Disparity in Context: Understanding how monocular image content interacts with disparity processing in human visual cortex

Abstract

Horizontal disparities between the two eyes’ retinal images are the primary cue for depth. Commonly used random ot tereograms (RDS) intentionally camouflage the disparity cue, breaking the correlations between monocular image structure and the depth map that are present in natural images. Because of the nonlinear nature of visual processing, it is unlikely that simple computational rules derived from RDS will be sufficient to explain binocular vision in natural environments. In order to understand the interplay between natural scene structure and disparity encoding, we used a depth-image-based-rendering technique and a library of natural 3D stereo pairs to synthesize two novel stereogram types in which monocular scene content was manipulated independent of scene depth information. The half-images of the novel stereograms comprised either random-dots or scrambled natural scenes, each with the same depth maps as the corresponding natural scene stereograms. Using these stereograms in a simultaneous Event-Related Potential and behavioral discrimination task, we identified multiple disparity-contingent encoding stages between 100 ~ 500 msec. The first disparity sensitive evoked potential was observed at ~100 msec after an earlier evoked potential (between ~50–100 msec) that was sensitive to the structure of the monocular half-images but blind to disparity. Starting at ~150 msec, disparity responses were stereogram-specific and predictive of perceptual depth. Complex features associated with natural scene content are thus at least partially coded prior to disparity information, but these features and possibly others associated with natural scene content interact with disparity information only after an intermediate, 2D scene-independent disparity processing stage.

1. Introduction

The visual system uses many different sources of information to estimate depth in the natural three-dimensional world. Depth cues such as linear perspective, texture gradients, shading and lighting all provide cues for inferring an object’s position in space. These cues are monoscopic in the sense that they can be seen by one eye. A direct volumetric sensation – known as stereopsis – comes from the specifically binocular depth cue of horizontal retinal disparity that is created by the image differences afforded by our laterally separated eyes (Wheatstone, 1838; Palmer, 1999; Howard and Rogers, 2002).

The neural basis of stereopsis has been frequently studied by isolating the disparity cue through the use of random-dot stereograms (RDS) (Julesz, 1960). By isolating the disparity component of the general depth perception mechanism with RDS, much knowledge has been gained regarding the perception of depth from disparity and its neural basis (Cumming and DeAngelis, 2001; Blake and Wilson, 2011; Welchman, 2016). Studies with RDS find that disparity is first encoded in primate V1 where cells are sensitive to absolute disparity (Cumming and Parker, 1999; Thomas et al., 2002), with sensitivity to relative disparity emerging in V2 (Thomas et al., 2002; Qiu and von der Heydt, 2005; Bredfeldt et al., 2009). Spatial modulations of disparity, e.g. relative disparities, are encoded macaque V2 (Nienborg et al., 2004; Bredfeldt and Cumming, 2006), V3A (Anzai et al., 2011), V4 (Umeda et al., 2007; Shiozaki et al., 2012) and IT (Janssen et al., 2001) and a limited form of relative disparity sensitivity can be seen in MT (Krug and Parker, 2011). Broadly similar patterns of disparity selectivity have been reported in studies with human fMRI (Goncalves et al., 2015; Welchman, 2016; Kohler et al., 2019).

The broader problem of depth extraction has also been approached by studying the combination of disparity information with other depth cues using simple stimuli to determine how different depth cues are combined into a unitary depth percept (Welchman, 2016). The combination of single cues is complex – one cue can veto others, or the cues can compete in a bi-stable/multi-stable fashion for perceptual access (Bülthoff and Mallot, 1988; Landy et al., 1995; Hillis et al., 2002; Knill and Saunders, 2003; Schiller et al., 2011; Dövencioğlu et al., 2013; Chen and Tyler, 2015). Cortical activations measured with fMRI for different depth configurations are more discriminable when shading or texture and disparity cues for depth agree (Dövencioğlu et al., 2013; Murphy et al., 2013), suggesting a form of cooperative combination.

While much has been learned about stereopsis and depth cue-combination through the use of simple stimuli, our sensory systems have evolved under the constraints imposed by natural tasks and the natural environment (Geisler, 2008). Visual function is thus intimately related to the properties of the stimulation commonly encountered in the natural environment (Felsen and Dan, 2005; Clifford et al., 2007). While disparity coding in natural scenes has been studied using computational methods (Hibbard, 2008; Burge and Geisler, 2014; Goncalves and Welchman, 2017), virtually nothing is known about the neural basis of disparity processing in natural scenes (Fischmeister and Bauer, 2006; Gaebler et al., 2014; Ogawa and Macaluso, 2015).

To study the neural basis of disparity processing in the context of naturalistic stimuli instead of in isolation, we previously measured human brain responses evoked by monsocopic and stereoscopic versions of a diverse range of natural scenes (Duan et al., 2018). Disparity-contingent responses were extracted by subtracting responses evoked by the 2D monoscopic images from the responses evoked by their corresponding 3D stereoscopic counterparts. Using this approach, we measured disparity-contingent evoked potentials for many different natural scenes. By controlling statistically for simple summary statistics of the image depth maps, we found that the disparity-contingent difference potential was positively correlated with neural responses driven by the higher-order scene statistics of the monocular half-images.

Motivated by this finding, the present study used high-density EEG recordings and a disparity discrimination task to determine more directly how monocular half-image content interacts with disparity processing both neurally and perceptually. Here, we experimentally manipulated the relationship between monoscopic image content and disparity by using novel stereograms that differed in whether the half-images were comprised of the original natural scene, visually scrambled textures or random dots. Taking advantage of the millisecond-scale precision of EEG recording, we provide evidence that the initial stage of the disparity computation is independent of identifiable features and objects, but that later stages are. By relating the magnitude of disparity-contingent activity to behavioral responses during the recordings, we show that activity in the later stages, but not the earlier stage of disparity processing is predictive of discrimination accuracy.

2. Methods

2.1. Participants

Fifty healthy adults (24 males) aged between 18 and 44 years (mean = 23.4 years) participated in this study. All participants had normal or corrected-to-normal visual acuity and the average logMar visual acuities of their left and right eyes were each −0.03 (corresponding to a Snellen acuity of ~20/20). They reported no difficulty perceiving stereo-scopic depth when viewing 3D pictures, and their average stereoacuity as measured by Randot^® stereotest (Stereo Optical, Inc., Chicago, IL) was 20.3 arcsec. The study was approved by the Stanford University Institutional Review Board and all participants gave written informed consent prior to the experiment. The procedures were in accordance with the Declaration of Helsinki.

2.2. Stimulus construction and trial structure

We selected our images from a natural scene data-base that included both stereo half-images as well as ground truth depth-maps. A comprehensive description of the natural-scene data-base and image capture pipeline can be found in Burge et al. (2016) and the database is available at http://natural-scenes.cps.utexas.edu/db.shtml. Briefly, each image pair was collected using two camera station-points spaced 65mm apart, mimicking the average distance between the two eyes of adult males (Dodgson, 2004). The corresponding depth map for each image was obtained using a scanning laser range finder. Forty high-quality stereo image pairs of outdoor scenes from the database were selected. The scenes included trees, lawns, buildings, signs and fences. All images were resampled to a resolution of 1920 pixels width × 1080 pixels height. The images were presented at a 3-meter viewing distance and this resulted in images of natural size (ortho-stereoscopic presentation) with minimal conflict between vergence and accommodation.

By presenting the right-eye image to both left and right eyes, we created monoscopic, two-dimensional (2D) images. To disrupt the relationship between monoscopic depth cues and stereoscopic cues we took two approaches. In one, we generated scrambled versions of each scene by applying the Portilla-Simoncelli algorithm (http://www.cns.nyu.edu/~lcv/texture/) to the monocular half images. In the other, we used random dot stereograms (RDS) that are devoid of monocular cues for depth structure. Depth Image Based Rendering (DIBR, see below) was used to transfer the natural scene depth map to texture-scrambled and random dot stereograms on a scene-by-scene basis. Each natural scene thus had a 2D and a 3D version and corresponding texture-scrambled and random dot 2D and 3D versions.

To create monoscopically scrambled stereograms that shared common low-level image statistics, the half-image synthesis (scrambling) algorithm started with a random noise half-image and an intact natural scene half-image. Through an iterative matching procedure, several image statistics were matched between the original natural image and the synthetic scrambled image (Portilla and Simoncelli, 2000). The algorithm (http://www.cns.nyu.edu/~lcv/texture/) employs a multi-scale, oriented Gabor-filter reconstruction pyramid and the matching process equates the pyramid filter responses between synthetic and natural images and thus their power spectrum. By nature of the iterative matching procedure employed by the algorithm, the intact and scrambled images have the same nominal mean luminance, minimum and maximum pixel luminance, variance, skew and kurtosis. The algorithm also matches a histogram of second- order correlations over filter locations, scales and orientations, as well as certain cross-orientation phases.

To determine the extent to which the synthesis algorithm, as we applied it, was able to match low-level statistics between intact and scrambled natural scenes, we measured space and frequency domain summary statistics for the intact and scrambled natural scenes. We found that the pixel standard deviations were matched to within 16%, with the scrambled images being higher. We used 2D Fourier transforms to measure band-limited differences between natural and synthesized spatial frequency spectra as a cross-check. To do this, we converted the images to gray-scale values (0–255) and cropped the images to 1040 × 1040 pixels. We used the MATLAB functions “fft2” and “fftshift” to compute the 2D Fourier amplitudes of each image. These amplitudes were then averaged separately over the exemplars of the intact and scrambled natural scenes. These amplitude spectra were summarized using a one-dimensional slice that averaged over orientation and are plotted on log amplitude vs log spatial frequency to better visualize the spectral slopes (Field, 1987). To convert the amplitude spectral values into interpretable visibility units, we converted them to Fourier contrast by dividing the average spectral amplitude at each spatial frequency by the DC value, multiplying the result by a factor of two to account for positive and negative frequencies (Hess et al., 1983). We then computed the difference in contrast between image types so that we could relate the magnitude of the residual differences in the images to estimates from the literature of thresholds for detecting band-limited contrast changes embedded in high contrast broadband targets such as natural images or Gaussian noise.

2.3. Depth Image Based Rendering of synthetic stereograms

Since depth information is available for each point in the images for each eye from the ground-truth depth maps, we applied a depth-image-based rendering technique (McMillan, 1997) to produce synthetic 3D images for each natural scene that had the original depth map, but whose monocular half-images were comprised of either scrambled textures or random dots. The approach, illustrated schematically in Fig. 1, starts from a monoscopic image (scrambled texture or random dots; top middle panel) and the separate left- and right-eye depth maps whose pixel coordinates match those of the source natural scene. To create stereopairs with the specified depth map, separate and identical target left and right eye half-images (bottom panes) are first created. In the left/right output half-images, the depth at each pixel from the left or right eye depth map is used to calculate the corresponding location in the source texture image which should be used to assign color for the output pixel (Fig. 1, the black arrows indicating pixel shift based on depth). Since each pixel in the left/right output has a valid depth value associated with it, we are able to perform this texture-lookup for each output pixel without running into the problem of holes or missing regions due to disocclusions. The resulting monocular half-images were smoothly varying textures with no visible discontinuities. Note that while the dis-occluded areas get filled with unmatched texture, they have the correct binocular disparity relative to the monoscopic texture (Fig. 1, regions highlighted in red). In the example, the depth map contains two disparate regions, a background and a disk, each with different but constant depth values. The disparity value of a given point in the depth map is used to replace the color at the shifted (disparate) location with that from the original pixel location in the source texture using opposite directions of shift in the left and right eye target textures.

Fig. 1.

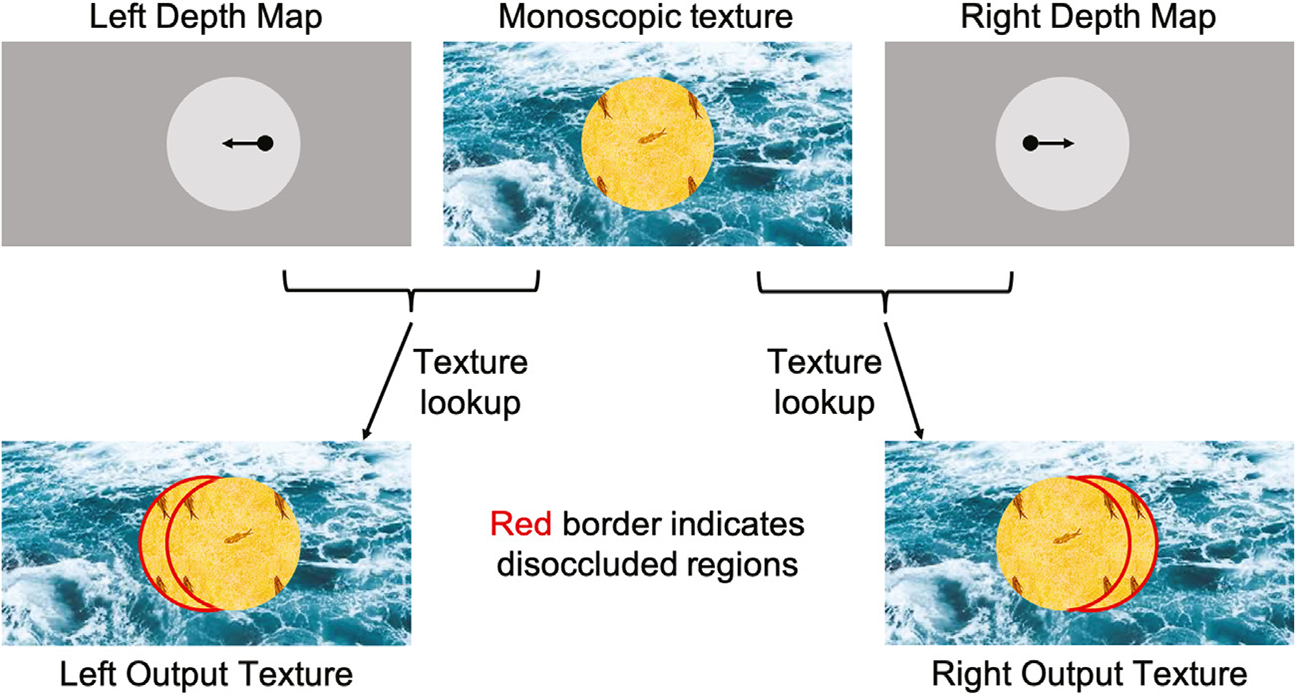
A high-level block diagram of depth-image-based synthesis. The top row shows the monoscopic source texture in the middle and the left and right input depth maps on either side. In each depth map, we can use the depth value for a pixel to compute where it maps to in the monoscopic texture image (shifts shown in black arrows). The corresponding output textures generated using texture-lookup are shown in the bottom row. Dis-occluded areas are highlighted with a red border.

The same depth rendering procedure was used to create a 3D random-dot stereogram for each scene from a 2D random dot image with 3.5 arcmin dot size and 25% dot density and the corresponding depth map. In the end, we thus had three different stereogram classes in monoscopic and stereoscopic formats: full natural scenes, scrambled scenes without recognizable content, and random dot images with no scene-related information. An example of three stereogram classes is shown in Fig. 2.

Fig. 2.

An example of three different stereograms based on a common natural-scene depth map. Left: Natural scene stereogram. Middle: Scrambled-scene stereogram with matched depth map. Right: Random Dot Stereogram with matched depth map. Note: For illustration purposes, the images shown here are stereopairs for a blue-red anaglyph. In the experiment, the images were viewed through a pair of shutter glasses.

Image pairs were presented using in-house software on a Sony Bravia (model XBR-65HX929) 3D TV (143.4 × 80.7 cm) at a resolution of 1920-by-1080 pixels. Active shutter glasses were used to present separate images to each eye. The images were either a disparate stereo-pair in the 3D conditions, or copies of the right eye image in the 2D conditions. A single trial was constructed as a 750 msec gray screen prelude followed by a 750 msec image presentation, during which a 2D monoscopic or 3D stereoscopic image of a natural scene, a scrambled scene or a random dot image was presented in random order (see Fig. 3). During each trial, a cross was placed in the center of the prelude image at the plane of the screen when viewed stereoscopically. The cross was removed when the test images were presented. Stereo disparities of the 3D images were rendered behind the fixation cross. The participant was instructed to maintain fixation on the cross and to reduce blinks and movements to a minimum.

Fig. 3.

Experiment trial structure. A mean luminance matched prelude image was displayed with a fixation cross in the center for 750 msec, followed at random by a natural image, a scrambled image, or a random dot image in either 2D or 3D formats. 2D images comprised identical image pairs to left and right eyes. 3D images comprised 3D disparate half-images to left and right eyes. A block consisted 240 trials, with each version of scene presented once. A uniform gray background was displayed between each trial until the response was made.

A two-alternative temporal forced choice procedure with a response deadline of 750 msec was used in which the participants were instructed to respond as quickly and as accurately as possible with a button press to indicate whether the image they saw was 2D or 3D (see Fig. 3). A block consisted of 240 trials, in which each version of a scene was shown once. A total of four blocks of trials were administered to each participant and the scene presentation order within each block was randomized.

2.4. EEG acquisition and preprocessing

The EEG data were collected using 128-channel HydroCell Geodesic Sensor Nets and a NetAmp 400 system (Electrical Geodesics Inc., Eugene, OR). The EEG was bandpass filtered from 0.3 to 50 Hz and digitized at a rate of 420 Hz. Individual electrodes were adjusted until impedances were below 50 kΩ before starting the recording. Artifact rejection was performed off-line according to a sample-by-sample threshold procedure to remove noisy electrodes, replacing them with the average of the six nearest neighboring electrodes. On average, less than 5% of the electrodes were substituted; these electrodes were mainly located near the forehead or the ears, and substituting them is unlikely to impact our results. The EEG was then re-referenced to the common average of all the remaining electrodes. Epochs with more than 15% of the data samples exceeding 30 μV were excluded on a sensor-by-sensor basis. Typically, these epochs included movements or blinks. A 130 msec delay between the onset of EEG recording and the stimulus onset caused by the EEG recording system (65 msec) and the BRAVIA monitor (65 msec) has been corrected in analysis.

2.5. Behavioral data statistical analysis

The response time (RT) and response accuracy for discriminating 2D vs. 3D images were averaged across all participants within each stereogram condition. Because of the repeated measurements within each participant, their behavioral data were then compared across conditions using a linear mixed model (Bates et al., 2014b), where stereogram condition was set as a fixed effect and individual participants were defined as random effects. Post-hoc Tukey tests were then administered for pair-wise comparisons between different conditions (Hothorn et al., 2017).

2.6. Analysis of EEG global field power

Global field power (GFP) is a single, reference-independent measure of brain response strength. The GFP equals the root mean square (RMS) across the average-referenced electrode values at a given instant in time,

$$\mathrm{G}\mathrm{F}\mathrm{P}(\mathrm{t})=\sqrt{\frac{\sum _{i=1}^N{\left(V_i(t)-\overline{V(t)}\right)}^2}{N}}$$

where $\mathrm{N}$ is the number of electrodes, and $\mathrm{V}$ is the voltage at a specific electrode. GFP provides a single number summary across the electrode montage of the response strength (Lehmann and Skrandies, 1980; Murray et al., 2008) as a function of time. It has been demonstrated to be an unbiased dimension-reduction method that can determine time points that have maximal field strength (Hamburger and van der Burgt, 1991). The participants’ time-locked Visual Evoked Potentials were summarized by GFP waveforms for each of the 6 image types (i.e. 2D or 3D natural scenes, scrambled scenes, and random dot stimuli).

Disparity-contingent potentials were calculated by subtracting 2D responses from 3D responses for each scene condition. In a first analysis, these difference potentials were converted to GFPs that were analyzed across the three different stereogram types by randomization statistics implemented in the RAGU software package (Koenig et al., 2011; Habermann et al., 2018). Briefly, a global measure of GFP cross-stereogram differences at each time point is defined as

$$s=\sum _{i=i}^c\sqrt{{\left(\overline{GF{P}_i}-\overline{GFP}\right)}^2}$$

where $c$ is the number of conditions, $\overline{GF{P}_i}$ is the average GFP over subjects within condition $\mathrm{i}$ and $\overline{GFP}$ is the grand mean GFP across all subjects and conditions. We would like to know if the value of $\mathrm{s}$ depends solely on the random variance across subjects and conditions, but not on the differences across conditions. To assess the statistical significance of s, we generated a distribution of $\mathrm{s}$ under the null hypothesis by randomly shuffling the condition assignment in each subject, recomputing $\mathrm{s}$ 5000 times. The significance of the effect is then given by the percent of randomly obtained values of $\mathrm{s}$ that are larger than or equal to the value of $\mathrm{s}$ obtained with the real data. After testing the significance of $\mathrm{s}$ at each time point, a multiple comparison correction was implemented by estimating how likely it was that the overall duration of a period of significant effects would have been observed by chance (König and Garcia, 2009).

2.7. Topographical analysis of variance

The GFP metric does not provide any information about how the potential is distributed across the electrodes – i.e. where large and small potentials were measured. The different stimulus conditions could alter the shape of the scalp topography without changing its magnitude. To compare the disparity-specific scalp maps in terms of their topographic distribution and thus their underlying neural generators across different scene conditions, the voltages of the scalp field maps were first normalized so that any differences across conditions were not merely due to a scaling factor that is common for all active sources. If differences still exist after map normalization, the active intracerebral sources must have had at least partially different locations and/or orientations. The normalized disparity-contingent scalp fields were compared through randomization statistics implemented in the RAGU software (Koenig et al., 2011; Habermann et al., 2018). The statistical testing procedure is similar to that described in the previous section, except that the global measure of scalp field differences s is defined as below:

$$s=\sum _{i=i}^c\sqrt{\frac{\sum _{j=1}^n{\left(\overline{v_{ij}}-{\overline{\bar{v}}}_j\right)}^2}{n}}$$

Where $\mathrm{c}$ is the number of conditions and group, $\mathrm{n}$ is the number of electrodes, $\overline{v_{ij}}$ is the voltage of the grand mean across subjects of condition $\mathrm{i}$ at electrode $\mathrm{j}$, and ${\overline{\overline{v}}}_j$ is the grand mean across subjects and conditions of the voltage at electrode $\mathrm{j}$.

2.8. Micro-state analysis

The configuration of the evoked scalp field changes over time, but we can identify “micro-states” – consecutive scalp fields that remain stable during a prolonged period. The change of the potential distribution can be quantified by an index called topographical dissimilarity (DISS), which calculates the standard deviation between successive maps at each time point:

$${\mathrm{D}\mathrm{I}\mathrm{S}\mathrm{S}}_{\mathrm{u},\mathrm{v}}=\sqrt{\frac{1}{n}\mathrm{*}\sum _{i=1}^n{\left(\frac{u_i}{GF{P}_u}¯\frac{v_i}{\mathrm{G}\mathrm{P}{F}_v}\right)}^2}$$

where $\mathrm{u}$ and $\mathrm{v}$ represent two consecutive scalp field maps, and $n$ is the number of electrodes (Lehmann and Skrandies, 1980; Skrandies, 1990). A number close to 0 indicates topographic homogeneity.

2.9. Correlational analysis of behavioral and neural data

To determine whether behavioral and electrophysiological patterns observed in the group averages are also consistently present in individuals (Fisher et al., 2018), we correlated the average disparity-sensitivity GFP during each microstate with the response accuracy using a repeated measure correlation analysis (Bakdash and Marusich, 2017). Repeated measures correlation (R package ‘rmcorr’ version 0.3.0) is a statistical technique for determining the common within-individual association for paired measures assessed on two or more occasions for multiple individuals. Specifically, since each participant provides three GFP measurements and a corresponding response accuracy for the same three scene conditions, the assumption of independence is violated. Using analysis of covariance, rmcorr accounts for non-independence among observations and statistically adjusts for inter-individual variability. After removing measured variance between participants, rmcorr provides the best linear fit for each participant using parallel regression lines with varying intercepts. The common regression slope is thus the association shared among individuals.

3. Results

3.1. Behavioral results

We measured the accuracy (Fig. 4, left) and response time (Fig. 4, right) for discrimination of 2D vs. 3D versions of each image type in order to make sure that the participants could perceive depth for each image class and as an attentional control during the EEG recordings. Discrimination accuracy was high for each of the three image classes. The accuracy of 2D vs. 3D discrimination was 87.6% (se = 0.009, N = 50) for natural images, 90.1% (se = 0.006, N = 50) for scrambled images and 94.7% (se = 0.005, N = 50) for random dot images. Accuracy differed across the three conditions as measured by an omnibus repeated measures ANOVA (χ² (50, 2) = 49. 0, p < 0. 001) (R package ‘lme4’ (Bates et al., 2014a)). In order to determine which pairwise differences contributed to the omnibus effect, we performed post-hoc Tukey tests that provide a more controlled Type I error than a set of independent pairwise T-tests (R package ‘multcomp’ (Hothorn et al., 2017)). Post-hoc Tukey tests indicated that the accuracy for random dot images was significantly higher than for scrambled images (Z = 4.48, p < 0.001) and natural images (Z = 6.90, p < 0.001). Accuracy for scrambled images was significantly higher than for natural images (Z = 2.42, p = 0.041).

Fig. 4.

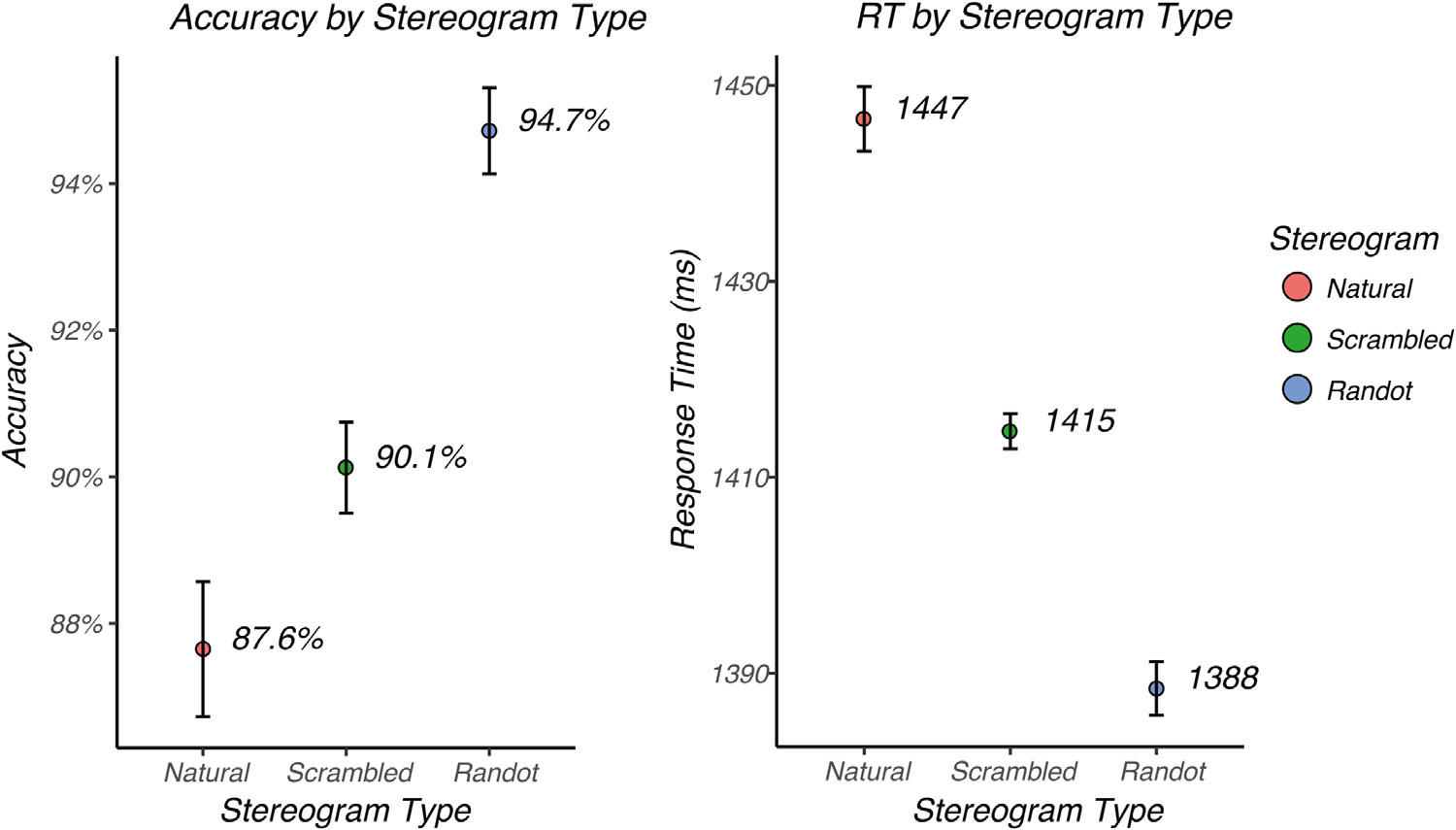
Mean accuracy and response time for the different image conditions. Left: Mean accuracy averaged across subjects plotted for natural images (red), scrambled images (green) and random dot images (blue). Right: Mean response time, averaged across subjects, plotted for natural images (red), scrambled images (green) and random dot images (blue). Error bars represent the standard error of the mean corrected for within-subject correlations (Morey, 2008).

Image conditions that were discriminated more accurately also led to faster response times (Fig. 4, right). The mean response time was 1388 msec (se = 2.73, N = 50) for random dot images, 1415 msec (se = 1.80, N = 50) for scrambled images and 1447 msec (se = 3.29, N = 50) for natural images. Response times differed cross the three conditions as measured by an omnibus repeated measures ANOVA (χ²(50, 2) = 235. 7, p < 0. 001). Post-hoc Tukey tests indicated that the response time for random dot images was significantly faster than that for scrambled images (Z = 6.9, p < 0.0001) and natural images (Z = 15.3, p < 0.0001). Response time for scrambled images was significantly faster than for natural images (Z = 8.4, p < 0.0001).

3.2. Evoked responses generated by monoscopic image content

As a first point of reference for the sequence of stimulus encoding, we measured the earliest timepoint at which responses to the three monoscopic (2D) image classes can be differentiated, either in terms of the brain response amplitude, the topographical distribution of sources, or both. This analysis sets a limit on when responses to different types of monoscopic image structure first become available and when they are differentiable. As a measure of the temporal evolution of the signal magnitude across conditions, we measured the global field power (GFP) as a function of time after image onset for each image class. The GFP is the standard deviation across the average-referenced electrode values and it provides a summary measure of response strength at a given instant in time. The results are shown in Fig. 5a as red curves for 2D natural images, green for 2D scrambled images and blue for 2D random dot images. Fig. 5b shows a zoomed-in view over the first 100 msec of the trial that includes the I initial rising phase of the responses. The onset of responses to 2D image contrast starts at around 50 msec for each image type. After response onset, the responses to the three image types are tightly coupled between and have a common GFP time-course between 50 ~ 100 msec (Fig. 5b). Randomization statistics were used to compare mean GFPs across the three conditions. The purple/grey bars on the horizontal axis indicate the time points at which a significant difference occurred, with gray uncorrected for multiple comparisons. Runs surviving multiple comparison correction are indicated by purple. The GFP time-course first begins to differ around 100 msec for the different stereogram classes (indicated by purple bars on the time-axis of Fig. 5a). Periods of significant differences among the three classes occurred between 100 ~ 140 msec, 180 ~ 320 msec, and 635 ~ 680 msec, as indicated by the purple bars above the x-axis of Fig. 5.

Fig. 5.

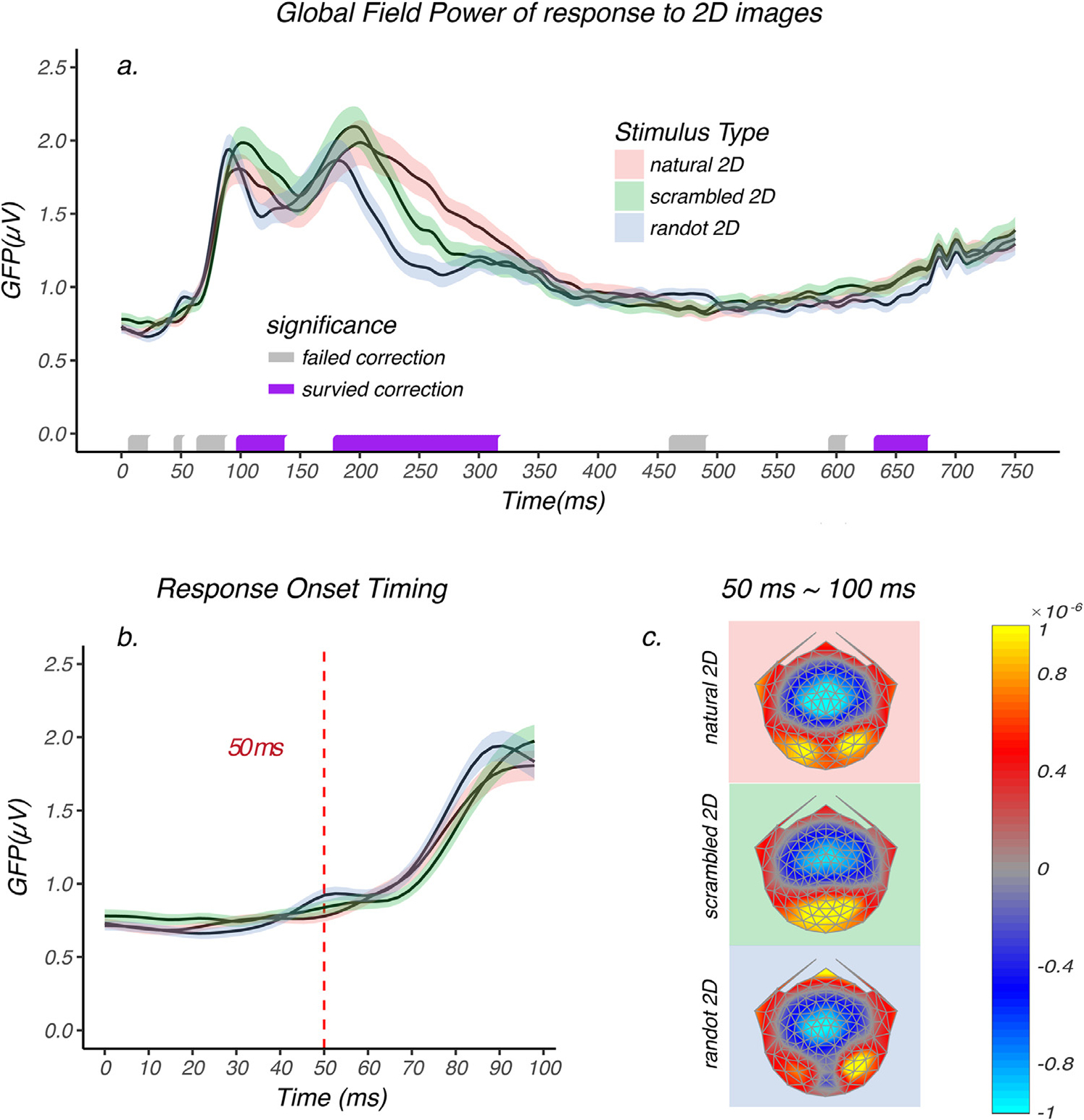
Global field power of 2D image response and average brain topographies between 50 ~ 100 msec. a.) GFP of 2D natural image (red), 2D scrambled image (green), and 2D random dot image (blue) responses are plotted as a function of time. Shaded area represents the standard error of the mean. Randomization statistics were used to compare mean GFPs across the three conditions. The purple/grey bars on the horizontal axis indicate the time points at which a significant difference occurred, uncorrected for multiple comparisons. Runs of significant values surviving multiple comparison correction are indicated by purple, while those failing correction are indicated by grey. The monocular images start to elicit differential brain response between 100 ~ 140 msec, 180 ~ 320 msec and 635 ~ 680 msec. b.) A zoomed in view over the first 100 msec. The GFPs of each image condition rise from baseline starting at around 50 msec, which is indicated by the dashed red line. Between 50 ~ 100 msec the GFPs were tightly coupled and no significant difference was observed during this time period. c.) The average scalp field maps during 50 ~ 100 msec for each 2D image condition and different underlying sources can be directly observed in this visualization.

The GFP analysis is only sensitive to amplitude differences across conditions, but not to possible differences in response topography caused by shifting of the locations of the underlying activity over time. To check whether the response topography differed between 50 ~ 100 msec across the three image classes, we plotted the average brain topographies over 50 ~ 100 msec. As can be seen in Fig. 5c, the different stimulus conditions do not share the same topography – despite having the same GFP profile. The reliability of these apparent topographic differences was assessed by first normalizing the scalp field maps to remove any amplitude differences between conditions, followed by a permutation test called Topographical Analysis of Variance (TANOVA) that compared the topographies resulting from the presentation of the three 2D image types. The significance was computed as a function of time and was controlled for Type II error (see methods section for details). The TANOVA indicated that the topographies differed starting at or very near the time that the response left baseline (~50 msec) and continued to differ up to ~500 msec and then again between 510 ~ 750 msec. Thus, although the amplitudes during 50 ~ 100 msec period are not different, the topographies and thus the underlying source distributions were not the same across conditions.

It is not surprising that early latency activity might differ between the random-dot half-images and the intact and scrambled natural scenes, given that the random-dot stimuli are comprised of binary achromatic elements while the other two stimuli comprise continuous-tone chromatic images. However, the topographies of the intact and scrambled natural scenes also differ over this time frame. Could this difference be due to uncontrolled differences in low-level image statistics? To begin to answer this question, we determined whether the synthesis algorithm was able to match commonly used low-level summary statistics. We computed the pixel-level standard deviations and also the band-limited differences in the 2D spatial frequency spectra for the two image classes. The pixel standard deviations were matched to within 16%. We also computed the Fourier amplitude of the intact and scrambled natural scenes as a function of spatial frequency (Fig. 6a; blue symbols: natural images, red symbols: scrambled images), averaging the amplitudes over images within a scene type. From these two average spectra, we computed the residual differences (black symbols). These differences are expressed as a percentage difference in Fig. 6b (see Methods). Fractional differences are largest at spatial frequencies above about ~10 c/deg where amplitudes were higher for the original images. Below ~10 c/deg amplitudes were higher for the scrambled images, but by a smaller amount. To relate these between-condition differences to their likely visibility, we converted the Fourier amplitudes to units of contrast (see Methods). As can be seen in Fig. 6c, the differential contrast values are low. They are particularly low at higher spatial frequencies where contrast in the images is low, offsetting the impact of the larger fractional differences at higher spatial frequencies. These differences in image contrast between scene types are likely to be below the observers’ contrast discrimination thresholds based on the threshold levels reported in prior psychophysical studies of contrast discrimination of bandlimited targets embedded in high contrast broad band backgrounds such as Gaussian noise or natural images (Lu and Dosher, 1999; Chandler and Hemami, 2003; Hemami et al., 2006; Bex et al., 2007).

Fig. 6.

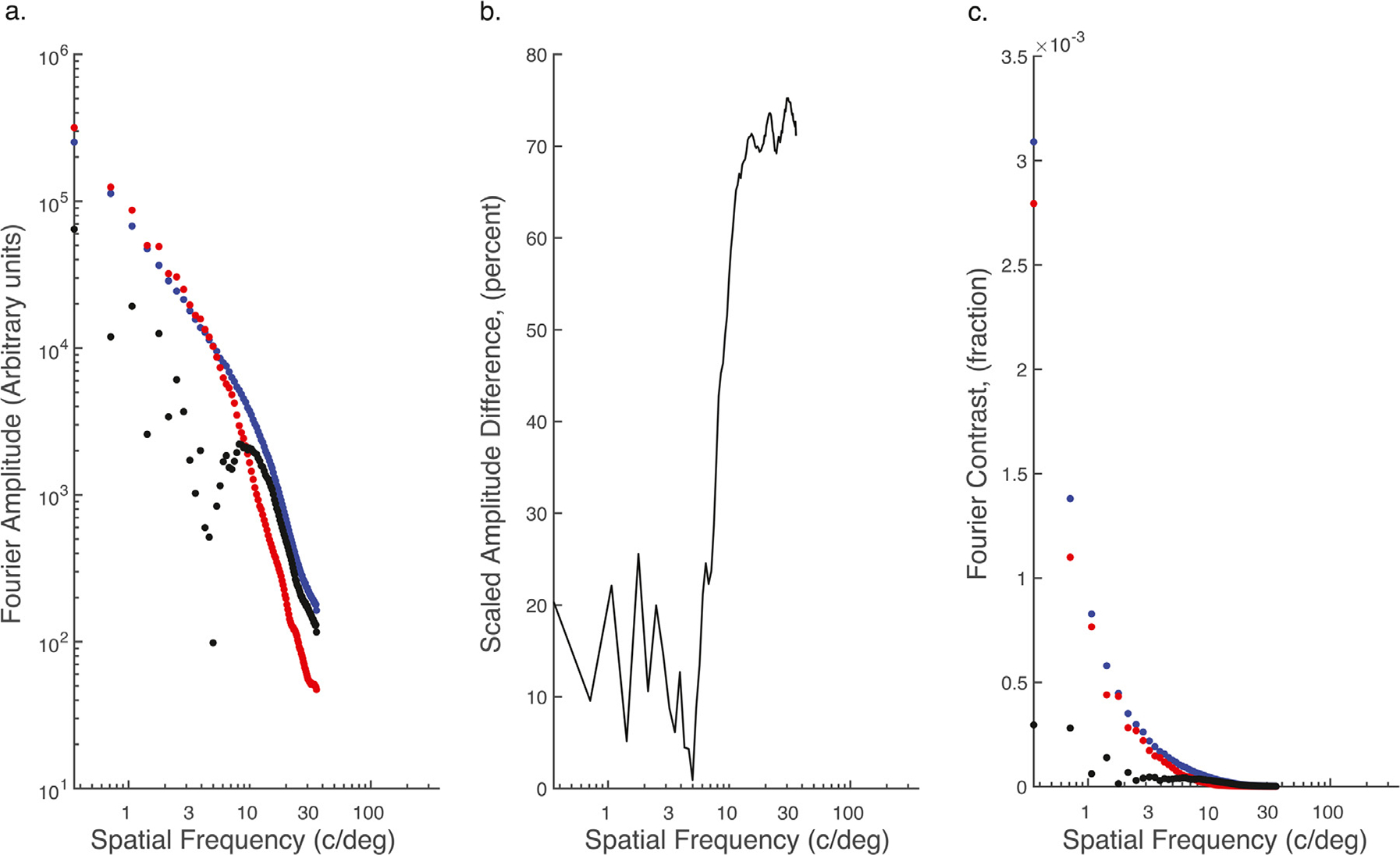
Comparison of summary statistics of intact and scrambled natural scenes. a) Amplitude spectra for intact natural scenes (blue), scrambled scenes (red) and the difference (black). b) Difference in amplitude between intact and scrambled scenes scaled to scene with largest amplitude. c) Fourier contrast as a function of spatial frequency for intact (blue) and scrambled scenes (red) and the difference (black).

3.3. Evoked responses generated by binocular disparity

The main interest of the present study was determining how monocular scene content interacts with complex patterns of horizontal disparity provided by a common set of depth maps. By design, the only difference between the monoscopic and stereoscopic versions of each of the different stereogram types was the presence of horizontal binocular disparity as provided by the ground truth depth maps. Therefore, we isolated disparity-contingent responses by subtracting the monoscopic responses from the stereoscopic responses for each stereogram type. This subtraction tests the linear summation model of the total response being equal to the sum of a response to monoscopic image content plus a response to disparity. If monocular image content doesn’t have any effect on disparity processing, the differential responses should not differ for the natural, scrambled and random dot versions, as they are generated from matched depth maps. If, on the other hand the measured responses differ across stereogram types, then there is a non-linear interaction between monoscopic scene content and disparity.

Fig. 7a shows the GFP of the difference between monoscopic and stereoscopic responses as a function of time for natural, scrambled, and random dot images. A disparity-contingent response rises from baseline starting at around 100 msec (see Fig. 7a, and the inset 7b). Between 100 and ~ 150 msec, the amplitude of the disparity-contingent response is the same for all three conditions, consistent with the disparity response being independent of monoscopic scene content. Between 150 ~ 300 msec, the amplitude of disparity-contingent responses depended on stimulus type, with response for random dot images being largest, followed by the scrambled and natural image responses (Fig. 7a). Between 310 ~ 510 msec, the disparity-evoked response to the random dot images has an extra peak that was not present in the other two conditions. After 150 msec, monoscopic and stereoscopic scene content interact in a non-linear fashion. Note that the GFP of the difference between 2D and 3D conditions would have been sensitive to either amplitude or topographic differences between the two conditions, had they been present in the raw data.

Fig. 7.

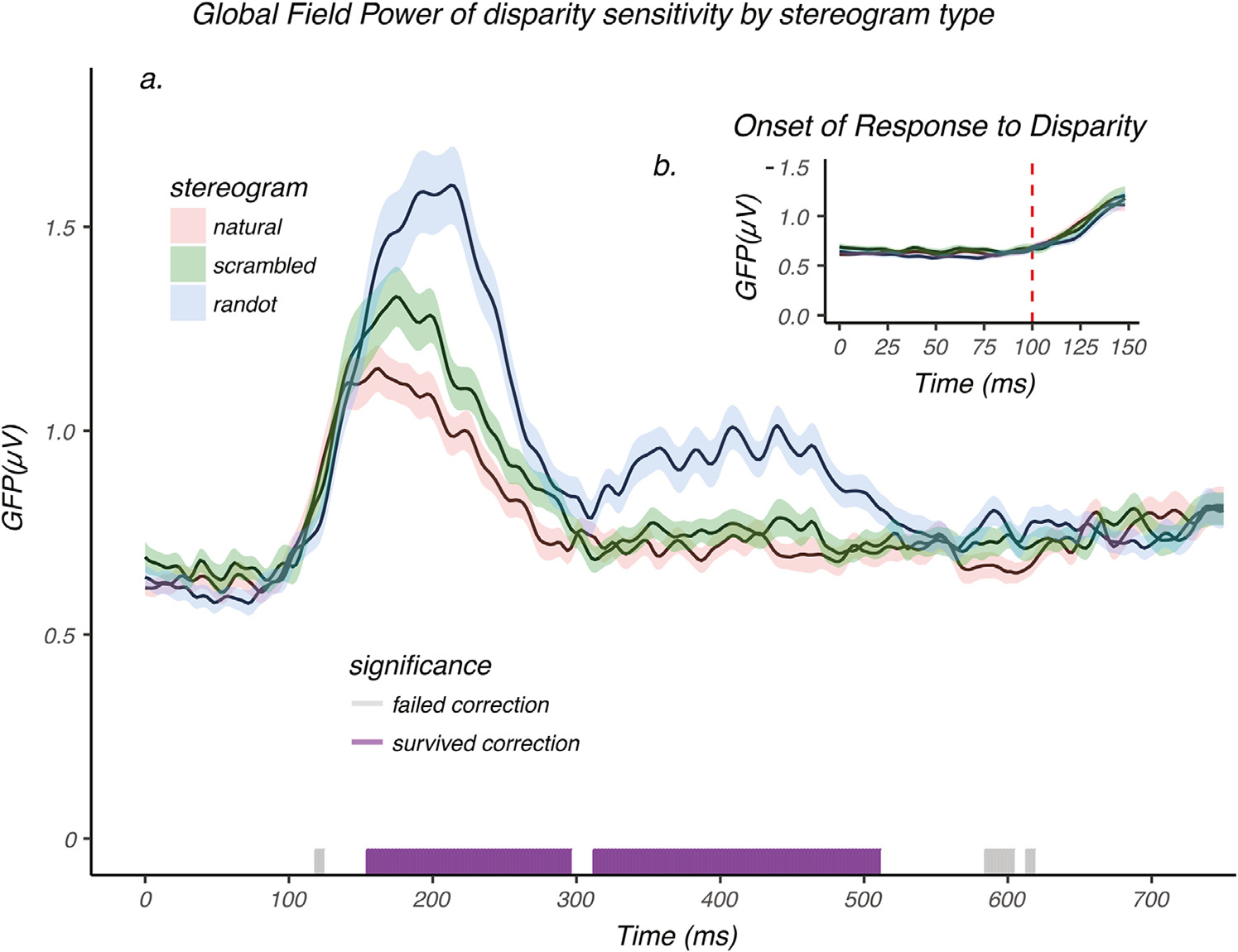
Global Field Power of disparity-contingent responses. a.) GFP of disparity-contingent responses for natural images (red), scrambled image (green), and random dot image (blue), plotted as a function of time. Shaded areas represent the standard error of the mean (N = 50). An analysis of GFP using randomization statistics was used to compare the mean GFP across the three conditions. The purple/grey bars on the horizontal axis indicate the time points at which a significant difference occurred. Runs of significant values surviving multiple comparison correction are indicated by purple, while those failing correction are indicated by grey. Disparity sensitivity starts to elicit a differential brain response between 150 ~ 300 msec, and between 310 ~ 510 msec. b.) A zoomed in view over the first 150 msec after stimulus onset. The GFPs for disparity-sensitivity across the three image conditions each rise from baseline starting at around 100 msec as indicated by the dashed red line. Between 100 ~ 150 msec the GFPs were tightly coupled and no significant differences were observed during this time period.

Because we found topographic differences in the absence of a GFP difference in the 2D image-onset responses, we also compared the disparity-contingent scalp topographies using TANOVA. Fig. 8a shows time-resolved topographies for the three stimulus conditions that were submitted to TANOVA. TANOVA indicated that at least partially non-overlapping sources were recruited for disparity processing between 180 ~ 310 msec, 350 ~ 490 msec and 570 ~ 650 msec (purple bars). Post hoc tests for pairwise comparisons between natural, scrambled and random dot images indicate that all pair-wise differences are significant during at least one time period both in terms of response amplitudes) and their topography/underlying neural generators.

Fig. 8.

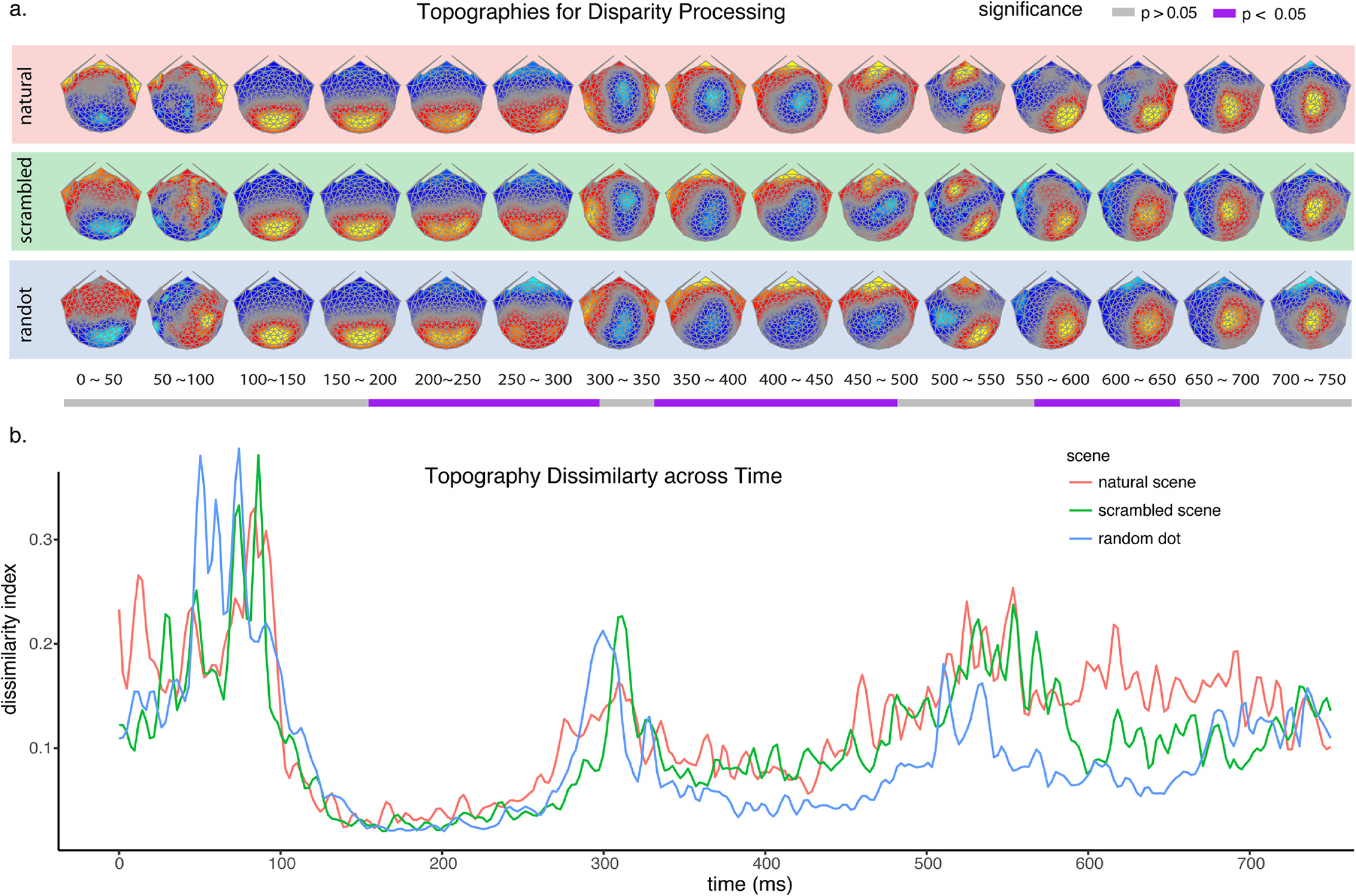
The normalized topographies of disparity-contingent responses for different image types and how they change over time. a. Normalized brain topographies of disparity-contingent responses for natural, scrambled, and random dot images. The topographies differed during 180 ~ 310 msec, 350 ~ 490 msec and 570 ~ 650 msec, corrected for multiple comparisons, as indicated by the purple bands below the timeline. b. A global map dissimilarity index was plotted for each of the image types, indicating the spatial correlation between pairs of successive topographies. Two highly stable micro-states were identified during 150 ~ 300 msec and 300 ~ 500 msec.

As can be seen in the disparity-contingent scalp field topographies in Fig. 8a, there are multiple stable scalp topographies, suggesting stable underlying source configurations/processing stages that unfold after stimuli presentation. To assess the stable periods and times of transition between different scalp field topographies for each image condition, we calculated a global dissimilarity index on the normalized scalp field maps over successive time points in order to categorize the brain activity into different “micro-states” (Skrandies, 1990). The index is in the form of 1 minus the spatial correlation between pairs of successive topographies. Fig. 8b displays the resulting dissimilarly index as a function of time. The figure shows an initial high dissimilarity period between 0 ~ 100 msec. This is expected because the analysis is based on difference maps between 2D and 3D images. This interval is before the onset of the disparity-contingent response which occurs around 100 msec (cf Fig. 8a,b) and the difference maps are thus expected to very noisy and unstable. The first stable micro-state occurs after the onset of the disparity-contingent response for each image type and is captured by the relatively low dissimilarity indices for each image type between 100 ~ 300 msec which correspond to gradually shifting topographies centered over the posterior occipital cortex (Fig. 8a).

The second micro-state is captured by another period of relatively low dissimilarity index that occurs between 300 ~ 500 msec, following a surge of dissimilarity at around 300 msec. The surge of dissimilarity indicates a change of the underlying sources, which can be seen in the visualization of topographies in Fig. 8a, where occipital activity switched to a parieto-central activity that remained relatively stable within an image type until 500 msec. The last stable phase of brain activity is during 500 ~ 750 msec that has a more complex topography over parietal-occipital cortex. Compared to the highly stable source distributions for the first two microstates, the last phase is less reliable in our measurements, as indicated by its elevated dissimilarity index. The results from amplitude differences, source differences, and micro-states analysis suggest a segmentation of the interaction between monocular image content and disparity into three distinct stages: stage I 150 ~ 300 msec, stage II 300 ~ 500 msec, and stage III 500 ~ 750 msec. Within each of these stages, the maps for each image type are relatively stable within an image type but differ from each across the different image types and this pattern is recapitulated across the three stages that involve distinct topographies.

3.4. Relationship between neural responses and perception

An important goal of studying neural responses is to use that information to predict or understand behavioral phenomena. In the case of disparity processing, a link between neural activity and depth perception could occur as soon as disparity-contingent activity is present, given that the behavioral task was a simple 2D vs 3D discrimination. On the other hand, monocular image content interacts with disparity processing starting from 150 msec and goes through three distinct processing stages (cf Fig. 8b). To determine which time-points contribute to perception, we used repeated measures correlation (Bakdash and Marusich, 2017) to correlate the behavioral accuracy on the 2D/3D discrimination task with the GFP of disparity-contingent responses measured simultaneously during the different processing stages (see Fig. 9). The correlation procedure determines whether individual-participant data can be explained by common regression parameters across the three stimulus conditions (see Methods). Not surprisingly, neural responses during the processing of monocular-image content between 50 and 100 msec, e.g. prior to the onset of disparity-contingent responses did not predict the discrimination accuracy (r = −0.09, p > 0.05). Interestingly, the neural responses between 100 and 150 msec when disparity sensitivity is present but is insensitive to monocular image content also did not predict discrimination accuracy (r = −0.16, p > 0.05). However, during the period between 150 ~ 300 msec when disparity responses do depend on monocular image content, the higher the GFP, the more accurate the discrimination is (r = 0.36, p < 0.001). A similar correlation pattern occurs between 300 ~ 500 msec (r = 0.40, p < 0.001). Finally, during the last phase we identified from the micro-state analysis (500 to 750 msec), the neural response no longer predicted the behavioral accuracy (r = 0.04, p > 0.05), suggesting this phase reflects post-encoding activity.

Fig. 9.

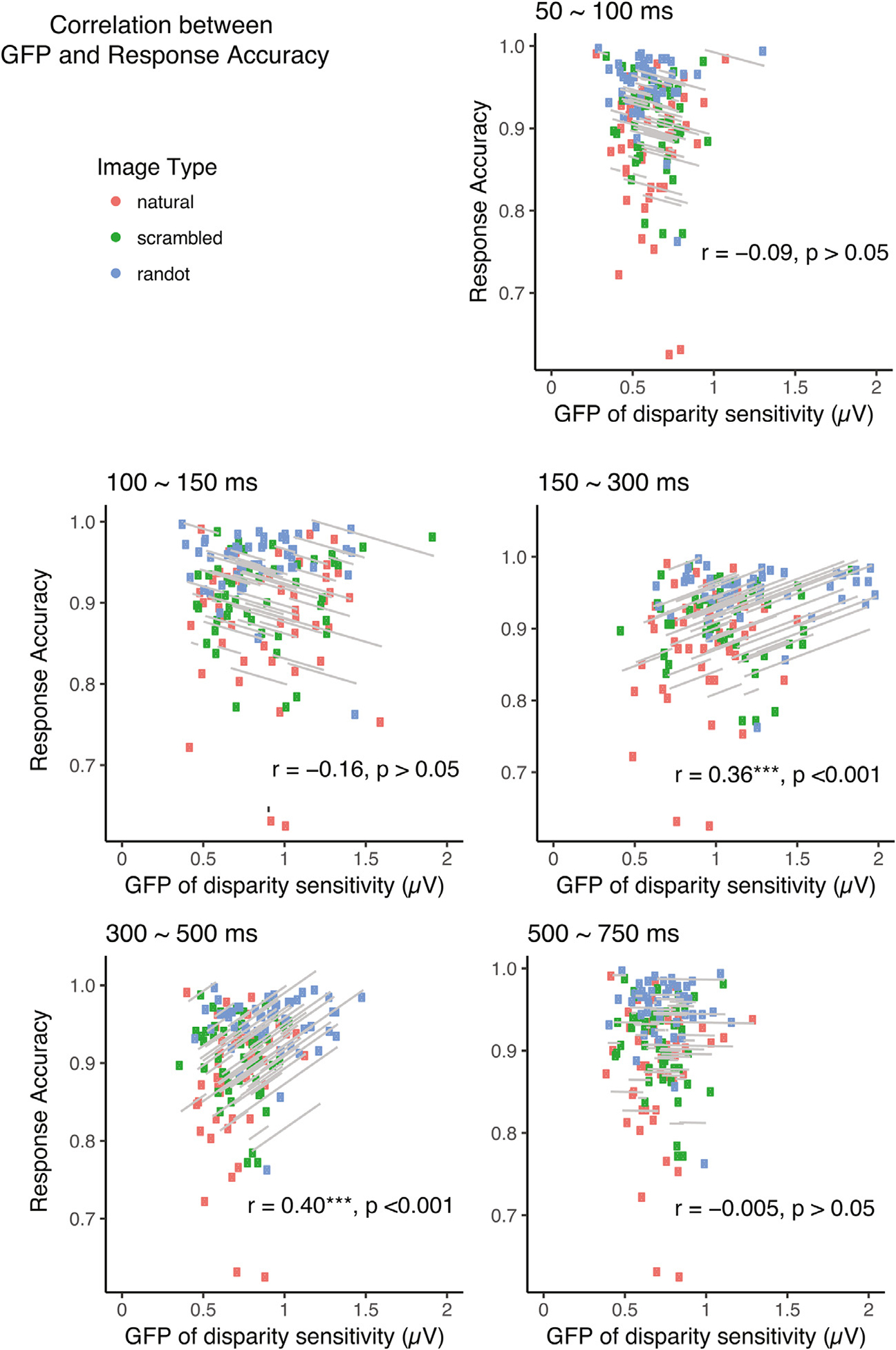
Correlation between GFP of disparity-contingent responses and 2D/3D discrimination accuracy across different time bins. The grey regression lines indicate the common slope fitted to each individual’s repeated measurements across three stimulus types. GFP of disparity-contingent response is predictive of behavioral accuracy of 2D/3D discrimination tasks between 150 ~ 300 msec (r = 0.36, p < 0.001), and between 300 ~ 500 msec (r = 0.40, p < 0.001). The correlation coefficients and their significance levels are annotated as insets in each panel (N = 50).

4. Discussion

Bela Julesz, when first describing the RDS posed the question of whether binocular parallax is determined by recognizing and then matching objects or contours in the monocular half-images or by first searching for patterns in the fused binocular field or both (Julesz, 1960). By showing that parallax could be estimated in the absence of monocularly identifiable and familiar features, he argued that binocular pattern matching was sufficient to extract parallax. Here we considered the converse – the extent to which matches between monoscopic and stereoscopic features influence the extraction of depth. Implicit in Julesz’s simple models was an implied order of processing. If monocular pattern recognition precedes the computation of parallax, then we might expect that the different stereogram types would lead to differences in the early time-course of disparity processing given that the monoscopic images differ so dramatically. If the latter was true, we might expect a period of common processing comprising this binocular matching process. We find evidence that the early time course of disparity processing is not measurably affected by monoscopic scene content, but that the later stages are. The pattern of results we observe suggests a “late fusion” model of the integration of stereoscopic and monoscopic depth cues in which rudimentary features of the depth map are extracted without reference to possibly larger-scale monoscopic content.

4.1. Image onset response timing

The earliest evoked responses we measure occur at around 50 msec after the onset of monoscopically visible contrast (Fig. 5), consistent with prior intra-cranial studies of the latency for information to reach primary visual cortex in human (Yoshor et al., 2007; Regev et al., 2018; Martin et al., 2019). In macaque the shortest single-cell onset latencies in V1 have been estimated to be 20–31 msec (Maunsell and Gibson, 1992), 27 msec (Nowak et al., 1995), 34 msec (Schmolesky et al., 1998) and 25–30 msec (Bair et al., 2002), as typical examples. The earliest image-onset latencies in macaque V1 to dynamic random dot stereograms were measured to be ~20–40 msec, median 54 msec (Gonzalez et al., 2001). Another study has measured macaque V1 image-onset times for RDS patterns as the time to 60% peak response (Nienborg et al., 2005), a more conservative estimator than that used by Gonzalez et al., (2001). Nienborg et al.’s onset latencies on this criterion ranged between 42 and 208 msec, with a median of ~67 msec. To accurately compare latencies across species, previous studies have derived a 5/3 species conversion factor (Schroeder et al., 1995; Chen et al., 2007). Our 50 msec image-onset latency would translate to 30 msec in macaque, which is in line with the earliest reported image-onset latencies in macaque.

The response amplitudes we measure between 50 and 100 msec have a common amplitude trajectory for each image type as indexed by the GFP profile, but the underlying neural generators as indexed by the topographic dissimilarity metric differ almost as soon as visual cortex starts to process these images. Direct interpretation of some of these results is complicated by the fact that we did not explicitly equalize the power spectra of the monocular half-images and thus both low-level and higher-level statistics of the half-images differed. In particular, the power spectra and chromaticity distribution of the random dot patterns were very different from those of the scrambled and intact 2D natural images. These latter images were approximately matched to each other on several summary statistics, but there were residual differences especially at higher spatial frequencies (see Fig. 6b). Our analysis of the contrast of the residual spectral differences between intact and scrambled natural scenes indicates that these differences are small in terms of visual contrast and are unlikely to dominate the response differences we observe. While the match over commonly used summary statistics appears adequate, we have not explored other image-based features or statistics that could drive the measured differences. We conclude that the measured topographic differences in Fig. 5 arise from differences in low-level features, as well as higher-order features in the case of the dot vs intact natural images and primarily, if not exclusively, from differences in higher-order statistics not controlled by our application of the synthesis algorithm in the case of the intact vs scrambled natural scenes. These differences are sufficient to shunt activity to different cortical areas, starting at very early time-points, a pattern that is difficult to appreciate in the single-unit literature due to the area-onset latencies being measured in separate experiments.

4.2. Onset latency for disparity-contingent responses

After the initial transient response to image onset occurs, disparity-contingent responses depart from baseline at around 100 msec for all three types of stereograms (Fig. 7). The timing of the onset of disparity-contingent responses is broadly similar to previous studies that measured disparity-evoked responses in human with random-dot stereograms (DRDS) that isolate the disparity cue (Regan and Spekreijse, 1970; Lehmann and Julesz, 1978; Neill and Fenelon, 1988; Michel et al., 1992; Fahle et al., 2003; Şahinoğlu, 2004).

In macaque V1, Durand et al. (2007) have measured the onset latency for disparity tuning and compared it to the onset-latency for orientation tuning. These selectivity-onset latencies were summarized with respect to the individual-cell latencies to image onset. They found that the onset of disparity selectivity lagged the image-onset response by an average of 77 msec with a semi-interquartile range of 22–148 msec. By contrast, the onset of orientation selectivity occurred at an average of 9 msec (2–55 msec). These results indicate that tuning for a monoscopically available feature – orientation – occurs shortly after cells begin to respond to image onset and well before tuning for binocular disparity emerges. The 77 msec average relative delay of stereoscopic processing with respect to image onset in the Durand et al. study converts to 128 msec in human. We find this relative delay to be 50 msec (e.g.100 msec after stimulus onset) which is more in line with their earliest relative delays (22 msec macaque/37 msec human).

In our paradigm and in the great majority of single-unit studies of disparity selectivity, the onset of image contrast occurs simultaneously with the onset of disparity. Multiple studies of disparity-selective cells in macaque have measured population responses for disparity sensitive cells responding to preferred vs non-preferred disparities under these conditions. A common feature of these time-courses is an initial response period where the cell response is above baseline but is not disparity selective. In macaque V2 (Nienborg and Cumming, 2006), the single-unit population response histogram leaves baseline at ~30 msec after image onset for both preferred and non-preferred disparities (50 msec human equivalent). However, it is not until ~125 msec (208 msec human equivalent) that responses to preferred and null disparities diverge. This pattern of a non-selective initial transient response to image onset, followed by a disparity-selective sustained response has also been observed in MT (Uka and DeAngelis, 2004; Ruff and Born, 2015), V4 (Tanabe et al., 2004; Shiozaki et al., 2012), IT (Janssen et al., 1999; Janssen et al., 2001, 2003; Uka et al., 2005), TEO (Alizadeh et al., 2018) and ventral premotor cortex (Theys et al., 2012b). In AIP, one study of 3D curvature selectivity showed a difference between image onset latency and disparity selectivity (Theys et al., 2012a) that an earlier study with similar stimuli did not (Srivastava et al., 2009). Of more direct relevance to the present study is work from the same group (Romero et al., 2013) that recorded responses in AIP to real-world objects presented in 2D vs 3D formats – a mode similar to our presentation of 2D vs 3D scenes. They found that the response to image onset occurred at ~45 msec, while the differential response to 2D vs 3D occurred at ~105 msec, a difference of 60 msec, somewhat longer than what we observe with the species conversion.

All of the studies of population response time-courses, except for Durand et al., (2007) did not measure the onset of disparity selectivity with respect to the individual-cell image onset latency, so there may have been some blurring of the profiles due to variability in onset latency across the population (Kiani et al., 2005). A relative delay of disparity-contingent responses – as we observe in human is, nonetheless seen in the clear majority of these macaque population-average time courses.

Why is the initial cortical response not disparity tuned, even in cells that are disparity selective? One possibility is that an abrupt onset of the monoscopic image drives cells into saturation and disparity tuning can only be expressed once rapid adaptation has occurred. While the initial contrast transient supports rapid decoding of stimulus orientation (Muller et al., 2001; Durand et al., 2007), the same might not be true for disparity. Alternatively, as in the case of orientation tuning (Ringach et al., 2003), disparity tuning may emerge after a period of recurrent intracortical cortical processing has occurred. The Durand et al (2007) results suggest either that orientation tuning is more robust to image contrast transients or that the period of recurrent processing needed to develop disparity selectivity is longer. Studies are needed that dissociate the onset of image contrast from the onset of disparity to separate these two possibilities.

4.3. Stereogram-independent, disparity-contingent responses between 100 ~ 150 msec

Disparity-contingent responses to each stereogram type emerge by 100 msec, but they are tightly coupled and not measurably different between 100 ~ 150 msec despite the large differences in their monoscopic appearance. By design, the stereogram classes were equated for disparity and one interpretation of this result is that responsiveness at early time-points is limited to a local feature analysis, such as that described by the disparity energy model (Ohzawa et al., 1990, 1997). Notably, in the present context, the disparity energy model of complex cells explicitly removes a dependence between disparity tuning and the position of features in the monocular half-images. Such an operation would make it difficult to distinguish the different relationships between disparity edges and monoscopic edges in our different stereogram types. Alternatively, it is always possible that our scalp recordings are insensitive to differences that might be present and measurable by other means, e.g. absence of evidence is not evidence of absence.

4.4. Interaction between monocular image content and disparity processing

After 150 msec, our measurements indicate that monoscopic and stereoscopic image content interact. We previously showed that the disparity-contingent response to natural scenes, measured as the difference potential between monoscopic and steroscopic scenes, was larger for scenes that had a larger difference potential between intact and scrambled monoscopic scenes (Duan et al., 2018). Scenes with “stronger” monoscopic content supported a larger disparity-contingent response, suggesting that monoscopic scene content interacts with disparity. While that analysis was consistent with an interaction between monoscopic and stereoscopic image content, it was not time- resolved and lacked a direct experimental manipulation of the relationship between monoscopic and stereoscopic image content. Here we find response amplitudes for the three types of depth-map-matched stereograms differed from 150 msec (Fig. 7a), indicating that interaction between monocularly available image content and the structure of the depth maps occurs no later than this time-point. At this point, it is not clear exactly which monoscopic image features interact with disparity. We can say that these features are higher-order than those preserved by the scrambling algorithm.

Previous work on interactions between disparity and monocular depth cues has used synthetic stimuli portraying pairs of depth cues rather than natural scenes that contain multiple cues. Observers have been shown combine information from texture and disparity when judging surface orientation (Hillis et al., 2002) and disparity and shading information when judging perceived depth (Lovell et al., 2012). Human imaging studies have similarly examined combinations of pairs of depth cues generated in synthetic images (Welchman et al., 2005; Ban et al., 2012; Dovencioglu et al., 2013; Murphy et al., 2013), implicating second-tier extra-striate visual areas such as V3B/KO. Single-unit recordings in macaque have found evidence for combination of disparity and texture/perspective cues in Caudal Intraparietal (CIP) cortex (Taira et al., 2000; Tsutsui et al., 2001; Rosenberg and Angelaki, 2014) and disparity and relative motion in MT of macaque (Armendariz et al., 2019) and V3B/KO in human (Ban et al., 2012). While these previous studies have implicated some important higher-order cues such as shading and perspective as interacting with disparity, the previous literature has not addressed the multi-stage temporal evolution of monoscopic and stereoscopic processing as done here. Importantly, while an earlier stage of disparity processing (100 ~ 150 msec) can be probed equivalently by the RDS and other stereograms, RDS-based experiments may not fully reflect depth processing in natural scenes due to the non-linear effects we demonstrate here at later time-points.

4.5. Temporal stages of disparity processing and association with perceptual decision making

We find two stable disparity-contingent cortical micro-states between 150 to 300 and between 300 to 500 msec (Fig. 8), both occurring well before the motor responses that occur roughly 1 sec later. It is therefore unlikely that activity during either of these microstates reflects motor response preparation or execution, rather these micro-states may reflect a temporally extended period of joint encoding of monoscopic and stereoscopic cues that is accomplished within at least two broad but distinct cortical networks. Based on the scalp topographies, the first is likely to be located in posterior occipital and temporal areas and the second in dorsal occipital and parietal areas (see Fig. 8). Importantly, within each of these stable micro-states, the detailed topography and thus underlying sources differ across stereogram types (Fig. 8b).

Perceptual read-out of depth appears to rely on these two stages of processing that start at ~150 msec, rather than on the earlier stage of processing between 100 and 150 msec that is disparity contingent, but not stereogram dependent (see Fig. 9). This relatively late perceptual access to the internal disparity response is consistent with a recent study of the temporal order of binocular depth perception that suggested that perceptual access occurs at around 200 msec after stimulus onset (Caziot et al., 2015). Data from single-unit electrophysiology also suggests relatively late perceptual access. For example, responses to anti-correlated RDS that support disparity tuning but not perceptual depth are progressively rejected from V1 to V4 and IT (Janssen et al., 2003; Tanabe et al., 2004). Similarly, sensitivity to relative disparity, key to perceptual stereopsis and extracting shape from disparity is poor in V1 and increases as the cortical hierarchy is ascended (Anzai et al., 1997; Cumming and Parker, 1999; Janssen et al., 2001; Thomas et al., 2002; Umeda et al., 2007). Finally, and more directly relevant to the present work, choice probability for surface orientation defined by disparity and texture cues is found in CIP, but not in V3A of macaque (Elmore et al., 2019).

We linked brain and behavior by exploiting the co-variation of individual differences in the amplitude of the disparity response and individual differences in discrimination accuracy. Importantly, the pattern of response amplitudes seen in the group data (Fig. 5 and 7) is also reflected at the individual level: the pattern of GFP amplitude over the three stimulus conditions is predictive of accuracy on an individual-subject basis, indicating a causal relationship between brain response amplitudes and perceptual accuracy. One thing worth noting in our experiment is that the response time is around 1400 msec after stimuli onset, with the best performance not faster than 1290 msec. It is possible that the two stages of disparity processing just described are both involved in disparity encoding, with the perceptual decision being reached after an extended period of evidence accumulation. The stimulus-locked analysis we have performed here favors the former over the latter. It would be useful to analyze responses that are locked to the time of the motor response to better explore the hypothesized accumulation stage (Cottereau et al., 2014).

5. Conclusions

By experimentally controlling for image depth maps and systematically manipulating monoscopic image content, we identified multiple disparity-encoding stages, with the earliest stage between 100 ~ 150 msec being insensitive to monoscopic image content. This stage is followed by two additional disparity-contingent stages between 150 ~ 500 msec that were image-content sensitive and predictive of behavioral accuracy on a disparity-discrimination task. Our results demonstrate that while the earliest stage of disparity processing can be effectively probed with RDS, the results may not fully reflect the nature of depth processing in natural scenes. Further work with more sophisticated experiments involving a combination of natural and naturalistic stimuli will be necessary to clarify the role of monocular image statistics and monocular depth cues in relationship to disparity processing.

Data sharing:

EEG data and study images and are archived at the Open Science Framework https://osf.io/hqgvf/