Tumor growth inhibition modeling in patients with second line biliary tract cancer and first line non‐small cell lung cancer based on bintrafusp alfa trials

Abstract

This analysis aimed to quantify tumor dynamics in patients receiving either bintrafusp alfa (BA) or pembrolizumab, by population pharmacokinetic (PK)‐pharmacodynamic modeling, and investigate clinical and molecular covariates describing the variability in tumor dynamics by pharmacometric and machine‐learning (ML) approaches. Data originated from two clinical trials in patients with biliary tract cancer (BTC; NCT03833661) receiving BA and non‐small cell lung cancer (NSCLC; NCT03631706) receiving BA or pembrolizumab. Individual drug exposure was estimated from previously developed population PK models. Population tumor dynamics models were developed for each drug‐indication combination, and covariate evaluations performed using nonlinear mixed‐effects modeling (NLME) and ML (elastic net and random forest models) approaches. The three tumor dynamics’ model structures all included linear tumor growth components and exponential tumor shrinkage. The final BTC model included the effect of drug exposure (area under the curve) and several covariates (demographics, disease‐related, and genetic mutations). Drug exposure was not significant in either of the NSCLC models, which included two, disease‐related, covariates in the BA arm, and none in the pembrolizumab arm. The covariates identified by univariable NLME and ML highly overlapped in BTC but showed less agreement in NSCLC analyses. Hyperprogression could be identified by higher tumor growth and lower tumor kill rates and could not be related to BA exposure. Tumor size over time was quantitatively characterized in two tumor types and under two treatments. Factors potentially related to tumor dynamics were assessed using NLME and ML approaches; however, their net impact on tumor size was considered as not clinically relevant.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Clinical trials of the investigational agent bintrafusp alfa in first‐line non‐small cell lung cancer (1L NSCLC) and second‐line biliary tract cancer (2L BTC) did not meet the primary efficacy end points.

• WHAT QUESTION DID THIS STUDY ADDRESS?

Are there patient‐specific factors that explain the variability in antitumor activity in the respective clinical trials and can this be assessed using population tumor dynamic models with a comprehensive covariate assessment including machine‐learning (ML) algorithms?

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

Although an exposure effect on tumor shrinkage was demonstrated for BA in 2L BTC, no exposure‐effect relationship could be discerned in 1L NSCLC and no clinically relevant covariate effects were identified in both populations.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

Viewed from a broader perspective, these analyses illustrate a two‐pronged approach incorporating both classical pharmacometrics and ML to covariate analyses, thereby contributing to the emerging area of pharmacometrics enhanced by advanced analytics, with opportunities to enable model‐informed precision medicine.

INTRODUCTION

Bintrafusp alfa (BA; MSB0011359C or M7824) is a first‐in‐class bifunctional fusion protein composed of the extracellular domain of the transforming growth factor‐β receptor II (a TGF‐β “trap”) fused to a human immunoglobulin G1 antibody blocking programmed death ligand 1 (PD‐L1), ¹ that thereby has potential to inhibit two key immunosuppression pathways in the tumor microenvironment simultaneously. ² Two recent BA clinical trials, versus pembrolizumab in first‐line non‐small cell lung cancer (1L NSCLC; NCT03631706), ³ and in second‐line biliary tract cancer (2L BTC; NCT03833661), ⁴ failed to replicate the encouraging results from earlier studies, warranting investigation to elucidate potential factors that might indicate sensitivity or resistance to BA or pembrolizumab treatment, as well as further elucidation of hyperprogression, defined as an unexpected rapid progression of disease in patients receiving immunotherapy, ⁵ also detected in these trials.

Previously, modeling and simulation approaches have been used to characterize the pharmacokinetics (PKs) of BA in various tumor types ⁶ and to support selection of the recommended phase II dose. ⁷ Furthermore, more recently population PK and exposure‐safety analyses have been used to inform risk management of bleeding toxicities. ⁸ None of the analyses, however, investigated tumor dynamics under BA treatment so far. Tumor growth inhibition modeling enables estimation of drug exposure effects, identification of significant covariates on tumor dynamics parameters, and quantification of their effects, thus potentially informing hypotheses around patient populations that might show higher or lower sensitivity to treatment. Moreover, machine‐learning (ML) methods are increasingly being applied in different stages of drug discovery and development, ⁹ , ¹⁰ including more recent applications to guiding population model development, ¹¹ and of particular interest in screening of covariates. ¹²

The objectives of this analysis were to quantify tumor dynamics under BA and pembrolizumab treatment by tumor growth inhibition modeling, and to identify covariates that may explain the variability in tumor dynamics by using traditional pharmacometric covariate analysis and ML techniques.

METHODS

Clinical trial design and patients

This analysis (Figure 1) included data from two multicenter, international, open‐label trials, in BTC and NSCLC. The BTC trial ¹³ was a phase II, single‐arm trial designed to evaluate BA monotherapy in patients with locally advanced or metastatic BTC previously treated with 1L platinum‐based chemotherapy. The 159 patients enrolled received BA at a dose of 1200 mg i.v. every 2 weeks (q2w). The NSCLC trial ¹⁴ was an adaptive phase III, randomized, controlled trial in patients with advanced NSCLC with high PD‐L1 tumor expression (≥80% PD‐L1 positive tumor cells). Patients (n = 304) who have not received previous treatment were enrolled and randomly assigned to receive either BA at a dose of 1200 mg i.v. q2w or pembrolizumab at a dose of 200 mg q3w in a 1:1 ratio. Schedule of tumor size (TS) assessments and PK sampling are given in Table S1.

FIGURE 1.

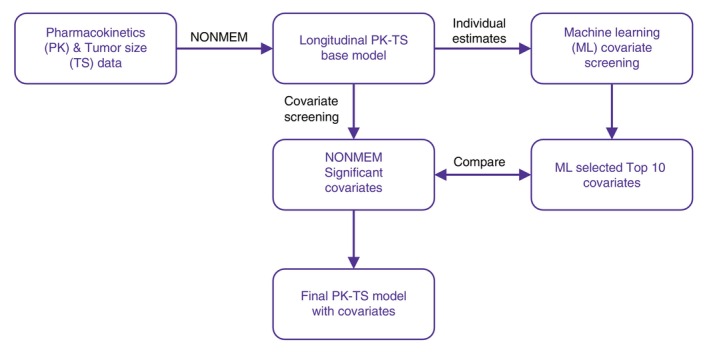
Overview of the analysis workflow.

Pharmacokinetics

The previously developed BA population PK model ⁸ was used to estimate the individual drug exposure (dynamic area under the concentration‐time curve [AUC]) for BA for both trials, using the actual dosing information that accounts for treatment interruptions. In the absence of pembrolizumab concentration data in the current study, a previously developed population PK model was used to characterize pembrolizumab exposure. ¹⁵ Therefore, pembrolizumab exposure (AUC) reflects the value for a typical subject as defined by the covariate model alone instead of individual patient exposure.

Tumor size modeling

The TS measure used in this analysis was the sum of longest diameters, as per the Response Evaluation Criteria in Solid Tumors (RECIST). ¹⁶ In NSCLC the TS was measured mainly using computed tomography (CT) or X‐ray; in BTC mainly CT and/or magnetic resonance imaging were used. In addition, patients' tumor growth was characterized as being hyperprogressive using the method described in Matos et al. ⁵ that is, “based on RECIST [1.1] as progressive disease (PD) in the first 8 weeks after treatment initiation and minimum increase in the measurable lesions of 10 mm plus: (i) increase of ≥40% in sum of target lesions compared with baseline [which represents doubling in unidimensional target lesions compared with classic RECIST PD criterion (20%)]; and/or (ii) increase of ≥20% in sum of target lesions compared with baseline (the classic RECIST PD criterion) plus the appearance of new lesions in at least two different organs.” ⁵ In NSCLC, all patients in the two arms had at least two tumor measurements. In BTC, there was one patient with only one tumor measurement, and this patient was retained in the analysis.

Several published models of tumor dynamics were evaluated, including: (1) the Claret et al. ¹⁷ model, which described an exponential decrease in the rate of tumor shrinkage to empirically account for resistance development, (2) a modified turnover model of Tham et al., ¹⁸ (3) a simpler turnover model with first order growth and decay, ¹⁹ , ²⁰ (4) a Gompertz function that described sensitive and resistant cell subpopulations, ²¹ and (5) a more complex model described by Chatterjee et al. ²² as a more physiologically based function that described a fraction of the tumor that is shrinking and a fraction that is not affected by the treatment.

Covariate evaluations

As one of the objectives of this work was to identify covariates that might explain variability in tumor dynamics, baseline values of preselected covariates were tested. Overall, the herein reported analyses evaluated covariates that were preselected for their potential association with the mechanism of action of the drug and its efficacy, or with the disease, including biology of the drug targets and tumor. These included demographics (e.g., sex, age, and body size), disease‐related characteristics (e.g., Eastern Cooperative Oncology Group status, histology, and necrotic tissue), disease‐related laboratory values (e.g., albumin, C‐reactive protein [CRP] and lymphocytes), therapy‐related (e.g., prior therapy, anti‐drug antibody status, and time since diagnosis to first dose), and genetic mutations (e.g., IDH1, KDR mutation, and minor allele frequency for all detected somatic variants in the sample). Detailed lists of covariates investigated for the BTC and NSCLC analyses are given in Supplementary Methods. Missing covariate information was imputed by the median value for continuous covariates and by the mode for categorical covariates. Covariate assessment comprised multiple steps, including (1) univariable covariate runs, (2) full covariate model followed by reduction, and (3) covariate evaluations using ML approaches.

Covariate evaluations via nonlinear mixed‐effects approach

Single covariate selection was based on the log‐likelihood criterion, goodness‐of‐fit plots, parameter precision, and scientific plausibility. All covariates resulting in a significant (p < 0.01) reduction in the objective function (i.e., χ²(1 df) > 6.635) and a reduction in interindividual variability (IIV) for the modeled parameter compared to that for the base model were combined into a full model. Subsequently, a backward elimination step was conducted whereby the covariates were sequentially set to their null value and those that resulted in a statistical worsening of the model objective function (p < 0.001) or were poorly estimated (relative standard errors [RSEs] >50%) were eliminated from the model, resulting in the final models.

For all non‐linear mixed‐effects (NLME) modeling analyses NONMEM (version ≥7.4.4; ICON Development Solutions) ²³ , ²⁴ was used, and SAS version 9.4 (SAS Institute) was used for the exploratory analysis, model development, and post‐processing of NONMEM output. In addition, Xpose version 4.4.0 ²⁵ PsN (psn.sourceforge.net), ²⁶ , ²⁷ and R ²⁸ software packages were used.

Covariate evaluations via ML approach

In addition to the NLME modeling approach, ML was implemented to evaluate the baseline covariates of interest on empirical Bayes parameter estimates. Data assembly and ML methods used the Python Data Analysis Library, pandas 1.1.5., ²⁹ NumPy 1.21.6. ³⁰ and scikit‐learn library 1.0.2. Values were standardized and redundant features showing strong multicollinearity were dropped from the analysis dataset prior to modeling. Two different ML algorithms were used for the screening procedure: (1) a regularized linear regression and (2) tree‐based model with recursive feature elimination. The methods for covariate selection are described below with further details provided in Supplementary Methods.

Within the elastic net model, L1, L2 penalties, and alpha weighting values for each covariate model were selected using grid search over a range of values. Indicators of the importance of each feature for the final elastic net covariate model were: (1) absolute values of the normalized co‐efficient, (2) permutation importance, and (3) Shapley (SHAP) Feature Importance.

Within the random forest (RF) model, parameters for each random forest regressor covariate model were tuned via grid search over a range of different values. These parameters were: (1) number of estimators or trees, (2) maximum tree depth, and (3) minimum number of samples at which to split. Indicators of the importance of each feature in the final RF covariate model were: (1) impurity based feature importance (gini), (2) permutation importance, and (3) SHAP.

RESULTS

Structural tumor dynamic model across treatment and tumor types

The tumor trajectories by study and treatment are presented in Figure S1. Hyperprogression was identified in BA arms (43 and 11 patients with hyperprogression in 2L BTC and 1L NSCLC, respectively), but not in pembrolizumab arm. In all three evaluated cases, that is, under both treatments and for both tumor types, the model with log‐normally distributed exponential tumor shrinkage component (describing the treatment‐induced tumor shrinkage over time that would result in reducing the tumor size asymptomatically toward zero), linear tumor growth component, ³¹ and residual variability modeled using log‐transform both sides approach with an additive error model described the data best:

$${\mathrm{TS}}_i\left(t\right)={\mathrm{BTS}}_i\bullet e^{-{k\mathrm{s}}_i\bullet t}+{\mathit{kg}}_i\bullet t$$ (1)

where TS _i (t) is the tumor size at time t (weeks) for the i‐th individual, BTS _i is the baseline tumor size, ${\mathit{ks}}_i$ is the exponential tumor shrinkage rate constant, and ${\mathit{kg}}_i$ is the linear tumor growth rate constant;

$$\ln \left(Y_{\mathit{ij}}\right)=\ln \left({\mathrm{TS}}_{\mathit{ij}}\right)+{\epsilon }_{\mathit{ij}}$$ (2)

where Y _ij denotes the observed tumor size for the ith individual at time j, TS _ij denotes the corresponding predicted tumor size, and ε _ij denotes the residual random effect, which is assumed to have a normal distribution with a zero mean and variance σ. ²

The model structure provided a good fit for all three herein investigated cases (i.e., both BA and pembrolizumab data in both BTC and NSCLC). The parameter estimates for k _s were 0.0159, 0.0368 and 0.0307 week⁻¹ for BA in BTC, BA in NSCLC and pembrolizumab in NSCLC, respectively. Typical values for k _g were 0.624, 0.728, and 0.643 mm/week for BA in BTC, BA in NSCLC, and pembrolizumab in NSCLC, respectively.

Tumor dynamics and covariate assessment under BA treatment in 2L BTC

Of the 157 subjects assigned to treatment with BA, 143 (91.1%) had evaluable PK and tumor size data. In this subpopulation, the median age was 65 years (range: 39 to 83 years), median body weight 65 kg (range: 38 to 100 kg), and 85 patients (59.4%) were men.

The tumor dynamics model parameters were well‐estimated (Table 1). Although some of the identified covariate parameters had relatively high standard errors (70.1%), IIV for baseline TS, k _g and k _s (50, 72.7, and 103.4% coefficient of variation [CV], respectively) was moderate to high, and estimated with acceptable accuracy (RSE < 20% CV). Shrinkage for the three tumor dynamic model parameters was low (<20%), allowing for covariates assessments (Table S2). The final model included effect of AUC on tumor shrinkage portion of the tumor size equation, with increasing rate of tumor shrinkage with increasing AUC, and the following covariates: minor allele frequency (+), time since diagnosis (−), aspartate aminotransferase (AST; +), CRP; (+) and Asian race on baseline TS (−), IDH1 mutation on k _s (+), and minor allele frequency (+), IDH1 mutation (+), CRP (+), and blood tumor mutational burden (+) on k _g (Table 1).

TABLE 1.

Parameters of the tumor dynamics model for BTC under 2 L bintrafusp alfa treatment.

Parameter (units)	Typical value	%RSE
Baseline TS (mm)	51.3	11.4
k s (week−1)	0.0159	26.7
k g (mm/week)	0.624	20
AUC effect	0.339	15.9
Proportional residual unexplained variability (% CV)	15.6	6.2
Minor allele frequency on baseline TS	0.106	26.2
Time since diagnosis on baseline TS	−0.151	35.9
AST on baseline TS	0.189	54
CRP on baseline TS	0.0777	43.8
Asian race on baseline TS	−0.2	35.2
IDH1 mutation on k s	2.13	55.4
Minor allele frequency on k g	0.262	33.2
IDH1 mutation on k g	1.17	51.5
CRP on k g	0.152	55.1
Blood tumor mutational burden on k g	0.629	70.1
IIV baseline TS (% CV)	50	6.5
IIV k s (% CV)	103.4	17
IIV k g (% CV)	72.7	12.3
Corr(baseline TS, k s)	−0.362	NE
Corr(baseline TS, k g)	0.465	NE
Corr(k s, k g)	−0.845	NE

Abbreviations: AST, aspartate aminotransferase; AUC, area under the curve; BTC, biliary tract cancer; CRP, C‐reactive protein; CV, coefficient of variation; IIV, interindividual variability, k _g, tumor growth rate constant; k _s, tumor shrinkage rate constant; NE, not evaluable; RSE, relative standard error; TS, tumor size.

Of the investigated covariates, the univariable NLME analyses identified several covariates as significant on baseline TS (10 covariates), k _g (10 covariates), and k _s (5 covariates). Likewise, ML identified numerous covariates for baseline TS, k _s and k _g. Goodness of fit metrics for the ML models is provided in Table S3. A summary of the comparison of the covariates identified by ML and univariable NLME analyses is provided in Table S4. SHAP plots have been provided as Figure S3.

Tumor dynamics and covariate assessment under BA treatment in 1L NSCLC

Of the 152 subjects assigned to treatment with BA, 139 (91.4%) had evaluable PK data as well as TS data. The median age in this subpopulation was 67 years (range: 42 to 90), median body weight 66.5 kg (range: 35.0 to 104.3), and 111 patients (79.9%) were men.

The tumor dynamics model parameters were generally well‐estimated (Table 2). IIV for baseline TS, k _g and k _s (55.4, 122.9, and 62.8% CV, respectively) were moderate to high, estimated with high accuracy (RSE < 30% CV). Shrinkage for the three tumor dynamic model parameters was acceptable (≤20%), allowing for covariate assessments (Table S2).

TABLE 2.

Parameters of the tumor dynamics model for NSCLC under 1 L bintrafusp alfa and pembrolizumab treatment.

Parameter (units)	Bintrafusp alfa		Pembrolizumab
	Typical value	%RSE	Typical value	%RSE
Baseline TS (mm)	81.1	5.75	80.4	4.91
k s (week−1)	0.0368	12.8	0.0307	9.06
k g (mm/week)	0.728	17.9	0.643	12.9
Proportional residual unexplained variability (% CV)	12.8	2.29	11.3	2.42
Effect of CRP on baseline TS	0.125	23.8	–	–
Effect of lymphocyte as percentage of total leukocytes on k g	−0.623	43.7	–	–
IIV baseline TS (% CV)	55.4	14.0	55.5	13.02
IIV k s (% CV)	62.8	26.3	70.1	24.03
IIV k g (% CV)	122.9	22.1	92.7	20.7
Corr(baseline TS, k s)	−0.0411	NE	−0.0228	NE
Corr(baseline TS, k g)	0.423	NE	0.288	NE
Corr(k s, k g)	−0.0639	NE	−0.0834	NE

Abbreviations: CRP, C‐reactive protein; CV, coefficient of variation; IIV, interindividual variability; k _g, tumor growth rate constant; k _s, tumor shrinkage rate constant; NE, not evaluable; NSCLC, non‐small cell lung cancer; RSE, relative standard error; TS, tumor size.

Covariates (list available in Supplementary Methods) were evaluated on all three tumor dynamic model parameters (baseline TS, k _g, and k _s). As AUC was not found to be a significant explanatory factor, herein presented are the covariate assessments performed without AUC in the model. However, as a sensitivity analysis, the covariate assessment was performed both without and with AUC in the model, with the results being virtually identical as expected with the inclusion/exclusion of a nonsignificant covariate.

With the NLME modeling approach the covariates were independently, univariably assessed for significance on baseline TS, k _g, and k _s. The univariable analyses identified the following covariates as significant: γ‐glutamyl transferase and CRP on baseline TS; lymphocytes as a percentage of total leukocytes on k _g; and no covariates had significant effect on k _s. Of these, CRP on baseline TS (+) and lymphocytes as a percentage of total leukocytes on k _g (−) met the criteria for retainment in the final model after backward elimination step (Table 2).

Similarly, ML did not identify any strong covariates for k _g and k _s; the normalized coefficient and feature importance as well as permutation importance indicated similar likelihood of all covariates evaluated. For baseline TS, on the other hand, the ML algorithm identified the following covariates as being potentially important: Asian race, creatinine, γ‐glutamyl transferase, CRP, monocyte, and lymphocyte levels (with goodness‐of‐fit metrics in Table S3). SHAP plots have been provided as Figure S4.

Tumor dynamics and covariate assessment under pembrolizumab treatment in 1L NSCLC

Of the 152 subjects assigned to treatment with pembrolizumab, 143 (94.1%) had evaluable PK and TS data. The median age of this subpopulation was 67 years (range: 36 to 88 years), median body weight 66.9 kg (range: 40.0 to 141.5 kg), and 111 patients (77.6%) were men.

The parameters of tumor dynamics model under pembrolizumab treatment were well‐estimated (Table 2). IIV in baseline TS, k _g, and k _s (55.5, 92.7, and 70.1% CV, respectively) were moderate to high, estimated with high accuracy (RSE < 25% CV), and acceptable shrinkage (<20%; Table S2).

The analysis of pembrolizumab was performed in the same manner as described above for BA and the same set of covariates was evaluated. Similar to BA, as AUC was not significant, the results below stem from covariate analysis without AUC in the model. Univariable analyses identified the proportion of necrotic tissue in the whole tumor region and fibroblast density in the whole tumor region as significant covariates on baseline TS; no covariates were identified as significant with respect to k _g and k _s. None of the covariates was retained in the final model after the backward elimination step.

Similarly, and using the same criteria as for BA (i.e., similar feature and permutation importance with all evaluated covariates) no covariates for k _g or k _s were identified using ML. For baseline TS, the following covariates were identified as important by ML: lymphocytes as a percentage of total leukocytes, minor allele frequency, AST, and lymphocyte level (with goodness‐of‐fit metrics in Table S3). SHAP plots have been provided as Figure S5.

DISCUSSION

In this work, we report tumor dynamics’ models for patients with BTC and NSCLC treated with BA or pembrolizumab which, together with ML methods, made it possible to identify factors that describe part of the variability in tumor dynamics. Although artificial intelligence (AI)/ML approaches are valuable to assist with model selection, ¹¹ the scope of application of ML algorithms in this analysis was limited to covariate evaluations and the model building step relied on conventional pharmacometric approaches that are established for modeling tumor growth dynamics. ³²

The developed tumor growth models for patients with BTC receiving 2 L BA treatment and patients with NSCLC receiving 1 L BA or 1 L pembrolizumab treatment all performed well (as assessed by standard diagnostics, e.g., goodness‐of‐fit plots and visual predictive checks). Regardless of the tumor type (BTC vs. NSCLC) or treatment (BA vs. pembrolizumab), tumor growth rates were of similar and overlapping extent (Figure 2). However, tumor shrinkage rates differed, being 59% lower in the BTC population than the NSCLC population, whereas they were comparable between BA and pembrolizumab arms of the NSCLC trial (Figure 2). The effect of BA exposure (AUC) on tumor shrinkage was significant in the BTC model, whereas neither BA nor pembrolizumab exposure was significant in the corresponding NSCLC models. The final models also included significant covariates on the tumor dynamics parameters (baseline TS, k _g, and/or k _s). Under the BTC setting (Table 1), several covariates were found significant, including patient‐related (race), disease‐related (AST and CRP), and genomic factors (minor allele frequency, IDH1 mutation, and tumor mutational burden). Although the covariates did explain some of the variability in tumor growth and shrinkage parameters, the net impact on tumor size over time (illustrated in Figure 3a–h) was of very limited extent for all covariates, indicating them clinically unimportant as contributors to overall variability in tumor dynamics. The only covariate identified to be related to tumor shrinkage was IDH1 mutation, in accordance with the previous reports of better prognosis in patients with IDH1 mutation, ³³ however, IDH1 was at the same time directly related to tumor growth, resulting in a more complex relationship with TS change over time (Figure 3f). In contrast to BTC, the NSCLC analysis identified only two covariates (Figure 3i,j) as significant in the BA arm, and none in the pembrolizumab arm. In the BA arm, baseline TS was found to be related to CRP concentration, which was expected as CRP is related to the disease severity, and lymphocyte percentage was inversely related to tumor growth rate, which is in accordance with the previous reports of low lymphocyte percentage as an indicator of poor prognosis in lung cancer. ³⁴ Interestingly, none of the covariates was identified as related to the tumor shrinkage rate.

FIGURE 2.

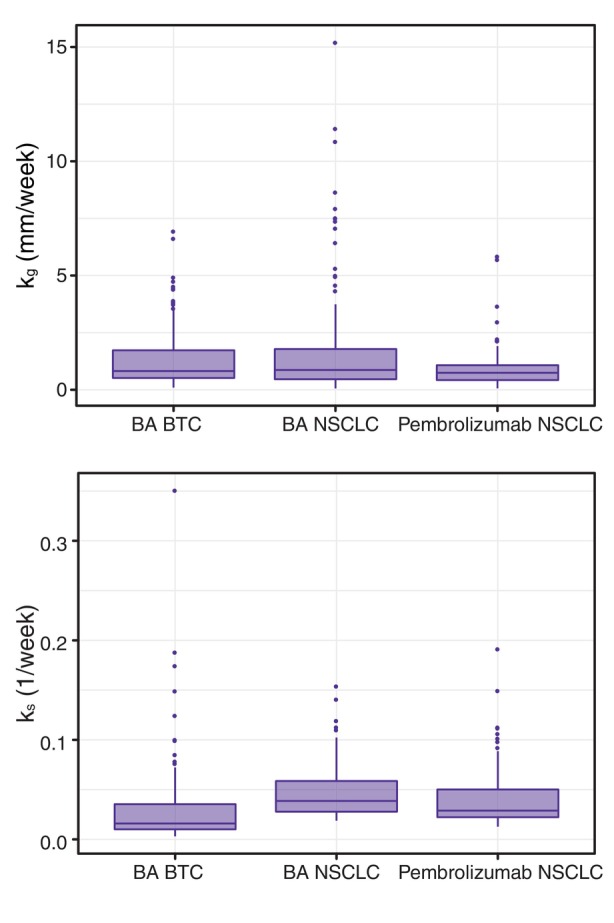
Distribution of tumor growth (upper panel) and tumor shrinkage (lower panel) rate constants among the developed tumor dynamics models. AST, aminotransferase; AUC, area under the curve; MAF, minor allele frequency; TS, tumor size.

FIGURE 3.

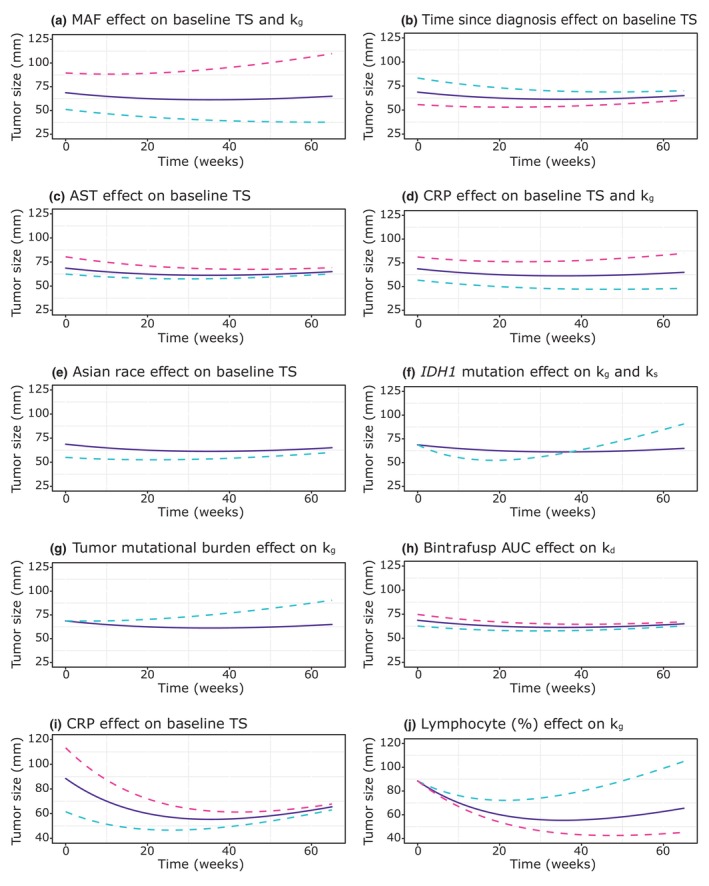
Effects of covariates identified as significant in the analysis of BTC trial (a–h) and NSCLC trial (i, j) data on tumor size dynamics. For continuous covariates purple full line denotes median, blue dashed line 5th percentile, and red dashed line 95th percentile; for categorical covariates purple full line denotes the reference category (non‐Asian race, no IDH1 mutation, and blood tumor mutational burden [TMB] <50th percentile) and blue dashed line the significant category (Asian race, IDH1 mutation, and blood TMB ≥50th percentile). BTC, biliary tract cancer; NSCLC, non‐small cell lung cancer.

A second part of this analysis utilized ML and univariable NLME approaches to identify trends in relationships between covariates and tumor dynamics, at the same time enabling comparison of these approaches. In BTC analysis, there was an overall agreement among covariates identified as significant by univariable NLME analyses and top features identified by ML (Table S4). Overall, the identified covariates fit into expected categories, including genomic (minor allele frequency, tumor mutational burden, and IDH1 mutation), disease‐related (CRP, lymphocytes, and alkaline phosphatase), and patient‐related factors (Asian race). Of note, the race was found only to be related to baseline TS and the overall magnitude of the effect was low (Figure 3e). In NSCLC analyses, there was a limited agreement between the two approaches, which might be partly attributable to the overall lack of significance of covariates in these analyses. Furthermore, whereas in the NLME setting there are clear statistical criteria that define significance, with ML assignment of significance relies on human intervention and decision in setting a predefined parameter (threshold or a predefined number of the top or most important covariates), thus influencing the comparisons of the two methods. In the BA arm analysis, covariates identified by NLME analysis were also captured by ML, but ML identified further covariates not captured by NLME. No covariates were associated with k _s with either of the methods; and the one covariate on k _g identified by NLME was not captured by ML. In the pembrolizumab arm analysis, neither of the methods linked any covariates to k _g nor k _s, whereas the covariates identified by the two methods for baseline TS differed without overlap. In summary, there was lower agreement between the two methods for NSCLC than for the BTC trial, and for BA than for pembrolizumab. As a phase I analysis in esophageal carcinoma ³⁵ suggested that immune‐excluded phenotype might be related to response to BA, our covariate analyses included the immune phenotype, these were, however, not found to be significant in any of our analyses. Similarly, the proportion of necrotic tissue in the tumor area ³⁶ and inflammatory microenvironment (macrophage, lymphocyte, and fibroblast density) ³⁷ were considered of interest, but none of them were found to be significant in our analyses.

As a primary purpose of the present research was to identify sources of variability (i.e., covariates) that may explain the observed heterogeneity in tumor growth dynamics in the evaluated datasets, it was important to qualify the developed population tumor dynamics models as having adequately low shrinkage (<20%) in the parameters where IIV could be described. In ML‐enabled covariate analyses, making the evaluation of shrinkage in model parameters is important. When shrinkage is high, the individual parameter estimates are not reflective of the actual individual patient making covariate identification difficult. Of note, the parameters for all developed models had little shrinkage in the present evaluation, supporting the results of the covariate analyses. It is important to acknowledge that the deployed ML methods in the analyses also do not take into account correlation between model parameters. However, covariate evaluations using ML run more quickly than with traditional modeling, and there is no need to create multiple model files to test each, making ML useful, particularly when model run times are long and many covariates need to be evaluated. Although AI/ML has shown great potential in assisting model selection, ¹¹ this model building step relied on conventional approaches.

Finally, because tumor hyperprogression was observed in certain patients, a subanalysis in the BA treatment groups compared patients who had experienced hyperprogression to patients who had not. With respect to tumor dynamics, the patients who experienced hyperprogression could be identified by higher tumor growth rate and lower tumor kill rate in both BTC and NSCLC (Figure S2). Interestingly, no meaningful difference in the BA exposure (first cycle AUC) was observed between these two patient subgroups (Figure S2d,h), suggesting that BA exposure was not a driver for hyperprogression, that is, that factors beyond BA treatment warrant further investigation with respect to hyperprogression. Due to the low number of hyperprogressing patients in our data, these findings warrant further research.

In conclusion, the herein reported analyses quantitatively characterized TS change over time in two different tumor types and under different two treatments. These studies did not meet the primary end point, thus, the main focus of this work was to assess the potential existence of subpopulations who might be sensitive to the effects of BA. To this purpose, two approaches, NLME and ML, were used to identify factors potentially related to the tumor dynamics. Given their demonstrated potential to mine and assess covariates in the high‐dimensional space, ¹² ML approaches were run to complement conventional methods in a comprehensive investigation. Results were generally consistent across methods, and several covariates were suggested to have an effect on population variability in model parameters characterizing tumor dynamics. However, their net impact on TS was not considered clinically relevant. Viewed from a broader perspective, these analyses illustrate a two‐pronged approach incorporating both classical pharmacometrics and ML to covariate analyses, thereby contributing to the emerging area of pharmacometrics enhanced by advanced analytics, with opportunities to enable model‐informed precision medicine. ¹⁰ , ³⁸ , ³⁹

AUTHOR CONTRIBUTIONS

A.‐M.M.‐G., N.T., D.R.M., Y.V., P.G., K.V., and A.K. wrote the manuscript. A.‐M.M.‐G., N.T., D.R.M., Y.V., P.G., K.V., and A.K. designed the research. All authors performed the research and analyzed the data. All authors read and approved the final manuscript.

FUNDING INFORMATION

Funding for the two trials (NCT03631706, NCT03833661) and analyses reported here was provided by the healthcare business of Merck KGaA, Darmstadt, Germany (CrossRef Funder ID: 10.13039/100009945).

CONFLICT OF INTEREST STATEMENT

A.‐M.M.‐G., T.M., and A.K. are employees of the healthcare business of Merck KGaA, Darmstadt, Germany. D.M. reports personal fees from the healthcare business of Merck KGaA, Darmstadt, Germany during the conduct of the study. Y.V., A.M., and K.V. are employees of EMD Serono. N.T. and P.G. are employees of Quantitative Pharmacology, Ares Trading S.A., Lausanne, Switzerland, an affiliate of Merck KGaA, Darmstadt, Germany.

Supporting information

Data S1

Milenković‐Grišić A‐M, Terranova N, Mould DR, et al. Tumor growth inhibition modeling in patients with second line biliary tract cancer and first line non‐small cell lung cancer based on bintrafusp alfa trials. CPT Pharmacometrics Syst Pharmacol. 2024;13:143‐153. doi: 10.1002/psp4.13068