Comparison of two‐stage and joint TGI‐OS modeling using data from six atezolizumab clinical studies in patients with metastatic non‐small cell lung cancer

Abstract

Two‐stage and joint modeling approaches are the two main approaches to investigate the link between longitudinal tumor size data and overall survival (OS) and anticipate clinical trial outcome. We here used a large database composed of one phase II and five phase III clinical trials evaluating atezolizumab (an immunotherapy) in monotherapy or in combination with chemotherapies in 3699 patients with non‐small cell lung cancer to evaluate the differences between both approaches in terms of parameter estimates, magnitude of covariate effects, and ability to predict OS. Although the two‐stage approach may underestimate the magnitude of the impact of tumor growth rate (K _G) on OS compared to joint modeling approach (hazard ratios [HRs] of 0.42–2.52 vs. 0.25–2.85, respectively, for individual K _G varying from the 5th and 95th percentiles), this difference did not lead into poorer performance of the two‐stage approach to describe the OS distribution in the six clinical studies. Overall, two‐stage and joint modeling approaches accurately predicted OS HR with a median (range) difference with the observed OS HR of 0.02 (0.01–0.18) and 0.03 (0.00–0.19), in all cases considered, respectively (e.g., for IMpower150: 0.80 [0.66–0.95] vs. 0.82 [0.70–0.95], respectively, whereas the observed OS HR was 0.80). In our setting, the two‐stage approach accurately predicted the benefit of atezolizumab on OS. Further work is needed to verify if similar results are achieved using phase Ib or phase II clinical trials where the number of patients and measurements is limited as well as in other cancer indications.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

The association between tumor size data and overall survival (OS) may be estimated using either a two‐stage or a joint modeling approach. However, there is still a lack of understanding of the differences between those two approaches regarding clinical trial analysis and decision making.

• WHAT QUESTION DID THIS STUDY ADDRESS?

We compared the performances of the two approaches in terms of parameter estimates, magnitude of covariate effects, and ability to predict OS using a large database of six randomized atezolizumab clinical trials in non‐small cell lung cancer (NSCLC).

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

There are no major differences in terms of parameter estimates, covariate effects, and prediction of OS between two‐stage and joint modeling approaches. Both approaches showed that tumor growth rate was highly associated with OS leading to an accurate prediction of OS distributions and hazard ratio in all six studies.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

The two‐stage approach may be suitable and less computationally intensive to predict the outcome of clinical studies in NSCLC.

INTRODUCTION

Over the last decades, immunotherapies have revolutionized the field of oncology by increasing the probability of durable response and prolonged survival compared to chemotherapies in various cancer indications. ¹ , ² , ³ , ⁴ Mathematical models have been widely used to support oncologic drug development, notably by characterizing the association between tumor growth inhibition (TGI) and long‐term clinical outcomes, such as overall survival (OS), allowing one to anticipate the outcome of clinical trials by the analysis of tumor dynamic response. ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ However, there is still a lack of consensus regarding the appropriate statistical model to characterize the association between tumor dynamics and OS. The two‐stage approach is one of the most widely used, consisting of (i) characterizing the tumor dynamics using a nonlinear mixed‐effects model and (ii) injecting individual tumor dynamic metric to be used as a predictor of OS in a parametric survival model. However, this approach has been criticized, as it may be prone to bias because it ignores the survival bias (i.e., the fact that the observation of tumor dynamics is conditional to the patient's survival). ¹¹ In order to correct this potential bias, an alternative approach is to use joint modeling in which both TGI and OS data are simultaneously fitted in an integrated manner. ¹² , ¹³ , ¹⁴ However, this comes at a certain cost, with higher computational times due to the numerical complexity of maximizing the likelihood while fitting both processes simultaneously. Although joint modeling has been successfully used to elucidate the association between tumor size and OS and enabled individualized medicine by providing an accurate prediction of individual survival, ⁵ , ⁷ , ¹⁵ the two‐stage approach remains a more practical and actionable approach during drug development to analyze clinical trials and conclude on treatment efficacy. ⁸ , ⁹ , ¹⁶

For that purpose, we here used a large database of six clinical studies evaluating atezolizumab (an immunotherapy) in monotherapy or in combination with chemotherapies in 3699 patients with non‐small cell lung cancer (NSCLC) to evaluate the differences of both approaches in terms of parameter estimates, magnitude of covariate effects, and ability to predict OS.

MATERIALS AND METHODS

Data

The data used in the following comparison consisted of a pooled dataset of six clinical trials in patients treated for NSCLC and already analyzed in Chan et al. ⁶ Studies were conducted in agreement with the Declaration of Helsinki and approved by institutional review boards or independent ethics committees.

A total of 4220 patients were treated either with atezolizumab (in monotherapy or combination with chemotherapies) or chemotherapy. However, for this analysis, only patients with at least one tumor size measurement (including the baseline scan) and non‐missing baseline characteristics were included. Conversely, patients with missing baseline characteristics and regardless of their number of tumor size measurements were excluded from the analysis (n = 521). Study protocols and results have been previously described ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ , ²¹ , ²² and are summarized in Table 1.

TABLE 1.

Description and summary of clinical trial used in the analysis.

Trial name	Atezolizumab‐containing arm (A)	Control arm (C)	Number of treated patients (A/C)	Number of analyzed patients (A/C)	Number of tumor size measurements (A/C)
POPLAR (NCT01903993)	Atezolizumab	Docetaxel	142/135	134/127	779/494
OAK (NCT02008227)	Atezolizumab	Docetaxel	421/401	364/373	1997/1457
IMpower130 (NCT02367781)	Atezolizumab + carboplatin + nab‐paclitaxel	Carboplatin + nab‐paclitaxel	472/232	437/214	3107/1087
IMpower131 (NCT02367794)	Atezolizumab + carboplatin + nab‐paclitaxel	Carboplatin + nab‐paclitaxel	334/334	317/309	2295/1550
IMpower132 (NCT02657434)	Atezolizumab + cisplatin/carboplatin + pemetrexed	Cisplatin/carboplatin + pemetrexed	291/274	160/140	696/513
IMpower150 (NCT02366143)	Arm A: Atezolizumab + carboplatin + paclitaxel Arm B: Atezolizumab + carboplatin + paclitaxel + bevacizumab	Arm C: carboplatin + paclitaxel + bevacizumab	399(A) 393(B) 392(C)	384(A) 370(B) 370(C)	2601(A) 2900(B) 2208(C)
Overall			4220 (2452/1768)	3699 (2166/1533)	21,684 (14,375/7309)

Model building

TGI and OS submodels were developed separately, as suggested by Kerioui et al. ²³ Two‐stage and joint modeling approaches only differ in the way they account for the link function between TGI and OS processes. TGI, OS submodels, and implementation of the link function for both methods are described in the subsequent sections.

TGI model

The TGI model consisted of a biexponential model ²⁴ defined as:

$$\mathrm{TS}\left(t\right)=\left\{\begin{array}{c}{\mathrm{TS}}_0\times e^{K_{\mathrm{G}}\times t},\text{if}t<0\\ {\mathrm{TS}}_0\times \left(e^{-K_{\mathrm{S}}\times t}+e^{K_{\mathrm{G}}\times t}-1\right),\text{if}t\ge 0\end{array}\right.$$

where t is the time (days) with time 0 at the start of treatment; TS is the tumor size (mm), TS₀ is the tumor size at start of treatment (mm); K _G is the tumor growth rate constant (d ⁻¹); and K _S is the tumor shrinkage rate constant (d ⁻¹). Of note, baseline covariates were not investigated on TGI‐related parameters.

Overall survival model

The OS model consisted of a parametric proportional hazard model. Exponential, Weibull, Gaussian, lognormal, logistic, and loglogistic baseline hazard functions have been tested and the one providing the lowest Akaike Information Criteria (AIC) was selected. Baseline covariates were considered for inclusion in the model, including age, gender, body weight, race, C‐reactive protein level, neutrophil‐to‐lymphocyte ratio, number of metastatic sites, albumin level, lactate dehydrogenase level, PD‐L1 status, Eastern Cooperative Oncology Group (ECOG) score, treatment line, presence of liver metastasis, smoking history, and tumor histology. First, baseline covariates were tested univariately and those leading to a loss of more than two points in the AIC were included in a multivariate model. Then, baseline covariates were selected following a backward deletion based on the AIC. Of note, continuous covariates were log‐transformed and centered around the median for the sake of model stability.

Link function

Modeling approaches differ in the way they account for the time‐to‐event process. Although the two‐stage approach assumes a complete independence of the TGI dynamics and the time‐to‐event processes, the joint model assumes an independence conditionally on the random effects of the longitudinal process. Therefore, for the two‐stage approach, we used the Empirical Bayes Estimate of log(K _G) as individual predictor of OS because it has been shown to be a strong predictor of OS in atezolizumab trials for NSCLC. ⁶ , ²⁴ Eventually, covariates that were no longer significant after the inclusion of log(K _G) were removed from the model based on the Wald test (p < 0.001).

In our main setting, log(K _G) was also used as a predictor of OS using the joint modeling approach but also investigated time‐varying predictors, such as the current tumor size over time (TS(t)) and the current first derivative (slope) of tumor size over time (dTS(t)), as alternatives to log(K _G). The general formulation of the OS model considering p continuous covariates and q categorical covariates and including the link function reads as follows:

$$h_i\left(t\right)=h_0\left(t\right)\times \exp \left(\sum _{j=1}^p{\gamma }^j\left(z_i^j-\text{median}\left(z^j\right)\right)+\sum _{j=p+1}^{p+q}{\gamma }^j{z}_i^j\right)\times \exp \left(\beta \left({\mathrm{\lambda }}_i-{\lambda }_{\mathrm{pop}}\right)\right)$$

where h ₀(t) is the parametric baseline hazard function; exp(${\gamma }^j$) is the hazard ratio (HR) associated to one unit of the jth continuous covariate or the zth modality of the jth categorical covariate; and exp($\beta$) is the HR associated to the link function ${\lambda }_i$. Of note, when investigating log(K _G) as a link function it was normalized by the typical log(K _G), noted ${\lambda }_{\mathrm{pop}}$, found during the analysis of tumor size data alone.

Parameter estimation

We assumed lognormal distributions for interindividual variability of TGI parameters with mean 0 and standard deviation ω and a correlation between K _G and K _S ($\rho$ K _G‐K _S). The residual variability was assumed to be additive and normally distributed with mean 0 and standard deviation σ. Differences in tumor size dynamics across treatment arms were accounted for by estimating distinct fixed effects for K _G and K _S within each treatment arm. Model parameters were estimated using the Stochastic Approximation Expectation–Maximization algorithm implemented in Monolix software (version 2020R1, Lixoft ²⁵ ). Of note, the two‐stage OS model was initially developed in R software (version 4.0.2) using the “survival” package and then implemented within Monolix for sake of comparison with the joint modeling approach.

Model comparison

The results from both two‐stage and joint modeling approaches were compared with respect to population parameter estimates and associated relative standard errors (RSE%), magnitude of the covariate effects, survival simulations, and their ability to reproduce the observed OS distribution and OS HR within each study. The magnitude of a covariate effect was calculated in a univariate manner and are presented as a tornado plot. Supposing that all covariates, except the one of interest, remained fixed at their median value or reference category, the magnitude of continuous and categorical covariate effects was derived from $\exp \left({\gamma }^j\left(z_i^j-\text{median}\left(z^j\right)\right)\right)$ or $\exp \left({\gamma }^j{z}_i^j\right)$, respectively. For each continuous covariate, we calculated the associated effect at the 5th and 95th percentile of the covariate distribution. For model evaluation, we performed 500 Monte Carlo simulations using the model parameter estimates and associated uncertainties and the covariate information from the original dataset. The 5th and 95th percentiles of the predicted OS distribution curves were calculated and overlayed to the observed OS distribution. Finally, we derived from those simulations the OS HR (median and 95% prediction intervals) using a Cox model with arm as the only covariate, hence comparing atezolizumab‐containing versus control arm in each study in the pooled dataset.

RESULTS

Data

A summary of the clinical trials composing the pooled dataset is presented in Table 1. A spaghetti plot of absolute tumor size and percent change from baseline are presented in Figure 1. Patients had a median of five scans (range: 1–19 scans) and a median follow‐up duration of 168 days (range: −36 to 959 days). Among the 3699 patients, 286 (7.7%) had only one baseline scan. Summary statistics of baseline characteristics are presented in Table S1.

FIGURE 1.

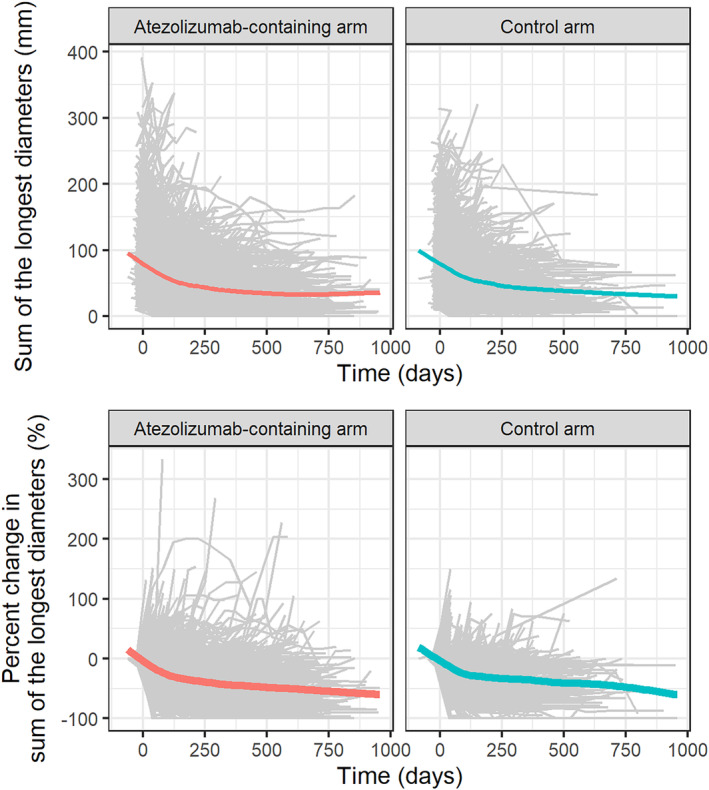
Tumor size profiles over time in atezolizumab‐containing arms and control arms. Absolute sum of the longest diameters (top) and percent change in sum of the longest diameters (bottom). Gray lines are the individual profiles of the sum of longest diameters. Colored lines are the local polynomial regression smooth curves across individual data.

TGI model

The TGI model was well able to capture the tumor dynamic profiles using either the two‐stage or joint modeling approach as shown in the goodness‐of‐fit plots presented in Figures S1 and S2.

Figure 2 presents the K _G estimates obtained with both approaches. K _G estimates tended to be lower with the two‐stage model compared to the joint model (e.g., in IMpower150 K _G Atezo + CP + B = 0.00088 day⁻¹ (95% confidence interval, CI_95% = [0.00079; 0.0010]) vs. K _G Atezo + CP + B = 0.0010 day⁻¹ (CI_95% = [0.0009; 0.0011]), respectively). Regardless of the modeling approach, the K _G was slower in the atezolizumab‐containing arms than in the corresponding control arm. The parameter estimates are presented in Table S2. All parameters were precisely estimated and had RSEs below 15%, irrespective of the modeling approach used.

FIGURE 2.

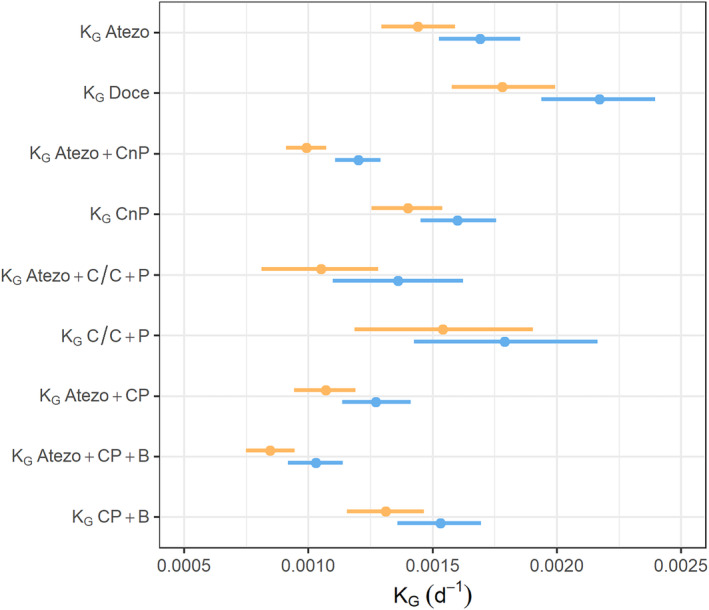
Comparison of K _G estimates of TGI submodel using two‐stage (orange) or joint (blue) modeling approaches. Points are the point estimates of K _G or K _S. Lines represent the 95% confidence intervals. Atezo, atezolizumab; B, bevacizumab; C/C, cisplatin or carboplatin; CnP, carboplatin + nab‐paclitaxel; CP, carboplatin + paclitaxel; Doce, docetaxel; K _G, tumor growth rate; K _S, tumor shrinkage; P, pemetrexed; TGI, tumor growth inhibition.

OS model

We found that a loglogistic baseline hazard function of the OS model with scale parameter (Te) and a shape parameter (s) and given by the following formula $h_0\left(t\right)=\frac{\frac{s}{\mathrm{Te}}\times {\left(\frac{t}{\mathrm{Te}}\right)}^{\left(s-1\right)}}{\left(1+{\left(\frac{t}{\mathrm{Te}}\right)}^s\right)}$ best described the data (Table S3).

In terms of baseline predictors of OS, patients receiving first‐line therapy with lower ECOG score, lower C‐reactive protein level, lower neutrophil‐to‐lymphocyte ratio, lower lactate dehydrogenase level, lower number of metastatic sites, no liver metastasis, positive PD‐L1 status, higher albumin level, or being Asian tended to have longer OS than other patients.

Both approaches provided precise parameter estimates and hinted that log(K _G), C‐reactive protein, and ECOG were the three most impactful predictors of OS. Overall, joint modeling tended to provide smaller effect sizes of baseline covariates and a larger one for log(K _G) (Table 2). However, models also differ by their scale parameter estimate (644 vs. 750 days, with the two‐stage and joint model, respectively) which makes direct comparison of effect sizes difficult. To override this issue, we calculated the HR associated with each covariate. The joint modeling approach provided a larger range of the effect of K _G compared to the two‐stage approach (HRs of [0.25–2.85] vs. [0.42–2.52] for individual K _G's varying from the 5th to the 95th percentiles, respectively, see Figure 3). Both modeling approaches were well able to reproduce the observed OS distribution as presented in Figure 4 which shows OS distributions of OAK (second + line therapy) and IMpower150 (first line of therapy; see Figure S3 for other studies).

TABLE 2.

Comparison of parameter estimates of OS submodel using two‐stage or joint modeling approaches.

Parameter	Unit or Group	Two‐stage model			Joint model
		Estimate	RSE%	Wald test statistic	Estimate	RSE%	Wald test statistic
Scale	day	640	3.1	–	750	3.2	–
Log(K G)	–	0.73	4.1	24	1.0	4.1	25
C‐reactive protein	mg/L	0.26	7.5	13	0.23	8.5	12
ECOG	1 vs. 0	0.52	9.2	11	0.41	9.9	10
Treatment line	2+ vs. 1	0.33	10	9.6	0.22	18	5.6
Neutrophil‐to‐Lymphocyte ratio	–	0.23	15	6.7	0.21	18	5.6
Liver metastasis	Yes vs. no	0.29	19	5.2	0.23	24	4.2
Asian	Yes vs. no	−0.35	20	4.9	−0.36	24	4.2
Number of metastatic sites	–	0.22	21	4.7	0.19	25	4.0
Albumin	g/L	−0.70	21	4.7	−0.63	27	3.7
Lactate dehydrogenase	U/L	0.18	22	4.5	0.17	25	4.1
PD‐L1 status	IC or TC >0 vs. IC and TC = 0	−0.14	25	4.0	−0.14	29	3.4
Shape	–	1.8	1.2	–	1.7	1.1	–

Note: The covariate model for OS for the two‐stage approach was initially developed in R and refitted within Monolix. Of note, all the included covariates in R where still significant when implemented in Monolix. Continuous covariates were log‐transformed and centered around the median. Covariates are ordered from the most to the less significant one using a Wald‐test in the two‐stage setting.

Abbreviations: ECOG, Eastern Cooperative Oncology Group performance status; K _G, tumor growth rate constant; OS, overall survival; RSE, relative standard error.

FIGURE 3.

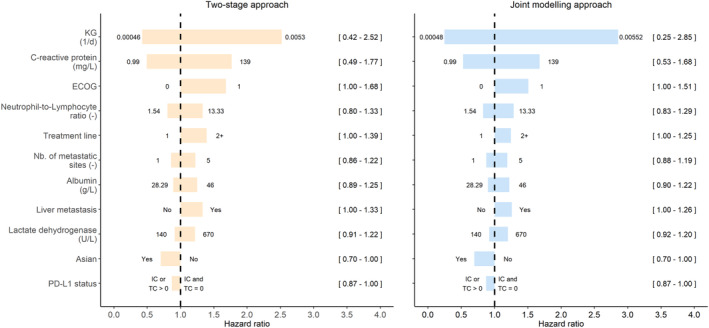
Tornado plot of covariate effects included in the OS model using the two‐stage (left) or joint modeling (right) approaches. For continuous covariates effects are centered around medians. Numbers between brackets are the hazard ratio associated with the modalities of categorical covariates or to the 5th and 95th percentiles of the continuous covariate distributions. Modalities of categorical covariates and percentiles of continuous covariates are at the edges of horizontal bars. ECOG, Eastern Cooperative Oncology Group; K _G, tumor growth rate; OS, overall survival.

FIGURE 4.

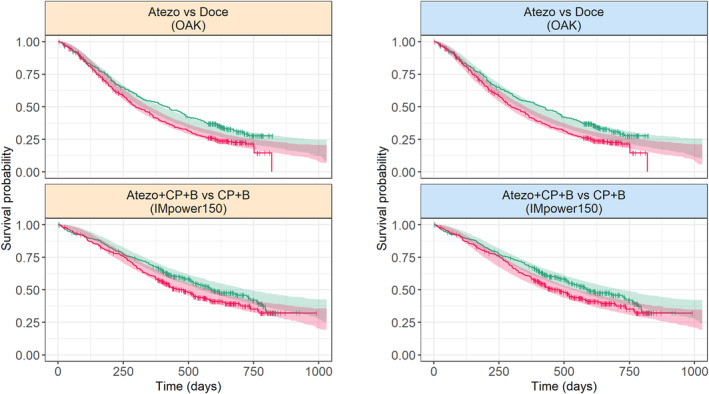
Simulated OS distribution obtained with the two‐stage (left) or joint modeling (right) approaches. Lines: observed Kaplan–Meier distributions; Shaded areas are 95% prediction intervals; Atezo, atezolizumab; B, bevacizumab; CP, carboplatin + paclitaxel; Doce, docetaxel; OS, overall survival.

Predicted and observed OS HR are summarized in Figure 5. Predicted HRs with the two approaches are close with a maximum absolute difference of 0.03. For studies investigating atezolizumab as first line therapy (i.e., IMpower130, IMpower131, IMpower132, and IMpower150) both methods accurately predicted OS HR and associated 95% prediction interval and well captured the observed OS HR. However, in studies investigating atezolizumab as second or third line therapy (i.e., POPLAR and OAK) both approaches predicted higher (i.e., less favorable) OS HR than observed that tended to be slightly outside the prediction interval for the two‐stage approach, but inside the prediction interval for the joint modeling due to larger prediction intervals.

FIGURE 5.

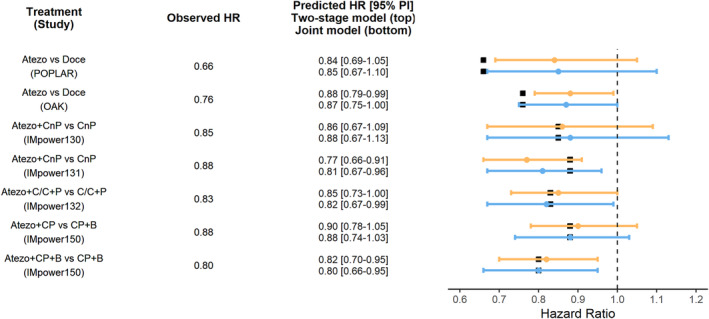
Comparison of predicted OS HRs using two‐stage (orange) or joint modeling (blue) approaches. Black squares represent the observed HR. Dots and error represent the predicted HR and 95% prediction interval, respectively. Atezo, atezolizumab; B, bevacizumab; C/C, cisplatin or carboplatin; CnP, carboplatin + nab‐paclitaxel; CP, carboplatin + paclitaxel; Doce, docetaxel; HR, hazard ratio; OS, overall survival; P, pemetrexed; PI, prediction interval.

DISCUSSION

This work aimed to identify putative differences between two‐stage and joint modeling of longitudinal (TGI) and time‐to‐event data (OS) in terms of parameter estimates, covariate effect sizes, and survival predictions. Both approaches were used to characterize the association between tumor size data and OS in a large historical database of 3699 patients with NSCLC treated with chemotherapy or atezolizumab ± chemotherapy.

A bi‐exponential model with distinct shrinkage and growth rates by treatment arm was well able to characterize the tumor size dynamics using both two‐stage and joint modeling. On the comparison of parameter precision, both approaches provided low and comparable RSE% and η‐shrinkage on TGI parameters. This finding may be attributed to the fact that the estimation relied on a large database of 21,684 tumor size measurements enabling a robust and precise estimation of the tumor dynamics. Atezolizumab‐containing arms had lower K _G (i.e., slower growth rate), than associated control arms using both approaches, consistent with the observation that the atezolizumab has shown significant improvements in OS over control in all of the trials. ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ , ²¹ , ²² Of note, baseline covariates were not investigated on the TGI model because the main objective of the analysis was to simulate OS conditionally on estimated individual K _G (and tumor dynamics) and baseline covariates.

The OS model showed that several baseline covariates were associated with OS including ECOG, C‐reactive protein, neutrophil‐to‐lymphocyte ratio, LDH, metastatic sites, liver metastasis, positive PD‐L1 status, albumin, and being Asian. Although the stepwise covariate modeling approach used is prone to selection bias, ²⁶ , ²⁷ all the above‐mentioned covariates make sense biologically and are in agreement with the results found in Chan et al. ⁶ However, our model differs by the baseline hazard function selected. Although we selected a loglogistic baseline hazard function, Chan et al. selected a lognormal function. This discrepancy may be attributable to the fact that all treated patients were included in this analysis whereas patients without post‐baseline tumor size measurement have previously been excluded. Such patients may have died or left the study early which may cause differences in the OS distribution and therefore in the baseline hazard function that best fits the data. Among the prognostic factors in the final OS model, K _G was the covariate that was the most associated with OS, showing that slower K _G is associated with extended survival. This is in line with a retrospective study conducted by the US Food and Drug Administration where they found that K _G was inversely associated with OS using 24 clinical trials investigating checkpoint inhibitors or target therapies in NSCLC. ²⁸ In addition, K _G was found to be the only metric to be successfully associated with survival in the POPLAR and OAK studies evaluating atezolizumab versus chemotherapy, whereas standard clinical end points, such as the objective response rate and the progression‐free survival were similar between the atezolizumab and control groups. ²⁴ The magnitude of HR associated with changes in individual log(K _G) estimates was larger using the joint modeling approach as compared with the two‐stage approach. This result is consistent with what has been found in linear mixed effect models ¹³ , ²⁹ or in a simulation study ¹² where the parameter of association between tumor size and OS was underestimated using a two‐stage approach. This may be attributed to the fact that the two‐stage approach ignores the informative dropout and may lead to biased parameter estimates. ³⁰ Although the two‐stage approach led to a lower magnitude of HR associated with log(K _G), it well captured the observed OS distribution and predicted the OS HR of atezolizumab versus control within each study, except the POPLAR and OAK studies (investigating atezolizumab as second‐ or third‐line treatment) contrary to Chan et al. where observed OS HR was adequately captured. ⁶ In this article and contrary to Chan et al., patients with only one baseline scan were included in the analysis. As those patients are likely to die early or leave the study, predicted OS distributions may be less favorable to atezolizumab. The multistate model that allows for simultaneous estimation of transition hazards of intermediate events (RECIST response status) along with tumor model‐derived metrics offers an alternative approach to predicting OS distributions ³¹ and particularly OS HR when it is confounded by the introduction of subsequent (e.g., second‐line) treatments after disease progression. ³²

Recently, Chen et al. presented a comparison of joint and two‐stage approaches using data from a phase I/II investigating durvalumab in patients with metastatic urothelial cancer. ³³ They concluded the joint modeling more accurately predicted OS than the two‐stage approach based on the associated concordance index and Brier score. In contrast with Chen et al., we here relied on a large database of over 3600 patients with both experimental and control arms and found that the results of the two models were largely similar. This suggests that joint models could be more appropriate in early phases when the information available in each individual is limited and requires to control for both the uncertainty of tumor dynamics and the survival bias. An advantage of the joint model is the capability to investigate for additional metrics, such as the time‐continuous tumor size, TS(t). Although none of these metrics provided a better fit to the data than log(K _G) (see Table S4), these metrics could nonetheless be useful to understand in greater detail other effects of treatment, in particular on the between‐lesion variability. ⁵ , ¹⁵

To conclude, our study supports that the modeling approach used both two‐stage and joint models provide to link tumor size data and OS may not play an essential role in largely similar results and accurately predicting the outcome of clinical trials in NSCLC. In addition, the two‐stage approach is the easiest to implement and a computationally much faster viable alternative. Further work is needed to evaluate the appropriateness of the two‐stage approach to support early decisions with short‐term follow‐up and anticipate the probability of success of a phase III clinical trial and to extend this work to other cancer indications.

AUTHOR CONTRIBUTIONS

A.G., M.M., and R.B. wrote the manuscript. A.G., M.M., P.C., J.Y.J., J.G., and R.B. designed the research. A.G. and M.M. performed the research and analyzed the data.

FUNDING INFORMATION

This project was funded by Roche and Genentech.

CONFLICT OF INTEREST STATEMENT

A.G. and M.M. are Certara employees and were under contract with Genentech/Roche for this project. P.C., J.Y.J., and R.B., are Genentech/Roche employees and hold Roche stock or stock options. J.G. was a consultant for Genentech‐Roche for this work.

Supporting information

Data S1

Gonçalves A, Marchand M, Chan P, Jin JY, Guedj J, Bruno R. Comparison of two‐stage and joint TGI‐OS modeling using data from six atezolizumab clinical studies in patients with metastatic non‐small cell lung cancer. CPT Pharmacometrics Syst Pharmacol. 2024;13:68‐78. doi: 10.1002/psp4.13057