Abstract
Persistent neural activity associated with working memory (WM) lasts for a limited time duration. Current theories suggest that its termination is actively obtained via inhibitory currents, and there is currently no theory regarding the possibility of a passive memory-loss mechanism that terminates memory persistent activity. Here, we develop an analytical-framework, based on synaptic strength, and show via simulations and fitting to wet-lab experiments, that passive memory-loss might be a result of an ionic-current long-term plateau, i.e., very slow reduction of memory followed by abrupt loss. We describe analytically the plateau, when the memory state is just below criticality. These results, including the plateau, are supported by experiments performed on rats. Moreover, we show that even just above criticality, forgetfulness can occur due to neuronal noise with ionic-current fluctuations, yielding a plateau, representing memory with very slow decay, and eventually a fast memory decay. Our results could have implications for developing new medications, targeted against memory impairments, through modifying neuronal noise.
1. Introduction
In many daily activities, such as maintaining telephone number digits, a small amount of information can be held and used even after the stimulus vanishes [1]. According to many physiological studies, the neural basis of this working memory (WM) ability, relates to persistent firing of the neurons [1], [2]. The phenomenon, termed persistent activity, was recorded in animal models showing neurons with sustained elevated firing rates, after the stimulus disappeared [3], [4], [5], [6]. The mechanism of persistent activity is often associated with the intrinsic properties of the neurons themselves where ionic currents keep the spiking [7], [8], or with connectivity within the neural circuit as a self-sustained network state [2], [9]. However, it is not fully known, in particular for the self-sustained network state model, what finally terminates the persistent activity. While currently it is suggested that active addition of external inhibitory currents terminates the persistent activity [9], we suggest here a new mechanism where WM persistent activity is spontaneously terminated due to internal passive mechanisms of either passive stochastic or passive deterministic environments. Based on a self-sustained network state model, the Hopfield model [10], [11], that describes the effect of synaptic strength on ionic-current, we provide an analytical description for spontaneous passive memory loss.
The self-sustained network state mechanism simulates WM persistent activity by analyzing the averaged firing rate, specifically analyzing the averaged firing rate vs. synaptic strengths [2], [12], [13]. Using those models, the persistent activity (WM) of a consistent firing rate could be achieved. However, describing the firing rate vs. synaptic strengths in a model is complex and cannot be studied analytically. In those models the average firing rate is obtained as the inverse of the average first passage time, and the equations are solved using numerical integration, hence analytical expressions cannot be formulated. In the present work, we base our analysis on an alternative representation of the WM model, that is on the ionic current vs. synaptic strengths (instead of the firing rate). Based on a simple current model, the Hopfield network model, we could perform a detailed mathematical analysis, which leads us to novel understandings of the persistent activity termination conditions.
The existing electrophysiological studies, using Hopfield network model, suggest that the mechanism to terminate WM is based on inhibition currents [9], [14]. In these studies the persistent activity is analyzed using a phase diagram of the current vs. the afferent stimulating current. Using this modeling, the persistent activity appears as a current plateau, i.e. having approximately constant high values for a long time before it decays. However, in order to terminate the plateau, that represent the loss of memory, an inhibitory current must be added to the model. Here we suggest natural mechanisms that terminate the persistent activity without using inhibitory currents. In contrast to earlier studies, we propose here to analyze the behavior of the current vs. synaptic strengths (instead of current vs. the afferent stimulating current). In this case our alternative approach leads us to develop a theory suggesting a new mechanism in which the WM persistent activity terminates passively, and hence elucidates the yet unknown aspects of forgetfulness. Our results suggest that persistent activity shows a plateau behavior that ends spontaneously, without the need of active inhibition currents. Specifically, we suggest two spontaneous mechanisms for forgetfulness based either on: (i) deterministic dynamics properties when converging slowly from an unstable to a stable state. This we find to emerge in the Hopfield network model, causing the current to very slowly decrease (almost constant) in a plateau fashion, which finally decays to zero abruptly or (ii) natural neuronal noise that we introduce into the Hopfield network modeling, which we find to enable forgetfulness abruptly after a period of persistent activity.
Our WM analysis, is supported by results of electrophysiological experiments in young and old rats, measured by excitatory postsynaptic potentials (EPSP) [15], provoking long-term potentiation (LTP). LTP is a phenomenon that describes long lasting increase of the EPSP after stimulation. Many aspects of LTP are still unknown, and the common belief is that LTP is the physiological basis of memory that accompanies plasticity in synaptic connections [15] - which are represented by the synaptic strength ω in our modeling. There are many indications that LTP cannot act according to the same mechanism as long term memory (LTM) that lasts years, mainly as LTP never lasts more than couple of weeks (usually few days) [15]. Thus, LTP is an excellent candidate having much in common with persistent activity, due to its persistent electrophysiological activity characteristics [16]. Moreover, we show resemblance between the dynamics of LTP and the persistent activity of Hopfield network model in Fig. 2 d and Fig. 3 d. While it is yet unknown how to describe the relation between the time duration of LTP experiments and average synaptic strength ω, our framework here suggests such analytical relationship and demonstrates it for aged and young rats as observed in the EPSP experiments. Specifically, our calculation of ω suggests that LTP protocol, in both young and aged rats, produces weak synaptic strength.
Figure 2.
Deterministic plateau. (a) Deterministic scenario describing current just below the criticality. Due to the closeness to the fixed point, the current decreases towards zero very slowly, such that a pseudo memory emerges. (b) Below criticality, ω < ωc, the average current decays to zero, however close to criticality there is a long slow decay like a plateau, which is similar to a steady state. This quasi-steady state plateau increases its time length, plateau duration, when simulated for smaller values of Δω/ωc. (c) The duration of the plateau, T, scales as Δω−1/2 such as predicted by Eq. (10). Note that the decay of T with an exponent −1/2 is analogous to critical interdependent networks [22], [23]. Here we show averaged values of simulations over 10 realizations assuming Gaussian distribution for the synaptic weights. Simulations in panels (b) and (c) were performed with τ = 1, C = 2 and N = 100 neurons, (i.e., without Mean-Field (MF) approximation). (d) Experimental data of anesthetized aged rats [15] (blue dots), shows a very good agreement with our theoretical simulation results (red line) for our suggested state variable Δω/ωc = 0.04 (i.e., ω = 0.96ωc). All stimulations use constant values of: I0 = 14, C = 2 and τ = 1 [min] (as assumed in sleep brain models [26]). The simulation results are shown for normalized I/C and thus have no units. This is since different scales of C, and hence of I, have no affect on the temporal dynamics but only their ratio. The EPSP units, in panel (d) and in the next Fig. 3 d, are shown in percentage [15], which indicate increase in EPSP slope relative to pre-stimulation baseline.
Figure 3.
Persistent activity temporal decay. (a) The current converges to a positive steady state because the average synaptic weight ω is above criticality ω > ωc and the system is in the active region. However, we identify two different typical time constants, long and short, for the decay of the memory. Far from the steady state there is a universal short time decay τ while close to the final state (gray area) there is a larger time decay τLT. (b) The decay of the average current I with time is exponential with fast (at the beginning) and slow (towards the end) exponential decay. The fast and slow exponents represent characteristic time constants τ and τLT, respectively, and fit well to their theoretical values in Eq. (12) and Eq. (13), which are marked in dashed lines. (c) Here we provide support for the analytical approximation, Eq. (14), for small Δω, showing a power-law with exponent −1/2. Simulations in panels (b) and (c) were obtained for a network of size N = 100 neurons (i.e., without using Mean-Field (MF) approximation), threshold of C = 2, τ = 0.25 and initial condition (by stimulating current IAff) of I0 = 150. (d) Empirical memory data as collected from anesthetized young rats model [15] (blue) compared to our model (red) with C = 2, τ = 3, I0 = 16 and Δω/ωc = 0.006 (i.e., ω = 1.006 ⋅ ωc) yielding τLT ≈ 27 min. Note that the value of ω/ωc = 1.006 is normalized, and therefore is not affected by units or scaling parameters which affect both τ and τLT (see Eq. (14)). Hence, while other parameters sets might yield same current temporal configuration, the value of ω/ωc is resilience and fixed per configuration.
2. Theoretical background
A common model of WM persistent activity is based on sustained excitation activity of highly connected neuronal cells. This concept was introduced in the Hopfield model [10], [11], which describes the variables as the neuronal membrane potential [11] or current [9], [14]. The WM persistent activity model was formalized as [9], [14],
| (1) |
where represents the current in neuron i and τ is the time constant. Here, is the Heaviside step function, determining an excitation threshold C, where only above C the current of neuron j impacts neuron i. is the external current excitation, which is obtained by an external stimulation (e.g., sensory stimulation). In Eq. (1), represents the interaction strength (synaptic strength) between neurons i and j, constructed as a complete graph (each neuron is connected to all neurons).
We hypothesize here that the weights vary with a value that is imprinted by the neurons' individual characteristics. Moreover, we assume that depends also upon the strength of the external stimulation, specifically, high external input yields high neuronal connections . Therefore, our analysis here will be, in contrast to earlier approaches, based on a memory phase diagram in the ω-space as shown in Fig. 1, where ω is the average over all weights .
Figure 1.

Memory phase diagram. The phase diagram in ω-space obtained from Eq. (5). The blue and the red continuous lines represent the steady states solutions, while the dashed green line represents an unstable solution separating between the two basins of attraction. Note that according to Eq. (4), the value of ω(N − 1) is actually the mean synaptic weight. See also the fixed points and stability analysis in Fig. S3 (Supplementary).
Next, we analyze Eq. (1) using a Mean-Field (MF) approximation [17] by replacing the varying interaction term by an averaged quantity, and by that we obtain a single equation for the average current (see Supplementary Section S.2). Specifically, in order to execute complex tasks such as memory, the brain neurons become highly connected [18], [19], [20], with networking properties close to a complete graph, which makes the MF solution more accurate. The obtained single MF equation is
| (2) |
where
| (3) |
and with defining ω as
| (4) |
Thus, I is the average current across the neurons (Eq. (3)), and ω is the average interaction weight between neurons (Eq. (4)).
Concerning memory, it is of importance to study the sustained current when , using,
| (5) |
We next track the fixed points of Eq. (5) by setting , which yields three solutions for the average current I as a function of the average weight ω: two stable solutions and one unstable solution. The ω-space splits into two areas. Indeed, Fig. 1 (see also Fig. S3 in Supplementary) shows exactly this: small values of ω yield a single dormant state (red), whereas large ω yields three fixed points (including two steady states, active (blue) and dormant (red)). We assume that the active state enables the existence of a persistent activity (i.e., WM) for large enough ω, while for small ω the memory cannot stay for long (no-activity).
Next we find the critical (tipping) point () of the transition from no-activity to persistent activity, while noticing that this point is a junction of a stable fixed point (continuous blue line in Fig. 1) and an unstable one (dashed green line). This requirement yields (see Supplementary Section S.4),
| (6) |
We conclude, from Eqs. (2) - (6), that is the condition for the creation of persistent activity, otherwise the memory is not preserved and the current decays to zero, hence the range of is a non-activity region.
In the following analyses we explore the impact of the interaction (synaptic) weights on the fundamental temporal memory characters through theoretical and simulation results as well as experimental wet-lab studies. The experimental wet-lab relates our theory to hippocampal of anesthetized young and aged rats model [15]. Note that using hippocampal model is a widely accepted paradigm of simple brainlike structures [21].
3. Results
Next we specify and show results that support our hypothesis about the possible mechanisms of passive persistent activity forgetfulness. Our suggestion, based on solutions of Eq. (5) (Fig. 1), for two mechanisms are: (i) A current flow that shows a natural long-term plateau with very slow decay under certain conditions. The memory is represented as an almost constant current for a limited time followed by a natural fast decay to zero, (ii) Neuronal noise fluctuations of the ionic-currents that lead to its fast decay, with persistent activity duration that is described by a ‘first passage time’ analysis.
3.1. Passive deterministic forgetfulness: deterministic plateau
Here we describe the passive mechanism for loss of persistent activity based on deterministic dynamic analysis, that we find to emerge in the transition from unstable to stable state in the Hopfield model, Eq. (2). Before explicitly presenting our theory regarding memory persistent activity forgetfulness, note that an intuitive explanation and demonstration is provided in Supplementary section Fig. S1.
We describe the passive mechanism for forgetfulness, based on a plateau formation shape of the current, which takes place near criticality just below the critical point. Specifically, we simulate the current in the region (gray area in Fig. 2 a) of a weak synaptic strength, which includes only the dormant steady state. However, due to its closeness to the persistent-activity area, the forgetting process is slow, and might include a long plateau which acts as a quasi-steady state, for some period. This means that, in the ω-space, this plateau scenario is for , i.e., , therefore I converges to zero, but since ω is near criticality (Δω is small) the current decays very slowly in a plateau shape, see Fig. 2 a - b (see also the analogous plateau phenomena in percolation of interdependent networks [22], [23]). The duration of this slow decaying plateau depends on the proximity of ω to , i.e., on Δω, as depicted next (based on [24]). In order to analytically estimate the time duration of the plateau, T, we focus on the region around the plateau formation, that is: and current close to , i.e., the time duration where is small. In general, for two such currents, close to , with 2ϵ currents difference between them, their time interval, T, can be described as:
| (7) |
To calculate the argument of the integral, we analyze the behavior of Eq. (5) in the limit of and (see Eq. (6)). We further use Eq. S.26 (Supplementary) for small Δω, keeping also the second order term of δI,
| (8) |
Placing Eq. (8) into Eq. (7), yields,
| (9) |
where and . Note that in Eq. (9) we replaced the integration limits to ±∞, since the integral is governed by small values of x and large values do not change the leading term.
Since is small, we finally get the plateau duration,
| (10) |
We note that, according to our analysis, the deterministic plateau duration also depends on τ. Hence environmental physiological conditions, such as sleep/anesthesia that affect τ, will accordingly change the time scale of T. Moreover, note that Eq. (10) depends on the same parameters (though with different scalings) as Eq. S.28 (Supplementary), which refers to the typical time decay of the current at conditions where there is no plateau formations.
Fig. 2 c illustrates the good fit between the theory, Eq. (10) (red line), and the simulation results (blue dots). As expected, this fit is better at low values of Δω, i.e., when ω is closer to criticality.
Furthermore, a closer look on recent empirical studies, Fig. 2 d, performed with EPSP measuring memory of rats models [15], [25], shows memory with a quasi-steady state long plateau similar to our theory and simulation results. Fig. 2 d compares between memory of aged rats [15] (blue dots) and simulating the current with ω close to criticality (). The excellent agreement between the plateau simulations and the EPSP measurements supports our theory and further suggests that the average synaptic strength with respect to the critical synaptic strength is for this case, . We note that similar plateau behavior has been also observed for EPSP measurements of memory in pilocarpine-treated rats [25].
3.2. Passive stochastic forgetfulness: stochastic plateau
In the previous Section we obtained a plateau from a state just below criticality. In the present Section we show that a plateau can be formed also at a state just above criticality. We will demonstrate, next, that for this scenario to take place, stochastic conditions must be present, as indeed occurs physiologically due to neuronal noise. For that matter, we first analyze persistent activity without considering forgetfulness and analyze EPSP of young rats. Specifically, we will show that by adding neuronal noise a plateau is formed even at certain conditions above criticality.
3.2.1. Persistent activity analysis
In this Section we study the regime in ω-space (Fig. 1) of , where persistent activity is maintained, and analyze the memory dynamic when converging to a steady state. We study here persistent activity, since we wish to better understand the effect of ω in young rats EPSP data, which is concluded at the end of the present section. Specifically, we show that the current converges to its stable state exponentially with a typical time constant (representing the memory length) that depends on the average weight ω.
For a steady state memory solution, the derivative of the current vanishes in Eq. (5) and thus obtaining:
| (11) |
where is the persistent current that yields the memory persistent activity (steady-state solution). Without intervention, such as the active inhibitor currents, this could have yielded a long term (LT) memory (LTM) solution. Here we study this region of persistent activity, whereas in the next Section we study how it could be still terminated to forgetfulness.
Next we are interested in describing the dynamics of LTM using Eq. (5) in two different limits: (i) and (ii) when I approaches (when ).
(i) In the first limit (), the behavior is trivial: since I is very large it can be assumed that , so that Eq. (5) can be written approximately as , and therefore an exponential decay with a typical time τ is obtained,
| (12) |
(ii) In the second limit, close to (when ), we expand Eq. (5) as where δI is small (see details in Supplementary Section S.5), and obtain,
This implies an exponential decay with a typical time decay,
| (13) |
Note that this exponential decay is valid under the condition as aforementioned, namely within a region above the steady memory, see Fig. 3 a. The range of this validity region is getting narrower close to criticality.
Fig. 3 b shows results from simulating Eq. (1) with for the LTM case, that is for and , showing the average current, I, temporal decay. Each colored line is for a different value of . Particularly, for all values of two exponential decays can be observed. The first exponent, at short time scales, t, (in the beginning of the simulations), is τ, which appears for all values, in accordance to Eq. (12) (Fig. 3 b dashed orange line). The second exponent, shows up at long time scales (towards the end of the simulation time and close to the steady state), representing a more moderate decay with an exponential value that fits well to the in Eq. (13) (Fig. 3 b, four dashed lines). Note that the first exponent, τ, is smaller than the second exponent, , which also fits well Eq. (13) implying that indeed, .
Next, we evaluate when ω is close to the critical value from above. To track the behavior in proximity of (for small Δω), we expand Eq. (11) using and (see Supplementary). Recalling that , and (Eq. (6)) we get
Substituting this into Eq. (13), we finally obtain,
| (14) |
This relation, Eq. (14), is in excellent agreement with our simulation results as illustrated in Fig. 3 c. Fig. 3 c summarizes the values of the time decay exponent, , as obtained from the simulations of the current I close to its steady state (the gray area in Fig. 3 a and the straight lines close to steady-state in Fig. 3 b). It is clearly seen that the relation between and is a power law with an exponent , supporting Eq. (14). Note, as expected, that for small values of , i.e. when ω is close to , the simulation results in Fig. 3 c, are more accurately described by a slope.
After investigating the model theoretically and verifying it by simulations, we explore the theoretical parameter ω and its relation to actual electrophysiological experiments of measuring memory data of EPSP. We used empirical EPSP data of long-term potentiation (LTP) [15], which is a phenomenon observed in brain areas involved in memory storage such as the hippocampus, and it describes long lasting increase of the EPSP after stimulation. The common belief is that LTP is the physiological basis of memory which accompanies plasticity in synaptic connections [15]. Fig. 3 d shows the LTP dynamics as experimentally measures in young rats [15] (blue dots) compared to our theoretical model of current dynamics as simulated for (red line). The excellent agreement between the data and the model suggests indeed that the average weight ω relation to the critical weight is . Thus, in this data of anesthetized young rats, the average synaptic weight is fairly close to the critical LTM weight, and just above it. However, in this LTP memory data, after one week [15] the memory eventually decays to zero, much faster than the common LTM. In the next Section we explain how this system could move from just above critical point to forgetfulness.
3.2.2. Passive stochastic forgetfulness: stochastic plateau - effect of neuronal noise
To consider neuronal noise inflations, we extend the model in Eq. (2) so that it includes neuronal noise of normal distribution with std σ and zero mean, using the stochastic differential equation:
| (15) |
where is a white noise. We assume that the stimulating current , which initiates the memory, has terminated so that now the neurons are influenced by the neuronal noise that fluctuates around zero. Note that here we analyze the average current, which is averaged over all neurons, same as in the definition, Eq. (2).
Next, we ask: when will the average current I, which here evolves randomly, cross down a critical value (the threshold, C, in the average case), and consequently the system will collapse to the dormant state regime, i.e., fully forgetfulness state. In fact, this phenomenon actually describes the problem known as the ‘first passage time’ of a stochastic process [27]. Specifically, we wish to examine the time when the mean current I crosses down for the first time the threshold C, and consequently decays to the forgetfulness state. In order for this memory-loss scenario to occur, ω must have a value slightly above the critical , so that the noise could push it towards the dormant state regime. This occurrence starts as persistent activity state, and terminated passively in the presence of neuronal noise.
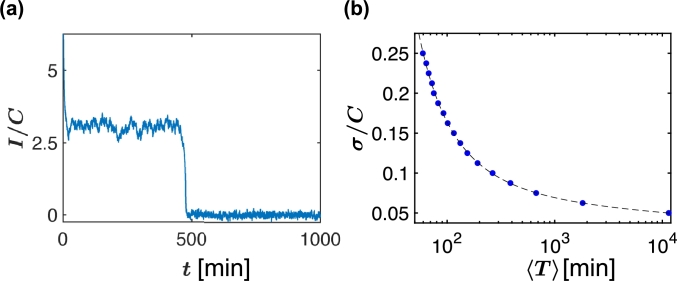
In Fig. 4 a we simulate Eq. (15), i.e., the stochastic plateau for values, and , that is ω is slightly above . Starting at persistent activity state close to the critical , due to the neuronal noise fluctuations, the current I rapidly drops to zero at around [min], hence the memory state is terminated passively. The results of 1000 realizations of simulating Eq. (15), all with but with different values of noise levels σ, are shown in Fig. 4 b. The average forgetfulness time , of all realizations, shows an inverse relation to σ, seen by the dashed line.
Figure 4.
Stochastic plateau: Simulations of neuronal noise (white noise). (a) In the persistent activity phase near criticality, there is a chance that afferent input noise will lead to crossing the criticality towards the forgetting region. The average current evolves in time according to Eq. (15). Simulating the case Δω/ωc = 0.006 and σ = 0.17, yields a first passage time T, where the current I sharply decays below the threshold C, at around T ≈ 400 [min]. (b) We repeat the simulation of panel (a) for different values of noise level σ. For each σ value, simulation has been repeated over 1,000 realizations in order to obtain a mean value of 〈T〉. The average time until forgetting 〈T〉 is marked in blue circles. As σ decreases, the mean time duration 〈T〉 increases inversely with 〈T〉, see the dashed line. From this graph, given 〈T〉 the noise level σ can be calculated (the threshold C value is generally known). All simulations have been performed with τ = 1 [min] (in accordance with sleep brain models [26]), C = 80pA[28] and N = 100. The units of 〈T〉 are in [min], same as the units of τ.
Our LTP data analysis in Fig. 3 d of young rats shows ω slightly above criticality (also ), where the memory has been reported to vanish eventually after a week [15], much shorter than expected from LTM (lasting many years). Hence this case fits well to our definition. According to our findings of the ω values, we suggest that while aged rats could show deterministic plateau (slightly below the critical , with , Fig. 2 d), young rats might show stochastic plateau (ω slightly above , with Fig. 3 d).
Theoretically, we can use the simulation results in Fig. 4 b to evaluate the neuronal noise σ. Assuming the termination of the LTP memory data after one week [15], i.e., , it yields according to Fig. 4 b a value of . Thus, since for rats' current excitability threshold is [28], the average neuronal noise is . This value of σ is in agreement with the estimated value of current noise of a single neuron, as was suggested when investigating cultured neurons from rat hippocampus held near activation potential [29].
In conclusion, we presented in the last two Sections, two possible scenarios for memory plateau formations and loss: (i) deterministic plateau: just below criticality (Fig. 2), the plateau emerges and drops fast when the current reaches from unstable state to the steady-state of (no-activity) in the Hopfield network model, or (ii) stochastic plateau: close and above criticality with noisy current fluctuations that at a certain time drops below criticality (Fig. 4 a), and terminates fast due to natural neuronal noise. Both options terminate persistent activity passively and yield similar current trajectories, however, originate from two different mechanisms.
4. Discussion
In the present work we describe analytically the fundamental dynamics of memory persistent activity, by exploring the phase diagram under changes in the strength of the neuronal network synaptic connections and its effects on memory decay with time. Generally, our theory explains and shows, from self-sustained network state model perspective, that forgetfulness can be achieved in two ways, either passively via deterministic considerations that yield a plateau in the current as a result of being close but below criticality, or via stochastic noise perturbations that yield a plateau even at state just above criticality. Our analytical results suggest a new fundamental understanding of the memory termination. It ends spontaneously in contrast to the contemporary belief, which suggests that forgetfulness has an active mechanism (derives from inhibitor currents).
We note that at ω values far from criticality the active inhibitor currents might be relevant, but suggest here that at values near (above or below) criticality the memory-loss can be passive and spontaneously. Based on empirical LTP rats data, we also show that physiologically ω can indeed takes values near criticality. Our results suggest that ω of young rats is just above criticality (). Thus, it is quite interesting to find that, for the same experimental protocol, aged rats show values just below criticality (), i.e., smaller than young rats. The relationship between LTP to memory was not fully understood, while memories last decades, LTP has been observed only for days (up to couple of weeks). Thus, excellent fit between LPT data and our simulations in Fig. 2 d, Fig. 3 d and Fig. 4, supports our hypothesis that LTP could represent just a persistent activity which does not involve all of the LTM mechanisms changes. We suggest that LTP does not evolve to long lasting memory since it produces too weak synaptic strength, with values only just above or just below criticality () for young and aged anesthetized rats respectively, which are probably not strong enough to produce substantial long lasting remodifications.
Note that the LTP is an artificial memory, which has some differences when compared to the naturally obtained (e.g., via visual stimulation) memory. Nevertheless, LTP is an excellent tool to study memory, in particularly using analytical models such as the Hopfield network model. Interestingly, our analysis and simulations results show that both our passive deterministic and passive stochastic plateau temporal values, as well as the typical time decaying exponents (see Eq. S.23 and Eq. S.28 (Supplementary)) depends on and τ. This might explain the empirical findings of correlations [30], [31] between all memory types.
Equation (10) and Fig. 4 describe analytically and via simulations the typical time duration of the deterministic plateau and the stochastic plateau cases respectively. While for the deterministic plateau case we offer deterministic stability approach, for the stochastic plateau case we offer a stochastic ‘first passage time’ mechanism. From Fig. 4 we conclude that as the noise level σ increases, the memory terminates earlier and there is a higher probability to return to the stable dormant state (no-memory state). However, the opposite scenario, i.e., obtaining memory from the no memory state due to synaptic weight noise, is not possible according to our simulations. Adding synaptic noise to the model during the stable dormant state could not change the state, i.e., can not produce memory, even in proximity to the critical value. This points to a possible protection mechanism that prevents maintaining false memories, due to merely noise, at the long term (see also Supplementary Fig. S5).
The neuronal noise is of clinical importance, that spans diverse clinical implications [26], [32]. Our simulation results based on our framework for persistent activity in Fig. 4, suggest that medications for reducing neuronal noise level could prolong memory, and hence might therefore prevent fall risk in dementia patients [33]. On the other spectrum of memory malfunctions, are diseases that are characterized by excessive memory, such as in post-traumatic stress disorder (PTSD). In those situations the patients might benefit from medications that promote forgetfulness by increasing synaptic noise. Generally, memory-loss is an important mechanism, allowing acquisition of new memories. Thus, our suggested passive forgetfulness mechanisms and analysis, could serve as an integral part of an healthy forgetfulness mechanism.
Several limitations of the present study, regarding the model simulations and the data interpretations should be noted. First, we compare our theoretical analyses and model simulations of persistent activity to experimental data as measured from EPSP of anesthetized rats [15]. However, the relation between EPSP protocol of anesthetized rats and memory performances is not fully understood yet [15]. Therefore, additional experimental platforms measuring memory should be compared to our model analysis.
Second, using our model simulations, we adjust the model time constant parameter to [min], in accordance with sleep brain models [26]. This τ parameter main effect is on the time scaling of the current I and EPSP, where smaller τ will achieve faster temporal dynamics. For example, changing the cognitive state or the experimental stimulation protocol, e.g., wakening or natural stimulations, could affect τ and therefore change the time scales (faster or slower time dynamic). Hence, future research should evaluate the τ values in different protocols.
Finally, note that in our persistent activity model analysis, we assume that the neuronal network connections strength affects the membrane currents through a logarithmic function (Eq. (1)), as in earlier studies on memory [9], [14]. Although other functions can be used, for example hyperbolic tangent [34] or with a delay [35], we still expect similar conclusions without changing the main inferences, though the ω-space diagram in Fig. 1, might be changed only quantitatively for other functions [36].
Funding
We thank the Israel Science Foundation (grant number 2830/23), the Binational Israel-China Science Foundation (grant number 3132/19), the European Union under the Horizon Europe grant OMINO (grant number 101086321).
H.Sanhedrai acknowledges the support of the Presidential Fellowship of Bar-Ilan University, Israel, and the Mordecai and Monique Katz Graduate Fellowship Program.
CRediT authorship contribution statement
Hillel Sanhedrai: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. Shlomo Havlin: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing. Hila Dvir: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.heliyon.2023.e23949.
Appendix A. Supplementary material
The following is the Supplementary material related to this article.
Extensions of our theoretical analysis are specified in the Supplementary material file.
Data availability
Data will be made available on request.
References
- 1.Zylberberg J., Strowbridge B.W. Mechanisms of persistent activity in cortical circuits: possible neural substrates for working memory. Annu. Rev. Neurosci. 2017;40:603–627. doi: 10.1146/annurev-neuro-070815-014006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wang X.-J. Macroscopic gradients of synaptic excitation and inhibition in the neocortex. Nat. Rev. Neurosci. 2020;21:169–178. doi: 10.1038/s41583-020-0262-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fuster J.M. Unit activity in prefrontal cortex during delayed-response performance: neuronal correlates of transient memory. J. Neurophysiol. 1973;36:61–78. doi: 10.1152/jn.1973.36.1.61. [DOI] [PubMed] [Google Scholar]
- 4.Kubota K., Iwamoto T., Suzuki H. Visuokinetic activities of primate prefrontal neurons during delayed-response performance. J. Neurophysiol. 1974;37:1197–1212. doi: 10.1152/jn.1974.37.6.1197. [DOI] [PubMed] [Google Scholar]
- 5.Barak O., Tsodyks M., Romo R. Neuronal population coding of parametric working memory. J. Neurosci. 2010;30:9424–9430. doi: 10.1523/JNEUROSCI.1875-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Zaksas D., Pasternak T. Directional signals in the prefrontal cortex and in area mt during a working memory for visual motion task. J. Neurosci. 2006;26:11726–11742. doi: 10.1523/JNEUROSCI.3420-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Egorov A.V., Hamam B.N., Fransén E., Hasselmo M.E., Alonso A.A. Graded persistent activity in entorhinal cortex neurons. Nature. 2002;420:173–178. doi: 10.1038/nature01171. [DOI] [PubMed] [Google Scholar]
- 8.Fraser D.D., MacVicar B.A. Cholinergic-dependent plateau potential in hippocampal ca1 pyramidal neurons. J. Neurosci. 1996;16:4113–4128. doi: 10.1523/JNEUROSCI.16-13-04113.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Durstewitz D., Seamans J.K., Sejnowski T.J. Neurocomputational models of working memory. Nat. Neurosci. 2000;3:1184–1191. doi: 10.1038/81460. [DOI] [PubMed] [Google Scholar]
- 10.Hopfield J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. 1982;79:2554–2558. doi: 10.1073/pnas.79.8.2554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Hopfield J.J. Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. 1984;81:3088–3092. doi: 10.1073/pnas.81.10.3088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Barbieri F., Brunel N. Can attractor network models account for the statistics of firing during persistent activity in prefrontal cortex? Front. Neurosci. 2008;2:114–122. doi: 10.3389/neuro.01.003.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Amit D.J., Brunel N. Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. New York, NY, 1991; 1997. pp. 237–252. [DOI] [PubMed] [Google Scholar]
- 14.Amit D.J., Brunel N. Learning internal representations in an attractor neural network with analogue neurons. Netw. Comput. Neural Syst. 1995;6:359–388. [Google Scholar]
- 15.Lynch M.A. Long-term potentiation and memory. Physiol. Rev. 2004;84:87–136. doi: 10.1152/physrev.00014.2003. [DOI] [PubMed] [Google Scholar]
- 16.Martin S.J., Grimwood P.D., Morris R.G. Synaptic plasticity and memory: an evaluation of the hypothesis. Annu. Rev. Neurosci. 2000;23:649–711. doi: 10.1146/annurev.neuro.23.1.649. [DOI] [PubMed] [Google Scholar]
- 17.Gao J., Barzel B., Barabási A.-L. Universal resilience patterns in complex networks. Nature. 2016;530:307–312. doi: 10.1038/nature16948. [DOI] [PubMed] [Google Scholar]
- 18.Solomon S., Shir B. Complexity; a science at 30. Europhys. News. 2003;34:54–57. [Google Scholar]
- 19.Ben-Naim E., Frauenfelder H., Toroczkai Z. vol. 650. Springer Science & Business Media; 2004. Complex Networks. [Google Scholar]
- 20.Gosak M., Markovič R., Dolenšek J., Rupnik M.S., Marhl M., Stožer A., Perc M. Network science of biological systems at different scales: a review. Phys. Life Rev. 2018;24:118–135. doi: 10.1016/j.plrev.2017.11.003. [DOI] [PubMed] [Google Scholar]
- 21.Stoop R.L., Stoop N., Kanders K., Stoop R. Excess entropies suggest the physiology of neurons to be primed for higher-level computation. Phys. Rev. Lett. 2021;127 doi: 10.1103/PhysRevLett.127.148101. [DOI] [PubMed] [Google Scholar]
- 22.Zhou D., Bashan A., Cohen R., Berezin Y., Shnerb N., Havlin S. Simultaneous first- and second-order percolation transitions in interdependent networks. Phys. Rev. E. 2014;90 doi: 10.1103/PhysRevE.90.012803. [DOI] [PubMed] [Google Scholar]
- 23.Gao J., Bashan A., Shekhtman L., Havlin S. IOP Publishing; 2022. Introduction to Networks of Networks. [Google Scholar]
- 24.Strogatz S.H. CRC Press; 2018. Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering. [Google Scholar]
- 25.Grosser S., Buck N., Braunewell K.-H., Gilling K.E., Wozny C., Fidzinski P., Behr J. Loss of long-term potentiation at hippocampal output synapses in experimental temporal lobe epilepsy. Front. Mol. Neurosci. 2020:143. doi: 10.3389/fnmol.2020.00143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Dvir H., Elbaz I., Havlin S., Appelbaum L., Ivanov P.C., Bartsch R.P. Neuronal noise as an origin of sleep arousals and its role in sudden infant death syndrome. Sci. Adv. 2018;4 doi: 10.1126/sciadv.aar6277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Redner S. Cambridge University Press; 2001. A Guide to First-Passage Processes. [Google Scholar]
- 28.Tateno T., Harsch A., Robinson H. Threshold firing frequency–current relationships of neurons in rat somatosensory cortex: type 1 and type 2 dynamics. J. Neurophysiol. 2004;92:2283–2294. doi: 10.1152/jn.00109.2004. [DOI] [PubMed] [Google Scholar]
- 29.Diba K., Lester H.A., Koch C. Intrinsic noise in cultured hippocampal neurons: experiment and modeling. J. Neurosci. 2004;24:9723–9733. doi: 10.1523/JNEUROSCI.1721-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Unsworth N. On the division of working memory and long-term memory and their relation to intelligence: a latent variable approach. Acta Psychol. 2010;134:16–28. doi: 10.1016/j.actpsy.2009.11.010. [DOI] [PubMed] [Google Scholar]
- 31.Was C.A., Woltz D.J. Reexamining the relationship between working memory and comprehension: the role of available long-term memory. J. Mem. Lang. 2007;56:86–102. [Google Scholar]
- 32.Dvir H., Kantelhardt J.W., Zinkhan M., Pillmann F., Szentkiralyi A., Obst A., Ahrens W., Bartsch R.P. A biased diffusion approach to sleep dynamics reveals neuronal characteristics. Biophys. J. 2019;117:987–997. doi: 10.1016/j.bpj.2019.07.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Sheridan P.L., Hausdorff J.M. The role of higher-level cognitive function in gait: executive dysfunction contributes to fall risk in Alzheimer's disease. Dement. Geriatr. Cogn. Disord. 2007;24:125–137. doi: 10.1159/000105126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lansner A. Associative memory models: from the cell-assembly theory to biophysically detailed cortex simulations. Trends Neurosci. 2009;32:178–186. doi: 10.1016/j.tins.2008.12.002. [DOI] [PubMed] [Google Scholar]
- 35.Leng S., Lin W., Kurths J. Basin stability in delayed dynamics. Sci. Rep. 2016;6:1–6. doi: 10.1038/srep21449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sanhedrai H., Gao J., Bashan A., Schwartz M., Havlin S., Barzel B. Reviving a failed network through microscopic interventions. Nat. Phys. 2022:1–12. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Extensions of our theoretical analysis are specified in the Supplementary material file.
Data Availability Statement
Data will be made available on request.