Abstract
Cellular membranes self-assemble from and interact with various molecular species. Each molecule locally shapes the lipid bilayer, the soft elastic core of cellular membranes. The dynamic architecture of intracellular membrane systems is based on elastic transformations and lateral redistribution of these elementary shapes, driven by chemical and curvature stress gradients. The minimization of the total elastic stress by such redistribution composes the most basic, primordial mechanism of membrane curvature-composition coupling (CCC). Although CCC is generally considered in the context of dynamic compositional heterogeneity of cellular membrane systems, in this article we discuss a broader involvement of CCC in controlling membrane deformations. We focus specifically on the mesoscale membrane transformations in open, reservoir-governed systems, such as membrane budding, tubulation, and the emergence of highly curved sites of membrane fusion and fission. We reveal that the reshuffling of molecular shapes constitutes an independent deformation mode with complex rheological properties. This mode controls effective elasticity of local deformations as well as stationary elastic stress, thus emerging as a major regulator of intracellular membrane remodeling.
Keywords: membrane elasticity, membrane curvature, thermodynamics, curvature-composition coupling, molecular shape
1. INTRODUCTION
The pace of life of eukaryotic cells can be seen through intracellular membrane dynamics, continuous and rapid remodeling of the endomembrane system. One of the major remodeling cascades is dedicated to functional membrane recycling, the basis of cellular homeostasis. The recycling, carried by small vesicular carriers, enables prompt delivery and removal of protein and lipid species to and from larger endomembrane subsystems. Synaptic membrane recycling takes less than 1 s during nerve impulse transmission (30, 144, 145), and the recycling of the whole surface membrane of a motile cell takes only 4 min (1, 51, 135). Membrane shuttling between intracellular organelles also can be extremely fast (59). Variations of membrane composition during the formation of a vesicular carrier can be quite dramatic, as these vesicles are tightly packed with accessory proteins and cargo (97, 110, 118, 146). Likewise, demixing of membrane species is characteristic for budding of enveloped viruses tightly packed with viral membrane proteins and thus excluding most of the host proteins (27, 115). Finally, a vesicle carrier is severed from the parent membrane by dedicated protein machinery, which organizes a membrane fission site with distinct protein and lipid compositions (118). In this article, we discuss how the compositional changes couple to local membrane deformations, rather than creating an additional energy barrier, enabling minimization of energy barriers and ensuring speed and reversibility of the deformations, imperative for fast membrane recycling.
Formation of vesicular compartments is generally associated with the self-assembly of a curved protein layer, an external coat, or an internal lining on the parent membrane (38, 47). Although such proteins encode vesicular geometry in their self-assembly patterns, they also sense membrane curvature, as the onset and development of the polymerization process depend on the curvature (94, 150). This curvature effect is due to elastic resistance of the lipid bilayer to bending: Coat self-assembly is easiest when membrane geometry coincides with that of the coat. To enforce membrane bending, coats rely on local curvature creators, such as auxiliary proteins and/or evolutionarily conserved protein domains coupled to membrane curvature (54, 72, 153). These domains both generate the curvature and sense it, as the curvature affects their membrane partitioning (54, 86). As coats, they have a preferred membrane curvature that matches their molecular geometry and optimizes their interaction with lipids (3). They migrate, or sort, toward similar curvatures in membrane curvature gradients, facilitating the formation of curved membrane domains (12, 83). Similar curvature-driven sorting has long been associated with the curvature-generating capacity of lipids (9, 23). The curvature-composition coupling (CCC) then is immanent in various components of the protein machinery driving the formation of vesicle carriers. CCC introduces elements of self-organization and mechanosensing into the formation of vesicular carriers, making it a stochastic process driven by various mechanical and environmental cues, with membrane curvature playing a key role in organization (43, 86, 105, 149).
The essence of CCC can be found in the dynamic adjustment of membrane composition during deformation, generally via molecular exchange with a reservoir or between membrane parts of different curvatures. Such an exchange is engrained in most of the membrane deformations in the cell. Cellular membranes rarely deform as a whole. Generally, a small membrane patch is transformed, remaining in connection with a relatively static parent membrane. The multicomponent parent membranes, along with cytoplasmic pools of proteins and lipids, provide reservoirs of molecular species for the deforming patch. CCC not only facilitates membrane deformation by a coat but also constitutes an entirely new mechanism of membrane morphogenesis. In the extreme forms of CCC, protein curvature creators could spontaneously demix, leading to coatfree membrane morphologies (109, 117, 129). Although such a strong CCC might constitute a stand-alone mechanism of membrane morphogenesis in minimal biomimetic systems or primordial membrane compartments, it was also implicated in ultrafast endocytosis triggered by changes in plasma membrane tension (117). Weak CCC, in turn, affects the elastic parameters of the membrane, reducing its compliance to bending due to the additional degree of freedom enabled by CCC during bending deformations (10, 128). This effect has long been known for cosurfactants exchanging between the monolayer and the bulk phases (65, 73) and is generally associated with dynamic membrane inhomogeneity (40, 88). The coupling of membrane deformation to both rotational and translational mobilities of anisotropic molecules leads to further membrane softening (39, 40). Whereas CCC for proteins might be impeded in crowded membrane systems, lipid migration is less restricted, especially during local, nanoscale membrane deformations. Hence, lipid CCC might emerge as a universal organizer and mechanical regulator of such deformation, with the local tuning of lipid composition playing a specific role in membrane fusion and fission (41, 118).
In this article, we discuss these emergent roles of CCC in local mesoscopic membrane deformations. We review the thermodynamics of local deformations of multicomponent lipid membranes and discuss the role of the membrane reservoir inherent to such systems, the reference states for the deformation, and the renormalization of the apparent mean curvature bending rigidity modulus and lateral tension of the membrane by CCC. Furthermore, using a simple model of a cylindrical lipid membrane nanotube (NT) connected to a planar membrane reservoir, we show that weak CCC can be considered an independent deformation mode controlled by the manifold of lipid shapes presented in the membrane. We support the theoretical analyses with experimental results obtained by multiple groups analyzing CCC from different perspectives, including membrane curvature and topology sensing by individual protein and lipid molecules, molecular sorting in membrane curvature gradients, and membrane softening by proteins and lipids. We conclude by discussing the rheology of CCC and its effect on membrane viscoelasticity.
2. CCC IN RETROSPECT: FROM EARLY IDEAS TO SINGLE-MOLECULE ANALYSES
The coupling between membrane shape and composition was first invoked to explain the peculiar geometry of erythrocytes (26, 33, 83, 133, 134). Membrane morphogenesis was linked to the ability, then hypothetical, of individual protein molecules to generate molecular-scale membrane curvature. Collective protein action transpires as a mesoscale curvature function of the local protein concentration. Nonuniform protein distribution over a membrane creates complex membrane shapes, such as that of erythrocytes (83). Stationary shapes were found at the membrane energy minima, considering the elastic energy of membrane bending and the entropic losses due to protein demixing from the reference uniform planar state (26, 83). In the energy minimization, membrane curvature and composition change self-consistently, resulting in local coupling between them (83).
The coupling originates from the dependence of the interaction energy between the protein molecule and the membrane on the membrane shape, defined by the principal curvatures of a reference membrane surface, and . The energy difference drives the protein redistribution in the membrane curvature gradients. Without knowing molecular details, Leibler (79) first modeled the linear elastic coupling to the mean curvature . The energy density was proposed, where is the coupling constant and is the membrane (its reference surface) area fraction occupied by the protein (79). is explicitly linked to the curvature generation activity of the protein. It can be shown that , where is the mean curvature bending rigidity modulus and is an approximation of the local membrane curvature intrinsic for the protein (9, 28, 79), for example, reflecting the shape of its membrane-interacting surface (86, 123). The CCC energy density becomes , illustrating that protein curvature generators migrate toward their intrinsic membrane curvatures. As is an elusive parameter, its mean-field analog, the spontaneous curvature , was introduced (83). At a given protein coverage defines the reference state for the mean curvature bending, the state characterized by the vanishing mean curvature bending moment in a free-standing membrane patch uniformly covered by the protein (71, 74).
Following the early theoretical analyses, CCC, often termed protein sorting, has been demonstrated experimentally for protein and lipid species. Strong CCC was associated primarily with proteins implicated in membrane remodeling (16, 54, 89, 119). Their sorting was detected in minimal membrane systems containing well-defined synthetic lipid membrane templates and purified proteins, such as annexin B12, amphiphysin, endophilin, reticulon, and IRSp53 (37, 77, 101, 117, 128, 150). In vitro reconstruction of CCC has been instrumental for the mechanistic analyses of this phenomenon. CCC was further associated with conserved protein domains coupled to membrane curvature via their shapes and membrane insertion motifs (86, 153). Sorting of crescentshaped Bin/Amphiphysin/Rvs (BAR) domains, omnipresent in membrane-remodeling proteins (119), toward positive or negative membrane curvature was correlated with their curvature generation activity (11, 21, 50, 119, 154). Amphipathic helices (AHs), creators of extremely high positive (25), drove protein sorting toward positive membrane curvature (28, 35, 68). The preferential partitioning of AHs into highly bent lipid monolayers was associated with the packing defects produced by extreme bending (5). As similar packing defects are generated by cone-shaped lipid species packed in a planar lipid monolayer (5), we argue below that CCC might account for the defect action as well.
Although strong coupling to membrane curvature might require specialized protein domains, any individual molecule in a heterogeneous lipid bilayer generally produces local deformations. The associated stress could be strong enough to support CCC. Such CCC, virtually unrelated to membrane remodeling processes in the cell, was detected for transmembrane proteins (2, 130), membrane-bound nanoparticles (112), and colloids (80). The general ability of peripheral membrane proteins to discriminate membrane curvature might be relevant for regulating spatial protein distribution in bacteria (102).
The CCC for lipids is important for our analysis in this article. Though generally weaker than that of proteins (69, 137), CCC was demonstrated experimentally for several lipid species of physiological importance, including dioleoylphosphatidylethanolamine (DOPE), cardiolipin, and lysolipids (9, 14, 17, 69). Coarse-grained modeling of lipid CCC confirmed the existence of the coupling (7, 32, 36). Lipid sorting is substantially enhanced in large gradients of membrane curvatures typical for structural intermediates of membrane fusion and fission (9, 70, 90). Accordingly, the lipid CCC was implicated in the regulation of membrane fission in the cell (96, 116). Demixing lipid species in weaker curvature gradients generally requires auxiliary driving forces coming from, for example, lipid phase separation (55, 107, 127, 148) or protein cosorting (109). Experimental detection of these driving forces suggested that CCC for lipids, as well as for proteins, can go beyond the linear coupling to mean membrane curvature outlined above.
Different CCC mechanisms were already considered in the early models of coupling. If the lipid and the protein species have the same , for example, in a planar lipid bilayer containing protein species with , demixing can still be produced by a mismatch between the protein and lipid rigidity (83). The corresponding energy density is proportional to , such that protein molecules are driven into or out of curved membrane parts depending on the sign of . The rigidity difference underlies lipid sorting associated with fluid phase separation (107, 138). Beyond the mean membrane curvature, linear coupling to deviatropic curvature was proposed for anisotropic molecules oriented in the membrane plane (19, 39, 40, 76). Sensing of deviatropic curvature by anisotropic membrane inclusions and peptides was documented in experiments (77) and simulations (49, 143). These results imply that protein molecules can discriminate membrane shape (e.g., distinguish a sphere from a cylinder of the same ) (77).
Membrane shape sensing implies strong local interactions, as not only translational but also rotational entropy of a molecule is diminished if the molecule is confined in a membrane part with certain mean and deviatropic curvatures. Accordingly, recent analyses demonstrated the CCC power at the single-molecule level (31, 49, 147). Single-molecule CCC is expectedly small for lipids, yet it could be detected as the difference in the residence time of lipid molecules in curved and flat membrane parts (31) (Figure 1a). The coupling is predictably stronger for proteins (e.g., for small oligomers of Dynamin1), creating substantial local membrane curvature (10). Although sensing of membrane curvature by Dynamin1 was associated with its helical oligomerization (108), small subhelical Dynamin1 oligomers show pronounced CCC, seen as preferential partitioning into highly curved membrane NTs (Figure 1b). Importantly, membrane curvature sensing by protein molecules might show cooperativity (63), due either to lateral interactions between the proteins or to membrane-mediated feedback.
Figure 1.
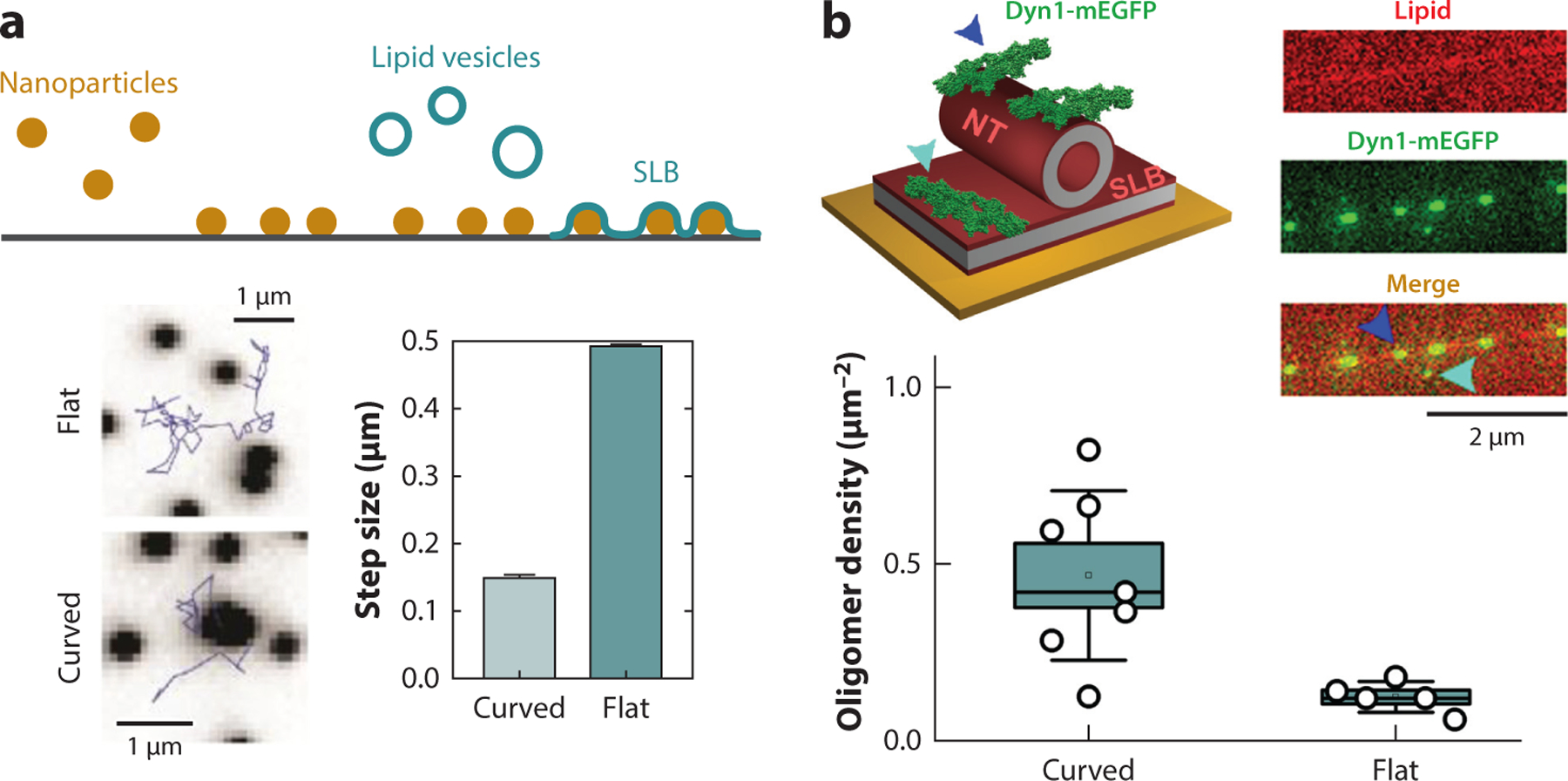
Experimental measurements of membrane curvature sensing by single molecules. (a) The schematic (top) shows the formation of a supported lipid bilayer (blue) containing flat and highly curved parts due to incorporated nanoparticles (brown). Two fluorescence microscopy images (bottom) show the trajectories of single fluorescently labeled lipid (1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine) moving over the flat part of the SLB (flat) and over or near the curved part (curved; black dot). The bar chart shows that the trajectory’s steps are smaller at or near the curved parts of the SLB, indicating preferred lipid partitioning to positively curved lipid monolayers. Panel a adapted from Reference 31. (b) Quantification of binding of small Dyn1-mEGFP oligomers (4–12mers) in an NT–SLB system. Lipid NTs were formed directly over flat SLB by the rolling technique (46). The protein oligomers (green) were seen bound to the NTs (blue arrow) and to SLB nearby (light blue arrow). The oligomer fluorescence intensity was used to determine the number of Dyn1-mEGFP monomers in the oligomers. The boxplot shows that the oligomer concentration was higher on the NT than on the SLB, in agreement with the positive membrane curvature sensing that is encoded in the arc-like architecture of small Dyn1 oligomers (104). Abbreviations: Dyn1, Dynamin1; mEGFP, monomeric enhanced GFP; NT, nanotube; SLB, supported lipid bilayer.
Although CCC can occur on nondeformable supported membrane templates in the form of pure curvature sensing (17, 63, 136) on soft, deformable membranes, CCC is intrinsically coupled to the generation of membrane curvature (12). Intuitively, CCC-driven accumulation of protein curvature generators on an appropriately curved membrane patch would increase the patch curvature. In fact, at high protein concentrations this positive feedback can trigger instability and phase-transition-like processes, where protein demixing leads to membrane shape transformations (66, 101, 117, 120, 122, 140, 152). Although these results are in line with earlier predictions about the morphological power of CCC (83), they also reveal that membrane transformations are generally described by a nonlinear CCC (12, 152). Yet the instabilities leading to the shape transformations could appear in linear CCC owing to related membrane softening.
It was noted in the original treatment of the linear CCC that coupling between the mean membrane curvature and composition leads to the decrease of the apparent bending rigidity of the membrane , where characterizes osmotic compressibility of the (diluted) protein solution in the lipid film (79). Coupling to deviatropic curvature causes a similar softening effect (40). As approaches zero, soft deformation modes emerge, leading to membrane shape instability (40, 79). Far from such instabilities, the reduction of associated with the coupling of the membrane composition to the mean curvature of the membrane, also termed mean-curvature-composition coupling (mCCC), was detected experimentally for proteins (37, 114, 128) and lipids (9, 58). Softening due to dynamic reorientation of a peptide in membrane undulations, evoking the deviatropic coupling, was also observed (93). The decrease of ranges from moderate (~30%) for lipid species to high (~85%) for membrane-inserting proteins. Such changes in substantially alter the energetics of membrane deformations. Near instability points even small changes in can trigger membrane remodeling, indicating that weak mCCC might critically affect membrane transformations during membrane fusion and fission (116).
The examples above highlight the complexity of the effects of CCC on membrane elasticity, mechanical stability, and membrane behavior under curvature stress in general. This mechanical side of CCC is somewhat overlooked compared with its role in molecular sorting and lateral self-organization of cellular membranes. In the next sections, we discuss in detail how CCC, particularly mCCC, affects bending elasticity, lateral tension, and the overall mechanics of the bending deformations of lipid and proteolipid membranes. We use linear mCCC as a prototype to describe the thermodynamics and basic molecular mechanisms of the softening effect in a multicomponent open membrane system.
3. THERMODYNAMICS OF MEMBRANE DEFORMATION IN MULTICOMPONENT OPEN MEMBRANE SYSTEMS
The thermodynamics of CCC has been extensively analyzed (12, 128, 138, 141). Here we follow conventional treatments to obtain simple analytical expressions for the changes to lateral tension and mean curvature bending rigidity of the membrane caused by mCCC. We first consider a homogeneous multicomponent lipid monolayer in contact with a reservoir, the most basic setup for the mCCC analysis (73). For an isothermal deformation, the differential of the Helmholtz free energy for the monolayer containing lipid species (74, 84) is
| 1. |
The right-hand side of Equation 1 includes the energy changes due to the changes in membrane composition and area via exchange with a reservoir, as well as the energy of membrane bending parameterized by the mean and Gaussian curvatures. The corresponding intensive variables are the chemical potentials , lateral tension , mean curvature , and Gaussian curvature bending moments (24, 74). The energy depends on the extensive variables as
| 2. |
To find how each chemical potential changes with deformation, we must uncouple the contributions of different lipid species to the deformation energy. In general, such uncoupling is complex, as it involves different reference states for different deformation modes (74, 84). To proceed, we make several common simplifications. We assume is much larger than the lipid monolayer thickness and consider deformation of the pivotal plane, where all lipid species have a fixed area , with the monolayer area . The fraction of the monolayer (pivotal plane) area occupied by the component is , with . We also omit the Gaussian curvature term in the general analysis and discuss the role of Gaussian and deviatropic curvatures separately. With these assumptions, Equation 2 could be solved straightforwardly for a two-component system, yielding the chemical potentials as the function of (73).
For the multicomponent monolayer, a renormalized chemical potential,
| 3. |
is introduced. The corresponding function has the total differential
| 4. |
with the integrals in Equations 3 and 4 taken from the same lower limit, which is generally associated with the reference membrane geometry, as depends only on and can be calculated for arbitrary and . Hence, Equation 3 is used to link the reference and arbitrary states.
3.1. The Reference State for Lipid Monolayer Bending
The reference state is defined as a minimum of the bending deformation energy, with infinitesimal bending of the membrane requiring no work. It follows from Equation 1 that at the absolute reference state and have to equal zero. The existence of the absolute reference state, where all deformation moments vanish, depends on the coupling between the deformation modes (e.g., bending and stretching/compression modes) (74). The reference state for the mean curvature bending (splay deformation) considered here is defined by . The corresponding geometry can be found in the linear elastic approximation (57):
| 5. |
This approximation remains valid until extremely high curvatures, as seen in experiments and simulations (45, 52, 125). However, as discussed in the literature (22, 52, 62), a higher-order expansion of might still be needed if the monolayer curvature differs significantly from . In Equation 5 is a single parameter characterizing the reference (spontaneous) monolayer state (71). We assume the additivity of so that , where is the spontaneous curvature of a lipid monolayer made of the component (25, 71, 83). With known exceptions (20, 34, 126), including cholesterol and lipid mixtures with a large mismatch of the lipid tail length, behaves as a robust molecular characteristic independent of the monolayer composition. The additivity of further indicates that does not depend on the rigidities of the membrane components as in a series of elastic springs. Accordingly, can be found using a simple Hookean law , where is the bending rigidity modulus of a lipid monolayer made of the component (83). Defined as such, is dominated by the softest membrane component. Stiffer constituents (e.g., proteins) transpire only at high membrane coverage. Equation 5 assumes that individual components affect the reference state only via their . This degeneracy vanishes if additional interactions between membrane components or between components and the curvature field, effectively linking and , are introduced. We discuss such interactions, as well as the coupling between two monolayers in the bilayer, in Sections 3.6 and 3.4, respectively.
We now find how the chemical potentials of membrane components change with the deformation from the reference state to an arbitrary state of curvature and tension . In the reference state , where corresponds to a single-component monolayer. From (Equation 3) we obtain
| 6. |
Of note, Equation 6 does not rely on linear elastic approximation, so and can be redefined to include nonlinear elastic contributions and extra coupling terms. Additional integrands can also be included to account for independent (e.g., saddle-splay) and mixed deformation modes (as discussed in Section 3.7). Finally, Equation 6 indicates that the lateral tension can be linked to the reference geometry, for example, via connecting the reference monolayer to a reservoir containing the lipid mixture of interest.
3.2. Reservoir Tension
Introduction of a reservoir(s) is appropriate for mimicking cellular membrane deformations. Pulling long membrane cylinders (tethers) from cellular membranes revealed that they are connected to relatively large sources of membrane material that maintain the membrane tension constant during tether elongation (60, 103, 132). Membrane folds, buds, budded microdomains, and membrane parts adhered to cytoskeleton all can contribute to buffering the tension during deformation (6, 78). Apart from membrane subsystems, the cytoplasm makes a large reservoir of peripheral membrane proteins. In the endoplasmic reticulum, lipid droplets can function as reservoirs linked to membrane tension changes (15, 91, 111). Similar bulk lipid reservoirs containing lipid solution in nonpolar organic solvents have been widely used to create biomimetic lipid bilayers in vitro, such as black lipid membranes (BLMs) (29, 139) and droplet interface bilayers (DIBs) (13). In these systems the membrane lipid composition is generally assumed to be similar to that of the reservoir mixture, due to empirical tests (e.g., phase separation) (61) or to independent partitioning of lipids into oil–water interface in diluted regimes (98, 131). The exchange with bulk micellar lipid reservoirs provides another means for controlling monolayer composition and creating asymmetric DIBs (13).
Though for local membrane deformations the most readily available reservoir is the parent membrane, its composition is also dynamically adjusted via molecular exchange with available reservoirs. Hence, unlike in preassembled closed membrane systems, such as giant unilamellar vesicles (GUVs), mCCC is applied to every membrane geometry in the system. Accordingly, we assume that the composition of the reference monolayer is defined by a set of reservoirs, with the chemical potentials of the membrane component in the reservoir remaining fixed during manipulations (extension and bending) of the monolayer. The associated lateral (reservoir) tension of the reference monolayer can be defined from Equation 6: . As at equilibrium, , it follows that
| 7. |
where the superscript in indicates that the reference monolayer is in equilibrium with the reservoir. The lateral tension here is defined at the pivotal plane of the monolayer and, as such, does not depend on external forces or moments. We also neglect the effect of the external forces on membrane undulations. We assume that is moderate to large [in the range of 0.01 to 1 mN/m, with the higher values typical for BLM and DIB systems and the lower values reported for the tubular endoplasmic reticulum (142)]. At such lateral tensions the effects of thermal-driven membrane undulation are minimal.
3.3. Lipid Monolayer Softening by CCC
We can now calculate the free energy density for the uniformly curved monolayer connected to the reservoir. Substituting Equations 6 and 7 into Equation 2 and subtracting the reservoir contribution, we recover a familiar form for the free energy density (12,23):
| 8. |
The three parts of the right-hand side of Equation 8 illustrate the sequence of the monolayer formation: (a) pulling the reference monolayer of the necessary area from the reservoir, (b) changing its composition at a fixed curvature via exchange with the reservoir, and (c) bending the monolayer at a fixed area and composition. For a linear elastic monolayer (Equation 5) the last integral in Equation 8 becomes
| 9. |
With the deviation of the concentrations from their reference values assumed to be small, we obtain from Equations 8 and 9
| 10. |
where is the bending modulus of the reference composition. Minimizing Equation 10 over and expanding to the second order in , we obtain (128)
| 11. |
where
| 12. |
is the effective bending modulus of the bilayer. Equation 12 is the key to understanding membrane softening via mCCC. Its right-hand side might be associated with two Hookean springs in series, with the spring constants and . The first constant is the mean curvature bending modulus , the material parameter defining elastic resistance for deformation with a fixed membrane composition (e.g., uniform bending of the whole membrane) (see Equation 10). The second constant, , defines the mCCC contribution, which diminishes to during local and nonuniform deformations. During such deformations, the total stress is distributed between the two springs as . We come back to this analogy in Section 4.1. Here we emphasize that, for stationary deformations, is the mean curvature bending modulus (74).
For a two-component monolayer with , Equation 12 reduces to the mCCC for the second component (12, 28, 128, 141):
| 13. |
For small Equation 13 yields , with , an expression well known for the softening effect in two-component membrane systems (e.g., 55) and also identical to an expression from the earliest linear mCCC model (79) (see Section 2). We next construct the lipid bilayer membrane from two monolayers governed by different reservoir systems [e.g., by different bulk reservoirs as in asymmetric DIB setups (13)].
3.4. CCC Effects on the Effective Bending Rigidity and Lateral Tension of Multicomponent Membranes
Making a bilayer from two different monolayers transforms Equation 11 into
| 14. |
where the monolayer bending rigidities (Equation 12) amount to
| 15a. |
the spontaneous state is defined from the bending moment balance as
| 15b. |
and the bilayer lateral tension becomes
| 15c. |
As both monolayers are free to exchange material with reservoirs, their area and composition are not fixed, so no area coupling between the monolayers exists (113). The spontaneous curvature of the bilayer (Equation 15b) is not zero unless the monolayers are connected to the same reservoir, as in the BLM systems. As is different from the spontaneous curvature of each monolayer, the tension (Equation 15c) is higher than the sum of the monolayer tensions, indicating hidden stress. For a symmetric bilayer, the stress (the last part on the right-hand side of Equation 15c) takes a familiar form, , associated with packing of lipid species with nonzero into planar membrane monolayers (74, 81, 82). However, in closed preassembled systems (such as GUVs or supported lipid bilayers), the stress is , defined by , the material parameters of the bilayer. The stress can be completely alleviated by bending to . In contrast, with the reservoir the stress at is minimal and cannot be diminished by deformation. This stress is intrinsic to monolayers and is ignored when the membrane is considered a single-layer system.
Next, we analyze how mCCC affects membrane systems containing differently curved parts, that is, systems with internal curvature gradients. We resort to the widely used membrane NT system (8, 42, 100). The NTs are highly curved membrane cylinders pulled by an external force from a large, low-curved parent membrane, such as a GUV or BLM (42, 46) (Figure 2). The NT energy is generally expressed through the tension of the planar part and the bending modulus of the NT membrane. With the reservoir-controlled parent membrane (the BLM system), the energy becomes
| 16. |
where is the NT length, is the pulling force, and is further augmented with respect to , reflecting the monolayers’ bending from the reference state to the (quasi)planar state:
| 17. |
Figure 2.
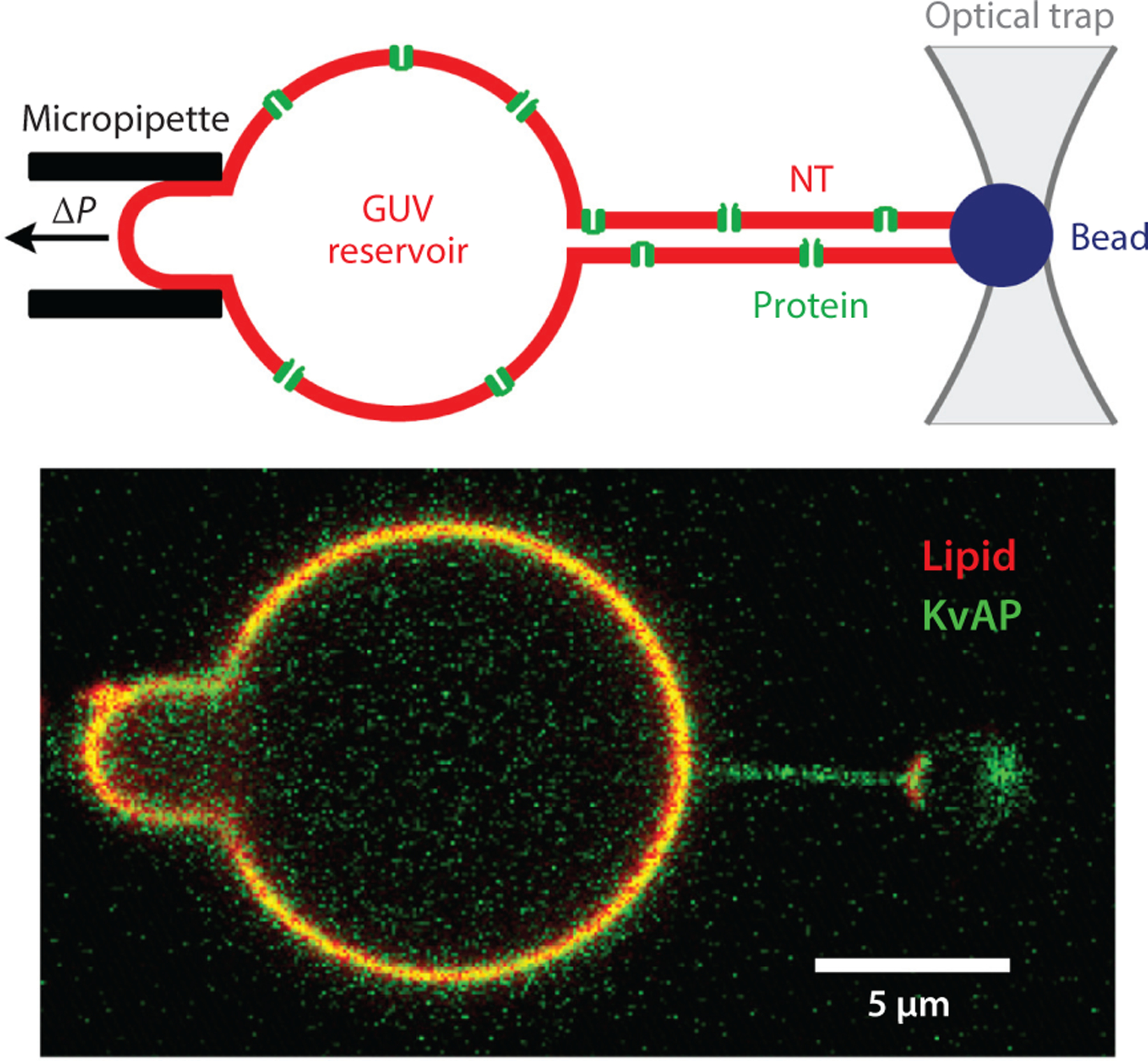
Membrane NTs connected to a reservoir GUV are widely used for quantitative analysis of CCC. (Top) The schematic shows an NT pulled from a GUV reservoir containing transmembrane protein (voltage-dependent K+ channel KvAP) (2). The GUV is held by a micropipette with negative hydrostatic pressure inside. The NT is pulled from the GUV by a microbead controlled by optical tweezers. (Bottom) The fluorescence microscopy image shows the membrane fluorescence coming from a lipid probe (red) and fluorescently labeled KvAP (green). Note that the green fluorescence prevails in the NT, indicating curvature-driven accumulation (sorting) of KvAP in the NT. Figure adapted with permission from Reference 2. Abbreviations: CCC, curvature-composition coupling; GUV, giant unilamellar vesicle; NT, nanotube.
Minimizing Equation 16 over and , we obtain
| 18. |
The ratio of to defines the radius and the pulling force of a multicomponent NT. Substitution of and produces the well-known equations for single-component NTs (106).
Equation 18 summarized the effects of mCCC on the effective bending rigidity and lateral membrane tension in the NT system. The NT system was instrumental in confirming these effects experimentally. For pure lipid NTs made of cone-shaped DOPE ( is high, approximately 0.4 nm−1) (44) and in cylinder-shaped dioleoylphosphatidylcholine (DOPC) is low, approximately 0.01 nm−1) (44) lipids, the measurements of via quantitative NT expansion by electric field revealed that decreased with the increase of DOPE concentration in the reservoir (9, 10) (Figure 3a, subpanel i). In agreement with Equation 13, is minimal at (P.V. Bashkirov & V.A. Frolov, unpublished data) when the mixing entropy peaks, enabling maximal softening. Curiously, tension also grows as predicted by Equation 17, indicating that the hidden stress is controlled by (Figure 3a, subpanel ii). Similar membrane softening with the epsin N-terminal homology (ENTH) domain (28) on one of the reference molecules was observed in mCCC research (129) (Figure 3b). For the NTs containing protein species, the decrease of the bending rigidity modulus due to mCCC could be detected via pulling force measurements by optical tweezers, with calculated using Equation 18, from linear regression of on (128) or on (37, 114).
Figure 3.
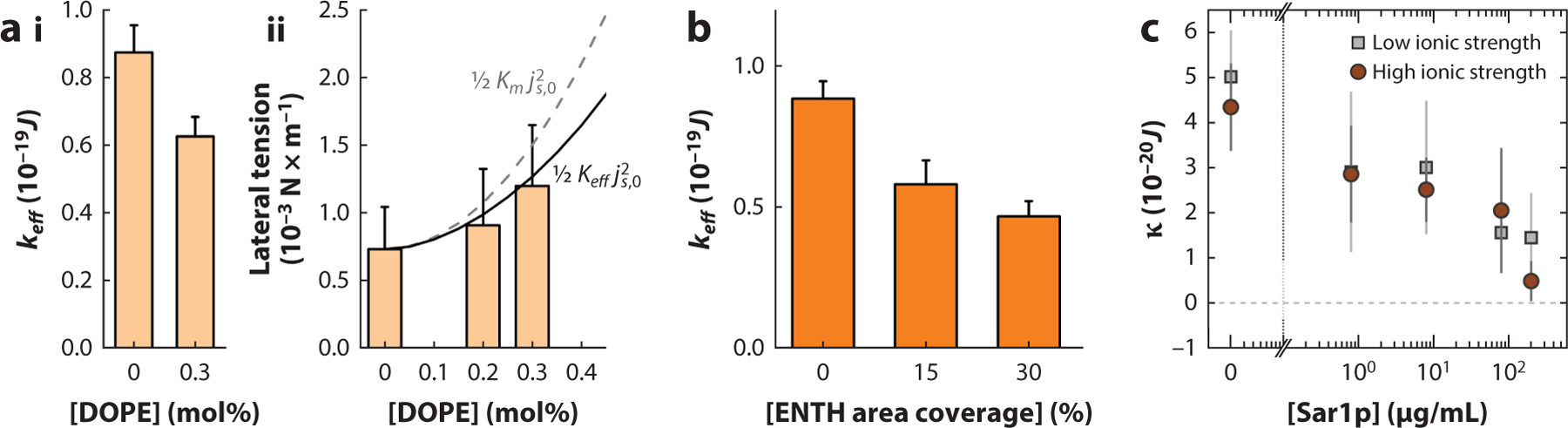
Changes in membrane elastic parameters by proteins and lipids with nonzero spontaneous curvature. Decrease of the effective bending rigidity and (ii) the increase of lateral tension of lipid membranes containing DOPE (9, 10). The solid and dashed lines show the tension increase calculated using Equation 17 or its modified version . (b) Decrease of effective bending rigidity as a function of the membrane coverage by ENTH; was measured as described in Reference 10. (c) Effective membrane rigidity decreases with the bulk concentration of the Sar1p GTPase implicated in membrane remodeling in COPII vesicle transport. Panel adapted with permission from Reference 114. Abbreviations: COPII, coat protein complex II; DOPE, dioleoylphosphatidylethanolamine; ENTH, epsin N-terminal homology domain.
The softening effect was also detected with membrane models other than NTs, for example, by analyzing alternations of the thermal undulations of GUVs by pore-forming peptides (18, 95) (Figure 3c) or lysolipids with high positive (58, 87). Nevertheless, mechanistic interpretation of the softening effect might be ambiguous, as the addition of a new membrane component also affects the material parameter . Though at low the effect is small, at higher can be layered, as observed with detergents, small solutes such as short alcohols, and pore-forming peptides (65, 92, 95). The reduction of was associated with a hydrophobic and geometric mismatch between the membrane components, causing membrane thinning (95, 151) and bulk structural alterations that led to changes to the transbilayer pressure profile (43). In general, CCC-related membrane softening can be distinguished from reduction by its rheological properties or via correlative analysis of the softening and redistribution of proteins in membrane curvature gradients.
3.5. Sorting and Softening
The relation of sorting and softening in the mCCC context is set by Equation 10. Its minimization over yields the absolute sorting coefficients, which measure deviation of the membrane composition from the reference composition:
| 19. |
Equation 19 identifies major parameters controlling curvature-driven sorting in the linear mCCC approximation: the average curvature frustration , the packing stress for individual components in the spontaneous state , and . It shows that addition of a soft component (or a component with high spontaneous curvature) diminishes the absolute sorting coefficients for the rest of the components in planar geometry but augments those at high membrane curvatures. This bidirectional action might account for the large stimulation of sorting (cosorting effect) of lipids by curvature-active proteins (109, 127). Equation 19 also shows that two components with opposite partition cooperatively, providing a plausible explanation for the stimulating effect of DOPE, but also the curvature-induced packing defect, on the membrane binding of AHs (5).
Equation 19 further yields the relative sorting coefficients , which quantify the component distribution between planar and curved monolayers. For the two-component system (Equation 13),
| 20. |
Equation 20 closely resembles equations derived for the protein sorting between the NT and the planar parent membrane (12, 37, 128). For two-component mixtures, Equation 20 can be straightforwardly modified to account for a larger area occupied by the protein component by substituting with . In the NT system, can be measured directly with fluorescently labeled proteins (28, 37) (Figure 2). Equations 13 and 20 are combined to find and for a given protein species from two independent sets of measurements (e.g., and pulling force ). For example, for ENTH, was obtained from the measurements (10) (Figure 3b). With defined by the size of the hydrophobic insertion of ENTH (~2 nm2) (124), , similar to the value obtained from the measurements (28). This similarity indicates that the ENTH-driven reduction of membrane rigidity is due primarily to mCCC. A similar comparison can be performed for DOPE. The intrinsic curvature of DOPE obtained from the measurements (Figure 3a), 0.4 nm−1, closely resembles that directly measured for stress-free DOPE monolayers in the hexagonal (HII) mesophase (44). Again, the correspondence between the intrinsic value and the value obtained from measurements confirms that reduction is driven by CCC.
We highlight one important feature of CCC-related softening: In the leading order, the effect does not depend on the sorting direction. That is, the addition of a molecule with positive spontaneous curvature, such as an AH, to either the internal, negatively curved NT monolayer or the external, positively curved NT monolayer should universally cause reduction and NT constriction (Equation 18). In particular, this softening effect might contribute to AH-driven membrane constriction and fission observed experimentally (85).
In summary, despite its simplicity, the linear mCCC model has generated several experimentally testable predictions about the effects of CCC on membrane deformations. However, the model has obvious limitations. Some of these have been mentioned in the text. In the following sections, we discuss these limitations in more detail in relation to common extensions of the linear mCCC model.
3.6. The Reference State for Bending Deformations of Proteolipid Membranes
Whereas linear mCCC developed for lipid membranes can be mapped to the protein-containing systems (as discussed above), the definition of becomes more involved. As discussed in Section 2, local interactions between proteins (membrane inclusion) and the lipid monolayer can affect the balance of bending moments in the reference bilayer state (Equation 15b). For example, peripheral membrane proteins forming an elastic scaffolding on the membrane surface can be considered as an additional elastic layer coupled to the lipid bilayer (64). To find the reference state in this system, akin to the asymmetric bilayer (Equation 15b), the local bending moments arising during coupling of the protein and lipid layers are to be balanced: , where and are the bending rigidities of the protein and lipid layers, respectively, and is the spontaneous curvature of the protein scaffold. The elastic part of the free energy (Equation 9) becomes . For a rigid protein , the protein behaves as a rigid membrane inclusion, with ) (see Equation 13 for a comparison). In the other limit , the bending energy becomes
| 21. |
which resembles the curvature mismatch model (76, 141).
Equation 21 effectively assumes that the protein-covered fraction of the membrane area has a different bending rigidity and is deformed independently from the lipid part (in contrast to the Hookean coupling assumed by Equation 12 for ). Explicit descriptions of local proteolipid interactions via a set of phenomenological interaction constants related to protein structure, particularly to anisotropy, constitute a plausible alternative to mCCC (53). Finding a reference state(s) for bending deformations, however, becomes a complex minimization problem for a nonhomogeneous membrane. For anisotropic molecules whose orientation in the membrane plane can be coupled to deviatropic curvature, the coupling renormalizes (39). Strong coupling that effectively freezes out the rotational degree of freedom might lead to geometries with periodically varying principal curvatures (40).
Although the reference state might be geometrically complex, can still be defined parametrically from the sorting coefficient obtained from the single molecule partitioning into membrane parts of different geometry. The linear mCCC model is applicable in this situation, as the first quantitative comparison with the curvature mismatch model showed (141). However, mapping to condensed regimes is not straightforward, as the additivity of might not hold. Overall, at high protein coverage, expansion of the mCCC model beyond the linear elastic approximation is likely to become necessary.
3.7. Gaussian Curvature, Entropic, and Differential Rigidity Contributions
Among the high-order contributions emerging upon such an expansion, the Gaussian curvature contributions ; Equation 1) are the most discussed. Although it can be considered a topological invariant for a special class of deformations of closed smooth surfaces, the Gaussian contribution is considered in the heterogeneous membrane systems (e.g., when the Gaussian modulus depends on the local membrane composition) or in the systems with boundaries, such as reservoir and domain boundaries as well as membrane inclusion boundaries. Equation 3 can be modified to include the energies of the saddle-splay and mixed deformations (24, 74). The corresponding contribution to the membrane bending energy can be estimated as
| 22. |
where the integrals are taken from the reference to the current state. The contribution of the saddle-splay deformation is on the order of and that of the mixed deformation can be estimated as (where is the mixed deformation modulus) (24, 74). For the heterogeneous systems (e.g., those containing protein inclusions), the local coupling to the deviatropic part of has been considered (19, 39, 40, 76). For anisotropic inclusions, quadrupolar coupling is generally considered, where is an angle between the inclusion director and the preferred principal curvature axis and is the corresponding interaction constant. For weak coupling, its contribution to the membrane deformation energy is proportional to , that is, (40). Although it follows that the above contributions could be neglected in the second-order analysis of mCCC, they must be taken into account beyond the linear expansion of (Equation 5).
Local membrane softening due to diminishing of the rotational degree of freedom of the inclusions is (40), analogous to Equation 13. This similarity suggests that membrane softening by weakly anisotropic membrane inclusions might have, in the leading order, two independent modes related to rotational and translational entropies. Their combined effect might be of importance for saddle-splay membrane deformations during membrane fusion and fission (41). Stronger molecular anisotropy complicates the interaction between the modes.
Besides modification of the bending energy contribution, beyond-quadratic (in ) treatment of the mixing entropy term becomes necessary. Different lattice and thermodynamic models have been proposed to account for instabilities and phase transitions observed in condensed protein solutions (127, 128, 140, 152). In general, the inclusion of protein–protein interactions (e.g., protein repulsion energy) was also necessary (55, 120, 128, 140). However, for a proteolipid mixture involving species with different , defining the mixing entropy becomes perplexing. Molecular level modeling seems to be a correct way to analyze CCC in such systems.
Finally, the third-order expansion of the free energy is to be used to recover the difference in the sorting coefficients of the molecules that have the same shape but different intrinsic rigidities (138). In a binary system, the coupling leads to membrane softening, as , where is the rigidity difference (138). These effects are especially important near phase transition points where chemical interaction between membrane species facilitates demixing (152). It follows that in the nonlinear regimes, extreme softening (79) can be achieved via a variety of pathways related to different softening mechanisms. However, further experimental assessments of critical membrane softening and associated curvature instabilities are needed to advance our understanding of the subject.
In summary, in open multicomponent membrane systems containing molecular species of different elastic properties, mCCC, in its various forms, universally increases membrane compliance to deformation. Furthermore, mCCC enables dynamic trading of the elastic stress of molecular deformation for the entropic stress of molecular demixing, thus facilitating both direct and reverse deformations. In the next section, we discuss this dynamic interplay between molecular demixing and membrane deformation.
4. MEMBRANE DEFORMATION VIA GRADUAL DEMIXING OF MOLECULAR SHAPES
4.1. Membrane Deformation via Compositional Adjustment
We come back to Equation 12 and analyze the Hookean relation in more detail. For that, we rewrite Equation 12 as
| 23. |
where . As with Equation 12, the right-hand side of Equation 23 can be interpreted as a Hookean relation for a sequence of springs in which each lipid species contributes two springs with the constants and . The first constant measures the bending stiffness of the lipid monolayer made of the lipid component. The second constant measures the entropic resistance to changing the concentration of the lipid component in the deforming membrane. This pure entropic constant is completely defined by the molecular geometry of the available lipid species and is reversely proportional to , such that lipid species with large diminish the most. For lipids, is commonly associated with an effective shape of the lipid molecule in the monolayer, with cylindrical and conical shapes corresponding to planar and curved monolayers, respectively (43). Following Equation 23, weak demixing or reshuffling of such lipid shapes constitutes an independent deformation mode, alternative to conventional bending with a fixed lipid composition (Figure 4a,b). To illustrate how membrane deformation can be conducted purely via reshuffling of molecular shapes, assume that is dominated by the entropic contribution of a single membrane component. With much larger than the rest of yet balanced by their sum so that , the effective bending rigidity becomes . In this hypothetical case using Equation 19, we obtain . That is, an arbitrary (small) deformation of the planar monolayer constructed as described can proceed exclusively via exchanging of the membrane component with the reservoir. For the planar bilayer made of two such monolayers, the deformation would effectively consist of the redistribution of the component of dominating between the monolayers.
Figure 4.
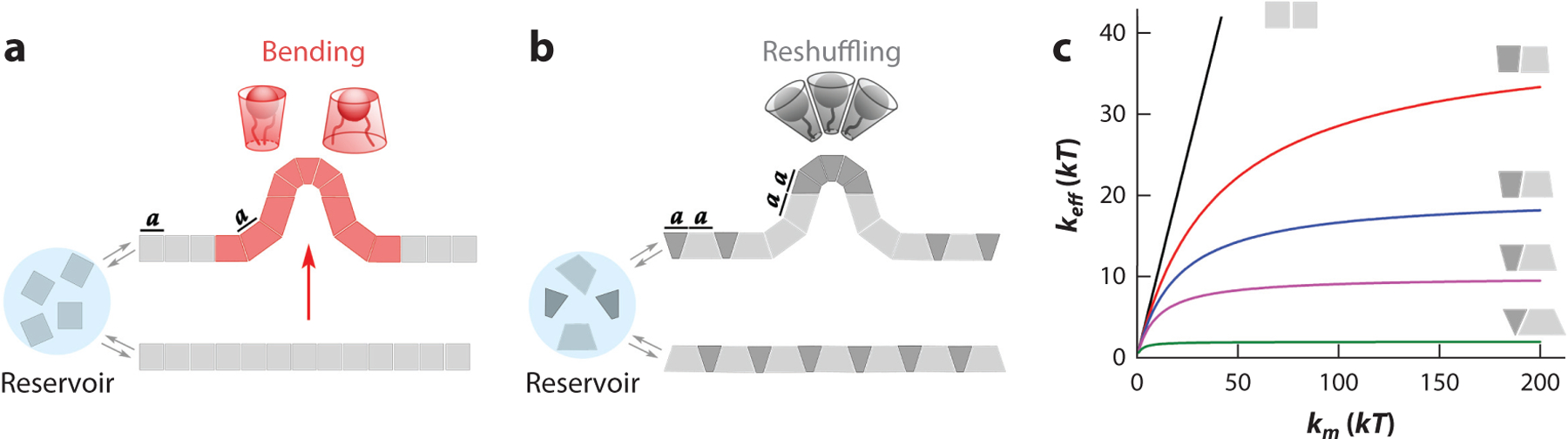
Different deformation modes of a multicomponent lipid monolayer. (a,b) Local deformation with a fixed composition of the deforming part (a) is compared with the similar-scale deformation achieved via curvature-composition coupling, by reshuffling of molecular shapes (b). The area occupied by the cylindrical (a) and cone-shaped (b) lipid species in the membrane reference surface remains constant during the deformation. (c) Dependence of the effective bending rigidity on material rigidity calculated with Equation 14 for a monolayer composed of conical lipids with similar and opposite . Note that with the increase of the absolute value of (from black to green lines), becomes independent of the material elasticity modulus, such that deformations proceed via molecular reshuffling.
The contribution of the (demixing) deformation mode depends on the ratio of to (Figure 4c). The addition of only 30 mol% of DOPE leads to a reduction of of approximately 30% (Figure 3a), showing that for lipids with oleoyl tails and are comparable. Reduction of by the addition of an established softener, a lipid species with a polyunsaturated tail, is similar in magnitude (99), corroborating the physiological relevance of the DOPE effect. The reduction of in protein-containing membranes is much higher (10) (Figure 3b), indicating that the protein redistribution might dominate the deformation energetics. The effect of protein demixing might be further amplified if linked to a source of energy, such as nucleotide hydrolysis. Measurements on GUVs revealed pronounced softening of active membrane by NTPases (4, 48). The ratio also determines the amount of elastic stress stored in the membrane, for example, in a vesicle carrier. The demixing part of the deformation energy does not contribute to the stress in the carriers detached from the parent membranes, whereas the demixing facilitates vesicle membrane deformations both before fission and after fusion. Similar regulation of the stored stress happens while lipids are recruited from a reservoir (Equations 15c and 17). Hence, the ratio might be considered as a measure of the regulatory action of weak mCCC on membrane deformations in the cell, particularly during vesicular transport and membrane recycling. Importantly, the ratio depends on the kinetics of the deformation, as reshuffling of molecular shapes takes time. The speed and extent of the reshuffling depend on those of the very deformation. In the next section, we discuss the basic rheological properties of mCCC seen in the NT system.
4.2. Rheology of Molecular Shape Reshuffling
CCC, and mCCC in particular, is based on migration of molecular species in membrane curvature gradients. Its rheology in a random geometry is fairly complex, not least because the curvature field is constantly changing in space and time due to CCC. Yet, in an important class of deformations, the curvature/concentration gradients are localized to a narrow boundary zone between the uniformly deforming membrane part and the reservoir. A narrow neck between a parent membrane and a budding vesicle, spherical or tubular, represents such a zone (37). In this situation, the migration is fast and the kinetics of CCC is limited by the diffusion within such a compartment (e.g., a vesicle or an NT). For an NT of the length , the characteristic time of the material exchange with the planar reservoir (Figure 2) is , where is the lateral diffusion coefficient. For a micron-long NT tube , such that faster NT deformations involve no compositional adjustment via CCC. In particular, the very NT formation upon the fast (~1 ms) narrowing of the catenoid membrane bridge driven by membrane tension (42, 66) (Figure 5a) shall proceed at virtually constant membrane composition. Hence, the NT system enables decoupling of the membrane deformation by a constant external force (tension) into two parts: the instant deformation and the slower adjustment of the NT shape and composition via mCCC. Indeed, if the NT membrane contains only a single lipid component or components of similar and (not demixable by curvature), its radius remains constant after the collapse (Figure 5b). When DOPE or ENTH, either of which reduces (Figure 3a,b), is added, the collapse is followed by slow NT constriction due to the diffusional adjustment of the NT membrane composition (Figure 5a,b). The extent of this additional constriction is proportional to of the corresponding molecular softener. Similar diffusional relaxation of the curvature stress was seen in the pulling force measurements upon an acute increase in the NT length (37, 56) (Figure 5c).
Figure 5.
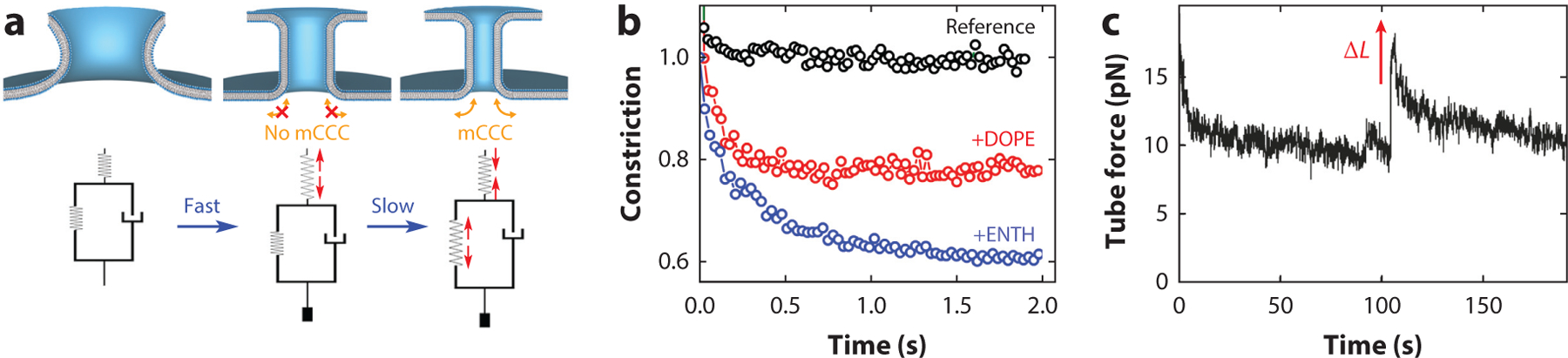
Rheology of CCC during the NT deformation. (a) The upper schematic shows the fast transformation of a catenoid membrane neck into a cylindrical NT (fast) followed by slow NT constriction due to moving of molecules into and out of the NT driven by CCC (slow). The lower schematic shows the corresponding rheological model consisting of two springs: The elastic spring is responsible for instant deformation and the entropic spring is responsible for slow NT deformation via CCC. The viscous-like (dashpot) element reflects the characteristic time of the membrane composition changes via CCC. (b) Experimental observation of the slow stage of the NT constriction shown in panel . The constriction is absent when the NT contains lipids with the same cylindrical geometry (no mCCC, black circles). The constriction is seen when the NT contains molecular species of nonzero spontaneous curvature, DOPE (red circles) or ENTH (blue circles), enabling mCCC. (c) Similar diffusional adjustment of the NT composition upon fast deformation (the length increase) is seen as the gradual decrease of the pulling force. Panel adapted with permission from Reference 56 (see also Equation 13). Abbreviations: CCC, curvature-composition coupling; DOPE, dioleoylphosphatidylethanolamine; ENTH, epsin N-terminal homology domain; mCCC, mean-curvature composition coupling; NT, nanotube.
This two-stage deformation process can be described by a simple rheological model containing and springs (Equations 12 and 23), the latter in parallel with a dashpot reflecting the slow adjustment of the NT composition to its curvature (Figure 5a). The model shows that with mCCC, fast deformations require a bigger force to progress to a certain curvature. In turn, the final elastic stress depends on the deformation speed: An instant deformation creates the largest molecular strain. These smart material properties are of importance for the mechanisms generating local membrane stresses that trigger membrane fusion and fission (41, 75). Specifically, fast and slow actions of the protein machinery mediating fusion and fission might trigger different deformational modes leading to different reaction pathways, with and without leakage (11). The model also points out possible CCC-related discrepancies in the bending modulus measurements by stationary and relaxation techniques.
Besides changing the effective bending rigidity, mCCC is also dynamically linked to the forces causing membrane bending. One force is the lateral membrane tension, which, in the reference or planar geometries, depends on the amount of hidden packing stress governed by mCCC (Equations 15c and 17). Hidden stress values become a function of the speed of the material exchange with bulk reservoirs: As with the NT, fast membrane extension (e.g., by osmotic stress) can be followed by slower correction of the membrane composition. The composition adjustment might also contribute to tension propagation or equilibration of tension gradients between different membrane compartments. Another force is membrane viscosity, a steep function of the protein concentrations (37). CCC might cause protein accumulation, or depletion, in the boundary of a deforming membrane part, thus dynamically regulating the friction drag for membrane material fluxes through the boundary (37). The corresponding shear thinning/thickening effects might be substantial, leading to membrane instability and fission, as was demonstrated for proteins implicated in the curvature creation in the tubular endoplasmic reticulum (37) and during endocytosis (121).
Overall, dynamic reshuffling of molecular shapes seems to provide a self-sufficient means of controlling the extent and dynamics of membrane deformation. In simple cylindrical geometry, the reshuffling constitutes an independent deformation mode dependent exclusively on the variety of molecular shapes present in the membrane. The mode displays interesting rheological properties, suggesting a new dynamic link between cellular membrane remodeling and motility. However, further experimental interrogation is needed to establish the role of this mode in cellular membrane morphogenesis.
5. CONCLUDING REMARKS
The endomembrane of a eukaryotic cell is a complex and dynamic self-assembly platform deeply implicated in the spatiotemporal coordination of multiple cellular processes. It is also a dynamic barrier that separates cellular compartments and protects a complex hierarchy of biochemical processes. The barrier function, fundamental for all membrane systems, is to be absolutely preserved during constant remodeling of the endomembrane subsystems required for their individual functions and for their functional integration. It has been long recognized that local membrane deformations, the foundation of intracellular membrane remodeling, are conducted in concert with demixing and segregation of membrane components, leading to the formation of distinct membrane domains and new membrane compartments. Quite importantly, the coupling between membrane shape and composition, CCC, also helps preserve the barrier function, minimizing local elastic stresses that threaten the structural stability of the lipid bilayer, the core of the membrane barrier. As we revealed in this article through an analysis of the vast literature on CCC, its elementary thermodynamics, and a few relevant experimental datasets, CCC provides a means of dynamically regulating fundamental parameters of the membrane deformations, apparent bending rigidity and local lateral tension. The regulation is based on weak demixing of membrane constituents of different intrinsic curvature—in other words, reshuffling of molecular shapes. As cellular membranes generally show a large variety of shapes, their reshuffling constitutes a versatile deformation mode that enables membrane remodeling with less force and less elastic stress, thus facilitating intracellular membrane recycling. The mode contributes to both regulating the energy barriers for membrane transformations and controlling local instabilities that lead to membrane fusion and fission. Although it has long been appreciated that the abundance of molecular shapes, specifically those of lipids, increases the morphological and topological flexibility of cellular membranes (43), we reiterate here that the shapes control various aspects of membrane remodeling by different, at times complex, means, in which not only the magnitude but also the variety of the intrinsic curvature of membrane components contributes to the regulation of membrane deformations.
ACKNOWLEDGMENTS
This work was partially supported by the National Institute of General Medical Sciences of the National Institutes of Health (NIH) under award R01GM121725 to V.A.F. (the content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH), Basque Government grant IT1270-19, and the Ministry of Science and Higher Education of the Russian Federation (P.I.K.). P.V.B. acknowledges support from the Center for Precision Genome Editing and Genetic Technologies for Biomedicine and the Federal Research and Clinical Center of Physical-Chemical Medicine of the Federal Medical Biological Agency.
Footnotes
DISCLOSURE STATEMENT
The authors are not aware of any affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.
LITERATURE CITED
- 1.Aguado-Velasco C, Bretscher MS. 1999. Circulation of the plasma membrane in Dictyostelium. Mol. Biol. Cell 10(12):4419–27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Aimon S, Callan-Jones A, Berthaud A, Pinot M, Toombes GES, Bassereau P. 2014. Membrane shape modulates transmembrane protein distribution. Dev. Cell 28(2):212–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Alimohamadi H, Rangamani P. 2018. Modeling membrane curvature generation due to membrane-protein interactions. Biomolecules 8(4):120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Almendro-Vedia VG, Natale P, Mell M, Bonneau S, Monroy F, et al. 2017. Nonequilibrium fluctuations of lipid membranes by the rotating motor protein F1F0-ATP synthase. PNAS 114(43):11291–96 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Antonny B 2011. Mechanisms of membrane curvature sensing. Annu. Rev. Biochem 80:101–23 [DOI] [PubMed] [Google Scholar]
- 6.Ayee MAA, Levitan I. 2018. Membrane stiffening in osmotic swelling: analysis of membrane tension and elastic modulus. Curr: Top. Membr: 81:97–123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Baoukina S, Ingólfsson HI, Marrink SJ, Tieleman DP. 2018. Curvature-induced sorting of lipids in plasma membrane tethers. Adv. Theory Simul 1(8):1800034 [Google Scholar]
- 8.Bashkirov PV.2007.Membrane nanotubes in the electric field as a model for measurement of mechanical parameters of the lipid bilayer. Biochem. Suppl. Ser. A Membr. Cell Biol 1(2):176–84 [Google Scholar]
- 9.Bashkirov PV, Chekashkina KV, Akimov SA, Kuzmin PI, Frolov VA. 2011. Variation of lipid membrane composition caused by strong bending. Biochem. Suppl. Ser. A Membr. Cell Biol 5(2):205–11 [Google Scholar]
- 10.Bashkirov PV, Kuzmin PI, Chekashkina K, Arrasate P, Vera Lillo J, et al. 2020. Reconstitution and real-time quantification of membrane remodeling by single proteins and protein complexes. Nat. Protoc 15(8):2443–69 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bassereau P, Jin R, Baumgart T, Deserno M, Dimova R, et al. 2018. The 2018 biomembrane curvature and remodeling roadmap. F. Phys. D Appl. Phys 51(34):343001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Baumgart T, Capraro BR, Zhu C, Das SL. 2011. Thermodynamics and mechanics of membrane curvature generation and sensing by proteins and lipids. Annu. Rev. Phys. Chem 62:483–506 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bayley H, Cronin B, Heron A, Holden MA, Hwang WL, et al. 2008. Droplet interface bilayers. Mol. Biosyst 4(12):1191–208 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Beltrán-Heredia E, Tsai F-C, Salinas-Almaguer S, Cao FJ, Bassereau P, Monroy F. 2019. Membrane curvature induces cardiolipin sorting. Commun. Biol 2(1):225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ben M’barek K, Ajjaji D, Chorlay A, Vanni S, Forêt L, Thiam AR. 2017. ER membrane phospholipids and surface tension control cellular lipid droplet formation. Dev. Cell 41(6):591–604.e7 [DOI] [PubMed] [Google Scholar]
- 16.Bhaskara RM, Grumati P, Garcia-Pardo J, Kalayil S, Covarrubias-Pinto A, et al. 2019. Curvature induction and membrane remodeling by FAM134B reticulon homology domain assist selective ER-phagy. Nat. Commun 10:2370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Black JC, Cheney PP, Campbell T, Knowles MK. 2014. Membrane curvature based lipid sorting using a nanoparticle patterned substrate. Soft Matter 10(12):2016–23 [DOI] [PubMed] [Google Scholar]
- 18.Bouvrais H, Méléard P, Pott T, Jensen KJ, Brask J, Ipsen JH. 2008. Softening of POPC membranes by magainin. Biophys. Chem 137(1):7–12 [DOI] [PubMed] [Google Scholar]
- 19.Božič B, Das SL, Svetina S. 2015. Sorting of integral membrane proteins mediated by curvature-dependent protein-lipid bilayer interaction. Soft Matter 11(12):2479–87 [DOI] [PubMed] [Google Scholar]
- 20.Brannigan G, Brown FLH. 2005. Composition dependence of bilayer elasticity. 7. Chem. Phys 122(7):074905. [DOI] [PubMed] [Google Scholar]
- 21.Breuer A, Lauritsen L, Bertseva E, Vonkova I, Stamou D. 2019. Quantitative investigation of negative membrane curvature sensing and generation by I-BARs in filopodia of living cells. Soft Matter 15(48):9829–39 [DOI] [PubMed] [Google Scholar]
- 22.Bubnis G, Risselada HJ, Grubmüller H. 2016. Exploiting lipid permutation symmetry to compute membrane remodeling free energies. Phys. Rev. Lett 117(18):188102. [DOI] [PubMed] [Google Scholar]
- 23.Callan-Jones A, Sorre B, Bassereau P. 2011. Curvature-driven lipid sorting in biomembranes. Cold Spring Harb. Perspect. Biol 3(2):a004648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Campelo F, Arnarez C, Marrink SJ, Kozlov MM. 2014. Helfrich model of membrane bending: from Gibbs theory of liquid interfaces to membranes as thick anisotropic elastic layers. Adv. Colloid Interface Sci 208:25–33 [DOI] [PubMed] [Google Scholar]
- 25.Campelo F, McMahon HT, Kozlov MM. 2008. The hydrophobic insertion mechanism of membrane curvature generation by proteins. Biophys. 7 95(5):2325–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Canham PB. 1970. The minimum energy of bending as a possible explanation of the biconcave shape of the human red blood cell. F. Theor. Biol 26(1):61–81 [DOI] [PubMed] [Google Scholar]
- 27.Cantin R, Méthot S, Tremblay MJ. 2005. Plunder and stowaways: incorporation of cellular proteins by enveloped viruses. 7. Virol 79(11):6577–87 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Capraro BR, Yoon Y, Cho W, Baumgart T. 2010. Curvature sensing by the epsin N-terminal homology domain measured on cylindrical lipid membrane tethers. 7. Am. Chem. Soc 132(4):1200–1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Castellana ET, Cremer PS. 2006. Solid supported lipid bilayers: from biophysical studies to sensor design. Surf. Sci. Rep 61(10):429–44 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chanaday NL, Cousin MA, Milosevic I, Watanabe S, Morgan JR. 2019. The synaptic vesicle cycle revisited: new insights into the modes and mechanisms. 7. Neurosci 39(42):8209–16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cheney PP, Weisgerber AW, Feuerbach AM, Knowles MK. 2017. Single lipid molecule dynamics on supported lipid bilayers with membrane curvature. Membranes 7(1):15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cooke IR, Deserno M. 2006. Coupling between lipid shape and membrane curvature. Biophys. 7 91(2):487–95 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Deuling HJ, Helfrich W. 1976. Red blood cell shapes as explained on the basis of curvature elasticity. Biophys. 7 16(8):861–68 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Dimova R 2014. Recent developments in the field of bending rigidity measurements on membranes. Adv. Colloid Interface Sci 208:225–34 [DOI] [PubMed] [Google Scholar]
- 35.Drin G, Casella J-F, Gautier R, Boehmer T, Schwartz TU, Antonny B. 2007. A general amphipathic -helical motif for sensing membrane curvature. Nat. Struct. Mol. Biol 14(2):138–46 [DOI] [PubMed] [Google Scholar]
- 36.Elías-Wolff F, Lindén M, Lyubartsev AP, Brandt EG. 2019. Curvature sensing by cardiolipin in simulated buckled membranes. Soft Matter 15(4):792–802 [DOI] [PubMed] [Google Scholar]
- 37.Espadas J, Pendin D, Bocanegra R, Escalada A, Misticoni G, et al. 2019. Dynamic constriction and fission of endoplasmic reticulum membranes by reticulon. Nat. Commun 10:5327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Faini M, Beck R, Wieland FT, Briggs JAG. 2013. Vesicle coats: structure, function, and general principles of assembly. Trends Cell Biol. 23(6):279–88 [DOI] [PubMed] [Google Scholar]
- 39.Fošnarič M, Bohinc K, Gauger DR, Iglič A, Kralj-Iglič V, May S. 2005. The influence of anisotropic membrane inclusions on curvature elastic properties of lipid membranes. 7. Chem. Inf. Model 45(6):1652–61 [DOI] [PubMed] [Google Scholar]
- 40.Fournier JB. 1996. Nontopological saddle-splay and curvature instabilities from anisotropic membrane inclusions. Phys. Rev. Lett 76(23):4436–39 [DOI] [PubMed] [Google Scholar]
- 41.Frolov VA, Escalada A, Akimov SA, Shnyrova AV. 2015. Geometry of membrane fission. Chem. Phys. Lipids 185:129–40 [DOI] [PubMed] [Google Scholar]
- 42.Frolov VA, Lizunov VA, Dunina-Barkovskaya AY, Samsonov AV, Zimmerberg J. 2003. Shape bistability of a membrane neck: a toggle switch to control vesicle content release. PNAS 100(15):8698–703 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Frolov VA, Shnyrova AV, Zimmerberg J. 2011. Lipid polymorphisms and membrane shape. Cold Spring Harb. Perspect. Biol 3(11):a004747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Fuller N, Rand RP. 2001. The influence of lysolipids on the spontaneous curvature and bending elasticity of phospholipid membranes. Biophys. 7 81(1):243–54 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Galimzyanov TR, Bashkirov PV, Blank PS, Zimmerberg J, Batishchev OV, Akimov SA. 2020. Monolayerwise application of linear elasticity theory well describes strongly deformed lipid membranes and the effect of solvent. Soft Matter 16(5):1179–89 [DOI] [PubMed] [Google Scholar]
- 46.Galvez JMM, Garcia-Hernando M, Benito-Lopez F, Basabe-Desmonts L, Shnyrova AV. 2020. Microfluidic chip with pillar arrays for controlled production and observation of lipid membrane nanotubes. Lab Chip 20(15):2748–55 [DOI] [PubMed] [Google Scholar]
- 47.Garoff H, Hewson R, Opstelten DJ. 1998. Virus maturation by budding. Microbiol. Mol. Biol. Rev 62(4):1171–90 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Girard P, Prost J, Bassereau P. 2005. Passive or active fluctuations in membranes containing proteins. Phys. Rev. Lett 94(8):088102. [DOI] [PubMed] [Google Scholar]
- 49.Gómez-Llobregat J, Elías-Wolff F, Lindén M. 2016. Anisotropic membrane curvature sensing by amphipathic peptides. Biophys. 7 110(1):197–204 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Habermann B 2004. The BAR-domain family of proteins: a case of bending and binding? EMBO Rep. 5(3):250–55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hao M, Maxfield FR. 2000. Characterization of rapid membrane internalization and recycling. 7. Biol. Chem 275(20):15279–86 [DOI] [PubMed] [Google Scholar]
- 52.Harmandaris VA, Deserno M. 2006. A novel method for measuring the bending rigidity of model lipid membranes by simulating tethers. 7. Chem. Phys 125(20):204905. [DOI] [PubMed] [Google Scholar]
- 53.Has C, Das SL. 2021. Recent developments in membrane curvature sensing and induction by proteins. Biochim. Biophys. Acta Gen. Subj 1865(10):129971. [DOI] [PubMed] [Google Scholar]
- 54.Haucke V, Kozlov MM. 2018. Membrane remodeling in clathrin-mediated endocytosis. 7. Cell Sci 131(17):jcs216812. [DOI] [PubMed] [Google Scholar]
- 55.Heinrich M, Tian A, Esposito C, Baumgart T. 2010. Dynamic sorting of lipids and proteins in membrane tubes with a moving phase boundary. PNAS 107(16):7208–13 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Heinrich MC, Capraro BR, Tian A, Isas JM, Langen R, Baumgart T. 2010. Quantifying membrane curvature generation of Drosophila amphiphysin N-BAR domains. 7. Phys. Chem. Lett 1(23):3401–6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Helfrich W 1973. Elastic properties of lipid bilayers: theory and possible experiments. Z. Naturforsch. C 28(11–12):693–703 [DOI] [PubMed] [Google Scholar]
- 58.Henriksen JR, Andresen TL, Feldborg LN, Duelund L, Ipsen JH. 2010. Understanding detergent effects on lipid membranes: a model study of lysolipids. Biophys. 7 98(10):2199–205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hirschberg K, Miller CM, Ellenberg J, Presley JF, Siggia ED, et al. 1998. Kinetic analysis of secretory protein traffic and characterization of Golgi to plasma membrane transport intermediates in living cells. 7. Cell Biol 143(6):1485–503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Hochmuth RM, Mohandas N, Blackshear PL. 1973. Measurement of the elastic modulus for red cell membrane using a fluid mechanical technique. Biophys. 7 13(8):747–62 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Honigmann A, Walter C, Erdmann F, Eggeling C, Wagner R. 2010. Characterization of horizontal lipid bilayers as a model system to study lipid phase separation. Biophys. 7 98(12):2886–94 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hossein A, Deserno M. 2020. Spontaneous curvature, differential stress, and bending modulus of asymmetric lipid membranes. Biophys. 7 118(3):624–42 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hsieh WT, Hsu CJ, Capraro BR, Wu T, Chen CM, et al. 2012. Curvature sorting of peripheral proteins on solid-supported wavy membranes. Langmuir 28(35):12838–43 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Hu J, Shibata Y, Voss C, Shemesh T, Li Z, et al. 2008. Membrane proteins of the endoplasmic reticulum induce high-curvature tubules. Science 319(5867):1247–50 [DOI] [PubMed] [Google Scholar]
- 65.Israelachvili JN. 2011. Intermolecular and Surface Forces. Amsterdam: Elsevier. 3rd ed. [Google Scholar]
- 66.Ivchenkov DV, Kuzmin PI, Galimzyanov TR, Shnyrova AV, Bashkirov PV, Frolov VA. 2021. Nonlinear material and ionic transport through membrane nanotubes. Biochim. Biophys. Acta Biomembr 1863(10): 183677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Jarin Z, Tsai F-C, Davtyan A, Pak AJ, Bassereau P, Voth GA. 2019. Unusual organization of I-BAR proteins on tubular and vesicular membranes. Biophys. F 117(3):553–62 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Jensen MB, Bhatia VK, Jao CC, Rasmussen JE, Pedersen SL, et al. 2011. Membrane curvature sensing by amphipathic helices: a single liposome study using -synuclein and annexin B12. F. Biol. Chem 286(49):42603–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kamal MM, Mills D, Grzybek M, Howard J. 2009. Measurement of the membrane curvature preference of phospholipids reveals only weak coupling between lipid shape and leaflet curvature. PNAS 106(52):22245–50 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Kawamoto S, Klein ML, Shinoda W. 2015. Coarse-grained molecular dynamics study of membrane fusion: curvature effects on free energy barriers along the stalk mechanism. 7. Chem. Phys 143(24):243112. [DOI] [PubMed] [Google Scholar]
- 71.Kozlov MM. 2018. Spontaneous and intrinsic curvature of lipid membranes: back to the origins. In Physics of Biological Membranes, ed. Bassereau P, Sens P, pp. 287–309. Cham, Switz.: Springer [Google Scholar]
- 72.Kozlov MM, Campelo F, Liska N, Chernomordik LV, Marrink SJ, McMahon HT. 2014. Mechanisms shaping cell membranes. Curr. Opin. Cell Biol 29:53–60 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Kozlov MM, Helfrich W. 1992. Effects of a cosurfactant on the stretching and bending elasticities of a surfactant monolayer. Langmuir 8(11):2792–97 [Google Scholar]
- 74.Kozlov MM, Leikin SL, Markin VS. 1989. Elastic properties of interfaces. Elasticity moduli and spontaneous geometric characteristics. 7. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys 85(4):277–92 [Google Scholar]
- 75.Kozlov MM, McMahon HT, Chernomordik LV. 2010. Protein-driven membrane stresses in fusion and fission. Trends Biochem. Sci 35(12):699–706 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Kralj-Iglič V, Svetina S, Žekž B. 1996. Shapes of bilayer vesicles with membrane embedded molecules. Eur: Biophys. 7 24(5):311–21 [DOI] [PubMed] [Google Scholar]
- 77.Larsen JB, Rosholm KR, Kennard C, Pedersen SL, Munch HK, et al. 2020. How membrane geometry regulates protein sorting independently of mean curvature. ACS Cent. Sci 6(7):1159–68 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Lavi I, Goudarzi M, Raz E, Gov NS, Voituriez R, Sens P. 2019. Cellular blebs and membrane invaginations are coupled through membrane tension buffering. Biophys. F 117(8):1485–95 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Leibler S 1986. Curvature instability in membranes. 7. Phys 47(3):507–16 [Google Scholar]
- 80.Li N, Sharifi-Mood N, Tu F, Lee D, Radhakrishnan R, et al. 2017. Curvature-driven migration of colloids on tense lipid bilayers. Langmuir 33(2):600–10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Lipowsky R 2013. Spontaneous tubulation of membranes and vesicles reveals membrane tension generated by spontaneous curvature. Faraday Discuss. 161:305–31 [DOI] [PubMed] [Google Scholar]
- 82.Lipowsky R 2014. Coupling of bending and stretching deformations in vesicle membranes. Adv. Colloid Interface Sci 208:14–24 [DOI] [PubMed] [Google Scholar]
- 83.Markin VS. 1981. Lateral organization of membranes and cell shapes. Biophys. 7 36(1):1–19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Markin VS, Kozlov MM, Leikin SL. 1988. Definition of surface tension at a non-spherical interface. 7. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys 84(8):1149–62 [Google Scholar]
- 85.Martyna A, Bahsoun B, Badham MD, Srinivasan S, Howard MJ, Rossman JS. 2017. Membrane remodeling by the M2 amphipathic helix drives influenza virus membrane scission. Sci. Rep 7:44695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.McMahon HT, Gallop JL. 2005. Membrane curvature and mechanisms of dynamic cell membrane remodelling. Nature 438(7068):590–96 [DOI] [PubMed] [Google Scholar]
- 87.Melero A, Chiaruttini N, Karashima T, Riezman I, Funato K, et al. 2018. Lysophospholipids facilitate COPII vesicle formation. Curr. Biol 28(12):1950–58.e6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Netz RR, Pincus P. 1995. Inhomogeneous fluid membranes: segregation, ordering, and effective rigidity. Phys. Rev. E 52(4):4114. [DOI] [PubMed] [Google Scholar]
- 89.Nguyen N, Shteyn V, Melia TJ. 2017. Sensing membrane curvature in macroautophagy. 7. Mol. Biol 429(4):457–72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Nishizawa M, Nishizawa K. 2010. Curvature-driven lipid sorting: coarse-grained dynamics simulations of a membrane mimicking a hemifusion intermediate. 7. Biophys. Chem 1(2):86–95 [Google Scholar]
- 91.Olzmann JA, Carvalho P. 2019. Dynamics and functions of lipid droplets. Nat. Rev. Mol. Cell Biol 20(3):137–55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Otten D, Brown MF, Beyer K. 2000. Softening of membrane bilayers by detergents elucidated by deuterium NMR spectroscopy. F. Phys. Chem. B 104(51):12119–29 [Google Scholar]
- 93.Pabst G, Danner S, Podgornik R, Katsaras J. 2007. Entropy-driven softening of fluid lipid bilayers by alamethicin. Langmuir 23(23):11705–11 [DOI] [PubMed] [Google Scholar]
- 94.Pak AJ, Grime JMA, Sengupta P, Chen AK, Durumeric AEP, et al. 2017. Immature HIV-1 lattice assembly dynamics are regulated by scaffolding from nucleic acid and the plasma membrane. PNAS 114(47):E10056–65 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Pan J, Tieleman DP, Nagle JF, Kucerka N, Tristram-Nagle S. 2009. Alamethicin in lipid bilayers: combined use of X-ray scattering and MD simulations. Biochim. Biophys. Acta Biomembr 1788(6):1387–97 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Parton RG, Kozlov MM, Ariotti N. 2020. Caveolae and lipid sorting: shaping the cellular response to stress. 7. Cell Biol 219(4)::201905071 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Pfeffer S 2003. Membrane domains in the secretory and endocytic pathways. Cell 112(4):507–17 [DOI] [PubMed] [Google Scholar]
- 98.Pichot R, Watson RL, Norton IT. 2013. Phospholipids at the interface: current trends and challenges. Int. 7. Mol. Sci 14(6):11767–94 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Pinot M, Vanni S, Pagnotta S, Lacas-Gervais S, Payet L-A, et al. 2014. Lipid cell biology. Polyunsaturated phospholipids facilitate membrane deformation and fission by endocytic proteins. Science 345(6197):693–97 [DOI] [PubMed] [Google Scholar]
- 100.Prévost C, Tsai F-C, Bassereau P, Simunovic M. 2017. Pulling membrane nanotubes from giant unilamellar vesicles. F. Vis. Exp 2017(130):56086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Prévost C, Zhao H, Manzi J, Lemichez E, Lappalainen P, et al. 2015. IRSp53 senses negative membrane curvature and phase separates along membrane tubules. Nat. Commun 6:8529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Ramamurthi KS, Lecuyer S, Stone HA, Losick R. 2009. Geometric cue for protein localization in a bacterium. Science 323(5919):1354–57 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Raucher D, Sheetz MP. 1999. Characteristics of a membrane reservoir buffering membrane tension. Biophys. F 77(4):1992–2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Reubold TF, Faelber K, Plattner N, Posor Y, Ketel K, et al. 2015. Crystal structure of the dynamin tetramer. Nature 525(7569):404–8 [DOI] [PubMed] [Google Scholar]
- 105.Reynwar BJ, Illya G, Harmandaris VA, Müller MM, Kremer K, Deserno M. 2007. Aggregation and vesiculation of membrane proteins by curvature-mediated interactions. Nature 447(7143):461–64 [DOI] [PubMed] [Google Scholar]
- 106.Roux A 2013. The physics of membrane tubes: soft templates for studying cellular membranes. Soft Matter 9:6726–36 [Google Scholar]
- 107.Roux A, Cuvelier D, Nassoy P, Prost J, Bassereau P, Goud B. 2005. Role of curvature and phase transition in lipid sorting and fission of membrane tubules. EMBO 7 24(8):1537–45 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Roux A, Koster G, Lenz M, Sorre B, Manneville J-B, et al. 2010. Membrane curvature controls dynamin polymerization. PNAS 107(9):4141–46 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Safouane M, Berland L, Callan-Jones A, Sorre B, Römer W, et al. 2010. Lipid cosorting mediated by Shiga toxin induced tubulation. Traffic 11(12):1519–29 [DOI] [PubMed] [Google Scholar]
- 110.Saheki Y, De Camilli P. 2012. Synaptic vesicle endocytosis. Cold Spring Harb. Perspect. Biol 4(9):a005645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Santinho A, Salo VT, Chorlay A, Li S, Zhou X, et al. 2020. Membrane curvature catalyzes lipid droplet assembly. Curr. Biol 30(13):2481–94.e6 [DOI] [PubMed] [Google Scholar]
- 112.Šarić A, Cacciuto A. 2013. Self-assembly of nanoparticles adsorbed on fluid and elastic membranes. Soft Matter 9:6677–95 [Google Scholar]
- 113.Seifert U, Berndl K, Lipowsky R. 1991. Shape transformations of vesicles: phase diagram for spontaneous-curvature and bilayer-coupling models. Phys. Rev. A 44(2):1182–202 [DOI] [PubMed] [Google Scholar]
- 114.Settles EI, Loftus AF, McKeown AN, Parthasarathy R. 2010. The vesicle trafficking protein Sar1 lowers lipid membrane rigidity. Biophys. 7 99(5):1539–45 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Shaw ML, Stone KL, Colangelo CM, Gulcicek EE, Palese P. 2008. Cellular proteins in influenza virus particles. PLOS Pathog. 4(6):e1000085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Shemesh T, Luini A, Malhotra V, Burger KNJ, Kozlov MM. 2003. Prefission constriction of Golgi tubular carriers driven by local lipid metabolism: a theoretical model. Biophys. F 85(6):3813–27 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Shi Z, Baumgart T. 2015. Membrane tension and peripheral protein density mediate membrane shape transitions. Nat. Commun 6:5974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Shnyrova AV, Frolov VA, Zimmerberg J. 2009. Domain-driven morphogenesis of cellular membranes. Curr. Biol 19(17):R772–80 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Simunovic M, Evergren E, Callan-Jones A, Bassereau P. 2019. Curving cells inside and out: roles of BAR domain proteins in membrane shaping and its cellular implications. Annu. Rev. Cell Dev. Biol 35:111–29 [DOI] [PubMed] [Google Scholar]
- 120.Simunovic M, Evergren E, Golushko I, Prévost C, Renard H-F, et al. 2016. How curvature-generating proteins build scaffolds on membrane nanotubes. PNAS 113(40):11226–31 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Simunovic M, Manneville JB, Renard HF, Evergren E, Raghunathan K, et al. 2017. Friction mediates scission of tubular membranes scaffolded by BAR proteins. Cell 170(1):172–84.e11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Simunovic M, Šarić A, Henderson JM, Lee KYC, Voth GA. 2017. Long-range organization of membrane-curving proteins. ACS Cent. Sci 3(12):1246–53 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Simunovic M, Voth GA, Callan-Jones A, Bassereau P. 2015. When physics takes over: BAR proteins and membrane curvature. Trends Cell Biol. 25(12):780–92 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Snead WT, Hayden CC, Gadok AK, Zhao C, Lafer EM, et al. 2017. Membrane fission by protein crowding. PNAS 114(16):E3258–67 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Sodt AJ, Pastor RW. 2013. Bending free energy from simulation: correspondence of planar and inverse hexagonal lipid phases. Biophys. F 104(10):2202–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Sodt AJ, Venable RM, Lyman E, Pastor RW. 2016. Nonadditive compositional curvature energetics of lipid bilayers. Phys. Rev. Lett 117(13):138104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Sorre B, Callan-Jones A, Manneville JB, Nassoy P, Joanny JF, et al. 2009. Curvature-driven lipid sorting needs proximity to a demixing point and is aided by proteins. PNAS 106(14):5622–26 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Sorre B, Callan-Jones A, Manzi J, Goud B, Prost J, et al. 2012. Nature of curvature coupling of amphiphysin with membranes depends on its bound density. PNAS 109(1):173–78 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Steinem C, Meinecke M. 2021. ENTH domain-dependent membrane remodelling. Soft Matter 17(2):233–40 [DOI] [PubMed] [Google Scholar]
- 130.Strahl H, Ronneau S, González BS, Klutsch D, Schaffner-Barbero C, Hamoen LW. 2015. Transmembrane protein sorting driven by membrane curvature. Nat. Commun 6:8728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Suezaki Y 1978. Statistical mechanical analysis of interfacial tension of black lipid membrane. 7. Theor. Biol 71(3):279–94 [DOI] [PubMed] [Google Scholar]
- 132.Sun M, Graham JS, Hegedüs B, Marga F, Zhang Y, et al. 2005. Multiple membrane tethers probed by atomic force microscopy. Biophys. 7 89(6):4320–29 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Svetina S, Kralj-Iglič V, Žekš B. 1990. Cell shape and lateral distribution of mobile membrane constituents. In Biophysics of Membrane Transport: Tenth School on Biophysics of Membrane Transport, Part II, ed. Kuczera J, Przestalski S, pp. 139–55. Wrocław, Pol.: Agric. Univ. Wrocław [Google Scholar]
- 134.Svetina S, Sekš B. 1990. The mechanical behaviour of cell membranes as a possible physical origin of cell polarity. F. Theor. Biol 146(1):115–22 [DOI] [PubMed] [Google Scholar]
- 135.Tanaka M, Kikuchi T, Uno H, Okita K, Kitanishi-Yumura T, Yumura S. 2017. Turnover and flow of the cell membrane for cell migration. Sci. Rep 7(1):12970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Tanaka M, Komikawa T, Yanai K, Okochi M. 2020. Proteomic exploration of membrane curvature sensors using a series of spherical supported lipid bilayers. Anal. Chem 92(24):16197–203 [DOI] [PubMed] [Google Scholar]
- 137.Tian A, Baumgart T. 2009. Sorting of lipids and proteins in membrane curvature gradients. Biophys. 7 96(7):2676–88 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Tian A, Capraro BR, Esposito C, Baumgart T. 2009. Bending stiffness depends on curvature of ternary lipid mixture tubular membranes. Biophys. 7 97(6):1636–46 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Tien HT. 1967. Black lipid membranes in aqueous media: interfacial free energy measurements and effect of surfactants on film formation and stability. 7. Phys. Chem 71(11):3395–401 [DOI] [PubMed] [Google Scholar]
- 140.Tozzi C, Walani N, Le Roux AL, Roca-Cusachs P, Arroyo M. 2021. A theory of ordering of elongated and curved proteins on membranes driven by density and curvature. Soft Matter 17(12):3367–79 [DOI] [PubMed] [Google Scholar]
- 141.Tsai F-C, Simunovic M, Sorre B, Bertin A, Manzi J, et al. 2021. Comparing physical mechanisms for membrane curvature-driven sorting of BAR-domain proteins. Soft Matter 17(16):4254–65 [DOI] [PubMed] [Google Scholar]
- 142.Upadhyaya A, Sheetz MP. 2004. Tension in tubulovesicular networks of Golgi and endoplasmic reticulum membranes. Biophys. 7 86(5):2923–28 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Walani N, Torres J, Agrawal A. 2014. Anisotropic spontaneous curvatures in lipid membranes. Phys. Rev. E 89(6):062715. [DOI] [PubMed] [Google Scholar]
- 144.Watanabe S, Rost BR, Camacho-Pérez M, Davis MW, Söhl-Kielczynski B, et al. 2013. Ultrafast endocytosis at mouse hippocampal synapses. Nature 504(7479):242–47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Watanabe S, Trimbuch T, Camacho-Pérez M, Rost BR, Brokowski B, et al. 2014. Clathrin regenerates synaptic vesicles from endosomes. Nature 515(7526):228–33 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Wilhelm BG, Mandad S, Truckenbrodt S, Kröhnert K, Schäfer C, et al. 2014. Composition of isolated synaptic boutons reveals the amounts of vesicle trafficking proteins. Science 344(6187):1023–28 [DOI] [PubMed] [Google Scholar]
- 147.Woodward X, Stimpson EE, Kelly CV. 2018. Single-lipid tracking on nanoscale membrane buds: the effects of curvature on lipid diffusion and sorting. Biochim. Biophys. Acta Biomembr 1860(10):2064–75 [DOI] [PubMed] [Google Scholar]
- 148.Wu QY, Liang Q. 2014. Interplay between curvature and lateral organization of lipids and peptides/proteins in model membranes. Langmuir 30(4):1116–22 [DOI] [PubMed] [Google Scholar]
- 149.Zeno WF, Day KJ, Gordon VD, Stachowiak JC. 2020. Principles and applications of biological membrane organization. Anпи. Rev. Biophys 49:19–39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Zeno WF, Snead WT, Thatte AS, Stachowiak JC. 2019. Structured and intrinsically disordered domains within Amphiphysin1 work together to sense and drive membrane curvature. Soft Matter 15(43):8706–17 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Zhan H, Lazaridis T. 2013. Inclusion of lateral pressure/curvature stress effects in implicit membrane models. Biophys. F 104(3):643–54 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Zhu C, Das SL, Baumgart T. 2012. Nonlinear sorting, curvature generation, and crowding of endophilin N-BAR on tubular membranes. Biophys. F 102(8):1837–45 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Zimmerberg J, Kozlov MM. 2005. How proteins produce cellular membrane curvature. Nat. Rev. Mol. Cell Biol 7(1):9–19 [DOI] [PubMed] [Google Scholar]
- 154.Zimmerberg J, McLaughlin S. 2004. Membrane curvature: how BAR domains bend bilayers. Curr. Biol 14(6):R250–52 [DOI] [PubMed] [Google Scholar]


