Feasibility of Dual-Energy Cone-Beam CT of Bone Marrow Edema Using Dual-Layer Flat Panel Detectors

Abstract

Purpose:

We investigated the feasibility of detection and quantification of bone marrow edema (BME) using dual-energy (DE) Cone-Beam CT (CBCT) with a dual-layer flat panel detector (FPD) and three-material decomposition.

Methods:

A realistic CBCT system simulator was applied to study the impact of detector quantization, scatter, and spectral calibration errors on the accuracy of fat-water-bone decompositions of dual-layer projections. The CBCT system featured 975 mm source-axis distance, 1,362 mm source-detector distance and a 430 × 430 mm² dual-layer FPD (top layer: 0.20 mm CsI:Tl, bottom layer: 0.55 mm CsI:Tl; a 1 mm Cu filter between the layers to improve spectral separation). Tube settings were 120 kV (+2 mm Al, +0.2 mm Cu) and 10 mAs per exposure. The digital phantom consisted of a 160 mm water cylinder with inserts containing mixtures of water (volume fraction ranging 0.18 to 0.46) - fat (0.5 to 0.7) - Ca (0.04 to 0.12); decreasing fractions of fat indicated increasing degrees of BME. A two-stage three-material DE decomposition was applied to DE CBCT projections: first, projection-domain decomposition (PDD) into fat-aluminum basis, followed by CBCT reconstruction of intermediate base images, followed by image-domain change of basis into fat, water and bone. Sensitivity to scatter was evaluated by i) adjusting source collimation (12 to 400 mm width) and ii) subtracting various fractions of the true scatter from the projections at 400 mm collimation. The impact of spectral calibration was studied by shifting the effective beam energy (± 2 keV) when creating the PDD lookup table. We further simulated a realistic BME imaging framework, where the scatter was estimated using a fast Monte Carlo (MC) simulation from a preliminary decomposition of the object; the object was a realistic wrist phantom with an 0.85 mL BME stimulus in the radius.

Results:

The decomposition is sensitive to scatter: approx. <20 mm collimation width or <10% error of scatter correction in a full field-of-view setting is needed to resolve BME. A mismatch in PDD decomposition calibration of ± 1 keV results in ~25% error in fat fraction estimates. In the wrist phantom study with MC scatter corrections, we were able to achieve ~0.79 mL true positive and ~0.06 mL false positive BME detection (compared to 0.85 mL true BME volume).

Conclusions:

Detection of BME using DE CBCT with dual-layer FPD is feasible, but requires scatter mitigation, accurate scatter estimation, and robust spectral calibration.

1. INTRODUCTION

Bone marrow edema (BME) presents as elevated fluid content within the fatty bone marrow. Detection of BME (also known as bone bruise) is an emerging application of Dual-Energy (DE) imaging using conventional CT, primarily for evaluation of subtle fractures in acute and subacute settings.^1–4 Here, we investigate the feasibility of implementing this capability in cone-beam CT (CBCT) using the recently introduced dual-layer flat-panel detector (FPD) combined with a two-stage (projection-domain followed by image-domain) three-material decomposition algorithm.⁵

The DE decomposition problem associated with BME imaging is particularly challenging because of poor spectral separation between fat and water. Therefore, a comprehensive evaluation of BME estimation sensitivity to projection non-idealities common in CBCT is an essential first step towards development of robust scanning and calibration protocols for this application. The results presented below will guide ongoing efforts to enable BME detection using CBCT.

2. METHOD

2.1. Dual-Layer Detector DE Acquisition and Three-Material Decomposition Protocols

A previously validated realistic x-ray system model was used to simulate single-scan DE CBCT using a dual-layer FPD. X-ray spectra, detector response and linear attenuation coefficients of all materials were obtained using Spektr3.0. Quantum and correlated electronic noise were included in the simulations. Monte Carlo (MC) simulations (with 10⁷ photon tracks and variance reduction) were used to obtain scatter estimates.^6,7

The 400 × 400 mm² dual-layer FPD, as shown in Fig. 1A, consisted of a top layer of a 0.2 mm CsI:Tl scintillator that provided the Low-Energy (LE) projections and a bottom layer of 0.55 mm CsI:Tl that provided the High-Energy (HE) data. The detector pixel size was 0.3 × 0.3 mm². A 1 mm Cu filter was sandwiched between two layers to improve spectral separation.⁸

Figure 1.

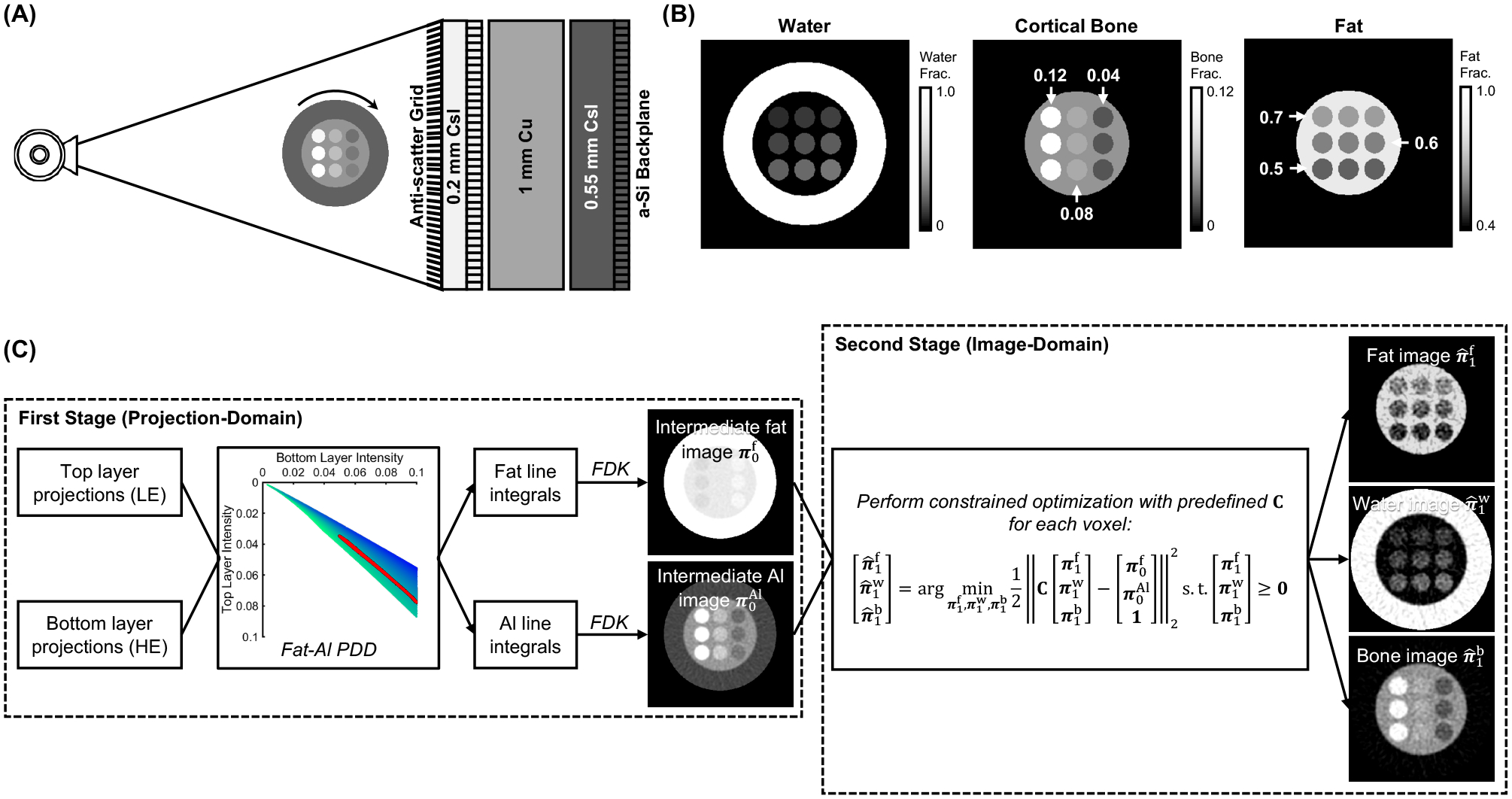
(A) Imaging configuration for DE CBCT of BME using dual-layer FPD. (B) The three-material phantom (axial views) used for validation. Bone and fat fractions of the inserts are marked on the image, the water fraction was given by the volume conservation principle. (B) The two-stage three-material DE decomposition pipeline.

The scan settings emulated the Siemens Healthineers Multitom Rax twin robotic x-ray system⁹: 974.7 mm source-axis distance and 1362.2 mm source-detector distance, 360° rotation with an angular step of 1°. The x-ray source was operated at 120 kV (+2 mm Al, +0.2 mm Cu) and 10 mAs per exposure. Vertically oriented Pb/Al anti-scatter grid¹⁰ with ratio of 13:1 was installed as illustrated in Fig. 1A.

DE imaging of BME was evaluated in an idealized multi-material digital extremity phantom simulated on a 0.5 × 0.5 × 0.5 mm³ voxel grid. The phantom, shown in Fig. 1B, was 500 mm long and consisted of an outer water cylinder of 160 mm diameter and an inner cylinder of 100 mm diameter made of a mixture of 0.07 of cortical bone and 0.93 of adipose (by volume fraction). Nine 20 mm diameter inserts were placed inside the inner cylinder, each filled with a unique mixture of water, bone, and fat. Each column of the insert pattern contained a fixed fraction of bone, decreasing from the leftmost column to the right. Each of the rows contained a fixed fraction of fat, decreasing from the topmost row. The water fractions in the inserts were assigned according to the volume conservation principle.¹¹ Within a single column, the severity of BME increased from top to bottom rows.

Fig. 1C illustrates the two-stage three-material DE decomposition pipeline applied to the simulated projections. The first stage involved projection-domain decomposition^9,12 (PDD) into fat and Al basis. PDD was implemented by interpolating in a precomputed 2D lookup table⁹ that related the measured LE and HE intensities to line integrals of Al and fat for a wide range of fat-Al mixtures. FDK algorithm was then applied (0.5 × 0.5 × 0.5 mm³ voxel size, ramp filter with 0.3x Nyquist frequency cutoff and Hann apodization) to obtain intermediate reconstructions of fat $\left({\pi }_0^{\text{f}}\right)$ and Al $\left({\pi }_0^{\text{Al}}\right)$ volume fractions. In the second stage, we assumed that ${\mu }^{\text{f}}(ϵ)$, ${\mu }^{\text{w}}(ϵ)$, ${\mu }^{\text{b}}(ϵ)\in \text{span}\left\{{\mu }^{\text{f}}(ϵ),{\mu }^{\text{Al}}(ϵ)\right\}$ (where ${\mu }^{\kappa }(ϵ)$ is the linear attenuation coefficients for material $\kappa$), and obtained a decomposition matrix $C$ that contained the linear combination weights that map ${\mu }^{\text{f}}(ϵ)$ and ${\mu }^{\text{Al}}(ϵ)$ onto ${\mu }^{\text{f}}(ϵ)$, ${\mu }^{\text{w}}(ϵ)$ and ${\mu }^{\text{b}}{(ϵ)}^4$. The matrix $C$ was also augmented with the volume conservation principle. A constrained least-squares problem using $C$ was solved using active-set method at each voxel to obtain fat $\left({\pi }_1^{\text{f}}\right)$, water $\left({\pi }_1^{\text{w}}\right)$ and bone $\left({\pi }_1^{\text{b}}\right)$ images from the intermediate fat-Al reconstructions from PDD. Essentially, the PDD stage converted the DE projections into a pair of base material images free of beam hardening artifacts (note that the choice of the two materials is arbitrary – e.g., photoelectric and Compton scatter interactions could be used instead). The second change-of-basis stage provided the means to incorporate the volume constraint, and converted these two base images into concentration maps of the three materials-of-interest.

2.2. Sensitivity of BME Imaging to Scatter and Spectral Calibration

The effects of scatter were investigated in a series of perturbation experiments, all assuming a 13:1 anti-scatter grid. DE decompositions were obtained from projections simulated without scatter and with scatter for a range of collimation widths: 12 mm, 20 mm, 80 mm and 400 mm (the entire detector). The sensitivity to scatter correction accuracy was studied for the 400 mm collimation data (full field-of-view). The following scatter corrections strategies were tested: 1) subtraction of a constant mean scatter estimate for each projection frame and energy channel; the estimate was obtained by finding a scatter fraction that yielded the optimal reduction of cupping artifacts in direct reconstructions of the LE and HE channels, 2) subtraction of a scatter field that matched the shape of the true distribution (i.e. the MC scatter injected into the original simulated data), but had incorrect magnitude; this error was introduced by scaling the MC scatter by a constant ranging from 0.8 to 1 (20% − 0% error), with the same constant applied to both energy channels. The scatter subtraction was applied before the PDD stage of the decomposition introduced in Sec. 2.1.

To study the impact of spectral mismatch in PDD calibration, we added/subtracted Cu filtration (ranging +1 mm Cu to −1 mm Cu) to the simulated source spectrum and regenerated the PDD lookup table with the resulting over- and underestimated spectral responses. The biased PDD lookup tables were then used in decomposition of the scatter-free data.

2.3. Realistic Wrist Phantom Study with Fast MC Scatter Estimation

We further evaluated the BME imaging framework using a realistic human wrist phantom generated from the segmentation of a high-resolution CT scan. The phantom was made of fat, water and cortical bone; its size is shown in Fig. 2A. A 0.85 mL BME stimulus, containing ~22% of cortical bone and equal fractions of water and fat, was placed in the shaft of the radius. Note that the BME lesion is not apparent in the single-energy FDK reconstruction in Fig. 2A, but is easy to identify in the Virtual Non-Calcium (VNCa)¹² image in Fig. 2B.

Figure 2.

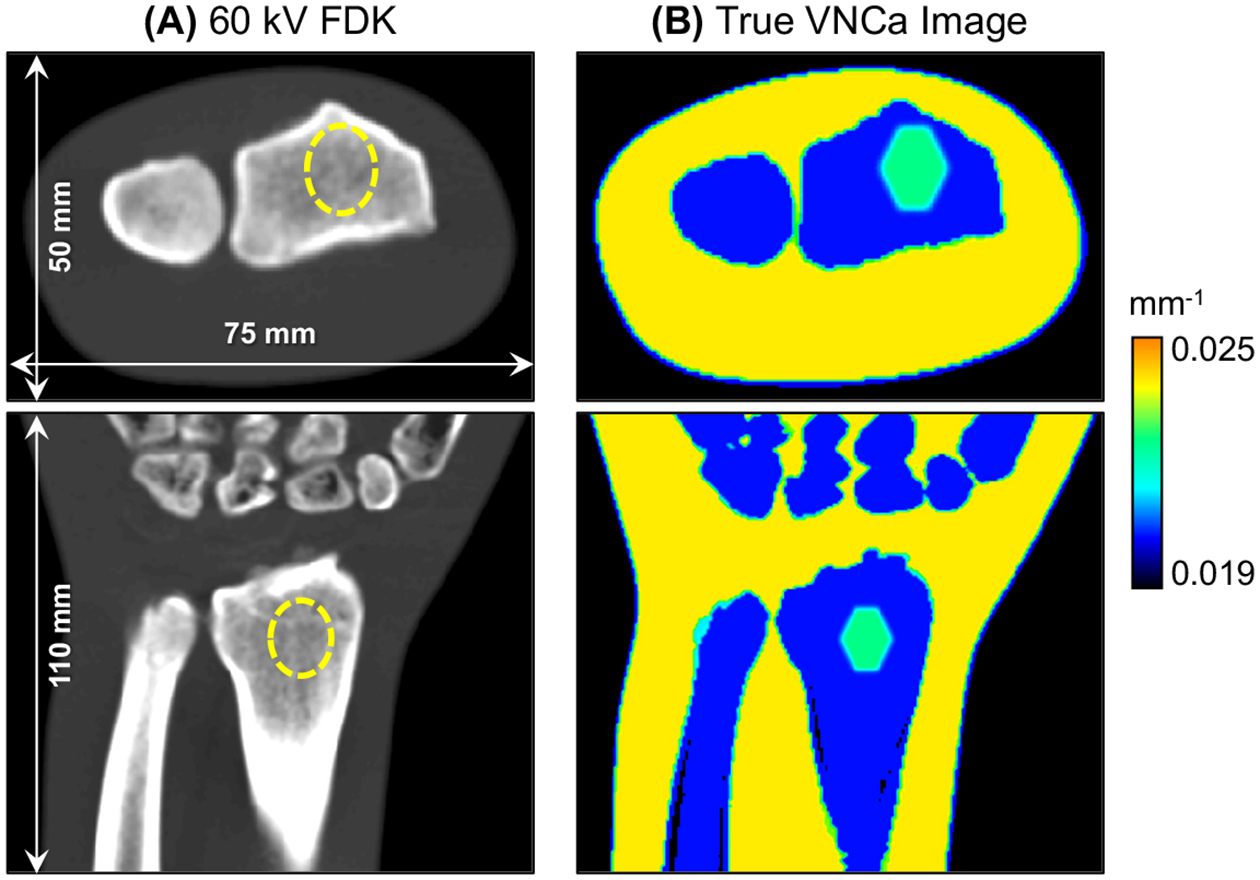
(A) 60 kV FDK reconstruction and (B) VNCa image of the realistic wrist phantom. The dashed line identifies the location of the BME stimulus in the FDK image. The BME lesion is easily detected as a region of increased VNCa attenuation within the bone marrow of the radius.

The primary DE projections and scatter were simulated using the same protocol as in Sec. 2.1. We applied a realistic scatter estimation framework to the simulated data. To this end, the two-stage three-material decomposition was first performed on the scatter-contaminated projections to generate a preliminary set of fat, water and bone images. These preliminary material density maps provided the object model for a fast MC scatter simulation with 10⁶ photons, variance reduction, and Gaussian smoothing (FWHM = 10 mm). Note that the number of photon realizations used during scatter estimation was 10-fold less than during the true scatter simulation. Three-material decomposition was performed again on the scatter-corrected projections to obtain the final images.

3. RESULTS

Fig. 3A illustrates scatter properties of dual-layer projection data. Without the anti-scatter grid, the scatter-to-primary ratio (SPR) in LE projections is substantially higher than in HE projections. This mismatch is partly alleviated by a grid, which reduces the SPR in both channels, by ~50% in the top layer and ~39% in the bottom layer (as measured at detector center). As shown in Fig. 3B, the introduction of the grid shifts the data closer to the scatter-free reference in the PDD lookup table. The application of narrow collimation (e.g., 12 mm) further improves the overlap with ideal data, although the intensity in both channels remains elevated.

Figure 3.

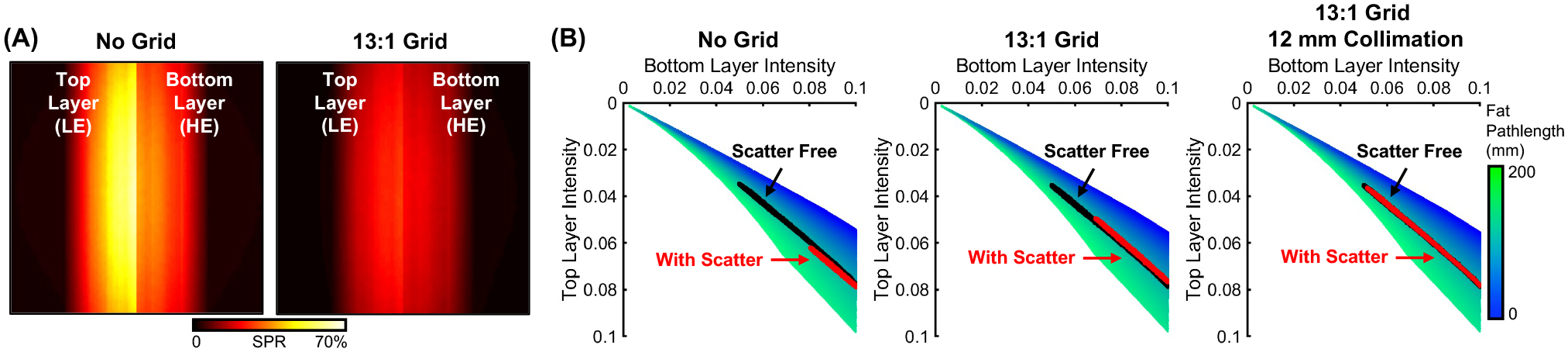
(A) SPR of the top and bottom detector layers without (left) and with (right) anti-scatter grid. (B) PDD fat lookup table without (left) and with (middle) anti-scatter grid, and with grid + narrow collimation (right).

Fig. 4 shows the effects of beam collimation and scatter correction error on BME estimates (all results with a 13:1 anti-scatter grid). Compared to the scatter-free reference (Fig. 4A), the decomposition with either 12 mm collimation (Fig. 4B) or full field-of-view and 5% scatter estimation error (Fig. 4C) result in relatively accurate visualization of the gradient of fat fractions (higher fractions in the top row of inserts). The performance of the decomposition deteriorates for wider x-ray beams and for higher scatter correction errors in the full field setting. Notably, the data corrected with a mean scatter estimate exhibits substantial spatial non-uniformity, underscoring the need to account for the shape of scatter distribution. Fig. 4D and E compare the quantitative accuracy of fat and cortical bone volume fractions. Bone concentration is fairly accurate already at 80 mm collimation or 20% scatter correction error in full field data. In contrast, the fat estimate is sensitive to crosstalk with the water image (not shown here), and requires more complete scatter rejections and/or more precise scatter corrections.

Figure 4.

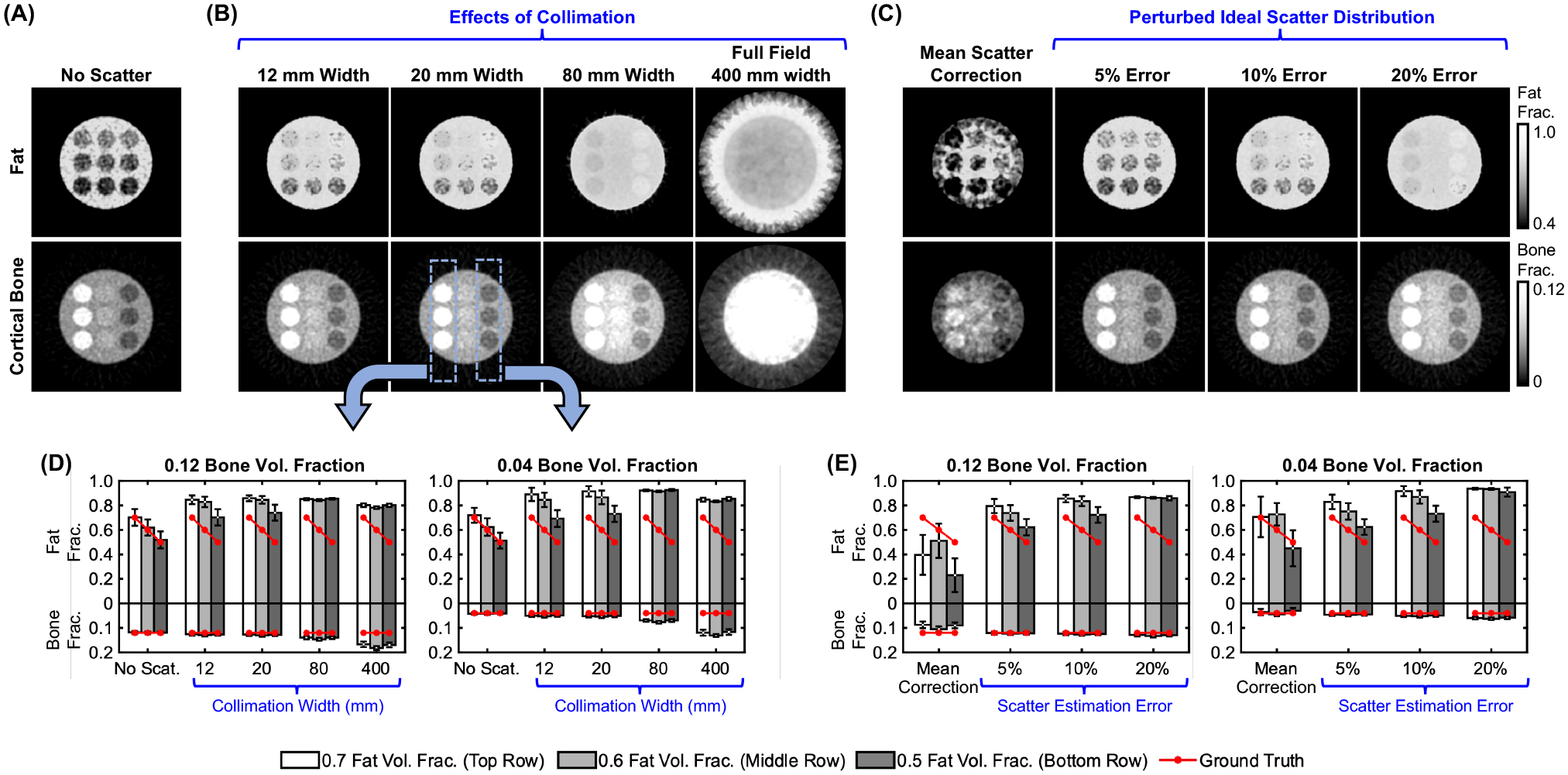
Adipose and bone concentration maps from (A) scatter-free DE projections, (B) DE projections with scatter for various collimation widths, and (C) full field-of-view DE projections with varied scatter correction error. Mean estimated fat/bone fractions for the leftmost and rightmost columns of inserts (marked on the image) for (D) the collimation study, and (E) the scatter correction study.

Fig. 5 compares selected scatter mitigation techniques in terms of BME quantification, here defined as the relative difference of fat fractions between the top row of inserts (no BME) and the bottom row of inserts (29% reduced fat fraction in the phantom). Although the decomposition is sensitive to scatter, all four methods in Fig. 4 can detect the decrease in fat fraction and estimate its magnitude with <50% error; the accuracy is higher at lower concentration of the cortical bone background (dark bars, i.e., rightmost column of inserts). For 5% scatter correction error, the detected change ranges from 22% to 26%, compared to the 29% ground truth change.

Figure 5.

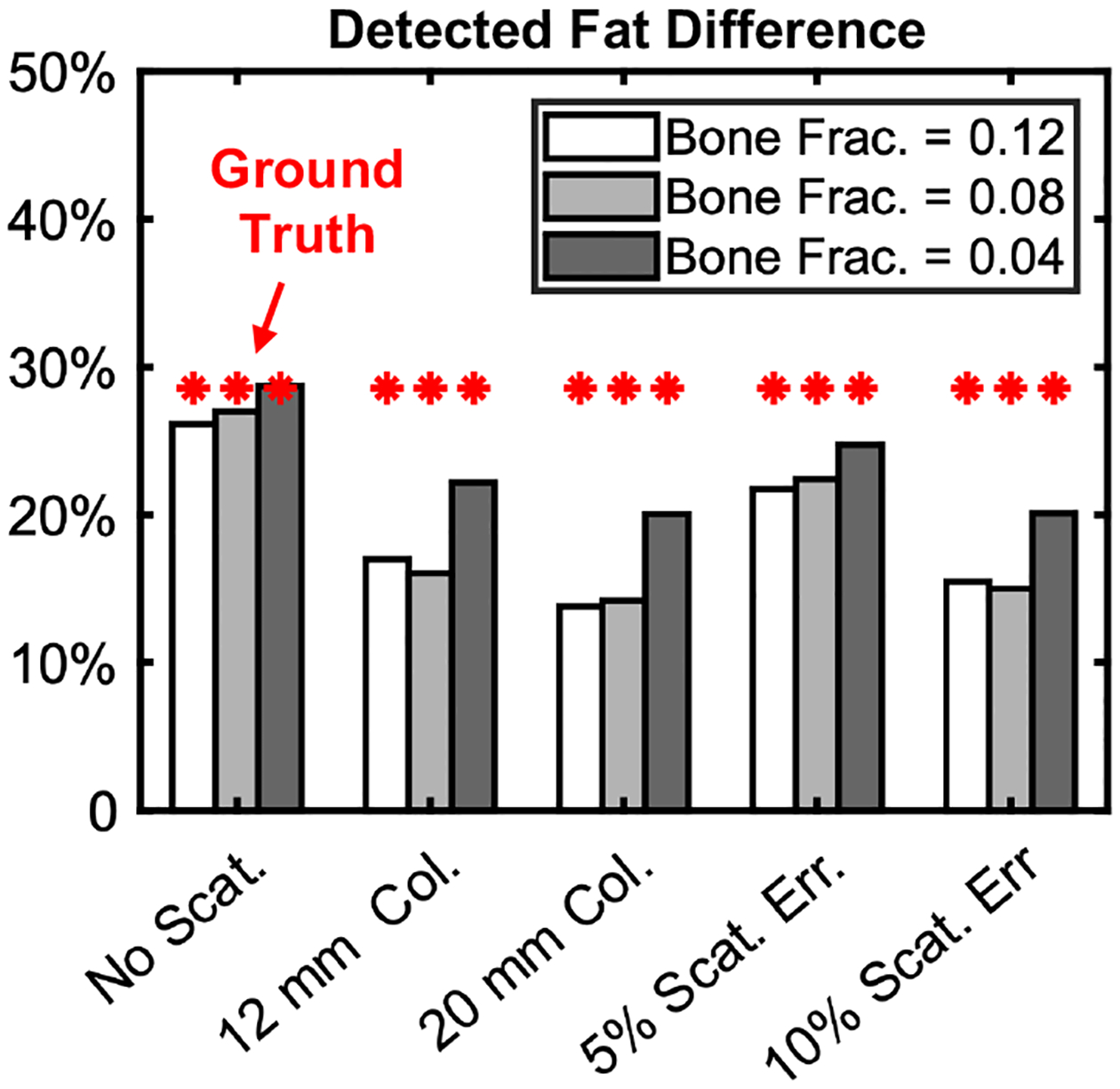
BME quantification accuracy for DE decompositions of scatter-free data (leftmost set of bars) and for different scatter mitigation strategies. The accuracy is represented by relative decrease in fat concentration measured between the top (true fat frac. = 0.7) and bottom (true fat frac. = 0.5) rows of inserts. Each bar represents one column of inserts.

Fig. 6 shows the effect of spectral calibration errors on the DE decomposition. When the effective beam energy is underestimated in the PDD tables, bone and fat are also underestimated to compensate for the spectrum assumed in the decomposition being less penetrating than the spectrum used in the measurements. The opposite effect is visible when effective energy is overestimated. Effective energy mismatch of ± ~1 keV (± 0.05 mm Cu) introduces moderate biases (e.g., ± 0.2 for fat fractions) and crosstalk between materials, but can still track the gradient of fat fractions (Fig. 6B). Severe mismatches (± >2 keV) lead to decomposition errors that will require empirical corrections during scan time.

Figure 6.

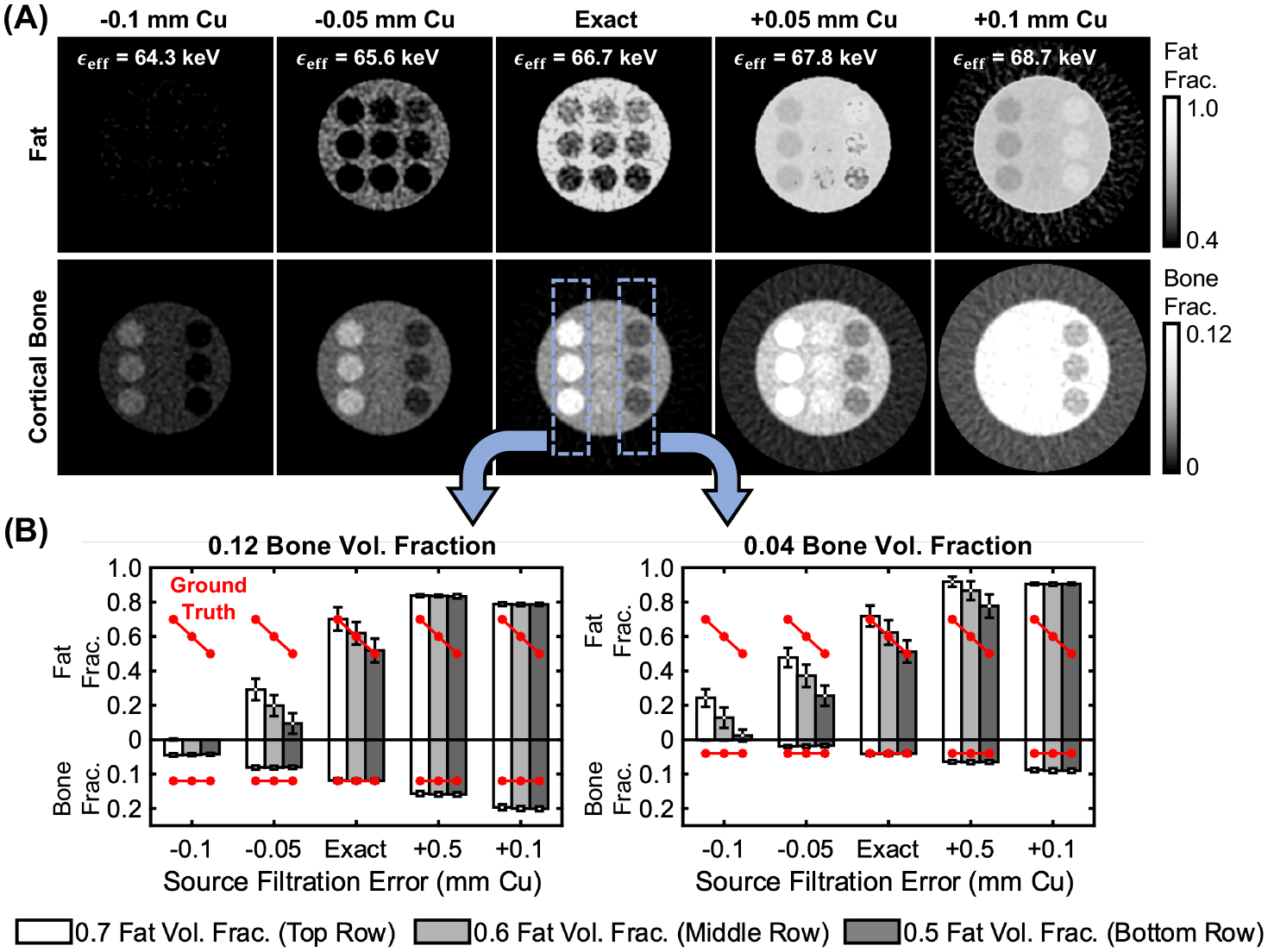
Effects of spectral calibration errors on decomposition accuracy. (A) Decomposed fat and bone fractions obtained using PDD decomposition tables that under/overestimated the effective energy of the x-ray beam. Mean estimated fat/bone fractions for the leftmost and rightmost columns of inserts are shown in (B).

Fig. 7 present the decomposition results (VNCa images) for the realistic wrist simulation before (Fig. 7A) and after (Fig. 7B) scatter correction. Visually, the VNCa image after the fast MC scatter estimation described in Sec. 2.3 appears to match the ground truth BME distribution in the digital phantom (Fig. 2) much better than the uncorrected decomposition. To quantify the accuracy of BME detection, we first segmented any cluster of voxels with VNCa > 0.0214 mm⁻¹ and a size of >1.5 mm diameter in the trabecular region of the wrist. We then computed true and false positive BME volumes relative to the ground truth BME. The decomposition after scatter correction (Fig. 7B) achieves ~0.79 mL true positive and ~0.06 mL false positive BME volume (note that the ground truth BME volume is 0.85 mL), which compares favorably to ~0.18 mL true positive volume produced before scatter correction (Fig. 7A).

Figure 7.

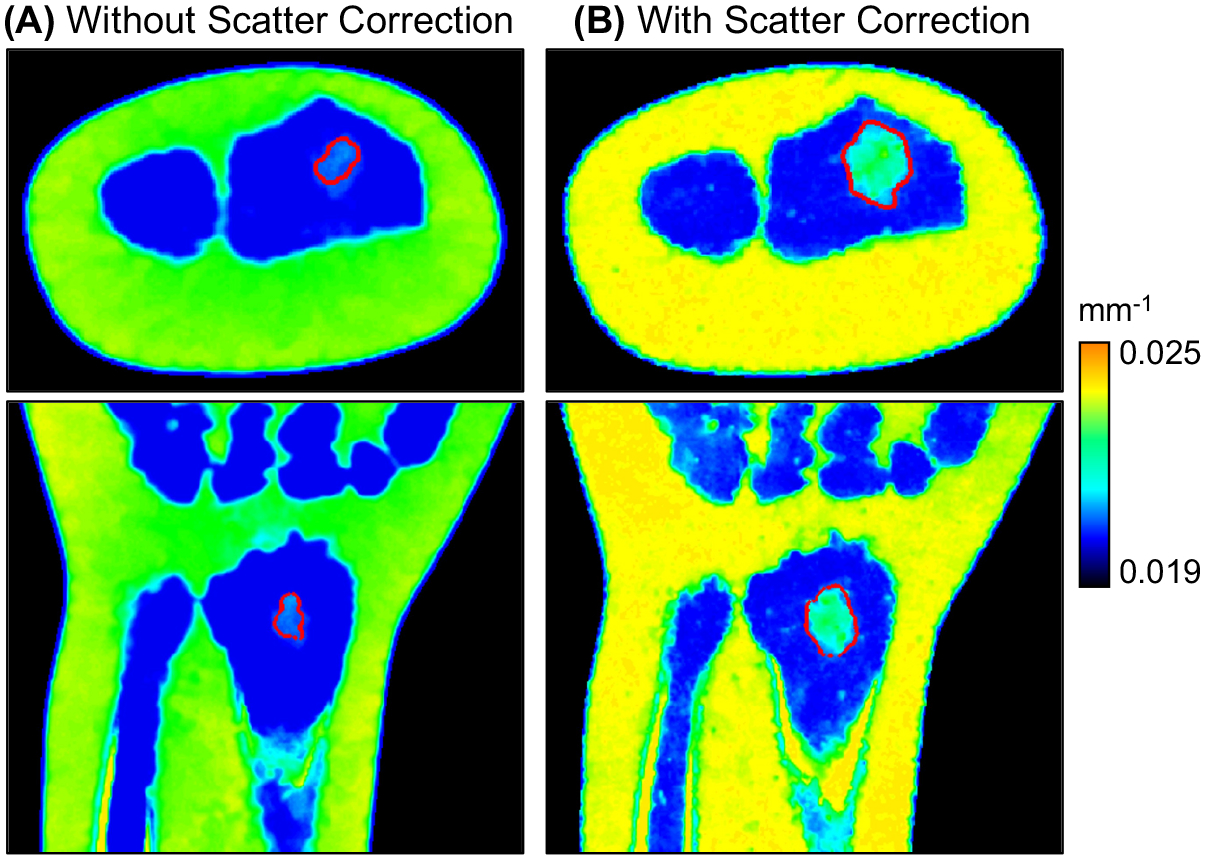
Decompositions (VNCa images) of the realistic wrist BME simulation without (A) and with (B) scatter correction. Compared to scatter simulation during projection generation, the scatter correction step involved an MC simulation with a reduced number of photon tracks and Gaussian smoothing of scatter profiles; the object model for this MC was a material map derived from a preliminary DE decomposition. Red lines indicate the segmented contour of the BME lesion (following the segmentation process described in Sec. 3).

4. DISCUSSION & CONCLUSION

We studied the effects of scatter and spectral calibration mismatch on fat-water-bone DE decompositions from dual-layer FPD data. The decomposition problem is challenging due to poor spectral separation between water and fat, and the relatively large overlap of LE (top layer) and HE (bottom layer) spectral responses. The volume conservation constraint introduces additional coupling between base materials, further increasing the sensitivity to projection nonidealities. Scatter is a substantial contributor to BME estimation errors. For the system geometry considered here, the x-ray beam needs to be either collimated to <20 mm, or the scatter correction needs to be accurate to <10% to detect ~30% BME. The decomposition is also sensitive to spectral calibration errors >1 keV effective energy shift. A fast MC scatter estimation approach was found to enable adequate visualization of a BME lesion in a realistic wrist phantom (assuming no spectral calibration error).

The results inform the ongoing development of DE CBCT protocols to mitigate scatter, e.g., scan orbits with extended air gap (possibly with collimation) that might be feasible using robotic systems¹⁴ such as the Multitom Rax. Furthermore, we are investigating robust scatter and spectral corrections with appropriate physical calibration standards deployed during imaging (similar to bone densitometry). In a parallel effort, we are translating the previously reported model-based DE three-material estimation algorithm (CMBMD)^15–17 to BME quantification.