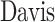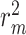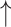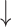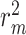Abstract
Identifying the binding affinity between a drug and its target is essential in drug discovery and repurposing. Numerous computational approaches have been proposed for understanding these interactions. However, most existing methods only utilize either the molecular structure information of drugs and targets or the interaction information of drug–target bipartite networks. They may fail to combine the molecule-scale and network-scale features to obtain high-quality representations. In this study, we propose CSCo-DTA, a novel cross-scale graph contrastive learning approach for drug-target binding affinity prediction. The proposed model combines features learned from the molecular scale and the network scale to capture information from both local and global perspectives. We conducted experiments on two benchmark datasets, and the proposed model outperformed existing state-of-art methods. The ablation experiment demonstrated the significance and efficacy of multi-scale features and cross-scale contrastive learning modules in improving the prediction performance. Moreover, we applied the CSCo-DTA to predict the novel potential targets for Erlotinib and validated the predicted targets with the molecular docking analysis.
Keywords: drug discovery, drug–target binding affinity, cross-scale, graph contrastive learning
INTRODUCTION
It takes an average of over a decade for a drug to get from the initial research and development stage to the commercialization stage [1–3], and the estimated cost for this process exceeds 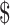 1 billion [4]. Developing new drug involves several stages, including target identification [5, 6], drug lead discovery [7, 8], preclinical development [9] and clinical trials [10]. A report reveals most drug development failures in clinical trials resulting from insufficient target validation[11]. The result highlights the significance and necessity of accurate drug screening for specific targets.
1 billion [4]. Developing new drug involves several stages, including target identification [5, 6], drug lead discovery [7, 8], preclinical development [9] and clinical trials [10]. A report reveals most drug development failures in clinical trials resulting from insufficient target validation[11]. The result highlights the significance and necessity of accurate drug screening for specific targets.
As a result, identifying interactions between drug molecules and receptor targets plays a crucial role in drug discovery. The goal is to identify compounds that can bind to disease targets with an activating or inhibiting effect, akin to matching a key to a lock [12]. These intermolecular interactions between compounds and targets occur within the pocket-like region of the protein, known as the binding site, where specific amino acid residues play a crucial role [13]. Compounds can engage with the protein targets in various orientations, influencing the efficacy and affinity of the binding process [14]. The binding affinity, along with the binding site and the binding conformation, form an interconnected system that influences the effectiveness of the interaction. Evaluating the binding affinity provides a key metric to assess the strength of interaction between a drug and its target. Experimentally determined parameters such as dissociation constant, inhibition constant and half-maximal inhibitory concentration are often used to indicate the binding strength between drugs and targets [15, 16]. However, determining these values by wet experiments is typically time-consuming and costly.
Over the past decades, computer-aided drug design technologies have had a revolutionary impact on the field of drug discovery. Molecular docking and dynamics simulation methods are frequently used to identify and predict potential drug targets, allowing researchers to accelerate the drug discovery and development process [17–19]. These methods can predict binding affinity by considering the geometric structural complementarity and binding free energy between ligand-acceptor molecules. These methods usually rely on the three-dimensional structures of the complexes. Although the tools like AlphaFold have enhanced the protein structure prediction, obtaining the dynamic protein structure and structure of protein complex is still challenging [20]. This limits the power of molecular docking and dynamics simulation methods.
Recent years have seen the emergence of artificial intelligence as a promising tool for drug–target prediction using machine learning and deep learning techniques. Unlike traditional computer-aided methods, these approaches do not strictly require the 3D structure of the ligand–receptor complex as input. Many studies have focused on binary drug–target interaction (DTI) prediction, and have achieved good results [21–27]. However, such type of prediction task may not adequately reflect the binding capacity of a drug and its target, nor accurately represent the efficacy of drug. As a result, more attention has been given to drug–target binding affinity (DTA) prediction recently, which can be defined as a regression task. Quite a few methods have been developed to address this task. For instance, Li et al. [28] proposed a docking scoring function based on a random forest model to predict affinity values between drugs and targets, and they found that low-quality data can also help improve the predictive performance of the machine-learning model. Pahikkala et al. [29] applied the regularized least squares method to predict the continuous DTA value. He et al. [30] presented a gradient-boosting tree model named SimBoost, which utilized informative features from the drug and target similarities to achieve the purpose of DTA prediction. And some methods use the sequence information of drugs and targets. For example, Öztürk et al. [31] employed double-independent convolutional neural network (CNN) blocks to extract features of drugs and targets from SMILES strings and protein sequences, respectively, and used learned representations for DTA prediction through a fully connected layer. Lin et al. [32] proposed a novel deep learning-based model named DeepGS. The model employs a CNN to learn representations of the target protein sequence and uses a graph attention network and a bidirectional gating recurrent unit to extract two types of drug features. These features are then concatenated with the protein sequence features to predict the binding affinity score. Li et al. [33] introduced the atom (in the compound)–residue (in the protein) pairwise interaction matrix to consider the non-covalent connections and predict the DTA. Zeng et al. [34] presented MATT\_DTI, which further used a self-attention block to encode the interaction information between drug representations and protein representations. Yuan et al. [35] proposed a multi-head linear attention mechanism to aggregate information for drugs and targets and applied knowledge distillation in the training stage. In practice, each drug molecule can be modeled as a graph with atoms as nodes and bonds as edges. With the recent advancements in graph neural networks, feature extraction for graph-structured data has become more convenient and effective. This has led to the development of various graph-based models for drug–target affinity prediction. Nguyen et al. [36] represented each drug as a molecular graph and introduced graph neural networks to learn the drug feature representations, and the target feature representations are extracted through CNN by capturing sequence information. Zhang et al. [37] presented SAG-DTA that introduced self-attention mechanisms when learning the representations of the molecular drug graph. However, these methods still treated the target proteins as sequential data for processing. Jiang et al. [38] utilized protein structure prediction (Pconsc4) to construct the protein contact map, and subsequently employed graph neural networks to learn features on the protein contact map and the molecular drug map. Most of the previous studies have utilized deep neural networks to learn feature representations of protein and drug molecules, which are then fed into a multilayer perceptron (MLP) for prediction. This framework is currently the foundation of machine learning models for predicting DTA. However, these methods only utilized the molecular structure information of drugs and proteins, with DTA information only appearing in the model training stage as the supervised task label. Existing methods did not consider the topology information of the drug–target network, which has proven to be useful in existing DTI prediction studies[21, 27]. These studies are achieved based on a drug–target network. In this network, drugs and targets are represented as nodes, and the connections between them are considered as edges, which correspond to the observed interactions between specific drugs and targets. Adopting this network-based approach enables us to predict unknown DTIs and understand the underlying mechanisms governing drug–target association [39, 40]. Molecular properties and drug–target network topology represent features of different scales. However, effectively capturing and integrating features from multiple scales remain a significant challenge.
To improve the performance of drug–target affinity prediction, we propose a novel cross-scale graph contrastive learning-based drug-target affinity prediction model, named CSCo-DTA, which differs from previous methods that primarily focus on using molecular features alone for DTA prediction. CSCo-DTA considers both network-scale feature and molecule-scale feature through a graph contrastive learning-based framework. CSCo-DTA consists of four main components, including molecule-scale feature extraction, network-scale feature extraction, contrastive learning across the molecule and network scales and DTA prediction. The proposed method specifically extracts network-scale features of drugs and proteins from the DTI network, as well as molecule-scale features of drugs and proteins from the drug and target molecule network, via graph neural networks. Next, using the feature representations of molecule-scale and network-scale, CSCo-DTA explores the consistency between the two perspectives through contrastive learning. Finally, an objective with a multi-task training strategy is designed to jointly optimize the representations of drugs and targets, as well as to predict DTA. We compare our method with existing methods on two benchmark datasets. The results demonstrate that CSCo-DTA performs the best on both datasets. Furthermore, we investigate the impact of multi-scale features of drugs and targets, as well as using cross-scale contrastive learning modules on the predictive performance of the model through the ablation experiment. The results demonstrate that these components significantly improve the accuracy of DTA prediction. Moreover, we conduct a case study on the potential targets of Erlotinib. The results indicate that our model can effectively predict the binding affinity of DTIs, which could have important implications for accelerating the drug discovery process. These findings highlight the potential of our approach to contribute to the development of more effective and targeted therapies for various diseases.
METHODS
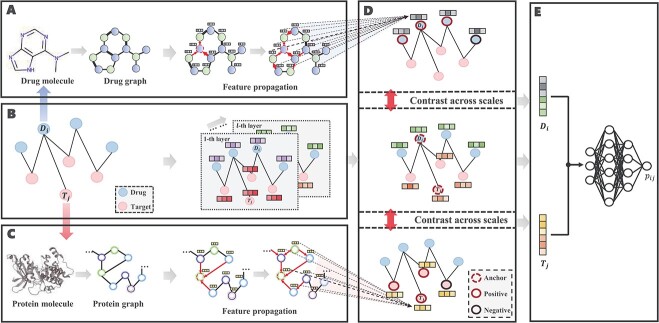
In this section, we first formulate the DTA prediction task as a regression problem and then propose a cross-scale graph contrastive learning-based drug-target affinity prediction model (CSCo-DTA). CSCo-DTA leverages graph neural network encoders to extract both molecule-scale and network-scale features, and maximizes the mutual information between these two scale features via a cross-scale graph contrastive learning component. Figure 1 illustrates the framework of the proposed model, which comprises four parts: the molecule-scale graph representation learning component (Figure 1A,C), the network-scale graph representation learning component (Figure 1B), the cross-scale graph contrastive component (Figure 1D) and the drug–target affinity prediction component (Figure 1E).
Figure 1.
The architecture of CSCo-DTA and its components are shown. A. The drug molecule is modeled as a drug graph and encoded as embeddings by GCNs. B. Graph representation learning in a drug–target network-scale view. C. The target molecule is modeled as a protein graph and encoded as embeddings by GCNs. D. The cross-scale graph contrastive learning component is used to maximize the mutual information between the above two scales. E. The drug–target affinity prediction component consists of an MLP that takes the learned embeddings as input to predict the affinity score.
Preliminaries
Before introducing the details of our method, we first formulate the DTA prediction as a regression problem and give the necessary notation used in our work. drug–target affinity prediction problem, drug–target bipartite network, drug molecular graph, protein molecular graph and the Laplacian matrix are defined as follows:
1) drug–target binding affinity (DTA) prediction. Given a set of drugs
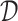 and a set of targets
and a set of targets 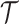 , the binding affinity values between drugs and targets can be organized into a matrix
, the binding affinity values between drugs and targets can be organized into a matrix 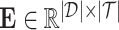 . Here, we aim to find a matrix
. Here, we aim to find a matrix 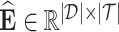 to approximate
to approximate  to predict the unobserved binding affinity value between the drug and the target.
to predict the unobserved binding affinity value between the drug and the target.- 2) drug–target bipartite network. The bipartite drug–target affinity network could be defined as
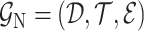 , where
, where 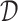 and
and 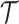 are the set of drugs and targets, respectively, and
are the set of drugs and targets, respectively, and 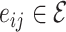 indicates the affinity between
indicates the affinity between 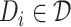 and
and 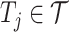 . The weight of edge
. The weight of edge 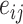 represents how tightly
represents how tightly 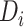 binds to
binds to 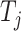 . The adjacent matrix
. The adjacent matrix 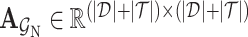 corresponding to the drug–target bipartite network can be defined as
corresponding to the drug–target bipartite network can be defined as
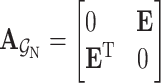
(1) 3) Drug molecular graph. Given a drug
 , the corresponding drug molecular graph can be formulated as
, the corresponding drug molecular graph can be formulated as  , where
, where 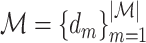 is the set of atoms of the drug, and
is the set of atoms of the drug, and 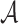 is the set of bonds of the drug,
is the set of bonds of the drug, 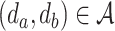 indicates the existence of a bond between the atom
indicates the existence of a bond between the atom 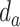 and atom
and atom 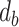 .
.4) Protein molecular graph. Each target protein can be regarded as a graph with amino acid residues as nodes. The molecule graph of the target
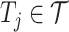 is denoted as
is denoted as 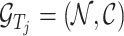 , where
, where 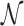 is a set consisting of amino acids and
is a set consisting of amino acids and 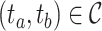 indicates that there is a contact between
indicates that there is a contact between 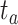 and
and 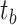 . It is noteworthy that the protein contact map is used in this paper, which is represented by a symmetric boolean matrix as a simplified representation of protein structure. The protein structure’s relevant characteristics can be obtained by analyzing the protein contact map.
. It is noteworthy that the protein contact map is used in this paper, which is represented by a symmetric boolean matrix as a simplified representation of protein structure. The protein structure’s relevant characteristics can be obtained by analyzing the protein contact map.
Graph representation learning components for different scales
In this part, we employ graph neural networks to obtain feature representations of drugs and proteins from both network-level and molecule-level perspectives based on the drug–target bipartite network and molecular graph, respectively. Details are shown as follows.
Graph representation learning in a drug–target network-scale view
The theory of network pharmacology models the interactions of drugs and their targets from the perspective of system biology. Also, it proves the importance of interactive information in the drug–target network [41]. Therefore, we perform feature extraction operations on the DTA bipartite network by utilizing the graph convolutional network (GCN). The essence of this operation is to dynamically filter the graph signal in the spectral domain to obtain low-frequency signal as the feature representations of drugs and targets in the network.
Mathematically, suppose 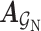 and
and 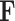 are the adjacent matrix and initial features corresponding to the DTA bipartite network, respectively, where
are the adjacent matrix and initial features corresponding to the DTA bipartite network, respectively, where 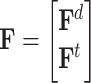 ,
, 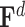 and
and 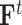 represent initial features for drugs and targets, respectively. The feature aggregation operator of GCN is defined as follows:
represent initial features for drugs and targets, respectively. The feature aggregation operator of GCN is defined as follows:
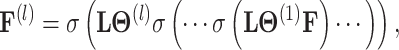 |
(2) |
where 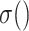 denotes the nonlinear activation function, such as ReLU [42].
denotes the nonlinear activation function, such as ReLU [42]. 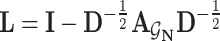 is the normalized Laplacian matrix,
is the normalized Laplacian matrix, 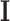 is the identity matrix and
is the identity matrix and 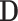 is the diagonal degree matrix defined as
is the diagonal degree matrix defined as 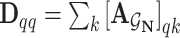 .
. 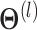 represents the trainable parameter matrix of the
represents the trainable parameter matrix of the 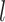 th-layer GCN.
th-layer GCN. 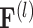 denotes the embedding matrix at the
denotes the embedding matrix at the 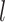 th-layer. Equation (2) describes the iterative process of learning the embedding of each node by aggregating information from their neighborhood and transforming the aggregated embeddings via multiplying a transformation matrix. Each vertex in the network gradually gains information from its high-order neighbors with the iterative process. Further, the final representation of the drug
th-layer. Equation (2) describes the iterative process of learning the embedding of each node by aggregating information from their neighborhood and transforming the aggregated embeddings via multiplying a transformation matrix. Each vertex in the network gradually gains information from its high-order neighbors with the iterative process. Further, the final representation of the drug 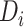 and the target
and the target 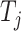 based on the network scale can be obtained as follows:
based on the network scale can be obtained as follows:
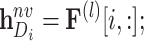 |
(3) |
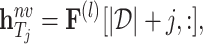 |
(4) |
where 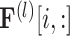 represents the
represents the 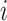 -th row of
-th row of 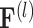 , and
, and 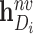 and
and 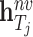 represent, respectively, the embedding of drug
represent, respectively, the embedding of drug 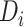 and target
and target 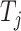 based on the molecular scale.
based on the molecular scale.
Graph representation learning in a molecule-scale view
In order to extract the molecule-level features, drug and target molecules are modeled as undirected graphs. For a drug molecular graph, nodes and edges in the graph represent atoms and bonds between atoms, respectively. For a protein molecular graph, nodes and edges in the graph represent residues and contacts between residues, respectively. The GCN is applied to encode the topology structure of a molecule-level graph.
More concretely, given a drug 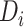 , let
, let 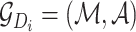 be the corresponding molecular graph (see the Preliminaries section for details). For the atom of a drug, the initial feature consists of several properties, including element type, bonding number, the count of attached hydrogen atoms, valence and whether the atom is an aromatic ring. For detailed information on the initial characteristics of nodes and edges in drug molecules, please refer to Supplementary Table 1. Based on initial atom features and molecular graph structure, we employ GCNs to learn an embedding vector for each atom and obtain the representation of the drug molecule through the readout function. Following the strategy of neighborhood aggregation, GCN produces the feature representation for each atom via aggregating embeddings of its neighbor atoms and itself iteratively. Formally, the feature aggregation in a single-layer GCN for the atom
be the corresponding molecular graph (see the Preliminaries section for details). For the atom of a drug, the initial feature consists of several properties, including element type, bonding number, the count of attached hydrogen atoms, valence and whether the atom is an aromatic ring. For detailed information on the initial characteristics of nodes and edges in drug molecules, please refer to Supplementary Table 1. Based on initial atom features and molecular graph structure, we employ GCNs to learn an embedding vector for each atom and obtain the representation of the drug molecule through the readout function. Following the strategy of neighborhood aggregation, GCN produces the feature representation for each atom via aggregating embeddings of its neighbor atoms and itself iteratively. Formally, the feature aggregation in a single-layer GCN for the atom 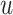 in the drug molecule is defined as
in the drug molecule is defined as
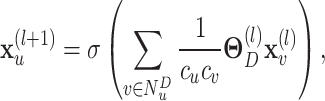 |
(5) |
where 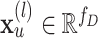 is the embedding of the atom
is the embedding of the atom 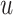 in the
in the 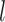 th-layer and
th-layer and 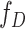 represents the dimension of the atom feature.
represents the dimension of the atom feature. 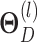 is the parameter matrix of the
is the parameter matrix of the 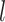 th-layer GCN.
th-layer GCN. 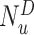 is the neighborhood set of the atom
is the neighborhood set of the atom 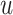 containing itself.
containing itself. 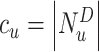 is a normalization constant.
is a normalization constant.
Given a target 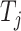 , let
, let 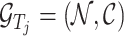 be the corresponding molecular graph (see the Preliminaries section for details). For the residue of a target, the initial feature consists of position-specific score, residue type, whether the residue is aromatic, residue weight and so on. For detailed information on the initial characteristics of nodes and edges in protein target molecules, please refer to Supplementary Table 2. We also define the feature aggregating operation for an amino acid residue
be the corresponding molecular graph (see the Preliminaries section for details). For the residue of a target, the initial feature consists of position-specific score, residue type, whether the residue is aromatic, residue weight and so on. For detailed information on the initial characteristics of nodes and edges in protein target molecules, please refer to Supplementary Table 2. We also define the feature aggregating operation for an amino acid residue 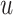 in the target molecule as follows:
in the target molecule as follows:
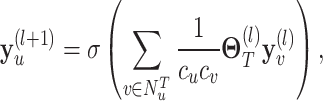 |
(6) |
where 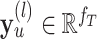 is the representation of the residue
is the representation of the residue 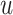 in the
in the 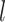 th-layer and
th-layer and 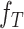 represents the dimension of residue feature.
represents the dimension of residue feature. 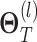 represents the parameter matrix of the
represents the parameter matrix of the 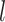 th-layer GCN.
th-layer GCN. 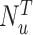 is the neighborhood set of the residue
is the neighborhood set of the residue 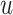 containing itself.
containing itself. 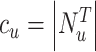 is a normalization constant.
is a normalization constant.
To sum up, the representation of each atom (amino acid residue) can be learned by the molecule-scale GCN, and the corresponding feature of the drug (protein) molecular can be further represented by a readout function as follows:
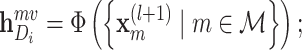 |
(7) |
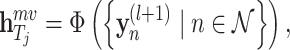 |
(8) |
where 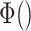 is the differentiable readout function, which is an add operation.
is the differentiable readout function, which is an add operation. 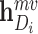 and
and 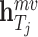 represent the embedding of drug
represent the embedding of drug 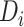 and target
and target 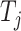 based on the molecular scale. Through this molecule-level feature extraction, we can gain the feature representation of drugs and proteins from a microscopic perspective.
based on the molecular scale. Through this molecule-level feature extraction, we can gain the feature representation of drugs and proteins from a microscopic perspective.
Cross-scale graph contrastive learning module
The molecule scale-based embeddings and the network scale-based embeddings represent drug and target features from different views, which may be related. In order to enhance feature representations by combining the molecule and network scales, we propose a cross-scale graph contrastive learning method to model embeddings based on different scales.
We first introduce the contrastive learning scheme for drugs. The scheme for targets is similar. After obtaining the drug representations of different scales by aforementioned graph neural network-based method, we first map them into the same feature space with an MLP, as shown in the following equation:
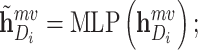 |
(9) |
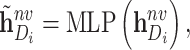 |
(10) |
where 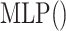 is a two-layer feedforward neural network. It is noted that
is a two-layer feedforward neural network. It is noted that 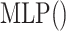 is shared by embeddings of different scales.
is shared by embeddings of different scales.
Afterwards, as shown in Figure 1D, the proposed model utilizes a contrastive learning scheme to optimize the representations. Given a drug as an anchor, its representation should be consistent with its positive samples and different from its negative samples across different scales. One of the key challenges of graph contrastive learning across scales is to define the positive and negative samples of a given anchor for providing self-supervised signals. In general, given an embedding of a drug 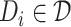 learned based on the network scale, its embedding learned from the molecular scale can be defined as the positive sample. In this study, to generate positive samples, we propose a novel sampling strategy, which includes molecular feature-based sampling and network structure-based sampling. For molecular feature-based sampling, the idea is that nodes with similar molecular structures are considered highly related and can be used as positive sample pairs. Specifically, the PubChem structure clustering tool [43] is used to calculate the molecular level drug–drug similarities, saved as
learned based on the network scale, its embedding learned from the molecular scale can be defined as the positive sample. In this study, to generate positive samples, we propose a novel sampling strategy, which includes molecular feature-based sampling and network structure-based sampling. For molecular feature-based sampling, the idea is that nodes with similar molecular structures are considered highly related and can be used as positive sample pairs. Specifically, the PubChem structure clustering tool [43] is used to calculate the molecular level drug–drug similarities, saved as 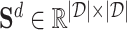 , and the Smith–Waterman algorithm [44] is used to calculate the protein sequence similarities, saved as
, and the Smith–Waterman algorithm [44] is used to calculate the protein sequence similarities, saved as 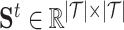 . Both drug–drug similarities and protein sequence similarities are molecular-level information. For network structure-based sampling, the idea is that nodes that share common neighbors in the network are related. We propose a meta-path-based method to calculate the similarity between drugs. The similarities between drugs are defined as the number of meta-path, which is drug–target-drug, between drugs in the drug–target network. The drug similarities are normalized and saved as
. Both drug–drug similarities and protein sequence similarities are molecular-level information. For network structure-based sampling, the idea is that nodes that share common neighbors in the network are related. We propose a meta-path-based method to calculate the similarity between drugs. The similarities between drugs are defined as the number of meta-path, which is drug–target-drug, between drugs in the drug–target network. The drug similarities are normalized and saved as 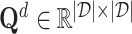 . Similarly, we obtained the target similarities, saved as
. Similarly, we obtained the target similarities, saved as 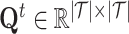 . Following aforementioned ways, we selected positive samples for each drug and each target according to molecule-level and network-level views. Specifically, to select positive samples for
. Following aforementioned ways, we selected positive samples for each drug and each target according to molecule-level and network-level views. Specifically, to select positive samples for 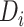 , we summed
, we summed 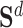 and
and 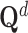 , then rank the samples with the
, then rank the samples with the 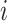 -th row in descending order. The top
-th row in descending order. The top 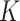 samples are selected as positive samples and the others are considered as negative samples.
samples are selected as positive samples and the others are considered as negative samples.
The embeddings of positive sample pair should be similar. The embeddings of negative sample pair should be different. Therefore, inspired by InfoNCE [45], the contrastive loss function of network scale is defined as follows:
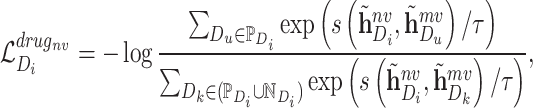 |
(11) |
where 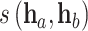 represents the cosine similarity between
represents the cosine similarity between 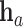 and
and 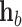 .
. 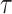 is a temperature parameter that used to adjust the similarity distribution of embeddings to better distinguish between positive and negative samples, and is typically set empirically.
is a temperature parameter that used to adjust the similarity distribution of embeddings to better distinguish between positive and negative samples, and is typically set empirically. 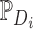 and
and 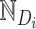 denote the positive and negative sample sets of
denote the positive and negative sample sets of 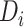 , respectively.
, respectively.
Similarly, the contrastive loss function of molecule scale is defined as follows:
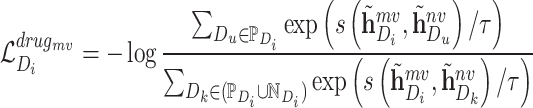 |
(12) |
In similar way, we can also define 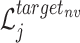 and
and 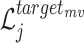 for the target
for the target 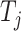 as follows:
as follows:
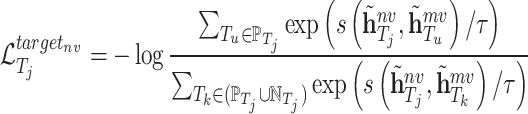 |
(13) |
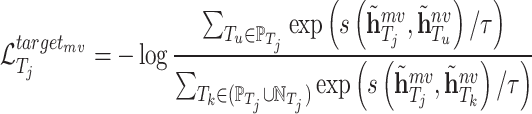 |
(14) |
In general, the part of the contrastive loss function is given as follows:
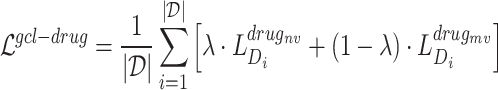 |
(15) |
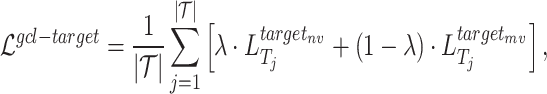 |
(16) |
where 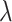 is a hyperparameter to balance the effect of both scales.
is a hyperparameter to balance the effect of both scales.
Objective with multi-task training strategy
We introduce a supervised-based loss by exploiting the original paired DTA data during training, in addition to the cross-scale contrastive-based loss. This approach allows us to fully utilize the existing labeled DTA data and maximize its potential.
In our approach, we learned the representations of drugs and targets from two different scales and projected them to the embedding space using an MLP. This results in two sets of embeddings for drugs and targets: 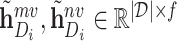 , and
, and 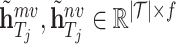 . To obtain the final representations for drugs and targets, we concatenated the mapped embeddings of both views, as shown below:
. To obtain the final representations for drugs and targets, we concatenated the mapped embeddings of both views, as shown below:
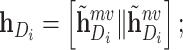 |
(17) |
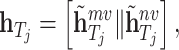 |
(18) |
where 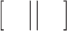 denotes the concatenation operation. We used the concatenated embeddings
denotes the concatenation operation. We used the concatenated embeddings 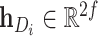 and
and 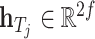 to predict the binding affinity score. The mean squared error (MSE) loss can be represented as follows:
to predict the binding affinity score. The mean squared error (MSE) loss can be represented as follows:
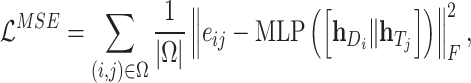 |
(19) |
where 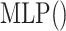 is a feedforward neural network and
is a feedforward neural network and 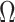 is used to denote the entries in the training set.
is used to denote the entries in the training set. 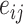 represents the experimentally verified binding affinity score between
represents the experimentally verified binding affinity score between 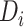 and
and 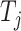 .
.
To summarize, the mathematical formulation for multi-task training in DTA prediction is as follows:
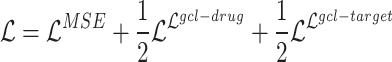 |
(20) |
By incorporating the cross-scale contrastive training objective into the DTA prediction task, we jointly optimized both objectives to improve the representations of drugs and targets during training.
RESULTS AND DISCUSSION
Data preparation
To comprehensively evaluate the performance of our proposed method, CSCo-DTA, we use two public drug–target affinity benchmark datasets: the Davis dataset [46] and the KIBA dataset [47]. The Davis dataset takes the negative logarithm of dissociation constants (pKd) as affinity values and includes 30 056 values between 68 drugs and 442 targets. The affinity scores range from 5.0 to 10.8 and indicate the binding strength of drug–target pairs. The KIBA dataset comprises 52 498 compounds and 467 kinase targets, and integrates the information of 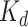 ,
, 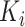 and
and 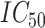 as drug–target affinity scores. The dataset was preprocessed following the method described in [30], resulting in 118 254 binding affinity scores between 2111 drugs and 229 targets, ranging from 0.0 to 17.2. In addition, each drug molecule was processed by RDKit [48] and target molecule was processed by PconsC4 [38, 49] to generate compound graph and protein contact map in the molecule-scale view (as described in Methods section). We compared our proposed method with other methods on these two datasets. The datasets were randomly divided into six subsets of equal size, with five subsets used for training, and one subset used as the test set [31, 34–36, 38]. To comprehensively evaluate the performance of the models, the MSE and
as drug–target affinity scores. The dataset was preprocessed following the method described in [30], resulting in 118 254 binding affinity scores between 2111 drugs and 229 targets, ranging from 0.0 to 17.2. In addition, each drug molecule was processed by RDKit [48] and target molecule was processed by PconsC4 [38, 49] to generate compound graph and protein contact map in the molecule-scale view (as described in Methods section). We compared our proposed method with other methods on these two datasets. The datasets were randomly divided into six subsets of equal size, with five subsets used for training, and one subset used as the test set [31, 34–36, 38]. To comprehensively evaluate the performance of the models, the MSE and 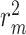 were used to assess the predictive performance of all methods.
were used to assess the predictive performance of all methods.
The performance evaluation of CSCo-DTA and baseline methods
We compared the proposed CSCo-DTA with the existing baseline methods, including DeepDTA [31], GraphDTA [36], DGraphDTA [38], MATT_DTI [34] and FusionDTA [35]. DeepDTA utilized CNNs to extract features from drug and target sequences, which were then used to predict their binding affinities. GraphDTA utilized graph neural networks to embed drug molecular graph and the target sequence embeddings were extracted through CNN. DGraphDTA utilized protein contact maps to represent the interaction between residue pairs in protein molecules, and employed graph neural networks to extract features from both protein contact maps and drug molecule graphs. MATT_DTI used 1D CNNs to learn the sequence representations of drugs and targets, and multiple attention blocks to establish the relationships between them. FusionDTA employed knowledge distillation and a novel multi-head linear attention mechanism, which aggregated global information using attention weights to make DTA predictions. In addition, we used CSCat-DTA for comparison, which directly concatenated the embeddings learned from network-scale and molecule-scale features via GCNs for fusion, and then used an MLP for prediction. The comparison methods were re-implemented based on the descriptions in the original publications. The experimental parameters for all comparison methods were set according to the model parameters given in the paper of each method.
The main hyperparameters of CSCo-DTA are as follows: (i) the temperature parameter 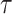 in the contrastive loss function, (ii) the biased item
in the contrastive loss function, (ii) the biased item 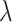 to balance the effect of two scales in the contrastive loss function, (iii) the number of positive samples
to balance the effect of two scales in the contrastive loss function, (iii) the number of positive samples 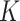 for each node in contrastive learning scheme, (iv) the number of GCN layers at the network-scale and (v) the number of GCN layers at the molecule-scale. Specifically, while keeping other parameters fixed, we systematically varied one parameter at a time to assess its influence on MSE to evaluate the effect of these parameters on the performance of CSCo-DTA. The effects of different parameter choices on model performance are presented in Supplementary Figure 1. We used
for each node in contrastive learning scheme, (iv) the number of GCN layers at the network-scale and (v) the number of GCN layers at the molecule-scale. Specifically, while keeping other parameters fixed, we systematically varied one parameter at a time to assess its influence on MSE to evaluate the effect of these parameters on the performance of CSCo-DTA. The effects of different parameter choices on model performance are presented in Supplementary Figure 1. We used 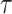 = 0.8,
= 0.8, 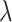 = 0.5,
= 0.5, 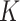 = 3, two layers of GCN in the network-scale, three layers of GCN in the molecule-scale and a learning rate of 2e-4 as experimental settings for CSCo-DTA.
= 3, two layers of GCN in the network-scale, three layers of GCN in the molecule-scale and a learning rate of 2e-4 as experimental settings for CSCo-DTA.
The performances of CSCo-DTA and other methods on the Davis dataset and KIBA dataset are shown in Table 1. The results indicate that CSCo-DTA achieves the best performance compared with the other baseline methods in most cases. Specifically, the results show significant improvement in CSCo-DTA and DGraphDTA compared with DeepDTA, which demonstrates the advantages of modeling drugs and targets as graphs to leverage their molecule structural information compared with modeling them as sequences. Moreover, CSCo-DTA outperforms DGraphDTA on both datasets, achieving 24.89% improvement in MSE and 12.95% improvement in 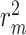 on the Davis dataset and 3.05% improvement in MSE and 1.38% improvement in
on the Davis dataset and 3.05% improvement in MSE and 1.38% improvement in 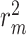 on the KIBA dataset. These results demonstrate that integrating molecule-scale and network-scale information can enhance drug–target affinity prediction. Compared with FusionDTA, the performance of CSCo-DTA achieves an average relative improvement of 20.19% in MSE and 3.60% in
on the KIBA dataset. These results demonstrate that integrating molecule-scale and network-scale information can enhance drug–target affinity prediction. Compared with FusionDTA, the performance of CSCo-DTA achieves an average relative improvement of 20.19% in MSE and 3.60% in 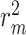 on the Davis dataset. The comparison between CSCo-DTA and CSCat-DTA indicates that the cross-scale graph contrastive learning component effectively improves DTA prediction performance in comparison with directly concatenating molecular scale and network scale features for prediction.
on the Davis dataset. The comparison between CSCo-DTA and CSCat-DTA indicates that the cross-scale graph contrastive learning component effectively improves DTA prediction performance in comparison with directly concatenating molecular scale and network scale features for prediction.
Table 1.
Comparison results of MSE and 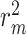 values for CSCo-DTA and baseline methods, proving our proposed method has improved performance compared with baseline methods on the Davis dataset and KIBA dataset. Lower MSE values indicate better performance. Higher
values for CSCo-DTA and baseline methods, proving our proposed method has improved performance compared with baseline methods on the Davis dataset and KIBA dataset. Lower MSE values indicate better performance. Higher 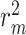 values indicate better performance
values indicate better performance
The predicted affinity scores are correlated with the experimental affinity scores
To further evaluate the performance of our proposed drug–target affinity prediction model, we conducted experiments to compare the predicted values with the measured values on two datasets. We visually presented the results in the form of scatterplots, as shown in Figure 2 and 3, where the x-axis represents the predicted values and the y-axis represents the true measured values. The red dashed line represents the line of perfect agreement between the predicted and true values, and closer data points to this line indicate higher prediction accuracy.
Figure 2.
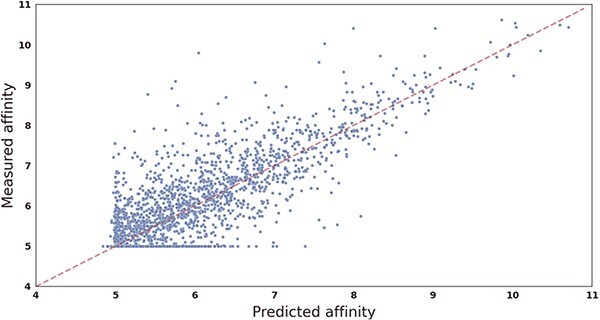
Scatter plot showing the correlation between CSCo-DTA’s predicted scores and measured binding affinities on the Davis dataset. The x-axis represents scores predicted by the CSCo-DTA model, and the y-axis represents true measured values.
Figure 3.
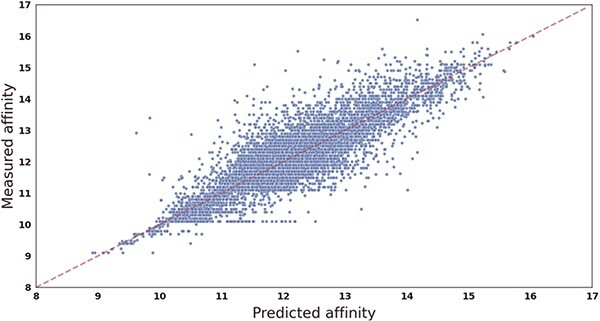
Scatter plot showing the correlation between CSCo-DTA’s predicted scores and measured binding affinities on the KIBA dataset. The x-axis represents scores predicted by the CSCo-DTA model, and the y-axis represents true measured values.
Our analysis reveals that for the Davis dataset, the dense region of data points is within the range of [5, 6], as more than half of the measured values (24 578/30 056) fall within this interval. Similarly, for the KIBA dataset, the dense region is within the range of [10, 14]. The results demonstrate that the CSCo-DTA model predicted the affinity scores very close to the ground-truth values, as evidenced by the data points from both datasets being distributed around the red dashed line. In summary, the experimental results support the high accuracy and reliability of our proposed model in predicting drug–target affinity scores, and highlight its potential in facilitating drug discovery and development efforts.
Multi-scale integration and contrastive learning enable CSCo-DTA to benefit
In this section, we conducted ablation studies to investigate the contribution of each component in our proposed model. Specifically, we examined the effectiveness of different level features and the cross-scale graph contrastive module by removing each component one by one and examining prediction performance. We conducted experiments on the Davis dataset, and the prediction performance results were shown in Figure 4 and Figure 5, which demonstrate the contribution of each component to the overall performance of the proposed model.
Figure 4.
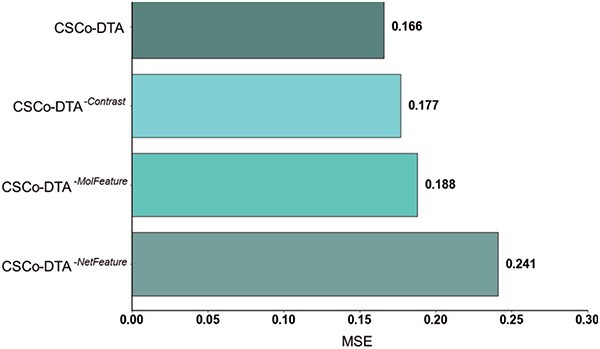
The MSE performance comparison of CSCo-DTA and its three variants on Davis dataset, proving the importance of features at different scales and the fusion of multi-scale features.
Figure 5.
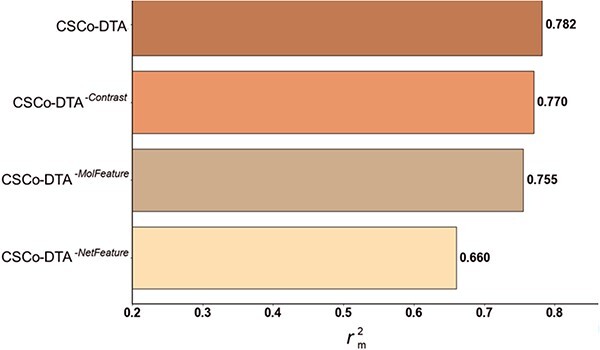
 performance comparison of CSCo-DTA and its three variants on Davis dataset, proving the importance of features at different scales and the fusion of multi-scale features.
performance comparison of CSCo-DTA and its three variants on Davis dataset, proving the importance of features at different scales and the fusion of multi-scale features.
The results in Figure 4 and Figure 5 indicate that using only molecule-scale feature (i.e. 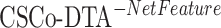 ) or network-scale feature (i.e.
) or network-scale feature (i.e. 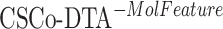 ) leads to decreased performance compared with the original model (CSCo-DTA). Specifically, the MSE values for
) leads to decreased performance compared with the original model (CSCo-DTA). Specifically, the MSE values for 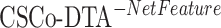 and
and 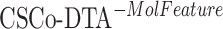 are 0.241 and 0.188, respectively, while the MSE value for CSCo-DTA is 0.166. This finding highlights the importance of both scale features in the performance of model, and underscores the necessity of integrating them to achieve optimal results. In addition, the MSE and
are 0.241 and 0.188, respectively, while the MSE value for CSCo-DTA is 0.166. This finding highlights the importance of both scale features in the performance of model, and underscores the necessity of integrating them to achieve optimal results. In addition, the MSE and 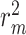 of the model without cross-scale graph contrastive component (i.e.
of the model without cross-scale graph contrastive component (i.e. 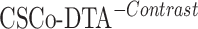 ) are reduced to 0.177 and 0.770, respectively. The results indicate that the cross-scale graph contrastive component plays a crucial role in improving the performance of the model. Thus, it can be concluded that each component of our proposed model contributes to the prediction performance of DTA.
) are reduced to 0.177 and 0.770, respectively. The results indicate that the cross-scale graph contrastive component plays a crucial role in improving the performance of the model. Thus, it can be concluded that each component of our proposed model contributes to the prediction performance of DTA.
Furthermore, we conducted experiments to assess the impact of input features on the performance, and the findings are presented in Supplementary Table 3. The results indicate that both node features and edge weights at the molecular and network scales are crucial to the performance. We further assessed the impact of drug–target network topology on the model’s performance through random edge removal and random edge swapping (Supplementary Tables 5 and 6).
Case study: predicting the new potential targets of Erlotinib
In this study, we applied the proposed CSCo-DTA model to predict potential targets for drug repositioning and performed molecular docking to validate the predicted targets. Specifically, we predicted the potential targets for Erlotinib, a tyrosine kinase receptor inhibitor used for the treatment of advanced or metastatic pancreatic cancer or non-small cell lung cancer [50–52]. Erlotinib was known to bind to the target receptor EGFR and inhibit its activity [53]. We obtained the potential targets for Erlotinib by ranking protein targets according to the prediction scores from CSCo-DTA, and found that 9 out of the top 10 targets with the highest predicted scores (Supplementary Table 4) had predicted value ranks consistent with their experimental activity ranks. To further validate our results, we performed molecular docking via LibDock [54] for the remaining target, IRAK4, which yielded a docking score of 118.115 compared with 122.603 for EGFR, suggesting a potential interaction between the drug and IRAK4. The docking results were visualized in Figure 6, which demonstrated that IRAK4 formed intermolecular forces with the amino acid residues of the targets. Furthermore, we performed the same experiment with the other method GraphDTA. The result show that IRAK4 is not included in the top 10 predicted targets for Erlotinib. This also indicates the effectiveness of our method on the drug target prediction. In conclusion, our study successfully predict potential protein targets for drugs using a computational model and validate the predicted target protein by molecular docking. These findings provide valuable insights into the mechanism of action of Erlotinib and its potential applications in the treatment of other diseases.
Figure 6.
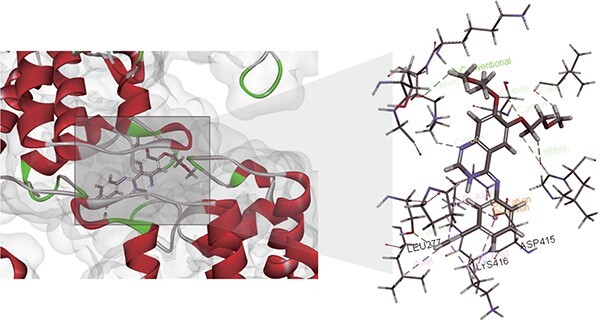
A case of the molecular docking visualization for the interaction between Erlotinib and IRAK4. The left part draws the DTIs. The right part further shows the visualization of the drug and the target pocket.
CONCLUSION
Predicting drug–target affinity is crucial for drug discovery and repurposing. In this study, we propose the CSCo-DTA approach to predict the binding affinity scores of drugs with targets. The proposed approach models the interactions between drugs and targets by learning representations from the drug–target affinity network. In addition, CSCo-DTA utilizes a GCN to extract molecule-level features of drugs or targets, and employs a contrastive learning framework to capture the potential relationship between the network-level and molecule-level views and make the learned representation more informative and integrated. Finally, we optimize the model using an objective with a multi-task training strategy. The evaluation results demonstrate that CSCo-DTA outperforms other methods in terms of MSE and 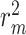 and different components of CSCo-DTA contributes to the performance improvement. We also apply CSCo-DTA to predict potential targets of Erlotinib. The results indicate that the CSCo-DTA may lead to the potential expansion of the therapeutic application of drugs.
and different components of CSCo-DTA contributes to the performance improvement. We also apply CSCo-DTA to predict potential targets of Erlotinib. The results indicate that the CSCo-DTA may lead to the potential expansion of the therapeutic application of drugs.
Key Points
We present a novel cross-scale contrastive learning-based method (CSCo-DTA) for predicting drug–target binding affinities.
CSCo-DTA utilizes graph convolutional network encoders to extract molecule-scale and network-scale features of drugs and targets. A contrastive learning framework is employed to maximize the mutual information between the features of two scales and explore their potential relationship.
The experimental results show that the CSCo-DTA outperforms state-of-the-art methods on both Davis dataset and KIBA dataset.
Supplementary Material
ACKNOWLEDGMENTS
We thank the anonymous reviewers for valuable suggestions. This paper was supported by the National Natural Science Foundation of China (62072376), Guangdong Basic and Applied Basic Research Foundation (2022A1515010144), Innovation Capability Support Program of Shaanxi (2022KJXX-75), the Fundamental Research Funds for the Central Universities (D5000230056).
Author Biographies
Jingru Wang is a doctoral student in the School of Computer Science at Northwestern Polytechnical University. Her research interests include computational biology and machine learning.
Yihang Xiao is a master student in the School of Computer Science at Northwestern Polytechnical University. His research interests include computational biology and machine learning.
Xuequn Shang is a professor in the School of Computer Science at Northwestern Polytechnical University. Her research interests include data mining and computational biology.
Jiajie Peng is an associate professor in the School of Computer Science at Northwestern Polytechnical University. His research interests include computational biology and machine learning.
Contributor Information
Jingru Wang, School of Computer Science, Northwestern Polytechnical University, Xi’an, 710072, China; Key Laboratory of Big Data Storage and Management, Northwestern Polytechnical University, Ministry of Industry and Information Technology, Xi’an, 710072, China; The National Engineering Laboratory for Integrated Aerospace-Ground-Ocean Big Data Application Technology, Xi’an, 710072, China.
Yihang Xiao, School of Computer Science, Northwestern Polytechnical University, Xi’an, 710072, China; Key Laboratory of Big Data Storage and Management, Northwestern Polytechnical University, Ministry of Industry and Information Technology, Xi’an, 710072, China.
Xuequn Shang, School of Computer Science, Northwestern Polytechnical University, Xi’an, 710072, China; Key Laboratory of Big Data Storage and Management, Northwestern Polytechnical University, Ministry of Industry and Information Technology, Xi’an, 710072, China; The National Engineering Laboratory for Integrated Aerospace-Ground-Ocean Big Data Application Technology, Xi’an, 710072, China.
Jiajie Peng, School of Computer Science, Northwestern Polytechnical University, Xi’an, 710072, China; Key Laboratory of Big Data Storage and Management, Northwestern Polytechnical University, Ministry of Industry and Information Technology, Xi’an, 710072, China; The National Engineering Laboratory for Integrated Aerospace-Ground-Ocean Big Data Application Technology, Xi’an, 710072, China; Research and Development Institute of Northwestern Polytechnical University in Shenzhen, Shenzhen, 518000, China.
CODE AND DATA AVAILABILITY
The implemented code and experimental dataset are available online at https://github.com/23AIBox/23AIBox-CSCo-DTA.
References
- 1. DiMasi JA. Assessing pharmaceutical research and development costs. JAMA Intern Med 2018;178(4):587. [DOI] [PubMed] [Google Scholar]
- 2. Wouters OJ, McKee M, Luyten J. Estimated research and development investment needed to bring a new medicine to market, 2009-2018. JAMA 2020;323(9):844–53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. DiMasi JA, Grabowski HG, Hansen RW. Innovation in the pharmaceutical industry: new estimates of R&D costs. J Health Econ 2016;47:20–33. [DOI] [PubMed] [Google Scholar]
- 4. Mullard A. New drugs cost US$2.6 billion to develop. Nat Rev Drug Disc 2014;13:877. [Google Scholar]
- 5. Duarte Y, Márquez-Miranda V, Miossec MJ, González-Nilo F. Integration of target discovery, drug discovery and drug delivery: a review on computational strategies. Wiley Interdiscip Rev Nanomed Nanobiotechnol 2019;11(4):e1554. [DOI] [PubMed] [Google Scholar]
- 6. Agamah FE, Mazandu GK, Hassan R, et al. Computational/in silico methods in drug target and lead prediction. Brief Bioinform 2020; 21(5):1663–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Blundell TL, Jhoti H, Abell C. High-throughput crystallography for lead discovery in drug design. Nat Rev Drug Discov 2002;1(1):45–54. [DOI] [PubMed] [Google Scholar]
- 8. Bruno A, Costantino G, Sartori L, Radi M. The in silico drug discovery toolbox: applications in lead discovery and optimization. Curr Med Chem 2019;26(21):3838–73. [DOI] [PubMed] [Google Scholar]
- 9. Honkala A, Malhotra SV, Kummar S, Junttila MR. Harnessing the predictive power of preclinical models for oncology drug development. Nat Rev Drug Discov 2022;21(2):99–114. [DOI] [PubMed] [Google Scholar]
- 10. Rubin EH, Gilliland DG. Drug development and clinical trials–the path to an approved cancer drug. Nat Rev Clin Oncol 2012;9(4):215–22. [DOI] [PubMed] [Google Scholar]
- 11. Arrowsmith J. Trial watch: phase II failures: 2008-2010. Nat Rev Drug Discov 2011;10(5):328–9. [DOI] [PubMed] [Google Scholar]
- 12. Du X, Li Y, Xia YL, et al. Insights into protein-ligand interactions: mechanisms, models, and methods. Int J Mol Sci 2016;17(2):144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Campbell SJ, Gold ND, Jackson RM, Westhead DR. Ligand binding: functional site location, similarity and docking. Curr Opin Struct Biol 2003;13(3):389–95. [DOI] [PubMed] [Google Scholar]
- 14. Dhakal A, McKay C, Tanner JJ, Cheng J. Artificial intelligence in the prediction of protein–ligand interactions: recent advances and future directions. Brief Bioinform 2022;23(1):bbab476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Ma W, Yang L, He L. Overview of the detection methods for equilibrium dissociation constant KD of drug-receptor interaction. J Pharm Anal 2018;8(3):147–52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Alves NJ, Stimple SD, Handlogten MW, et al. Small-molecule-based affinity chromatography method for antibody purification via nucleotide binding site targeting. Anal Chem 2012;84(18):7721–8. [DOI] [PubMed] [Google Scholar]
- 17. Vivo MD, Masetti M, Bottegoni G, et al. Role of molecular dynamics and related methods in drug discovery. J Med Chem 2016;59(9):4035–61. [DOI] [PubMed] [Google Scholar]
- 18. Kitchen DB, Decornez H, Furr JR, Bajorath J. Docking and scoring in virtual screening for drug discovery: methods and applications. Nat Rev Drug Discov 2004;3(11):935–49. [DOI] [PubMed] [Google Scholar]
- 19. Gorgulla C, Boeszoermenyi A, Wang ZF, et al. An open-source drug discovery platform enables ultra-large virtual screens. Nature 2020;580(7805):663–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Jumper J, Evans R, Pritzel A, et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021;596(7873):583–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Peng J, Wang Y, Guan J, et al. An end-to-end heterogeneous graph representation learning-based framework for drug-target interaction prediction. Brief Bioinform 2021;22(5):bbaa430. [DOI] [PubMed] [Google Scholar]
- 22. Luo Y, Zhao X, Zhou J, et al. A network integration approach for drug-target interaction prediction and computational drug repositioning from heterogeneous information. Nat Commun 2017;8(1):573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Wan F, Hong L, Xiao A, et al. NeoDTI: neural integration of neighbor information from a heterogeneous network for discovering new drug-target interactions. Bioinformatics 2019;35(1):104–11. [DOI] [PubMed] [Google Scholar]
- 24. An Q, Yu L. A heterogeneous network embedding framework for predicting similarity-based drug-target interactions. Brief Bioinform 2021;22(6):bbab275. [DOI] [PubMed] [Google Scholar]
- 25. Ye Q, Hsieh CY, Yang Z, et al. A unified drug-target interaction prediction framework based on knowledge graph and recommendation system. Nat Commun 2021;12(1):6775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Li Y, Qiao G, Wang K, Wang G. Drug-target interaction predication via multi-channel graph neural networks. Brief Bioinform 2022;23(1):bbab346. [DOI] [PubMed] [Google Scholar]
- 27. Zhao T, Hu Y, Valsdottir LR, et al. Identifying drug–target interactions based on graph convolutional network and deep neural network. Brief Bioinform 2021;22(2):2141–50. [DOI] [PubMed] [Google Scholar]
- 28. Li H, Leung KS, Wong MH, Ballester P. Low-quality structural and interaction data improves binding affinity prediction via random Forest. Molecules 2015;20(6):10947–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Pahikkala T, Airola A, Pietilä S, et al. Toward more realistic drug-target interaction predictions. Brief Bioinform 2015;16(2):325–37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. He T, Heidemeyer M, Ban F, et al. SimBoost: a read-across approach for predicting drug-target binding affinities using gradient boosting machines. J Chem 2017;9(1):24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Öztürk H, Özgür A, Ozkirimli E. DeepDTA: deep drug-target binding affinity prediction. Bioinformatics 2018;34(17):i821–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Lin X, Zhao K, Xiao T, et al. DeepGS: Deep Representation Learning of Graphs and Sequences for Drug-Target Prediction. The 24th European Conference on Artificial Intelligence (ECAI). Santiago de Compostela, Spain, 2020, 1301–8.
- 33. Li S, Wan F, Shu H, et al. MONN: a multi-objective neural network for predicting compound-protein interactions and affinities. Cell Systems 2020;10(4):308–322.e11. [Google Scholar]
- 34. Zeng Y, Chen X, Luo Y, et al. Deep drug-target binding affinity prediction with multiple attention blocks. Brief Bioinform 2021;22(5):bbab117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Yuan W, Chen G, Chen C. FusionDTA: attention-based feature polymerizer and knowledge distillation for drug-target binding affinity prediction. Brief Bioinform 2022;23(1):bbab506. [DOI] [PubMed] [Google Scholar]
- 36. Nguyen T, Le H, Quinn TP, et al. GraphDTA: predicting drug-target binding affinity with graph neural networks. Bioinformatics 2021;37(8):1140–7. [DOI] [PubMed] [Google Scholar]
- 37. Zhang S, Jiang M, Wang S, et al. SAG-DTA: prediction of drug-target affinity using self-attention graph network. Int J Mol Sci 2021;22(16):8993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Jiang M, Li Z, Zhang S, et al. Drug-target affinity prediction using graph neural network and contact maps. RSC Adv 2020;10(35):20701–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Sun M, Zhao S, Gilvary C, et al. Graph convolutional networks for computational drug development and discovery. Brief Bioinform 2020;21(3):919–35. [DOI] [PubMed] [Google Scholar]
- 40. Zeng X, Zhu S, Lu W, et al. Target identification among known drugs by deep learning from heterogeneous networks. Chem Sci 2020;11(7):1775–97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Nogales C, Mamdouh ZM, List M, et al. Network pharmacology: curing causal mechanisms instead of treating symptoms. Trends Pharmacol Sci 2022;43(2):136–50. [DOI] [PubMed] [Google Scholar]
- 42. Glorot X, Bordes A, Bengio Y. Deep sparse rectifier neural networks. J Mach Learn Res 2011;15:315–23. [Google Scholar]
- 43. Bolton EE, Wang Y, Thiessen PA, et al. PubChem: integrated platform of small molecules and biological activities. Annu Rep Comput Chem 2008;4:217–41. [Google Scholar]
- 44. Smith TF, Waterman MS. Identification of common molecular subsequences. J Mol Biol 1981;147(1):195–7. [DOI] [PubMed] [Google Scholar]
- 45. Oord A, Li Y, Vinyals O. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748. 2018.
- 46. Davis MI, Hunt JP, Herrgard S, et al. Comprehensive analysis of kinase inhibitor selectivity. Nat Biotechnol 2011;29(11):1046–51. [DOI] [PubMed] [Google Scholar]
- 47. Tang J, Szwajda A, Shakyawar S, et al. Making sense of large-scale kinase inhibitor bioactivity data sets: a comparative and integrative analysis. J Chem Inf Model 2014;54(3):735–43. [DOI] [PubMed] [Google Scholar]
- 48. Lovrić M, Molero JM, Kern R. PySpark and RDKit: moving towards big data in cheminformatics. Mol Inform 2019;38(6):e1800082. [DOI] [PubMed] [Google Scholar]
- 49. Michel M, Hurtado DM, Elofsson A. PconsC4: fast, accurate and hassle-free contact predictions. Bioinformatics 2019;35(15):2677–9. [DOI] [PubMed] [Google Scholar]
- 50. Yang Z, Hackshaw A, Feng Q, et al. Comparison of gefitinib, erlotinib and afatinib in non-small cell lung cancer: a meta-analysis. Int J Cancer 2017;140(12):2805–19. [DOI] [PubMed] [Google Scholar]
- 51. Cai H, Wang R, Guo X, et al. Combining gemcitabine-loaded macrophage-like nanoparticles and Erlotinib for pancreatic cancer therapy. Mol Pharm 2021;18(7):2495–506. [DOI] [PubMed] [Google Scholar]
- 52. Mountzios G, Syrigos KN. A benefit-risk assessment of erlotinib in non-small-cell lung cancer and pancreatic cancer. Drug Saf 2011;34(3):175–86. [DOI] [PubMed] [Google Scholar]
- 53. Bareschino MA, Schettino C, Troiani T, et al. Erlotinib in cancer treatment. Ann Oncol 2007;18:vi35–41. [DOI] [PubMed] [Google Scholar]
- 54. Rao SN, Head MS, Kulkarni A, LaLonde JM. Validation studies of the site-directed docking program LibDock. J Chem Inf Model 2007;47(6):2159–71. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The implemented code and experimental dataset are available online at https://github.com/23AIBox/23AIBox-CSCo-DTA.