High Q-Factor Plasmonic Surface Lattice Resonances in Colloidal Nanoparticle Arrays

Abstract

Surface lattice resonances (SLRs) sustained by ordered metal arrays are characterized by their narrow spectral features, remarkable quality factors, and the ability to tune their spectral properties based on the periodicity of the array. However, the majority of these structures are fabricated using classical lithographic processes or require postannealing steps at high temperatures to enhance the quality of the metal. These limitations hinder the widespread utilization of these periodic metal arrays in various applications. In this work, we use the scalable technique of template-assisted assembly of metal colloids to produce plasmonic supercrystals over centimeter areas capable of sustaining SLRs with high Q factors reaching up to 270. Our approach obviates the need for any postprocessing, offering a streamlined and efficient fabrication route. Furthermore, our method enables extensive tunability across the entire visible and near-infrared spectral ranges, empowering the design of tailored plasmonic resonant structures for a wide range of applications.

Introduction

Ordered metal nanostructures have captured the attention of the nanophotonics community due to their intriguing optical properties that surpass those of individual metallic particles.¹ These ensembles exhibit not only the well-known localized surface plasmon resonances (LSPRs) characteristic of a single particle but also a new optical resonance excited via the diffraction of the incoming wave by the array. These surface lattice resonances (SLRs) are originated by the coupling of the in-plane orders of diffraction known as Rayleigh-Wood anomalies (RAs) and the near field of each nanoparticle (NP).² The diffractive nature of the lattice resonances allows engineering of the spectral position of the SLR by adjusting the periodicity of the array. The collective response of the array effectively mitigates the inherent losses of the metal, leading to optical resonances with narrow spectral widths that extend beyond those sustained by individual nanosized particles (LSPRs).³ SLRs can be evaluated in terms of their quality factor (Q-factor), a significant figure of merit used to assess the performance of optical resonances. The Q-factor is inversely proportional to its bandwidth, which is defined as the ratio between the spectral position of the resonance (E_R) and the full width at half-maximum (fwhm) (Q = E_R/fwhm). From a physical standpoint, the Q-factor refers to the capacity of a resonance to accumulate and store energy and provides insight into the ratio of energy stored to the energy lost by an oscillator.⁴ In spectroscopic applications, high Q-factors translate into narrow and well-defined resonances; hence, an SLR with a high Q-factor will exhibit greater intensity and spectral selectivity in its optical response.

Several studies illustrate the direct relationship between the Q-factors of plasmonic nanostructure resonances and the associated near-field intensity distribution.^5,6 While LSPRs sustained by single metal NPs usually reach a value of Q = 5–10,^7,8 SLRs from ordered arrays can largely exceed these numbers, giving rise to sharp resonances that find application in a large number of fields. SLRs are ideal for sensing since they are susceptible to small changes in the refractive index of the surrounding environment with high sensitivity and specificity.⁹⁻¹² Furthermore, high Q-factor SLRs can be used to enhance the efficiency of light absorption and emission in optoelectronic devices by coupling the SLRs to an emitter, such as a quantum dot or a fluorescent molecule.^13,14

Nowadays, most metal NP arrays showing high Q-factor SLRs are produced via top-down approaches such as electron beam (EBL) or focused ion beam lithography. While these techniques offer impressive performance and design versatility, they do have certain limitations that hinder their implementation in high-demand applications: they need specialized equipment, expensive materials, and the manufacturing speed is slow (in series fabrication). The fabrication process is particularly relevant in this case since the overall size of the array strongly influences the resonance quality (small area arrays have lower Q-factors than bigger ones).¹⁵⁻¹⁷ The first SLRs experimental demonstrations were conducted independently in 2008 by Auguié, Chu, and Kravets.^5,18,19 The EBL-produced Au disc arrays yielded resonances with Q-factors ranging from 25 to 60. Subsequently, various optical configurations and geometries were explored to further improve these values.²⁰ For instance, the utilization of the Kretschmann configuration led to a Q-factor of 150 at 764 nm,²¹ while the implementation of nanostripe arrays on metal films achieved a remarkable Q-factor of 300 at 1500 nm.²² One of the most relevant alternatives to EBL fabrication is the PEEL method (Photolithography + Electro-beam deposition + Etching + Lift-off).²³⁻²⁶ Through the utilization of this technique, impressive Q-factors of 230 have been reported for arrays of Au disks,²⁷ which have been exploited to achieve lasing in several configurations.^27,28

In the vast majority of ordered metal nanostructures, the noble metal is introduced via thermal evaporation, which leads to polycrystalline deposits with high optical damping that limits the bandwidth of the optical resonance achieved, so careful attention to the deposition conditions is required.²⁹ In this regard, Gomez Rivas and co-workers directed their efforts toward modifying the rate of Ag deposition, thereby influencing its dielectric properties and surface roughness. This targeted approach resulted in achieving impressive Q-factors of 330 in 2D disc arrays.³⁰ Another strategy to improve the morphology and crystallinity of the deposited metal consists in performing a postannealing step involving temperatures as high as 700–1000 °C for several hours, which improves the quality of the resonance (Q = 430) sustained by thermally evaporated gold deposits,³¹ and is compatible with a bottom-up approach (Q = 230).³² Improving the crystalline quality of the noble metal via thermal postprocessing has given excellent results; however, it hinders the implementation of these periodic particle arrays onto many organic supports.

Bin-Salam et al. reported one of the largest Q-factors measured in plasmonic SLRs as high as Q = 2340 at λ = 1550 nm sustained by a thermally evaporated gold NP array defined by electron beam lithography and encapsulated with a silica cladding.¹⁶ One key aspect to achieve such an ultrahigh Q-factor was the utilization of a coherent illumination light source, specifically a supercontinuum laser, which also brings attention to the relevant role played by the optical set-up used to characterize the samples.

An interesting alternative to produce metal arrays with high quality over large areas is the use of colloids.³³ Chemically synthesized metallic colloidal NPs already present a high degree of crystallinity, tunable optical properties, and are compatible with scalable fabrication and solution processability.³⁴⁻³⁶ Several experimental approaches employed for the fabrication of plasmonic arrays using colloidal particles, including dip coating self-assembly,³⁷⁻⁴⁰ capillary-assisted particle assembly (CAPA),⁴¹⁻⁴³ templated-assisted self-assembly,⁴⁴⁻⁴⁶ among others,^47,48 are promising alternatives to top-down procedures. However, so far, the 2D lattices built with colloidal nanocrystals have not exhibited Q-factor values as high as their top-down counterparts. In dip coating self-assembly, a monolayer of NPs (typically core–shell metal@spacer) self-assembles at the water/air interface and is subsequently transferred onto a substrate.³⁷ This technique yields ordered domains of single Ag NPs encapsulated by poly(N-isopropylacrylamide) sustaining SLRs with Q-factors ranging from 14 to 26.^38,39 On the other hand, the CAPA method showed great potential for the formation of arrays consisting of single and few particles on prepatterned substrates. Q-factors of 36 were achieved using Au NPs on stretchable substrates,⁴⁹ while Q-values of 48 and 80 under normal and oblique incidence, respectively, were obtained using Ag nanocubes.^41,42

In template-assisted self-assembly, the colloids follow the patterns engraved in the reusable prepatterned templates, arranging into lattices of either single NPs or clusters (metamolecules) over square centimeter areas.^50,51 The process can be easily adapted to different colloid materials, shapes, sizes, solvents, and substrates. Q-factors close to 7 were observed in 54 nm diameter Au NP cluster arrays.⁴⁶ Subsequent studies revealed that the optical properties of similarly sized NP clusters could be improved through rapid thermal annealing processes, resulting in Q ≈ 25.⁴⁴ Further studies showed that the size of the nanocrystal composing the clusters strongly affects the optical properties of the arrays, with narrower SLRs obtained using smaller Au colloids (Q = 66, with 22 nm NPs).⁴⁵ In this context, colloid NPs template-assisted self-assembly might be a pivotal element to open up possibilities for large-scale fabrication of nanostructures with high Q-factor SLRs.

In this study, we use templated assembly to produce gold colloid NP arrays over large areas exhibiting high-quality factors as high as 270 under normal incidence from the visible spectral region up to 2400 nm in the IR without involving any thermal annealing process. We present a systematic analysis of the different experimental factors that influence the quality of the optical resonances sustained by the metal colloid arrays, including single particle versus cluster, and how they can be tuned to obtain Q-factors exceeding 250. Moreover, we show the effect of the near-field interaction (NP–NP coupling) on the array far-field optical response. Our findings offer a roadmap for developing high-throughput methods to fabricate plasmonic structures with super-sharp features on a variety of substrates and over large areas, within minutes.

This article is organized as follows: first, we briefly describe the template-assisted method used to produce plasmonic supercrystals from gold colloids of different sizes. Second, we compare the optical properties from 2D arrays produced with large Au colloids versus small colloids (single particle versus clusters in the unit cell) from both theoretical and experimental viewpoints. Third, we studied the relevance of the refractive index environment to achieve the highest Q-factors. Finally, by leveraging these optimized conditions, we demonstrate the production of plasmonic crystals that exhibit SLRs across the spectrum, spanning from the visible to the near-infrared region (NIR).

Experimental Methods

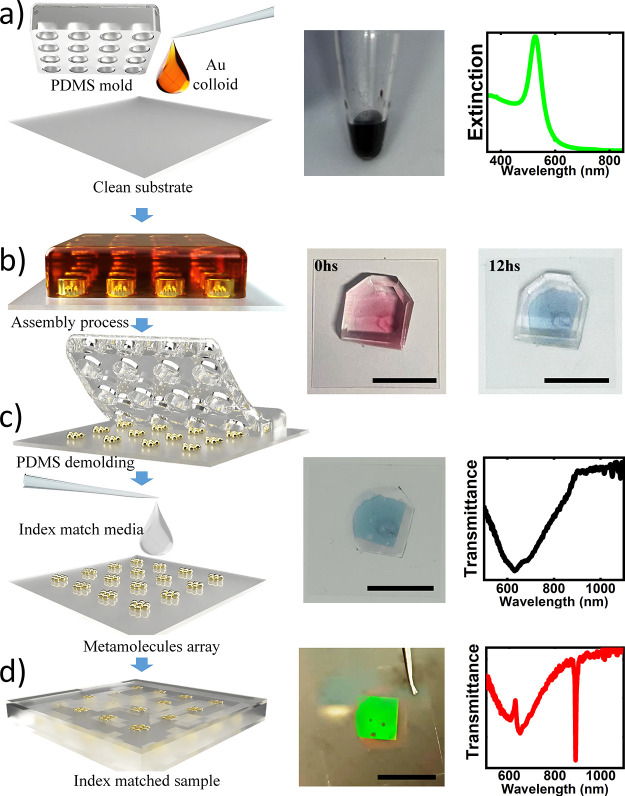
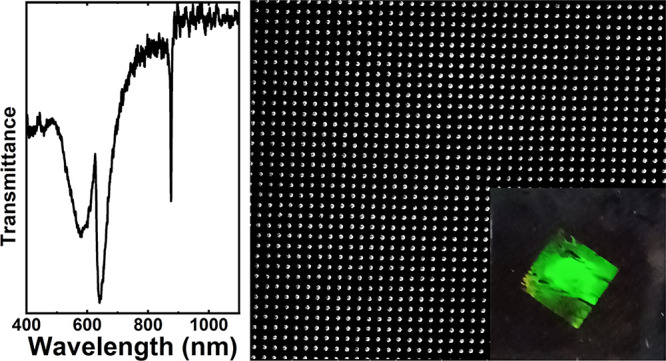
The template-assisted fabrication of the plasmonic supercrystals is summarized in Figure 1 following previous studies (see SI Video).^45,46 Basically, the technique derives from the soft lithography method as it employs prepatterned polydimethylsiloxane (PDMS) molds as printing stamps to induce the ordering of the colloidal dispersion upon drying. In this work, monodisperse spherical gold colloids with diameters between 30 and 115 nm were synthesized using the seed growth method.⁵² Prior to assembly, the surface of the particles was modified with thiolated poly(ethylene glycol) (PEG-SH) to facilitate ordering. The concentration of the colloid dispersion was kept between 10 and 50 mM of Au⁰ (see SI Table S1). An aliquot of 1–2 μL of the colloidal dispersion (Figure 1a) was placed onto the clean substrate and later covered by the patterned PDMS mold. Topographically patterned PDMS molds with square and hexagonal arrays of holes were used featuring lattice parameters between 400 and 1700 nm and hole diameters between 150 and 1020 nm (see SI Table S2) to produce lattice resonances covering the visible and NIR spectral range. Once the colloidal dispersion is encapsulated between the stamp and the glass, the system is left to evaporate undisturbed (Figure 1b). The initial coloration of the colloidal ink observed through PDMS is similar to that observed for NPs, but as the solvent evaporates, the newly formed film appears blue. Once dried, the PDMS mold is removed from the film (Figure 1c), leaving a nicely defined array determined by the geometric parameters of the mold, covering an area between 0.49 and 1 cm² and showing iridescence when observed at oblique angles. The transmittance measurements from the as-produced samples under normal incidence reveal a broad peak. As explained in the literature,⁵³ in order to observe a sharp SLR, the metal array must be surrounded by a homogeneous refractive index. Therefore, a superstrate layer is deposited on the samples in order to match the refractive index of the substrate; in the present study, we used glass and index matching oil; however, different substrate/superstrate combinations were considered, as shown in the Supporting Information Figure S3. After the incorporation of the superstrate (Figure 1d), the plasmonic array is immersed in a homogeneous dielectric environment and the SLR is clearly observable as a narrow band in the transmittance spectrum.

Figure 1.

Schematic representation of the template-induced assembly process of gold colloids. Namely, a concentrated drop of colloidal dispersion (a) is sandwiched between a prepatterned PDMS mold and the substrate (b). Upon evaporation of solvent (c), the colloids are assembled in the 2D pattern defined by the stamp. Finally, a superstrate medium is used to index match the glass substrate and produce sharp optical features (d). Inset images show photographs of the process and representative spectra. Scale bar = 1 cm.

In all cases, optical characterization was carried out using an FTIR spectrometer (Bruker Vertex 70) attached to an optical microscope with no focusing objective and under a tungsten-halogen light source. The inspected area in each case is approximately 1 mm² with the lowest numerical aperture achievable in the setup. It is worth noting that the experimental setup severely influences the Q factor that can be recorded, as we show in Figure S4, where different entrance objectives were considered. The different optical conditions used in this study are described in section 8 of the Supporting Information.

Results and Discussion

Single Particle versus Cluster-Based Plasmonic Supercrystals

The ideal 2D array of single Au nanospheres supports high-quality SLRs as reported in the literature.^2,4 In the ideal case, reducing the size of the modeled NP from 250 to 40 nm results in higher-quality resonances for a constant lattice parameter. Manjavacas and co-workers reported a dependence of the Q-factor with the geometrical parameters given by Q ≈ (LP/D)⁹, where LP is the array lattice parameter and D is the diameter of the NPs.⁶ As suggested by the exponent (ninth power), the Q-factor is dramatically enhanced to exorbitant values when small particles are considered. In summary, large areas of small single particles are required to support high Q-factor SLRs.

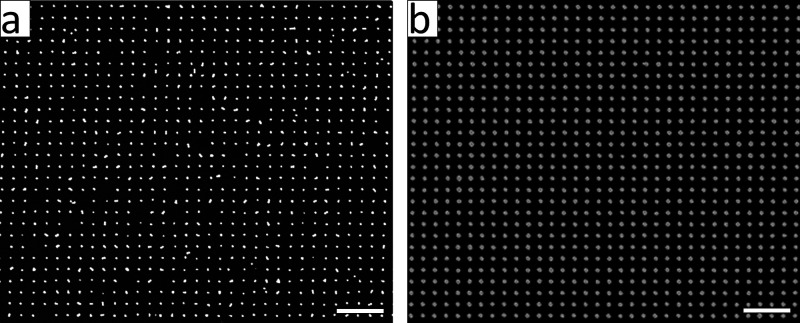
Experimentally, single NP assemblies have been reported in the literature, however, producing large-area defect-free arrays remains a challenging task.^47,48 Single metal NPs could be assembled via the CAPA method but in most cases only over relatively small areas. The template-assisted method for assembling metal colloids typically yields large patterned areas of clustered Au colloids, and producing single NP arrays remains a daunting challenge. Inherently to the process, the colloids confined within the cavities of the PDMS stamp tend to aggregate, forming “metamolecules” that eventually determine the optical properties of the array. Typically, 115 nm Au colloids in a 10 mM Au⁰ concentration were assembled under a PDMS stamp featuring 300 nm diameter cavities in a square lattice (Figure 2a,c) leading to metamolecule arrays. In order to reach a single NP array, we used PDMS molds with smaller diameters of 150 nm, hence limiting the number of colloids that can fit in a single cavity (Figure 2b,d). The concentration of the “cetyltrimethylammonium chloride” (CTAC) of the 115 nm Au nanospheres was increased to 150 μM during array fabrication to prevent aggregation under the smaller PDMS voids (see SI), while the concentration of the colloids was kept at 10 mM Au⁰. The reduction in the diameter of the cavity of the PDMS stamp leads to plasmonic crystals with fewer particles forming the unit cell, as can be seen comparing Figure 2a,b.

Figure 2.

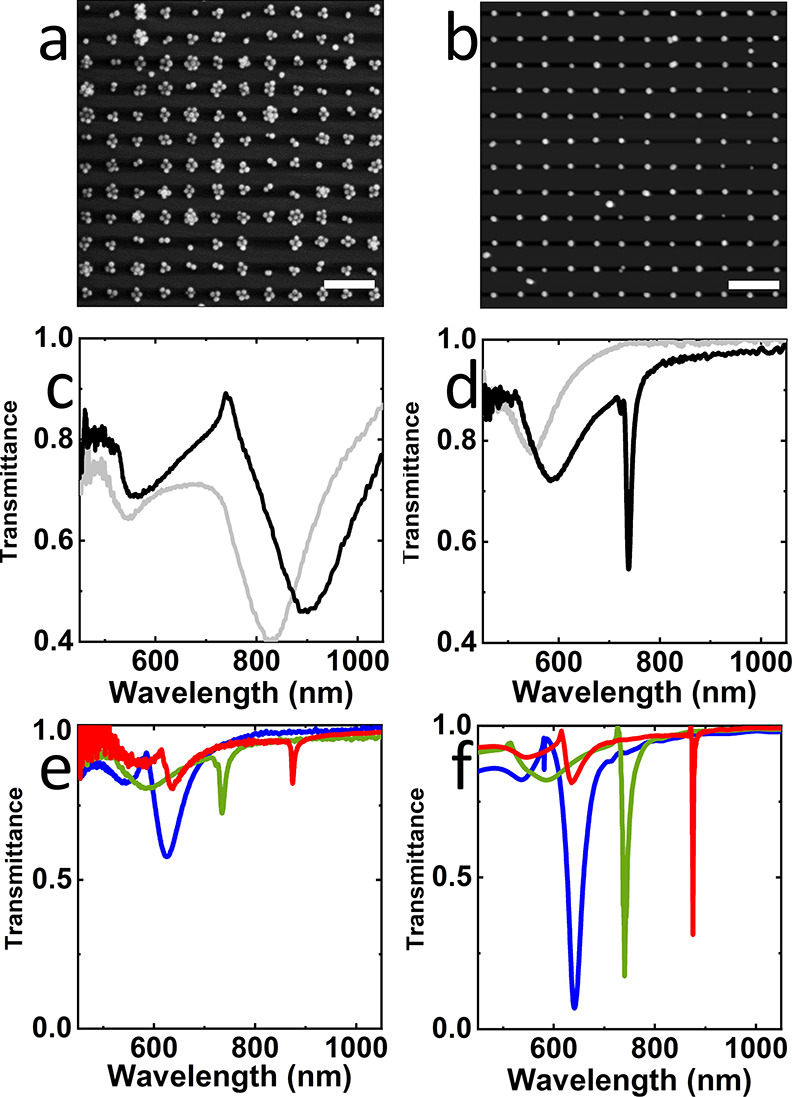
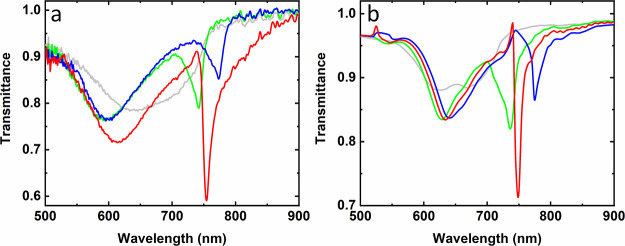
Scanning electron microscopy (SEM) images (a, b), experimental (c–e), and calculated (f) transmittance spectra at normal incidence of plasmonic meta-molecule arrays: multiple nanoparticles (a, c) and single nanoparticles per site (b, d, e, f). The nanoparticle size in all the samples is (115 ± 20) nm. The lattice parameter in (a–d) is 500 nm. The light gray lines in (c, d) represent the transmittance spectra without index matching, whereas the black lines display those with index matching. Experimental (e) and simulated (f) transmittance spectra from arrays with lattice parameters 400 (blue lines), 500 (green lines), and 600 nm (red lines). Scale bar = 1 μm.

The optical characterization of the plasmonic crystals made with 277 nm (Figure 2c) and 150 nm (Figure 2d) molds before index matching (plotted in gray solid lines) reveals a broad resonance near 550 nm attributed to the LSPR of individual particles in both cases. A broad lattice resonance is only observed in the plasmonic crystal constituted by clustered Au colloids (Figure 2c,d, gray lines). This resonance above 800 nm results from the near-field coupling of the metamolecule⁵⁴ and the diffraction by the grating, but no clear RA can be identified due to the inhomogeneous refractive index environment.⁵³ Upon incorporation of a refractive index matching layer, the single particle array clearly sustains a sharp resonance that can be attributed to a surface lattice mode, whereas the multiparticle array only shows a shift in the position of the resonance (Figure 2c,d, black lines). The different optical behavior of the single NP array with and without the index matching condition (Figure 2d) provides further evidence of this requirement. Prior to index matching, the transmittance in the 700–750 nm region is close to 100%, with the optical response solely due to the LSPR of individual particles, while the SLR is completely attenuated by the refractive index contrast at the substrate/air interface. However, when several NPs make up the unit cell of the lattice (Figure 2c), the index matching does not generate a narrow SLR; instead, the collective mode of the cluster shifts to longer wavelengths due to the higher effective index surrounding, and the RA becomes perfectly visible as a transmittance maximum at 750 nm, suggesting that the broad band located at 900 nm may have a hybrid character between LSPR and SLR.

We prepared single Au particle arrays with three different lattice parameters (400, 500, and 600 nm) and compared their experimental (Figure 2e) and theoretical (Figure 2f) transmittance spectra calculated using the finite difference time domain (FDTD) method. Both experiment and theory included a homogeneous environment (the index matching layer was applied to experimental samples), leading to a clear observation of SLRs. The spectral profile is dominated by an SLR whose spectral position depends on the lattice parameter used in each case. The experimental transmittance minima appeared at 624, 735, and 873 nm for lattice parameters 400, 500, and 600 nm, respectively. Despite the high structural quality of the samples, a slight broadening and reduced resonance amplitude are observed in the experimental samples as compared to the theory. The Q-factors obtained for the 400, 500, and 600 nm period lattices (12, 67, and 161, respectively) are not far from the theoretical limits (18, 74, and 365) predicted by FDTD simulations. Overall, single particle arrays obtained via template-induced assembly are more challenging to obtain over large areas since it is more difficult to achieve defect-free large areas. Also, the presence of defects, such as disorder, vacancies, dimers, or trimers, has a dramatic influence over the optical response of the plasmonic crystal, broadening the resonance (see FDTD simulations in Figure S5).⁵⁵

Single Au nanosphere arrays (115 nm in diameter) can be produced via template-assisted self-assembly with a high yield of single particles exhibiting high Q-factors as compared to previous reports.^45,49 However, from our perspective, the exploitation of this structure for high-quality optical resonances is hindered by the difficulty to fabricate large and defect-free areas as revealed by SEM inspection of the samples (Figures 3a and S6). In stark contrast, the use of smaller colloids (30 nm in size) greatly facilitates the production of large-area homogeneously ordered plasmonic crystals, as illustrated by the SEM image in Figure 3b. Although each unit cell composing the plasmonic crystal contains several Au NPs, the near-field coupling within each cluster is diminished due to the small colloid size,⁴⁵ hence high-quality resonances can be achieved (Figures 4, S8 and S9).

Figure 3.

Low magnification scanning electron microscopy (SEM) images of (a) 2D arrays made of single nanoparticles (Au colloid of 115 ± 20 nm) and (b) 2D arrays constituted of nanoparticle clusters (Au colloids of 30 ± 2 nm). Lattice parameter in both cases is 500 nm. Scale bar = 2 μm. A statistical analysis of the SEM images is presented in SI Figure S6.

Figure 4.

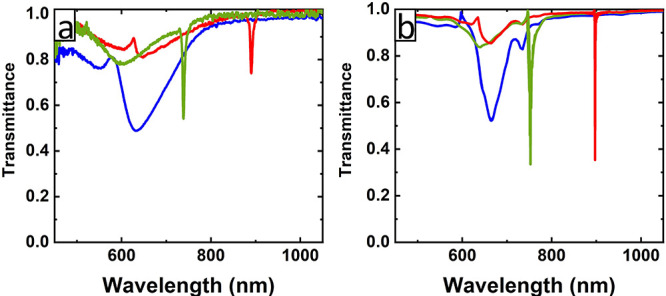
Experimental (a) and FDTD calculated (b) transmittance spectra at normal incidence of plasmonic meta-molecule arrays: 30 nm nanoparticle clusters. The lattice parameters are 400 (blue lines), 500 (green lines), and 600 nm (red lines).

Plasmonic Supercrystals Constituted by Clusters of 30 nm Au Colloids

The experimental and theoretical spectra of plasmonic crystals fabricated with 30 nm Au colloids for lattice parameters of 400, 500, and 600 nm under index-matching conditions are depicted in Figures 4 and S10. The experimental Q-factor values achieved by the 500 and 600 nm lattice parameter samples (Figure 4a) are 156 and 167, respectively, corresponding to fwhm values of 4.75 and 5.30 nm at normal incidence. To the best of our knowledge, these are among the highest Q-factor values reported for colloidal NP arrays. The second order of diffraction can also be identified in the spectral profile (more easily discernible for the 500 nm lattice parameter sample than in the single-particle array system). The spectrum for the 400 nm lattice parameter array (Figure 4, blue line) shows a significantly broader resonance for both theory and experiment, this is originated by the proximity of the LSPR and the SLR as reported in the literature.³⁰

The simulated transmittance spectra of plasmonic crystals with varying lattice parameters (400, 500, and 600 nm) made of clusters of 30 nm Au particles (Figure 4b) showed theoretical Q-factor values of 12, 241, and 1573, surpassing by far those obtained in calculations of larger single NP arrays (as depicted in Figure 2f). The exceptional performance of these plasmonic crystals constituted by arrays of small NP (30 nm) clusters is attributed to the weakened near-field coupling within a small NP cluster, which leads to a smaller bathochromic shift of the LSPR from the cluster compared to clusters of bigger particles. Additionally, the collective scattering of the particle cluster increases nonlinearly with the number of particles composing the cluster.⁴⁵ The scattering intensity is sufficient to observe the SLR, when its spectral position is out of the LSPR band from the NP cluster, in this case allowing the observation of SLRs at wavelengths greater than 600 nm.

Characterizing the Optical Properties of Plasmonic Supercrystals and the Influence of the Superstrate Refractive Index

There are several aspects that affect the value of the Q-factor that can be measured. The optical setup employed is of great importance (see Figure S4 for dependence with objectivès numerical aperture). To illustrate the relevance of the light source used, we collected transmission spectra from the arrays under a coherent light source (white laser). As recently reported by Boyd and Dolgaleva,¹⁶ coherent illumination can significantly increase the Q-factor values. For the plasmonic crystal with a 600 nm lattice parameter, a Q-factor exceeding 300 was obtained, which is twice as high as the value obtained with incoherent illumination (see Figure S11). The observed fwhm was 2.7–3.2 nm, which suggests that the Q-factor is likely even higher, limited only by the monochromator resolution, as described in the Experimental Section and SI.

Another relevant aspect of high-quality lattice resonances is the optimal index matching condition. For samples supported by glass, a superstrate layer is deposited on the plasmonic crystal to achieve the homogeneous environment condition. The relevance of the index matching layer is manifested in the experimental and theoretical spectra represented in Figure 5. The simulated optical response of a 500-nm lattice parameter plasmonic crystal whose unit cell is formed by 19–37 Au nanospheres of 28 nm diameter placed at the interface between air and a glass substrate reveals no sign of SLR. As described by Garcia de Abajo,⁵³ due to the in-plane nature of SLR, the asymmetries in the dielectric environment of the substrate (n = 1.49 at λ = 750 nm) relative to air (n = 1) result in the attenuation and broadening of its optical features, consequently the SLR becomes less distinct or undetectable. To illustrate the impact of the refractive index contrast between the substrate and superstrate (Δn = −0.49 for glass/air), we studied three different materials as superstrates (both experimentally and in the simulations): ethylene glycol (EG) with a refractive index of n = 1.419 at λ = 750 nm (green line), immersion oil (oil) with n = 1.506 at λ = 750 nm (red line), and an epoxy resist (SU-8) with n = 1.58 at λ = 750 nm (blue line), corresponding to Δn values of −0.071, 0.016, and 0.09, respectively. The effect of this superstrate layer is the clear observation of the SLR at 742, 754, and 773 nm for EG, oil, and SU-8, respectively. Remarkably, not only does the position of the SLR shift due to the influence of the superstrate but the Q factor also exhibits a significant dependence on the Δn value. When EG is employed as the superstrate (Δn = −0.071), the Q factor is 31.5, while for SU-8 (Δn = 0.09), it is 30. The optimized index matching condition for glass is immersion oil (Δn = 0.016), which results in a Q factor = 49 and displays the most intense and best-resolved resonance. Both the calculated and experimental spectra presented in Figure 5 illustrate well the relevance of the index matching condition in a plasmonic array to support well-defined lattice resonances.

Figure 5.

Experimental (a) and calculated (b) transmittance spectra at normal incidence of 500 nm lattice parameter plasmonic meta-molecule arrays (30 nm Au nanoparticle clusters). The glass substrate refractive index is n = 1.49 at λ = 750 nm, while the superstrates were air (n = 1, light gray line), ethylene glycol (n = 1.419 at λ = 750 nm, green line), immersion oil (n = 1.506 at λ = 750 nm, red line), and epoxy SU-8 (n = 1.58 at λ = 750 nm, blue line). The calculated structure is a plasmonic crystal composed of 19–37 Au clusters with the Au diameter is 28 and 2 nm interparticle distance.

Plasmonic Supercrystals in the NIR region

In what follows, we illustrate how the seamless fabrication of plasmonic crystals with 30 nm colloids allows for the fabrication of ordered arrays of NP clusters sustaining SLRs in the NIR/infrared (IR) region. Typically, reports of structures with resonances in this spectral range are achieved via top-down methods.^22,56,57 These structures are generally anisotropic, both in the morphology of the scatterers (so that one of the LSPR modes is significantly red-shifted, i.e., as in the case of the longitudinal mode of nanorods) and the lattice used, which is frequently rectangular rather than square. Furthermore, the spectral “distance” between the λ_LSPR of the clusters and the λ_SLR has an optimal value for achieving the highest Q-factor, as discussed in various articles.^16,30 Consequently, structures are typically designed on demand, including the unit cell and lattice parameter, to satisfy optimal conditions. Regarding previously reported ordered arrays of colloid NPs with resonances in the NIR/IR region, research in this area is scarce. Matricardi et al.⁴⁶ showed that clusters of 52 nm nanospheres with lattice parameters of 1600 nm exhibited resonances at wavelengths above 2000 nm.

In Figure 6, we represent the transmittance spectra of plasmonic crystals constituted by 30 nm Au colloids under index matching conditions operating from the visible to the NIR (diameters and periods are 280, 440, 700, 960 nm and 560, 740, 1140, 1600 nm, respectively). As can be seen in Figures 6a and S12, the arrays sustain well-defined SLRs along the visible and NIR regions. Q-factors with values exceeding 150 were obtained even when the resonance was above 2400 nm, where λ_SLR–λ_LSPR exceeds 1500 nm. As the lattice parameter increases (Figure 6d–g), the weak near-field coupling between small particles produces small redshifts to the LSPR from λ_LSPR = 580–730 nm. In the case of λ_RA and λ_SLRs, they are both directly proportional to the periodicity and the refractive index of the medium, undergoing an almost 1500 nm shift. In many cases, a second and even a third order of the lattice resonance are clearly visible (e.g., blue dashed line in Figure 6a).

Figure 6.

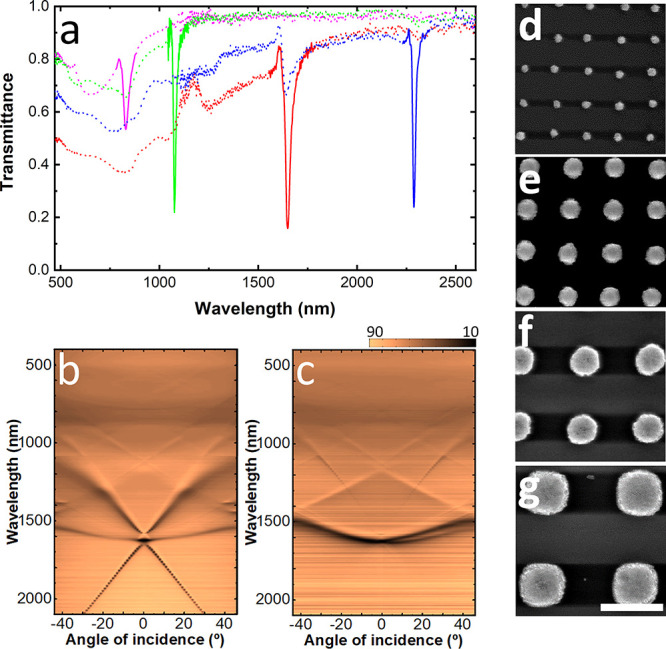
NIR operating plasmonic supercrystals. (a) Experimental transmittance spectra at normal incidence of plasmonic meta-molecule arrays (30 nm Au nanoparticle clusters) with varying lattice parameter L and diameter d. L = 560 nm and d = 280 nm (violet line), L = 740 nm, d = 440 nm (green line), L = 1140 nm, d = 700 nm (red line), and 1600 nm, d = 960 nm (blue line). Angle-resolved transmittance map measured with s- (b) and p-polarized (c) incident light of the sample with L = 1140 nm and d = 700 nm, corresponding to the red curve in panel a. SEM images corresponding to inspected samples: (d) violet, (e) green, (f) red, and (g) blue. Additional images are shown in Figure S13. Scale bar = 1 μm.

The angular-resolved characterization of a sample (set up described in Figure S2) with a lattice parameter of 1140 nm is shown in Figure 6b,c for s- and p-polarized light, respectively. The angular dispersion measurements reveal the distinct behavior of RA modes (0, ± 1) for s-polarized and (±1, 0) for p-polarized light. Whereas the first one is strongly affected by the angle of incidence of the light, the second has a small blue shift at high incidence angles. At shorter wavelength, the second-order RAs (±1, ± 1) are observed for both s- and p-polarization. These findings suggest that arrays of small NPs forming clusters exceeding several times their size are promising nanostructures for NIR/IR applications, such as those related to telecommunication C-band.

High Q-Factor Plasmonic Supercrystals

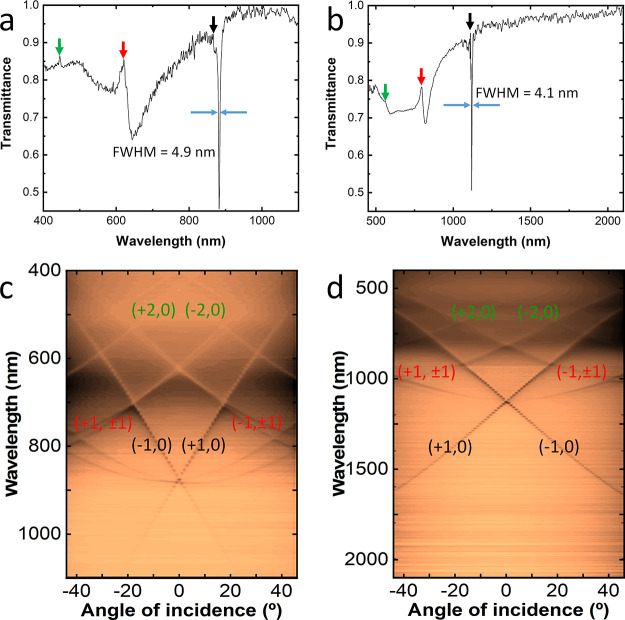
Finally, we present the spectra obtained under normal incidence and the angle-resolved transmittance maps for s-polarized light for our best-performing plasmonic arrays with lattice parameters of 600 and 780 nm (Figure 7). A notable characteristic observed in both arrays is the presence of SLRs with Q-factors surpassing 200 (additional high Q-factor samples in Figures S14–S15). Specifically, in Figure 7b, the SLR localized at 1150 nm demonstrates a remarkable Q-factor of 270 under an incoherent light source accompanied by a narrow fwhm of 4.1 nm. In both arrays, clear evidence of second-order and even third-order diffraction can be observed at respective wavelengths of 620 and 450 nm for the lattice parameter of 600, and 820 and 600 nm for the lattice parameter of 780 nm (see arrows). The angular behavior of these modes is depicted in Figure 7c,d. Under s-polarized light, the spectral dependence with respect to the incidence angle exhibits an approximately linear trend at small angles, resulting in the splitting of resonance peaks and SLRs at positions corresponding to (−1, 0) and (+1, 0) for the first order (Figure S16), and so forth for the subsequent diffracted orders. Notably, within this angular distribution, a remarkable phenomenon occurs at angles ranging from ±15 to 20°, where the first- and second-order modes intersect, leading to constructive interference and reinforcing the spectral characteristics. At larger angles, further intersections occur with the third and fourth orders with similar behavior.

Figure 7.

Experimental transmittance spectra at normal incidence of plasmonic meta-molecule arrays made with 30 nm Au nanoparticles for lattice parameters (a) 600 and (b) 780 nm. The blue arrows indicate the fwhm of each resonance. The RAs are also indicated by arrows: (±1, 0), (0, ± 1) (black), (±1, ± 1) (red), (±2, 0), (0, ± 2) (green). Angle-resolved transmittance map measured with s-polarized incident light for samples with lattice parameter 600 nm (c) and 780 nm (d).

Conclusions

We have successfully demonstrated high Q-factors (Q > 250) for plasmonic SLRs sustained by plasmonic crystals constituted by colloidal gold NP clusters. The Q-factors achieved in this study are comparable to those obtained via traditional lithography and thermal evaporation. We compared the performance of plasmonic supercrystals built from single 115 nm Au colloids with the arrays produced from smaller 30 nm Au colloids. The plasmonic crystals made from small colloids are easily produced over large areas, achieving larger defect-free areas and resulting in the best-performing arrays. Furthermore, our calculations indicate that arrays made with 30 nm NP clusters have the potential to reach Q-factors approaching 1000, surpassing their current performance. We have also stressed the relevance of the optical set-up conditions and the superstrate index matching, which are also key factors to achieve high Q resonances. Finally, we highlight that our fabrication procedure, the template assembly of metal colloids, is a simple and scalable technique that avoids the use of hazardous chemical reagents and specialized instruments (e.g., electron beam lithography). Our method makes efficient use of the materials involved as the NPs are directly deposited onto the array without leaving any residues. The template-assisted assembly provides great versatility in achieving resonances spanning across the visible and near-infrared range (from 600 to 2400 nm) and is compatible with a variety of substrates (soft/flexible) since no annealing step is required.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.3c08617.

• Details on materials, gold nanoparticle synthesis, stamp fabrication, supercrystal preparation steps with and without index matching, and additional SEM and TEM characterization; descriptions of the optical measurement setups used and the FDTD simulations; discussion on the supercrystal arrays on different substrates, geometries, illumination conditions, angular response; and additional examples of high-quality arrays (PDF)

• Video of the template-assisted self-assembly process of gold nanoparticles on a glass substrate(MP4)

Author Contributions

^† X.Q. and L.A.P. contributed equally to this work.

The authors declare no competing financial interest.