Modelling Health State Utilities as a Transformation of Time to Death in Patients with Non-Small Cell Lung Cancer

Abstract

Background

When utilities are analyzed by time to death (TTD), this has historically been implemented by ‘grouping’ observations as discrete time periods to create health state utilities. We extended the approach to use continuous functions, avoiding assumptions around groupings. The resulting models were used to test the concept with data from different regions and different country tariffs.

Methods

Five-year follow-up in advanced non-small cell lung cancer (NSCLC) was used to fit six continuous TTD models using generalized estimating equations, which were compared with progression-based utilities and previously published TTD groupings. Sensitivity analyses were performed using only patients with a confirmed death, the last year of life only, and artificially censoring data at 24 months. The statistically best-fitting model was then applied to data subsets by region and different EQ-5D-3L country tariffs.

Results

Continuous (natural) $\mathrm{Log}(TTD)$ and $1/\sqrt{\mathit{TTD}}$ models outperformed other continuous models, grouped TTD, and progression-based models in statistical fit (mean absolute error and Quasi Information Criterion). This held through sensitivity and scenario analyses. The pattern of reduced utility as a patient approaches death was consistent across regions and EQ-5D tariffs using the preferred $\mathrm{Log}(TTD)$ model.

Conclusions

The use of continuous models provides a statistically better fit than TTD groupings, without the need for strong assumptions about the health states experienced by patients. Where a TTD approach is merited for use in modelling, continuous functions should be considered, with the scope for further improvements in statistical fit by both widening the number of candidate models tested and the therapeutic areas investigated.

Supplementary Information

The online version contains supplementary material available at 10.1007/s40273-023-01314-2.

Key Points for Decision Makers

Time to death (TTD) health state utilities have been extensively used in immune-oncology, and generally estimated using discrete ‘groupings’ of TTD, typically in days or months to death.

The TTD approach can be generalized to use continuous functions of TTD, avoiding the need for strong assumptions regarding the construction of groups. The results show an improved model using fewer assumptions/variables.

TTD analysis generates consistent results across different regions and EQ-5D country tariffs, with a clear pattern of decreased utility in the final year (and particularly, the last 3 months) of life.

Introduction

Health state utility values (HSUVs) are necessary inputs to health economic models that use quality-adjusted life-years (QALYs) as a measure of value in health technology assessment. In oncology, health states have commonly been defined, and HSUV estimated, by disease progression status—an imperfect proxy of utilities for multiple reasons, including assessment schedules in clinical trials [1], and uncertainty regarding when quality of life falls relative to disease progression. More recently, a number of studies have used ‘time to death’ (TTD) groupings for health states [2, 3]. These HSUVs are then used in conjunction with survival probabilities to estimate QALYs.

Proximity to death and patient health-related quality of life have been shown to be linked [4] beyond a narrow application to modelling. Furthermore, recent retrospective analyses suggest that TTD may be more strongly correlated with health care costs than other factors, including age [5, 6]. Finally, a simulation study has provided an indication of the situations for which TTD utilities will more closely reflect the deterioration in quality of life as patients approach death than the progression-based utilities approach [7], thus offering a better differentiator of the value of competing interventions.

TTD utilities are particularly relevant and have frequently been used for immunotherapies, where patients may live for an extended period of time, potentially even with progressed disease [2, 8]. In published implementations of TTD utilities, patient utility has been aggregated by discrete groupings of proximity to death, henceforth referred to as groupings. The selection of these groupings (e.g., 0–4 weeks, 4–26 weeks, 26–52 weeks and 52+ weeks from death) appears largely arbitrary, without a strong rationale (either clinical or empirical) for the specific groupings chosen [7].

In order to understand the HSUV groupings used, the National Institute for Health and Care Excellence (NICE) website was searched to identify all immune-oncology appraisals completed by October 2022. NICE appraisals were used since a large amount of detail is publicly available, and includes most licensed medicines. In total, 55 immunotherapy appraisals were identified, of which 3 were terminated, leaving 52 appraisals. Of the 49 appraisals where the methods used were identifiable, 21 provided analysis by TTD groupings, with details split across the various documents (such as company submission, Evidence Review Group report, and decisions). Within the 21 appraisals, 10 distinct approaches to grouping were identified, where the approach used appeared to be linked more to the drug (and thus submitting company) than the disease area (Table 1). The TTD groupings used appear similar but are inconsistent between appraisals; consequently, it is difficult to establish if TTD was appropriate in these cases or to compare estimates without considerable structural uncertainty remaining. Given redaction to documents, it is possible that further groupings were also used but were not identifiable in public documents.

Table 1.

Groupings of time to death utilities in company base cases for completed NICE technology assessments to October 2022

NICE TA number	Year	Drug	Cancer type
Months: <1, 1–3, 3–6, 6–9, 9–12, 12+a Days: <30, 30–89, 90–179, 180–269, 270–359, 360+b
TA319a	2014	Ipilimumab	Melanoma
TA366b	2016	Pembrolizumab	Melanoma
TA428 b,c,d	2017	Pembrolizumab	NSCLC
Days: <30, 30–89, 90–179, 180+
TA357	2015	Pembrolizumab	Melanoma
Days: <30
TA384c	2016	Nivolumab	Melanoma
Days: <30, 30–179, 180–359, 360+
TA428d	2017	Pembrolizumab	NSCLC
TA531	2018	Pembrolizumab	NSCLC
TA557	2018	Pembrolizumab	NSCLC
TA600	2019	Pembrolizumab	NSCLC
TA650	2020	Pembrolizumab	RCC
TA737	2021	Pembrolizumab	Oesophageal/gastro-oesophageal
TA801	2022	Pembrolizumab	Breast
a Days: <30, 30–99, 100+ b Weeks: <4, 4–12, 12+
a TA517	2018	Avelumab	MCC
b TA691d	2021	Avelumab	MCC
Weeks: ≤5, 5–15, 15–30, 30+
TA520	2018	Atezolizumab	NSCLC
TA584	2019	Atezolizumab	NSCLC
TA638e	2020	Atezolizumab	SCLC
Days: <30, 31–60, 61–90, 91–180, 180–364, 365+
TA661	2020	Pembrolizumab	Head and neck SCC
Days: <35, 35–266, 267+
TA691d	2021	Avelumab	MCC
Days: <35, 35–74, 75–209, 210+
TA705	2021	Atezolizumab	NSCLC
Days: ≤28, 29–56, 57–84, 84+
TA736	2021	Nivolumab	Head and neck SCC

MCC Merkel cell carcinoma, NSCLC non-small cell lung cancer, NICE National Institute for Health and Care Excellence, RCC renal cell carcinoma, SCC squamous cell carcinoma, SCLC small cell lung cancer, TA technology assessment

^a,bare extremely similar, but differ in being defined by days vs. weeks

^cAlso included progression status as a variable

^dTwo models were included in the submission

^eAlso included a variable for ‘on treatment’

All details taken from publicly available documents hosted on the NICE website, with each TA accessible at https://www.nice.org.uk/guidance/TAXXX by substituting the TA number for ‘XXX’

The aim of this research was to investigate an alternative approach of modelling utility as a continuous function of proximity to death, avoiding the need to create discrete groupings and thus impose structural breakpoint assumptions implicit in this functional form. This was done using a large dataset in non-small cell lung cancer (NSCLC), pooling 5-year follow-up data from two international, randomized, phase III clinical studies, including regular self-reported EQ-5D-3L responses collected throughout the post-progression period [9]. The large number of patients included and the long duration of follow-up allows for more extensive analysis than typically feasible for the first analysis of a registrational study. Secondary aims were to verify that findings remained consistent across geographical regions, and using different EQ-5D-3L country tariffs.

Methods

Data Sources

Pooled data from the clinical studies of nivolumab versus docetaxel in pretreated metastatic squamous (CheckMate 017, NCT01642004) and non-squamous (CheckMate 057, NCT01673867) NSCLC was used to perform the analysis. As the studies continued to collect data beyond the registrational period, the 5-year long-term follow-up data were used, with a minimum follow-up of 64.2 and 64.5 months for CheckMate 017 and 057, respectively.

EQ-5D-3L assessment schedules were identical in the two studies. These were taken either every 4 weeks (nivolumab) or every 3 weeks (docetaxel) for the first 6 months, then every 6 weeks thereafter for the remainder of the treatment period. Follow-up EQ-5D-3L assessments were taken 30 and 100 days post treatment discontinuation, then every 3 months for the following 12 months, and then every 6 months until death. In total, the pooled datasets provided 4850 EQ-5D-3L responses from 788 patients. Over the study durations, 718 of these patients died, with a median TTD of 271 days (interquartile range 130–522).

Statistical Analysis

Following a prespecified statistical analysis plan, a number of models were fitted to the observed EQ-5D-3L data (scored using the UK value set) using the generalized estimating equation (GEE) to account for correlation at the patient level. The models tested used TTD (in days) as a linear continuous variable, as well as additional functional forms, including $\mathrm{Log}(TTD)$, ${\mathit{TTD}}^2$, ${\mathit{TTD}}^2+TTD$, $1/\sqrt{\mathit{TTD}}$, and $1/e^{\mathit{TTD}}$, all selected as the models had the ability to reflect increasingly impaired quality of life in proximity to death. The results of these continuous functions were then compared with fitted models using either models based on progression status, or previously published discrete TTD groupings of ≤ 4 weeks, 5–26 weeks, 27–52 weeks, and >52 weeks [10].

Model fits were compared using the mean absolute error (MAE) of the predicted-observed values, and the Quasi Information Criterion (QICu). The QICu mimics the Akaike Information Criterion (AIC), including penalization for the number of parameters included in the regression. Confirmatory analyses were then performed, repeating analyses in only the subset of patients who died within the study period, using data on the last year of life only, analyzed by treatment (nivolumab vs. docetaxel), and by study (due to the differing disease histologies). An additional analysis was also performed, artificially censoring the individuals at a maximum of 24 months follow-up to understand whether the same models would be preferred in the more common circumstances of less mature data, for example from early data cuts of registrational trials as are typically used for health technology assessment. This artificially censored dataset included 617 of the 718 observed deaths.

MAE and QICu were used to select a best-performing TTD model to carry forward to perform analysis by region and EQ-5D value set. The aim of this analysis was to verify that similar TTD trends were observed and to understand the magnitude of any observed differences between tariffs. The best-performing model was also applied to data split by geographic region of patients (Europe/North America (US and Canada)/rest of world), using the UK tariff value set to investigate whether the association found between patient utility and proximity to death is related to geography.

Results

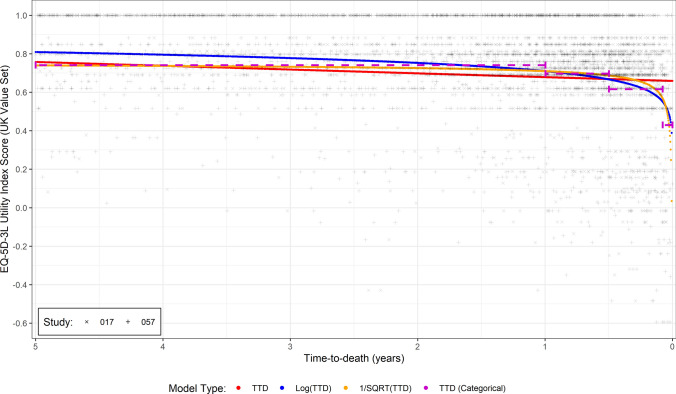
A visually perceptible trend between TTD and utility was evident in the dataset, with utility remaining relatively stable until the last year of life and then declining considerably until death. The different continuous functions of TTD were fitted to this data, with four of them converging (Fig. 1). Statistical metrics (the MAE and QICu) [Table 2] supported the perceived trend of stability followed by decline in the last year of life, shown by the poor performance of using only TTD in the regression model. To show this last year of life, electronic supplementary material (ESM) Fig. 1 is identical to Fig. 1 but showing only the final 12-month period.

Fig. 1.

EQ-5D-3L utility (UK value set) versus time to death (TTD) in the pooled CheckMate-017 and CheckMate-057 studies, including preferred model fits

Table 2.

Time to death models (TTD) applied to the pooled CheckMate-017 and CheckMate-057 EQ-5D-3L data using the UK value set

Statistical model	All patientsa [n = 788, N = 4850]		Confirmed death only used in model fits i.e. excluding censors [n = 718, N = 3627]		Last year of life only used in model fits [n = 587, N = 2007]		Artificially censoring at 24 months follow-up [n = 617, N = 2645]
	MAE	QICu	MAE	QICu	MAE	QICu	MAE	QICu
$\mathit{TTD}$	0.184	4853	0.183	3629	0.193	2009	0.184	2656
$\mathrm{L}\mathbf{o}\mathbf{g}(\mathit{T}\mathit{T}\mathit{D})$	0.173	4847	0.178	3628	0.190	2008	0.179	2656
$1/\sqrt{\mathit{TTD}}$	0.179	4847	0.177	3628	0.190	2008	0.180	2656
${1/e}^{\mathit{TTD}}$	NA	NA	NA	NA	0.201	2009	0.193	2652
${\mathit{TTD}}^2$	NA	NA	NA	NA	0.195	2009	0.186	2656
${\mathit{TTD}}^2+TTD$	NA	NA	NA	NA	0.190	2010	0.181	2657
Time to death grouping (≤4 weeks, 5–26 weeks, 27–52 weeks, ≥52 weeks)	0.175	4849	0.178	3631	0.191	2011	0.180	2658
Progression-based utilities (pre/post progression)	0.193	4852	0.191	3629	0.201	2009	0.194	2656

Bold formatting shows the preferred Log(TTD) model fit

n number of patients, N number of observations, MAE mean absolute error, QICu Quasi Information Criterion, TTD time to death (days), NA not applicable (model did not converge)

^aDate last known alive used as the date of death for continuous TTD models

Of the continuous functions, the $\mathrm{Log}(TTD)$ and $1/\sqrt{\mathit{TTD}}$ models performed the best; these models had the lowest QICu, with a slightly lower MAE for the $\mathrm{Log}\left(T,T,D\right)$ model. Comparing these models with progression-based utility models and the discrete TTD grouping models, the MAE and QICu were improved (i.e., lower), indicating a better fit to the data (MAE) and statistical fit accounting for the number of explanatory variables (QICu). For completeness, model parameters are presented in ESM Table 1.

Results remained consistent when analyzing only patients with a confirmed death in the study period and only using data in the last year of life (Table 2)—in both cases with MAE at least as good, and lower QICu for continuous functions. The $\mathrm{Log}(TTD)$ and $1/\sqrt{\mathit{TTD}}$ models performed comparably in this analysis subset, with the $\mathrm{Log}(TTD)$ model performing marginally better than the $1/\sqrt{\mathit{TTD}}$ model (<0.01 difference in the MAE). Analyzing by non-squamous versus squamous disease (implicitly by clinical study given the differences in patient populations) and by treatment, again gave consistent results (ESM Fig. 2, ESM Fig. 3). The analysis artificially censoring the data at the 24-month time period also showed a consistent pattern of a good fit to the data for continuous time models, without differences in coefficients, particularly $\mathrm{Log}(TTD)$ and $1/\sqrt{\mathit{TTD}}$ (Table 2).

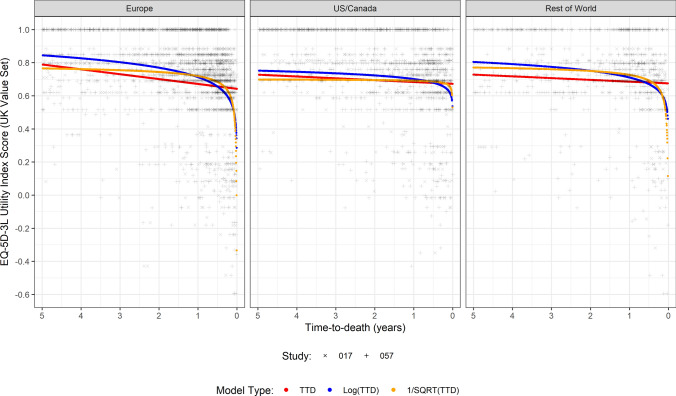
When comparing regional subgroup analyses using the $\mathrm{Log}(TTD)$ model, similar trends were observed, although with differences in the absolute utilities reported. For example, in North America, the mean utility fell from 0.678 at 180 days before death to 0.622 at 30 days before death. The corresponding values for Europe were 0.655 to 0.508, and for the rest of the world, 0.669 to 0.565 (Fig. 2). As a result, the continuous models fit showed similar patterns to when fit to the overall dataset, although with slight differences in coefficients.

Fig. 2.

Fitted utility models to EQ-5D-3L versus time to death (TTD) by region using the UK value set, including preferred model fits to CheckMate-017 and CheckMate-057 data

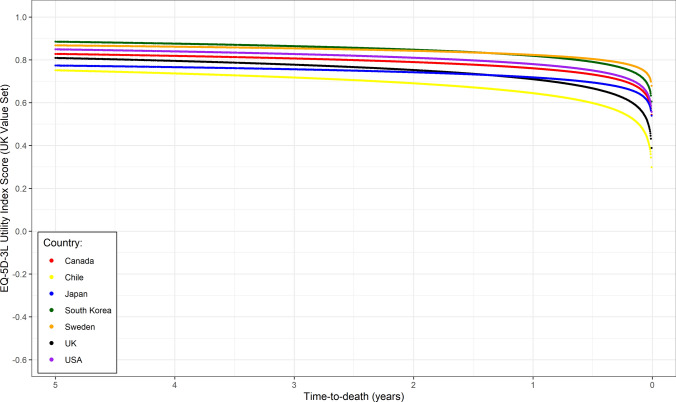
In selecting a preferred model for comparisons across regions and country tariffs, a case could be made for the use of both $\mathrm{Log}(TTD)$ and $1/\sqrt{\mathit{TTD}}$, with the $\mathrm{Log}(TTD)$ model used due to its marginally lower MAE, acknowledging that in practice a wider range of factors should be considered in choosing a preferred model than simply model fit statistics. The $\mathrm{Log}(TTD)$ model results were consistent across all relevant tariffs (Argentina, Australia, Belgium, Canada, Chile, China, Denmark, France, Germany, Italy, Japan, The Netherlands, New Zealand, Poland, Portugal, South Korea, Spain, Sweden, UK, US), with the fitted models presented in Fig. 3. Although some differences in absolute utility between tariffs are apparent, there was a high degree of consistency in the way utility fell before death across the value sets. This similarity can be seen in the predicted 90 days before death utilities, where across the country tariffs, the mean was 0.67, median 0.68, and standard deviation 0.08, i.e., a high degree of alignment between tariffs.

Fig. 3.

Log(time to death) model fits to pooled CheckMate-017 and CheckMate-057 EQ-5D-3L data applying (selected) country tariffs

Discussion

The main finding of the analysis was that predicting patient utility as a continuous function, as opposed to using a grouping approach, allows for a statistically better model fit (same or better MAE, with lower QICu) achieved without the need to impose groupings. Table 1 shows that 10 different cut-offs have been used in NICE appraisals to group time periods (ranging from 2 to 6 groups used), exemplifying the arbitrary nature of model selection with grouping; the use of a continuous function avoids such assumptions. Although the grouping approach did in some instances give an equal MAE to the continuous approaches, the additional parameters specified resulted in a worse statistical fit (as measured by the QICu), and therefore would not be preferred. This analysis also demonstrated that the continuous TTD models also provided an improvement in model fit compared with progression-based analyses, although this was not the primary comparison and may not be appropriate in all cases. As such, when a case is made for an approach to estimation of HSUVs, such statistical considerations should form a part of the reasoning, alongside the clinical rationale and assumptions implicit in the approach taken.

This finding was consistent in analyses using observations taken in the last year of life. Although multiple models appeared to provide a good fit to the data, $\mathrm{Log}(TTD)$ and $1/\sqrt{\mathit{TTD}}$ showed good performance in this dataset. There may also be other model forms that we did not test that could have provided a better fit; for example, given that much of the fall in utility occurs in the last year or so of life, a case for a ‘two-part’ model, with utility constant until a point at which utility begins to fall, could be considered. Support for such an approach can be seen from the artificial censoring at 24 months, a scenario more likely to be seen around the registration of new products where data are less mature and thus long-term estimates less available to inform longer-term fits. The consistency in the continuous TTD relationship estimated with full follow-up and artificial censoring datasets supports the validity of estimating TTD relationships with immature data, and indicates utility can reliably be extrapolated using a TTD approach for survival outside the range of the observed data. This in turn facilitates better estimates of quality of life in modelling, and thus, ultimately, in decision making at the population level. Care is still required however in the fitting of models. As highlighted by peer review, various models may asymptote if time is zero, and thus appropriate checks, adding 1 day (as with survival models), or limits may need to be applied. Equally, the variability of the data should be noted, with some patients having high utilities until extremely close to death. This heterogeneity is a feature of utility data and, indeed, is to be expected [11].

When comparing across regions, the findings of utility linked to TTD were highly consistent. In all three regions included, the same pattern of utility falling markedly in the last year of life was observed, even with different absolute baseline levels of self-reported utility. Similarly, the pattern of falls in utility towards the end of life was seen across the analyses, with only minimal differences seen between tariffs—the shape of curves was similar, with only small differences in absolute values. As such, we found no strong evidence to suggest that the relationship between TTD and utility varies substantially by region, providing further supporting evidence for the TTD approach.

The main strength of the analyses performed relates to the quantity of data available for analysis. With over 4000 EQ-5D observations with 5 years of follow-up, it represents an incredibly rich source for hypothesis testing. The main limitation of the findings is that they are derived from a contemporary clinical trial in NSCLC and may not be generalizable to other conditions or broader patient populations. Although there exists evidence that such patterns are seen in cancer patients in general [12], further research to understand where such patterns are evident is therefore required, both in different cancer areas and perhaps in non-oncology terminal diseases. Additional avenues for future research could also be including patient characteristics (such as response, performance status, or adverse events) to improve model fit, or expanding to joint models of survival and utility.

As a broader concern, the analysis performed illustrates another limitation of utility regressions—the schedule of assessments in a clinical trial often varies related to disease progression and length of follow-up. In the clinical trials examined here, assessments were more frequent while on treatment than in survival follow-up. It would seem plausible that patients are more likely to miss visits or not complete questionnaires as their health deteriorates, which would imply data are not missing at random and would be linked to utility values. Although an untestable assumption, if correct then the estimates produced from analyses (regardless of specification—continuous TTD, grouped TTD, or progression-based) may overestimate quality of life (despite values already seeming low in some instances).

Conclusions

Despite the limitations, this work represents the first application of continuous TTD functions using a large, long-term dataset. Although further analysis is required to ensure the replicability of findings and expansion of candidate models, the research indicates continuous functions represent an attractive and viable option for the modelling of utility data compared with groupings. Given the approach requires fewer assumptions than the use of groupings, it is also likely to increase the accuracy of estimates and thus acceptability to payers.

Supplementary Information

Below is the link to the electronic supplementary material.

Declarations

Author contributions

This study was conceptualized by AJH, MAC, JWS, JRP and RL; the analyses were performed by KF, AMK and RL; interpretation was provided by AJH, MAC, GM, AMK, JWS, JRP and RL; and the manuscript was drafted by AJH and RL. All authors read and approved the final version.

Conflicts of interest

Anthony J. Hatswell is an employee of Delta Hat, who were funded by BMS (the owners of the trial data) for their involvement in this study. Mohammad A. Chaudhary, James W. Shaw, and John R. Penrod are employees of BMS. Giles Monnickendam is an employee of Ceelos Consulting and a member of the NICE Technology Appraisal Committee. Alejandro Moreno-Koehler, Katie Frampton, and Rachael Lawrance are employees of Adelphi Values, who were funded by BMS for involvement in the study.

Funding

This study was funded by BMS.

Availability of data and material

This study used data from BMS clinical trials. BMS operate a data sharing request process whereby trial data can be requested, details can be found at https://www.bms.com/researchers-and-partners/independent-research/data-sharing-request-process.html.

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Code availability

Analyses were performed using SAS and R, and are designed to be reproducible using the methodology described in the article.