SMART Binary: New Sample Size Planning Resources for SMART Studies with Binary Outcome Measurements

Abstract

Sequential Multiple-Assignment Randomized Trials (SMARTs) play an increasingly important role in psychological and behavioral health research. This experimental approach enables researchers to answer scientific questions about how to sequence and match interventions to the unique, changing needs of individuals. A variety of sample size planning resources for SMART studies have been developed, enabling researchers to plan SMARTs for addressing different types of scientific questions. However, relatively limited attention has been given to planning SMARTs with binary (dichotomous) outcomes, which often require higher sample sizes relative to continuous outcomes. Existing resources for estimating sample size requirements for SMARTs with binary outcomes do not consider the potential to improve power by including a baseline measurement and/or multiple repeated outcome measurements. The current paper addresses this issue by providing sample size planning simulation procedures and approximate formulas for two-wave repeated measures binary outcomes (i.e., two measurement times for the outcome variable, before and after intervention delivery). The simulation results agree well with the formulas. We also discuss how to use simulations to calculate power for studies with more than two outcome measurement occasions. Results show that having at least one repeated measurement of the outcome can substantially improve power under certain conditions.

Introduction

Adaptive interventions (also known as dynamic treatment regimens) play an increasingly important role in various domains of psychology, including clinical (Véronneau et al., 2016), organizational (Eden, 2017), educational (Majeika et al., 2020), and health psychology (Nahum-Shani et al., 2015). Designed to address the unique and changing needs of individuals, an adaptive intervention is a protocol that specify how the type, intensity (dose), or delivery modality of an intervention should be modified based on information about the individual’s status or progress over time.

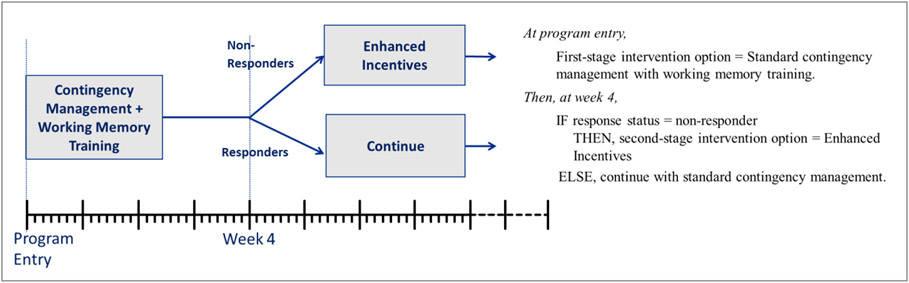
As an example, suppose the adaptive intervention in Figure 1 was employed to reduce drug use among youth with cannabis use disorder attending intensive outpatient programs. This example is based on research by Stanger and colleagues (2019) but was modified for illustrative purposes. In this example, youth are initially offered standard contingency management (financial incentives for documented abstinence) with technology-based working memory training (a commercially available digital training program to improve working memory for youth, involving 25 sessions with eight training tasks per session). As part of the intervention, drug use is monitored weekly via urinalysis and alcohol breathalyzer tests over 14 weeks. Second, at week 4, youth who test positive or do not provide drug tests are classified as non-responders and are offered enhanced (i.e., higher magnitude) incentives; otherwise, youth continue with the initial intervention.

Figure 1.

An example adaptive intervention to reduce drug use among youth with cannabis use disorder attending intensive outpatient programs

This example intervention is “adaptive” because time-varying information about the participant’s progress during the intervention (here, response status) is used to make subsequent intervention decisions (here, to decide whether to enhance the intensity of the incentives or continue with the initial intervention). Figure 1 shows how this adaptive intervention can be described with decision rules—a sequence of IF–THEN statements that specify, for each of several decision points (i.e., points in time in which intervention decisions should be made), which intervention to offer under different conditions. Note that this adaptive intervention includes a single tailoring variable: specifically, response status at week 4, measured based on drug tests. Tailoring variables are information used to decide whether and how to intervene (here, whether to offer enhanced incentives or not).

Importantly, an adaptive intervention is not a study design or an experimental design—it is an intervention design. Specifically, an adaptive intervention is a pre-specified protocol for use in practice (e.g., by health care professionals) to guide decisions about whether and how to intervene (Collins, 2018; Nahum-Shani & Almirall, 2019). However, in many cases, investigators have scientific questions about how to best construct an adaptive intervention; that is, how to select and adapt intervention options at each decision point to achieve effectiveness and scalability. Sequential multiple assignment randomized trials (SMARTs; Lavori & Dawson, 2000; Murphy, 2005) are increasingly employed in psychological research to empirically inform the development of adaptive interventions (for a review of studies see Ghosh et al., 2020). A SMART is an experimental design that includes multiple stages of randomizations and that can be used to provide information for choosing potential adaptive interventions. Each stage is intended to provide data for use in addressing questions about how to intervene and under what conditions at a particular decision point. A SMART is not itself an adaptive intervention; instead, it is a randomized trial intended to gather scientific information to optimize an adaptive intervention. Multiple potential adaptive interventions are embedded in the SMART, and data from the SMART can be used to make causal inferences concerning their relative effectiveness.

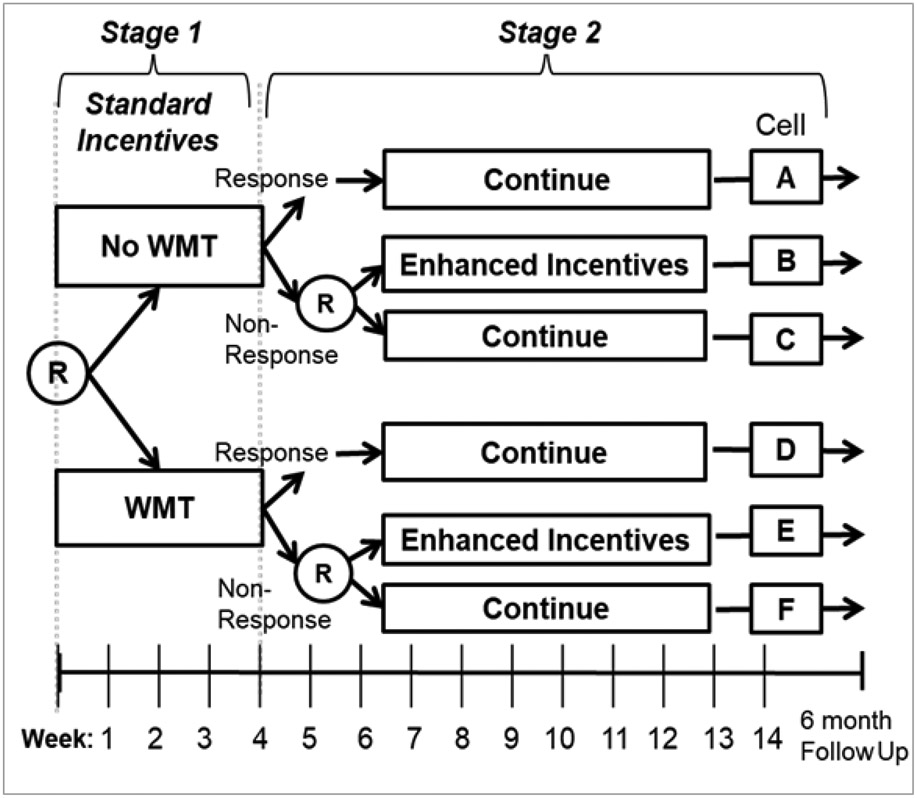
Consider the working memory training SMART in Figure 2, which was designed to collect data to empirically inform the development of an adaptive intervention for youth with cannabis use disorders (Stanger et al., 2019). This trial was motivated by two questions: in the context of a 14-week contingency management intervention, (a) is it better to initially offer a technology-based intervention that focuses on improving working memory or not? and (b) is it better to enhance the magnitude of incentives or not for youth who do not respond to the initial intervention? These questions concern how to best intervene at two decision points—the first is at program entry and the second is at week four. Hence, the SMART in Figure 2 includes two stages of randomizations, corresponding to these two decision points. Specifically, at program entry youth with cannabis use disorders were provided a standard contingency management intervention and were randomized to either offer working memory training or not. Drug use was monitored weekly via urinalysis and alcohol breath tests over 14 weeks. At week 4, those who were drug positive or did not provide drug tests were classified as early non-responders and were re-randomized to either enhanced incentives or continue with the initial intervention, whereas those who were drug negative were classified as early responders and continued with the initial intervention option (i.e., responders were not re-randomized).

Figure 2.

Working Memory Training (WMT) SMART Study

Notes: WMT denotes Working Memory Training. Circled R denotes randomization. All participants were offered standard contingency management initially.

The multiple, sequential randomizations in this example SMART give rise to four “embedded” adaptive interventions (see Table 1). One of these adaptive interventions, labeled “Enhanced working memory training” and represented by cells D+E, was described earlier (Figure 1). Many SMART designs are motivated by scientific questions that concern the comparison between embedded adaptive interventions (Kilbourne et al., 2018; Patrick et al., 2020; Pfammatter et al., 2019). For example, is it better, in terms of abstinence at week 14, to employ the “Enhanced working memory training” adaptive intervention (see Table 1; also represented by cells D, E in Figure 2), or the “Enhanced incentives alone” adaptive intervention (represented by cells A, B in Figure 2)?

Table 1.

SMART Design Used by Stanger and colleagues (2019)

Adaptive Intervention	$A_1$	$A_2$	Stage 1	Response Status	Stage 2	Cells (Fig. 1)
Enhanced working memory training	1	1	WMT+CM	Responder	Continue	D,E
				Nonresponder	Add EI
Working memory training alone	1	−1	WMT+CM	Responder	Continue	D,F
				Nonresponder	Continue
Enhanced incentives alone	−1	1	CM	Responder	Continue	A,B
				Nonresponder	Add EI
Standard contingency management	−1	−1	CM	Responder	Continue	A,C
				Nonresponder	Continue

Note: WMT = working memory training, CM = contingency management, EI = enhanced incentives.

Both adaptive interventions offer enhanced incentives to non-responders while continuing the initial intervention for responders, but the former begins with working memory training whereas the latter does not.

The comparison between embedded adaptive interventions is often operationalized using repeated outcome measurements in the course of the trial (Dziak et al., 2019; Nahum-Shani et al., 2020), such as weekly abstinence over 14 weeks measured via weekly drug tests. Repeated outcome measurements in a SMART have both practical and scientific utility (Dziak et al., 2019; Nahum-Shani et al., 2020). They can be leveraged not only to make more precise comparisons of end-of-study outcomes, but also to estimate other quantities, such as area under the curve (AUC; see Almirall et al., 2016), phase-specific slopes, and delayed effects (see Nahum-Shani et al., 2020). Dziak and colleagues (2019) and Nahum-Shani and colleagues (2020) provide guidelines for analyzing data from SMART studies in which the repeated outcome measurements are either continuous or binary. However, although sample size planning resources for SMART studies with numerical repeated outcome measurements have been proposed (e.g., by Seewald et al., 2020), sample size planning resources have yet to be developed for binary repeated outcome measurements. The current paper seeks to close this gap by developing sample size resources for planning SMART studies with binary repeated outcomes measurements.

We begin by reviewing existing sample size planning resources for SMARTs with only an end-of-study binary outcome (i.e., not repeated measurements). We then extend this approach to include a pre-randomization baseline assessment (here called pretest for convenience) and show that this can increase power for comparing adaptive interventions in terms of an end-of-study outcome (i.e., an outcome measured post randomizations which refer to as posttest). In this paper, we provide simulation-based procedures (and R code) to calculate sample size requirements, or power for a given sample size, in a SMART with binary outcomes and two or more measurement occasions. In the special case of two occasions, we also derive an asymptotic sample size formula which agrees well empirically with the simulation results in the reasonable scenarios considered. We separately consider how to use simulations, constructed appropriately for the SMART context, to calculate power for studies with more than two outcome measurements; an example simulation is given in Appendix 1. It was not practical to derive useful formulas for more than two measurement times. We show by simulations, however, that adding more outcome measurements beyond pretest and posttest may or may not lead to substantial gains in power, depending on the scenario. Nonetheless, these additional measurements may be useful in answering highly novel secondary research questions, such as about delayed effects (see Dziak et al., 2019; Nahum-Shani et al., 2020). For convenience we begin by reviewing the derivation of power and sample size formulas, and then discussing settings where approximations can reasonably be made and settings where simulations might be more beneficial.

Sample Size Planning for Binary SMART

Suppose that in the process of planning the working memory training SMART (Figure 2), investigators would like to calculate the sample size required for comparing the ‘enhanced working memory training’ and the ‘enhanced incentives alone’ adaptive interventions (see Table 1). Note that the working memory training SMART is considered a “prototypical” SMART (Ghosh et al., 2020; Nahum-Shani et al., 2022). A prototypical SMART includes two stages of randomization, and the second-stage randomization is restricted to individuals who did not respond to the initial intervention. That is, only non-responders (to both initial options) are re-randomized to second-stage intervention options. More specifically, the first randomization stage involves randomizing all experimental participants to first stage intervention options. Next, response status is assessed. Individuals classified as responders are not re-randomized and typically continue with the initial intervention option. Individuals classified as non-responders are re-randomized to second-stage intervention options. Here, response status is a tailoring variable that is integrated in the SMART by design; that is, this tailoring variable is included in each of the adaptive interventions embedded in this SMART (see Table 1).

Notation and Assumptions

Let $A_1$ denote the indicator for the first-stage intervention options, coded $+1$ for working memory training, or $-1$ for no working memory training; let $R$ denote the response status, coded 1 for responders and 0 for non-responders; and let $A_2$ denote the indicator for the second-stage intervention options among non-responders, coded $+1$ for enhanced incentives and $-1$ for continuing without enhanced incentives. Throughout, we use upper-case letters to represent a random variable, and lower-case letters to represent a particular value of that random variable. Each of the four adaptive interventions embedded in the working memory training SMART (Figure 1) can be characterized by a pair of numbers ($a_1$, $a_2$), each $+1$ or $-1$. We write that a participant in a SMART study “follows” or “is compatible with” an adaptive intervention ($a_1$, $a_2$) if this participant’s first-stage intervention is $a_1$, and if furthermore this participant is either responsive ($R=1$) to the first-stage intervention, or else is not responsive ($R=0$) and hence is offered second-stage intervention $a_2$. Notice that this representation includes responders who were not assigned to $a_2$ in practice, as long as they were assigned to $a_1$; the intuition is that they might have been assigned to $a_2$ if they had not responded. Thus, unlike in an ordinary randomized trial, the same participant (here, a responder) is compatible with more than one of the adaptive interventions being considered; data analytic approaches to handle this design feature are discussed further by Nahum-Shani and coauthors (2012) and Lu and coauthors (2016).

Let $i=1,\dots ,n$ denote study participants. We assume that, for each $i$, the binary outcomes $Y_{t,i}$ are observed at time points $t=1,\dots ,T$. Let $R_i(a_1)$ denote the potential outcome of the response status variable (see accessible introduction in Marcus et al., 2012) for person $i$ if that person is offered an adaptive intervention with initial option $a_1$. Let $Y_{t,i}^{(d)}$ or $Y_{t,i}(a_1,a_2)$ denote the potential outcome at time $t$ for person $i$ if offered an adaptive intervention $d$ defined by intervention options ($a_1$, $a_2$). It is assumed that if $R_i(a_1)=1$, then $Y_{t,i}(a_1,-1)=Y_{t,i}(a_1,+1)$, because responders cannot be impacted by the second-stage options, although they may still provide information about the effect of the first-stage options. Of course, for individuals with $R_i(a_1)=0,Y_{t,i}(a_1,-1)$ need not equal $Y_{t,i}(a_1,+1)$.

For the remainder of the manuscript, we assume that the investigator’s goal is to compare a pair of embedded adaptive interventions $d=(a_1,a_2)$ and $d^{\prime }=(a_1^{\prime },a_2^{\prime })$, in terms of outcome probability at end-of-study. We start by reviewing the $T=1$ case (final, end-of-study outcome only), then extend to $T=2$ (baseline outcome and final outcome), and then explore $T=3$ via simulations, using a flexible method that also allows for higher $T$. We assume for most of the paper that the logit link is being used, and that the estimand of interest $\Delta$ is the log odds ratio of the end-of-study outcome between a pair of adaptive interventions. Throughout, we assume that the investigator wishes to choose a sample size n to achieve adequate power to test the null hypothesis $\Delta =0$. Similar to Kidwell and colleagues (2019) and Seewald and colleagues (2020), we assume that the pair of embedded adaptive interventions being compared differs in at least the first-stage intervention option $A_1$. We also assume that there are no baseline covariates are being adjusted for. In general this is a conservative assumption because adjusting for baseline covariates sometimes improves power and usually does not worsen it (Kidwell et al., 2018).

Recall that the asymptotic sampling variance of a parameter is inversely proportional to the sample size. Across a very wide range of models, the required sample size $n$ to test a null hypothesis $\Delta =0$ with power $q$ and two-sided level $\alpha$ can be written as

$$n\ge {\left(z_q+z_{1-\alpha ∕2}\right)}^2\frac{{\sigma }_{\Delta }^2}{{\Delta }^2}$$ (1)

where $z_q={\Phi }^{-1}(q)$ is the normal quantile corresponding to the desired power, $\Delta$ is the parameter of interest, and ${\sigma }_{\Delta }^2$ is a quantity such that for a given sample size $n$, $\text{Var}(\widehat{\Delta })={\sigma }_{\Delta }^2∕n$ is its sampling variance; see Derivation 1 in the Appendix 2. The main challenge is to find a formula for ${\sigma }_{\Delta }^2$ which fits the model and design of interest, and which can be calculated from intuitively interpretable quantities, for which reasonable guesses could be elicited from a subject matter expert. In this paper we assume that the parameter of interest is the log odds ratio between outcomes for a comparison of two embedded adaptive interventions differing at least in first intervention option. That is, the null hypothesis is $\Delta =0$ where

$$\Delta =\log \text{it}({\mu }^{(d)})-\log \text{it}({\mu }^{(d^{\prime })})=\log \left(\frac{\frac{{\mu }^{(d)}}{1-{\mu }^{(d)}}}{\frac{{\mu }^{(d^{\prime })}}{1-{\mu }^{(d^{\prime })}}}\right),$$

where ${\mu }^{(d)}=E\left[Y^{(d)}\right]=P\left[Y^{(d)}=1\right]$ be the expected value of the binary end-of-study outcome for a participant who follows embedded adaptive intervention $d$. Other quantities of interest, such as the probability ratio, are also possible.

Parameters Required for Calculating Sample Size

Even after the parameter of interest has been defined and a proposed true value for it has been elicited, more information is still needed to estimate a sample size requirement. These pieces of information could be described as nuisance parameters, although some may be of secondary research interest in their own right. Specifically, let $r_d=E(R^{(d)}=1)$ be the probability that an individual given adaptive intervention $d$ will be a responder. We assume that $r_d$ depends only on $a_1$ and not on $a_2$, because the second-stage intervention is not assigned until after response status is assessed, but it is still convenient to use the $d$ subscript, with the understanding that $r_d$ and $r_{d^{\prime }}$ will be the same for adaptive interventions having the same $a_1$. In Appendix 2, we also make consistency assumptions that imply that ${\mu }^{(d)}=P(Y^{(d)}=1\mid A_1=a_1,A_2=a_2)$ and $r_d=P(R=1\mid A_1=a_1)$. ${\mu }^{(d)}$ is taken marginally over $R$, representing the overall average success probability for non-responders who were assigned to first-stage option $a_1$ and second-state option $a_2$, as well as for responders who were assigned to first-stage option $a_1$ only. Thus, ${\mu }^{(d)}$ is different from the mean response of individuals who were offered both $a_1$ and $a_2$ in practice.

Let ${\psi }^{(d0)}=P(Y^{(d)}=1\mid R^{(d)}=0)$ and ${\psi }^{(d1)}=P(Y^{(d)}=1\mid R^{(d)}=1)$ denote the end-of-study outcome probabilities for non-responders and responders, respectively, given intervention and response status. These parameters represent expected values which are conditional on $R$. These parameters can be elicited from investigators by asking them to specify the hypothesized probabilities that $Y=1$ in the six cells A-F in Figure 2. For adaptive intervention $d=(a_1,a_2)$, ${\psi }^{(d0)}$ corresponds to the probability that $Y=1$ for someone who did not respond to first-stage intervention option $a_1$ and was then offered second-stage intervention option $a_2$. Also, ${\psi }^{(d1)}$ corresponds to the probability that $Y=1$ for someone who responded to $a_1$. Because responders are not impacted by intervention option $a_2$, ${\psi }^{(d1)}$ is equal for any two adaptive interventions having the same $a_1$, whereas ${\psi }^{(d0)}$ is potentially different for each adaptive intervention. Although ${\psi }^{(d1)}$ in particular does not depend on the second-stage option comprising an adaptive intervention, it is still convenient to apply the shorthand superscript $d$ here instead of $a_1(d)$, because the adaptive intervention as a whole is assumed to be the target of inference in the analysis.

In the next section, we discuss two options for calculating sample size. The first option requires eliciting hypothetical values of the ${\psi }^{(d0)}$ and ${\psi }^{(d1)}$ parameters, which are the end-of-study outcome probabilities conditional on both the intervention options and response status. The second option requires eliciting hypothetical values of the ${\mu }^{(d)}$ parameters, which are the end-of-study outcome probabilities given the embedded adaptive interventions; these probabilities are conditional only on the intervention options and are marginal over (i.e., average across levels of) response status.

Sample Size Requirements for Posttest Only: A Single Measurement time

Let $V_d=E\left({\left(Y^{(d)}-{\mu }^{(d)}\right)}^2\right)$ be the variance of $Y^{(d)}$, marginal over $R$. Thus $V_d$ equals ${\mu }^{(d)}\left(1-{\mu }^{(d)}\right)$ because $Y^{(d)}$ is a binary outcome. Also, let $V_{d0}=\mathrm{E}\left({\left(Y^{(d)}-{\mu }^{(d)}\right)}^2\mid R=0\right)$ and $V_{d1}=\mathrm{E}\left({\left(Y^{(d)}-{\mu }^{(d)}\right)}^2\mid R=1\right)$ be the expected squared conditional residuals from the marginal expected outcome for a non-responder or responder, respectively, who follows embedded adaptive intervention $d$. By standard consistency assumptions (see Appendix 2), $V_{d0}$ can also be written as $\mathrm{E}((Y-\mu {)}^2\mid A_1=a_1(d)\phantom{)}$, $R=0$, $\phantom{(}{A}_2=a_2(d))$, and $V_{d1}$ can also be written as $\mathrm{E}((Y-\mu {)}^2\mid A_1=a_1(d),R=1)$, where $a_1(d)$ and $a_2(d)$ are the intervention options comprising adaptive intervention $d$. The quantities $V_{d0}$ and $V_{d1}$ can be calculated indirectly from the elicited probabilities, because

$$\begin{gathered} V_{d0}=\mathrm{E}\left({\left(Y^{(d)}-{\mu }^{(d)}\right)}^2\mid R=0\right) \\ =\mathrm{E}\left({\left(Y^{(d)}-{\psi }^{(d0)}\right)}^2\mid R=0\right)+\mathrm{E}\left({\left({\psi }^{(d0)}-{\mu }^{(d)}\right)}^2\mid R=0\right) \\ +2\mathrm{E}(\left(Y^{(d)}-{\psi }^{(d0)}\right)\left({\psi }^{(d0)}-{\mu }^{(d)}\right)\mid R=0) \\ ={\psi }^{(d0)}\left(1-{\psi }^{(d0)}\right)+{\left({\psi }^{(d0)}-{\mu }^{(d)}\right)}^2+0 \\ ={\psi }^{(d0)}\left(1-{\psi }^{(d0)}\right)+r_d^2{\left({\psi }^{(d1)}-{\psi }^{(d0)}\right)}^2, \end{gathered}$$

and similarly

$$\begin{gathered} V_{d1}=\mathrm{E}\left((Y^{(d)}-{\mu }^{(d)}{)}^2\mid R=1\right) \\ ={\psi }^{(d1)}(1-{\psi }^{(d1)})+(1-r_d{)}^2({\psi }^{(d1)}-{\psi }^{(d0)}{)}^2. \end{gathered}$$

Hence, $V_{d0}$ and $V_{d1}$ can be interpreted as the variances of $Y^{(d)}$ conditional on $R=0$ or $R=1$, plus an extra quantity that can be interpreted as the effect of response status.

These expressions lead to a sample size recommendation for a pairwise comparison of two adaptive interventions differing at least on stage-1 recommendation. Specifically,

$$n\ge \frac{{\left(z_q+z_{1-\frac{\alpha }{2}}\right)}^2\left(\frac{4(1-r_d)V_{d0}+2r_d{V}_{d1}}{V_d^2}+\frac{4(1-r_{d^{\prime }})V_{d^{\prime }0}+2r_{d^{\prime }}{V}_{d^{\prime }1}}{V_{d^{\prime }}^2}\right)}{{\Delta }^2},$$ (2)

where $\Delta$ is the true log odds ratio between the adaptive interventions.

Appendix 2 describes how we derived the expression above, using standard causal assumptions, from a sandwich covariance formula

$$\mathrm{Cov}(\widehat{\theta })=\frac{1}{n}{\mathit{B}}^{-1}{\mathit{MB}}^{-1}.$$

Here $\mathit{B}=E\left({\sum }_d{w}^{(d)}{V}_d{\mathit{x}}_d^T{\mathit{x}}_d\right)={\sum }_d{V}_d{\mathit{x}}_d^T{\mathit{x}}_d$ where ${\mathit{x}}_d$ is the design matrix expressing adaptive intervention $d$, $w^{(d)}$ is the weight of a given individual under adaptive intervention $d$, and

$$\mathit{M}=E\left({\left(\sum _d{w}^{(d)}{V}_d^{-1}{\mathit{x}}_d^T(Y-{\mu }^{(d)})\right)}^{\otimes 2}\right).$$

Note that weights are employed because non-responders are randomized twice (with probability ½ each time) whereas responders are randomized once (with probability ½), so that the former are under represented in the sample mean under a specific embedded adaptive intervention $d$ (i.e., they have ¼ change of folowing $d$ whereas responders have ½ chance). Thus, inverse probability weights are used (i.e., 4 for non-responders and 2 for responders) to correct for this underrepresentation (see details in Nahum-Shani et al., 2012 and Dziak et al., 2019). Because of the definition of the weights, $\mathit{M}$ simplifies to a diagonal matrix with entries

$$4(1-r_d)V_{d0}+2r_d{V}_{d1}.$$

It is assumed that the target contrast can be written as ${\mathit{c}}^T\theta$ for some vector $\mathit{c}$, where

$${\sigma }_{\Delta }^2=\frac{1}{n}\text{Var}({\mathit{c}}^T\theta )={\mathit{c}}^T\text{Var}\left(\frac{1}{n}\theta \right)\mathit{c}={\mathit{c}}^T({\mathit{B}}^{-1}{\mathit{MB}}^{-1})\mathit{c}.$$

In the case of the logistic regression model, this would be true for a pairwise log odds ratio. For a pairwise comparison between adaptive interventions $d$ and $d^{\prime }$, the researcher would set $c_d=+1$, $c_{d^{\prime }}=-1$, and other entries of $\mathit{c}$ to zero. After some algebra, the sandwich covariance therefore implies Equation (2). Details are given in Appendix 2.

It appears at first that formula (2) requires specifying hypothetical values for all probabilities, both conditional on $R$ and marginal over $R$, because $V_{d0}$ and $V_{d1}$ depend on both sets of probabilities. However, in practice only the conditional probabilities ${\psi }^{(d0)}$ and ${\psi }^{(d1)}$ for each adaptive intervention and the response rate need to be specified, because the marginal probabilities can then be computed by expectations: ${\mu }^{(d)}=(1-r_d){\psi }^{(d0)}+r_d{\psi }^{(d1)}$. However, although ${\mu }^{(d)}$ can be computed from ${\psi }^{(d0)}$, ${\psi }^{(d1)}$, and $r_d$, additional assumptions would be needed to compute ${\psi }^{(d0)}$ and ${\psi }^{(d1)}$ from ${\mu }^{(d)}$ and $r_d$.

Kidwell and colleagues (2018) provide an alternative formula, which (in terms of our notation) assumes that $V_{d0}\le V_d$, $V_{d1}\le V_d$, $V_{d^{\prime }0}\le V_{d^{\prime }}$, and $V_{d^{\prime }1}\le V_{d^{\prime }}$. Under these variance assumptions, the approximate required sample size is

$$n\ge 2\frac{{\left(z_q+z_{1-\alpha ∕2}\right)}^2}{{\Delta }^2}\left(\frac{2-r_d}{V_d}+\frac{2-r_{d^{\prime }}}{V_{d^{\prime }}}\right).$$ (3)

Under the further simplifying assumption that the proportion of responders is equal in the two adaptive interventions being compared ($r_d=r_{d^{\prime }}=r$), expression (2) simplifies to

$$n\ge 2(2-r)\frac{{\left(z_q+z_{1-\alpha ∕2}\right)}^2}{{\Delta }^2}\frac{1}{V_d+V_{d^{\prime }}}.$$

The sample size formula above is equivalent to a sample size formula for a two-arm RCT with binary outcome, multiplied by the quantity $2-r$, which Kidwell and colleagues (2018) interpreted as a design effect. In practice, this formula requires eliciting hypothetical values for the marginal outcome probabilities ${\mu }_d$ for each adaptive intervention of interest, and the response rate $r$. Based on these parameters, one can calculate the variance $V_d={\mu }_d(1-{\mu }_d)$ for each adaptive intervention and calculate the log odds ratio $=({\mu }_d∕(1-{\mu }_d))∕({\mu }_{d^{\prime }}∕(1-{\mu }_{d^{\prime }}))$.

Both formula (2) and formula (3) require that the proportion of responders be elicited. Kidwell and colleagues (2019) note that setting $r=0$ provides a conservative upper bound on required sample size, but the resulting approximation is very pessimistic and may lead to an infeasibly high recommendation.

Both formula (2), which we describe here as a conditional-probabilities-based (CPB) formula, and formula (3) which we describe as a marginal-probabilities-based (MPB) formula, have advantages and disadvantages. The marginal formula requires additional assumptions, but then requires fewer parameters to be elicited. Furthermore, the marginal probabilities are related directly to the marginal log odds ratio of interest for comparing embedded adaptive interventions. In other words, since the hypothesis concerns the comparison of two embedded adaptive interventions, it may be more straightforward for many investigators to specify parameters that describe the characteristics of these adaptive intervention, rather than their corresponding cells. However, other researchers may find the conditional probabilities for each cell comprising the adaptive interventions of interest more intuitive to elicit, as they directly correspond to the randomization structure of the SMART being planned. In the following section, we extend both formulas to settings with a baseline measurement of the outcome.

Sample Size Requirements for Pretest and Posttest: Two Measurement Times

Power in experimental studies can often be improved by considering a baseline (pre-randomization) assessment as well as the end-of-study outcome (see Benkeser et al., 2021; Vickers & Altman, 2001). These are sometimes described as a pretest and posttest; here, we refer to them as $Y_0$ and $Y_1$. The pretest is assumed to be measured prior to the initial randomization, and therefore causally unrelated to the randomly assigned interventions. The pretest could either be included as a covariate, or else could be modeled as a repeated measure in a multilevel model; we assume the latter approach in the sample size derivations. Below we provide formulas that are similar to (2) and (3), but take advantage of additional information from the baseline measurement.

Let ${\mu }^{(0)}=E(Y_0)$ be the expected value for the baseline measurement of the outcome at the beginning of the study. Here, neither $Y_0$ nor ${\mu }^{(0)}$ are indexed by adaptive intervention $d$, because $Y_0$ is measured prior to randomization. Let ${\mu }^{(d)}=E\left(Y_1^{(d)}\right)$ be the expected value for the end-of-study measurement of the outcome for an individual given adaptive intervention $d$. Then by Derivation 4 in Appendix 2, the approximate required sample size can be written as

$$n=\frac{{\left(z_q+z_{1-\alpha ∕2}\right)}^2}{{\Delta }^2}{\mathit{c}}^T{\mathit{B}}^{-1}{\mathit{MB}}^{-1}\mathit{c}$$ (4)

where the formulas for $\mathit{c}$, $\mathit{B}$, and $\mathit{M}$ are derived in Appendix 2. The derivation comes from a sandwich covariance formula as in the posttest-only case, and follows the general ideas of Lu and colleagues (2016) and Seewald and colleagues (2020). Specifically $\mathit{B}={\sum }_d{\mathit{X}}_d^T{\mathit{S}}_d{\mathit{X}}_d$ where ${\mathit{G}}_d$ is a $2\times 2$ diagonal matrix with entries $\text{Var}(Y_0^{(d)})$ and $\text{Var}(Y_1^{(d)})$, ${\mathit{R}}_d$ is the $2\times 2$ within-person correlation matrix between $Y_0^{(d)}$ and $Y_1^{(d)}$, and ${\mathit{S}}_d={\mathit{G}}_d^{\frac{1}{2}}{\mathit{R}}_d^{-1}{\mathit{G}}_d^{\frac{1}{2}}$. Under some assumptions (see Appendix 2), $\mathit{M}$ can be approximated by ${\sum }_{d}4(1-r_d){\mathit{D}}_d^T{\mathit{V}}_d^{-1}{\mathit{V}}_{d0}{\mathit{V}}_d^{-1}{\mathit{D}}_d+{\sum }_{d}2r_d{\mathit{D}}_d^T{\mathit{V}}_d^{-1}{\mathit{V}}_{d1}{\mathit{V}}_d^{-1}{\mathit{D}}_d$.

A formula like (4) can be implemented in code but provides little intuitive understanding. However, under the further assumption that the variance is independent of response status given adaptive intervention received, equation (4) simplifies to the following:

$$n=\frac{(2-r){\left(z_q+z_{1-\alpha ∕2}\right)}^2}{{\Delta }^2}\left(\frac{4-3{\rho }^2}{2V_d}-\frac{{\rho }^2}{\sqrt{V_d{V}_{d^{\prime }}}}+\frac{4-3{\rho }^2}{2V_{d^{\prime }}}\right).$$ (5)

The key to the simplifications used in deriving (5) is that $\mathit{B}$ and $\mathit{M}$ can each be expressed as an “arrowhead” matrix, i.e., a matrix which is all zeroes except for the main diagonal, the first row, and the first column, and therefore can be inverted by simple algebra, using the formula of Salkuyeh and Beik (2018). Details are given in Appendix 2.

Although in practice, it is very unlikely that variance will be independent of response status, we use this approximation to generate a formula that is more interpretable and accessible. The performance of this formula is evaluated later in the simulation studies, where the variance and response status are dependent. Expression (4) is again a CPB formula and Expression (5) is a MPB formula. If the pretest provides no information about the posttest, so that $\rho =0$, then expression (5) simplifies to expression (3), which was the sample size formula of Kidwell and colleagues (2019). In other words, using an uninformative pretest ($\rho =0$) is approximately the same as ignoring the pretest.

Beyond Pretest and Posttest: More than Two Measurement Times

For a SMART with more than two measurement times (i.e., more than pretest and posttest), an easily interpretable formula is not possible without making assumptions that would be unrealistic in the binary case. Seewald and colleagues (2020) provide both a general and a simplified sample size formula for comparing a numerical, end-of-study outcome in longitudinal SMARTs. However, the simplified formula relies on the assumption of homoskedasticity across embedded adaptive interventions and measurement occasions, and exchangeable correlation between measurement occasions. In a binary setting, these simplifying assumptions are less realistic because two binary random variables cannot have equal variance unless they also have either equal (e.g., .20 and .20) or exactly opposite means (e.g., .20 and .80). Determining sample size requirements via simulations would be a feasible alternative in this setting (see Appendix 1).

However, if the investigator prefers not to use simulations, then we propose using the two-measurement-occasion formulas as approximations for planning SMARTs with more than two measurement occasions. Simulations shown in Appendix 1 suggest that the resulting sample size estimates would be reasonable. Although taking more measurement occasions into account might provide somewhat higher predicted power, this would depend on the assumed and true correlation structure and the design assumptions of the SMART. The power could also depend on assumptions concerning the shape of change trajectories within the first- and second-stage of the design (e.g., linear, quadratic, etc.), which might become difficult to elicit. Therefore, although more sophisticated power formulas might be developed, they might offer diminishing returns versus a simpler formula or a simulation. In the next section we discuss the use of simulations to calculate power for settings with more than two measurement times and to investigate the properties of the sample size formulas described earlier.

Simulation Experiments

In order to test whether the proposed sample size formulas work well, it is necessary to simulate data from SMART studies with repeated binary outcome measurements. Furthermore, simulation code can be relatively easily extended to situations in which the simplifying assumptions of the formulas do not apply. Below we discuss two simulation experiments. The first is designed to assess performance of the power formulas. This is done by comparing, for fixed sample sizes, the power estimated based on the sample size formulas to the power calculated from simulations. The second is designed to assess the performance of the sample size formulas as well as to investigate the extent of reduction in required sample size obtainable by taking pretest into account. This is done by comparing, for a fixed target power, estimates of the required sample sizes given by the various formulas to simulated sample size requirements.

Simulation Experiment 1: Performance of Power Formulas

A factorial simulation experiment was performed based on a SMART design with two measurement times. This experiment investigates the ability of the sample size formulas to choose a sample size which is large enough to achieve 0.80 power under specified assumptions. All simulation code is available online at https://github.com/d3lab-isr/Binary_SMART_Power_Simulations or via https://d3lab.isr.umich.edu/software/ . The experiment is designed to answer the following questions: First, do the proposed sample size formulas accurately predict power compared to the power estimated via simulations? Second, how much does the estimated power change by using the CPB approach in Expression (2), versus the MPB approach in Expression (3)? Third, to what extent does using a pretest result in efficiency gains (i.e., higher power for a given sample size) when comparing adaptive interventions based on repeated binary outcome measurements? Fourth, if the pretest is to be used in the model, is there a relative advantage or disadvantage to including the pretest as a covariate (and only the posttest as an outcome), versus modeling both the pretest and the posttest in a repeated measurement model? We used simulations to answer these questions under a scenario with hypothesized true parameters described below.

Methods

Data was simulated to mimic a prototypical SMART study, similar to the working memory training SMART in Figure 1. Randomization probabilities were set to be equal (50% each) for first-stage intervention options for each simulated participant, as well as for second-stage intervention options for each simulated non-responder. We assume there are two outcome measurement occasions: a baseline measurement before randomization (pretest), and an end-of-study outcome measurement (posttest). 10,000 datasets were simulated and analyzed per scenario (combination of effect size and sample size).

We assumed that the contrast of interest is the end-of-study log odds of drug use between the “enhanced working memory” ($+1$, $-1$) and the “enhanced incentives alone” ($-1$, $+1$) adaptive interventions (Table 1). Also, the data were simulated under the assumption of no attrition (study dropout). In practice a researcher should inflate the final estimate of required sample size to protect against a reasonable estimate of attrition probability.

We compared the power predictions obtained by using the different formulas available for ${\sigma }_{\Delta }^2$, with simulated power estimates. Specifically, we considered power calculated from expression (1) using the CPB estimates and MPB estimates for ${\sigma }_{\Delta }^2$, which would correspond to the sample size recommendations in expressions (3) and (5), respectively. We generated samples of either $n=300$ or $n=500$, in which the true correlation structure was either independent ($\rho =0$) or correlated with correlation $\rho =.3$ or $\rho =.5$. The datasets were simulated using the approach described below.

Steps in Simulating Datasets.

We first generated a random dummy variable for baseline abstinence $Y_0$ with probability $E(Y_0)=A0$. Next, $A_1$ was randomly assigned to $+1$ or $-1$ with equal probability. Then, $R$ was generated as a random binary variable (0 or 1) such that the log odds of $R=1$ was set to $-.62+Y_0+.5A_1$. The intercept $-.62$ was chosen to give an overall response rate of about 56% in the $A_1=+1$ arm and 33% in the $A_1=-1$ arm, or about 45% overall. Thus, we assume that in general most participants are responders, with an advantage to those receiving working memory training. The correlation between $Y_0$ and $R$ was about .23.

Finally, the end-of-study outcome $Y_1$ was generated. For convenience, $A_2$ and $A_1\times A_2$ were set to have zero effect, and the effect of $A_1$ was set so that the marginal odds ratio between a pair of adaptive interventions differing on $A_1$ would be approximately 1.5, 2, or 3, depending on the condition. These values are within the ranges which would be considered small, medium and large, respectively, by Olivier, May and Bell (2017). The conditional expected value for the final outcome $Y_1$ is given by the model

$$\log \text{it}\left(E(Y_1\mid Y_0,A_1,R,A_2)\right)={\beta }_0+{\beta }_{Y_0}{Y}_0+{\beta }_{A_1}{A}_1+{\beta }_{R}R+{\beta }_{A_2}{A}_2+{\beta }_{A_1{A}_2}{A}_1{A}_2.$$ (6)

The values for ${\beta }_{A_2}$ and ${\beta }_{A_1{A}_2}$ were set to zero for simplicity, and the other values were determined by trial and error to give the desired marginal quantities and are provided in Table 2.

Table 2:

Data-Generating Parameters for End-of-Study Binary Outcomes in Simulations

Scenario		Parameters of Data-Generating Model
Pretest– Posttest Corr.	Effect Size (Odds Ratio)	Conditional Regression Parameters in (6)			Marginal Expected Values
		${\beta }_0$	${\beta }_{Y_0}$	${\beta }_{A_1}$	(−, −)	(−, +)	(+, −)	(+, +)
0.06	1.5	−0.44	0.00	0.100	0.45	0.45	0.55	0.55
0.06	2	−0.44	0.00	0.250	0.42	0.42	0.59	0.59
0.06	3	−0.44	0.00	0.460	0.37	0.37	0.63	0.64
0.3	1.5	−0.90	1.20	0.115	0.45	0.45	0.55	0.55
0.3	2	−0.90	1.20	0.290	0.42	0.42	0.59	0.59
0.3	3	−0.90	1.20	0.520	0.37	0.37	0.64	0.64
0.6	1.5	−1.55	3.00	0.220	0.45	0.45	0.55	0.55
0.6	2	−1.55	3.00	0.450	0.41	0.41	0.58	0.58
0.6	3	−1.55	3.00	0.780	0.37	0.37	0.64	0.64

Note. The conditional regression parameters refer to Expression (6). For simplicity, ${\beta }_R$ is set to 1 and ${\beta }_{A_2}={\beta }_{A_1{A}_2}=0$. This leads to an average percentage of responders across arms of 45%, with responder proportions of 56.5% and 33.5% for the $+1$ and $-1$ levels of $A_1$. Because of a small remaining indirect effect of $Y_0$ and $Y_1$ via $R$ (i.e., correlations between pretest, response variable and posttest), the lowest level of correlation considered here is still not exactly zero (about 0.06), despite specifying a zero parameter for the conditional effect of $Y_0$ and $Y_1$.

Analysis of Simulated Datasets.

The model was fit using weighted and replicated estimating equations (see Dziak et al., 2019; Lu et al., 2016; Nahum-Shani et al., 2020) with either working independence or working exchangeable correlation. The latter is equivalent here to working AR-1 because there are only two waves (measurement occasions). Three forms of the twowave model were fit separately: an analysis of the posttest adjusted for pretest as a covariate, a repeated measures analysis with working independence, and a repeated measures analysis with working exchangeable correlation. Tests were done at the standard two-sided Type 1 error rate of .05.

Computation of Marginal Correlation for Formulas.

Although the two-wave power formulas take the marginal pretest–posttest correlation as an input, this parameter was not directly specified in the simulation code, because a simulation requires fully conditional models to be specified. Therefore, for purposes of calculating power via the formula for a given condition, we used the average marginal correlation estimate obtained from applying the weighted and replicated analysis (marginal over R) to the simulated datasets generated for this specific condition.

Results

With respect to the first motivating question (do the proposed sample size formulas accurately predict power compared to the power estimated via simulations), the results of the simulations (Table 3) are very encouraging. First, at least under the conditions simulated, the proposed sample size formulas do predict power accurately compared to the power which is estimated via simulations. As would be expected, power is higher when the effects size is higher and/or the sample size is higher.

Table 3:

Predicted and Simulated Power for Fixed Effect Sizes

Scenario		One Wave			Two Wave
		Predicted Power		Simulated Power	Predicted Power		Simulated Power
Odds Ratio	Sample Size	MPB	CPB		MPB	CPB
Pre-post correlation 0.06
1.5	300	0.298	0.298	0.296	0.299	0.313	0.298
1.5	500	0.455	0.454	0.457	0.456	0.476	0.458
2	300	0.665	0.664	0.667	0.666	0.692	0.667
2	500	0.869	0.868	0.876	0.870	0.888	0.878
3	300	0.956	0.955	0.961	0.956	0.966	0.962
3	500	0.997	0.997	0.999	0.997	0.998	0.998
Pre-post correlation 0.3
1.5	300	0.286	0.286	0.279	0.312	0.324	0.305
1.5	500	0.437	0.437	0.449	0.475	0.493	0.484
2	300	0.672	0.671	0.677	0.716	0.737	0.722
2	500	0.874	0.874	0.880	0.904	0.917	0.908
3	300	0.957	0.957	0.963	0.971	0.977	0.976
3	500	0.997	0.997	0.999	0.999	0.999	0.999
Pre-post correlation 0.6
1.5	300	0.290	0.290	0.291	0.423	0.431	0.427
1.5	500	0.442	0.442	0.450	0.627	0.637	0.641
2	300	0.649	0.649	0.652	0.831	0.840	0.848
2	500	0.856	0.857	0.861	0.965	0.968	0.968
3	300	0.955	0.956	0.962	0.994	0.995	0.996
3	500	0.997	0.997	0.998	1.000	1.000	1.000

Notes. “MPB” = marginal-probabilities-based (expression 3); “CPB” = conditional-probabilities-based (expression 5), In all conditions, the proportion of responders was set to approximately 0.565 given $A_1=+1$ and 0.336 given $A_1=-1$; this difference is the reason why the pre-post correlation $\text{Cor}(Y_0,Y_1)$ could not be set to exactly zero. The odds ratio shown is for pairwise comparison of $+,-$ to $-,-$ adaptive interventions, which is equivalent here to the effect of $A_1$. For simplicity of interpretation, $A_2$ and the $A_1\times A_2$ interaction were set to have no effect on $Y_1$. The simulated power shown for the two-wave model uses the covariate adjustment approach (pretest as covariate); the repeated measures approach had approximately the same power, or in some conditions about 0.005% higher.

The second motivating question concerns the extent that the estimated power will change by using the CPB approach in Expression (2) versus the MPB approach in Expression (3). The results indicate that the MPB and the CPB formulas are equivalent in the one-wave (posttest–only) case. However, these formulas differ slightly from each other in the pretest–posttest scenarios, with the MPB approach being slightly conservative, and the CPB approach being sometimes slightly overly optimistic.

The third question motivating this experiment concerns the extent that using a pretest will result in efficiency gains when comparing adaptive interventions. The results indicate that power is often higher when using a pretest–posttest model than with a posttest-only model, although this depends on within-subject correlation. There is no difference in power between these approaches when the pretest–posttest correlation is negligible (0.06) and only a very small difference when the pretest–posttest correlation is small (0.3), but there is a large difference when the pretest–posttest correlation is sizable (0.6). For example, with an odds ratio of 2 and sample size of 200, the one-wave approach has unacceptably low power of 65%, while the two-wave approach has a much better power of 85%.

Finally, the fourth motivating question concerns the relative advantage or disadvantage to including the pretest as a covariate versus as a measurement occasion in a repeated-measurement model. For purposes of calculating power for comparing adaptive interventions, the working independence analysis was found to be exactly equivalent to a posttest-only analysis, and the covariate-adjusted analysis was essentially equivalent to the exchangeable analysis. Therefore, we focus on comparing results for the non-independent repeated-measures analysis versus the posttest-only analysis. Because we found the simulated power with a pretest covariate to be approximately the same as the simulated power with repeated measures, they are represented by the same column under the Two-Waves heading. This near equivalence may result from the intervention options being randomized in the current settings; had there been confounding, the two models might have dealt with it differently, leading to differences in power and accuracy.

Simulation Experiment 2: Performance of Sample Size Formulas

This simulation was intended to study the ability of the sample size formulas to choose a sample size which is large enough to achieve a specified power (set here to .80) under specified assumptions, but which is not too large to undermine the feasibility of the study. The questions were analogous to the previous three. First, do the proposed sample size formulas give similar sample size predictions to those obtained from simulations? Second, how much does the estimated sample size change by using the CPB sample size formulas (2) and (4) versus the MPB sample size formulas (3) and (5)? Third, to what extent can the required sample size be reduced, under given assumptions, by taking the pretest–posttest correlation into account?

Method

Ordinarily, Monte Carlo simulations do not directly provide a needed sample size, but only an estimated power for a given sample size. However, by simulating various points of a power curve and interpolating, it is practical to use simulations to approximate the required sample size. We consider the inverse normal (probit) transform of power, ${\Phi }^{-1}(q)$, to be approximately linearly associated with $N$, based on the form of Equation (1) and the fact that sampling variance is inversely proportional to $N$. That is, we assume ${\Phi }^{-1}(q)\approx \widehat{a}+\widehat{b}N$ for some $\widehat{a}$ and $\widehat{b}$. Therefore, using the same scenarios as in the previous experiment, we perform simulations for several sample sizes in the range of interest and fit a probit model to relate the predicted power to each sample size. The needed sample size is then roughly estimated as $N=({\Phi }^{-1}(.80)-\widehat{a})∕\widehat{b}.2,000$ datasets were simulated and analyzed per effect size scenario, each on a grid of 10 potential sample sizes.

Results

The first question motivating this simulation experiment focused on whether the proposed sample size formulas provide similar sample size predictions to those obtained from simulations. Consistent with the results of the first simulation experiment, the results of the current experiment (Table 4) indicate that the formulas approximately agree with each other, and with the simulations, on the required sample size.

Table 4.

Predicted and Approximate Simulated Sample Size Requirements N for Fixed Effect Sizes

Scenario	One Wave			Two Waves
	Predicted N Required		Simulated N Required	Predicted N Required		Simulated N Required
Odds Ratio	MPB	CPB		MPB	CPB
Pre-post correlation 0.06
1.5	1152	1154	1157	1149	1087	1153
2	414	415	413	413	389	412
3	176	176	167	175	165	165
Pre-post correlation 0.3
1.5	1209	1211	1210	1090	1040	1091
2	408	408	411	368	351	371
3	175	175	169	159	151	152
Pre-post correlation 0.6
1.5	1192	1191	1182	753	735	745
2	430	429	431	277	270	269
3	176	176	172	118	115	109

Notes. “MPB” = marginal-probabilities-based (expression 3); “CPB” = conditional-probabilities-based (expression 5). The data-generating model settings are the same as those used for Table 3.

The second motivating question concerns the extent that the estimated sample size changes by using the CPB versus the MPB sample size formulas. As in the first simulation experiment, we found the MPB approach and CPB approach to be practically equivalent in the posttest-only case. In the pretest–posttest case, the MPB approach was found to be slightly conservative and the CPB approach was found to be slightly anticonservative, probably making the MPB approach the safer choice.

Finally, the third question motivating this experiment concerned the extent to which the required sample size can be reduced by taking the pretest–posttest correlation into account. The results indicate that taking pretest–posttest correlation into account reduces the required sample size. As would be expected from the previous simulation experiment, results showed that the required sample size for adequate power can be reduced dramatically (possibly by hundreds of participants) by employing a pretest–posttest approach instead of posttest-only.

Discussion

The current manuscript addresses an important gap in planning resources for SMART studies by providing new sample size simulation procedures, as well as approximate asymptotic sample size formulas, for SMARTs with binary outcomes. These sample size resources enable researchers to consider the inclusion of a pretest when calculating sample size requirements for comparing adaptive interventions. Two simulation experiments show that the new formulas perform well under various realistic scenarios. Given the increased uptake of SMART studies in behavioral science (see Ghosh et al., 2020; Nahum-Shani et al., 2022) and the high prevalence of binary outcome data in many domains of psychological and behavioral health research, the proposed sample size formulas have the potential to contribute to the development of adaptive interventions across multiple fields.

Our simulation results show that taking into account the inclusion of a pretest (i.e., the pretest–posttest correlation) in power calculations leads to smaller sample size requirements than comparing end-of-study outcomes (i.e., posttest) alone. While the sample size savings in some scenarios are relatively small, in other scenarios they are quite substantial, making the SMART design more feasible when resources are limited. Overall, these results suggest that when planning SMART studies with binary outcomes, investigators can potentially improve power by including a baseline measurement. This pretest may be included either as a measurement occasion in a repeated measurement model, or as a covariate, with similar power benefits.

The results also indicate that modeling more outcome measurement occasions beyond pretest and posttest may have diminishing returns in terms of power for comparing end-of-study (posttest) outcomes between adaptive interventions. However, intermediate measurements between pretest and posttest may be vital for secondary research questions about other estimands, such as delayed effects, which are not considered here (see Dziak et al., 2019). Systematic investigation of the extent of efficiency gained per added measurement occasion is needed to better assess the tradeoff between adding measurement occasions versus adding participants to the study in terms of power for a given hypothesis.

For the pretest–posttest case, we provided both simple asymptotic formulas and simulation code. Simulations have the advantage of being more easily adapted to different designs or situations, and do not require as many simplifying approximations as the asymptotic formulas do, although of course both require assumptions about parameter values.

Limitations and Directions for Future Research

Careful consideration of assumptions, preferably with sensitivity analyses, is still important for sample size planning. It would not be reasonable to argue that planning sample size to achieve exactly .80 power (and no more) is the best approach in general. More conservative sample size approaches may provide more capacity to handle unexpected situations such as higher than anticipated attrition. However, in some cases, an unreasonably high estimated sample size requirement would make it difficult to justify the conduct of a study given realistic funding or participant recruitment constraints. Hence, calculating predicted power with as much precision as possible, for a given set of assumptions, is desirable.

In this paper we have used the ordinary Pearson correlation coefficient, even for describing the relationship between binary variables. This is valid and convenient, and it follows the way correlation is operationalized in, for instance, generalized estimating equations (Liang & Zeger, 1986). However, there are other alternative measures available such as tetrachoric correlation (Bonnett & Price, 2005) which could optionally be explored. One limitation which might be encountered when choosing parameters for simulations is that very high correlations might lead to complete separation (parameter unidentifiability due to frequentist estimates of certain conditional probabilities being at zero or one). This is a known limitation of binary data, but it might be avoided in simulations by specifying correlations that are not very high, yet still realistic, and in data analysis by either simplifying the model or using priors.

This paper has assumed that sample size calculations would be motivated by a primary question involving a pairwise comparison between two adaptive interventions. However, other estimands could be considered in secondary analyses once the data are gathered. Future studies may extend the sample size planning resources provided in this manuscript to accommodate other planned analyses of binary outcome data from a SMART, such as a multiple comparisons with the best adaptive intervention (Artman et al., 2020; Ertefaie et al., 2016).

Appendix 1

Simulation Illustrating Three-Wave Analysis

In this appendix we assume that there are two different follow-up times per participant, $Y_1$ and $Y_2$, instead of a single end-of-study (posttest) outcome $Y_1$, so that there are now three measurement occasions per participant. For simplicity we assume here that both follow-up times occur after the second treatment phase. Therefore, the variables for a given individual in the study would be observed in the following order: pretest $Y_0$, initial randomization $A_1$, tailoring variable $R$, second randomization $A_2$ for nonresponders, first follow-up $Y_1$, second follow-up $Y_2$. This results in a somewhat different and simpler setting compared to that of Seewald (2020), who considered (in the linear modeling case) a mid-study outcome taken about the same time as $R$, and preceding the second randomization.

In the current setting, the second outcome $Y_2$ can potentially depend on any of $Y_0$, $A_1$, $R$, $A_2$, and $Y_1$, making a very wide range of different DAGs and simulation scenarios possible. For simplicity, we chose scenarios in which $Y_2$ depends on $Y_1$ but is conditionally independent of most or all the other preceding variables given $Y_1$.

Specifically, we continue to assume the same parameters used in the “high” correlation setting from Simulations 1 and 2 when simulating $Y_0$ and $Y_1$. We then further assume one of two scenarios for the relationship of $Y_2$ to the preceding variables. In the “no delayed effect” scenario, $Y_2$ depends on the preceding variables only through $Y_1$, and is conditionally independent of all other variables given $Y_1$, as if in a Markov chain. Thus, the effect of $A_1$ on $Y_2$ is mediated entirely by $Y_1$. In the “delayed effect” scenario, $A_1$ has an effect on $Y_2$ which is only partly mediated by $Y_1$.

The conditional models used for these two scenarios are as follows. For the “no delayed effect” condition,

$$\log \text{it}\left(E(Y_2\mid Y_0,A_1,R,A_2,Y_1)\right)=\log \text{it}\left(E(Y_2\mid Y_1)\right)=-1.4+3Y_1.$$

For the “delayed effect” condition,

$$\log \text{it}\left(E(Y_2\mid Y_0,A_1,R,A_2,Y_1)\right)=\log \text{it}\left(E(Y_2\mid A_1,Y_1)\right)=-1.4+.275A_1+.5Y_1.$$

The conditional effect of $Y_1$ on $Y_2$ was set to be weaker in the delayed effect scenario, so that the total effect of $A_1$ on $Y_2$ (i.e., the direct effect conditional on $Y_1$ plus the indirect effect mediated through $Y_1$) would be comparable between scenarios. In particular, the resulting odds ratio for the contrast of interest, still assumed to be ($+1$, $-1$) versus ($-1$, $-1$), was 3.0 for $Y_1$ and 2.0 for $Y_2$.

We assume that the estimand of interest is comparison of embedded adaptive interventions on the final outcome, where final outcome is interpreted as either the early follow-up $Y_1$ or the later follow-up $Y_2$, in order to compare the simulated power for each. We fit one-wave models to predict $Y_1$ alone or $Y_2$ alone. We also fit two-wave models to predict $Y_1$ or $Y_2$ separately adjusting for $Y_0$, and assuming exchangeable correlation structure (equivalent to AR-1 for the two-wave model). These models only consider two of the measurement occasions available. Finally, we fit three-wave models to predict $Y_2$ adjusting for $Y_0$ and $Y_1$, by applying methods similar to Lu and colleagues (2016) and Dziak and colleagues (2020) and using working assumptions of either independence, AR-1 or exchangeable correlation structure. In the three-wave models, we assumed a separate piecewise linear trajectory from $Y_0$ to $Y_1$ and from $Y_1$ to $Y_2$ for each embedded adaptive intervention.

Each scenario was replicated in 10,000 datasets each for sample sizes $n=300$ and $n=500$. Simulated power for each model in each scenario is shown in Table 5. Power for models using $Y_1$ as the final outcome was very high, and much higher than those using $Y_2$ as the final outcome. However, this is not surprising because the effect size for $Y_1$ was also higher. More interesting is the power comparison among the five models for $Y_2$ (the rightmost five columns).

In the no-delayed-effect scenario, power was clearly higher for methods which used information from $Y_0$ to predict $Y_2$ (i.e., “$Y_2$ Adjusted for $Y_0$,” working AR-1, and working exchangeable) versus those which ignored $Y_0$ (“$Y_2$ Only” and working independence). However, there was very little additional benefit in using $Y_1$, possibly because $Y_1$ is on the causal chain between $Y_0$ and $A_1$ on the left, and $Y_2$ on the right. Also, as expected, power was higher for a working correlation that approximately fit the data-generating model (AR-1) than one which did not (exchangeable). Although neither structure corresponded exactly to the data-generating model, the exchangeable working structure made the unhelpful assumption that $\text{Corr}(Y_0,Y_1)=\text{Corr}(Y_0,Y_2)$. In contrast, in the delayed effect scenario, it made little difference which model was used. This was presumably because in this scenario $Y_0$ and $Y_1$ had relatively little value for predicting $Y_2$ once $A_1$ was accounted for.

There are many other possible data-generating models that could be explored in a three-wave simulation. For instance, we did not explore power for detecting an effect of $A_2$, or whether power might be different depending on the order and timing of the measurements. However, it appears that at least in some circumstances, a two-wave ($Y_0\to Y_2$) model provides about as much benefit as a three-wave model ($Y_0\to Y_1\to Y_2$) with less complexity, assuming that contrasts in expected values for $Y_2$ are of primary interest. Of course, for more complicated estimands (e.g., for studying whether the effect is delayed), more than two waves would be needed.

Table 5 (for Appendix 1).

Simulated power for different models in three-wave simulation

Scenario		Simulated power for first follow-up $Y_1$, by model		Simulated power for second follow-up $Y_2$, by model
Delayed Effect	Sample Size	$Y_1$ Only	$Y_1$ Adjusted for $Y_0$	$Y_2$ Only	$Y_2$ Adjust ed for $Y_0$	$Y_2$ Adjusted for $Y_0$ and $Y_1$
						(Indep.)	(AR-1)	(Exch.)
No	300	0.962	0.997	0.651	0.715	0.651	0.726	0.699
No	500	0.998	1.000	0.859	0.907	0.859	0.909	0.893
Yes	300	0.961	0.997	0.515	0.517	0.515	0.540	0.521
Yes	500	0.998	1.000	0.744	0.746	0.744	0.757	0.737

Notes. In all of these conditions, the average estimated odds ratio for the effect of $A_1$ was set to 3.0 for $Y_1$ and 2.0 for $Y_2$, in terms of the pairwise comparison of ($+$, $-$) to ($-$, $-$) adaptive interventions, which is equivalent here to the effect of $A_1$. For simplicity of interpretation, $A_2$ and the $A_1\times A_2$ interaction were set to have no effect. The conditions differ in the relationship of the simulated late follow-up $Y_2$ to the baseline assessment $Y_0$ and initial treatment $A_1$. The simulated decay in effect size over time between $Y_1$ and $Y_2$ is intended to be analogous to that found in many real-world clinical trials.