Buoyancy of underground structures and pore water pressure conduction law in silty clay strata

Abstract

Based on the effective stress principle, indoor model tests were conducted in this study to calculate the buoyancy of an underground structure and determine the law of pore water pressure conduction in silty clay strata. A comprehensive underground structure-water-soil interaction test system was established with four-in-one features: Elimination of lateral friction, controllable water head, circulating water supply and drainage, and simulation of groundwater flow. Four- and seven-gradient buoyancy continuous monitoring tests were completed using fine sand and silty clay, respectively, to verify the reliability and accuracy of the test system. The hydrostatic pressure and seepage-hydrostatic process of the silty clay strata were simulated separately to investigate the buoyancy of the underground structure of the strata, the buoyancy reduction coefficient, and the pore water pressure conduction law. The results show the reliability and accuracy of the comprehensive test system for underground structure-water-soil interaction. The concept of “buoyancy starting intercept” is proposed based on this system, where the underground water level value should be the head of water supply minus the “buoyancy starting intercept” when calculating buoyancy in weak permeable layers. Under hydrostatic action, the groundwater is phreatic, deeper burial depths show greater magnitude of this discount. When the groundwater is confined, the water head reduction coefficient increases with increase in the burial depth or hydraulic gradient. Buoyancy calculations of an underground structure within the range of confined water should not be reduced in this case. Whether in a seepage or hydrostatic state, the pore water pressure in the silty clay layer is below the theoretical value. The results of this work may provide a theoretical basis for further analysis of the pore water pressure conduction law and buoyancy reduction mechanism of clay soils. We also may provide a theoretical reference for the development of innovative underground structure-water-soil interaction comprehensive test systems.

1. Introduction

In 2022, China signed cooperation plans with the African Union, Morocco, and Cuba as part of the Belt and Road Initiative and as an extension of the “Planning Outline for the Construction of the China-Mongolia-Russia Economic Corridor”. The new construction, and reconstruction, of underground structures in many cities is in full swing; multiple layers of groundwater and other complex hydrogeological conditions at this depth range directly affect the safety and investment of underground structures. There is a significant value in fully understanding the buoyancy reduction and pore water pressure conduction law of underground structures.

The underground structure, together with water and soil, form a complex triadic system of interactions. Groundwater creates many geotechnical problems [[1], [2], [3]] and it is difficult to properly calculate the buoyancy of underground structures in clay soils [4,5]. For a foundation with strong permeability, such as sand or gravel soil, buoyancy is calculated according to the anti-floating fortification water level without reduction. The buoyancy of an underground structure in a weakly permeable or impermeable foundation is usually below the calculated value, however, which is referred to as “buoyancy reduction”. The extent of this reduction can be expressed as a buoyancy reduction coefficient [[6], [7], [8], [9]]. Designers typically apply the highest anti-floating water level to determine the buoyancy load on an underground structure, thereby overestimating buoyancy resistance. An unreasonable buoyancy value can create conditions for significant damage to the structure.

Many scholars have investigated buoyancy calculation in underground structures and the law of pore water pressure conduction. There has been important progress in regards to model testing methods and theories. Zhou et al. [10], for example, investigated the effects of groundwater buoyancy on underground water level changes, pore water pressure duration, and burial depth of underground structures using an indoor experimental model device. They found that the measured reduction in groundwater buoyancy can be expressed as a “reduction factor”. Zhang et al. [11] studied the effects of permeability coefficient, hydraulic gradient, and burial depth on the buoyancy of underground structures through model tests and proposed a simplified equation for calculating buoyancy. Song et al. [12] used the semi-interval search method for an experimental study of groundwater buoyancy of shallow foundations in saturated clay soil strata. They found that the measured buoyancy of clay soil foundations is less than the theoretical buoyancy, but the test setup did not account for lateral friction in the underground structure. Zhang et al. [13] studied the water buoyancy effect and buoyancy reduction coefficient of an underground grain silo in sandy and clay soil. Considering only the hydrostatic effect, the buoyancy reduction coefficient was 0.95 in the sandy layer and 0.79 in the saturated silty clay. Indeed, there have been numerous studies on the mechanism of groundwater buoyancy and pore water pressure conduction laws mostly focusing on indoor model tests [14,15] and numerical simulations [[16], [17], [18]]. However, there is a lack of in-depth research on the buoyancy reduction coefficients of underground structures with different types of groundwater action or on the pore water pressure conduction law of silty clay strata.

In the present study, we developed a comprehensive test system with universal applicability for underground structure-water-soil interactions. Our system allows for eliminating lateral friction, controlling the water head, circulating water supply and drainage, and simulating underground water flow. The test soil was simulated with fine sand and silty clay to carry out continuous monitoring tests of buoyancy to verify the reliability and accuracy of the system. We simulated groundwater in the silty clay strata as a hydrostatic action and seepage-hydrostatic process, then explored the buoyancy reduction and pore water pressure conduction law under these two conditions. The results of this work may provide a sound theoretical basis for further analyses of the pore water pressure conduction law and buoyancy reduction mechanism of silty clay. We also may provide workable guidance for the development of innovative, comprehensive underground structure-water-soil interaction test systems.

2. Underground structure-water-soil interaction test system and scheme

2.1. Underground structure-water-soil interaction comprehensive test system

We constructed a comprehensive test system of underground structure-water-soil interaction to explore the buoyancy and pore water pressure conduction law in a silty clay strata. The system consists of four devices: A model box, underground structure device, groundwater recharge device, and monitoring device. A two-dimensional sketch of the test setup is shown in Fig. 1 and a physical diagram is shown in Fig. 2.

Fig. 1.

Two-dimensional sketch of test setup.

Fig. 2.

Underground structure-water-soil interaction comprehensive test system.

The internal dimensions of the model box are 1 m × 1 m × 1.1 m (L × W × H). This is the main body of the test system which contains the soil, groundwater, and underground structural devices. To prevent the model box from deformation after being subjected to pressure, which affects its accuracy, a steel plate welded model box was selected for its sealing and rigidity. A ring beam was set at the top, middle, and bottom of the model box. The underground structural unit consists of a triangular pyramid, a rigid circular steel plate, and an enclosure that is not in direct contact with the sidewall thus eliminating lateral friction. The triangular pyramid provides force support for the strain-gauge type transducer. The enclosure is 400 mm high with an inner diameter of 350 mm and consists of a steel cylinder and waterproof rubber at the bottom. To ensure that the base plate moves freely in the vertical direction, the base plate was constructed from flexible waterproof silicone. Its movement is not transmitted to the side wall after bearing the water pressure but directly fed back to the strain-gauge type transducer. The interior of the enclosure stays dry throughout the test.

The groundwater recharge device consists of an electric hoist, inlet pipes, water supply tank, and counter filter layer. The electric hoist is used to adjust the height of the water tank. The inlet pipe is eight plastic hoses connecting the model box and the water supply tank. The water supply tank size is 1 m × 0.2 m × 0.3 m, with a volume of 60 L. A 10 cm thickness of medium sand counter filter layer was set at the bottom of the model box to provide uniform water supply for the upper test soil layer.

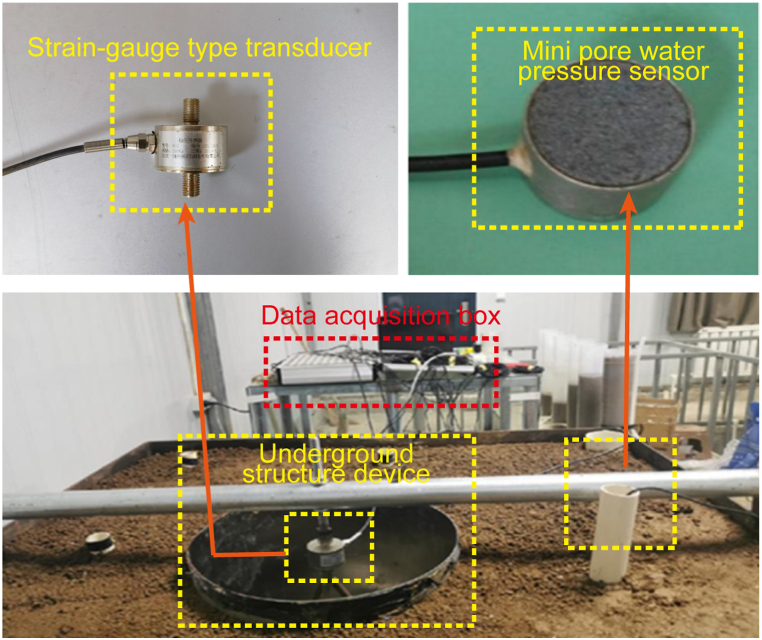
The monitoring device consists of mini pore water pressure sensors, a strain-gauge type transducer, and a data acquisition box (Fig. 3). The specific parameters of the sensor are shown in Table 1.

Fig. 3.

Monitoring device.

Table 1.

Sensor parameters.

Equipment name	Model	Diameter × Thickness (mm)	Combined error (%F.S)	Extreme overload (%F.S)	Temperature range (°C)	Material
Mini pore water pressure sensor	BWK	Φ18 × 12	≤0.5	120	−35∼80	Stainless steel
Strain-gauge type transducer	HYLY-019	Φ60 × 30	≤0.5	200	−30∼70	Stainless steel

The BWK mini pore water pressure sensor monitors pore water pressure variations at different depths in the soil layer. It is too small in size to affect the pore pressure conduction path or buoyancy of the underground structure. An HYLY-019 strain-gauge type transducer monitors the force on the bottom plate of the underground structure. A removable counterforce beam was arranged on the top of the model box and connected to the strain-gauge type transducer.

2.2. Comprehensive test system calibration program

Tests were conducted with four and seven gradients of continuous buoyancy monitoring using fine sand and silty clay, respectively, to verify the reliability and accuracy of the proposed four-in-one test system. The system was found to eliminate lateral friction, control the water head, circulate water supply and drainage, and effectively simulate groundwater flow. Each test was roughly a three-step process: Soil sample filling, external tank water supply, and gradient adjustment of tank height. The process is depicted in Fig. 4.

Fig. 4.

Test process.

The fine sand and silty clay used were taken from Changchun Urban Rail Transit Construction Line No. 3, China. In both cases, a 10 cm thickness of medium sand counter filter layer was laid at the bottom of the model box followed by filling of fine sand or silty clay. Geotextiles were laid at the junction of the medium sand layer and the silty clay to prevent soil particles from sinking into the bottom of the model box along the pores of the medium sand. Soil samples were compacted every 20 cm of fill and taken with a ring knife for geotechnical testing. The physical parameters of fine sand and silty clay after filling are shown in Table 2, Table 3. After the third layer of soil sample was filled, it was placed into the underground structure device as the remaining layers of soil samples continued to be filled.

Table 2.

Physical parameters of sand.

Soil sample	Water content w (%)	Density ρ (g/cm3)	Void ratio e (%)	Degree of saturation Sr (%)	Dry density ρd (g/cm3)	Permeability coefficient k (cm/s)
Fine Sand	21.6	1.89	0.61	96.1	1.63	3.70 × 10−3

Table 3.

Physical parameters of silty clay.

Soil layer	Density ρ (g/cm3)	Void ratio e (%)	Water content w (%)
Undisturbed soil	1.95	0.767	26.62
1 layer (0.1–0.3 m)	2.12	0.45	18.70
2 layer (0.3–0.5 m)	2.09	0.50	21.80
3 layer (0.5–0.7 m)	2.11	0.53	18.00
4 layer (0.7–0.9 m)	1.99	0.67	14.50
5 layer (0.9–1.05 m)	2.00	0.63	19.40

Unsaturated clay has water diffusion and volume compression in the infiltration stage, as well as a large suction matrix. If the test begins immediately after the water level is raised, the internal stress of the soil changes in a highly complex manner alongside seepage force, which affects the accuracy of the data. The large hydraulic gradient also destroys the soil structure, connecting pores of the soil and creating an excessive reduction coefficient. To remedy this, we injected water into the external water supply tank and gradually raised the height of the tank to continuously supply water to the model box. After each lifting of 10 cm, it was allowed to stand for 24 h. The process was repeated until the water supply head was kept level with the bottom plate of the underground structure device. Due to the poor permeability and timeliness of clay soil, the saturation process is relatively slow. Water should be continuously replenished to continuously monitor the water level of the soil layer in the box. The test soil layer below the underground structure device can be considered to be completely saturated once the water level is stable.

The electric hoist was used to lift the water supply head by stepwise adjusting the height of the water supply tank according to the gradient. The lifting amplitude of each gradient of water supply head depends on the water level of the soil layer and the response speed of buoyancy. At the beginning of each stage, we added water to the tank and maintained a stable water supply head for a certain period of time, then stopped adding water until the water level of the test soil layer was stable. We continued to raise the water supply level, then moved on to the next stage of the test. The water level and buoyancy were monitored in real time throughout. The bottom plate of the underground structural installation was used as the reference surface for each test, i.e., the zero point of the water head.

2.3. Buoyancy test scheme of silty clay strata under hydrostatic pressure

Three different underground water levels were set to monitor the buoyancy of the underground structure floor in the silty clay strata: 10 cm (level 1), 20 cm (level 2), and 30 cm (level 3) higher than the bottom of the underground structure. The test conditions are listed in Table 4. The test was started once the underground water level was raised to the bottom of the underground structural device, then raised stepwise to level 1, level 2, and level 3.

Table 4.

Buoyancy test conditions under hydrostatic pressure.

Conditions	Groundwater type	Test operation	Test content
1	Phreatic water	Close all valves and raise the water level of the model box by top filling	Buoyancy of underground structure and reduction coefficient
2	Confined water	Close the drain valve at the bottom of the model box, raise the water level of the model box by the groundwater recharge device

2.4. Groundwater seepage-hydrostatic process pore water pressure conduction law

The groundwater seepage-hydrostatic process is divided into a seepage pore pressure conduction stage and a hydrostatic pore pressure conduction stage. In the seepage pore pressure conduction stage, phreatic and confined water were supplied simultaneously. The phreatic water level was controlled to 97.5 cm and the elevation of confined water was held stable at 72.5 cm. This simulated the vertical seepage of groundwater in the silty clay layer under the combined action of phreatic and confined water. In the hydrostatic pore pressure conduction stage, the groundwater recharge device stopped supplying confined water and stabilized the phreatic water level. The phreatic water layer independently supplied the silty clay layer vertically at a consistent elevation of 97.5 cm. The changes in G1-G6 (heights of 875 mm, 800 mm, 625 mm, 375 mm, 188 mm, and 125 mm, respectively) piezometer heads in these two stages were tested to analyze the pore water pressure in seepage and hydrostatic states. This allowed us to determine the law of pore water pressure conduction in the silty clay layer.

3. Comprehensive test system calibration results analysis

3.1. Variation of groundwater buoyancy under gradient water supply in fine sand

Changes in the buoyant water head of fine sand under four gradient water supply conditions are shown in Fig. 5. We lifted the water supply head step-by-step in four gradients and checked the water supply head and buoyant water head every 10 min. Each time the tank is lifted, the water supply head has a buffer period of about 0.3 h after which it slowly decreases and eventually stabilizes. The buoyant water head can immediately respond to the gradient water supply. The first 1 h shows rapid growth followed by growth fatigue before gradually stabilizing. The water supply head and the buoyant water head eventually reach a critical value as the water head to each gradient is raised; we define this as the “critical water head”. When the fine sand medium is supplied with gradient water, the water supply head and the buoyant water head eventually grow infinitely close at the critical water head. The existence of the critical water head indicates that the fine sand medium can almost completely conduct pore water pressure.

Fig. 5.

Changes in water head with time (fine sand).

We measured the water supply head and buoyant water head of the fine sand medium after stabilization in the hydrostatic state as shown in Table 5. The buoyant water head reduction coefficient of the fine sand layer is 0.957–0.986 (i.e., almost not reduced at all) and increases with the water supply head. The buoyancy of a structure in a fine sand medium can be calculated according to Archimedes law. The measured value of the buoyancy of the underground structure in the strong permeable layer is similar to the theoretical value in our case with no reduction phenomenon. Due to the large porosity of soil particles in the strong permeable layer, the water pressure can be effectively transferred to the bottom of the underground structure, so that the buoyancy at the bottom of the underground structure is almost equal to that in pure water. When the permeability is further increased, the reduction coefficient of buoyancy of underground structure will be correspondingly larger and larger, and finally close to 1.

Table 5.

Buoyancy reduction coefficient of fine sand in hydrostatic state.

Test gradient	Stable water supply head (mm)	Stable buoyant water head (mm)	Reduction coefficient
Gradient 1	94	90	0.957
Gradient 2	195	190	0.974
Gradient 3	305	300	0.983
Gradient 4	386.5	381	0.986

3.2. Groundwater buoyancy in silty clay under gradient water supply

The changes in the buoyant water head of silty clay under seven gradient water supply conditions are shown in Fig. 6. The water supply head was raised step-by-step according to seven gradients and checked, alongside the buoyant water head, every 10 h. After each lifting of the water tank, the water supply head dropped slowly and eventually stabilized. The buoyant water head fed back to the gradient water supply is slowly and increased slowly over time. The total test time of the seven gradients was about 560 h. After each gradient water supply, the buoyant water head took an average of 80 h to stabilize. After stabilization, there was a marked difference between the buoyant water head and water supply head; the buoyant water head was significantly smaller. The measurements for both heads of silty clay after stabilization in the hydrostatic state are listed in Table 6. The reduction coefficient of the buoyant water head of the silty clay layer is 0.780–0.864 and increases with increase in the water supply head.

Fig. 6.

Changes in water head with time (silty clay).

Table 6.

Buoyancy reduction coefficient of silty clay in hydrostatic state.

Test gradient	Stable water supply head (mm)	Stable buoyant water head (mm)	Reduction coefficient
Gradient 1	100	78	0.780
Gradient 2	179	140	0.782
Gradient 3	208.5	165	0.791
Gradient 4	272	215	0.790
Gradient 5	328	270.5	0.825
Gradient 6	360	311	0.864
Gradient 7	410	351.5	0.857

We continuously monitored buoyancy in a fine sand medium and silty clay gradient water supply using the proposed system while exploring the relationship between the water supply head and buoyant water head. We found that the measured value of buoyancy in the underground structure with a strong permeable layer is basically consistent with the theoretical value, and that there is no reduction phenomenon. The measured value of underground structure buoyancy in the weak permeable layer is smaller than the theoretical value and there is a reduction phenomenon, which is in accordance with previous research results [19]. In effect, ours is a complete integrated test system. It can fully realize the preset functions (e.g., eliminating lateral friction, controlling water head, simulating groundwater flow). It effectively simulates the hydrostatic effect and seepage-hydrostatic process. It is a reliable indoor model for exploration of the buoyancy and pore water pressure conduction law in silty clay strata. It also may be further developed into more innovative, comprehensive test systems for underground structure-water-soil interaction.

3.3. Relationship between water supply head and buoyant water head in steady state

The water supply head and buoyant water head stabilize after each stage of supplying water to where the two values remain unchanged. At this point, all groundwater in the test system is in a static state. We conducted linear fitting analysis of the relationship between the water supply head and buoyant water head in the stable state of the fine sand medium and silty clay (Table 5, Table 6) as shown in Fig. 7(a). The linear fitting relationship of fine sand is a straight line with a slope of approximately 1. Although there is an intercept of 3.7636 mm, it is almost negligible considering the likelihood of some test error.

Fig. 7.

Supply water head and buoyant water head relationship fitting curve.

The water supply head and buoyant water head in the stable state of the silty clay layer are not proportional, but a straight line that does not pass through the origin (Fig. 7(b)). The relational expression is $y=0.8943\left(x-20.781\right)$. The x-axis positive intercept of the underground water level at the bottom of the underground structure is 20.781 mm. We define this intercept of the x-axis as the “buoyancy starting intercept”. When the head of water supply is below the buoyancy starting intercept, the underground water level cannot be raised above the bottom plate of the underground structure because there is no seepage of groundwater in the test soil layer, therefore, the buoyancy of the underground structure device is zero. When the water supply head exceeds the buoyancy starting intercept, the seepage in the test soil layer is strong enough to lift the underground water level beyond the bottom of the underground structure.

In the critical seepage state, the initial hydraulic gradient i₀ is equal to the ratio of the water head difference Δh₀ to the corresponding seepage path L₀ in the critical seepage state:

$$i_0=\Delta h_0/L_0$$ (1)

The water head difference Δh₀ under the critical seepage state is the buoyancy starting intercept. When calculating buoyancy in the aquitard, the groundwater level should be the water supply head minus the buoyancy starting intercept.

4. Buoyancy change of silty clay strata under hydrostatic pressure

The pressure heads at different depths under “condition 1” are shown in Fig. 8(a). As depth increases, the pore water pressure of the silty clay strata gradually deviates from the theoretical value and the pressure heads at each point are reduced to varying degrees. There is a certain nonlinear trend at larger depths. In the vertical direction, the reduction is higher at deeper buried depths and the silty clay is hindered more intensely by water pressure conduction. In the soil-filling process, lower soil layers are subjected to multiple compactions and overburdening pressure created by the upper soil. The lower soil is denser and has stronger ability to resist penetration. Therefore, the reduction phenomenon is more obvious at deeper buried depths.

Fig. 8.

Test results of condition 1.

The water head reduction coefficient at different depths is shown in Fig. 8(b). This coefficient decreases as depth increases, which is consistent with our previous observations. The coefficient also increases slightly after the underground water level is raised, which indicates that an increase in the hydraulic gradient shrinks the reduction range. Fig. 8(c) shows the buoyancy of the underground structure at three water levels, where each value is less than the theoretical buoyancy to varying extent. The buoyancy of the underground structure is high as per the highest water level without discounting.

The pressure heads at different depths in silty clay under “condition 2” are shown in Fig. 9(a). Under the action of confined water at the bottom, the measured pressure head at the buried depth of 50–90 cm is different from the theoretical water head. The distribution of the water head at each point along the depth gradient is almost linear. The head reduction is stronger when the piezometer is buried at shallower depths. When buried 90–100 cm, there is only a slight difference between the measured pressure head and the theoretical value. Under the action of confined water, the pore water pressure decreases linearly in the vertical direction with decrease in burial depth due to the obstruction of pore pressure conduction by the silty clay.

Fig. 9.

Test results of condition 2.

As shown in Fig. 9(b), the head reduction coefficient increases as depth increases. The difference in distribution along the depth is significant, mainly due to the different locations of the confined water and phreatic water relative to the weak permeable layer. The internal reduction phenomenon is less obvious in the soil within the range of the action of confined water; the reduction coefficient tends toward 1 at depths of 90–100 cm. The bottom water supply simulated confined water in condition 2, so pore water pressure was transmitted upward from the bottom plate of the weak permeable layer and the pressure head gradually attenuated upward. As the hydraulic gradient increases, the hindering effect of silty clay on the conduction of pore water pressure decreases and the ability of the clay to hinder seepage is reduced. Under a higher hydraulic gradient, small pores expand to form a dominant seepage channel as the head reduction coefficient increases.

Fig. 9(c) shows the buoyancy of the bottom plate determined on a strain-gauge type transducer after stabilization under three water levels. The buoyancy of the bottom plate is less than the theoretical value, but only slightly. Confined water places buoyancy force on the silty clay layer, which weakens the reduction effect. The buoyancy of underground structure within the scope of confined water should not be reduced.

5. Pore water pressure conduction law of groundwater seepage-hydrostatic process in silty clay strata

5.1. Pressure head variation with time

The G1-G7 pressure head variation curve with time is shown in Fig. 10. The pressure head increased slowly with time and leveled off between 9 d and 15 d. The hydrostatic pore water pressure conduction stage was tested based on the seepage stage. After closing the confined water supply valve, the pressure heads of G4, G5, and G6 decreased rapidly towards a valley value on the 18th day, then increased until stabilizing. The stable value of the pressure head in the hydrostatic stage is 1.14–1.47 times that in the seepage stage. Groundwater seepage causes head loss, which has an important effect on the buoyancy of underground structures. The vertical pore water pressure decreased as the stratum flowed from phreatic to confined water, so buoyancy could not be calculated according to the groundwater level in the phreatic water layer.

Fig. 10.

Pressure head versus time curve.

5.2. Vertical variation of pressure head

The seepage-stage (3–15 d) and hydrostatic-stage (18–30 d) vertical variation curve of the pressure head is shown in Fig. 11(a)-(b). The theoretical hydrostatic pressure head is shown in Fig. 11(c). In the seepage stage, the pressure head at each depth deviates from the linear distribution. The curve shows where, in the case of downward seepage of phreatic water, the water head is distributed in a bow along the depth and ultimately trends toward a straight line, but is consistently less than the theoretical value. In the hydrostatic stage, the pressure head gradually deviates from the theoretical value as depth increases alongside different degrees of reduction. Pore water pressure is related to soil saturation, head loss and other factors. Under actual conditions, the soil saturation is difficult to reach 100 %. In the process of water seepage, the measured pore water pressure is slightly smaller than the theoretical value due to the existence of pore gas in the pore and bearing part of the pressure. At the same time, due to the differences in soil compactness and seepage path in the actual soil layer, the head loss caused by the resistance along the seepage process is greater than the theoretical value, resulting in the measured pore water pressure is slightly smaller than the theoretical value. The pressure head in silty clay layer is less than the theoretical value regardless of whether it is in the seepage state or hydrostatic state.

Fig. 11.

Vertical pressure head variation curve.

6. Conclusion

We evaluated the accuracy of a comprehensive underground structure-water-soil test system. We examined the buoyancy of an underground structure and the pore water pressure conduction law of a silty clay strata based on hydrostatic and seepage-hydrostatic processes, respectively. Our results can be summarized as follows.

• 1)We found that the measured buoyancy of the underground structure in the strong permeable layer is basically consistent with the theoretical value, with no reduction. The measured buoyancy of the underground structure in the weak permeable layer is smaller than the theoretical value and there is a reduction phenomenon. The indoor model device has functions including eliminating lateral friction, controlling the water head, circulating water supply and drainage, and accurately simulating groundwater flow. It is a complete underground structure-water-soil comprehensive test system for studying buoyancy and pore water pressure conduction laws.
• 2)Based on the proposed test system, we established “critical water head” and “buoyancy starting intercept” concepts. The head difference Δh₀ under the critical seepage condition is the buoyancy starting intercept. When calculating buoyancy in the weak permeable layer, the underground water level should be the head of the water supply minus the buoyancy starting intercept.
• 3)Under hydrostatic conditions, when it is phreatic water, the greater the buried depth, the greater the reduction, and the stronger impediment of the silty clay to the transfer of water pressure, according to the highest water level without reduction to calculate the buoyancy of underground structures will be large. When the groundwater is confined, the water head reduction coefficient increases with depth or hydraulic gradient.
• 4)The vertical pore water pressure is reduced as the stratum flows from phreatic to confined water. Buoyancy cannot be calculated only according to the groundwater level in the phreatic water layer. The pressure head in silty clay layer is less than the theoretical value regardless of whether it is in a seepage or hydrostatic state.

Data availability statement

Some or all data, models, or code that support the findings of this study are available from the corresponding author upon reasonable request. Data will be made available on request.

Additional information

No additional information is available for this paper.

CRediT authorship contribution statement

Haotian Guo: Writing - review & editing, Writing - original draft, Funding acquisition, Conceptualization. Runjian Zhou: Writing - original draft, Software. Chao Sun: Supervision, Conceptualization. Yuli Lin: Data curation. Jinchao Xie: Resources, Investigation, Conceptualization.

Declaration of competing interest

No conflict of interest exits in the submission of this manuscript, and manuscript has been approved by all authors for probable publication. I would like to declare on behalf of my co-authors that the work described was an original research that has not been published previously, and not under consideration for publication elsewhere, in whole or in part. All the authors listed have approved the manuscript that is enclosed.