Surface-based anthropomorphic bone structures for use in high-resolution simulated medical imaging

Abstract

Objective.

Virtual imaging trials (VITs) enable efficient assessment and optimization of medical image devices and techniques via simulation rather than physical studies. These studies require realistic, detailed ground-truth models or phantoms of the relevant anatomy or physiology. Anatomical structures within computational phantoms are typically based on medical imaging data; however, for small and intricate structures (e.g., trabecular bone), it is not reasonable to use existing clinical data as the spatial resolution of the scans is insufficient. In this study, we develop a mathematical method to generate arbitrary-resolution bone structures within virtual patient models (XCAT phantoms) to model the appearance of CT-imaged trabecular bone.

Approach.

Given surface definitions of a bone, an algorithm was implemented to generate stochastic bicontinuous microstructures to form a network to define the trabecular bone structure with geometric and topological properties indicative of the bone. For an example adult male XCAT phantom (50^th percentile in height and weight), the method was used to generate the trabecular structure of 46 chest bones. The produced models were validated in comparison with published properties of bones. The utility of the method was demonstrated with pilot CT and photon-counting CT simulations performed using the accurate DukeSim CT simulator on the XCAT phantom containing the detailed bone models.

Main Results.

The method successfully generated the inner trabecular structure for the different bones of the chest, having quantiative measures similar to published values. The pilot simulations showed the ability of photon-counting CT to better resolve the trabecular detail emphasizing the necessity for high-resolution bone models.

Significance.

As demonstrated, the developed tools have great potential to provide ground truth simulations to access the ability of existing and emerging CT imaging technology to provide quantitative information about bone structures.

Introduction

Anthropomorphic virtual phantoms are an increasingly popular tool in medical imaging simulation studies. When combined with accurate computational models of an imaging process, virtual phantoms can be used to conduct virtual imaging trials (VITs) to evaluate and optimize imaging technologies efficiently and safely via computerized simulation (Abadi et al., 2020b). For these simulation results to be capable of driving clinical decisions, it is essential that the virtual phantoms provide realistic models of the relevant patient anatomy and physiology.

The 4D extended cardiac-torso (XCAT) phantoms were developed in our laboratory to provide a series of diverse virtual anthropomorphic models to be used in simulated medical imaging applications (Segars et al., 2013). The XCAT phantoms include thousands of anatomical features, including many detailed structures of the chest (Abadi et al., 2018b). The phantoms have been widely used in imaging research with use in radiation dosimetry (Sahbaee et al., 2017a, Sahbaee et al., 2017b, Hoye et al., 2019, Fu et al., 2021) and imaging protocol optimization for ionizing imaging modalities such as computed tomography (CT) (Tanaka et al., 2019, Abadi et al., 2019a, Abadi et al., 2020,_S1_Reference4, Abadi et al., 2021, Shankar et al., 2022, Sotoudeh-Paima et al., 2022). A current limitation to the XCAT phantoms is they do not model the inter-tissue heterogeneity for organs or bones. This heterogeneity can convey diagnostic information and therefore is necessary to adequately evaluate image quality. Without it, the simulated CT images of the phantoms would not be realistic enough to meaningfully inform clinical data acquisition.

In previous work, we improved the realism of our digital XCAT phantom cohort by developing a voxel-based power-law noise model to give the characteristic appearance of trabecular bone under CT imaging (Abadi et al., 2019b) based on the anatomical images of the Visible Human Female (Zhang et al., 2006). The algorithm was able to synthesize textures with a similar power-law texture having exponent β = 2.2 in correspondence with real anatomical images and resulted in more realistic trabecular bone regions in simulated CT images of XCAT phantoms. However, the trabecular bone structure was simply approximated using volumetric texture images and, therefore, did not include the true underlying anatomy.

At the same time, CT imaging is showing great potential to objectively assess structural and physiological abnormalities of bones. The effectiveness of CT is even more promising with the emergence of photon-counting CT (PCCT). Though not currently widely available, PCCT units allow for medical images with finer resolution and more robust material discrimination than previously possible with clinical CT (Hsieh et al., 2020, Flohr et al., 2020, Sandstedt et al., 2021). Simulations of the relevant anatomy and physiology (Sauer et al.) and imaging physics (Abadi et al., 2018a) can be combined in order to determine the optimal use of this technology. However, it is important to have models that have sufficient phantom-domain detail as the increased image fidelity of PCCT has the potential to demonstrate new imaging indications of disease only if the underlying anatomical detail is present at the time of CT simulation (Si-Mohamed et al., 2022a, Si-Mohamed et al., 2022b, Thomsen et al., 2022).

In this work, we develop a new, mathematical surface-based mesh method to generate realistic chest bone structures (sternum, backbone, ribs, scapulas, and clavicles) with accurate morphological and topological detail for the XCAT phantoms. This method defines the spatial extent of the complementary bone–marrow structures (shown to scale in Fig. 1) that are the root cause of the characteristic image texture (Laib and Rüegsegger, 1999, Lespessailles et al., 2006, Chappard et al., 2008, da Silva et al., 2014) and provides a transition from using image-informed characteristic power law textures to a ground-truth model with exact morphology. Enhanced XCAT phantoms with the detailed bone structures can be input into the accurate DukeSim CT simulator (Abadi et al., 2018a) to produce CT images with a phantom-defined known truth to quantiatively evaluate current and emerging CT technologies used for bone disease characterization.

Figure 1:

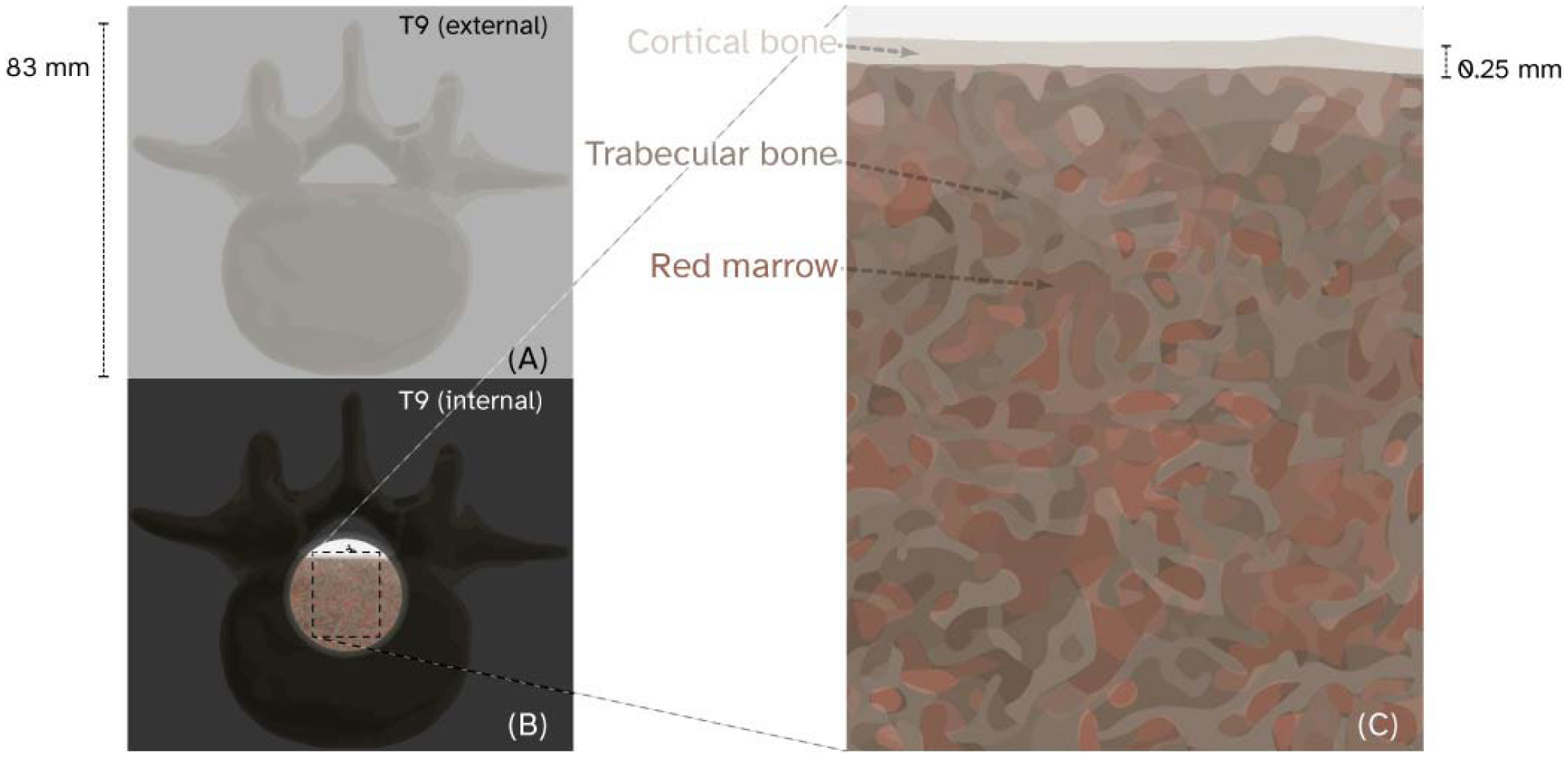
Ninth thoracic vertebrae (T9) shown to scale as an opaque cortical shell in (A) and with a region of cortical bone cut away (B) to show the trabecular bone and red marrow structures (C).

Methods

Overview

Cortical shells from XCAT phantom bones most relevant to cardiothoracic imaging—ribs (24), thoracic and lumbar vertebrae (17), scapula (2), clavicles (2), and sternum (1)—were used to inform the spatial extent and location of stochastic 3D microstructure surfaces. The microstructure surfaces were modified to have geometric and topological properties similar to trabecular bone. Trabecular bone structures for anatomy with similar size and bounding box dimensions were generated in corresponding subsets to optimize throughput. With 128 GB RAM, up to 4 total bones from among the ribs, clavicle, sternum per iteration; up to 10 vertebrae per iteration; or, up to one scapula per iteration were created in parallel. The primary output of the algorithm, for each bone, was triangle meshes defining the trabecular and cortical bone volumes. The bone volume output also implicitly defined the corresponding red marrow volume for each bone (volume within the bone that is not cortical or trabecular). The bone structures were voxelized at 0.10 mm isotropic resolution for a 50^th percentile adult male XCAT and subject to CT simulation with DukeSim for demonstration.

3D trabecular volume generation for the chest bones

Generation of the inner trabecular structure

Each of the XCAT bones used started from their NURBS surface definitions and were exported to an .STL file format. This file format contains a numbered list of vertex coordinates and a list of relationships between adjacent vertex numbers that describe the faces of a surface. The cortical thickness for each of the bones was determined to be approximately 0.25 mm (Dyson et al., 1970). Per-vertex surface normals from the outer cortical shell were inverted and displaced inward by 0.25 mm to create a surface to represent the inner-cortical boundary.

The distinction between cortical and trabecular bone was temporarily necessary to define an efficient, lightweight set of surfaces that include well-defined volumetric regions of marrow and bone. From the vertex values of the inner-cortical surface of each bone, a bounding box (having dimensions B_Δx, B_Δy, B_Δz mm) was determined and used to create three arrays containing sets of X, Y, and Z coordinates reshaped into an array with a linear sampling density in each direction of ρ_x,y,z = 5 samples per mm (to be able to capture trabecular bone struts of thickness 0.25 mm (Dyson et al., 1970, Whitehouse et al., 1971b, Whitehouse and Dyson, 1974, Blain et al., 2008). A small buffer length ε = 0.5 mm and total size ρ_x,y,z · (B_Δx + 2ε, B_Δy + 2ε, B_Δz + 2ε) were used to represent the sampling locations in a way that allows for efficient vectorization. The components of the sampling array were combined into the term R_n, given the evaluation location for each wave n and basis direction, with each generated 3-vector q_n. The vector q_n had a random unit direction uniformly distributed over the solid angle 4π about the geometric center of the bone and random phase θ_n uniformly distributed over the range (0,2π]. This was then used to evaluate the function G at each sampling point:

$$G=\sqrt{\frac{2}{N}}\sum _{n=1}^N\text{cos}\left(R_n\cdot q_n+{\theta }_n\right).$$ (1)

The trabecular-only bone volume ratio D was used to define the value of the level set iso-value:

$$\xi =-\sqrt{2}\cdot {\text{erf}}^{-1}(2D-1),$$ (2)

which denotes the numerical contour value at which an isosurface implicitly described by G is extracted. The output for each bone were structures as shown in Fig. 2.

Figure 2:

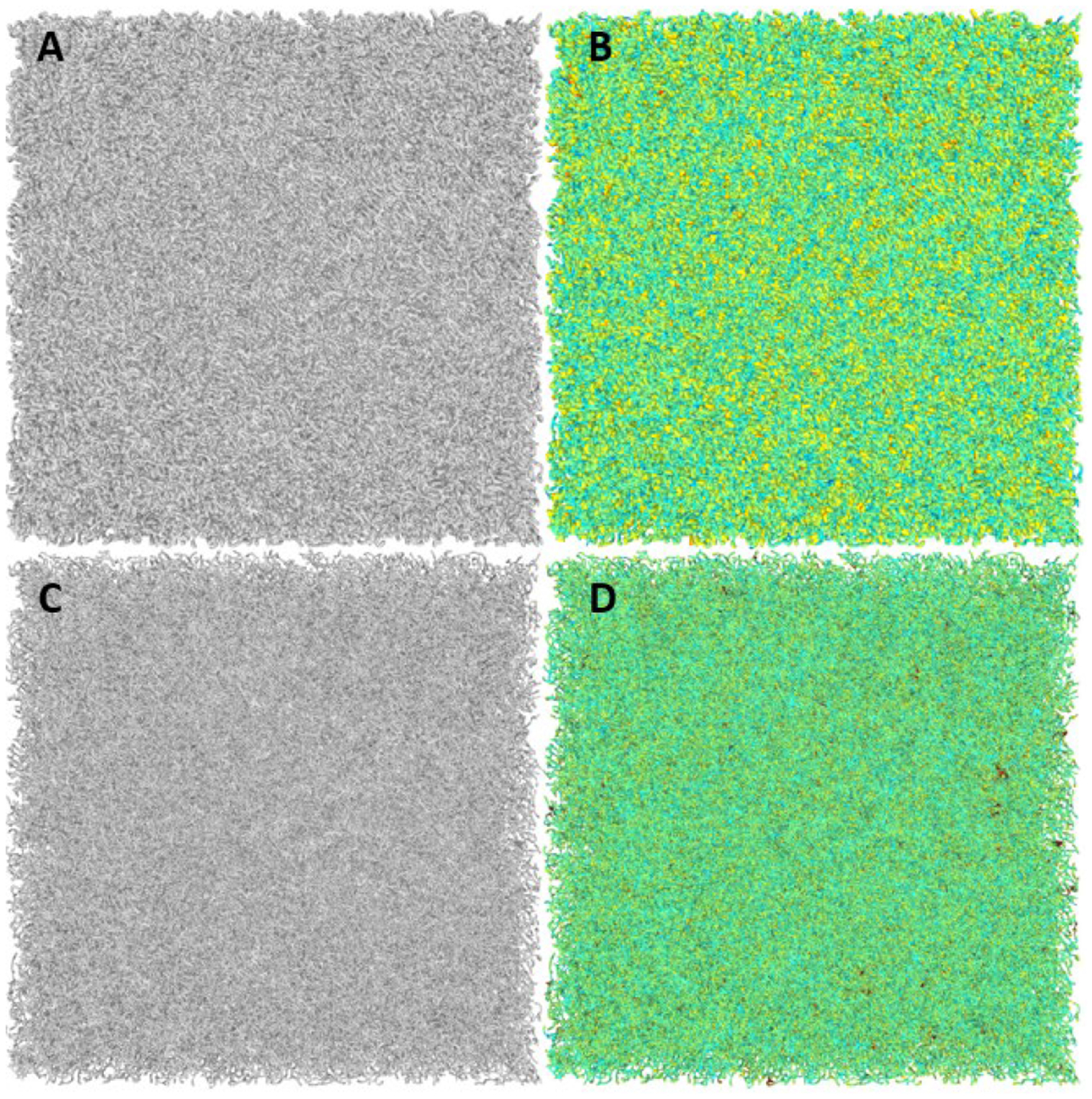
A shows an output stochastic cube structure that is approximately 20% the volume of its convex hull; B shows the same cube with color added to indicate approximate local thickness as determined using the shape diameter function (SDF). C shows the structure in A but procedurally thinned in locations where the connecting struts of the structure were too thick to model trabecular bone. D shows the same morphology as C but again with added color indicating that the disparities in the size of trabecular struts have been resolved using the SDF as proposed by Shapira (Shapira et al., 2008).

Given surface definitions for the outer-cortical boundary and the inner-cortical boundary components of a bone, we implemented an algorithm to generate the trabecular bone structure using stochastic bicontinuous structures (Soyarslan et al., 2018, M Moerman, 2018). The generated stochastic microstructures were discrete 2-manifolds (i.e., triangular mesh surfaces), which were watertight (having well-defined volume and no self-intersections) and high genus (large number of distinct “handle” structures).

To extract continuous structures in the shape of the bone from the initial mesh, PyMeshLab (Zhou et al., 2016, Muntoni and Cignoni, 2021) was used for cutting volumes of the cube-shaped trabecular bone structure that are outside the bone of interest (the Boolean intersection operations). The output of each Boolean operation was a surface composed of one or more connected components. The largest connected component was taken to represent the trabecular bone structure mesh.

Output mesh repair and modification

Repair and modification of the meshes was performed automatically using postprocessing scripts within PyMeshLab. Any output mesh which had non-manifold topology (e.g., combinatorially non-manifold vertices and non-manifold edges), non-watertight geometry (e.g., “holes” that would prevent direct calculation of the volume inside the surface), and non-manifold geometry (e.g., self-intersecting faces) was first analyzed for non-manifold vertices, which were split without vertex displacement (combinatorially split) to avoid modifying connectivity. Any remaining non-manifold edges were repaired by removal of each face incident on each non-manifold edge and closing any holes, resulting in a structure that was topologically 2-manifold with non-watertight geometry. Self-intersecting faces were selected along with all border edges (i.e., edges which belong only to one face) and were removed from the mesh, after which the border edges and all incident faces were removed from the mesh, giving a discrete 2-manifold with non-watertight geometry and no self-intersections. Holes in the mesh were then iteratively closed by alternately patching border edges and repairing any incidental non-manifold topology caused by this repair process, with the size of the holes allowed to be closed increasing by an order of magnitude each time.

Each resulting discrete surface was topologically 2-manifold with genus O(10⁵) and had watertight geometry. Each surface was then subject to a geodesic remeshing with 0.020 mm node displacment constraint. The average edge length of a representative trabecular surface was 0.25 mm with an average volume of 23000 mm³. The Euler characteristic of each surface was calculated (typically O(−10⁵), which allowed for quick calculation of the zeroth, first, and second Betti number (higher-order Betti numbers were 0). These measures were calculated for both the trabecular-only bone structures as well as full (cortical and trabecular) bone structures. These measures also provided information for the marrow structure, since these bone and marrow structures are topological duals(Pontrjagin, 1934, Laib and Rüegsegger, 1999, Lespessailles et al., 2006, Chappard et al., 2008, da Silva et al., 2014).

Properties of the repaired and remeshed surface were then measured using the shape diameter function (SDF) as described by Shapira (Shapira et al., 2008) and made available with PyMeshLab (Muntoni and Cignoni, 2021). Each vertex of the surface had 120 rays cast centered about the inverted (inward-pointing) vertex normal vectors and randomly distributed over a cone angle of 120° with peeling iteration set to the minimum acceptable value. The average ray length was calculated per vertex and stored along with the vertices and faces as a polygon mesh (.PLY) vertex quality attribute (double-precision, scalar), along with the outward-pointing set of vertex normals.

Vertices were treated differently as a function of their “thickness” value T. Thickness values less or equal to than empirically-observed (Kuhn et al., 1990, Goulet et al., 1994) thickness values (T_{mesh vertex i} − T_{anthropomorphic} ≤ 0) for trabeculae were not modified—they are specifically considered later to fine-tune topological and geometric properties of the mesh; thickness values greater than reported (T_{mesh vertex i} − T _{anthropomorphic} = 2δ > 0) were each translated along their inward-normal by one-half the difference between the excess thickness and the anthropomorphic value (NewPosition_{mesh vertex i} = OldPosition_{mesh vertex i} + δ · (InwardNormal_{mesh vertex i})).

The resulting meshes had thickness value distributions calculated again via the SDF(Shapira et al., 2008), with distributions closer to anthropomorphic geometry but having a number of (small) very thinly-connected regions. These thin structures were used to tune the connectivity parameter of the mesh which is the genus (number of “handle” structures on the mesh divided by its volume giving a result generally between 1–8 handles/mm³ in agreement the equivalent results of “Euler # per mm³” as reported by Goulet (Goulet et al., 1994). When the connectivity value was too high, the thinnest structures were thinned and remeshed further until their connectivity was restricted to individual topologically and geometrically non-manifold vertices. The vertex was repaired by via geometric vertex splitting, thereby decreasing the genus of the mesh with relatively small effect on the mesh volume.

Phantom-specific bones

Cortical and trabecular bone volume

As mentioned previously, the outer cortical shell of the phantom bones were used to define the inner-cortical surface by inverting their vertex normals and displacing along them each set of vertices by 0.25 mm (Treece et al., 2010). The inner cortical shell was used as a bounding volume for the trabecular structures generated in the shape of the bounding box of each bone. A Boolean intersection operation was implemented to extract the part of the cube structure that occupied the same volumetric space as the bone. The resulting output mesh aligned exactly with the inside faces of the inner cortical boundary (a property of the exact Boolean operations proposed by Zhou (Zhou et al., 2016)). Any topologically non-manifold vertices in the output mesh were repaired via zero-displacement splitting, resulting in a manifold mesh. Any small connected components not connected to the full structure (i.e., structures not directly connected to the largest structure) were removed from the mesh.

For the ribs, which are curved structures, the trabecular structures were generated in a cylindrical coordinate system (Fig. 3.A.) and warped to match the shape of each rib without disturbing the structures (Fig. 3.B.).

Figure 3:

Example rib structure shaping. The calculation time benefits from generating the bone surface in a small, axis-aligned region and smoothly warping it to follow the contour of each individual rib.

The bone-shaped trabecular volume was then subject to a Boolean union operation with the cortical volume (where cortical volume was defined as “outer cortical surface” minus “inner cortical surface”) and unioned with the trabecular surface:

$$\text{Total bone}=(\text{Outer cortical surface}\setminus \text{Inner cortical surface })\cup (\text{Trabecular surface}).$$ (3)

The resulting total bone surface was again subject to non-manifold vertex repair by zero-displacement vertex splitting, resulting in a manifold mesh that describes the trabecular bone volume in one connected structure.

Trabecular-complement red marrow volume

The dual structure (Total bone)^C (Pontrjagin, 1934) of each bone volume includes the marrow volume. The marrow surface was generally defined implicitly in this process to aid in fast and robust voxelization of the surfaces and reduce the memory footprint of these structures; however, because of the exact nature of the Boolean operations performed previously, the double-precision marrow structure fits exactly inside the bone structure and is shown alongside a cortical-only and trabecular-only visualization of XCAT virtual adult male 50^th percentile vertebrae T9 in Fig. 4.

Figure 4:

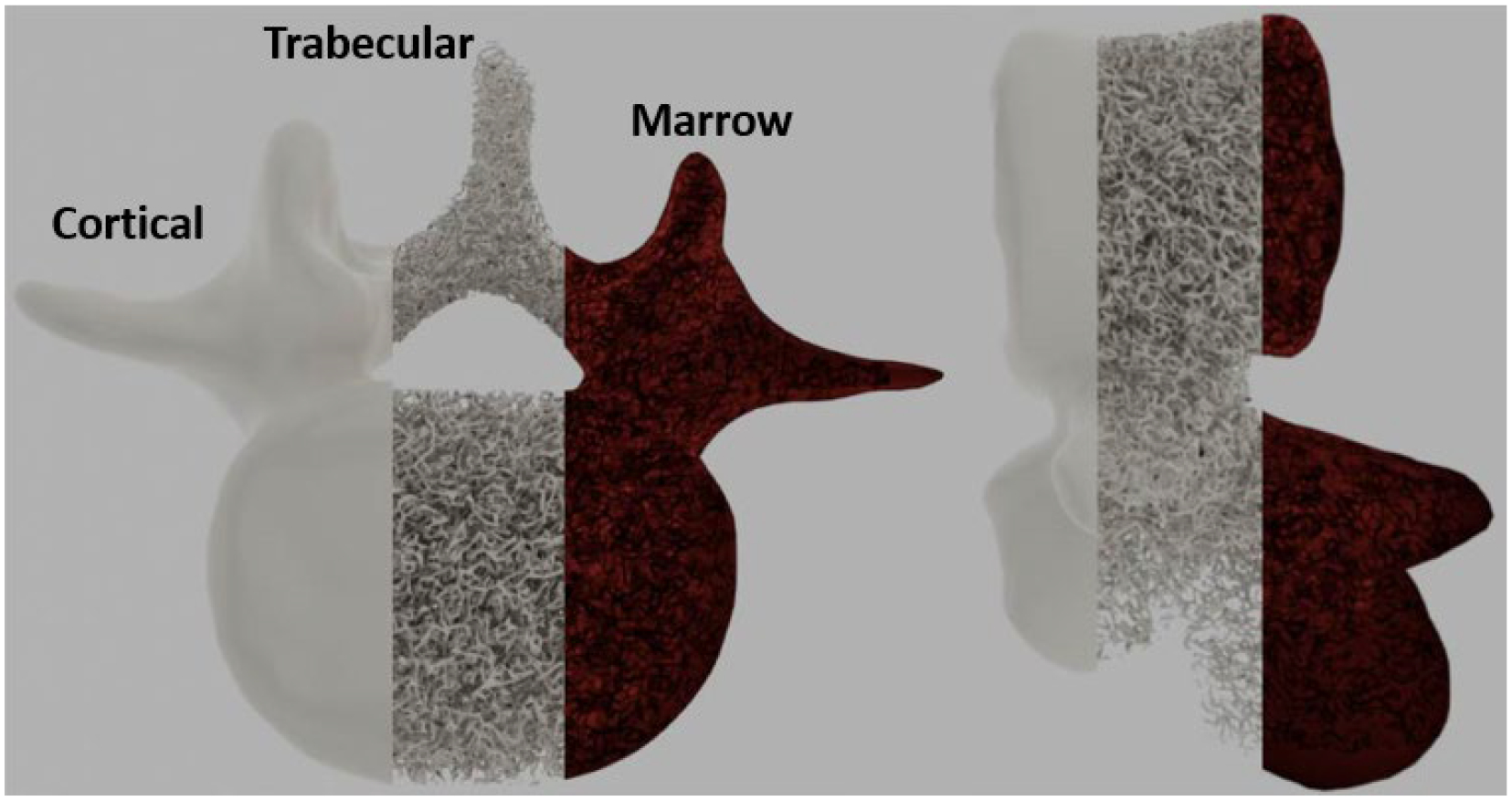
XCAT virtual adult male 50th percentile T9 trabecular bone as produced by the method. Cortical, trabecular, and marrow volumes are shown in two views. The trabecular bone volume as a fraction of the total bone volume was 19%.

External model validation

To ensure that the generated trabecular bone models were in agreement with the range of typical values in a healthy adult male population, topological and geometric features of the models were calculated and compared to reported values. Both CT imaging and histological data were used in this comparison: the histology data was used to assess the adherence of the models to the expected overall population-level ground truth. The CT imaging data was used to compare the observed simulation HU values to what is expected based on clinical observations. The histological validation step took place prior to the image-based consistency check, which was after voxelization but prior to CT simulation.

Observed quantities included: trabecular bone volume per combined trabecular–marrow volume (BV/TV, dimensionless), trabecular bone surface area per combined trabecular–marrow volume (BS/TV, mm⁻¹), number of “handle” structures per cubic millimeter (Genus/mm³, 1/mm³, Conn.D), trabecular bone surface area per trabecular bone volume (BS/BV, mm⁻¹), trabecular thickness (Tb.Th, mm), and the complementary marrow thickness (or trabecular separation, Tb.Sp, mm). All quantities were calculated based on the original triangulated surface models. Values were averaged across all similar bone types (e.g., ribs).

All properties were readily calculated on CPU-based systems except Tb.Th and Tb.Sp, which were calculated primarily using an NVIDIA Tesla K80 since the task involved per-vertex ray-tracing.

CT Image acquisition

The example 50th percentile adult male XCAT phantom with added bone structures was imaged using the scanner-specific CT simulator DukeSim. The virtual acquisitions were done by modeling commercial photon-counting detector (PCD) CT (NAEOTOM Alpha, Siemens) and conventional energy-integrating detector (EID) CT (FORCE, Siemens) scanners at a CTDI_vol of 40 mGy, with a pitch of 0.8, and a rotation time of 0.5 s. The PCCT images were acquired at two spatial resolution modes: (1) ultra-high resolution with beam collimation of 120×0.2 mm (PCD UHR) and (2) high resolution with beam collimation of 144×0.4 mm (PCD HR). The EID acquisitions used a beam collimation of 0.96×0.6 mm. All acquisitions utilized a tube voltage of 120 kV, and the PCD acquisitions used detector thresholds of 20 and 65 keV. The images were reconstructed using a vendor-specific reconstruction software (ReconCT, Siemens) with a FOV of 400 mm. All acquisitions were reconstructed with two renditions. The first used reconstruction settings optimized for bone quantification: the smallest slice thickness available (0.2 mm for PCD UHR, 0.4 mm for PCD HR, and 0.75 mm for EID), a sharp kernel (PCD: Br56, EID: Br49), and a 1024×1024 matrix size (McCabe et al., 2023). The second used reconstruction settings to represent a general chest-abdomen-pelvis scan: a slice thickness of 1.0 mm, a smooth kernel (PCD: Br40, EID: Br36), and a 512×512 matrix size. Kernels between scanners were chosen based on matching MTF curves.

Results

Generated trabecular bone models

The method successfully generated the inner trabecular structures for the different bones of the chest. Figures 5–7 show 3D renderings of the structures; the renderings were produced using the Blender modeling software (www.blender.org). Figure 5 shows the inner structures generated for all 46 bones of the 50th percentile male XCAT phantom. Figure 6 shows a close-up of the trabecular bone for the vertebrae. Figure 7 provides an illustration of how the method can generate variable trabecular bone structures.

Figure 5:

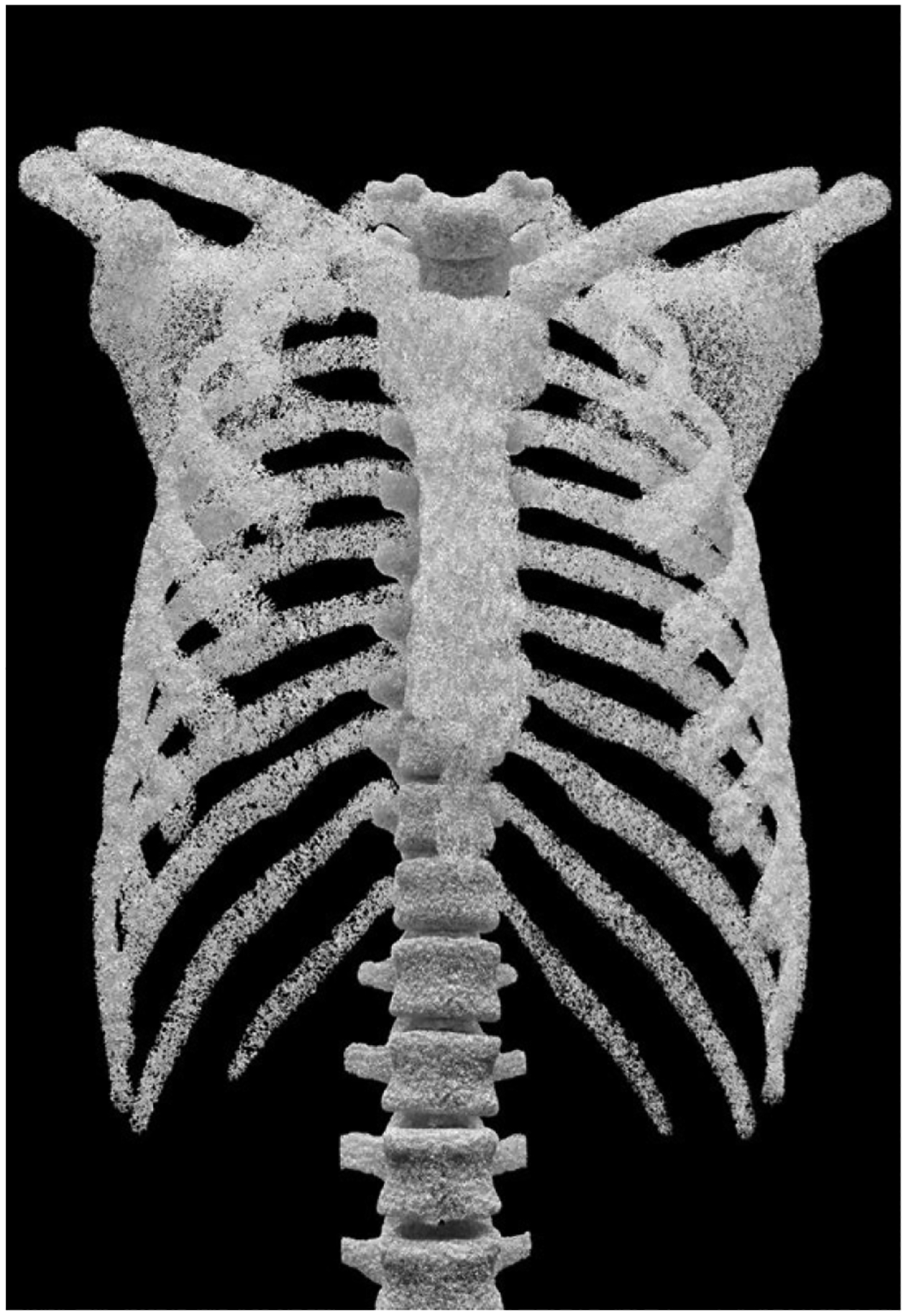
Trabecular bone model for 46 bones of the chest generated for the XCAT adult male phantom.

Figure 7:

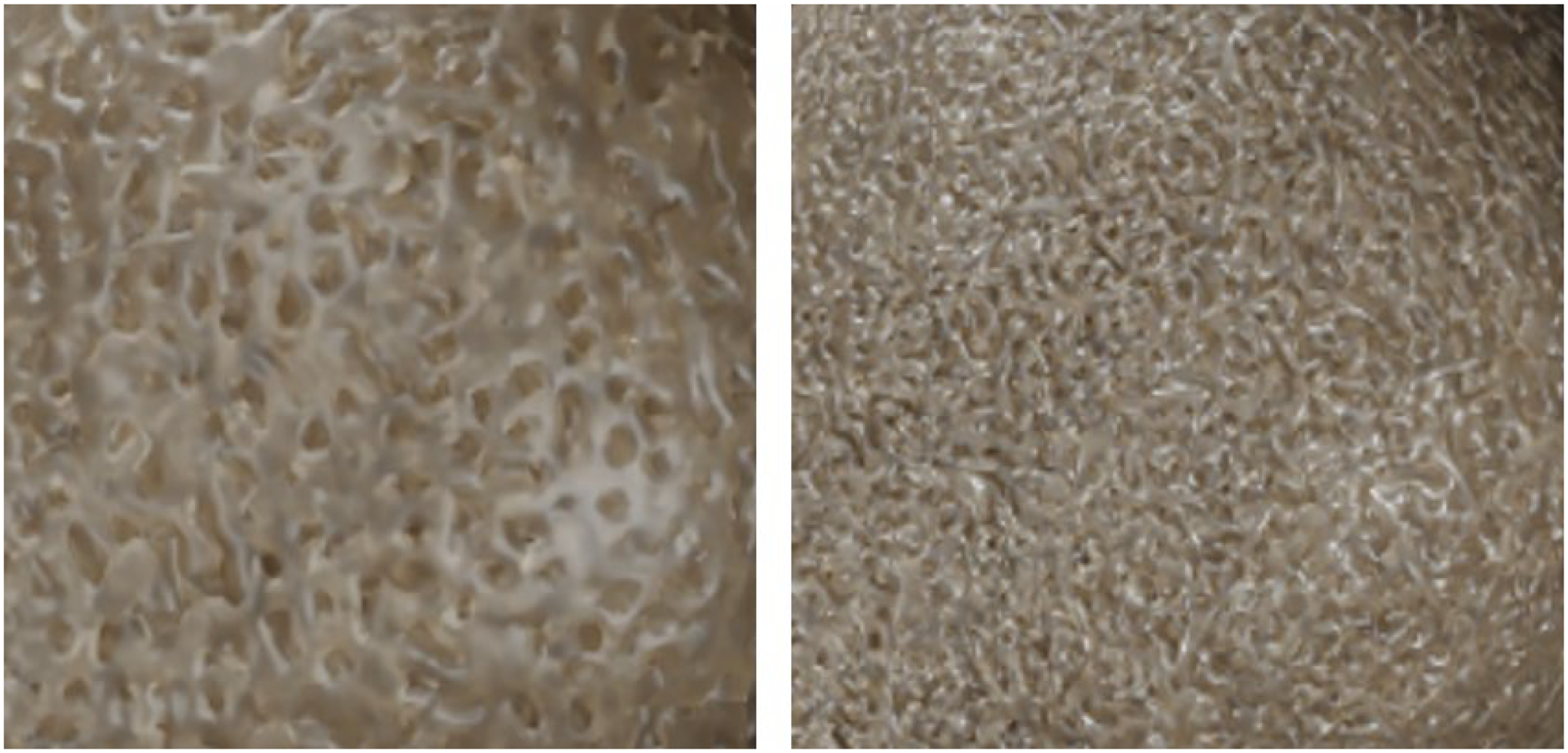
Close-up view of the trabecular bone model generated with variable trabecular bone volume fractions (trabecular volume divided by the total bone volume) of 50% (left) and 65% (right).

Figure 6:

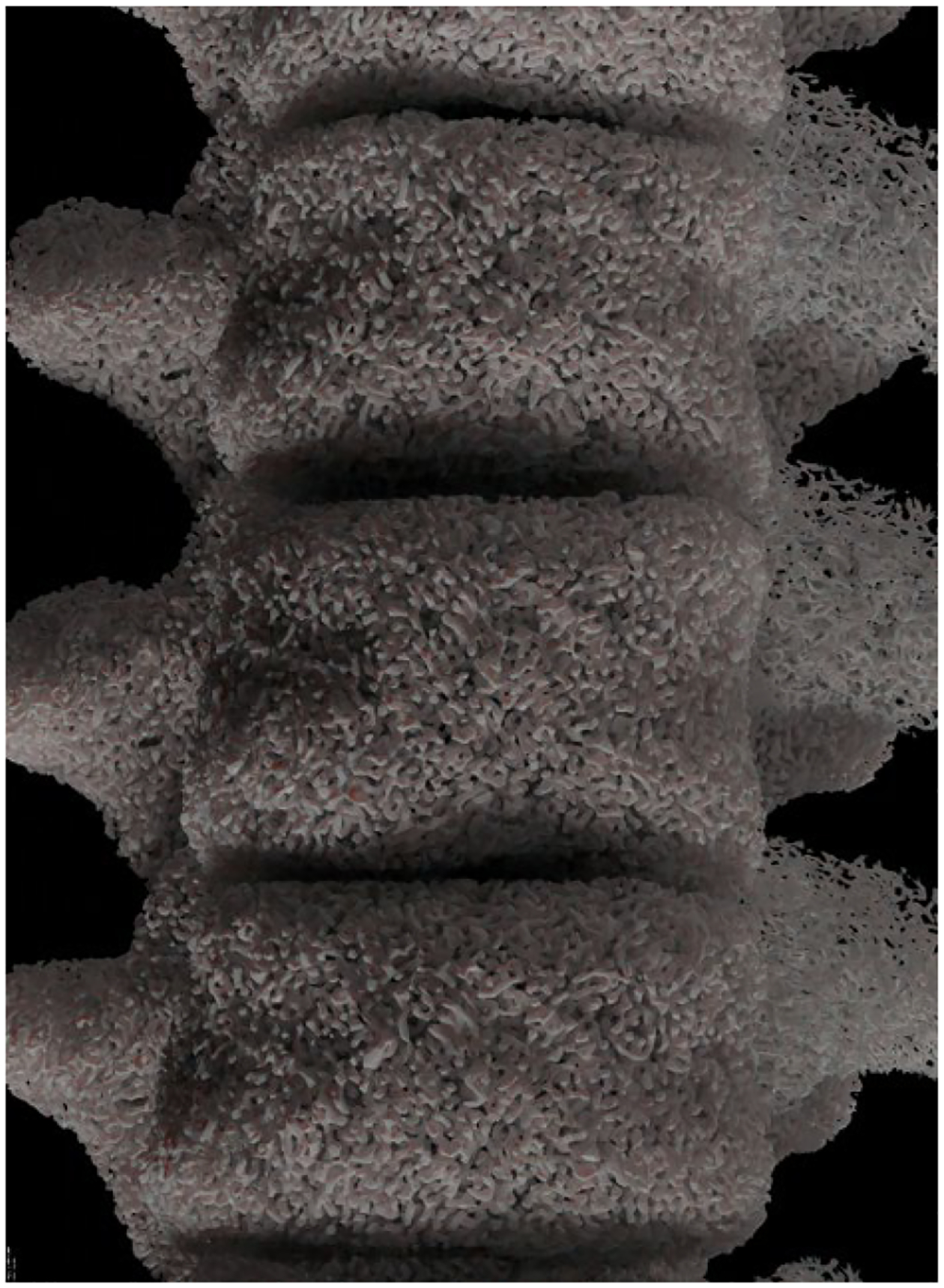
Trabecular bone generated for the XCAT vertebrae.

Model validation

The model validation process used published data acquired from micro-CT, histology, and scanning electron microscopy of human trabecular bone in the torso. Due to sometimes extreme differences in reported values between studies, even within the same modality, all reported values are listed as a range.

The values observed for this validation were geometric and topological properties of the trabecular bone structures including trabecular bone volume (Bone Volume, BV), trabecular bone surface area (Bone Surface, BS), combined trabecular and marrow volume (Total Volume, TV); connectivity density (Conn.D), trabecular thickness (Tb.Th), and marrow thickness (Tb.Sp)—these values are summarized in Table 1 as a reference for the additional derived metrics as reported in Tables 2–6.

Table 1:

Symbols for common bone geometric and topological property measurements

Svmbol	BV	BS	TV	Conn.D	Tb.Th	Tb.Sp
Units	mm3	mm2	mm3	mm−3	mm	mm
Description	Trabecular volume	Trabecular surface area	Trabecular+Marrow volume	Genus / Trabecular volume	Trabecular length	Marrow length

Table 2:

Mean value (μ) of empirical and modeled topological properties of human vertebral trabecular bone. The percent error for the model (ε) was calculated if μ fell outside the empirical range.

Vertebra (T1–L5)
Modeled	BV/TV (%)	BS/TV (mm −1 )	Conn.D (mm −3 )	BS/BV (mm −1 )	Tb.Th (mm)	Tb.Sp (mm)
	μ=13.1	μ=3.7	μ=5.1 ε = 2.0%	μ=28.3 ε = 1.1%	μ=0.16	μ=0.76
Empirical	BV/TV (%)	BS/TV (mm −1 )	Conn.D (mm −3 )	BS/BV (mm −1 )	Tb.Th (mm)	Tb.Sp (mm)
	μ=[8–27] (Maquer et al., 2015, Banse et al., 2002, Merz and Schenk, 1970, Goulet et al., 1994, Ulrich et al., 1999, Hildebrand et al., 1999)	μ=[1.6–4.5] (Goulet et al., 1994)	μ=[2–5] (Odgaard and Gundersen, 1993)	μ=[12–28] (Whitehouse et al., 1971a, Kuhn et al., 1990, Ulrich et al., 1999, Hildebrand et al., 1999)	μ=[0.10–0.17] (Hildebrand et al., 1999)	μ=[0.66–1.0] (Hildebrand et al., 1999)

Table 6:

Mean value (μ) of empirical and modeled topological properties of human trabecular bone of the torso.

Pooled trabecular bone
Empirical	BV/TV (%)	BS/TV (mm −1 )	Conn.D (mm −3 )	BS/BV (mm −1 )	Tb.Th (mm)	Tb.Sp (mm)
Pooled	μ=[13–27] (Goulet et al., 1994)	μ=[1.6–4.5] (Goulet et al., 1994)	μ=[2–5] (Odgaard and Gundersen, 1993)	μ=[10–27] (Goulet et al., 1994, Hildebrand et al., 1999)	μ=[0.10–0.19] (Goulet et al., 1994, Hildebrand et al., 1999)	μ=[0.4–0.88] (Goulet et al., 1994)

Quantification of the bone structure properties from both the models and from available data are included in Tables 2–6. General values for the quantities used for validation can be found in the “Pooled” row at the bottom of Table 6.

Each of Tables 2–6 refer to a particular type of bone (vertebrae, ribs, etc.). Measurements of the modeled parameters are included in the upper portion of each table under the heading “Modeled”. These values were calculated from the voxelized ground-truth models at a 0.01mm resolution using BoneJ (Doube et al., 2010). The mean (μ) was reported for all bone metrics. If the mean value of the model did not fall within the empirical range, the percent error (ε) was reported in the table.

The lower portion of each of Tables 2–6 reports empirical observations of the same geometric and topological properties for the bones; in the case of some of the less common parameters being unavailable, pooled statistics are included for comparison. The pooled statistics are reported in Table 6. The quantiative measures from the modeled bones can be seen to agree considerably with the published values. For the sternum and scapula, they can be seen to vary more from empirical measurements of BS/BV, ratio of the trabecular surface area to the trabecular volume. Additional operations (mesh decimation or smoothing) may be needed to better match this measure by reducing the trabecular surface area while preserving the volume.

Simulated CT and PCCT images of the bone structures were also found to be in good agreement with the histologically observed values for BV/TV, BS/TV, Conn.D, BS/BV, and Tb.Th to the extent that data was available for each quantity and type of bone modeled here. Modeled vertebral bone density (BV/TV) was measured to be approximately 13% by volume; BS/TV varied from 1–2 mm⁻¹; Conn.D from 1–5 mm⁻³; BS/BV from 10–20 mm⁻¹; trabecular thickness (Tb.Th) from 0.05–0.35 mm; and marrow thickness (Tb.Sp) from 0.5–4.0 mm. The simulated images are shown in Figs. 7–8. The PCCT images were better able to resolve the trabecular structures of the phantom when compared to the EID images, demonstrating that it is indeed necessary to have a model at such a high resolution for future medical imaging simulations focused on bone and bone texture.

Figure 8:

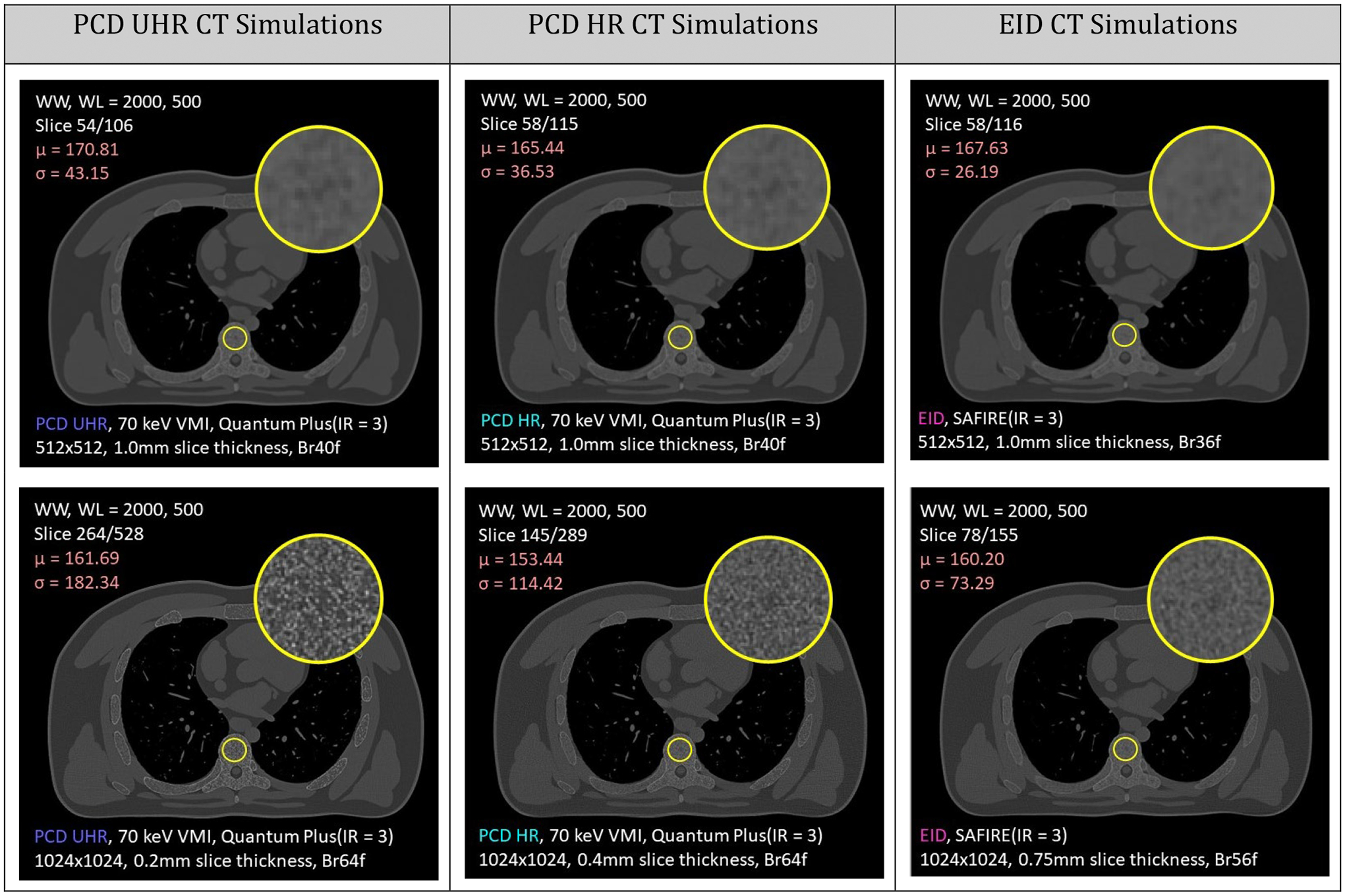
Simulation comparison of photon-counting detector (PCD) PCCT versus conventional energy-integrating detector (EID) CT. Different acquisition parameters are detailed in white at the bottom of each image. The top row represents a routine chest reconstruction, and the bottom row utilizes optimized reconstruction parameters for bone quantification.

Software package

The complete software required to produce the bone models was developed as standalone Podman(Kurtzer et al., 2017) and Docker(Merkel, 2014) images with the minimum necessary runtime environment (totaling ~ 10 GB as a compressed archive). Most features of the software run in a reasonable amount of time on a CPU-based machine; however, a NVIDIA Tesla K80 GPU board was necessary to calculate some physical properties of the bone tissue (like local thickness) within a reasonable amount of time. Use of pre-generated models does not specifically require a highly parallel computing architecture. Using GPU, the bone structure generation process was several orders of magnitude faster than with CPU and has been optimized for GPU computation to maximize throughput.

The stand-alone application will be distributed like the XCAT software. The bone models it produces can be read by the XCAT program as user-defined objects with user-defined materials to add within the anatomies for simulations.

CT simulation

Simulated CT images from the voxelized phantom can be seen below in Fig. 8 for both PCD and EID CT. Photon counting detectors appear to be able to resolve the trabecular structures with higher fidelity than standard energy integrating detectors and are better able to distinguish between marrow and trabecular tissue. This demonstrates the necessity of a high-resolution anthropomorphic model of trabecular bone when evaluating properties of bone tissue under CT imaging.

Discussion

In this work, we developed a procedure to generate realistic computational trabecular bone structures of the torso with an exactly-known ground-truth morphology which are suitable for use in simulated medical imaging. The method can be used to generate trabecular bone structures variable in density, local thickness, and connectivity for phantoms of differing body habitus or bone shape. Through alteration of the method’s parameters, models for disease such as osteoporosis can also be generated. This work presents the first use of this new tool for generation of bone structures of the torso and subsequent CT and PCCT simulation.

Additionally, this work brings us closer to the goal of achieving fast, robust, and representative generation of realistic small-scale morphology that is adherent to known clinical texture properties of CT-imaged bone structures—and which are readily available to the entire XCAT phantom cohort. This effort also assists in the goal of realizing realistic simulated chest imaging for not only ionizing imaging modalities but any simulated imaging modality which can benefit from a sub-clinical resolution bone tissue morphology (e.g., magnetic resonance imaging, positron emission tomography).

Prior work has consisted of smaller 3D models and image-domain synthesis efforts; however, smaller-scale 3D models were intended to represent small regions of bone and complementary marrow structures (rather than for 46 bones on the scale of an adult male torso). Similarly, image-domain-only synthesis of realistic textures used as a stand-in for exactly-known morphology enables the correct appearance under current imaging, but does not provide a phantom-domain direct correspondence to histological ground-truth. Plus, as imaging methods are improved, such as in photon-counting CT, texture models fall apart in not providing the underlying structure which can now be resolved.

A critical consequence of this work is that the results shown here indicate that imaging-based quantification of trabecular and cortical structures are almost universally prone to overestimating the spatial extent of the bone structures (i.e., these measurements are biased such that attempts at quantification of these structures from simulated or clinical images alone leads to a consistently hyper-thick estimation which is only apparent when compared to histological data—or, in this case, known ground-truth morphology. The larger implication of the image-based overestimation of bone density for computational simulation and phantom work is that validation of any proposed model that purports to be realistic must be validated by an external source of information. That external information must also not be directly supplied to the simulator. Failure to validate with a truly external source of information can lead to circularity and compromise efforts to create a reproducible validation of a proposed model.

This work had several limitations. First, the computational demand of some of the methods used in generating the trabecular bone structures may limit the accessibility of this model in terms of both model generation and simulation, which may in turn limit its usability. Second, additional operations may be needed to better match the bones for the sternum and scapula in terms of the surface area and volume of the generated trabecular structures. Additionally, there was not incorporation of realistic bone structure anisotropy that matched body habitus and inter-vertebral stress gradients (e.g., load-bearing orientation) as would be seen in vivo.

In future work, it will be possible to address the issue of the relative isotropy of the bone structures generated here. Specifically, topology optimization using finite element analysis will allow for patient-specific application of loads due to general body habitus and patient-specific inter-vertebral position—this will allow for incremental changes to the trabecular structure morphology to remove material from locations of low stress and reinforce locations of high stress. Because this optimization technique mimics the actual physiological changes that occur due to loading and unloading of bone tissue, it may be possible to use it to create anisotropic bone structures that are unique to individual patients.

Additionally, the trabecular structures generated here are also randomly oriented. This results in some characteristic trabecula orientations and thicknesses that are not representative of what would be found in vivo. It is possible to use an approach known as “topology optimization”(Zhou et al., 2019, Wu, 2018, Hoshina et al., 2018, Oh et al., 2021, Kegl, 2000, Abdi et al., 2014, Holmberg et al., 2013, Cheng, 1995, Brittain et al., 2011, Sokołowski, 2003, Maute and Ramm, 1995, Yago et al., 2020) in order to give the bone structures generated a realistic (functionally-informed) anisotropy. This approach is motivated by Wolff’s law(Turner, 1992, Frost, 2001, Rubin and Hausman, 1988, Jang and Kim, 2008, Frost, 1990, Cowin, 1986, Pearson and Lieberman, 2004, Teichtahl et al., 2015, Ruff et al., 2006, Mullender and Huiskes, 1995) which is supported by observations of bone microstructures gradually reinforcing over time due to repetitive load stimulus. Additionally, this approach has allowance for a reduction of material in under-utilized regions. Loads may be applied to each vertebra (cortical–trabecular–marrow model) on the region of contact with the superior intervertebral disc and assigning the inferior intervertebral disc contact region to be a fixed boundary condition.

Conclusion

This work enables the generation and post-hoc parameter modification of a set of computational models of human trabecular bones of the chest for use in virtual imaging simulations. Enhanced phantoms with detailed models of the bones can provide a vital tool to evaluate emerging imaging techniques such as photon-counting CT that offer improved spatial resolution and reduced noise.

Table 3:

Mean value (μ) of empirical and modeled topological properties of human rib and clavicular trabecular bone. The percent error for the model (ε) was calculated if μ fell outside the empirical range.

Rib and clavicle
Modeled	BV/TV (%)	BS/TV (mm −1 )	Conn.D (mm −3 )	BS/BV (mm −1 )	Tb.Th (mm)	Tb.Sp (mm)
Rib	μ=15.3	μ=3.6	μ=2.5	μ=23.3	μ=0.19	μ=0.51
Clavicle	μ=16.9	μ=3.9	μ=2.5	μ=22.8	μ=0.20	μ=0.57
Empirical	BV/TV (%)	BS/TV (mm −1 )	Conn.D (mm −3 )	BS/BV (mm −1 )	Tb.Th (mm)	Tb.Sp (mm)
Rib with Pooled Statistics	μ=[13–27] (Goulet et al., 1994)	μ=[1.6–4.5] (Goulet et al., 1994)	μ=[2–5] (Odgaard and Gundersen, 1993)	μ=[10–27] (Goulet et al., 1994, Hildebrand et al., 1999)	μ=[0.15–0.20] (Whitehouse et al., 1971a)	μ=[0.4–0.88] (Goulet et al., 1994)

Table 4:

Mean value (μ) of empirical and modeled topological properties of human sternum trabecular bone. The percent error for the model (ε) was calculated if μ fell outside the empirical range.

Sternum
Model	BV/TV (%)	BS/TV (mm −1 )	Conn.D (mm −3 )	BS/BV (mm −1 )	Tb.Th (mm)	Tb.Sp (mm)
	μ=10.8	μ=3.4	μ=2.0	μ=31.0 ε=34%	μ=0.14	μ=0.56
Empirical	BV/TV (%)	BS/TV (mm −1 )	Conn.D (mm −3 )	BS/BV (mm −1 )	Tb.Th (mm)	Tb.Sp (mm)
	μ=[9–17] (Maquer et al., 2015, (Arbabi, 2009, Whitehouse, 1975, Ulrich et al., 1999)	μ=[1.6–4.5] (Goulet et al., 1994)	μ=[2–5] (Odgaard and Gundersen, 1993)	μ=[17.6–23.1] (Arbabi, 2009, Whitehou se, 1975, Ulrich et al., 1999)	μ=[0.088–0.150] (Whitehouse, 1975, Ulrich et al., 1999, Ulrich et al., 1999)	μ=[0.4–0.88] (Goulet et al., 1994)

Table 5:

Mean value (μ) of empirical and modeled topological properties of human scapular trabecular bone. The percent error for the model (ε) was calculated if μ fell outside the empirical range.

Scapula
Model	BV/TV (%)	BS/TV (mm −1 )	Conn.D (mm −3 )	BS/BV (mm −1 )	Tb.Th (mm)	Tb.Sp (mm)
	μ=14.6	μ=4.4	μ=3.7	μ=30.2 ε=12%	μ=0.17	μ=0.66
Empirical	BV/TV (%)	BS/TV (mm −1 )	Conn.D (mm −3 )	BS/BV (mm −1 )	Tb.Th (mm)	Tb.Sp (mm)
Scapula with Pooled Statistics	μ=[7–25] (Li et al. 2015)	μ=[1.6–4.5] (Goulet et al., 1994)	μ=[2–5] (Odgaard and Gundersen, 1993)	μ=[10–27] (Goulet et al., 1994, Hildebrand et al., 1999)	μ=[0.12–0.18] (Li et al. 2015)	μ=[0.54–1.18] (Li et al. 2015)