Brain rhythms have come of age

Abstract

Neuronal oscillations offer access to neuronal operations, bringing microscopic and macroscopic mechanisms, experimental methods, and explanations to a common platform. The field of brain rhythms has become the agora of discussions from temporal coordination of neuronal populations within and across brain regions to cognitive phenomena, including language and brain diseases.

Introduction

Studies of neuronal oscillations are as old as neuroscience itself. Yet, in-depth inquiry of neuronal oscillations had its earnest start only three decades ago. This pivotal change was mainly due to works that focused on the neuronal spike content of the various rhythms, their biophysical and circuit mechanisms, and drug responsiveness, which provided a link to circuit functions and, in turn, to cognitive phenomena. This mesoscopic link created a new platform, the field of “neuronal oscillations,” which has become one of the fastest growing disciplines in neuroscience, and allowed for a fruitful conversation between cellular and network neuroscience on the one hand and cognitive, neurology, and psychiatry on the other. The term “brain rhythm” has become a household word beyond neuroscience. Our community has moved from the early critical questions (“Do oscillations exist?” or “Do network oscillations assist brain computation?”) to “how” neuronal oscillations contribute to circuit operations and behavior.¹ Now it is time to relate current major challenges of contemporary neuroscience to brain rhythms.

The new problem: Time is neuronal space in the brain

Simultaneity of two (or more) events may be deemed synchronous (i.e., occurring within a defined time interval of an observer) even if the two events occur at vastly different times. For example, action potentials arriving at the same time onto the dendrite of a reader neuron from a nearby and distant neuron exert a cooperative impact on discharge of the reader (target) neuron, even though the spikes in the two upstream neurons were generated tens of milliseconds apart (Figure 1A). Conversely, action potentials that are generated at the same (clock) time in a nearby and distant neuron will arrive to the reader neuron tens of milliseconds apart (i.e., asynchronously; Figure 1B). This observer- or reader-defined synchrony is critical in brain operations. If the action potentials from many upstream neurons arrive within the membrane time constant of the target (reader) neuron (τ: 10–50 ms for a typical pyramidal neuron), their combined action is cooperative because each of them contributes to the discharge of the reader neuron. Action potentials arriving later can only contribute to initiating another action potential. Thus, from the reader neuron’s point of view, upstream partners that contribute to its spike discharge constitute a functional assembly (integrated by the membrane time constant), whereas spikes outside this time window can only be part of another assembly.² This simple functional measure can thus both integrate and segregate upstream neurons into discrete assemblies, irrespective of whether they are interconnected or not. The entire goal of synchronous cooperation is to have an impact, i.e., trigger an action potential in target neurons. Neurons that achieve this joint impact can be considered as a fundamental assembly. When the reader mechanism can integrate over longer time scales (e.g., NMDA channels or neuronal circuits), several fundamental assemblies can be concatenated.

Figure 1. Time is neuronal space.

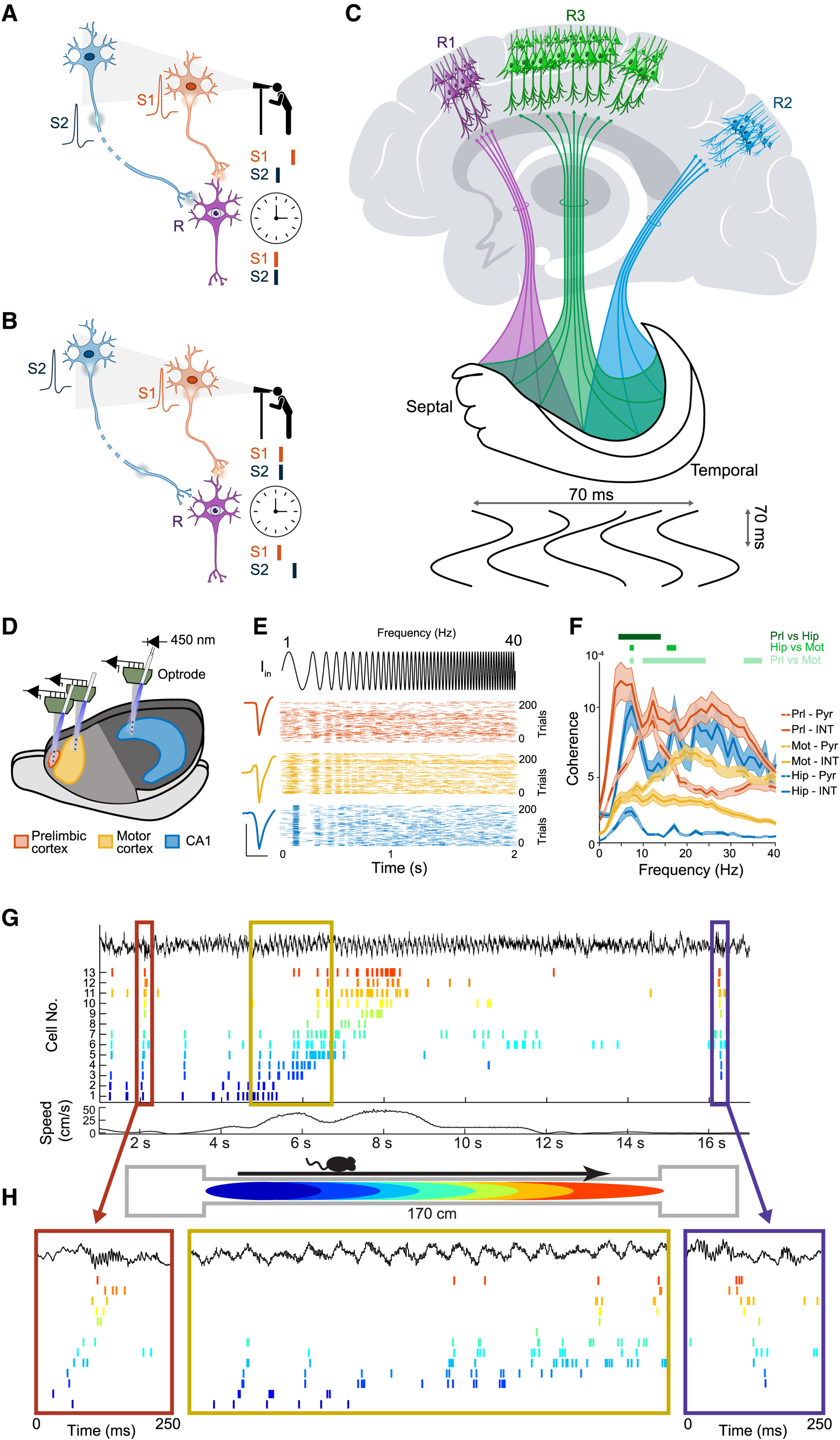
(A–C) (A and B) Observer/reader-dependent definition of synchrony. (A) Spikes from upstream neurons (sender 1 and sender 2, S1 and S2, respectively) arrive “at the same time” to the dendrites of a reader neuron (R), but these spikes were initiated at different times by S1 and S2. (B) Spikes initiated at the same time in S1 and S2 arrive at different times to the R. The R-centric classification of spikes generalizes to populations as well. (C) Space-duration readout of neuronal messages. Spikes from the hippocampus that arrive within the time constant of the neocortical reader circuits R1 or R2 are integrated. Upstream (hippocampal) neurons that send these spike messages are considered separate assemblies by R1 and R2, respectively, because of timing of spikes and anatomical connectivity. The hypothetical reader circuit R3 has a “preformed anticipatory schema” with a shared cipher (theta cycle frame) that helps to select features that are characteristic for anticipated events or activities and their change. Marking the message boundaries by cyclic inhibition partitions a continuous stream of events into discrete units and forms the hypothetical basis for extraction and synthesis of new information (a process called “abstraction”). In the example, the message sent from the entire hippocampus occurs in half a theta cycle (~70 ms).

(D–F) Circuit-specific resonance. (D) Neuronal activity was recorded from cingulate (Cin, orange), motor cortex (Mot, yellow), and hippocampus (Hip, blue) with silicon probes in transgenic mice expressing channelrhodopsin-2 selectively in Cam-KII-expressing excitatory cells. (E) Top: “chirp” pattern optogenetic stimulation signal (1–40 Hz, 2s). Example pyramidal cells from these different brain regions show preferred frequency response (n = 200 trials; scale bar, 100 μV and 1 ms). (F) Spiking resonance (mean ± SEM) for pyramidal cells (Pyr, dashed line) and interneurons (INT, solid line). Significant region differences are highlighted (green lines, p < 0.01; Mann-Whitney U test with Bonferroni correction).

(G and H) Time compression of neuronal assembly sequences. (G) Spike trains of hippocampal neurons (color ticks) before, during, and after a single lap. The top black trace illustrates the local field potential; the bottom black line illustrates the locomotion speed of the rat. (H) Spike sequences within single theta cycles are compressed versions of the place field spiking activity on the track (2-s segment highlighted in the yellow box). These theta sequences gradually shift as the animal moves from left to right down the track. On each end of the tack (red and purple boxes), spiking during ripples reflects forward and reverse replay of the sequences on the track, respectively. Figure adapted from Diba and Buzsáki.³.

This reader-centric view becomes of utmost importance when one wants to understand communication across brain regions, such as the hippocampus and neocortex (Figure 1C). Because of the slow communication across neurons via the relatively slow conducting axons and charge time of the neuronal membrane, computation and messaging are not instant but protracted over time. This slow propagation of the activity within and across networks is reflected at the mesoscopic level as “traveling waves.”⁴ For example, population activity travels from the dorsal to the ventral pole of the hippocampus in half a theta cycle (~70 ms; Figure 1C). Therefore, the question that arises when the entire hippocampus takes part in a particular computation is: how does the neocortical reader integrate (i.e., decode) neuronal messages from the hippocampus? As is the case in human language communication, where even the last word of the sentence can change the meaning of the sentence, the reader structure should know both the beginning and end of each message—in our example, the spikes from the entire hippocampal volume within 70 ms time frames.

For the messages to become information, certain requirements must be in place, of which syntactical rules are most important. We should emphasize that separation of networks into senders and receivers serve only didactic purposes. In the complex networks of the brain, most structures are bidirectionally connected and can serve as both senders and receivers, whose functions can change rapidly by shifting the phases of the sender and receiving partners.

Syntax for communication across brain circuits by neuronal rhythms

In a general sense, communication is an agreement between a sender and receiver. This “agreement” is called the cipher known to both parties. A key aspect of the cipher is a method by which the messages are broken down into smaller information chunks or segments, the modus operandi by which the sent messages are transcribed and translated by the receiver. Chunking of messages by agreed rules allows the generation of and reading (i.e., “de-ciphering”) virtually infinite combinations from a finite number of elements in human, sign, body, artificial, and computer languages, music, and mathematical logic, and, presumably, the brain. This small set of rules, usually referred to as syntax, governs the combination and temporal progression of discrete elements (such as letters or musical notes) into ordered and hierarchical relations (words, phrases, and sentences or chords and chord progressions) that allow the generation of messages, which, when interpreted by the receiver, become information. Syntax is exploited in all systems where messages are coded and transmitted, searched for, and decoded.

A potential substrate for a hypothetical neuronal syntax in the brain is the constellation of brain rhythms.⁵ The neurophysiological basis of this hypothesis is that virtually all known network oscillations (>1 Hz) are based on inhibition, which creates temporal frames for parsing and chunking of neuronal spiking activity into cell assemblies and sequences of assemblies for the effective exchange of neuronal messages among neuronal networks. Communications via rhythms is effective because neuronal oscillators have a separate “duty” or sending phase when spiking information is transferred and a perturbation or “receiving” phase.⁶ These types of oscillators can synchronize robustly and rapidly in a single cycle, making them ideal for segmentation of spiking information in both time and space. Thus, neuronal oscillations have a dual function in brain networks: they are influenced by spiking inputs and, in turn, affect timing of spike outputs. In addition, rhythm cycles across regions can provide the information about message frames. In the absence of segmentation and a mutually agreed cipher, messages would remain meaningless gobbledygook.

Brain rhythms cover more than four orders of magnitude in frequency, from the infraslow (<0.01 Hz) to ultrafast (200 Hz) rhythms, and include at least ten interactive oscillation classes. Integrated over a long temporal scale, the power distribution of the various frequencies has the appearance of 1/frequencyⁿ “noise,” partly reflecting the fact that slow oscillations generate large, synchronous membrane-potential fluctuations in many neurons in brain-wide networks, whereas faster oscillations are associated with smaller changes in membrane potential in a limited number of cells that are synchronized only within a restricted neural volume. The different oscillations generated in cortical and subcortical networks show a hierarchical relationship via cross-frequency phase-amplitude coupling, meaning that the amplitude of the faster oscillation varies predictably as a function of the phase of the slower oscillator, akin to how daylight duration is modulated by the seasons (spring, summer, fall, and winter) of the year.⁷ For example, the ultrafast oscillatory “ripple” waves (150–200 Hz) in the hippocampus are phase locked to hippocampal sharp-wave events, and the magnitude of the sharp-wave ripples (SPW-R) is modulated by the phase of thalamocortical sleep spindles. The spindle events, in turn, are phase modulated by cortical delta oscillations, which are nested in brain-wide 0.1 Hz and 0.02 infra- and ultra-slow oscillations. At the neuronal level, such multi-level nesting of phase-amplitude coupling reflects local-global computation, which is how distributed local processes are integrated into globally ordered states. The results of local computations are broadcast to wide-spread brain areas, and in the reverse direction, local computations and the direction of the activity flow of signals are coordinated by the phase of a global mechanism. We suggest that this global-local integration computation is the neurophysiological basis of various psychological constructs, known as “executive,” “attentional,” “contextual,” or “top-down” control. Prominent examples include the hippocampal theta phase coupling of neocortical gamma events so that the results of multiple neocortical computations can be delivered to the non-refractory phase of the theta cycle to integrate multiple modalities and the contextual control of primary visual cortex by higher-order areas via slower (alpha) oscillations.

The well-known brain network oscillation classes are also phase modulated by slower body rhythms with 50 s, 15 min, 90 min, ultradian 6 h, and the circadian cycles, yet little is known about the significance of these body-modulated excitability changes in the brain. Despite a 17,000-fold variability in brain volume across mammalian species, the temporal scales and dynamics of neuronal coordination within and across brain networks and between brain and the body remain remarkably similar. A final argument in favor of brain rhythms for providing a syntactic framework for exchanging neuronal messages is that, to date, no other alternative theory has been advanced.

Oscillations as coordinators and compressors of neuronal activity

Keeping neurons in an excitable state is most effectively achieved by fluctuating the membrane potential close to the action potential threshold. In principle, this can be achieved by “noise,” sustained by balanced inhibitory and excitatory inputs. In line with this reasoning, improvement of behavioral performance in various tasks is often accompanied by reduced (i.e., asynchronous) spike correlation among cortical neurons. These experimental observations led to the suggestion that decorrelated spike fluctuations among neurons are advantageous for population coding because they increase the entropy and reduce the redundancy in the network and thus maximize the processing and storage capacity of neurons. This “independent” single-neuron view stands in contrast to the constraint of spike times by network oscillations and the postulated need for temporal coordination of neuronal assemblies to effectively discharge their downstream target partners. Oscillatory excitatory inputs with their parallel feedforward inhibition offer an economic compromise for the beneficial effect of noise by keeping networks in an excitatory state (i.e., a substitute for noise) as well as forming neuronal coalitions by shared cycle phases across the population, resulting in relatively random baseline firing of principal cells, yet synchronizing their actions when needed. Indeed, gamma oscillations, ubiquitous in all circuits with excitatory and inhibitory dynamics, reflect a tug of war between excitation and inhibition. Therefore, increased local field potential (LFP) gamma power, transient or sustained, is a telltale of increased local excitability. Gamma wave periods match the membrane time constant of pyramidal neurons, which explains why coalitions of neurons in this time frame (i.e., the fundamental assembly or neuronal “letter”) are most effective in discharging their postsynaptic targets. In short, gamma rhythms offer all the advantages of noisy regime for individual neurons while also allowing the network to readily switch to synchrony.

While separation of the sending and receiving phases of neuronal oscillations provide alternating refractoriness and amplification within each cycle, frequency resonance of neuronal circuits offers amplification at a longer timescale and can route and promote propagation of activity even through weak connections. Resonance refers to a selective response of a receiving circuit to signals that arrive in phase with the oscillation best supported by the circuit. Such selective amplification is demonstrated experimentally by using a “chirp” signal that continuously varies from slow to fast oscillatory waves (Figures 1D–1F). Because networks have different resonant frequency properties, they can selectively and differentially read out spike messages from upstream senders.

Oscillations and synchrony are often used synonymously, and gamma oscillations exemplify this relationship. However, temporal coordination and synchrony refer to different mechanisms.⁸ Hippocampal theta oscillations illustrate this difference. Firing of neighboring assemblies (within successive gamma waves) in the theta cycle are correlated with the travel distance representation of the assembly pairs while the rat is walking on a track so that the assembly representing the current location of the rat fires at the trough of the theta cycle, whereas cell assemblies of the previously and subsequently visited places discharge on the descending and ascending phases (Figures 1G and 1H), spanning almost the entire theta cycle (thus forming a “neuronal letter”). Therefore, while pyramidal cells are temporally coordinated, they do not discharge synchronously but are separated by orderly delays, as illustrated by their negative spike correlations. The fraction of negatively correlated neuron pairs also increases in the neocortex during “activated” focused attention. Thus, precise temporal coordination (“metachrony”) and synchrony have different meanings, mechanisms, and consequences. In summary, brain states with theta oscillations, and possibly other slow rhythms, serve to counter synchrony among neurons and distribute cell assemblies within the theta cycle.

Time compression of stimulus and event “representation” can vary with brain-state-dependent oscillation patterns. A prime example is the compression of sequences and walked distances in the maze by SPW-Rs (Figures 1G and 1H). From the temporal order of spikes, phase locked to successive ripple waves, the experimenter can reconstruct the virtual travel of the animal during consummatory behaviors, including non-REM sleep. Even at this fast (<100 ms) temporal scale, inhibition protracts excitatory synchrony so that instead of the “same time,” neuronal assemblies are discretized into multiple short (~6 ms) information packages. Presumably, these compressed sequences are also important for the downstream reader structures because perturbation of SPW-Rs leads to memory deficit. As in rodents, “replay” events in the human brain are also present in accelerated temporal sequences compared with actual experience. Importantly, replay does not simply recapitulate sensory experience but instead follows an order implied by learned abstract knowledge, embedded in the brain’s preexisting knowledge base, thus grounding the relevance of new knowledge.

Oscillations as the neuronal basis of human language

Our analogy of brain syntax to the regenerative nature of human language may be more than just a metaphor. The co-evolution of the brain and body may have constrained the way brain rhythms control the motor system and produce sound. Language is also produced by combining elements, such as sentences, which have new qualities not present in the individual words, separated by gaps. The prosodic features of speech, such as intonation, stress, and pause, are characteristic of individuals, yet they also share common features among all people, varying between 0.3 Hz and 2 Hz (delta band). Syllables (“beat”) also repeat somewhat rhythmically 4 to 8 times per second (theta band), while phonemes and fast transitions are characterized by a frequency band between 30 and 80 Hz (gamma band). Thus, the time-varying dynamics of syllable sequences can be faithfully tracked by the amplitude of theta oscillations and the phase-coupled amplitude of gamma activity. In turn, the edges of the sound envelope of speech can reset the phase of slow brain oscillations.⁹

In a multi-talker environment (“Cocktail Party”), brain activity preferentially tracks attended, relative to ignored, speech streams using both the phase of low-frequency neural activity (1–7 Hz) and the power of high gamma power activity (70–150 Hz). In higher-order brain regions, the difference between attended and ignored speech increases and this selectivity itself sharpens as a sentence unfolds. These findings thus suggest that oscillations not only track the prosodic features of speech but may also involve semantic extraction. In support of this claim, it has been shown that the magnitude of theta-gamma phase coupling is stronger when the listener extracts semantic meaning of speech compared to when the same words in a sentence are randomly shuffled or played backwards.

While it may not be surprising that the prosodic features of speech correlate with brain rhythms, semantic information is expected to arise from the combinatorics of spikes, not detectable directly from low frequency-band LFP (known as the “inverse problem” of EEG). Yet, each spike may produce a small synaptic response (i.e., a transmembrane current) in the target neurons, which, in principle, is detectable in the extracellular space. When large enough LFP sensors are available, the population vector of space-time-varying LFP traces (“synapsembles”) can be used to indirectly extract spikingrelated activity. As mentioned above, hippocampal neurons discharge selectively when the rat is at certain locations (Figures 1G and 1H), while LFPs at single anatomical sites exhibit no such place tuning. Nonetheless, because the representation of position is sparse and distributed, such information can be recovered from multiple-site LFP recordings. When LFPs are sampled at high spatial density, distributions of phases and amplitudes of the LFP theta waves across brain volume correlate with the rat’s position as robustly as neuronal spiking populations. The synapsemble hypothesis may explain why virtually any motor or cognitive behavior or semantic information can be tracked and extracted from high-density recordings of brain oscillations, as amply illustrated by the rapidly growing numbers of ECoG studies over the past three decades.

Moving forward

Because a large part of the extracellularly recorded LFP signal is due to the summed activity of time-overlapping transmembrane potentials, brought about by spike-induced postsynaptic currents (synapsembles), any non-physiological alternation of neuronal assembly coordination can also be recovered from in-depth analysis of LFP patterns. Although detection of epileptic activity from LFP is the most frequently used diagnostic tool, nearly all psychiatric conditions may be characterized by some level of “oscillopathy” or “rhythmopathy.”¹⁰ The relationship between spike assemblies and synapsembles can be also exploited for controlling computers, robots, or other artificial actuators. The advantage of measuring spatially distributed LFP features is their long-term stability compared to multisite recording of single units, which are sensitive to microscopic movements.

Finally, future works in artificial intelligence may exploit oscillatory networks for computation. This may be a win-win outcome because implementation of evolution-tested network operations may lead to novel predictive-semantic architectures and, in return, may assist neuroscience in discovering generative rules of neuronal patterning, their coding, and decoding abilities.