Abstract
The awake cortex is characterized by a higher level of ongoing spontaneous activity, but it has a better detectability of weak sensory inputs than the anesthetized cortex. However, the computational mechanism underlying this paradoxical nature of awake neuronal activity remains to be elucidated. Here, we propose a hypothetical stochastic resonance, which improves the signal-to-noise ratio (SNR) of weak sensory inputs through nonlinear relations between ongoing spontaneous activities and sensory-evoked activities. Prestimulus and tone-evoked activities were investigated via in vivo extracellular recording with a dense microelectrode array covering the entire auditory cortex in rats in both awake and anesthetized states. We found that tone-evoked activities increased supralinearly with the prestimulus activity level in the awake state and that the SNR of weak stimulus representation was optimized at an intermediate level of prestimulus ongoing activity. Furthermore, the temporally intermittent firing pattern, but not the trial-by-trial reliability or the fluctuation of local field potential, was identified as a relevant factor for SNR improvement. Since ongoing activity differs among neurons, hypothetical stochastic resonance or “sparse network stochastic resonance” might offer beneficial SNR improvement at the single-neuron level, which is compatible with the sparse representation in the sensory cortex.
Keywords: microelectrode array, non-linear firing rate distribution, signal-to-noise ratio, sound detection, temporal firing pattern
Introduction
The ability to robustly detect weak sensory stimuli is crucial for survival. In the cortex, however, evoked responses to small sensory inputs are generally weak and sparse among notoriously variable ongoing spontaneous activities (Burns and Webb 1976; Takahashi et al. 2004; Faisal et al. 2008; Funamizu et al. 2013). Moreover, cortical neurons are heterogeneous in terms of selectivity and response magnitude to sensory stimuli and ongoing activity levels (Ohki et al. 2005; Van Hooser et al. 2005; Ch'ng and Reid 2010; Clancy et al. 2015; Tischbirek et al. 2019). This suggests that a small subset of neurons in the sensory cortex is crucial for the representation of a specific stimulus (DeWeese et al. 2003; Olshausen and Field 2004; Hromádka et al. 2008; Tolhurst et al. 2009). However, how such sparse representation with heterogeneous neuronal populations could achieve a reliable detection of weak sensory inputs with a sufficient signal-to-noise ratio (SNR) against variable ongoing activities remains to be elucidated.
Ongoing activity should not be considered as noise for the detection of weak signals but rather as a representation of brain states (Gilbert and Sigman 2007), which interact with bottom-up information of sensory stimuli (Ferezou and Deneux 2017). Sensory-evoked activities thus depend on brain states, such as up/down states and sleep/anesthetized/wake states. Importantly, an awake neuronal state is characterized by a higher level of ongoing activity but with a better detectability of weak sensory inputs than anesthetized or unconscious brain states (Alkire 2008; Harris and Thiele 2011; Noda and Takahashi 2015). This suggests that the ongoing activity plays an active role in improving the SNR in perception (Azouz and Gray 1999; Haider et al. 2007; Hasenstaub et al. 2007; Reig et al. 2015). Thus, the ongoing activity might represent a repertoire of available functional patterns used for stimulus encoding (Arieli et al. 1996; Luczak et al. 2009) and have profound influences on perceptual decision-making and motor output (Hesselmann et al. 2008; de Lange et al. 2013).
Here, we hypothesize that the nonlinear interaction between ongoing spontaneous activities and sensory-evoked activities is crucial for improving the SNR of weak sensory inputs. Such interactions are reminiscent of stochastic resonance, which has been widely reported in neural systems from insects to humans (Douglass et al. 1993; Collins et al. 1996; Levin and Miller 1996). Stochastic resonance has been characterized as an SNR, depending on the level of the external background noise (Hänggi 2002; Manjarrez et al. 2003). However, there is limited knowledge on whether the level of internal activity—that is, the ongoing spontaneous activity—plays a potential role in determining the SNR in the neural representation of the sensory cortex. Because ongoing activity differs among neurons, our hypothetical stochastic resonance might work at the single-neuron level, therefore offering compatibility with the sparse representation in the sensory cortex.
We have previously demonstrated that, in the auditory cortex, single-unit activities (SUAs) provided more enhanced encoding capacity to the tone stimuli as well as the higher level of ongoing activity in the awake state than in the anesthetized state (Noda and Takahashi 2015). However, the computational mechanism behind the enhanced capacity, especially to weak inputs, has not yet been elucidated in the context of the increased ongoing activity. This study investigated whether and how the SNR depends on the level of the ongoing activity using the dataset of electrophysiological recordings of hundreds of neurons from the entire auditory cortex in awake and anesthetized rats. Our hypothetical stochastic resonance predicts that the SNR is optimized at a certain level of ongoing activity, specifically in response to weak stimulus inputs. We then characterized the temporal firing pattern and firing reliability in both ongoing and tone-evoked activities to reveal the underlying neural mechanisms of stochastic resonance with the ongoing activity. These hypothetical mechanisms were verified with a simulation model of spiking neurons. Based on our findings, we proposed a schematic model of sensory representation in a local network, which allows each neuron in a heterogeneous neural population to robustly detect weak sensory stimuli.
Materials and methods
Experimental design and subject details
We reanalyzed a previously published dataset from Noda and Takahashi (2015), where the full experimental procedure is detailed. The experimental protocol was approved by the Committee on the Ethics of Animal Experiments at the Research Center for Advanced Science and Technology at the University of Tokyo (Permit Number: RAC09107). Briefly, we used 5 adult male Wistar rats (11- to 12-week-old, 270–340 g mass; CLEA Japan, Inc., Tokyo, Japan) and performed surgery under isoflurane anesthesia (3.5% at induction and 2.0–2.5% for maintenance) to implant a custom-made head holder (Noda and Takahashi 2015) onto the rats’ skulls around 10 days before recording. The holder was a U-shaped polyacetal plastic covering the temporal cortex, including the entire auditory cortical area. Within the area of the U-shaped holder, all the skin and muscles were removed and the temporal bone was exposed and thinned. Additionally, we performed a small craniotomy near the bregma to embed a reference electrode with electrical contact to the dura mater. During and up to 3 days after surgery, an antiphlogistic analgesic drug (ketoprofen: 3.3 mg/kg body weight) and antibiotics (ampicillin sodium: 17 mg/kg) were injected intramuscularly. After a few days of recovering from surgery, we trained the rats for approximately 7 days to adapt to the head-restrained experimental conditions under which electrophysiological recordings were carried out in a sound-attenuating chamber (AMC-4015; O’Hara & Co. Ltd, Tokyo, Japan). During the training sessions, the heads were restrained with a custom-made stainless-steel fixation device, and the bodies were covered with a loose-fitting plastic half-round tube. We continued the daily training until the rats were able to stay still and maintain the resting state for >3 h, similar to the entire duration of the experiment. In the initial stages of training, the head-fixed situation may have caused fear or stress in rats. Therefore, we periodically provided sucrose water as a reward for maintenance of the resting state.
We performed all electrophysiological experiments in a sound-attenuating chamber used in training as previously described (Noda and Takahashi 2015). The microelectrode array used in this study comprised a grid of 10 × 10 silicon probes with an interelectrode distance of 400 μm in 4 × 4 mm2 substrates (ICS-96 Array; Blackrock Microsystems Inc., Salt Lake City, UT, United States). The array covered the rat auditory cortex with an area of approximately 3 × 4 mm. Neural signals were simultaneously obtained from 96 electrodes. Under isoflurane anesthesia (1.4–2.2%), but without any other analgetic agent nor local anesthesia, we placed the ground electrode under the cervical neck skin, removed the temporal skull and dura mater, and exposed the temporal cortex just before recording. Using a custom-made inserter, we inserted the array to a depth of approximately the upper 600 μm below the pial surface, that is, cortical layer IV (Barbour and Callaway 2008; Pernia et al. 2020), to measure the multiunit activities (MUAs) and LFPs. MUAs and LFPs were obtained with an amplification gain of 1,000 and digital bandpass filters of 0.25–7.5 and 0.3–500 Hz and sampling frequencies of 30 and 1 kHz, respectively (Cerebus data acquisition system; Cyberkinetics Inc., Salt Lake City, UT, United States). We conducted recordings under isoflurane anesthesia. We observed a negative deflection of tone-evoked LFP, confirming the recording depth to around layer 4 (Szymanski et al. 2011; Stolzberg et al. 2012). After the recordings, the delivery of the anesthetic drug was stopped. Subsequently, we confirmed that the rats were awake by observing their subtle voluntary limb movements. At least 30 min after halting the anesthetic delivery, we reconfirmed wakefulness by ongoing high-frequency LFP oscillations (Eckhorn et al. 1993). Finally, we collected recordings in the awake state, provided that no sign of increased stress, for example, large movements associated with electromyographic artifacts, was observed. The animals did not receive any analgetic during recordings in awake state. After the recordings, the animals were deeply anesthetized with isoflurane and euthanized by the intraperitoneal injection of pentobarbital (65–110 mg/kg).
Stimulus induction
To characterize the frequency response area (FRA) on the basis of spike discharges at each estimated single unit, sound stimuli were presented as tone bursts that were 30 ms in duration and with 5-ms linear rise and fall ramps. The frequencies of the stimuli ranged between 1.6 and 64 kHz with one-third octave increments and intensities between 20- and 80-dB sound pressure level (SPL) with 10-dB increments. A total of 126 test tones were used with 18 test frequencies and 7 intensities. Each tone was presented 20 times in a pseudorandom order with an intertone interval of 600 ms. The stimuli were presented both in the awake and anesthetized states, and the order of the tones was the same across rats and states. These stimuli were delivered to both the left and right pinnas through a free-field speaker (EAS-10TH800; Panasonic Corp., Osaka, Japan) located 15 cm from the front of the center of both the right and left pinnas. The speaker was calibrated with a one-fourth inch microphone at the pinnas (4939; Bruel & Kjær, Nærum, Denmark).
Data analysis
Spike sorting
The detailed procedure for single-unit isolation has been previously described by Noda and Takahashi (2015). Briefly, we first extracted biologically plausible spike waveforms based on 4 heuristic criteria. Then, we projected the extracted spike waveforms into 3 major principal components using principal component analysis. A clustering method (Harris 2000) was used to compress data in the principal component space with an appropriate number of clusters using the open source software, KlustaKwik. Subsequently, we extensively examined the waveforms of each clustered sample and discarded the clusters that did not seem physiologically plausible by visual inspection. Lastly, we defined SUAs as activities in the remaining clusters and identified them as well-isolated SUs in a subset of recording sites.
Definition of FRA
The tone-evoked response for each single unit was characterized as the average z-score of spikes at 5–45 ms after the stimulus onset. The detailed procedure to define the characteristic frequency (CF), FRA, minimum threshold (MT), and response quality (d’) was previously described (Noda and Takahashi 2015). Briefly, the FRA was measured as an area in the frequency-dB SPL plane, where z-scores had larger values than the threshold. The threshold is determined by the maximal value of the second-order differentials of a smoothed z-score histogram, that is, the inflection point (Guo et al. 2012). The statistical distance of distributions was defined as d’, which is between the responsive and nonresponsive areas in each FRA of the corresponding unit (Guo et al. 2012; Noda and Takahashi 2015). Monotonicity of the rate-level function of FRA was then characterized by the monotonicity ratio, which is the ratio of the response value at 80 dB SPL to the maximum response value at the CF (Sutter and Schreiner 1995; Moshitch et al. 2006).
Quality criteria
Based on the criteria used in the previous study (Guo et al. 2012), we excluded single units with a low d’ (<3.0) from tone-responsive units (279 units in total) under either anesthetized or awake condition (exclusion of 10 units) and units with an extremely high (>10 times) or low (<0.1 times) d’ between anesthetized and awake condition (exclusion of 6 units) such that d’ is evenly distributed in the 2-dimensional space of anesthetized and awake conditions. This led to 263 tone-responsive qualified units.
Receiver operating characteristic analysis
We defined test tones with 60–80 and 20–40 dB SPL as high sound level and low sound level, respectively, as the similar intensity ranges were suggested as high and low levels, respectively, in prior studies (Polley et al. 2006; Duque et al. 2012). Within the range of each high level and low level, the frequency condition F(i) was set as the CF of each single unit and the SPL condition, and SPL(j) was pseudorandomly selected within the FRA of the unit (Fig. 1A). To avoid any biased variability of the spiking activity in a specific frequency–SPL condition due to the relatively small number of trials, we lumped the spiking activities in 5 neighboring frequency–SPL conditions together, that is, (F(i − 1), SPL(j)), (F(i + 1), SPL(j)), (F(i), SPL(j − 1)), (F(i), SPL(j + 1)), and (F(i), SPL(j)). Any case in which the neighboring condition was out of the FRA or out of each high-/low-level input was excluded from further analyses. This allowed us to focus on the effect on the spiking activity in each high-/low-level input condition rather than the effect of a specific sound frequency and SPL, with a reliable number of trials up to 100. Then, we referred to the combination of frequency–SPL conditions in each high-/low-level input as a high/low sound-level condition. Prestimulus ongoing spiking activity and tone-evoked response were defined for each trial at 45–5 ms before and 5–45 ms after the stimulus onset, respectively. For each single unit, these activities were time-averaged for each trial and were averaged across the trials.
Fig. 1.
Responsiveness to weaker tones and relationship between ongoing and evoked firing rates differ between awake and anesthetized states in the auditory cortex. A) Frequency responsive areas (FRAs) of representative neurons under awake (left) and anesthetized states (right). Asterisks denote the center of high sound-level conditions (within 60–80 dB SPL); circles, low sound-level conditions (within 20–40 dB SPL). The high and low sound-level conditions were pseudorandomly selected within the FRA. The low sound-level condition was below the MT of FRA under anesthesia but not less than the MT under awake. Representative FRAs with MTs (AW < AN). B) Pie chart of sample neurons categorized by the MT in awake and anesthetized states. Colors: orange (AW<AN for n = 164), neurons whose MT was lower under awake than anesthetized states; green (AW = AN for n = 57), neurons with the comparable MTs under awake and anesthetized sates; cyan (AW>AN for n = 42), neurons whose MT was higher under awake than anesthetized states. Neurons with MT >40 dB SPL under awake state were included in the hatched area in the orange. C) Exemplary trial-averaged peri-stimulus time histograms of a single unit for high (top) and low (bottom) sound levels in the awake state. D) Tone-evoked firing rate as a function of prestimulus firing rate in the awake state. Each sample represents an individual single unit (n = 156) from all 5 rats. Firing rates were averaged across time and trials (see Materials and methods). The left and right panels indicate the scatter plot for high and low sound levels, respectively. The Pearson’s correlation coefficient R and its corresponding P value are provided as insets. Various fitting curves are overlaid on the scatter plot and color-coded as follows: blue, linear function; red, power function; and green, nonparametric spline function (see Materials and methods). E) Same as D but in the anesthetized state.
We obtained the receiver operating characteristic (ROC) curve to assess the discriminability between the prestimulus and tone-evoked firing rates. The prestimulus and tone-evoked distributions of firing rates were acquired from the time-averaged firing rates in each trial. For a given threshold of firing rates, ranging from 0 to 500 Hz, true-positive and false-positive rates of prestimulus versus tone-evoked classification were plotted on the ordinate and abscissa, respectively, as the ROC curve. An area under the ROC curve, i.e. area under curve (AUC), was characterized as a measure of discriminability, or SNR, between the prestimulus and tone-evoked activities. We also calculated the ROC using the probability distributions of the prestimulus and tone-evoked firing rates with a threshold of likelihood instead of the firing rate itself. This was done to evaluate whether the spike firing rate-based ROC is more likely to result in a nonconcave function with values <0.5 than the likelihood-based ROC.
Kullback–Leibler divergence
Kullback–Leibler divergence (KL divergence) was also used as another measure of SNR between the prestimulus and tone-evoked activities. KL divergence is an information-theoretic measure that quantifies how far a (signal) probability distribution (P) is from another (noise) probability distribution (q) and is calculated as follows:
 |
where N is the total number of trials. For each SUA, P and q were calculated from the tone-evoked and prestimulus firing rate distributions (Fig. 2A).
Fig. 2.
SNR of weak-tone-evoked firing is maximized at an intermediate level of prestimulus firing rates under awake state. A) Definition of SNR in a representative single unit. Based on the histograms of the prestimulus and tone-evoked firing rates (left), the AUC was derived using ROC analysis (right). B) Summary scatter plots of AUC as a function of prestimulus firing rate of pooled data across subjects: top left, awake high level; top right, awake low level; bottom left, anesthetized high level; bottom right, anesthetized low level. The median (solid line) values with upper and lower quartiles (shaded band) are indicated with a binning of 5.25 Hz. The black arrows indicate the bin with the maximum AUC (max bin). The black horizontal bars indicate that the AUC in these bins is significantly lower than that in the max bin; gray horizontal bars indicate no statistical significance. C) Summary bar plot of AUC for low, middle, and high prestimulus firing units in the awake state. The middle level of prestimulus firing rate was defined at the local maximum of AUC, and the low- and high-level prestimulus firing rates were defined thereafter (see Materials and methods). Kruskal–Wallis test was applied across the 4 conditions: intermediate prestimulus firing rate, high prestimulus firing rate, and high and low sound-level conditions for each level of firing rate. Then, robust rank-order test between the middle- and high prestimulus firing rates for each sound level was applied after Bonferroni–Holm correction. Data are presented as the mean ± SEM. *P < 0.05.
Criteria for the low-, mid-, and high-firing rate groups
Based on the prestimulus firing rates, we categorized single units into low-, mid-, and high-firing rate groups. The midfiring rate group was defined as the bin (width of 5 Hz) of the firing rate, which includes the maximum AUC (e.g. Fig. 2C) for each high and low sound-level conditions. The boundaries for the low- and high-firing rate groups were defined to make a distinct difference in the absolute firing rate from the midfiring rate group. The lower boundary of the high-firing rate group was also considered to have a comparable number of samples with the midfiring rate group (for high sound level: n = 30 and 34 units in the mid- and high-firing rate groups; for low sound level: n = 22 and 25 units in the mid- and high-firing rate groups, respectively) for further statistical analysis. Accordingly, for the high sound level, the ranges of prestimulus firing rate for low (lowS), mid (middles), and high (highS) were defined as 0–5.0, 5.4–10.4, and 18.0–65.0 Hz, respectively; for the low sound level, low (lowW), mid (middleW), and high (highW) were defined as 0–5.5, 10.0–15.0, and 25.0–65.0 Hz, respectively.
Curve fitting
To approximate tone-evoked firing rates as a function of prestimulus firing rates, we attempted linear and nonlinear fittings with a polynomial function, power function, Weibull function, and nonparametric spline function across SUs. For nonparametric spline fitting, the piecewise polynomial function was used. Furthermore, we used a cubic function and a 2-term exponential function to fit interspike interval (ISI) kurtosis and ISI skewness as a function of the prestimulus firing rate (e.g. Figs. 5 and 6). Each function used in the analysis was as follows:
Fig. 5.
Trial-by-trial reliability does not account for the SNR of tone-evoked firing. A) Representative raster plots across 100 trials in response to low sound-level inputs with relatively reliable (left) and unreliable responses (right) in the awake state. B) FF of tone-evoked firing with a time window of 4 ms (Tw = 4 ms) as a function of a prestimulus firing rate for high (leftmost inset) and low (second from right) sound-level conditions. Data from all rats (n = 5) were plotted, overlaid with bars of median and upper/lower quartile with a binning of 5 Hz. Summary bar plots of FF for the 3 different levels of prestimulus firing rate (second inset from left and rightmost inset). *P < 0.05. C) FF of tone-evoked firing as a function of AUC for high (left) and low (right) sound-level conditions. Dark, neutral, and light gray dots represent middle, high, and low prestimulus firing units, respectively. Plus symbols (+) indicate the means of the middle or high prestimulus firing rate units. The solid line represents the linear boundary between the middle and high prestimulus firing rate units. The Pearson’s correlation coefficient R and P values are indicated. †P < 0.075. D) Change in FF (ΔFF) from prestimulus firing to tone-evoked firing as a function of AUC: left, high sound level; right, low sound level. The mean and SEM are overlaid in each inset. E) FF (Tw = 4 ms) of tone-evoked firing rate as a function of a tone-evoked firing rate for high (left) and low (right) sound-level conditions.
Fig. 6.

LFP does not account for the SNR of tone-evoked firing. A) Representative LFP traces under awake (left) and anesthetized (right) states: top, grand average of prestimulus (left) and tone-evoked LFP traces (right) from 2 different recording sites; bottom, trial-by-trial LFP traces corresponding to the traces in the top. The amplitude at tone onset was subtracted from the LFP. B) Tone-evoked LFP amplitude as a function of prestimulus LFP amplitude (rms) for high and low sound levels: left, awake state; right, anesthetized state. The prestimulus LFP amplitude was defined as the rms of the LFP across all recording sites. Data from all animals (n = 5) were plotted. C) AUC of the LFP amplitude as a function of prestimulus LFP amplitude for high and low sound levels: left, awake state; right, anesthetized state. The median (solid dark gray line) and upper and lower quartiles (shaded gray band) are indicated with a binning of 45 μV. D) Same as C, but AUC of the delta–theta-band-specific LFP amplitude as a function of prestimulus delta–theta-band LFP amplitude. The dark gray line and shaded gray band are depicted as the same with C, but with a binning of 50 μV. E) Same as C but, AUC of the alpha-band-specific LFP amplitude as a function of prestimulus alpha -band LFP amplitude. The dark gray line and shaded gray band are depicted as the same with C, but with a binning of 40 μV. F) Same as C but, AUC of the beta-band-specific LFP amplitude as a function of prestimulus beta -band LFP amplitude. The dark gray line and shaded gray band are depicted as the same with C, but with a binning of 35 μV. G) Same as C but, AUC of the gamma-band-specific LFP amplitude as a function of prestimulus gamma-band LFP amplitude. The dark gray line and shaded gray band are depicted as the same with C, but with a binning of 10 μV.
Linear function: 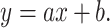
Power function: 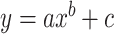 .
.
Weibull function: 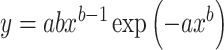 .
.
Cubic function: 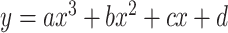 .
.
Two-term exponential function: 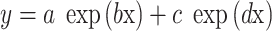 .
.
To minimize fitting errors, we used the nonlinear least squares method with the Trust-Region algorithm (max iteration: 400) and termination tolerance on a model value of 10−6 (MATLAB function “fit”).
To evaluate fittings, that is, how the variation of the data was explained, we used the sum of squared errors (SSE) and degrees of freedom adjusted R-square (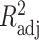 ). To compare fitting across functions, we applied the Akaike’s information criteria and Bayesian information criteria.
). To compare fitting across functions, we applied the Akaike’s information criteria and Bayesian information criteria.
Simulation of SNR
To demonstrate how the numerical fitting curves captured the SNR characteristics of the experimental data, we simulated the AUC of ROC from the fitting curves based on the assumption that both the prestimulus and tone-evoked firing rates across trials are lognormally distributed (Roxin et al. 2011; Mizuseki and Buzsaki 2013; Petersen and Berg 2016; Mongillo et al. 2018). To define the lognormal distribution, the MATLAB function, “makedist” was used with the “lognormal” option. In this lognormal distribution, the mean (μ) was derived from the natural logarithm of output of the fitting curve (y), and the SD (σ) was set as 1.05 for prestimulus and as 0.85 for tone-evoked firing distribution. These values were based on the SD of the observed firing rate distribution in the experiments. A firing distribution of each unit was lognormally fitted with the MATLAB function “fitdist,” and the σ was estimated across the units in all 5 rats.
Analysis of ISI distribution
To characterize the temporal properties of prestimulus and tone-evoked firing patterns, the coefficient of variation (CV), skewness, kurtosis, and hyperskewness of the ISI distribution were evaluated (Kang and Amari 2008; Schwalger et al. 2010; Mar 2019). Skewness (s) and kurtosis (k) of the ISI values (∆t) were obtained from pooled data across all trials without bias correction as follows:
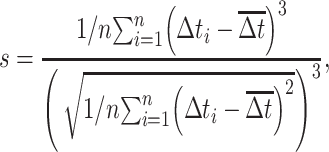 |
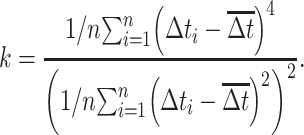 |
Hyperskewness focused on the tail of skewed distribution rather than the entire distribution. It is defined as the fifth moment without bias correction (Veestraeten 2015; Fischer and Schumann 2018; Mar 2019).
 |
Concavity index
To quantify the downward opening distribution of a given test parameter as a function of the prestimulus firing rate, we defined the concavity index, 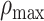 , which is a measure of the maximum degree of concave downward (or convex upward) in the distribution. To calculate
, which is a measure of the maximum degree of concave downward (or convex upward) in the distribution. To calculate 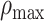 , we first divided the data into M bins based on the prestimulus firing rate. We then searched for a bin that has a local maximum by comparing the values in the neighboring bins, as follows:
, we first divided the data into M bins based on the prestimulus firing rate. We then searched for a bin that has a local maximum by comparing the values in the neighboring bins, as follows:
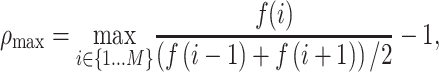 |
where 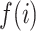 is the median of the distribution of interest at the ith bin of M test bins, where the distribution can be ISI skewness, kurtosis, or hyperskewness distribution. To capture the shape of the distribution, M was heuristically determined, while referring to Freedman–Diaconis rule (Freedman and Diaconis 1981) in determining a reasonable width of a bin in the histogram. When
is the median of the distribution of interest at the ith bin of M test bins, where the distribution can be ISI skewness, kurtosis, or hyperskewness distribution. To capture the shape of the distribution, M was heuristically determined, while referring to Freedman–Diaconis rule (Freedman and Diaconis 1981) in determining a reasonable width of a bin in the histogram. When 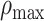 has a high positive value, the test distribution includes a clear concave function; by contrast, when it is close to 0 or has a negative value, the distribution is either a nonconcave or even a convex function, respectively. In order to achieve a population estimation, we applied bootstrap sampling for the data in individual test bins, computed median of them with MATLAB “bootstrp” function, and calculated the concavity index. We repeated the procedure 100 times to statistically compare any difference in the concavity index between different conditions.
has a high positive value, the test distribution includes a clear concave function; by contrast, when it is close to 0 or has a negative value, the distribution is either a nonconcave or even a convex function, respectively. In order to achieve a population estimation, we applied bootstrap sampling for the data in individual test bins, computed median of them with MATLAB “bootstrp” function, and calculated the concavity index. We repeated the procedure 100 times to statistically compare any difference in the concavity index between different conditions.
Reliability across trials
The trial-by-trial reliability of firing rates was quantified using the Fano factor (FF), σ2/μ. Prestimulus and tone-evoked FFs were characterized as the average in each time window defined as follows: at 50–0 ms before the stimulus onset and 5–55 ms after the stimulus onset, respectively. As the FF depended on the time window for calculating the variance (Warzecha and Egelhaaf 1999), we used different sliding time windows (Tw) of 4, 8, 25, and 50 ms, the range of which aligns with that of a previous study conducted in the auditory cortex (Kayser et al. 2010). To quantify the discrimination boundary between the middle and high prestimulus firing groups in the FF and AUC plane, we used linear discriminant analysis (LDA) for these groups with the MATLAB classifier function, “fitcdiscr.” We presumed that the LDA model had the same covariance matrix for each class and that only the means varied.
Local field potential analysis
We calculated the root mean square (rms) of LFP 45–5 ms before the onset of sound stimulus as a prestimulus spontaneous activity. For the tone-evoked response, we evaluated the negative peak value during the 5–45-ms poststimulus latency after subtracting the offset value at the stimulus onset (0 ms). To assess the relationship between SUA and LFP surrounding a given unit, we investigated the SNR between SUA and LFP in the same electrode where the unit was extracted. To characterize the SNR, we scaled the prestimulus LFP rms such that these LFPs (hundreds of μV) could settle in a range comparable to the tone-evoked firing rate of single units (tens of Hz). To analyze the different frequency components in LFP, we divided the measured LFP into 4 frequency bands using digital bandpass filtering: delta–theta, 1–8 Hz; alpha, 8–13 Hz; beta, 13–30 Hz; and gamma, 45–60 Hz. The measured LFP signals were digitally filtered using the sixth-order Butterworth filter and zero phase filtering using the MATLAB “filtfilt” function. The filtered signals were then transformed into analytic signals of instantaneous amplitude and phase using the Hilbert transform. For each frequency band, the amplitude represented the grand average of analytic amplitude across the prestimulus and poststimulus time windows.
Model simulation
We investigated in a simulation model whether and how SNR depended on the relationship between the prestimulus and tone-evoked firing. The test relationship was just set a priori as either (i) supralinear, (ii) linear, or (iii) lognormal random. In the simulation, the trial average of prestimulus firing rates across neurons was fit to have a lognormal distribution with the mean and SD set at 8.0 and 1.0, respectively, and the maximum prestimulus firing rate was limited to 60 Hz. These characteristics were comparable to those observed in our physiological experiments. The number of model neurons were set at n = 300. Each neuron generated ongoing spontaneous activity, i.e. the prestimulus firing, using the Poisson process. The mean of the Poisson distribution was set at the trial average of firing rate, which was determined and sampled from the lognormal distribution of population activities. The number of trials and time window in the simulation was set as 200 and 0.1 s, respectively. For each relationship, the tone-evoked firing across neurons was normalized to have a comparable median, 95th and 5th percentiles. The tone-evoked firing was also comparably distributed with that observed under the awake low-level condition. The supralinear relationship between the prestimulus firing rate x and the tone-evoked firing rate y was defined as:
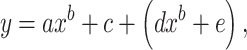 |
where a = 10.2, b = 0.5, c = −5, d = 5.6 × (r − 0.5), e = 13 × (r − 0.5) + 1, and r was a uniformly distributed random number in the interval (0, 1). The linear relationship was defined as:
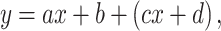 |
where a = 1.3, b = 13, c = 1.2 × (r − 0.5), and d = 4.0 × (r − 0.5). For the lognormal random relationship, the tone-evoked firing rate was characterized as a lognormal random distribution, where the mean and SD were derived from the distribution of tone-evoked firing in the supralinear relationship.
Tone-evoked firing was generated by the leaky-integrate-and-fire (LIF) model (Gerstner et al. 2014) with parameters adapted from previous studies (Reig et al. 2015; Lopez-Jury et al. 2020):
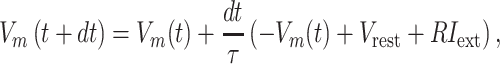 |
where 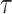 is the membrane time constant,
is the membrane time constant, 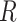 is the membrane resistance,
is the membrane resistance, 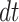 is the time resolution,
is the time resolution, 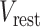 is the resting potential, and
is the resting potential, and 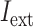 is the input membrane current. We varied some of these parameters to evaluate whether and how temporal patterns of firing depend on these parameters. We set
is the input membrane current. We varied some of these parameters to evaluate whether and how temporal patterns of firing depend on these parameters. We set  = 10 or 20 ms;
= 10 or 20 ms;  = 10, 100, and 200 MΩ;
= 10, 100, and 200 MΩ;  = 1 ms; and
= 1 ms; and 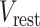 = −60 or −70 mV. If the voltage reaches the spike threshold
= −60 or −70 mV. If the voltage reaches the spike threshold  , then a spike is registered, the voltage is instantly reset at
, then a spike is registered, the voltage is instantly reset at 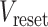 , and the dynamics continue.
, and the dynamics continue.
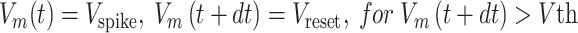 |
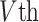 was set at −50 mV, the reset potential
was set at −50 mV, the reset potential 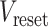 was set at −80 mV, the spike potential
was set at −80 mV, the spike potential 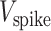 = +20 mV, and the absolute refractory period
= +20 mV, and the absolute refractory period 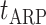 = 2 ms.
= 2 ms.
I
ext was set as a step function varying in timing and strength, as a simplified form of the observed summation of auditory-evoked thalamo-cortical presynaptic inputs. The timing of the input onset and the duration of input was defined as gaussian distributions 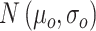 and
and 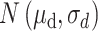 , respectively, where
, respectively, where 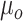 and
and 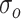 were 15 and 4 ms, whereas
were 15 and 4 ms, whereas 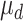 and
and  were 20 and 8 ms, respectively. Input membrane current was defined as follows:
were 20 and 8 ms, respectively. Input membrane current was defined as follows:
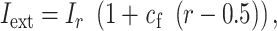 |
where  = 1.75,
= 1.75,  varied from 10−6 to 10−5 mA. In the time window except for the auditory-evoked synaptic inputs,
varied from 10−6 to 10−5 mA. In the time window except for the auditory-evoked synaptic inputs, 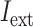 was replaced by the Poisson process with the mean event frequency
was replaced by the Poisson process with the mean event frequency 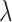 and the strength
and the strength 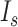 , which ranged [4, 45] and [0.5, 7.0] × 10−6
, which ranged [4, 45] and [0.5, 7.0] × 10−6 respectively. The combination of the parameters of
respectively. The combination of the parameters of 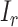 ,
, 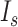 , and
, and 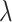 were redefined and selected according to the distribution of the tone-evoked firing rate in each relationship condition. Then, we derived the SNR and ROC–AUC and characterized the ISI distribution as described in the analyses of physiological experiments.
were redefined and selected according to the distribution of the tone-evoked firing rate in each relationship condition. Then, we derived the SNR and ROC–AUC and characterized the ISI distribution as described in the analyses of physiological experiments.
Results
Prestimulus versus tone-evoked firing rates
We recorded tone-evoked activities with a dense microelectrode array at layer IV in the entire auditory cortex of head-fixed rats under awake and anesthetized states. We isolated SUAs from each electrode and determined the FRA by presenting tone bursts with various test frequencies and SPLs. As quality control, we quantified the response quality, d’, as the statistical distance of distributions between the responsive and nonresponsive areas in each FRA (Guo et al. 2012; Noda and Takahashi 2015). We excluded the units with a low response quality, d’ (d’ < 3), in both the states, and units with extremely different response quality between the states (see Materials and methods). Finally, we obtained 263 tone-responsive qualified units (n = 5 rats). We compared the FRA of the same unit between awake and anesthetized states and found that tone-evoked responses were weaker in the anesthetized state than in the awake state (Fig. 1A).
Population analysis in Fig. 1B and Supplementary Fig. 1B showed that 62% of the test units (n = 164 out of 263 in total) exhibit a lower MT in the awake state than in the anesthetized state (AW < AN; e.g. units #1 and #2 in Fig. 1A), 22% (n = 57) exhibit a comparable MT between the 2 states (AW = AN; unit #4 in Supplementary Fig. 1A), and 16% (n = 42) exhibit a higher MT in the awake state (AW > AN; unit #3 in Supplementary Fig. 1A). Thus, in most auditory cortical neurons, low SPL tones around the CF elicited tone-evoked activities in the awake state, but not in the anesthetized state. To address why the awake state achieved a better tone detection than the anesthetized state, we studied the majority of units and excluded 38% of the units (AW > AN and AW = AN) from further analyses.
Since the majority of the test units exhibited monotonic FRA as a function of tone intensity level for both the awake and anesthetized conditions, and the fractions of monotonic FRA were comparable between the 2 states (74.9% of the units with monotonicity ratio > 0.80 in awake state, and 71.9% in anesthetized state in Supplementary Fig. 1C), we compared the neural activities in response to high sound levels (60–80 dB SPL) and low sound levels (20–40 dB SPL) (Fig. 1C and Supplementary Fig. 1D). High-level condition was defined for each unit such that tone-evoked spikes were observed in both the awake and anesthetized states, whereas low-level condition was defined where tone-evoked spikes were observed only in the awake state. The test tone under high-level condition had an SPL of not less than the MT in the awake state, but below the MT in the anesthetized state. This definition of the low-level condition excluded units of MT > 40 dB SPL in the awake state (n = 8) from further analyses (Fig. 1B), which left 156 units in the end for the main analyses. We also confirmed that the response quality of the test units included in the main analyses below is comparable in the awake and anesthetized states (Supplementary Fig. 1E, 2-sided Wilcoxon signed rank test, P = 0.15).
The CF was statistically comparable between the awake and anesthetized states in the same unit (Pearson’s correlation, R = 0.695, P = 8.4 × 10−24; Mann–Whitney U test, P = 0.71), confirming that the frequency selectivity in the awake state was almost identical to that in the anesthetized state (Supplementary Fig. 1F). Additionally, CF was widely distributed from 1.6 to 40 kHz, indicating that our test units did not have a sampling bias of CF. Furthermore, the test frequencies of the low-level condition were selected at CF and CF ± 1/4 octave of the awake state (see Materials and methods). For the high-level condition, the test frequencies were in principle set at CF and CF ± 1/4 octave and were always the same between the awake and anesthetized states. While CF of the same unit is mostly equivalent between these states, if the CF is different among them for the high sound level, we selected the CF of the anesthetized condition because the test frequency within the awake state’s FRA tends to be broader than that of the anesthetized state. (Noda and Takahashi 2015). The test SPL were pseudorandomly selected within both the awake and anesthetized FRAs.
To address how intrinsic fluctuations of the ongoing activity affected signal detection, we characterized how tone-evoked firing depended on prestimulus ongoing firing. The dynamic range of the ongoing firing rate fit with previous studies in auditory or other sensory-motor cortices (Supplementary Fig. 1H and I) (Hromádka et al. 2008; O'Connor et al. 2010; Roxin et al. 2011; Petersen and Berg 2016). Under both awake and anesthetized states and under both high- and low-level conditions, tone-evoked firing rates were highly positively correlated with the prestimulus ongoing firing rates (Fig. 1D and E; R = 0.72, P = 3.5 × 10−26 in high-level condition under awake state; R = 0.82, P = 1.2 × 10−38 in low-level condition under awake state; R = 0.77, P = 2.9 × 10−32 in high-level condition under anesthetized state; R = 0.84, P = 3.1 × 10−42 in low-level condition under anesthetized state). However, upon close inspection, prestimulus firing rates were lower in the anesthetized state than in the awake state (Fig. 1D and E; anesthesia vs. awake: 2.4 vs. 7.0 Hz for median; 14.9 vs. 33.6 Hz for 95 percentile), and the reduction in prestimulus firing rate from the awake to anesthetized state was observed even for each corresponding single unit (Supplementary Fig. 1G, Wilcoxon signed-rank test, P = 6.5 × 10−10). More interestingly, curve fitting analyses suggested that the relationship between prestimulus and evoked firing depended on both the state and the condition. Evoked firing rates were best characterized as a power function (nonlinear, concave function) of the prestimulus firing rate in the awake state (Fig. 1D and statistical comparison in Table 1) and as a linear function as well as a nonlinear function in the high-level condition under the anesthetized state (Fig. 1E, left). Nonparametric spline fitting also confirmed that nonlinear curves with a concave shape best explained our experimental data in the awake state (Table 1). The difference of nonlinearity or linearity in fitting between awake and anesthetized states was not due to specific SUs with extremely low firing rates or extremely high firing rates. This was assessed by evaluating the goodness of fit when curve fitting was applied only to the subset of the distribution without the SUs of especially high prestimulus firing rates or the SUs of especially low prestimulus firing rates, or without both the SUs of especially high and low prestimulus firing rates (Supplementary Table 1). This supralinear relationship between prestimulus and evoked firing suggested that a subset of units exhibits a relatively large tone-evoked response in the awake state, that is, a larger SNR, when the level of prestimulus ongoing firing was intermediate.
Table 1.
Evaluation of fitting of tone-evoked firing with prestimulus firing.
| Awake state | ||||||||
|---|---|---|---|---|---|---|---|---|
| High sound level | Low sound level | |||||||
| Linear function | Power function | Weibull function | Spline function | Linear function | Power function | Weibull function | Spline function | |
| SSE | 0.0810 | 0.0719a | 0.0731 | 0.0657 | 0.0363 | 0.0292a | 0.0302 | 0.0269 |
| RMSE | 0.0238 | 0.0225a | 0.0226 | 0.0224 | 0.0157 | 0.0141a | 0.0143 | 0.0142 |
| R adj | 0.434 | 0.494b | 0.489 | 0.499 | 0.582 | 0.662b | 0.653 | 0.659 |
| AIC | −672.48 | −688.63a | −687.45 | - | −814.62 | −846.17a | −842.04 | - |
| BIC | −666.61 | −679.87 | −681.58a | - | −808.69 | −837.32a | −836.11 | - |
| Leave-one-out method for estimation of generalization error | ||||||||
| RMSE | 24.015 | 22.702a | 22.806 | - | 15.805 | 14.215a | 14.423 | - |
| MAE | 19.688 | 18.048a | 18.341 | - | 12.620 | 10.997a | 11.222 | - |
| Anesthetized state | ||||||||
| High sound level | Low sound level | |||||||
| Linear | Power | Weibull | Spline | Linear | Power | Weibull | Spline | |
| SSE | 0.0342 | 0.0341a | 0.0367 |

|
0.0032 | 0.0031a | 0.0031a | 0.005210 |
| RMSE | 0.0158a | 0.0158a | 0.0164 |

|
0.0049 | 0.0048a | 0.0048a | 0.00646 |
| R adj | 0.581b | 0.579 | 0.549 |

|
0.707 | 0.716 | 0.718b | 0.480 |
| AIC | −758.59a | −757.90 | −748.62 |

|
−1086.9 | −1091.0 | −1092.1a | - |
| BIC | −752.81a | −749.27 | −742.84 |

|
−1081.1 | −1082.4 | −1086.3a | - |
| Leave-one-out method for estimation of generalization error | ||||||||
| RMSE | 15.893a | 15.965 | 16.513 | - | 4.892 | 4.827 | 4.796a | - |
| MAE | 12.018a | 12.127 | 12.057 | - | 3.546 | 3.479 | 3.458a | - |
SSE, sum of squared error; RMSE, root-mean-squared error; Radj, adjusted R-square; AIC, Akaike’s information criterion; BIC, Bayesian information criterion; MAE, mean absolute error; hyphen (-): not measured.
aSmallest value out of the linear and nonlinear fitting curves (except for spline function), indicating a better fit.
bLargest value out of the linear and nonlinear fitting curves (except for spline function), indicating a better fit.
Stochastic resonance with ongoing firing for low sound level in the awake state
For every condition and state, we attempted to characterize the SNR of the tone-evoked firing rate as a function of the prestimulus ongoing firing rate. As shown in Fig. 2A, the distribution of the tone-evoked firing rate shifted toward larger values than that of the prestimulus firing rate. To evaluate the SNR from the difference in these distributions, we conducted a ROC analysis and quantified the AUC (Fig. 2A). Pooled data also showed that the relationship between the AUC and the prestimulus firing rate depended on the condition and state (Fig. 2B, statistical comparison in Table 2). For high sound level in the awake state (awake high-level condition), the AUC increased with the prestimulus firing rate and reached a plateau at the intermediate firing rate via multiple comparison analyses of AUC between bins with different prestimulus firing rates (Fig. 2B, upper left), whereas the AUC in the awake low-level condition exhibited a local maximum at the intermediate firing rate at approximately 13 Hz (Fig. 2B, black arrow) and decreased at the high firing rate (Table 2). The AUCs in the anesthetized states were essentially different from those under the awake state, owing to the lower prestimulus firing rate (Fig. 2B, lower inset). The AUC in the anesthetized high-level condition increased with the prestimulus firing rate (Fig. 2B, lower left inset), but the prestimulus firing rate did not exceed approximately 25 Hz. The AUC in the anesthetized low-level condition was low at approximately 0.5 Hz, indicating that there were small differences between the prestimulus and tone-evoked firing rates (Fig. 2B lower right inset). These findings confirm that the test SPL of low sound level was below the MT of FRA in the anesthetized state.
Table 2.
Statistical evaluation of Fig. 2B.
| P value for each bin of prestimulus firing rate with a bin size of 5.25 Hza | ||||||||
|---|---|---|---|---|---|---|---|---|
| Center of prestimulus firing rate bin | ||||||||
| Prestimulus firing rate with max AUC |
2.6 Hz | 7.9 Hz | 13.1 Hz | 18.4 Hz | 23.6 Hz | 28.9 Hz | 34.1 Hz | |
| Awake state—high-level condition | 0.853 at 7.9 Hz |
P = 3.27 × 10−12 |
b | P = 0.26 | P = 0.36 | P = 0.62 | P = 0.072 | P = 0.48 |
| Awake state—low-level condition | 0.829 at 13.1 Hz |
P = 4.12 × 10−11 |
P = 0.177 | b |
P = 2.04 × 10−5 |
P = 0.0040 | P = 0.177 | P = 0.0040 |
| Anesthetized state—high-level condition | 0.877 at 18.4 Hz |
P < 1.0× 10−3 |
P = 0.0064 | P = 0.153 | b | N.A. | N.A. | N.A. |
| Anesthetized state—low-level condition | 0.57 at 7.9 Hz |
P = 7.11 × 10−9 |
b | P = 0.375 | P = 0.375 | N.A. | N.A. | N.A. |
| P value for each bin of prestimulus firing rate with a bin size of 5.0 Hz | ||||||||
| Prestimulus firing rate with max AUC |
2.5 Hz | 7.5 Hz | 12.5 Hz | 17.5 Hz | 22.5 Hz | 27.5 Hz | 32.5 Hz | |
| Awake state—high-level condition | 0.85 at 7.5 Hz |
P = 6.92 × 10−14 |
b | P = 0.15 | P = 0.15 | P = 0.55 | P = 0.43 | P = 0.24 |
| Awake state—low-level condition | 0.82 at 12.5 Hz |
P = 7.77 × 10−16 |
P = 0.036 | b | P = 0.0032 |
P = 1.04 × 10−5 |
P = 0.0402 |
P = 4.64 × 10−4 |
| P value for each bin of prestimulus firing rate with bin size of 5.5 Hz | ||||||||
| Prestimulus firing rate with max AUC |
2.7 Hz | 8.3 Hz | 13.8 Hz | 19.3 Hz | 24.7 Hz | 30.2 Hz | 35.8 Hz | |
| Awake state—high-level condition | 0.87 at 8.3 Hz |
P = 1.64 × 10−8 |
b | P = 0.205 | P = 0.53 | P = 0.86 | P = 0.53 | P = 0.86 |
| Awake state—low-level condition | 0.82 at 13.8 Hz |
P = 3.52 × 10−13 |
P = 0.067 | b |
P = 1.90 × 10−6 |
P = 0.013 | P = 0.034 | P = 0.013 |
N.A., data are not available
a P values were calculated using 1-sided, 2-sample robust rank-order test by comparing between the bin of prestimulus firing rate with max AUC and the other bins, with Bonferroni–Holm correction for multiple comparison.
bThe bin with the local maximum, also meaning the bin to test for comparison.
However, the above-mentioned multiple comparison analysis that compared the bin yielding the maximum AUC with the other bins having different prestimulus firing rates might overestimate significant differences between these bins. Therefore, we also applied a permutation test by shuffling AUC values across units with different prestimulus firing rates. First, we applied the permutation test across all the ranges of prestimulus firing rate bins from 0 to 40 Hz. Since the AUC values were highly dispersed across different prestimulus firing rates, it resulted in the significantly lower deviation of AUC at the lowest prestimulus firing rate bin across all the conditions and the significant higher deviation of AUC for all the conditions except for anesthetized high-level condition (Supplementary Fig. 2A and B, top insets). This suggests that the lower AUC values in the distribution pull down the statistical center of AUC distribution and make the higher AUC values easily significant in the permutation test. In fact, the result of Kruskal–Wallis test was significant for all the conditions. Thus, a permutation test was applied again, but after removing the units with the lower AUC values at the lowest prestimulus firing rate bin. As a result, there were significantly higher AUC values at the bin of intermediate prestimulus firing rate only for awake high-level condition, but not for the other 3 conditions (Supplementary Fig. 2A and B, bottom insets, this was also the case in Kruskal–Wallis test in Supplementary Fig. 2A and B).
Note that, in some cases, the calculation of AUC based on the threshold on the likelihood is more appropriate than the threshold on the firing rate; we also calculated AUC based on the probability distributions of the prestimulus and tone-evoked firing rates with a threshold of likelihood. The likelihood-based AUC distributions were almost identical with the firing rate-based AUC distributions for all the vigilance states and the sound intensity conditions (Supplementary Fig. 2E). Therefore, we continued to adopt the firing rate-based AUC distributions for further analyses.
We determined whether the AUC was a nonmonotonic function of the prestimulus firing rate. For each condition, we categorized prestimulus firing rates into low, mid, and high groups (see Materials and methods) such that the maximum AUC was included in the midgroup of firing rates (black arrows in Fig. 2B) and the low and high groups included units with distinctly lower and higher firing rates than the midgroup, respectively. The AUC depended on the difference of sound levels as well as prestimulus firing rates according to the group comparison between them (Kruskal–Wallis test across high and low sound levels and high and midprestimulus firing rates, χ2 = 12.4, P = 0.0061). For the low sound level, the AUC was significantly lower in the high prestimulus firing group than in the midgroup (Fig. 2C; robust rank-order test with Bonferroni–Holm correction, P = 0.0056); no significant difference was observed for the high sound level (Fig. 2C; P = 0.0824).
To confirm the above ROC analyses, we also characterized the SNR using KL divergence, an information-theoretic approach that quantifies the distance of probability distribution between tone-evoked (signal) and prestimulus firing rates (noise). Scatter plots between KL divergence and prestimulus firing rate also exhibited a local maximum only in the awake low-level condition (Supplementary Fig. 2A, statistical comparison in Supplementary Table 2). The group analysis also confirmed that KL divergence in the midfiring group was significantly higher than that in the high firing group for the low sound level (Supplementary Fig. 2B, right; Mann–Whitney U test, P = 0.030), but not for the high sound level (Supplementary Fig. 2B, left; Mann–Whitney U test, P = 0.58). Thus, an intermediate level of prestimulus ongoing firing is likely to have an advantage in the detection of weak signals. This result fits the broad definition of stochastic resonance, where the SNR improves at an intermediate level of (internal neuronal) noise.
We then examined whether this SNR improvement or hypothetical stochastic resonance was predictable from the relationship between the prestimulus and tone-evoked firing rates (Fig. 1C). We performed a simple simulation to test how different types of fitting curve used in Fig. 1 for evoked firing rates along prestimulus firing rates can explain the experimental SNR features, meaning that we focused on the 3 curves: linear, supralinear, and nonparametric fitting curves. To characterize the firing rate distributions for the calculation of AUC in the simulation, we also assumed that both the prestimulus and tone-evoked firing rates across trials are lognormally distributed based on the previous studies (Roxin et al. 2011; Mizuseki and Buzsaki 2013; Petersen and Berg 2016). Intriguingly, our simulation confirmed that the AUC is predicted as a nonmonotonic function of the prestimulus firing rate with a local maximum at its intermediate firing rate when the tone-evoked firing rate was fit with either the supralinear parametric (power) or nonparametric (spline) function of prestimulus firing rates (Fig. 3B and C; sum of squared errors [SSE] = 3.67 for power function; SSE = 2.22 for spline function), but not with a linear function (Fig. 3A; SSE = 4.23; Supplementary Fig. 3). Thus, the hypothetical stochastic resonance we observed was an emergent property of the supralinear relationship between the prestimulus and tone-evoked firing rates.
Fig. 3.
Supralinear fitting curves for distribution of tone-evoked firing rate to prestimulus firing rate could best simulate the SNR. A–C) Prediction of AUC outline from the curve fitting analyses in awake low-level conditions. The linear, power, and spline functions in Fig. 1D (also shown as a small panel at top-right inset here) were used to predict the outline of AUC in the left, middle, and right insets, respectively.
Temporal pattern of firing underlying stochastic resonance
Next, we asked whether any other features of the prestimulus and tone-evoked firing patterns underlie the nonmonotonic SNR improvements in the hypothetical stochastic resonance. First, we assessed the temporal profiles of firing from the ISI distributions. In a representative unit, shown in Fig. 4A (left), the tone-evoked ISI distribution was more highly skewed toward 0 than the prestimulus ISI distribution. In another representative unit (Fig. 4A, right), the prestimulus ISI distribution was roughly similar in shape to the tone-evoked ISI distribution. Thus, the temporal profiles of the firing rates differed among units.
Fig. 4.
Concave function in temporal intermittency is observed in tone-evoked activities but not in prestimulus activities. A) ISI distributions of prestimulus (light gray) and tone-evoked (dark gray) activities across all trials as shown in representative single units. B) Scatter plots of ISI hyperskewness. Prestimulus and tone-evoked ISI hyperskewness were plotted as a function of a prestimulus firing rate in prestimulus (light gray) and tone-evoked firing (dark gray). The median and upper/lower quartile values are shown as dots with error bars, with a binning of 5 Hz. Left, high sound-level condition; right, low sound-level condition. Data from all rats (n = 5) were plotted. C) Summary bar plots of ISI hyperskewness: left, high sound level; right, low sound level. For the low, middle, and high prestimulus firing units, prestimulus and tone-evoked ISI hyperskewness were compared for high sound level (leftmost inset). The mean and SEM are shown for each bar. Second from left: box plots of change in ISI hyperskewness (ΔISI hyperskewness) from prestimulus to tone-evoked firing for each middle and high prestimulus firing units, respectively. In each box, the central line indicates the median and the top and bottom edges of the box the 75th and 25th percentiles. The whiskers extend to the most extreme points in the ΔISI hyperskewness data. Second inset from right and rightmost inset are the same as leftmost inset and second inset from left, respectively, but for low sound level. The mean and SEM are shown for each bar. †P < 0.075. D) Concavity index of ISI hyperskewness calculated from the distributions in B. For low and high sound levels, prestimulus (pre) and tone-evoked (post) activities were compared by Kruskal–Wallis test. The tone-evoked ISI hyperskewness for low sound level was compared to the other conditions by Mann–Whitney U test with FDR correction. ***P < 0.001. E) Separation of SUs into high SNR units and low SNR units based on SNR values, but not based on tone-evoked firing rate. The SUs within a certain range of tone-evoked firing rate (40–120 Hz for high sound level; 25–75 Hz for low sound level) were selected and divided by the rounded average of AUC (0.85 and 0.75 for high and low sound-level conditions, respectively) in these selected units as a threshold. Tone-evoked firing rate (top) and AUC (bottom) between high SNR units and low SNR units for high (left) and low (right) sound levels. F) Comparison of ISI hyperskewness between high SNR units and low SNR units for high and low sound levels. *P < 0.05. Kruskal–Wallis test across all the conditions and thereafter Mann–Whitney U test with FDR correction between the low SNR units for low sound level and the others were applied.
To quantify these individual differences, we determined the extent to which the ISI distribution was asymmetrically distorted from the prestimulus period to the poststimulus period in each condition. We examined the hyperskewness of ISI, which is a measure of the relative importance of tails versus the center of an ISI distribution in causing skewness and is considered to focus more on the shape of tail part of distribution than skewness. Prestimulus ISI hyperskewness was characterized as a monotonic function of the prestimulus firing rate (Fig. 4B, Pearson’s correlation between prestimulus firing rate and prestimulus ISI hyperskewness: R = 0.52, P = 1.95 × 10−10 for high sound level and R = 0.58, P = 4.20 × 10−14 for low sound level). Contrastingly, in tone-evoked ISI hyperskewness, no significant difference between mid and high prestimulus firing rates was observed for the high sound level (Fig. 4C, left; Mann–Whitney U test, P = 0.57; midprestimulus firing rate: 37.62 ± 7.14; high prestimulus firing rate: 35.63 ± 3.71). Similarly, the increase in ISI hyperskewness (ΔISI hyperskewness) from prestimulus to tone-evoked firing was not different between the midprestimulus and high prestimulus firing rates (P = 0.13); for low sound level, the midprestimulus firing rate units exhibited a higher ISI hyperskewness than the high-firing rate units (Fig. 4C, right; midprestimulus firing rate: 47.13 ± 10.58; high prestimulus firing rate: 33.83 ± 4.94), although the difference was not significant (P = 0.073). In fact, ΔISI hyperskewness was significantly higher in midprestimulus firing rate than that in high prestimulus firing rate (Fig. 4C, Mann–Whitney U test, P = 0.025). From low to midprestimulus firing rates, the tone-evoked ISI hyperskewness increased for both high and low sound levels (high sound level: 17.25 ± 3.71 at low firing rates; low sound level: 16.16 ± 2.95 at low firing rates). To characterize the nonmonotonic, concave shape in the distribution of ISI hyperskewness, we applied the concavity index to the distribution divided into M bins, which quantifies the concavity of a bin by comparing the value of the bin with the values in the neighboring bins and searches the maximum degree of concavity across the bins and repeated these procedure by bootstrapping. The inverse of M or width of bin was heuristically determined as 5 Hz from the data, while referring to the Freedman–Diaconis rule (Freedman and Diaconis 1981), where the reasonable width is 4.9 Hz in the awake high-level condition and 5.4 Hz in the awake low-level condition. According to the population estimation of the concavity index to the distribution of ISI hyperskewness, the tone-evoked ISI hyperskewness exhibited significantly higher the concavity index for low sound level than those for the other conditions (Fig. 4D, Kruskal–Wallis test, χ2(3, 396) = 67.77, P = 1.28 10−14; Mann–Whitney U test with FDR correction, prehigh level vs. postlow level: 6.68
10−14; Mann–Whitney U test with FDR correction, prehigh level vs. postlow level: 6.68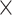 10−10; posthigh level vs. postlow level: 6.43
10−10; posthigh level vs. postlow level: 6.43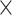 10−14; prelow level vs. postlow level: 1.71
10−14; prelow level vs. postlow level: 1.71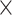 10−14). Thus, we observed the local maximum of ISI hyperskewness at the intermediate prestimulus firing rate, specifically during tone-evoked period for low sound level. However, since the tone-evoked firing rate also changed with prestimulus firing rate, it is not clear whether the nonmonotonicity of the ISI hyperskewness could be due to the concave properties of the SNR or merely due to the change in tone-evoked firing rate. To test this, we first selected a group of single units within a certain range of tone-evoked firing rate and then split these units according to the SNR into high SNR units and low SNR units by the rounded average of the SNR distribution as a threshold for each high- and low-level condition (Fig. 4E, AUC = 0.85 for high level, AUC = 0.75 for low level). The high SNR units showed clearly a much higher SNR than the low SNR units by definition (Mann–Whitney U test, for high sound level: P = 2.63
10−14). Thus, we observed the local maximum of ISI hyperskewness at the intermediate prestimulus firing rate, specifically during tone-evoked period for low sound level. However, since the tone-evoked firing rate also changed with prestimulus firing rate, it is not clear whether the nonmonotonicity of the ISI hyperskewness could be due to the concave properties of the SNR or merely due to the change in tone-evoked firing rate. To test this, we first selected a group of single units within a certain range of tone-evoked firing rate and then split these units according to the SNR into high SNR units and low SNR units by the rounded average of the SNR distribution as a threshold for each high- and low-level condition (Fig. 4E, AUC = 0.85 for high level, AUC = 0.75 for low level). The high SNR units showed clearly a much higher SNR than the low SNR units by definition (Mann–Whitney U test, for high sound level: P = 2.63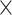 10−11; for low sound level: P = 5.10
10−11; for low sound level: P = 5.10 10−14), while the tone-evoked firing rate was not different between the 2 groups of units (P = 0.17 for high sound level, P = 0.14 for low sound level). When comparing ISI hyperskewness across the groups of SNR units, the high SNR units demonstrated a significantly higher ISI hyperskewness than did the low SNR units for low sound level, but it was not the case for high sound level (Fig. 4F, Kruskal–Wallis test, χ2(3136) = 8.34, P = 0.040; Mann–Whitney U test with FDR correction, for high SNR units vs. low SNR units at low sound level, P = 0.034; for high SNR units vs. low SNR units at high sound level, P = 0.16), and ISI hyperskewness in the low SNR units for low sound level was also smaller than that in the high SNR units for high sound level (Fig. 4F, P = 0.034). This suggests that the high SNR is the dominant factor for the skewness of ISI or temporal sparseness of firing.
10−14), while the tone-evoked firing rate was not different between the 2 groups of units (P = 0.17 for high sound level, P = 0.14 for low sound level). When comparing ISI hyperskewness across the groups of SNR units, the high SNR units demonstrated a significantly higher ISI hyperskewness than did the low SNR units for low sound level, but it was not the case for high sound level (Fig. 4F, Kruskal–Wallis test, χ2(3136) = 8.34, P = 0.040; Mann–Whitney U test with FDR correction, for high SNR units vs. low SNR units at low sound level, P = 0.034; for high SNR units vs. low SNR units at high sound level, P = 0.16), and ISI hyperskewness in the low SNR units for low sound level was also smaller than that in the high SNR units for high sound level (Fig. 4F, P = 0.034). This suggests that the high SNR is the dominant factor for the skewness of ISI or temporal sparseness of firing.
Similarly, when we quantify the skewed or distorted ISI distribution with other higher-order moments like kurtosis and skewness, we observed similar behaviors with ISI hyperskewness: the increase of the higher-order moments of ISI distribution during tone-evoked period from the prestimulus period was prominent at the intermediate prestimulus firing rate only for low sound level (Supplementary Fig. 4A, B, E, and F); this leads to larger concavity index of the distributions (Supplementary Fig. 4C and G). We again confirmed that the high values of the higher-order moments of ISI distribution were due to the high SNR (Supplementary Fig. 4D and H). We also demonstrated the nonmonotonicity or the local maximum of the distribution in the higher-order moments of ISI during tone-evoked period along the prestimulus firing rate by permutation test (Supplementary Fig. 5A–C).
We evaluated the temporal firing patterns based on the distribution of the ISI from all the trials. However, if the firing frequency differs from trial to trial, these higher-order moments can also be high even if the temporal firing patten within the individual trials did not clearly contribute to the nonmonotonicity of the distribution of these higher-order moments. To test this, we removed the information of the ISI distribution within each trial by calculating the median of ISI for each trial and used the ISI median as the representative temporal firing information in each trial. Then, we constructed the distribution of the ISI median across trials. If the nonmonotonicity of the distribution in the higher-order moments of ISI was purely due to the trial-by-trial variability of ISI, we should observe comparable nonmonotonic distributions of the higher-order moments from the ISI median across trials with what we have shown in Fig. 4 and Supplementary Fig. 4. However, the distributions of the higher-order moments from the ISI median exhibited a large variability along the prestimulus firing rate and did not show any clear nonmonotonicity or local maximum during tone-evoked period (Supplementary Fig. 5D–I). This indicates that the temporal firing patterns within individual trials do contribute to the nonmonotonicity of the distribution in the higher-order moments of ISI with a local maximum at the midprestimulus firing rate during the tone-evoked period.
Conversely, when we analyzed the temporal firing properties under anesthesia, the higher-order moments of the ISI distribution showed a monotonic increase with the prestimulus firing rate during both prestimulus and tone-evoked periods for both high and low sound levels and did not exhibit any nonmonotonic, concave shape of the distributions with a local maximum (Supplementary Fig. 6A, C, and E). In fact, the concavity index of the distribution of the higher-order moments during the tone-evoked period was not different from or even smaller than that during the prestimulus period for low sound level (Supplementary Fig. 6B, D, and F). As shown in the monotonic distribution of SNR in Fig. 2, the higher-order moments of ISI distribution demonstrated not concave but monotonic distributions as a function of prestimulus firing rate under anesthesia.
Thus far, our results suggest that, in response to low but not high sound level stimuli, the ISI of evoked activities was more heavily tailed and skewed in the units with midprestimulus firing rates under the awake state but not the anesthetized state, that is, temporally intermittent firing patterns alternating between silence and burst firing were elicited.
We also evaluated the temporal variability by the CV of ISI. For both prestimulus and tone-evoked ISI, CV increased with prestimulus firing rate and reached a plateau at approximately 1 at a high firing rate (Supplementary Fig. 6G and H). Thus, the temporal variability was not characterized as a nonmonotonic function of the prestimulus firing rate.
Trial-by-trial reliability of firing does not account for SNR
The trial-by-trial reliability of tone-evoked firing differed across single units (Fig. 5A). We evaluated whether the trial-by-trial reliability underlies the nonmonotonic SNR improvement in hypothetical stochastic resonance. To quantify the trial-by-trial reliability, we calculated the FF of the tone-evoked firing rate (see Materials and methods) with different sizes of time windows. For both high and low sound levels, the FF significantly negatively correlated with prestimulus firing rates, especially when the Tw was short (Fig. 5B; when Tw = 4 ms, R = −0.60, P = 9.4 × 10−17 for high sound level and R = −0.61, P = 5.4 × 10−17 for low sound level; Supplementary Fig. 7A; when Tw = 8 ms, R = −0.37, P = 2.8 × 10−6 for high level, and R = −0.28, P = 3.5 × 10−4 for low level; Supplementary Fig. 7B; when Tw = 25 ms, R = −0.18, P = 0.025 for high level, and R = −0.096, P = 0.23 for low level; Supplementary Fig. 7C; when Tw = 50 ms, R = −0.077, P = 0.34 for high level, and R = −0.052, P = 0.52 for low level). This result suggests that the trial-by-trial reliability of tone-evoked firing increased with prestimulus firing rates and did not change nonmonotonically with prestimulus firing rates.
We further analyzed the relationship between FF and SNR. For both high- and low-level conditions, the FF with a Tw of 4 ms was negatively correlated with the AUC (Fig. 5C; R = −0.70, P = 7.4 × 10−24 for high sound level, and R = −0.41, P = 1.4 × 10−7 for low sound level), indicating that the SNR increased with the trial-by-trial reliability of tone-evoked firing. However, when the mid and high prestimulus firing units were compared, the midfiring group with the highest AUC showed a higher FF than the high firing group for high sound levels (Fig. 5C; Mann–Whitney U test of FF, P = 0.074) and low sound levels (P = 0.030). To confirm that the general trend of the AUC–FF relationship is inconsistent with the difference between the mid and high prestimulus firing units, especially for low sound level, we performed a LDA to visualize and quantify the boundary between the mid and high prestimulus units in an AUC–FF plane (Fig. 5C, red lines). The loss function was smaller for the low sound level (Ls = 0.20) than for the high sound level (Ls = 0.26), and the slope of the boundary was steeper for the low sound level (−0.19) than for the high sound level (−0.16), indicating that the FF difference between the mid and high prestimulus firing units was more distinct for the low sound level than for the high sound level. The FF with a longer Tw of 8 ms also exhibited a similar trend, but a weaker correlation with AUC (between FF and SNR, R = −0.13, P = 0.094 for high sound level, and R = −0.006, P = 0.94 for low sound level), and the FF with a longest Tw of 25 and 50 ms yielded no correlation with AUC (25 ms: R = −0.06, P = 0.94; 50 ms: R = −0.12, P = 0.12 for low sound level). The difference in FF with these longer time windows between the mid and high prestimulus firing units was not significant (Supplementary Fig. 7E and F). Thus, the midprestimulus firing units had higher SNRs with a trial-by-trial reliability of less than or equal to that of the high prestimulus firing units.
Lastly, we confirmed that the changes in FF from prestimulus to tone-evoked firing rates did not show any statistical difference between the mid and high prestimulus firing units for both high and low sound-level conditions (Fig. 5D; Tw = 4 ms, Mann–Whitney U test, P = 0.68 for high sound level and P = 0.40 for low sound level). These results were similarly observed at a Tw of 25 ms (P = 0.22 for high level and P = 0.86 for low level).
Collectively, the trial-by-trial response reliability was correlated with a prestimulus firing rate and is likely to depend on the magnitude of tone-evoked responses because FF also displayed a clear negative correlation with the tone-evoked firing rate (Fig. 5E). However, the trial-by-trial reliability was independent of the SNR or ISI distribution.
Local population activity is irrelevant to stochastic resonance with ongoing firing
Our next question was whether the nonmonotonic SNR with respect to an ongoing firing rate emerged from the local population activities which are based on the summation of synaptic current across many neurons or from a single-neuron mechanism. As shown in the representative traces in Fig. 6A, a recording site with large fluctuations in the ongoing LFP exhibited a large tone-evoked LFP. Population analysis revealed that the tone-evoked LFP peak amplitude positively correlates with the rms of prestimulus LFP in all conditions (Fig. 6B; R = 0.61, P = 1.57 × 10−17 for awake high-level condition; R = 0.57, P = 5.36 × 10−15 for awake low-level condition; and R = 0.57, P = 7.10 × 10−15 for anesthetized low-level condition), except for the anesthetized high-level condition (R = 0.10, P = 0.20).
The SNR at the LFP level, that is, LFP AUC, was generally higher for high sound level (Fig. 6C; 0.94, awake high level and 0.92 for anesthetized high-level conditions, respectively) than low sound level (0.80 for awake low level and 0.54 for anesthetized low-level conditions). Although the LFP AUC had a slightly negative correlation with the prestimulus LFP rms (R = −0.21, P = 0.0070 for awake low level; R = −0.20, P = 0.013 for anesthetized high level; R = −0.19, P = 0.018 for anesthetized low level) except for the awake high-level condition (R = 0.10, P = 0.21), the AUC showed a considerable fluctuation in each state condition compared with the single-unit AUC, shown in Fig. 2, and nonmonotonicity in the AUC was not observed. In the awake state, the AUC did not show any local maxima across prestimulus LFP rms when the AUC distribution was divided into 45 μV bins of LFP (Kruskal–Wallis test: P = 0.24 for high sound level; P = 0.23 for low sound level). In the anesthetized state, the AUC tended to exhibit a local maximum at a lower prestimulus LFP rms (for high sound level: 32.5 μV bin, Kruskal–Wallis test: P = 5.0 × 10−4; for low sound level: 122.5 μV bin, P = 0.11), which was significantly higher than the AUC only at a higher prestimulus LFP (for high sound level: Mann–Whitney U test with Bonferroni–Holm correction: P = 0.44, 0.022, 0.31, 0.14, and 2.0 × 10−4 for 32.5, 122.5, 167.5, 212.5, and 257.5 μV bin vs. 77.5 μV bin, respectively), indicating a monotonic decrease in the AUC with prestimulus LFP. These results ruled out the possibility that the hypothetical stochastic resonance occurred at the level of local population activity.
Since it is known that LFPs in different frequency bands contribute differently to ongoing activity as well as tone-evoked response (Kayser et al. 2009; Noda et al. 2013), we asked the possibility that tone-evoked LFP peak amplitude in a specific frequency band uniquely behaves against the prestimulus LFP amplitude. We then split LFP signals into 4 different frequency bands by digital bandpass filtering: delta–theta, 1–8 Hz; alpha, 8–13 Hz; beta, 13–30 Hz; and gamma, 45–60 Hz, where these bands were designed based on our previous studies (Noda et al. 2013; Noda and Takahashi 2015). Across all the frequency bands tested, we observed the strong positive correlation between prestimulus LFP amplitude and tone-evoked LFP peak amplitude across both high and low sound levels and across both awake and anesthetized conditions (delta–theta: at least R ≥ 0.84, P ≤ 3.8 10−43 across all the 4 conditions; alpha: R ≥ 0.98, P ≤ 6.6
10−43 across all the 4 conditions; alpha: R ≥ 0.98, P ≤ 6.6 10−109; beta: R ≥ 0.89, P ≤ 1.6
10−109; beta: R ≥ 0.89, P ≤ 1.6 10−53; gamma: R ≥ 0.46, P ≤ 1.9
10−53; gamma: R ≥ 0.46, P ≤ 1.9 10−9). Then, we characterized the SNR of tone-evoked peak amplitude of band-specific LFP with respect to the prestimulus band-specific LFP amplitude by calculating the AUC from the ROC curve.
10−9). Then, we characterized the SNR of tone-evoked peak amplitude of band-specific LFP with respect to the prestimulus band-specific LFP amplitude by calculating the AUC from the ROC curve.
In general, the tone-evoked LFP in lower frequency bands (delta–theta and alpha) displayed the relatively lower AUC values (Fig. 6F and G); on the other hand, the LFP in higher frequency bands (beta and gamma) showed the higher AUC values (Fig. 6D and E), probably because the slow frequency components could not capture the tone-evoked response transient well. From delta to beta bands, the AUC basically increased with prestimulus LFP amplitude for either high and low sound level and under both awake and anesthetized states, except for anesthetized low-level condition (Fig. 6E–G, Table 3), and none of the conditions demonstrated nonmonotonic distribution of the AUC with any local maximum along prestimulus LFP amplitude (Table 3). In gamma band, the distribution of AUC did not depend on or monotonically decreased with prestimulus LFP amplitude (Fig. 6D, Table 3). Overall, the LFP in any frequency band did not exhibit nonmonotonic behavior of SNR along prestimulus LFP across any sound level and under both awake and anesthetized states.
Table 3.
Statistical evaluation of band-specific LFPs in Fig. 6.

| |||||||||

|
aRobust rank-order test with Bonferroni correction, P values were calculated using 2-sample robust rank-order test and were compared between the bin of prestimulus LFP amplitude with maximum AUC and the other bins, with Bonferroni correction for multiple comparison.
bThe bin with the local maximum, also meaning the bin to test for comparison.
We further evaluated the relationship between the prestimulus LFP and SNR of tone-evoked firing rates in each unit. We plotted the AUC of tone-evoked firing rates obtained in Fig. 2 with respect to the prestimulus LFP rms in the corresponding recording channel (Supplementary Fig. 8). We did not find any correlation between them for both high and low sound levels under both awake and anesthetized states (awake high level: R = −0.064, P = 0.43; awake low level: R = −0.061, P = 0.45; anesthetized high level: R = −0.023, P = 0.78; anesthetized low level: R = 0.026, P = 0.74), meaning that the SNR at the single-unit level has no relation to the prestimulus LFP level.
Therefore, the nonmonotonic SNR with respect to prestimulus activity was observed only at a single-unit level and was independent of local population activity. The source of the observed stochastic resonance was prestimulus firing at a single neuron level rather than fluctuation of the LFP level.
Modeling the network stochastic resonance effect
To test whether the relationship between the prestimulus and tone-evoked firing patterns was sufficient for the nonmonotonic SNR improvement across single units and for the nonmonotonic temporal intermittency of firing across single units, we simulated population activities of spiking neurons and their temporal firing patterns when the relationship of prestimulus and tone-evoked firing was set to either (i) supralinear, (ii) linear, or (iii) lognormally random. Our physiological data suggested that (i) the supralinear relationship was primarily observed under the awake low-level condition, whereas (ii) the linear relationship was primarily observed under anesthetized condition; the lognormally random relationship (iii) served as a control condition here. Assuming that ongoing firing, i.e. the prestimulus firing, in each neuron was described by the Poisson process, the trial average of prestimulus firing rates across neurons was designed to have lognormal distribution, the mean and SD of which were comparable to those in our physiological data. For tone-evoked firing activities, each neuron was modeled as a LIF model (Fig. 7A).
Fig. 7.

Simulation demonstrates that the supralinear relationship between prestimulus and tone-evoked firing rates is sufficient for the nonmonotonic SNR improvement and the temporal intermittency. A) Simulated prestimulus and tone-evoked spike series of an example neuron across 200 trials. Spontaneous spike series were generated by the Poisson process. Tone-evoked spike series were generated by a LIF model (see Materials and methods). B) Simulated distribution of prestimulus and tone-evoked firing rates for the supralinear (left), linear (middle), and lognormally random relationships (right) (n = 300). Fitting curves here were overlaid via gaussian process factor analysis of each distribution after. C) Scatter plots of SNR (AUC) as a function of prestimulus firing rate of the simulated data in B. The supralinear relationship exhibited the nonmonotonic SNR improvement, whereas SNRs monotonically decreased with prestimulus firing rate for the linear and lognormal random relationships. D) Scatter plots of ISI skewness as a function of prestimulus firing rate in prestimulus (light dots) and tone-evoked firing (dark dots) periods. Conventions comply with Fig. 4B. E) Summary bar plots of ΔISI skewness for the low, middle, and high prestimulus firing units. The mean and SEM are shown for each bar. ***P < 0.001, **P < 0.01, *P < 0.05. F) Summary bar plots of ΔISI kurtosis for the low, middle, and high prestimulus firing units. G) Summary bar plots of ΔISI hyperskewness for the low, middle, and high prestimulus firing units. H) Box plot for change of ISI skewness (ΔISI skewness) in the high prestimulus firing rate from that in the middle prestimulus firing rate across different model parameters. Observation is the ΔISI skewness from the experimental data in Supplementary Fig. 4. Mann–Whitney U test of ISI skewness between high prestimulus firing rate versus middle prestimulus firing rate for each parameter condition. *P < 0.05.
In the supralinear relationship (Fig. 7B, left), the resulting SNR changed nonmonotonically with the prestimulus firing rates and exhibited a local maximum at the intermediate firing rate (Fig. 7C, left). However, in either the linear or lognormally random distribution (Fig. 7B, middle and right), the SNR monotonically decreased with the prestimulus firing rates (Fig. 7C, middle and right).
Furthermore, as observed in our physiological data, the nonmonotonic SNR improvement was associated with specific characteristics of ISI. In the supralinear relationship, the prestimulus ISI skewness monotonically increased with the prestimulus firing rate, while the tone-evoked ISI skewness reached a plateau at the intermediate firing rate (Fig. 7D, left). Therefore, the change of ISI skewness from prestimulus to tone-evoked period, i.e. ΔISI skewness, was characterized as a nonmonotonic change with the local maximum at the midprestimulus firing units (Fig. 7E, left). However, in the linear relationship, both the prestimulus and tone-evoked ISI skewness monotonically increased in parallel with the prestimulus firing rates (Fig. 7D, middle), and therefore the ΔISI skewness of each unit did not depend on the prestimulus firing (Fig. 7E, middle). In the lognormally random relationship, because the tone-evoked ISI skewness did not increase with the prestimulus firing rate (Fig. 7D, right), the ΔISI skewness monotonically decreased with the prestimulus firing rates (Fig. 7E, right). Similarly, the supralinear relationship tended to exhibit nonmonotonic ΔISI kurtosis (Fig. 7F) as well as nonmonotonic ΔISI hyperskewness (Fig. 7G) with the local maxima at the midprestimulus firing units, while the linear relationship exhibited monotonically increasing ΔISI kurtosis (Fig. 7F) and ΔISI hyperskewness (Fig. 7G) with the prestimulus firing levels and the lognormally random relationship showed monotonically decreasing ΔISI kurtosis and ΔISI hyperskewness.
We also tested different LIF model parameters to investigate which parameters are contributing to the nonmonotonic SNR improvement and the nonmonotonic change of temporally intermittent firing in the supralinear relationship. Especially, we changed the membrane resistance (inverse leak conductance) which determines how far the membrane potential is driven by an input current, and the time constant which is the decay time for the membrane potentials to decay exponentially to the equilibrium potential, and the resting membrane potential (see Materials and methods). When the input current and the other model parameters are fixed, increase of the membrane resistance elevates the firing rate in the model, while the increase of the time constant decreases it. Meanwhile, the relationship between the resting membrane potential and the reset potential affects the membrane potential fluctuation, especially in case that the resting potential is far higher than the reset potential and close to the spike threshold. The spike threshold generally affects regularity in the spiking output in the model. In our model simulation, the distribution of the average firing rate was predetermined such that change of these model parameters should not affect the average firing rate, but the distribution of firing rate across trials and temporal firing patterns in individual trials. Even though we changed these parameters, the nonmonotonic SNR was robustly observed as long as the relationship between the prestimulus firing rate and the evoked firing rate was supralinear (Supplementary Fig. 9). The moderate change in the resting membrane potential between −60 and −70 mV did not induce any qualitative difference in the temporal firing pattern, e.g. ΔISI skewness in the model (Fig. 7 and Supplementary Fig. 9). On the other hand, the nonmonotonic behavior of temporal firing pattern especially depended on the membrane resistance and the time constant: When a longer time constant (20 ms) or a larger membrane resistance (200 MΩ) was set in the model, the ISI skewness, ISI kurtosis, and ISI hyperskewness during the tone-evoked period monotonically and more sharply increased with the prestimulus firing rate than during prestimulus period, leading to the monotonic behavior of ΔISI skewness, ΔISI kurtosis, and ΔISI hyperskewness with the different prestimulus firing levels (Supplementary Fig. 9). However, the combination of a longer time constant (20 ms) and a relatively large membrane resistance (100 MΩ) again resulted in nonmonotonic distribution of ΔISI skewness (Fig. 7H), meaning that the balance between these parameters which affect input-driven firing in the mutually opposite direction could be important.
Taken together, the nonmonotonic ISI features with respect to the prestimulus firing rates, as well as to the nonmonotonic SNR improvement, were observed in the supralinear relationship, supporting our hypothesis that the supralinear relationship between prestimulus and tone-evoked firing rates led to the nonmonotonic SNR improvement through the temporally intermittent firing at an intermediate prestimulus activity level.
Discussion
We found that the relationship between the prestimulus ongoing activity and the tone-evoked firing activity differed between the awake and anesthetized states (Fig. 1D and E). Evoked firing in the anesthetized state increased linearly with prestimulus firing, where the ongoing activity is generally suppressed, whereas that in the awake state increased supralinearly. This supralinear property distinguishes tone-evoked firing from the ongoing activity and achieves a better SNR for weak inputs, which are subthreshold under anesthesia. This SNR improvement is reminiscent of stochastic resonance, which offers a clear advantage at a certain level of input (Fig. 8A and B). This hypothetical mechanism suggests that a smaller number of units, or a subpopulation in the auditory cortex, gains the benefit of SNR improvement (Fig. 8A). Furthermore, the temporally intermittent firing pattern, but not the trial-by-trial reliability or the LFP fluctuation, could be the neural mechanism underlying SNR improvement (Fig. 8B). Our simulation also verified that the supralinear relationship between tone-evoked and ongoing firing is sufficient for the nonmonotonic SNR improvement and temporal intermittent firing pattern. We believe that this mechanism works in a sparse microcircuit in the auditory cortex (Fig. 8A) and refer to it as the “sparse network stochastic resonance.”
Fig. 8.
Proposed schematic representation of the “sparse network stochastic resonance” phenomenon. A) Population representation before and after sound input. The SNR for weak sound inputs depends on the prestimulus activity of each neuron among a neuronal population in the auditory cortex. Only a small number of neurons showed a high SNR to weak inputs. B) Schematic summary of our findings. Firing reliability monotonically increased with prestimulus firing rates; however, SNR was optimized at an intermediate prestimulus firing rate with temporally intermittent tone-evoked firing pattern (middle).
Ongoing activity and sensory processing
We showed that single units with different ongoing spontaneous activities differ in tone-evoked firing rates, temporal patterns, and reliability. The brain state, or fluctuation of ongoing activity, is likely to play several critical roles in sensory processing (Hartmann et al. 2015) according to the following evidence: (i) The ongoing activity level often positively correlated with the sensory-evoked activity level (see the section below for more detail); (ii) spatio-temporal ongoing activity patterns outlined the sensory-evoked response patterns (Arieli et al. 1996; Luczak et al. 2009); (iii) ongoing spontaneous activity predicted perceptual and behavioral outcomes specifically in response to ambiguous stimuli (Hesselmann et al. 2008); and (iv) during learning and development, the ongoing activity self-organized neuronal circuits (Babola et al. 2018) and the sensory-evoked activity pattern coevolved with ongoing activity patterns (Han et al. 2008; Lewis et al. 2009; Berkes et al. 2011). These contributions of ongoing activity onto evoked activity seem to be generally observed at different stages of sensory pathway in the brain, especially with respect to item (iv) (Babola et al. 2018). However, ongoing spontaneous and evoked activities are differently modulated in subcortical regions by inputs from a sensory cortex or from other brain regions (Blackwell et al. 2020; Aizenberg et al. 2019). For example, spontaneous activities between the auditory thalamus and auditory cortex contributed differently during task engagement and prediction (Otazu et al. 2009). Future studies need to probe the detailed relationship between the ongoing and sensory-evoked activities in different subcortical regions. Thus, ongoing activity is critical for the understanding of cortical sensory processing.
Regarding the evidence for the item (i), a positive correlation between the ongoing activity and stimulus-evoked activity levels has been previously observed in both the anesthetized and awake states in either different cortical regions, sensory modalities, or species, as illustrated in the following examples: the auditory cortex of awake marmoset monkeys (Bender et al. 2016), the somatosensory cortex of anesthetized mice (Clancy et al. 2015), the visual cortex of anesthetized cats (Azouz and Gray 1999), awake rats and cats (Ch'ng and Reid 2010), and the lateral geniculate nucleus of anesthetized mice (Tang et al. 2016). However, the relationship in terms of linearity or nonlinearity was not characterized. We partly attribute this observation of linearity/nonlinearity to the differences in experimental and analytical conditions among studies. By examining both awake and anesthetized neural activities, this study was able to define weak stimuli, which are suprathreshold in the awake state but subthreshold in anesthetized state. This level of stimulus is most likely to gain SNR through stochastic resonance. Furthermore, ongoing firing varied more widely in the awake state than in the anesthetized state, indicating the existence of sparse network stochastic resonance, where some, but not all, neurons gain benefits from ongoing activity. Thus, our experimental design could be a major contributing factor to our findings. We confirmed that most auditory-evoked responses ceased within a few hundred milliseconds after the tone offset, as previously reported (Hromádka et al. 2008; Otazu et al. 2009; Nir et al. 2015), and determined the intertone interval at 600 ms to avoid the possible effects of preceding tones on ongoing activity. However, because stimuli were delivered every 600 ms, prediction of stimulus delivery might modulate the ongoing activity specifically in the awake state (Funamizu et al. 2013; Noda et al. 2017). We speculate that top-down prediction and attention develop a specific brain state, that is, a specific profile of ongoing activity, to improve SNRs in a given stimulus context in the proposed framework. Whether and how the brain actively utilizes sparse network stochastic resonance warrants further investigation.
Stochastic resonance in the neural system
Classically, stochastic resonance is defined as the improved detection of weak periodic input in the presence of a certain amount of noise in crayfish mechanoreceptors (Wiesenfeld and Moss 1995). This definition was extended into a broadband, aperiodic weak input (e.g. interneurons in the cricket’s abdominal ganglion; Levin and Miller 1996). These pioneering studies have discussed SNR improvements with different levels of noise in a specific type of cell. Recently, suprathreshold stochastic resonance has been defined as the net output of a neuron population (Durrant et al. 2011).
Our sparse network stochastic resonance is similar to these previous studies in that SNR is optimized at a certain level of noise; however, this study offers several novel perspectives. First, because the SNR improvement we observed was derived from a subset of heterogeneous neuronal populations, our model is compatible with the notion of sparse network representation of sensory stimuli (Olshausen and Field 2004; Hromádka et al. 2008; Bullmore and Sporns 2009). Second, instead of external noise added to the stimuli, the internal noise of the neural system is utilized to improve the SNR. Internal noise in neural systems has been extensively investigated as a stochastic mechanism. For example, synaptic connections have been characterized as a stochastic neurotransmitter release (Tsodyks and Markram 1997; Manwani and Koch 1999; Steinmetz et al. 2000; Branco and Staras 2009). Baseline membrane potentials fluctuate, owing to the stochastic gating of ion channels and membrane noise (Lecar and Nossal 1971; Diba et al. 2004; Kole et al. 2006). These subthreshold fluctuations underlie the ongoing spiking activities of neural populations, and the interaction between ongoing and stimulus-evoked activities determines the SNR of stimulus representation, as previously demonstrated in experiments (Sakata and Harris 2009; Issa and Wang 2013; Meir et al. 2018) and model studies (Brinkman et al. 2016; Feng et al. 2018). Our schematic model integrates these insights with the idea of stochastic resonance.
Temporal firing pattern and temporal coding
The ISI of ongoing activity in the auditory cortex exhibits a skewed distribution (Yague et al. 2017), which can be maximized when the temporal pattern of the noise input lies between deterministic and stochastic process (Schwalger et al. 2010). Consistently, our findings on the prestimulus temporal firing pattern showed that ISI skewness depends on the ongoing activity level and reaches the maximum at an intermediate prestimulus activity.
Analysis of the ISI distribution revealed that the poststimulus firing pattern is neither periodic nor random. The test tone frequency was too high for neuronal firing to phase lock with the cycle of the sound wave; instead, the tone stimulus made the firing pattern temporally intermittent. This particular firing pattern was observed in a synchronous firing sequence called a synfire chain (Ikegaya et al. 2004). The rich repertoire of sequences is often discussed in the theory of self-organized criticality (SoC), or neuronal avalanches, where the size distribution of intermittent firing patterns is characterized as a power law, indicating that the spike generation is far from a Poisson process (Benayoun et al. 2010; Yada et al. 2017; Plenz et al. 2021). Both experimental and model studies have demonstrated that information transmission is maximized when the SoC is achieved under balanced excitation and inhibition (Shew et al. 2011; Vazquez-Rodriguez et al. 2017). Thus, we believe that SoC plays a role in the generation of intermittent firing patterns and SNR improvement in sparse network stochastic resonance.
SNR and trial-by-trial reliability
The trial-by-trial variability (i.e. FF) decreased with higher tone-evoked firing rates; however, this relationship did not necessarily lead to the highest SNR. This is in line with a more faithful signal transmission at a high noise level (Stein et al. 2005) and a more reliable sensory-evoked firing activity at a high spontaneous activity level (Azouz and Gray 1999). Neuronal variability in the ongoing activity is quenched by external stimuli (Ponce-Alvarez et al. 2013); thus, the reliability of stimulus-evoked responses increases with response magnitude. The variability of firing determines the reliability of and contributes to the SNRs. However, SNRs mainly depend on the difference in the distribution between the signal and noise. This could explain why response reliability is irrelevant to the nonlinear behavior of the SNR.
We demonstrate hypothetical stochastic resonance for weak auditory input in the awake state, which could be derived from the supralinear relationship between the ongoing activity and auditory-evoked response. Future experiments will be expected to characterize the SNR improvement from the ongoing activity for more defined brain states, such as states during REM/NREM sleep, quiet waking, attention, or during locomotion.
Supplementary Material
Acknowledgments
Current affiliation of TN is Institute of Physiology, University Medical Center, Johannes Gutenberg-University, Hanns-Dieter-Hüsch Weg 19, 55128 Mainz, Germany.
Contributor Information
Takahiro Noda, Department of Mechano-informatics, Graduate School of Information Science and Technology, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan.
Hirokazu Takahashi, Department of Mechano-informatics, Graduate School of Information Science and Technology, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan.
Authors’ contributions
Takahiro Noda (Formal analysis, Investigation, Methodology, Validation, Visualization, Writing—original draft) and Hirokazu Takahashi (Conceptualization, Funding acquisition, Investigation, Project administration, Supervision, Writing—review & editing)
Funding
This work was supported in part by JSPS KAKENHI (23H03465, 23H04336), JST (JPMJMS2296), AMED (JP22dm0307009), NEDO (18101806-0), the Asahi Glass Foundation, and the Naito Foundation.
Conflict of interest statement: None declared.
Data availability
Data will be available from the corresponding author upon reasonable request.
References
- Aizenberg M, Rolon-Martinez S, Pham T, Rao W, Haas JS, Geffen MN. Projection from the Amygdala to the Thalamic Reticular Nucleus Amplifies Cortical Sound Responses. Cell Rep. 2019:28(3):605–615 e604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alkire M. Consciousness and anesthesia. Science. 2008:322(5903):876–880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arieli A, Sterkin A, Grinvald A, Aertsen A. Dynamics of ongoing activity: explanation of the large variability in evoked cortical responses. Science. 1996:273(5283):1868–1871. [DOI] [PubMed] [Google Scholar]
- Azouz R, Gray CM. Cellular mechanisms contributing to response variability of cortical neurons in vivo. J Neurosci. 1999:19(6):2209–2223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Babola TA, Li S, Gribizis A, Lee BJ, Issa JB, Wang HC, Crair MC, Bergles DE. Homeostatic control of spontaneous activity in the developing auditory system. Neuron. 2018:99(3):511–524 e515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbour DL, Callaway EM. Excitatory local connections of superficial neurons in rat auditory cortex. J Neurosci. 2008:28(44):11174–11185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benayoun M, Cowan JD, Drongelen W, Wallace E. Avalanches in a stochastic model of spiking neurons. PLoS Comput Biol. 2010:6(7):e1000846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bender DA, Ni R, Barbour DL. Spontaneous activity is correlated with coding density in primary auditory cortex. J Neurophysiol. 2016:116(6):2789–2798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berkes P, Orbán G, Lengyel M, Fiser J. Spontaneous cortical activity reveals hallmarks of an optimal internal model of the environment. Science. 2011:331(6013):83–87. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blackwell JM, Lesicko AM, Rao W, De Biasi M, Geffen MN. Auditory cortex shapes sound responses in the inferior colliculus. Elife. 2020:9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Branco T, Staras K. The probability of neurotransmitter release: variability and feedback control at single synapses. Nat Rev Neurosci. 2009:10(5):373–383. [DOI] [PubMed] [Google Scholar]
- Brinkman BA, Weber AI, Rieke F, Shea-Brown E. How do efficient coding strategies depend on origins of noise in neural circuits? PLoS Comput Biol. 2016:12(10):e1005150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 2009:10(3):186–198. [DOI] [PubMed] [Google Scholar]
- Burns BD, Webb AC. The spontaneous activity of neurones in the cat’s cerebral cortex. Proc R Soc Lond B. 1976:194(1115):211–223. [DOI] [PubMed] [Google Scholar]
- Ch'ng YH, Reid RC. Cellular imaging of visual cortex reveals the spatial and functional organization of spontaneous activity. Front Integr Neurosci. 2010:4(20):1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clancy KB, Schnepel P, Rao AT, Feldman DE. Structure of a single whisker representation in layer 2 of mouse somatosensory cortex. J Neurosci. 2015:35(9):3946–3958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins JJ, Imhoff TT, Grigg P. Noise-enhanced tactile sensation. Nature. 1996:383(6603):770. [DOI] [PubMed] [Google Scholar]
- Lange FP, Rahnev DA, Donner TH, Lau H. Prestimulus oscillatory activity over motor cortex reflects perceptual expectations. J Neurosci. 2013:33(4):1400–1410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeWeese MR, Wehr M, Zador AM. Binary spiking in auditory cortex. J Neurosci. 2003:23(21):7940–7949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diba K, Lester HA, Koch C. Intrinsic noise in cultured hippocampal neurons: experiment and modeling. J Neurosci. 2004:24(43):9723–9733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douglass JK, Wilkens L, Pantazelou E, Moss F. Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature. 1993:365(6444):337–340. [DOI] [PubMed] [Google Scholar]
- Duque D, Perez-Gonzalez D, Ayala YA, Palmer AR, Malmierca MS. Topographic distribution, frequency, and intensity dependence of stimulus-specific adaptation in the inferior colliculus of the rat. J Neurosci. 2012:32(49):17762–17774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durrant SJ, Taylor C, Cairney S, Lewis PA. Sleep-dependent consolidation of statistical learning. Neuropsychologia. 2011:49(5):1322–1331. [DOI] [PubMed] [Google Scholar]
- Eckhorn R, Frien A, Bauer R, Woelbern T, Kehr H. High frequency (60-90 Hz) oscillations in primary visual cortex of awake monkey. Neuroreport. 1993:4(3):243–246. [DOI] [PubMed] [Google Scholar]
- Faisal AA, Selen LP, Wolpert DM. Noise in the nervous system. Nat Rev Neurosci. 2008:9(4):292–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feng T, Chen Q, Yi M, Xiao Z. Improvement of signal-to-noise ratio in parallel neuron arrays with spatially nearest neighbor correlated noise. PLoS One. 2018:13(7):e0200890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferezou I, Deneux T. Review: How do spontaneous and sensory-evoked activities interact? Neurophotonics. 2017:4(3):031221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer S, Schumann A. A distribution-free ordinal classification of floods based on moments. Hydrol Sci J. 2018:63(11):1605–1618. [Google Scholar]
- Freedman D, Diaconis P. On the histogram as a density estimator:L2 theory. Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete. 1981:57(4):453–476. [Google Scholar]
- Funamizu A, Kanzaki R, Takahashi H. Pre-attentive, context-specific representation of fear memory in the auditory cortex of rat. PLoS One. 2013:8(5):14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstner W, Kistler W, Naud R, Paninski L. Neuronal dynamics: from single neurons to networks and models of cognition. Cambridge: Cambridge University Press; 2014. [Google Scholar]
- Gilbert CD, Sigman M. Brain states: top-down influences in sensory processing. Neuron. 2007:54(5):677–696. [DOI] [PubMed] [Google Scholar]
- Guo W, Chambers AR, Darrow KN, Hancock KE, Shinn-Cunningham BG, Polley DB. Robustness of cortical topography across fields, laminae, anesthetic states, and neurophysiological signal types. J Neurosci. 2012:32(27):9159–9172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haider B, Duque A, Hasenstaub AR, Yu Y, McCormick DA. Enhancement of visual responsiveness by spontaneous local network activity in vivo. J Neurophysiol. 2007:97(6):4186–4202. [DOI] [PubMed] [Google Scholar]
- Han F, Caporale N, Dan Y. Reverberation of recent visual experience in spontaneous cortical waves. Neuron. 2008:60(2):321–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hänggi P. Stochastic resonance in biology how noise can enhance detection of weak signals and help improve biological information processing. ChemPhysChem. 2002:3(3):285–290. [DOI] [PubMed] [Google Scholar]
- Harris KD. Accuracy of tetrode spike separation as determined by simultaneous intracellular and extracellular measurements. J Neurophysiol. 2000:84(1):401–414. [DOI] [PubMed] [Google Scholar]
- Harris KD, Thiele A. Cortical state and attention. Nat Rev Neurosci. 2011:12(9):509–523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartmann C, Lazar A, Nessler B, Triesch J. Where's the noise? Key features of spontaneous activity and neural variability Arise through learning in a deterministic network. PLoS Comput Biol. 2015:11(12):e1004640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasenstaub A, Sachdev RN, McCormick DA. State changes rapidly modulate cortical neuronal responsiveness. J Neurosci. 2007:27(36):9607–9622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hesselmann G, Kell CA, Eger E, Kleinschmidt A. Spontaneous local variations in ongoing neural activity bias perceptual decisions. Proc Natl Acad Sci U S A. 2008:105(31):10984–10989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hromádka T, DeWeese MR, Zador AM. Sparse representation of sounds in the unanesthetized auditory cortex. PLoS Biol. 2008:6(1):0124–0137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ikegaya Y, Aaron G, Cossart R, Aronov D, Lampl I, Ferster D, Yuste R. Synfire chains and cortical songs: temporal modules of cortical activity. Science. 2004:304(5670):559–564. [DOI] [PubMed] [Google Scholar]
- Issa EB, Wang X. Increased neural correlations in primate auditory cortex during slow-wave sleep. J Neurophysiol. 2013:109(11):2732–2738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kang K, Amari S. Discrimination with spike times and ISI distributions. Neural Comput. 2008:20(6):1411–1426. [DOI] [PubMed] [Google Scholar]
- Kayser C, Montemurro MA, Logothetis NK, Panzeri S. Spike-phase coding boosts and stabilizes information carried by spatial and temporal spike patterns. Neuron. 2009:61(4):597–608. [DOI] [PubMed] [Google Scholar]
- Kayser C, Logothetis NK, Panzeri S. Visual enhancement of the information representation in auditory cortex. Curr Biol. 2010:20(1):19–24. [DOI] [PubMed] [Google Scholar]
- Kole MH, Hallermann S, Stuart GJ. Single Ih channels in pyramidal neuron dendrites: properties, distribution, and impact on action potential output. J Neurosci. 2006:26(6):1677–1687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lecar H, Nossal R. Theory of threshold fluctuations in nerves. Biophys J. 1971:11(12):1068–1084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levin JE, Miller JP. Broadband neural encoding in the cricket cereal sensory system enhanced by stochastic resonance. Nature. 1996:380(6570):165–168. [DOI] [PubMed] [Google Scholar]
- Lewis CM, Baldassarre A, Committeri G, Romani GL, Corbetta M. Learning sculpts the spontaneous activity of the resting human brain. Proc Natl Acad Sci U S A. 2009:106(41):17558–17563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopez-Jury L, Mannel A, Garcia-Rosales F, Hechavarria JC. Modified synaptic dynamics predict neural activity patterns in an auditory field within the frontal cortex. Eur J Neurosci. 2020:51(4):1011–1025. [DOI] [PubMed] [Google Scholar]
- Luczak A, Bartho P, Harris KD. Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron. 2009:62(3):413–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manjarrez E, Rojas-Piloni G, Méndez I, Flores A. Stochastic resonance within the somatosensory system effects of noise on evoked field potentials elicited by tactile stimuli. J Neurosci. 2003:23(6):1997–2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manwani A, Koch C. Detecting and estimating signals in noisy cable structures, I: neuronal noise sources. Neural Comput. 1999:11(8):1797–1829. [DOI] [PubMed] [Google Scholar]
- Mar JC. The rise of the distributions: why non-normality is important for understanding the transcriptome and beyond. Biophys Rev. 2019:11(1):89–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meir I, Katz Y, Lampl I. Membrane potential correlates of network decorrelation and improved SNR by cholinergic activation in the somatosensory cortex. J Neurosci. 2018:38(50):10692–10708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizuseki K, Buzsaki G. Preconfigured, skewed distribution of firing rates in the hippocampus and entorhinal cortex. Cell Rep. 2013:4(5):1010–1021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mongillo G, Rumpel S, Loewenstein Y. Inhibitory connectivity defines the realm of excitatory plasticity. Nat Neurosci. 2018:21(10):1463–1470. [DOI] [PubMed] [Google Scholar]
- Moshitch D, Las L, Ulanovsky N, Bar-Yosef O, Nelken I. Responses of neurons in primary auditory cortex (A1) to pure tones in the halothane-anesthetized cat. J Neurophysiol. 2006:95(6):3756–3769. [DOI] [PubMed] [Google Scholar]
- Nir Y, Vyazovskiy VV, Cirelli C, Banks MI, Tononi G. Auditory responses and stimulus-specific adaptation in rat auditory cortex are preserved across NREM and REM sleep. Cereb Cortex. 2015:25(5):1362–1378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noda T, Takahashi H. Anesthetic effects of isoflurane on the tonotopic map and neuronal population activity in the rat auditory cortex. Eur J Neurosci. 2015:42(6):2298–2311. [DOI] [PubMed] [Google Scholar]
- Noda T, Amemiya T, Shiramatsu TI, Takahashi H. Stimulus phase locking of cortical oscillations for rhythmic tone sequences in rats. Frontiers in Neural Circuits. 2017:11:2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noda T, Kanzaki R, Takahashi H. Stimulus phase locking of cortical oscillation for auditory stream segregation in rats. PLoS One. 2013:8(12):e83544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O'Connor DH, Peron SP, Huber D, Svoboda K. Neural activity in barrel cortex underlying vibrissa-based object localization in mice. Neuron. 2010:67(6):1048–1061. [DOI] [PubMed] [Google Scholar]
- Ohki K, Chung S, Ch'ng YH, Kara P, Reid RC. Functional imaging with cellular resolution reveals precise micro-architecture in visual cortex. Nature. 2005:433(7026):597–603. [DOI] [PubMed] [Google Scholar]
- Olshausen BA, Field DJ. Sparse coding of sensory inputs. Curr Opin Neurobiol. 2004:14(4):481–487. [DOI] [PubMed] [Google Scholar]
- Otazu GH, Tai LH, Yang Y, Zador AM. Engaging in an auditory task suppresses responses in auditory cortex. Nat Neurosci. 2009:12(5):646–654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pernia M, Diaz I, Colmenarez-Raga AC, Rivadulla C, Cudeiro J, Plaza I, Merchan MA. Cross-modal reaction of auditory and visual cortices after long-term bilateral hearing deprivation in the rat. Brain Struct Funct. 2020:225(1):129–148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen PC, Berg RW. Lognormal firing rate distribution reveals prominent fluctuation–driven regime in spinal motor networks. elife. 2016:5:e18805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plenz D, Ribeiro TL, Miller SR, Kells PA, Vakili A, Capek EL. Self-organized criticality in the brain. Front Phys. 2021:9:639389. [Google Scholar]
- Polley DB, Steinberg EE, Merzenich MM. Perceptual learning directs auditory cortical map reorganization through top-down influences. J Neurosci. 2006:26(18):4970–4982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponce-Alvarez A, Thiele A, Albright TD, Stoner GR, Deco G. Stimulus-dependent variability and noise correlations in cortical MT neurons. Proc Natl Acad Sci U S A. 2013:110(32):13162–13167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reig R, Zerlaut Y, Vergara R, Destexhe A, Sanchez-Vives MV. Gain modulation of synaptic inputs by network state in auditory cortex in vivo. J Neurosci. 2015:35(6):2689–2702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roxin A, Brunel N, Hansel D, Mongillo G, Vreeswijk C. On the distribution of firing rates in networks of cortical neurons. J Neurosci. 2011:31(45):16217–16226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakata S, Harris KD. Laminar structure of spontaneous and sensory-evoked population activity in auditory cortex. Neuron. 2009:64(3):404–418. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwalger T, Fisch K, Benda J, Lindner B. How noisy adaptation of neurons shapes interspike interval histograms and correlations. PLoS Comput Biol. 2010:6(12):e1001026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shew WL, Yang H, Yu S, Roy R, Plenz D. Information capacity and transmission are maximized in balanced cortical networks with neuronal avalanches. J Neurosci. 2011:31(1):55–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein RB, Gossen ER, Jones KE. Neuronal variability: Noise or part of the signal? Nat Rev Neurosci. 2005:6(5):389–397. [DOI] [PubMed] [Google Scholar]
- Steinmetz PN, Manwani A, Koch C, London M, Segev I. Subthreshold voltage noise due to channel fluctuations in active neuronal membranes. J Comput Neurosci. 2000:9(2):133–148. [DOI] [PubMed] [Google Scholar]
- Stolzberg D, Chrostowski M, Salvi RJ, Allman BL. Intracortical circuits amplify sound-evoked activity in primary auditory cortex following systemic injection of salicylate in the rat. J Neurophysiol. 2012:108(1):200–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutter ML, Schreiner CE. Topography of intensity tuning in cat primary auditory cortex: single-neuron versus multiple-neuron recordings. J Neurophysiol. 1995:73(1):190–204. [DOI] [PubMed] [Google Scholar]
- Szymanski FD, Rabinowitz NC, Magri C, Panzeri S, Schnupp JW. The laminar and temporal structure of stimulus information in the phase of field potentials of auditory cortex. J Neurosci. 2011:31(44):15787–15801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi H, Nakao M, Kaga K. Distributed representation of sound intensity in the rat auditory cortex. Neuroreport. 2004:15(13):2061–2065. [DOI] [PubMed] [Google Scholar]
- Tang J, Ardila Jimenez SC, Chakraborty S, Schultz SR. Visual receptive Field properties of neurons in the mouse lateral geniculate nucleus. PLoS One. 2016:11(1):e0146017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tischbirek CH, Noda T, Tohmi M, Birkner A, Nelken I, Konnerth A. In vivo functional mapping of a cortical column at single-neuron resolution. Cell Rep. 2019:27(5):1319–1326 e1315. [DOI] [PubMed] [Google Scholar]
- Tolhurst DJ, Smyth D, Thompson ID. The sparseness of neuronal responses in ferret primary visual cortex. J Neurosci. 2009:29(8):2355–2370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsodyks MV, Markram H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc Natl Acad Sci U S A. 1997:94(2):719–723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Hooser SD, Heimel JA, Chung S, Nelson SB, Toth LJ. Orientation selectivity without orientation maps in visual cortex of a highly visual mammal. J Neurosci. 2005:25(1):19–28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vazquez-Rodriguez B, Avena-Koenigsberger A, Sporns O, Griffa A, Hagmann P, Larralde H. Stochastic resonance at criticality in a network model of the human cortex. Sci Rep. 2017:7(1):13020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veestraeten D. A recursion formula for the moments of the first passage time of the Ornstein-Uhlenbeck process. J Appl Probab. 2015:52(2):595–601. [Google Scholar]
- Warzecha AK, Egelhaaf M. Variability in spike trains during constant and dynamic stimulation. Science. 1999:283(5409):1927–1930. [DOI] [PubMed] [Google Scholar]
- Wiesenfeld K, Moss F. Stochastic resonance and the benefits of noise: from ice ages to crayfish and SQUIDs. Nature. 1995:373(6509):33–36. [DOI] [PubMed] [Google Scholar]
- Yada Y, Mita T, Sanada A, Yano R, Kanzaki R, Bakkum DJ, Hierlemann A, Takahashi H. Development of neural population activity toward self-organized criticality. Neuroscience. 2017:343:55–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yague JG, Tsunematsu T, Sakata S. Distinct temporal coordination of spontaneous population activity between basal forebrain and auditory cortex. Front Neural Circuits. 2017:11:64. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data will be available from the corresponding author upon reasonable request.








