Selective formation of metastable polymorphs in solid-state synthesis

Abstract

Metastable polymorphs often result from the interplay between thermodynamics and kinetics. Despite advances in predictive synthesis for solution-based techniques, there remains a lack of methods to design solid-state reactions targeting metastable materials. Here, we introduce a theoretical framework to predict and control polymorph selectivity in solid-state reactions. This framework presents reaction energy as a rarely used handle for polymorph selection, which influences the role of surface energy in promoting the nucleation of metastable phases. Through in situ characterization and density functional theory calculations on two distinct synthesis pathways targeting LiTiOPO₄, we demonstrate how precursor selection and its effect on reaction energy can effectively be used to control which polymorph is obtained from solid-state synthesis. A general approach is outlined to quantify the conditions under which metastable polymorphs are experimentally accessible. With comparison to historical data, this approach suggests that using appropriate precursors could enable targeted materials synthesis across diverse chemistries through selective polymorph nucleation.

Metastable polymorphs with low surface energy are made accessible by reactions with large thermodynamic driving force.

INTRODUCTION

Creating specific polymorphs through targeted synthesis remains one of the great unsolved challenges of rational materials design. Metastable compounds often exhibit desirable properties for advanced technologies related to pharmaceuticals, semiconductors, catalysis, and energy. However, their synthesis is challenging due to competition with lower-energy phases (1, 2), and there are few guidelines available to understand which metastable compounds are experimentally accessible. Thermodynamic competition for metastable phases may appear as decomposition into phases with different compositions (phase separation) or as a phase at the same composition but with a different structure that exhibits lower free energy (polymorphism) (3). A compound that is metastable with respect to phase separation can sometimes be retained by keeping the synthesis temperature low, thereby restricting the long-range diffusion needed to form the competing phases (4)—an approach that has been used to synthesize metastable compounds in thin films (5). In contrast, polymorphism remains difficult to control.

The ground state for a given composition often competes with many different structures in a narrow energy range (2), and it is not well understood what determines the specific conditions under which each structure can form. These structures can occasionally be stabilized by modifying their synthesis conditions. For instance, high-temperature and high-pressure polymorphs like diamond (from graphite) and β-quartz (from α-quartz) can be produced under such conditions and subsequently returned to ambient conditions quickly enough to retain their metastable state. Precursor selection can also play a role in stabilizing certain metastable polymorphs. CaCO₃ is a well-studied example of this, where the choice of precursor species and concentrations each have a notable effect on the polymorph that first nucleates (6). Despite these recent advances, there remains no general set of rules to determine the specific conditions under which a metastable polymorph can form. There exist more than 10,000 polymorphs in the Materials Project (7) that are predicted to be close (≤20 meV/atom) to the convex hull formed by thermodynamically stable compounds, but have yet to be synthesized experimentally.

It has been widely reported that certain metastable polymorphs with low surface energy can be stabilized at small particle size, particularly when using solution-based synthesis routes (3). This principle has been leveraged to synthesize metastable polymorphs of binary oxides (8) and metal chalcogenides (9) from solutions. For example, nanosized TiO₂ is a well-studied system where the metastable anatase polymorph forms before the rutile one, despite the latter phase having a lower bulk free energy (10). Similar observations have also been made regarding the crystallization of metastable polymorphs from melts (11, 12), vapors (13), and amorphous media (14, 15). In this work, we demonstrate that surface-stabilized polymorphs are also prevalent in solid-state synthesis. Building on classical nucleation theory, we show that the first polymorph to form is determined by the reaction energy, which can be deliberately controlled by the choice of precursors. Using more reactive precursors with a large driving force to produce the desired compound effectively lowers the critical radius required for nucleation, which in turn favors the formation of polymorphs with low surface energy. This understanding creates opportunities to synthesize metastable materials using a scalable, solid-state route.

LiTiOPO₄ (LTOPO) is used as a prototype system to demonstrate the validity of our framework. This compound has been reported in two polymorphs: one with orthorhombic Pnma symmetry and the other with triclinic $P\overline{1}$ symmetry. Yet, the factors that govern the formation of each polymorph remain undetermined. Density functional theory (DFT) calculations performed in this work reveal that the metastable polymorph of LTOPO has a lower surface energy than the ground state and, as such, may nucleate first at small particle size. We show that by using precursors with a large reaction energy to form LTOPO, the critical radius for nucleation is kept small enough to favor the metastable polymorph, whose formation is confirmed with in situ x-ray diffraction (XRD). In contrast, the use of precursors that form low-energy reaction intermediates requires larger critical nuclei to form LTOPO, delaying the formation of its metastable polymorph and reducing its yield. These findings support the hypothesis that reaction energy and its change along the synthesis path dictate the influence of surface energy on solid-state reaction outcomes, for which rational precursor selection can enable the targeted synthesis of metastable materials.

RESULTS

Thermodynamics of nucleation-controlled polymorph selection

In a process controlled by nucleation, the selectivity of competing polymorphs can be assessed by comparing their nucleation rates. According to classical nucleation theory (16), the rate of nucleation (Q) for a given phase is related to its surface energy (γ) and the bulk free energy change (∆G) associated with its formation by the equation:

$$Q=A\text{exp}\left[-\frac{16{\mathrm{\pi \gamma }}^3}{3n^2{k}_{\mathrm{B}}T{(∆G)}^2}\right]$$ (1)

where n is the number of atoms per unit volume, T is temperature, k_B is Boltzmann’s constant, and A is a pre-factor. According to Langer theory, A is a product of the dynamic pre-factor κ, which is related to the growth rate of critical clusters, and the statistical pre-factor Ω₀, which provides a measure of the phase space volume available for the nucleation (17).

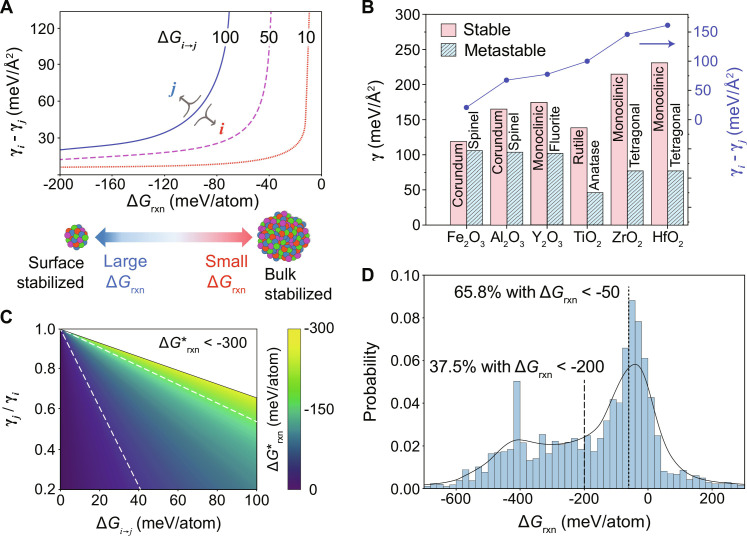
In the context of solid-state synthesis, we refer to the bulk free energy change as the reaction energy (∆G_rxn). Whereas the surface energy of a phase is relatively constant in a given medium, assuming its nucleation is homogeneous, the reaction energy can be varied by modifying the reagents from which the phase forms. To illustrate the effects of surface and reaction energies, Fig. 1A plots several boundaries where the nucleation rate of a stable polymorph (i) is equal to that of a metastable polymorph (j) at the same composition. Each boundary represents a specific value of the bulk energy difference between the two polymorphs (∆G_i→j) and is plotted as a function of two metrics: (i) the difference between the surface energies of the two polymorphs (γ_i − γ_j) and (ii) the reaction energy to form the stable polymorph (∆G_rxn). Note that we assume γ_j < γ_i in our analysis; otherwise, polymorph j can never achieve an energetic advantage during nucleation.

Fig. 1. Opportunity windows for polymorph selection in solid-state synthesis.

(A) Boundaries at which the nucleation rates of a stable polymorph (i) and metastable polymorph (j) with the same composition are equal. Axes denote the bulk reaction energy (∆G_rxn) and surface energy difference (γ_i − γ_j). Each curve is calculated for a distinct polymorph energy difference (∆G_i→j) given in meV/atom on the graph. Schematic at the bottom shows the polymorph selectivity influenced by the bulk reaction energies that is tunable by precursor selection. (B) A contour plot showing the critical reaction energy ( ${\mathrm{\Delta }G}_{\text{rxn}}^{*}$ ) required for preferential nucleation of a metastable polymorph at various ΔG_i→j and γ_j/γ_i. (C) Reported calorimetry-measured surface energies of anhydrous binary metal oxides Fe₂O₃ (60), Al₂O₃ (61), Y₂O₃ (62), TiO₂ (63), ZrO₂ (20), and HfO₂ (18, 19). (D) Reaction energy distribution of solid-state reactions reported in the literature using a text-mined dataset (24, 25) and energies calculated at 500°C.

In Fig. 1A, the region to the upper left of each boundary represents the conditions where the metastable polymorph (j) nucleates faster than the stable one (i), signifying an opportunity window to form the metastable phase. The range of this window depends on the bulk energy difference between the polymorphs. For a small energy difference, such as 10 meV/atom, preferential nucleation of the metastable polymorph occurs for a wide range of reaction energies (typically ΔG_rxn < −20 meV/atom) even if its surface energy is only slightly lower (>5 meV/Ų) than that of the stable polymorph. A larger polymorph energy difference requires more extreme conditions to favor the metastable phase. For example, to access a polymorph with energy ≈ 100 meV/atom above the stable phase, the surface energy of the metastable phase must be ~20 meV/Ų lower than that of the stable phase to make its nucleation plausible. At the same time, the reaction energy must be more negative than −80 meV/atom to ensure that the metastable polymorph nucleates before the stable one.

The trends shown in Fig. 1A suggest that reaction energy is an effective handle to control the selectivity between two competing polymorphs. Figure 1B further illustrates this by plotting the critical reaction energy, ${\mathrm{\Delta }G}_{\text{rxn}}^{*}$ (note S1), below which a metastable polymorph (j) nucleates faster than its stable counterpart (i), against the ratio of the polymorph surface energies (γ_j/γ_i) and their bulk energy difference (ΔG_i→j). The plot shows that when two competing polymorphs have similar bulk formation energies, i.e., small ΔG_i→j, only a small reaction energy is required to preferentially nucleate a metastable phase with lower surface energy (γ_j/γ_i < 1). In contrast, when polymorphs have a large bulk energy difference but similar surface energies, larger reaction driving force is required to access the metastable phase (e.g., ΔG_rxn < −200 meV/atom). Such large reaction driving force is less common, as it requires highly reactive precursors that directly contribute to the product’s formation without creating stable intermediates that consume the thermodynamic driving force.

The scales of the variables shown in Fig. 1 (A and B) were chosen based on historical data from the literature such that these diagrams cover the range of conditions where metastable polymorph nucleation is reasonably accessible. In the well-studied cases of metastable binary metal oxides synthesized from solution, polymorph surface energy differences have been reported to reach ~150 meV/Ų (Fig. 1C) (18, 19). For example, both ZrO₂ and HfO₂ adopt a monoclinic polymorph as their ground state (18–20). However, a metastable tetragonal polymorph is often observed when these compounds are synthesized at the nanoscale. Prior work has attributed this observation to the fact that the metastable polymorph has a surface energy that is 130 to 150 meV/Ų less than the monoclinic ground state (18–20). Coupled with the small difference between the bulk formation energies of the two polymorphs (40 to 50 meV/atom), our framework suggests that the metastable phase should nucleate first when its reaction energy exceeds ~60 meV/atom. Such a moderate driving force is accessible using a wide range of precursors. Furthermore, lower reaction energies would be required in cases where the surface energy difference is increased through heterogeneous nucleation on a surface that favors the metastable polymorph, e.g., when the product shares structural similarities with the precursors (21, 22) or the substrate on which it is grown (23).

Bulk reaction energies span a similarly wide range of values. Figure 1D shows the distribution of reaction energies from 7562 prior solid-state synthesis experiments (24, 25), calculated at a common lower bound of solid-state synthesis temperature of 500°C (Materials and Methods). Approximately 65.8% of reactions have ΔG_rxn < −50 meV/atom, whereas 37.5% have ΔG_rxn < −200 meV/atom. These results highlight the availability of precursors with large reaction energies, which may provide access to synthesize metastable polymorphs with low surface energies. These reported reaction energies will be reduced in the event of intermediate phase formation, emphasizing the need for accurate modeling techniques that can predict reaction pathways, in addition to the use of in situ characterization techniques to directly observe such pathways.

LTOPO polymorphs

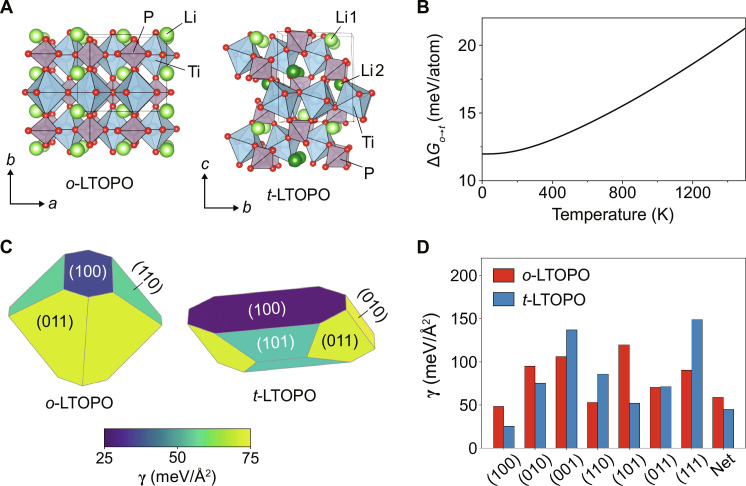
We test the validity of our framework for selectivity in the synthesis of two competing LTOPO polymorphs. The polymorph with orthorhombic Pnma symmetry, hereafter referred to as o-LTOPO, adopts structure based on the sillimanite (Al₂SiO₅) framework. It consists of edge-sharing TiO₆ octahedra forming one-dimensional chains, which are connected through PO₄ tetrahedra and octahedrally coordinate Li. The polymorph with triclinic $P\overline{1}$ symmetry, hereafter referred to as t-LTOPO, adopts a similar structure to o-LTOPO but with different orientations of the PO₄ tetrahedra and reduced coordination of Li to square pyramidal. The unit cell structure of each polymorph is shown in Fig. 2A and fig. S1.

Fig. 2. LTOPO polymorph structures and energetics.

(A) Crystal structures of the orthorhombic (o-LTOPO, Pnma) and triclinic (t-LTOPO, $P\overline{1}$ ) polymorphs for LTOPO. (B) DFT-calculated free energy difference between o- and t-LTOPO from 0 K to 1490 K. (C) Wulff constructions showing the equilibrium particle shape of each polymorph. (D) DFT-calculated surface energies of all low-index surfaces comprising the Wulff construction of each polymorph. The net surface energies are also shown as the rightmost bars on the graph, revealing that t-LTOPO has a more stable surface than o-LTOPO.

DFT calculations reveal that o-LTOPO is the ground state, whereas t-LTOPO is metastable with 12 meV/atom higher energy at 0 K. Nevertheless, both polymorphs have been observed experimentally, although the factors that dictate the selectivity of each polymorph were yet unclear. Previous studies have shown that t-LTOPO forms before o-LTOPO at low temperatures when using a solid-state route (26), whereas an opposite relation to temperature was observed during cooling-crystallization experiments (27), suggesting that temperature by itself does not dictate the polymorph selectivity. Our investigation of temperature effects based on vibrational entropy (Fig. 2B) confirms that the metastability of t-LTOPO remains unchanged throughout 0 to 1490 K, with the energy difference ΔG_o→t increasing from 12 meV/atom to 21 meV/atom as the temperature rises.

The persistent metastability of t-LTOPO in its bulk form suggests that its experimental formation may be related to its nucleation kinetics at small particle size, where surface energies become important. The more favorable surface energy of t-LTOPO was verified using DFT calculations on slabs representing the low-index Miller indices for each polymorph. In Fig. 2C, we display the equilibrium particle shapes of o- and t-LTOPO determined using the Wulff construction. Consistent with the principle outlined by Navrotsky (3, 28), which states that metastable polymorphs often have lower surface energies than their stable counterparts, the net surface energy of t-LTOPO (44.85 meV/Ų, or 0.717 J/m²) is lower than that of o-LTOPO (58.65 meV/Ų, or 0.938 J/m²). The enhanced stability of the metastable polymorph’s surface can largely be attributed to the low energy of its (100) facet, which constitutes 49% of the total surface area in the Wulff construction. As shown by the surface energy for each set of Miller indices in Fig. 2D, the (100) surface of t-LTOPO is more stable than any others of each polymorph, which we attribute to a reduced number of broken bonds along this termination (note S2).

Although particles formed via solid-state synthesis may not adopt a perfect Wulff shape, the net surface energies computed using the Wulff construction are generally thought to provide a reasonable estimate of each phase’s surface energy under realistic conditions. Previous work has reported good agreement between DFT-calculated and experimentally measured surface energies for a variety of elemental crystals, even when those crystals showed varying particle shapes (29). We can also show that for LTOPO specifically, the exact particle shape has little effect on the relative stability of either polymorph. For example, after recalculating the net surface energy of each polymorph based on a simple particle shape resembling a sphere (fig. S2), t-LTOPO still has a lower surface energy (72.87 meV/Ų, or 1.165 J/m²) than o-LTOPO (84.92 meV/Ų, or 1.357 J/m²). This result confirms that the metastable phase would be favored at small particle size, even if the kinetics of diffusions were insufficient to form a perfect Wulff shape.

In situ characterization of LTOPO synthesis

The stabilization of t-LTOPO by its low surface energy makes it an excellent candidate to probe the factors that influence polymorph selectivity. To this end, we performed solid-state synthesis experiments targeting LTOPO and monitored their phase evolution with in situ synchrotron XRD. Two precursor sets were investigated, differing only by their phosphate source—P₂O₅ versus NH₄H₂PO₄—while using Li₂CO₃ and TiO₂ as the Li and Ti sources. Both precursor mixtures were ball-milled at 450 rpm for 20 hours to ensure intimate mixing. In situ synchrotron XRD measurements were then carried out on each mixture (in air) while heating at a rate of 25°C/min to 700°C, followed by a 3-hour hold at this temperature. The selected precursors and conditions were chosen based on previous work where LTOPO was synthesized (26, 27, 30–32). The phosphate source was changed to vary the reactivity of the starting precursor mixture, which we will show has a prominent effect on the resulting synthesis pathway and product selectivity.

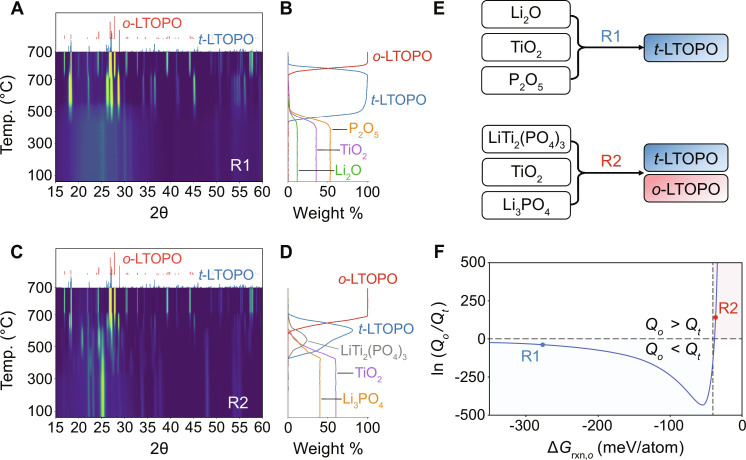
Precursor set 1: Li₂CO₃ + TiO₂ + P₂O₅

Figure 3A shows a heatmap of the XRD intensities measured from precursor set 1 as it was heated to 700°C. At low temperature, the patterns show only a few well-defined peaks that can be attributed to TiO₂. The other precursors become amorphous after ball milling, as evidenced by diffuse scattering in the XRD patterns (fig. S3). Near 500°C, several peaks associated with t-LTOPO appear and continue to grow upon further heating, at the expense of the TiO₂ precursors whose signal decays between 500° and 700°C. The weight fraction of each phase is plotted as a function of temperature in Fig. 3B. Since the sample was mostly amorphous at low temperature, we set the initial weight fraction of each phase (Li₂O, TiO₂, and P₂O₅) to its expected value based on the starting precursor stoichiometry, assuming CO₂ loss during milling.

Fig. 3. Phase evolution and polymorph selection during solid-state synthesis of LTOPO.

(A and C) In situ synchrotron XRD patterns (2θ converted to Cu K_α) measured while heating to 700°C, followed by a 3-hour hold, using starting precursors of (A) Li₂CO₃, TiO₂, and P₂O₅ or (C) Li₂CO₃, TiO₂, and NH₄H₂PO₄. (B and D) Phase fraction evolution estimated from the peak intensity in (A) and (C), respectively. Amounts of amorphous phases were calibrated based on the starting materials. (E) Reaction pathways denoted R1 and R2 correspond to the results shown in (A) and (C), respectively. (F) Relative polymorph nucleation rates between o-LTOPO and t-LTOPO as a function of reaction energy (ΔG_rxn,o). The minimum thermodynamic driving force required to form the metastable t-LTOPO is denoted by ${\mathrm{\Delta }G}_{\text{rxn}}^{*}$ . The two points (R1, R2) along the curve represent different reactant combinations that led to the initial formation of LTOPO.

Rapid t-LTOPO growth occurs from 500° to 550°C, followed by slower growth between 550° and 650°C as the precursors are completely consumed and t-LTOPO becomes phase pure. This metastable polymorph remains present until 700°C, at which point several new peaks associated with o-LTOPO appear. This stable polymorph continues to grow as the sample is held at 700°C, with the weight fraction of o-LTOPO following a clear S-shape that agrees well with the Avrami equation, until it becomes the only remaining phase. The delayed formation of o-LTOPO, despite being the ground state, can be attributed to the need for enhanced reaction kinetics, which are in this case provided by higher temperatures.

All the reactions observed in situ are believed to occur in the solid state. Although set 1 contains phases with potentially low melting points (e.g., P₂O₅), our measurements based on Thermogravimetric Analysis (TGA) and Differential Scanning Calorimetry (DSC) do not detect any substantial heat flow associated with melting as the sample reaches the temperature at which t-LTOPO forms (fig. S4). Scanning electron microscopy (SEM) measurements on the synthesis product also reveal particles that are randomly shaped and agglomerated (fig. S5), not well faceted, which suggests that t-LTOPO formed via solid-state reactions and not from a melt.

Precursor set 2: Li₂CO₃ + TiO₂ + NH₄H₂PO₄

In situ synchrotron XRD measurements performed on precursor set 2 (Fig. 3C) reveal that Li₂CO₃ and NH₄H₂PO₄ reacted in the ball milling step, as evidenced by the appearance of Li₃PO₄ at low temperature. The weight fraction of each phase is plotted as a function of temperature in Fig. 3D. Upon heating, the partially reacted mixture of TiO₂ and Li₃PO₄ proceeds through a notably different reaction pathway than set 1. Both t-LTOPO and LiTi₂(PO₄)₃ form as intermediates at 500°C, consuming TiO₂ and Li₃PO₄ (Fig. 3C). Peaks corresponding to o-LTOPO appear at 600°C, accompanied by a reduction in the intensity of peaks attributed to LiTi₂(PO₄)₃, TiO₂, and Li₃PO₄. Further heating to 700°C causes a phase transition from t-LTOPO to o-LTOPO, as was observed in the reaction pathway of set 1.

Ex situ characterization of LTOPO synthesis

The reaction pathway followed by set 1 reveals a temperature window where the metastable t-LTOPO polymorph forms without impurities (500° to 700°C), presenting a viable route to synthesize this phase. A separate synthesis procedure was performed by heating set 1 to 500°C at a rate of 25°C/min and holding for 1 hour, after which ex situ XRD confirmed the presence of t-LTOPO without any detectable impurities. The XRD pattern (fig. S6) remains unchanged even after holding the sample at 500°C for 12 hours, suggesting that the phase transformation of LTOPO depends on temperature more strongly than time. This finding is further supported by additional experiments where a slower heating rate of 1°C/min was used, resulting in the same product (t-LTOPO).

In contrast to set 1, the combination of precursors in set 2 does not provide an effective route to synthesize the metastable t-LTOPO, as it never appears without any impurities in the reaction pathway. Ex situ XRD performed on a sample made by heating set 2 to 500°C reveals a mixture of t-LTOPO and LiTi₂(PO₄)₃, each of which forms regardless of the heating rate used (fig. S6). This distinct path forms the stable o-LTOPO directly from intermediates, rather than from t-LTOPO. Holding the sample at 500°C for 12 hours did not lead to any noticeable changes to the XRD pattern, which suggests that the transformation from LiTi₂(PO₄)₃ to o-LTOPO only occurs at higher temperatures owing to its low driving force. Once o-LTOPO is formed at 700°C, it remains the only majority phase even after cooling to room temperature. We also re-annealed the sample at two different temperatures (500°C or 600°C) with a long hold time of 48 hours. As shown in fig. S7, the XRD pattern remains completely unchanged in either case, confirming that o-LTOPO is indeed the ground state at all temperatures considered.

Effect of reaction energy on LTOPO selectivity

On the basis of the phase evolution observed through in situ synchrotron XRD measurements (Fig. 3, A and C), we identify two reactions that resulted in the formation of LTOPO (Fig. 3E):

$$\mathrm{R}1:{\text{Li}}_2\mathrm{O}+2 {\text{TiO}}_2+{\mathrm{P}}_2{\mathrm{O}}_5\to 2 {\text{LiTiOPO}}_4(\mathrm{\Delta }{G}_{\text{rxn},o}=-279 \text{meV}/\text{atom})$$

$$\mathrm{R}2:{\text{LiTi}}_2{({\text{PO}}_4)}_3+{\text{Li}}_3{\text{PO}}_4+2 {\text{TiO}}_2\to 4 {\text{LiTiOPO}}_4(\mathrm{\Delta }{G}_{\text{rxn},o}=-40 \text{meV}/\text{atom})$$

We performed in situ XRD analyses starting directly from reactants of R1 and R2 using a laboratory diffractometer equipped with a heating stage (Anton Paar HTK 1200 N) and Cu K_α radiation. To ensure that each set of precursors remains unreacted before heating, we avoided the use of high-energy ball milling and instead mixed the samples by hand. The corresponding experiments (figs. S8 and S9) confirm that R1 leads to the formation of t-LTOPO at a low temperature of 400°C, which remains the sole product until the sample is further heated above 700°C. In contrast, R2 causes only transient formation of t-LTOPO with low purity at temperatures between 670° and 750°C. This is followed by the formation of o-LTOPO as the remaining precursors are consumed upon further heating to 800°C. In summary, these findings demonstrate that R1 provides clear benefits over R2 when used to synthesize LTOPO in its metastable polymorph.

The key difference between R1 and R2 lies in their reaction energies. DFT calculations indicate that R1 has a much larger reaction energy (−279 meV/atom) than R2 (−40 meV/atom). Figure 3F gives the logarithm of the relative nucleation rates for o-LTOPO (Q_o) and t-LTOPO (Q_t) throughout a wide range of reaction energies. The resulting curve highlights two distinct regimes for each polymorph to preferentially nucleate, separated by the critical reaction energy ( ${\mathrm{\Delta }G}_{\text{rxn}}^{*}$ ), which we define as the minimum thermodynamic driving force required to nucleate the metastable polymorph faster than the stable one (i.e., Q_t > Q_o). To preferentially nucleate the metastable polymorph of LTOPO, we find a critical reaction energy of ${\mathrm{\Delta }G}_{\text{rxn}}^{*}$ = −45 meV/atom (note S3). Given that the calculated reaction energy for R1 is substantially larger than this threshold, it falls well within the regime where t-LTOPO is expected to nucleate first (denoted in blue). Calculation of relative nucleation rates (note S3) suggests that t-LTOPO nucleates ~10¹⁷ times faster than o-LTOPO when formed by R1.

In comparison to R1, the precursors in R2 have a smaller reaction energy of −40 meV/atom to form LTOPO. This increases the critical radius required for nucleation, thereby favoring larger particles with more stable bulk energies (such as o-LTOPO). However, the computed reaction energy of R2 lies very close to the critical reaction energy for LTOPO ( ${\mathrm{\Delta }G}_{\text{rxn}}^{*}$ = −45 meV/atom), and therefore, one might expect that nucleation of either phase is competitive at high temperature. This was confirmed using the in situ XRD measurements discussed earlier, which showed that both polymorphs begin to form within a relatively narrow temperature window of ~80°C. Therefore, although both reaction pathways can form t-LTOPO to some extent, R1 presents a more effective route to obtaining the metastable polymorph with high purity throughout a wide range of temperatures (400° to 700°C).

To further demonstrate the importance of reaction energy in controlling the nucleation rates of competing polymorph, we tested two additional sets of precursors with reaction energies that lie in between the two extremes of R1 and R2. The anticipated reactions for these precursor sets are listed below:

$$\mathrm{R}3:{\text{Li}}_3{\text{PO}}_4+3 {\text{TiO}}_2+{\mathrm{P}}_2{\mathrm{O}}_5\to 3 {\text{LiTiOPO}}_4(\mathrm{\Delta }{G}_{\text{rxn},o}=-104 \text{meV}/\text{atom})$$

$$\mathrm{R}4:{\text{LiTi}}_2{({\text{PO}}_4)}_3+{\text{Li}}_2{\text{TiO}}_3\to 3 {\text{LiTiOPO}}_4(\mathrm{\Delta }{G}_{\text{rxn},o}=-73 \text{meV}/\text{atom})$$

From the in situ XRD measurements shown in figs. S10 and S11, we find that the first reaction (R3) produces t-LTOPO with a majority yield at temperatures between 560° and 750°C, before later forming o-LTOPO upon further heating. The second reaction (R4) produces t-LTOPO with less yield and over a smaller range of temperatures (620°to 700°C). Combining these results with the outcomes of reactions R1 and R2, we plot in Fig. 4 the temperature window over which the metastable polymorph (t-LTOPO) is observed for each precursor set. The temperature window is plotted as a function of each precursor set’s reaction energy, revealing a clear and direct correlation between the two quantities. Such correlation agrees well with our proposed framework for polymorph selectivity, which states that larger reaction energies favor the polymorph with lower surface energy (in this case, t-LTOPO). By lowering its nucleation barrier relative to any competing polymorphs, the surface-stabilized phase can form at lower temperatures, well before the ground state can appear (as observed in R1).

Fig. 4. Correlation between t-LTOPO stability window and reaction energy.

The temperature window over which t-LTOPO is observed, plotted with respect to the reaction energy, for each precursor set tested here. This includes R1: Li₂O + TiO₂ + P₂O₅, R2: LiTi₂(PO₄)₃ + TiO₂ + Li₃PO₄, R3: Li₃PO₄ + TiO₂ + P₂O₅, and R4: LiTi₂(PO₄)₃ + Li₂TiO₃. The vertical dashed line represents the critical reaction energy, below which o-LTOPO formation is predicted to be favorable.

DISCUSSION

The targeted synthesis of metastable polymorphs bolsters current approaches to materials design by enabling access to a vastly enlarged space beyond thermodynamically stable materials. The formation of metastable phases with lower surface energy has long been studied in solution-based methods, where the small particle size enables surface energy to dictate reaction outcomes. Related work in thin films and amorphous media has demonstrated that metastable polymorphs can also be accessed by modifying the surface energy through structural templating or epitaxial growth (21–23), i.e., by engineering the rate of heterogeneous nucleation. We have shown in this work that metastable polymorphs are also accessible in traditional solid-state synthesis where controlled modification of the surface energy is typically considered to be more challenging.

Our work demonstrates that the reaction energy, easily modifiable by changing precursors, can be used as an additional handle to control the relative nucleation rates of competing polymorphs. Larger reaction energies effectively reduce the critical radius required for nucleation, thereby increasing the ratio of surface area to bulk volume in the corresponding nuclei (Fig. 1A). As such, nucleation events driven by large reaction energies tend to favor the formation of products with low surface energies. This principle was successfully applied to synthesize a metastable polymorph of LTOPO, whose formation is made possible by (i) its surface energy being lower (more stable) than that of the ground state and (ii) the use of precursors that maintain a large reaction energy to form it. Since the persistence of surface-stabilized metastable polymorphs relies on small particle size and a slow transformation rate toward the ground state, we more generally recommend that low temperatures be used for their synthesis. Commonly used procedures like regrinding and reheating should be avoided to maintain the metastable product, which can often be formed rapidly and with high purity in a single step (without reheating) if sufficiently reactive precursors are used.

The framework for polymorph selectivity presented here operates under the assumption that solid-state reactions proceed through nucleation and growth. This is supported by recent efforts that used high-resolution electron microscopy to study solid phase transitions at the atomic scale. Peng et al. (33) first reported that solid phase transitions in a polymer take place through a two-step process involving the formation of liquid nuclei as intermediates, from which crystalline products can nucleate and grow. Later work by Fei et al. (34) confirmed these findings and revealed a similar nucleation mechanism for solid-state reactions involving inorganic compounds. While the two-step nucleation process differs in some respects from classical nucleation theory, both models share relevant quantities such as the critical radius and energetic barrier for nucleation. Accordingly, we approximate these quantities in the current work by assuming that classical nucleation theory is qualitatively accurate, enabling a comparative assessment of nucleation rates for competing polymorphs.

Our framework also assumes that nucleation is homogeneous in nature. In reality, nuclei tend to form heterogeneously at the interfaces between different particles, as well as at the surface of the sample container, leading to reduction in the nucleation barrier. However, accounting for such effects in a quantitative manner is difficult using first-principles calculations, and we believe that our methodology can still be used to provide approximate guidance for polymorph selectivity in solid-state synthesis as heterogeneous nucleation only influences a fraction of the nucleating solid’s surface. In general, the guidance provided by our framework is most likely to hold true in extreme cases (e.g., large surface energy differences), as demonstrated for LTOPO.

Our approach highlights the importance of ab initio computations, which are needed to evaluate the relative stability of competing polymorphs and determine the reaction energies of various precursor sets. Both factors help identify systems where metastable compounds may be accessible. With the advent of large-scale ab initio databases such as the Materials Project, which contains DFT-computed properties for >150,000 compounds, rapid screening of suitable polymorphs is now possible. The DFT computations made available in such databases can be further supplemented with recently developed machine learning algorithms (35) that can describe finite-temperature contributions to the free energy (e.g., from vibrational entropy). Nevertheless, the accuracy of DFT is not universal and can become more limited when dealing with strongly correlated systems. To address this, more advanced functionals are being developed. For example, the Materials Project has recently transitioned from PBE to SCAN, which more accurately describes properties such as the formation energy, even on many strongly correlated systems (36, 37). Such advancements promise to improve our predictive capabilities, enabling broader application of the framework described in this work.

The data presented in Fig. 1 suggests that there exists a wide range of conditions under which surface-stabilized metastable polymorphs may be obtained through solid-state synthesis. A key requirement for this task is the selection of optimal precursors that not only start with a large reaction energy to form the desired target but also maintain it should any intermediates form. To this end, our framework for polymorph selectivity may benefit from integration with existing techniques for the design (38–40) and optimization (41) of reaction pathways. These techniques predict the intermediates formed by a set of precursors and use ab initio computations to determine the reaction energy that remains to produce the targeted polymorph from these intermediates. Such methods can be used to screen various precursor sets and identify reaction pathways with a large thermodynamic driving force at the target-forming step, thereby favoring the nucleation of surface-stabilized polymorphs in accordance with the framework outlined in this work. The use of in situ characterization (22, 42) is also critical to verify any proposed reaction pathways, enabling a complete understanding of the factors that dictate the synthesis of metastable polymorphs in the solid state.

MATERIALS AND METHODS

Synthesis and characterizations

Li₂CO₃, TiO₂, P₂O₅, NH₄H₂PO₄, Li₃PO₄, and Li₂O were purchased from Sigma-Aldrich and used directly for the synthesis of LTOPO. LiTi₂(PO₄)₃ was synthesized from Li₂CO₃, TiO₂, and NH₄H₂PO₄ by solid-state reaction at 800°C for 12 hours. To prepare precursor mixtures, chemicals were weighed and loaded into a ZrO₂-lined jar in an Ar-filled glovebox. Excess Li₂CO₃ (10 wt %) was added to compensate for any Li loss during high-energy ball milling or high-temperature treatment. The powder was mixed using 10 ZrO₂ grinding balls with 10 mm diameter and milled at 450 rpm for 20 hours in a Retsch PM 400 planetary ball mill. After ball milling, the powder was scraped from the jar and then pelletized. For in situ synchrotron XRD studies, the pellets were broken to small pieces to fit into a quartz capillary. For in situ laboratory XRD studies, powders were pressed manually and loaded into an Al₂O₃ sample holder, which was then loaded into a Bruker D8 Advance diffractometer (Cu K_α radiation) equipped with an Anton Paar heating stage. For ex situ studies, heat treatment on the pellets was conducted in a box furnace in the air. After heating, the pellets were removed from the furnace and fast cooled in the air. Pellets were pulverized to fine powder using a mortar and pestle. Ex situ XRD was performed using a Rigaku Miniflex 600 diffractometer with Cu K_α radiation. SEM images were obtained on a Zeiss Gemini Ultra-55 analytical field-emission SEM. Thermal analysis was performed on a Mettler Toledo TGA/DSC 3+ instrument with 10 ml/min N₂ flow.

In situ synchrotron XRD

In situ synchrotron XRD was performed at beamline 11-ID-B at the Advanced Photon Source (APS) of Argonne National Laboratory with a constant wavelength of 0.2115 Å. Samples were loaded into 1.1-mm quartz capillaries and mounted in a flow cell optimized for the collection of diffraction data in transmission geometry (43). The flow cell was mounted at the beamline on an x-y stage for ease of alignment. Samples were heated with compact resistive heating elements to temperatures up to 700°C at a ramp rate of 25°C/min under air without any gas flow. Diffraction data were acquired every 15 s on an amorphous silicon-based area detector (PerkinElmer XRD1621) positioned at a nominal distance of 1000 mm from the sample. Calibration of the beam center, sample-detector distance, rotation, and tilt angle were performed in GSAS-II using a CeO₂ standard (44). Reduction of the two-dimensional images to one-dimensional patterns was performed in GSAS-II.

All XRD patterns were analyzed using a recently developed machine learning package, XRD-AutoAnalyzer (45), which automates the identification of crystalline phases using a convolutional neural network trained on entries from the Inorganic Crystal Structure Database (ICSD). We manually verified the presence of any phases identified using this automated approach. Their weight fractions were then assessed by performing Rietveld refinement to optimize the fit between the calculated and experimentally observed XRD patterns. We only varied the lattice parameters, particle size, and weight fraction of each phase during refinement to ensure that the process could be performed in high throughput without any errors. All other parameters (e.g., site occupancies and displacements) were kept fixed according to the ICSD entry reported for each compound. The lattice parameters of each LTOPO polymorph, obtained from this fitting procedure, are plotted in fig. S12.

Bulk free energies

For all solid phases studied in this work, bulk free energies were calculated using DFT calculations performed with the Vienna ab initio simulation package (VASP) (46–49). Starting structures were taken from Materials Project (7) and relaxed using the projector augmented wave (PAW) method with the strongly constrained and appropriately normed (SCAN) functional (50). This functional has been shown to outperform more traditional DFT functionals, like PBE and PBEsol, when used to compute solid formation energies (51), enabling the relative stability of competing polymorphs to be assessed with a high degree of accuracy (37). A cutoff energy of 600 eV was imposed on the plane wave basis sets. For each structure, the Brillouin zone was sampled with Gaussian smearing (0.05 eV width) on a Γ-centered mesh containing at least 25 k-points per Å⁻¹. Unit cells and atomic positions were relaxed until all forces were less than 10⁻² eV/Å. On the final structures, electronic optimization was performed using the tetrahedron method with Blöchl corrections (52) and a convergence criterion of 10⁻⁶ eV.

To account for finite-temperature effects, vibrational entropies were computed for both LTOPO polymorphs through application of the quasi-harmonic approximation (QHA) based on density functional perturbation theory (DFPT), as implemented in the Phonopy package (53). Supercells of size 2 × 2 × 1 were prepared based on the DFT-relaxed structure of each polymorph. To apply QHA, the volumes (V) of these supercells were expanded and compressed to form nine distinct structures with linear strains Δε ∈ {−3%, −2%, −1%, −0.5%, 0%, 0.5%, 1%, 2%, 3%}. DFPT calculations were performed using the Perdew-Burke-Ernzerhof generalized gradient approximation (GGA) (54) and PAW method (55). An energy cutoff of 520 eV and a stricter energy convergence criterion of 10⁻⁸ eV were used for the DFPT calculations. After obtaining the vibrational entropies (S), the Gibbs free energy (G) was calculated as a function of temperature (T) for each LTOPO polymorph:

$$G=H-\mathit{TS}$$

where H is the enthalpy of each phase, approximated by the DFT-calculated energy. For all other phases considered in this work, temperature-dependent Gibbs free energies were estimated using the machine-learned descriptor developed by Bartel et al. (35), which can closely approximate the vibrational entropies in solid phases.

Surface energies

For each polymorph of LTOPO, the surface energy was determined by performing DFT calculations on surface slabs generated using the efficient creation and convergence scheme (56), as implemented in the Python Materials Genomic (Pymatgen) package (57). Only low-index surfaces were considered, including Miller indices (hkl) with $h,k,l\in \{\overline{1},0,1\}$ . Slabs were generated with a thickness of at least 10 Å and a 15-Å vacuum. Atomic positions within each slab were relaxed while keeping the unit cell fixed to maintain the interlayer vacuum. The parameters used for the DFT calculations performed here were the same as those used for the bulk free energy calculations, except for the k-point mesh, where only the Γ point was sampled along the direction normal to the surface. From the final energies of the relaxed slabs (E_slab), surface energies (γ) were calculated as follows:

$$\mathrm{\gamma }=\frac{1}{2A}(E_{\text{slab}}-N{E}_{\text{bulk}})$$

where A is the surface area of the slab, N is the number of atoms it contains, and E_bulk is the normalized (per atom) energy of the bulk phase. The Wulff construction was used to determine the equilibrium particle shape for each polymorph of LTOPO, from which total surface energies were calculated.

Text-mining dataset

To investigate distribution of reaction energies in solid-state synthesis experiments, we extracted the information associated with 7562 solid-state reactions from a previously reported dataset that was formed by text-mining the scientific literature (24, 25). For each reaction, the difference in the Gibbs free energies of the product(s) and the precursor(s) was calculated using thermochemical data from the Materials Project (7). Each chemical formula was mapped to the lowest-energy structure or a linear combination of them available in the Materials Project for that composition. Since all Materials Project energies are calculated at 0 K, we approximate the finite-temperature Gibbs free energy of each phase at 500°C using the machine-learned descriptor developed by Bartel et al. (35). For gaseous species such as O₂ and CO₂, the temperature-dependent enthalpy and entropy were taken from the FREED (58) and NIST (59) experimental databases. For materials containing CO₃²⁻ anions, an empirical correction of −1.2485 eV/CO₃ was applied to compensate for systematic errors in DFT. This value was calibrated based on experimental enthalpies of common carbonates (24).

From our analysis, 14.7% of all reactions considered have a positive (unfavorable) reaction energy at 500°C. This result is unexpected given that reactions can occur experimentally only if they are thermodynamically favorable. However, we identify three sources of error that may have led to these positive reaction energies. First, an error rate of 7% has been reported when extracting reported precursors and synthesis targets from the literature (25). Second, discrepancies may exist between the modeled and actual synthesis conditions. Quantities related to the atmospheric conditions are sometimes not reported in the papers considered when mining the literature. We also only computed the reaction energies at 500°C, whereas the actual experiments may have been performed at different a temperature. Third, there is some uncertainty in the computed reaction energies as we used a finite-temperature estimation technique with a root mean square error of about 61 meV/atom (35).

Supplementary Materials

This PDF file includes:

Notes S1 to S3

Figs. S1 to S13

References