Universal orbit design for metal artifact elimination

Abstract

Objective.

Metal artifacts are a persistent problem in CT and cone-beam CT. In this work, we propose to reduce or even eliminate metal artifacts by providing better sampling of data using non-circular orbits.

Approach.

We treat any measurements intersecting metal as missing data, and aim to design a universal orbit that can generally accommodate arbitrary metal shapes and locations. We adapted a local sampling completeness metric based on Tuy’s condition to quantify the extent of sampling in the presence of metal. A maxi-min objective over all possible metal locations was used for orbit design. A simple class of sinusoidal orbits was evaluated as a function of frequencies, maximum tilt angles, and orbital extents. Experimental implementation of these orbits were performed on an imaging bench and evaluated on two phantoms, one containing metal balls and the other containing a pedicle screw assembly for spine fixation. Metal artifact reduction (MAR) performance was compared amongst three approaches: non-circular orbits only, algorithmic correction only, and a combined approach.

Main results.

Theoretical evaluations of the objective favor sinusoidal orbits with large tilt angles and large orbital extents. Furthermore, orbits that leverage redundant azimuthal angles to sample non-redundant data have better performance, e.g. even or non-integer frequency sinusoids for a 360° acquisition. Experimental data support the trends observed in theoretical evaluations. Reconstructions using even or non-integer frequency orbits present less streaking artifacts and background details with finer resolution, even when multiple metal objects are present and even in the absence of MAR algorithms. The combined approach of non-circular orbits and MAR algorithm yields the best performance. The observed trend in image quality is supported by quantitative measures of sampling and severity of streaking artifact.

Significance.

This work demonstrates that sinusoidal orbits are generally robust against metal artifacts and can provide an avenue for improved image quality in interventional imaging.

1. Introduction

Metal artifacts are a persistent problem in CT and cone-beam CT (CBCT). In image-guided interventional procedures, such artifacts are especially prevalent due to the presence of surgical hardware, embolization materials, fixation devices, etc. Projection data from x-rays passing through metal exhibit beam hardening and/or photon starvation, which results in biased and/or noisy measurements leading to bright and dark streaks in tomographic reconstructions. These artifacts are exacerbated when the metallic component is large or when multiple metal objects are present, often completely obliterating anatomical details in surrounding regions of interest(ROI).

Numerous algorithmic solutions have been proposed for metal artifact ‘correction,’ most aiming at alleviating the appearance of streaks (Mouton et al 2013, Gjesteby et al 2016, Katsura et al 2018, Wellenberg et al 2018, Khodarahmi et al 2019). A major category of algorithms attempt to replace projection data contaminated by metal—i.e. inpainting, based on interpolation using neighbouring measurement data and/or estimates using prior knowledge of the anatomy. Such methods can effectively mitigate streaking artifacts and lead to visually pleasing reconstructions. However, anatomical information occluded by metal is inherently missing and usually cannot be recovered by algorithmic approaches alone. More specifically, when projection data through metal suffer from severe beam hardening and photon starvation, any frequency content sampled by those views will be misrepresented or missing from the affected ROIs in the reconstruction.

Modern robotic c-arms in interventional suites are increasingly equipped with capabilities for flexible acquisition geometries around the patient. Although primarily intended for fluoroscopy, such capabilities can be leveraged for volumetric imaging as well. In this work, we propose to fundamentally solve the metal artifact problem by designing non-circular orbits such that data missing in any view can be compensated for in other views. We reformulate metal artifact as a sampling problem and treat any x-rays passing through metal as missing data. Using this approach, if an orbit can completely sample an object in the presence of metal, the reconstruction will effectively be metal-artifact-free. We thus draw parallels between metal artifact and well-known missing data problems such as the null-cone in cone beam CT (i.e. cone-beam artifacts), which allows us to leverage established theory of data completeness (Tuy 1983, Smith 1985) for orbit design and optimization.

There has been a long history of investigations into the effect of orbits on data completeness. Various non-circular orbits have been proposed to acquire complete data and eliminate cone-beam artifacts in a large volume. Example orbits include orthogonal circles (Tuy 1983), helix (Katsevich 2002), circle and line (Zeng and Gullberg 1992), and saddle (Pack and Noo 2005) trajectories.

More recently, the advent of robotic imaging systems considerably increased the range of achievable orbits for CBCT scanners. Furthermore, the improvement in reconstruction speed for model-based methods also allowed investigation of wider classes of orbits which may not be amenable to existing analytic reconstruction methods. This increased flexibility in orbit selection has motivated a body of work on designing and optimizing orbits for various imaging scenarios and image quality goals. The authors previously proposed an orbit design method that relies on a prior scan of the patient and prior knowledge of metal placement to maximize detectability index of a pre-specified binary signal detection task around metal (Stayman and Siewerdsen 2012, Stayman et al 2019). Using detectability as a performance metric, orbits were optimized either view-by-view using a greedy approach (i.e. choosing the next best view) or parameterized as a linear combination of periodic basis functions the coefficients of which are obtained using an optimizer. A similar approach was adopted for industrial CT where a prior image based on a CAD model of the object was used for object-specific designs (Fischer et al 2016). Several other groups have investigated designs using different objective functions (e.g. point spread function, Tuy completeness metric, etc.) and orbit specifications (e.g. arcs accounting for kinematic constraints, limited number of projections, etc.) (Hatamikia et al 2020, Herl et al 2020, Bauer et al 2021, Hatamikia et al 2021, Herl et al 2021). Thies et al proposed a greedy, online design approach that does not require prior knowledge of the patient anatomy. Rather, the next best view was selected based on detectability index predicted from a deep learning model (Thies et al 2020). Two previous investigations have specifically sought non-circular orbits for metal artifact avoidance. Herl et al used a local data completeness metric to avoid highly attenuating views (Herl et al 2020). Wu et al proposed a spectral shift metric that measures the difference between monoenergtic and polyenergetic projections of pre-identified metal objects (Wu et al 2020).

All of the investigations cited in the previous paragraph rely on prior knowledge of at least one of the following: an attenuation map of the object, the location and shape of the metal component, the region of interest, and the imaging task. While bigger gains in image quality are theoretically possible with such patient-specific, task-specific designs, implementing different orbits for individual patients poses significant logistic challenges in the clinic in terms of calibration and quality assurance. In addition, prior knowledge of the patient anatomy and exact shape/location of the metal (e.g. from pre-operative planning data) may not be available or may be different from actual placement during the procedure. Furthermore, in the case of metal artifacts, the dominant source of photon starvation and beam hardening is attributed to metal rather than patient anatomy. Because of these reasons, we aim to investigate feasibility of a ‘universal’ orbit, where a single orbit can mitigate artifact from metal components of general shapes and at different locations within the object. Preliminary results for this investigation can be found in Gang et al (2020a, 2020b). This manuscript presents detailed orbit design methods, additional results and analysis, and more in-depth discussions. While the focus of this work is on orbit design, we included performance comparisons with an example metal artifact reduction (MAR) algorithm.(Kalender et al 1987) The extent of MAR is compared amongst three categories of methods: non-circular orbits only, MAR algorithm only, and a combined non-circular orbit and algorithm approach.

2. Theoretical methods

2.1. Design principle

In this work, we treat data intersecting metal as missing data. That is, any measurements containing metal are assumed to carry no information and not considered to be sampled. Under this paradigm, any location in the image volume that is completely sampled should be free of metal artifact. If an orbit can be found such that complete data can be collected for all locations of interest in the presence of metal, one can effectively eliminate metal artifact.

The design principle is illustrated in a toy problem in figure 1(a) where we wish to image line pair objects in the presence of a metal ball at the isocenter. For simplicity, we assume a parallel beam geometry and consider two line pairs objects at locations $l_1$ (in-plane with the metal ball) and $l_2$ (out of plane with the metal ball). Using a circular orbit in-plane, rays parallel to the line pair pattern at $l_1$ are blocked by the metal ball; i.e. the Radon plane corresponding to the frequency of the line pairs is not sampled and the line pair pattern would therefore not be visible in the reconstruction. We may tilt the orbit such that line pair at $l_1$ is out of plane with the metal and is thus fully sampled. However, line pair at $l_2$ is now occluded by the metal. To sample both line pairs, we may collect non-redundant data using a ‘folded’ orbit consisting of half of each of the previous two circular orbits such that each half samples a different line pair. The goal of this work is to extend the two location problem to every reasonable location in the image and to identify orbits such that all these locations are completely sampled.

Figure 1.

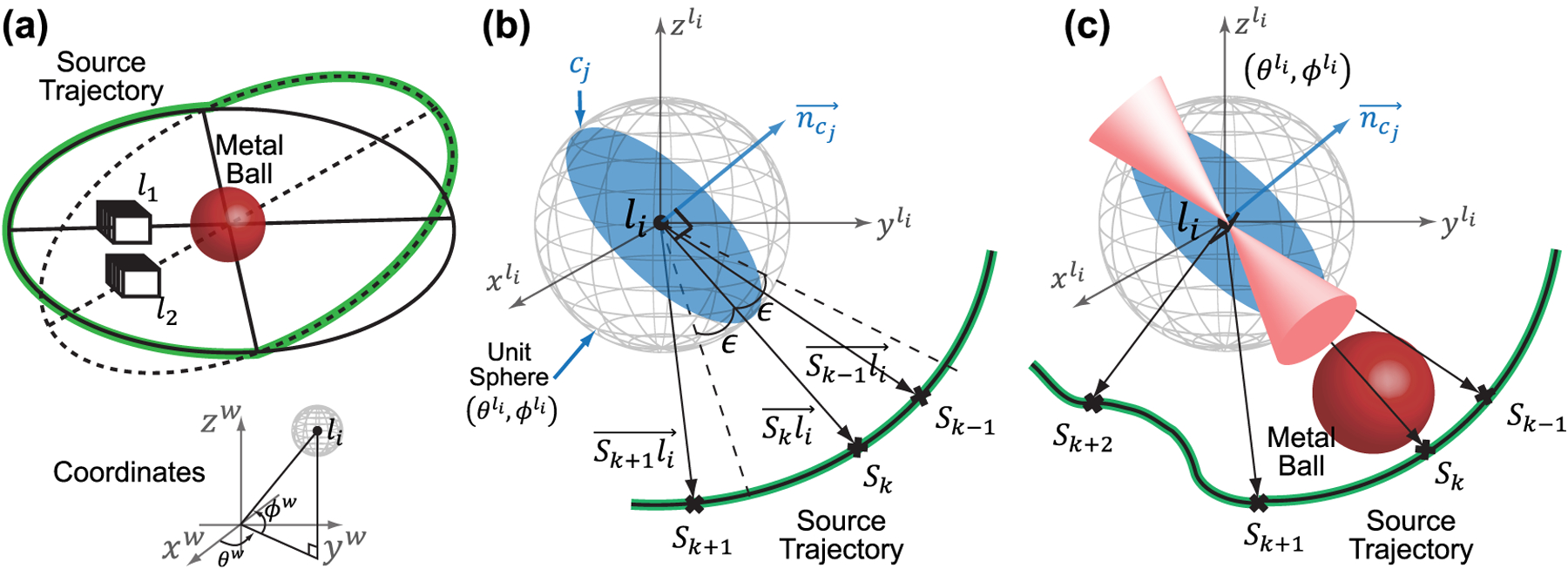
(a) The design principle is illustrated in a toy problem containing a metal ball and two line pairs at locations $l_1$ and $l_2$. Assuming a parallel beam geometry, it is possible to completely eliminate metal artifact at these two locations using a ‘folded’ orbit with source trajectory indicated in green. The world coordinate system (superscript $w$) in both Cartesian and polar are shown. (b) Illustration of an example plane, $c_j$, through a location, $l_i$, being sampled by two source positions $S_k$ and $S_{k-1}$. (c) Sampling of $c_j$ in the presence of a metal ball. Both $S_k$ and $S_{k-1}$ are occluded by metal and no long contribute to sampling. However, one can design orbits such that another source position, e.g. $S_{k+2}$, still samples $c_j$.

2.2. Data completeness in the presence of metal

To design orbits following the above principle, we first need a quantitative metric to describe data completeness in the presence of metal. Quantitation methods for data completeness has been extensively investigated in previous work (Metzler et al 2003, Liu et al 2012, Sun et al 2014, Clackdoyle and Noo 2019). Here, we adopt Tuy’s condition (Tuy 1983) in a local context and quantify a voxel-wise completeness criterion using the sampling completeness metric proposed by Metzler et al (2003). Briefly, the local Tuy’s condition states that a single voxel in the image is considered completely sampled if all planes passing through it (or equivalently, great circles on the Orlov sphere of that voxel) intersect the orbit. The sampling completeness metric, denoted as ${\mathbb{S}}_{l_i}$ at voxel $l_i$, computes the percentage of intersecting planes.

Our method for computing ${\mathbb{S}}_{l_i}$ has similarities with Sun et al (2014) and Liu et al (2012). Through an arbitrary voxel $l_i$ in the image volume, we discretely sampled an ensemble of planes, each denoted $c_j$ with unit normal $\overrightarrow{n_{c_i}}$. Figure 1(b) shows one example plane and its unit normal through an example location $l_i$. The planes are selected such that their unit normals intersect a unit sphere centered at $l_i$ (with local spherical coordinates denoted as $\left({\theta }^{l_i},{\varphi }^{l_i}\right)$) at points that approximate uniform sampling of the unit sphere (Deserno 2004). In this work, we sampled ${\varphi }^{l_i}$ from 0° to 90° at 1° increment, and evenly distributed ${\theta }^{l_i}$ between 0° and 360° at $1^{°}/\text{cos}\left({\varphi }^{l_i}\right)$ increment—i.e. the increment between adjacent ${\theta }^{l_i}\mathrm{s}$ is 1° at the equator $\left({\varphi }^{l_i}=0^{°}\right)$ and progressively increasing towards the poles. A total of 20 620 planes were sampled at each voxel.

A particular source position, $S_k$, is considered to intersect the plane $c_j$ if the vector connecting $S_k$ and $l_i,\overrightarrow{S_k{l}_i}$, is perpendicular to $\overrightarrow{n_{c_j}}$. To account for discrete sampling of both the planes and source positions, we allow a small tolerance angle, $ϵ$, and consider $S_k$ and $c_j$ to intersect if the aforementioned angle is within ${90}^{°}\pm ϵ$. In this work, we chose $ϵ$ to be 1°. The sampling completeness metric, ${\mathbb{S}}_{l_i}$, is equal to the percentage of total planes that intersects any source positions in an orbit. In figure 1(b), $\overrightarrow{S_k{l}_i}$ is at 90° to $\overrightarrow{n_{c_j}}$ and therefore intersects $c_j;\overrightarrow{S_{k-1}{l}_i}$ is considered to intersect $c_j$ due to the tolerance angle $ϵ$, while $\overrightarrow{S_{k+1}{l}_i}$ does not intersect $c_j$. The plane $c_j$ intersects the orbit and hence counts towards the sampling completeness percentage. Note that each source position can intersect many planes through $l_i$.

In the presence of metal, we modify the ${\mathbb{S}}_{l_i}$ metric such that any planes sampled by source positions intersecting metal no longer count towards sampling. As illustrated in figure 1(c), the presence of a metal ball occludes any vectors falling within the red cones from intersecting planes through the location $l_i$, e.g. $S_k$ and $S_{k-1}$ now no longer sample $c_j$. However, $c_j$ can still contribute to ${\mathbb{S}}_{l_i}$ if another source position intersects the plane, e.g. $S_{k+2}$. The range of source positions masked by metal is dependent on the shape and size of the metal, as well as the relative distance of the metal to $l_i$. For general metal shapes, these source positions can be identified through intersections between forward projections of the metal objects and $l_i$. If we can approximate the shape of the metal by spheres or ellipsoids, we may simplify computation by analytically computing their projections on to the unit sphere surrounding $l_i$. Specifically for spherical metal objects, defining all terms in local spherical coordinates $\left({\theta }^{l_i},{\varphi }^{l_i},r^{l_i}\right)$, the range of discounted source positions can be approximated by two anti-symmetric elliptical masks according to distortions of spheres under an equirectangular projection (Snyder 1982). For a metal sphere of radius $r$ and centered at $\left({\theta }_{l_i}^m,{\varphi }_{l_i}^m,r^m\right)$, the centers of the elliptical masks are simply $\left({\theta }_{l_i}^m,{\varphi }_{l_i}^m\right)$ and $\left({\theta }_{l_i}^m+{180}^{°},-{\varphi }_{l_i}^m\right)$, with major and minor axes given by:

$$d_{\varphi }=\text{arcsin}\left(r/r^m\right),d_{\theta }=\frac{\text{arcsin}\left(r/r^m\right)}{\text{cos}\left({\varphi }_{l_i}^m\right)}.$$ (1)

The masks at six example locations around a metal ball are illustrated in figure 2. Any planes intersected by source positions falling within the masks are no longer counted towards ${\mathbb{S}}_l$.

Figure 2.

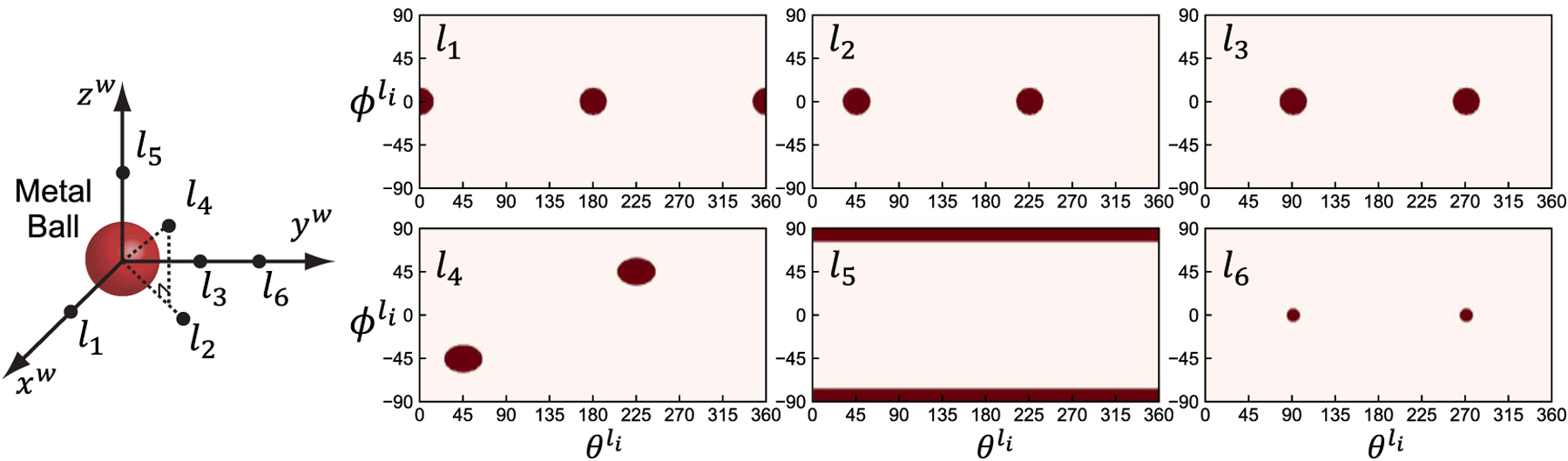
Assuming the presence of a metal ball at isocenter (red), local regions of $\left({\theta }^{l_i},{\varphi }^{l_i}\right)$ occluded by metal is shown for six relative locations in red masks. Source positions falling within the red masks do not contribute to the sampling completeness percentage.

2.3. Orbit design

The sampling completeness metric developed in section 2.2 forms the basis for an objective function which can be used for metal-tolerant orbit designs. By maximizing $\mathbb{S}$ at locations of interest in the presence of metal, one can minimize or even eliminate metal artifacts if the orbit achieves 100% completeness. The design process can be adapted based on the specific imaging scenario and design requirements. For example, if prior information of the patient (including location and shape of metal components) is available, one can perform a patient-specific design using optimization approaches similar to previous works by simply replacing the objective function (Stayman et al 2019). When prior information about the patient anatomy or metal objects are not available, and/or when patient-specific orbits are not realistic due to logistic concerns (e.g. calibration, quality assurance), it is desirable to have a universal orbit that is robust against arbitrary metal shapes and locations within the patient. Intuitively, such an orbit should provide maximal sampling in the allowable $\left({\theta }^w,{\varphi }^w\right)$ space. For example, the space filling orbit proposed in Kingston et al (2018), which consists of regularly spaced source positions at intervals satisfying the Crowther criterion, should be the most robust against arbitrary metal shapes and locations. However, such orbits are often impractical for medical imaging applications due to acquisition speed, radiation dose concerns, and limited achievable source positions due to mechanical constraints of the imaging system and/or other equipment in the operating room. Therefore, we focus on designs that can be accomplished in a continuous acquisition, under dose constraints specified by the total number of projections. Furthermore, we assume that the isocenter, source-to-axis distance (SAD), and source-to-detector distance (SDD) are fixed, and define the orbit in terms of a discrete set of source positions designated by pairs of rotation angle $\left({\theta }^w\right)$ and elevation angle $\left({\varphi }^w\right)$.

2.3.1. Imaging phantom and design objective

For this investigation, we assume the metal object is smaller than or equal to an 18 mm diameter ball. We further assume that it may appear anywhere within a central cylindrical field of view (FOV) with radius of 17 cm and height of 10 cm. For optimization purposes, we sampled an ensemble of potential metal locations along a rectangle grid at 2.5 cm interval along each dimension within the FOV. Note that only a single metal location is considered at a time. A total of 185 metal locations are sampled as illustrated in figure 3(a).

Figure 3.

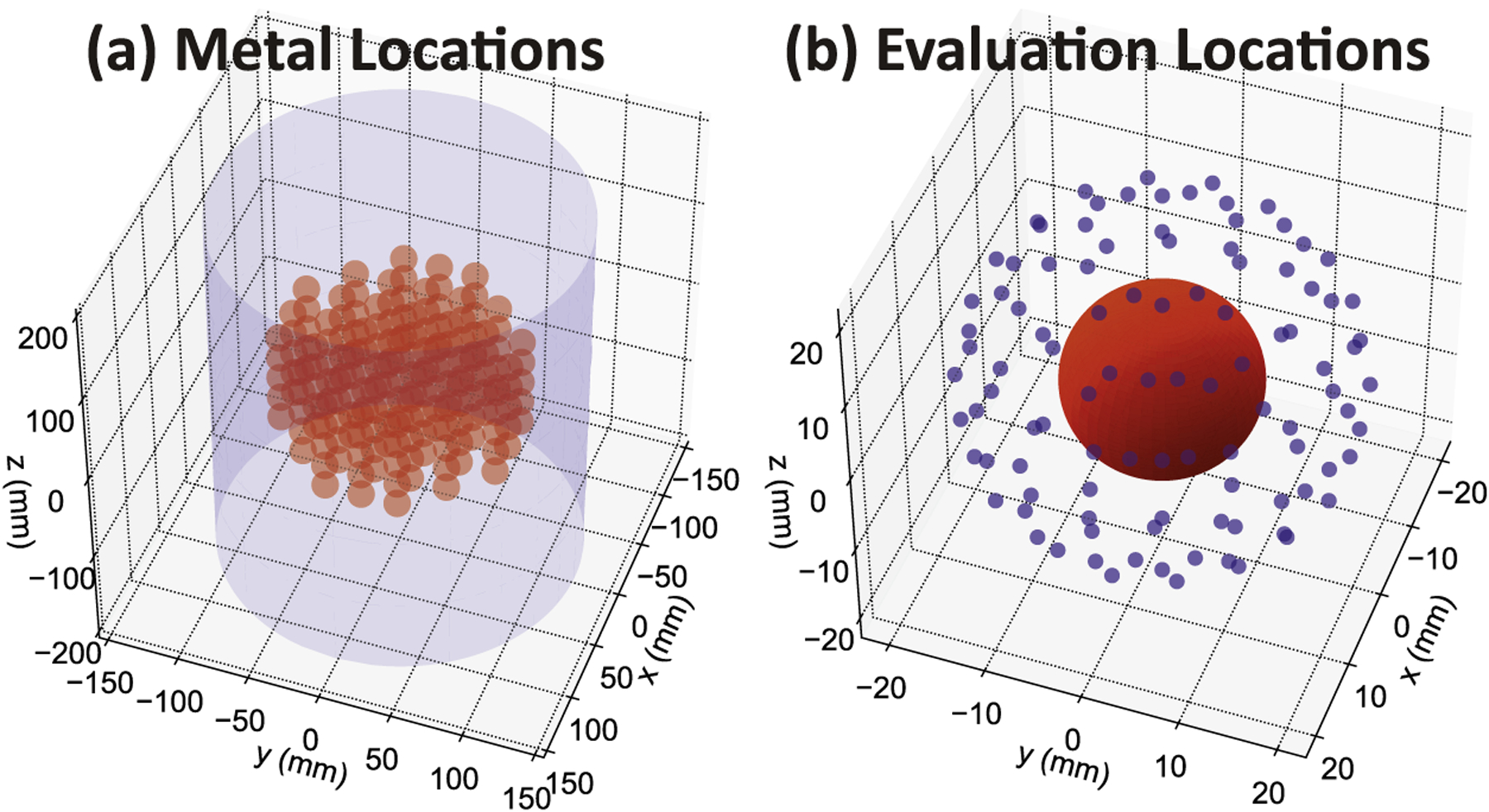
(a) The ensemble of potential metal locations used for optimization. Note that only a single metal location is considered at a time. (b) The evaluation locations around each metal location where the sampling completeness metric, $\mathbb{S}$, is computed.

For each metal location, we would ideally compute and maximize sampling completeness at every other location within the image. However, such evaluations are computationally expensive. Furthermore, locations most susceptible to metal artifacts are those close to the metal object. Therefore, for each metal location, we only computed the sampling completeness metric for an ensemble of evaluation locations distributed along a spherical shell 1 cm away from the metal surface. We did not explicitly consider locations even closer to the metal surface since, intuitively, the closer the locations are to metal, the higher the source tilt angle has to be in order to avoid the metal. The evaluation locations are chosen to approximate equal sampling on a sphere, similar to the method used to sample planes through a voxel in section 2.2 (Deserno 2004). We chose 20 equidistributed $\theta$ on the equator between $\left[\mathrm{0,2}\pi \right)$, and 11 equidistributed $\varphi$ between $[-\pi /2,\pi /2]$. A total of 102 evaluation locations were selected for each metal location.

For each orbit, $\mathbb{S}$ is computed for each metal location and its surrounding evaluation location. The objective function for orbit design was chosen to maximize the minimum $\mathbb{S}$ for all potential metal locations and all evaluations locations:

$${\text{argmax}}_{\Omega }\underset{l_m,l_e}{\mathrm{m}\mathrm{i}\mathrm{n}} {\mathbb{S}}_{l_e;l_m}\left(\Omega \right),$$ (2)

where $\Omega$ denotes an orbit, detailed in the next section. The subscript $l_e;l_m$ denotes the evaluation location, $l_e$, around a corresponding metal location, $l_m$, where $\mathbb{S}$ is computed. Such a performance criterion tends to enforce a high, but uniform level of sampling across evaluation locations and metal positions.

2.3.2. Sinusoidal orbits

Optimization adopted in previous work (Stayman et al 2019) relied on finding the coefficients for a low dimensional parameterization of orbits (e.g. using sinusoidal basis functions, local Gaussian basis functions, splines, etc.). We performed initial investigations using such optimization methods and found that there are a large number of orbits that can achieve a similar level of sampling completeness (Gang et al 2020b). While it is possible to narrow down the classes of orbits by imposing other constraints (e.g. fixed starting angle, maximum elevation angle, maximum velocity or acceleration etc.), we focus our investigation on simple classes of sinusoidal orbits.

We consider orbits where the elevation angle of the source, ${\varphi }^w$, varies as a sinusoidal function of a fixed set of rotation angles, ${\theta }^w$:

$${\varphi }^w={\varphi }_{\text{max}}\text{sin}\left(f{\theta }^w\right),$$ (3)

where ${\varphi }_{\text{max}}$ denotes the maximum achievable elevation or tilt angle, and $f$ denotes the frequency of the sinusoid. According to the coordinate definitions in figure 1, $f=0$ corresponds to a circular orbit while $f=1$ corresponds to a tilted circular orbit at ${\varphi }_{\text{max}}$ to the $\left(x^w,y^w\right)$ plane. We evaluated the maximin objective function in equation (2) for these orbits as a function of ${\varphi }_{\text{max}}$ (from −50° to 50° at 5° increments) and $f$ (from 0.25 to 8 at 0.25 increments) to compare performance. We further evaluated two different orbital extents—${\theta }^w$ ranging from 1° to 360° and from 1° to 540°, both at 1° increments.

3. Experimental methods

3.1. Imaging phantoms

To assess performance of the designed orbits in physical experiments, we constructed two phantoms with different sets of metal objects. As shown in figure 4(a), both phantoms were housed in an acrylic cylinder of ~15 cm diameter and ~13 cm height. In the first phantom, we inserted 3/8″ diameter stainless steel metals balls surrounded by 3D printed radial line pair patterns (Peopoly Moai 200, Los Angeles, CA). The line pairs were aligned with the center of the metal balls and placed within axial planes in the image domain. The spatial frequencies corresponding to these line pairs would be the most challenging to sample due the metal artifact resulting from a circular orbit. We placed three of such structures in the central axial plane and one ~2 cm away from the central plane. In the second phantom, we placed spine fusion hardware consisting of two pairs of stainless steel pedicle screw assembly, each consisting of three screws connected by a metal rod. The central pair of screws is approximately within the central axial plane. To provide structural details around the metal objects in both phantoms, we constructed a cluttered background (Gang et al 2010) by filling the cylinder with plastic spheres of different sizes and contrasts.

Figure 4.

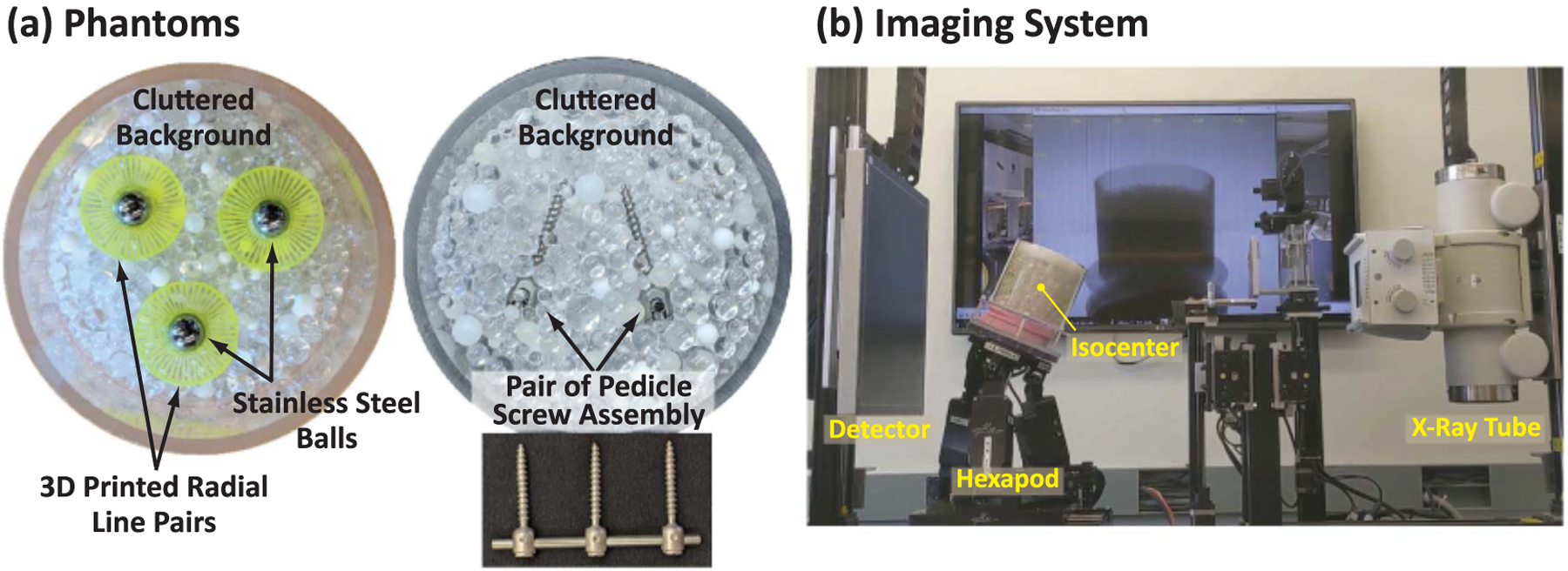
(a) Two imaging phantoms use for this study, one with metal balls and surrounding radial line pairs, one with pedicle screw pairs. Both phantoms contain cluttered background to provide structural details. (b) The imaging bench where non-circular orbits are implemented via a hexapod motion stage.

3.2. Orbit implementation on an imaging bench

Imaging experiments were performed on a CBCT imaging bench shown in figure 4(b). The bench consists of an x-ray tube (Varex Rad-94, Salt Lake City, UT), a flat-panel detector (Varex 4343CB, Salt Lake City, UT), and a hybrid hexapod stage (Alio Industries, Arvada, CO) capable of motion with six degrees of freedom. Non-circular orbits were implemented by tilting and rotating the object via the hexapod. We additionally allowed synchronous z-motion of the source and detector to simulate additional tilt. The isocenter of the orbits was fixed at the center of the phantom. With this setup, a maximum tilt angle of ${\varphi }_{\text{max}}={24}^{°}$ can be achieved. We implemented sinusoidal orbits at several frequencies with the azimuthal angle ${\theta }^w$ ranging from 1° to 360° at 1° increment. System geometry was set to a source to axis distance of 83 cm and source to detector distance of 111 cm. Data acquisitions were performed at 100 kV and 0.4 mAs for each projection.

3.3. Calibration and reconstruction

Data acquired from the imaging bench were calibrated using a 2D-3D registration method detailed in Ouadah et al (2016), where a prior image of the object was used to identify the projection matrix of each view. In this work, we segmented the metal objects from an FBP reconstruction of data acquired under a circular orbit and used the resulting metal image as the prior. The pose of the metal was found to be sufficient to identify the geometry.

To reconstruct data from non-circular orbits, we adopted a statistical modeled-based reconstruction method suitable for accommodating arbitrary acquisition geometries. Specifically, the algorithm relies on a penalized likelihood (PL) objective with a quadratic penalty:

$$\hat{\mu }={\text{argmax}}_{\mu }\left[L\right(y;\mu )-\beta R(\mu \left)\right].$$

Here, $\hat{\mu }$ is the reconstruction, $\mu$ is the image estimate, and $y$ is the measurement data. The data fidelity term, $L(y;\mu )$, describes the log-likelihood for Poisson distributed measurements. We used a quadratic penalty, $R\left(\mu \right)={\mu }^T\mathbf{R}\mu$, applied to first-order voxel neighbors in 3D. For all reconstructions of this work, the regularization strength, $\beta$, was set to 10⁴. All reconstructions were performed at an isotropic voxel size of 0.75 mm.

To highlight the effect of orbits on metal artifacts, we first performed PL reconstructions with no additional metal artifact correction. In addition, we performed reconstructions on projection data corrected by a simple MAR algorithm (Kalender et al 1987) to illustrate the combined effect of both orbits and algorithmic corrections. Briefly, the metal artifact correction was applied as follows. We first segmented the metal objects using simple thresholding (threshold = 0.055 mm⁻¹) in an uncorrected PL reconstruction. Projection data containing metal were then identified through a forward projection of the segmented metal image and replaced by linear interpolation.

3.4. Image quality assessment

We presented reconstructions to provide visual assessment of metal artifact in terms of the severity of streaks. The visibility of the radial line pair patterns provides additional visual indicators for the extent of sampling around the metal ball. To complement visual assessment, we additionally computed the sampling completeness maps as a direct measure of sampling for different metal configurations and orbits. The maps were generated by evaluating ${\mathbb{S}}_{l_i}$ along a fine rectangular grid within the phantoms followed by linear interpolation. The minimum and mean values of the maps were also computed for regions within the phantom but approximately 1 cm away from metal surfaces as measures of global performance in terms of sampling. To further support visual assessment of the severity of streaking and shading, we computed the variance of voxel values within select uniform background spheres in-plane with the three metal balls. The presence of streaking and shading artifact would result in high variance values.

4. Results

figure 5 plots the objective function values for a single metal ball in equation (2)—i.e. the minimum sampling completeness over all metal and evaluation locations as illustrated in figure 3, for sinusoidal orbits as a function of different frequencies, $f$, and maximum tilt, ${\varphi }_{\text{max}}$. The orbital extent or maximum azimuthal angle, ${\theta }_{\text{tot}}$, is 360° in (a) and 540° in (b). The objective value is the lowest when ${\varphi }_{\text{max}}=0$ for circular orbits. The values are comparable for orbits at $f=1.0$ which correspond to tilted circular orbits at different ${\varphi }_{\text{max}}\mathrm{s}$. This indicates poor completeness in the presence of metal for these two orbits. Increasing ${\varphi }_{\text{max}}$ generally results in an increase in the objective. We observe an interesting trend where even frequencies perform better than odd frequencies. This is because even frequency sinusoids can make use of azimuthal angles that are otherwise redundant to increasing sampling in the $\left({\theta }_l,{\varphi }_l\right)$ space. For example, at the isocenter, views at $\theta$ and $\theta +{180}^{°}$ are completely redundant for odd frequency orbits. Thus, any source positions occluded by metal between $\theta =1^{°}-{180}^{°}$ would remain so between $\theta ={181}^{°}-{360}^{°}$. On the other hand, most views are non-redundant for even frequency orbits. Therefore, a greater portion of $\left({\theta }^l,{\varphi }^l\right)$ would be sampled by these orbits, which increases their robustness against arbitrary metal placements. For the increased orbital extent of 540°, all integer frequencies orbits now have redundant data. Therefore, a similar reasoning as above explains improved performance of all non-integer frequencies orbits.

Figure 5.

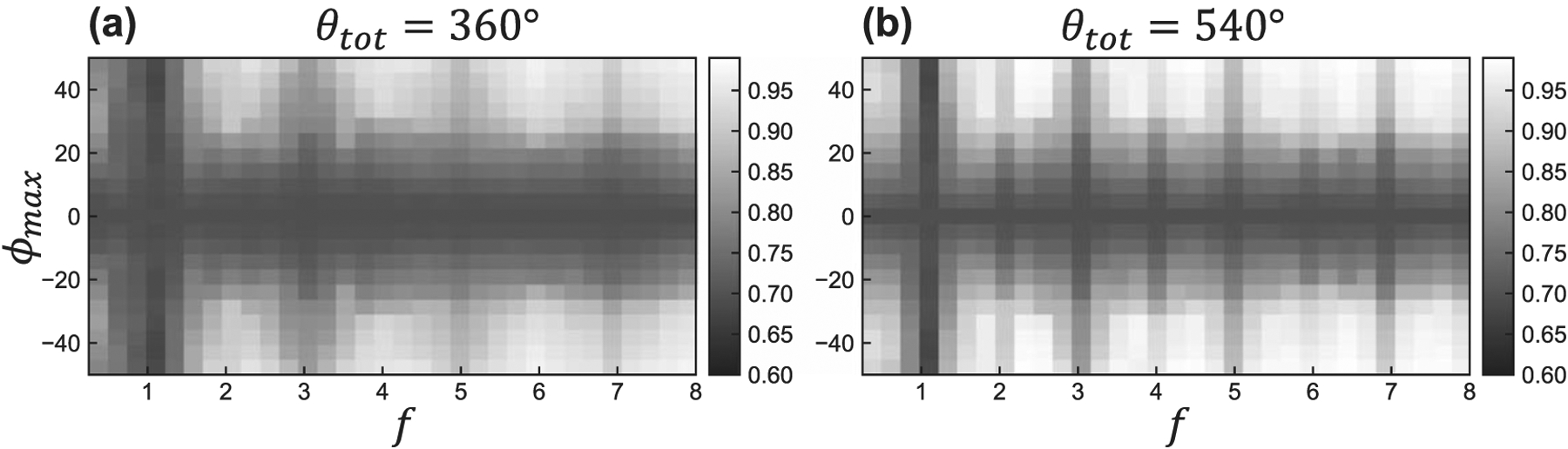
The maximin objective function values in equation (2) evaluated a function of the frequency, $f$, and maximum elevation angle, ${\varphi }_{\text{max}}$, of sinusoidal orbits. The total orbital extent is 360° for (a) and 540° for (b).

To visualize the effect of metal on sampling completeness at different spatial locations and provide additional understanding on the trends observed in figure 5, we plot the sampling completeness maps for a metal ball placed at the center of the FOV in figure 6. We selected a few example sinusoidal orbits of varying frequency, magnitude, and orbital extent $\left(\theta \right)$. When not explicitly specified, the nominal orbit parameters are: ${\varphi }_{\text{max}}={24}^{°}$, consistent with the limit on the imaging bench, and ${\theta }_{\text{tot}}={360}^{°}$. As expected, the lowest sampling completeness for all orbits occur for location immediately adjacent to the metal ball. Sampling completeness maps for the rest of the locations are determined by the particular orbits. For a circular orbit with the metal ball in-plane, the sampling completeness is the lowest at the center and slowly improves as we move away from the metal ball. For a tilted circular orbit, the locations where the scan plane bisects the central axial plane suffers from low sampling completeness but other locations have close to 100% completeness since a tilted circular orbit shifts the metal artifact out of plane. For a sinusoidal orbit with $f=2.0$, the locations that suffer from low sampling completeness occurs around redundant/overlapping rays when $\theta ={45}^{°}$ and $\theta ={135}^{°}$. This explains the trends seen in $f=3.0$ as well. When the maximum tilt ${\varphi }_{\text{max}}$ is increased to 50°, the sampling completeness improves overall, especially for locations close to the metal. When a non-integer frequency is used $(f=2.6)$ and the orbital extent is 540°, the sampling completeness map is more uniform and is approximately 100% at locations further away from the metal ball.

Figure 6.

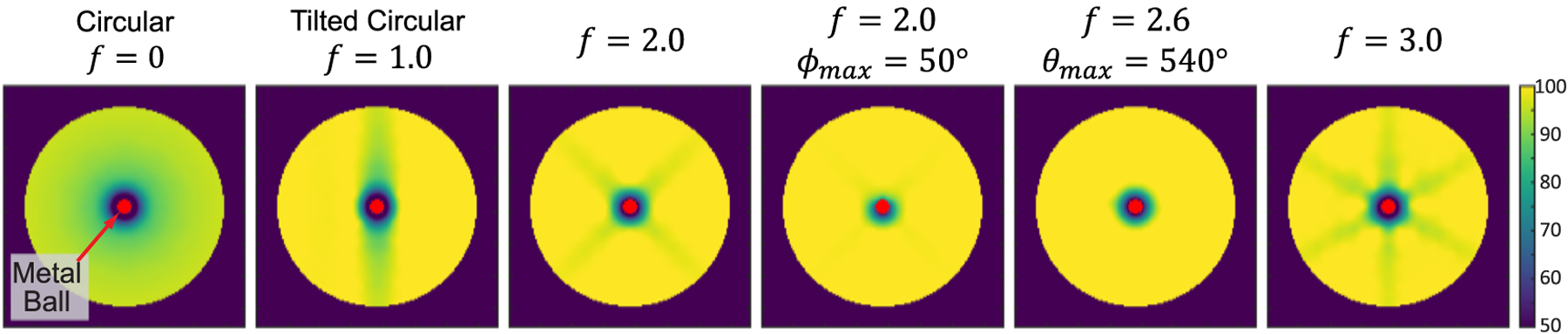
The sampling completeness maps within a cylindrical FOV when a metal ball is located at isocenter. When not explicitly mentioned in the subtitles, the nominal parameters for the sinusoidal orbits are ${\varphi }_{\text{max}}={24}^{°}$ and ${\theta }_{\text{tot}}={360}^{°}$.

Reconstructions for different frequency sinusoidal orbits for the metal ball phantom are shown in figures 7 and 8. Figure 7 shows an axial slice of the reconstruction containing a single metal ball approximately 2 cm away from the central axial plane. Both uncorrected and MAR reconstructions are shown, with the segmented metal mask for the latter overlaid in red. All orbits have an orbital extent ${\theta }_{\text{tot}}={360}^{°}$. Results for a circular orbit with MAR correspond to a pure algorithmic solution under conventional acquisition geometry; uncorrected reconstruction results for orbits with frequency greater than $1(f>1)$ correspond to mitigation strategies using only orbit designs; and results for non-circular orbit with MAR correspond to a combined approach. The visibility of the radial line pair patterns surrounding the metal ball serves as a visual indicator of the extent of missing sampling around the metal. Under a circular orbit, the radial line pairs are not visible all around. For the tilted circular orbit, the line pairs are not visible along one direction as the metal artifacts are tilted out-of-plane. For higher frequency sinusoids, the edges of the line pair object are variably visible depending on the sampling patterns of the sinusoids. How close to the metal we can see the line pairs is limited by the maximum tilt angle achievable on the imaging system. If we can image with a greater tilt angle (>24°), the line pairs should be visible closer to the metal, similar to the trend illustrated in the sampling completeness map in figure 6. The MAR reconstructions show the same trend-line pair regions that are not visible in the uncorrected reconstruction are not recovered by MAR. Figure 8 presents an axial slice containing three metal balls and a sagittal slice. In the uncorrected circular orbit reconstruction, bright and dark streaks typical of metal artifacts can be observed between adjacent metal objects. The circular orbit reconstruction with MAR, corresponding to a pure algorithmic solution using conventional acquisition geometry, are effective in eliminating the streaks but have difficulty resolving the radial line pairs and the spheres in the background. The streaking artifacts for the tilted circular orbit only occur for two metal balls that are both in the tilted scan plane. The higher frequency sinusoids perform better both in terms of mitigated streaking artifacts, visibility of the radial line pairs, and the resolution of the background spheres. As a quantitative measure of the severity of streaking artifacts, the variance of voxel values inside the purple mask (shown in the Circular, Uncorrected axial reconstruction) from left to right is: 2.86 × 10⁻⁵, 1.07 × 10⁻⁵, 7.00 × 10⁻⁶, 5.65 × 10⁻⁶, and 4.32 × 10⁻⁶ mm⁻². Consistent with visual assessment, such variance measure is dominated by dark bands in the circular and tilted circular orbits, and gradually improves for sinusoidal orbits. Furthermore, we present the sampling completeness maps for the same axial slice under different orbits as a direct measure of sampling. The observed trend of image quality is supported by the completeness maps, where lower percentages correspond to regions with more severe artifacts. We further computed the minimum and mean sampling completeness percentages over the axial slice within the phantom but sans circular areas within $1\mathrm{c}\mathrm{m}$ away from the metal surface (as indicated by the black dotted circles). The minimum sampling completeness percentages from left to right are: 44.1%, 59.7%, 66.6%, 62.6%, and 76.0%; the mean percentages are: 76.5%, 90.7%, 95.6%, 91.3%, and 96.6%.

Figure 7.

Reconstruction of the metal ball phantom. An axial slice through a single metal ball is shown for a circular, a tilted circular, and higher frequency sinusoidal orbits. Reconstructions are shown for both data with (labeled ‘MAR’) and without metal (labeled ‘Uncorrected’) artifact correction. The segmented mask containing metal is overlaid in the former in red.

Figure 8.

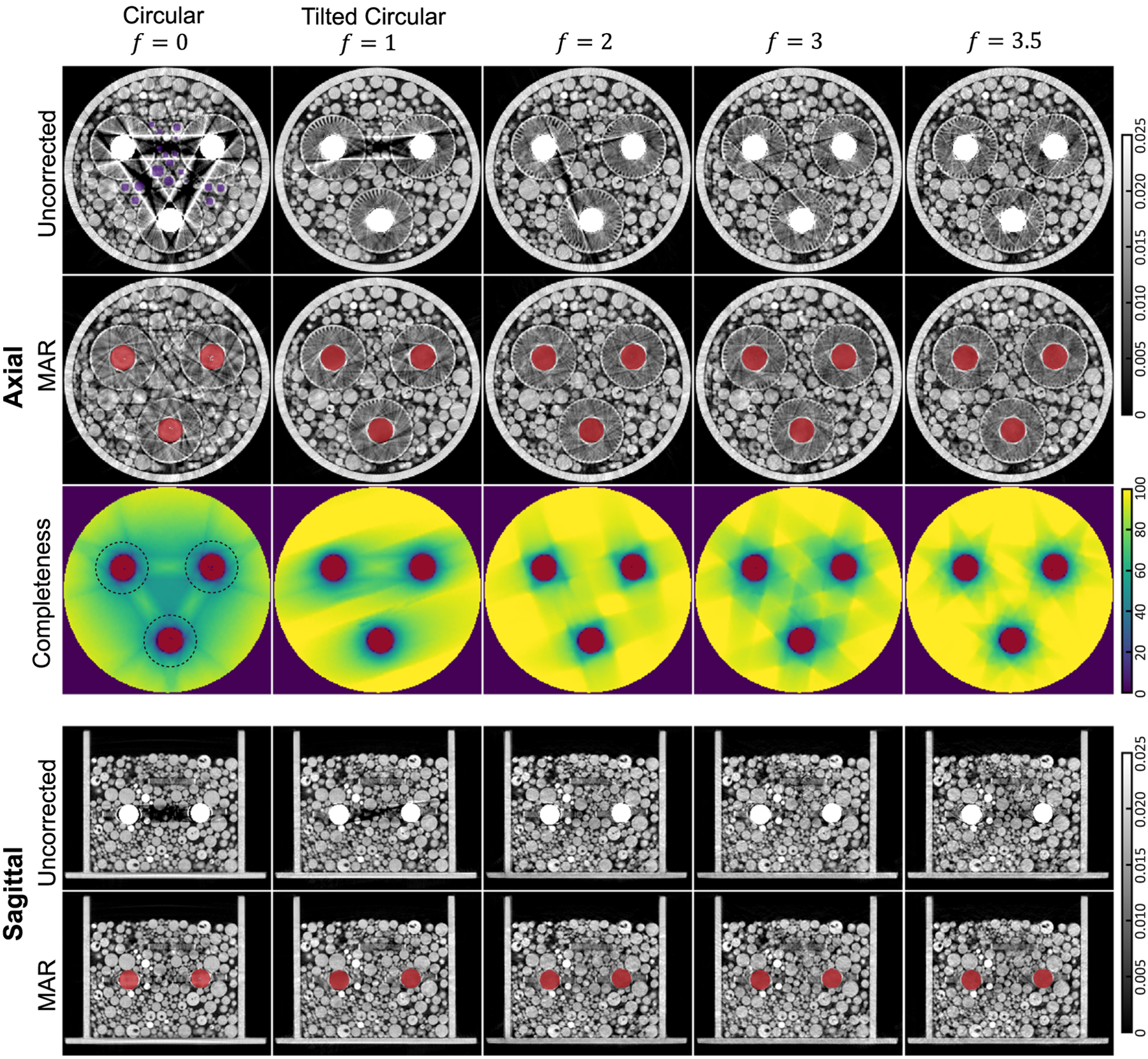
Reconstruction of the metal ball phantom for different orbits with and without metal artifact correction. An axial slice containing three metal balls and the corresponding sampling completeness map are shown for each orbit. A sagittal slice through two metal balls is also presented.

Among the different higher frequency sinusoids, the performance is dependent on the ROI due to different spatial sampling patterns, as observed in both the reconstructions and the completeness maps. Though the even frequency orbit $f=2$ outperforms the odd frequency orbit $f=3$ in terms of improved sampling completeness percentages over a larger area, both exhibit residual artifacts in the uncorrected reconstructions. Consistent with results for the single metal ball case (figure 5), orbits that leverage redundant azimuthal angles to increase sampling $(f=2.0,f=3.5)$ are more robust to metal artifacts, even when multiple metal objects are present. The $f=3.5$ orbit, especially, results in visible line pairs in almost all directions around all three metal balls in the uncorrected reconstruction. These trends are reflected in the minimum and mean sampling completeness percentages as well. We note that visibility of the line pairs is worse in the MAR reconstruction due to inconsistent data resulting from the interpolation process. In addition to metal artifacts, the circular orbit exhibit cone-beam artifacts evident as blurry edges across base of the phantom (evident in the sagittal images). Such artifact is improved for all other orbits. Figure 9 shows slices from reconstructions of the pedicle screw phantom—an axial slice through the middle screw pair, and a sagittal slice through the screw heads and metal rods. Similar trends in image quality are observed compared to figure 8, where both the screw boundary and background structures are obscured for a circular orbit. A tilted circular orbit shifts artifact out-of-plane, while the higher frequency sinusoids are better at reconstructing structures between the screw pairs. For this metal object, both the $f=2$ and $f=3.33$ orbits are fairly robust against metal artifacts, as seen from both reduced streaking artifact and improved sampling completeness maps. Similar to the metal ball base, we computed the minimum and mean of the sampling completeness maps for areas within the object at approximately 1 cm away from the metal surface (indicated by the black outline). From left to right, the minimum percentages are: 12.3%, 37.4%, 52.9%, 45.4%, 64.9%; the mean is 62.4%, 88.9%, 94.1%, 90.1%, 93.8%. Again, performance trends from visual assessment are supported by the numbers with $f=2$ and $f=3.3$ outperforming the rest. Note that the highest frequency sinusoid is slightly different from figure 8 $(f=3.33$ versus $f=3.5)$. The performance of both orbits should be comparable.

Figure 9.

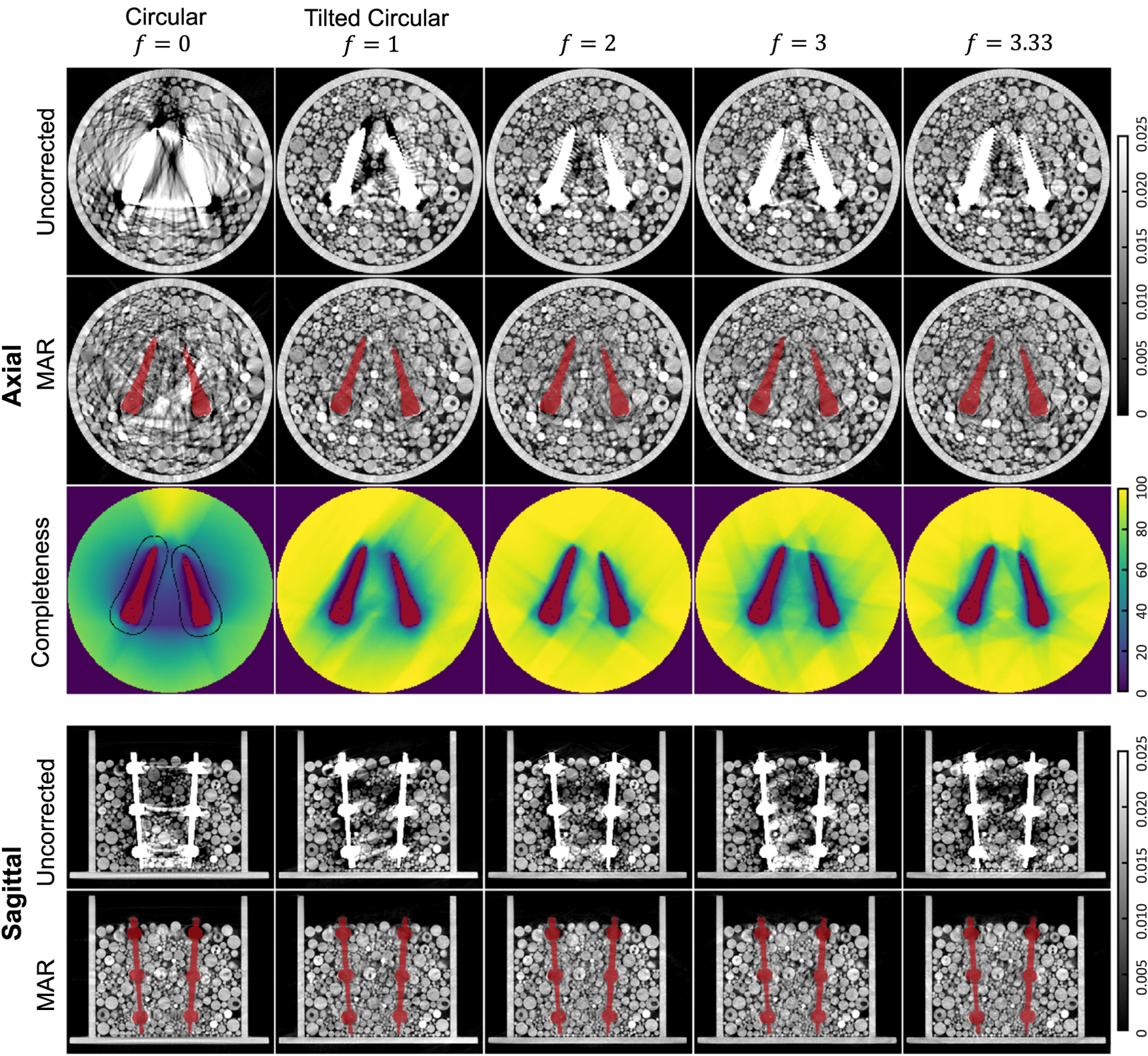
Reconstruction of the pedicle screw phantom for different orbits with and without metal artifact correction. The axial slice contains the middle screw pair and the sagittal slice contains the screw heads and metal rods. The sampling completeness maps for the axial slice are also presented for each orbit.

From figures 8 and 9, we observe image quality improvements with sinusoidal orbits for the cases of three metal balls and pedicle screws. Results from both phantoms indicate that a pure algorithmic solution relying only on MAR performs poorly, especially for challenging cases with multiple metal objects in the same axial slice. Mitigation strategies relying only on orbit designs are able to significantly reduce metal artifacts but still have residual streaks and shading when it is not possible to achieve 100% sampling completeness at all locations. Results combining both orbit designs and MAR exhibit the best performance with little to no shading or streaking. Consistent with trends observed in figure 5, even frequencies and non-integer frequencies perform better than odd frequencies due to reduced redundancy resulting in improved sampling.

5. Discussion and conclusion

In this work, we presented orbit designs for MAR. Distinct from previous work, we focus on general, universal orbits that can be applied to arbitrary anatomy and metal configurations. We treated data intersecting metal as missing, and used a classic metric of data completeness in an objective function for orbit design. We found that when considering arbitrary anatomy and metal configurations, there exist many designs that can achieve similar levels of data completeness. We therefore focused on simple sinusoidal orbits and investigated the effect of frequency, maximum tilt angle, and orbital extent on imaging performance. These sinusoidal orbits were implemented on an experimental test bench with phantoms containing different metal objects. Higher frequency and higher maximum tilt angles were found to improve data completeness in the presence of metal. In particular, orbits that have less redundant rays—e.g. orbits capable of leveraging redundant azimuthal angles to sample a different part of the $\left({\theta }_l,{\varphi }_l\right)$ space are found to be more robust against metal artifacts.

The simple sinusoidal orbits investigated in this paper should be relatively easy to implement on clinical robotic C-arms Since these orbits are tolerant to metal artifacts regardless of the position of the metal, they can be thought of as universal and applied in general circumstances when metal is expected to be present. Such fixed orbits can be individually calibrated and present less challenges for clinical translation than orbits designed for a specific patient or metal implant scenario.

While the work presented here shows the potential benefits of designed non-circular orbits, there are many ways in which it can be refined. For example, the sinusoidal orbits were parameterized using evenly spaced $\theta$ values. For high frequency sinusoids, even sampling in $\theta$ that can result in unequal arc lengths between adjacent views. Sinusoidal orbits with equally spaced arcs may be more desirable. Other orbital parameterizations and constraints can likely achieve similar levels of performance as well but may have other advantages in an interventional suite (e.g. avoiding obstacles, accounting for device motion limitations, and or velocity and acceleration limits).

The proposed design metric based on completeness can also be modified. In its current form, the metric does not distinguish between sampling patterns of equal completeness percentage. For example, a sampling completeness percentage of 80% where all the missing 20% are concentrated together would have a more visible undersampling artifact as compared a case where the missing planes are evenly distributed. Another drawback of the current optimization is that it optimized only for single metal object locations (though that object can be anywhere in the FOV). While we have observed a robustness in orbital design for multiple metal objects, a more sophisticated optimization could consider metal object pairs, triples, or more general classes of metal distribution.

The orbits identified using purely the sampling completeness metric favors large tilt angles, high frequency sinusoids, and large orbital extent. The solution is not surprising considering the more ‘spacing filling’ property of these orbits. While such orbits are more favorable for sampling, they may not be ideal for other image quality or patient safety considerations. For example, rays at higher tilt angles are usually highly attenuated and have higher noise; a larger orbital extent with a greater number of projections generally incurs more radiation dose. It is possible to include a noise and/or dose penalty/constraint into the design process, assuming an approximate anatomical model (e.g. an elliptic cylinder for abdominal imaging).

The above topics are subjects of ongoing and future work which could provide additional advantages and further facilitate the clinical translation of these scanning methods. While not the focus of our work, similar methods can be used to design orbits for industrial applications. Implementation on a clinical C-arm and evaluation using anthropomorphic phantoms will help establish the feasibility of non-circular orbits and their tolerance to metal artifacts in interventional imaging.