Abstract
Replica exchange with solute tempering (REST) is a highly effective variant of replica exchange for enhanced sampling in explicit solvent simulations of biomolecules. By scaling the Hamiltonian for a selected “solute” region of the system, REST effectively applies tempering only to the degrees of freedom of interest but not the rest of the system (“solvent”), allowing fewer replicas for covering the same temperature range. A key consideration of REST is how the solute-solvent interactions are scaled together with the solute-solute interactions. Here, we critically evaluate the performance of the latest REST2 protocol for sampling large-scale conformation fluctuations of intrinsically disordered proteins (IDPs). The results show that REST2 promotes artificial protein conformational collapse at high effective temperatures, which seems to be a designed feature originally to promote the sampling of reversible folding of small proteins. The collapse is particularly severe with larger IDPs, leading to replica segregation in the effective temperature space and hindering effective sampling of large-scale conformational changes. We propose that the scaling of the solute-solvent interactions can be treated as free parameters in REST, which can be tuned to control the solute conformational properties (e.g., chain expansion) at different effective temperatures and achieve more effective sampling. To this end, we derive a new REST3 protocol, where the strengths of the solute-solvent van der Waals interactions are re-calibrated to reproduce the levels of protein chain expansion at high effective temperatures. The efficiency of REST3 is examined using two IDPs with nontrivial local and long-range structural features, including the p53 N-terminal domain and the kinase inducible transactivation domain of transcription factor CREB. The results suggest that REST3 leads much more efficient temperature random walk and improved sampling efficiency, which also further reduces the number of replicas required. Nonetheless, our analysis also reveals significant challenges of relying on tempering alone for sampling large-scale conformational fluctuations of disordered proteins. It is likely that more efficient sampling protocols will require incorporating more sophisticated Hamiltonian replica exchange schemes in addition to tempering.
Introduction
Atomistic simulations of proteins in explicit solvent have greatly benefited from significant recent advances in both GPU-enabled molecular dynamics (MD) algorithms1–6, which can provide over 100-fold acceleration compared to traditional CPU-based approaches, and accurate general-purposed force fields7–12, which have been extensively rebalanced for describing folded as well as unfolded proteins. Nonetheless, direct atomistic simulations of large-scale conformational fluctuations and transitions of proteins remain extremely challenging. For example, re-analysis of a 30-μ𝑠 simulation of a relatively small 40-residue Aβ40 peptide generated using special purpose supercomputer ANTON 27, 13 revealed a surprisingly limited level of convergence at both the secondary and tertiary structure levels14. This highlights the critical need for so-called enhanced sampling techniques for generating statistically representative structural ensembles of proteins15–23. This is particularly true in studies of intrinsically disordered proteins (IDPs)24–27, an important class of proteins that rely on structural plasticity for function and need to be described using heterogeneous conformational ensembles28–32. Arguably, the functional mechanism of an IDP is encoded in how its disordered ensembles respond to various cellular stimuli and signals, such as the binding of ligands and cofactors, changes in cellular environments, and post-translational modifications32–35. There is a critical need to generate well-converged disordered ensembles of an IDP and resolve their differences in various states in order to establish the molecular basis of its function36–38.
For high-dimensional and diffusive processes such as IDP conformational fluctuations, temperature-based replica exchange (T-RE)16, 39, 40 has proven to be one of the most powerful enhanced sampling techniques in general. In T-RE, multiple copies of the system (“replicas”) are simulated in parallel at different temperatures and periodically attempt to exchange simulation temperatures according to Metropolis criteria that maintain the detailed balance. As a result, replicas can undergo random walk in the temperature space to promote barrier crossing and conformational sampling. T-RE has played an instrumental role in recent implicit and explicit solvent force field optimizations, by helping to provide converged conformational distributions of model peptides8, 41–43. An important limitation of T-RE for explicit solvent simulations is that the number of replicas required for a given temperature range scales as , where is the total number of atoms16. The number of replicas required can become prohibitive for explicit solvent simulation of even modestly sized IDPs that require very large water boxes to accommodate the conformational flexibility. Replica exchange with solute tempering (REST) is a powerful variant of T-RE designed to dramatically reduce the number of replicas required17, 44–46. The basic idea is to use Hamiltonian rescaling to achieve effective tempering, such that different regions of the system can be simulated under different effective temperatures17. This allows only the selected “solute” region (e.g., the protein) to be subjected to tempering while the rest of the system (“solvent”) is maintained at the same temperature for all replicas. As a result, only interactions related to the “solute” contribute to the Metropolis criteria of replica exchange and a much smaller number (by 3- to 10-fold) of replicas is required to cover the desired temperature range. For example, only 16 replicas were required in REST simulations of the disordered N-terminal domain of p53 (p53-NTD, residues 1–61)12, 37, 38, achieving ~25% acceptance rates from 298 to 500 K. A comparable T-RE simulation of the same solvated system (~72,000 atoms) would require over 100 replicas to ensure sufficient exchange acceptance rates (e.g., ~20%). Importantly, the solute region in REST simulations does not need to include the whole protein, allowing flexible tempering of selected protein regions of interest 46–48. REST can be further generalized to only include selected energy terms for tempering to further reduce the number of replicas required49.
Despite the great flexibility of REST in targeted tempering, how well it translates into better efficiency in sampling large scale protein conformational transitions is not always clear. Disrupting the delicate balance between protein-protein, protein-water and water-water interactions due to the re-scaling of different components of the Hamiltonian can result in elevated energy barriers and actually end up hindering the sampling50. In the improved REST2 protocol, the solute-solvent interactions were increasingly weakened at higher effective temperature conditions compared to the original protocol. As a result, the protein remains more compact at higher temperatures, which apparently could allow REST2 to generate more reversible folding transitions of beta-hairpin peptides44. In this work, we critically analyzed the efficacy of REST2 for the simulation of disordered protein conformational ensembles using two model IDPs with nontrivial local and long-range structural features. The results reveal an alarmingly strong tendency of REST2 to generate increasingly compact ensembles at higher temperatures, especially for larger and more flexible IDPs. Importantly, the overly compact conformations at high temperatures could rarely be exchanged to low temperatures, leading to the segregation of replicas and greatly reducing the efficiency of random walk in the temperature space. We propose that the scaling factors of solute-solvent van der Waals (vdW) interactions can be treated as free parameters to control the solute conformational properties at different temperatures for maximizing sampling efficiency. To this end, we design a new REST3 protocol that aims to reproduce the levels of protein chain expansion at high temperatures. The new protocol eliminates the exchange bottleneck and greatly improves the efficiency of random walk in the temperature space, realizing similar conformational convergence with a smaller number of replicas. Nonetheless, our analysis also reveals that tempering has important limitations in driving cooperative local and global conformational transitions of proteins, due to the entropic nature of the associated free energy barriers51. It is likely that more efficient sampling protocols will require incorporating more sophisticated Hamiltonian replica exchange schemes in addition to effective tempering51–55.
Methods
REST algorithm.
REST allows tempering on only a selected region of interest (e.g., “solute”) while keeping the rest of the system (e.g., “solvent”) at a single temperature. This can significantly reduce the number of DOFs that contribute to the Metropolis criteria of replica exchange, and thus a much smaller number of replicas is needed to cover the same temperature range17, 44. The energy of the whole system can be divided into three parts: the solute-solute energy , the interaction energy between solute and solvent , and the self-interaction energy between the solvent molecules . The scaled Hamiltonian at condition is then given as,
| (1) |
where denotes the system coordinates and ’s are the scaling factors of the three components. The scaling factor of solvent-solvent interactions will be kept constant (e.g., 1) at all conditions in REST. The solute-solute interaction scaling factor , on the other hand, is adjusted for each condition to achieve the desired effective temperature of , which is usually exponentially spaced between (the temperature of interest) and with total replicas,
| (2) |
Note that all replicas are simulated at the same apparent temperature of in REST. The two existing variants of REST protocols differ in how the solute-solvent energy term is scaled. The original REST protocol17 is equivalent to having:
| (3) |
where and is the Boltzmann constant. However, it has found that REST showed limited efficiency in driving large conformational transitions and led to exchange bottlenecks between low and high temperature conditions50. In the revised REST2 protocol44,
| (4) |
The geometric averaging scaling scheme for setting in REST2 weakens the solute-solvent interactions compared to the original REST protocol, and the weakening effect is maximal at condition . Note that weakening solute-solvent interactions in REST2 was intentional, for artificially maintaining more compact conformations at high temperatures to facilitate refolding and potentially drive faster reversible folding transitions of beta-hairpins and mini-proteins44. It remains unclear whether this is an optimal scaling scheme to simulate the dynamic and potentially more extended ensemble of IDPs. In this work, we propose a new REST3 protocol by introducing an additional calibration factor for vdW interactions between the solute and solvent, and more details can be found in the third session of Results and Discussion.
System setup and simulation protocols.
Two well-studied IDPs were used to evaluate the REST protocols in this work. The kinase inducible transactivation domain (KID) of transcription factor CREB includes residues 119–146 (TD SQKRR EILSR RPSYR KILND LSSDA P). p53-NTD includes residues 1–61 of p53 (MEEPQ SDPSV EPPLS QETFS DLWKL LPENN VLSPL PSQAM DDLML SPDDI EQWFT EDPGP D). The N- and C- termini were capped with acetyl and N-methyl amide groups, respectively. Both proteins have been extensively characterized by MD, NMR and other biophysical approaches12, 56–64. Unless otherwise noted, we ran two independent simulations (control and folding) for each protocol starting from two distinct conformations to evaluate simulation convergence. The control simulation was initiated from a helical state and the folding simulation from an extended state (see Figure S1). Except for the control simulations of KID, the proteins were solvated in truncated octahedron boxes, where the shortest distance between two opposite hexagons was ~10.0 nm for KID (folding, with ~25000 water molecules) and ~9.8 nm for p53-NTD (both control and folding, with ~23500 water molecules), respectively. In KID control simulations, the folded initial conformation was solvated in an ~8.5 nm cubic box using about 20000 water molecules. Na+ or Cl− ions were added to neutralize the systems. The periodic boundary conditions were utilized in all simulations, and simulation boxes were large enough to prevent the protein from significant interactions with the periodic images (e.g., see Figure S2).
All initial conformations were first energy minimized using a steepest descent algorithm for 6000 steps in GROMACS65, 66. 100 ps NVT simulations at 298 K followed by 1 ns of NPT simulations at 298 K and 1 atm were then performed with protein heavy atoms harmonically restrained with a 1000 kJ/mol/nm2 force constant. The systems were equilibrated under the same NPT condition for another 1 ns without restraints before the standard MD or REST production simulations. All new simulations in this work were carried out in the a99SB-disp protein force field7, which is arguably one of the best for simulating dynamic protein conformations12. The vdW interactions were smoothly switched off at 1.0 nm, and the long-range electrostatic interactions were treated using the particle mesh Ewald (PME) method67. The lengths of hydrogen-containing bonds were constrained using the LINCS algorithm68.
The REST2 and REST3 simulations were carried out using GROMACS65, 66 patched with PLUMED 2.3.069–71. As summarized in Table S1, a total of eight REST simulations were performed. These simulations include either 16 replicas spanning an effective temperature of 298 K to 500 K or 8 replicas spanning 298 K to 450 K. Detail configurations of all REST2 and REST3 protocols are given in Table S2. Replica exchange was attempted every 2 ps. The total lengths of simulations are 1 μ𝑠 per replica for KID and 2 μ𝑠 per replica for p53-NTD. Only folding REST3 simulations were performed for p53-NTD due to the longer simulation length. We have previously performed REST2 simulations of p53-NTD in six force fields12, where each simulation was ~ 1 μ𝑠 per replica. Here, the p53-NTD simulations in a99SB-disp with REST2 were extended to 2 μ𝑠/replica for both control and folding runs. In addition, two 500 ns standard MD simulations were performed at 500 K for p53-NTD to guide our design of the REST3 protocol.
Analysis.
Unless otherwise noted, the first 200 ns of all REST2 and REST3 simulations were excluded in subsequent analysis, which was performed using a combination of GROMACS, in-house scripts, and the MDTraj package72. The helical propensities were identified using the standard Dictionary of Secondary Structure of Proteins (DSSP) protocol73. For KID simulations, the error bars were estimated from the difference between the folding and control runs. For p53-NTD simulations, the 2 μ𝑠 folding trajectories were divided into two parts (0.9 μ𝑠 each excluding the first 200 ns) for error bars calculation. Principal component analysis (PCA) was performed using the python SciKit-learn package74 to evaluate the sampling efficiency as well as to visualize the simulated ensembles. For this, snapshots were taken every 100 ps from the entire trajectories to collect all conformations sampled at 298 K (including the first 200 ns). For each peptide, the ensembles generated from REST2 and REST3 simulations were combined and aligned using the backbone atoms before performing the PCA analysis to derive a common set of principal components. The PCA analysis was performed based on the coordinates of Cα atoms. The free energy surfaces were derived directly from the 2D probability distributions along the first two principal components (PCs). All molecular visualizations were done using VMD75.
Results and Discussion
Severe over-compaction at high temperatures in REST2
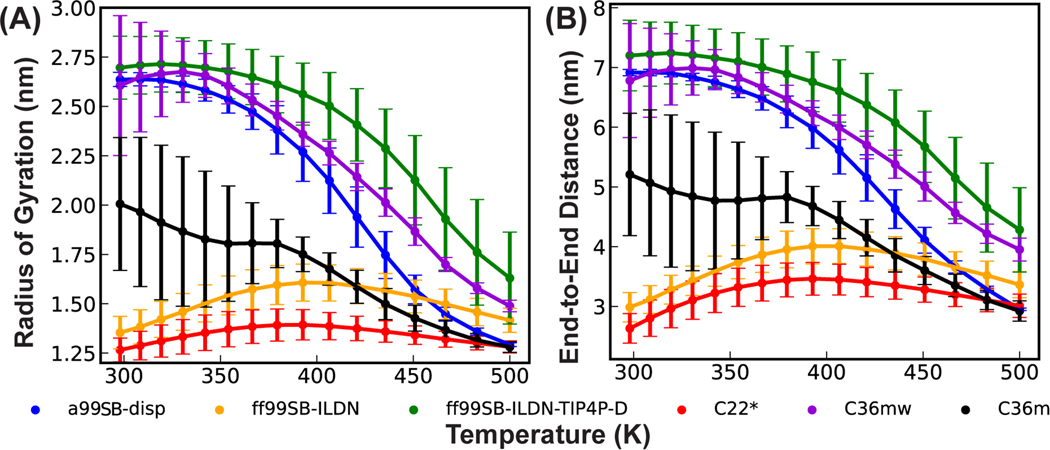
We previously utilized REST2 to evaluate the performance of six latest protein force fields for their ability to describe various local and long-range structures of p53-NTD12. These force fields include CHARMM36m (C36m)8 and its variant C36mw8, CHARMM22* (C22*)76–78, Amber ff99SB-ILDN79, 80 and ff99SB-ILDN-TIP4P-D79, 81, and a99SB-disp7. Curiously, the level of convergence depends strongly on the force field even with ~1 μs/replica simulation time. It was further found that some helical states appeared to be long-lived in C36m and C36mw in REST2, even though these states would readily unfold during standard MD at 298K within 1 μs12. The implication is that the rescaling scheme of protein-protein and protein-water interactions in REST2 may result in elevated energy barriers for helix-coil transitions. Here, we further analyze the conformational properties of p53-NTD as a function of effective temperature from these REST2 simulations in all six force fields. As summarized in Figure 1 and S2, p53-NTD adopts spuriously compact ensembles under high temperature conditions in all six force fields, leading to smaller radius of gyration and end-to-end distance. The helicity level also often increases together with an elevated level of compaction at high temperatures (e.g., in a99SB-disp, Figure S2C). Ensembles for p53-NTD at 500 K are 1.5–2 times more compact than the ensembles generated at the lowest temperature of 298 K, except for the ff99SB-ILDN and C22* that lead to severe over compaction at 298 K. Even for these two later force fields, the scaling scheme of REST2 (Eq. 4) drives further compaction above 400 K after a modest chain expansion between 298 to 400 K. Similar observations can also be made on REST2 simulation of the smaller and less flexible KID in a99SB-disp (Figure S3), demonstrating that this behavior is force field and protein independent. Interestingly, temperature-induced compaction was also observed in a previous REST2 simulation of a short model peptide Q15, but it appeared to reflect a true property of this peptide in the Amber03ws force field82.
Figure 1.
Overall protein chain expansion of p53-NTD as a function of temperature in REST2 simulations in six explicit solvent protein force fields. (A) Average radius of gyration and (B) end-to-end distance. The error bars were calculated as the differences between results from the control and folding REST2 simulations. The first 200 ns was excluded from both the control and folding runs.
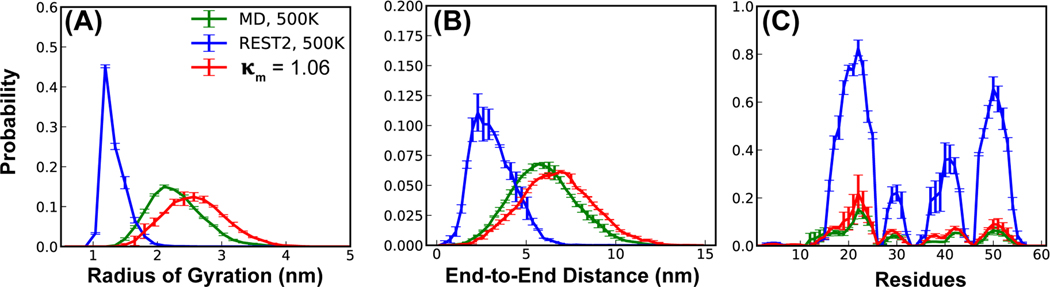
Importantly, the collapsed ensembles at high effective temperatures in REST2 are artificial. In Figure 2, we compare the REST2 ensemble in a99SB-disp at an effective temperature of 500 K to the one generated by standard MD simulations at 500 K using the unscaled force field. Clearly, the protein does not become severely compact (Figure 2A and B, blue vs green trace) or highly helical (Figure 2C, blue vs green trace) in standard 500 K MD simulations with the original unscaled Hamiltonian. These results suggest that the scaling scheme in REST2 weakens solute-solvent interactions too much compared to solute-solute interactions and that the level of imbalance becomes more severe at higher temperatures. The observation that IDPs are driven to undergo severe compaction at high effective temperatures likely contributes to the challenges of REST2 protocol in achieving convergence during 1 μs/replica simulations of p53-NTD using C36m or C36mw in the previous study12.
Figure 2.
Conformational properties of p53-NTD using unscaled (MD) and scaled Hamiltonians (as in REST2 and REST3 or = 1.06; see Table S2), including (A) radius of gyration, (B) end-to-end distance, and (C) residue helicity profile. The distributions at 500 K with the unscaled Hamiltonian were calculated from the last 400 ns of two independent 500ns runs and the error bars show the difference between these two runs. Results for REST2 and REST3 at 500 K were calculated from the last 1.8 μs of the ensembles and the error bars were estimated as the difference between the first and second 0.9 μs of these ensembles.
Over-compaction at high temperatures can lead to replica segregation in REST2
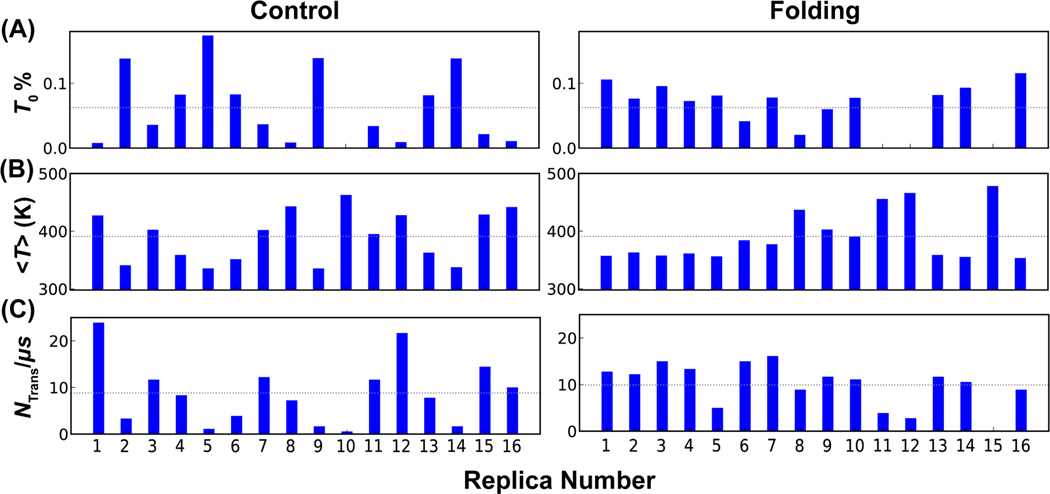
To evaluate the consequence of compaction at high temperatures, we analyzed the efficiency of replica random walk in the temperature space in both control and folding REST2 simulations of p53-NTD in a99SB-disp (Table S1). Inspection of the temperature evolution of all replicas (Figures S4 and S5) reveals substantial segregation in the temperature space. For example, several replicas including 11, 12 and 15 occupy the high temperature conditions exclusively throughout the folding REST2 simulation (Figure S5). We calculated a set of metrics to further evaluate the consequence of segregation in the temperature space, including the average occupancies at the lowest temperature, average effective temperatures and total number of round trips between the lowest and highest conditions for each replica. In an ideal replica exchange simulation, all replicas undergo efficient random walk in the temperature space and should be equivalent to each other. However, the results, summarized in Figure 3, show that all metrics are highly non-uniform for replicas in both control and folding REST2 simulations of p53-NTD. Only subsets of replicas contribute to the ensemble at 298 K and several replicas take few round trips between the lowest and highest temperature conditions. The segregation is particularly severe in the control REST2 simulation. Overall, there are only about 8.82/μs and 9.93/μs round trips per replica in the control and folding runs, respectively. Further analysis showed that inefficient temperature random walk in REST2 hampered conformational samplings, which will be discussed in the following sections. Importantly, the observed replica segregation in the temperature space is not due to inefficiency in neighboring replica exchanges; the acceptance rates are relatively uniform at ~25% in both control and folding REST2 runs. Instead, it should be attributed to the conformational trapping of replicas, particularly at high temperatures. For example, the three replicas trapped at high temperature regions in the folding REST2 simulations (11, 12 and 15) are all trapped in compact conformational states with very small radius of gyration (Figure S5, blue traces). With worse temperature mixing and strong potential bias introduced by the folded initial conformation during the control REST2 run, we will mainly focus on the analysis of folding simulations of p53-NTD in the following sessions.
Figure 3.
Efficiency of replica exchange in REST2 simulations of p53-NTD, as reflected in (A) occupancy at the lowest temperature (, 298 K), (B) average effective temperature, and (C) the number of temperature round trip per μs for each replica in control (left) and folding (right) runs. The dashed lines in A and B mark the expected values if perfect random walk occurs ( = 0.06; = 390.9 K). The dashed line in C indicates the average per μs of all 16 replicas, which is 8.82/μs and 9.93/μs in the control and folding runs, respectively.
Re-balancing the solute-solvent interactions in REST3
The artificial conformational collapse at high effective temperatures and resulting replica segregation in the temperature space are a direct consequence of the scaling scheme in the REST2 protocol (Eq. 4), which is intentional and designed to drive more reversible folding transitions of mini-proteins and beta-hairpins. This limitation may thus be addressed by re-balancing of solute-solvent and solute-solute interactions in the REST protocol (Eq. 1). In particular, we propose that the scaling of the solute-solvent interactions in REST does not need to follow prescribed mixing rules such as Eq. 2 and Eq. 3. Instead, may be treated as free parameters that can be carefully tuned to control the solute conformational properties (e.g., chain expansion) at different effective temperatures for more efficient sampling. We note that scaling of solute-solute electrostatic interactions is achieved by scaling of all solute partial charges, such that the use of PME requires the solute-solvent electrostatic interactions to follow the geometric mixing rule of Eq. 3. However, the solute-solvent van der Waals (vdW) interactions could be independently tuned. As such, we recast Eq. 1 in REST3 as,
| (5) |
where is the additional scaling factor for the solute-solvent vdW interactions at condition . Setting = 1 for all conditions recovers the REST2 protocol.
As a proof of concept, we recalibrated the solute-solvent relative interaction strength by matching the conformational properties of p53-NTD at high temperatures, where the artificial compaction is particularly severe in REST2 simulations (Figures S2, S3, and 4).The results show that a modest increase in the solute-solvent vdW interactions with = 1.06 is sufficient to largely recover both local and global structural properties of p53-NTD at 500 K (Figure 2), as compared to results from standard MD using the original unscaled s99SB-disp force field. Based on this, we simply use a linear relationship to set for other conditions in REST3,
Note that = 1 for the first four conditions, because the artificial collapse of p53-NTD appears to be minimal at low effective temperatures (see Figure 1). Detailed values of all scaling factors of the REST3 protocol tested below can be found in Table S2.
REST3 eliminates conformational trapping at high temperatures and replica segregation
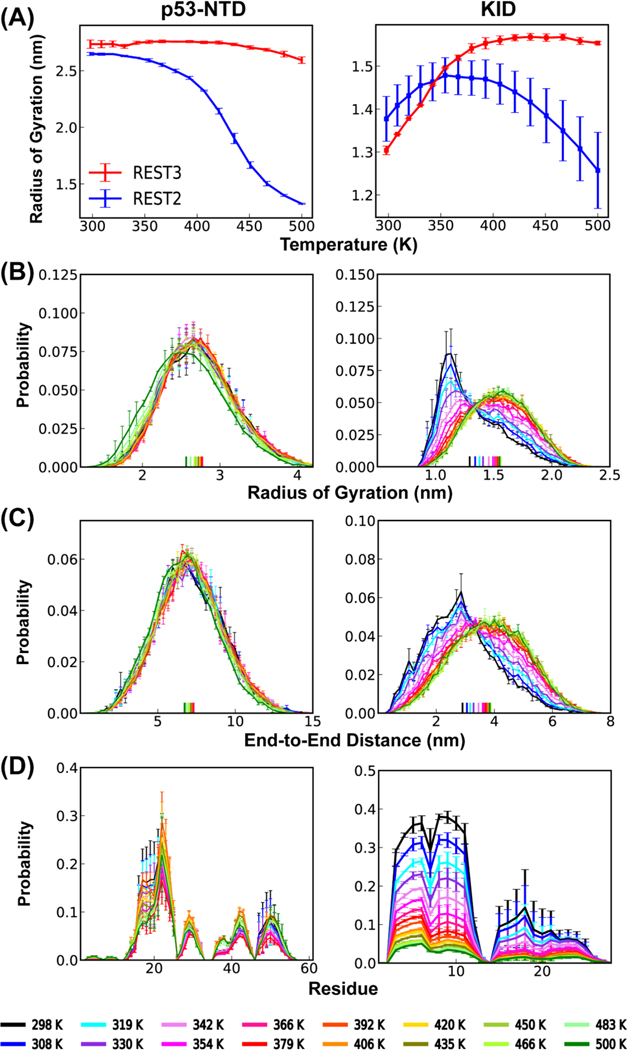
We first performed one folding REST3 simulation of p53-NTD in a99SB-disp to evaluate the new protocol’s efficiency in driving replica random walk in the temperature space and conformational sampling. As summarized in Figure 4 (left column), rescaling of the solute-solvent vdW interactions in REST3 (Eq. 5 and 6) eliminates the artificially increasing compactness at higher temperatures. Note that p53-NTD is a highly dynamic IDP with a large radius of gyration at room temperature (experimental value ~ 2.39 nm58); it apparently does not undergo further chain expansion as the temperature is increased from 298 K to 500 K (Figure 4A, top left). This is also confirmed in standard MD simulations of p53-NTD at 500 K using the original, unscaled a99SB-disp force field (Figure 2). However, the residual helicity does gradually decrease at increasing temperature in REST3 (Figure 4D, left). This is in contrast to artificially elevate helicity at high temperatures in REST2 (Figures 2C and S2C). Therefore, the new REST3 protocol seems to be able to largely recapitulate the expected conformational properties of p53-NTD within the simulation temperature range.
Figure 4.
Conformational properties as a function of temperature from REST3 simulations of p53-NTD (left, folding) and KID (right, control and folding simulations) in a99SB-disp, including (A) average radius of gyration, (B) distributions of radius of gyration, (C) distribution of end-to-end distance, and (D) average residue helicity profiles. Results from REST2 run are also shown in panel (A) for comparison. See Methods for calculation of error bars.
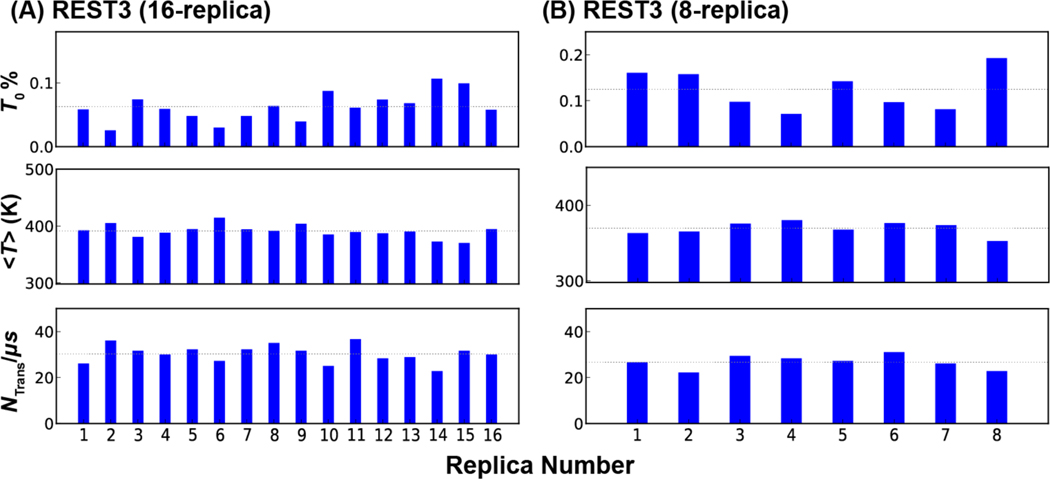
Removing artificial compaction at high temperatures leads to much more efficient replica random walk in REST3. As summarized in Figure S6, all REST3 replicas undergo rapid random diffusion throughout the temperature range. Importantly, all replicas are completely free of trapping in compact states and appear to efficiently sample a wide range of conformational states with different levels of compaction (Figure S6, blue traces for radius of gyration). Reflecting much more efficient mixing, all replicas in REST3 have similar average temperatures, number of round trips between the lowest and highest temperatures, and contribute similarly to the lowest temperature ensemble (Figure 5), which are hallmarks of well-converged replica exchange simulations. In particular, the average number of temperature round trips increase to 30.3/μs per replica, compared to 9–10/μs per replica in REST2 runs (see Figures 3). Note that the average exchange acceptance rates are essentially identical (~25%) in these REST2 and REST3 runs. The dramatic improvement in the efficiency of random walk in the temperature space is a direct result of eliminating the artificial conformational compaction at higher temperatures (Figures S4 and S5).
Figure 5.
Efficiency of replica exchange in REST3 folding simulation of p53-NTD using 16 or 8 replicas, as reflected in occupancy at the lowest temperature ( at 298 K), average effective temperature , and the number of temperature round trip per μs for each replica. The average per μs are 30.3/μs and 26.7/μs for 16-replica or 8-replica runs, respectively (as indicated by the dash lines).
We further evaluate the efficacy and transferability of REST3 in preventing conformational trapping and replica segregation using KID, which is a smaller and more structured IDP64. As summarized in Figure 4 (right column), REST2 also leads to modest artificial conformational compaction and increased structural level for KID. REST3 effectively eliminates the artificial compaction and generates ensembles that show appropriate temperature-dependent conformational properties at both secondary and global levels. Interestingly, the efficiency of replica exchange in REST2 does not appear to deteriorate as much compared to the case of p53-NTD (Figure 3 vs S7). As such, the replica exchange efficiency does not benefit significantly from the new REST3 protocol. This observation should not be surprising, considering that KID is a smaller IDP and adopts much more compact conformational ensembles even at 298 K (Figure 4A). The artificial over compaction is much less severe than the highly flexible p53-NTD. Nonetheless, as will be discussed later, ensembles derived from the folding and control REST3 runs appear to be better converged at all temperatures. Taken together, REST3 is an effective protocol free of artificial compaction at high effective temperatures and much more suitable for the simulation of dynamic protein conformational ensembles compared to REST2 in general.
Conformational sampling and convergence of REST2 and REST3
Examination of the evolution of the conformations of replicas in REST2 vs. REST3 as a function of simulation time clearly demonstrates more efficient exploration of different conformational spaces in REST3. For example, all REST3 replicas reversibly sample diverse conformations with a wide range of radius of gyration throughout the 2 μs simulation time (Figure S6, blue traces). In contrast, many REST2 replicas rarely sample conformations of different sizes (Figure S4 and S5, blue traces) and the lack of sampling by individual replicas is particularly prominent in the control run. Nonetheless, it is also known that the apparent convergence of the lowest temperature ensemble of a replica exchange simulation can arise due to replica mixing even in the presence of substantial replica segregation and conformational trapping51, 83. Indeed, with 1 or 2 μs sampling per replica, the current REST2 and REST3 simulations generated highly consistent disordered ensembles at 298 K for both KID and p53-NTD in the a99SB-disp force field, with similar local and global structural properties such as radius of gyration distributions and residue helicity profiles (Figure S8). Closer inspection of the structural ensembles generated by independent folding and control runs, however, suggests that certain structural properties are better converged in REST3 simulations. For example, substantial differences persist between the 2D distributions of the radius of gyration and end-to-end distance derived from folding and control REST2 runs (Figure 6 A vs B), while the distributions are far more consistent from REST2 runs (Figure 6 C vs D).
Figure 6.
2D probability distributions of the radius of gyration and end-to-end distance of KID at 298 K, derived from independent REST2 and REST3 control and folding simulations (Table S1). The first 200 ns of all trajectories were excluded as the equilibrium phase. All probability distributions were first converted into the free energy surface before plotting.
We further assess the sampling and convergence of REST2 and REST3 by performing the PCA analysis of the disordered ensembles at 298 K, which allows the heterogenous ensembles to be projected in principal axes with the largest variances (see Methods). The results confirm a higher level of consistency between ensembles of KID generated by folding and control runs of REST3 compared to those of REST2, but at the same time reveal substantial residual differences even for REST3 simulations (Figure 7A). The later observation is somewhat surprising, considering the small size of KID and the apparent convergence of various 1D distributions with 1 μs per replica sampling time (e.g., Figure S8). On the other hand, this really illustrates the critical challenge of sampling disordered protein conformational ensembles in explicit solvent even for modest-sized IDPs32. For p53-NTD, REST3 appears to be capable to sample broader metastable states (e.g., areas with free energy < 0.5 kcal/mol, Figure 7B), but the ensembles generated by the two REST protocols are much more similar compared to those of KID. Besides the longer sampling time of 2 μs per replica, the better convergence of p53-NTD ensembles may also be attributed to its more extended and less structured nature despite the longer sequence (Figure S8).
Figure 7.
Distribution of conformational ensembles at 298 K generated by REST2 and REST3 control and folding simulations of KID (A) and folding simulation of p53-NTD (B) in the a99SB-disp force field. The ensembles were projected along the same first two principal components derived from PCA analysis of all conformations sampled from both REST2 and REST3 runs of each individual protein. All probability distributions were first converted into the free energy surface before plotting.
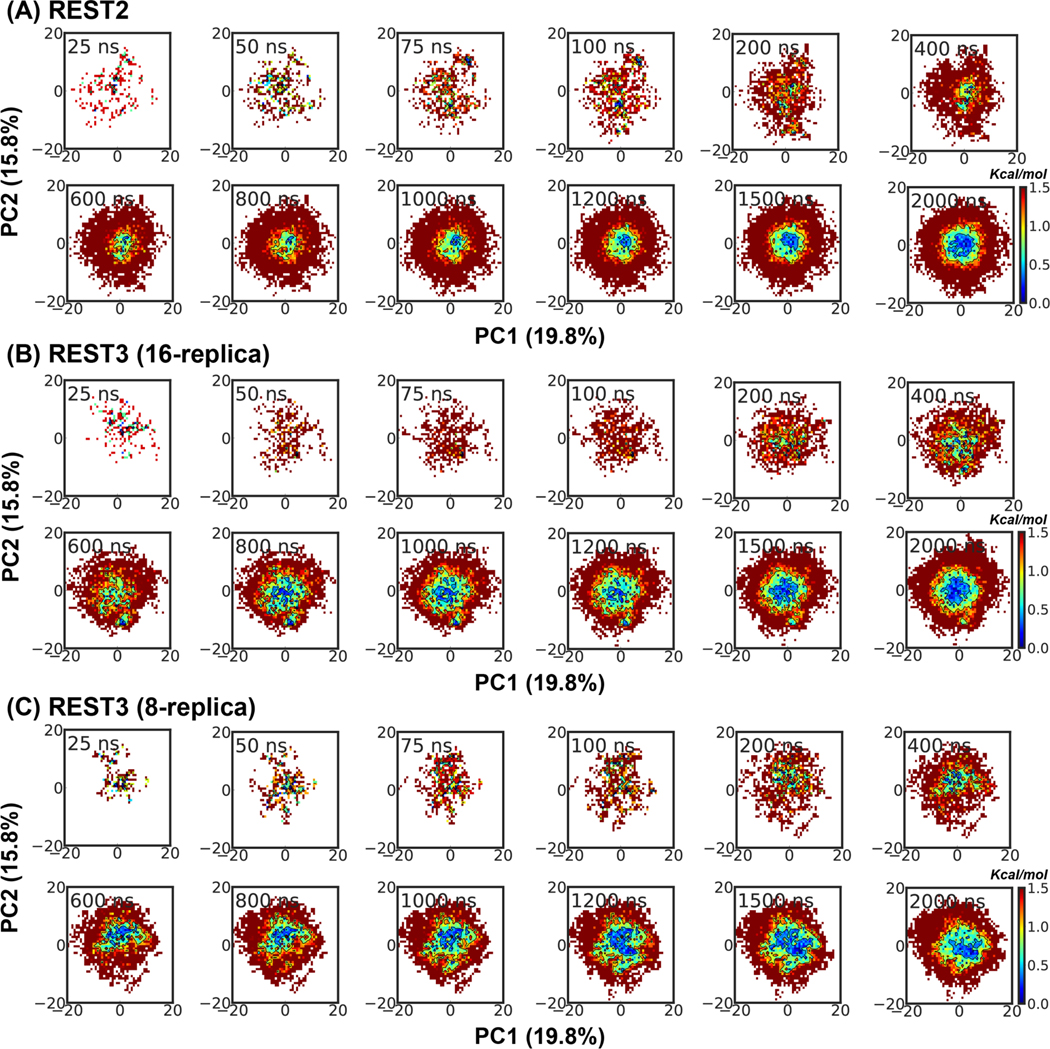
To directly compare the convergence rates, we further analyze the evolution of the disordered ensembles at 298 K as a function of REST2 and REST3 simulation time. For KID, we focus on the sampling of transient partial helices, as analysis of the global structural properties already reveals improved convergence with REST3 (e.g., Figure 6 and 7). For this, we calculated the probabilities of partial helices as identified by their starting positions and lengths. The results, summarized in Figure S9, again highlight the challenge of sampling disordered protein conformations, as the helical substate distributions remain significantly different between 1-μs control and folding runs for both REST2 and REST3. Even longer sampling time is likely required for achieving better convergence at the helical substate level. Nonetheless, there appears to be an overall improvement in the convergence of the populations of helical substates in REST3 compared to REST2. For example, the populations of partial helices starting around residue 1 (red arrows in Figure S9 B and D) reach plateaus by ~600 ns during the REST3 folding run, but continue to increase and only reach similar (converged) levels near the end of the 1 μs REST2 folding run. Similar observations can be made for some helical states in the control runs (e.g., purple arrows in Figure S9 A and C). For p53-NTD, the 2 μs REST2 and REST3 simulations yield highly similar ensembles, as reflected in various 1D distributions (Figure S8) and PCA analysis (Figure 7B). Examination of the evolution of the disordered ensemble at 298 K as a function of simulation time suggests that REST2 and REST3 are quite similar in achieving the overall convergence (Figure 8 A vs B), despite substantial differences in conformational coverage of individual replicas (Figure S4 and S5 vs S6, blue traces). This again highlights how replica mixing itself can lead to apparent convergence in replica exchange simulations. Nonetheless, it is also clear that REST3 is able to sample broader free energy basin with shorter simulation times (e.g., regions with free energy < 0.5 kcal/mol). Taken together, detailed conformational analyses above support that improved replica exchange efficiency and conformational sampling of individual replicas in REST3 can indeed further improve the convergence of the disordered ensembles generated at the lowest temperature condition.
Figure 8.
Evolution of the conformational ensemble of p53-NTD at 298 K during (A) REST2, (B) REST3 (16-replica), and (C) REST3 (8-replica) folding simulations in a99SB-disp. The ensembles were projected along the same first two principal components derived from PCA analysis of all conformations sampled from REST2 and REST3 runs. All probability distributions were first converted into free energy surface before plotting.
REST3 can further reduce the required number of replicas
The observation that REST2 does not appear to suffer significantly from conformational trapping and replica segregation at high effective temperatures suggests that smaller number of replicas may be sufficient for the simulation of p53-NTD using the REST3 protocol. Here, we evaluate a REST3 protocol with only 8 replicas spanning 298 K to 450 K (see Table S2) and perform a folding simulation of p53-NTD for 2 μs per replica. Although the larger temperature spacing leads to smaller average replica exchange acceptance (~6.5%), all replicas can efficiently explore the whole temperature space and are free of conformational trapping (Figure S10). As a result, all replicas contribute significantly to the lowest temperature ensemble and have similar average temperatures (Figure 5B), which are hallmarks of well-converged replica exchange simulations. The average temperature round-trip transition rate is 26.7/μs per replica, compared to that of ~30.3/μs for the 16-replica REST3 run. Importantly, the resulting disordered ensemble at 298 K is highly similar to those generated by both REST2 and REST3 protocols (Figure S11). Comparison of the 298 K ensembles as a function of simulation time (Figure 8 C) further demonstrates that the convergence rate of the 8-replica REST3 protocol is similar to that of the 16-replica REST3 protocol and superior to that of the 16-replica REST2 protocol. Taken together, it is evident that the better-balanced solute-solute and solute-solvent interactions in REST3 allow it to effectively sample disordered protein conformational ensembles with much less computational sources.
Conclusions
REST is one of the most effective enhanced sampling approaches for biomolecular simulations that is particularly suitable for explicit solvent simulations by dramatically reducing the number of replicas required. In this work, we critically evaluated the replica exchange and sampling efficiency of the latest REST2 protocol for simulation of disordered protein ensembles. Our results reveal that REST2 leads to artificial conformational compaction at high effective temperatures. This is due to the imbalanced scaling of solute-solute and solute-solvent interactions, which was originally designed to promote reversible folding of mini-proteins and beta-hairpins44. Importantly, the artificial over compaction at high temperatures leads to conformational trapping and segregation of replicas in the temperature space during REST2 simulations. These problems can be particularly severe for highly flexible IDPs such as p53-NTD, where some replicas can completely fail to contribute to the lowest temperature ensemble.
We propose that the scaling of solute-solvent vdW interactions can be treated as a free parameter in REST protocols, which can be optimized to carefully control the conformational properties of the protein solute at various temperature conditions and achieve more efficient conformational sampling. To this end, we describe a new REST3 protocol that has been tuned to generate conformational distributions throughout the temperature range similar to those expected using the unscaled Hamiltonian. With a better balance between solute-solute and solute-solvent interactions, REST3 completely eliminates conformational trapping at high temperatures and the resulting replica segregation problem as observed in REST2. All REST3 replicas can undergo highly efficient random walk in the temperature space and sample a broad range of conformational space. As a result, REST3 can further improve the convergence of the disordered protein conformational ensemble at both local and global structure levels. Importantly, REST2 often relies on replica mixing for achieving the apparent convergence instead of true conformational sampling of individual replicas. We also show that REST3 allows one to further reduce the number of replicas required for sufficient sampling. Our tests suggest that at least about half of the computational sources can be saved compared to REST2 when simulating the moderately sized IDPs such as p53-NTD.
Our critical analyses of REST2 and REST3 protocols further reveal significant challenges of relying on tempering alone for sampling large-scale conformational fluctuations of disordered proteins. Sampling of many detailed conformational substates has limited convergence even with 1 to 2 μs per replica sampling and significant differences often persist between independent runs initiated from drastically different initial conformations. This challenge can be attributed to the entropic nature of the barriers involved in folding transitions of local and/or global (transient) structures51, such that the transition rates will only depend weakly on the simulation temperature. As such, further improvement of the REST protocol will likely require incorporating of more advanced Hamiltonian replica exchange in addition to tempering.
Supplementary Material
Acknowledgements
All simulations were performed on the pikes GPU cluster housed in the Massachusetts Green High-Performance Computing Cluster (MGHPCC). This work was supported by National Institutes of Health Grant R35 GM144045 (J. C.).
Footnotes
Supporting Information accompanies this paper at doi: xxxx.
Competing interests: The authors declare no competing interests.
References
- 1.Brooks BR; Brooks CL; Mackerell AD; Nilsson L; Petrella RJ; Roux B; Won Y; Archontis G; Bartels C; Boresch S; Caflisch A; Caves L; Cui Q; Dinner AR; Feig M; Fischer S; Gao J; Hodoscek M; Im W; Kuczera K; Lazaridis T; Ma J; Ovchinnikov V; Paci E; Pastor RW; Post CB; Pu JZ; Schaefer M; Tidor B; Venable RM; Woodcock HL; Wu X; Yang W; York DM; Karplus M, Charmm: The Biomolecular Simulation Program. J. Comput. Chem 2009, 30, 1545–1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Case DA, D. S. C., Cheatham TE III, Darden TA, Duke RE, Giese TJ, Gohlke H, Goetz AW, Greene D, Homeyer N, Izadi S, Kovalenko A, Lee TS, LeGrand S, Li P, Lin C, Liu J, Luchko T, Luo R, Mermelstein D, Merz KM, Monard G, Nguyen H, Omelyan I, Onufriev A, Pan F, Qi R, Roe DR, Roitberg A, Sagui C, Simmerling CL, Botello-Smith WM, Swails J, Walker RC, Wang J, Wolf RM, Wu X, Xiao L, York DM and Kollman Amber PA 2017, University of California, San Francisco. 2017. [Google Scholar]
- 3.Eastman P; Friedrichs MS; Chodera JD; Radmer RJ; Bruns CM; Ku JP; Beauchamp KA; Lane TJ; Wang L-P; Shukla D; Tye T; Houston M; Stich T; Klein C; Shirts MR; Pande VS, Openmm 4: A Reusable, Extensible, Hardware Independent Library for High Performance Molecular Simulation. J. Chem. Theory Comput 2012, 9, 461–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Abraham MJ; Murtola T; Schulz R; Páll S; Smith JC; Hess B; Lindahl E, Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25.
- 5.Phillips JC; Braun R; Wang W; Gumbart J; Tajkhorshid E; Villa E; Chipot C; Skeel RD; Kal L; Schulten K, Scalable Molecular Dynamics with Namd. J. Comput. Chem 2005, 26, 1781–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gotz AW; Williamson MJ; Xu D; Poole D; Le Grand S; Walker RC, Routine Microsecond Molecular Dynamics Simulations with Amber on Gpus. 1. Generalized Born. J. Chem. Theory Comput 2012, 8, 1542–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Robustelli P; Piana S; Shaw DE, Developing a Molecular Dynamics Force Field for Both Folded and Disordered Protein States. Proc. Natl. Acad. Sci. U. S. A 2018, 115, E4758–E4766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Huang J; Rauscher S; Nawrocki G; Ran T; Feig M; de Groot BL; Grubmuller H; MacKerell AD Jr., Charmm36m: An Improved Force Field for Folded and Intrinsically Disordered Proteins. Nat. Methods 2017, 14, 71–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Robertson MJ; Tirado-Rives J; Jorgensen WL, Improved Peptide and Protein Torsional Energetics with the Opls-Aa Force Field. Journal of Chemical Theory and Computation 2015, 11, 3499–3509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Piana S; Donchev AG; Robustelli P; Shaw DE, Water Dispersion Interactions Strongly Influence Simulated Structural Properties of Disordered Protein States. J Phys Chem B 2015, 119, 5113–23. [DOI] [PubMed] [Google Scholar]
- 11.Nerenberg PS; Jo B; So C; Tripathy A; Head-Gordon T, Optimizing Solute-Water Van Der Waals Interactions to Reproduce Solvation Free Energies. J Phys Chem B 2012, 116, 4524–4534. [DOI] [PubMed] [Google Scholar]
- 12.Liu X; Chen J, Residual Structures and Transient Long-Range Interactions of P53 Transactivation Domain: Assessment of Explicit Solvent Protein Force Fields. J. Chem. Theory Comput 2019, 15, 4708–4720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Shaw DE; Grossman JP; Bank JA; Batson B; Butts JA; Chao JC; Deneroff MM; Dror RO; Even A; Fenton CH; Forte A; Gagliardo J; Gill G; Greskamp B; Ho CR; Ierardi DJ; Iserovich L; Kuskin JS; Larson RH; Layman T; Lee LS; Lerer AK; Li C; Killebrew D; Mackenzie KM; Mok SYH; Moraes MA; Mueller R; Nociolo LJ; Peticolas JL; Quan T; Ramot D; Salmon JK; Scarpazza DP; Ben Schafer U; Siddique N; Snyder CW; Spengler J; Tang PTP; Theobald M; Toma H; Towles B; Vitale B; Wang SC; Young C, Anton 2: Raising the Bar for Performance and Programmability in a Special-Purpose Molecular Dynamics Supercomputer. Int Conf High Perfor 2014, 41–53.
- 14.Chen JL; Liu XR; Chen JH, Targeting Intrinsically Disordered Proteins through Dynamic Interactions. Biomolecules 2020, 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhang WH; Chen JH, Accelerate Sampling in Atomistic Energy Landscapes Using Topology-Based Coarse-Grained Models. J Chem Theory Comput 2014, 10, 918–923. [DOI] [PubMed] [Google Scholar]
- 16.Sugita Y; Okamoto Y, Replica-Exchange Molecular Dynamics Method for Protein Folding. Chem. Phys. Lett 1999, 314, 141–151. [Google Scholar]
- 17.Liu P; Kim B; Friesner RA; Berne BJ, Replica Exchange with Solute Tempering: A Method for Sampling Biological Systems in Explicit Water. Proc. Natl. Acad. Sci. U. S. A 2005, 102, 13749–13754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mittal A; Lyle N; Harmon TS; Pappu RV, Hamiltonian Switch Metropolis Monte Carlo Simulations for Improved Conformational Sampling of Intrinsically Disordered Regions Tethered to Ordered Domains of Proteins. J. Chem. Theory Comput 2014, 10, 3550–3562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Peter EK; Shea JE, A Hybrid Md-Kmc Algorithm for Folding Proteins in Explicit Solvent. Phys. Chem. Chem. Phys 2014, 16, 6430–6440. [DOI] [PubMed] [Google Scholar]
- 20.Zhang C; Ma J, Enhanced Sampling and Applications in Protein Folding in Explicit Solvent. J. Chem. Phys 2010, 132, 244101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zheng LQ; Yang W, Practically Efficient and Robust Free Energy Calculations: Double-Integration Orthogonal Space Tempering. J. Chem. Theory Comput 2012, 8, 810–823. [DOI] [PubMed] [Google Scholar]
- 22.Yang W, Advanced Sampling for Molecular Simulation Is Coming of Age. J. Comput. Chem 2016, 37, 549-549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zuckerman DM, Equilibrium Sampling in Biomolecular Simulations. Annual Review of Biophysics 2011, 40, 41–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wright PE; Dyson HJ, Intrinsically Disordered Proteins in Cellular Signalling and Regulation. Nat. Rev. Mol. Cell Biol 2015, 16, 18–29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Uversky VN, Intrinsically Disordered Proteins and Their “Mysterious” (Meta)Physics. Front Phys-Lausanne 2019, 7. [Google Scholar]
- 26.Hatos A; Hajdu-Soltesz B; Monzon AM; Palopoli N; Alvarez L; Aykac-Fas B; Bassot C; Benitez GI; Bevilacqua M; Chasapi A; Chemes L; Davey NE; Davidovic R; Dunker AK; Elofsson A; Gobeill J; Foutel NSG; Sudha G; Guharoy M; Horvath T; Iglesias V; Kajava AV; Kovacs OP; Lamb J; Lambrughi M; Lazar T; Leclercq JY; Leonardi E; Macedo-Ribeiro S; Macossay-Castillo M; Maiani E; Manso JA; Marino-Buslje C; Martinez-Perez E; Meszaros B; Micetic I; Minervini G; Murvai N; Necci M; Ouzounis CA; Pajkos M; Paladin L; Pancsa R; Papaleo E; Parisi G; Pasche E; Barbosa Pereira PJ; Promponas VJ; Pujols J; Quaglia F; Ruch P; Salvatore M; Schad E; Szabo B; Szaniszlo T; Tamana S; Tantos A; Veljkovic N; Ventura S; Vranken W; Dosztanyi Z; Tompa P; Tosatto SCE; Piovesan D, Disprot: Intrinsic Protein Disorder Annotation in 2020. Nucleic Acids Res. 2020, 48, D269–D276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chen J, Towards the Physical Basis of How Intrinsic Disorder Mediates Protein Function. Arch. Biochem. Biophys 2012, 524, 123–31. [DOI] [PubMed] [Google Scholar]
- 28.Ganguly D; Chen J, Structural Interpretation of Paramagnetic Relaxation Enhancement-Derived Distances for Disordered Protein States. J. Mol. Biol 2009, 390, 467–77. [DOI] [PubMed] [Google Scholar]
- 29.Das RK; Ruff KM; Pappu RV, Relating Sequence Encoded Information to Form and Function of Intrinsically Disordered Proteins. Curr. Opin. Struct. Biol 2015, 32, 102–112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fisher CK; Stultz CM, Constructing Ensembles for Intrinsically Disordered Proteins. Curr. Opin. Struct. Biol 2011, 21, 426–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Levine ZA; Shea JE, Simulations of Disordered Proteins and Systems with Conformational Heterogeneity. Curr Opin Struct Biol 2017, 43, 95–103. [DOI] [PubMed] [Google Scholar]
- 32.Chen J; Liu X; Chen J, Targeting Intrinsically Disordered Proteins through Dynamic Interactions. Biomolecules 2020, 10, 743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ferreon AC; Ferreon JC; Wright PE; Deniz AA, Modulation of Allostery by Protein Intrinsic Disorder. Nature 2013, 498, 390–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Garcia-Pino A; Balasubramanian S; Wyns L; Gazit E; De Greve H; Magnuson RD; Charlier D; van Nuland NA; Loris R, Allostery and Intrinsic Disorder Mediate Transcription Regulation by Conditional Cooperativity. Cell 2010, 142, 101–11. [DOI] [PubMed] [Google Scholar]
- 35.Berlow RB; Dyson HJ; Wright PE, Expanding the Paradigm: Intrinsically Disordered Proteins and Allosteric Regulation. J. Mol. Biol 2018, 430, 2309–2320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Liang C; Savinov SN; Fejzo J; Eyles SJ; Chen J, Modulation of Amyloid-Beta42 Conformation by Small Molecules through Nonspecific Binding. J. Chem. Theory Comput 2019, 15, 5169–5174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Schrag LG; Liu X; Thevarajan I; Prakash O; Zolkiewski M; Chen J, Cancer-Associated Mutations Perturb the Disordered Ensemble and Interactions of the Intrinsically Disordered P53 Transactivation Domain. J. Mol. Biol 2021, 433, 167048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zhao J; Blayney A; Liu X; Gandy L; Jin W; Yan L; Ha JH; Canning AJ; Connelly M; Yang C; Liu X; Xiao Y; Cosgrove MS; Solmaz SR; Zhang Y; Ban D; Chen J; Loh SN; Wang C, Egcg Binds Intrinsically Disordered N-Terminal Domain of P53 and Disrupts P53-Mdm2 Interaction. Nat. Commun 2021, 12, 986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Swendsen RH; Wang JS, Replica Monte-Carlo Simulation of Spin-Glasses. Phys. Rev. Lett 1986, 57, 2607–2609. [DOI] [PubMed] [Google Scholar]
- 40.Hansmann UHE; Okamoto Y, Numerical Comparisons of Three Recently Proposed Algorithms in the Protein Folding Problem. J. Comput. Chem 1997, 18, 920–933. [Google Scholar]
- 41.Chen J; Im W; Brooks CL, Balancing Solvation and Intramolecular Interactions: Toward a Consistent Generalized Born Force Field. J. Am. Chem. Soc 2006, 128, 3728–3736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Best RB, Computational and Theoretical Advances in Studies of Intrinsically Disordered Proteins. Curr. Opin. Struct. Biol 2017, 42, 147–154. [DOI] [PubMed] [Google Scholar]
- 43.Best RB; Zheng W; Mittal J, Balanced Protein-Water Interactions Improve Properties of Disordered Proteins and Non-Specific Protein Association. J. Chem. Theory Comput 2014, 10, 5113–5124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wang L; Friesner RA; Berne BJ, Replica Exchange with Solute Scaling: A More Efficient Version of Replica Exchange with Solute Tempering (Rest2). J. Phys. Chem. B 2011, 115, 9431–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Terakawa T; Kameda T; Takada S, On Easy Implementation of a Variant of the Replica Exchange with Solute Tempering in Gromacs. J. Comput. Chem 2011, 32, 1228–34. [DOI] [PubMed] [Google Scholar]
- 46.Moors SL; Michielssens S; Ceulemans A, Improved Replica Exchange Method for Native-State Protein Sampling. J Chem Theory Comput 2011, 7, 231–7. [DOI] [PubMed] [Google Scholar]
- 47.Pang X; Zhou HX, Disorder-to-Order Transition of an Active-Site Loop Mediates the Allosteric Activation of Sortase A. Biophys. J 2015, 109, 1706–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Liu XR; Jia ZG; Chen JH, Enhanced Sampling of Intrinsic Structural Heterogeneity of the Bh3-Only Protein Binding Interface of Bcl-Xl. J. Phys. Chem. B 2017, 121, 9160–9168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kamiya M; Sugita Y, Flexible Selection of the Solute Region in Replica Exchange with Solute Tempering: Application to Protein-Folding Simulations. J. Chem. Phys 2018, 149, 072304. [DOI] [PubMed] [Google Scholar]
- 50.Huang X; Hagen M; Kim B; Friesner RA; Zhou R; Berne BJ, Replica Exchange with Solute Tempering: Efficiency in Large Scale Systems. J Phys Chem B 2007, 111, 5405–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zhang W; Chen J, Efficiency of Adaptive Temperature-Based Replica Exchange for Sampling Large-Scale Protein Conformational Transitions. J. Chem. Theory Comput 2013, 9, 2849–2856. [DOI] [PubMed] [Google Scholar]
- 52.Faraldo-Gomez JD; Roux B, Characterization of Conformational Equilibria through Hamiltonian and Temperature Replica-Exchange Simulations: Assessing Entropic and Environmental Effects. J. Comput. Chem 2007, 28, 1634–1647. [DOI] [PubMed] [Google Scholar]
- 53.Yang MJ; Huang J; MacKerell AD, Enhanced Conformational Sampling Using Replica Exchange with Concurrent Solute Scaling and Hamiltonian Biasing Realized in One Dimension. J. Chem. Theory Comput 2015, 11, 2855–2867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Roe DR; Bergonzo C; Cheatham TE, Evaluation of Enhanced Sampling Provided by Accelerated Molecular Dynamics with Hamiltonian Replica Exchange Methods. J. Phys. Chem. B 2014, 118, 3543–3552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zhang W; Chen J, Accelerate Sampling in Atomistic Energy Landscapes Using Topology-Based Coarse-Grained Models. J. Chem. Theory Comput 2014, 10, 918–923. [DOI] [PubMed] [Google Scholar]
- 56.Lee H; Mok KH; Muhandiram R; Park KH; Suk JE; Kim DH; Chang J; Sung YC; Choi KY; Han KH, Local Structural Elements in the Mostly Unstructured Transcriptional Activation Domain of Human P53. J. Biol. Chem 2000, 275, 29426–29432. [DOI] [PubMed] [Google Scholar]
- 57.Huang F; Rajagopalan S; Settanni G; Marsh RJ; Armoogum DA; Nicolaou N; Bain AJ; Lerner E; Haas E; Ying L, Multiple Conformations of Full-Length P53 Detected with Single-Molecule Fluorescence Resonance Energy Transfer. Proceedings of the National Academy of sciences 2009, 106, 20758–20763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Lowry DF; Stancik A; Shrestha RM; Daughdrill GW, Modeling the Accessible Conformations of the Intrinsically Unstructured Transactivation Domain of P53. Proteins: Structure, Function, and Bioinformatics 2008, 71, 587–598. [DOI] [PubMed] [Google Scholar]
- 59.Wells M; Tidow H; Rutherford TJ; Markwick P; Jensen MR; Mylonas E; Svergun DI; Blackledge M; Fersht AR, Structure of Tumor Suppressor P53 and Its Intrinsically Disordered N-Terminal Transactivation Domain. Proc. Natl. Acad. Sci. U. S. A 2008, 105, 5762–5767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lum JK; Neuweiler H; Fersht AR, Long-Range Modulation of Chain Motions within the Intrinsically Disordered Transactivation Domain of Tumor Suppressor P53. J. Am. Chem. Soc 2012, 134, 1617–1622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Zhan YA; Wu HW; Powell AT; Daughdrill GW; Ytreberg FM, Impact of the K24n Mutation on the Transactivation Domain of P53 and Its Binding to Murine Double-Minute Clone 2. Proteins 2013, 81, 1738–1747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Radhakrishnan I; PerezAlvarado GC; Parker D; Dyson HJ; Montminy MR; Wright PE, Solution Structure of the Kix Domain of Cbp Bound to the Transactivation Domain of Creb: A Model for Activator:Coactivator Interactions. Cell 1997, 91, 741–752. [DOI] [PubMed] [Google Scholar]
- 63.Radhakrishnan I; Perez-Alvarado GC; Dyson HJ; Wright PE, Conformational Preferences in the Ser(133)-Phosphorylated and Non-Phosphorylated Forms of the Kinase Inducible Transactivation Domain of Creb. FEBS Lett. 1998, 430, 317–322. [DOI] [PubMed] [Google Scholar]
- 64.Ganguly D; Chen J, Atomistic Details of the Disordered States of Kid and Pkid. Implications in Coupled Binding and Folding. J. Am. Chem. Soc 2009, 131, 5214–5223. [DOI] [PubMed] [Google Scholar]
- 65.Abraham MJ; Murtola T; Schulz R; Páll S; Smith JC; Hess B; Lindahl E, Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar]
- 66.Pall S; Abraham MJ; Kutzner C; Hess B; Lindahl E, Tackling Exascale Software Challenges in Molecular Dynamics Simulations with Gromacs. Lect Notes Comput Sc 2015, 8759, 3–27. [Google Scholar]
- 67.Darden T; York D; Pedersen L, Particle Mesh Ewald: An N-Log (N) Method for Ewald Sums in Large Systems. The Journal of Chemical Physics 1993, 98, 10089. [Google Scholar]
- 68.Hess B; Bekker H; Berendsen HJC; Fraaije JGEM, Lincs: A Linear Constraint Solver for Molecular Simulations. J. Comput. Chem 1997, 18, 1463–1472. [Google Scholar]
- 69.Tribello GA; Bonomi M; Branduardi D; Camilloni C; Bussi G, Plumed 2: New Feathers for an Old Bird. Computer Physics Communications 2014, 185, 604–613. [Google Scholar]
- 70.Terakawa T; Kameda T; Takada S, On Easy Implementation of a Variant of the Replica Exchange with Solute Tempering in Gromacs. Journal of computational chemistry 2011, 32, 1228–1234. [DOI] [PubMed] [Google Scholar]
- 71.Bussi G, Hamiltonian Replica Exchange in Gromacs: A Flexible Implementation. Mol Phys 2014, 112, 379–384. [Google Scholar]
- 72.McGibbon RT; Beauchamp KA; Harrigan MP; Klein C; Swails JM; Hernandez CX; Schwantes CR; Wang LP; Lane TJ; Pande VS, Mdtraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys J 2015, 109, 1528–32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Law SM; Frank AT; Brooks CL 3rd, Pcasso: A Fast and Efficient Calpha-Based Method for Accurately Assigning Protein Secondary Structure Elements. J. Comput. Chem 2014, 35, 1757–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Pedregosa F; Varoquaux G; Gramfort A; Michel V; Thirion B; Grisel O; Blondel M; Prettenhofer P; Weiss R; Dubourg V; Vanderplas J; Passos A; Cournapeau D; Brucher M; Perrot M; Duchesnay E, Scikit-Learn: Machine Learning in Python. J Mach Learn Res 2011, 12, 2825–2830. [Google Scholar]
- 75.Humphrey W; Dalke A; Schulten K, Vmd: Visual Molecular Dynamics. J. Mol. Graph 1996, 14, 33-&. [DOI] [PubMed] [Google Scholar]
- 76.MacKerell AD; Feig M; Brooks CL, Extending the Treatment of Backbone Energetics in Protein Force Fields: Limitations of Gas-Phase Quantum Mechanics in Reproducing Protein Conformational Distributions in Molecular Dynamics Simulations. Journal of computational chemistry 2004, 25, 1400–1415. [DOI] [PubMed] [Google Scholar]
- 77.MacKerell AD; Bashford D; Bellott M; Dunbrack RL; Evanseck JD; Field MJ; Fischer S; Gao J; Guo H; Ha S; Joseph-McCarthy D; Kuchnir L; Kuczera K; Lau FTK; Mattos C; Michnick S; Ngo T; Nguyen DT; Prodhom B; Reiher WE; Roux B; Schlenkrich M; Smith JC; Stote R; Straub J; Watanabe M; Wiorkiewicz-Kuczera J; Yin D; Karplus M, All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [DOI] [PubMed] [Google Scholar]
- 78.Piana S; Lindorff-Larsen K; Shaw DE, How Robust Are Protein Folding Simulations with Respect to Force Field Parameterization? Biophys J 2011, 100, L47–L49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Lindorff-Larsen K; Piana S; Palmo K; Maragakis P; Klepeis JL; Dror RO; Shaw DE, Improved Side-Chain Torsion Potentials for the Amber Ff99sb Protein Force Field. Proteins 2010, 78, 1950–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Hornak V; Abel R; Okur A; Strockbine B; Roitberg A; Simmerling C, Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins 2006, 65, 712–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Piana S; Donchev AG; Robustelli P; Shaw DE, Water Dispersion Interactions Strongly Influence Simulated Structural Properties of Disordered Protein States. J Phys Chem B 2015, 119, 5113–5123. [DOI] [PubMed] [Google Scholar]
- 82.Hicks A; Zhou HX, Temperature-Induced Collapse of a Disordered Peptide Observed by Three Sampling Methods in Molecular Dynamics Simulations. J. Chem. Phys 2018, 149, 072313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Periole X; Mark AE, Convergence and Sampling Efficiency in Replica Exchange Simulations of Peptide Folding in Explicit Solvent. J. Chem. Phys 2007, 126, 014903. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.