Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Jan 3;18(2):1563–1572. doi: 10.1021/acsnano.3c09265

Surface Reconstructions in II–VI Quantum Dots

Jordi Llusar †, Indy du Fossé ‡, Zeger Hens ∥, Arjan Houtepen ‡,*, Ivan Infante †,§,*
PMCID: PMC10795476  PMID: 38169474

Abstract

graphic file with name nn3c09265_0007.jpg

Although density functional theory (DFT) calculations have been crucial in our understanding of colloidal quantum dots (QDs), simulations are commonly carried out on QD models that are significantly smaller than those generally found experimentally. While smaller models allow for efficient study of local surface configurations, increasing the size of the QD model will increase the size or number of facets, which can in turn influence the energetics and characteristics of trap formation. Moreover, core–shell structures can only be studied with QD models that are large enough to accommodate the different layers with the correct thickness. Here, we use DFT calculations to study the electronic properties of QDs as a function of size, up to a diameter of ∼4.5 nm. We show that increasing the size of QD models traditionally used in DFT studies leads to a disappearance of the band gap and localization of the HOMO and LUMO levels on facet-specific regions of the QD surface. We attribute this to the lateral coupling of surface orbitals and the formation of surface bands. The introduction of surface vacancies and their a posteriori refilling with Z-type ligands leads to surface reconstructions that widen the band gap and delocalize both the HOMO and LUMO. These results show that the surface geometry of the facets plays a pivotal role in defining the electronic properties of the QD.

Keywords: quantum dots, density functional theory, semiconductors, surface states, surface reconstructions

Introduction

Computational studies have played a crucial role in the advancement of our understanding of colloidal quantum dots (QDs) over the past two decades.1−4 Density functional theory (DFT) calculations have allowed the investigation of QD models with realistic structures and ligand-terminated surfaces that closely resemble experimental observations.1,5 However, despite significant improvements in computational power, most DFT studies still rely on model systems that are considerably smaller than real QDs found in experiments.1,6−8 For example, excluding ligands, a spherical CdSe QD with a diameter of 5 nm contains approximately 2400 atoms, while DFT models typically consist of fewer than 500 atoms (∼3 nm diameter).9−14 Although smaller models are suitable for studying local surface configurations,13−15 they may overlook surface localized states that emerge when the size of a QD, and thus of its facets, is expanding. Hence, these models likely do not provide an accurate representation of larger QDs. Moreover, for a precise description of core/shell(/shell) particles, QD models are needed that represent core and shell(s) with the correct thickness, which would make these models nearly identical in size to their experimental counterparts.

Previous investigations of QD systems with diameters of >5 nm have employed various computational methods. Tight-binding calculations have been effective for accurately reproducing experimentally observed absorption spectra.16−19 Pseudopotential methods are useful for studying carrier dynamics and the electronic structure of QDs.20−23 However, both methods are less suitable to predict the geometry of the QD surface.5 Furthermore, these calculations often employ pseudohydrogen passivation,17,18,20,21,24 which does not resemble the experimentally present carboxylate or amine ligands and, as such, is not appropriate for a chemical description of the QD surface.5 The pseudohydrogen passivation turns all surface atoms of a QD into four-coordinated surface species, a situation that neglects the possibility that the abrupt termination of a QD by different facets yields undercoordinated surface atoms.13,14,25,26 Recent developments in classical force fields tailored specifically to QDs have enabled the study of large QDs with realistic ligand capping at a fraction of the computational cost.27,28 However, these force field methods cannot predict the electronic structure of the QD, and thus the formation of localized states through, for example, electron charging and discharging. For detailed analyses of surface states and their impact on the electronic properties of QDs, DFT remains the most effective choice.5

Nevertheless, the literature on DFT studies of QD models containing over 500 atoms is severely limited. Some reports employ pseudohydrogen passivation, similar to pseudopotential and tight-binding studies, but this approach fails to accurately describe the chemical nature of the QD surface.29,30 In 2014, Voznyy and Sargent presented a CdSe QD model comprising approximately 1200 atoms, excluding the ligands, that was passivated with chloride ions. However, the HOMO and LUMO of this QD were localized on surface facets and separated by a negligible HOMO–LUMO gap.31 A similar surface localization of the HOMO resulted from DFT calculations on CdSe nanoplatelets.32 These findings are inconsistent with the well-established particle-in-a-box model of QDs,33,34 which predicts delocalized orbitals, as experimentally observed with scanning tunneling microscopy,24,35,36 and size-tunable band gap of QDs.37,38

Surface localized orbitals with energy inside the bulk band gap may result from the reduced coupling of atomic orbitals to surface atoms. For flat semiconductor surfaces in vacuum, the formation of facet specific 2D surface bands is well-known and is often countered by the spontaneous formation of surface vacancies. To address this facet truncation problem, Voznyy and Sargent have indeed introduced surface vacancies, leading to a slightly n-doped QD with delocalized states.31 Nonetheless, additional studies are needed to explore the impact of surface vacancies and other factors on the QD electronic properties.

In the present study, we show that larger Cd- and Zn-chalcogenide model QDs that are terminated by low-index bulk facets feature increasingly surface localized HOMO and LUMO states with a negligible HOMO–LUMO gap. We demonstrate that this deviation from experimental findings can be addressed by introducing reconstructed surfaces that feature surface vacancies analogous to those observed on flat semiconductor surfaces. Additionally, we explore refilling these vacancies with Z-type ligands and find that it leads to similar delocalization of the HOMO–LUMO levels. This enables us to put forward a QD model without vacancies that retains a high ligand concentration as observed for experimental QDs and displays delocalized HOMO and LUMO levels separated by a sizable HOMO–LUMO gap, in line with experimental findings. Finally, we demonstrate that this approach can be used to build models for so-called type-I and type-II core–shell QDs that avoid, again, surface localization of HOMO and LUMO.

Results and Discussion

Issue with Large QD Models

The zinc blende Cd68Se55Cl26 model system, which is illustrated in the leftmost part of Figure 1A, served as a reference structure for multiple previous studies.13,15,43−48 This model system, henceforth termed Cd68, is roughly spherical, cation-rich, and charge balanced. Charge balance is achieved through passivation with chloride ligands in lieu of the experimentally often-employed oleate ligands. Ligand distribution on the facets is primarily based on a previous work by Cosseddu and co-workers.45 The diameter of this QD model is approximately 1.8 nm, as measured from one corner of a ⟨111⟩-facet to the furthest corner of the ⟨111⟩-facet on the opposite side; a size significantly smaller than a typical experimental CdSe QD. The density of states (DOS), as well as the shapes of the HOMO and LUMO, are shown in Figure 1B,C, respectively. For the Cd68 model, both the HOMO and the LUMO are delocalized over the entire QD and separated by a HOMO–LUMO gap of 1.5 eV. Further details of this system may be found elsewhere.13

Figure 1.

Figure 1

Open in a new tab

Effect of increasing the size of the QD model. (A) Structure of CdSe QD models with compositions of Cd68Se55Cl26, Cd176Se147Cl58, Cd360Se309Cl102, and Cd640Se561Cl158, respectively. (B) DOS for each QD with their respective HOMO and LUMO gap energies. Every horizontal line corresponds to an MO. The length of the colored line segments indicates the contribution of each element to an MO. Levels below the dotted line are filled with two electrons; levels above the line are empty. (C) Contour plots of the HOMO and LUMO of each system.

In line with the prediction of a particle-in-a-box model, increasing the QD diameter to 2.7 nm (Cd176) causes a decrease in the HOMO–LUMO gap. However, Figure 1C shows that the HOMO of this model QD no longer uniformly extends across the entire QD. Further increasing the QD size to 3.6 (Cd360) and 4.5 nm (Cd640) results in clearly surface localized HOMO and LUMO states—specifically on the Se-terminated 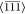Inline graphic- and Cd-terminated ⟨111⟩-facets, respectively—separated by a negligible HOMO–LUMO gap.

A versatile tool commonly used for quantifying the degree of localization of the wave function is the inverse participation ratio (IPR), which ranges from 1/Natoms for complete delocalization to 1 for complete localization, where Natoms are the number of atoms in the system. To compare systems of various sizes, it is more convenient to use a normalized participation ratio (PR), defined below, which ensures a value of 0% (for complete localization) and 100% (for complete delocalization) regardless of the number of Cd and Se atoms in the system:

graphic file with name nn3c09265_m002.jpg

Here, (I)PRi (%) is the (inverse) fractional participation ratio of the ith molecular orbital (MO)i, Pα,i is the weight of the (MO)i on atom α, and NCd and NSe are the numbers of Cd and Se atoms in the inorganic QD core, respectively. Note that the number of ligand atoms is specifically not included, since their contribution near the band edges is generally small.

Figure 2A shows that the HOMO and LUMO of Cd68 are delocalized over ∼10–60% of the atoms in the model QD. The HOMO and LUMO levels, represented by the black horizontal lines, exhibit similar participation ratios, indicating no significant localization for this QD size. For Cd640, shown in green in Figure 2A, the PRs of the levels deep inside the VB and CB are similar to those of Cd68. However, the PRs decrease significantly near the HOMO and LUMO, which reflects the localization of these states at the QD surface; see Figure 1C. Figure 2B displays the PRs of the HOMO and LUMO for all four QD sizes, where especially the PRs of the HOMO drop from ∼13% for Cd68 to ∼1–2% for the three largest QDs.

Figure 2.

Figure 2

Open in a new tab

Left panel: Effect of surface reconstruction. (A) PR of Cd68 and Cd640. Each data point corresponds to a MO. The horizontal and vertical lines indicate the PR and energy of the HOMO and LUMO of both systems. (B) PRs of the HOMO (filled circles and dashed lines) and LUMO (filled triangles and dotted lines) as the size of the QD increases. (C) HOMO–LUMO gap of different sizes of QDs. The blue lines stand for nonpassivated QDs, whereas the yellow lines represent QDs with surface vacancies. (D) Structures of Cd640 with no passivation and surface vacancies.

Likewise, the PRs of LUMO monotonically decrease from ∼47 to 1.5%. Figure 2C shows that the HOMO–LUMO gap concomitantly decreases with increasing QD size, reaching a negligibly small value of 0.08 eV for Cd360 and Cd640, which would render such QDs metallic. These results confirm and quantify the conclusion that increasing the size of the QD leads to surface localization of the band edges; see Figure 1C and, for further discussion, Section S2 in the Supporting Information (SI).

The localization of HOMO and LUMO on the QD surface and the disappearance of the HOMO–LUMO gap do not agree with multiple experimental findings. The possibility of attaining near-unity photoluminescence quantum yield (PLQY),49,50 the size-tuneability of the band gap,37,38 and the delocalized orbitals measured by scanning tunneling microscopy24,35,36 are consistent with the traditional description of the band edges through particle-in-a-box models, which predict fully delocalized HOMO and LUMO states and a HOMO–LUMO gap larger than the bulk band gap.33,34 Therefore, we assume that these computational results represent a situation that is not found in real QDs. This can have two possible causes: (1) the computational method is flawed, or (2) the atomistic structure of the modeled QD is wrong.

In the first case, we know from previous works that the PBE functional underestimates the band gap;51 however, it still predicts a band gap of approximately 0.5 eV for bulk CdSe, which should therefore be the limit for large QDs. Additionally, as described in more detail in the SI, the choice of the basis set or the exchange–correlation functional does not qualitatively affect the results. We conclude that the computational method is not at fault here. In the second case, the atomistic structure of the model QD might fail to reproduce the key characteristics of the QDs observed in experiments. One possible explanation is that ligands play a pivotal role in modulating the band gap of QDs. In experiment, QDs are often completely covered with X-type oleate ligands, L-type ligands like amines or phosphines, and Z-type ligands like CdCl2 or Cd(RCOO)2. Previous studies have shown that the addition of L-type ligands or the replacement of chloride X-type ligands with thiolates has little effect on the electronic structure of small Cd68 models.13 Interestingly, as illustrated in Figure S2, these results hold true for the large Cd360 model, aligning with the earlier conclusion for Cd68. The effect of adding Z-type ligands will be discussed below.

Another potential distinction between the modeled and real structures may lie in the intrinsic instability of the QD facets derived from cutting the QD out of the bulk material. This instability resembles that observed in flat semiconductor surfaces,43 where localized levels within the band gap might emerge at facets, edges, and corners of a finite crystal. In the SI, we provide an in-depth exploration of the formation of intragap localized states at the edges of 1D diatomic chains and beyond, based on a tight-binding approach developed by Harrison.52 In essence, within a 1D diatomic chain and under a regime of weak coupling between neighboring orbitals, the uppermost valence band state would be a purely antibonding combination of Cd and Se s orbitals, while the lowermost conduction band state a fully bonding combination of Cd and Se p orbitals; see Figure S5. In contrast, as the coupling between adjacent atomic orbitals increases, these two bands invert (band inversion). As illustrated in Figure S6, under such conditions, two surface states emerge between band-edge states: one localized on the anion at the chain’s left edge and the other on the cation at its right edge. This logic can be extended to 2D, where intragap localized states manifest at the edge of the 2D lattice (Figure S7) and to 3D diatomic crystals. In the latter, following the same rationale, the localized state becomes facet-specific. Therefore, we can infer that, in binary AB crystals with an s-like antibonding CB minimum and p-like bonding VB maximum, like CdSe or InP, the presence of surface localized states in finite 3D crystals is a common occurrence and should be recognized as an inherent feature rather than a flaw in the computational methodology. However, under these conditions, these facets can still become intrinsically unstable and can reconstruct under experimental conditions. Such surface reconstructions are discussed next.

Surface Reconstructions

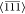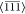It is well-known from studies on the surfaces of bulk semiconductors that facets obtained by cutting the bulk are not always stable.43 As indicated in Figure 1A, our model QDs exhibit ⟨100⟩-, ⟨111⟩-, and Inline graphic-facets, which all have been shown to reconstruct for flat surfaces in vacuum.53 Although much of the previous research on surface reconstructions of compound semiconductors has been conducted on GaAs surfaces, the findings are expected to be applicable to II–VI compounds.53 In general, the ⟨100⟩-facets contain a significant amount of dicoordinated Cd ions. However, the introduction of X-type ligands effectively passivates these ions, yielding bulklike 4-fold coordination. 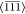In contrast, the ⟨111⟩- and Inline graphic-facets exhibit a higher prevalence of tricoordinated Cd and Se, respectively. In the model systems we employ, these facets are not as effectively passivated by ligands compared to the ⟨100⟩-facets, and they can undergo a reconstruction commonly observed in GaAs ⟨111⟩ surfaces, as shown in Figure 3A, where 25% of the surface cations are replaced by a vacancy.53−55 This particular reconstruction has also been predicted for ZnSe,56 and similar results have been obtained for wurtzite CdSe.57 For the Inline graphic surface, multiple structures have been proposed, as will be discussed below.

Figure 3.

Figure 3

Open in a new tab

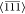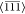Possible reconstructions of ⟨111⟩- and Inline graphic-facets in the Cd640 model. (A) Reconstruction of the ⟨111⟩-facet based on a cation vacancy. (B) Reconstruction of the Inline graphic-facet as proposed by Chadi.60 (C) and (D) reconstructions of the 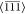Inline graphic-facet as observed by Biegelsen et al.61 The columns depict the unreconstructed model, the addition or removal of atoms (white circles), the pattern for adding or removing atoms, and the final reconstructed model. Note that the structures, for depiction purposes, are not optimized since this can lead to small distortions of the reconstructions near the edge or corner sites. White and red dotted lines indicate the treated facets.

Formation of Superficial Cation Vacancies

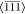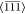We explored various possibilities for incorporating surface reconstructions into our QD models. For the ⟨111⟩-facets, the cation-vacancy reconstruction depicted in Figure 3A stands out as the most favorable option. This specific reconstruction presents the sole pattern mentioned in the experimental literature for zinc blende materials.54,58,59 In contrast, for the Inline graphic-facets, three surface reconstructions have been reported that could fit on the relatively small facets of the Cd640 model: (1) the first is based on the work by Chadi,60 who proposed a multivacancy model in which both cation and anion vacancies lead to the ring structure displayed in Figure 3B. This reconstruction features a suitably small unit cell that can be accommodated within a typical QD facet. It is obtained by simultaneously removing one Cd and one Se atom to preserve the overall charge balance of the system without requiring the addition or removal of Cl ions at other facets. (2) The second reconstruction is based on the work by Biegelsen et al.,61 who utilized scanning tunneling microscopy to demonstrate the formation of a trimer of anion-adatoms forms on the GaAs Inline graphic surface as depicted in Figure 3C.

We have however discarded this trimer structure due to charge balance concerns: to introduce numerous anions onto the 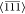Inline graphic-facets, it would be necessary to remove chloride ligands from the ⟨100⟩-facets, which, in turn, would significantly destabilize these facets.43 (3) The final reconstruction—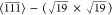Inline graphic—is displayed in Figure 3D and could, as stated in ref (60) for GaAs, be experimentally obtained by annealing the reconstructed structure—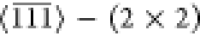Inline graphic—in Figure 3B.61 Note that the structure of Figure 3B can be obtained from Figure 3D by shifting the hexagonal structures of the latter so that the protruding cations are turned into bridging atoms.60,61 The structure in Figure 3D however presents challenges due to its large unit cell size, making it difficult to fit onto a QD facet. Moreover, due to the higher cation/anion ratio compared to the structure in Figure 3B, additional chloride ligands need to be placed on the ⟨111⟩-facets. As demonstrated in Figure S8 for Cd640, this leads to the formation of undesired localized states. Taking into account all of these factors, we have opted to proceed with option 1 on the Inline graphic-facets, i.e., the reconstruction shown in Figure 3B.

The introduction of surface reconstructions, as depicted in Figure 2C, leads to an increase in the HOMO–LUMO gap for all QD sizes. The effect is particularly pronounced for Cd360 and Cd640, with the band gap transitioning from a metallic nature (∼0 eV) to values exceeding 1.0 eV. Figure 2B demonstrates similar improvements in the delocalization of HOMO and LUMO orbitals. Regardless of the QD size, the LUMO exhibits delocalization of approximately 40%. Note that, due to the introduction of vacancies, the number of Cd atoms is slightly lower than that indicated by the name (i.e., 68, 176, 360, and 640), the total compositions being Cd56Se43Cl26, Cd152Se123Cl58, Cd324Se281Cl86, and Cd592Se517Cl150, respectively. To explain the reversal of the HOMO–LUMO gap closure, one can refer to the autocompensation effect observed on bulk surfaces. This effect arises from the formation of an equal number of cation- and anion-dangling bonds on their respective facets, prompting a spontaneous rearrangement of surface atoms to eliminate the metallic surface band. This process resembles a Peierls transition.53

Backfilling of the Surface Vacancies with Z-Type Ligands

While the model with vacancies has successfully addressed the problem of preventing the formation of localized states on QD facets, the QD model with vacancies on the 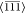Inline graphic and ⟨111⟩ features a ligand surface concentration of only 2.8 nm–2, which is below the 3.5 nm–2 typically reported in experiments.62 Therefore, we considered that this model does not represent the actual surface composition of the experimental QDs and decided to refill the previously introduced vacancies by adding a CdCl2 Z-type ligand to each vacant site. This backfilling process provides a quite uniform distribution of Cl ligands, unlike the traditional QD model illustrated in Figure 4A, where the ligands are placed largely on the ⟨100⟩ surfaces.

Figure 4.

Figure 4

Open in a new tab

Comparison among QD structures along different directions. (A) Sketch of a pure (without vacancies) QD, (B) full-vacancies QD, and (C) completely backfilled QD. Red lines provide a guide-to-eye to delimit the correspondent facets. Unlike panel C, both panels A and B are referred to as old structures since they are not considered the definitive structures.

To perform the backfilling on the Cd360 QD model and obtain a uniform distribution of ligands, we decided to make our approach as general as possible. Although not needed to obtain delocalized HOMO and LUMO levels, we have additionally created vacancies on the ⟨100⟩-facets, using the pattern shown in Figure S9, to explore a wider range of surface modifications. 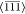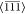Therefore, the geometry depicted in Figure 4B(i–iii), which has an initial ligand density of 1.8 ligands/nm2, is our starting point for increasing the CdCl2 surface coverage by refilling one by one all of the vacancies with CdCl2 molecules following a specific order: ⟨100⟩, Inline graphic, and ⟨111⟩, as shown in Figure 4C(i–iii), respectively. This order is not arbitrary, because we expect that the dicoordinated Cd atoms on the ⟨100⟩-facets make this facet more reactive. Consequently, it becomes filled first.63−65 On the other hand, the Inline graphic- and ⟨111⟩-facets are expected to exhibit similar ligand stabilization, although it remains unclear which of the two facets is more stable. To assess the stability of each facet, we computed the complexation energy, ΔEcomp,

graphic file with name nn3c09265_m015.jpg

where n represents the number of ligand monomers in vacuum, E[NC–ligand] is the energy of the complexed-nanocrystal energy, E[ligand] is the energy of the ligand monomers in vacuum, and E[NC] is the energy of the noncomplexed nanocrystal.

We obtained average complexation energies of −50.5, −32.1, and −22.6 kcal/mol for the ⟨100⟩-, 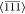Inline graphic-, and ⟨111⟩-facets, respectively. To do so, we considered as the initial system the one depicted in Figure 4B(i) and gradually added CdCl2 on each facet. Interestingly, after implementing this backfilling procedure, the HOMO–LUMO gap energy remains wide open and both the HOMO and the LUMO continue to exhibit delocalization consistently, even when all vacant sites are filled.

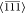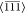This result stems from the uniform rearrangement of the CdCl2 molecules across the whole QD, especially those placed on Inline graphic- and ⟨111⟩-facets, allowing both the Cd and Se to maintain a high coordination number larger than or equal to 3. The final QD model presents a high ligand density at approximately 5 ligands/nm2, which is larger than the experimentally observed value of 3.5 ligands/nm2.62 This indicates that to prepare a QD model for calculations that match the experimental ligand density, it is important to follow the order of complexation energies. 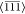To achieve a ligand density of 3.5 ligands/nm2, one should first completely fill the ⟨100⟩-facets, followed by 45% filling of the Inline graphic-facets. The ⟨111⟩-facets remain ligand free in this case. We note that, since the procedure starts from the vacancy-rich structures depicted in Figure 4B, the ⟨111⟩-facets remain full of vacancies and the Inline graphic-facets contain 55% of the vacancies. Once this experimental ligand density is achieved, the theoretical Cd:Se ratio yields 1.19. This value falls within the range of Cd/Se ratios reported in the studies by Karel Čapek et al.66 and Fritzinger et al.,67 which are 1.16 and 1.23, respectively. This procedure indicates that for ligand passivated surfaces, stable solutions with considerable HOMO–LUMO gap energies can be obtained without introduction of vacancies. The effects of vacancies and ligand passivation are similar in the sense that both prevent the formation of surface bands.

Transferability to Other QD Models

To test the generality of these results, we extended the approach developed for the Cd360 model to different II–VI systems: CdS, CdTe, ZnSe, ZnS, and ZnTe for the case of maximum surface coverage. Interestingly, we did not observe any significant differences; indeed, similarly to the Cd360 structure, all of these QD models featured delocalized HOMO and LUMO states and also wide HOMO–LUMO gap energies; see Figure 5. Note that the HOMO–LUMO gap energies obtained in this work show the same trend among II–VI structures with relation to the bulk band gap energy when using PBE functionals.68 This implies that the formation of surface localized states, and their elimination by appropriate passivation with Z-type ligands, is a general feature of II–VI zinc blende QDs and, in turn, a general feature of II–VI and III–V.13 We have also tested the recently developed AK13 functional that should provide a better estimate of the band gaps and do indeed find that the band gaps follow the expected trend for different semiconductors and are roughly in line with the band gaps expected for these QD sizes.68

Figure 5.

Figure 5

Open in a new tab

(A) Sketch of the different Cd(Zn)360 models used. (B) Evolution of the HOMO–LUMO gap energy as a function of the composition of the QD. The colors displayed on the names of the materials represent the atom colors in part A. Notice the comparison between functionals PBE (orange) and AK13 (blue). (C) Contour plots of the HOMO and LUMO of each system. (D) HOMO–LUMO gap energy tuning based on the percentage of Cd(Zn)Cl2 monomers backfilled in the different QDs. Blue and black-gray tonality lines represent QDs that are comprised of Cd and Zn cations, respectively.

As reconstruction of the QD surface makes it possible to create larger QD models that still show the expected behavior (i.e., a band gap and delocalized band edges), the fully reconstructed model of Cd360 can now also be used to create archetypal core/shell structures, such as type-I and type-II heterostructures. First, in Figure 6, we compare the Cd360 model with a CdSe/ZnS core/shell QD, both without and with surface reconstruction. The core/shell model consists of a Cd68Se55 core (that is, the smallest QD model in Figure 1) and ∼2 layers of ZnS shell, leading to a total composition of Cd68Se55/Zn292S254Cl102 and Cd68Se55/Zn292S226Cl158 for the unreconstructed and reconstructed models, respectively (see Figure S10 for a view of the inside of the reconstructed core/shell QD). The unreconstructed CdSe/ZnS model in Figure 6A(iii) clearly shows surface localized HOMO and LUMO wave functions and a metallic DOS, very similar to the pure CdSe model of the same size in Figure 6A(i). This shows that the appearance of a band of surface localized states is a property of the surface facet and is not sensitive to the core. The reconstructed CdSe/ZnS system shown in Figure 6A(iv) exhibits significantly delocalized HOMO and LUMO wave functions and a well-defined HOMO–LUMO gap.

Figure 6.

Figure 6

Open in a new tab

Comparison of the Cd360 model with the CdSe/ZnS core/shell system with and without surface reconstruction. Only the reconstructed versions of CdSe/ZnS and CdSe/ZnTe core/shell models are compared one to each other. (A) Structures of both the unreconstructed and reconstructed core-only and the CdSe/ZnS core/shell models and reconstructed CdSe/ZnTe core/shell model. (B) DOS of each system with their respective HOMO–LUMO gap energies. (C) Contour plots of the HOMO and LUMO of each system.

We notice that, in the reconstructed CdSe/ZnS system, the HOMO is overall mainly localized on the CdSe core with some leakage to the ZnS shell, while the LUMOs are mainly in the shell. This can be seen in the HOMO and LUMO wave function plots in Figure 6C and more clearly in the relative contributions of core (orange) and shell (dark blue) to the HOMO and LUMO levels in the density-of-states plot in Figure 6B(iv).

Employing a typical band-alignment classification, this suggests a quasi-type-I band alignment against the expected pure type-I. Second, contrary to the CdSe/ZnS system, the CdSe/ZnTe core/shell QD, with composition Cd68Se55/Zn292Te226Cl158, displays features of a type-II alignment in agreement to that observed in the bulk, e.g., the VB edge delocalized in the shell and CB mostly defined in the core; see Figure 6C. In QDs quantum confinement of the core and shell can influence the relative alignment of the two materials. Furthermore, the band alignment will be sensitive to the charge distribution on the surface and in the ligand shell, which in the calculations could still deviate from the experimental surface composition. This may explain why in these relatively small (but computationally large) core–shell models, the observed alignment differs from what is expected in the bulk. Therefore, for further study of these core/shell models, the effect of the core and shell size and surface composition must be carefully considered. However, these results show that given proper termination of the QD surface DFT can be used to study larger QDs and core/shell systems.

Conclusions

In conclusion, we used DFT calculations to study the electronic properties of larger QDs (up to ∼4.5 nm in diameter) with realistic surface passivation. It is found that increasing the size of traditional QD models leads to the disappearance of the band gap and the localization of HOMO and LUMO on the surface. We have shown that the introduction of surface reconstructions on all of the ⟨100⟩-, 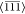Inline graphic-, and ⟨111⟩-facets gives rise to the delocalization of both the HOMO and LUMO and a significant increase in the band gap. Furthermore, refilling these surface reconstructions with Z-type ligands resulted in a similar delocalization of the HOMO and LUMO levels along with the appearance of band gap energies closely aligned with the experimental values. These results show that the QD surface plays a pivotal role in the delocalization of the wave function, which depends not only on the presence of (in)organic ligands but also on the surface geometry of the QD facets. The new surface geometries identified in this work enable the study of quantum dots of realistic sizes as well as technologically important core–shell QDs with density functional theory methods.

Methods

Geometry optimizations were performed at the DFT level using a Perdew–Burke–Ernzerhof exchange–correlation functional (PBE)39 and double-ζ basis set, as implemented in the CP2K quantum chemistry software package.40 Relativistic effects were considered through the effective core potentials. The structures were relaxed until the following criteria were met: max_force, 4.5 × 10–4 Ha/bohr; rms_force, 3.0 × 10–4 Ha/bohr; max_step, 3.0 × 10–3 bohr; rms_step, 1.5 × 10–3 bohr. For the core/shell QD without surface reconstructions, it was necessary to increase max_force to 2.5 × 10–3 Ha/bohr, which could be indicative of strain at the core/shell interface. The isosurface value used for the charge density plots is |0.005| (e–/bohr3)1/2. The inverse participation ratio (IPR) and the crystal orbital overlap population (COOP) (the computational details of which have been discussed previously)41 were calculated using the workflows implemented in the nano-QMFlows package.42 Further details can be found in the main text and the appendix of ref (42).

Acknowledgments

A.H. acknowledges the European Research Council Horizon 2020 ERC Grant Agreement No. 678004 (Doping on Demand) for financial support. This work was sponsored by NWO Exact and Natural Sciences for the use of supercomputer facilities and was carried out on the Dutch national e-infrastructure with the support of the SURF Cooperative. This study was supported by IKUR Strategy under the collaboration agreement between Ikerbasque Foundation and BCMaterials on behalf of the Department of Education of the Basque Government. Z.H. acknowledges support from FWO-Vlaanderen (Projects G0B2921N and G0C5723N) and Ghent University (01G02124).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.3c09265.

  • Additional computing details including different methods and software packages, effects of using formate ligands instead of chlorides, limitations observed in the pattern shown in Figure 3D, details on the pattern used for the ⟨100⟩-facets, and modeling features of the CdSe/ZnS core/shell model (PDF)

Author Contributions

⊥ J.L. and I.d.F. contributed equally to this work.

The authors declare no competing financial interest.

Supplementary Material

nn3c09265_si_001.pdf (1.9MB, pdf)

References

  1. Pascazio R.; Zito J.; Infante I. An Overview of Computational Studies on Colloidal Semiconductor Nanocrystals. Chim. Int. J. Chem. 2021, 75, 427–434. 10.2533/chimia.2021.427. [DOI] [PubMed] [Google Scholar]
  2. Prezhdo O. V. Photoinduced Dynamics in Semiconductor Quantum Dots: Insights from Time-Domain Ab Initio Studies. Acc. Chem. Res. 2009, 42, 2005–2016. 10.1021/ar900157s. [DOI] [PubMed] [Google Scholar]
  3. Kilina S. V.; Tamukong P. K.; Kilin D. S. Surface Chemistry of Semiconducting Quantum Dots: Theoretical Perspectives. Acc. Chem. Res. 2016, 49, 2127–2135. 10.1021/acs.accounts.6b00196. [DOI] [PubMed] [Google Scholar]
  4. Hong Y.; Wu Y.; Wu S.; Wang X.; Zhang J. Overview of Computational Simulations in Quantum Dots. Isr. J. Chem. 2019, 59, 661–672. 10.1002/ijch.201900026. [DOI] [Google Scholar]
  5. Hens Z.; De Roo J. Atomically Precise Nanocrystals. J. Am. Chem. Soc. 2020, 142, 15627–15637. 10.1021/jacs.0c05082. [DOI] [PubMed] [Google Scholar]
  6. Eichkorn K.; Ahlrichs R. Cadmium Selenide Semiconductor Nanocrystals: A Theoretical Study. Chem. Phys. Lett. 1998, 288, 235–242. 10.1016/S0009-2614(98)00306-6. [DOI] [Google Scholar]
  7. Puzder A.; Williamson A. J.; Gygi F.; Galli G. Self-Healing of CdSe Nanocrystals: First-Principles Calculations. Phys. Rev. Lett. 2004, 92, 217401. 10.1103/PhysRevLett.92.217401. [DOI] [PubMed] [Google Scholar]
  8. Deglmann P.; Ahlrichs R.; Tsereteli K. Theoretical Studies of Ligand-Free Cadmium Selenide and Related Semiconductor Clusters. J. Chem. Phys. 2002, 116, 1585–1597. 10.1063/1.1427718. [DOI] [Google Scholar]
  9. Voznyy O. Mobile Surface Traps in CdSe Nanocrystals with Carboxylic Acid Ligands. J. Phys. Chem. C 2011, 115, 15927–15932. 10.1021/jp205784g. [DOI] [Google Scholar]
  10. Snee P. T. DFT Calculations of InP Quantum Dots: Model Chemistries, Surface Passivation, and Open-Shell Singlet Ground States. J. Phys. Chem. C 2021, 125, 11765–11772. 10.1021/acs.jpcc.1c02874. [DOI] [Google Scholar]
  11. Rusishvili M.; Wippermann S.; Talapin D. V.; Galli G. Stoichiometry of the Core Determines the Electronic Structure of Core–shell III–V/II–VI Nanoparticles. Chem. Mater. 2020, 32, 9798–9804. 10.1021/acs.chemmater.0c03939. [DOI] [Google Scholar]
  12. Yazdani N.; Bozyigit D.; Vuttivorakulchai K.; Luisier M.; Infante I.; Wood V. Tuning Electron-Phonon Interactions in Nanocrystals through Surface Termination. Nano Lett. 2018, 18, 2233–2242. 10.1021/acs.nanolett.7b04729. [DOI] [PubMed] [Google Scholar]
  13. Houtepen A. J.; Hens Z.; Owen J. S.; Infante I. On the Origin of Surface Traps in Colloidal II-VI Semiconductor Nanocrystals. Chem. Mater. 2017, 29, 752–761. 10.1021/acs.chemmater.6b04648. [DOI] [Google Scholar]
  14. Voznyy O.; Thon S. M.; Ip A. H.; Sargent E. H. Dynamic Trap Formation and Elimination in Colloidal Quantum Dots. J. Phys. Chem. Lett. 2013, 4, 987–992. 10.1021/jz400125r. [DOI] [PubMed] [Google Scholar]
  15. Du Fossé I.; Boehme S. C.; Infante I.; Houtepen A. J. Dynamic Formation of Metal-Based Traps in Photoexcited Colloidal Quantum Dots and Their Relevance for Photoluminescence. Chem. Mater. 2021, 33, 3349–3358. 10.1021/acs.chemmater.1c00561. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Groeneveld E.; Delerue C.; Allan G.; Niquet Y. M.; De Mello Donegá C. Size Dependence of the Exciton Transitions in Colloidal CdTe Quantum Dots. J. Phys. Chem. C 2012, 116, 23160–23167. 10.1021/jp3080942. [DOI] [Google Scholar]
  17. Keuleyan S. E.; Guyot-Sionnest P.; Delerue C.; Allan G. Mercury Telluride Colloidal Quantum Dots: Electronic Structure, Size-Dependent Spectra, and Photocurrent Detection up to 12 Mm. ACS Nano 2014, 8, 8676–8682. 10.1021/nn503805h. [DOI] [PubMed] [Google Scholar]
  18. Allan G.; Delerue C. Tight-Binding Calculations of the Optical Properties of HgTe Nanocrystals. Phys. Rev. B - Condens. Matter Mater. Phys. 2012, 86, 165437. 10.1103/PhysRevB.86.165437. [DOI] [Google Scholar]
  19. Moreels I.; Lambert K.; Smeets D.; De Muynck D.; Nollet T.; Martins J. C.; Vanhaecke F.; Vantomme A.; Delerue C.; Allan G.; Hens Z. Size-Dependent Optical Properties of Colloidal PbS Quantum Dots. ACS Nano 2009, 3, 3023–3030. 10.1021/nn900863a. [DOI] [PubMed] [Google Scholar]
  20. Califano M.; Gómez-Campos F. M. Universal Trapping Mechanism in Semiconductor Nanocrystals. Nano Lett. 2013, 13, 2047–2052. 10.1021/nl4003014. [DOI] [PubMed] [Google Scholar]
  21. Gómez-Campos F. M.; Califano M. Hole Surface Trapping in CdSe Nanocrystals: Dynamics, Rate Fluctuations, and Implications for Blinking. Nano Lett. 2012, 12, 4508–4517. 10.1021/nl3016279. [DOI] [PubMed] [Google Scholar]
  22. Wang L.-W.; Zunger A. Pseudopotential Calculations of Nanoscale CdSe Quantum. Phys. Rev. B - Condens. Matter Mater. Phys. 1996, 53, 9579–9582. 10.1103/PhysRevB.53.9579. [DOI] [PubMed] [Google Scholar]
  23. Fu H.; Zunger A. InP Quantum Dots: Electronic Structure, Surface Effects, and the Redshifted Emission. Phys. Rev. B - Condens. Matter Mater. Phys. 1997, 56, 1496–1508. 10.1103/PhysRevB.56.1496. [DOI] [Google Scholar]
  24. Delerue C. J.; Lannoo M.. Nanostructures: Theory and Modeling; Springer: Berlin, Heidelberg, 2004. 10.1007/978-3-662-08903-3. [DOI] [Google Scholar]
  25. McIsaac A. R.; Goldzak T.; Van Voorhis T. It Is a Trap!: The Effect of Self-Healing of Surface Defects on the Excited States of CdSe Nanocrystals. J. Phys. Chem. Lett. 2023, 14, 1174–1181. 10.1021/acs.jpclett.2c03317. [DOI] [PubMed] [Google Scholar]
  26. Yu M.; Fernando G. W.; Li R.; Papadimitrakopoulos F.; Shi N.; Ramprasad R. First Principles Study of CdSe Quantum Dots: Stability, Surface Unsaturations, and Experimental Validation. Appl. Phys. Lett. 2006, 88, 231910 10.1063/1.2209195. [DOI] [Google Scholar]
  27. Cosseddu S.; Infante I. Force Field Parametrization of Colloidal CdSe Nanocrystals Using an Adaptive Rate Monte Carlo Optimization Algorithm. J. Chem. Theory Comput. 2017, 13, 297–308. 10.1021/acs.jctc.6b01089. [DOI] [PubMed] [Google Scholar]
  28. Pascazio R.; Zaccaria F.; Van Beek B.; Infante I. Classical Force-Field Parameters for CsPbBr3 Perovskite Nanocrystals. J. Phys. Chem. C 2022, 126, 9898–9908. 10.1021/acs.jpcc.2c00600. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Zhang H.; Ma X.; Lin Q.; Zeng Z.; Wang H.; Li L. S.; Shen H.; Jia Y.; Du Z. High-Brightness Blue InP Quantum Dot-Based Electroluminescent Devices: The Role of Shell Thickness. J. Phys. Chem. Lett. 2020, 11, 960–967. 10.1021/acs.jpclett.9b03567. [DOI] [PubMed] [Google Scholar]
  30. Voigt D.; Bredol M.; Gonabadi A. A General Strategy for CuInS2 Based Quantum Dots with Adjustable Surface Chemistry. Opt. Mater. (Amst) 2021, 115, 110994 10.1016/j.optmat.2021.110994. [DOI] [Google Scholar]
  31. Voznyy O.; Sargent E. H. Atomistic Model of Fluorescence Intermittency of Colloidal Quantum Dots. Phys. Rev. Lett. 2014, 112, 157401. 10.1103/PhysRevLett.112.157401. [DOI] [PubMed] [Google Scholar]
  32. Singh S.; Tomar R.; Ten Brinck S.; De Roo J.; Geiregat P.; Martins J. C.; Infante I.; Hens Z. Colloidal CdSe Nanoplatelets, A Model for Surface Chemistry/Optoelectronic Property Relations in Semiconductor Nanocrystals. J. Am. Chem. Soc. 2018, 140, 13292–13300. 10.1021/jacs.8b07566. [DOI] [PubMed] [Google Scholar]
  33. Brus L. Electronic Wave Functions in Semiconductor Clusters: Experiment and Theory. J. Phys. Chem. 1986, 90, 2555–2560. 10.1021/j100403a003. [DOI] [Google Scholar]
  34. Chukwuocha E. O.; Onyeaju M. C.; Harry T. S. T. Theoretical Studies on the Effect of Confinement on Quantum Dots Using the Brus Equation. World J. Condens. Matter Phys. 2012, 02, 96–100. 10.4236/wjcmp.2012.22017. [DOI] [Google Scholar]
  35. Nienhaus L.; Goings J. J.; Nguyen D.; Wieghold S.; Lyding J. W.; Li X.; Gruebele M. Imaging Excited Orbitals of Quantum Dots: Experiment and Electronic Structure Theory. J. Am. Chem. Soc. 2015, 137, 14743–14750. 10.1021/jacs.5b09272. [DOI] [PubMed] [Google Scholar]
  36. Maltezopoulos T.; Bolz A.; Meyer C.; Heyn C.; Hansen W.; Morgenstern M.; Wiesendanger R. Wave-Function Mapping of Inas Quantum Dots by Scanning Tunneling Spectroscopy. Phys. Rev. Lett. 2003, 91, 196804 10.1103/PhysRevLett.91.196804. [DOI] [PubMed] [Google Scholar]
  37. Shirasaki Y.; Supran G. J.; Bawendi M. G.; Bulović V. Emergence of Colloidal Quantum-Dot Light-Emitting Technologies. Nat. Photonics 2013, 7, 13–23. 10.1038/nphoton.2012.328. [DOI] [Google Scholar]
  38. Donega C. d. M. Synthesis and Properties of Colloidal Heteronanocrystals. Chem. Soc. Rev. 2011, 40, 1512–1546. 10.1039/C0CS00055H. [DOI] [PubMed] [Google Scholar]
  39. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–6868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  40. Hutter J.; Iannuzzi M.; Schiffmann F.; Vandevondele J. CP2K: Atomistic Simulations of Condensed Matter Systems. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 15–25. 10.1002/wcms.1159. [DOI] [Google Scholar]
  41. Du Fossé I.; Mulder J. T.; Almeida G.; Spruit A. G. M.; Infante I.; Grozema F. C.; Houtepen A. J. Limits of Defect Tolerance in Perovskite Nanocrystals: Effect of Local Electrostatic Potential on Trap States. J. Am. Chem. Soc. 2022, 144, 11059–11063. 10.1021/jacs.2c02027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Zapata F.; Ridder L.; Hidding J.; Jacob C. R.; Infante I.; Visscher L. QMflows: A Tool Kit for Interoperable Parallel Workflows in Quantum Chemistry. J. Chem. Inf. Model. 2019, 59, 3191–3197. 10.1021/acs.jcim.9b00384. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Du Fossé I.; Ten Brinck S.; Infante I.; Houtepen A. J. Role of Surface Reduction in the Formation of Traps in N-Doped II-VI Semiconductor Nanocrystals: How to Charge without Reducing the Surface. Chem. Mater. 2019, 31, 4575–4583. 10.1021/acs.chemmater.9b01395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Du Fossé I.; Lal S.; Hossaini A. N.; Infante I.; Houtepen A. J. Effect of Ligands and Solvents on the Stability of Electron Charged CdSe Colloidal Quantum Dots. J. Phys. Chem. C 2021, 125, 23968–23975. 10.1021/acs.jpcc.1c07464. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Cosseddu S.; Pascazio R.; Giansante C.; Manna L.; Infante I. Ligand Dynamics on the Surface of CdSe Nanocrystals. Nanoscale 2023, 15, 7410–7419. 10.1039/D2NR06681E. [DOI] [PubMed] [Google Scholar]
  46. Anderson N. C.; Hendricks M. P.; Choi J. J.; Owen J. S. Ligand Exchange and the Stoichiometry of Metal Chalcogenide Nanocrystals: Spectroscopic Observation of Facile Metal-Carboxylate Displacement and Binding. J. Am. Chem. Soc. 2013, 135, 18536–18548. 10.1021/ja4086758. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Greaney M. J.; Couderc E.; Zhao J.; Nail B. A.; Mecklenburg M.; Thornbury W.; Osterloh F. E.; Bradforth S. E.; Brutchey R. L. Controlling the Trap State Landscape of Colloidal CdSe Nanocrystals with Cadmium Halide Ligands. Chem. Mater. 2015, 27, 744–756. 10.1021/cm503529j. [DOI] [Google Scholar]
  48. Voznyy O.; Zhitomirsky D.; Stadler P.; Ning Z.; Hoogland S.; Sargent E. H. A Charge-Orbital Balance Picture of Doping in Colloidal Quantum Dot Solids. ACS Nano 2012, 6, 8448–8455. 10.1021/nn303364d. [DOI] [PubMed] [Google Scholar]
  49. Kirkwood N.; Monchen J. O. V.; Crisp R. W.; Grimaldi G.; Bergstein H. A. C.; Du Fossé I.; Van Der Stam W.; Infante I.; Houtepen A. J. Finding and Fixing Traps in II-VI and III-V Colloidal Quantum Dots: The Importance of Z-Type Ligand Passivation. J. Am. Chem. Soc. 2018, 140, 15712–15723. 10.1021/jacs.8b07783. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Page R. C.; Espinobarro-Velazquez D.; Leontiadou M. A.; Smith C.; Lewis E. A.; Haigh S. J.; Li C.; Radtke H.; Pengpad A.; Bondino F.; Magnano E.; Pis I.; Flavell W. R.; O’Brien P.; Binks D. J. Near-Unity Quantum Yields from Chloride Treated CdTe Colloidal Quantum Dots. Small 2015, 11, 1548–1554. 10.1002/smll.201402264. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Azpiroz J. M.; Ugalde J. M.; Infante I. Benchmark Assessment of Density Functional Methods on Group II-VI MX (M = Zn, Cd; X = S, Se, Te) Quantum Dots. J. Chem. Theory Comput. 2014, 10, 76–89. 10.1021/ct400513s. [DOI] [PubMed] [Google Scholar]
  52. Harrison W. Tight-Binding Theory of Surface States in Metals. Phys. Scr. 2003, 67 (3), 253–259. 10.1238/Physica.Regular.067a00253. [DOI] [Google Scholar]
  53. Duke C. B. Semiconductor Surface Reconstruction: The Structural Chemistry of Two-Dimensional Surface Compounds. Chem. Rev. 1996, 96, 1237–1260. 10.1021/cr950212s. [DOI] [PubMed] [Google Scholar]
  54. Chadi D. J. Vacancy-Induced 2 × 2 Reconstruction of the Ga(111) Surface of GaAs. Phys. Rev. Lett. 1984, 52, 1911–1914. 10.1103/PhysRevLett.52.1911. [DOI] [Google Scholar]
  55. Haberern K. W.; Pashley M. D. GaAs(111) A-(2 × 2) Reconstruction Studied by Scanning Tunneling Microscopy. Phys. Rev. B 1990, 41, 3226–3229. 10.1103/PhysRevB.41.3226. [DOI] [PubMed] [Google Scholar]
  56. Chadi D. J. Atomic Structure of Polar (111) Surfaces of GaAs and ZnSe. J. Vac. Sci. Technol. A: Vacuum, Surfaces, and Films 1986, 4, 944–946. 10.1116/1.573761. [DOI] [Google Scholar]
  57. Manna L.; Wang L. W.; Cingolani R.; Alivisatos A. P. First-Principles Modeling of Unpassivated and Surfactant-Passivated Bulk Facets of Wurtzite CdSe: A Model System for Studying the Anisotropic Growth of CdSe Nanocrystals. J. Phys. Chem. B 2005, 109, 6183–6192. 10.1021/jp0445573. [DOI] [PubMed] [Google Scholar]
  58. Tong S. Y.; Xu G.; Mei W. N. Vacancy-Buckling Model for the (2 × 2) GaAs (111) Surface. Phys. Rev. Lett. 1984, 52, 1693. 10.1103/PhysRevLett.52.1693. [DOI] [Google Scholar]
  59. Srivastava G. P. Theory of Semiconductor Surface Reconstruction. Rep. Prog. Phys. 1997, 60, 561–613. 10.1088/0034-4885/60/5/002. [DOI] [Google Scholar]
  60. Chadi D. J. Atomic Structure of the (2 × 2) Reconstructed GaAs(1̅1̅1̅) Surface: A Multivacancy Model. Phys. Rev. Lett. 1986, 57, 102–105. 10.1103/PhysRevLett.57.102. [DOI] [PubMed] [Google Scholar]
  61. Biegelsen D. K.; Bringans R. D.; Northrup J. E.; Swartz L.-E. Reconstructions of GaAs(1̅ 1̅ 1̅) Surfaces Observed by Scanning Tunneling Microscopy. Phys. Rev. Lett. 1990, 65, 452–455. 10.1103/PhysRevLett.65.452. [DOI] [PubMed] [Google Scholar]
  62. Singh S.; Leemans J.; Zaccaria F.; Infante I.; Hens Z. Ligand Adsorption Energy and the Postpurification Surface Chemistry of Colloidal Metal Chalcogenide Nanocrystals. Chem. Mater. 2021, 33, 2796–2803. 10.1021/acs.chemmater.0c04761. [DOI] [Google Scholar]
  63. Saniepay M.; Mi C.; Liu Z.; Abel E. P.; Beaulac R. Insights into the Structural Complexity of Colloidal Cdse Nanocrystal Surfaces: Correlating the Efficiency of Nonradiative Excited-State Processes to Specific Defects. J. Am. Chem. Soc. 2018, 140, 1725–1736. 10.1021/jacs.7b10649. [DOI] [PubMed] [Google Scholar]
  64. Lv L.; Li J.; Wang Y.; Shu Y.; Peng X. Monodisperse CdSe Quantum Dots Encased in Six (100) Facets via Ligand-Controlled Nucleation and Growth. J. Am. Chem. Soc. 2020, 142, 19926–19935. 10.1021/jacs.0c06914. [DOI] [PubMed] [Google Scholar]
  65. Liu L.; Zhuang Z.; Xie T.; Wang Y. G.; Li J.; Peng Q.; Li Y. Shape Control of CdSe Nanocrystals with Zinc Blende Structure. J. Am. Chem. Soc. 2009, 131, 16423–16429. 10.1021/ja903633d. [DOI] [PubMed] [Google Scholar]
  66. Karel Čapek R.; Moreels I.; Lambert K.; De Muynck D.; Zhao Q.; Van Tomme A.; Vanhaecke F.; Hens Z. Optical Properties of Zincblende Cadmium Selenide Quantum Dots. J. Phys. Chem. C 2010, 114 (14), 6371–6376. 10.1021/jp1001989. [DOI] [Google Scholar]
  67. Fritzinger B.; Čapek R. K.; Lambert K.; Martins J. C.; Hens Z. Utilizing Self-Exchange to Address the Binding of Carboxylic Acid Ligands to CdSe Quantum Dots. J. Am. Chem. Soc. 2010, 132 (29), 10195–10201. 10.1021/ja104351q. [DOI] [PubMed] [Google Scholar]
  68. Tran F.; Blaha P. Importance of the Kinetic Energy Density for Band Gap Calculations in Solids with Density Functional Theory. J. Phys. Chem. A 2017, 121, 3318–3325. 10.1021/acs.jpca.7b02882. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn3c09265_si_001.pdf (1.9MB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES