Nonrandom Exposure to Exogenous Shocks

Abstract

We develop a new approach to estimating the causal effects of treatments or instruments that combine multiple sources of variation according to a known formula. Examples include treatments capturing spillovers in social or transportation networks and simulated instruments for policy eligibility. We show how exogenous shocks to some, but not all, determinants of such variables can be leveraged while avoiding omitted variables bias. Our solution involves specifying counterfactual shocks that may as well have been realized and adjusting for a summary measure of non-randomness in shock exposure: the average treatment (or instrument) across shock counterfactuals. We use this approach to address bias when estimating employment effects of market access growth from Chinese high-speed rail construction.

1. Introduction

Many questions in economics involve the causal effects of treatments which are computed from multiple sources of variation, and sometimes observed at different “levels,” according to a known formula. Consider three examples. First, when estimating spillovers from a randomized intervention, one might count the number of an individual’s neighbors who were selected for the intervention. This spillover treatment combines variation in who was selected with variation in who neighbors whom. Second, in studies of transportation infrastructure effects, one might measure the growth of regional market access: a treatment computed from the location and timing of transportation upgrades and the spatial distribution of economic activity in a country. A third example is a treatment capturing individual eligibility for a public program, such as Medicaid, which is jointly determined by the eligibility policy in the individual’s state and her household’s demographics and income.¹

This paper develops a new approach to estimating the effects of such composite variables when some, but not all, of their determinants are generated by a true or natural experiment. We ask, for example, how one can estimate market access effects by leveraging the timing of new railroad line construction as exogenous shocks, when the other determinants of market access (such as the pre-determined location of large markets and planned lines) are non-random.

We first show that omitted variable bias (OVB) may confound conventional regression approaches in such settings. Bias arises from different observations receiving systematically different values of the treatment because of their individual non-random “exposure” to the exogenous shocks. For example, even when construction is delayed for a random set of lines, regions that are economically or geographically more central will tend to see a larger growth in market access because they are closer to a typical potential line (and thus closer to a typical constructed line). Regression estimation of market access effects then fails without an additional assumption on the exogeneity of economic geography: that more exposed (e.g., central) regions do not differ in their relevant unobservables, such as changes in local productivity or amenities. Intuitively, randomizing transportation upgrades does not randomize the market access growth generated by them.

Our solution to the OVB challenge is based on the specification of counterfactual exogenous shocks that might as well have been realized. This approach views the observed shocks as one realization of some data-generating process—what we call the shock assignment process—which can be simulated to obtain counterfactuals. In a true experiment, the shock assignment process is given by the randomization protocol. In natural experiments, shock counterfactuals make explicit the contrasts which the researcher wishes to leverage, for instance by specifying permutations of the shocks that were as likely to have occurred. For example, if line construction delays are considered as-good-as-random, one might produce counterfactual network maps by randomly exchanging the lines which were completed earlier and later.

Valid shock counterfactuals can be used to avoid OVB by a “recentering” procedure which involves measuring and appropriately adjusting for a single confounder: the expected treatment. To do so, a researcher draws counterfactual shocks from the assignment process and recomputes the instrument many times. Then, for each observation, the treatment is averaged across these many draws to obtain the expected treatment. Finally, the expected treatment is subtracted from the realized treatment to obtain the recentered treatment. We show that using this recentered treatment as an instrument for the realized treatment removes the bias from non-random shock exposure. Intuitively, observations only get high vs. low values of the recentered treatment because the observed shocks were drawn instead of the counterfactuals, which is assumed to happen by chance. For example, when the expected treatment is constructed by permuting the timing of new line construction, regressions that instrument with recentered market access growth compare regions which received higher vs. lower market access growth because proximate lines were constructed early vs. late, and not because of the economic geography. Another closely related solution to OVB is to include the expected treatment as a control in the regression of an outcome on the realized treatment; this can be viewed as recentering the treatment while also removing some residual variation in the outcome, in a control function approach.²

This approach to causal inference with composite variables, in which some determinants are labeled as exogenous and characterized by an assignment process, can be seen as formalizing the natural experiment of interest and bringing composite variables to familiar econometric territory.³ Indeed, the conditions we impose on the exogenous shocks are similar to those which might be used if the shocks were directly used as treatments: e.g., if shocks to the timing of railroad line upgrades were used in a regression of outcomes defined at the “level” of those lines. Recentering ensures identification from the natural experiment, even when the regression is estimated at a different level (e.g., across regions instead of lines).

Our framework further allows the treatment to have endogenous or unobserved determinants. In this case one may construct candidate composite instruments based on the treatment’s exogenous and predetermined components. The same OVB problem arises in this instrumental variable (IV) case, and it can again be solved by recentering the candidate instrument by its expectation over the shock assignment process. Controlling for the expected instrument is again another solution.

We establish several attractive properties of the recentering approach, beyond our primary results on OVB. First, recentered estimators are consistent provided the exogenous shocks induce sufficient cross-sectional variation in the instrument and treatment—regardless of the correlation structure of unobservables. Second, shock counterfactuals can be used for exact finite-sample inference and specification tests via randomization inference (RI). Finally, while our consistency and RI results rely on an assumption of constant treatment effects, recentered IV estimators generally capture a convex average of heterogeneous effects under a natural first-stage monotonicity condition.

We apply this framework to estimate the employment effects of market access (MA) growth due to new high-speed railway system in China. We show how recentering can help leverage variation in the timing of transportation upgrades to purge OVB. Simple regressions of employment growth on MA growth suggest a large and statistically significant effect, which is only partially reduced by conventional geography-based controls. But this effect is eliminated when we adjust for expected MA growth, measured by permuting constructed HSR lines with similar ones that were planned but not built. The unadjusted estimates thus reflect the fact that employment grew in regions which were more exposed to planned high-speed rail construction, whether or not construction actually occurred.

Econometrically, expected treatment and instrument adjustment is similar to propensity score methods for removing OVB (Rosenbaum and Rubin 1983), with two key differences. First, we propose using the structure of composite treatments and instruments to compute their expectation from more primitive assumptions on the assignment process for exogenous shocks. This approach is similar to how Borusyak et al. (2022) and Aronow and Samii (2017) address OVB when using linear shift-share instruments and network treatments, respectively. It differs from conventional methods of directly estimating propensity scores; such methods are typically infeasible in the settings we consider because the exposure to exogenous shocks is intractably high-dimensional. Second, our regression-based adjustment differs from conventional approaches of weighting by or matching on propensity scores.⁴ Regression adjustment is more popular in applied research, avoids practical issues of limited overlap (due to, e.g., propensity scores that are close to zero or one), does not require the treatments or instruments to be binary, and is natural for estimating constant structural parameters or convex averages of heterogeneous treatment effects.

The remainder of this paper is organized as follows. The next section motivates our analysis with three examples related to network spillovers, market access effects, and Medicaid eligibility effects. Section 3 develops our general framework and results. Section 4 presents our application, and Section 5 concludes. Additional results and extensions are given in an earlier working paper, Borusyak and Hull (2021, henceforth BH).

2. Motivating Examples

We develop three stylized examples, inspired respectively by the settings of Miguel and Kremer (2004), Donaldson and Hornbeck (2016), and Currie and Gruber (1996), to illustrate the main insights of this paper. In each example we consider estimating the parameter $\beta$ of a causal or structural model which relates an outcome $y_i$ to a treatment $x_i$,

$$y_i={\beta x}_i+{\epsilon }_i,$$ (1)

for a set of units $i=1,\dots ,N$ with an unobserved error ${\epsilon }_i$. The common feature of the examples is that $x_i$ is computed from multiple sources of variation by a known formula.

Network spillovers:

Suppose $y_i$ is student $i$’s educational achievement and $x_i$ counts the number of $i$’s neighbors who have been dewormed in an intervention:

$$x_i=\sum _{k=1}^{N}N{eighbor}_{ik}{Dewormed}_k.$$

Here ${Dewormed}_k\in \{0,1\}$ is an indicator for student $k$ being selected for the deworming intervention and ${Neighbor}_{ik}\in \{0,1\}$ indicates that $i$ and $k$ are neighbors (i.e., connected by an observed network link). The error term ${\epsilon }_i$ captures $i$’s educational outcome when none of her neighbors are dewormed. This example is a stylized version of the main specification in Miguel and Kremer (2004).⁵

Market access:

Suppose $y_i$ is the growth of land values in region $i$ between two dates $t\in \{0,1\}$ and $x_i=\log M{A}_{i1}-\log M{A}_{i0}$ is the growth of regional market access (MA) due to improvements to the interregional railroad network. Market access is computed

$${MA}_{it}=\sum _{j=1}^N\frac{{Pop}_j}{\tau ({Network}_t,{Loc}_i,{Loc}_j)},$$

following standard models of economic geography (e.g. Redding and Venables (2004)). Here ${Pop}_j$ is the time-invariant population of region $j$, ${Network}_t$ is the set of railway lines and other types of transit which comprise the transportation network in operation at time $t$, ${Loc}_j$ is the location of region $j$ on the map, and $\tau (\cdot )$ is a function giving the travel time between regions $i$ and $j$. The error term ${\epsilon }_i$ captures location $i$’s land value growth in the absence of market access growth, due to some regional amenity and productivity shocks. Similar market access growth specifications are considered in, for example, Donaldson and Hornbeck (2016).

Medicaid eligibility:

Suppose $y_i$ is individual $i$’s health outcome and $x_i\in \{0,1\}$ indicates her eligibility for Medicaid. Let ${IncDem}_i$ be a vector of individual income and demographics, ${State}_i\in \{1,\dots ,50\}$ index $i$’s state of residence, and ${Policy}_k$ be state $k$’s eligibility policy: i.e. the set of income and demographic groups eligible for Medicaid in that state. Then

$$x_i=1[{IncDem}_i\in {Policy}_{{State}_i}].$$

The error term ${\epsilon }_i$ captures individual $i$’s outcome when she is ineligible for Medicaid. This example comes from Currie and Gruber (1996).

To estimate $\beta$ in each example, we consider a true or natural experiment that manipulates some of the determinants of $x_i$. Formally, we partition the variables from which $x=(x_1,\dots ,x_N)$ is computed into two groups: a set of shocks $g$ and a set of predetermined variables $w$. The shocks $g=(g_1,\dots ,g_K)$ are assumed to be exogenous, i.e. independent of the errors $\epsilon =({\epsilon }_1,\dots ,{\epsilon }_N)$. Shock exogeneity combines two conceptually distinct assumptions—that $g$ is as-good-as-randomly assigned, and that this assignment only affects the outcome of each unit $i$ via its treatment $x_i$ (an exclusion restriction). The shocks can be assigned at a different “level” than the observations, with $K\ne N$. The remaining variables $w$ have an arbitrary structure and $f_i(\cdot ;w)$ governs the mapping from the exogenous shocks to each unit’s treatment, i.e. the observation’s “exposure” to the shocks.⁶ We assume that $w$ is determined prior to the (natural) experiment and is unaffected by the shocks.

Network spillovers (cont.)

Suppose deworming is assigned in a randomized control trial (RCT) and ${\beta x}_i$ fully captures its spillover effects. Then $g={({Dewormed}_k)}_{k=1}^K$ collects the exogenous shocks, for $K=N$.⁷ The remaining determinants of the spillover treatments of all units, $w={({Neighbor}_{ik})}_{i,k=1}^N$, are fixed in the experiment.

Market access (cont.)

Suppose the timing of new railroads is exogenous. Specifically, suppose that among $K$ lines planned to be constructed by $t=1$ some are randomly delayed by unexpected engineering problems (unrelated to the trends in regional land values). Suppose also the model of economic geography is correctly specified, so $\beta \log M{A}_{it}$ fully captures the effects of transportation upgrades. Then $g={({Open}_k)}_{k=1}^K$ collects the exogenous shocks, where ${Open}_k$ is an indicator for whether planned line $k$ faces no delays. Assuming no other changes to the network at $t=1$, we can partition the determinants of MA growth into $g$ and $w=\left({({Loc}_i,{Pop}_i)}_{i=1}^N,{Network}_0\right)$ as ${Network}_1$ is fully determined by ${Network}_0$ and the set of newly opened lines.

Medicaid eligibility (cont.)

Suppose Medicaid policies across the $K=50$ states are exogenous, i.e. are chosen irrespective of the potential health outcomes and affect individual outcomes only via Medicaid eligibility. Then $g={({Policy}_k)}_{k=1}^K$ collects the exogenous shocks, with the other determinants of eligibility collected in $w={({IncDem}_i,{State}_i)}_{i=1}^N$.

The first point of this paper is that ordinary least squares (OLS) estimation of $\beta$ can suffer from OVB, despite the experimental variation underlying $x_i$.⁸ The OVB problem arises because some units receive systematically higher values of $x_i$ than others, as a consequence of their non-random exposure to the shocks. This systematic variation may be cross-sectionally correlated with the errors ${\epsilon }_i$, generating bias in OLS estimation of equation (1).

Network spillovers (cont.)

Even when deworming is randomly assigned to students, those with more neighbors (e.g., because they live in dense urban areas) will tend to have more dewormed neighbors and therefore be more exposed to the deworming intervention. Urban areas may have different educational outcomes for reasons unrelated to deworming, generating OVB.

Market access (cont.)

Even when the opening status of lines is as-good-as-randomly assigned, regions in the economic and geographic center of the country will tend to see more market access growth than peripheral regions as the former are closer to a typical potential line. Central regions may face different amenity and productivity shocks, generating OVB.

Medicaid eligibility (cont.)

Even when Medicaid policies are as-good-as-randomly assigned to states, poorer individuals will tend to see higher rates of eligibility. Poor individuals may face different health shocks, generating OVB.

Our second insight is that this OVB problem has a conceptually simple solution, which follows from viewing the set of realized $g$ as one draw from a shock assignment process and considering what counterfactual sets of exogenous shocks could have as likely been drawn. The specification of such counterfactuals allows one to measure and remove the systematic component of variation in the treatment which drives OVB. Specifically, the researcher recomputes the treatment $x_i$ of each unit $i$ across many counterfactual sets of shocks and takes their average to measure the expected treatment, ${\mu }_i$. We show that this ${\mu }_i$, which is co-determined by the exposure of $x_i$ to the shocks $g$ and the shock assignment process, is the sole confounder in equation (1). OVB can then be purged by “recentering” the treatment, i.e. instrumenting $x_i$ with ${\tilde{x}}_i=x_i-{\mu }_i$ in equation (1), or by simply adding ${\mu }_i$ as a control in OLS estimation. The key to removing bias with this approach is thus to credibly specify and average over shock counterfactuals—a task which is trivial in true experiments and which otherwise formalizes the natural experiment of interest.

Network spillovers (cont.)

With deworming assigned in an RCT, the shock assignment process is given by the known randomization protocol. If, say, each student has a 30% chance of being dewormed, the expected number of $i$’s dewormed neighbors over repeated draws of deworming shocks ${\mu }_i$ is 0.3 times their number of neighbors ${\sum }_{k=1}^K{Neighbor}_{ik}$. OVB is thus purged by controlling for the number of neighbors, or by using the recentered number of dewormed neighbors ${\tilde{x}}_i=x_i-{\mu }_i$ to instrument for $x_i$. With either adjustment, the regression will only compare students who had more neighbors dewormed than expected (given the network) to those with fewer-than-expected dewormed neighbors.

Market access (cont.)

The as-good-as-random assignment of opening status can be formalized by each planned line facing an equal and independent chance of opening. Then, if ${\sum }_{k=1}^K{Open}_k=K_1$ railway lines open by $t=1$, every counterfactual network in which $K_1$ lines from the plan opened was as likely to have occurred. One can thus compute expected MA growth ${\mu }_i$ as the average MA growth of region $i$ across these counterfactuals (or a random subset of them). Recentering by or controlling for this ${\mu }_i$ ensures that the regressions only compare regions which saw higher MA growth than expected—given pre-existing economic geography and the plan—to those which saw less-than-expected MA growth.

Medicaid eligibility (cont.)

The as-good-as-random assignment of Medicaid policies can be formalized by each state randomly drawing from a pool of potential policies, such that every permutation of the realized policies was equally likely to have occurred. Averaging individual $i$’s eligibility across these permutations yields an expected eligibility ${\mu }_i$ which equals the share of states in which she would be eligible. Our solution is to instrument actual eligibility with recentered eligibility $x_i-{\mu }_i$, or control for ${\mu }_i$ in an OLS regression. Either approach would, for example, effectively remove from the sample “always-eligible” or “never-eligible” individuals (with $x_i={\mu }_i=1$ or $x_i={\mu }_i=0$) whose income and demographics make them unaffected by policy variation.

The recentering solution generally dominates more conventional ones, such as instrumenting directly by the shocks or controlling for the other determinants of $x_i$. Instrumenting with the shocks is infeasible when the shocks are assigned at a different level than the units, and generally discards variation in treatment due to $w$. Controlling for an observation’s non-random shock exposure flexibly is typically infeasible, because such exposure is high-dimensional. Conversely, low-dimensional controls are only guaranteed to purge OVB (absent additional non-experimental restrictions on the error term) when they linearly span ${\mu }_i$, which is difficult to establish except when ${\mu }_i$ is known and recentering is feasible. If either the assignment process or shock exposure mapping is complex, ${\mu }_i$ is unlikely to be a simple function of observed characteristics.

Network spillovers (cont.)

Using student $i$’s own deworming status as an instrument is infeasible as it does not predict the number of dewormed neighbors; incorporating the non-random network adjacency matrix is necessary. Controlling for the entire row of the adjacency matrix (which characterizes student’s exposure) is also infeasible, as it would absorb all cross-sectional variation in the treatment. Controlling for the number of $i$’s neighbors is enough to purge OVB under completely random assignment of deworming, since this control is proportional to ${\mu }_i$. However, such simple controls would not linearly span ${\mu }_i$ with more complex randomization protocols, such as with two tiers (by school, then by student) or stratification (e.g., with girls dewormed with a known higher probability). Simple controls are also generally insufficient with more complex specifications of spillovers.⁹

Market access (cont.)

Railroad timing shocks vary at the level of lines, so it is infeasible to use them as instruments for regional market access without incorporating some non-random features of economic geography. Controlling perfectly for these features is also infeasible, as each region’s market access depends on the entire spatial distribution of economic activity. Simple sets of controls, such as polynomials in the latitude and longitude of a region, need not linearly span ${\mu }_i$ given the complexity of $x_i$, and thus are not guaranteed to purge OVB.

Medicaid eligibility (cont.)

Currie and Gruber (1996) propose instrumenting individual eligibility with a measure of the overall policy generosity of her state—a so-called “simulated instrument.” Such instruments are simple functions of ${Policy}_k$ for all individuals in state $k$ and are thus exogenous and relevant under random policy assignment. However they discard relevant within-state variation in $i$’s income and demographics and are thus likely to yield a less powerful first-stage prediction of $x_i$ than recentered eligibility.¹⁰

We conclude this section by noting that the OVB problem and recentering solution both extend to the case with an arbitrary endogenous $x_i$ and a candidate instrument $z_i$ which is constructed from exogenous shocks and other variables by a known formula. This approach is natural when the treatment can be represented as a function of exogenous shocks $g$, predetermined variables $w$, and endogenous (and possibly unobserved) variables $u$: i.e. when $x_i=h_i(g,w,u)$ for a known $h_i(\cdot )$. An intuitive candidate instrument for $x_i$ is the prediction of $x_i$ in the scenario when the $u$ shocks are ignored: $z_i=h_i(g,w,0)$. Our framework shows that these candidate instruments are generally invalid, again because of the non-random exposure of $z_i$ to $g$. Yet OVB can again be purged by measuring the expected instrument ${\mu }_i$—the average $z_i$ across counterfactual $g$—and either instrumenting $x_i$ with the recentered IV ${\tilde{z}}_i=z_i-{\mu }_i$ or controlling for ${\mu }_i$ while instrumenting with $z_i$.

Market access (cont.)

Suppose population sizes also change between $t=0$ and $t=1$, and the observable changes $u={({Pop}_{i1}-{Pop}_{i0})}_{i=1}^N$ are not exogenous (e.g. they respond to house price shocks in $\epsilon$). Then one can consider instrumenting the realized change in MA by a predicted change in MA which keeps population sizes fixed at $t=0$ levels. Without recentering, this IV regression may suffer from the same OVB as the OLS regression discussed above. OVB is now avoided by recentering the MA prediction via counterfactual railroad networks.

Medicaid eligibilty (cont.)

Suppose one is interested in the effects of Medicaid takeup, instead of eligibility. Takeup is the product of eligibility and $1-{NeverTaker}_i$, where ${NeverTaker}_i$ indicates that individual $i$ would decline Medicaid if eligible and $u={({NeverTaker}_i)}_{i=1}^N$ is unobserved. Under the appropriate exclusion restriction one can consider instrumenting takeup with eligibility; our recentering strategy then again removes OVB from non-random variation in policy exposure.

3. Theory

We now develop a general econometric framework for settings with non-random exposure to exogenous shocks. We introduce the baseline setting, develop our approach to estimation based on the recentering procedure, and discuss how this recentering can be performed by specifying counterfactual shocks in Sections 3.1-3.3. We then discuss conditions for consistency of recentered IV estimators in Section 3.4, and how inference can be conducted in Section 3.5. Several extensions are summarized in Section 3.6.

3.1. Setting

We consider estimation of $\beta$ in the causal or structural model

$$y_i={\beta x}_i+{\epsilon }_i,$$ (2)

from a dataset of scalar and demeaned $y_i$ and $x_i$, $i=1,\dots ,N$. Below we discuss extensions to heterogeneous causal effects, nonlinear models, multiple treatments, and additional control variables. Although we use a single index of $i$ for observations, we note our framework accommodates repeated cross-sections and panel data.

Importantly for the applicability of our framework, we do not assume that the observations of $y_i$ and $x_i$ are independently or identically distributed ($iid$) as when arising from random sampling. This allows for complex dependencies across the units due to their common exposure to observed and potentially unobserved shocks. It is also consistent with settings where the $N$ units represent a population—for example, all regions of a country—and conventional random sampling assumptions are inappropriate (Abadie et al., 2020).¹¹

We suppose that to estimate $\beta$ a researcher has constructed a candidate instrument

$$z_i=f_i(g;w),$$ (3)

where $f_1(\cdot ),\dots ,f_N(\cdot )$ is a list of known non-stochastic functions, $g$ is a $K\times 1$ vector of shocks, and $w$ is a list of other variables of unrestricted dimension. Equation (3) is very general: any $z_i$ that can be computed from a set of observed data, according to a known formula, can be described in this way.¹² It also allows $x_i=z_i$, in which case $\beta$ is the causal effect of the composite treatment.

We assume that the shocks $g$ are exogenous, which we formalize by their conditional independence from the vector of errors given the other sources of instrument variation:

Assumption 1. (Shock exogeneity): $g⫫\epsilon \mid w$

As noted in Section 2, this notion of shock exogeneity combines two conceptually distinct conditions. First, it imposes an exclusion restriction, reflecting an economic model of how $g$ can affect $y$. Second, it requires as-good-as-random shock assignment. This latter condition is satisfied when the shocks are fully randomly assigned, as in an RCT (i.e., $g⫫(\epsilon ,w)$), but also allows $w$ to contain variables that govern the shock assignment process.¹³ Importantly, Assumption 1 allows $\mathbb{E}[{\epsilon }_i\mid w]$ to vary arbitrarily across $i$; this reflects the lack of non-experimental assumptions, such as parallel trends, constraining the error in equation (2).¹⁴ Assumption 1 is consistent with a two-step data-generating process, where $w$ is determined prior to the realization of shocks $g$ and errors $\epsilon$ which then together determine ($x,y$).¹⁵

We start by considering an instrumental variable (IV) regression of $y_i$ on $x_i$ that instruments with $z_i$. As usual, this strategy requires $z_i$ to be relevant to the treatment and orthogonal to the error term. In our non-$iid$ setting, we formalize these two conditions in terms of the full-sample IV moments $\mathbb{E}\left[\frac{1}{N}{\sum }_i{z}_i{x}_i\right]$ and $\mathbb{E}\left[\frac{1}{N}{\sum }_i{z}_i{y}_i\right]$. Since (2) implies $\mathbb{E}\left[\frac{1}{N}{\sum }_i{z}_i{y}_i\right]=\beta \mathbb{E}\left[\frac{1}{N}{\sum }_i{z}_i{x}_i\right]+\mathbb{E}\left[\frac{1}{N}{\sum }_i{z}_i{\epsilon }_i\right]$, $\beta$ is recoverable from the ratio of these moments (what we term identification) under the relevance condition of $\mathbb{E}\left[\frac{1}{N}{\sum }_i{z}_i{x}_i\right]\ne 0$ and the orthogonality condition of $\mathbb{E}\left[\frac{1}{N}{\sum }_i{z}_i{\epsilon }_i\right]=0$.¹⁶ To start we assume the two IV moments are known, in order to focus on the potential for OVB when the orthogonality condition fails. We discuss conditions for consistent estimation in Section 3.4.

3.2. OVB and Instrument Recentering

We define the expected instrument ${\mu }_i=\mathbb{E}[f_i(g;w)\mid w]$ as the average value of $z_i$ across different realizations of the shocks, conditional on $w$. Our first result shows that OVB may arise when predetermined exposure to the natural experiment is endogenous, and that the potential for such bias is entirely governed by the relationship between ${\mu }_i$ and the error ${\epsilon }_i$. Formally, under Assumption 1 instrument orthogonality need not hold: $\mathbb{E}\left[\frac{1}{N}{\sum }_i{z}_i{\epsilon }_i\right]\ne 0$ in general. Rather,

$$\mathbb{E}\left[\frac{1}{N}\sum _i{z}_i{\epsilon }_i\right]=\mathbb{E}\left[\frac{1}{N}\sum _i{\mu }_i{\epsilon }_i\right].$$ (4)

This result follows from the law of iterated expectations: $\mathbb{E}[z_i{\epsilon }_i]=\mathbb{E}[\mathbb{E}[f_i(g;w){\epsilon }_i\mid w]]=\mathbb{E}[{\mu }_i\mathbb{E}[{\epsilon }_i\mid w]]=\mathbb{E}[{\mu }_i{\epsilon }_i]$ for all $i$, where the second equality uses Assumption 1 and the definition of ${\mu }_i$.

The central role of ${\mu }_i$ in governing OVB suggests the recentering solution: even though OVB results from potentially high-dimensional variation in units’ exposure to shocks, adjustment for the one-dimensional confounder ${\mu }_i$ is sufficient for instrument orthogonality. We adjust $z_i$ by defining the recentered instrument ${\tilde{z}}_i=z_i-{\mu }_i$. By equation (4), orthogonality always holds for this instrument:

$$\mathbb{E}\left[\frac{1}{N}\sum _i{\tilde{z}}_i{\epsilon }_i\right]=\mathbb{E}\left[\frac{1}{N}\sum _i{z}_i{\epsilon }_i\right]-\mathbb{E}\left[\frac{1}{N}\sum _i{\mu }_i{\epsilon }_i\right]=0.$$

Thus, if ${\tilde{z}}_i$ is also relevant, $\beta$ is identified by the IV regression which uses the recentered instrument ${\tilde{z}}_i$ instead of $z_i$.¹⁷

A closely related solution, also suggested by equation (4), is to include the expected instrument ${\mu }_i$ as a control in specification (2) while using the original $z_i$ as the instrument in a control function approach (Wooldridge, 2015). Controlling for ${\mu }_i$ can be thought of as recentering $z_i$ while also removing the residual variation in $y_i$ which is cross-sectionally correlated with ${\mu }_i$. As usual, removing this residual variation may generate precision gains in large samples; similar gains may arise from including (a fixed number of) any predetermined controls in a recentered IV regression.¹⁸

Equation (4) further shows that adjusting for ${\mu }_i$ is generally necessary for identification, absent additional restrictions on the unobserved error. Conventional controls and fixed effects are only guaranteed to purge OVB when they linearly span ${\mu }_i$: a condition that is difficult to verify except when recentering is also feasible.¹⁹

Adjustments based on ${\mu }_i$, as the sole confounder of $z_i$, are similar to more conventional propensity score methods. There are three key differences, concerning the setting, adjustment method, and computation of ${\mu }_i$. First, propensity score methods have mostly been applied to binary treatments, starting from Rosenbaum and Rubin (1983). While generalizations to binary instruments (e.g. Abadie (2003)) and non-binary treatments (e.g. Imbens (2000)) have been proposed, our setting allows for arbitrary treatments or instruments. Second, the propensity score literature has mostly used non-regression adjustment methods, such as matching or binning (Abadie and Imbens, 2016; King and Nielsen, 2019). A notable exception is the E-estimator of Robins et al. (1992), which similarly leverages linearity of an outcome model like (2) to recenter by a scalar variable. Third, and most importantly, propensity scores are usually estimated from the data by relating the treatment to a vector of observation-specific covariates. This approach is generally not feasible because exposure to exogenous shocks is high-dimensional: for instance, as noted in Section 2, the expected market access of any region $i$ depends on the entire economic geography of the country. We therefore take a different approach to computing ${\mu }_i$, which we turn to next.

3.3. Computing the Expected Instrument via Shock Counterfactuals

We propose computing the expected instrument by specifying an assignment process for the shocks, drawing many sets of counterfactual shocks from this process, recomputing the candidate instrument each time, and averaging it across the counterfactuals. Here we formalize this approach, discuss general ways in which counterfactual shocks can be specified, and highlight the advantages of our approach over alternatives.

We define the shock assignment process as the conditional distribution of $g\mid w$, with cumulative distribution function $G(g\mid w)$. When $G(\cdot )$ is known, the expected instrument ${\mu }_i=\int f_i(\gamma ;w)dG(\gamma \mid w)$ can be computed and either used to recenter $z_i$ or added as a regression control.²⁰ To emphasize the importance of a known shock assignment process, we write it as an assumption:

Assumption 2. (Known assignment process): $G(g\mid w)$ is known in the support of $w$.

This assumption is unrestrictive when the shocks are determined by a known randomization protocol, as in an RCT or with policy randomizations (such as tie-breaking lottery numbers in centralized assignment mechanisms; Abdulkadiroglu et al. (2017)). The assignment process may also be given by scientific knowledge when the shocks are randomized naturally, such as when $g$ captures weather or seismic shocks governed by meteorological or geological processes (e.g., Carvalho et al. (2021); Madestam et al. (2013)). Policy discontinuities (as in regression discontinuity designs) can also yield a known $G(\cdot )$ when viewed as generating local randomization around known cutoffs (Lee, 2008; Cattaneo et al., 2015).

In observational data, where the distribution of shocks is unknown, Assumption 2 can be satisfied by specifying some permutations of shocks that were as likely to have occurred. For instance, if one is willing to assume the shocks $g_k$ are $iid$ across $k$, it follows that all permutations of the observed $g$ are equally likely. In this case $G(g\mid w)$ is uniform when $w$ is augmented by the permutation class $\Pi (g)=\{\pi (g)\mid \pi (\cdot )\in {\Pi }_K\}$, where ${\Pi }_K$ denotes the set of permutation operators $\pi (\cdot )$ on vectors of length $K$ (e.g. Lehmann and Romano, 2006, p. 634). The distribution of each $g_k$ (conditionally on other components of $w$) then needs not be specified; the expected instrument is the average $z_i$ across all permutations of shocks, which serve as counterfactuals:

$${\mu }_i=\frac{1}{K!}\sum _{\pi (\cdot )\in {\Pi }_K}{f}_i(\pi (g);w).$$

Such ${\mu }_i$ are easy to compute (or approximate with a random set of permutations).

Similar expected instrument calculations follow under weaker shock exchangeability conditions, such as when the $g_k$ are $iid$ within, but not across, a set of known clusters and the class of within-cluster permutations is used to draw counterfactuals. We illustrate this approach in Section 4. In BH we discuss how our framework can also apply with $G(g\mid w)$ specified up to a low-dimensional vector of consistently estimable parameters (Appendix C.5); we also show how Assumption 2 can derive from an economic model (e.g. of transportation network formation) with stochastic shocks or from symmetries of the joint shock distribution (Appendices D.1 and D.2)

We note that even when $G(\cdot )$ is challenging to specify, a possibly incorrect specification can be useful as a sensitivity check. Specifically, if Assumption 1 holds and there is already no OVB because the included regression controls perfectly capture either the endogenous features of exposure or the expected instrument, then controlling for any candidate expected instrument $m_i(w)$ cannot introduce bias. In this case the researcher may safely control for one or several $m_i(w)$ based on some guesses of the assignment process.²¹ More generally, researchers may achieve additional robustness by controlling for multiple candidate $m_i(w)$ based on multiple shock assignment process guesses; only one such guess needs to be right to purge OVB.

3.4. Recentered IV Consistency

With the ratio of recentered IV moments identifying $\beta$, we now consider whether the corresponding IV estimator $\widehat{\beta }=(\frac{1}{N}{\sum }_i{\tilde{z}}_i{y}_i)∕(\frac{1}{N}{\sum }_i{\tilde{z}}_i{x}_i)$ is consistent, i.e. whether $\widehat{\beta }\stackrel{p}{\to }\beta$ as the number of observed outcomes and treatments grows large ($N\to \infty$). To formalize consistency in our $non\text{-}iid$ context we consider a sequence of distributions $P_N$ for the complete data ($y,x,g,w$). Only in this section, to make the asymptotic sequence explicit, we index moments by $P_N$: e.g., we write the recentered IV moments as ${\mathbb{E}}_{P_N}\left[\frac{1}{N}{\sum }_i{\tilde{z}}_i{y}_i\right]$ and ${\mathbb{E}}_{P_N}\left[\frac{1}{N}{\sum }_i{\tilde{z}}_i{x}_i\right]$. We allow the number of observed shocks, $K_N=\text{dim}(g)$, and the dimensions of $w$ to change arbitrarily with $N$.

We first consider mean-square convergence of $\frac{1}{N}{\sum }_i{\tilde{z}}_i{\epsilon }_i$ to ${\mathbb{E}}_{P_N}\left[\frac{1}{N}{\sum }_i{\tilde{z}}_i{\epsilon }_i\right]=0$ under Assumption 1: i.e., whether ${\text{Var}}_{P_N}\left[\frac{1}{N}{\sum }_i{\tilde{z}}_i{\epsilon }_i\right]\to 0$. Since $\widehat{\beta }=\beta +\left(\frac{1}{N}{\sum }_i{\tilde{z}}_i{\epsilon }_i\right)∕\left(\frac{1}{N}{\sum }_i{\tilde{z}}_i{x}_i\right)$ by (2), such convergence implies $\widehat{\beta }\stackrel{p}{\to }\beta$ so long as the instrument is asymptotically relevant (a condition we return to below). We establish this convergence under a regularity condition on ${\epsilon }_i$ and a substantive restriction on ${\tilde{z}}_i$, which we term weak mutual dependence:

Assumption 3. (Weak mutual dependence):

$${\mathbb{E}}_{P_N}\left[\frac{1}{N^2}\sum _{i,j}\mid {\text{Cov}}_{P_N}[{\tilde{z}}_i,{\tilde{z}}_j\mid w]\mid \right]\to 0.$$

Proposition 1. Suppose Assumptions 1-3 hold and ${\mathbb{E}}_{P_N}\left[{\epsilon }_i^2\mid w\right]\le U_{\epsilon }$ uniformly across $N$ and $i=1,\dots ,N$. Then ${\text{Var}}_{P_N}\left[\frac{1}{N}{\sum }_i{\tilde{z}}_i{\epsilon }_i\right]\to 0$.

Proof. See Appendix D.

Assumption 3 holds when the shocks induce rich cross-sectional variation in the recentered instrument, through heterogeneous exposure, such that most pairs of (${\tilde{z}}_i,{\tilde{z}}_j$) have a weak covariance across possible realizations of $g$. The proof shows this is enough for a law of large numbers to apply to $\frac{1}{N}{\sum }_i{\tilde{z}}_i{\epsilon }_i$.²²

Note that in line with our approach to identification, Proposition 1 makes no substantive restrictions on the errors ${\epsilon }_i$ beyond Assumption 1 (in particular, it puts no restrictions on the dependence of ${\epsilon }_i$ across observations). In the absence of such restrictions, Proposition 2 in Appendix C shows the Assumption 3 is not only sufficient for ${\text{Var}}_{P_N}\left[\frac{1}{N}{\sum }_i{\tilde{z}}_i{\epsilon }_i\right]\to 0$ but, under regularity conditions, also necessary. Of course, more conventional restrictions on the mutual dependence of errors (such as $iid$ or clustered ${\epsilon }_i$) may also suffice for convergence when weak mutual dependence of ${\tilde{z}}_i$ fails.

Three additional results in Appendix C, which extend the results on consistency with linear shift-share instruments from Borusyak et al. (2022), unpack Assumption 3 further. First, a large number of exogenous shocks is essentially necessary for the recentered instrument to not have many strong cross-sectional dependencies. Proposition 3 formalizes this intuition by showing that, with sufficiently smooth $f_i(\cdot ;w)$, Assumption 3 can only hold with $K_N\to \infty$. Moreover, the concentration of exposure to this growing number of shocks matters. Proposition 4 formalizes this idea by considering a concentration measure for average shock exposure which is similar to a Herfindahl-Hirschman Index (HHI): ${\mathbb{E}}_{P_N}\left[{\sum }_{k=1}^{K_N}{\left(\frac{\partial \overline{f}(g;w)}{{\partial g}_k}\right)}^2\right]$, where $\overline{f}(g;w)=\frac{1}{N}{\sum }_i(f_i(g;w)-{\mu }_i)$. For binary $g_k$ and weakly monotone $f_i(\cdot ;w)$ (as in the network spillovers and market access examples) and with mutually-independent shocks, Assumption 3 is satisfied when this measure converges to zero such that the impact of any finite set of shocks on $\frac{1}{N}{\sum }_i{\tilde{z}}_i$ vanishes.²³ Proposition 5 considers a different low-level condition in a case covering the medicaid eligibility example: Assumption 3 holds when most pairs of observations of ${\tilde{z}}_i$ are affected by non-overlapping sets of shocks.

Convergence of $\frac{1}{N}{\sum }_i{\tilde{z}}_i{\epsilon }_i$ implies consistency of the recentered IV estimator so long as (i) ${\mathbb{E}}_{P_N}\left[\frac{1}{N}{\sum }_i{\tilde{z}}_i{x}_i\right]$ remains bounded away from zero and (ii) $\frac{1}{N}{\sum }_i{\tilde{z}}_i{x}_i-{\mathbb{E}}_{P_N}\left[\frac{1}{N}{\sum }_i{\tilde{z}}_i{x}_i\right]\stackrel{p}{\to }0$.²⁴ Condition (i) follows when the relationship between $z_i$ and $x_i$ is strong and when most observations of ${\tilde{z}}_i$ have exposure concentrated in a small number of exogenous shocks, such that ${\text{Var}}_{P_N}[{\tilde{z}}_i]$ does not dissipate even as $K_N\to \infty$. Proposition 6 in Appendix C formalizes these conditions with a linear first stage model of $x_i={\pi z}_i+u_i$, with $g⫫u\mid w$, and a different measure of shock exposure concentration: the HHI of the effects of different shocks on ${\tilde{z}}_i$, ${\sum }_{k=1}^{K_N}{\left({\mathbb{E}}_{P_N}\left[\frac{{\partial f}_i(g;w)}{{\partial g}_k}\mid w\right]\right)}^2$, averaged across observations $i$. In the case of mutually-independent binary shocks, we require $\pi \ne 0$ and that the expectation of this concentration measure is bounded above zero. The HHI conditions from Propositions 4 and 6 may simultaneously hold when most observations are mostly exposed to a small number of shocks, differentially across a large number of shocks. Conditions similar to Assumption 3 can be derived to ensure convergence of the sample first stage, (ii).²⁵

3.5. Randomization Inference and Specification Tests

In some applications of our framework, natural assumptions on the mutual independence of ${\tilde{z}}_i$ or ${\epsilon }_i$ across observations can make conventional (e.g. clustered) asymptotic inference valid. Generally, however, the common exposure of observations to observed and unobserved shocks generates complex dependencies across observations making conventional asymptotic analysis inapplicable.²⁶ In such cases, it may be attractive to construct confidence intervals for the constant effect $\beta$ and tests for Assumptions 1 and 2 based on the specification of the shock assignment process, following a long tradition of randomization inference (RI; Fisher, 1935). The RI approach guarantees correct coverage in finite samples of both observations and shocks.²⁷ We focus on a particular type of RI test which is tightly linked to the recentered IV estimator $\widehat{\beta }$.

RI tests and confidence intervals for $\beta$ are based on a scalar test statistic $T=𝒯(g,y-bx,w)$, where $b$ is a candidate parameter value. Under the null hypothesis of $\beta =b$ and Assumption 1, the distribution of $T=𝒯(g,\epsilon ,w)$ conditional on $\epsilon$ and $w$ is implied by the shock assignment process $G(g\mid w)$. One may simulate this distribution, by redrawing the $g$ shocks and recomputing $T$. If the original value of $T$ is far in the tails of the simulated distribution, one has grounds to reject the null. Inversion of such tests yields confidence interval for $\beta$ by collecting all $b$ that are not rejected. These intervals have correct size, both conditionally on ($\epsilon ,w$) and unconditionally (see Appendix C.3 of BH for details).

We propose addressing the practical issue of choosing a randomization test statistic by picking a $T$ that is tightly linked to the recentered IV estimator, building on the theory of Hodges and Lehmann (1963) and Rosenbaum (2002). Specifically, we consider the sample covariance of the recentered instrument and implied residual: $T=\frac{1}{N}{\sum }_i(f_i(g;w)-{\mu }_i)\cdot (y_i-{bx}_i)$. Lemma 2 of BH shows that $\widehat{\beta }$ is a Hodges-Lehmann estimator corresponding to this $T$, meaning that $\widehat{\beta }$ equates $T$ with its expectation across counterfactual shocks (specifically, zero).²⁸ This connection makes RI tests and confidence intervals based on $T$ inherit the consistency of $\widehat{\beta }$: the test power asymptotically increases to one for any fixed alternative $b\ne \beta$ under additional regularity conditions (Proposition S2 of BH).²⁹

Randomization inference can also be used to perform falsification tests on our key Assumptions 1 and 2. Recentering implies a testable prediction that ${\tilde{z}}_i$ is orthogonal to any variable $r={(r_i)}_{i=1}^N$ satisfying $g⫫r\mid w$, such as any function of $w$ or other observables (either predetermined or contemporaneous) thought to be conditionally independent of $g$. To test this restriction, one may check that the sample covariance $T=\frac{1}{N}{\sum }_i{\tilde{z}}_i{r}_i$ is sufficiently close to zero by drawing counterfactual shocks and checking that $T$ is not in the tails of its conditional-on-($w,r$) distribution. Multiple falsification tests, based on a vector of predetermined variables $R_i$, can be combined by an appropriate RI procedure, e.g. by taking $T$ to be the sample sum of squared fitted values from regressing ${\tilde{z}}_i$ on $R_i$.³⁰

Falsification tests can be useful in two ways. First, when $r_i$ is a lagged outcome or another variable thought to proxy for ${\epsilon }_i$, they provide an RI implementation of conventional placebo and covariate balance tests of Assumption 1. While the use of RI for inference on causal effects may be complicated by treatment effect heterogeneity, the sharp hypothesis of zero placebo effects is a natural null. Second, RI tests will generally have power to reject false specifications of the shock assignment process, i.e. violations of Assumption 2, even when $r_i$ does not proxy for ${\epsilon }_i$. For $r_i=1$, for example (which is trivially conditionally independent of $g$), the test verifies that the sample mean of $z_i$ is typical for the realizations of the specified assignment process. Setting $r_i={\mu }_i$ instead checks that the recentered instrument is not correlated with the expected instrument that it is supposed to remove.

3.6. Extensions

While we analyze the constant-effect model (2), identification by ${\mu }_i$-adjusted regressions extends to settings with heterogeneous treatment effects. Namely, Appendix C.1 of BH shows that the recentered IV estimator generally identifies a convex-weighted average of heterogeneous effects under an appropriate monotonicity condition, extending Imbens and Angrist (1994). The weights are proportional to the conditional variance of ${\tilde{z}}_i\mid w$ across counterfactual shocks, ${\sigma }_i^2$. These ${\sigma }_i^2$, like ${\mu }_i$, are given by the shock assignment process (Assumption 2) and therefore can be computed by the researcher. Moreover, they can be used to identify more conventional weighted average effects. For example, in reduced-form models of the form $y_i={\beta }_i{z}_i+{\epsilon }_i$ a recentered and rescaled IV $(z_i-{\mu }_i)∕{\sigma }_i^2$ identifies the average effect $\mathbb{E}\left[\frac{1}{N}{\sum }_{i=1}^N{\beta }_i\right]$. Similarly, in IV settings with binary $x_i$ and $z_i$, this rescaled instrument identifies the local average treatment effect of Imbens and Angrist (1994).³¹

Further extensions are given in the appendix of BH. Appendix C.6 shows how predetermined observables can be included as regression controls to reduce residual variation and potentially increase power. Appendix C.7 discusses identification and inference with multiple treatments or instruments. Finally, Appendix C.8 extends the framework to nonlinear outcome models.

4. Application: Effects of Transportation Infrastructure

We now present an empirical application showing how our theoretic framework can be used to avoid OVB in practice. Specifically, we estimate the effect of market access growth on Chinese regional employment growth over 2007–2016, leveraging the recent construction of high-speed rail (HSR). We show how counterfactual HSR shocks can be specified, and how correcting for expected market access growth can help purge OVB.

The recent construction of Chinese HSR has produced a network longer than in all other countries combined (Lawrence et al., 2019). The network mostly consists of dedicated passenger lines and has developed rapidly since 2007.³² Construction objectives included freeing up capacity on the low-speed rail network and supporting economic development by improving regional connectivity (Lawrence et al., 2019; Ma, 2011). While affordable fares make HSR popular for multiple purposes, business travel is an important component of rail traffic, ranging between 28% and 62%, depending on the line (Ollivier et al., 2014; Lawrence et al., 2019). The role of HSR may also extend beyond directly connected regions, as passengers frequently transfer between HSR and traditional lines (and between intersecting HSR lines). An early analysis by Zheng and Kahn (2013) finds positive effects of HSR on housing prices, while Lin (2017) similarly finds positive effects on regional employment.

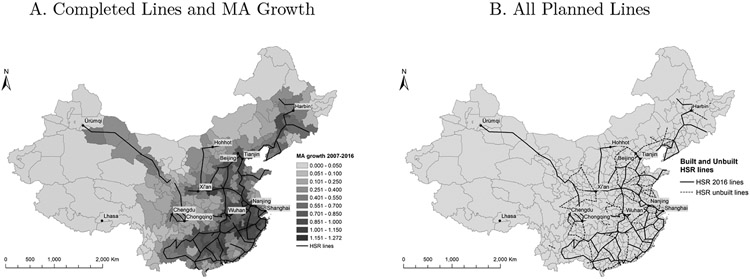
We analyze HSR-induced market access effects for 340 sub-province-level administrative divisions in mainland China, referred to as prefectures.³³ We measure market access growth between 2007 and 2016 by combining data on the development of the HSR network and each prefecture’s location and population (as measured in the 2000 census). A total of 83 HSR lines opened between these years, with the first in 2008; a further 66 lines were completed or under construction as of April 2019.³⁴ We compute a simple market access measure in each prefecture $i$ and year $t$ based on the formula in Zheng and Kahn (2013): ${MA}_{it}={\sum }_j\text{exp}(-0.02{\tau }_{ijt})\cdot {Pop}_{j,2000}$, where ${Pop}_{j,2000}$ denotes the year-2000 population of prefecture $j$ and ${\tau }_{ijt}$ denotes predicted travel time between regions $i$ and $j$ in year $t$ (in minutes). Travel time predictions are based on the operational speed of each HSR line as well as geographic distance, which proxies for the travel time by car or a low-speed train. We relate MA growth, $x_i=\log {MA}_{i,2016}-\log {MA}_{i,2007}$, to the corresponding growth in prefecture’s urban employment $y_i$ from Chinese City Statistical Yearbooks. This yields a set of 275 prefectures with non-missing outcome data; see Appendix A for details on the sample construction and MA measure. Panel A of Figure 1 shows the Chinese HSR network as of the end of 2016, along with the implied MA growth of relative to 2007.

Figure 1:

Chinese High Speed Rail and Market Access Growth, 2007-2016 A. Completed Lines and MA Growth B. All Planned Lines Notes: Panel A shows the completed China high-speed rail network by the end of 2016, with shading indicating MA growth (i.e. log-change in MA) relative to 2007. Panel B shows the network of all HSR lines, including those planned but not yet completed as of 2016.

Column 1 of Table I, Panel A, reports the coefficient from a regression of employment growth on MA growth.³⁵ The estimated elasticity of 0.23 is large. With an average MA growth of 0.54 log points, it implies a 12.4% employment growth attributable to HSR for an average prefecture—almost half of the 26.6% average employment growth. The estimate is also highly statistically significant using Conley (1999) spatially-clustered standard errors.

Table I:

Employment Effects of Market Access: Unadjusted and Recentered Estimates

	Unadjusted OLS (1)	Recentered IV (2)	Controlled OLS (3)
Panel A: No Controls
Market Access Growth	0.232 (0.075)	0.084 (0.097) [−0.245, 0.337]	0.072 (0.093) [−0.169, 0.337]
Expected Market Access Growth			0.317 (0.096)
Panel B: With Geography Controls
Market Access Growth	0.133 (0.064)	0.056 (0.089) [−0.135, 0.280]	0.047 (0.092) [−0.146, 0.280]
Expected Market Access Growth			0.214 (0.073)
Recentered	No	Yes	Yes
Prefectures	275	275	275

Notes: This table reports coefficients from regressions of employment growth on MA growth in Chinese prefectures from 2007–2016. MA growth is unadjusted in Column 1. In Column 2 this treatment is instrumented by MA growth recentered by permuting the opening status of built and unbuilt HSR lines with the same number of cross-prefecture links. Column 3 instead estimates an OLS regression with recentered MA growth as treatment and controlling for expected MA growth given by the same HSR counterfactuals. The regressions in Panel B control for distance to Beijing, latitude, and longitude. Standard errors which allow for linearly decaying spatial correlation (up to a bandwidth of 500km) are reported in parentheses. 95% RI confidence intervals based on the HSR counterfactuals are reported in brackets.

Panel A of Figure 1, however, gives reason for caution against causally interpreting the OLS coefficient. Prefectures with high MA growth, which serve as the effective treatment group, tend to be clustered in the main economic areas in the southeast of the country where HSR lines and large markets are concentrated. A comparison between these prefectures and the economic periphery may be confounded by the effects of unobserved policies, both contemporaneous and historical, that differentially affected the economic center.

We quantify the systematic nature of spatial variation in MA growth in Column 1 of Table II, by regressing it on a prefecture’s distance to Beijing, latitude, and longitude. These predictors capture over 80% of the variation in MA growth (as measured by the regression’s $R^2$), reinforcing the OVB concern: for a causal interpretation of the Table I regression, one would need to assume that all unobserved determinants of employment growth (e.g. local productivity shocks) are uncorrelated with these geographic features. While one could of course control for the specific geographic variables from Table II (as we explore below), controlling perfectly for geography is impossible without removing all variation in $x_i$.

Table II:

Regressions of Market Access Growth on Measures of Economic Geography

	Unadjusted	Recentered
	(1)	(2)	(3)	(4)
Distance to Beijing	−0.291 (0.062)	0.069 (0.039)		0.088 (0.045)
Latitude/100	−3.324 (0.646)	−0.342 (0.276)		−0.182 (0.319)
Longitude/100	1.321 (0.458)	0.485 (0.237)		0.440 (0.240)
Expected Market Access Growth			0.026 (0.056)	0.054 (0.069)
Constant	0.536 (0.029)	0.018 (0.018)	0.018 (0.021)	0.018 (0.018)
Joint RI p-value		0.443	0.711	0.492
$R^2$	0.824	0.083	0.010	0.086
Prefectures	275	275	275	275

Notes: This table reports coefficients from regressing the unadjusted and recentered MA growth of Chinese prefectures (2007–2016) on geographic controls. Recentering is done by permuting the opening status of built and unbuilt lines with the same number of cross-prefecture links. All regressors are measured for the prefecture’s main city and demeaned such that the constant in each regression captures the average outcome. Distance to Beijing is measured in 1,000km. Standard errors which allow for linearly decaying spatial correlation (up to a bandwidth of 500km) are reported in parentheses. Joint RI p-values are based on the 1,999 HSR counterfactuals and the sum-of-square fitted values statistic, as described in footnote 30.

Our solution is to view certain features of the HSR network as realizations of a natural experiment. By specifying a set of counterfactual HSR networks we can compute the appropriate function of geography ${\mu }_i$ which removes the systematic variation in MA growth.

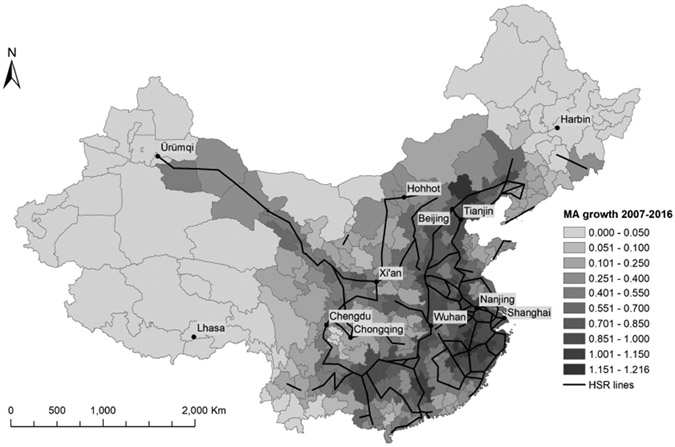
Our specification of counterfactuals exploits the heterogeneous timing of HSR construction. Specifically, we permute the 2016 completion status of the built and unbuilt (but planned) lines, assuming that the timing of line completion is conditionally as-good-as-random. Panel B of Figure 1 compares the built and unbuilt lines which form our counterfactuals. Unbuilt lines tend to be concentrated in the same areas of China as built lines, reinforcing the fact that construction is not uniformly distributed in space. Moreover, built lines tend to connect more regions: the average number of cross-prefecture “links” is 3.19 and 2.44 for built and unbuilt lines, respectively, with a statistically significant difference (p = 0.048). To account for this difference we construct counterfactual upgrades by permuting the 2016 completion status only among lines with the same number of links. For example the main Beijing to Shanghai HSR line, which has the greatest number of links, is always included in the counterfactuals. This procedure generates 1,999 counterfactual HSR maps that are visually similar to the actual 2016 network; Appendix Figure A1 gives an illustrative example.

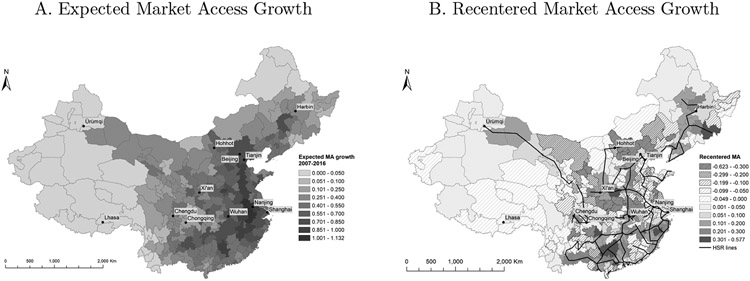
Columns 2–4 of Table II validate this specification of the HSR assignment process by the test described in Section 3.5. Column 2 shows that this recentering successfully removes the systematic geographic variation in market access. Specifically, we regress recentered MA growth on a constant and the same geographic controls as in Column 1. The regression coefficients and $R^2$ fall dramatically relative to Column 1, while a permutation-based p-value for their joint significance (based on the regression’s sum-of-squares, as suggested in footnote 30) is 0.44. Columns 3 and 4 further show that recentered MA growth is uncorrelated with expected MA growth.³⁶

Figure 2 plots expected and recentered MA growth given by the permutations of built and unbuilt lines. The effect of recentering is apparent by contrasting the solid and striped regions in Panel B of Figure 2 (indicating high and low recentered MA growth) with the dark- and light-shaded regions in Panel A of Figure 1 (indicating high and low MA growth). The recentered treatment no longer places western prefectures in the effective control group, as their MA growth is as low as expected. Similarly, some prefectures in the east (such as Tianjin) are no longer in the effective treatment group, as they saw an expectedly large increase in MA. At the same time, recentering provides a justification for retaining other regional contrasts. Hohhot, for example, expected higher MA growth than Harbin due to the planned connection to Beijing. This line was still under construction in 2016, however, resulting in lower MA growth in Hohhot than Harbin.

Figure 2: Expected and Recentered Market Access Growth from Chinese HSR.

Notes: Panel A shows the variation in expected 2007–16 MA growth across Chinese prefectures, computed from 1,999 HSR counterfactuals that permute the opening status of built and unbuilt lines with the same number of cross-prefecture links. Panel B plots the variation in corresponding recentered MA growth: the difference between the MA growth shown in Panel A of Figure 1 and expected MA growth. The HSR network as of 2016 is also shown in this panel.

Column 2 of Table I, Panel A, shows that instrumenting MA growth with recentered MA growth reduces the estimated employment elasticity substantially, from 0.23 to 0.08. Controlling for expected MA growth yields a similar estimate of 0.07 in Column 3. Neither of the two adjusted estimates is statistically distinguishable from zero according to either Conley (1999) spatial-clustered standard errors or permutation-based inference (which yields a wider confidence interval in this setting). The difference between the unadjusted and adjusted estimates is explained by the fact that employment growth is strongly predicted by expected MA growth. In Column 3 we find a large coefficient on ${\mu }_i$, of 0.32, meaning that employment grew faster in prefectures that were more highly exposed to potential HSR construction, whether or not the nearby lines were built yet.

Panel B of Table I shows that the geographic controls from Table II do not isolate the same variation as expected MA growth adjustment. Including these controls in the unadjusted regression of Column 1 yields a smaller but still economically and statistically significant coefficient of 0.13. In contrast, Columns 2 and 3 show that the finding of no significant MA effect after adjusting for ${\mu }_i$ is robust to including geographic controls. The ${\mu }_i$ adjustment alone appears sufficient to remove the geographic dependence of MA, as Table II also showed.³⁷

While our primary interest is to illustrate the recentering approach, we note that there are several possible explanations for the substantive finding of a small employment effect of MA. Unlike other transportation networks used for trading goods, the Chinese HSR network primarily operates passenger trains. Its scope for directly affecting production is therefore smaller, although it could still facilitate cross-regional business relationships. In addition, the employment effects of growing market access could be positive for some regions but negative for others, as easier commuting between regions relocates employers. We leave analyses of such mechanisms and heterogeneity for future study.

In BH we discuss how market access recentering relates to other approaches in the long literature estimating transportation infrastructure upgrade effects (Redding and Turner, 2015). We first contrast the well-known challenge of strategically chosen transportation upgrades with the less discussed problem that regional exposure to exogenous upgrades may be unequal. We then explain how common strategies to address the former issue (e.g. by leveraging historical routes or inconsequential places) can be incorporated in our framework, at least in principle. At the same time, we highlight that recentering may still be needed to address the latter issue. We further discuss how some of the existing approaches naturally yield specifications of counterfactual networks (e.g. the placebos in Donaldson (2018) and Ahlfeldt and Feddersen (2018)) and summarize the conceptual and practical advantages of our approach relative to employing more conventional controls. We emphasize that even when it is challenging to obtain a convincing specification of counterfactuals, any specification can yield a robustness check on these alternative strategies (see footnote 21).

5. Conclusion

Many studies in economics use treatments or instruments which combine multiple sources of variation, which are sometimes observed at different “levels,” according to a known formula. We develop a general approach to causal inference when some, but not all, of this variation is exogenous. Non-random exposure to the exogenous shocks can bias conventional regression estimators, but this problem can be solved by specifying a shock assignment process: namely, a set of counterfactual shocks that might as well have been realized. Averaging the treatment or instrument over these counterfactuals yields a single ${\mu }_i$ which can be adjusted for to achieve identification and consistency. The specification of counterfactuals also yields a natural form of valid finite-sample inference.

In practice, researchers face a choice in how to use ${\mu }_i$ in a regression analysis: recentering by it or controlling for it. When the assignment process is given by a true randomization protocol, as in a RCT, we recommend researchers recenter first to purge OVB. Then any predetermined controls (i.e. functions of exposure) can be included to remove variation in the error term and likely increase estimation efficiency. While ${\mu }_i$ is one possible control, which automatically recenters the treatment or instrument, it need not be the best choice in terms of predicting the residual variation. Our recommendation is different in natural experiments where assumptions must be placed on the assignment process. Then controlling for candidate ${\mu }_i$ instead of recentering can have a valuable “double-robustness” property. Researchers can compute and control for several candidate ${\mu }_i$ based on different assignment processes, such that OVB is purged if at least one of the processes is specified correctly (or if there is no OVB to begin with).

We conclude by noting that our framework bears practical lessons for a range of common treatments and instruments, well beyond the market access measure in our empirical application. In our working paper (Borusyak and Hull, 2021), we discuss and illustrate some of these implications for policy eligibility treatments, network spillover treatments, linear and nonlinear shift-share instruments, model-implied instruments, instruments from centralized school assignment mechanisms, “free-space” instruments for mass media access, and weather instruments. We expect other settings may also benefit from explicit specification of shock counterfactuals and appropriate adjustment for non-random shock exposure.

A. Data Appendix

Our analysis of market access effects uses data on 340 prefectures of mainland China. This excludes the islands of Hainan and Taiwan and the special administrative regions of Hong Kong and Macau, but includes six sub-prefecture-level cities (e.g. Shihezi) that do not belong to any prefecture. We use United Nations shapefiles to geocode each prefecture by the location of its main city (or, in a few cases, by the prefecture centroid).³⁸

We use a variety of sources to assemble a comprehensive database of the HSR network in 2016 as well as the lines planned (and in many cases under construction) as of April 2019 but not opened yet by the end of 2016. Our starting points are Map 1.2 of Lawrence et al. (2019), China Railway Yearbooks (China Railway Yearbook Editorial Board, 2001-2013), and the replication files of Lin (2017). We cross-check network links across these sources and use Internet resources such as Wikipedia and Baidu Baike to confirm and fill in missing information. Our database includes various types of HSR lines, including the National HSR Grid (4+4 and 8+8) and high-speed intercity railways. However, we only consider newly built HSR lines, excluding traditional lines upgraded to higher speeds. We do not put further restrictions on the class of trains (e.g. to G- and D-classes only) or specify an explicit minimum speed. The operating speed therefore ranges between 160 and 380kph, although the majority of lines are at 250kph. For each line we collect the date of its official opening (if it has opened), the actual or planned operating speed, and the list of prefecture stops. When different sections of the same line opened in a staggered way, we classify each section as a separate line for the purposes of constructing our 1,999 counterfactuals, following the definition of a line in footnote 34. We include only one contiguous stop per prefecture and drop lines that do not cross prefecture borders.

We compute travel time ${\tau }_{ijt}$ between all pairs of prefectures $i$ and $j$ as of the ends of 2007 and 2016 for both the actual and counterfactual networks. Travel time combines traditional modes of transportation (car or low-speed train) with HSR, where available. We allow for unlimited changes between different HSR lines and between HSR and traditional modes without a layover penalty, as HSR trains tend to operate frequently and traditional modes also involve downtime. Following the existing literature, we proxy for travel time by traditional modes by the straight-line distance, and specify the speed of 100 = 120/1.2kph, where 120kph is their typical speed and the 1.2 adjustment for actual routes that are longer than a straight line. For two prefectures connected by an HSR line, we compute the distance along the line as the sum of straight-line distances between adjacent prefectures on the line. We use the operating speed of each line divided by an adjustment factor of 1.3 to capture the fact that the average speed is lower than the nominal speed we record. Computing MA further requires the population of each of the 340 prefectures from the 2000 population Census, which we obtain from Brinkhoff (2018).³⁹

We measure prefecture employment in the 2008–2017 China City Yearbooks (China Statistics Press, 2000-2017).⁴⁰ Each yearbook covers the previous year (so our data cover 2007–2016). While the yearbooks provide several employment variables, we use “The Average Number of Staff and Workers” (from the “People’s Living Conditions and Social Security” chapter), as measured in the entire prefecture and not just the main urban core. This employment series has by far the lowest number of strong year-to-year deviations which may indicate data quality issues.

We finally apply a data cleaning procedure to the outcome variable. We first mark a prefecture-year observation as exhibiting a “structural break” if ($i$) the outcome changes by more than twice in either direction relative to the previous non-missing value for the prefecture, ($ii$) it is not followed by a change in the opposite direction that is between 3/4 and 4/3 as large in terms of log-changes (which we view as a one-off jump and ignore), and ($iii$) the previous change does not satisfy (i). We view the outcome change between 2007 and 2016 as valid only if there are no structural breaks in any year in between. This reduces the sample from 283 to the final set of 275 prefectures.

B. Additional Exhibits

Figure A1: Simulated HSR Lines and Market Access Growth.

Notes: This figure shows an example map of simulated Chinese HSR lines and market access growth over 2007–2016, obtained by permuting the opening status of built and unbuilt lines with the same number of cross-prefecture links.

C. Additional Results

Throughout the results and later proofs we omit the phrase “almost surely with respect to $w$” for brevity. We also abbreviate weak mutual dependence (Assumption 3) as WMD.

Proposition 2 (Convergence for all errors implies WMD). Suppose ${\text{Var}}_{P_N}[{\tilde{z}}_i\mid w]\le U_z$ uniformly. If, for some $U_{\epsilon }>0$, ${\text{Var}}_{P_N}\left[\frac{1}{N}{\sum }_i{\tilde{z}}_i{\epsilon }_i\right]\to 0$ for every sequence of distributions of $\epsilon$ such that ${\text{Var}}_{P_N}[{\epsilon }_i]\le U_{\epsilon }$ for all $N$ and $i=1,\dots ,N$ then WMD holds.

Proposition 3 (WMD implies growing number of shocks). Suppose the support of $g_k$ is bounded uniformly across across $N$ and $k=1,\dots ,K_N$. Suppose further that, uniformly across $N$, ${\tilde{f}}_i(g;w)\equiv f_i(g;w)-{\mathbb{E}}_{P_N}[f_i(g;w)\mid w]$ is Lipschitz-continuous in $g$ with the Lipschitz constant below $U_{Lip}$ and that ${\text{Var}}_{P_N}\left[{\tilde{f}}_i(g;w)\mid w\right]\ge L_z>0$ for at least $N\cdot L_V$ units $i$, with $L_V>0$. Then WMD implies $K_N\to \infty$.

Proposition 4 (WMD and dispersed shock exposure). Suppose $f_i(g;w)$ is weakly monotone in $g$ for all $i$, the components of $g$ are jointly independent conditionally on $w$, and ${\text{Var}}_{P_N}[g_k\mid w]\in [L_{\sigma },U_{\sigma }]$ for $0<L_{\sigma }<U_{\sigma }<\infty$. Consider three cases: conditionally on $w$, ($i$) all components of $g$ are normally distributed and ${\mathbb{E}}_{P_N}\left[\mid \frac{\partial \overline{f}(g)}{{\partial g}_k}\mid \mid w\right]<\infty$, (ii) all components of $g$ have the Bernoulli distribution, or (iii) $\overline{f}$ is linear in $g$. In each case:

1. If ${\sum }_k{\mathbb{E}}_{P_N}\left[{\left(\frac{\partial \overline{f}(g;w)}{{\partial g}_k}\right)}^2\right]\to 0$, WMD holds;

2. If WMD holds, ${\mathbb{E}}_{P_N}\left[{\sum }_k{\left({\mathbb{E}}_{P_N}\left[\frac{\partial \overline{f}(g;w)}{{\partial g}_k}\mid w\right]\right)}^2\right]\to 0$,

where we define $\frac{\partial \overline{f}(g)}{{\partial g}_k}\equiv \overline{f}(g_1,\dots ,g_{k-1},1,g_{k+1},\dots ,g_{K_N})-\overline{f}(g_1,\dots ,g_{k-1},0,g_{k+1},\dots ,g_{K_N})$ in the Bernoulli shock case.

Proposition 5 (WMD and non-overlapping exposure sets). For each $N$, let $G_1(\cdot ),\dots ,G_N(\cdot )$ be a fixed set of functions of $w$ to subsets of $\{1,\dots ,K_N\}$ such that $f_i(\cdot ;w)$ does not depend on $g_k$ for any $k\notin G_i(w)$. Suppose the components of $g$ are jointly independent conditionally on $w$, and ${\text{Var}}_{P_N}[{\tilde{z}}_i\mid w]\le U_z$, uniformly across $N$ and $i=1,\dots ,N$. Then WMD holds if ${\mathbb{E}}_{P_N}\left[\frac{1}{N^2}{\sum }_{i,j=1}^{N}1[G_i(w)\cap G_j(w)\ne \varnothing ]\right]\to 0$.

Proposition 6 (First stage and concentrated individual exposure). Suppose $x_i={\pi z}_i+u_i$ with $u_i⫫g\mid w$, for all $i$ and $\pi \ne 0$. Suppose further, conditionally on $w$, the components of $g$ are mutually independent with ${\text{Var}}_{P_N}[g_k\mid w]\ge L_{\sigma }>0$ uniformly across $N$ and $k=1,\dots ,K_N$. Moreover, one of three conditions hold: ($i$) all components of $g$ are mutually independent and ${\mathbb{E}}_{P_N}\left[\mid \frac{\partial {\tilde{f}}_i(g;w)}{{\partial g}_k}\mid w\mid \right]<\infty$, (ii) all components of $g$ have the Bernoulli distribution, or (iii) all ${\tilde{f}}_i(\cdot ;w)$ are linear in $g$. Then ${\mathbb{E}}_{P_N}\left[\frac{1}{N}{\sum }_i{\sum }_k{\left({\mathbb{E}}_{P_N}\left[\frac{\partial {\tilde{f}}_i(g;w)}{{\partial g}_k}\mid w\right]\right)}^2\right]\ge L_{HHI}>0$ uniformly across $N$, ${\mathbb{E}}_{P_N}\left[\frac{1}{N}{\sum }_i{x}_i{\tilde{z}}_i\right]$ is also uniformly bounded away from zero (by $\mid \pi \mid \cdot L_{HHI}{L}_{\sigma }$.

D. Proofs

We drop the $P_N$ subscripting of moments for all proofs to simplify notation. We again abbreviate weak mutual dependence (Assumption 3) as WMD.

Proof of Proposition 1. By Assumption 1 and the Cauchy-Schwarz inequality

$$\begin{gathered} \text{Var}\left[\frac{1}{N}\sum _i{\tilde{z}}_i{\epsilon }_i\right]=\mathbb{E}\left[{\left(\frac{1}{N}\sum _i{\tilde{z}}_i{\epsilon }_i\right)}^2\right]=\frac{1}{N^2}\sum _{i,j}\mathbb{E}[{\tilde{z}}_i{\tilde{z}}_j{\epsilon }_i{\epsilon }_j] \\ =\frac{1}{N^2}\sum _{i,j}\mathbb{E}[\mathbb{E}[{\tilde{z}}_i{\tilde{z}}_j\mid w]\mathbb{E}[{\epsilon }_i{\epsilon }_j\mid w]] \\ \le \frac{1}{N^2}\sum _{i,j}\mathbb{E}\left[\mid \mathbb{E}[{\tilde{z}}_i{\tilde{z}}_j\mid w]\mid \sqrt{\mathbb{E}\left[{\epsilon }_i^2\mid w\right]\mathbb{E}\left[{\epsilon }_j^2\mid w\right]}\right] \\ \le U_{\epsilon }\mathbb{E}\left[\frac{1}{N^2}\sum _{i,j}\mid \text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w]\mid \right]\to 0. \end{gathered}$$ (5)

When ${\mu }_i$ is approximated by $\frac{1}{S}{\sum }_{s=1}^S{z}^{(s)}$ for $z_i^{(s)}=f_i(g^{(s)};w)$ and for a finite number $S$ of random draws $g^{(s)}$ from $G(g\mid w)$, the same argument holds with a variance upper bound that is at most twice as large. Indeed, since

$$\begin{gathered} \mathbb{E}\left[\left(z_i-\frac{1}{S}\sum _s{z}_i^{(s)}\right)\left(z_j-\frac{1}{S}\sum _s{z}_j^{(s)}\right)\mid w\right] \\ =\text{Cov}\left[z_i-\frac{1}{S}\sum _s{z}_i^{(s)},z_j-\frac{1}{S}\sum _s{z}_j^{(s)}\mid w\right]+\mathbb{E}\left[z_i-\frac{1}{S}\sum _s{z}_i^{(s)}\mid w\right]\mathbb{E}\left[z_j-\frac{1}{S}\sum _s{z}_j^{(s)}\mid w\right] \\ =\frac{S+1}{S}\text{Cov}[z_i,z_j\mid w]=\frac{S+1}{S}\text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w], \end{gathered}$$

we have, repeating the steps in (5),

$$\text{Var}\left[\frac{1}{N}\sum _i{\epsilon }_i\left(z_i-\frac{1}{S}\sum _s{z}_i^{(s)}\right)\right]\le \frac{S+1}{S}{U}_{\epsilon }\mathbb{E}\left[\frac{1}{N^2}\sum _{i,j}\mid \text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w]\mid \right]\to 0.$$

Proof of Proposition 2. For each $N$ consider $\epsilon =\sqrt{U_{\epsilon }∕U_z}\cdot \tilde{\epsilon }$ where ($\tilde{\epsilon }$, $w$) is distributed as ($\tilde{z}$, $w$), and $\tilde{\epsilon }⫫g\mid w$. Then $\text{Var}[{\epsilon }_i]=U_{\epsilon }\text{Var}[{\tilde{z}}_i]∕U_z\le U_{\epsilon }$. Moreover,

$$\begin{gathered} \text{Var}\left[\frac{1}{N}\sum _i{\tilde{z}}_i{\epsilon }_i\right]=\frac{1}{N^2}\sum _{i,j=1}^N\mathbb{E}[\mathbb{E}[{\tilde{z}}_i{\tilde{z}}_j\mid w]\mathbb{E}[{\epsilon }_i{\epsilon }_j\mid w]] \\ =\frac{U_{\epsilon }}{U_z}\cdot \frac{1}{N^2}\sum _{i,j=1}^N\mathbb{E}\left[\mathbb{E}{\left[{\tilde{z}}_i{\tilde{z}}_j\mid w\right]}^2\right] \\ =\frac{U_{\epsilon }}{U_z}\cdot \frac{1}{N^2}\sum _{i,j=1}^N\mathbb{E}\left[\text{Cov}{[{\tilde{z}}_i{\tilde{z}}_j\mid w]}^2\right]\to 0. \end{gathered}$$

By the Cauchy-Schwarz inequality, $\frac{1}{N^2}{\sum }_{i,j=1}^N\mid \text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w]\mid \le {\left(\frac{1}{N^2}{\sum }_{i,j=1}^N\text{Cov}{[{\tilde{z}}_i,{\tilde{z}}_j\mid w]}^2\right)}^{0.5}$.

And by Jensen’s inequality, $\mathbb{E}\left[\frac{1}{N^2}{\sum }_{i,j=1}^N\mid \text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w]\mid \right]\le \mathbb{E}\left[{\left(\frac{1}{N^2}{\sum }_{i,j=1}^N\text{Cov}{[{\tilde{z}}_i,{\tilde{z}}_j\mid w]}^2\right)}^{0.5}\right]\le \mathbb{E}{\left[\frac{1}{N^2}{\sum }_{i,j=1}^N\text{Cov}{[{\tilde{z}}_i,{\tilde{z}}_j\mid w]}^2\right]}^{0.5}\to 0$.

Proof of Proposition 3.⁴¹ We prove this result by contradiction. Without loss of generality suppose $K_N=K$ is constant along the asymptotic sequence; whenever $K_N\nrightarrow \infty$, there is a subsequence of $K_N$ bounded by some $K$, and the proof follows for that subsequence without change. Also without loss, we condition on $w$ and suppress the $w$ notation. We denote the upper bound on the support of $\mid g_k\mid$ by $U_g∕2$ and extend the domain of each ${\tilde{f}}_i$ to ${[-U_g∕2,U_g∕2]}^K$ preserving its Lipschitz constant, by the Kirszbraun theorem.

Let $ℝ(x)=\text{min}\{\lceil x∕\delta \rceil \cdot \delta ,U_g∕2\}$ denote the upward-rounding function for some $\delta >0$. Consider ${\check{f}}_i(g)=ℝ\left({\tilde{f}}_i(ℝ(g_1),\dots ,ℝ(g_K))\right)$ which rounds both the shocks and the values of ${\tilde{f}}_i$ Note that

$$\mid {\check{f}}_i(g)-{\tilde{f}}_i(g)\mid \le \mid {\check{f}}_i(g)-{\tilde{f}}_i(ℝ(g_1),\dots ,ℝ(g_K))\mid +\mid {\tilde{f}}_i(ℝ(g_1),\dots ,ℝ(g_K))-{\tilde{f}}_i(g)\mid \le \delta +{\delta U}_{Lip}\sqrt{K},$$

where the second inequality uses the Lipschitz condition and ${\Vert g-(ℝ(g_1),\dots ,ℝ(g_K))\Vert }_2\le \delta \sqrt{K}$ since $\mid g_k-ℝ(g_k)\mid \le \delta$ for each $k$.

By the Lipschitz condition $\mid {\tilde{f}}_i(g_A)-{\tilde{f}}_i(g_B)\mid \le U_{Lip}{U}_g\sqrt{K}$ for any $g_A,g_B\in {[-U_g∕2,U_g∕2]}^K$. Since $\mathbb{E}\mid {\tilde{f}}_i(g)]=0$ and $g\in {[-U_g∕2,U_g∕2]}^K$, this implies $\mid {\tilde{f}}_i(g)\mid \le U_{Lip}{U}_g\sqrt{K}$ and consequently $\mid {\check{f}}_i(g)\mid \le U_{Lip}{U}_g\sqrt{K}+\delta +{\delta U}_{Lip}\sqrt{K}$. Thus, for all $N$ and $i=1,\dots ,N$ there is only a finite number $U_R$ of possible “rounded” ${\check{f}}_i(\cdot )$ functions. Therefore, at least ${NL}_V∕U_R$ of observations $i$ with $\text{Var}\left[{\tilde{f}}_i(g)\right]\ge L_z$ have the same rounded function, and thus there are at least ${({NL}_V∕U_R)}^2$ such pairs of observations ($i,j$). For any such pair, since $\mathbb{E}\left[{\tilde{f}}_i(g)-{\tilde{f}}_j(g)\right]=0$,

$$\begin{gathered} 2\text{Cov}\left[{\tilde{f}}_i(g),{\tilde{f}}_j(g)\right]=\text{Var}\left[{\tilde{f}}_i(g)\right]+\text{Var}\left[{\tilde{f}}_j(g)\right]-\mathbb{E}\left[{\left({\tilde{f}}_i(g)-{\tilde{f}}_j(g)\right)}^2\right] \\ \ge {2L}_z-\mathbb{E}\left[{\left(\mid {\tilde{f}}_i(g)-{\check{f}}_i(g)\mid +\mid {\check{f}}_i(g)-{\check{f}}_j(g)\mid +\mid {\tilde{f}}_j(g)-{\check{f}}_j(g)\mid \right)}^2\right] \\ \ge {2L}_z-\mathbb{E}\left[{\left(\delta \left(1+U_{Lip}\sqrt{K}\right)+0+\delta \left(1+U_{Lip}\sqrt{K}\right)\right)}^2\right]. \end{gathered}$$

Setting $\delta =\frac{\sqrt{L_z}}{2(1+U_{Lip}\sqrt{K})}$, we have $\text{Cov}\left[{\tilde{f}}_i(g),{\tilde{f}}_j(g)\right]\ge \frac{L_z}{2}>0$, and therefore

$$\frac{1}{N^2}\sum _{i,j=1}^N\mid \text{Cov}\left[{\tilde{f}}_i(g),{\tilde{f}}_j(g)\right]\mid \ge \frac{1}{N^2}\cdot {\left(\frac{{NL}_V}{U_R}\right)}^2\frac{L_z}{2}=\frac{L_V^2{L}_z}{{2U}_R^2}\nrightarrow 0.$$

Thus, weak mutual dependence does not hold, establishing the contradiction.

To establish Proposition 4, we first state and prove four lemmas. We assume all moments relevant for those lemmas exist.

Lemma 1. $h:{\mathbb{R}}^K\to \mathbb{R}$ is weakly increasing and random variables $g_1,\dots ,g_K$ are independent, then for any $k\in \{1,\dots ,K-1\}$ the conditional expectation $\mathbb{E}[h(g_1,\dots ,g_K)\mid g_1,\dots ,g_k]$ is weakly increasing.

Proof. Fix ${\gamma }_1,\dots ,{\gamma }_k$ and ${\gamma }_1^{\prime },\dots ,{\gamma }_k^{\prime }$ such that ${\gamma }_r^{\prime }\ge {\gamma }_r$ for $r=1,\dots ,k$, and define the $K\times 1$ vectors $g=({\gamma }_1,\dots ,{\gamma }_k,g_{k+1},\dots ,g_K)$ and $g^{\prime }=({\gamma }_1^{\prime },\dots ,{\gamma }_k^{\prime },g_{k+1},\dots ,g_K)$. Note $h(g^{\prime })\ge h(g)$. For $r=k+1,\dots ,K$, denote the cumulative distribution function of $g_r$ by $G_r(\cdot )$. Then

$$\begin{gathered} \mathbb{E}[h(g^{\prime })]=\int \cdots \int h(g^{\prime }){dG}_{k+1}(g_{k+1})\dots {dG}_K(g_K) \\ \ge \int \cdots \int h(g){dG}_{k+1}(g_{k+1})\dots {dG}_K(g_K)=\mathbb{E}[h(g)]. \end{gathered}$$

Lemma 2. For any weakly increasing $h_1$, $h_2:{\mathbb{R}}^K\to \mathbb{R}$, $\text{Cov}[h_1(g),h_2(g)]\ge 0$ for $g=(g_1,\dots ,g_K)$ with independent components.

Proof. For $K=1$ this is well known. The proof for $K>1$ follows by induction. Suppose it is true for $K-1$. Then by the law of total covariance

$$\text{Cov}[h_1(g),h_2(g)]=\mathbb{E}[\text{Cov}[h_1(g),h_2(g)\mid g_1]]+\text{Cov}[\mathbb{E}[h_1(g)\mid g_1],\mathbb{E}[h_2(g)\mid g_1]].$$

The first term is the expectation of a covariance of two monotone (by Lemma 1) functions of $K-1$ variables. The second term, again by Lemma 1, is a covariance of two monotone functions of random scalars. Thus both terms are non-negative.

Lemma 3. If $f_i(g;w)$ is weakly monotone in $g$ for all $i$ and components of $g$ are jointly independent conditionally on $w$, then $\text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w]\ge 0$ for all $i$ and $j$. Furthermore WMD simplifies to $\text{Var}[\overline{z}]\to 0$ for $\overline{z}=\frac{1}{N}{\sum }_i{\tilde{z}}_i$.

Proof. Applying Lemma 2 to ${\tilde{z}}_i=f_i(g;w)-\mathbb{E}[f_i(g;w)\mid w]$ and ${\tilde{z}}_j=f_j(g;w)-\mathbb{E}[f_j(g;w)\mid w]$ (or their negations, if $f_i(g;w)$ is weakly decreasing) and conditioning on $w$ everywhere, we obtain $\text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w]\ge 0$. Thus, WMD simplifies to

$$\begin{gathered} \mathbb{E}\left[\frac{1}{N^2}\sum _{i,j}\mid \text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w]\mid \right]=\mathbb{E}\left[\frac{1}{N^2}\sum _{i,j}\text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w]\right] \\ =\mathbb{E}\left[\text{Var}\left[\frac{1}{N}\sum _i{\tilde{z}}_i\mid w\right]\right]=\text{Var}\left[\frac{1}{N}\sum _i{\tilde{z}}_i\right]\to 0, \end{gathered}$$

where the second line rearranges terms and the third line follows by $\mathbb{E}[\frac{1}{N}{\sum }_i{\tilde{z}}_i\mid w]=0$.

Lemma 4. Suppose $g=(g_1,\dots ,g_K)$ is jointly independent with ${\sigma }_k^2\equiv \text{Var}[g_k]$ and consider a scalar function $h$ on the support of $g$. Then if $(i)$ all components of $g$ are normally distributed and $\mathbb{E}\left[\mid \frac{\partial h(g)}{{\partial g}_k}\mid \right]<\infty$ or (ii) all components of $g$ have the Bernoulli distribution,

$$\sum _k{\sigma }_k^2{\left(\mathbb{E}\left[\frac{\partial h(g)}{{\partial g}_k}\right]\right)}^2\le \text{Var}[h(g)]\le \sum _k{\sigma }_k^2\mathbb{E}\left[{\left(\frac{\partial h(g)}{{\partial g}_k}\right)}^2\right],$$ (6)

with $\frac{\partial h}{{\partial g}_k}$ defined in the Bernoulli case as in Proposition 4. Further, (iii) if $h$ is linear, (6) holds with equalities, regardless of the distributions of the components of $g$.

Proof. For part (i), the lower bound is established by Cacoullos (1982, Proposition 3.7), and the upper bound on $\text{Var}[h(g)]$ is established by Chen (1982, Corollary 3.2). For part (ii), the lower bound follows from restricting the results for binomial distributions in Cacoullos and Papathanasiou (1989, p. 355), and the upper bound is similarly a special case of the result in Cacoullos and Papathanasiou (1985, p. 183). Part (iii) follows trivially from the fact that $\partial h∕{\partial g}_k$ is non-stochastic.

Proof of Proposition 4. By Lemma 3, WMD is equivalent to $\text{Var}\left[\overline{f}(g;w)\right]=\mathbb{E}\left[\text{Var}\left[\overline{f}(g;w)\mid w\right]\right]\to 0$. Applying Lemma 4 conditionally on $w$ and using the bounds on $\text{Var}[g_k\mid w]$,

$$\mathbb{E}\left[\sum _k{L}_{\sigma }{\left(\mathbb{E}\left[\frac{\partial \overline{f}(g;w)}{{\partial g}_k}\mid w\right]\right)}^2\right]\le \text{Var}[\overline{f}(g;w)]\le \mathbb{E}\left[\sum _k{U}_{\sigma }\mathbb{E}\left[{\left(\frac{\partial \overline{f}(g;w)}{{\partial g}_k}\right)}^2\mid w\right]\right].$$

The upper bound, the law of iterated expectations, and $U_{\sigma }>0$ imply that if $\mathbb{E}\left[{\sum }_k{[\left(\frac{\partial \overline{f}(g;w)}{{\partial g}_k}\right)}^2\right]\to 0$, $\text{Var}\left[\overline{f}(g;w)\right]\to 0$, and thus WMD holds. The lower bound and $L_{\sigma }>0$ imply that if WMD holds and thus $\text{Var}\left[\overline{f}(g;w)\right]\to 0$, we have $\mathbb{E}\left[{\sum }_k{\left(\mathbb{E}\left[\frac{\partial \overline{f}(g;w)}{{\partial g}_k}\mid w\right]\right)}^2\right]\to 0$.

Proof of Proposition 5. For any $N$ and fixed $\overline{w}$ in the support of $w$ and for $i$ and $j$ such that $G_i(\overline{w})\cap G_j(\overline{w})=\varnothing$ we have ${\tilde{z}}_i⫫{\tilde{z}}_j\mid w=\overline{w}$ because $f_i$ and $f_j$ are functions of two non-overlapping subvectors of $g$, the components of which are conditionally independent. Thus $\text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w=\overline{w}]=0$ for such ($i$, $j$) pairs, and we obtain

$$\begin{gathered} \frac{1}{N^2}\sum _{i,j}\mid \text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w]\mid =\frac{1}{N^2}\sum _{i,j}1[G_i(w)\cap G_j(w)\ne \varnothing ]\mathbb{E}[\mid \text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w]\mid ] \\ \le \frac{1}{N^2}\sum _{i,j}1[G_i(w)\cap G_j(w)\ne \varnothing ]\mathbb{E}\left[\sqrt{\text{Var}[{\tilde{z}}_i\mid w]\text{Var}[{\tilde{z}}_j\mid w]}\right] \\ \le U_z\cdot \frac{1}{N^2}\sum _{i,j}1[G_i(w)\cap G_j(w)\ne \varnothing ] \end{gathered}$$

and therefore $\mathbb{E}\left[\frac{1}{N^2}{\sum }_{i,j}\mid \text{Cov}[{\tilde{z}}_i,{\tilde{z}}_j\mid w]\mid \right]\to 0$.

Proof of Proposition 6. By the law of iterated expectations, $\mathbb{E}\left[\frac{1}{N}{\sum }_i{x}_i{\tilde{z}}_i\right]=\pi \mathbb{E}\left[\frac{1}{N}{\sum }_i{\tilde{z}}_i^2\right]=\pi \mathbb{E}\left[\frac{1}{N}{\sum }_i\text{Var}[{\tilde{z}}_i\mid w]\right]$. The result then follows directly from Lemma 4 applied to each ${\tilde{f}}_i(g;w)$:

$$\frac{1}{N}\sum _i\text{Var}[{\tilde{z}}_i\mid w]\ge \frac{1}{N}\sum _i\sum _k\text{Var}[g_k\mid w]{\left(\mathbb{E}\left[\frac{\partial {\tilde{f}}_i(g;w)}{{\partial g}_k}\mid w\right]\right)}^2\ge L_{\sigma }\cdot \frac{1}{N}\sum _i\sum _k{\left(\mathbb{E}\left[\frac{\partial {\tilde{f}}_i(g;w)}{{\partial g}_k}\mid w\right]\right)}^2,$$

and thus $\mid \mathbb{E}\left[\frac{1}{N}{\sum }_i{x}_i{\tilde{z}}_i\right]\mid \ge \mid \pi \mid \cdot L_{\sigma }{L}_{HHI}$.