RASCH ANALYSIS OF THE FORGOTTEN JOINT SCORE IN PATIENTS WITH TOTAL HIP ARTHROPLASTY

Abstract

Objective

To assess the internal construct validity, including local independence, unidimensionality, monotonicity, and invariance, reliability, and targeting of the Forgotten Joint Score within the Rasch Measurement Theory framework.

Design

Cross-sectional study.

Patients

A total of 111 patients with total hip arthroplasty at least 3 months after surgery.

Methods

The Forgotten Joint Score was submitted to each subject during their rehabilitative treatment in an Italian centre and then to Rasch analysis.

Results

The base Rasch analysis showed a satisfactory fit to the model with strict unidimensionality and no differential item functioning. However, monotonicity (11 out of 12 items showed disordered thresholds) and local independence were violated. After rescoring 10 items and creating 5 subtests to account for local dependence, the scale satisfied all the other Rasch model requirements (i.e. invariance, local independence, monotonicity, unidimensionality, and multi-group invariance), with reliability indexes (> 0.850) for measurement at the individual level and proper targeting. A raw-score-to-measure conversion table was provided.

Conclusion

After structural (i.e. collapsing items categories) and non-structural (i.e. creating subtests) strategies, the Forgotten Joint Score satisfied the measurement requirements of the Rasch model, and it can be used in patients with total hip arthroplasty in clinical and research settings.

LAY ABSTRACT

The Forgotten Joint Score (FJS) is a questionnaire used to quantify a patient’s ability to forget their operated prosthetic joint. A recent study suggested shortcomings in FJS unidimensionality; that is, the ability to measure a single variable. Therefore, this study performed a deep psychometric analysis in 111 patients with total hip replacement. Most item thresholds were disordered, meaning patients could not coherently discriminate between the score categories. Furthermore, local dependence between items was found, showing that item responses were dependent among them. After structural modifications, that is, collapsing item categories to solve the disordered thresholds and non-structural modifications, that is, creating subtests to solve the local dependence, the FSJ showed good psychometric properties. Although the number of observations was sufficient for a calibration sample, further studies are needed to confirm these results. A conversion table has been provided to enable clinicians and researchers to use the FJS as an interval measure.

Total hip arthroplasty (THA) is considered the standard care for treating end-stage hip osteoarthritis (1), providing pain relief, and improving function (2) and quality of life (3). In Italy in 2020, 30,980 hip arthroplasty interventions were performed, despite a decrease of 25% from 2019 due to the SARS-CoV-2 (COVID-19) pandemic period (4).

Patient-reported outcome measures (PROMs) showcase the effectiveness of THA from the patient’s perspective (5). PROMs encompass data reported directly by people about their symptoms, physical functioning, and quality of life (6), which may differ from those detected by healthcare professionals (7).

The Forgotten Joint Score (FJS) is a PROM consisting of 12 items, developed by Behrend et al. (8) to quantify “the patient’s ability to forget the operated joint” in everyday life in patients with THA or total knee arthroplasty (TKA), which is indirectly related to the patient’s quality of life after surgery. The items composing the questionnaire have a 5-Likert ordinal scale and assess the person’s awareness regarding the presence of a joint prosthesis while performing various activities of daily living (ADLs), such as lying in bed at night or sitting on a chair.

Although preliminary analyses supported the internal consistency, test-retest reliability (8), external construct validity, and responsiveness of the FJS in patients with THA (9), we recently conducted a psychometric study on the Italian FJS version in 111 patients with THA (10), evaluating the internal construct validity within the classical test theory (CTT) psychometric framework. After translation and cross-cultural adaptation of the FJS into Italian, the high internal consistency, both in terms of Cronbach’s alpha (= 0.944) and inter-item correlations (all correlations > 0.6), and the excellent test-rest reliability (intraclass correlation coefficient = 0.958) were confirmed. However, a confirmatory factor analysis (CFA) showed the initial data misfit to a 1-factor model, suggesting a lack of unidimensionality for the total score and the presence of local dependence between items FJS06 and FJS09. After accounting for this local dependence, the FJS fit to a 1-factor CFA improved significantly, except for the root mean square error of approximation (= 0.087), which was slightly above the recommended threshold (≤ 0.08) (11). Hence, the CFA findings highlighted the need for a more in-depth assessment of the internal construct validity of the FJS within the Rasch measurement theory framework.

Rasch analysis (12–15) is a statistical technique assessing the fit of subjects’ responses to a given scale or questionnaire according to the Rasch model requirements. Rasch measurement theory helps to identify and address potential violations of the internal construct validity model’s requirements and enables the evaluation of separation reliability and scale targeting to the sample. Given the properties of the Rasch model, it is possible to estimate item difficulties and person abilities on the same measurement continuum when data conforms to the model’s requirements. Moreover, the total score can be transformed from an ordinal to a linear interval-level scale, with the logit as the unit of measurement (12, 14).

Therefore, the aim of this study was to assess the internal construct validity, including local independence, unidimensionality, monotonicity and measurement invariance, reliability, and targeting of the FJS in patients with THA through Rasch analysis.

METHODS

Subjects and setting

Complete details of the study methodology, including the enrolment procedures, the setting, the sample and the scale descriptive statistics, have been published previously (10).

In summary, 111 adults (> 18 years old) who had undergone THA at least 3 months before the study were enrolled through a convenient sample method. Subjects with a poor understanding of the Italian language or with hip replacement revision or neurological, visual, or cognitive impairment were excluded.

The Italian FJS version (10) was administered to each subject during the rehabilitative treatment at the Rehabilitation Service “San Giovanni di Dio”, Adelfia, Italy, from December 2020 to December 2021.

The ethics commitee of IRCCS San Raffaele, Italy, approved the study protocol (number: RP 20/17)), which followed the principles outlined in the Declaration of Helsinki. Participants gave written informed consent to participate in the study.

Outcome measure

The FJS (8) comprises 12 items, investigating the patient’s awareness of the joint prosthesis during different ADLs. Each item is scored on a 5-point Likert scale: 0 = never, 1 = almost never, 2 = seldom, 3 = sometimes, 4 = mostly. According to the authors of the original version (8), all item responses must be summed and divided by the number of completed items. This mean value is subsequently multiplied by 25 to obtain a total score range from 0 to 100 points. Finally, the score is subtracted from 100 to change the direction of the final score in a way that high scores indicate a high degree of “forgetting” the prosthetic joint, that is, a low degree of awareness. A higher score indicated a higher ability to forget THA daily.

The current study calculated the total score by summing each item score, based on a previous Rasch analysis study on the FJS in patients with TKA by Niama Natta et al. (16), obtaining a measure of “awareness” of the prosthetic joint for each patient.

Rasch analysis

The FJS data were subjected to fitting to the Rasch model (12). Rasch analysis, which involves the evaluation of the Rasch model’s assumptions and requirements, has been discussed extensively elsewhere (12–15). This study was conducted utilizing the partial credit parameterisation of the Rasch model, which does not impose any restrictions on the item threshold parameters (17).

The methods employed to interpret the Rasch analysis output have been comprehensively described in previous publications (18–20). In summary, to elucidate the analysis outputs, the following summary statistics were reported:

• Fit to the Rasch model: this pertains to the stochastically invariant ordering of the item. It is evaluated through the mean and standard deviation (SD) of the item and person fit residuals, as well as a summary χ² interaction statistic. An acceptable fit to the model is attained when all individual item and person fit residuals are within ± 2.5. As a summary measure, the grouped SD value of the item and person fit residuals should also be ≤ 1.4 to indicate adequate fit (12). In addition, the summary item χ² should not be significant after Bonferroni’s correction, indicating no deviation from the model’s expectations (21). The current study also evaluated the item characteristic curves, representing the discrepancy between the observed and predicted responses for each item based on the probabilistic relationship between a person’s ability and the item difficulty (12, 15).

• Internal construct validity requirements:

  • ◦Unidimensionality: each scale item must measure a single underlying variable (13, 14). To evaluate this requirement, the current study employed a paired t-test on the separate person parameter estimates for each subject, obtained from 2 subsets of items identified through a principal component analysis of the residuals (22). Unidimensionality was ascertained by examining the proportion of significant tests (PST) and the lower limit of the binomial confidence interval for proportions (BCI), which was considered “strict” if less than 5%. We regarded unidimensionality as “acceptable” if only the BCI were below 5% (23).
  • ◦Monotonicity: this dictates that the likelihood of endorsing an FJS item or response option reflects the patient’s awareness about their operated joint. As per this principle, the increase in the underlying latent trait, i.e., awareness of their properly operated joint, should correspond to a parallel increase in the probability of endorsing items related to higher awareness (14, 24). The adequacy of this requirement is evaluated based on the percentage of items with disordered thresholds, with a value of 0% deemed optimal for ensuring adequate monotonicity.
  • ◦Local independence: this denotes that a person’s ability accounts for all the variation in their responses to an item, with no other systematic association between responses for a given ability level. To evaluate local independence, we used a local dependence relative cut-off (LDRC), calculated by adding 0.2 to the mean of the residual correlations after removing each item’s correlation with itself (i.e. equal to 1) (18, 25).
  • ◦Absence of differential item functioning (DIF): this requires that an item remain invariant across relevant subgroups or person factors (e.g. sex). This indicates that different groups of individuals, with equivalent levels of underlying characteristics within a given person factor, should respond similarly regardless of their group affiliation. The current study considered uniform and non-uniform DIF. To assess the presence of DIF, this study conducted a 2-way analysis of variance (ANOVA) for each item, comparing scores across each level of the person factor. DIF occurs when the ANOVA p-values fall significantly below the Bonferroni correction (14, 24). Specifically, we analysed sex (male vs female) and age (< 61 years vs ≥ 61 years, based on the median value of the sample) as person factors in the DIF analysis.

• Targeting and reliability:

  • ◦Targeting: this pertains to the degree of matching between a scale measurement range and the distribution of the calibrating sample (14, 15). The floor and ceiling effects and the targeting index were examined to evaluate targeting. The targeting index was calculated as the ratio between the mean person location and the standard error of the measurement. Based on this assessment, the targeting was deemed “good” and “fair” within 1 standard error and 2 standard errors, correspondingly (26).
  • ◦Separation reliability: this refers to the ability of a scale to distinguish persons effectively based on their ability level. This was measured by various indices, including the Person Separation Index (PSI), Cronbach’s alpha (α), and the number of statistically distinct levels (strata) (14, 15, 26, 27). In addition, in cases where mistargetting was a concern, the Distribution-Independent Person Separation Index (DI-PSI) and the number of statistically Distinct Levels of Performance Ability (DLPA) were calculated (28). For individual person and group-level measurements, PSI or DI-PSI values of ≥ 0.85 and ≥ 0.70, respectively, are considered sufficient (29, 30).

When the data demonstrated non-conformity with the Rasch model, we progressively adjusted the scale to account for the violations of the internal construct validity requirements.

This iterative process was achieved through a post-hoc modification of individual items, which can be statistical and structural. The first, referred to as “statistical”, involves adjustments to the scale structure while keeping the total score range intact. These adjustments, such as “subtest creation” (13, 31, 32) and “item splitting” (14), primarily impact the conversion of total scores into estimates of the ability to address local independence violations and uniform DIF, respectively. Differently, the second approach, known as “structural”, actively modifies the scale structure through “item rescoring” (14, 15, 33) in case of disordered thresholds, or “item deleting” in case of misfitting or non-uniform DIF (31). These modifications affect the total score range and are used to resolve monotonicity violations and persistent model misfits, respectively. “Item rescoring” is accomplished by collapsing adjacent response categories and following established guidelines (34) to optimize statistical and clinical meaning (13, 33), while “item deleting” is employed as a last resort when other modifications have failed.

Given that the FJS has already been published and widely used as a questionnaire, our objective would be to prioritize the statistically conservative approach while minimizing the implementation of structure-modifying strategies, particularly in cases where the scale fails to attain satisfactory internal construct validity. Consequently, the fit of the scale to the Rasch model, internal construct validity requirements, reliability, and targeting were evaluated during the initial analysis of the scale. Subsequently, following each scale modification, these parameters were reassessed to confirm that the model fit was adequate. This process was iteratively conducted until no further alterations were necessary or feasible.

Should DIF be detected in the solution obtained so far, the influence of the item/ subtest splitting on the person estimates would be tested using the procedure presented by Maritz et al. (32). After item/subtest splitting, we would anchor the “split” solution on the “un-split” one, using an item/subtest free from the DIF, and compare the person estimates of the two solutions, calculating an effect size (Cohen’s d) of the paired t-test of the difference. A Cohen’s d < 0.2 would be considered negligible; thus, the DIF would not be adjusted for (32). Otherwise, the “split” solution would be chosen as the final (32).

Should a final fitting solution following the above modifications be found, its total score would be transformed into interval-level measurements, whose unit is the logit (12, 14, 15).

The Rasch analysis was conducted using the RUMM2030 software (version 5.4 for Windows. RUMM Laboratory Pty Ltd, Perth, Australia: 1997–2010; www.rummlab.com), employing a pairwise maximum likelihood estimation algorithm. A significance value of 0.05 was used throughout and adjusted for the number of tests by Bonferroni correction (35). A sample size of 111 observations would be sufficient to estimate item difficulty, with a significance level of 0.05 to ± 0.5 logits, irrespective of the targeting of persons to the items (36). The RUMM Logbook^TM, an ad hoc Excel 2007^TM application developed using Microsoft Visual Basic^TM macros, was used to facilitate interpreting the results of each Rasch analysis (available on request to the corresponding author).

RESULTS

Sample characteristics

This study included 111 subjects (mean ± SD age = 63.7 ± 11.9 years; 59.5% male). The enrolled patients’ main demographic and clinical characteristics are reported in Table I. Detailed sample characteristics are available elsewhere (10).

Table I.

Main demographic and clinical characteristics of the sample (N = 111)

Characteristics
Age, years, mean ± SD	63.7 ± 11.9
Body mass index, kg/m2, mean ± SD	27.6 ± 4.7
Days after the surgery, mean ± SD	1084.3 ± 1448.1
Sex, n (%)
Male	66 (59.5)
Female	45 (40.5)
Occupation, n (%)
Retired	38 (34.2)
Housewife	29 (26.1)
Employee	24 (21.6)
Self-employment	14 (12.6)
Unemployed	6 (5.4)
Aetiology, n (%)
Osteoarthritis	78 (70.3)
Fracture	24 21.6)
Cancer	1 (0.9)
Other	8 (7.2)
Replacement side, n (%)
Right	75 (67.6)
Left	36 (32.4)

SD: standard deviation.

Rasch analysis summary

The base Rasch analysis showed an adequate fit to the Rasch model for the questionnaire (Table II, “Base analysis”), which satisfied the item homogeneity or invariance requirement (χ²_df = 15.8₁₂; p = 0.199). Indeed, also at the item level, there was no model overfit or underfit with fit residuals within ± 2.5. Beyond this, there were no significant χ² for all the items, which indicates the satisfaction of the stochastic invariance of the item hierarchy. Also, the scale showed a strict unidimensionality, as the PST was 3.8%, and the Lower Bound of the BCI for proportions (LBCI) was 0%. However, there were disordered thresholds for 11 items out of 12, suggesting a violation of the monotonicity requirement. In addition, 5 pairs of items had residual correlations above the LDRC (here set at 0.116, indicative of a violation of the local independence requirement).

Table II.

Results of Rasch analysis for the Forgotten Joint Score (FJS) (N = 111)

N	Analysis name	Fit to the Rasch model						Internal construct validity requirements					Reliability and targeting
		FitRes Items		FitRes Persons		Item-trait interaction		Unidimensionality		Other internal construct validity requirements			Separation reliability		Targeting
		Mean	SD	Mean	SD	χ2df	p-value	PSTa	LBCIa	T-DTb	LDc	T-DIFd	PSIe	αe	PL Mean	PL SD	SEMf	Targeting indexg
1	Base analysis	0.102	0.940	–0.283	1.460	15.812	0.199	3.8%	0.0%	91.7%	5	0	0.899	0.944	–0.260	1.484	0.472	–0.551
2	After rescoring	0.062	0.889	–0.317	1.423	11.812	0.458	8.6%	3.8%	0%	4	0	0.907	0.940	–0.425	1.730	0.528	–0.806
3	After subtesting	0.275	0.617	–0.344	1.197	1.965	0.854	1.0%	0.0%	0%	0	0	0.879	0.909	–0.342	1.399	0.487	–0.702
Recommended values		[–2.5, 2.5]	< 1.4	[–2.5, 2.5]	< 1.4	–	< p-value corrected for Bonferroni	< 5.0a	< 5.0	0%	0	0	≥ 0.85e	≥ 0.85e	0.000	–	–	[–2, 2]g

^aUnidimensionality is achieved when PST is < 5% or the lower bound of its BCI is < 5%.

^bThe T-DT statistic is calculated as the percentage of items with disordered thresholds out of the total items. The values range from zero to 100%, where zero indicates the absence of items with disordered thresholds.

^cLD value shows the number of item pairs with adjusted residual correlations above the local dependence relative cut-off, calculated as the mean of all the residual correlations (excluding the correlation of items with themselves) plus 0.2.

^dThe T-DIF summary statistic is calculated as the absolute value of the base 10 logarithms of all p-values for uniform and non-uniform DIF across all items and all person factors below the Bonferroni-corrected p-value. The values range from zero to infinite, where zero indicates no DIF.

^eA value > 0.850 indicates the measurement precision at the individual level, whereas a value > 0.700 indicates precision only at the group level. Values < 0.700 will make the instrument unsuitable for any measurement, as it cannot distinguish 2 groups of persons at the very least.

^fSEM is calculated with the formula: $SD\times \sqrt{1-reliability}$, where SD is the person location standard deviation, and reliability is the PSI with extremes.

^gThe targeting index is calculated as the ratio between the mean person measures and the SEM. Targeting is good and respectively fair when the mean person measure is beyond [–1 +1] and [–2, +2] SEM the mean item measure (set by default at 0 logits).

N: analysis number; FitRes: fit residual; SD: standard deviation; χ2df: χ2 and its degrees of freedom; p: Bonferroni-corrected χ2 probability value; PST: the proportion of significant t-test carried out on the estimates: that within a principal component analysis of residuals: loaded positively and negatively (factor loading >±0.3) on the first component; LBCI: lower bound confidence interval at 95% for PST; T-DT: percentage of items with disordered thresholds; LD: number of item pairs with residual correlations above the local dependence relative cut-off; T-DIF: total DIF load; PSI: person separation index; α: Cronbach’s alpha; PL mean: person location mean; PL SD: person location standard deviation; SEM: standard error of measurement of the person locations.

In the next steps of analysis, several item modifications were performed to achieve a final fitting solution of the scale:

• All items, except for items FJS11 and FJS08, which recovered ordered thresholds after the rescoring of the other items, were rescored as they showed disordered thresholds (Table II, “After rescoring analysis”, Table III). The responses “almost never” and “seldom” were collapsed consistently for all rescored items;

• “Subtests” were created between clusters of items that demonstrated some left-over local dependence, obtaining a 5-subtest solution (FJS01-FJS02; FJS03-FJS11; FJS04-FJS05-FJS07; FJS06-FJS12; FJS08-FJS09-FJS10).

Table III.

Item parameters and fit statistics for the Forgotten Joint Score (FJS) (N = 111, analysis “number 2 – After rescoring” and “number 3 – After subtesting”)

Analysis “number 2 – After rescoring”	Item parameters and fit statistics					Scoring model
Item label	Loc	SE	FR	χ2	p *	0	1	2	3	4
FJS08 – Awareness when standing up from a low-sitting position?	–0.845	0.115	0.856	0.23	0.631	0	1	2	3	4
FJS11 – Awareness taking a walk/hiking?	–0.506	0.110	–0.58	0.33	0.566	0	1	2	3	4
FJS07 – Awareness walking on uneven ground?	–0.177	0.140	–0.924	0.97	0.324	0	1	1	2	3
FJS09 – Awareness standing for long periods of time?	–0.168	0.132	–0.198	0.02	0.903	0	1	1	2	3
FJS03 – Awareness when you are walking for more than 15 min?	–0.075	0.135	0.930	0.22	0.636	0	1	1	2	3
FJS06 – Awareness climbing stairs?	–0.049	0.136	0.724	1.93	0.164	0	1	1	2	3
FJS02 – Awareness sitting on a chair for more than 1 h?	0.016	0.134	0.818	0.41	0.524	0	1	1	2	3
FJS10 – Awareness doing housework or gardening?	0.083	0.136	–0.285	0.41	0.521	0	1	1	2	3
FJS12 – Awareness doing your favourite sport?	0.126	0.144	–0.014	0.18	0.676	0	1	1	2	3
FJS05 – Awareness traveling in a car?	0.312	0.137	–1.188	3.78	0.052	0	1	1	2	3
FJS01 – Awareness in bed at night?	0.593	0.137	1.533	2.35	0.125	0	1	1	2	3
FJS04 – Awareness taking a bath/shower?	0.691	0.138	–0.934	1.02	0.312	0	1	1	2	3
Analysis “number 3 – After subtesting”	Item parameters and fit statistics					Scoring model
Subtest label	Loc	SE	FR	χ2	p **
FSJ03 – FSJ11	–0.314	0.074	0.422	0.14	0.712	0–7
FSJ08 – FSJ09 – FSJ10	–0.296	0.063	0.339	0.24	0.623	0–10
FSJ06 – FSJ12	0.119	0.088	0.526	0.03	0.874	0–6
FSJ04 – FSJ05 – FSJ07	0.162	0.067	–0.769	1.43	0.232	0–9
FSJ01– FSJ02	0.329	0.085	0.859	0.13	0.714	0–6

FJS items and subtests are ordered by progressively increasing the difficulty from top to bottom. The location is expressed in logits.

For analysis “number 2 – After rescoring”, the degree of freedom for each χ² was 1 for all items.

^*The Bonferroni-corrected p-value indicating statistical significance at the 0.05 level was 0.004.

For analysis “number 3 – After subtesting”, the degrees of freedom for each χ² were 1 for all subtests.

^**The Bonferroni-corrected p-value indicating statistical significance at the 0.05 level was 0.008.

FJS: Forgotten Joint Score; Loc: Location; SE: standard error; FR: fit residual; χ2: chi-square; p: χ2 probability.

After these modifications, the final solution for the FJS showed a good fit to the Rasch model (χ²_df = 1.96₅; p = 0.854) (Table II, After subtesting analysis”). In addition, the scale satisfied all the other internal construct validity requirements in terms of monotonicity (no disordered thresholds), local independence (no pairs of residual correlations of items above the LDRC), strictly unidimensionality (overall PST = 1.0%, LBBCI = 0%), and invariance at the subgroup level (no DIF for the person factors assessed: sex, age). The item parameters and fit statistics for this analysis are reported in Table III.

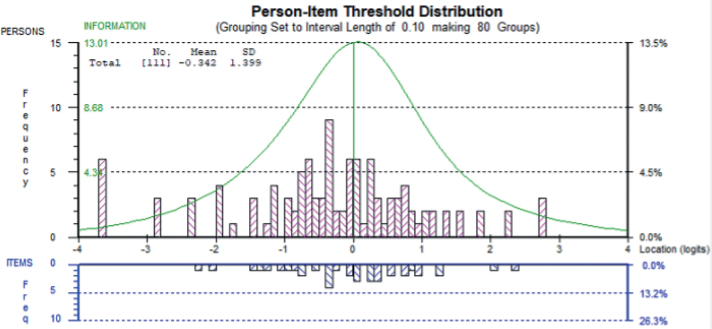
All the subjects’ responses fitted the model except for 4 under-fitting subjects, showing fit residuals > 2.5. The targeting FJS graph (Fig. 1) of the final analysis (Table II, “After subtesting analysis”) highlighted that persons were spread across 7 logits, with a negligible floor (5.4%) and no ceiling effects (0%).

Fig. 1.

Targeting of the Forgotten Joint Score (FJS) (N = 111, analysis “number 3 –After subtesting”). In the figure, persons and items are displayed, respectively, in the upper and the lower part of the graph, separated by the logit scale. Grouping set to interval length of 0.10, making 80 groups. Freq: frequency; No: number; SD: standard deviation.

The mean person ability of –0.342 logits and a targeting index of –0.702 indicated a proper matching between person ability and item difficulty, set by default at 0 logits.

The separation reliability, expressed as PSI and Cronbach’s alpha, was 0.879 and 0.909, respectively, indicating the precision of measurement at the individual level. Therefore, given the PSI, persons could be separated into 3.9 strata, the statistically distinct levels of awareness of the operated hip reliably distinguished by the scale.

The item hierarchy (Table III, “After rescoring analysis”) suggested that the activities in which the awareness of the operated hip is higher for most people are linked to postural changes and walking (FJS08: standing up from a low-sitting position, FJS11: taking a walk/hiking, FJS07: walking on uneven ground). Conversely, the activities in which the awareness of the operated hip is lower concern maintaining a static, fixed position (FJS05: travelling in a car, FJS01: in bed at night, FJS04: taking a bath/shower).

Based on the item calibration, it was possible to construct a table to convert the scale raw scores into interval-level estimates of the awareness of the prosthetic hip (Table IV).

Table IV.

Raw-score-to-measure-estimates conversion table for the Forgotten Joint Score (FJS) – Italian (analysis “number 3 – After subtesting”)

Rai score	Logit scale	± 95% CI	0–60 original scaling	± 95% CI
0	–3.679	2.319	0.0	9.4
1	–2.875	1.648	6.6	6.7
2	–2.336	1.286	10.9	5.2
3	–1.975	1.090	13.9	4.4
4	–1.702	0.966	16.1	3.9
5	–1.481	0.878	17.9	3.6
6	–1.297	0.811	19.4	3.3
7	–1.138	0.759	20.7	3.1
8	–0.998	0.717	21.8	2.9
9	–0.872	0.682	22.9	2.8
10	–0.759	0.653	23.8	2.7
11	–0.655	0.627	24.6	2.6
12	–0.558	0.608	25.4	2.5
13	–0.468	0.590	26.2	2.4
14	–0.382	0.576	26.9	2.3
15	–0.301	0.564	27.5	2.3
16	–0.223	0.557	28.2	2.3
17	–0.147	0.551	28.8	2.2
18	–0.072	0.545	29.4	2.2
19	0.001	0.543	30.0	2.2
20	0.074	0.543	30.6	2.2
21	0.147	0.545	31.2	2.2
22	0.221	0.547	31.8	2.2
23	0.296	0.553	32.4	2.3
24	0.373	0.561	33.0	2.3
25	0.453	0.572	33.7	2.3
26	0.536	0.586	34.3	2.4
27	0.623	0.602	35.1	2.5
28	0.717	0.623	35.8	2.5
29	0.818	0.649	36.6	2.6
30	0.928	0.680	37.5	2.8
31	1.052	0.721	38.6	2.9
32	1.195	0.772	39.7	3.1
33	1.363	0.847	41.1	3.4
34	1.571	0.943	42.8	3.8
35	1.842	1.082	45.0	4.4
36	2.216	1.298	48.0	5.3
37	2.793	1.691	52.7	6.9
38	3.684	2.413	60.0	9.8

Person estimates are expressed in logits and into a 0–60 scale (FJS original scaling).

This conversion table can only be used if patients are assessed on all items of the FJS (i.e. without missing responses). The modified raw scores are to be used for the FJS items, as detailed in Table III.

DISCUSSION

This paper analysed the internal construct validity, reliability, and targeting of the FJS within the Rasch measurement theory framework in patients with THA. After assessing the same properties within the CTT framework in a previous study (10), we concluded the need for a more in-depth assessment of its internal construct validity based on an root mean square error of approximation (RMSEA) value slightly above the recommended threshold shown by CFA results. In this work, after structural and non-structural strategies to cope respectively with the violation of the monotonicity and local independence requirements, the FJS confirmed the satisfaction of all the internal construct validity requirements of the Rasch model (i.e., unidimensionality, invariance, local independence, monotonicity, multi-group invariance), with reliability indexes adapted for individual-level measurement and proper targeting. A raw-score-to-measure conversion table was provided, which can be used in clinical and research settings for patients with THA. Although the number of available observations was sufficient for a calibration sample, further studies would be needed to confirm these results.

In comparing the two described analysis frameworks of the internal construct validity (CTT vs Rasch measurement theory), both expressed a good fit of all items to the different requested requirements. Furthermore, it is possible to find a difference in the violation of local dependence highlighted by the CFA and the Rasch analysis. Indeed, CFA showed a significant modification index between only 2 items (10). Differently, in the Rasch analysis context with more in-depth analysis based on measures of person estimates (vs ordinal scores in CFA), 5 pairs of items signalled a significant residual, which highlighted that responses to these items were governed by the response to other items and not only by the degree of the latent trait (i.e. “response dependence”) (37). The presence of response dependence was also sustained by the reduction of the reliability estimate (PSI delta = 0.03), compared to the anaysis n°3 “After subtesting”, in which we accounted for local dependence, and the previous one (37). Given the common presence of local dependence in Rasch analyses on health outcome scale data, its detailed assessment is fundamental considering its impact on the scale’s internal construct validity (38). Our analysis strategy was to manage local dependency based on clinical and statistical considerations. Although the clinical conceptual perspective of the highlighted dependence was unclear in some cases, we attempted to provide a clinical rationale for the item content that made up the subtests. For example, FJS01 and FJS02 concern static positions, FJS08, FJS09, and FJS10 quantify activities performed in a standing position, and FJS03 and FJS11 refer to gait. Finally, in the subtest composed of FJS04, FJS05, and FJS07, the first two items refer to activities that involve maintaining a position for a prolonged period. At the same time, the FSJ07 refers to walking on uneven ground. All three activities may be related to postural control and balance requests in different positions to maintain stability and prevent falls, especially when taking a bath/shower or walking on uneven ground. However, this conceptual rationale only partially explains these correlations, and we cannot exclude that this result was due to the relatively small sample size.

To our knowledge, this is the first study reporting on the Rasch analysis of the Italian version of the FJS in patients with THA. Previously, Giesinger et al. in 2013 (39) developed a computer-adaptive version of the FJS in patients with THA and TKA after running a Rasch analysis, and recently, in 2019, Niama Natta et al. (16) performed a Rasch analysis of the FJS in patients undergoing knee arthroplasty.

Considering the Rasch analyses, it can be initially shown that a different parameterization of the Rasch model was used between the three studies. In our work, as previously indicated, the partial credit model was used, which does not impose any restrictions on the item threshold parameters (17). In Giesinger (39) and Niama Natta’s (16) studies, the rating scale model was used, which provides that thresholds do not have to be equally spaced within an item, but the threshold constraints are equal across all items (17), having obtained a non-significant likelihood-ratio test.

Comparing the base analyses, the questionnaire showed an overall satisfactory fit to the model (current study: χ² = 15.8₁₂, p-value = 0.12; Giesinger’s study (39): RMSEA = 0.11; Niama Natta’s study (16): χ² = 34.1₁₂, p-value = 0.08), and almost all items showed disordered thresholds for two of the samples (current: 11/12; Niama Natta: 9/12), while Giensinger et al. (39) found no disordered thresholds using the rating scale model.

Regarding local dependence, the other two articles (16, 39) found fewer items with significant residual correlations. In this regard, it is essential to note that, in Giesinger (39) and Niama Natta’s (16) studies, respectively, a fixed cut-off of 0.25 and 0.30 were considered, unlike the current study, in which the cut-off was calculated about each analysis and so lower than the fixed. This difference may have led to a possible underdetection of local dependence in these samples. In addition, no analogies were highlighted between the pairs of items involved in significant residual correlations of the considered studies.

After the common item rescoring of the disordered score categories in the current analysis and in Niama Natta’s one, where the “almost never” category was consistently combined with the “seldom” one in a single category, going from 5 scoring categories to 4 scoring categories, a notable difference between the three Rasch analyses was the analytical strategy. Given the presence of local dependence between pairs of items, the analytical approach of Niama Natta et al. (16) was “structural”. Indeed, 3 FJS items (FJS03, FJS05 and FJS11) were deleted as they had residual correlations with other items above the cut-off of 0.3 and worse psychometric characteristics. In contrast, this violation has been managed through a conservative “statistical” technique called “item subtesting” in the current study. Finally, in Giesinger’s work (39), no strategy was reported to handle local dependence.

Considering the final solutions obtained, we noticed how using a more conservative analytical strategy allowed us to keep the 12 original items, unlike Niama Natta’s final version composed of 9 items (16). Both scales showed an excellent fit to the Rasch model, a satisfactory unidimensionality, and an optimal targeting of the item’s difficulty compared with the subject’s ability. The measurement range of FJS for TKA (Niama Natta) was wider than approximately 1 logit. Still, the scale showed a slightly lower separation reliability level (PSI = 0.84 vs 0.88) due to the lower scoring thresholds (27 vs 38) caused by deleting the above 3 items. On the contrary, Giesinger’s paper did not realize any modifications to the scale, keeping the initial solution and obtaining the already cited satisfactory fit to the model and a Cronbach’s alpha value (= 0.97) higher than the current sample (= 0.91). This discrepancy could be due to the reduced number of items (5 subtests) of our final version on which we calculated this statistic and the unsolved local dependence in Giesinger’s sample. It is well known that Cronbach’s alpha is sensitive to the item number, i.e. the higher the item number, the higher the alpha value, and it is also inflated by positive local dependence (37). Furthermore, the discrepancy in internal consistency findings between the two studies may be due to our FJS versions’ lower total score than Giesinger’s version, as we rescored several items that presented disordered thresholds while they did not. No further information was available in Giensinger’s study about targeting. Finally, no items of the three samples were affected by DIF by sex and age, as already proved by Behrend et al. (8) in the original version.

Furthermore, given the item hierarchy shown in the three studies’ results, it is interesting to note that among the activities in which the awareness of the operated hip was higher for most people, there is the postural change from a low-sitting position to the standing position, both in patients with the knee (Niama Natta) (16) and hip prostheses (current study), and the standing for longer period and the walking on uneven ground are present in the two THA samples (39). On the other hand, among the activities in which the awareness of a knee or hip prosthesis is lower, being in bed at night and taking a bath/shower are reported by all three studies. From a biomechanical and neurophysiological point of view, the observed similarity in results could be attributed to the fact that individuals with THA and TKA may have kinesthetic and proprioceptive impairments on the ipsilateral lower limb (40), which can cause persistent static stability dysfunction, muscle weakness, and range of motion restrictions (41, 42). Thus, the awareness of having a joint prosthesis will probably increase during movement and functional activities, especially in demanding tasks and weight-bearing, which may provide sensory feedback and proprioceptive input, increasing the perception of prosthesis awareness. On the other hand, prosthesis awareness may decrease when a patient is required to maintain a specific position for a long time.

Finally, our and Niama Natta’s (16) studies developed raw-score-to-measure conversion tables usable in clinical and research contexts for patients with THA and those with TKA. As in previous works, the current results highlight the importance of using interval-level measures, which support the appropriate use of parametric statistics in clinical trials and the correct interpretation of the variable changes intra- and inter-subject, unlike the raw scores (18, 19). However, the conversion table can be used only if no missing items are present and the raw scores of the rescored items are modified, as detailed in Table III (section “Scoring model”).

This study has some limitations. Although the number of available observations was sufficient for a calibration sample, a larger sample would have further minimized the risk of capitalizing on chance concerning the fit to the model. Given this limitation, it would be desirable to conduct further studies with internal construct validity assessment of the FJS in the Rasch measurement theory framework on other samples, also composed of subjects with different aetiologies in which an internal construct validity assessment has already been performed within the CTT psychometric framework (e.g. anterior cruciate ligament reconstruction, patellar dislocation, quadriceps tendon rupture reconstruction). Moreover, the rescoring changes were made post-hoc, so these might not be the same if new response categories were presented to subjects completing the scale.

In conclusion, after structural and non-structural strategies, this study supports the internal construct validity, reliability, and targeting of the FJS within the Rasch measurement theory framework in a sample of patients with THA.

Funding Statement

The study protocol was approved by the IRCCS San Raffaele, Italy (number: RP 20/17).