Indirect Electrochemical Cooling: Model-Based Performance Analysis and Working Fluid Selection

Abstract

The rising energy demand for cooling and heating requires efficient and sustainable technologies. Vapor-compression systems represent the state of the art but suffer from downscaling limits and maintenance needs. These disadvantages may be overcome by recently proposed electrochemical processes. However, their potential has not been explored systematically. This work quantifies the thermodynamic potential of an indirect electrochemical cooling process that replaces the vapor compressor of a standard refrigeration cycle with an electrochemical cell. An equilibrium-based process model evaluates the process performance of a working fluid, depending on its composition and temperatures in the process. After screening an extensive database for possible working fluids, an electrochemical cooling process is analyzed and optimized for the coefficient of performance (COP) to operate between two heat reservoirs at 20 °C (heat source) and 35 °C (heat sink). The majority of the investigated working fluids yield smaller or similar efficiencies than vapor-compression refrigeration, with COPs between 3.0 and 4.0. However, 35 promising working fluids that achieve higher efficiencies are identified with a COP up to 9.63, corresponding to 49% of Carnot. These working fluids are worthy of further investigation as their use in the electrochemical cooling process possibly outperforms standard vapor-compression refrigeration.

1. Introduction

Cooling is essential for human living and consumes 3900 TWh/a of electricity worldwide,¹ corresponding to 16% of the total electricity consumption. With growing populations and economies, the global heating and cooling energy demand will increase substantially in the coming decades.^1,2 Given the increasing standards of living and climate change, in particular, a significant increase is anticipated for the cooling demand. Prospectively, the number of globally installed cooling devices will increase from 3.6 billion devices in 2019 to 9.5 billion in 2050.¹ A substantial share of the growing cooling demand is allocated to space cooling. Today’s electricity demand for space cooling of 2000 TWh/a is expected to triple by 2050.¹

Due to this expected increase, improving the energy efficiency of cooling processes was recently highlighted by Henry et al.³ as one of five thermal energy grand challenges for decarbonization. Doubling the efficiency of air conditioning would reduce the required global power generation by 1.300 GW until 2050.¹ This value equals China and India’s combined coal-based power generation capacity in 2019.¹ Hence, increasing cooling technologies’ efficiency could massively reduce the required expansion of renewable electricity production and is a crucial step to enable the transition to a sustainable energy supply.

Today, the state-of-the-art technology for cooling devices and heat pumps is a vapor-compression system. In vapor-compression systems, evaporation drives heat absorption, enabling high capacities. Furthermore, the technology is very mature and applicable to wide capacity ranges.⁴ Extensive research has been carried out to improve vapor-compression cycles in previous decades.⁵⁻⁷ Despite the major progress achieved, some disadvantages, such as environmentally harmful working fluids, high noise emissions, and vibrations, have not been overcome so far. Alternative technologies to vapor-compression systems can break new ground toward more efficient and sustainable cooling.

Various alternative technologies⁸⁻¹¹ to vapor-compression refrigeration have been investigated: gas processes (e.g., Brayton), caloric processes (magnetocaloric, electrocaloric, and elastocaloric), thermoacoustic and thermoelectric processes, and sorption and chemical cooling processes. To date, none of these technologies can exceed vapor-compression processes for space cooling applications in terms of efficiency and specific cooling capacity⁹ and has achieved significant market penetration yet. However, these technologies might be promising for applications with specific constraints (e.g., noise or space).

Lately, alternative cooling technologies based on electrochemistry have garnered interest.^11,12 Advantageous configurations with no (or very few) moving parts promise high efficiencies and the potential to outperform vapor-compression refrigeration.¹³ Generally, electrochemical cooling systems are classified into direct and indirect systems depending on the thermodynamic effect exploited: direct electrochemical cooling systems employ the heat absorbed or rejected from electrochemical reactions.¹⁴⁻¹⁶ Conversely, indirect electrochemical cooling systems utilize a secondary effect arising from an electrochemical reaction (e.g., phase change or pressure change) to generate a cooling effect.¹³

In pioneering work, Gerlach and Newell¹⁵ developed a thermodynamic model of a direct electrochemical cooling system. They found that a lower current density improves the performance by reducing the ohmic losses in the electrochemical cell. Duan et al.¹⁶ presented an extended thermodynamic model of a direct electrochemical cooling system using the Fe²⁺/Fe³⁺ and VO²⁺/VO⁺₂ redox couples. Their results indicate that direct electrochemical cooling systems are competitive with vapor-compression refrigeration when low current densities are applied.¹⁶

A promising indirect electrochemical cooling process combines parts of standard vapor-compression refrigeration with an electrochemical cell:¹⁷ as in standard vapor-compression refrigeration, evaporating the working fluid enables high cooling capacities. However, in this hybrid cooling process, the working fluid condenses through a composition change during a redox reaction in an electrochemical cell (e.g., proton exchange reaction). Standard vapor-compression refrigeration often requires a large pressure difference to enable evaporation and condensation at specified source and sink temperatures. Consequently, the compression of the vaporous working fluid requires a significant amount of work and reduces the process’s overall performance. In particular, the compressor’s exergetic losses are substantial in most heat pumps and refrigerators.¹⁸ In the indirect electrochemical cooling process, the condensation in the electrochemical cell shifts the compression from the vapor to the liquid phase and thus substantially reduces the compression work compared to standard vapor-compression refrigeration.

For such an indirect electrochemical cooling process, James et al.¹⁷ introduced an equilibrium-based thermodynamic model assuming complete conversion in the electrochemical cell and calculating the cell work based on the reversible cell work and a fixed cell efficiency. Feasible working fluids for indirect electrochemical cooling are molecule pairs. A molecule pair is a combination of species A and B, which can be converted into each other by a redox reaction. James et al.¹⁷ evaluated nine redox reactions with proton exchange for a case study: T_source = 20 °C, T_sink = 35 °C, ΔT_approach = 5 K, η_pump = 0.8, η_cell = 0.6. The authors identified isopropanol/acetone (IPA) as the best-performing molecule pair. Employing IPA as the working fluid in the electrochemical cooling process results in a coefficient of performance (COP) of 8.1, improving the COP by 20% compared to standard vapor-compression refrigeration.

In the following work, James¹⁹ developed a 2D cell model accounting for ohmic, activation (Butler–Volmer), and concentration overpotentials (Nernst). The model considers thermodynamic equilibria to account for incomplete reactions in the cell and fluid mixtures in the system (Van-Laar model). In comparison to their first study,¹⁷ the extended model predicts lower COPs, e.g., COP = 1.75 instead of 8.1 for IPA. James¹⁹ associated the COP decrease with the concentration overpotential growing during the reaction in the cell. Following up on James et al.,¹⁷ Kim et al.²⁰ investigated the correlation between system performance and cell area for the electrochemical cooling process using IPA. For a 7 kW residential application, Kim et al.²⁰ calculate a required cell area of 2451 m² corresponding to 3000 8-cell stacks. Furthermore, Kim et al.²¹ extended the previous model by an iterative determination of the extent of reaction and the cell temperature and, consequently, found that lower conversion in the cell increases the cell temperature to sufficiently reject heat from the cell. Elevated cell temperatures increase the process pressures, subsequently reducing the evaporator’s heat uptake. Consecutively, Kim et al.²² showed experimentally for IPA that condensation through composition change in the electrochemical cell is possible. In a recent model-based study, Kim et al.²³ evaluated the performance of 13 molecule pairs in an electrochemical cooling process to identify decisive properties for selecting molecule pairs. They found the difference in boiling point temperature of the pure species, the reversible cell voltage, and the chemical equilibrium constant to be key metrics of molecule pairs for heat pumping applications. Still, their process model underlies the assumption of a complete reaction and thereby neglects mixture effects.

The studies mentioned above^17,19−22 show that the electrochemical cooling process’ performance is heavily dependent on the employed molecule pair. Assessing the performance capability of molecule pairs requires a certain model complexity. Estimating the cell work from the reversible cell work and a cell efficiency, analogous to James et al.,¹⁷ has the risk of underestimating the cell work and consequently overestimating the potential of the respective molecule pair and the electrochemical cooling process. Furthermore, incomplete reactions require calculating the cell work and all other process units depending on the mixture composition. Hence, reconsidering the selection of molecule pairs with a more complex process model and a broader search space seems beneficial. However, the more complex process models developed by James et al.^17,19 and Kim et al.²⁰⁻²² include detailed cell models and require extensive computational time, causing tedious analyses for numerous different molecule pairs.

This paper aims to evaluate the potential of the indirect electrochemical cooling process and identify promising molecule pairs. For that purpose, we developed an equilibrium-based thermodynamic process model that includes the key design aspects while allowing for an extensive molecule pair screening. To compare molecule pairs consistently, molecule-pair-dependent optimal working fluid compositions in the process are determined. Thereby, our model considers the working fluid composition change in an electrochemical cell when calculating the cell work and the entire process.

We first screen an extensive database for molecule pairs feasible in the indirect electrochemical cooling process. In the next step, we simulate their performance in the electrochemical cooling process. Here, we evaluate the thermodynamic efficiency limits of the electrochemical cooling process and compare the performance to standard vapor-compression refrigeration. In the final step, we identify important molecule pair properties affecting the performance of indirect electrochemical cooling.

2. Modeling

2.1. Process Model

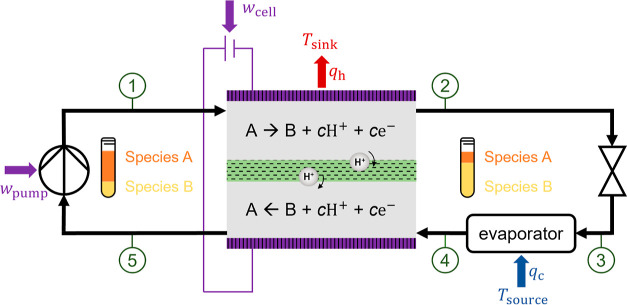
Four basic units comprise the investigated electrochemical cooling process: an electrochemical cell, a throttle to decrease the pressure, an evaporator, and a pump to increase the pressure (Figure 1). In this hybrid cycle, the working fluid consists of a binary mixture of species A and B. Heat is absorbed by evaporating the working fluid, analogous to standard vapor-compression cycles. However, recondensation of the working fluid and heat rejection are accomplished in an electrochemical cell through a change in working fluid composition in a reversible electrochemical reaction. The process model is subject to the following assumptions.

Figure 1.

Schematic of the electrochemical cooling process (process adapted from James et al.¹⁷). The encircled numbers define the thermodynamic states. w_pump and w_cell are the molar-specific works required in the pump and cell, respectively. q_c and q_h are the molar-specific heat uptake and rejection, respectively.

• 1.Negligible pressure losses.
• 2.Isenthalpic working fluid expansion in the throttle.
• 3.Negligible overpotentials associated with ohmic resistance, mass transport, and kinetics in the electrochemical cell.
• 4.Pure proton transport through the membrane.

Since the process model neglects these loss mechanisms, the resulting performance is expected to overestimate the real-life behavior. Still, the model captures the main process characteristics and thus allows for molecule pair screening.

The developed model incorporates five thermodynamic states (Figure 1) at two pressure levels: p_high (states 1 and 2) and p_low (states 3, 4, and 5).

The bubble-point pressure at cell temperature T_cell (= T₂) and the composition at the outlet of the upper half-cell x_A,2 (state 2) define the high process pressure p_high.

1

Setting p_high to the bubble-point pressure at cell temperature ensures that saturated liquid enters the throttle.

The low process pressure p_low (states 3, 4, and 5) is defined by the bubble-point pressure at cell temperature T_cell (= T₅) and outlet composition of the lower half-cell x_A,5 (state 5) to enable the pumping of a liquid working fluid.

2

Therefore, the pressure difference results exclusively from a difference in the working fluid composition. A pinch model accounts for the heat exchangers and calculates the constant cell (T_cell at states 2 and 5) and evaporation (T_evap at state 4) temperatures from the heat sink (T_sink) and source (T_source) temperatures. Hence, the cell and evaporation temperatures are defined by the application and a minimal approach temperature ΔT_approach.

3

4

The thermodynamic process states are defined as follows.

• State ① = f (p_high, h₁ = h₅ + w_pump, x_A,1).

• State ② = f (p_high, T_cell, x_A,2), saturated liquid.

• State ③ = f (p_low, h₂, x_A,2).

• State ④ = f (p_low, T_evap, x_A,2).

• State ⑤ = f (p_low, T_cell, x_A,1), saturated liquid.

For each of the five process states, the thermal and caloric properties of the working fluid are determined with an equilibrium-based thermodynamic property model (Section 2.3). The process variables are calculated from the process states, as explained in the following.

2.1.1. Pumping Work

The molar-specific pumping work w_pump is determined by employing an isentropic pump efficiency η_pump.

5

with

6

2.1.2. Cell Reaction and Work

The working fluid composition in the half-cells changes in flow direction. Thus, the Gibbs free energy change during the electrochemical reaction depends on the location y in the half-cells. The electrochemical reaction in the upper high-pressure half-cell (Figure 1) is described by the spacial extent of reaction ζ.

7

ζ describes the change in the mole fraction of species A, from the inlet (state 1) to a particular position y along the reaction in the cell Δx_A,1–y, related to the overall change between the inlet (state 1) and the outlet (state 2) Δx_A,1–2. In the lower half-cell (low-pressure), the reverse reaction occurs (Figure 1). The cell work is calculated from the change in Gibbs free energy resulting from the electrochemical reactions in the two half-cells. We distinguish between the endergonic and the exergonic half-cell reaction to calculate the work required in the electrochemical cell. The overall molar amount of the working fluid does not change during the cell reaction. Thus, the cell work is calculated as a molar-specific value.

2.1.2.1. Exergonic Half-Cell Reaction

The exergonic reaction from ζ = 1 to ζ = 0 occurs in the low-pressure half-cell. The maximum cell work produced in the exergonic reaction w_out depends on the cell temperature T_cell, the pressure in the exergonic half-cell p_low, and the composition change in the reaction Δx_A,1–2.

8

2.1.2.2. Endergonic Half-Cell Reaction

The opposite reaction to the exergonic half-cell occurs in the endergonic high-pressure half-cell. Here, the change in Gibbs free energy during the reaction varies along the location from ζ = 0 to ζ = 1. Thus, applying a charge profile along the electrode would be necessary to optimally account for the composition change in flow direction. However, due to the very high electrode conductivity, adjusting the electrode’s charge to the changing working fluid composition at the electrode surface is not possible if only one electrode (or cell) is utilized. Therefore, the cell work needed to drive the endergonic reaction w_in is determined from the reaction’s change in the Gibbs free energy Δ_rg, assuming that ζ = 1 = const.: the charge required to achieve the outlet working fluid composition is applied to the entire electrode. The endergonic reaction takes place at the cell temperature T_cell and pressure of the endergonic half-cell p_high.

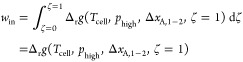9

2.1.2.3. Cell Work

The total molar-specific work needed in the electrochemical cell to keep the reactions running w_cell is the difference between the work required in the endergonic half-cell reaction w_in and the work provided by the exergonic half-cell reaction w_out.

10

2.1.3. Heat Uptake in the Evaporator

The molar-specific heat uptake in the evaporator q_c is the difference between the enthalpy at the outlet h₄ (state 4) and the inlet h₃ (state 3) of the evaporator.

11

2.1.4. Coefficient of Performance

The COP is used to evaluate the performance of the electrochemical cooling process. The COP describes the ratio between the molar-specific heat uptake in the evaporator q_c and the molar-specific work needed in the process.

12

As for standard vapor-compression refrigeration, the performance of the electrochemical cooling is limited by the Carnot-efficiency COP_limit that is calculated from the heat sink and heat source temperatures.

13

2.2. Optimization of the Working Fluid Composition

The working fluid composition is optimized for each molecule pair to evaluate the overall potential of electrochemical cooling. For a case study, the following parameters are kept constant: the temperature of heat sink T_sink and heat source T_source, the minimal approach temperature ΔT_approach, and the isentropic pump efficiency η_pump. The remaining degrees of freedom in the calculation of the COP are

• The mole fraction of species A in state 1: x_A,1

• The change in the mole fraction of species A in the upper half-cell of the electrochemical cell (state 1 to state 2): Δx_A,1–2.

The absolute value of the change in the lower half-cell is identical to Δx_A,1–2.

For each molecule pair analyzed, we maximize the COP by optimizing the working fluid composition as defined in the following optimization problem (eq 14).

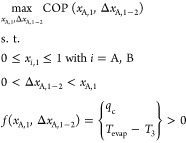14

The optimization problem is solved subject to (s.t.) constraints: first, the mole fractions of all species i in state 1 x_i,1 need to be between 0 and 1. Furthermore, 0 < Δx_A,1–2 < x_A,1 must be kept, as the initial amount of species A at the upper half-cell’s inlet x_A,1 limits the quantity of species A that can react to species B. To achieve cooling, the enthalpy change in the evaporator q_c needs to be greater than zero. Furthermore, the evaporation temperature T_evap needs to be greater than the temperature of state 3 T₃ to enable heat uptake.

The optimization problem is solved in Python using the minimize function with the sequential least squares programming (SLSQP) method from the SciPy package, which includes a nonlinear programming (NLP) solver. As NLP optimization usually does not guarantee a global optimum, the optimization is conducted five times with randomized starting points for each molecule pair. Subsequently, the optimization result with the highest COP is selected. Optimizing for one molecule pair takes 5–10 min on a standard computer.

2.3. Property Model

The working fluid in the electrochemical cooling process is a binary mixture consisting of species A and B. To determine vapor–liquid equilibria for the process, Antoine coefficients of pure fluids are fitted using vapor–liquid equilibrium data from DIPPR 801 correlations.²⁴ Caloric properties for pure fluids are calculated using the molar-specific isobaric ideal gas heat capacity and the Peng–Robinson equation of state²⁵ to consider deviations from the ideal gas. The following necessary input data for pure fluid properties are taken from the DIPPR 801 database:²⁴ the critical pressure and temperature, the standard state absolute entropy, the standard state heat of formation, the acentric factor, and coefficients for the molar-specific isobaric ideal gas heat capacity.²⁴ When choosing the values from the DIPPR 801 database, the values classified as accepted values are selected to ensure working with consistent and reliable fluid properties.²⁶

The φ–γ approach implemented in the Phasepy package to calculate mixture properties²⁷ allows the calculation of real mixture behavior in the process. In the φ–γ approach, vapor phase deviations φ are expressed by virial expansion, calculated with the Abbott–Van Ness correlation.²⁸ For liquid phase deviations γ, a g^E model is used. In this study, an NRTL model is used with parameters obtained from SPT-NRTL.²⁹ SPT-NRTL is a natural language processing model for the thermodynamically consistent prediction of binary activity coefficients from the SMILES code. The SPT-NRTL model is trained on 26 million data points of a synthetic COSMO-RS data set and fine-tuned with experimental data. Winter et al.²⁹ state that the mean absolute error in predicting the binary activity coefficients (ln γ) is between 0.1 and 0.2, exceeding the prediction accuracy of the known group contribution model UNIFAC.²⁹

2.4. Case Study

Following James et al.,¹⁷ we use typical conditions of domestic air conditioners for the case study.

• Temperature of the heat source T_source = 20 °C.

• Temperature of the heat sink T_sink = 35 °C.

• Minimum approach temperature for the electrochemical cell and evaporator ΔT_approach = 5 K.

• Isentropic efficiency of the pump η_pump = 0.8.

2.5. Screening for Possible Molecule Pairs

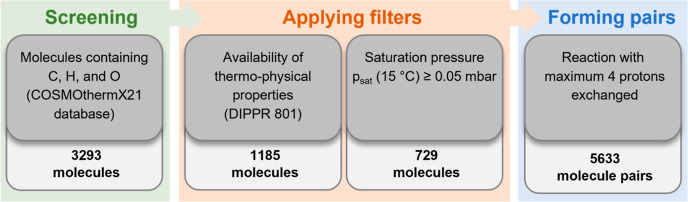
Figure 2 presents the molecule pair preselection procedure of this study: first, the comprehensive COSMOthermX21 database³⁰ is screened for molecules only containing carbon, hydrogen, and oxygen atoms. Our study focuses on this molecular composition to limit the selection regarding possible side products and environmental impact; 3293 molecules are retained.

Figure 2.

Procedure to preselect suitable molecule pairs to be evaluated with the process model.

After the identification of possible molecules in the screening step, two filters are applied to the list of possible molecules. As described in the previous section, the thermodynamic properties are taken from the DIPPR 801 database to model the electrochemical cooling process. Considering only molecules with sufficient data in the DIPPR 801 database reduces the number of molecules from 3293 to 1185. Furthermore, the minimal saturation pressure at the evaporation temperature is set to 0.05 mbar. This criterion excludes mixtures that are probably in a solid state at the evaporation temperature and reduces the number of suitable molecules to 729. In the real electrochemical cooling process, such low pressures are not desirable. However, it must be noted that the evaporation pressure in the process depends on the properties of the two molecules and their interaction. Setting the pure fluid minimum saturation pressure at evaporation temperature to this low value excludes molecules that are certainly not suitable but avoids excluding too many pure fluids in the preselection that might be suitable.

Proton exchange membranes (PEMs) are frequently used in electrochemical cells. Their typical temperature range, stable up to 85–90 °C,³¹ fits reasonably the temperatures of the electrochemical cooling process. Thus, a PEM is considered in the electrochemical cell of this study. Hence, in the next step, molecule pairs that can undergo (de)hydrogenation reactions are formed from the molecules identified. The maximal number of protons exchanged is set to four, and 5633 molecule pairs are found.

In the final step, the electrochemical cooling process is evaluated with the optimization model employing the 5633 obtained molecule pairs as the working fluid, with the endergonic reaction occurring in the upper half-cell. The results of the process evaluation step are discussed in the following sections.

3. Results

3.1. Thermodynamic Evaluation

The 5633 molecule pairs obtained in the preselection of the screening are evaluated with the process model. The electrochemical cooling process is feasible for 606 molecule pairs. For the other 5027 molecule pairs, the optimizer does not find adequate working fluid compositions meeting the optimization constraints because, e.g.

• Condensation in the electrochemical cell is not achievable even with complete conversion at cell temperature and pressure.

• Even assuming complete conversion, the temperature after the throttle T₃ is higher than the maximum evaporation temperature, inhibiting cooling.

The COP of standard vapor-compression refrigeration (benchmark) is determined to be between 3.8 and 4.7 (R410A, superheating: 5 K, isentropic compressor efficiency: 0.52–0.64) for the selected case study.

Figure 3 shows the histogram and cumulative distribution of the optimized COP for the 606 molecule pairs found. 78% of the molecule pairs yield a COP between 3.0 and 4.0 and thus are no promising candidates. For our detailed study, the focus is on molecule pairs achieving a COP greater than 4.0, as they can potentially compete with standard vapor-compression refrigeration. 35 molecule pairs (5.8%) achieve a COP greater than 4.0. These promising molecule pairs are listed in Table 1. Within the 35 promising molecule pairs, 12 yield a COP higher than 4.7 and, hence, possibly outperform standard vapor-compression refrigeration (COP = 3.8–4.7, highlighted in green in Table 1).

Figure 3.

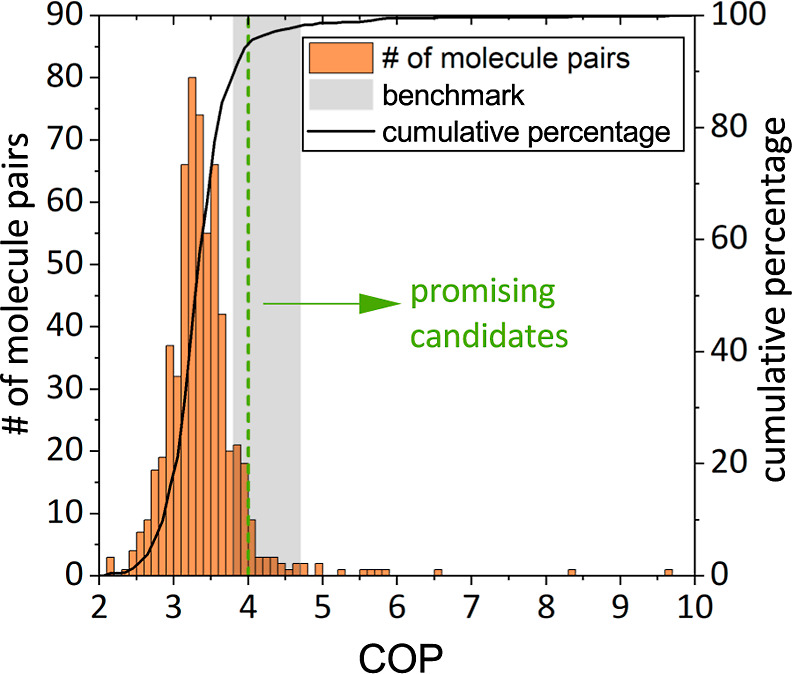
Histogram (orange, bin width = 0.1) and cumulative percentage distribution of COP (black line) for the 606 molecule pairs. The gray area represents the benchmark (vapor-compression refrigeration, COP = 3.8–4.7); promising molecule pairs have a COP greater than 4.0 (green dashed line).

Table 1. List of Promising Molecule Pairs^a.

^aMolecule pairs with COP values higher than 4.7 are highlighted in green.

The mixture of ethylene glycol and acetic acid yields the maximum COP of 9.63 (COP_limit = 19.5). Species A of the best-performing molecule pair, ethylene glycol, is employed in various industrial and commercial applications, including polyester resins for fiber or polyethylene terephthalate (PET) containers, as a functional fluid for antifreeze, deicing, and heat transfer and as a solvent.³² The corresponding species B of the best-performing molecule pair, acetic acid, is employed in the food industry as an acidulant and preservative or used as an herbicide, microbiocide, fungicide, or pH-adjusting agent in manufacturing.³³ Thus, both species are known and market-available. However, to the best of our knowledge, no experimental investigation of the electrochemical reaction kinetics between ethylene glycol and acetic acid has been published.

Previous studies^17,19−23 of electrochemical cooling consider models with different model complexity (cf. Table A1). The low-complexity model of James et al.¹⁷ considered only nine molecule pairs, while the more sophisticated models exclusively focused on the IPA pair.¹⁹⁻²² Consequently, our results cannot be directly compared. Even for the IPA pair, comparisons are challenging due to variations in case studies.²⁰⁻²² The low-complexity model¹⁷ assumed complete reaction within the electrochemical cell and a constant cell efficiency. Compared with this model, our calculations result in lower COPs for most of the molecule pairs. The lower COPs are expected since our model covers more losses, e.g., the concentration overpotential at the electrode surface. Only propylene glycol/1-hydroxy-2-propanone (PGLY) yields a higher COP in our model than in the calculation of James et al.¹⁷ While PGLY performs well in our study with a COP of 5.53, James et al.¹⁷ determined a COP of 1.18. Here, the optimized working fluid compositions in the process and the consideration of mixtures could explain the deviation.

Table A1. Comparison of Different Models for Electrochemical Cooling^a.

	James et al.17	James19	Kim et al.20	Kim et al.21	Kim et al.22	Kim et al.23	this work
cell model	overall cell efficiency	2D-discretized	2D-discretized	2D-discretized	overpotential	overall cell efficiency	concentration-dependent cell work
composition change in cell	complete	variable	variable	iterative	variable	complete	optimized
activation overpotentials	no	yes	yes	yes	yes	no	no
ohmic overpotentials	no	yes	yes	yes	yes	no	no
concentration overpotentials	no	yes	yes	yes	yes	no	yes
mixtures in process	no	yes (Van-Laar)	yes (Van-Laar)	yes (Van-Laar)	yes (Van-Laar)	no	yes (φ–γ)
pressure losses	no	yes	yes	yes	no	no	no
constant Tcell	yes	yes	yes	no	yes	yes	yes
number of molecule pairs	9	1 (IPA)	1 (IPA)	1 (IPA)	1 (IPA)	5	5633
COP for IPA Tsource = 20 °C Tsink = 35 °C	8.1	1.75				8.1	2.97

^aThe COP for IPA is listed when evaluated for T_source = 20 °C and T_sink = 35 °C.

James et al.¹⁷ identified IPA as the best-performing working fluid with a calculated COP of 8.1, while our model yields a significantly lower COP of 2.97. However, Kim et al.²⁰ used a 2D cell model to determine a cell voltage of 0.1 V for IPA. Compared to the original model from James et al.,¹⁷ the cell voltage is increased by a factor of 3. The cell work increases nearly linearly with the cell voltage. Neglecting changes in the pumping work and the molar-specific heat uptake in the evaporator, the COP is reciprocal to the cell work (eq 12). Following this, the expected COP for IPA with a cell voltage of 0.1 V is approximately 2.7 and thus close to the COP calculated with our model (COP = 2.97). In later work, James¹⁹ recalculated the COP using the 2D cell model for different working fluid compositions in a process model and found a COP of 1.75 for IPA. This COP is significantly lower than the COP calculated with James et al.’s previous model (COP = 8.1).¹⁷

However, the comparison with previous results from James et al.¹⁷ for IPA emphasizes that considering the composition change of the working fluid in the process significantly impacts the COP. Our model considers a working fluid- and composition-dependent cell work, while James et al.¹⁷ assumed a non working fluid-dependent constant cell efficiency of 0.6. Kim et al.²¹ state a simulation time of nearly 30 min for one data point when solving their multivariable (cell temperature and extent of reaction) optimization process with the implemented discretized cell model. In contrast, optimizing for one molecule pair takes less than 10 min with this work’s model. Considering the reduced computational effort and comparing our model results with those obtained with the more complex models from James¹⁹ and Kim et al.²⁰ demonstrate that our model offers a good compromise between complexity and effort. The calculated COPs appear to be in a realistic value range and enable a reliable performance evaluation of certain molecule pairs. Moreover, the required model inputs are available for many molecules, enabling a large screening.

3.2. Important Molecule Pair Properties for Electrochemical Cooling

Based on the 606 molecule pairs identified (Section 3.1), molecule pair properties are determined that benefit the electrochemical cooling process. According to eq 12, the COP depends on the heat uptake in the evaporator q_c and the works added in the electrochemical cell w_cell and the pump w_pump. As the major part of the work is added in the electrochemical cell, the pumping work can be neglected for qualitative analysis.

15

Thus, high heat uptake q_c in the evaporator and low cell work w_cell are desired to achieve high COPs.

3.2.1. Heat Uptake in the Evaporator q_c

Under the assumption of full evaporation, the heat uptake in the evaporator depends on the enthalpy of vaporization of both pure fluids (h_evap,A and h_evap,B), the mixture composition x_A,3, the steam quality at the inlet of the evaporator χ₃ (state 3), and the enthalpy of mixing Δh^E.

16

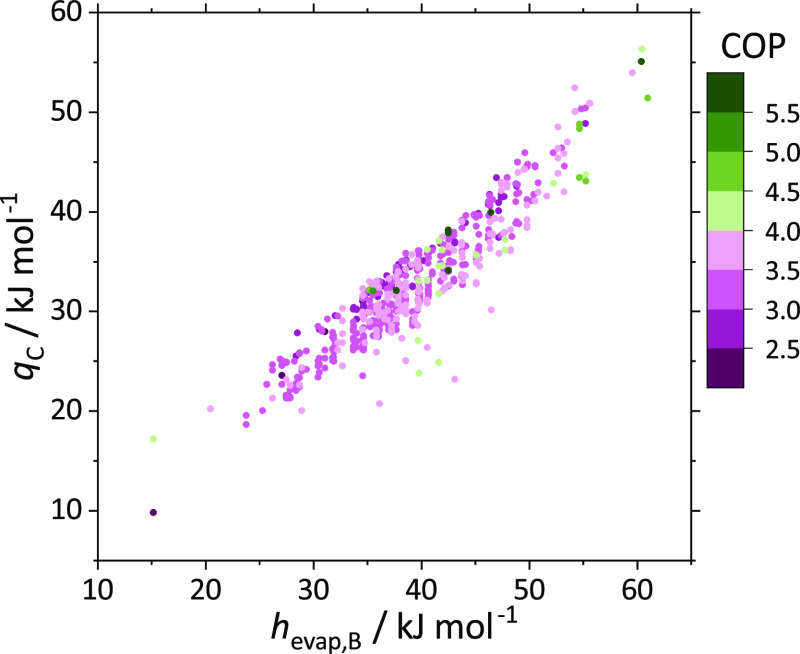
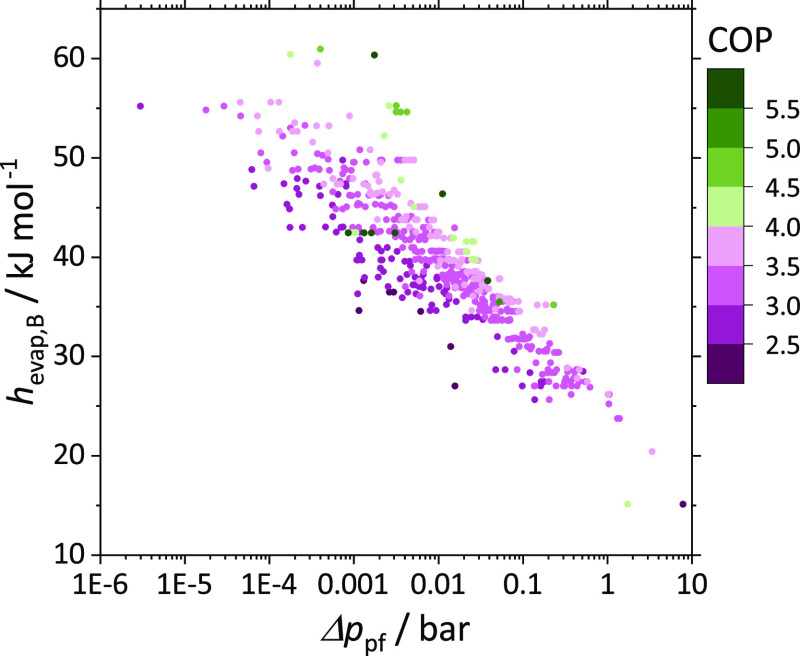
The steam quality at the evaporator inlet is expected to be similar for all molecule pairs since the working fluid entering the throttle (state 2) is always a saturated liquid. The evaporating mixture consists mainly of species B (x_B,3 > x_A,3) as species B is the more volatile species. Hence, a large enthalpy of vaporization of species B is the key factor for high heat uptake.

Figure 4 displays the relation between the specific heat uptake in the evaporator q_c and the enthalpy of vaporization of species B h_evap,B. Promising candidates yielding COP values greater than 4.0 are colored in green tones. Figure 4 confirms that species B’s enthalpy of vaporization has a major impact on the COP. Generally, higher enthalpies of vaporization of species B increase the heat uptake in the evaporator and tend to result in higher COPs. Most of the molecule pairs with the potential to outperform standard vapor-compression refrigeration (COP > 4.7) have enthalpies of vaporization of species B greater than 42 kJ/mol (cf. Table 1).

Figure 4.

Specific heat uptake in the evaporator q_c as a function of the enthalpy of vaporization of species B h_evap,B for the 606 molecule pairs. The colors represent the optimized COP. Promising candidates with a COP greater than 4.0 are colored in green tones, and less promising pairs (COP < 4.0) are colored in purple tones.

3.2.2. Cell Work w_cell

The cell work depends on the working fluid composition change in the electrochemical cell Δx_A,1–2 (eqs 8–10). Molecule pairs with low working fluid composition changes in the electrochemical cell Δx_A,1–2 seem to be advantageous as the cell work tends to decrease with decreasing Δx_A,1–2. Decreasing the cell work subsequently increases the COP of the electrochemical cooling process. The correlation between the composition change of the working fluid and thermodynamic properties of the molecule pairs is investigated to identify molecule pairs that enable low cell work while achieving a cooling effect.

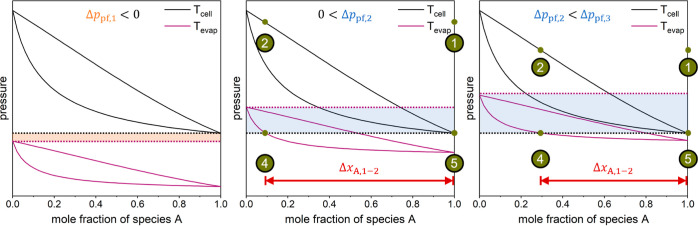
As explained in Section 2.1, the process pressures are defined as the bubble-point pressures of the working fluid at cell temperature (states 2 and 5 in Figure 1). To realize cooling through evaporation in the process, the species-B-rich mixture (states 2, 3, and 4) must be liquid at high pressure and cell temperature (state 2) and vaporous or in a two-phase state at low pressure and evaporation temperature (state 4). In turn, the species-A-rich mixture (states 1 and 5) needs to be liquid at low pressure and cell temperature (state 5) to enable the pumping of a liquid. Figure 5 displays the dew and boiling lines for evaporation and cell temperatures in pressure–mole fraction diagrams for three cases. The left plot presents an infeasible process, since a phase change of the working fluid in the electrochemical cell is unachievable even for a complete reaction. Here, it is impossible to find a pressure at which the species-A-rich mixture (state 5) is liquid, but the species-B-rich mixture (state 4) is not liquid. The center and right plots show feasible processes but with different composition changes in the electrochemical cell Δx_A,1–2.

Figure 5.

Pressure–mole fraction diagrams of molecule pairs with dew and boiling lines at cell temperature (black line) and evaporation temperature (purple line). Additionally, the saturation pressure of species B at evaporation temperature p_sat,B (T_evap) (purple dotted line) and the saturation pressure of species A at cell temperature p_sat,A (T_cell) (black dotted line) are displayed. Green circles indicate the process states. The pressure difference Δp_pf is highlighted in orange (left, negative value) and blue (center and right, positive value) and increases from left to right. Left: infeasible process for zeotropic mixtures. Center and right: feasible processes.

The pressure difference Δp_pf between the saturation pressure of species B at evaporation temperature p_sat,B (T_evap) and the saturation pressure of species A at cell temperature p_sat,A (T_cell) is calculated with eq 17.

17

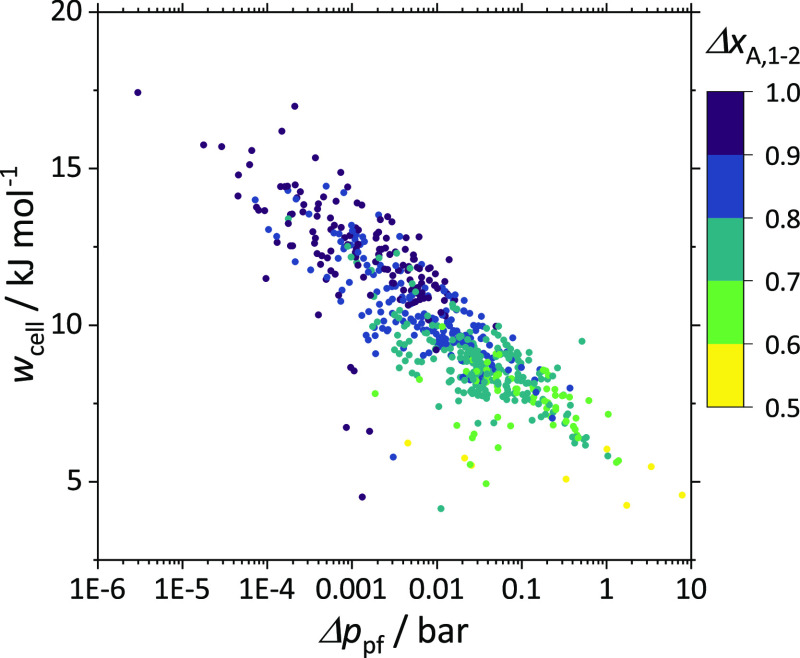
As shown in Figure 5 by the highlighted areas (orange and blue), the pressure difference Δp_pf is a good indicator of the feasibility of the process and the required composition change. If Δp_pf is smaller than zero (orange area in Figure 5 left), the process is infeasible for zeotropic mixtures. For feasible processes (Δp_pf > 0), the required composition change in the electrochemical cell decreases with increasing Δp_pf (Figure 5, center and right). Hence, molecule pairs with a large Δp_pf are expected to have a small cell work. Figure 6 confirms this correlation. Here, the cell work w_cell is shown as a function of the pressure difference Δp_pf. The pressure difference varies between 10^–6 and 10¹ bar as the thermo-physical properties of the 606 investigated molecule pairs differ.

Figure 6.

Required cell work w_cell depending on the difference between the saturation pressure of species B at evaporation temperature and the saturation pressure of species A at cell temperature Δp_pf for 606 molecule pairs. The color represents the working fluid composition change Δx_A,1–2 in the electrochemical cell. For better visualization of all molecule pairs, the x-axis is logarithmic.

Generally, molecule pairs with a higher pressure difference Δp_pf enable lower composition changes in the electrochemical cell and lower cell work.

3.2.3. Coefficient of Performance

Low cell work and high heat uptake in the evaporator lead to high COPs of electrochemical cooling. Figure 7 presents the optimized COP as a function of species B’s enthalpy of vaporization h_evap,B and the pressure difference Δp_pf.

Figure 7.

Optimized COP for the 606 molecule pairs as a function of the enthalpy of vaporization of species B h_evap,B and the difference between the saturation pressure of species B at evaporation temperature and the saturation pressure of species A at cell temperature Δp_pf. Promising candidates with a COP greater than 4.0 are colored in green tones, and less promising pairs (COP < 4.0) are colored in purple tones.

Species B’s enthalpy of vaporization substantially affects the COP (cf. Figure 4). For similar enthalpies of vaporization of species B, molecule pairs with a higher difference between the saturation pressure of species B at evaporation temperature and the saturation pressure of species A at cell temperature tend to have a higher COP (cf. Figure 6). In general, molecule pairs with high enthalpies of vaporization of species B and a high difference between the saturation pressure of species B at evaporation temperature and the saturation pressure of species A at cell temperature seem beneficial for electrochemical cooling. The present analysis thus identifies the key thermodynamic properties of molecule pairs that could be employed in a broader screening relying on less data.

4. Conclusions

This study investigates the potential of indirect electrochemical cooling as a promising alternative to standard vapor-compression refrigeration. Assessing the performance of 606 molecule pairs allows for estimating the potential of the electrochemical cooling process with (de)hydrogenation reactions in the electrochemical cell. After screening the COSMOthermX21 database³⁰ for possible molecule pairs, an equilibrium-based thermodynamic model of the electrochemical cooling process is used to evaluate the molecule pairs’ performance. The equilibrium-based thermodynamic model accounts for molecule pair-dependent optimal working fluid compositions that influence the performance of the electrochemical cooling process. The optimal working fluid compositions are determined with an optimization routine, ensuring a systematic and consistent comparison of the molecule pairs’ performance in the electrochemical cooling process.

Most molecule pairs achieve COPs between 3.0 and 4.0. However, 35 promising molecule pairs are identified, which yield COPs greater than 4.0 and may have the potential to outperform standard vapor-compression refrigeration. The mixture of ethylene glycol and acetic acid is predicted to perform best in the electrochemical cooling process, yielding the maximum COP of 9.63, corresponding to 49% of Carnot.

The efficiency of this electrochemical cooling process heavily depends on the thermo-physical properties of the pure fluids and the mixture behavior. A high vaporization enthalpy of species B and a large difference between the saturation pressures of the pure fluids at evaporation temperature (pure species B) and cell temperature (pure species A) are beneficial for a large COP. These results provide insights into preselecting potential working fluids for an electrochemical cooling process.

The efficiencies determined in this work may deteriorate when taking more losses in the electrochemical cell (activation, ohmic) or the process (heat exchanger) into account. However, the most promising working fluids identified in this study are a good basis for prospective studies that address more detailed models or experiments.

Glossary

Nomenclature

COP

coefficient of performance

Δ_rg

molar-specific reaction’s change in the Gibbs free energy,

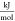
Δh^E

molar-specific enthalpy of mixing,

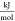
Δh_evap

molar-specific enthalpy of vaporization,

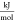
h

molar-specific enthalpy,

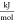
p

pressure, bar

q

molar-specific heat,

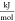
s

molar-specific entropy,

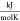
T

temperature, °C

w

molar-specific work,

x

mole fraction,

Glossary

Greek letters

Δ

change of a variable

γ

activity coefficient

η

efficiency

φ

fugacity coefficient

χ

steam quality

ζ

reaction parameter

Glossary

Subscripts

A

first species of binary mixture

B

second species of binary mixture

bp

bubble point

c

cooling

evap

evaporation

h

heating

pf

pure fluid

s

isentropic

sat

saturated

sink

heat sink

source

heat source

1,2,3,4,5

process states

Glossary

Acronyms and Abbreviations

DIPPR

design institute for physical properties

IPA

isopropanol/acetone

NLP

nonlinear programming

NRTL

nonrandom two-liquid

PEM

proton exchange membrane

PET

polyethylene terephthalate

PGLY

propylene glycol/1-hydroxy-2-propanone

SLSQP

sequential least squares programming

SMILES

simplified molecular input line entry system

SPT

SMILES to properties transformer

UNIFAC

universal quasi-chemical functional group activity coefficients

Appendix

Table A1 compares different models for electrochemical cooling.

The authors declare no competing financial interest.