Masking repeats while clustering ESTs

Abstract

A problem in EST clustering is the presence of repeat sequences. To avoid false matches, repeats have to be masked. This can be a time-consuming process, and it depends on available repeat libraries. We present a fast and effective method that aims to eliminate the problems repeats cause in the process of clustering. Unlike traditional methods, repeats are inferred directly from the EST data, we do not rely on any external library of known repeats. This makes the method especially suitable for analysing the ESTs from organisms without good repeat libraries. We demonstrate that the result is very similar to performing standard repeat masking before clustering.

INTRODUCTION

EST sequences are an abundant source of information about gene structure and expression. To organize this information and improve sequence length and quality, EST sequences are often clustered together. Clustering methods differ, but they all rely on grouping overlapping sequences together, based on the idea that overlapping sequences represent the same gene or transcript.

One problem in clustering is the presence of repeats. Repeats are common sequence motifs duplicated hundreds of times in the genome (1). Since coding sequences do usually not contain repeats, the frequency of repeats is much smaller in ESTs than in genomic sequences. However, repeats can still be present in UTR regions of transcripts, and also in retained intron sequences. Repeat sequences lead to false overlaps of unrelated ESTs, sometimes resulting in oversized clusters.

The usual solution to the problem is to remove repeats by masking. The most commonly used program for masking repeats is RepeatMasker by Smit and Green (http://www.repeatmasker.org). It is based on Smith–Waterman alignment with a library of known repeats, as well as algorithms for detecting low-complexity regions. While this usually works well, there are two problems. One is speed. Repeat masking is sometimes much more time-consuming than the clustering itself. Methods for speedup exist (2), but masking of large datasets remains a substantial task.

The second problem is that it can only find known repeats (except for low-complexity regions), which is a major drawback when working with new species. Approaches to repeat identification from genomic sequence alone have been made (3,4), but this requires a time-consuming all-against-all comparison of the genome to itself.

We present a method to eliminate problematic repeats during the process of clustering. The method is fast and library independent. It is based on the fact that an EST containing a common repeat sequence will generate many more matches in the repeat region than in the rest of the EST. The repeat can thus be identified and masked. Despite the diversity of many known repeat elements, this seems to work surprisingly well. The method is implemented in a program called RepeatBeater.

We emphasize that this method cannot find all repeat sequences like a library search could do, since it will only find common repeats in the actual dataset. However, this is exactly what causes problems in clustering. Our goal is to remove clustering artifacts caused by repeats, and not to identify all repeats. Nevertheless, we demonstrate that the method finds a large proportion of repeats of certain types. We also show that the resulting clusterings are similar to the clusterings obtained with traditional repeat masking, which is an indication that repeat types not discovered do not present a major obstacle for EST clustering.

In the following sections, we first describe the method and how to tune the parameters, and then we present and discuss a verification on example datasets.

MATERIALS AND METHODS

Datasets

For parameter tuning, we use a test dataset containing 1873 human ESTs. These sequences constitute the largest cluster obtained when clustering a dataset containing 105 991 human ESTs that were chosen randomly from the UniGene Human EST collection (5).

After masking for human repeats with RepeatMasker's default options, this single cluster containing the 1873 ESTs is separated into 253 clusters plus 186 singletons. We will refer to this clustering as the reference clustering.

Additionally, we used the following datasets for verification of the method and parameters: the first 100 000 Arabidopsis thaliana ESTs from UniGene (build 43) featuring ‘cDNA’ in the description line, the first 50 000 Oryza sativa ESTs from UniGene (build 51) featuring ‘cDNA’ in the description line and the first 100 000 C.elegans ESTs from UniGene (build 15).

MASKING METHOD

Terminology and definitions

To calculate all matches in a dataset, we used the freely available xsact tool, which was also used to perform all clusterings (5). Clustering is based on identifying the maximal set of exactly matching subsequences between each pair of sequences. The word size (k parameter) was set to 20, meaning that only exactly matching substrings of that length or longer will be detected.

Consequently, we define a ‘match’ as the occurrence of identical words of length ≥20 in two sequences. The two sequences containing a match constitute a ‘matching pair’.

Each nucleotide position in a sequence is included in zero or more matches. We call the distribution of the number of matches over the positions in a sequence the ‘match distribution’.

The term ‘repeat’ will be used for subsequences which ideally should be masked in the clustering process due to multiple occurrences in different genes.

Outline of the method

The method can be outlined as follows:

1. Find all matches and calculate the match distribution for every sequence.

2. Identify regions to be considered as repeats.

3. Close short gaps between masked regions, and remove short masked regions.

The two last steps are detailed below.

Identification of repeats

Obviously, sequence positions included in repeats are likely to be part of more matches than other positions. Consequently, these regions feature local maxima in the match distribution. Not every peak in the match distribution describes a repeat, however. In particular, when a cluster contains few sequences, a small number of hits can still be identified as a repeat. As an additional criterion, we therefore require the number of matches to exceed a ‘minimum match threshold’, k, before being considered a repeat.

First, the average μ₁ and the SD, σ₁, of the match distribution are calculated. Position i is considered as a repeat if

$$m\left(i\right)>max(k,{\mu }_1+f{\sigma }_1).$$ 1

where m(i) describes the number of matches for position i.

In the next section, we will discuss the choice of the parameters f (the ‘multiplier’) and k (the ‘minimum match number’).

Again the average μ₂ and the SD σ₂ are calculated, but this time disregarding already masked positions. Every remaining position is masked as repeat, if it satisfies Equation 1 with μ₁, and σ₁ replaced by μ₂ and σ₂. We repeat this procedure until no more masking is performed.

Post-processing of the masking

Because of variability of the repeats and read errors in ESTs, repeat regions will often contain short regions not identified as repeats. Therefore, it is necessary to close gaps between masked regions. This is conceptually an easy task, but we need to determine the minimal gaps allowed between masked regions. This threshold is called the ‘minimum gap size’. The next section describes the differences in the results gained with different gap sizes.

After connecting neighbouring masked regions, there are still very short masked regions left. Though small regions are statistically repeated very often, it does not fit in our definition of a repeat as used in the repeat masking process. We therefore parse the masking again, and unmask short masked regions. The next section will also discuss different minimum sizes of a masked region, the ‘minimum length’.

RESULTS

Tuning of the parameters

Our masking method depends on four parameters which have to be adjusted. To determine these, we ran the algorithm for a large selection of parameter choices, and clustered the masked sequences in each case. The result was then compared with the clustering produced with masking performed with RepeatMasker.

Minimum length of masked region and minimum gap size

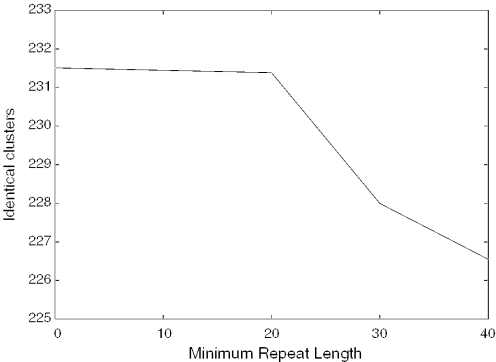
The influence of the minimum length threshold on the clusterings is marginal. Figure 1 illustrates the average changes of identical clusters with the reference clustering at different minimum length thresholds. The shown gradient is independent of the other parameters, all parameter choices result in a similar curve.

Figure 1.

Number of identical clusters as a function of the minimum length threshold.

The highest number of identical clusters is attained by keeping all the masked regions (i.e. setting the minimum length to 0). However, we still recommend to unmask short regions with a threshold of 20 as a useful minimum size of repeats. The impact on the clustering is small, and the masked regions correspond more closely to RepeatMasker's output. RepeatMasker creates 1264 masked regions in the test dataset, only 2 of them are <20 nt.

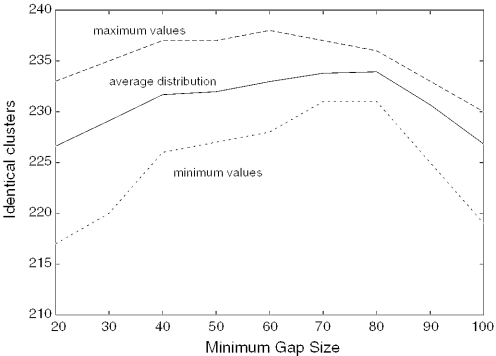
Figure 2 shows the effect on the number of identical clusters when varying the minimum gap size parameter. The curves show the maximum, average and minimum number of identical clusters as the other parameters are varied. RepeatBeater appears very robust against changes of this parameter. In the range from 40 to 80 nt, we observe small changes. As the gap size increases beyond this, too much of the sequences is masked, and consequently clusters are split. Based on these curves, we choose 70 as the minimum gap size.

Figure 2.

Number of identical clusters as a function of the minimum gap size parameter.

The multiplier f and the minimum match number k

Now that the post-processing of the masking is adjusted, we focus on the parameters involved in the first step of masking: the detection of the masked regions.

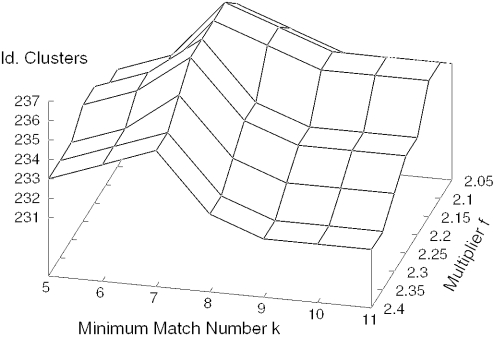
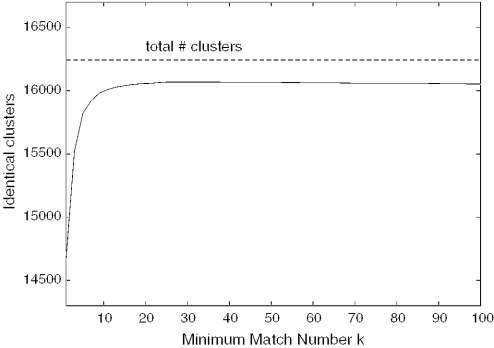
Figure 3 visualizes the results of the tests with differing f and k. We set f to 2.15, which is optimal for a large range of values of k. The optimal choice of k depends on the size of the dataset. Figure 4 illustrates the influence of k in our original dataset consisting of 105 991 ESTs (from which we extracted the test dataset). A raw clustering gives 15 938 clusters. After masking with RepeatMasker, 16 243 clusters and 978 new singletons are formed: 15 823 of the clusters are identical. We see from Figure 4 that the number of identical clusters increase quickly for low k, but that it is relatively constant for k > 15, with a slow decline for k > 40. We therefore set k to 30.

Figure 3.

Number of identical clusters as a function of minimum match number and multiplier.

Figure 4.

For varying minimum match number, the number of clusters identical to clusters produced when masking is performed by RepeatMasker. The dataset is the ∼100 000 sequences from which the test dataset was constructed.

Table 1 shows the distribution of cluster sizes in the test data in three cases: masking with RepeatBeater, masking with RepeatMasker and no masking.

Table 1.

Comparison of different clustering results for our test dataset

Cluster size	Number of clusters after masking with
	RepeatBeater	RepeatMasker	Unmasked
1	168	186
2	65	67
3–4	59	62
5–8	67	64
9–16	40	41
17–32	20	19
33–64
65–128
129–256
257–512
513–1024
1025–2048			1

An examination of the regions masked by the two methods shows that out of the total sequence, 15.2% of the nucleotides are masked by both methods, 5.7% are masked only by RepeatMasker and 0.8% are masked only by RepeatBeater.

Verification on different datasets

The method was also tested on other datasets of different sizes, using ESTs of species with existing repeat libraries. We present cluster size distributions of the clusterings after using RepeatMasker, after using RepeatBeater and after clustering the unmasked dataset. Additionally, we compared it to the corresponding distribution for the UniGene clustering.

We ran RepeatMasker with RepBase update 9.01 (1,6). For our own masking, we used the recommended parameter setting from the previous section.

The datasets used are described previously.

For A.thaliana (Table 2), the differences between clusterings appear to be very small concerning the percentage of equal clusters. The effect of repeats in this dataset becomes clear when comparing the largest cluster in each clustering. The clustering produced using RepeatBeater features a much smaller largest cluster than the other clusterings. But compared with the UniGene clustering, even our largest cluster is oversized.

Table 2.

Cluster size distribution of clusterings of 100 000 A.thaliana ESTs

Cluster size	UniGene	Number of clusters after masking with
		RepeatBeater	RepeatMasker	Unmasked
1	204	3017	3010	2988
2	363	1792	1790	1786
3–4	918	2243	2240	2232
5–8	1798	2161	2152	2147
9–16	1905	1433	1408	1403
17–32	1012	701	667	654
33–64	402	321	298	293
65–128	107	110	103	100
129–256	39	41	33	27
257–512	9	10	9	10
513–1024	4	6	5	3
1025–2048		1	1	1
2049–4096			0	0
4097–8192			1	0
8193–16 384				1
16 385–32 768

For O.sativa (Table 3) as well, the clusterings of the rice ESTs feature an oversized cluster compared to the UniGene clustering. Though RepeatBeater does not split this particular cluster, the results are still similar to the clustering after using RepeatMasker.

Table 3.

Cluster size distribution of clusterings of 50 000 Oryza sativa ESTs

Cluster size	UniGene	Number of clusters after masking with
		RepeatBeater	RepeatMasker	Unmasked
1	505	597	700	576
2	192	229	232	227
3–4	445	417	417	412
5–8	718	666	678	647
9–16	814	719	709	656
17–32	502	404	409	353
33–64	221	179	176	138
65–128	92	76	73	46
129–256	18	13	14	7
257–512	2	0	0	0
513–1024	1	0	1	0
1025–2048		0	0	0
2049–4096		0	0	0
4097–8192		0	0	0
8193–16 384		1	1	0
16 385–32 768				1

For C.elegans (Table 4), we also suspect an insufficient RepeatMasker masking. The differences between the clustering after masking with RepeatMasker and the one resulting from the unmasked sequences are marginal. Using RepeatBeater again reduces the largest cluster and increases the similarity with the UniGene clustering, but still the differences to the RepeatMasker clustering are small.

Table 4.

Cluster size distribution of clusterings of 100 000 C.elegans ESTs

Cluster size	UniGene	Number of clusters after masking with
		RepeatBeater	RepeatMasker	Unmasked
1	785	4688	4666	4642
2	2296	3187	3175	3173
3–4	1926	2842	2788	2784
5–8	1520	2140	2073	2070
9–16	1248	1353	1305	1305
17–32	961	643	575	572
33–64	397	269	235	233
65–128	133	96	74	71
129–256	55	52	31	32
257–512	9	9	5	5
513–1024		2	0	0
1025–2048		1	0	0
2049–4096			0	0
4097–8192			0	0
8193–16 384			1	1

DISCUSSION

Analysis of masked regions

While the focus of RepeatBeater is the impact of masking on clustering, it is also interesting to examine the masked regions to determine what kinds of repeats are masked. We compared the masked regions to the repeats detected and classified by RepeatMasker (see Table 5). The most common family is SINE/Alu, which is at least partially detected by our tool in 97% of the cases. In 53 cases (5.7%), it is exactly the same region, in many others nearly the same. If we mask only SINE/ALU-repeats with RepeatMasker, we get 96.3% agreement with RepeatBeater at the nucleotide level, compared to 93.5% when all repeat types are masked.

Table 5.

Comparison of masked regions

Repeat family	Total	Found
SINE/Alu	919	893
Low complexity	77	17
Simple repeat	59	12
SINE/MIR	53	0
LINE/L2	34	3
LINE/L1	34	1
DNA/MER1 type	23	2
LTR/MaLR	17	1
DNA/MER2 type	14	1
LTR/ERV1	10	0
Other	24	0
Sum	1264	930

The second column shows how many regions of the given type that were identified by RepeatMasker, and the third column shows how many of these were found by RepeatBeater. A region counts as found if there is at least a partial overlap with a RepeatBeater masked region.

For the other repeat types, RepeatBeater masks them in very few cases (most of these cases being low complexity or simple repeat), and no matches are exact. This is not surprising, since they occur much less frequently than SINE/Alu. Of course, our method cannot find repeats which are rare in the actual dataset.

Segments that are masked by RepeatBeater but not by RepeatMasker deserve special attention, since they can improve clustering quality by removing false positives not classified as known repeats. We investigated further the test dataset containing 1873 sequences in a single cluster. There are 182 segments of length 20–199 masked only by RepeatBeater. Perhaps surprisingly, 43% of them turned out to contain simple poly-T or poly-A sequences of length 6–18, which clearly should be masked to avoid false positives. In order to classify the other segments, we compared them with the Swissprot and Refseq databases. The masked segments alone are usually too short to give significant hits, so we used the complete ESTs containing those segments. A search using Blastx confirmed that the sequences containing segments masked by RepeatBeater have more hits than other sequences on average (data not shown). We did not find any overrepresentation of specific protein families, however.

In conclusion, the presented results show that masking repeats in the clustering process can be done without libraries. The resulting clusterings are very similar to the clustering gained after masking with RepeatMasker, and probably even better when good organism-specific libraries are unavailable. In addition, the method has the potential to be performed as a part of the clustering process, and avoid a separate (and time-consuming) masking step.