Doubly robust evaluation of high-dimensional surrogate markers

Summary

When evaluating the effectiveness of a treatment, policy, or intervention, the desired measure of efficacy may be expensive to collect, not routinely available, or may take a long time to occur. In these cases, it is sometimes possible to identify a surrogate outcome that can more easily, quickly, or cheaply capture the effect of interest. Theory and methods for evaluating the strength of surrogate markers have been well studied in the context of a single surrogate marker measured in the course of a randomized clinical study. However, methods are lacking for quantifying the utility of surrogate markers when the dimension of the surrogate grows. We propose a robust and efficient method for evaluating a set of surrogate markers that may be high-dimensional. Our method does not require treatment to be randomized and may be used in observational studies. Our approach draws on a connection between quantifying the utility of a surrogate marker and the most fundamental tools of causal inference—namely, methods for robust estimation of the average treatment effect. This connection facilitates the use of modern methods for estimating treatment effects, using machine learning to estimate nuisance functions and relaxing the dependence on model specification. We demonstrate that our proposed approach performs well, demonstrate connections between our approach and certain mediation effects, and illustrate it by evaluating whether gene expression can be used as a surrogate for immune activation in an Ebola study.

1. Introduction

When evaluating the effectiveness of a treatment, policy, or intervention, the desired measure of effectiveness may be expensive to collect, not routinely available, or may take a long time to occur. In these cases, it is sometimes possible to identify a surrogate outcome that can more easily, quickly, or cheaply capture the effect of interest. For example, when evaluating an intervention designed to delay dementia onset, the time required to observe enough dementia diagnoses is often very long, and surrogates that have been considered for intervention evaluation include mild cognitive impairment, adiponectin levels, neuroimages, amyloid plaques, and neurofibrillary tangles (Small, 2006; Teixeira and others 2013). Similarly, in studies evaluating treatments to prevent diabetes, surrogate measures for diabetes onset have included changes in body weight, fasting plasma glucose, and hemoglobin A1c (Caveney and Cohen, 2011; Choi and others 2011). And it is presently obvious that a surrogate marker for SARS-CoV-2 vaccine efficacy is required to develop the second generation of vaccines adapted to novel variants of concern (Karim, 2021).

Theory and methods for evaluating the strength of surrogate markers have been well studied in the context of a single surrogate marker measured in the course of one or more randomized clinical studies—see the detailed review in Joffe and Greene (2009). In particular, model-based approaches have been proposed for continuous (Alonso and others, 2004) and binary surrogates (Alonso and others, 2016) in meta-analysis and in the principal stratification framework (Gilbert and Hudgens, 2008). Robust nonparametric methods have been proposed in Parast and others (2020) and Parast and others (2016). However, fully nonparametric methods are not available or not reliable when the number of markers is more than one or two. In these cases, a parametric approach to evaluate a high-dimensional surrogate may be considered as proposed in Zhou and others (2022), which requires the correct specification of two high-dimensional linear models. Alternatively, an initial model may be used to reduce the dimensionality of the surrogate (Agniel and Parast, 2021; Parast and others 2016). However, the mis-specification of the parametric models or an inappropriate initial model may produce badly biased estimates of the utility of the surrogate.

In this work, we propose a robust and efficient method for evaluating multiple surrogate markers, with particular attention to the possibility that surrogates may be high-dimensional. Our approach revives the spirit of the estimator in Freedman and others (1992), itself based on the pioneering work of Prentice (1989) to draw on a connection between quantifying the utility of a surrogate marker and the most fundamental tools of causal inference: namely, methods for estimating the average treatment effect. This connection does not appear to have been made before in the surrogate marker literature, despite the extensive connections made between mediation and surrogacy (Taylor and others, 2005; Joffe and Greene, 2009). Making this connection facilitates the use of all of the machinery now available to robustly and efficiently estimate average treatment effects. Specifically, we take advantage of state-of-the-art methods for incorporating flexible machine learning and/or sparse high-dimensional models into the estimation of treatment effects. These methods based estimation on the efficient influence function of key quantities and use sample splitting to ensure convenient asymptotic distributions and inference while putting minimal restrictions on what types of estimators may be used. Furthermore, we show that our proposed approach has connections to certain mediation estimands when the assumptions underlying mediation analysis are satisfied.

One key benefit of our approach is that it does not require randomization of treatment, which has been required by previous nonparametric approaches to evaluating surrogate markers (Agniel and Parast, 2021; Parast and others, 2016). Assessments of surrogate markers are not solely limited to studies of randomized treatment (Obirikorang and others, 2012). In fact, using surrogate outcomes based on complex observational data is finding purchase in all corners of science (Wang and others, 2020). In Section 6, we give an example where researchers are interested in studying whether gene expression can be used as a surrogate for immune activation in an observational setting. Our approach exploits insights from observational causal inference to estimate all relevant quantities and thus is equally applicable in both observational and randomized settings.

The structure of the rest of the article is as follows. In Section 2, we lay out the notation and the setting in which we are working, and we motivate the importance of evaluating surrogate markers in light of recent advances in the surrogate marker literature. In Section 3, we detail assumptions necessary for identifying and interpreting parameters of interest. We discuss the identification, estimation, and the asymptotic behavior of our estimator in Section 4 and discuss variance estimation and inference. We evaluate the performance of the proposed approach using a simulation study in Section 5, and in Section 6, we investigate whether gene expression could be used as a surrogate for immune response to Ebola infection. We give final remarks and draw connections to other methods for evaluating surrogate markers in Section 7.

2. Evaluation of surrogate markers

2.1. Notation

Let 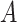denote a binary treatment, and let the primary outcome of the study be 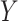. Let there be a vector 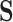of potential surrogate information, and let 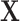be a vector of pretreatment covariates. The primary quantity of interest is the treatment effect on the outcom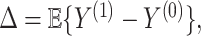e where 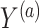is the potential or counterfactual outcome that would have been observed if treatment were 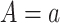, possibly contrary to fact. Similarly, let 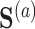be the potential/counterfactual value the vector of surrogates would take if 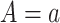. Let the data observed in the current study be 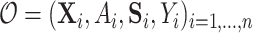, 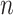iid realizations of .

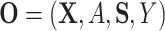2.2. Importance of quantifying surrogate strength

Understanding the strength of a potential surrogate is important for many reasons. In practice, information about surrogate strength will inform decisions regarding whether to measure the surrogate in a future study (especially if it is costly or invasive to measure) and/or whether to use the surrogate to assess treatment effectiveness in a future study. In addition, a number of novel statistical methods for using surrogates in future studies can only be applied when the surrogate is strong. For example, Parast and others (2019) propose a robust nonparametric procedure to test for a treatment effect using surrogate marker information measured prior to the end of the study in a time-to-event outcome setting, but they rely on the assumption that the surrogate is sufficiently strong. As another example, Price and others (2018) propose constructing a function 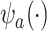of the surrogates that leads to some optimality properties, but it can be shown that this method should only be used with a strong surrogate.

Specifically, they construct an optimal transformation of the surrogates 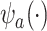in terms of minimizing the following mean squared error

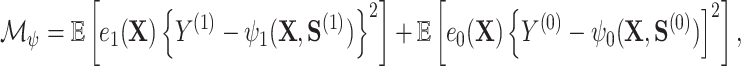(2.1)

with 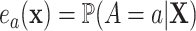, under the constraint that it satisfies the so-called Prentice definition:

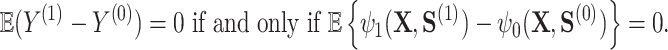The optimal transformations in this case are shown to be 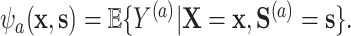In addition to this appealing optimality property, this proposal also resolves the so-called “surrogate paradox.” The paradox states that the treatment could have a positive causal effect on a univariate surrogate 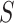which could have a positive correlation with the outcome, but the treatment could yet have a negative effect on the outcome. The Price surrogate resolves the surrogate paradox by definition. The treatment effect on the transformed surrogate is by definition equivalent to the treatment effect on the outcome: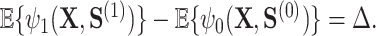

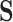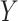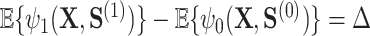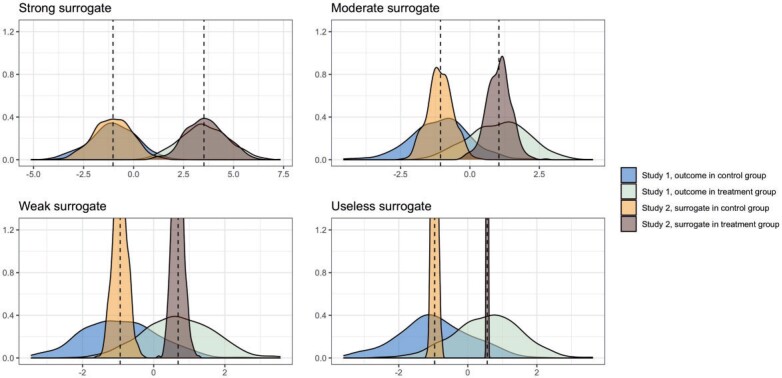
However, the Price surrogate’s resolution of the surrogate paradox is in some sense too good. The surrogate paradox is thus resolved for every potential set of surrogates, good and bad. Even if the surrogates are completely unrelated to the outcome , . In fact, the power to detect a treatment effect in a future study using 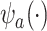actually increases as the surrogate becomes weaker (explaining less of the treatment effect), if the Prentice definition does not hold. Consider the toy example depicted in Figure 1 (see Appendix A of the Supplementary material available at Biostatistics online for details of the data generation). As the strength of the surrogate increases, 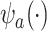becomes more like the true outcome 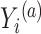. As the surrogate becomes weaker, 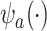becomes more like 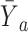the mean outcome in treatment group 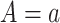from the first study. This means that a weak surrogate ensures that the treatment effect in the second study will be identical to the treatment effect in the first study because the distribution of 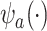will cluster closely around the estimate of 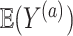from the first study (see specifically, the fourth panel of Figure 1). In this scenario, the second study is providing no new information about the treatment. Thus, the Price surrogate should only be used with a strong 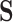, and its use with a weak or possibly even moderately strong set of surrogates may not be advisable.

Fig. 1.

Distribution of outcomes 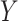in an initial study (Study 1) and surrogate functions (approximating the outcome) 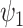(surrogate in the treatment group) and 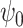(surrogate in the control group) in a future study (Study 2) based on simulated data, arranged according to the strength of the surrogate marker—i.e., the capacity of the surrogate to explain the treatment effect. The wider distribution on the left corresponds to the control group in Study 1, the wider distribution on the right to the treated group in Study 1, the narrower distribution on the left to 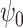in Study 2, and the narrower distribution on the right to 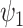in Study 2. Vertical dotted lines correspond to the means of the treatment groups in the first study. See Appendix A of the Supplementary material available at Biostatistics online for simulation details. Surrogate functions 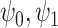were estimated via a correctly specified linear regression in the first study and then applied to the second study population. When the surrogate was strong, the distribution of the surrogate in the second study was quite close to the distribution of the outcome in the first study. However, when the surrogate was weak, the distribution of the surrogate in the second study clustered around the group mean from the first study.

Therefore, for both decision-making purposes and to use statistical methods that take advantage of strong surrogates, methods are needed to rigorously quantify the strength of the proposed set of surrogates before using (functions of) the surrogates in practice. In the following section, we propose an efficient method for estimating the strength of a possibly high-dimensional set of surrogates in observational studies. Our aim is for this proposed method to complement existing work, like that of Parast and others (2019) and Price and others (2018), that rely on the availability of a strong surrogate but currently lack tools to assess surrogate strength, particularly in a high-dimensional surrogate setting.

2.3. Quantity to evaluate surrogate strength

In this section, we present a general method for evaluating the usefulness of a set of surrogates. This can be used to evaluate the suitability of any set of surrogates or surrogate transformations and is appropriate for 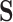of any dimension. To evaluate the surrogates’ usefulness, we use the proportion of treatment effect explained by 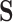(PTE) defined as 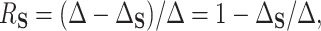with 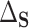the residual treatment effect, or the treatment effect that remains after controlling for the surrogate information. This measure has been used frequently in the evaluation of surrogate markers, as far back as the pioneering works of Prentice (1989) and Freedman and others (1992) and more recently in Parast and others (2020; 2016) and Agniel and Parast (2021). If 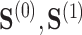are independent of 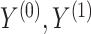conditional on , then and 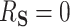. In contrast, if all of the treatment effects can be attributed to 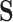, then 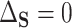and .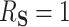

In the more recent works using this PTE, 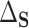is defined in terms of a particular reference distribution, e.g., taking 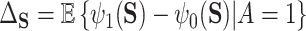to be the residual treatment effect among the treated group. This choice of reference distribution is often arbitrary and was not required by the older (model-based) approaches. To obviate the need for this choice of reference distribution and to take advantage of the extensive development in average treatment effect estimation (and the associated intuition and machinery that have been built up around it), we define 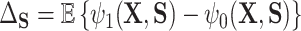, the average treatment effect conditional on the distribution of 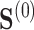and 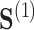both being equal to the distribution of 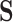(all conditional on 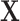). Other choices of reference distribution could be used when there are substantive reasons to prefer them. When there are no interactions with treatment – 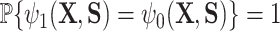– choice of reference distribution does not change 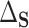. See Section 7 for further connections in this vein to Agniel and Parast (2021) and similar recent methods.

This formulation of PTE also has deep connections to quantities important to mediation analysis without requiring some of the restrictive assumptions common in the mediation literature. In particular, we show in Appendix B of the Supplementary material available at Biostatistics online that 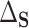is a function of conditional natural direct effects and that 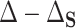is a function of conditional natural indirect effects (Joffe and Greene, 2009; VanderWeele 2013), when the assumptions for identifying those effects are met. While many previous reviews of surrogate methods identify the causal effects framework for surrogate evaluation solely with mediation (Joffe and Greene, 2009; Conlon and others, 2017), we use causal tools without requiring all of the assumptions necessary for mediation. Importantly, we do not require that all confounders of the surrogate–outcome relationship are measured and included in the study because the aims of mediation and surrogate marker evaluation are different (VanderWeele, 2013). The aim of identifying a mediator is determining whether the effect of treatment operates through the mediator itself, e.g., through some biological pathway. Often, a good surrogate marker is similarly conceptualized as a variable through which the treatment operates, but this is not necessarily required; a variable can be a good surrogate if it captures the treatment effect on the outcome, even if the treatment effect does not operate through the variable itself (sometimes called a nonmechanistic correlate of protection; Plotkin and Gilbert, 2012).

3. Assumptions

3.1. Identifying assumptions

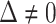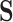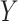We first require , without which requirement the goals of identifying surrogate markers are practically and theoretically not meaningful. We further make the three typical assumptions of treatment effect estimation: consistency, positivity, and no unmeasured confounding. Specifically, we assume that the observed values of and when 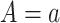are identical to the counterfactuals 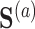and 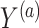such that 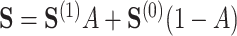and 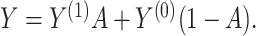We furthermore assume that 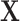contains all confounders of the effects of 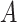on the surrogates and the outcome, such that the treatment 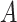is as good as randomized conditional on the covariates 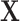: (A.1) 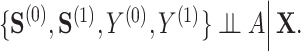In addition, we assume two forms of positivity, which ensures that individuals in the two study arms are not too different from one another. First, the usual positive probability of receiving either treatment for some 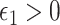, 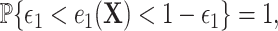and a related assumption that further conditions on the surrogates, 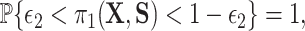for som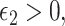e where 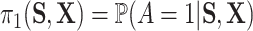. Notably, letting 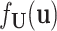be the density of the random variable 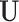evaluated at 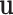, because 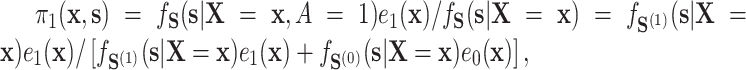these two positivity conditions ensure that the conditional distribution of the counterfactual surrogates under treatment and control cannot be too different from one another, i.e., ensuring overlap. When the treatment has a large effect on , this additional overlap requirement may be suspect—e.g., there may be some values of such that 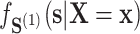approaches 0 and thus 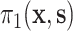also approaches 0. We discuss a generalization of our approach that removes this overlap condition in Appendix C of the Supplementary material available at Biostatistics online.

3.2. Required assumptions to ensure interpretation of 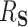as a proportion

The interpretation of 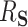as the PTE depends on it actually being a proportion, lying between 0 and 1. We adapt conditions in Wang and Taylor (2002) and Agniel and Parast (2021) which ensure that 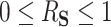. These conditions are as follows (assuming without loss of generality that 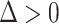): (A.2)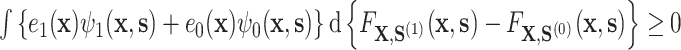; and (A.3) 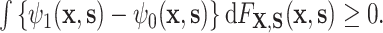The condition (A.3) ensures that 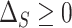, i.e., that the residual treatment effect is in the same direction as the overall treatment effect 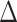. Condition (A.2), which ensures that 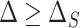, requires that, roughly speaking, a propensity-weighted mixture of the two conditional mean functions 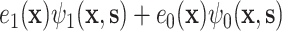is larger when 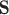takes values from the distribution of the counterfactual surrogates under treatment than if it took values from the distribution under control. These two conditions are analogs of conditions (A6) and (A7) in Agniel and Parast (2021). See Appendix D of the Supplementary material available at Biostatistics online for an alternative approach that may be considered if these conditions are not or unlikely to be met, though the alternative approach lacks the interpretability and connections to previous literature of the proposed approach.

4. Identification, estimation, and inference

4.1. Identifiability

In this section, we show that the effects of interest are identifiable, propose a robust and efficient estimation procedure, and describe the asymptotic properties of our proposed estimators. The effects of interest may be identified as average treatment effects identifiable from the data, one of which conditions on the surrogates (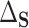) and one which does not (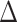). In particular, the residual treatment effect may be identified as

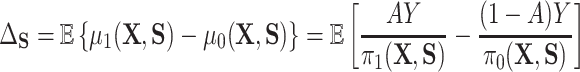(4.2)

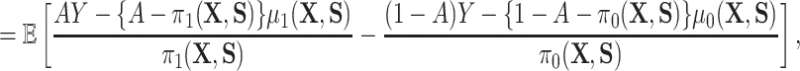(4.3)

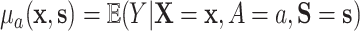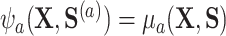where . The result in the first equality of (4.2) follows from the definition of and the fact that because of (A.1), and the other results follow shortly thereafter, following familiar paths as arguments for the identification of the average treatment effect in other contexts. These results show that the residual treatment effect may be identified without knowledge of the mean function for the outcome via the second equality in (4.2) and gives an augmented inverse probability weighting (Bang and Robins, 2005) version of the estimand (4.3). may also be identified, following similar standard arguments and using similar functionals with 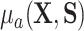replaced by 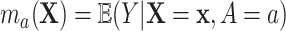and 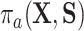replaced by .

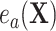4.2. Proposed estimation

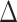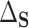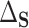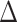This identification of and in terms of average treatment effects allows us to take advantage of the rich literature on robust estimation of these quantities. We propose to estimate and as

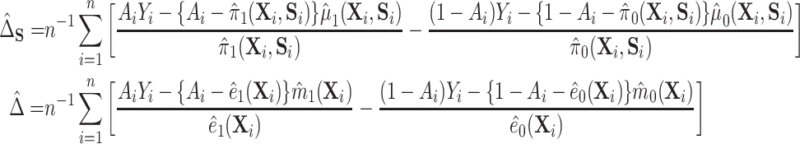and thus, estimate as , where we leave estimation of the components: 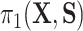, , 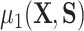, , 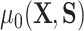, 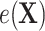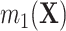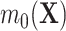to be quite general. We propose and evaluate two different versions of this proposed estimator: one where we estimate these components using the Super Learner (Van der Laan and others, 2007), which finds an optimal combination of a set of candidate models or learners (denoted “DR-SL”) and another that uses the relaxed lasso (Meinshausen, 2007) (denoted “DR-lasso”). In addition, our proposed estimators use a sample-splitting scheme (Chernozhukov and others, 2017), which we describe in detail in Appendix C of the Supplementary material available at Biostatistics online, to avoid placing restrictive conditions on the estimation of the nuisance functions.

Remark 1.

While depends on the counterfactual quantities and is thus not the same target treatment effect estimated by Chernozhukov and others (2017), because it is identified by the same observed data quantities in (4.3), we can use the same machinery used in Chernozhukov and others (2017), though requiring the stronger assumption (A.1).

4.3. Inference

Under very general conditions, including the standard causal assumptions identified in Section 3.1, 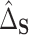will converge at the parametric 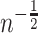rate and be asymptotically normal (Chernozhukov and others, 2017; Farrell, 2015) so long as

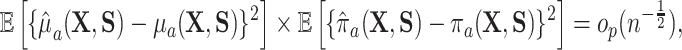(4.4)

with similar results holding for 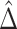if

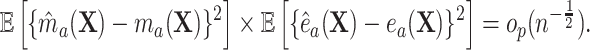(4.5)

As these estimators are built on the efficient influence functions, they are also semiparametrically efficient. Furthermore, as we show in Appendix C of the Supplementary material available at Biostatistics online, as long as the sample splits are the same for 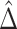and 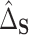, we will have 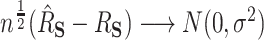if both (4.4) and (4.5) hold. Specifically, we have that

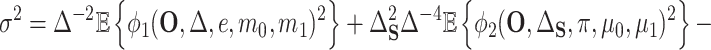(4.6)

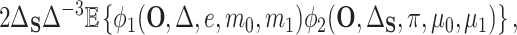(4.7)

where

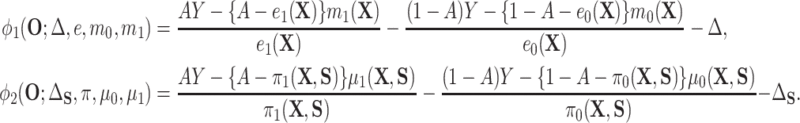Remark 2.

When the dimension of is not high, (4.4) and (4.5) are not in general restrictive, as many parametric and nonparametric methods are able to achieve the slow rates required of the estimators under certain conditions, including the lasso (Tibshirani, 1996), random forests (Wager and Walther, 2015), and deep neural networks (Farrell and others, 2021), when used with a sample-splitting scheme. Ensemble methods such as the Super Learner (Van der Laan and others, 2007) may also be used to combine these and other methods to obtain good performance if any of the methods achieves the required rates of consistency. As described in the prior section, our proposed approach combines both ensemble estimation of nuisance functions and sample splitting; we demonstrate the good performance of this approach in finite samples in Section 5.

In higher dimensions, the convergence in (4.4) and (4.5) is more difficult to ensure without further restrictions. If only is high-dimensional, then a typical approach is to assume that may be specified as a sparse linear model and may be specified as a sparse logistic regression model for , and with sparse enough to ensure (4.4). Because of the fact that is related to , restricting to this class of models is unproblematic so long as is low-dimensional and may be estimated nonparametrically (i.e., without being restricted to the class of sparse linear models). However, if is also high-dimensional, sparse logistic models for and may not in general be compatible with one another because of the well-known noncollapsibility of logistic regression (Guo and Geng, 1995), unless (which would imply ) or (which would imply that does not confound the relationship between and ). In these cases, the approach of Tan (2020) may be used to estimate the nuisance functions, in which case only one of and are required to be a correctly specified logistic regression. However, this approach did not appear to perform well in our simulations in Section 5. Despite these theoretical considerations, our simulations suggest that an ensemble approach using the Super Learner may outperform approaches based on sparse linear models, as in Tan (2020) or in the version of our estimator that uses only lasso regression. More theoretical development in this area may be warranted.

5. Simulations

5.1. Simulation overview

Our proposed estimator based on the Super Learner (“DR-SL”) is implemented using the package (Polley and others, 2021) in 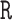. The candidate learners we included were the lasso, ridge regression, ordinary least squares, support vector machines, and random forests for 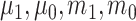and the lasso, logistic regression, linear discriminant analysis, quadratic discriminant analysis, support vector machines, and random forests for 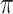and 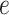. Our second estimator using the relaxed lasso (“DR-lasso”) is implemented using the package (Friedman and others, 2010), to estimate all needed functions. For all simulations, we truncated estimates of the propensity and surrogate scores so that 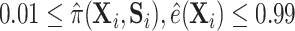for all . We used the default cross-validation procedure to select the tuning parameters for the Super Learner. For the DR-lasso estimator, we used the default crossvalidation to select the tuning parameters. It is possible that performance could be improved by tweaking the tuning parameters for the candidate learners.

It is our understanding that there are no currently available methods to robustly estimate the PTE of a high-dimensional surrogate. However, since there are available methods to measure the strength of high-dimensional mediators, we compare our proposed approach to these available methods. While the goals of mediation analysis and surrogate markers analysis are different and the necessary assumptions differ, this allows us to offer some reasonable comparison to methods that are currently available, rather than no comparison at all. Thus, to fairly compare, we set up the majority of our simulations such that 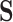is a mediator in that it lies on the causal pathway between 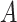and 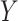. While mediation methods are attempting to estimate a distinct quantity from 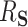, in three of the four following simulation settings, the estimation of the “proportion mediated” (which is used in mediation) and 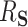are the same.

In our simulations, we compare our proposed approach to: high-dimensional mediation analysis (HIMA, Zhang and others, 2016) as implemented in the 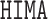package (Zheng and others, 2018); Bayesian mediation analysis (BAMA, Song and others, 2020) as implemented in the 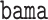package (Rix and Song, 2021); and high-dimensional linear mediation analysis (Zhou and others, 2020) as implemented in the 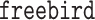package. All three of these methods propose 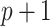linear models: 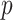models for the surrogates/mediators— 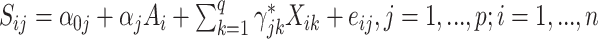— and one outcome model— — though the implementation of does not allow for the inclusion of covariates 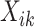. Using these models, the overall treatment effect can be identified as 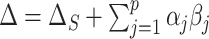, and as above the PTE (or proportion mediated) may be identified as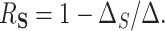

We computed 95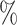 confidence intervals (CIs) for 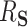as 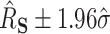, where 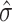is an estimate of (4.6). We computed 95 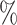credible intervals for the BAMA estimator from the 2.5 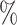and 97.5 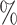quantiles of the posterior distribution of 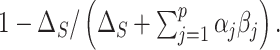CIs were not computed for the HIMA and freebird implementations because they are not available.

5.2. Simulation setup

We constructed four sets of simulations for a total of 18 simulation settings to assess the performance of our proposed approach in both low- and high-dimensional settings.

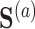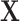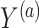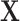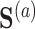For the first set of simulations, the data-generating mechanism for was linear in , the data-generating mechanism for was linear in and , and the propensity score was linear on the log-odds scale. Given this data-generating mechanism, we would expect that all methods (proposed and comparisons) should perform reasonably well. We set the dimension of 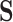(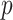) and of 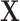(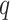) to be 100. We let 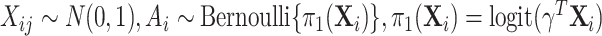, where 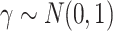. The surrogates were generated as 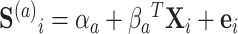, where 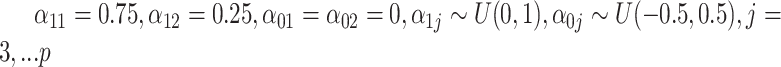. And only five of the covariates were important for determining the surrogate: 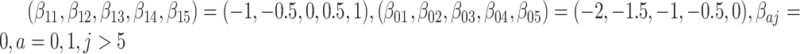. The outcome counterfactuals were given by 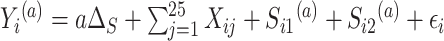, suggesting that only the first two surrogates and 25 of the covariates were important for determining the outcome. The errors 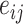and 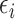were 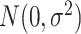. We let the sample size vary between 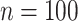and 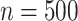and the level of noise between 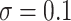and 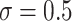—for a total of four settings—and we set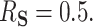

In the second set of simulations (six more settings), the data-generating mechanism was less linear, including interactions between covariates in both the propensity score and the model for 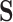, though the outcome model was still a simple linear combination of 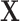and 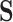. In the third set of simulations (two more settings), the dimension of the surrogates (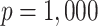) was much larger than the sample size (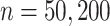), and correct specification of the outcome functions also included nonlinear terms. These simulations should mimic what may happen in practice since all models are typically subject to some amount of mis-specification. We expected the nonlinearity to induce bias in the competing methods (which require linear models to hold). In the fourth set of simulations (six more settings), we specified 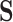so that it was not a mediator but was instead downstream of a true mediator. We performed 1000 replications for each simulation setting. We give full details and results for these simulations in Appendix E of the Supplementary material available at Biostatistics online.

5.3. Results

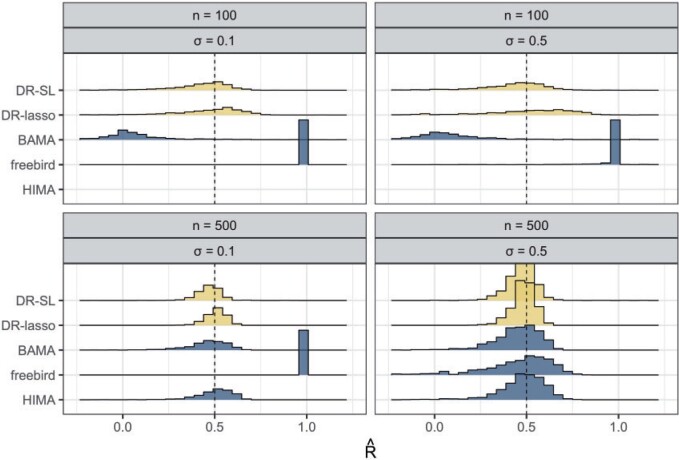
As expected, the first data-generating mechanism was well approximated using linear models. When the sample size was large (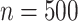) and 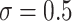, all methods performed well, with a relatively small bias (see Figure 2). The median 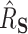estimates were 0.46 (BAMA), 0.48 (freebird), 0.49 (HIMA), 0.48 (DR-SL), and 0.49 (DR-lasso), all of which compare favorably to the true 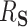value of 0.5. The distribution of estimates for the proposed approaches was a bit tighter than for the competing methods. The empirical 2.5 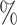and 97.5 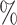quantiles were 0.32 and 0.60 for DR-SL, 0.35 and 0.59 for DR-lasso, 0.15 and 0.67 for HIMA, 0.11 and 0.63 for BAMA, and 0.85 and 0.71 for freebird. Results were similar for the sample size with less noise (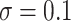), except for the freebird approach which began to estimate the PTE to be exactly 1 in almost all simulations: the empirical 2.5 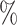and 97.5 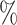quantiles of the 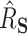distribution for freebird were exactly 1. At the lower sample size (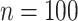), HIMA did not run, while BAMA estimates tended to be near 0 and freebird estimates were again clustered tightly around 1. Our proposed approaches had median 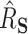values of 0.45 (DR-SL) and 0.56 (DR-lasso), though with more variability than when 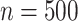. The median absolute deviation (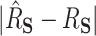) was smaller for both DR-SL and DR-lasso than any of the competing approaches for all settings.

Fig. 2.

Distribution of estimates of 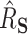in the first data-generating mechanism. Lighter shaded regions represent the distribution of the proposed estimators (“DR-SL” and “DR-lasso”); darker shaded regions represent the distribution of the comparison estimators (“BAMA,” “freebird,” and “HIMA”). The true value of 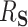is given as a vertical dotted line at 0.5. At the lower sample size (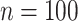), HIMA did not run and so is not shown.

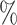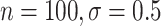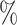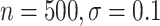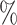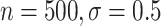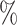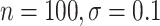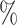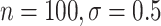CI coverage for the proposed estimators tended to be quite good for DR-SL in all settings: coverage was 95 (), 96 (), 94 (), and 97 (). Coverage for the DR-lasso estimator was worse in general: coverage was 88 (), 82 (), 89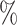 (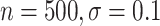), and 96 ()

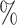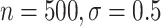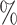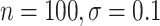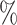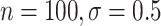However, BAMA CIs also did not uniformly obtain nominal coverage: 96 (), 99 (), 92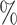 (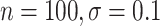), and 85 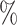(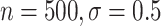). Even when BAMA CIs had nominal coverage, they were more than four times larger than the CIs for the proposed estimators: for example, BAMA CI half-lengths were 1.40 (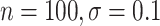) and 1.61 (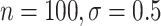), while the corresponding half-lengths were 0.25 and 0.30 for DR-SL and 0.28 and 0.44 for DR-lasso.

The proposed estimators also outperformed the competing methods in the additional simulation settings where models were subject to mis-specification and the dimensionality of the surrogates was much larger than the sample size. See Appendix E of the Supplementary material available at Biostatistics online for complete results.

6. Ebola immune response application

The concentration of binding antibodies is often used as the primary outcome of interest in studies of Ebola vaccine efficacy, being itself a surrogate of vaccine efficacy as measured by the effect on the incidence of infections (Roozendaal and others, 2020). Because gene expression is the means by which DNA is turned into RNA and eventually proteins, it is associated with cellular function. Thus, the establishment of the humoral immune response may be captured by changes in gene expression as suggested by early works on systems vaccinology (Li and others, 2014). Furthermore, gene expression changes may occur days or even weeks before traditional measures of immune function (Rechtien and others, 2017). If gene expression can act as a surrogate for immune response, then it could possibly be used to shorten vaccine trials or to quickly measure the effect of vaccination in a population. Finally, genome-wide expression data offer the opportunity at looking at very different ways of influencing the response to intervention which constitutes potential surrogate markers. In this study, we sought to use observational data on long-term Ebola survivors and healthy controls to shed light on the possibility of gene expression’s use as a surrogate for antibody response to Ebola virus. This aim is inspired by the study of potential surrogates of protection among Ebola disease survivors (Sullivan and others, 2009).

In total, 26 Ebola survivors of the 2013–2016 Ebola outbreak in West Africa were recruited from the Postebogui cohort (Etard and others, 2017) as well as 33 healthy donors as described in Wiedemann and others (2020), each of whom had an expression for 29 624 genes quantified from whole blood RNA-seq (freely available from the Gene Expression Omnibus repository with accession code GSE143549) as well as the concentration of specific Ebola binding antibodies measured. Clearly, this is a setting where the number of potential surrogate markers (the genes) is substantially larger than the sample size. Given the superior performance of the DR-SL in our simulation study, and the high-dimensional setting, we focus only on using the DR-SL estimator to quantify how much of the overall difference in humoral immune response between survivors and healthy donors could be captured by the measured gene expression data. We used the same candidate learners as specified in Section 5. Propensity and surrogate scores (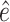 and 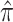) were truncated at 0.05 and 0.95 to prevent instability due to extreme weights, and 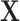included age and sex.

Ebola survivors were estimated to have a much higher abundance of Ebola-specific antibodies (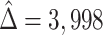, SE 851.5). Using DR-SL, the residual treatment effect, 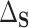, was estimated as 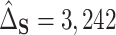with SE 727.8, and the proportion of the difference explained by gene expression was estimated as 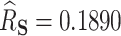, with a SE of 0.07923. Thus, a large part of the humoral immune response cannot be explained by the differences in gene expression. Of note, we assumed no unmeasured confounding factors although it cannot be guaranteed in such a real-life context where survivors and healthy volunteers are two selected populations. If unmeasured confounding inflated both 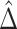and 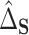roughly equally, this could have the effect of artificially deflating 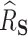. Another explanation for the low estimated 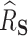could be that, while gene expression measured shortly after infection may potentially be a good surrogate, measuring it long after infection (as in this study), does not capture the treatment effect as well. Measurement error in 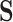could also deflate the PTE. Importantly, one other potential violation of our assumptions is that about one-third of the observations have truncated surrogate scores— 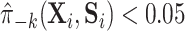or 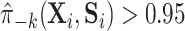. This suggests that positivity might be (nearly) violated. We discuss this further in Appendix C of the Supplementary material available at Biostatistics online along with a potential solution.

7. Discussion

We have proposed a very general approach to evaluating surrogate markers which can be applied in randomized experiments or in observational studies and can be used regardless of the dimensionality of the surrogates. Our approach is robust in that we have defined the PTE of the surrogates without reference to any models, and we have shown how machine learning approaches like Super Learner may be used to very flexibly estimate nuisance functions. Our simulation results suggest that our Super Learner estimator (DR-SL) outperforms competing methods even when the underlying data-generating mechanism is linear and still gives reasonable results even when high-dimensional linear models are mis-specified.

Our approach here is intimately tied to previous approaches for evaluating surrogate markers. The approaches in Agniel and Parast (2021) and in Parast and others (2016) can be seen to be similar to a version of our approach where the average treatment effect among controls is estimated under further assumptions. In Agniel and Parast (2021), they further require strict randomization of treatment, and they assume that 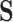is a realization of a smooth continuous function. Parast and others (2016) make similar assumptions but take 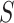to be a scalar surrogate. They estimate a version of (4.2) among controls: 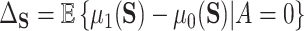using kernel smoothing and taking advantage of the fact that treatment is randomized. Their estimates have the form 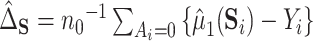, where 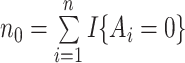and 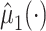is estimated via kernel smoothing (possibly after dimension reduction). Our approach here could easily be adapted to estimate a similar quantity by using methods for doubly robust estimation of the average treatment effect on the treated (Shu and Tan, 2018; Moodie and others, 2018; Chernozhukov and others, 2017) by, for exampl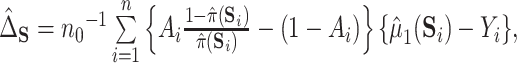e, where 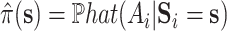may be estimated using a model similar to the one used for 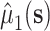. Furthermore, our approach could be used to facilitate the use of machine learning methods in the estimation of 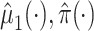, to include covariates to control for confounding, or to simplify or strengthen asymptotic results. For example, results for the kernel estimator used in Agniel and Parast (2021) obtain rates of convergence of 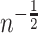only under very limited technical conditions, but using sample-splitting parametric rates of convergence could be obtained under very general conditions.

8. Software

We include software to implement our proposed methods in the R package available at github.com/denisagniel/crossurr.

Supplementary material

Supplementary material is available online at http://biostatistics.oxfordjournals.org.