Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2024 Jan 4;128(2):723–731. doi: 10.1021/acs.jpcc.3c06300

Computational Study of the Enhancement of Graphene Electrodes for Use in Li–Ion Batteries via Forming Superlattices with Transition Metal Dichalcogenides

Edward Allery David Baker 1,*, Conor Jason Price 1, Steven Paul Hepplestone 1,*
PMCID: PMC10801692  PMID: 38264433

Abstract

graphic file with name jp3c06300_0005.jpg

In our study, we examined nine transition metal dichalcogenide (TMDC)–graphene superlattices as potential Li–ion intercalation electrodes. We determined their voltages, with ScS2–graphene in T- and R-phases showing the highest at around 3 V, while the others ranged from 0 to 1.5 V. Most superlattices exhibited minimal volumetric expansion (5 to 10%), similar to NMC (8%), except for SnS2-T and NiS2-T, which expanded up to nearly 20%. We evaluated their capacities using a stability metric, EIS, and found that ScS2-T, ScS2-R, and TiS2-T could be intercalated up to two Li ions per MX2 unit without decomposing to Li2S, yielding capacities of 306.77 mA h/g for both ScS2 phases and 310.84 mA h/g for TiS2-T, roughly equivalent to LiC2. MoS2-T could accept Li up to a limit of a = 15/16 in LiaMoS2Cb, corresponding to a capacity of 121.29 mA h/g (equivalent to LiC4). Examining the influence of graphene layers on MoS2-T, we observed a voltage decrease and an initial EIS decrease before effectively flat lining, which is due to charge donation to the middle graphene layer, reducing the electron concentration near the TMDC layer. As graphene layers increased, overall volume expansion decreased with Li intercalation, which is attributed to the in-plane expansion changing. Our results underscore the potential of TMDC–graphene superlattices as Li–ion intercalation electrodes, offering low volumetric expansions, high capacities, and a wide voltage range. These superlattices all show an increase in the capacity of the graphene.

Introduction

Li–ion-based batteries are the most widely used energy storage medium for portable electronic devices, seeing use in anything from phones to electric cars and most devices in between. The electrodes of a Li–ion battery determine their voltage and capacity, with many different types of materials having been used and investigated as Li–ion battery electrodes. These materials mainly consist of layered van der Waals structures following the discovery and use of TiS2 as a Li–ion intercalation electrode in the 1970s,1−3 which was followed by LiCoO2 in 1980.4 From this, many other layered materials were investigated, such as graphite,5 the nonlayered spinel structure LiMn2O4,6,7 and MoS2,8−16 before the currently commercially used NMC17−19 and NCA20 were discovered.

Many electrode materials share the layered structure of transition metal dichalcogenides (TMDCs), which are made of one part transition metal (M) and two parts chalcogen (S, Se, or Te, denoted as X) with the general formula MX2.21 Since the investigations into TiS2,1−3 TMDCs have remained a prevalent electrode,22−25 with sulfur-based TMDCs often being looked at over other TMDCs as they are lighter and have been shown to have higher capacities than selenium- and tellurium-based TMDCs.26 The large van der Waals gap TMDCs possess allows for the rapid insertion and extraction of intercalants, as demonstrated by systems such as VS2,27 while maintaining relatively low volume changes of 8% for materials such as NMC.28 This has led to more of these TMDCs to be investigated for use as Li–ion battery electrodes, such as WS2,29 NbSe2,30 ReSe2,16 and most recently, ScS2.31 Nb- and Ta-based materials32 have been shown to be intercalatable up to ratios of 1:1 Li/MX2, but their heavier masses result in lower theoretical capacities below 170 mA h/g. MoS2 is widely studied8−16 in the field of TMDCs and has been the subject of numerous investigations, demonstrating a capacity of 167 mA h/g but poor conductivity. ScS2 in particular has recently been suggested as a promising electrode,31 promising an ideal maximum cathode voltage of 4.5 V, a reversible capacity of 183 mA h/g, and a volumetric expansion of 7.5%. In addition, in spite of the ready conversion into Li2S and Sn, SnS2 also shows considerable promise as an electrode material.33−40

Recent studies have looked at improving many of the properties of TMDCs needed for their use as electrode materials with the aim of extending device operation, increasing the intercalant capacities, and improving conductivity. Morphology control8,41,42 and composite formation,27,43−48 particularly through the inclusion of graphitic carbon49,50 or other layered materials, have been used to improve electrical and ionic conductivity, provide mechanical support, and improve the resultant capacity. Carbon is also often used as the anode in Li–ion batteries and can be obtained in multiple forms. The most basic of these is graphite, which can be intercalated up to the LiC6 limit (equivalent to 339.18 mA h/g).51 Graphene has been shown to achieve a higher capacity, but this is often suspended in monolayers, which are unrealistic in a normal battery electrode.52

Constructing superlattices is an attractive approach for tailoring the properties of two-dimensional materials due to the comparative ease with which they can be made (such as via exfoliation53) and has been applied to TMDCs.54−58 Given the layered structure of many battery electrodes in use today, such as NMC, NCA, LiCoO2, and graphite, superlattices could be made from these to modify their voltages, capacities, thermal stability, and more in order to improve their overall performance. Some TMDC–graphene superlattices have already been investigated as intercalation electrodes, showing promise as anodes,59−62 with MoS2–graphene superlattices showing voltages of 1.5 V and conversion reactions to Li2S at 2.3 V.61 Experimental evaluations of the MoS2/graphene systems have indicated62 that such systems offer improvements in terms of diffusion pathways and could be used for dual Li–Mg systems.

In this article, we have investigated the effect that forming superlattices (alternating TMDC/graphene multilayer systems) with graphene has on a wide variety of sulfur-based TMDCs using density functional theory (DFT). We have calculated the voltages and capacities by looking at the thermodynamic relation between the TMDCs and byproducts that are often formed when these breakdown in the presence of Li, Li2X. We have also investigated the effect that additional graphene layers have on T-phase MoS2.

Methods

Density Functional Theory

First-principles DFT calculations were performed using the projector augmented wave (PAW)63,64 method implemented in the Vienna Ab initio Simulation Package (VASP).65−68 The calculations utilize Perdew–Burke–Ernzerhof electron exchange correlation functions.69,70 The plane wave energy cutoff and augmentation were both 500 eV, with a Γ-centered Monkhorst-pack grid71 of at least 3 × 3 × 3 was used for the supercells due to their size, denser grids were used for smaller supercells. van der Waals interactions were included using the DFT-D3 method of Grimme72 to account for the weak interactions between the 2D-layered materials. The structures were geometrically relaxed until the forces between the atoms were less than 0.01 eV/Å using a combination of the conjugate gradient algorithm73 and a quasi-Newtonian relaxation algorithm, RMM-DIIS.74 PAW pseudopotentials were used for core electrons, and the electrons that have been treated as valence are Mo 4d55s1, W 5d46s2, Sn 5s25p2, Sc 3d14s2, Ni 3d84s2, Mn 3d54s2, Ti 3d24s2, S 3s23p4, C 2s22p2, and Li 1s22s1.

In order to minimize the strain between the TMDCs and graphene, large supercells have been created with anywhere from 4 to 16 MX2 units, an example of which is shown in Figure 1. These supercells have been generated using the ARTEMIS75 package, which carries out a series of rotational matchings of two layers and produces a unit cell with minimal strain, alongside estimating the interlayer distances. The supercells were generated with and without Li (a = 0 and a = 2) for the 9 different TMDCs investigated, and these were then modified to get additional Li concentrations (a = 1, 15/16, 17/16). For such large supercells, the number of configurations for a = 1 would result in, for example, 60,000,000 calculations (for one system) and only provide an intermediary voltage. As such, we have focused on only the key points of intercalation (a = 0, 1, 2). For a = 1, we have chosen 2 configurations based on previous results for TMDCs,26 one with the Li filling every other interlayer region between graphene and the TMDC, and the second where the Li is evenly spread between the interlayer regions. The precise geometry of the relevant unit cells and how these additional concentrations were made are provided in the Supporting Information, Section S3. These were all calculated from a graphene supercell of the same size as in the TMDC–graphene superlattices, the exact sizes of these are given in Table 1, and a single unit cell of the TMDCs, the only exception to this is MnS2 T, for which we used a TMDC supercell of the same size, the reason for this is given in the Supporting Information, Section S3. Volume expansion with increasing Li content was calculated in the standard method, 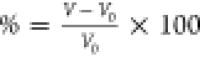Inline graphic where V0 is the volume of an unintercalated superlattice (a = 0).

Figure 1.

Figure 1

Open in a new tab

Schematic of ScS2 with graphene with Li from the top (a) and side (b) and without Li from the top (c) and side (d). This has 13 MX2 units and 56 carbon atoms.

Table 1. Ratios of MX2 to C Along With the Strain Associated with Each Layer for the 9 Supercells Generated Using the ARTEMIS75 Package and the Formation Energies per Unit Areaa.

TMDC no. MX2 C/MX2 ratio (b) strain on TMDC (%) strain on graphene (%) formation energy (meV/Å2)
MoS2 H 16 3.3750 0.98 –0.36 0.86
MoS2 T 16 3.3750 –0.59 –0.02 –8.95
WS2 H 16 3.3750 0.89 –0.35 0.043
SnS2 T 4 4.5000 0.65 –0.15 6.53
ScS2 R 13 4.3077 –3.44 0.018 13.38
ScS2 T 13 4.3077 –0.24 0.018 19.82
NiS2 T 13 3.8462 –3.44 –0.53 5.80
MnS2 T 7 3.7143 –4.74 –0.20 64.30
TiS2 T 16 3.8750 0.29 –0.27 11.69
Open in a new tab
a

The strains are calculated for the TMDCs with no Li compared with their superlattices with no Li (a = 0).

Voltages and Stability

The voltages, V, of these superlattices at different levels of Li intercalation can be expressed as

graphic file with name jp3c06300_m002.jpg 1

where ΔG is the change in Gibbs free energy, the total Li content a2 > a1, E(LiaMX2Cb) is the energy of an MX2–graphene superlattice with a Li and b carbon per MX2 unit, and E(Li) is the energy of Li in its bulk form. The Gibbs free energy can be approximated as the internal energy, as the pressure–volume and vibrational entropy contributions are known to be negligible in TMDCs76 and graphite/graphene.77

The thermodynamic stability of these superlattices was assessed by looking at the favorability of the formation of the secondary product Li2X. In Li–ion batteries, the formation of secondary products like Li2X indicates a loss of the desired layered structure, leading to a loss in capacity. We can determine the maximum Li intercalation limit by finding a region in phase space where Li2X is less favorable than an intercalated superlattice, where an unintercalated structure is less favorable, and where the elemental bulks are less favorable. These limits are expressed as

graphic file with name jp3c06300_m003.jpg 2
graphic file with name jp3c06300_m004.jpg 3
graphic file with name jp3c06300_m005.jpg 4

where ΔH(A) is the enthalpy of formation of compound A with respect to the bulk constituents and ΔμA is given by ΔμA = μA – μ0A, μA being the chemical potential of species A when in LiaMX2Cb, with A = Li, M, X, and C. If we consider the maximum difference in ΔμLi in eqs 2 and 3 when ΔμM = ΔμC = 0, we can qualitatively determine if a region of stability exists for LiaMX2Cb, we define this quantity as EIS, and it is given by

graphic file with name jp3c06300_m006.jpg 5

A positive EIS means that LiaMX2Cb is thermodynamically favorable, and a negative EIS means that Li intercalated to this capacity is not stable and will result in the formation of Li2S. Hence, determining the limit of intercalation, a, for when EIS = 0, determines the maximum amount of Li that can be intercalated and therefore the capacity. For these superlattices, we have also considered the formation of LiC6 from the lithiated superlattices (a > 0) and show that this is always unfavorable. The origin of the limits that EIS is derived from and the results looking at the formation of LiC6 can be found in Supporting Information, Sections S1 and S2.

Results and Discussion

General Properties

To establish the viability of these TMDC–graphene superlattices for the intercalation of Li, we first need to examine the resultant strains and formation energies. The exact number of MX2 units and the carbon to MX2 ratio (b) is given in Table 1, along with the strain associated with each layer and the formation energy per unit area. These are calculated for the TMDCs with no Li compared with their respective superlattices with no Li (a = 0). Details of this are given in the Supporting Information, Section S3. As can be seen, the strains are all less than ±0.6% for graphene and less than ±5% for the TMDCs. All of the formation energies for these structures are less than ±0.02 eV/Å2, with the exception of MnS2. However, in all cases, these supercells are both energetically viable and have sufficiently low strains to not dramatically affect the resultant properties. In general, the graphene shows minimal strain, whereas the TMDCs are more strained; however, these are lower than the expansion that these materials undergo due to Li intercalation. It is of note that, in all cases, the inclusion of graphene has made these superlattices both conductive, which is required for them to be used as electrodes, and decreased the diffusion barriers (see Supporting Information).

Voltages

The voltage is one of the most fundamental properties of an electrode and is used to determine if it is considered an anode or a cathode. Anodes normally have voltages lower than 2 V vs Li/Li+, ideally between 0.5 and 1.5 V, cathodes normally have voltages higher than 3 V, ideally between 3 and 4.5 V.78Figure 2a shows how the voltage of the TMDC–graphene superlattices varies as a in LiaMX2Cb is increased, calculated using eq 1.

Figure 2.

Figure 2

Open in a new tab

Open circuit voltages (a), volumetric expansions (b), in-plane lattice expansions (c), and out-of-plane lattice expansions (d) for the TMDC–graphene superlattices as a increase in LiaMX2-G.

Most of the TMDC–graphene superlattices display voltages that lie in the anode range. MoS2-H, MoS2-T, WS2-H, SnS2-T, NiS2-T, MnS2-T, and TiS2-T all have voltages between ≈1.5 and 0 V, meaning that these would be suitable as anodes. Despite how similar MoS2-H and MoS2-T are in composition, the change in TMDC phase leads to MoS2-T having a far higher voltage for a = 0 → 1, this may be caused by the large rearrangement that this system has undergone, having changed from T-phase to T′-phase (a distortion of T-phase with alternating Mo–Mo distances) and back to T-phase for a = 0 → 1 → 2. MoS2–H has a very flat voltage, which is far more preferable when looking for a Li intercalation battery electrode. SnS2-T has a flat voltage from a = 0 to a = 2, as neither of the a = 1 configurations was more favorable than a combination of the a = 0 and a = 2 structures. Our results for MoS2-T with graphene agree with those of the experiment, where a voltage of ≈1.5 V has been seen, as well as irreversible conversion reactions occurring above this voltage.61 We note that WS2, ScS2-R, and ScS2-T all show a significant drop in their voltages.

ScS2-R and ScS2-T both start with much higher voltages, closer to 3 V for a = 0 → 1, before dropping down to an anode-like voltage, around 1.15 V for a = 1 → 2. This puts them in an odd situation where they are not quite high enough to be considered a cathode but start too high to be considered an anode for their whole intercalation range at this ratio of MX2 to carbon. This suggests that ScS2-based cathodes should have low levels of carbon such that their voltages are not as significantly decreased.

Comparison of the TMDC–graphene voltages with those of their bulk TMDCs shows that the voltage is generally decreased. The details of this are shown in Supporting Information, Section S4. The lowest decrease was shown when mixing WS2–H with graphene, which was only decreased by 1.4%. The highest decrease in voltage was the mixing of MoS2–H with graphene, which showed a decrease in voltage of 0.72 V without graphene to 0.43 V with graphene. In general, our results show that the addition of graphene decreases the voltages of the TMDCs, with values ranging from 1.44 to 40.38% in the range a = 0 → 1. Clearly, the inclusion of graphene increases the effectiveness of these materials as anodes but is detrimental to the performance of cathodes.

Volumetric Expansion

When investigating Li–ion intercalation electrodes, it is important to look at how the volume of these materials changes during cycling, as this can be a cause of degradation of these materials that leads to a loss of usable capacity. Figure 2b shows how the volume of the TMDC–graphene superlattices varies as a in LiaMX2Cb is increased. As expected, for all superlattices investigated, we can see a general increase in volume when Li is intercalated. The superlattices at a = 1 and a = 2 all show smaller volumetric expansions to their respective bulk TMDCs at a = 1, with the exception of WS2-H and SnS2-T, which expand more at a = 2, these are given in the Supporting Information, Section S5. Bulk MnS2-T has actually shrunk when Li is intercalated into it; this is due to the aligned spins on the manganese atoms going from 3 up with no Li to 2 up with Li; the aligned spins repulse each other, leading to a decrease in volume. This is not observed in our MnS2-T superlattice, as the manganese atoms are more spatially separated due to the inclusion of graphene between the TMDC layers.

The observed expansions of the superlattices can be split into three groups, showing slightly different trends. MoS2-H, WS2-H, ScS2-T, MnS2-T, and TiS2-T have a large increase in volume for a = 0 → 1 with a much smaller increase in volume for a = 1 → 2, this is what we expect to happen for the vast majority of the investigated superlattices as Li prefers to be split between both sides of the TMDC layer instead of all on one side, meaning that both gaps between the TMDC and graphene layers are spread apart by Li. Although Li ScS2-T prefers to all be on one side when a = 1, breaking this “trend”. SnS2-T has a constant expansion from a = 0 → 2 due to the a = 1 configuration not being favorable. MoS2-T, ScS2-R, and NiS2-T all show an odd behavior of contracting when going from a = 1 → 2, this is also observed experimentally for materials such as NMC, which has the largest out-of-plane lattice constant near 50% Li content.28

From the lattice constant expansions shown in Figure 2c,d, we can see that the expansion of the out-of-plane lattice is the biggest contributor to the volumetric expansion. This is due to the van der Waals gaps between the layers being forced apart by Li as it is intercalated; this is seen in many other intercalation electrodes.28 We see volumetric expansions in the range of 5 to 10% for all materials except for SnS2-T and NiS2-T. This level of expansion is comparable to that seen in materials used in commercial batteries, such as NMC, with an expansion of 8%.28 SnS2-T and NiS2-T both undergo expansion in the range of 10 to 20%, which could lead to the significant formation of cracks during cycling, which accelerate degradation and limit capacity.79

Chemical Stability and Capacity

We can determine the maximum amount of Li that the TMDC–graphene superlattices can accommodate by determining when EIS ≈ 0 by using eq 5. Figure 3 shows how EIS varies as the level of intercalated Li, a, is increased. In these structures, we investigate strictly one layer of carbon with one layer of TMDC. For all the systems that have positive EIS, a similar or better Li to carbon ratio than that of graphene on (LiC6) its own is achieved. This indicates that the capacity of the carbon has been increased. The superlattices that show this improvement involve the TMDCs ScS2-R, ScS2-T, TiS2-T, and MoS2-T. Conversely, the remaining TMDCs are considered to readily decompose into Li2S at a = 1. These may still be able to intercalate Li without undergoing conversion; however, intercalation for a < 1 will lead to low capacities that are not suitable for electrodes.

Figure 3.

Figure 3

Open in a new tab

EIS for the TMDC–graphene superlattices as the intercalation level, a, increases in LiaMX2Cb for a = 1 and a = 2. Value for EIS has been included for these without graphene as well. For MoS2, extra points have been included for a = 15/16 and a = 17/16.

To further explore the limits of mixing these systems, we expand on the results for MoS2-T with graphene. For MoS2-T at a = 1 and a = 2, the EIS is negative, meaning that it is unfavorable to intercalate this TMDC even to just one Li per unit. However, the value of EIS at a = 1 was very low, equal to −0.191 eV. We have considered Li concentrations of a = 15/16 and a = 17/16 (±1 Li compared to a = 1). From this, we can confirm that EIS does become positive for a = 15/16, equal to 0.242 eV, meaning that MoS2-T with graphene is able to be intercalated and has a capacity equal to 121.29 mA h/g. If we look at the graphene layer, this is roughly equivalent to the limit of LiC4. We can also see that the value of EIS at a = 17/16 is between the values of EIS at a = 1 and a = 2. Thus, we can state that the MoS2–graphene boundary shows a small increase in capacity compared to the pure graphene region and a slight decrease in performance when compared to pure MoS2. This result agrees with Larson et al.59 who showed, for LiaMoS2C3.125 (50C: 16 MoS2), that the limit of intercalation is a ≈ 1.

ScS2-R, ScS2-T, and TiS2-T are all resistant to the formation of Li2S up to an intercalation of a = 2, meaning that these can be intercalated up to at least 2 Li per MX2 unit without decomposing. When ScS2-R and ScS2-T are compared to graphene, this is almost approaching LiC2, a large improvement over the LiC6 limit of graphene. When TiS2 is compared to graphene, it is equivalent to going slightly beyond LiC2. Both ScS2-R and ScS2-T have a capacity of 306.77 mA h/g, and TiS2 has a capacity of 310.84 mA h/g.

Comparing the EIS of the TMDC–graphene superlattices to their respective TMDCs at a = 1, we can see that the addition of graphene has decreased the stability of the TMDC against intercalation for all systems with the exception of WS2-H. This is shown by a general decrease in EIS, we find that this decrease compared to the bulk TMDC ranges from 1.09 to 0.17 eV, excluding WS2-H, which increases by 0.01 eV.

Changing the Ratio of Carbon to TMDC

In order to investigate the effect of graphene further, we looked at what happens when the ratio of graphene to MoS2-T is increased. This system is of particular relevance as MoS2 does not conduct without an additive, such as hard carbons. We have used MoS2-T at Li contents of a = 0 and a = 1 for this, varying the number of graphene layers between 0 and 3, which is equivalent to b = 0, 3.375, 6.750, and 10.125 (intermediate cases are discussed in the Supporting Information). For all cases where b ≠ 0, the same local structure of MoS2-T and Li has been used, as was found for a = 1 and b = 3.375, no additional Li is added as the amount of carbon is increased, a schematic of this is shown in Figure 4c. From these results, we can assess the effect that more carbon has on the local stability, volume expansion, and voltage of the MoS2-T layer. The voltage, EIS and volumetric, and local expansions are shown in Figure 4 and are given in the Supporting Information, Section S6.

Figure 4.

Figure 4

Open in a new tab

(a) Open circuit voltage and (b) EIS for MoS2-T as the number of layers of graphene is increased for a Li content of a = 0 and a = 1. (c) Shows both the total volumetric expansion in green and the local expansion in the z-axis in black. For the superlattices, this is measured from the graphene layer below the TMDC to the graphene layer above; for the TMDC on its own, we have used the distance between the closest sulfur atoms in the two neighboring TMDC layers, (d) is a schematic showing how additional carbon has been added to these systems as additional layers.

Our results show that the voltage (from a = 0 to a = 1) decreases as the amount of carbon, b, is increased. As we have limited our search to just the interface region, this suggests that a truly mixed MoS2/hard carbon system (which has bulk regions of both materials) will observe three peaks in its voltage behavior. The first peak will occur at around 1.7 V and be associated with bulk MoS2 intercalation. The second peak will occur at 1.5 and be associated with the interface, and the final much lower peak will be associated with hard carbon (typically of the order of 0.5–1 V depending on the carbon). This has been observed in the experiment by Wenelska et al.61 where the interface peak occurs as a shoulder to the main bulk MoS2 peak with an additional peak at 2.3 V, which corresponds to the breakdown into Li2S.

Looking at the overall expansion of the various carbon superlattices, we can see that the volume expansion decreases with the amount of graphene layers. Given that we are not adding any additional Li as we increase the number of graphene layers, we need to instead look at how the local environment around the TMDC changes. In order to understand this local environment better, we have also included the local change in the out-of-plane direction, which is measured from the graphene layer just below the TMDC to the graphene layer just above. From this, we can actually see that the amount of out-of-plane space occupied by the TMDC and Li increases as the number of graphene layers increases. This indicates that the overall decrease in volume expansion as the amount of carbon increases is due to changes in the in-plane lattice expansion.

Our results also show that the local stability of the MoS2-T layer is also decreasing compared to bulk MoS2-T, with EIS dropping as the amount of carbon b is increased. We can also see that both the voltage and EIS change in unison, decreasing by roughly the same amount as b is increased. Initially, we see a decrease in EIS. This is due to the donated charge from the Li mainly being absorbed by the TMDC, with the graphene not absorbing significant amounts. However, we do see a slight increase in EIS going from b = 6.750 to 10.125, where Bader charge analysis80 indicates that some of the donated charge is now spread to the third graphite layer, which reduces the total charge in the vicinity of the Li-TMDC region and could be responsible for this improvement in stability, details of this are provided in the Supporting Information, Section S6.

Conclusions

In this work, we have investigated the performance of 9 different TMDC–graphene superlattices for their potential use as Li–ion intercalation electrodes. We have calculated their voltages, finding that ScS2–graphene in both the T- and R-phases possesses voltages nearing 3 V, while the other 7 TMDC–graphene superlattices are between 0 and 1.5 V. The vast majority of these superlattices also show very little volumetric expansion in the range of 5–10%, similar to that of NMC at 8%; the only exceptions to this are SnS2-T and NiS2-T, which expanded up to nearly 20%.

Looking at the breakdown of these superlattices into Li2S, LiC6, and their constituent transition metals, we assess their capacities using a metric of stability, EIS. From all of the superlattices investigated, we found that ScS2 in both T- and R-phases and TiS2-T are able to be intercalated up to two Li ions per MX2 unit (Li2MX2Cb), leading to large capacities of 306.77 mA h/g for both ScS2 phases and 310.84 mA h/g for TiS2-T, which were both roughly equivalent to a limit of LiC2. MoS2-T was also found to be able to accept Li up to a limit of a = 15/16 in LiaMoS2Cb, agreeing with results seen in other studies.59 This corresponds to a capacity of 121.29 mA h/g, which is equivalent to a limit of LiC4.

To further explore the effects of graphene in these superlattices, we investigated what would happen to MoS2-T as additional layers of graphene were added. This showed that adding more layers of graphene decreased the voltage, while our metric of stability, EIS, initially decreased before effectively flatlining. A Bader charge analysis revealed that this may be due to charge being donated to the middle graphene layer, reducing the amount of electrons near the TMDC layer. The overall volume expansion of these superlattices decreases with Li intercalation as the number of graphene layers increases, while the local expansion around the TMDC layer increases.

Our results highlight the effects of forming superlattices with TMDCs and graphene for use as Li–ion intercalation electrodes, with low volumetric expansions and high capacities with a wide range of voltages. All of the superlattices investigated became conductive due to the addition of graphene.

Acknowledgments

The authors thank the University of Exeter CDT for Metamaterials, with funding from the EPSRC (EP/L015331/1). Via our membership of the UK’s HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202, EP/R029431), this work used the ARCHER and ARCHER 2 UK National Supercomputing Services (http://www.archer.ac.uk).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpcc.3c06300.

  • Derivation of EIS, formation of LiC6, lattice constants, stresses, strains, voltages, volumetric expansions, effects of additional graphene and MoS2, charge analysis, diffusion barriers, and AIMD stability (PDF)

Author Contributions

E.A.D.B.: conceptualization, data curation, formal analysis, methodology, writing original draft, and review and editing. C.J.P.: formal analysis and methodology. S.P.H.: conceptualization, funding acquisition, supervision, writing original draft, and review and editing.

The authors declare no competing financial interest.

Supplementary Material

jp3c06300_si_001.pdf (1.4MB, pdf)

References

  1. Whittingham M. S. Electrical Energy Storage and intercalation chemistry. Science 1976, 192, 1126–1127. 10.1126/science.192.4244.1126. [DOI] [PubMed] [Google Scholar]
  2. Thompson A. H. Lithium ordering in LixTiS2. Phys. Rev. Lett. 1978, 40, 1511–1514. 10.1103/PhysRevLett.40.1511. [DOI] [Google Scholar]
  3. Umrigar C.; Ellis D. E.; Wang D.-S.; Krakauer H.; Posternak M. Band structure, intercalation, and interlayer interactions of transition-metal dichalcogenides: TiS2 and LiTiS2. Phys. Rev. B: Condens. Matter Mater. Phys. 1982, 26, 4935–4950. 10.1103/PhysRevB.26.4935. [DOI] [Google Scholar]
  4. Mizushima K.; Jones P.; Wiseman P.; Goodenough J. LixCoO2 (x-1): A new cathode material for batteries of high energy density. Mater. Res. Bull. 1980, 15, 783–789. 10.1016/0025-5408(80)90012-4. [DOI] [Google Scholar]
  5. Yazami R.; Touzain P. A reversible graphite-lithium negative electrode for electrochemical generators. J. Power Sources 1983, 9, 365–371. 10.1016/0378-7753(83)87040-2. [DOI] [Google Scholar]
  6. Yoshio M.; Inoue S.; Hyakutake M.; Piao G.; Nakamura H. New lithium manganese composite oxide for the cathode of rechargeable lithium batteries. J. Power Sources 1991, 34, 147–152. 10.1016/0378-7753(91)85034-T. [DOI] [Google Scholar]
  7. Gummow R. J.; Thackeray M. M. An investigation of spinel-related and orthorhombic LiMnO2 Cathodes for rechargeable lithium batteries. J. Electrochem. Soc. 1994, 141, 1178–1182. 10.1149/1.2054893. [DOI] [Google Scholar]
  8. Li H.; Li W.; Ma L.; Chen W.; Wang J. Electrochemical lithiation/delithiation performances of 3D flowerlike MoS2 powders prepared by Ionic liquid assisted hydrothermal route. J. Alloys Compd. 2009, 471, 442–447. 10.1016/j.jallcom.2008.03.133. [DOI] [Google Scholar]
  9. Fang X.; Hua C.; Guo X.; Hu Y.; Wang Z.; Gao X.; Wu F.; Wang J.; Chen L. Lithium storage in commercial MoS2 in different potential ranges. Electrochim. Acta 2012, 81, 155–160. 10.1016/j.electacta.2012.07.020. [DOI] [Google Scholar]
  10. Stephenson T.; Li Z.; Olsen B.; Mitlin D. Lithium ion battery applications of molybdenum disulfide (MoS2) nanocomposites. Energy Environ. Sci. 2014, 7, 209–231. 10.1039/C3EE42591F. [DOI] [Google Scholar]
  11. Xia J.; Wang J.; Chao D.; Chen Z.; Liu Z.; Kuo J.-L.; Yan J.; Shen Z. X. Phase evolution of lithium intercalation dynamics in 2H-MOS2. Nanoscale 2017, 9, 7533–7540. 10.1039/C7NR02028G. [DOI] [PubMed] [Google Scholar]
  12. Zhang L.; Sun D.; Kang J.; Feng J.; Bechtel H. A.; Wang L.-W.; Cairns E. J.; Guo J. Electrochemical reaction mechanism of the MoS2 electrode in a lithium-ion cell revealed by in situ and Operando X-ray absorption spectroscopy. Nano Lett. 2018, 18, 1466–1475. 10.1021/acs.nanolett.7b05246. [DOI] [PubMed] [Google Scholar]
  13. Imanishi N.; Toyoda M.; Takeda Y.; Yamamoto O. Study on lithium intercalation into MoS2. Solid State Ionics 1992, 58, 333–338. 10.1016/0167-2738(92)90137-E. [DOI] [Google Scholar]
  14. George C.; Morris A. J.; Modarres M. H.; De Volder M. Structural evolution of electrochemically lithiated MoS2 nanosheets and the role of carbon additive in Li-Ion Batteries. Chem. Mater. 2016, 28, 7304–7310. 10.1021/acs.chemmater.6b02607. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Lu Y.; Yao X.; Yin J.; Peng G.; Cui P.; Xu X. MOS2 nanoflowers consisting of nanosheets with a controllable interlayer distance as high-performance lithium ion battery anodes. RSC Adv. 2015, 5, 7938–7943. 10.1039/C4RA14026E. [DOI] [Google Scholar]
  16. Nadar A.; Arora Y.; Thakur P.; Narayanan T.; Bhattacharya A.; Khushalani D. ReS2 vs MoS2: Viable electrodes for batteries and capacitors. Electrochem. Commun. 2022, 139, 107313. 10.1016/j.elecom.2022.107313. [DOI] [Google Scholar]
  17. Liu Z.; Yu A.; Lee J. Y. Synthesis and characterization of LiNi1–x–yCoxMnyO2 as the cathode materials of secondary lithium batteries. J. Power Sources 1999, 81–82, 416–419. 10.1016/S0378-7753(99)00221-9. [DOI] [Google Scholar]
  18. Yoshio M.; Noguchi H.; Itoh J.-i.; Okada M.; Mouri T. Preparation and properties of LiCoyMnxNi1–x–yO2 as a cathode for lithium ion batteries. J. Power Sources 2000, 90, 176–181. 10.1016/S0378-7753(00)00407-9. [DOI] [Google Scholar]
  19. Park S.; Yoon C.; Kang S.; Kim H.-S.; Moon S.-I.; Sun Y.-K. Synthesis and structural characterization of layered li[Ni1/3Co1/3MN1/3]O2 cathode materials by ultrasonic spray pyrolysis method. Electrochim. Acta 2004, 49, 557–563. 10.1016/j.electacta.2003.09.009. [DOI] [Google Scholar]
  20. Wang Y.; Jiang J.; Dahn J. The reactivity of delithiated Li(Ni1/3Co1/3Mn1/3)O2, Li(Ni0.8Co0.15Al0.05)O2 or LiCoO2 with non-aqueous electrolyte. Electrochem. Commun. 2007, 9, 2534–2540. 10.1016/j.elecom.2007.07.033. [DOI] [Google Scholar]
  21. Chhowalla M.; Shin H. S.; Eda G.; Li L.-J.; Loh K. P.; Zhang H. The chemistry of two-dimensional layered transition metal dichalcogenide nanosheets. Nat. Chem. 2013, 5, 263–275. 10.1038/nchem.1589. [DOI] [PubMed] [Google Scholar]
  22. Whittingham M. S. The role of ternary phases in cathode reactions. J. Electrochem. Soc. 1976, 123, 315–320. 10.1149/1.2132817. [DOI] [Google Scholar]
  23. Whittingham M. S. Chemistry of intercalation compounds: Metal guests in chalcogenide hosts. Prog. Solid State Chem. 1978, 12, 41–99. 10.1016/0079-6786(78)90003-1. [DOI] [Google Scholar]
  24. Gao Y.-P.; Wu X.; Huang K.-J.; Xing L.-L.; Zhang Y.-Y.; Liu L. Two-dimensional transition metal diseleniums for Energy Storage Application: A review of recent developments. CrystEngComm 2017, 19, 404–418. 10.1039/C6CE02223E. [DOI] [Google Scholar]
  25. Gao Y.-P.; Xu J.; Huang K.-J.; Lu H.; Pang Y.-X.; Li G.-q. An overview of the current status and prospects of cathode materials based on transition metal sulfides for magnesium-ion batteries. CrystEngComm 2021, 23, 7546–7564. 10.1039/D1CE01029H. [DOI] [Google Scholar]
  26. Price C. J.; Baker E. A. D.; Hepplestone S. P. First principles study of layered transition metal dichalcogenides for use as electrodes in Li-ion and Mg-ion batteries. J. Mater. Chem. A 2023, 11, 12354–12372. 10.1039/D3TA00940H. [DOI] [Google Scholar]
  27. Qi H.; Wang L.; Zuo T.; Deng S.; Li Q.; Liu Z.; Hu P.; He X. Hollow structure VS2@reduced graphene oxide (RGO) architecture for enhanced sodium-ion battery performance. ChemElectroChem 2020, 7, 78–85. 10.1002/celc.201901626. [DOI] [Google Scholar]
  28. Woodcox M.; Shepard R.; Smeu M. First principles investigation into the interwoven nature of voltage and mechanical properties of the LixNMC-811 cathode. J. Power Sources 2021, 516, 230620. 10.1016/j.jpowsour.2021.230620. [DOI] [Google Scholar]
  29. Nandi D. K.; Sen U. K.; Dhara A.; Mitra S.; Sarkar S. K. Intercalation based tungsten disulfide (WS2) Li-ion battery anode grown by atomic layer deposition. RSC Adv. 2016, 6, 38024–38032. 10.1039/C6RA00468G. [DOI] [Google Scholar]
  30. Hitz E.; Wan J.; Patel A.; Xu Y.; Meshi L.; Dai J.; Chen Y.; Lu A.; Davydov A. V.; Hu L.; et al. Electrochemical intercalation of lithium ions into NbSe2 nanosheets. ACS Appl. Mater. Interfaces 2016, 8, 11390–11395. 10.1021/acsami.5b11583. [DOI] [PubMed] [Google Scholar]
  31. Price C. J.; Pitfield J.; Baker E. A. D.; Hepplestone S. P. First principles study of layered scandium disulfide for use as Li-ion and beyond-Li-ion batteries. Phys. Chem. Chem. Phys. 2023, 25, 2167–2178. 10.1039/D2CP05055B. [DOI] [PubMed] [Google Scholar]
  32. Murphy D. W.; Di Salvo F. J.; Hull G. W.; Waszczak J. V. Convenient preparation and physical properties of lithium intercalation compounds of group 4b and 5b layered transition metal dichalcogenides. Inorg. Chem. 1976, 15, 17–21. 10.1021/ic50155a005. [DOI] [Google Scholar]
  33. Morales J.; Perez-Vicente C.; Tirado J. Chemical and electrochemical lithium intercalation and staging in 2H SnS2. Solid State Ionics 1992, 51, 133–138. 10.1016/0167-2738(92)90190-Z. [DOI] [Google Scholar]
  34. Seo J.-w.; Jang J.-t.; Park S.-w.; Kim C.; Park B.; Cheon J. Two-dimensional SnS2 nanoplates with extraordinary high discharge capacity for lithium ion batteries. Adv. Mater. 2008, 20, 4269–4273. 10.1002/adma.200703122. [DOI] [Google Scholar]
  35. Zai J.; Wang K.; Su Y.; Qian X.; Chen J. High stability and superior rate capability of three-dimensional hierarchical SnS2 microspheres as anode material in lithium ion batteries. J. Power Sources 2011, 196, 3650–3654. 10.1016/j.jpowsour.2010.12.057. [DOI] [Google Scholar]
  36. Luo B.; Fang Y.; Wang B.; Zhou J.; Song H.; Zhi L. Two dimensional graphene–SnS2 hybrids with superior rate capability for lithium ion storage. Energy Environ. Sci. 2012, 5, 5226–5230. 10.1039/C1EE02800F. [DOI] [Google Scholar]
  37. Zhang Q.; Li R.; Zhang M.; Zhang B.; Gou X. SnS2/reduced graphene oxide nanocomposites with superior lithium storage performance. Electrochim. Acta 2014, 115, 425–433. 10.1016/j.electacta.2013.10.193. [DOI] [Google Scholar]
  38. Gao P.; Wang L.; Zhang Y.-Y.; Huang Y.; Liao L.; Sutter P.; Liu K.; Yu D.; Wang E.-G. High-resolution tracking asymmetric lithium insertion and extraction and local structure ordering in SnS2. Nano Lett. 2016, 16, 5582–5588. 10.1021/acs.nanolett.6b02136. [DOI] [PubMed] [Google Scholar]
  39. Wang M.; Huang Y.; Zhu Y.; Wu X.; Zhang N.; Zhang H. Binder-free flower-like SnS2 nanoplates decorated on the graphene as a flexible anode for high-performance lithium-ion batteries. J. Alloys Compd. 2019, 774, 601–609. 10.1016/j.jallcom.2018.09.378. [DOI] [Google Scholar]
  40. Li R.; Miao C.; Zhang M.; Xiao W. Novel hierarchical structural SnS2 composite supported by biochar carbonized from chewed sugarcane as enhanced anodes for lithium ion batteries. Ionics 2020, 26, 1239–1247. 10.1007/s11581-019-03288-8. [DOI] [Google Scholar]
  41. Wang Q.; Jiao L.; Han Y.; Du H.; Peng W.; Huan Q.; Song D.; Si Y.; Wang Y.; Yuan H. CoS2 hollow spheres: Fabrication and their application in lithium-ion batteries. J. Phys. Chem. C 2011, 115, 8300–8304. 10.1021/jp111626a. [DOI] [Google Scholar]
  42. Song Y.; Liao J.; Chen C.; Yang J.; Chen J.; Gong F.; Wang S.; Xu Z.; Wu M. Controllable morphologies and electrochemical performances of self-assembled nano-honeycomb WS2 anodes modified by graphene doping for lithium and sodium ion batteries. Carbon 2019, 142, 697–706. 10.1016/j.carbon.2018.07.060. [DOI] [Google Scholar]
  43. Xu X.; Rout C. S.; Yang J.; Cao R.; Oh P.; Shin H. S.; Cho J. Freeze-dried WS2 composites with low content of graphene as high-rate lithium storage materials. J. Mater. Chem. A 2013, 1, 14548. 10.1039/c3ta13329j. [DOI] [Google Scholar]
  44. Liu Y.; Zhu M.; Chen D. Sheet-like MoSe2/C composites with enhanced Li-ion storage properties. J. Mater. Chem. A 2015, 3, 11857–11862. 10.1039/C5TA02100F. [DOI] [Google Scholar]
  45. Sung G.-K.; Jeon K.-J.; Park C.-M. Highly reversible and superior Li-storage characteristics of layered GeS2 and its amorphous composites. ACS Appl. Mater. Interfaces 2016, 8, 29543–29550. 10.1021/acsami.6b10994. [DOI] [PubMed] [Google Scholar]
  46. Pomerantseva E.; Gogotsi Y. Two-dimensional heterostructures for energy storage. Nat. Energy 2017, 2, 17089. 10.1038/nenergy.2017.89. [DOI] [Google Scholar]
  47. Bediako D. K.; Rezaee M.; Yoo H.; Larson D. T.; Zhao S. Y.; Taniguchi T.; Watanabe K.; Brower-Thomas T. L.; Kaxiras E.; Kim P. Heterointerface effects in the electrointercalation of van der waals heterostructures. Nature 2018, 558, 425–429. 10.1038/s41586-018-0205-0. [DOI] [PubMed] [Google Scholar]
  48. Xiang Huang Z.; Liu B.; Kong D.; Wang Y.; Ying Yang H. SnSe2 quantum dot/RGO composite as high performing lithium anode. Energy Storage Mater. 2018, 10, 92–101. 10.1016/j.ensm.2017.08.008. [DOI] [Google Scholar]
  49. Entwistle J.; Ge R.; Pardikar K.; Smith R.; Cumming D. Carbon binder domain networks and electrical conductivity in lithium-ion battery electrodes: A critical review. Renewable Sustainable Energy Rev. 2022, 166, 112624. 10.1016/j.rser.2022.112624. [DOI] [Google Scholar]
  50. Qi X.; Blizanac B.; DuPasquier A.; Lal A.; Niehoff P.; Placke T.; Oljaca M.; Li J.; Winter M. Influence of thermal treated carbon black conductive additive on the performance of high voltage spinel CR-doped LiNi0.5Mn1.5O4 composite cathode electrode. J. Electrochem. Soc. 2015, 162, A339–A343. 10.1149/2.0401503jes. [DOI] [Google Scholar]
  51. Kaskhedikar N. A.; Maier J. Lithium storage in carbon nanostructures. Adv. Mater. 2009, 21, 2664–2680. 10.1002/adma.200901079. [DOI] [PubMed] [Google Scholar]
  52. Yoo E.; Kim J.; Hosono E.; Zhou H.-s.; Kudo T.; Honma I. Large Reversible Li Storage of Graphene Nanosheet Families for Use in Rechargeable Lithium Ion Batteries. Nano Lett. 2008, 8, 2277–2282. 10.1021/nl800957b. [DOI] [PubMed] [Google Scholar]
  53. Jia X.; Shao Q.; Xu Y.; Li R.; Huang K.; Guo Y.; Qu C.; Gao E. Elasticity-based-exfoliability measure for high-throughput computational exfoliation of two-dimensional materials. npj Comput. Mater. 2021, 7, 211. 10.1038/s41524-021-00677-4. [DOI] [Google Scholar]
  54. Nutting D.; Felix J. F.; Tillotson E.; Shin D.-W.; De Sanctis A.; Chang H.; Cole N.; Russo S.; Woodgate A.; Leontis I.; Fernandez H. A.; Craciun M. F.; Haigh S. J.; Withers F. Heterostructures formed through abraded van der Waals materials. Nat. Commun. 2020, 11, 3047. 10.1038/s41467-020-16717-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Rawat A.; Ahammed R.; Sharma D.; Jena N.; Mohanta M. K.; De Sarkar A. Solar energy harvesting in type II van der waals heterostructures of Semiconducting Group III monochalcogenide Monolayers. J. Phys. Chem. C 2019, 123, 12666–12675. 10.1021/acs.jpcc.9b03359. [DOI] [Google Scholar]
  56. Mohanta M. K.; Rawat A.; Jena N.; Sharma D.; Ahammed R.; De Sarkar A. Interfacing boron monophosphide with molybdenum disulfide for an ultrahigh performance in thermoelectrics, two-dimensional excitonic solar cells, and Nanopiezotronics. ACS Appl. Mater. Interfaces 2019, 12, 3114–3126. 10.1021/acsami.9b16866. [DOI] [PubMed] [Google Scholar]
  57. Ren J.; Zhang C.; He C.; Ouyang T.; Li J.; Tang C.; Zhong J. Optoelectronic properties of type-II SePtTe/InS van der waals heterojunction. J. Appl. Phys. 2020, 128, 043103. 10.1063/5.0007359. [DOI] [Google Scholar]
  58. Ahammed R.; Rawat A.; Jena N.; Sharma D.; Mohanta M. K.; De Sarkar A. ZrS3/MS2 and ZrS3/MXY (M = Mo, W; X, y = S, Se, Te; x ≠ y) type-II van der waals hetero-bilayers: Prospective candidates in 2D excitonic solar cells. Appl. Surf. Sci. 2020, 499, 143894. 10.1016/j.apsusc.2019.143894. [DOI] [Google Scholar]
  59. Larson D. T.; Fampiou I.; Kim G.; Kaxiras E. Lithium intercalation in graphene–MoS2 heterostructures. J. Phys. Chem. C 2018, 122, 24535–24541. 10.1021/acs.jpcc.8b07548. [DOI] [Google Scholar]
  60. Yousaf M.; Wang Y.; Chen Y.; Wang Z.; Firdous A.; Ali Z.; Mahmood N.; Zou R.; Guo S.; Han R. P.; et al. A 3D trilayered CNT/MoS2/C heterostructure with an expanded MoS2 interlayer spacing for an efficient sodium storage. Adv. Energy Mater. 2019, 9, 1900567. 10.1002/aenm.201900567. [DOI] [Google Scholar]
  61. Wenelska K.; Adam V.; Thauer E.; Singer L.; Klingeler R.; Chen X.; Mijowska E. Fabrication of 3D graphene/MoS2 spherical heterostructure as anode material in Li-Ion Battery. Front. Energy Res. 2022, 10, 960786. 10.3389/fenrg.2022.960786. [DOI] [Google Scholar]
  62. Yu X.; Zhao G.; Liu C.; Wu C.; Huang H.; He J.; Zhang N. A MoS2 and Graphene Alternately Stacking van der Waals Heterstructure for Li+/Mg2+ Co-Intercalation. Adv. Funct. Mater. 2021, 31, 2103214. 10.1002/adfm.202103214. [DOI] [Google Scholar]
  63. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
  64. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  65. Kresse G.; Hafner J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 558–561. 10.1103/PhysRevB.47.558. [DOI] [PubMed] [Google Scholar]
  66. Kresse G.; Hafner J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 49, 14251–14269. 10.1103/PhysRevB.49.14251. [DOI] [PubMed] [Google Scholar]
  67. Kresse G.; Furthmüller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  68. Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
  69. Perdew J. P.; Burke K.; Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  70. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 1396. 10.1103/PhysRevLett.78.1396. [DOI] [PubMed] [Google Scholar]
  71. Monkhorst H. J.; Pack J. D. Special points for Brillouin-zone integrations. Phys. Rev. B: Condens. Matter Mater. Phys. 1976, 13, 5188–5192. 10.1103/PhysRevB.13.5188. [DOI] [Google Scholar]
  72. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  73. Tribbey W. Numerical Recipes. ACM SIGSOFT Software Engineering Notes 2010, 35, 30–31. 10.1145/1874391.187410. [DOI] [Google Scholar]
  74. Pulay P. Convergence acceleration of iterative sequences. the case of scf iteration. Chem. Phys. Lett. 1980, 73, 393–398. 10.1016/0009-2614(80)80396-4. [DOI] [Google Scholar]
  75. Taylor N. T.; Davies F. H.; Rudkin I. E. M.; Price C. J.; Chan T. H.; Hepplestone S. P. ARTEMIS: Ab initio restructuring tool enabling the modelling of interface structures. Comput. Phys. Commun. 2020, 257, 107515. 10.1016/j.cpc.2020.107515. [DOI] [Google Scholar]
  76. Aydinol M.; Kohan A.; Ceder G. Ab initio calculation of the intercalation voltage of lithium-transition-metal oxide electrodes for rechargeable batteries. J. Power Sources 1997, 68, 664–668. 10.1016/S0378-7753(96)02638-9. [DOI] [Google Scholar]
  77. Persson K.; Hinuma Y.; Meng Y. S.; Van der Ven A.; Ceder G. Thermodynamic and kinetic properties of the Li-graphite system from first-principles calculations. Phys. Rev. B: Solid State 2010, 82, 125416. 10.1103/PhysRevB.82.125416. [DOI] [Google Scholar]
  78. Eftekhari A. Low voltage anode materials for lithium-ion batteries. Energy Storage Mater. 2017, 7, 157–180. 10.1016/j.ensm.2017.01.009. [DOI] [Google Scholar]
  79. Hausbrand R.; Cherkashinin G.; Ehrenberg H.; Gröting M.; Albe K.; Hess C.; Jaegermann W. Fundamental degradation mechanisms of layered oxide Li-ion battery cathode materials: Methodology, insights and novel approaches. Mater. Sci. Eng., B 2015, 192, 3–25. 10.1016/j.mseb.2014.11.014. [DOI] [Google Scholar]
  80. Yu M.; Trinkle D. R. Accurate and efficient algorithm for Bader Charge Integration. J. Chem. Phys. 2011, 134, 064111. 10.1063/1.3553716. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jp3c06300_si_001.pdf (1.4MB, pdf)

Articles from The Journal of Physical Chemistry. C, Nanomaterials and Interfaces are provided here courtesy of American Chemical Society

RESOURCES