Platform-independent estimation of human physiological time from single blood samples

Significance

The importance of circadian rhythm in health is evident in studies from metabolic disorders to Alzheimer’s disease. However, translating these observations to the clinic remains stymied due to the burden of measuring physiological time. Methods to assess physiological time using blood biomarkers address this issue, but they must be accurate and generalizable across protocols and platforms. Here, we present TimeMachine, an algorithm that can estimate the circadian phase from a single blood sample. Validation on four distinct datasets shows TimeMachine accurately recovers phase estimates from a single-timepoint gene expression profile of human peripheral blood mononuclear cells across varied protocols and technologies, an important advance over current methods. This algorithm offers a feasible approach for incorporating circadian biomarkers in research and clinical care.

Abstract

Abundant epidemiological evidence links circadian rhythms to human health, from heart disease to neurodegeneration. Accurate determination of an individual’s circadian phase is critical for precision diagnostics and personalized timing of therapeutic interventions. To date, however, we still lack an assay for physiological time that is accurate, minimally burdensome to the patient, and readily generalizable to new data. Here, we present TimeMachine, an algorithm to predict the human circadian phase using gene expression in peripheral blood mononuclear cells from a single blood draw. Once trained on data from a single study, we validated the trained predictor against four independent datasets with distinct experimental protocols and assay platforms, demonstrating that it can be applied generalizably. Importantly, TimeMachine predicted circadian time with a median absolute error ranging from 1.65 to 2.7 h, regardless of systematic differences in experimental protocol and assay platform, without renormalizing the data or retraining the predictor. This feature enables it to be flexibly applied to both new samples and existing data without limitations on the transcriptomic profiling technology (microarray, RNAseq). We benchmark TimeMachine against competing approaches and identify the algorithmic features that contribute to its performance.

The circadian rhythm is an endogenous, evolutionarily conserved timekeeping system that regulates biological processes in time with the Earth’s daily cycle. In mammals, the rhythm is generated in each cell via a transcription–translation feedback loop, which in turn orchestrates 24-h transcriptional rhythms in nearly half of all genes in a tissue-specific manner (1). Numerous studies have demonstrated that dysregulation of circadian rhythms is associated with various health issues, including obesity, diabetes, cardiovascular disease, and cancer (2–4). In the past decade, it has become clear that aligning drug dosing time with the internal circadian clock can enhance the effectiveness of treatments and reduce side effects, particularly for cancer (5–7). However, the current gold standard measure of circadian phase, dim-light melatonin onset (DLMO), is time-consuming and expensive to obtain, requiring hourly saliva/plasma samples over a 24-h period. The expense of consecutive sample collection and the availability of a sleep clinic are major barriers to implementing circadian measures in research studies and clinical settings. The development of simple measurement of circadian phase is necessary to facilitate the translation of circadian-based medicine on a population scale.

Transcriptomic profiling technologies and machine learning algorithms offer a promising approach to assess the circadian phase by using gene expression in blood samples as a readout of the endogenous circadian rhythm. Prior to the availability of human circadian datasets, methods were developed to predict time of day using a single–time–point expression profile for mouse tissues. “Molecular Timetable,” developed by Ueda et al., used 168 time-indicating genes to estimate peak time of cycling genes via cosine fitting in mouse liver tissues (8). While this approach performed well in mice under laboratory conditions, the need for an accurate biomarker applicable to humans spurred the development of more sophisticated algorithms (9–11).

The first of these, Hughey et al.’s “ZeitZeiger” is a supervised machine learning method to predict time-of-day from gene expression data using smooth periodic splines and sparse principal components (12). Originally developed using the same mouse data as Molecular Timetable, it was later extended to human data (9) and optimized specifically using monocytes assayed with the NanoString platform (13). More recently, Laing et al. developed a multivariate model based on partial least squares regression (PLSR) that takes a single sample of gene expression profile as input to predict the melatonin phase in humans (10). This PLSR-based model was trained and validated on a mixture of two human circadian gene expression datasets profiled by the same microarray platform and reported to predict 54% of the samples with an error under 2 h.

However, each of these methods has limitations that hampered their generalizability. For example, when ZeitZeiger is applied to a new batch of data, the training data and the new data are renormalized with batch correction, followed by retraining the machine after the batch correction is done. This can present challenges for interpretability, as the predictor itself may differ from batch to batch. Moreover, application of batch correction necessitates multiple samples from the same batch and thus cannot be used for a single new sample (as would be expected in clinical application). While the PLSR-based model developed by Laing et al. does not require batch correction, it instead relies on quantile normalization to the same reference array of training data. This means that new data must measure the same features as the training data ($\sim {10}^4$ transcripts), including genes that are not part of the predictor itself (which comprises $\sim {10}^2$ genes). It has also been shown that this normalization may not adequately address systematic batch differences, making the predictor inaccurate when applied across platforms (11).

To address the need for a generalizable predictor that could be used without batch correction or retraining, Braun et al. proposed “TimeSignature,” an elastic-net regression model with a within-subject normalization step (11, 14). TimeSignature was validated against three different studies using distinct microarrays and RNA-sequencing platforms and demonstrated accuracy across platforms and studies without the need for batch correction, retraining, or fitting platform-specific models. Its generalizability across datasets was shown to significantly outperform ZeitZeiger and the one sample PLSR-based method. However, TimeSignature requires two samples from each subject to compute the within-subject normalization, and the two samples need to be at least 8 h apart for peak accuracy. While still simpler than assaying DLMO, this requirement limits prospective application to settings where two samples can be collected and cannot be applied retrospectively to previously collected single samples.

In this study, we introduce a single-timepoint algorithm for predicting circadian phase in humans, emphasizing its simplicity and generalizability. The TimeMachine algorithm offers two variants—ratio TimeMachine (rTM) and $Z$-score TimeMachine (zTM). Both variants only require gene expression measurements for 37 genes from a single blood draw and achieve similar performance. No constraints are placed on the assay (microarray, RNAseq, etc). To evaluate its performance, we trained and tested the model on one human circadian gene expression dataset (divided subject-wise into training and testing subsets) and validated it on three independent datasets with different microarray and RNA-seq platforms. Our results indicate that, once trained, the TimeMachine predictor can be applied directly to new data without retraining the model or any batch corrections. TimeMachine achieves a median absolute error of $\sim$2.5 h, performing as well or better than other single-sample methods. It utilizes fewer genes and is only around 20 to 40 min less accurate than methods requiring two draws. We also investigated factors associated with uncertainties in TimeMachine’s predictions, such as the amplitude of the regression model and sampling time, which offer valuable insights for future applications.

Results

TimeMachine Algorithm.

The framework of TimeMachine starts with a feature selection and within-sample rescaling step, followed by fitting the predictor, and finally applying it to samples from separate studies. To demonstrate the performance of the TimeMachine algorithm, we acquired four published datasets of human whole–blood transcriptome profiles from the NCBI Gene Expression Omnibus (GEO) repository: GSE39445 (TrTe) (15), GSE48113 (V1) (16), GSE56931 (V2) (17), and GSE113883 (V3) (11). Details of each dataset can be found in Materials and Methods. We will refer to these datasets as TrTe, V1, V2, and V3 throughout the manuscript. Only genes in common to all four datasets were retained for analysis, yielding a total of 7,615 genes.

Identifying predictor genes.

The first step of the algorithm is to identify genes that contain phase information and would thus be promising biomarkers of time.

Existing methods, including ZeitZeiger (9), the PLSR-based method (10), and TimeSignature (11), offer distinct strategies for identifying genes with rhythmic patterns that can predict circadian phases in human blood transcriptomic data in PBMCs.

We applied the aforementioned algorithms using the provided code from the original authors to our training data, which comprises half of the subjects selected at random from TrTe. This process led to the identification of 24, 100, and 41 time-indicating genes, respectively (as shown in SI Appendix, Table S1). Because previous findings have demonstrated that the predictor genes identified by these algorithms rarely overlap, even when employed on the same dataset (10), we consider the union of these genes—135 genes in total (SI Appendix, Table S1)—as candidate phase markers.

Of these, we expect that genes that exhibit the strongest cycling patterns will better reflect circadian time. To this end, we identify those that show the most robust cycling via JTK_Cycle analysis (18, 19). Thirty-seven genes yield JTK_Cycle $P<0.1$ (SI Appendix, Table S2). These 37 genes are used as the inputs to the TimeMachine predictor.

Sample-wise normalization.

The diverse transcriptomic profiling platforms often generate gene expression data on different scales. This poses a significant challenge for developing a predictor that performs well independently of the specific profiling platform. Key techniques, such as batch correction, quantile normalization, or the subject-wise normalization used in TimeSignature, are implemented to ensure that the data are expressed on a comparable and consistent scale. Here, we propose two normalization approaches: 1) pairwise gene ratios and 2) $Z$-score transformation. Both approaches are based on the conjecture that the relative expression of the predictor genes, rather than their absolute magnitudes, are the biologically relevant features, and that these will be better preserved across platforms than the absolute expression values. As demonstrated further below, the two techniques offer similar performance. To distinguish between the normalization schemes, we will refer to the algorithm as ratio TimeMachine (rTM) when employing pairwise gene ratios, and as $Z$-score TimeMachine (zTM) when applying $Z$-score transformation in the subsequent sections.

Pairwise gene ratios.

We denote the log2 expression of gene $j$ in sample $i$ collected at time $t_i$ as $x_{i,j}$, where $j=1,\cdots ,37$. For the given sample $i$, the difference between the log2 expressions (i.e., the ratio of a pair of gene expressions) is:

$$z_{i,jk}=x_{i,j}-x_{i,k},$$

where $j=1,\cdots ,36$ and $k>j$. The resulting vector ${\overrightarrow{z}}_i$ is thus a $1\times 666$ vector representing the ratio of gene expressions at time $t_i$.

$Z$-score transformation.

For a given sample $i$ collected at time $t_i$, the log2 expression of 37 genes are denoted as ${\overrightarrow{x}}_i$ (a $1\times 37$ vector). Calculating the $Z$-score transformation on the sample yields

$${\overrightarrow{z}}_i=\frac{{\overrightarrow{x}}_i-\overline{{\overrightarrow{x}}_i}}{s_i},$$

where $i=1,\cdots ,n$; $\overline{{\overrightarrow{x}}_i}$ is the sample mean; and $s_i$ represents the sample SD.

Notably, no batch correction or other normalization is conducted, so that the predictor can be directly applied to future data simply by selecting these 37 genes and applying the ratio or $Z$-score sample-wise normalization.

Fitting the predictor.

Both ratio TimeMachine and $Z$-score TimeMachine use a bivariate regression model with elastic net regularization to predict physiological time as a function of gene expression. Here, the target (dependent) variables are the Cartesian coordinates corresponding to the angle on a 24-h clock,

$$\begin{array}{c}\hfill Y_{(N\times 2)}={\left[\begin{array}{c}cos\left(\frac{2\pi }{24}{t}_i\right)\\ sin\left(\frac{2\pi }{24}{t}_i\right)\end{array}\right]}^{\mathsf{T}}={\beta }_0+Z_{(N\times P)}{\beta }_{(P\times 2)}+{\eta }_{(N\times 2)},\end{array}$$ [1]

where $t_i$ is the physiological time (e.g. hours since DLMO, otherwise known as “melatonin phase”) for sample $i$; $Z$ is an $N$ (observations) $\times$P (features) matrix after the normalization described above ($P=37$ for $Z$-score TimeMachine; $P=666$ for ratio TimeMachine); and $\eta$ is a Gaussian error term.

To obtain a more accurate and parsimonious model, we find coefficients $\beta$ that minimize the cost function with elastic net regularization (20):

$$\begin{array}{cc}\hfill {\displaystyle \underset{({\mathit{\beta }}_0,\mathit{\beta })\in {\mathbb{R}}^{(P+1)\times 2}}{min}}& [\frac{1}{2N}{\displaystyle \sum _{i=1}^N}\Vert \overrightarrow{y_i}-{\mathit{\beta }}_0-{\mathit{\beta }}^{\mathsf{T}}{\overrightarrow{z}}_i{\Vert }_F^2\hfill \\ \hfill & +\lambda ((1-\alpha )\Vert \mathit{\beta }{\Vert }_F^2/2+\alpha {\displaystyle \sum _{j=1}^P}\sqrt{{\beta }_{j1}^2+{\beta }_{j2}^2})],\hfill \end{array}$$ [2]

where $\lambda$ is the regularization penalty and $\alpha$ balances the $L_1$ and $L_2$ penalty terms. The value of $\alpha$ ranges from 0 to 1. Both $\alpha$ and $\lambda$ are tuned by cross-validation within the training data.

Once the model coefficients are fit, the model can be applied to predict $\widehat{Y}=\left[\widehat{y_{i1}},\widehat{y_{i2}}\right]$ from a new sample. This output is then transformed back into a time measurement via

$$\widehat{t_i}=\frac{24}{2\pi }(\mathrm{atan}2(\widehat{y_{i1}},\widehat{y_{i2}})mod2\pi ).$$ [3]

The absolute prediction error for sample $i$ can then be calculated as

$${ϵ}_i= min(|\widehat{t_i}-t_i|,24-|\widehat{t_i}-t_i|).$$ [4]

Validation: Cross-Study and Cross-Platform Accuracy.

To assess the performance of ratio TimeMachine and $Z$-score TimeMachine across varied datasets and platforms, we randomly selected half of the subjects from TrTe for training. We then used the remaining data from TrTe, along with the two independent datasets with melatonin data (V1 and V3), to compare algorithms’ accuracy with respect to the true melatonin phase—specifically, the time since DLMO (Fig. 1). (Here, we exclude dataset V2, as it did not include publicly accessible melatonin data; we return to it further below.)

Fig. 1.

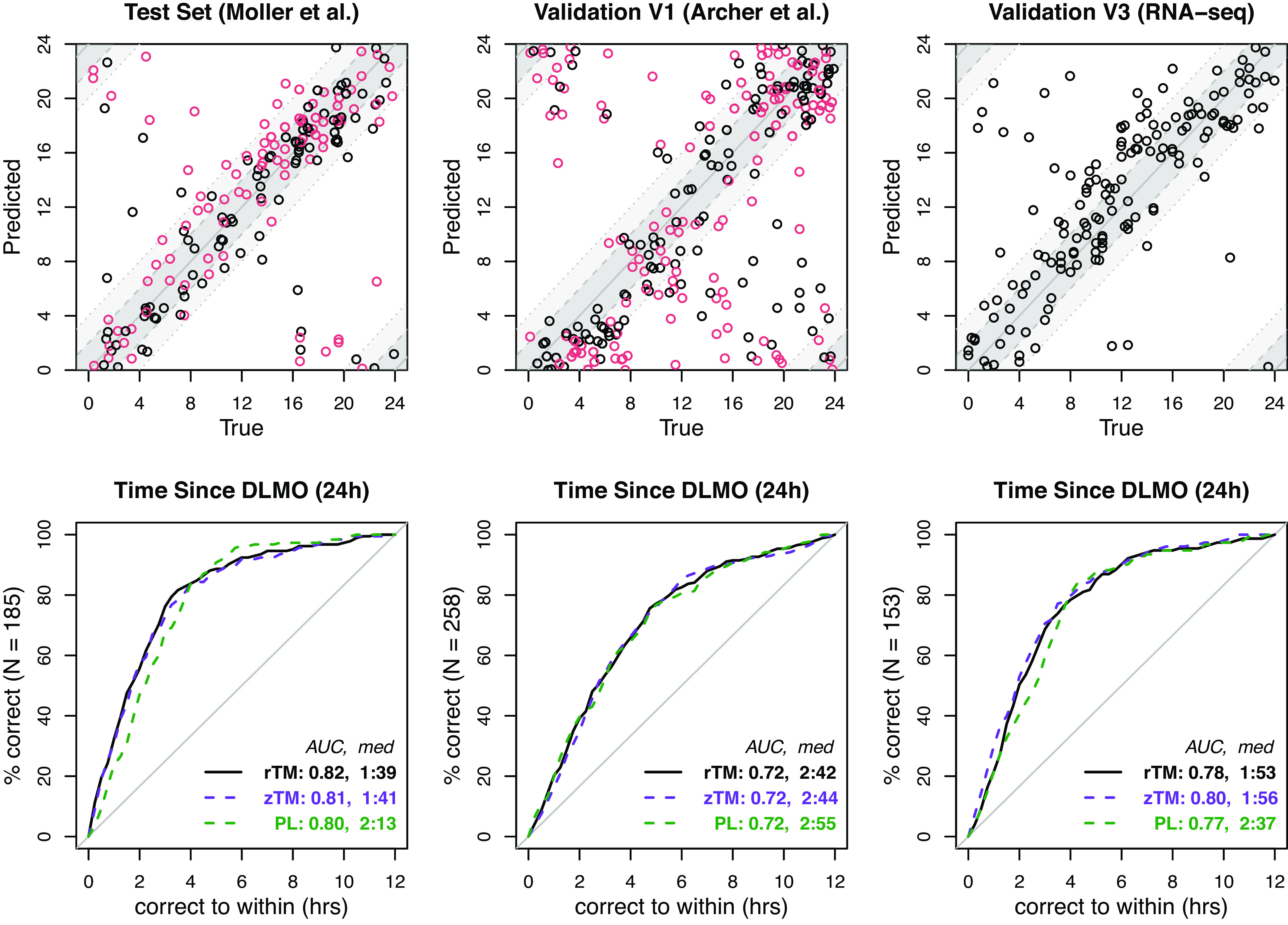
TimeMachine predictions of melatonin phase (time since DLMO) on data from three distinct studies. Both variants of the TimeMachine algorithm, ratio TimeMachine (rTM) and $Z$-score TimeMachine (zTM), were trained on a subset of subjects from the Möller et al. study (TrTe) and then applied to the remaining test subjects in Möller et al. along with two independent datasets V1 (Archer et al.) and V3 (RNA-Seq) for validation. The top row shows the agreement of predictions from ratio TimeMachine with the measured melatonin phase (time since DLMO) for each sample. Dark and light gray bands indicate an error range of $\pm$2 and $\pm$4 h. The color of the point represents experimental protocols: Black denotes control condition, and red denotes sleep restriction (Möller et al.) and forced desynchrony (Archer et al.), respectively. In the bottom row, we plot the fraction of correctly predicted samples for each study vs. prediction errors for the ratio TimeMachine algorithm (solid black), in comparison to the other variant, $Z$-score TimeMachine algorithm (dashed purple), and the single-sample PLSR algorithm (dashed green), along with the normalized area under the curves (AUC) and median absolute errors for each algorithm.

Within the training set, we used 10-fold cross-validation to tune the penalty parameter. The optimal Elastic Net penalty resulted in a ratio–TimeMachine model with 71 (out of 666) predictive features and a $Z$-score TimeMachine with all 37 (out of 37) predictive features. We then applied the trained predictor to both the held-out data from TrTe and the independent datasets without any cross-platform normalization or batch correction, yielding results shown in Fig. 1. To assess performance, we compute the median absolute error and the normalized area under the error CDF curve (AUC). Here, a predictor with an AUC of 0.5 performs no better than random chance, while a perfect predictor would have an AUC of 1.

For the unseen TrTe data, ratio TimeMachine had a median absolute error of 1:39 h, with 55.7% of predictions within $\pm$2 h and 83.8% within $\pm$4 h. Despite the study employing two sleep protocols (control versus sleep restriction), sleep restriction did not significantly affect ratio TimeMachine’s transcriptomic phase estimates ($P=0.1$; Wilcoxon rank-sum test).

We also evaluated ratio TimeMachine’s performance on two independent datasets where experimental conditions and profiling platforms differed. V1 used the same microarray platform as the training data, but had different experimental conditions. V3 not only had different experimental conditions, but also profiled samples using RNA-Seq rather than microarray. Importantly, we did not perform any batch correction or additional data manipulation beyond the sample-wise normalization described in the previous section.

In V1, ratio TimeMachine accurately predicted the melatonin phase (i.e., time since DLMO) within $\pm$2 h and $\pm$4 h in 39.5% and 65.9% of samples, respectively, yielding a median absolute error of 2:41 h. Comparison of the error distribution between the two sleep protocols in the V1 dataset suggests that predictions became less accurate when sleep misaligned with melatonin ($P=0.002$; Wilcoxon rank-sum test), corroborating findings from prior studies (10).

Using V3, we showed that ratio TimeMachine can be generalized to gene expression data across technical variability. Despite being trained on microarray data, when applied to RNA-Seq data, it yielded a median absolute error of 1:53 h. Specifically, it predicted the melatonin phase within $\pm 2$ h for 50.3% of samples and within $\pm 4$ h for 78.4%, further emphasizing TimeMachine’s consistent performance across platforms.

The $Z$-score variant of TimeMachine displayed comparable performance on the validation datasets (SI Appendix, Table S3). There was no significant difference between ratio TimeMachine and $Z$-score TimeMachine across all datasets ($P=\{0.71;0.77;0.3\}$ for dataset TrTe, V1, and V3, respectively; Wilcoxon rank-sum test). This consistency suggests both normalization methods perform equivalently for the purpose of inferring circadian phase from blood transcriptomics across platforms.

Comparison with Competing Methods.

We compared TimeMachine to the state-of-the-art machine-learning algorithm that to date provides the most accurate predictions of the circadian phase from a single blood draw. Laing et al. proposed an approach based on partial least squares regression (PLSR), which selects a set of 100 predictor genes from thousands of genes to predict the melatonin phase (10). In their work, the authors trained the PLSR model using a subset of combined samples from both Möller et al. and Archer et al., processed by batch correction and quantile normalization, and tested it on the remaining samples in the mixed datasets. With these data, the PLSR-based method outperformed both ZeitZeiger and Molecular Timetable. However, as both datasets were processed by identical microarray platforms and mixed during the training, it remained unclear whether the trained predictor is robust enough to infer circadian time using data from other high-throughput technologies. We adopted the authors’ code to train the PLSR model using the same training samples as TimeMachine, using all genes for the quantile normalization as described in ref. 10. We then applied the trained PLSR model to the independent validation datasets.

As depicted in Fig. 1, TimeMachine’s performance was as good or better than PLSR’s, which exhibited a median absolute error of 2:13 h for the unseen TrTe testing data, 2:55 h for V1, and 2:37 h for V3 (Fig. 1). While the PLSR method comes close to the performance of TimeMachine, we note that both the quantile normalization step and the PLSR step itself require many more genes (all 7,615 genes and 100 genes, respectively) than are required for TimeMachine. In the testing subset of TrTe, ratio TimeMachine significantly outperforms the PLSR predictor ($P=0.01$; Wilcoxon rank-sum test). However, its performance paralleled PLSRs in the V1 and V3 datasets ($P=\{1,0.33\}$ for V1 and V3, respectively; Wilcoxon rank-sum test). Still, TimeMachine accurately predicted the melatonin phase within $\pm 2$ h for $>$50% of the V3 samples, versus $\sim 40\%$ for PLSR (SI Appendix, Table S3). As noted above, similar accuracy was achieved by rTM and zTM. Comparison of $Z$-score TimeMachine and PLSR shows that the $Z$-score variant provided statistically better predictions than PLSR for datasets TrTe and V3, but not V1 ($P=\{0.035,0.76,0.047\}$ for TrTe, V1, and V3, respectively; Wilcoxon rank-sum test).

We further note that the performance of ratio and $Z$-score TimeMachine’s performance is only slightly worse than that of reported state-of-the-art two-timepoint methods (11, 14), with a median absolute error that is $\sim$20 min larger for the TrTe testing subset and $\sim$40 min larger for the validation sets V1 and V3.

In order to further assess TimeMachine’s generalizability, we apply it across all four distinct studies (including V2), covering two different microarray platforms and the RNA-Seq. Because melatonin data are unavailable for V2, the local time of the blood draw was used as a proxy. We justify this choice on the basis of the fact that the selection criteria for all four studies restricted participants to healthy, intermediate-chronotype individuals, for whom the circadian phase is expected to be well aligned to local time. Indeed, for the studies where both melatonin and local time data are available (TrTe, V1, and V3), it was previously demonstrated that melatonin phase is closely correlated with local time (14). Using local time gives us the opportunity to demonstrate TimeMachine’s performance with a completely distinct sleep protocol and microarray platform from the other studies.

When trained on the same samples as in Fig. 1 to predict local time, ratio TimeMachine matched PLSR’s accuracy for dataset V3 ($P=0.41$; Wilcoxon rank-sum test). However, ratio TimeMachine outperformed PLSR across the three microarray datasets with statistical significance ($P<0.001$ for TrTe, V1, and V2; Wilcoxon rank-sum test). Notably, ratio TimeMachine achieved a median absolute error that was $\sim$1 h less than that of PLSR for data sourced from microarray platforms and predicted 10 to $15\%$ more samples within the window of $\pm 2$h and $\pm 4$ h (SI Appendix, Table S3). As shown in Fig. 2, ratio TimeMachine’s predictions of local time had a median absolute error of $\sim$2.5 h in all datasets, including V2 (a dataset from a different microarray platform than TrTe and V1). In contrast, PLSR’s quantile normalized approach (labeled as PL in Fig. 2) exceeded a median absolute error of 3 h.

Fig. 2.

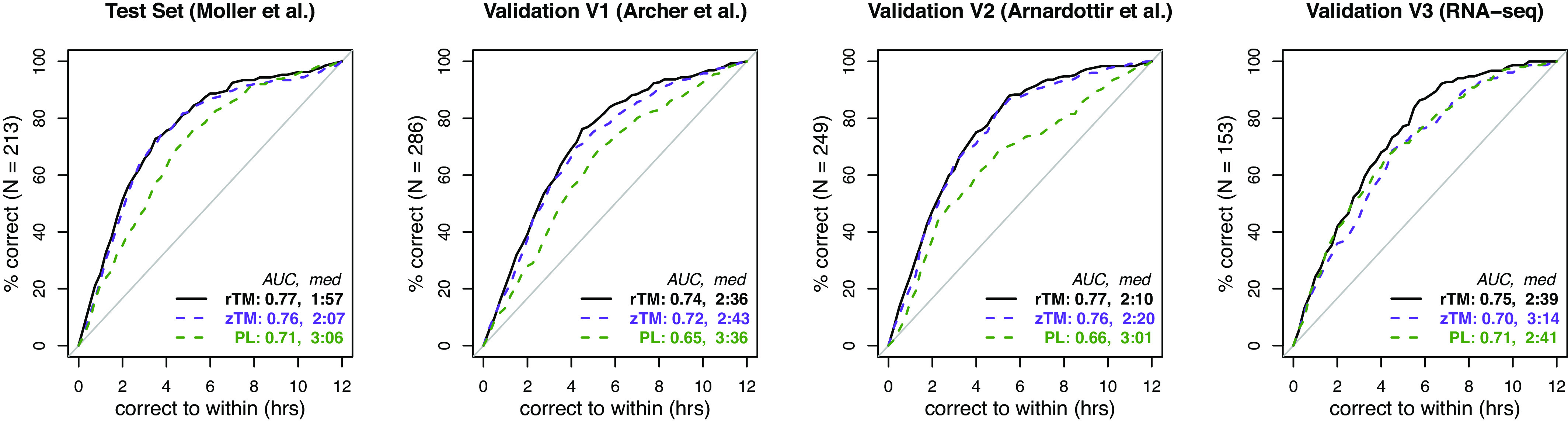
Accuracy of one-timepoint methods on predicting the blood draw-time. Instead of predicting the melatonin phase as in Fig. 1, we trained and applied ratio TimeMachine (solid black), $Z$-score TimeMachine (dashed purple), and PLSR (dashed green) to obtain time-of-day predictions on four distinct datasets.

Furthermore, ratio TimeMachine and $Z$-score TimeMachine displayed similar error distribution when forecasting the local blood-draw times across all datasets ($P=\{0.51,0.38,0.59,0.11\}$ for TrTe, V1, V2, and V3, respectively; Wilcoxon rank-sum test). Comparing $Z$-score TimeMachine with PLSR revealed that, akin to ratio TimeMachine, the $Z$-score variant generated statistically superior predictions for datasets TrTe, V1, and V2. However, the error distributions were indistinguishable for dataset V3 (P$=$ {0.005, 0.002, $<$0.001, 0.48} for TrTe, V1, V2 and V3, respectively; Wilcoxon rank-sum test). Overall, this indicates that either normalization technique—pairwise ratio or $Z$-score transformation—of the chosen 37 genes significantly enhanced prediction accuracy in predicting blood-draw timings.

Properties of TimeMachine.

Beyond demonstrating ratio TimeMachine and $Z$-score TimeMachine’s robustness across datasets, we aim to understand the factors that affect the algorithm’s performance.

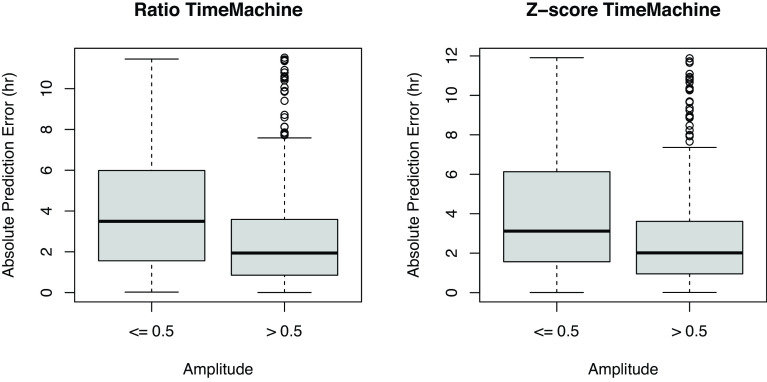
We expect that it may be harder to predict time in samples with a low amplitude of gene expression, simply due to the fact that the signal is low. In this case, we might expect that samples whose Cartesian prediction coordinates (Eq. 1) lie close to the origin will have larger errors in the time prediction (Eq. 4) than those that lie close to or beyond the unit circle. To investigate this, we calculate the “gene expression amplitude” as the magnitude of the mapping output, i.e., $\sqrt{{\widehat{y_{i1}}}^2+{\widehat{y_{i2}}}^2}$. We find the resulting amplitude of predictions can easily deviate from the unit circle when the trained predictor is applied to the validation data. We observe that a smaller prediction amplitude yields a larger prediction error, as expected. Fig. 3 shows that for ratio TimeMachine, the absolute prediction error is significantly larger when the associated output amplitude is below 0.5 ($P<0.001$; Wilcoxon rank-sum test), suggesting that the output amplitude may serve as a proxy for quantifying the confidence of predictions. While ratio TimeMachine and $Z$-score TimeMachine take in different normalized data as the input, they both utilize a bivariate regression model. Thus, ratio TimeMachine and $Z$-score TimeMachine shared the same properties, where the absolute prediction error is significantly larger when the associated output amplitude is below 0.5 ($P<0.001$; Wilcoxon rank-sum test).

Fig. 3.

Relationship between prediction accuracy and its predicted amplitude for ratio TimeMachine and $Z$-score TimeMachine. The amplitude here is defined as the magnitude of the predictor $\widehat{Y}$. Predicted amplitudes $\le$0.5 yield a significantly less accurate time prediction than higher amplitudes for both variants of TimeMachine ($P<0.001$; Wilcoxon rank-sum test).

Moreover, when we categorize samples by phase into 2-h intervals, a significant difference in amplitude over time becomes evident ($P<0.01$, Kruskal–Wallis test). Visually examining the data suggests an inverse relationship between error distributions and predicted amplitude (SI Appendix, Figs. S1 and S2); that is, as amplitude decreases, error increases. Across all time bins, a predicted amplitude below 0.5 is associated with significantly higher error ($P<0.001$). Furthermore, a lower predicted amplitude (below 0.5) is also associated with a significantly higher error even after adjusting for variation between individual subjects ($P<0.001$). These findings are consistent for both ratio TimeMachine and $Z$-score TimeMachine, suggesting that the predicted amplitude serves as a useful measure of prediction confidence, irrespective of time or individual variation.

Discussion

We have introduced a machine-learning method called TimeMachine (with two variants, ratio TimeMachine and $Z$-score TimeMachine) that can predict physiological time using the expression of 37 genes from a single blood draw. In contrast to existing methods, our approach yields results that robustly generalize across platforms and study protocols without requiring batch correction or retraining. This feature is important for two reasons. First, it makes it possible to apply TimeMachine to future samples without constraining the transcriptomic profiling platform, and potentially devise small “kits” for its application. Second, it opens the possibility of applying TimeMachine to the wealth of existing, untimed data for secondary analysis, again without constraints on the platform.

The normalization step is crucial for achieving cross-platform accuracy, suggesting that normalization and machine learning algorithms may be optimized separately for best performance. Our algorithm presents two distinct within-sample normalization techniques: $Z$-score transformation ($Z$-score TimeMachine) and pairwise ratio of gene expression (ratio TimeMachine). No significant performance difference was found between ratio TimeMachine and $Z$-score TimeMachine on different datasets. Both the pairwise ratios and $Z$-score normalization operate on the assumption that relative gene abundances—rather than their absolute magnitudes—are both biologically relevant and faithfully captured across different platforms. We believe this is a reasonable assumption for both RNA-seq and PCR, and previous studies using pairwise gene ratios suggest that microarrays also preserve relative expression differences with enough fidelity to serve as robust predictors (21–23). Our empirical results with the 37 predictor genes corroborate this assumption. However, future studies should explore the strength of this assumption, particularly for older microarrays not considered in the current study.

TimeMachine performs at least as well as the state-of-the-art PLSR method and in some cases performs significantly better. However, although the PLSR-based approach yielded performance close to TimeMachine in several of our tests, we note that as described in ref. 10 it requires quantile normalization across the complete dataset, implying the need to assay all 7,615 genes in subsequent applications (not only the 100 PLSR predictor genes). In contrast, TimeMachine relies on just 37 genes, making it a more practical choice for future usage. Our findings suggest that assaying and normalizing the full complement of genes may not be necessary for predicting circadian time. In fact, our results indicate that the selection and preprocessing steps matter as much as the ML method (TimeMachine’s ElasticNet versus PLSR; SI Appendix, Fig. S3). This is unsurprising, considering that both ElasticNet and PLSR are regularized regression techniques, and should thus achieve comparable performance. It also underscores the benefits of thoughtful feature selection prior to any machine learning algorithm.

We also note the appearance of a recently proposed algorithm (tauFisher) (24) that employs a regression model on the principal components of the pairwise gene ratios of core clock genes (BMAL1, BDP, NR1D1, NR1D2, PER1, PER2, PER3, CRY1, and CRY2) along with the top 10 rhythmic genes, following smoothing and rescaling of their expression profiles (24). This approach has been shown to predict circadian time in single-cell scRNA-seq mouse SCN and skin samples, based on training with bulk microarray and RNA-seq mouse SCN and skin data. These findings independently corroborate our observation that the pairwise gene ratio likely maintains the circadian dynamics between genes, providing predictive features for circadian time, even across different assay platforms. However, at the time of this writing, the extent to which tauFisher can be generalized to human data and across platforms or sleep conditions, remains unclear.

In addition to introducing a method for predicting circadian phase, we also investigated the factors that influence the accuracy of our predictions. We notice that low predicted amplitudes from the TimeMachine model (including both variants) are associated with a less accurate prediction of physiological time. This relationship suggests that the amplitude may be used as a rough measure of confidence in the prediction. Yet while there is some practical utility in the amplitude prediction, we must emphasize that it has no physiological interpretation, since the training data were assumed by fiat to have amplitude 1. Because only the circadian phase varied in the training data (and was the underlying prediction target), it may be of interest for future studies to consider instead a one-dimensional model using circular regression to predict time as a circular variable, rather than transforming time to a Cartesian plane as in Eqs. 1–3. In this case, the optimization would select $\beta$ coefficients that minimize angular error alone, rather than the overall distance in the 2-d plane (as in Eq. 2). However, it will still be necessary to include a regularization penalty to inhibit overfitting. Solving the optimization problem for circular penalized regression remains an interesting avenue for future work.

From a practical perspective, TimeMachine’s single-sample requirement enhances its usability and feasibility, but greater accuracy can be achieved with two-sample methods such as TimeSignature ($\sim$20 to $\sim$40 min improvement in the median absolute error). Using just one sample, TimeMachine predicted $>$50% of TrTe and V3 samples, and $\sim$40% of V1 samples within a $\pm 2$ h range. In contrast, TimeSignature, using two samples taken 12 h apart, predicted $\sim$70% of TrTe and V3 samples and $\sim$45% of V1 samples within the same time frame. Therefore, where possible, we still recommend using two blood draws, at least 8 and ideally 12 h apart (11), to assay circadian phase.

For applications requiring yet greater accuracy, we propose that TimeMachine’s performance could be used to identify the optimal sample collection window for melatonin studies, reducing the need for burdensome sampling. Until now, determining the gold-standard phase marker, DLMO, has been both costly and time-consuming, requiring hourly saliva or plasma samples for at least 6 to 8 h around the expected melatonin onset time. In cases where prior knowledge of melatonin onset is unknown, such as in people with sleep disorders, samples must be taken throughout an entire circadian cycle. TimeMachine inferences could be used to optimize this collection to a smaller window.

It is important to highlight that the selection of the 37 predictor genes is not necessarily unique. As previous studies have discussed, many genes cycle in phase, and could be equally good predictors; a different training set might yield an alternate set of predictor genes (9–11). Moreover, the circadian transcriptomics datasets used in this study (11, 15–17) only include young, healthy, intermediate-chronotype individuals. Previous studies in animal models have shown that factors such as sex, sleep disorders, shift work, and aging can lead to significant changes in gene expression rhythms (25–30), and it is likely that similar changes occur in humans as well. Such populations may benefit the most from circadian-based treatments, but temporal gene expression data from diverse human populations (such as night shift workers and various disease groups) largely remains lacking. It remains critical to collect more data to explore the performance of all time inference methods (including TimeMachine) in diverse populations. In previous work, for instance, we demonstrated that the two-draw TimeSignature method is robust to changes in healthy aging (31), but sensitive to changes during critical illness (32). We expect that TimeMachine may have similar properties that could be explored in future studies.

Related to this, we find that being out of sync with melatonin (rather than mere sleep deprivation) can lead to a greater deviation between TimeMachine’s predicted time and the actual melatonin phase. This trend parallels findings from predictions involving two-timepoint approaches (10). Research has demonstrated that being out of phase with melatonin leads to a reduction of rhythmic transcripts from $6.4\%$ to a mere $1\%$ (16), causing desynchrony between the peripheral circadian rhythm in blood transcriptome and the central circadian rhythm of melatonin.

By training the algorithm to predict melatonin phase, we use the transcriptional dynamics in blood as a proxy for rhythms in the brain. However, emerging evidence shows that peripheral clocks in other tissues may be affected by factors distinct from those influencing the central clock in the brain—for example, food and exercise for peripheral clocks as opposed to light for the central clock (33, 34). These peripheral clocks may also exhibit phase differences relative to those in the brain or blood. Therefore, additional studies are needed to draw inferences about phases in different organs, and to understand how the interplay between rhythms in the brain, blood, and other tissues impacts health outcomes.

Our study is an important step toward the use of circadian biomarkers in wide–ranging applications. While the importance of the circadian rhythm in human health has been highlighted in multiple studies, the inclusion of circadian biomarkers in medical research and clinical use has been hampered by the challenge of assaying physiological time. TimeMachine addresses this gap by providing predictions that show good agreement with in-lab DLMO data and blood draw time, along with an indicator of reliability (amplitude). TimeMachine requires only a single-timepoint gene expression profile of human peripheral blood mononuclear cells (PBMCs), making it a practical tool for real-world implementation. TimeMachine’s generalizability is a significant advantage. It enables prospective application, wherein TimeMachine is applied to new samples (e.g., for the purpose of customizing the timing of light intervention based on an individual’s circadian phase), without the need for data to be collected on a specific platform. Additionally, TimeMachine enables retrospective circadian analysis of existing data by providing a platform-free way to infer time label for existing untimed samples. By inferring these labels, secondary analyses of vast quantities of existing PBMC expression data could be mined for associations with circadian time, shedding light on the role of circadian rhythms in diseases from neurodegeneration to cancer.

Materials and Methods

Data Sources.

We analyzed published data of human whole–blood transcriptome profiles from four independent studies. Data were obtained from the NCBI Gene Expression Omnibus (GEO) repository under the following accession numbers and imported into R:

GSE39445 (training and testing [TrTe]) consists of 427 blood samples from 26 subjects in total (15). Each subject underwent two protocols in a crossover design: a sleep-restriction protocol (6 h of sleep opportunity per night) and a control protocol (10 h of sleep opportunity per night). Following the sleep opportunity, blood samples were collected every 3 h over a 27-h period under constant routine conditions. Samples were assayed using a Whole Human Genome 4$\times$44K custom Agilent microarray platform (G2514F, AMADID 026817) as described in ref. 15. We split the data subject-wise at random into training and testing subsets for the purpose of the present study.

GSE48113 (validation dataset V1) consists of 287 blood samples from 22 subjects under a forced-desynchrony protocol, where the sleep–wake cycle of all subjects was scheduled for a 28-h day (16). Each subject went through two conditions, sleeping in phase and out of phase with their melatonin rhythm. Blood samples were collected every 4 h for both conditions. Samples from V1 were assayed using the same microarray platform as the training/testing data (Aligent; G2514F, AMADID 026817) as described in ref. 16.

GSE56931 (validation dataset V2) consists of 249 samples from 14 subjects. For each subject, blood samples were collected every 4 h during a 3-d study. Samples were processed using a different microarray platform (Rosetta/Merck Human RSTA Custom Affymetrix 2.0 microarray) from the previous two, as described in ref. 17.

GSE113883 (validation dataset V3) comprises 11 subjects whose whole blood samples were collected every 2 h over a 28-h constant routine, yielding a total of 165 samples (11). In contrast to the previous three datasets, transcriptional profiling of samples from V3 was processed by RNA sequencing.

The processing of microarray and RNA-Seq data, as well as transcript alignment, has been previously carried out by the original authors (11, 15–17), and these procedures remained unaltered for our present study. In the case of microarray data, gene expression was averaged when multiple probes represented the same gene. More details of the individual datasets can be found in refs. 11 and 15, 16, 17.

Availability of Melatonin Data.

In conjunction with blood transcriptome, melatonin levels were also available for all datasets except V2. Dim–light melatonin onset (DLMO) is used in these studies the gold–standard reference marker for the human circadian phase. As in refs. 11 and 14, we also consider local time in an analysis that includes V2 (which lacks public melatonin data).

Supplementary Material

Appendix 01 (PDF)

Data, Materials, and Software Availability

Code data have been deposited in GitHub (https://github.com/pepperhuang/TimeMachine) (35). All other data are included in the manuscript and/or SI Appendix. Previously published data were used for this work (GSE39445 (36), GSE48113 (37), GSE56931 (38), and GSE113883 (39) were obtained from the NCBI Gene Expression Omnibus repository).