Significance
During collective cellular processes, cells often dynamically shape and respond to their chemical environments. Our understanding of these processes is limited by the ability to measure these chemical profiles in real time. For example, the Patlak–Keller–Segel model has widely been used to describe collective chemotaxis toward self-generated gradients in various systems, albeit without direct verification. Here, we used a biocompatible fluorescent protein sensor to directly observe attractant gradients created and chased by collectively migrating bacteria. Doing so uncovered limitations of the standard chemotaxis model at high cell densities and allowed us to establish an improved model. Our work demonstrates the potential for fluorescent protein sensors to measure the spatiotemporal dynamics of chemical environments in cellular communities.
Keywords: fluorescent sensor, collective behavior, bacterial chemotaxis, Patlak–Keller–Segel model, self-generated gradient
Abstract
Chemotactic bacteria not only navigate chemical gradients, but also shape their environments by consuming and secreting attractants. Investigating how these processes influence the dynamics of bacterial populations has been challenging because of a lack of experimental methods for measuring spatial profiles of chemoattractants in real time. Here, we use a fluorescent sensor for aspartate to directly measure bacterially generated chemoattractant gradients during collective migration. Our measurements show that the standard Patlak–Keller–Segel model for collective chemotactic bacterial migration breaks down at high cell densities. To address this, we propose modifications to the model that consider the impact of cell density on bacterial chemotaxis and attractant consumption. With these changes, the model explains our experimental data across all cell densities, offering insight into chemotactic dynamics. Our findings highlight the significance of considering cell density effects on bacterial behavior, and the potential for fluorescent metabolite sensors to shed light on the complex emergent dynamics of bacterial communities.
Motile bacteria, such as Escherichia coli, navigate complex and changing chemical signals (1) by performing a biased random walk (2): Rotating its flagella counterclockwise propels the bacterium forward, until one or more motors reverse rotation direction, causing the cell to tumble and quickly reorient. By modulating their tumbling rate based on perceived changes in chemical concentration along their swimming trajectory (3, 4), E. coli cells can climb gradients of attractants and descend gradients of repellents. This process, called chemotaxis, plays a critical role in bacterial pathogenesis (5), among numerous other phenomena.
Bacteria also actively modify their chemical environment and respond to these self-generated perturbations. For example, by consuming attractants and responding to the resulting gradients, populations of E. coli cells can migrate collectively (6–23). This process generates cell density waves such as traveling bands and rings that can migrate over large distances. In eukaryotes, such signaling molecule-induced collective cell migration events underlie cancer dynamics (24), immune system function (25), and development (26, 27), among others.
The Patlak–Keller–Segel (PKS) model (28, 29), and its extension to include growth and replication (12, 15, 18, 19, 30–33), is a standard mathematical framework for modeling chemotaxis, in particular collective migration, that has been widely used by researchers to investigate the interplay between bacterial collective behavior and chemical signaling (17, 18, 31–38). This standard chemotaxis model has proven to be a powerful tool for predicting emergent features observed in experiments, such as self-aggregation (9, 21), pattern formation (39), and collective transport (10, 21). However, the PKS model has never been directly verified, and more broadly our understanding of the intertwined dynamics of bacteria and their chemical environments is limited, due to the lack of techniques for measuring chemical concentration in real time.
Here, we present a method to directly measure aspartate (Asp) concentration with high spatial and temporal resolution, in situ, using a protein fluorescent-based sensor (40–42). With this sensor, we measure dynamic gradients generated by bacterial consumption during collective migration and test the validity of the standard PKS chemotaxis model. While the model agreed well with our data at low cell densities, it diverged at high cell densities. The inconsistencies between our experimental measurements and the PKS model can be resolved by introducing simple, biophysically motivated modifications, in which both attractant consumption and bacterial chemotaxis are suppressed at higher cell densities. We expect that fluorescent protein-based sensors like the one used here will be valuable tools for accessing the spatiotemporal dynamics of chemical profiles in a variety of cellular systems.
Results
Fluorescent Sensor Reveals Spatiotemporal Dynamics of Bacteria-Generated Gradients during Chemotaxis.
To visualize self-generated gradients during collective bacterial migration, we repurposed a fluorescent sensor [jAspSnFR3 (42)] for the attractant Asp (Fig. 1A), which some of us originally developed for use in neuronal systems (40, 41). The sensor backbone is constructed from GltI, the periplasmic component of E. coli’s ABC transporter complex for import of the amino acids glutamate and Asp. Two point mutations in the binding domain (S27A and S72P) make the sensor highly specific for Asp and insensitive to glutamate (SI Appendix, Fig. S1). This ligand-binding domain is fused to circularly permuted superfolder green fluorescent protein (GFP) to produce the fluorescent sensor. Upon binding to Asp, the sensor changes conformation, increasing its fluorescence emission intensity. We measured the calibration curve between fluorescence intensity and Asp concentration in microfluidic channels by mixing 1 μM of purified jAspSnFR3 protein with varying concentrations of Asp (Methods). These data fit an equilibrium binding model with a binding affinity of Kd = 20 ± 1 μM (Fig. 1B).
Fig. 1.

Fluorescent sensor reveals spatiotemporal dynamics of bacterially generated gradients during collective migration. (A) Bacteria (E. coli, red) respond to environmental chemical stimuli (attractant Asp, green) that they themselves influence by consumption, enabling them to migrate collectively. (B) We repurposed a fluorescent sensor that changes conformation and increases fluorescence intensity after binding to Asp. The plot shows the calibration curve from Asp concentration to sensor emission intensity. Data points are averages over an entire sweep of images along the microfluidic device. The same device was used for all Asp concentrations. Error bars are the SD of pixel intensity over the entire sweep of images. Uncertainty of is the 95% CI of the fit. Shading is 95% CI of the binding model’s predictions. (C) Time-lapse imaging of E. coli cells expressing the fluorescent protein mCherry2 (red) and the sensor (green) during collective migration in a microfluidic device (Inset). (Scale bar, 1 mm.) Inset: The microfluidic device consists of a long linear channel of length 20 mm, width 1.2 mm, and depth 100 µm, with two holes punched at the ends for filling in liquid medium (small hole) and inoculating bacteria (big hole).
Using the same microfluidic device and media as in the sensor calibration experiments, we generated collectively migrating waves of red fluorescent protein (RFP)-labeled E. coli (Methods). Using 1 μM of sensor and 100 μM Asp ensured that the concentration of Asp in the wave was well within the range of sensitivity of the sensor and limited any potential effects of the sensor sequestering Asp from the bacteria. With this experimental setup, we used time-lapse imaging to simultaneously measure the spatial density of bacteria and the dynamic profile of Asp (Fig. 1C and Methods). From the typical wave speeds, gradient length scales, and image exposure times, we expect minimal blurring or other imaging artifacts (Methods). By separately measuring RFP fluorescence intensity for several known densities of bacteria, we interpolated the absolute density of bacteria in the traveling waves, in units of optical density (OD) at 600 nm. Thus, we directly measured both the concentrations of bacteria and attractant with high spatial resolution and in real time.
The Standard Model for Collective Chemotactic Migration Describes the Bacterial Wave at Low Cell Density but Breaks Down at High Cell Density.
Numerous theoretical and experimental studies have used variations of the classic PKS model to describe collective chemotactic migration (28, 29). This model consists of two coupled partial differential equations (PDEs) that describe the dynamics of Asp concentration and bacterial density . The Asp dynamics include diffusion and consumption by the bacteria:
| [1] |
where is the diffusion coefficient of Asp in water (17, 18, 43–45), is the maximum consumption rate, and is the Asp concentration at which bacteria consume Asp at half-maximal rate (17, 18, 46). The bacterial dynamics include cell diffusion, chemotaxis, and growth:
| [2] |
Here, is the cells’ perceived signal, where (47–49) and are the receptor-ligand dissociation constants when receptors are in the inactive and active states, respectively (50). and are the diffusion and chemotaxis coefficients of the bacteria, and is the growth rate, which we measured to be under our experimental conditions (Methods). Eqs. 1 and 2 are supplied with a complicated initial condition near , the inoculation site, and boundary conditions at : , as and , as , where is the initial concentration of attractant in the channel.
With the ability to directly measure both bacterial density and in situ Asp concentration, we could assess the PKS model of collective bacterial migration. During collective migration along the linear channel in our device, the profiles of both the bacterial density and Asp concentration reached a quasi-steady state. That is, the profiles essentially stopped changing in the frame of reference moving with the bacterial wave, defined by , where is the speed of the traveling wave, and is defined as the peak of bacterial density. Converting Eqs. 1 and 2 to the co-moving frame and rearranging terms so that all unknown parameters are on the right-hand side (RHS), we arrive at:
| [3] |
| [4] |
In the moving reference frame, the boundary conditions become , as and , as . The consumption parameters and , although measured before under other conditions (17, 18), can vary with bacterial strain, growth media, temperature, experimental media, etc., as can and . Therefore, to test the ability of this model to quantitatively capture our data, we fit these unknown model parameters by computing the left-hand side (LHS) of Eqs. 3 and 4 from the data and then minimizing the sum of squared deviations with the RHS (Methods).
These PDEs fit the data well for low cell density bacterial waves (peak cell density ) with , and 300 ± 230 μM2/s(Fig. 2 A–C). The fit values are in reasonable ranges, compared to the literature (17, 18, 51–53). However, the model predictions with the same parameters values clearly deviated from the data in high cell density waves (peak cell density ) (Fig. 2 D–F). For model predictions on intermediate-density waves, see SI Appendix, Fig. S2. Quality of the fit was assessed using the mean squared error (MSE) between the left and RHSs of each equation (see SI Appendix for details); values closer to 0 indicate better fits. We arrive at the same conclusion if we fit the high cell density data first and then predict the low cell density data (SI Appendix). Our findings reveal that the standard model for chemotaxis fails to accurately describe the behavior of high-density bacterial populations.
Fig. 2.
The standard model for chemotaxis, the PKS model, describes the bacterial wave at low cell density but breaks down at high density. (A) The quasi-steady state profiles in the co-moving frame, of bacteria density (red) and attractant Asp concentration (green), during low cell density migration . (B) Fitting the Asp dynamics of the PKS model to experimental data (above).( and ) are the Asp concentration and the bacteria density, respectively, is the wave speed, is the molecular diffusion of Asp, is the maximum consumption rate, is the half-max of the consumption rate, and is the coordinate in the co-moving frame ( is defined as the peak of bacterial density). Green: LHS of the Asp dynamics equation with and measured and (17, 18, 43–45). Throughout, uncertainty of is the SEM. Magenta: RHS of the Asp dynamics equation with measured, and and fit to match the LHS. The MSE between the LHS and RHS at the best-fit parameters is shown on each panel (see SI Appendix for details). (C) Fitting the bacteria dynamics of the PKS model to experimental data (above). is the cells’ perceived signal [ and (47–49)], is the effective bacterial diffusivity, is the chemotactic coefficient, and is the measured growth rate (Methods). Red: LHS of the bacteria dynamics equation with , , and measured. Cyan: RHS of the bacterial dynamics equation with and fit to match the LHS. (D–F) is the same as (A–C) for a high cell density wave. (E and F) magenta and cyan lines are predicted using the same parameter values for , , , as in (B and C). Here, . The shading represents the SD across replicates. replicates for (A–C) and for (D–F). Uncertainties for the RHS of each equation are not shown for clarity but were included in the calculation of the MSE (SI Appendix).
Attractant Dynamics Are Consistent with Cell Density-Dependent Consumption Rate.
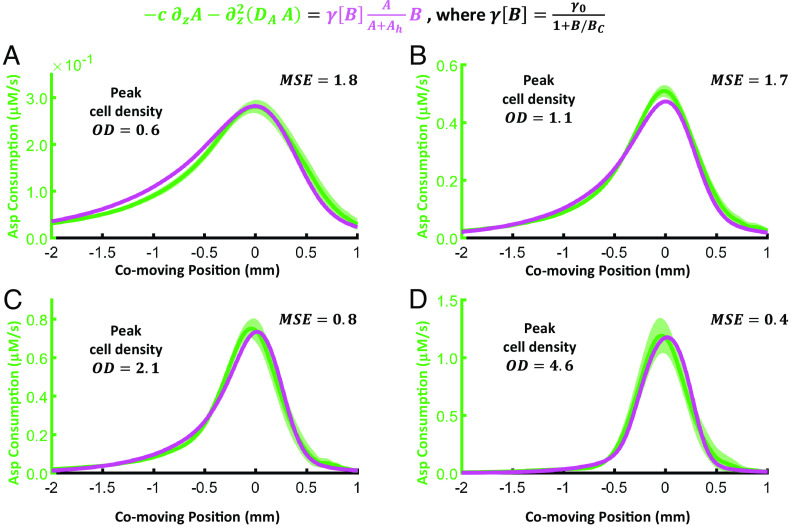
At high cell densities, the model fails to describe both Asp and bacterial dynamics. The predictions of Asp dynamics break down because they overestimate the rate at which bacteria consume the attractant near , where cell density is highest (Fig. 2E). This disagreement gets worse as bacterial density increases (SI Appendix, Fig. S2 H and K). Therefore, we propose the following phenomenological correction to the maximum consumption rate, in which the bacteria consume Asp more slowly at higher local cell density:
| [5] |
Introducing this modification into Eq. 3, we find that for the parameter values , , and , the RHS is in reasonable agreement with the LHS of Eq. 3, for the entire range of wave cell densities observed (Fig. 3). The fit values for and are also reasonable compared to the literature (17, 18). Eq. 3 only depends on the bacterial dynamics through the measured bacterial density ; therefore, we were able to perform this fit independently of the parameters and , which we consider in the following section.
Fig. 3.
Asp dynamics are consistent with cell density–dependent consumption rate. Top: modified Asp consumption rate. Green: Asp consumption rate (LHS) calculated from the data. Magenta: Asp consumption rate (RHS) with parameters , and fit to match the LHS. The MSE between the LHS and RHS at the best-fit parameters is shown on each panel (see SI Appendix for details). These are shown for waves with peak bacterial cell density of (A), (B), (C), and (D). The parameters were fit to all data simultaneously. The shading represents the SD across replicates: for (A), for (B), for (C), and for (D). Uncertainties for the RHS of each equation are not shown for clarity but were included in the calculation of the MSE (SI Appendix).
One plausible mechanism for a cell density-dependent consumption rate of Asp is spatial variations in the concentration of dissolved oxygen, which is required by E. coli to consume Asp (17) (see also refs. 54 and 55). Oxygen is consumed by E. coli (6, 17), but it can be replenished by permeation through the PDMS (polydimethylsiloxane) chip (56). In microfluidic devices where the channel depth is much smaller than the width of the traveling wave, these two effects can balance out such that the local drop in oxygen concentration is directly proportional to the local cell density (see SI Appendix for derivation). Indeed, in a similar microfluidic system, oxygen levels in traveling waves of bacteria were shown to be lower in regions of higher cell density (17).
The Shape of the Attractant Gradient Reveals a Reduction of the Chemotactic Coefficient at High Cell Density.
The standard PKS model prediction for the flux of bacteria also deviates from our observations in waves with high cell density. Like the Asp consumption dynamics, this disagreement between theory and experiment increases with cell density. The deviation is most notable behind (Fig. 2F), i.e., the region behind the peak of cell density, where the bacterial flux is dominated by chemotaxis (29, 32). Therefore, we inspected the profile of perceived signal , whose gradient drives chemotactic waves. As the maximum cell density in the wave increased (Fig. 4A), the perceived signal exhibited regions with two different slopes: a steeper slope near the peak of cell density and a shallower slope behind it (Fig. 4B). These two regions were even more apparent when we plotted the gradient of perceived signal (Fig. 4C), which showed a distinct peak close to the peak of cell density that increased with maximum cell density.
Fig. 4.
The gradient of the measured perceived signal cannot be explained by the standard model for chemotaxis. (A) Cell density profile for four waves with increasing peak cell density: (purple, ), (cyan, ), (green, ), and (red, ). Shade is SD across replicates. (B) Corresponding perceived signal exhibits a sudden change of slope at the back of the wave that becomes more prominent with higher cell density. Inset: Simulations of the PKS model using the proposed cell density-dependent Asp consumption rate but a constant chemotactic coefficient show no sharp change in the slope of the perceived signal. Simulations with (full line) and without (dashed line) the contribution of phenotypic diversity. (C) Corresponding gradient of the perceived signal shows a distinct peak that becomes more prominent for high-cell-density waves. Inset: plots from the PKS simulations as in (B) show that PKS equations cannot explain this feature even with the effects of phenotypic diversity (17) included.
This drastic change in the slope of the attractant gradient arguably provides the clearest evidence for a breakdown of the standard PKS model. The speed of the wave is set by how fast the cells deplete the attractant (29). Then, to travel at that speed, the local gradient steepness must be related to the chemotactic coefficient of the traveling cells according to (29, 32, 33). The two slopes indicated that the bacteria dynamics cannot be explained by a single value of the chemotactic coefficient. Simulations confirmed that two distinct slopes do not emerge in the PKS model, even after including our modification to the Asp consumption rate in Eq. 5 (Fig. 4 B and C, Insets).
Phenotypic diversity is known to cause individual cells to have different chemotactic coefficients (57, 58). Since the gradient is shallow at the front of the wave and steeper towards the back, high-performing phenotypes (high- cells) localize to the front, and low-performing phenotypes localize further back, equalizing migration speed throughout the wave (17, 59). This arrangement is stable to perturbations in the region where the perceived gradient monotonically increases with position from front to back: When a cell moves away from its stable point in the wave, the steeper gradient behind that point makes the cell speed up, while the shallower gradient ahead makes it slow down, returning the cell to the stable point in both cases.
However, this arrangement cannot explain why cells are still able to travel together in the region of the wave where the gradient is decreasing toward the back, which becomes pronounced in the high cell density case. In this region, the cells’ chemotactic coefficients must increase instead of decrease toward the back, which should not be stable according to the logic described above. Simulations of the PKS model with and without phenotypic diversity confirmed that spatial sorting alone could not explain the emergence of a peak in the signal gradient at high cell density (Fig. 4 B and C, Insets). Therefore, there must be another, unknown mechanism that maintains the stability of an arrangement in which some cells with high are located behind cells with low , particularly in waves with high cell density.
Stability requires that this mechanism be a local, dynamic effect on top of cells’ intrinsic chemotactic coefficients, . In particular, we propose a phenomenological model in which cells’ chemotactic coefficients are reduced in regions of high cell density:
| [6] |
In this model, can vary among cells, but it is divided by a cell density-dependent factor. When a cell in the high-density region falls behind, although the gradient gets shallower, its dynamic increases according to Eq. 6, and the net effect is to return the cell to the high-density region. Fitting the RHS to the LHS of Eq. 4 using this correction showed good agreement with the data for all cell densities observed (Fig. 5), with parameter values , , and .
Fig. 5.
Bacterial dynamics are consistent with a reduction of the chemotactic coefficient when cell density becomes large. Top: modified chemotactic coefficient. Red: rate of change of cell density (minus growth) (LHS) calculated from the data. Cyan: spatial derivative (divergence) of the flux of cell density (RHS) with parameters , , fit to match the LHS. The MSE between the LHS and RHS at the best-fit parameters is shown on each panel (see SI Appendix for details). These are shown for waves with peak bacterial cell densities of (A), (B), (C), and (D). The parameters were fit to all data simultaneously. Uncertainties for the RHS of each equation are not shown for clarity but were included in the calculation of the MSE (SI Appendix).
We note that chemotaxis to oxygen can also affect group migration of E. coli (6). However, chemotaxis to oxygen would produce the opposite of the observed effect: An oxygen gradient would point forward at the front and backward at the back, since the local drop in oxygen is proportional to the local cell density (SI Appendix). With an additional chemotactic signal like this, coherent migration would require that the Asp gradient be shallower at the front and steeper at the back, contrary to our experimental observations. Thus, chemotaxis to oxygen gradients cannot explain the shape of the measured gradient.
Reduction of the chemotactic coefficient with increasing cell density has been reported before in experiments measuring the drift velocity of individual cells in a fixed gradient of the non-metabolizable attractant methyl-Asp (60). In the theory of that paper, has almost the same form as Eq. 6, except with an additional, higher-order term in the denominator. The cell density at which this effect becomes significant in our data is similar to the value reported there. When we fit the full functional form, we found that the coefficient multiplying the quadratic term was near zero; therefore, we did not include that term. Comparing agent-based simulations to experiments, those authors found that hydrodynamic interactions among cells increased their effective rotational diffusion at high cell densities, thus impairing their ability to bias their swimming direction in response to chemical signals. Here, we find that this cell density–dependent reduction in the chemotactic coefficient steepens the attractant gradient in the region where cell density is highest, compensating for the reduction in chemotactic coefficient there.
Discussion
By repurposing a fluorescent sensor for the amino acid Asp, here we have directly measured dynamic chemoattractant gradients generated by bacterial cells, with high spatial and temporal resolution. Using these measurements, we tested a classic and extensively used model of collective chemotactic migration, the PKS model (28, 29), extended to include growth (12, 15, 18, 19, 30–33). We found that while the standard PKS model provides a satisfactory description of traveling waves at low cell density, it fails to explain experimental observations at high cell densities. Specifically, Asp consumption is lower than predicted at high densities, and the perceived signal behind the peak of the wave exhibits two increasingly distinct slopes. We find that phenomenological extensions to the PKS model, in which Asp consumption and chemotaxis performance decrease with increasing cell density, explain the data over a wide range of cell densities. Our findings imply that the impacts of cell density on bacterial collective behavior are profound, even when the cell volume fraction is small (<1%). In even more crowded systems, direct cell–cell collisions are expected to further suppress chemotaxis performance (61). Although we “manually” chose functional forms for the modifications to the Asp consumption rate and the chemotaxis coefficient, in principle one could try to learn these corrections, and the entire PDEs, directly from data (62).
Our understanding of many cell-biological processes, such as wound healing (63, 64), development (65), and biofilm formation (66–69), is likely limited by the difficulties of measuring the spatiotemporal dynamics of chemical concentrations experienced by and shaped by cells. Julius Adler performed the first measurements of cell density and attractant concentrations in traveling waves of bacteria (6), but they were limited to a spatial resolution of a centimeter and temporal resolution of an hour. Here by contrast, we measured the dynamics of Asp concentration with micron and minute resolution, with the latter limited by the time needed to take sweeps of images over a large field of view. Common approaches typically involve fixation (70, 71), which can provide spatial structure and snapshots, but with limited dynamic information—and frequent damage to the processes under study. Other alternatives include invasive probes (72) or small molecule dyes that are toxic to cells but can be encapsulated in lipids (73, 74). Biocompatible, protein-based fluorescent sensors like the one used here provide a powerful method for addressing these difficulties.
Methods
Microfluidic Device Design and Fabrication.
Microfluidic devices were constructed from the biocompatible and oxygen-permeable silicone polymer PDMS on coverslips following standard soft lithography protocols. The master mold for the device is a silicon wafer featuring a long linear channel of width 1.2 mm, length 2 cm, and height 100 µm, created using ultraviolet (UV) photoresist lithography with SU-8 negative resist (SU8 3010, Microchem). The resists were then cured using UV light exposure through photomasks designed in CAD software and printed by CAD/Art Services, Inc. (Bandon, Oregon), again following photoresist manufacturer specifications. Subsequently, the wafer was baked, and the uncured photoresist was dissolved. After curing the SU-8 coat, the features were baked further, and after completion, a protective coat of silane was applied by vapor deposition.
To cast the device, the wafer was coated with a 5-mm layer of degassed 10:1 PDMS-to-curing agent (Sylgard 184, Dow Corning). The layer was baked overnight at 70 °C and allowed to cool. Then, the devices were cut out, and holes of diameter size 2 mm and 0.25 mm were punched at the two ends of the long linear channel, making external connections with the channel from the outside. The PDMS devices were cleaned with transparent adhesive tape (Magic Tape, Scotch) followed by rinsing with (in order) isopropanol, methanol, and Millipore filtered water, air-drying between each rinse. The glass was rinsed the same way, with acetone, isopropanol, methanol, and Millipore-filtered water. The PDMS was tape-cleaned an additional time, and then the devices and 24 mm 50 mm glass coverslips (#1.5) were placed in a plasma treatment oven (Harrick Plasma) under vacuum for 60 s. The PDMS was then laminated to the coverslip and baked on a hotplate at 80°C for 15 mins to establish a covalent bond. Devices were stored at room temperature and used within 12 h.
Protein Purification.
The Asp sensor used here, jAspSnFR3 (42), is a precursor of iGluSnFR3 (75), with additional mutations to the binding pocket, S27A and S72P. Plasmids carrying the sensor were transformed into E. coli BL21(DE3) cells (lacking pLysS). Protein expression was induced by growth in liquid auto-induction medium supplemented with 100 μg/mL ampicillin at 30 °C (76). Proteins were purified by immobilized Ni-NTA affinity chromatography (77) in 0.1 M sodium phosphate buffer containing 1 M NaCl, pH 7.4. The sensor protein was eluted with a 120-mL gradient from 0 to 200 mM imidazole. Final concentrations of sensor were typically ~100 µM.
Strains, Growth Conditions, and Sample Preparation.
The bacterial strain used in this study is HE205 (18), a motile variant of E. coli K-12 strain NCM3722 whose physiology has been well-characterized (78–84). HE205 was transformed with plasmid pZA31 carrying genes for the RFP mCherry2 (85) and chloramphenicol antibiotic resistance, both under the constitutive promoter pTet. We grew cells in MOPS glycerol medium, made from 100 mL/L 10× MOPS N-C-, with additional components added in the following order to avoid precipitation of salts: 83.7 g/L MOPS adjusted to pH 7.0 with KOH, 7.12 g/L tricine adjusted to pH 7.0 with KOH, 0.0278 g/L FeSO4 7H2O, 0.481 g/L K2SO4, 0.000555 g/L CaCl2, 1.06 g/L MgCl2·6H2O, 29.1 g/L NaCl, 0.230 g/L K2PO4, 20 mM NH4Cl, and 4 mL/L glycerol, and then sterile filtered. The medium used in the traveling wave experiments is the same as the growth medium but with Asp added to a final concentration of 100 μM and jAspSnFR3 added to a final concentration 1 μM.
Cells first grew overnight, then were diluted 100× and regrown until mid-exponential phase . After that, cells were washed twice in the growth medium and resuspended in the experimental medium at cell densities (OD600) of 0.1, 0.3, 3.0, and 6.0 to generate waves of different cell densities. After filling the microfluidic device with 8 μL of experimental medium from the smaller hole, that hole was sealed with a piece of transparent adhesive tape (Magic Tape, Scotch) to prevent flow during the experiment caused by differences in hydrostatic pressure across the device. Cells were then inoculated in the larger hole, and a drop of mineral oil was also added to prevent evaporation.
Imaging Procedure.
Migrating waves were imaged on an inverted microscope (Nikon Eclipse Ti-E) equipped with a custom environmental chamber (50% humidity and 30 °C). A custom MATLAB script was used to control the microscope and its automated stage (Prior) via the MicroManager interface (86). Time-lapse images (fluorescence: RFP and GFP) of the bacteria and the Asp sensor were acquired using a Hamamatsu ORCA-Flash4.0 V2 camera (2,048 × 2,048 array of 6.5 μm × 6.5 μm pixels), a 10× objective (Nikon CFI Plan Fluor, N.A. 0.30, W.D. 16.0 mm), and an LED illuminator (Lumencor SOLA light engine, Beaverton, OR). Starting at the origin (closed beginning of the long linear channel) with a specified color channel, the motorized stage moved along the channel and paused every the width of one frame to take fluorescence images (exposure time 122 ms for both channels). All images in the mCherry2 (RFP) channel were taken first, followed by images in the jAspSnFR3 (GFP) channel. Image sweeps were taken every 5 min.
We expect that the errors in our estimates of the gradient steepness are small. All errors should be largest in experiments where the waves travel fastest and the gradients are steepest, so we focus on the high-cell density case for all calculations that follow. The fastest waves travel at ~8 . At its steepest point (at in Fig. 4B), the gradient of perceived signal is roughly linear in : , with and (Fig. 4C). First, we estimate the effects of blurring in a single image due to finite image exposure times. With the exposure time of 0.2 s used here, the wave moves in the time it takes to capture one image. In this time, the relative change in perceived signal at the steepest point is , or 0.016%. This small change indicates that there is very little blurring in any single image. Another potential source of blurring is due to taking multiple images of the wave in one image sweep, which are then stitched them together. The time between consecutive images in a sweep is about 0.5 s. Furthermore, we take images with 2/3 overlap, so one field of view is recorded in 3 images, and therefore any given point in the wave is included in at most 3 images, which takes about 1.5 s. By the same analysis above, the wave moves about during this time, and the maximum relative change in perceived signal is , or 1.2%.
Image Analysis.
Raw RFP and GFP images from each sweep were first stitched together into “frames.” Then, each frame was normalized by the first GFP frame, which was taken before the cells entered the channel, to eliminate the effects of variations in the height of the channel on fluorescence intensity. The normalized frames were then rotated so that the channel was aligned with the horizontal axis, and pixels outside of the channel were cropped out. Finally, the fluorescence intensity inside the channel was averaged over the width the channel, i.e., the direction perpendicular to the direction of motion of the wave. Spatial derivatives were computed by approximating the measured profiles with smoothing spline functions using the MATLAB function fit with the “smoothingspline” option and computing the derivative of the splines. Asp concentration profiles and cell density profiles were averaged over replicates with similar peak cell density. Models were fit to data from all cell density conditions simultaneously by minimizing the sum of squared deviations between the data and the model, using the MATLAB function lsqnonlin, specifically in the 3 mm region around the cell density peak. Details of the error analysis and calculation of the MSE are provided in SI Appendix.
Growth Rate Measurement.
Cells were grown overnight in the experimental medium (without Asp), then diluted and grown to OD 0.25, as above [Asp has a small effect on the growth rate in this medium (18)]. Then, cells were inoculated in the microfluidic device, as above. The device with cells was loaded onto the microscope with the environmental chamber and imaged by taking sweeps of the RFP channel every 5 min for 6 h. Images were analyzed as above to extract the average RFP intensity, which was converted to OD. The growth rate was estimated by fitting a line to the logarithm of OD versus time during exponential growth.
Simulation.
Simulations were performed using the same custom MATLAB code reported recently (33), with the Asp consumption rate modified as in Eq. 5.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
We thank Thomas Lamot for extensive help setting up the experimental assay. We also thank Jeremy Moore, Keita Kamino, Jyot Antani, and Truong H. Cai for helpful discussions. This work was supported by NIH awards R01GM138533 (T.E.) and F32GM131583 (H.H.M.).
Author contributions
T.V.P., H.H.M., and T.E. designed research; T.V.P., H.H.M., and L.V. performed research; J.S.M. and L.L.L. contributed new reagents/analytic tools; T.V.P., H.H.M., and T.E. analyzed data; H.H.M. performed simulations; L.L.L. edited final manuscript; T.E. supervised the research; and T.V.P., H.H.M., and T.E. wrote the paper.
Competing interests
The authors have patent filings to disclose, US20190376964A1.
Footnotes
This article is a PNAS Direct Submission.
Data, Materials, and Software Availability
Simulation code is available at https://github.com/emonetlab/ks (87). Experimental data is available at https://doi.org/10.5061/dryad.37pvmcvqx (88). The jAspSnFR3 sensor is available on the public repository addgene at https://www.addgene.org/203458/ (89) or upon request from Jonathan Marvin.
Supporting Information
References
- 1.Sourjik V., Wingreen N. S., Responding to chemical gradients: Bacterial chemotaxis. Curr. Opin. Cell Biol. 24, 262–268 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Berg H. C., E. coli in Motion (Biological and medical physics series, Springer, New York, 2004), vol. 1, p. 133. [Google Scholar]
- 3.Segall J. E., Block S. M., Berg H. C., Temporal comparisons in bacterial chemotaxis. Proc. Natl. Acad. Sci. U.S.A. 83, 8987–8991 (1986). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Parkinson J. S., Hazelbauer G. L., Falke J. J., Signaling and sensory adaptation in Escherichia coli chemoreceptors: 2015 update. Trends Microbiol. 23, 257–266 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zhou B., Szymanski C. M., Baylink A., Bacterial chemotaxis in human diseases. Trends Microbiol. 31, 453–467 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Adler J., Chemotaxis in bacteria. Science 153, 708–716 (1966). [DOI] [PubMed] [Google Scholar]
- 7.Holz M., Chen S. H., Quasi-elastic light scattering from migrating chemotactic bands of Escherichia coli. Biophys. J. 23, 15–31 (1978). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wolfe A. J., Berg H. C., Migration of bacteria in semisolid agar. Proc. Natl. Acad. Sci. U.S.A. 86, 6973–6977 (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Park S., et al. , Influence of topology on bacterial social interaction. Proc. Natl. Acad. Sci. U.S.A. 100, 13910–13915 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lambert G., Liao D., Austin R. H., Collective escape of chemotactic swimmers through microscopic ratchets. Phys. Rev. Lett. 104, 168102 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Saragosti J., et al. , Directional persistence of chemotactic bacteria in a traveling concentration wave. Proc. Natl. Acad. Sci. U.S.A. 108, 16235–16240 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Koster D. A., Mayo A., Bren A., Alon U., Surface growth of a motile bacterial population resembles growth in a chemostat. J. Mol. Biol. 424, 180–191 (2012). [DOI] [PubMed] [Google Scholar]
- 13.Emako C., Gayrard C., Buguin A., de Almeida L. N., Vauchelet N., Traveling pulses for a two-species chemotaxis model. PLOS Comput. Biol. 12, e1004843 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ni B., et al. , Evolutionary remodeling of bacterial motility checkpoint control. Cell Rep. 18, 866–877 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fraebel D. T., et al. , Environment determines evolutionary trajectory in a constrained phenotypic space. Elife 6, e24669 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Morris R. J., et al. , Bacterial population solitary waves can defeat rings of funnels. New J. Phys. 19, 035002 (2017). [Google Scholar]
- 17.Fu X., et al. , Spatial self-organization resolves conflicts between individuality and collective migration. Nat. Commun. 9, 2177 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Cremer J., et al. , Chemotaxis as a navigation strategy to boost range expansion. Nature 575, 658–663 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Liu W., Cremer J., Li D., Hwa T., Liu C., An evolutionarily stable strategy to colonize spatially extended habitats. Nature 575, 664–668 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gude S., et al. , Bacterial coexistence driven by motility and spatial competition. Nature 578, 588–592 (2020). [DOI] [PubMed] [Google Scholar]
- 21.Phan T. V., et al. , Bacterial route finding and collective escape in mazes and fractals. Phys. Rev. X 10, 031017 (2020). [Google Scholar]
- 22.Bhattacharjee T., Amchin D. B., Ott J. A., Kratz F., Datta S. S., Chemotactic migration of bacteria in porous media. Biophys. J. 120, 3483–3497 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bhattacharjee T., Amchin D. B., Alert R., Ott J. A., Datta S. S., Chemotactic smoothing of collective migration. Elife 11, e71226 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Roussos E. T., Condeelis J. S., Patsialou A., Chemotaxis in cancer. Nat. Rev. Cancer 11, 573–587 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Oppenheim J. J., Yang D., Alarmins: Chemotactic activators of immune responses. Curr. Opin. Immunol. 17, 359–365 (2005). [DOI] [PubMed] [Google Scholar]
- 26.Shellard A., Mayor R., Chemotaxis during neural crest migration. Semin. Cell Dev. Biol. 55, 111–118 (2016). [DOI] [PubMed] [Google Scholar]
- 27.Mayor R., Etienne-Manneville S., The front and rear of collective cell migration. Nat. Rev. Mol. Cell Biol. 17, 97–109 (2016). [DOI] [PubMed] [Google Scholar]
- 28.Patlak C. S., Random walk with persistence and external bias. Bull. Math. Biophys. 15, 311–338 (1953). [Google Scholar]
- 29.Keller E. F., Segel L. A., Traveling bands of chemotactic bacteria: A theoretical analysis. J. Theor. Biol. 30, 235–248 (1971). [DOI] [PubMed] [Google Scholar]
- 30.Lapidus I. R., Schiller R., A model for traveling bands of chemotactic bacteria. Biophys. J. 22, 1–13 (1978). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lauffenburger D., Kennedy C. R., Aris R., Traveling bands of chemotactic bacteria in the context of population growth. Bull. Math. Biol. 46, 19–40 (1984). [Google Scholar]
- 32.Narla A. V., Cremer J., Hwa T., A traveling-wave solution for bacterial chemotaxis with growth. Proc. Natl. Acad. Sci. U.S.A. 118, e2105138118 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mattingly H. H., Emonet T., Collective behavior and nongenetic inheritance allow bacterial populations to adapt to changing environments. Proc. Natl. Acad. Sci. U.S.A. 119, e2117377119 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Scribner T. L., Segel L. A., Rogers E. H., A numerical study of the formation and propagation of traveling bands of chemotactic bacteria. J. Theor. Biol. 46, 189–219 (1974). [DOI] [PubMed] [Google Scholar]
- 35.Novick-Cohen A., Segel L. A., A gradually slowing travelling band of chemotactic bacteria. J. Math. Biol. 19, 125–132 (1984). [DOI] [PubMed] [Google Scholar]
- 36.Horstmann D., From 1970 until present: The Keller-Segel model in chemotaxis and its consequences (2003). https://www.semanticscholar.org/paper/From-1970-until-present%3A-the-Keller-Segel-model-in-Horstmann/332f8dd39b966aedc849956161ef644a11efa0e3.
- 37.Wang Z. A., Mathematics of traveling waves in chemotaxis (Review paper). DCDS-B 18, 601–641 (2012). [Google Scholar]
- 38.Seyrich M., Palugniok A., Stark H., Traveling concentration pulses of bacteria in a generalized Keller-Segel model. New J. Phys. 21, 103001 (2019). [Google Scholar]
- 39.Brenner M. P., Levitov L. S., Budrene E. O., Physical mechanisms for chemotactic pattern formation by bacteria. Biophys. J. 74, 1677–1693 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Marvin J. S., et al. , An optimized fluorescent probe for visualizing glutamate neurotransmission. Nat. Methods 10, 162–170 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Marvin J. S., et al. , Stability, affinity, and chromatic variants of the glutamate sensor iGluSnFR. Nat. Methods 15, 936–939 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Davidsen K., Marvin J. S., Aggarwal A., Brown T. A., Sullivan L. B., An engineered biosensor enables dynamic aspartate measurements in living cells. Elife 12, RP90024 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hazel J. R., Sidell B. D., A method for the determination of diffusion coefficients for small molecules in aqueous solution. Anal. Biochem. 166, 335–341 (1987). [DOI] [PubMed] [Google Scholar]
- 44.Ribeiro A. C. F., Barros M. C. F., Verissimo L. M. P., Lobo V. M. M., Valente A. J. M., Binary diffusion coefficients for aqueous solutions of l-aspartic acid and its respective monosodium salt. J. Solution Chem. 43, 83–92 (2014). [Google Scholar]
- 45.Cremer J., et al. , Effect of flow and peristaltic mixing on bacterial growth in a gut-like channel. Proc. Natl. Acad. Sci. U.S.A. 113, 11414–11419 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Monod J., Wyman J., Changeux J. P., On the nature of allosteric transitions: A plausible model. J. Mol. Biol. 12, 88–118 (1965). [DOI] [PubMed] [Google Scholar]
- 47.Neumann S., Hansen C. H., Wingreen N. S., Sourjik V., Differences in signalling by directly and indirectly binding ligands in bacterial chemotaxis. EMBO J. 29, 3484–3495 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Yang Y., et al. , Relation between chemotaxis and consumption of amino acids in bacteria. Mol. Microbiol. 96, 1272–1282 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Moore J. P., Kamino K., Kottou R., Shimizu T., Emonet T., Sensory diversity and precise adaptation enable independent bet-hedging strategies for multiple signals at the same time. bioRxiv [Preprint] (2023). 10.1101/2023.02.08.527720. [DOI] [Google Scholar]
- 50.Mello B. A., Tu Y., An allosteric model for heterogeneous receptor complexes: Understanding bacterial chemotaxis responses to multiple stimuli. Proc. Natl. Acad. Sci. U.S.A. 102, 17354–17359 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Colin R., Zhang R., Wilson L. G., Fast, high-throughput measurement of collective behaviour in a bacterial population. J. R. Soc. Interface 11, 20140486 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Dufour Y. S., Gillet S., Frankel N. W., Weibel D. B., Emonet T., Direct correlation between motile behavior and protein abundance in single cells. PLOS Comput. Biol. 12, e1005041 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Mattingly H. H., Kamino K., Machta B. B., Emonet T., Escherichia coli chemotaxis is information limited. Nat. Phys. 17, 1426–1431 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Adler J., Effect of amino acids and oxygen on chemotaxis in Escherichia coli. J. Bacteriol. 92, 121–129 (1966). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Adler J., Templeton B., The effect of environmental conditions on the motility of Escherichia coli. Microbiology 46, 175–184 (1967). [DOI] [PubMed] [Google Scholar]
- 56.Vollmer A. P., Probstein R. F., Gilbert R., Thorsen T., Development of an integrated microfluidic platform for dynamic oxygen sensing and delivery in a flowing medium. Lab Chip 5, 1059–1066 (2005). [DOI] [PubMed] [Google Scholar]
- 57.Waite A. J., et al. , Non-genetic diversity modulates population performance. Mol. Syst. Biol. 12, 895 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Salek M. M., Carrara F., Fernandez V., Guasto J. S., Stocker R., Bacterial chemotaxis in a microfluidic T-maze reveals strong phenotypic heterogeneity in chemotactic sensitivity. Nat. Commun. 10, 1877 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Bai Y., et al. , Spatial modulation of individual behaviors enables an ordered structure of diverse phenotypes during bacterial group migration. Elife 10, e67316 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Colin R., Drescher K., Sourjik V., Chemotactic behaviour of Escherichia coli at high cell density. Nat. Commun. 10, 5329 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Amchin D. B., Ott J. A., Bhattacharjee T., Datta S. S., Influence of confinement on the spreading of bacterial populations. PLoS Comput. Biol. 18, e1010063 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Psarellis Y. M., et al. , Data-driven discovery of chemotactic migration of bacteria via machine learning. arXiv [Preprint] (2022). http://arxiv.org/abs/2208.11853. [Google Scholar]
- 63.Gurtner G. C., Werner S., Barrandon Y., Longaker M. T., Wound repair and regeneration. Nature 453, 314–321 (2008). [DOI] [PubMed] [Google Scholar]
- 64.de Oliveira S., Rosowski E. E., Huttenlocher A., Neutrophil migration in infection and wound repair: Going forward in reverse. Nat. Rev. Immunol. 16, 378–391 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Di Talia S., Vergassola M., Waves in embryonic development. Ann. Rev. Biophys. 51, 327–353 (2022). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Flemming H. C., et al. , Biofilms: An emergent form of bacterial life. Nat. Rev. Microbiol. 14, 563–575 (2016). [DOI] [PubMed] [Google Scholar]
- 67.Liu J., et al. , Metabolic co-dependence gives rise to collective oscillations within biofilms. Nature 523, 550–554 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Prindle A., et al. , Ion channels enable electrical communication in bacterial communities. Nature 527, 59–63 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Liu J., et al. , Coupling between distant biofilms and emergence of nutrient time-sharing. Science 356, 638–642 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Petkova M. D., Tkačik G., Bialek W., Wieschaus E. F., Gregor T., Optimal decoding of cellular identities in a genetic network. Cell 176, 844–855.e15 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Díaz-Pascual F., et al. , Spatial alanine metabolism determines local growth dynamics of Escherichia coli colonies. Elife 10, e70794 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Jo J., Cortez K. L., Cornell W. C., Price-Whelan A., Dietrich L. E., An orphan cbb3-type cytochrome oxidase subunit supports Pseudomonas aeruginosa biofilm growth and virulence. Elife 6, e30205 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Douarche C., Buguin A., Salman H., Libchaber A. E., Coli and oxygen: A motility transition. Phys. Rev. Lett. 102, 198101 (2009). [DOI] [PubMed] [Google Scholar]
- 74.Bouvard J., Douarche C., Mergaert P., Auradou H., Moisy F., Direct measurement of the aerotactic response in a bacterial suspension. Phys. Rev. E 106, 034404 (2022). [DOI] [PubMed] [Google Scholar]
- 75.Aggarwal A., et al. , Glutamate indicators with improved activation kinetics and localization for imaging synaptic transmission. Nat. Methods 4, 1–10 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Studier F. W., Protein production by auto-induction in high-density shaking cultures. Protein Expr. Purif. 41, 207–234 (2005). [DOI] [PubMed] [Google Scholar]
- 77.Crowe J., et al. , “6xffis-Ni-NTA chromatography as a superior technique in recombinant protein expression/purification” in Protocols for Gene Analysis, Harwood A. J., Ed. (Methods in Molecular Biology, Humana Press, Totowa, NJ, 1994), vol. 31, pp. 371–387, 10.1385/0-89603-258-2:371. [DOI] [PubMed] [Google Scholar]
- 78.Soupene E., et al. , Physiological studies of Escherichia coli strain MG1655: Growth defects and apparent cross-regulation of gene expression. J. Bacteriol. 185, 5611–5626 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Lyons E., Freeling M., Kustu S., Inwood W., Using genomic sequencing for classical genetics in E. coli K12. PLoS One 6, e16717 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.You C., et al. , Coordination of bacterial proteome with metabolism by cyclic AMP signalling. Nature 500, 301–306 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Hui S., et al. , Quantitative proteomic analysis reveals a simple strategy of global resource allocation in bacteria. Mol. Syst. Biol. 11, 784 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Brown S. D., Jun S., Complete genome sequence of Escherichia coli NCM3722. Genome Announc. 3, e00879-15 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Basan M., et al. , Overflow metabolism in Escherichia coli results from efficient proteome allocation. Nature 528, 99–104 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Basan M., et al. , A universal trade-off between growth and lag in fluctuating environments. Nature 584, 470–474 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Shen Y., Chen Y., Wu J., Shaner N. C., Campbell R. E., Engineering of mCherry variants with long Stokes shift, red-shifted fluorescence, and low cytotoxicity. PLoS One 12, e0171257 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Edelstein A., Amodaj N., Hoover K., Vale R., Stuurman N., Computer control of microscopes using µManager. Curr. Protoc. Mol. Biol. 92, 14.20.1–14.20.17 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Mattingly H. H. and Emonet T., Code for simulating a Keller-Segel type of collective bacterial migration with multiple phenotypes, growth, and inheritance, in liquid and porous environments. Github. https://github.com/emonetlab/ks. Deposited 5 May 2022. [Google Scholar]
- 88.Phan T. V., et al. , Direct measurement of dynamic attractant gradients reveals breakdown of the Patlak-Keller-Segel chemotaxis model. Data dryad. 10.5061/dryad.37pvmcvqx. Deposited 2 June 2023. [DOI] [PMC free article] [PubMed]
- 89.Davidsen K., Marvin J. S., Aggarwal A., Brown T. A., Sullivan L. B., pRSET-jAspSnFR3. Addgene. https://www.addgene.org/203458/. Deposited 28 November 2023.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
Simulation code is available at https://github.com/emonetlab/ks (87). Experimental data is available at https://doi.org/10.5061/dryad.37pvmcvqx (88). The jAspSnFR3 sensor is available on the public repository addgene at https://www.addgene.org/203458/ (89) or upon request from Jonathan Marvin.