A viscoelastic constitutive model for human femoropopliteal arteries

Abstract

High failure rates present challenges for surgical and interventional therapies for peripheral artery disease of the femoropopliteal artery (FPA). The FPA’s demanding biomechanical environment necessitates complex interactions with repair devices and materials. While a comprehensive understanding of the FPA’s mechanical characteristics could improve medical treatments, the viscoelastic properties of these muscular arteries remain poorly understood, and the constitutive model describing their time-dependent behavior is absent. We introduce a new viscoelastic constitutive model for the human FPA grounded in its microstructural composition. The model is capable of detailing the contributions of each intramural component to the overall viscoelastic response. Our model was developed utilizing fractional viscoelasticity and tested using biaxial experimental data with hysteresis and relaxation collected from 10 healthy human subjects aged 57 to 65 and further optimized for high throughput and automation. The model accurately described the experimental data, capturing significant nonlinearity and hysteresis that were particularly pronounced circumferentially, and tracked the contribution of passive smooth muscle cells to viscoelasticity that was twice that of the collagen fibers. The high-throughput parameter estimation procedure we developed included a specialized objective function and modifications to enhance convergence for the common exponential-type fiber laws, facilitating computational implementation. Our new model delineates the time-dependent behavior of human FPAs, which will improve the fidelity of computational simulations investigating device-artery interactions and contribute to their greater physical accuracy. Moreover, it serves as a useful tool to investigate the contribution of arterial constituents to overall tissue viscoelasticity, thereby expanding our knowledge of arterial mechanophysiology.

1. Introduction

Peripheral Artery Disease (PAD) is often understood as an occlusion of the arteries of the lower extremities, leading to reduced blood flow to the tissues of the limbs. This condition affects millions worldwide, causing severe pain, tissue damage, and the loss of toes and limbs [1]. Although PAD accounts for less than 5% of all cardiovascular diseases [2], it is one of the most expensive vascular diseases to treat on a per-patient basis [3]. This is primarily due to the frequency of surgical repairs and interventions failing and requiring repeated care. The development of longer-lasting treatments requires a thorough understanding of the mechanical behavior of the arteries in the lower extremities, which can then inform computational modeling of device-artery interactions and improve the efficacy of treatment modalities.

The femoropopliteal artery (FPA) is the main artery in the lower limb. Although its mechanical properties have been extensively studied [4–9], the focus so far has been on its hyperelastic behavior. The FPA is a muscular artery. Compared to elastic arteries such as the aorta, it demonstrates a greater amount of hysteresis with a directional preference. This viscoelastic response is not well studied in the literature and is likely enabled by arterial microstructural characteristics. The FPA has a complex intramural structure, which includes longitudinally-oriented elastic fibers that facilitate longitudinal pre-stretch, reduce arterial kinking during limb flexion, and ensure energy-efficient FPA function [10]. In addition, circumferentially oriented smooth muscle cells regulate the diameter of the artery in response to downstream tissue oxygen demands, and helically-arranged collagen fiber families strengthen the artery and protect it from overstretching [4,11,12]. It remains unclear which of these FPA constituents primarily cause viscous dissipation, how much of it is direction-dependent, and what functional purpose FPA viscoelasticity serves. It is known that viscoelasticity in other arteries reduces the magnitude and temporal variation of circumferential stress and strain and causes reduced radial wall movement [13]. A greater viscoelastic response may also confer benefits such as increased resistance to abrupt deformations and a quicker rate of mechanical energy dissipation [14]. Regardless, it is important to account for the viscoelastic properties when designing medical devices that will interact with these arteries over millions of cycles, which can have significant consequences on both device durability and repair patency.

Traditional methods [15,16] for modeling arterial viscoelasticity mainly integrate rate effects using differential equations based on spring and dashpot elements. These approaches generally require many material parameters and extensive experimental data to describe the directional dependence and the nonlinearity of soft tissues. In addition, the optimal model form has yet to be determined and tested for its ability to fit and predict the response of specific types of arteries. In recent studies, fractional viscoelasticity has been used to model the behavior of soft tissue [17,18] by representing the material with a continuous viscoelastic relaxation spectrum. This approach typically uses only one or two additional variables to model the viscoelastic response. The physical meaning of these parameters is also more intuitive to understand as the degree of viscoelasticity varies from no rate dependence (elastic) to pure stress rate dependence. This makes the approach very practical as it extends to the existing hyperelastic models and allows the study of individual intramural component contributions to the overall viscoelastic response [19–21].

We aimed to develop a new constitutive formulation that can describe the nonlinear anisotropic viscoelastic behavior of human FPAs. Specifically, we aim to separately identify the major contributors to the mechanical response, especially its viscoelastic component, without compromising the identifiability of the resulting parameters. To this end, we utilized the fractional viscoelasticity approach and a strain-energy function motivated by the extracellular matrix (ECM) structure of the FPA. We further enriched the optimization problem by integrating multiple data sources to improve material parameter estimation and optimized it for high through-put and automation. The proposed pipeline was tested on FPA tissues from 10 healthy middle-aged human subjects, and the results were analyzed to examine the relationship between the underlying microstructure and the mechanical response of the FPA.

In the following, we first provide an overview of the FPA microstructure and discuss the experimental data used for this study. We will then review the kinematic and hyperelastic constitutive formulations designed for the FPA. This will be followed by the viscoelastic extension of the constitutive model and the description of the algorithm and procedure for optimized parameter estimation. Finally, we will present the experimental data for ten human subjects and discuss the ability of our model to portray them.

2. Materials and methods

2.1. Microstructure of the femoropopliteal artery

The FPAs need to support two important physiological functions: cardiac cycle pulsation and the flexion-induced deformations of the lower limbs [22–25]. The former is facilitated by the smooth muscle cells (SMCs) of the tunica media, while the latter is supported by the elastic fibers in the external elastic lamina (EEL) located at the junction between the tunica media and the adventitia [10]. The structural orientations of these components are also specialized to facilitate these roles (Fig. 1). The SMCs are predominantly circumferentially oriented to enable regulation of the vessel diameter. On the other hand, the elastic fibers in the EEL are predominantly longitudinally oriented to allow mature, healthy arteries to maintain axial tension and avoid buckling during fore-shortening induced by limb flexion [24,26]. Tunica adventitia supports the FPA from the outside and prevents vessel overstretching through families of undulated type I collagen fibers mixed with dispersed elastic fibers and fibroblasts [27]. Together, these circumferentially oriented SMCs, longitudinally oriented elastic fibers, and helically-organized type I collagen fiber families constitute the primary load-bearing components of the FPA wall. They are embedded in a matrix of medial type IV collagen and glycosaminoglycans (GAGs) that surround the SMCs and appear to have no preferred orientation.

Fig. 1.

Structural composition of the human femoropopliteal artery (FPA) from a representative middle-aged subject with longitudinally-oriented elastic fibers in the external elastic lamina (first row, Verhoeff-Van Gieson stain, elastin is black) and circumferential smooth muscle cells (SMCs) in the media (second row, Masson’s Trichrome stain, SMCs are red), surrounded by medial collagen (blue) and two diagonally-oriented families of collagen type I fibers in the adventitia (third row, multiphoton microscopy, second harmonic generation signal (blue)). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.2. Mechanical data

Five male and five female FPAs from tissue donors, ages 57 to 65, were obtained by Live On Nebraska within 24 h of death after receiving consent from the next of kin. All arteries were free of gross vascular pathology (Table 1). Planar biaxial extension tests were conducted on fresh tissues using a CellScale BioTester (CellScale, Waterloo, ON, Canada) with 2.5 N load cells. The tests were performed on 13 × 13 mm specimens immersed in 0.9% phosphate-buffered saline (PBS) at 37 °C with the longitudinal and circumferential directions of the arteries aligned with the test axes. To ensure a repeatable response, all arteries were preconditioned for 20 loading-unloading cycles at the maximum estimated strain, which was in line with our prior experimental protocols aimed to achieve a repeatable response (see Fig. 9 of Nordsletten et al. [20]). After preconditioning, we used 21 strain-controlled loading cycles with different strain ratios to characterize arterial mechanical properties (Fig. 2). These included 10 longitudinal to circumferential strain ratios of 1:1 to 1:0.1 with a step size of 0.1, 10 ratios of 1:1 to 0.1:1, and a final ratio of 1:1. The three equibiaxial loading cycles were interspersed at the beginning, middle, and end of the testing sequence to verify that the tissue did not accumulate damage and remained within the viscoelastic range. Loading and unloading were done at a strain rate of 0.01 s ⁻¹. The experiment ended with a relaxation protocol in which the tissue was held under constant equibiaxial strain, and the decreases in longitudinal and circumferential forces were recorded over 600 s. The deformation gradient was measured by tracking the movements of graphite markers using a top-mounted camera, and the unloaded state before preconditioning was set as the reference configuration. Due to the model’s sensitivity to strain rate and strain history, we filtered the experimental data to remove outliers and high-frequency noise (see Appendix A).

Table 1.

Specimen age, biological sex (M for male, F for female), and intimal thickening determined using histology.

ID	Age	Sex	Intimal Thickening
1	64	M	Moderate
2	59	M	Low
3	61	M	Low
4	65	M	Moderate
5	60	M	Moderate
6	61	F	None
7	62	F	Moderate
8	60	F	Low
9	62	F	Moderate
10	57	F	Moderate

Fig. 2.

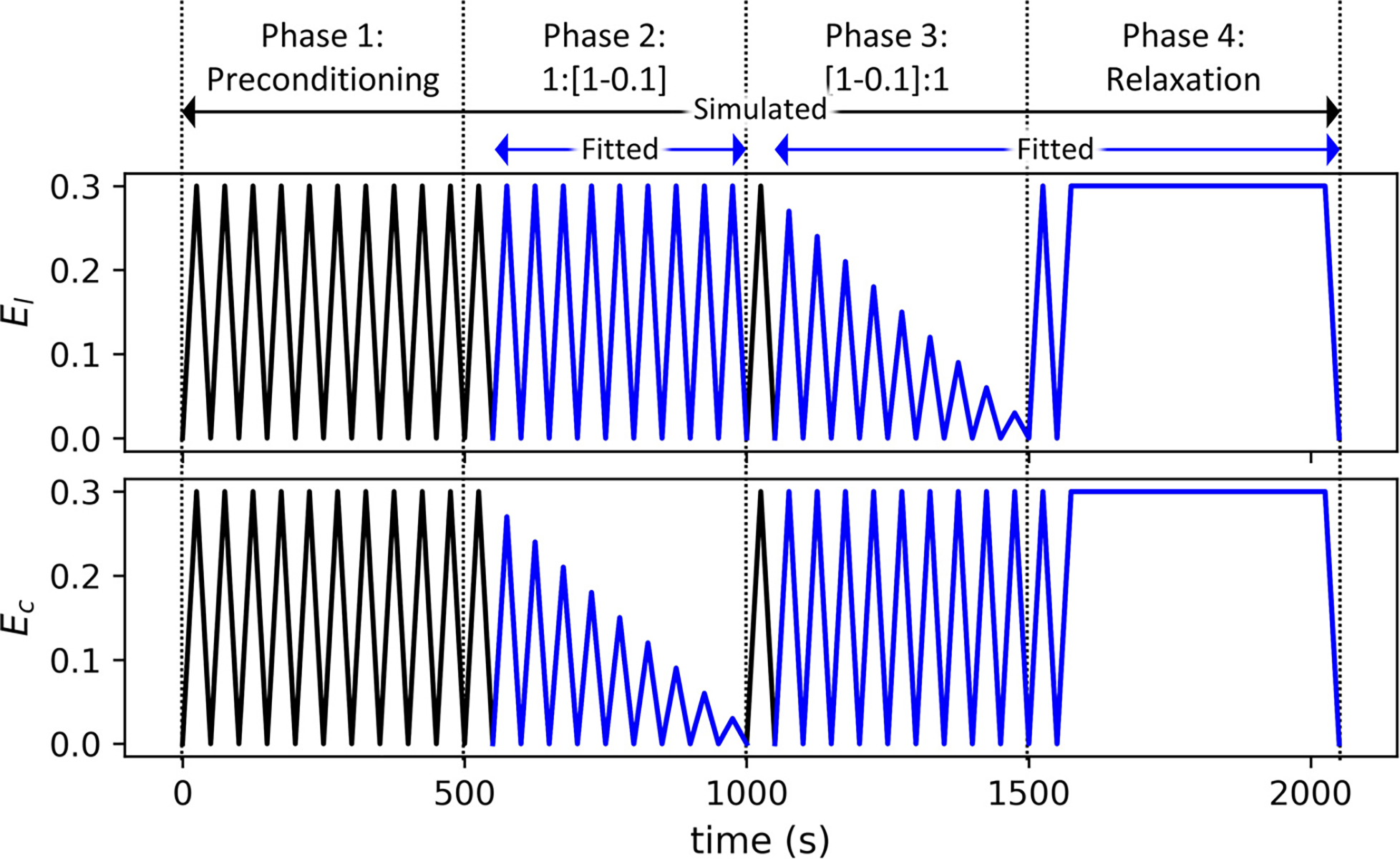
Graphical representation of the loading protocols showing the stretch ${\mathrm{\lambda }}_l$ in the longitudinal direction and ${\mathrm{\lambda }}_c$ in the circumferential direction of each cycle. There are four phases: preconditioning, decreasing ratios of circumferential stretch, decreasing ratios of longitudinal stretch, and stress relaxation. Black curves are simulated, but only the blue curves are used in parameter estimation. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.3. Kinematics and kinetics

Deformation can be characterized by the mapping from the reference configuration ${\mathrm{\Omega }}_0\subset {\mathbb{R}}^3$ to the physical configurations at time $t$, ${\mathrm{\Omega }}_t\subset {\mathbb{R}}^3\forall t\in [0,T]$, where $\mathbf{X}\in {\mathrm{\Omega }}_0$ denoting the material points in the reference configuration and $\mathbf{x}\in {\mathrm{\Omega }}_t$ the corresponding spatial points in the deformed physical configurations [28–30]. The relative motion is defined by a displacement field $\mathbf{u}\in {\mathrm{\Omega }}_0\times [0,T]$ such that $\mathbf{x}(\mathbf{X},t)=\mathbf{u}(\mathbf{X},t)+\mathbf{X}$. The deformation gradient, which describes the stretch and shear of the material as well as the changes in volume, is characterized by the tensor $\mathbf{F}={\nabla }_{\mathbf{X}}\mathbf{u}+\mathbf{I}$ and its determinant $J=\mathrm{d}\mathrm{e}\mathrm{t}\mathbf{F}>0$ [30].³ Arteries are often assumed to be incompressible [31], i.e., $J\equiv 1$, although there is a debate on this issue in the literature [32–35].

The invariants of the right and left Cauchy–Green tensors $\mathbf{C}={\mathbf{F}}^{\mathrm{T}}\mathbf{F}$ and $\mathbf{b}={\mathbf{F}\mathbf{F}}^{\mathrm{T}}$ often provide the basis for developing constitutive relations (e.g., [28]), i.e.,

$$I_{\mathbf{C}}=\mathbf{C}:\mathbf{I},I{I}_{\mathbf{C}}=\mathbf{C}:\mathbf{C},I{II}_{\mathbf{C}}=\mathrm{d}\mathrm{e}\mathrm{t}\mathbf{C}.$$ (1)

Like most biological tissues, arteries are often anisotropic due to embedded structural fibers such as collagen and elastin. SMCs, which are highly organized, can also be a source of tissue anisotropy. For developing constitutive models, it is useful to incorporate the structural orientation using pseudo-invariants that compute the strain along the structural axes. For example,

$$I_a=\mathbf{C}:{\mathbf{a}}_0\otimes {\mathbf{a}}_0={\mathbf{a}}_0\cdot \left(\mathbf{C}{\mathbf{a}}_0\right)=\mathbf{a}\cdot \mathbf{a}$$ (2)

computes the squared stretch along ${\mathbf{a}}_0$, a unit normal vector in the material configuration. Here, ${\mathbf{a}}_0$ can represent the local orientation of collagen fibers, elastic fibers, or SMCs, and $\mathbf{a}={\mathbf{F}\mathbf{a}}_0$ represents the deformed vector. A generalized way of representing the orientation of these structural components, when they are not well-aligned to a single direction, is to replace the tensor ${\mathbf{a}}_0\otimes {\mathbf{a}}_0$ with the structure tensor

$$\mathbf{H}=\frac{1}{4\pi }{\int }_S\rho (\mathbf{a})\mathbf{a}\otimes \mathbf{a}\mathrm{d}S,\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{t}\mathrm{r}\mathbf{H}=1,$$ (3)

where $\rho (\mathbf{a})$ is the 3D orientation distribution, i.e., the probability that the fiber is oriented in the direction of $\mathbf{a}$, while the integration is over the unit sphere $S$ [36].

Stresses are primarily defined from the reactions via the Cauchy stress formula $\mathbf{t}=\mathit{\sigma }\cdot \mathbf{n}$, which is expressed in the deformed domain [28–30]. Alternatively, the first Piola-Kirchhoff stress tensor $\mathbf{P}$ is expressed with respect to the reference domain and is related to the Cauchy stress tensor $\mathit{\sigma }$ by the Piola transformation [30]

$$\mathbf{P}=J\mathit{\sigma }{\mathbf{F}}^{-\mathrm{T}}.$$ (4)

Another Piola transformation can be applied to calculate the second Piola-Kirchhoff stress tensor $\mathbf{S}$, i.e.,

$$\mathbf{S}=J{\mathbf{F}}^{-1}\mathit{\sigma }{\mathbf{F}}^{-\mathrm{T}},$$ (5)

where the introduction of $\mathbf{S}$, along with its strain conjugate $\mathbf{E}=\frac{1}{2}(\mathbf{C}-\mathbf{I})$, are convenient for constitutive modeling since it is defined entirely in the reference configuration.

2.4. Hyperelastic model

The hyperelastic model for the FPAs was previously formulated and used to describe arterial behavior during loading [9]. It had four distinct components, including collagen, $c$, elastin, $e$, passive SMCs, $s$, and the ground matrix, $g$, that is comprised of the remaining ECM. The strain energy is given by

$$\mathrm{\Psi }={\mathrm{\Psi }}_g+{\mathrm{\Psi }}_c+{\mathrm{\Psi }}_e+{\mathrm{\Psi }}_s-p(J-1),$$ (6)

where $p(J-1)$ is the incompressibility constraint. In terms of the second Piola Kirchhoff stress tensor, the ground matrix is represented by a neo-Hookean material, i.e.

$${\mathrm{\Psi }}_g=\frac{{\mu }_g}{2}\left(I_{\mathbf{C}}-3\right),{\mathbf{S}}_g=2\frac{\partial {\mathrm{\Psi }}_g}{\partial \mathbf{C}}={\mu }_g\mathbf{I},$$ (7)

where ${\mu }_g$ is a material parameter related to the ground matrix, while collagen, elastin, and SMCs are all modeled as Holzapfel-type fiber families sharing a similar form as

$${\mathrm{\Psi }}_k=\frac{{\mu }_k}{4b_k}\left(e^{b_k{I}_k^2}-1\right),{\mathbf{S}}_k=2\frac{\partial {\mathrm{\Psi }}_k}{\partial \mathbf{C}}={\mu }_k{I}_k{e}^{b_k{I}_k^2}{\mathbf{H}}_k,I_k=\mathbf{C}:{\mathbf{H}}_k-1,$$ (8)

but different structure tensors ${\mathbf{H}}_k$. Here, ${\mu }_k$ is the modulus parameter, $b_k$ is the exponent parameter controlling the nonlinearity of the material, and $k\in \{c,e,s\}$ are indices for collagen, elastin, and SMCs, respectively. Elastin and smooth muscle cells are modeled as simple, uniformly aligned fiber families with

$${\mathbf{H}}_e={\mathbf{m}}_e\otimes {\mathbf{m}}_e,{\mathbf{H}}_s={\mathbf{m}}_s\otimes {\mathbf{m}}_s.$$ (9)

In comparison to other major arteries, the important distinction of the FPA is that its elastic fibers are oriented longitudinally, SMCs are aligned mainly circumferentially, and adventitial collagen type I consists of two major fiber families crisscrossed at angles $\alpha$ and $-\alpha$ with the longitudinal axis ${\mathbf{m}}_e$. This is in accordance with the functional role and observed microstructure of the FPA (Section 2.1). The two fiber families are modeled using the structure tensor approach [36], i.e.

$${\mathbf{H}}_{c,i}=A\mathbf{I}+B{\mathbf{m}}_i\otimes {\mathbf{m}}_i+\left(1-3A-B\right){\mathbf{m}}_n\otimes {\mathbf{m}}_n,i\in \left\{4,6\right\},$$ (10)

where ${\mathbf{m}}_4$ and ${\mathbf{m}}_6$ are the mean orientation of each collagen fiber family, $A$ and $B$ are the shape parameters used to parameterize the orientation distributions ($\rho (\mathbf{a})$ in Eq. (3)) and ${\mathbf{m}}_n$ is the out-ofplane direction. The parameters $A$ and $B$ are typically derived by experimentally measuring $\rho (\mathbf{a})$ [9,36] and fitting the resulting data while assuming that the mean preferred direction lies in-plane and that there is symmetry about the mean.

The material orientations are not necessarily the same at the Cartesian coordinates representing the testing axes, i.e., the specimens may not be perfectly cut and aligned (Fig. 3). The difference between the two can be represented by a rotation $\theta$ in the plane. Hence the mean material orientations are

$$\begin{array}{ll}& \left[{\mathbf{m}}_e\right]=[\mathrm{c}\mathrm{o}\mathrm{s}\theta ,\mathrm{s}\mathrm{i}\mathrm{n}\theta ],\left[{\mathbf{m}}_s\right]=[\mathrm{c}\mathrm{o}\mathrm{s}(\theta +\pi /2),\mathrm{s}\mathrm{i}\mathrm{n}(\theta +\pi /2)]\\ & \left[{\mathbf{m}}_4\right]=[\mathrm{c}\mathrm{o}\mathrm{s}(\theta +\alpha ),\mathrm{s}\mathrm{i}\mathrm{n}(\theta +\alpha )],\left[{\mathbf{m}}_6\right]=[\mathrm{c}\mathrm{o}\mathrm{s}(\theta -\alpha ),\mathrm{s}\mathrm{i}\mathrm{n}(\theta -\alpha )].\end{array}$$ (11)

Fig. 3.

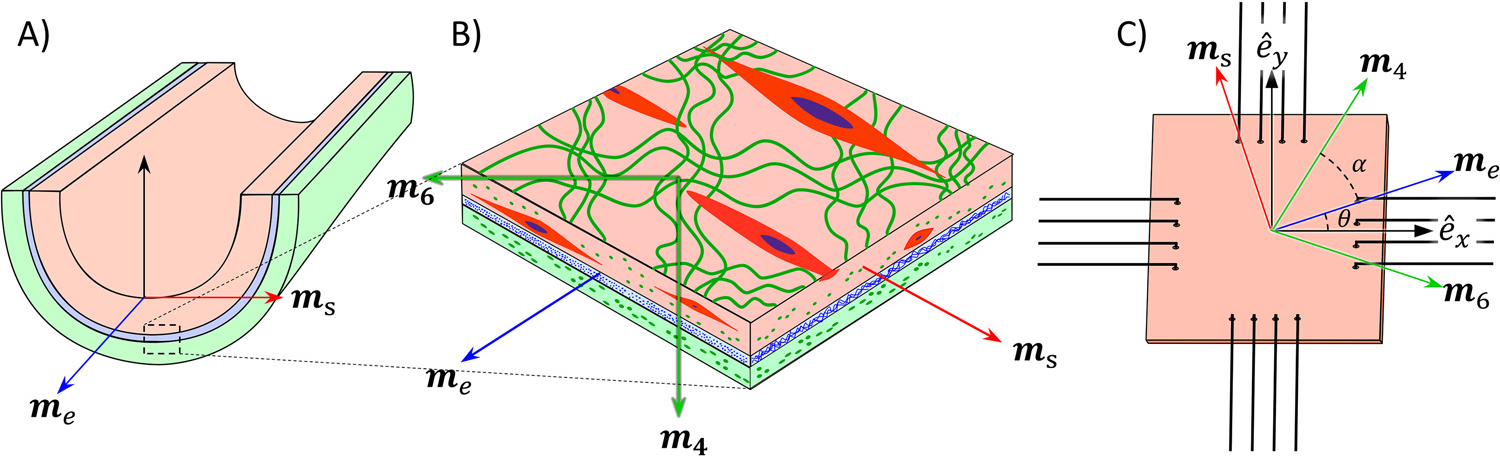
An illustration of the material axes of the smooth muscle cells (${\mathbf{m}}_s$), elastin (${\mathbf{m}}_e$), and collagen (${\mathbf{m}}_c$) used in the model: A) relative to the intact specimen, B) showing the tissue components, and C) relative to the Cartesian coordinate for mechanical testing $\stackrel{\mathbf{ˆ}}{\mathbf{e}}$. The color and subscript correspond to the components: collagen (green, $c$), elastin (blue, $e$), and SMCs (red, $s$). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.5. Normalized fiber model

To facilitate the parameterization, we used the scaling approach described in [37] with some minor updates. The parameters ${\mu }_k$ and $b_k$ in Eq. (8) are covariant because the parameter $b_k$ increases the value of the curve as a whole like the parameter ${\mu }_k$ (Fig. 4 A vs. B). Therefore, a similar quality of fit can be achieved by increasing the value of $b_k$ and decreasing the value of ${\mu }_k$ or vice versa (Fig. 4C). With this in mind, we can introduce linear scaling according to

$${\mathbf{S}}_k^{\mathrm{*}}={\beta }_k{\mathbf{S}}_k,$$ (12)

where

$${\beta }_k=\frac{1}{I_{\max ,k}}{e}^{-b_k{l}_{\max ,k}^2},I_{\max ,k}=\underset{t}{\max }{I}_k(t).$$ (13)

Fig. 4.

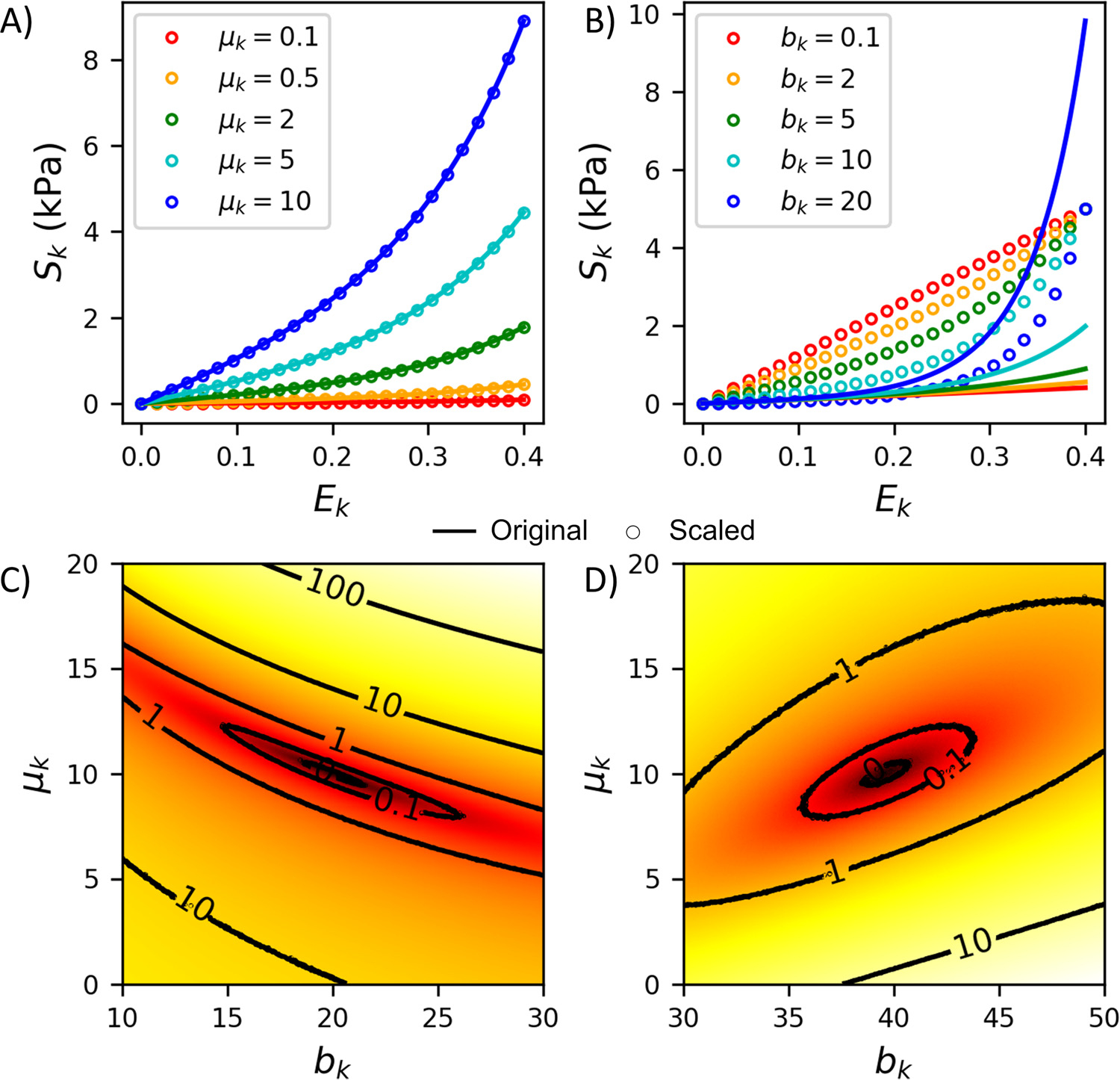
Illustration of how varying the modulus $\left({\mu }_k\right)$ and exponent $\left(b_k\right)$ of the fiber model (Eq. (8)) changes after applying the scaling (Eq. (14)). A) Changes in the stress-strain curve as the modulus (${\mu }_k$ and the equivalent scaled modulus ${\mu }_k^{\mathrm{*}}$) is varied. B) Changes in the stress-strain curve as the exponent $b_k$ is varied. The local contours for the objective function with C) the original (Eq. (8)) and D) the scaled models (Eq. (14)) are also shown.

With this, ${\mathbf{S}}_k^{\mathrm{*}}={\mu }_k$ when $\mathbf{C}={\mathrm{m}\mathrm{a}\mathrm{x}}_t\mathbf{C}(t)$, allowing $b_k$ to only affect the nonlinearity of the curve (Fig. 4 B). For collagen, which consists of two fiber families, we take the greater of the two $I_{\mathrm{m}\mathrm{a}\mathrm{x}}$. This approach modifies the topology near the objective function and, in particular, makes it more elliptical, significantly improving most optimization algorithms’ performance. This modification does not change the constitutive model response. All parameter values are mapped one-to-one, with the exponent $b_k$ having the same value in both forms. The modulus in the scaled case ${\mathbf{u}}_k^{\mathrm{*}}$ is related to the unscaled case by

$${\mu }_k=\frac{{\mu }_k^{\mathrm{*}}}{I_{\mathrm{m}\mathrm{a}\mathrm{x}}}{e}^{-b{I}_{\mathrm{m}\mathrm{a}\mathrm{x}}^2}.$$ (14)

All one-to-one parameter sets also have the same objective function value, which means that the topology of the optimization problem is fundamentally the same. As long as the algorithms converge successfully, the same parameter values are obtained and can be mapped back and forth. Another benefit of this approach is that the value of ${\mu }_k^{\mathrm{*}}$ is more consistent and physically meaningful. In this scaled form, ${\mu }_k^{\mathrm{*}}$ represents each component’s stress contribution at maximum strain. If each component of the tissue can be tested individually, then ${\mu }_k^{\mathrm{*}}$ can simply be set to the maximum stress encountered.

2.6. Viscoelastic extension

Studies have shown that fractional viscoelasticity – a class of viscoelastic models – captures some of the key viscoelastic behaviors of soft tissues [38–41]. Conceptually, viscoelasticity in soft biological tissues arises from a hierarchical distribution of relaxation mechanisms [42,43]. Instead of modeling the resulting viscoelastic relaxation spectrum using discrete independent elements, e.g., in a generalized Maxwell model, the fractional model represents the entire continuous spectrum using one constant, the order of the fractional derivative $v$. Each $v$ characterizes a spectrum ranging from $v=0$, purely elastic, to $v=1$, purely viscous. A frequently used definition is the Caputo derivative [44], i.e.

$$D_t^{v}g=\frac{1}{\mathrm{\Gamma }(1-v)}{\int }_0^t(t-s{)}^{-v}\dot{g}\left(s\right)ds,v\in \left[0,1\right],$$ (15)

which has the advantage that the Caputo derivative of any constant is 0. This approach was used to model viscoelasticity in a variety of soft tissues [18,45–48], including the heart [20,49], lung [50], liver [19], breast [51], heart valves [52], and arteries [21,53,54].

2.7. Final model form

Combining the above, the entire model in terms of the second Piola-Kirchhoff stress tensor is given by

$$\mathbf{S}={\mathbf{S}}_g+D_t^{v_c}\left[{\mathbf{S}}_{c,4}+{\mathbf{S}}_{c,6}\right]+{\mathbf{S}}_e+D_t^{v_s}\left[{\mathbf{S}}_s\right]-p{\mathbf{C}}^{-1}.$$ (16)

Here, as commonly done in the literature, we considered elastin to be elastic in alignment with its functional role. Current studies on isolated elastin do not demonstrate significant viscoelasticity [55]. The ground matrix was also considered elastic because of its small contributions to the total stress. See further discussion in Sections 4.5 and 4.6, respectively. The invariant $I_k$ is defined in Eq. (8) and the structure tensors ${\mathbf{H}}_k$ are defined in Eqs. (10) and (11). The parameters needed to characterize this form are $\xi =\left\{{\mu }_g,{\mu }_c^{\mathrm{*}},b_c,{\mu }_e^{\mathrm{*}},b_e,{\mu }_s^{\mathrm{*}},b_s,\theta ,\alpha ,v_c,v_s\right\}$. The parameters ${\mu }_k$ are the modulus parameters of each structural component of the tissue, and $b_k$, $k\in \{c,e,s\}$ are the corresponding exponents, see Eq. (8). The parameter $\alpha$ is the angle of the collagen fiber families in Eqs. (10) and (11). The structure tensor parameters in Eq. (10) should ideally be obtained from imaging. However, noticing that these values were relatively consistent in our previous study, we set them to $A=0.155$ and $B=0.4243$, i.e., the average of the values from the previous work [9]. In addition, $\theta$ is the specimen alignment, and $v_c$ and $v_s$ are the viscoelasticity constants for the fractional derivative of the collagen and SMCs.

2.8. Fractional 2PK stress update formula

The challenge with using fractional derivatives for modeling viscoelasticity is the computation of the time integral. If implemented naively, this results in a computation time complexity of $𝒪\left(N_t^2\right)$ and a memory complexity of $𝒪\left(N_t\right)$ for storing the strain history, where $N_t$ is the number of time steps. Following efforts towards more efficient approximations by Yuan and Agrawal [56] and others [57,58], we developed an improved approach with better convergence properties and discussed its implementation for finite element problems [59]. In short, fractional derivatives of a tensor can be approximated using the Prony series, i.e.

$${\widehat{\mathit{D}}}_t^v\mathbf{A}:={\beta }_0{\mathbf{A}}^{\prime }(t)+\sum _{k=1}^{N_p}{\int }_0^t{\beta }_k\exp (\frac{s-t}{{\tau }_k}){\mathbf{A}}^{\prime }(s)\text{d}s,$$ (17)

where ${\beta }_0,\dots ,{\beta }_{N_p}$ and ${\tau }_1,\dots ,{\tau }_{N_p}$ are $2N_p+1$ parameters optimized to match the decay for a given $\alpha$. This can be related to the generalized Maxwell model, where these parameters must be determined individually. A discrete approximation can be made by taking advantage of an intermediate variable ${\mathbf{Q}}_k$, i.e.

$${\widehat{\mathit{D}}}_n^v\mathbf{A}:=\frac{{\beta }_0}{\Delta t}({\mathbf{A}}^n-{\mathbf{A}}^{n-1})+\sum _{k=1}^{N_p}{\mathbf{Q}}_k^n,{\mathbf{Q}}_k^n=e_k^2{\mathbf{Q}}_k^{n-1}+e_k{\beta }_k({\mathbf{A}}^n-{\mathbf{A}}^{n-1}),$$ (18)

and $e_k=\mathrm{e}\mathrm{x}\mathrm{p}\left[-\mathrm{\Delta }t/\left(2{\tau }_k\right)\right]$. This provides $𝒪\left(N_t\right)$ scaling for computation time and $𝒪(1)$ scaling for memory (for ${\mathbf{Q}}_k^n$). The parameters ${\beta }_k$ and ${\tau }_k$ can be precomputed independently from the function being differentiated [59].

2.9. Parameter optimization

We propose a three-part objective function

$$ℱ(\xi )=[\chi (\xi )+\varphi (\xi )](1+𝒫(\xi )),$$ (19)

where $\chi$ is the residual function, $𝒫$ is a penalty/regularization term for the parameters, and $\varphi$ is additional fitted data - in this case, the hysteresis of each loading cycle. See Appendix B for a more thorough exploration of these terms and their impact. For the stress residuals, we used the weighted $L^2$ norm, i.e.

$$\chi (\xi )=\sum _{i\in 1,2}\sum _{p=1}^{n_p}{𝒲}_{ii}^p\sum _{k=N_0^p}^{N_e^p}{\left(S_{ii}^k(\xi )-{\widehat{S}}_{ii}^k\right)}^2,$$ (20)

which generally converges with the fewest iterations. Only the normal stresses are considered due to testing limitations, and the inability to provide all the necessary information for accurately calculating the shear stresses [60]. Here, ${𝒲}_{ii}^p$ are the weights for each loading cycle $p$ and stress tensor component $S_{ii}$. $N_0^p$ and $N_e^p$ denote the initial and final index of each loading cycle, respectively. The weights are defined as

$${𝒲}_{ii}^p=\left[1+\frac{1}{4}{\left(\frac{p}{n_p}\right)}^2\right]{\left(\sum _{k=N_0^p}^{N_e^p}{\widehat{S}}_{ii}^k+\frac{1}{n_p}\sum _{k=0}^{N_e^{n_p}}{\widehat{S}}_{ii}^k\right)}^{-1}.$$ (21)

The first term represents an increase in confidence for the later cycles, with values in the range [1,1.25]. This increases the robustness of the parameter estimation against errors during testing by favoring the later loading cycles, of which the relaxation protocol is especially important for determining the viscoelastic constants (see Appendix B). The second term balances the weight of each loading cycle during optimization. Without this, the loading cycles with low-stress ratios are being biased against due to lower total stress. Considerations must also be given for the low-stress loading cycles being more prone to errors, bias, and noises. Thus, this term is the sum of the norm of each loading cycle plus the norm of the average of all loading cycles (see Appendix B).

The hysteresis is calculated by the midpoint rules, i.e., for loading cycle $p$, the hysteresis ${\mathscr{H}}_{ii}^p$ is given by

$${\mathscr{H}}_{ii}^p(\mathbf{S},\mathbf{C})=\sum _{k=N_0^p+1}^{N_e^p}\frac{1}{2}(S_{ii}^k+S_{ii}^{k-1})(C_{ii}^k-C_{ii}^{k-1}).$$ (22)

The full contribution to the objective function is given by

$$\varphi (\xi )=\sum _{i\in 1,2}\sum _{p=1}^{n_p}\frac{({\sum }_p{N}_p^e-N_p^0)}{n_p}{𝒲}_{ii}^p{\left({\mathscr{H}}_{ii}^p(\mathbf{S}(\xi ),\hat{\mathbf{C}})-{\mathscr{H}}_{ii}^p(\hat{\mathbf{S}},\hat{\mathbf{C}})\right)}^2.$$ (23)

Because our objective function did not include shear stresses, there was less data for coupling between the material axes. This complicates the unique determination of the specimen orientation, $\theta$, and the collagen fiber orientation, $\alpha$. As a result, collagen tends to align with one of the material axes. From a modeling perspective, the directional responses became entirely decoupled, and the data were fit independently. Experimentally, however, the specimen orientation was close to the test axes, and the collagen fibers formed two families crossed between the material axes. Adding two small penalties on $\theta$ and $\alpha$ to account for these effects, i.e.,

$$\begin{gathered} 𝒫(\mathit{\xi })=0.001{\theta }^2+0.01{\left(\alpha -\frac{\pi }{4}\right)}^2+{\left(v_c-v_{\text{long}}\right)}^2 \\ +{\left[\frac{1}{2}\left(v_c+v_s\right)-v_{\text{circ}}\right]}^2, \end{gathered}$$ (24)

mitigated these issues and produced more consistent parameter fits. The scaling constants for these two terms are deliberately small, so they only affect the results significantly when the minimum is ambiguous (See Appendix B). The precomputed viscoelastic constants on $v_{\text{long}}$ and $v_{\text{circ}}$ are obtained by fitting the relaxation data ${\hat{S}}_{i,k}$ along each axis, i.e.

$$v_i=argmi{n}_v\sum _k{(\frac{{\widehat{S}}_{i,k}}{{\widehat{S}}_{i,0}}-t_k^{-v})}^2\text{for}i\in \{\text{long},\text{circ}\}.$$ (25)

Due to the structural orientation of collagen and SMCs, only collagen affects the stress decay in the longitudinal direction, while both collagen and SMCs can affect stress decay circumferentially.

2.10. Optimization algorithm

To perform the optimization, we leveraged the differential evolution algorithm in the SciPy optimization and root-finding package [61]. Differential evolution attempts to find the global minimum by mutating a population of randomly seeded parameter vectors. Polishing allowed the best seeds to be grafted using the L-BFGS-B gradient method. To improve the search radius, 64 seeds per parameter (704 combined) were used along with a mutation factor of [0.7, 1.7] and a recombination ratio of 0.7. The constitutive model was coded in C++ and compiled as a Python module using the Cython framework [62].

Leveraging the scaling method (Section 2.5), all modulus parameter bounds, i.e. for ${\mu }_g$, ${\mu }_c^{\mathrm{*}}$, ${\mu }_e^{\mathrm{*}}$, and ${\mu }_s^{\mathrm{*}}$, were set to [10⁻⁴, 300] kPa. For our experimental protocol, no specimens were loaded with stresses greater than 300 kPa. A different upper bound can be chosen for other experimental protocols. A modulus of zero leads to total ambiguity of the exponents, requiring a non-zero lower bound. A more adaptive bound was required for the exponent parameters. Following the observed trend, i.e., stiffer specimens required a larger exponent to exhibit nonlinearity, the bounds were set to $b_c\in \left[0.0,30.0/\left(C_{\mathrm{m}\mathrm{a}\mathrm{x}}-\right.\right.1.0)]$, $b_e\in \left[0.0,15.0/\left(C_{\mathrm{m}\mathrm{a}\mathrm{x}}-1.0\right)\right]$, and $b_s\in \left[0.0,15.0/\left(C_{\mathrm{m}\mathrm{a}\mathrm{x}}-1.0\right)\right]$. Finally, $\theta \in [-\pi /4,\pi /4]$ and $\alpha \in [0,\pi /2]$ represented the entire possible search space. The viscoelastic constants were in the range of [0,0.5]. In addition, we require that $b_c>b_e$ and $b_c>b_s$ since collagen is generally stiffer than elastin and SMCs.

3. Results

We investigated the viscoelastic properties of FPAs from five healthy male and five female individuals aged 57 to 65 (Table 1). The resulting parameters are summarized in Table 2. The scaled modulus is an estimation of the stress fractions at the maximum strain (Eq. (14)). Using this metric, the SMCs were the dominant contributor to the total stress with a scaled modulus of ${\mu }_s^{\mathrm{*}}=57.5\pm 26.2\mathrm{k}\mathrm{P}\mathrm{a}$, followed by collagen ${\mu }_c^{\mathrm{*}}=37.7\pm 16.7\mathrm{k}\mathrm{P}\mathrm{a}$, and elastin ${\mu }_e^{\mathrm{*}}=17.8\pm 5.3\mathrm{k}\mathrm{P}\mathrm{a}$. (Table 2). The contribution of the ground matrix, represented by a neo-Hookean model, was usually insignificant, i.e., ${\mu }_g=1.4\pm 1.7\mathrm{k}\mathrm{P}\mathrm{a}$. A substantial portion of the variations of these values were due to the amount of stress experienced by the specimens during the test. When normalized by the stresses at maximum strain, the SMCs accounted for a consistent 81 ± 9% of the circumferential stress and elastin for 31 ± 8% of the longitudinal stress. The collagen fibers, composed of two fiber families orientated between the axes, were generally more closely aligned with the longitudinal axis than the circumferential axis, allowing the collagen to absorb most of the longitudinal stress.

Table 2.

11 best-fit parameters for each of the 10 specimens. The subscripts are $g$ for ground matrix, $c$ for collagen, $e$ for elastin, and $s$ for SMCs; The μ’s are the moduli and * indicates that it is the scaled variant, i.e., Eq. (14); b’s are the exponents where applicable, α denotes the orientation of the collagen fiber families around the longitudinal axis and θ is the overall orientation of the specimen in radians. $R^2$ is the coefficient of determination.

ID	Hyperelastic							Structural		Viscoelastic		${\mathit{R}}^2$
	${\mathit{\mu }}_{\mathit{g}}(\mathbf{k}\mathbf{P}\mathbf{a})$	${\mathit{\mu }}_{\mathit{c}}^{\mathbf{*}}(\mathbf{k}\mathbf{P}\mathbf{a})$	${\mathit{b}}_{\mathit{c}}$	${\mathit{\mu }}_{\mathit{e}}^{\mathbf{*}}(\mathbf{k}\mathbf{P}\mathbf{a})$	${\mathit{b}}_{\mathit{e}}$	${\mathit{\mu }}_{\mathit{s}}^{\mathbf{*}}(\mathbf{k}\mathbf{P}\mathbf{a})$	${\mathit{b}}_{\mathit{s}}$	θ(Rad)	$\mathit{\alpha }(\mathbf{R}\mathbf{a}\mathbf{d})$	$v^c$	$v^s$
1	1.47	43.70	15.52	24.36	0.00	44.15	3.22	−0.08	0.01	0.023	0.048	0.991
2	0.94	35.61	19.48	18.48	1.52	22.68	1.60	0.23	0.29	0.021	0.092	0.996
3	0.00	22.80	36.47	7.72	0.43	52.30	28.32	−0.13	0.68	0.028	0.021	0.998
4	3.58	59.23	18.61	14.52	0.00	61.94	5.18	0.26	0.59	0.023	0.061	0.994
5	0.00	66.98	23.68	19.04	0.00	78.22	8.62	0.24	0.51	0.020	0.039	0.996
6	0.31	29.21	20.18	24.00	0.00	109.30	9.15	0.33	0.03	0.038	0.049	0.993
7	4.87	35.02	12.40	25.36	0.00	88.35	11.13	0.29	0.69	0.016	0.032	0.996
8	2.14	24.58	15.49	15.78	0.00	23.32	1.53	−0.22	0.23	0.041	0.082	0.996
9	0.86	50.54	9.74	13.00	0.00	45.84	5.60	−0.15	0.48	0.027	0.038	0.994
10	0.00	9.75	8.12	15.48	0.24	48.72	2.25	0.35	0.08	0.022	0.035	0.995

The most significant differences between these specimens were the exponent parameters $b_c$, $b_e$, and $b_s$ (Table 2). They exhibited a strong correlation with the extensibility of the specimens. Initial analysis indicates a potential inverse correlation between the modulus of elastin ${\mu }_e$ and the exponent of collagen $b_c$, but a larger sample size is required to validate this relationship. Aligning with traditional perspectives, the collagen fibers demonstrated the most nonlinearity, followed by the SMCs and the elastic fibers, which generally displayed a near linear behavior, i.e., $b_e\approx 0$. A higher elastin exponent sometimes occurred in stiffer specimens, where there was no protruding toe region in the longitudinal direction.

We also observed a larger average viscoelastic constant for the SMCs (i.e., $v_s=0.0497\pm 0.0214$) compared to the collagen fibers (i.e., $v_c=0.0259\pm 0.0075$) (Table 2). This difference was generally difficult to perceive from the relaxation curves alone (Fig. 5 A), which is a mix of responses from the viscoelastic collagen and SMCs as well as the hyperelastic components of elastin and the ground matrix. Moreover, the effects of preconditioning led to an alteration in the reference configuration, which resulted in the inability to adequately capture the peak stress of the relaxation protocol, inducing a downward shift in the model’s entire relaxation response when compared to the experimental data. The underestimation of peak stress can skew the calculation of viscoelastic constants because greater viscoelasticity would lead to a more pronounced stress decay, allowing the latter part of the relaxation protocol to align more accurately. One approach to counterbalance this effect includes the integration of hysteresis and an initial approximation of viscoelastic constants described in Section 2.9.

Fig. 5.

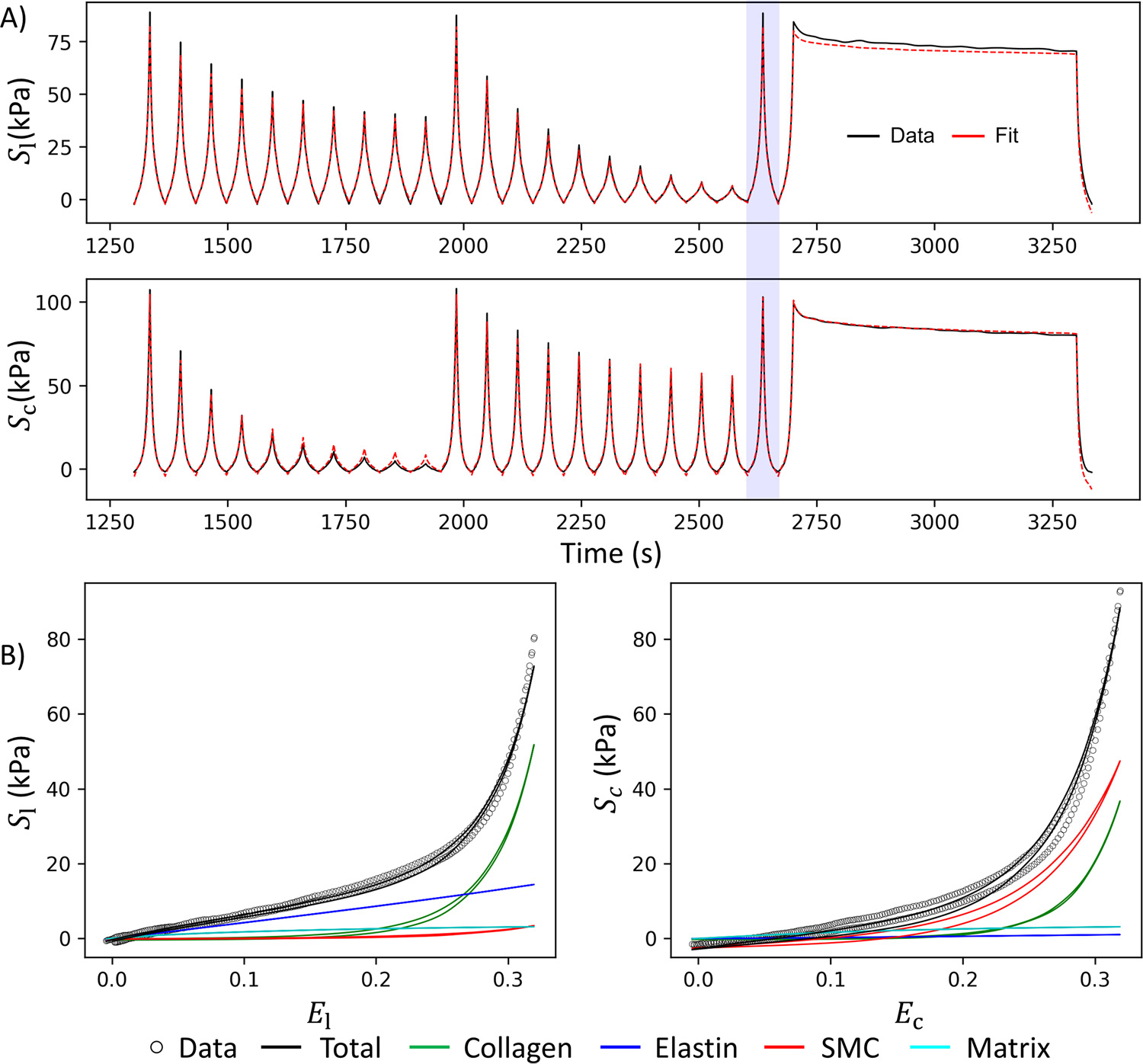
Representative fit of the experimental data: A) Data versus fit over time for all loading cycles after preconditioning, including the unfitted cycles. B) Best fit for the last equibiaxial loading cycle (blue shaded curve in A) illustrating the hysteresis and contribution of each tissue component. $S_l$ is the second Piola-Kirchhoff stress in the longitudinal direction, and $S_c$ is the stress in the circumferential direction, while ${\mathrm{\lambda }}_l$ and ${\mathrm{\lambda }}_c$ are the stretches in the longitudinal and circumferential directions, respectively.

On average, the specimens demonstrated a more significant amount of hysteresis circumferentially, e.g., Fig. 5 B right, than longitudinally. Since the SMCs are primarily oriented in the circumferential direction (Fig. 1), this provides a reasonable way of separating the viscoelasticity of SMCs from that of the collagen. This was reasonably successful, where the entire relaxation curve of the model shifted relative to the experimental data rather than resulting in a large discrepancy with the rate of decay (Fig. 5 A). These results highlight the importance of incorporating hysteresis as a distinct component within the objective function to estimate viscoelastic parameters.

The separated stress-strain curves for the individual ECM components of the last equibiaxial protocol of a representative specimen are presented in Fig. 5 B. There was a prominent and nearly linear toe region longitudinally, which may be attributed to the presence of elastin. Due to the low exponent value, elastin contribution was generally small at maximum strain. In contrast, the toe region in the circumferential direction was much less prominent, and the curve was significantly more nonlinear. The amount of hysteresis circumferentially was also considerably larger, which cannot be explained by the collagen alone without affecting the longitudinal curves.

The best-fit curves for all loading cycles are also presented in Fig. 6. Although most of the longitudinal nonlinearity was due to the collagen fibers, the SMCs were consistently responsible for a significant portion of the nonlinear response circumferentially. This is reflected in the circumferential-longitudinal coupling of the mechanical response. It was common to observe a substantial decrease in the nonlinearity of the longitudinal response for the loading cycles in phase 2 as the maximum circumferential strain decreased (Fig. 6 A left). On the contrary, the circumferential response for the loading cycles in phase 3 remained significantly nonlinear as the maximum longitudinal strain decreased (Fig. 6 B right). The former finding can be attributed to the diminished recruitment of collagen fibers in cross directions, leading to the curves approaching a nearly linear response, a characteristic typically associated with elastic fibers. Similarly, there was also a reduction in the recruitment of collagen fibers when the maximum longitudinal strain decreased in phase 3. However, the ensuing response suggests that the supportive structural component, the SMCs, diverges significantly from the behavior of elastin. These observations align with the microstructural composition of the FPA described in Section 2.1.

Fig. 6.

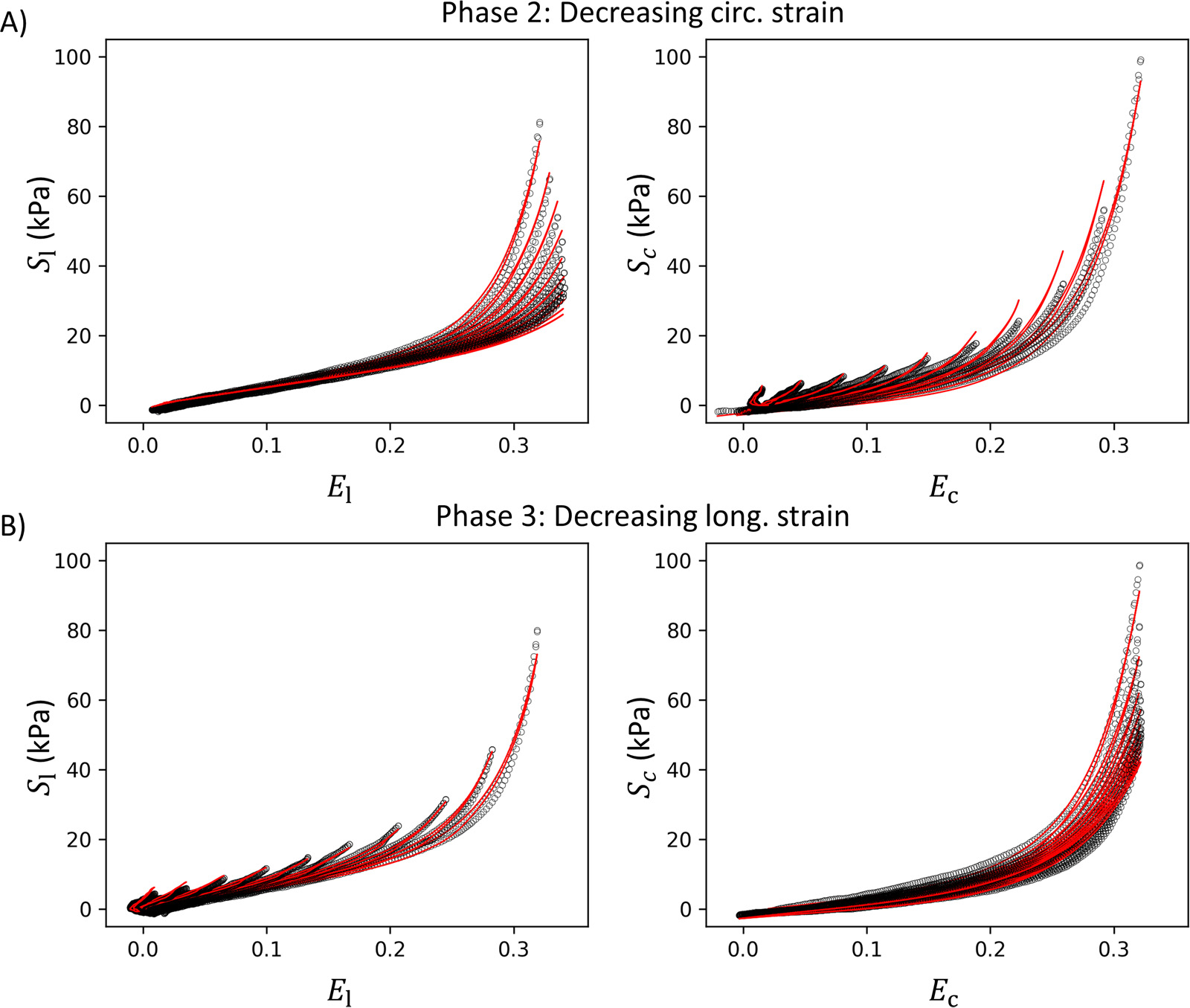
Individual fits for individual loading curves with different axial strain ratios: A) Phase 2 with decreasing circumferential strain. B) Phase 3 with decreasing longitudinal strain. $S_l$ is the second Piola-Kirchhoff stress in the longitudinal direction, while $E_l$ and $E_c$ are the Green-Lagrange strains in the longitudinal and circumferential directions, respectively.

The correlation coefficient between the viscoelastic constants and the other material parameters was very low – a maximum of 0.26 for $v_s$ and 0.38 for $v_c$ (Table 3), suggesting they may be unique. In comparison, the correlation between the hyperelastic parameters of collagen, elastin, and SMCs was sometimes quite high, e.g., the correlation of ${\mu }_c$ and $b_c$ of −0.97 and the correlation of ${\mu }_s$ and $b_s$ of −0.98. For clarity, a correlation coefficient of 1.0 implies that the outcomes derived from modifying one parameter are indistinguishable from the consequences of altering the other parameter, which means that the corresponding parameters cannot be uniquely determined. After applying the parameter scaling (Section 2.5), the correlation coefficient reduced to −0.27 for ${\mu }_c^{\mathrm{*}}$ and $b_c$ and 0.37 for ${\mu }_s^{\mathrm{*}}$ and $b_s$. The results were not perfect due to the complexity of the full model (Eq. (16)). For instance, the correlation between ${\mu }_c$ and ${\mu }_e$ increased from −0.22 to 0.87. However, the overall outcomes represent a substantial improvement. Consequently, the scaled model required less than half the average number of iterations to achieve convergence compared to the original model. Notably, both methodologies converged to the same minimum value (Table 3 bottom).

Table 3.

The correlation matrix between the parameters for the representative specimen 7 is shown using (top) the original model (Eq. (8)) and (middle) the scaled model (Eq. (14)). A correlation value of 1 on the off-diagonal means that the optimization problem is singular. (Bottom) The final best-fit parameters of both models are shown along with the average number of iterations (Nit) required to reach the minimum from 10 runs with different random seeds. The parameters for the scaled model are mapped back to the original with Eq. (14).

		${\mathit{\mu }}_{\mathit{g}}$	${\mathit{\mu }}_{\mathit{c}}$	${\mathit{b}}_{\mathit{c}}$	${\mathit{\mu }}_{\mathit{e}}$	${\mathit{b}}_{\mathit{e}}$	${\mathit{\mu }}_{\mathit{s}}$	${\mathit{b}}_{\mathit{s}}$	${\mathit{v}}_{\mathit{c}}$	${\mathit{v}}_{\mathit{S}}$
Original Model	${\mu }_g$	1.00	−0.48	0.42	−0.63	0.57	−0.76	0.71	0.25	0.40
	${\mu }_c$	−0.48	1.00	−0.97	−0.22	−0.37	0.06	−0.09	−0.36	0.02
	$b_c$	0.42	−0.97	1.00	0.30	0.21	0.00	0.01	0.37	0.03
	${\mu }_e$	−0.63	−0.22	0.30	1.00	−0.62	0.68	−0.63	0.09	−0.36
	$b_e$	0.57	−0.37	0.21	−0.62	1.00	−0.43	0.47	0.22	0.09
	${\mu }_s$	−0.76	0.06	0.00	0.68	−0.43	1.00	−0.98	−0.12	−0.24
	$b_s$	0.71	−0.09	0.01	−0.63	0.47	−0.98	1.00	0.13	0.22
	$v_c$	0.25	−0.36	0.37	0.09	0.22	−0.12	0.13	1.00	−0.27
	$v_s$	0.40	−0.02	0.03	−0.36	0.09	−0.24	0.22	−0.27	1.00

		${\mu }_g$	${\mu }_c$	$b_c$	${\mu }_e$	$b_e$	${\mu }_s$	$b_S$	$v_c$	$v_s$
Scaled Model	${\mu }_g$	1.00	−0.46	0.52	0.24	0.38	0.19	0.32	0.32	0.13
	${\mu }_c$	−0.46	1.00	−0.27	−0.87	−0.72	−0.67	−0.12	−0.30	0.17
	$b_c$	0.52	−0.27	1.00	0.29	−0.15	0.06	−0.41	0.19	0.05
	${\mu }_e$	0.24	−0.87	0.29	1.00	0.73	0.57	−0.07	0.38	−0.26
	$b_e$	0.38	−0.72	−0.15	0.73	1.00	0.47	0.36	0.31	−0.14
	${\mu }_s$	0.19	−0.67	0.06	0.57	0.47	1.00	0.37	0.19	−0.07
	$b_s$	0.32	−0.12	−0.41	−0.07	0.36	0.37	1.00	0.11	−0.01
	$v_c$	0.32	−0.30	0.19	0.38	0.31	0.19	0.11	1.00	−0.42
	$v_s$	0.13	0.17	0.05	−0.26	−0.14	−0.07	−0.01	−0.42	1.00

	${\mu }_g$	${\mu }_c$	$b_c$	${\mu }_e$	$b_e$	${\mu }_s$	$b_s$	$v_c$	$v_s$	Nit
Original	4.868	11.38	12.40	43.54	0.0	2.86	11.13	0.016	0.032	1673
Scaled	4.867	11.38	12.40	43.54	0.0	2.86	11.13	0.016	0.032	687

When characterizing the hyperelastic response, it is common to adjust the reference configuration, since hyperelastic models cannot produce non-zero stresses at zero strain. Viscoelastic modeling differs due to the need to account for the strain history. In particular, the same reference configuration must be maintained throughout the experiment, so its choice is less clear. We tested the modeling analysis with different reference configurations, and the results demonstrate that choosing the first point before preconditioning as a reference led to the closest match between the unloaded stresses at the end of each loading cycle afterward (Fig. 7). This suggests that viscoelasticity accounts for a significant portion of the changes in the unloaded configurational over time.

Fig. 7.

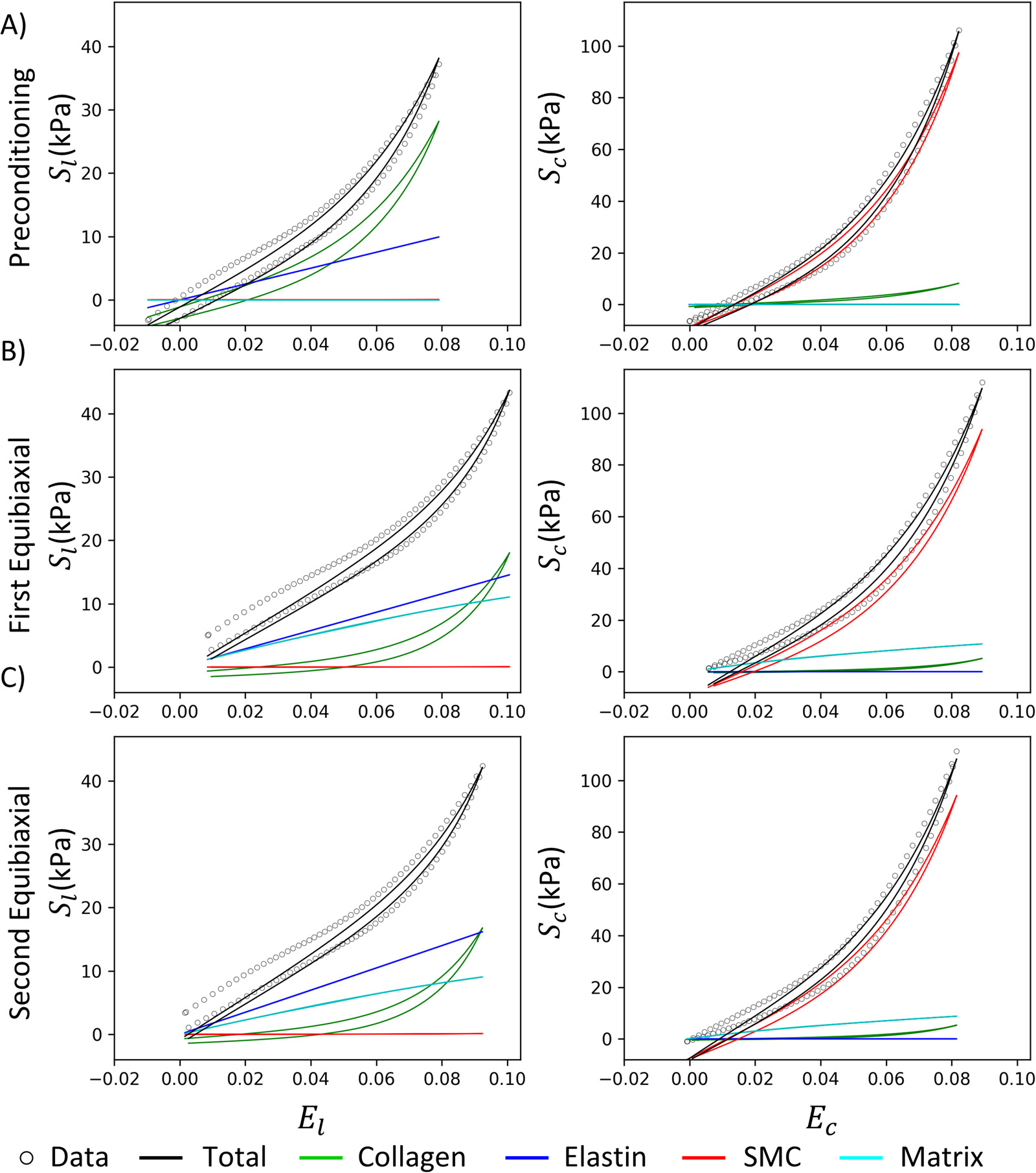
Best-fit stress-strain curve of the last equibiaxial protocol with separate contributions, if the reference state is assumed to be A) before preconditioning, B) before the first equibiaxial protocol, and C) before the second equibiaxial protocol. $S_l$ is the second Piola-Kirchhoff stress in the longitudinal direction, and $S_c$ is the stress in the circumferential direction, while $E_l$ and $E_c$ are the Green Lagrange strains in the longitudinal and circumferential directions, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

The quality of the fits was generally excellent, with an average $R^2$ value of 0.995 (Table 2) and similar levels of the root mean squared error (RMSE) for each loading curve (Fig. 8). Even the first two equibiaxial protocols not used for fitting matched well. Due to the weights and the inclusion of the a priori estimate of $v$ and the hysteresis, the RMSE tended to increase towards the low-stress protocols but remained within the acceptable range.

Fig. 8.

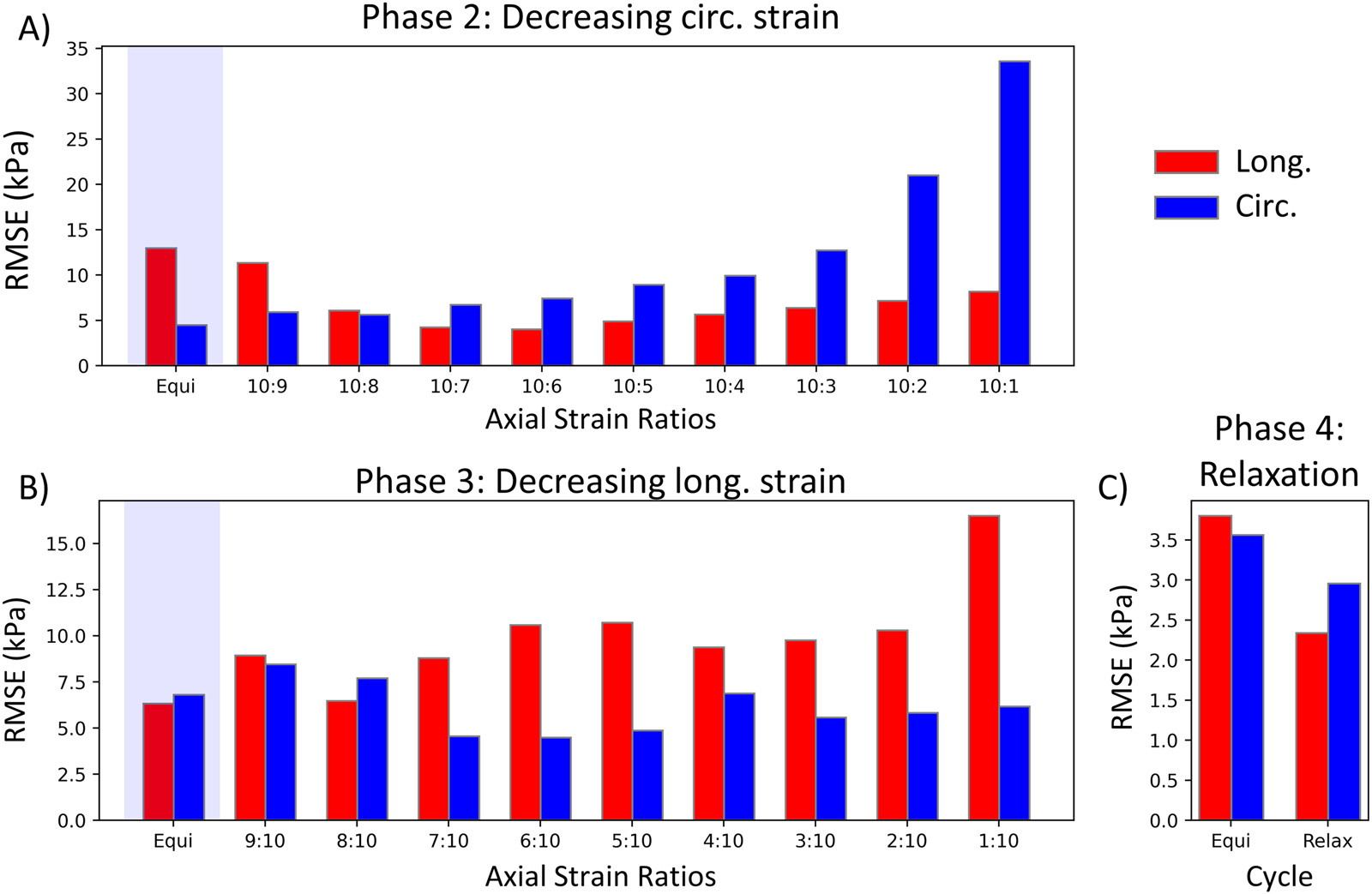
The root mean squared error (RMSE) of the individual loading cycles for the representative specimen in Fig. 5: A) RMSE for the loading cycles in phase 2 of Fig. 2, where the circumferential strain decreases cycle by cycle. B) RMSE for the loading cycles in phase 3, where the longitudinal strain decreases. C) RMSE for the loading cycles in phase 4, where the relaxation testing was performed. Red bars represent the RMSE for the longitudinal stress, while blue bars represent the circumferential stress. The blue-shaded loading curves were not used for fitting. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

4.1. Viscoelasticity in the FPA

Collagen fibers and SMCs are major contributors to the viscoelastic response of the muscular FPA. On average, the viscoelastic constant for the SMCs was twice that of collagen, which is not surprising given that the experimental mechanical data indicates significantly more hysteresis circumferentially, i.e., along the SMC orientation (e.g., Fig. 5). The complex machinery of the SMCs with their actin and myosin proteins was reported to produce a direction-dependent viscoelastic response with more significant hysteresis along the cell direction [63]. Physiologically, this may suggest that peripheral arteries that are farther from the heart experience a lower pressure gradient, and therefore energy efficiency may be less important than viscoelastic damping during diameter regulation. Conversely, a more elastic longitudinal behavior may be desirable to withstand the hostile biomechanical environment of the flexing lower limbs where the artery undergoes axial extension and compression during locomotion [22–25].

Importantly, the viscoelastic constants obtained in this study are very consistent, with the SMCs from nine of the ten specimens showing more viscoelasticity than collagen. For eight of the ten specimens, the SMC viscoelastic constants were 50% to 100% higher than for collagen (Table 2). The ten specimens we selected for this study were all from a similar age group (57–65 years) (Table 1) and did not exhibit gross pathology that could significantly alter the biomechanical response. However, as expected for most soft biological tissues, they exhibited some variability in their responses, particularly regarding the degree of extensibility captured by the exponent b _k parameters (Table 2). Overall, however, the consistency in the viscoelastic parameters was good, suggesting that they were likely determined reliably. From a theoretical point of view, this makes sense since soft tissue extensibility is generally related to the degree of collagen fiber crimping in the reference configuration, which should not affect the innate properties of the intramural constituents. This consistency of the determined viscoelastic constants is encouraging as it opens up the possibilities to study how they change with the broader subject population and vascular pathology known to drive the change in intramural FPA composition [8,27]. We leave these questions to future studies.

4.2. Stress contribution of collagen, elastin, and SMCs

The stress fraction of collagen, elastin, and SMCs were relatively consistent in magnitude, although some variations were observed. If, instead, the values were analyzed relative to the maximum axial stress, the SMCs consistently accounted for 81 ± 9% of the circumferential stress at maximum deformation. Likewise, elastin was responsible for 31 ± 8% of the longitudinal stress at maximum deformation. In addition, differences can also be affected by the variations in loading. However, it is encouraging that the values were similar among the analyzed specimens, which represented a relatively uniform group. The contribution of collagen was less straightforward to analyze because collagen families do not align with any of the material axes, and their orientation may vary between specimens. However, the collagen stress fraction was 63 ± 31% of the maximum stress value in the longitudinal direction and 18 ± 14% of the maximum stress value in the circumferential direction. It would be interesting to investigate how this contribution shifts with FPA aging as the elastin degrades and more of the cross-linked collagen takes on the redistributed load, causing a shift in the stress-strain toe region.

4.3. The importance of hysteresis

Incorporating hysteresis into the objective function and its weight relative to the residual stress is crucial for the reliable estimation of viscoelastic constants. The significance of the hysteresis term is on par with or exceeds the residuals in the objective function. It is not uncommon for the viscoelasticity along an axis to be overlooked in pursuit of a superior on-axis fit at high stresses. Moreover, the viscoelasticity also affects the unloaded state after each cycle. Consequently, any bias in the reference configuration due to preconditioning or other permanent set effects could result in suboptimal estimates of the viscoelastic constants (e.g., Fig. 7). This situation is compounded by the requirement for a continuous strain history. Given that the hysteresis is unaffected by the reference configuration, it serves as a valuable metric for estimating viscoelasticity.

4.4. Preconditioning and viscoelasticity

Preconditioning is typically used to achieve a repeatable response when assessing the hyperelastic behavior of postmortem tissues. After death, the adenosine triphosphate molecule that separates the actin-myosin bridges and causes muscle relaxation is no longer produced, and the cross-bridging locks the muscles in place until either decomposition or mechanical stretching breaks them apart. Partly for this reason (and partly due to the reorientation of other microstructural components such as collagen), the reference configuration is usually taken after the preconditioning to ensure a repeatable response. However, due to the importance of strain history for the viscoelastic response, there is no luxury for adjusting reference configuration for individual loading curves to produce congruent stress-strain data. Due to the need to continuously simulate all loading cycles over time, it is not clear what the reference configuration should look like. For all ten specimens tested in our study, the choice of the first data point, i.e., before preconditioning, led to the smallest difference in stresses after the unloading of the last equibiaxial loading cycle (e.g., Fig. 7). This suggests that viscoelasticity also plays an important role in the changes in the reference configuration during testing. For the ten specimens in this study, these viscoelastic effects were comparable to the preconditioning effects.

4.5. Viscoelasticity of elastin

Elastin is well known for its contribution to the elastic recoil of arteries and other soft biological tissues. The more elastic the mechanical response of the tissue, the more efficiently it adapts to the physiological cardiac cycle loading. Despite this, the viscoelastic response of elastin has been described in several studies [55,64–68] but the observed stress decay poses several interpretative challenges. First, most experiments involved elastin undergoing dehydration and immersion in various solutions [64–68]. Isolated elastic structures reveal substantial stress decay within the first few seconds, but medium- to long-term decay curves exhibited a tendency to flatten [55], typical of elastic materials. Second, elastin demonstrates no creep [55]. Third, it is difficult to argue that the aggressive process of extracting elastin from soft biological tissue, which usually involves decellularization and destruction of the remaining extracellular matrix, does not impact the mechanical response of the constituents. All these issues likely contribute to the inconsistencies in the reported experimental findings. Although the viscoelastic response of undisturbed elastin is likely minor, its inclusion in the model would have introduced an additional variable, thereby complicating the determination of other parameters.

4.6. Viscoelasticity of the ground matrix and GAGs

The viscoelasticity of the ground matrix is an interesting topic of discussion. By definition, these are the remaining components of the extracellular matrix but not the main structural components. This is commonly done in biomechanics since the mechanical response of the remaining matrix components tends to be insignificant. This also means that the ground matrix includes GAGs, proteoglycans, and other viscoelastic molecular structures. It is, therefore, natural to expect the ground matrix to be viscoelastic. However, considering that the overall response of the ground matrix is marginal (contributing less than 1% of the total stress, Fig. 5 B), it is unlikely that it could make a significant contribution to the overall viscoelastic response.

4.7. Optimization algorithm and objective function modification

The optimization algorithm is always an important consideration in any constitutive modeling problem. Gradient algorithms are superior in terms of speed, but they also depend heavily on the initial parameter estimate. More often than not, unimodality, convexity, and ellipticity are not guaranteed due to imperfect data and constitutive model nonlinearity and complexity. One approach is bootstrapping [69], but this can become quite expensive. Although the search space can be narrowed by examining the data, this is challenging with a large data set. Global algorithms like differential evolution are an attractive alternative with pseudo-randomized initial seeds and non-gradient-based exploration. Of course, genetic algorithms lend themselves to a more thorough exploration of the objective function, but there is still a significant investment of time.

Another avenue is to improve the objective function itself. Exponential-type constitutive models are well known for their banana-shaped rather than elliptic objective function surfaces, leading to slow convergence [37,70,71], e.g., Fig. 4 B. Applying our scaling modification (Section 2.5) led to significant gains in convergence even with a non-gradient algorithm, highlighting the importance of ellipticity. This can also be seen in the improvement of the correlations between parameters (Table 3), which become more decoupled after scaling. Since this modification is one-to-one and maintains the same objective function value, the same minimum is reached (Table 3, bottom). Since the original parameters are easily recoverable, there is no downside. For our problem, this led to an acceptable 5 to 20 min per specimen parameter estimation when run on 16 processors.

The optimal theoretical scenario would consider a model of the form $S_f=a{e}^{b{E}_f}$ and fitting $\mathrm{l}\mathrm{o}\mathrm{g}{S}_f$ with the parameter $\mathrm{l}\mathrm{o}\mathrm{g}a$ whereby the optimization problem could be formulated as follows

$$\underset{a,b}{\min }\sum _i{(S_f(E_{f,i})-S_{f,i})}^2\to \underset{A,b}{\min }\sum _i{\left[b{E}_{f,i}+A-\log (S_{f,i})\right]}^2,$$ (26)

where $A=\mathrm{l}\mathrm{o}\mathrm{g}a$, i.e. fitting to a straight line. This is the underlying reason why such parameter transformation approaches are effective in pure in silico studies like [70,71]. In practice, there are numerous problems with this approach. Using the logarithm skews the fit to the low-stress data and amplifies the noise in that range. It does not tolerate zero and negative stresses, which can be produced by reference configuration shifts and shear deformations. Finally, and most relevant to this work, negative stresses make perfect sense in the context of viscoelasticity.

4.8. Potential implications

While structurally motivated hyperelastic models to describe arterial behavior have been established for some time [72], the focus has been predominantly on elastic arteries, like the aorta, where viscoelastic effects are not as pronounced as in muscular arteries. Vessels such as the FPA are structurally different to facilitate their function further away from the heart. The exact reasons necessitating their greater viscoelasticity remain somewhat elusive, though the biomechanical environment provides some indication. A greater viscoelastic response of the FPA may confer benefits such as increased resistance to abrupt deformations from external mechanical factors like limb flexion and a quicker rate of mechanical energy dissipation [14]. The predominantly muscular composition also allows arteries like the FPA to control the body’s blood pressure and flow through vasoconstriction and vasodilation, which requires a higher degree of viscoelasticity to accommodate frequent and rapid structural changes. Regardless of the precise physiological underpinnings driving the pronounced circumferential viscoelasticity of the FPA, it is important to account for these viscoelastic properties when designing medical devices that will interact with these arteries over millions of cycles. This understanding can significantly optimize the longevity and effectiveness of the repair devices and contribute to improved repair patency.

4.9. Study limitations

Our study introduces a new viscoelastic constitutive model for human FPA and provides an algorithmic implementation to make it usable for large data sets. Nevertheless, the results must be seen in the context of study limitations. First, since our specimens were collected postmortem, assessing their active mechanical properties was not possible, and we have only considered the passive SMC response. The active SMC tone has a major effect on the mechanical properties of muscular arteries in animals [73], and there is no reason to believe it does not have a similar effect in humans.

Secondly, estimating shear stress in biomechanical testing is quite difficult because of the heterogeneity of the specimens and the lack of attachment systems that can apply traction homogeneously to the edge. The best way to achieve this is to use self-equilibrating pulleys and sutures [60], but the problem of creating a homogeneous internal stress field remains. Additionally, applying suture attachments to small samples is technically challenging, time-consuming, and can result in tissue damage if done improperly. Most existing testers utilize rakes or clamped boundaries, which are much easier to use, and the off-axis forces are not even measured, so shear stresses cannot be estimated. There is no easy way to get around this limitation, but in our previous work with the self-equilibrating pulley system, the FPA shear effects were small when the test axes were aligned with the arterial directions [74], justifying the use of a rake system in our subsequent experiments [7–9]. In this study, we applied small corrections to the specimen orientation and collagen splay angle to compensate for the potential influence of specimen misalignment, and using a global algorithm and quality fits, we were able to achieve consistent results despite the uncertainties in the reference configuration caused by preconditioning.

Thirdly, the microstructure of the ECM has a major impact on the overall response of biological tissues. It determines the anisotropy and the axial coupling response, which can be quite complicated in tissues like the FPA that undergo complex deformations. Ideally, microstructural information should be obtained experimentally [9,36,75], but this requires special equipment, is very time-consuming and technical, and is generally not feasible for large specimen numbers. To compensate for this, we allowed the orientation of the specimen to vary. Due to the heterogeneity of the tissue, it can be challenging to align the specimen perfectly using visual cues alone. However, this can have a significant effect on the quality of the fit and the estimation of viscoelastic properties since poor fit quality naturally also affects the viscoelastic response. For example, over-estimating the maximum stress will result in a higher viscoelastic constant so that the stress will decay faster toward the experimental data. In addition, based on previous hyperelastic models [9], where the relative orientation of collagen fibers can vary significantly, the parameter $\alpha$ was also necessary. To alleviate the ambiguity of these parameters, we added small penalty terms for $\theta$ and $\alpha$.

Lastly, it is likely that the three layers of the arterial wall: intima, media, and adventitia affect the overall viscoelasticity of the tissue differently, and their separation may provide additional in-sights into the viscoelastic FPA behavior. We did not perform this separation for two main reasons: (i) it would have disrupted tissue integrity and residual stresses, which could also contribute to viscoelastic effects, and (ii) such a separation is technically challenging (and often not feasible) in many healthy FPA tissues. Nevertheless, our approach allowed us to analyze the contributions of individual intramural components to the overall viscoelastic behavior, and we hope to be able to apply this methodology to a larger number of specimens in our future studies.

5. Conclusions

We have introduced a fractional nonlinear viscoelastic constitutive model for human FPAs and the methodology necessary for the high-throughput analysis of their biaxial mechanical responses. Our model enhances current hyperelastic formulations by facilitating the discernment of the individual properties of collagen and SMCs. Tested on 10 FPA specimens from individuals aged 57 to 65, our approach consistently produced high-quality fits and stable viscoelastic constants. Our results demonstrate that the values of the viscoelastic parameters for SMCs were twice as high as those for collagen, with SMCs contributing 81% to the circumferential response and elastin influencing 31% of the longitudinal behavior. As the fiber families’ angles varied across each specimen, collagen’s contribution exhibited greater variability. The algorithmic implementation of this model bolstered the consistency and speed of parameter estimation, facilitating the creation of an effective pipeline for large-scale arterial data set analysis. This approach will enable further exploration of the influence of demographics and vascular pathology on tissue viscoelasticity.

Statement of significance.

The demanding biomechanical environment of the femoropopliteal artery (FPA) necessitates complex interactions with repair devices and materials, but the viscoelastic properties of these muscular arteries remain poorly understood with the constitutive model describing their time-dependent behavior being absent. We hereby introduce the first viscoelastic constitutive model for the human FPA grounded in its microstructures. This model was tested using biaxial mechanical data collected from 10 healthy human subjects between the ages of 57 to 65. It can detail the contributions of each intramural component to the overall viscoelastic response, showing that the contribution of passive smooth muscle cells to viscoelasticity is twice that of collagen fibers. The usefulness of this model as tool to better understand arterial mechanophysiology was demonstrated.

Appendix A. Hermite filtering

Sudden and instantaneous data changes, such as high-frequency noise and data outliers due to sensor errors, pose a challenge for viscoelastic models, whose stress is directly proportional to the rate of deformation. An automatic algorithm is required to filter the input data while preserving the underlying response. Common filters in signal processing are usually not sufficient, as they significantly alter the data in the event of sudden changes, e.g., in the area of the transition between loading and unloading. For this reason, an interpolation strategy is generally more appropriate. Here, we need C ⁰ continuity throughout the entire test and C ¹ continuity within each loading cycle. Under these conditions, Hermite polynomials are a natural choice. One way to express this is

$$\begin{array}{ll}& f(s)=\left\{\begin{array}{ll}{p}_0{\varphi }_0^p(s)+q_0{\varphi }_0^q(s)+p_1{\varphi }_1^p(s)+q_1{\varphi }_1^q(s)& \text{if}s\in [0,1],\\ 0,& \text{otherwise,}\end{array}\right.\\ & {\varphi }_0^p(s)=2s^3-3s^2+1,{\varphi }_0^q(s)=s^3-2s^2+s,\\ & {\varphi }_1^p(s)=-2s^3-3s^2,{\varphi }_1^q(s)=s^3-s^2,\end{array}$$ (A.1)

where $p_0$ and $p_1$ are the nodal values and $q_0$ and $q_1$ are the derivatives at the nodes. Neighboring Hermite elements share the nodal values $p$. If these neighboring elements are also in the same loading cycle, they share the same derivative values $q$.

Multiple Hermite elements are required for each loading curve to maintain the underlying response, and the length of each Hermite element needs to be sufficient not to be affected by noise. In this study, we used 12 Hermite elements per loading or unloading curve. Let $x=g_e(t)$ for each element $e$ and $\xi =\left\{p_0,q_0,p_1,q_1,\dots ,p_m,q_m\right\}$ be the collection of nodal values, the full interpolation function with m elements is then given by

$$\begin{gathered} 𝒴(t)=\sum _{e=1}^m{\xi }_{2e-2}{\varphi }_0^p(g_e(t))+{\xi }_{2e-1}{\varphi }_0^q(g_e(t)) \\ +{\xi }_{2e}{\varphi }_1^p(g_e(t))+{\xi }_{2e+1}{\varphi }_1^q(g_e(t)). \end{gathered}$$ (A.2)

Fig. A.1.

Flowchart of the algorithm for filtering data. $𝒴\left(t_j\right)$ is the interpolation of $y_j$ at $t_j$.

Given the data $\left(t_i,y_i\right)$ for $i\in \{0,1,\dots ,n\}$ then the Hermite parameters $\xi$ can be determined by solving $y_i=A_{ij}{\xi }_j$ (summation over $j$ is implicit here), where the interpolation matrix $\mathbf{A}$ can be determined from Eq. (A.2). Assuming that the rank of $\mathbf{A}$ is $m$, i.e., there are sufficient data points within the range of each Hermite element, then there exists a Moore-Penrose inverse ${\mathbf{A}}^{+}$, where ${\mathbf{A}}^{+}\mathbf{A}=\mathbf{I}$ so that

$${\xi }_j=A_{ji}^{+}{y}_i.$$ (A.3)

Considering that $\mathbf{A}$ only depends on $t_i$, the same ${\mathbf{A}}^{+}$ can be used to determine the Hermite element parameters for all components of the displacements and forces and $\mathbf{A}$ can be used to interpolate for the filtered outputs.

Let ${\xi }_j^c={\left(A^c\right)}_{ji}^{+}{y}_i^c$ be the Hermite system for each curve $c$ and let ${\xi }_l=A_{lk}^{+}{y}_k$ be the generalization of one loading curve to the global system for the entire data set. Assuming that there are $N$ loading curves, the cost of computing $A_{lk}^{+}$ from $A_{kl}$ has a time complexity of $𝒪\left(N^3{m}^3\right)$, which could become intractable. As an alternative strategy, note that the interpolation of each curve is independent except at the junctions. Let $k_i^c$ and $l_j^c$ be the mapping of the local curve index to the global index and $m$ be the number of Hermite elements per curve, as above. At the junctions, ${\xi }_0^c={\xi }_{2m+1}^{c-1}$, i.e., ${\left(A^c\right)}_{0,i}^{+}{y}_i^c={\left(A^{c-1}\right)}_{2m+1,i}^{+}{y}_i^c$. For $N$ loading curves, the global Moore-Penrose inverse can be assembled by

$$A_{l_j^c,k_i^c}^{+}=\left\{\begin{array}{ll}\frac{1}{2}\left[{\left(A^c\right)}_{0,i}^{+}+{\left(A^{c-1}\right)}_{2m+1,i}^{+}\right]& \text{if}j=0\vee j=2m+1,\\ {\left(A^c\right)}_{j,i}^{+}& \text{otherwise.}\end{array}\right.$$ (A.4)

Assembling $A_{lk}^{+}$ this way has a time complexity of only $𝒪\left({Nm}^3\right)$, where $m$ is also capped.

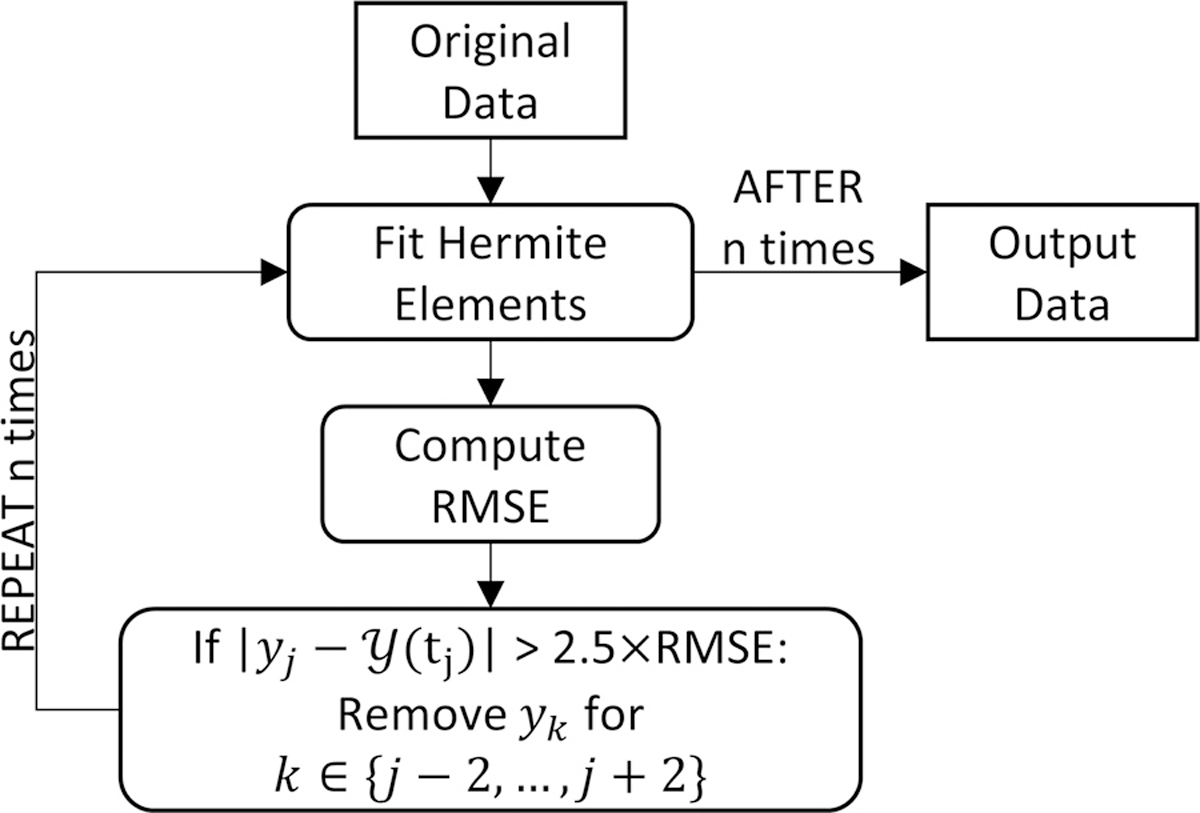
For filtering, we assume that outliers in the data are the points that are more than 2.5 times the RMSE of the best fit of the Hermite elements. Thus, the filter can be applied through the following steps:

1. Fit data to Hermite elements

2. Compute root mean squared error

3. Find outliers that are more than 2.5×RMSE away from the interpolation

4. Remove outliers and their neighbors from the data set

5. Repeat step 1 for a set number of times

6. Return data

   1. Remove outliers only: fill missing values with interpolated values

   2. Remove outliers and noise: return interpolated values

An example algorithm is illustrated in Fig. A.1. Outliers can have a significant effect on the RMSE. By nesting the filter, we converge to the true RMSE resulting from the noise. Typically, we observed that the RMSE does not change significantly after three repetitions. This approach is very effective. Fig. A.2 A shows the filtered marker position versus the raw measured data in an example where the tracking of a marker was temporarily lost. The underlying data and noise were well preserved, with all outliers gone. Fig. A.2 B shows an example of noise removal. Here, the properties of the data are retained.

Fig. A.2.

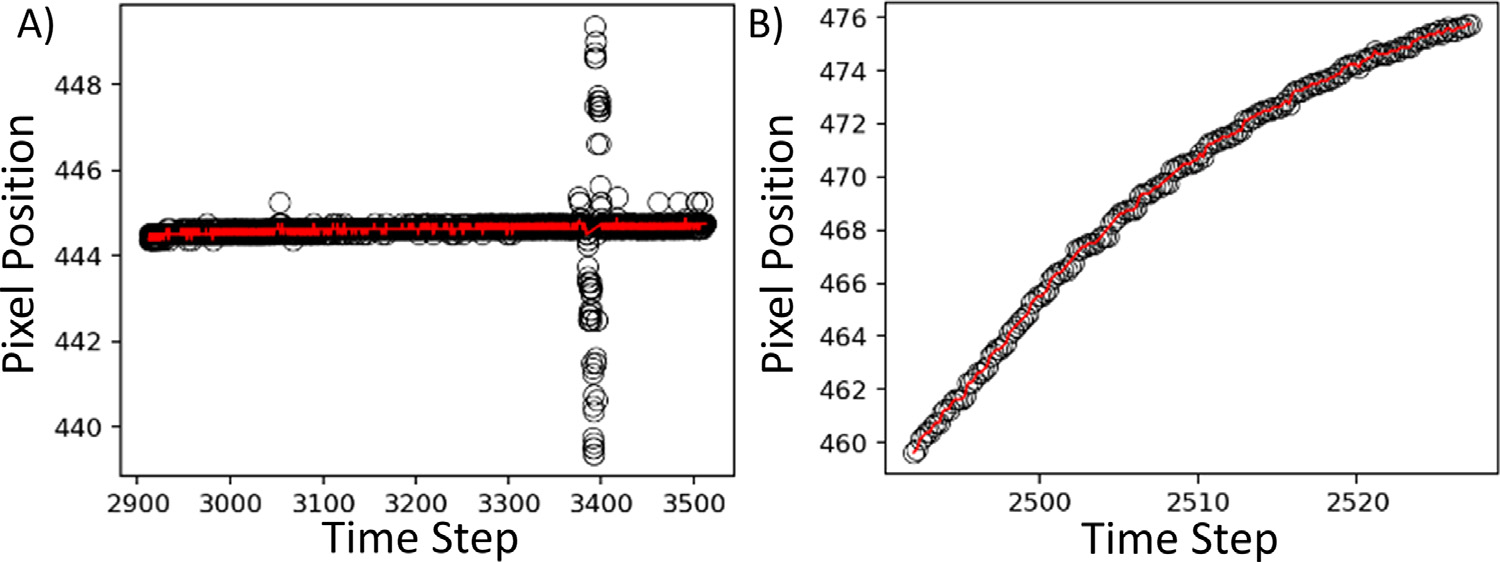
A) Filtered results for data with outliers. B) Filtered results for noisy data.

Appendix B. The form of the objective function

In developing the objective function presented in Section 2.9, our focus was on robustness (in terms of tolerating errors in the data), repeatability, convergence rate, and physiological accuracy. There were several methods we considered for achieving these goals, including the parameter estimation algorithm, changing the model form, changing the residual norm, changing the stress weighting, applying additional penalties on the material parameters, and incorporating multiple data sources. The optimization algorithm, the scaled model form, and the incorporation of hysteresis and relaxation data are presented in Sections 2.10, 2.5, and 2.9, respectively, and are discussed in the discussion. We have done extensive testing of various residual norms and various combinations of parameter penalties prior to arriving at the final form.

In summary, there are 3 main components in the objective function (Eq. (19)): the residual, the hysteresis, and the penalties,

$$ℱ\left(\xi \right)=\left[\chi \left(\xi \right)+\varphi \left(\xi \right)\right]\left(1+𝒫\left(\xi \right)\right),$$ (19 revisited)

The hysteresis data are incorporated as a separate sum to the stress residuals. The relaxation data, on the other hand, are incorporated indirectly into the stress residuals and hysteresis, and directly as terms in the penalty for the viscoelastic constants. As such, the weights of these penalty terms are 2 to 3 magnitude greater than the penalty terms on the orientation of the specimen, $\theta$, and the orientation of the collagen fiber families, $\alpha$.

Fig. B.1.

Example best fit A) without the weights in Eq. (21) and B) with only the protocol-specific part of the weights.

Fig. B.2.

Example showing discrepancy occurring in the data from testing. A) Shows the full protocol over time; the redundant equibiaxial loading curves at B) and C) are used to show differences in the curves. Weights are used to bias the fit to curve C).

Table B.1.

Comparing best-fit values with different residual norms (Eqs. (B.1)–(B.3)).

	Hyperelastic							Viscoelastic
	${\mathit{\mu }}_{\mathit{g}}(\mathbf{k}\mathbf{P}\mathbf{a})$	${\mathit{\mu }}_{\mathit{c}}^{\mathbf{*}}(\mathbf{k}\mathbf{P}\mathbf{a})$	${\mathit{b}}_{\mathit{c}}$	${\mathit{\mu }}_{\mathit{e}}^{\mathbf{*}}(\mathbf{k}\mathbf{P}\mathbf{a})$	${\mathit{b}}_{\mathit{e}}$	${\mathit{\mu }}_{\mathbf{s}}^{\mathbf{*}}(\mathbf{k}\mathbf{P}\mathbf{a})$	${\mathit{b}}_{\mathit{s}}$	${\mathit{y}}_{\mathit{c}}$	${\mathit{v}}_{\mathit{s}}$	${\mathit{R}}^2$	${\mathit{N}}_{\text{iter}}$
Quadratic (B.1)	4.87	35.02	12.40	25.36	0.00	88.35	11.13	0.016	0.032	0.996	747
Absolute (B.2)	4.32	39.25	13.73	23.01	0.00	93.25	12.34	0.014	0.034	0.988	1161
Cubic (B.3)	4.75	42.88	11.22	24.53	0.00	75.62	10.40	0.017	0.029	0.998	1620

Fig. B.3.

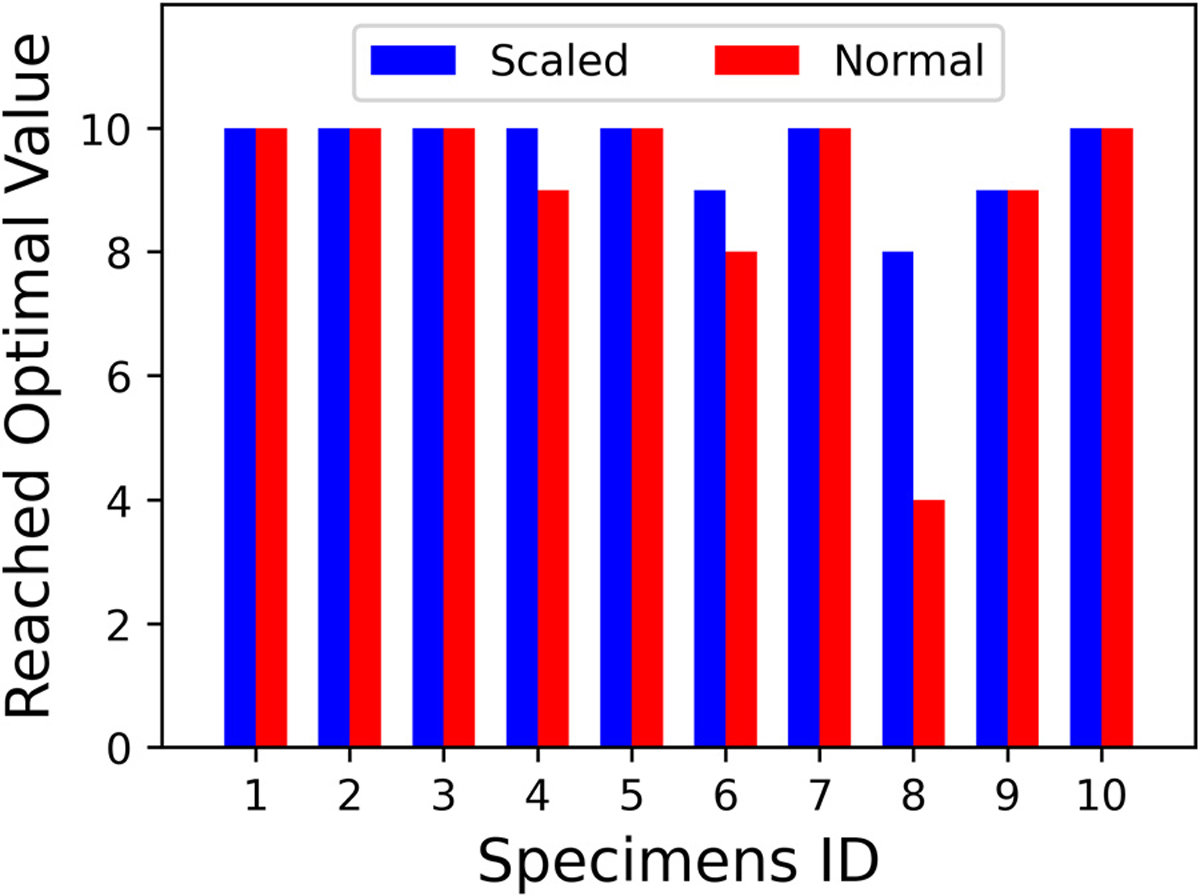
The number of specimens that converged to the best-fit values. The scaled fiber model (Eq. (12)) is shown in blue, and the normal fiber model (Eq. 8) is shown in red. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

$$\begin{gathered} 𝒫(\xi )=0.001{\theta }^2+0.01{\left(\alpha -\frac{\pi }{4}\right)}^2 \\ +{\left(v_c-v_{\text{long}}\right)}^2+{\left[\frac{1}{2}\left(v_c+v_s\right)-v_{\text{circ}}\right]}^2. \end{gathered}$$ (24 revisited)

We are only applying generic penalties to the two parameters $\theta$ and $\alpha$. The penalties are also sufficiently small, i.e., approximately 1% of the total objective function value, so they do not play a major role in determining the parameters with the exception of when there is a lack of uniqueness, i.e., the objective function is relatively flat. For this reason, the penalties are applied as a multiplier to the sum of the residuals and the difference in hysteresis to avoid the need to scale and normalize the penalties to the data. The weights are further chosen such that they have the smallest base power of 10 such that the penalties still produce the desired effect.

The weight introduced in Eq. (21) looks complex, but the idea behind it is simple.

$${𝒲}_{ii}^p=\left[1+\frac{1}{4}{(\frac{p}{n_p})}^2\right]{\left(\sum _{k=N_0^p}^{N_e^p}{\widehat{S}}_{ii}^k+\frac{1}{n_p}\sum _{k=0}^{N_e^{n_p}}{\widehat{S}}_{ii}^k\right)}^{-1}.$$ (21 revisited)

These are loading-cycle-specific weighting that has two aims: 1) recalibrate the importance of each loading cycle to the overall fit and 2) robustness and protection against errors during testing. Fitting the sum of squares error carries the inherent assumption of the data being random Gaussian distributed errors about a curve. However, we do not have perfect constitutive descriptions of biological materials. Idealization, homogenization, and utilization of a continuum approach are necessary. This means the errors are biased. Although there are theories for tackling this problem in maximum likelihood estimation, they require significantly more data that are often not obtainable – playing a part in the lack of their popularity. Because the true errors are biased, this places undue weight on the high-stress data in determining the overall fit. The equibiaxial loading cycle and other loading cycles that are nearly equibiaxial are therefore disproportionately weighted in comparison to the low-ratio loading cycles. However, the entire spectrum of loading ratios is important for describing the axial coupling of the material, e.g., the orientation of the collagen fibers. Due to the lack of shear stress, these low-ratio loading cycles should not be neglected (Fig. B.1 A). Thus, we introduced a balancing weight, ${\sum }_{k=N_0^p}^{N_e^p}{\hat{S}}_{ii}^k$, that scales by the total stress of each loading path. On the other hand, the low-ratio loading cycles are usually also the most error-prone and can negatively affect the overall fit (Fig. B.1 B). To mitigate this, the weight was balanced with the average stress of all cycles, $\frac{1}{n_p}{\sum }_{k=0}^{N_e^{n_p}}{\hat{S}}_{ii}^k$.

The second part of the weight establishes a slight bias to the weights, i.e., the last loading cycle, the relaxation curve, can weigh 25% more than the first cycle. Most often, we do not observe a difference in the best-fit parameters with this value. However, the testing protocol (Section 2.2, Fig. 2) for the data sets is very long, sometimes over an hour. Within this period, there can sometimes be a slight shift in the grip of the attachment or a change in load cell voltage. While the overall mechanical response does not change significantly, it can shift and become somewhat inconsistent, thereby introducing multiple local minima. To resolve this, we introduced a bias in the selection of local minima. Because the relaxation data was from the last loading cycle, this weight was more favorable to the later loading cycles. Fig. B.2 B illustrates the equibiaxial behavior before such an event, and Fig. B.2 C illustrates the equibiaxial behavior after this event. The value of 25% may not be optimal but through our preliminary testing, it was found sufficient.

We also examined multiple residual norms used for the objective function,

$$\chi (\xi )=\sum _{i\in 1,2}\sum _{p=1}^{n_p}{𝒲}_{ii}^p\sum _{k=N_0^p}^{N_e^p}{(S_{ii}^k(\xi )-{\widehat{S}}_{ii}^k)}^2,$$ (B.1)

$$\chi (\xi )=\sum _{i\in 1,2}\sum _{p=1}^{n_p}{𝒲}_{ii}^p\sum _{k=N_0^p}^{N_e^p}\left|S_{ii}^k(\xi )-{\widehat{S}}_{ii}^k\right|,$$ (B.2)

$$\chi (\xi )=\sum _{i\in 1,2}\sum _{p=1}^{n_p}{𝒲}_{ii}^p\sum _{k=N_0^p}^{N_e^p}{\left|S_{ii}^k(\xi )-{\widehat{S}}_{ii}^k\right|}^3,$$ (B.3)

These produced slight differences in the final parameters (Table B.1) due to the bias towards the high-stress data for the cubic, Eq. (B.3), and low-stress data for the absolute value, Eq. (B.2). The magnitude of the corresponding parameters did not change significantly, but the number of iterations to converge was clearly favorable for the quadratic norm. Because we are already using weights to balance the high-stress data, the quadratic form was chosen.

Finally, we investigated the uniqueness and reproducibility of the material fits. Some of the work on examining the parameter correlation and the quality of the global minimum was shown in Fig. 3. In general, we found sufficiently low parameter correlations to find the minimum. We also conducted a trial of 100 runs with randomized initial parameter seeds, 10 per specimen, and checked how many converged to the global minimum. Here, we assume that the global minimum is the parameter set with the best $R^2$ value for each specimen. Although not perfect, only 4 of 100 runs failed to converge to the optimal values (Fig. B.3). In comparison, 10 of 100 failed without implementing the scaling approach. Also, specimens with more linear behavior subjected to low stresses were more difficult to fit.