Abstract
A mechanistic, dynamic model was developed to calculate body composition in growing lambs by calculating heat production (HP) internally from energy transactions within the body. The model has a fat pool (f) and three protein pools: visceral (v), nonvisceral (m), and wool (w). Heat production is calculated as the sum of fasting heat production, heat of product formation (HrE), and heat associated with feeding (HAF). Fasting heat production is represented as a function of visceral and nonvisceral protein mass. Heat associated with feeding (HAF) is calculated as ((1 − km) x MEI), where km is partial efficiency of ME use for maintenance, and MEI = metabolizable energy intake) applies at all levels above and below maintenance. The value of km derived from data where lambs were fed above maintenance was 0.7. Protein change (dp/dt) is the sum of change in the m, v, and w pools, and change in fat is equal to net energy available for gain minus dp/dt. Heat associated with a change in body composition (HrE) is calculated from the change in protein and fat with estimated partial efficiencies of energy use of 0.4 and 0.7 for protein and fat, respectively. The model allows for individuals to gain protein while losing fat or vice versa.
When evaluated with independent data, the model performed better than the current Australian feeding standards (Freer et al., 2007) for predicting protein gain in the empty body but did not perform as well as for gain of fat and fleece-free empty body weight. Models performed similarly for predicting clean wool growth. By explicit representation of the major energy using processes in the body, and through simplification of the way body composition is computed in growing animals, the model is more transparent than current feeding systems while achieving similar performance. An advantage of this approach is that the model has the potential for wider applicability across different growth trajectories and can explicitly account for the effects of systematic changes on energy transactions, such as the effects of selective breeding, growth manipulation, or environmental changes.
Keywords: body composition, growth, modeling, metabolism, nutrition, ruminant
This paper presents a revised dynamic, mechanistic model of heat production and body composition in sheep where heat production is calculated internally as the sum of fasting heat production, heat associated with feeding, and heat from changes in bodily protein and fat pools. The resulting model reflects the variation in heat production that arises both from feed, the animal, and the intersection of these two sources, and is a simpler and more flexible way to predict energy requirements and heat production in growing ruminants than traditional feeding systems.
Introduction
Traditional feeding systems calculate energy transactions from fasting heat production and energy density of the feed (Freer et al., 2007; NASEM, 2016). The current Australian feeding standards for ruminants (Freer et al., 2007), otherwise known as the CSIRO model, is based on metabolizable energy and defines variation in the efficiency of energy use for maintenance as a function of metabolizable energy density and type of feed. Energy content of gain is computed from historical data on fat and protein content and adjusted for weight relative to maturity scaled by standard reference weight to account for differences in size due to breed. However, this does not adequately capture the relationship between feed eaten and prior growth pattern on the gain of protein and fat in the period in which animal’s transition to the new equilibrium state. Moreover, the attribution of variation in energy use to energy density of feed alone does not account for the effect of variation in HP from fat and protein deposition on energy use for gain (Marcondes et al., 2013).
The underlying basis for variation in heat loss from ingested feed in growing ruminants is complex and has been attributed to a range of mechanisms including—conversion of energy-yielding substrates, principally VFA to ATP (Blaxter, 1962), variation in use of ATP due to protein turnover and Na-K ATPase activity (McBride et al. 1985) and relative differences in the size of organs each with different energy expenditure (Ferrell, 1988). Baldwin and Black (1979) outlined a framework to incorporate these sources of variation in responses to animal growth to feed into a computer program. Subsequently (Baldwin et al., 1987; Black et al., 1987; Gill et al., 1989) incorporated aspects of metabolic control of nutrient utilization into research scale models, without explicit consideration of the effects of relative contributions of different organs. Di Marco and Baldwin (1989) and Di Marco et al. (1989) developed a model that simplified organ size and protein turnover and energy expenditure into two pools (viscera and nonviscera), and Sainz and Wolffe (1990) devised a model of sheep growth using four protein pools (carcass, viscera, skin, and wool). In contrast to current feeding systems, these models require data inputs that are not readily available or easily estimated, precluding their use in practice. More empirical approaches as used in current feeding systems work relatively well when applied to typical production practices. However, much research in animal nutrition has been done to address deficiencies in the feeding systems used, and the model presented in this paper lies somewhere in between the two approaches while expanding the input needs to eventually provide more robust predictions as production practices and animal genetics progress.
Oltjen et al. (1986) introduced a simplified model of growth using a single protein pool and energy transactions derived from the California Net Energy system. At the time it predicted growth at least as well as the NRC (1976), but it underpredicted protein gain and over-predicted fat gain on high-energy diets (Arnold and Bennett, 1991). An alternate approach that used two protein pools and a traditional method for describing energy transactions (Corbett et al., 1990) was developed by Soboleva et al. (1999) using data from growth path studies of sheep in which nutrient supply varied from restricted to ad libitum and which permitted marked variation in growth including the opportunity for compensatory growth (Ferrell et al., 1986). This model was further developed by Oltjen et al. (2006) who suggested HP could be estimated from protein dynamics.
The work described here extends the model of Oltjen et al. (2006) by calculating HP internally within the model and features revised protein pool equations and the addition of a wool protein pool. The current paper describes the development of the revised model and the use of new data to evaluate the prediction ability of the model compared to the traditional methods used by the current Australian ruminant feeding standards (Freer et al., 2007).
Materials and Methods
Data used in the work reported here came from previously published studies. No new animal experiments were conducted in this work. As such, no animal care and use committee approvals were needed to conduct this work.
Underlying assumptions
The work presented in the current paper is based on axioms of animal growth articulated by Soboleva et al. (1999) and elsewhere in the history of this model (Oltjen et al., 1986, 2000, 2006; Oddy et al., 2019, 2021, 2022; Dougherty et al., 2020, 2022a–d). Specifically, there are six assumptions in the model.
(1) Growth is driven by energy intake, and for the purposes of the current model, other nutrients (amino acids, vitamins, and minerals) are assumed nonlimiting.
(2) Protein in the fleece-free empty body (FFEB) can be classified into two pools based on relative turnover rates and their respective rates of energy use/HP per gram of tissue protein. The smaller protein pool consists of tissues with high rates of protein turnover and high specific HP. This pool, called viscera (v), consists of the empty gut, liver, kidneys, heart, and lungs. The other pool is larger with a slower turnover rate and lower HP per unit of tissue protein. This pool, called “muscle” (m), contains not just muscle protein but protein in all nonvisceral tissues in the FFEB (muscle, skin, head, hocks, blood, and bone). Wool (w) is a separate protein pool that acts as a protein sink.
(3) Protein in visceral and nonvisceral pools have their own respective upper bounds. In nonvisceral tissue, this upper bound, m*, is defined as mature protein mass and is calculated from mature size and composition, factoring in the effects of breed and sex. No consideration is given in this iteration of the model of the effects of stunting due to nutritional deprivation. In visceral protein, this upper bound, v*, is a function of feed intake, feed characteristics, and the relative maturity of the animal. This upper bound is not a fixed target like m*. Rather, because visceral tissues are more sensitive to energy supply than nonvisceral tissues, v* represents “equilibrium” visceral mass for a given feed and feeding level combined with the stage of maturity of the animal.
(4) When energy intake is close to the point where retained energy (RE) equals 0, animals can gain protein while mobilizing fat. This potential for protein gain diminishes in nonvisceral tissue as animals reach maturity, but not in viscera or in wool.
(5) The gain of protein in the nonvisceral (“muscle”) pool is proportional to net energy available for gain (NEG) and relative protein deposition potential, as defined by the animal’s relative maturity.
(6) Energy not lost as heat production, or used for protein gain in wool, viscera, and nonvisceral tissue, is deposited as fat.
Description of previous version of model
Oltjen et al. (2006) used lamb growth and body composition data from Ferrell et al. (1986) to evaluate and investigate a prior version of the model (Soboleva et al., 1999; Oltjen et al., 2000).
The model of Oltjen et al. (2006) is:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
where v and m are the visceral and nonvisceral pools, f is the fat pool, NEG is net energy available for gain, all in kJ. In Equations (1)–(8), km and kv are rate constants for the partitioning of retained energy (RE) into muscle and viscera, respectively; cm × fa is an adjustment to account for continued deposition of protein in muscle when retained energy is negative, and the terms cm, e2, cs1, c2, b1,b2, b3, and b4 are constants. As described above, m* is the upper bound on the m pool, specifically nonvisceral protein at maturity, and v* is the upper bound on visceral crude protein for a given level of intake (MEI) and animal size (m). Change in empty body weight (EBW) is calculated from the change in the energetic content of the protein and fat pools (kJ/d), where 0.2201 is the crude protein content of 1 kg of fat-free tissue, and 23.8 and 39.6 are the energy density (MJ/kg) of protein and fat, respectively. This was the starting point for the revised model presented here.
Data used for development and evaluation
The Oltjen et al. (2006) model described above was revised using individual feed intake and lamb growth and body composition (fat, protein, ash, and dry matter) data from the final phases of the studies reported by Hegarty et al. (1999) and Dougherty et al. (2022a). These were the only available serial slaughter studies of sheep fed a pelleted diet at different rates of energy and escape protein supply (Hegarty et al., 1999) and with ad libitum intake of pelleted diets differing in energy density and escape protein (Dougherty et al., 2022a) on which individual data on intake and body composition were available. Unlike the study of Ferrell et al. (1986) in which the animals were fasted for 4 d prior to slaughter with commensurate changes in mass of viscera, the animals used here were fed between 2 and 12 h before slaughter. The combined data from the final phases of these studies is shown as development data in Table 1.
Table 1.
Summary of data from studies used in development and evaluation of the model
| Measure | Development data (n = 187)1 | Evaluation data (n = 121)2 | ||||
|---|---|---|---|---|---|---|
| Mean | SD | Range | Mean | SD | Range | |
| Initial age, m | 7.63 | 0.91 | 6.7 to 8.5 | 5.43 | 2.09 | 2.9 to 11.0 |
| SRW, kg | 70 | 0 | 70 to 70 | 76.2 | 6.98 | 70 to 100 |
| MEI, MJ/d | 11.8 | 4.03 | 4.9 to 22.8 | 12.3 | 3.04 | 5.0 to 15.3 |
| M/D, MJ/kg DM | 9.87 | 1.25 | 7.7 to 12.7 | 10.9 | 0.53 | 8.5 to 11.3 |
| DOF, d | 89 | 5.1 | 75 to 99 | 63 | 15.4 | 36 to 207 |
| Initial LWT, kg | 38.7 | 8.97 | 24.3 to 58.0 | 34.7 | 6.27 | 20.0 to 51.0 |
| Initial %EBF | 24.4% | 3.51% | 19.5% to 33.2% | 16.1% | 3.43% | 8.2% to 25.4% |
| Final LWT, kg | 49.7 | 7.49 | 31.1 to 69.8 | 42.3 | 7.49 | 25.0 to 60.5 |
| Final %EBF | 26.7% | 4.57% | 15.4% to 36.7% | 22.9% | 4.66% | 11.4% to 31.7% |
| CWG, g/d clean | 7.4 | 1.98 | 3.6 to 13.1 | 9.3 | 1.24 | 5.3 to 9.9 |
| ADG of FFEB, kg/d | 0.11 | 0.07 | −0.05 to 0.29 | 0.11 | 0.07 | −0.07 to 0.24 |
| RE in FFEB, MJ/d | 1.80 | 1.51 | −1.95 to 5.49 | 6.50 | 2.88 | −0.31 to 11.4 |
Notes: Values shown are mean, standard deviation (SD) and range of traits.
ADG of FFEB, average daily gain of fleece free empty body; CWG, clean wool growth; DOF, days on feed; EBF, empty body fat as % Empty BW; LWT, liveweight; M/D, metabolizable energy density of the feed offered; MEI, metabolizable energy intake; RE in FFEB, energy retained in FFEB.
1Individual lamb data from the final (experimental) phases of Hegarty et al. (1999) and Dougherty et al. (2022a);
2Individual lamb data from Keogh et al. (2023), and the preliminary phase of Dougherty et al. (2022a) and treatment means from Turgeon et al. (1986).
The model was evaluated against data not used in development (evaluation data described in Table 1). Individual lamb data from three experiments where body composition was measured in Merino cross lambs of similar ages but with different weights, growth rates, and nutritional histories (the preliminary period of Dougherty et al., 2022a; Keogh et al., 2023), together with nine treatment means from a similar study with Suffolk × Rambouillet lambs by Turgeon et al. (1986). Lambs used in Dougherty et al. (2022a) were castrated males, while Turgeon et al. (1986) and Keogh et al. (2023) used a mix of females and castrated males. Energy intake varied from below maintenance to ad libitum and feed intake was recorded daily. For the serial slaughter studies of Turgeon et al. (1986) and Dougherty et al. (2022a), tissue and organ weights were recorded at harvest, and body composition was measured by postmortem chemical analysis. For Keogh et al. (2023), the composition of the fleece-free empty body was estimated via CT scan. Diets were pelleted except those of Turgeon et al. (1986) in which a mixed forage and concentrate diet was used. Estimations of gain of body weight, fat, and protein from the revised model were compared with those obtained from the CSIRO model (Freer et al., 2007) using the evaluation data described in Table 1.
Statistical analysis
The model was developed in R (R Core Team, 2023) as a dynamic, mechanistic model with a daily timestep. Model parameter values were estimated in three stages: this approach was chosen due to the performance limitations found when optimizing many parameters simultaneously.
The coefficients in the revised v* equation (CMEI, Cm, and CMD) were estimated from experimental data (Oddy et al., 1997; Hegarty et al., 1999; Dougherty et al., 2022a) via multiple regression in Minitab (Minitab LLC, 2022). This was done by using the final observed visceral energy as an estimate of v* because the experimental period was long enough for the visceral tissues to have reached a steady state for each of the feeds (>40 d; Burrin et al., 1990; Freetly et al. 1995). These initial values were then refit in R using the optim() function (R Core Team, 2023) to minimize the prediction error for the data from Hegarty et al. (1999) and Dougherty et al. (2022a).
The remaining parameters were optimized in two stages within the dynamic mechanistic model. First, the parameters in the dm/dt equation (pm and e0) were optimized by using observed RE in place of estimated NEG since this allows these parameters to be decoupled from the effects of other parameters and equations. In this stage, goodness of fit was calculated using the RMSE of the residuals of final muscle energy.
Finally, the remaining parameters (pv and the HP coefficients) were estimated using the full model. For this stage, it is necessary to calculate an overall goodness of fit for the three nonlinear response variables (muscle protein, visceral protein, and fat) simultaneously, because the parameter values affect all three tissue pools. Parameter estimation and optimization must therefore consider the different scales and variances of these pools, as well as the covariances of the residuals. This was done by minimizing the determinant of the residual matrix as described by Bates and Watts (1988). This corresponds to the maximum likelihood estimate for multivariate normal residuals. For an (N × 3) matrix R of residuals for N data points and three response variables, the (3 × 3) residual matrix is the matrix calculated by matrix multiplication as RT × R.
For both stages of parameter estimation within the dynamic mechanistic model, initial parameter estimates were derived from literature values and then parameter optimization was performed using the L-BFGS-B (Byrd el al., 1995) and Nelder and Mead (1965) methods of the optim() function in R (R Core Team, 2023) to minimize the prediction error for the data from Hegarty et al. (1999) and Dougherty et al. (2022a). The parameter estimates were cross-checked using the Metro_Hastings function from the MHadaptive package (Chivers, 2012) using Markov Chain Monte Carlo methods and a Metropolis-Hastings algorithm with 100,000 runs (Tanner, 1996). This also provided measures of the correlations between model parameters.
Prediction error was calculated as the determinant of the residuals matrix for the response variables (muscle protein, visceral protein, and fat). Parameter values were varied within a specified range and relative error for a specific parameter was calculated iteratively by running the model with the specific parameter value, taking the determinant of the residuals matrix, and dividing that value by the lowest value of the determinant from prior runs in that range of parameter value runs.
Models were evaluated using mean square prediction error (MSPE), which was then decomposed into mean bias, slope bias, and random error using the methods of Bibby and Toutenberg (1977) and expressed as a proportion of MSPE. The root mean square error (RMSPE) is used to report prediction error in the same units as observed values and is here expressed as a percentage of the observed mean for ease of assessment and comparison. The coefficient of variation of the observations (CV) and coefficient of determination (r2) are also reported. Model residuals were plotted against centered predictions and linear regression trendlines (y = ax + b) were plotted for each model to allow for visual assessment of mean and slope bias, as by Dougherty et al. (2017).
Results and Discussion
Model revision and parameter estimation—retained energy
The major changes from Oltjen et al. (2006) are 1) simplification of the method for calculation of dm/dt and dv/dt, 2) inclusion of wool as a protein sink, and 3) re-working of the manner in which HP is represented. The representation of a fat pool (f), as shown above in equation (5), remains unchanged from Oltjen et al. (2006).
Nonvisceral empty body protein
Oltjen et al. (2006) utilized the data from Ferrell et al. (1986), in which body component weights were measured after 4 d of fasting and obtained values of e2 = 3.4 and cm = 1,340 kJ/d for the continued protein gain in the NVEB pool equations when NEG < 0 (equations (1) and (2), as described above). However, when these equations were fitted to the data of Hegarty et al. (1999) and Dougherty et al. (2022a), the value for e2 was determined to be 0.25 (SE = 0.99); i.e., not different from zero. Accordingly, the value of equation (2) approaches 1 and equation (1) can be simplified with a single term, e0, to account for protein gain when NEG < 0, as shown in equation (9).
| (9) |
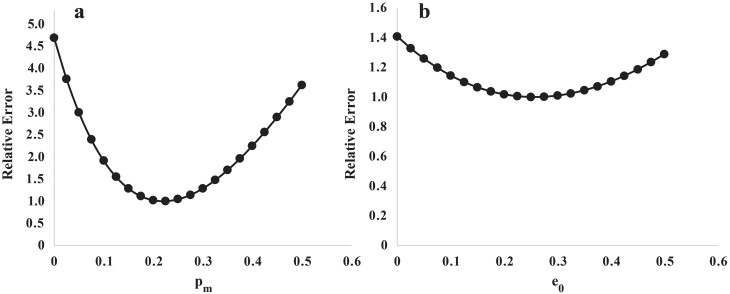
An initial estimate for pm was obtained from data on protein gain measured by A-V difference in the hindlimb of growing lambs (Early et al., 1988; Harris et al., 1992; Oddy and Owens, 1996) and an estimate of NEG from the same data. This suggested that pm may lie in the range of 0.18 to 0.24. On the basis of a summary of the literature reporting the relationship between nitrogen and energy balance (Graham, 1964a–c, 1969; Wainman et al., 1970; Black and Griffiths, 1975) and from the hindlimb A-V difference studies summarized by Oddy (1993), a value for e0 between 0.16 and 0.3 MJ/d was expected. When pm and e0 were fitted simultaneously to data from Hegarty et al. (1999) and Dougherty et al. (2022a), the values obtained were; pm= 0.226 (±0.016) (Figure 1a) and e0 = 0.2486 (± 0.034) (Figure 1b).
Figure 1.
Relative error vs. values for (a) pm and (b) e0 (parameters for representation of dm/dt) fitted one at a time against data from Hegarty et al. (1999) and Dougherty et al. (2022a). Relative error was calculated iteratively by running the model with the specific parameter value, taking the determinant of the residuals matrix, and dividing that value by the lowest value of the determinant from prior runs in the range of parameter values used.
Dougherty et al. (2020, 2022b) provided a method to calculate m* from standard reference weight (SRW; Freer et al., 2007) and noted the importance of accounting for variation in mature body composition by breed and sex. The CSIRO (Freer et al., 2007) model defines SRW as the average fleece-free weight of a mature ewe in average condition, while NASEM (2007) states that a mature sheep at SRW is assumed to have approximately 25% fat. However, data from the continuous growth of animals suggest that fatness at maturity (SRW) can be over 40% (Searle and Griffiths, 1976; Butterfield, 1988). More data on variation in mature size and composition is needed to more accurately underpin estimates of SRW and/or m* to improve the ability of the model to capture variation in mature size and its effects on animal growth rates.
Visceral protein
Visceral protein (v) refers to protein in visceral tissue, i.e., empty reticulo-rumen and gastrointestinal tract, liver, kidneys, heart, and lungs. The rate of change of visceral protein in the revised model is calculated as described by Oltjen et al. (2006):
| (10) |
where pv (kv by Oltjen et al. 2006) is the rate of change in visceral organ protein energy content following a change in energy intake, and v* is the upper bound of protein in viscera.
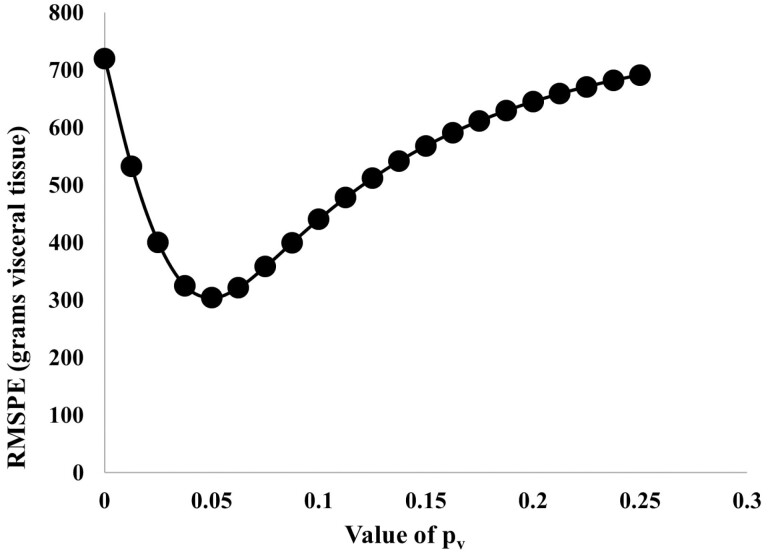
Estimation of pv requires data on visceral protein mass measured during the period in which viscera is responding to changes in feeding level. Studies in which data on oxygen uptake by the splanchnic bed (Burrin et al., 1989) and in which visceral organ weights were recorded at 14 d intervals (Burrin et al., 1990) were used to derive an estimate of pv of 0.05 (Figure 2). This value of pv is similar to 0.093, the value obtained by Freetly et al. (1995) for the rate constant for change in oxygen consumption by the splanchnic bed in response to changes in diet; this is similar to the value for the lag in energy expenditure (0.05, corresponding to a lag of 20 d) derived by Soboleva et al. (1999) using the data of Ferrell et al. (1986).
Figure 2.
RMSE (grams of visceral tissue) vs. value of pv (rate constant in estimation of dv/dt) for data from Burrin et al. (1990).
The maximal amount of visceral protein mass for any given energy intake, energy density of feed, and stage of maturity is v*. For practical purposes, it is the mass of visceral protein achieved after 8 wk of eating the same feed (the time to reach equilibrium visceral mass, estimated from data of Burrin et al. (1990) and Freetly et al. (1995)). Analysis of data from Hegarty et al. (1999) and Dougherty et al. (2022a) using pelleted diets, and Oddy et al. (1997) who used mixtures of hays and protein supplements, indicated that MEI, the energy density of the feed (M/D) and mass of NVEB protein affected equilibrium visceral protein mass as shown in equation (11).
| (11) |
where CMEI, Cm, and CMD are coefficients describing the effects of energy intake, nonvisceral protein, and dietary energy density (M/D, MJ/kg DM) on v*, respectively, as described by Oddy et al. (2021).
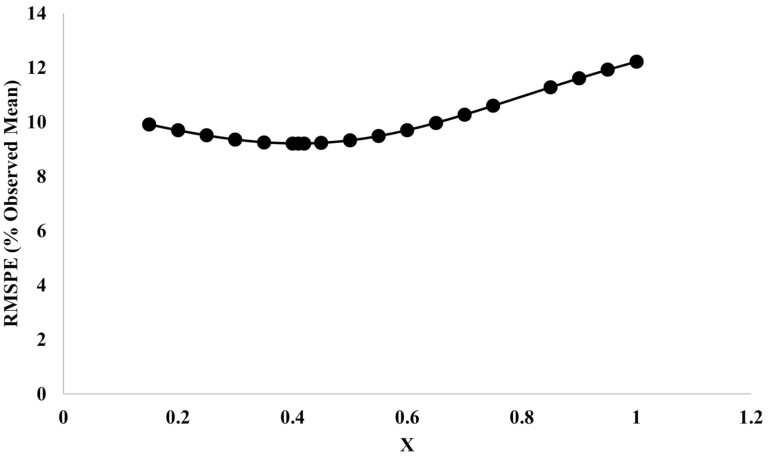
The v* term was derived from data on growing sheep eating different amounts of various diets (Oddy et al., 1997; Hegarty et al., 1999; Dougherty et al., 2022a). Records were selected from lambs that had been fed the same diet for at least 42 d prior to slaughter and v* was estimated by regressing observed visceral protein against MEI (MJ/d), dietary energy density (M/D, MJ ME/kg DM), and nonvisceral protein (m) in the fleece-free empty body (FFEB). The curvilinear relationship between v* and m (Figure 3) is consistent with observations by Butterfield (1988) that visceral tissues are “early maturing.
Figure 3.
RMSE (%observed mean) for visceral protein (MJ) vs. exponent on muscle crude protein (MX) in v* equation which relates potential visceral protein energy content to MEI, M/D, and m*.
The equation for v* is:
| (12) |
In the data used to develop equation (12) the RMSE for visceral protein was 1.49 MJ (9.21% of the observed mean) with a mean bias of −0.0017 MJ (−0.07g). When applied only to the data of Hegarty et al. (1999) and Dougherty et al. (2022a), the RMSE for visceral protein was 9.24% of the observed mean, with mean bias of 0.27 MJ (11.3g). This suggests that the form of the feed eaten affects v*, and is consistent with the observations of Blaxter and Boyne (1978) that the partial efficiency of energy use for maintenance, km, was best estimated separately for different types of feeds (pelleted, forages, and mixed diets). Sheep and cattle eating predominantly roughage diets have larger stomach and intestines than those eating concentrates (Sun et al., 1994, Sainz and Bentley, 1997, Meyer et al., 2015).
Wool growth
Daily clean wool growth is calculated based on the methods of CSIRO (Freer et al. 2007, 2012) and is calculated as a lagged function of the weighted sum of today’s daily (instantaneous) wool growth (Wt) and the prior day’s wool growth (dw/dt−1), where:
| (13) |
| (14) |
W t is a function of breed (WBr), energy intake (MEI), and relative maturity (WZ), where Z is the current liveweight/standard reference weight (SRW).
Wool growth is an important part of sheep production and metabolism but is often omitted from studies on growth and body composition. Wool is a protein sink and cannot be mobilized to support bodily protein or energy requirements, unlike muscle and viscera. However, at low levels of growth and/or intake, such as in mature animals or animals close to maintenance, a large proportion of nitrogen and therefore energy balance is retained in wool (Hegarty et al., 1999; Dougherty et al., 2022a). Accordingly, if total RE is close to or at zero, wool growth and its concomitant RE gain requires the mobilization of resources from the rest of the body (Hegarty et al., 1999; Dougherty et al., 2022a).
Heat production
Oltjen et al. (2006) suggested an alternative for calculation of heat production could be
| (15) |
where b1, …, b4 represent heat produced per unit of protein mass or their respective rates of change. Estimates of b1, …, b4 were obtained from fitting the data of Ferrell et al. (1986). Oddy et al. (2019) attempted to derive estimates of b1 through b4 independently from blood flow and A-V data of oxygen and amino acid fluxes. It was found that estimates of b1 and b2 were identifiable, b3 was somewhat identifiable, but it was not possible to independently estimate b4, the oxygen consumption (heat production) associated with visceral protein gain because of an inability to quantify protein gain due to the simultaneous deposition and secretion of protein from the liver and gastrointestinal tract. Attempts to fit equation (15) to data from Ferrell et al. (1986), Hegarty et al. (1999), and Dougherty et al. (2022a) by combining dm/dt and dv/dt to dP/dt (where dP/dt = dm/dt + dv/dt) to estimate HP from protein gain did not improve the fit to the data. Moreover, the fitting process found HP was consistently associated with MEI. The form of the equation that best fitted the data of Ferrell et al. (1986), Hegarty et al. (1999), and Dougherty et al. (2022a) was
| (16) |
Note that b1 = bm and b2 = bv in the remainder of this paper.
Estimation of fasting heat production
Equation (16) implies that as MEI approaches 0, bm × m + bv × v approaches FHP, so that
| (17) |
Initial estimates of bm and bv were obtained by setting MEI to 0, using the FHP observed by Graham et al. (1974) and the observation of Ortigues and Durand (1995) that in sheep fed between half maintenance and maintenance, half of the whole-body oxygen consumption (HP) was in the splanchnic bed. Initial values of nonvisceral empty body (NVEB) protein and visceral protein were derived from the proportion of tissue masses in the fat-free mass (summarized by Butterfield, 1988), and the proportion of protein in NVEB (0.21) and viscera (0.16) reported by Dougherty et al. (2020).
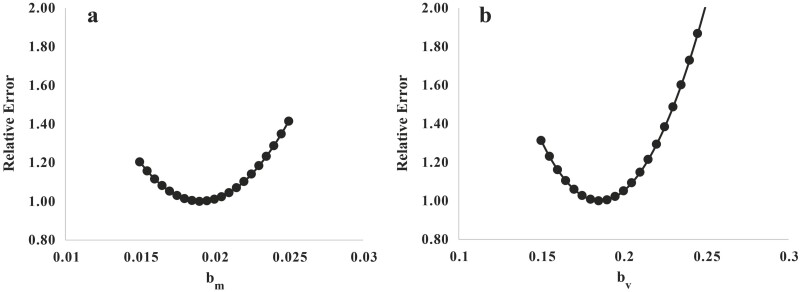
The initial estimates of bm (0.017) and bv (0.17) obtained as above were similar to those subsequently obtained from fitting bm and bv to the development data (Table 1), respectively, bm (0.019 ± 0.0057) and bv (0.185 ± 0.048). Equation (17) allows for variation in FHP due to variation in the protein content of the body and the distribution of protein between viscera and NVEB. This represents the effects of the prior level of feeding on FHP (Marston, 1948; Graham et al., 1974; Ferrell et al., 1986) through effects directly on visceral protein mass relative to the protein mass of the remainder of the body. Accordingly, bm × m + bv × v varies with prior level of feeding and stage of maturity. This model can recapitulate the relationship between FHP and EBW, and FHP and fat-free mass reported in sheep by Graham et al. (1974) as shown by Dougherty et al. (2021).
Fasting heat production is relatively constant per kg liveweight and LWT0.75 in the same animal over extended periods of time (Blaxter, 1962). FHP is used as the baseline for energy expenditure in most feeding systems (ARC 1980; Freer et al. 2007; NASEM, 2007). Graham et al., (1974) summarized a range of studies of fasting heat production in sheep (FHP, called basal metabolic rate in Graham et al., 1974), some of which had different growth rates prior to measurement. In these studies, Graham observed a close to linear relationship between fat-free tissue mass of weaned sheep and FHP and noted that there was systematic variation in FHP due to prior growth rate and/ or feed intake. Ferrell (1988) presented data to show that much of the variation in FHP was due to variation in visceral organ size. Subsequent studies (Eisemann and Neinaber, 1990; Reynolds et al., 1991; Ortigues and Durand, 1995) have demonstrated that the splanchnic bed (liver, reticulo-rumen, and gastrointestinal tract) has a rate of oxygen consumption as much as 10 times higher than peripheral tissues (predominantly muscle).
Contribution of protein and fat gain and ME intake to heat production
All MEI is converted to heat at maintenance (where RE = 0) or below. However, some of the MEI (~30%) is lost as heat due to energy costs of eating, digestion, and metabolism in the body. This is the basis for the calculation of the partial efficiency of ME use for maintenance km (where km = FHP/MEm). There is systematic variation in km due to the type of feed eaten (pellets, forages, and mixed diets) and the ME density of the feed (M/D); on average, for sheep on forage-based diets km has a value of 0.7, such that 1 − 0.7 = 0.3 of MEI is lost as heat (Blaxter and Boyne,1978; Clayton et al., 2022).
It has been assumed that when RE > 0, the efficiency of gain (kg) is due to variation in composition of feed (Lofgreen and Garrett, 1968; Blaxter and Boyne, 1978; ARC, 1980; Freer et al., 2007; NASEM, 2007, 2016), composition of gain (Rattray et al., 1973; Ferrell et al., 1979) or a combination of both (Tedeschi, 2019, 2023, Williams and Jenkins, 2003). Williams andJenkins (2003) developed a construct to describe HP above maintenance that accounted for separate contributions of HP from gain of fat and protein and to the amount of ME ingested above maintenance:
| (18) |
where HiEr is heat produced from fat and protein gain and HiEv is heat produced from support functions and is proportional to MEI.
Williams and Jenkins (2003) presented evidence that heat produced above maintenance due to everything other than gain of protein and fat was 30% to 33% across a range of breeds of cattle. This proportion of heat produced by support functions is similar to the accepted mean for heat associated with MEI at and below maintenance and suggests that the arguments used to justify HP as a function of MEI below maintenance (cost of eating, rumen fermentation, digestion, and excretion) may also apply above maintenance and contribute to the variation in HP associated with gain.
Not accounting for HP due to MEI above RE = 0 overestimates HP due to protein and fat gain. For example, estimates of the partial efficiency of protein and fat gain using multiple regression, which assumes no loss of energy due to eating the additional feed above maintenance other than that due to energy cost of protein and fat deposition, are 12% to 13% for protein and 67% for fat (Rattray et al., 1973; Ferrell et al., 1979). This efficiency of protein gain is substantially less than that reported in other species (~47%; Owens et al., 1995). The corresponding estimate of efficiency of fat gain (67%) is also less than the mean of that reported in other species (76%; Owens et al. 1995) and the theoretical costs of fat synthesis (70% to 72%; Baldwin, 1968).
The ideas of Williams and Jenkins (2003) were incorporated into the understanding of the b0 * MEI term of equation (16) by extending the concept of heat produced by support functions above maintenance but explicitly describing it as the heat associated with feeding (HAF) at any level of feed intake. The heat produced by gain of protein and fat is HrE, which is the heat of product formation (NRC, 1981).
This allows a description of total HP as (Figures 4 and 5):
Figure 4.
Relative error vs. parameter values for (a) bm and (b) bv (parameters used in estimation of FHP) obtained from the combined dataset of Hegarty et al. (1999) and Dougherty et al. (2022a). Relative error was calculated as described in Figure 1.
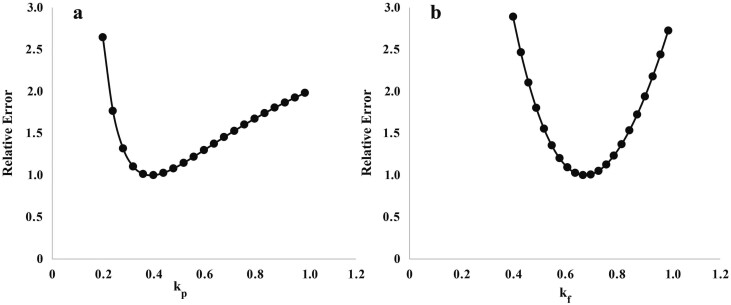
Figure 5.
Relative error vs. values for (a) kp and (b) kf (parameters to estimate HP from protein and fat gain) fitted one at a time against data from Hegarty et al. (1999) and Dougherty et al. (2022a). Relative error was calculated as described in Figure 1.
| (19) |
where FHP = bm × m + bv × v is as described above, the derivation of HrE and HAF are described below.
Heat associated with gain of protein can be calculated as ((1/kp) − 1) × dp/dt and heat associated with gain of fat as ((1/kf) − 1) × df/dt. Therefore:
| (20) |
Heat associated with feeding (HAF) at any level of MEI can be calculated by iteratively fitting values for kp, kf, and HAF to data. The estimate of HAF derived in this way for the data of Hegarty et al. (1999) and Dougherty et al. (2022a) is 0.3 × MEI, i.e., if bMEI = 0.3 then km = 0.7.
It is not possible to obtain useful estimates of the heat produced from gain of protein, gain of fat and heat associated with feeding using multiple regression because of the high correlations between (MEI – MEm), dP/dt and df/dt (Bernier et al., 1987). Accordingly, an iterative process was used in which estimates of heat produced by gain of fat and protein, MEI were initially informed by consensus estimates from the literature. These were then tested in the entire model to determine goodness of fit for the final traits. The estimates of kp, kf, and bMEI, which provided the best fit of the model using the development data set (Table 2), were values of 0.4, 0.7, and 0.3, respectively. These estimates of partial efficiencies of fat and protein gain (0.7 and 0.4, respectively) were close to values observed in monogastric species (Owens et al., 1995). The value of kp is consistent with the energetic efficiency of protein gain calculated from the rate of whole-body protein synthesis relative to protein gain observed in growing lambs (Oddy et al., 1997).
Table 2.
Model parameter values ± standard error and units for revised model
| Term | Definition | Value | Units |
|---|---|---|---|
| b m | Heat production from muscle protein | 0.019 ± 0.006 | d−1 |
| b v | Heat production from visceral protein | 0.185 ± 0.048 | d−1 |
| b p | Heat production from change in body protein | If dP/dt <0, bp = 0; else, bp = 1.5 |
Unitless |
| b f | Heat production from change in body fat | If dF/dt <0, bf = 0; else, bf = 0.43 |
Unitless |
| b MEI | Heat production per MJ of MEI | 0.3 or (1 − km) where km = 0.5 + 0.02 × M/D |
Unitless |
| p m | Rate constant for partitioning of energy into nonviscera protein | 0.226 ± 0.016 | d-1 |
| e0 | Energy lost as fat to sustain energy gain in protein when energy balance = 0 | 0.249 ± 0.034 | MJ/d |
| p v | Rate constant for partition of energy into visceral protein | 0.05 ± 0.035 | d-1 |
| C MEI | Regression coefficient for the relationship between MEI and v* | 0.676 ± 0.282 | MJ d−1 |
| C m | Regression for the relationship between m0.41 and v* | 2.061 ± 1.555 | MJ0.41 |
| C MD | Regression for the relationship between M/D and v* | −0.53 ± 0.997 | MJ/kg DM |
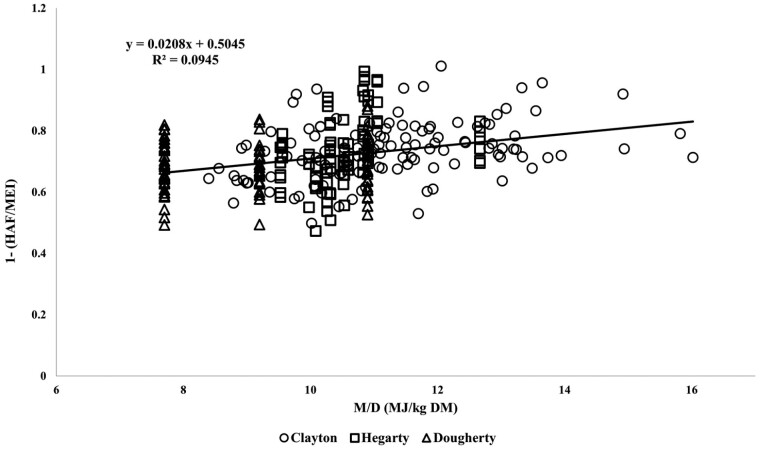
It is possible that HAF is systematically related to M/D (Freer et al. 2007; NASEM 2007, 2016). The relationship between 1 − (HAF/MEI) and M/D obtained from this study was overlaid on that of km vs. M/D from 91 ruminant calorimetry studies in which km was estimated at or below maintenance (Clayton et al., 2022). Figure 6 shows that km as determined from independent data (Clayton et al., 2022) and 1 − (HAF/MEI) as determined by Hegarty et al. (1999) and Dougherty et al. (2022a) are equivalent. The data from the animals fed above maintenance fit within the distribution of data used to estimate the relationship between M/D and km at or below maintenance, which suggests that heat associated with feeding (HAF) is similar at maintenance and above.
Figure 6.
Efficiency of energy use for maintenance (km) vs. dietary energy density (M/D, MJ/kg DM) for sheep data as summarized in the review of Clayton et al. (2022) and an estimate of km above maintenance (1 − HAF/MEI) calculated from the data of Hegarty et al. (1999) and Dougherty et al. (2022) using the methods described in this paper.
For the combined data (Figure 6), the relationship between km and 1 − HAF/MEI was 0.02 * M/D + 0.5, similar to the accepted relationship between km and M/D (Freer et al., 2007). There was considerable variation in the data and the relationship was not strong (R2 = 0.1) suggesting other factors may also contribute to variation in km and/or 1 − (HAF/MEI) (Blaxter and Boyne, 1978). The model represents visceral protein as a function of v*, which itself is a function of M/D, and it is possible that the relationship between M/D and v* may be stronger than that of km and M/D. For the data of Hegarty et al. (1999) and Dougherty et al. (2022a), there was no statistical advantage in a variable km, and the relationship between km and M/D was weak, as seen elsewhere (Clayton et al., 2022).
Accordingly, it is suggested that unless M/D differs widely from a mean of 10 MJ ME/kg DM then a fixed value of 0.7 for km (i.e., bMEI = 0.3) can be used for calculation of HAF from MEI above and below MEI where RE = 0. Otherwise, the standard relationship between km and M/D can be used, where km = 0.02 × M/D + 0.5 (Freer et al., 2007; Figure 6).
Final model structure and parameter values
The final model structure and its equations are shown in Figure 7, with terms as defined above and in Table 2. Model coefficient values and their standard errors are shown in Table 2. The revised model uses MJ for all pool sizes and MJ/d for rates of change. As in Oltjen et al. (2006), the model defines the energetic value of protein as 23.8 MJ/kg, and fat as 39.6 MJ/kg.
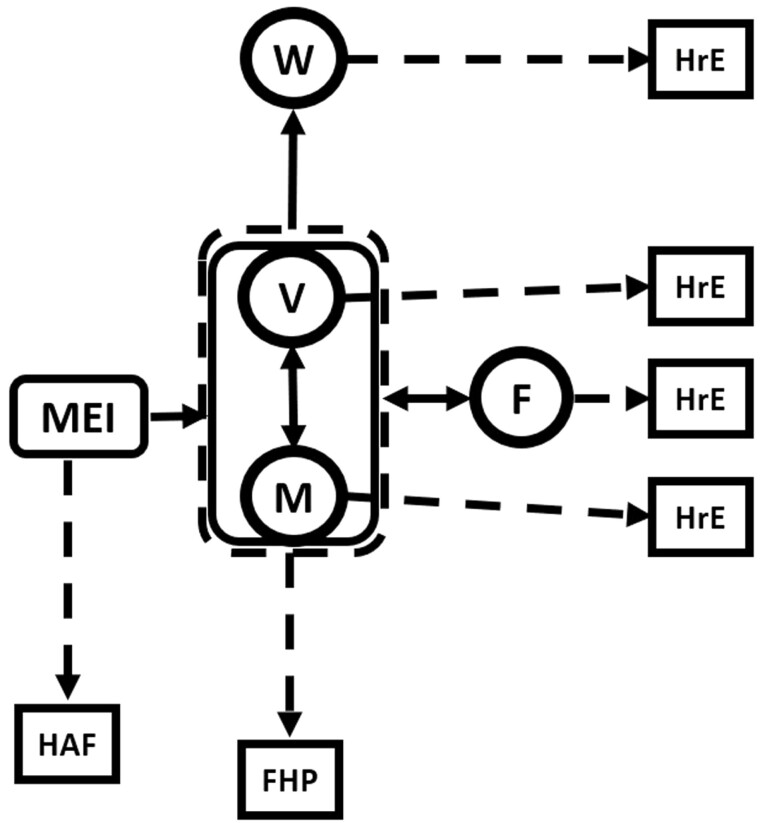
Figure 7.
The complete model is described above. MEI = metabolizable energy intake; M, V, W are protein pools representing nonvisceral (M), viscera (V), and wool (W) depots, respectively, and F is the fat pool. The solid arrows represent mass and energy flows and the dotted arrows loss of energy as heat. All fluxes are MJ/d. The equations which describe this model are:
NEG = MEI – HP;
HP = FHP + HrE + HAF;
dm/dt = (pm × NEG + e0) × (1 − m/m*);
dv/dt = pvx (v* − v);
v* = CMEI × MEI + Cm × (m0.41) − CMD × M/D;
dw/dt = fn(dw/dt(t−1)t, WBrt, Wz, MEI);
dP/dt = ∑(dm/dt + dv/dt + dw/dt);
dF/dt = NEG – dm/dt − dv/dt − dw/dt;
FHP = bm × m + bv × v;
HrE = bp × dP/dt + bf × dF/dt;
HAF = bMEI * MEI.
The values of each parameter are shown in Table 2.
Model evaluation
The revised model was evaluated and compared with that of CSIRO (Freer et al., 2007) using independent data from three experiments where body composition was measured in Merino cross lambs of similar ages but with different weights, growth rates, and nutritional histories (Table 1). A fixed value of km = 0.7 was used for the evaluation, as discussed above; this was thought appropriate as the values of km estimated from reported M/D were close to 0.7 for all datasets (0.7 ± 0.03 for development data, 0.72 ± 0.01 for evaluation data). Standard reference weight (SRW) was derived using available information about the breeds of lambs used in each study and all lambs within a study were assumed to have the same SRW. The lambs from Hegarty et al. (1999) and Dougherty et al. (2022a) were sourced from the same research flock; therefore, SRW was assumed the same for lambs in both studies. SRW was used to calculate mature nonvisceral protein mass, as described in Dougherty et al. (2020, 2022b). The models were evaluated for their ability to predict final fleece-free empty body composition (MJ protein and fat), fleece-free empty body weight (FFEBW, kg), and clean wool growth (g/d) (Tables 3 and 4, Figures 8 and 9).
Table 3.
Comparison of the model presented here vs. the CSIRO for the model final body composition, fleece-free EBW, and wool growth (n=187) using the development data (Table 1), The measured traits are as described in Table 1
| Measure | Protein in fleece-free empty body (MJ) | Empty body fat (MJ) | Fleece-free empty body weight (kg) | Clean wool growth (g/d) | ||||
|---|---|---|---|---|---|---|---|---|
| Mean of observed values | 138.25 | 426.62 | 39.60 | 7.40 | ||||
| CV of observations | 12.56 | 30.43 | 16.19 | 26.70 | ||||
| Model | Model | CSIRO | Model | CSIRO | Model | CSIRO | Model | CSIRO |
|---|---|---|---|---|---|---|---|---|
| Mean of predicted values | 138.33 | 126.98 | 422.89 | 433.57 | 39.52 | 37.22 | 5.35 | 5.82 |
| Mean bias | −0.08 | 11.27 | 3.73 | −6.95 | 0.09 | 2.39 | 2.06 | 1.58 |
| Mean bias %obs mean | −0.06% | 8.15% | 0.87% | −1.63% | 0.22% | 6.02% | 27.77% | 21.37% |
| RMSE | 8.63 | 14.42 | 58.73 | 59.59 | 2.03 | 3.24 | 3.46 | 3.42 |
| RMSE (%obs mean) | 6.24 | 10.43 | 13.77 | 13.97 | 5.13 | 8.18 | 46.69 | 46.20 |
| r 2 | 0.75 | 0.74 | 0.81 | 0.81 | 0.91 | 0.90 | 0.00 | 0.01 |
| Mean bias | 0.01 | 61.05 | 0.40 | 1.36 | 0.18 | 54.21 | 35.37 | 21.40 |
| Slope bias | 1.06 | 2.08 | 9.01 | 9.81 | 8.07 | 6.33 | 32.09 | 45.74 |
| Random error | 98.93 | 36.87 | 90.58 | 88.83 | 91.74 | 39.46 | 32.54 | 32.85 |
CV, coefficient of variation (%).
Table 4.
Comparison of the model presented here vs. the CSIRO model (Freer et al., 2007) for prediction of evaluation data on final body composition, fleece-free EBW, and wool growth (n = 121). The measured traits are as described in Table 1.
| Measure | Protein in fleece-free empty body (MJ) | Empty body fat (MJ) | Fleece-free empty body weight (kg) | Clean wool growth (g/d) | ||||
|---|---|---|---|---|---|---|---|---|
| Mean of observed values | 127.73 | 327.10 | 35.06 | 9.31 | ||||
| CV of observations | 17.30 | 35.66 | 20.54 | 13.35 | ||||
| Model | Model | CSIRO. | Model | CSIRO | Model | CSIRO | Model | CSIRO |
|---|---|---|---|---|---|---|---|---|
| Mean of predicted values | 129.78 | 131.35 | 279.73 | 302.94 | 34.15 | 35.22 | 5.35 | 5.64 |
| Mean bias | −2.06 | −3.62 | 47.37 | 24.15 | 0.91 | −0.16 | 3.96 | 3.67 |
| Mean bias %obs mean | −1.61% | −2.84% | 14.48% | 7.38% | 2.58% | −0.45% | 42.57% | 39.39% |
| RMSPE | 9.69 | 8.83 | 69.58 | 56.21 | 2.94 | 2.54 | 4.20 | 3.87 |
| RMSPE (%obs mean) | 7.58 | 6.92 | 21.27 | 17.18 | 8.39 | 7.23 | 45.09 | 41.59 |
| r 2 | 0.82 | 0.87 | 0.83 | 0.83 | 0.86 | 0.88 | 0.45 | 0.49 |
| Mean bias | 4.51 | 16.83 | 46.35 | 18.46 | 9.48 | 0.39 | 89.12 | 89.71 |
| Slope bias | 0.87 | 0.01 | 5.10 | 8.41 | 6.18 | 4.17 | 6.09 | 5.12 |
| Random error | 94.62 | 83.17 | 48.55 | 73.13 | 84.33 | 95.43 | 4.79 | 5.17 |
CV, coefficient of variation (%).
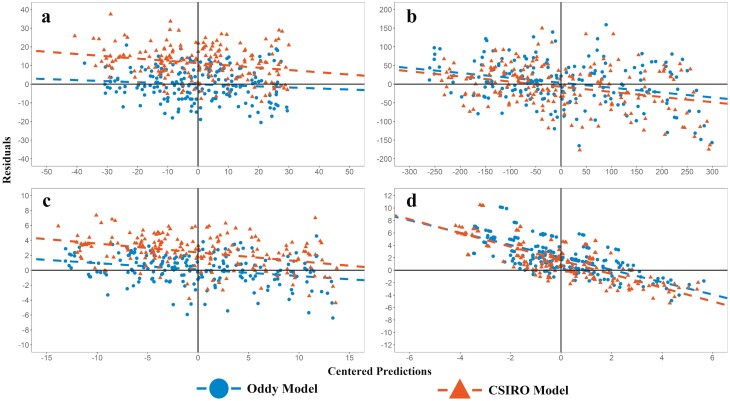
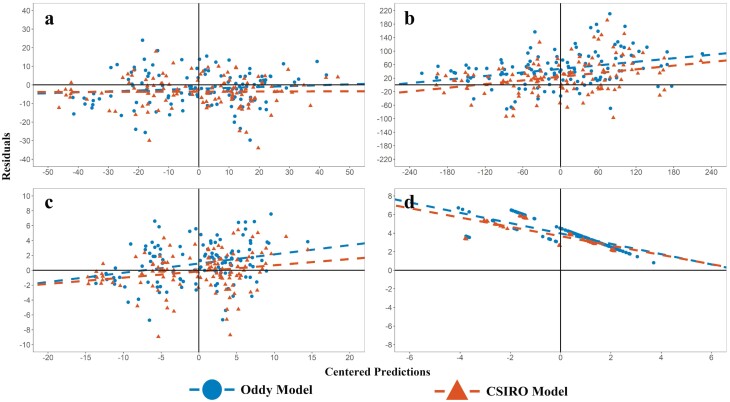
Figure 8.
Comparison of model and CSIRO model predictions v’s observed for the development data shown in Table 1. The graphs are residuals vs. centered predictions for (a) Protein in fleece-free EBW (MJ), (b) Fat (MJ), (c) fleece-free EBW (kg), and (d) Clean wool growth (g/d).
Figure 9.
Residuals vs. centered predictions for (a) Protein in fleece-free EBW (MJ), (b) Fat (MJ), (c) fleece-free EBW (kg), (d) Clean wool growth for the evaluation data set (g/d; Table 1).
Development dataset
For the development dataset (Table 3), the protein was predicted with a higher accuracy by the model compared with Freer et al (2007, CSIRO model) (Figure 8a), with lower RMSE (% observed mean) and mean bias. The CSIRO model underpredicted protein by an average of 474 g (11.3 MJ), while the model overpredicted protein by 3.41 g (0.08 MJ). Within the protein pools, the RMSE for muscle and visceral protein were 6.95% and 9.08%, respectively. The model overpredicted muscle protein by an average of 9.22 g, but underpredicted viscera protein by 5.81 g. Mean bias and slope bias were higher for viscera than for muscle, but both terms were <1% of the total error decomposition for both protein pools, and mean bias was <1% of the observed mean for muscle and viscera (data not shown).
Both models had similar RMSEs for predicting final empty body fat (EBF) in the development dataset, but the proposed model had lower mean bias than the CSIRO model, underpredicting fat in the empty body (EBF) by 94.2 g (3.73 MJ), while the CSIRO model overpredicted EBF by 176 g (6.95 MJ). Variation in EBF was higher than in other measures, and error for both models increased as observed fat increased, trending toward overpredicting fat in lambs that were fatter at slaughter (Figure 8b). It should be noted that in the proposed model, fat gain is predicted by difference, so all errors in predicting protein gain and heat production accumulate in the fat pool. The RSR for protein and fat was <0.5, indicating satisfactory ability to capture the observed variation in the data (Moriasi et al., 2007).
The model had lower mean bias and RMSE than the CSIRO model for prediction of fleece-free EBW (FFEBW) in the development dataset. On average, both models underpredicted FFEBW, though the CSIRO model underpredicted EBW for a larger proportion of data than the model (Figure 8c). Both models substantially underpredicted wool growth in the development dataset (Figure 8d), with a high mean bias (>20% of observed mean). Neither model predicted wool growth adequately. Further work is required to develop a better model of wool growth for inclusion in simple models of animal growth.
Evaluation dataset
When compared to evaluation data, the model performed better for estimation of protein in the empty body than the CSIRO model but less well for EBF and FFEBW (Table 4, Figure 9). Both models overpredicted protein for the evaluation dataset (Figure 9a), the CSIRO model had a lower RMSPE (% observed mean), while the model had a lower mean bias. The model predicted muscle protein better than visceral protein (RMSPE 8.03% vs. 16.2%), overpredicting muscle protein by 162 g but underpredicting visceral protein by 75.6 g; visceral protein had higher mean and slope bias than muscle protein (data not shown). The CSIRO model predicted EBF better than the model for the evaluation dataset, with lower RMSPE and lower mean bias (610 g vs. 1,196 g). However, both models underpredicted EBF, and the degree of underprediction tended to be higher in lambs that were fatter at slaughter (Figure 9b). On average, the CSIRO model tended to overpredict FFEBW in the evaluation dataset, while the model tended to underpredict (Figure 9c); however, the CSIRO model had lower mean bias and RMSPE for FFEBW than the model. As in the development dataset, neither model predicted wool growth adequately (Figure 9d).
Average lean protein mass was similar between the development and evaluation datasets, differing by only 0.44 kg, or ~8%. However, the average final empty body fat was 2.5 kg lower in the independent dataset than in development dataset, a difference of 23%, and between-individual variation was higher in the evaluation data. This difference in fatness between datasets may have contributed to the higher error seen by both models when predicting fat for the evaluation data. Differences in experimental methods used to measure protein and fat content of the body between the two datasets may have also contributed to differences in model performance; the majority of the data in the evaluation dataset was individual lamb data from Keogh et al. (2023), who estimated body composition and tissue weights from CT scan data; the other studies used in model development and evaluation were serial slaughter trials where tissue weights were obtained postmortem and body composition was measured chemically.
Both models substantially underpredicted wool growth. This may be due to the nature of the wool data available, which was less detailed than data on body composition—the only study where individual wool growth data was available was the experimental period of Dougherty et al. (2022a), and treatment means or other estimates of wool production were used for the other datasets. These limitations meant that there was poorer linkage between variation in body composition and variation in wool growth, reducing predictive power for both models and to a lesser extent, overall model predictive capacity for other measures. Wool growth is an important contributor to whole-body energy transactions, and a significant component of RE when RE is close to 0. It is necessary to include wool to fully account for energy transactions. The wool growth equations used in the proposed model were derived from Freer et al., (2007). Neither model predicted wool growth well. In the data sets used here, energy intake had a significant effect on wool growth, but protein supply did not, so it is unlikely that poor prediction was due to inadequate representation of the response to amino supply in the models. The wool growth equations used within both the CSIRO model and this model require revision to improve prediction of wool growth.
General discussion
The model presented here extends the work of Oltjen et al. (2006) on modeling of energetics and body composition in sheep. A novel aspect of the revised model is the calculation of HP internally within the model. Unlike current feeding systems it combines, information on both heat associated with feeding and heat generated by protein and fat transactions in the body with an internal representation of FHP as a function of the mass of protein in visceral and nonvisceral tissues. Body composition and composition of gain are derived dynamically, with a flexible relationship between fat and protein that allows for situations where fat is mobilized to support body protein reserves. Recognition of the substantial role wool has as an energy sink has allowed estimates of HP from protein gain congruent with estimates of efficiency of protein gain reported in other species (Owens et al., 1995). The method of estimating deposition of energy in protein and allowing the balance of energy not lost as heat to accrue as fat provides estimates of body composition not dissimilar to those obtained by regression analysis of past studies that have underpinned current feeding systems (ARC, 1980; NRC, 1981; Freer et al., 2007; NASEM 2007, 2016).
The current model construct is more flexible in that short-term variation in body composition arising from changes in feed supply and composition relative to maturity is accommodated without recourse to fixed proportions of protein and fat deposition used in existing feeding systems. The addition of a wool protein pool is necessary to allow for more accurate representation of energy utilization. Estimation of HP can be obtained internally within the model, although that calculation relies on initial estimates of parameters for HP initially obtained from A-V difference and blood flow measurements not traditionally associated with feeding systems. It is well known that accurate estimation of parameters for highly correlated components of a system is difficult to achieve. As much independent evidence as possible was assembled to support initial parameter values, followed by iteration to minimize errors for the entire suite of output parameters, rather than rely on the interpretation of regression coefficients. This has resulted in a description of the underlying processes such as the relationships between energy costs associated with visceral and nonvisceral protein informing the basis of FHP; the contribution of heat associated with eating and heat of product formation for protein and fat gain. Although this approach yields similar estimates of body composition as traditional methods it has the advantage of exposing the factors contributing to variation in HP which in turn allows a somewhat more rational understanding of the causes of variation in HP and protein and fat deposition in sheep.
Conclusions and Implications
The revised model presented here is simpler than current Australian feeding standards (Freer et al., 2007) and better represents the underlying biology of the system. Through explicit representation of the major energy using processes in the body, and through simplification of the way body composition is computed in growing animals, the model is more transparent than current feeding systems while achieving similar performance. The model then has the advantage of potentially wider applicability across different growth trajectories and can explicitly account for the effects of systematic changes on energy transactions, such as the effects of selective breeding, growth manipulation, or environmental changes. When evaluated against independent data, the revised model performed at least as well as the current CSIRO model (Freer et al., 2007) for protein gain in the body, but less well for fat and empty body weight gain. Neither model performed well at predicting wool growth, highlighting the need to include a more realistic representation of the relationship between nutrition, body composition, and wool growth. In general, more data on body composition and tissue weights in animals at lower planes of nutrition are required to improve estimates of composition of gain, along with additional data on mature body size and composition at maturity. In particular data on the relationship between visceral protein mass from animals eating feeds of different physical structures (long, chopped, ground, and pelleted) are required. Future developments to the revised model include the representation of pregnancy and lactation, the energetic cost of activity, and internal calculation of gut fill. It is anticipated that the structure of this model will enable the representation of genetic variation in protein and fat deposition and hence production outcomes in the future. Work is underway on a beef cattle version of this model, based on the same underlying structures and principles presented here for sheep.
Though additional data are needed for further development, the model presented here provides a mechanistic, flexible, and transparent approach to calculating body composition and HP in sheep. This approach is structurally equivalent to traditional feeding systems but provides a biological explanation to model terms and parameters.
Acknowledgments
The authors thank Drs J.L. Black and R.C. Dobos for helpful discussions during this work. Financial support was provided by Meat & Livestock Australia Donor Company, Grant P.PSH.0998 “Revise Australian feeding standards to better achieve product specifications and improve ruminant efficiency”.
Glossary
Abbreviations:
- ADG
average daily Gain
- ATP
adenosine triphosphate
- A-V
arteriovenous
- BW
body weight
- BWG
body weight gain
- DMI
dry matter intake (kg/d)
- EBF
empty body fat
- EBW
empty body weight
- FFEB
fleece-free empty body
- FFEBW
fleece-free empty body weight
- FFLWT
fleece-free liveweight
- FHP
fasting heat production
- HAF
heat associated with feeding
- HP
heat production
- HrE
heat of product formation
- k m
efficiency of energy use for maintenance
- k g
efficiency of energy use for gain
- LWT
liveweight
- M/D
energetic density of feed/diet (MJ ME/ kg DM)
- ME
metabolizable energy
- MEI
metabolizable energy Intake (MJ/d)
- MEm
metabolizable energy requirement for maintenance (MJ/d)
- NEG
net energy available for gain (MJ/d)
- NVEB
nonvisceral empty body
- RE
retained energy (MJ)
- RMSE
root mean squared error
- RMSPE
root mean squared prediction error
- SRW
standard reference weight
- VFA
volatile fatty acid
- Z
relative maturity
Appendix: Model Initialization
The model requires initial values for masses of protein in the m and v pools (mInit and vInit, respectively), as well as initial wool, fat (fInit), and fleece-free empty body weight (FFEBW). Initial wool cover is provided by the user, but where initial FFBEW, protein, and fat are not available, they can be calculated from fleece-free liveweight (FFLWT), Z, and SRW as follows, using equations derived from Butterfield et al. (1988) and Searle and Griffiths (1976):
GutFillInit (kg) = (2.487 x Z – 1.482 x Z2 + 0.001) x 9.1 x (SRW/100) [A1]
ShrinkInit (%) = ((FFLWT – GutFillInit)/FFLWT) x (0.35 + 0.106 x M/D – 0.004 x M/D2) [A2]
FFEBWInit (kg) = FFLWT x ShrinkInit [A3]
v Init (MJ) = SRW x (2.732 x Z – 1.731x Z2 – 0.0014) x SexFac x 23.8 x 0.157 [A4]
f Init (MJ) = ((98.797 x Z – 38.035 x Z2 – 14.499)/100) x fleece-free Liveweight x 39.6 [A5]
m Init (MJ) = (FFEBWInit – (vInit/23.8/0.157) – (fInit/39.6)) x 23.8 x 0.21 [A6]
where GutFillInit is initial gut fill, ShrinkInit is the conversion factor for converting FFLWT to FFEBW, M/D is energy density of the previous diet (MJ/kg DM), SexFac is 0.047 for intact males, 0.051 otherwise, 0.157 and 0.21 are the crude protein content of fat-free viscera and muscle, respectively (Dougherty et al., 2021, 2022a); and 23.8 and 39.6 are the energy density (MJ/kg) of protein and fat, respectively (Oltjen et al., 2006; Oddy et al., 2019).
Contributor Information
Victor Hutton Oddy, NSW Department of Primary Industries, Extensive Livestock Centre, University of New England, Armidale, NSW, Australia; Department of Animal Science, University of New England, Armidale, NSW, Australia.
James C H Dougherty, NSW Department of Primary Industries, Extensive Livestock Centre, University of New England, Armidale, NSW, Australia; CSIRO Agriculture & Food, St. Lucia, QLD, Australia; Department of Animal Science, University of New England, Armidale, NSW, Australia.
Mark Evered, NSW Department of Primary Industries, Extensive Livestock Centre, University of New England, Armidale, NSW, Australia.
Edward H Clayton, NSW Department of Primary Industries, Wagga Wagga, NSW, Australia.
James W Oltjen, Department of Animal Science, University of California, Davis, CA, USA.
Conflict of Interest Statement: The authors declare no real or perceived conflicts of interest.
Literature Cited
- Agricultural Research Council (ARC). 1980. The Nutrient Requirements of Ruminant Livestock. Slough, United Kingdom: CAB International. Commonwealth Agricultural Bureaux. [Google Scholar]
- Arnold, R. N., and Bennett G. L... 1991. Evaluation of four simulation models of cattle growth and body composition: Part II—Simulation and comparison with experimental growth data. Agric. Sys. 36:17–41. doi: 10.1016/0308-521x(91)90106-k [DOI] [Google Scholar]
- Baldwin, R. L. 1968. Estimation of theoretical calorific relationships as a teaching technique: a review. J. Dairy Sci. 51:104–111. doi: 10.3168/jds.s0022-0302(68)86928-0 [DOI] [Google Scholar]
- Baldwin R.L. and Black J.L... 1979. Simulation of the effects of nutritional and physiological status on the growth of mammalian tissues: description and evaluation of a computer program. Melbourne, Victoria, Australia: CSIRO. procite:cf7ee74f-2788-404a-a612-0c818004ffb0. doi: 10.25919/zcnv-x252 [DOI] [Google Scholar]
- Baldwin, R. L., France J., and Gill M... 1987. Metabolism of the lactating cow I. Animal elements of a mechanistic model. J. Dairy Res. 54:77–105. doi: 10.1017/s002202990002522x [DOI] [PubMed] [Google Scholar]
- Bates, D.M. and Watts D.G... 1988. Nonlinear regression and its applications. New York, USA: John Wiley & Sons. [Google Scholar]
- Bernier, J. F., Calvert C., Famula T. R., and Baldwin R. L... 1987. Energetic efficiency of protein and fat deposition in mice with a major gene for rapid postweaning gain. J. Nutr. 117:539–548. doi: 10.1093/jn/117.3.539 [DOI] [PubMed] [Google Scholar]
- Bibby, J.H. and Toutenberg H... 1977. Prediction and improved estimation in linear models. Minneappolis, USA: John Wiley & Sons. [Google Scholar]
- Black, J. L., and Griffiths D. A... 1975. Effects of liveweight and energy intake on nitrogen balance and total N requirement of lambs. Br. J. Nutr 33:399–413. doi: 10.1079/BJN19750044 [DOI] [PubMed] [Google Scholar]
- Black, J. L., Gill M., Beever D. E., Thornley J. H. M., and Oldham J. D... 1987. Simulation of the metabolism of absorbed energy-yielding nutrients in young sheep: efficiency of utilization of acetate. J. Nutr. 117:105–115. doi: 10.1093/jn/117.1.105. [DOI] [PubMed] [Google Scholar]
- Blaxter, K. L. 1962. The fasting metabolism of adult wether sheep. Br. J. Nutr. 16:615–626. doi: 10.1079/bjn19620060 [DOI] [PubMed] [Google Scholar]
- Blaxter, K. L., and Boyne A. W... 1978. The estimation of the nutritive value of feeds as energy sources for ruminants and the derivation of feeding systems. J. Agric. Sci. 90:47–68. doi: 10.1017/s0021859600048589 [DOI] [Google Scholar]
- Burrin, D. G., Ferrell C. L., Eisemann J. H., Britton R. A., and Nienaber J. A... 1989. Effect of level of nutrition on splanchnic blood flow and oxygen consumption in sheep. Br. J. Nutr. 62:23–34. doi: 10.1079/bjn19890005 [DOI] [PubMed] [Google Scholar]
- Burrin, D. G., Ferrell C. L., Britton R. A., and Bauer M... 1990. Level of nutrition and visceral organ size and metabolic activity in sheep. Br. J. Nutr. 64:439–448. doi: 10.1079/bjn19900044 [DOI] [PubMed] [Google Scholar]
- Butterfield, R. 1988. New concepts of sheep growth. Netley, South Australia, Australia: The Department of Veterinary Anatomy, University of Sydney. Griffin Press Limited. [Google Scholar]
- Byrd, R. H., Lu P., Nocedal J., and Zhu C... 1995. A limited memory algorithm for bound constrained optimization. SIAM J. Sci. Comput. 16:1190–1208. doi: 10.1137/0916069. doi: 10.1137/0916069 [DOI] [Google Scholar]
- Chivers, C. 2012. MHadaptive: general Markov Chain Monte Carlo for Bayesian inference using adaptive Metropolis-Hastings sampling. http://cran.nexr.com/web/packages/MHadaptive/MHadaptive.pdf
- Clayton, E. H., Oltjen J. W., Evered M., Dougherty H. C., and Oddy V. H... 2022. Predicting the efficiency of utilization of energy for maintenance (km) or gain (kg) for sheep and cattle from feed quality components. Anim Sci. Proc. 13:248–249. doi: 10.1016/j.anscip.2022.07.015 [DOI] [Google Scholar]
- Corbett, J.L., Freer M., Hennessy D.W., Hodge R.W., Kellaway R.C., McMeniman N.P. and Nolan J.V... 1990. Feeding standards for Australian livestock: Ruminants. Melbourne, Victoria, Australia: Standing Committee on Agriculture, CSIRO. http://hdl.handle.net/102.100.100/256672?index=1 [Google Scholar]
- Di Marco, O. N., and Baldwin R. L... 1989. Implementation and evaluation of a steer growth model. Agric. Sys. 29:247–265. doi: 10.1016/0308-521x(89)90055-3 [DOI] [Google Scholar]
- Di Marco, O. N., Baldwin R. L., and Calvert C. C... 1989. Simulation of DNA, protein and fat accretion in growing steers. Agric. Sys. 29:21–34. doi: 10.1016/0308-521x(89)90068-1 [DOI] [Google Scholar]
- Dougherty, H. C., Kebreab E., Evered M., Little B. A., Ingham A. B., Hegarty R. S., Pacheco D., and McPhee M. J... 2017. The AusBeef model for beef production: I. Description and evaluation. J. Agric. Sci. (Camb.) 155:1442–1458. doi: 10.1017/S0021859617000429 [DOI] [Google Scholar]
- Dougherty, H. C., Evered M., Oltjen J. W., Hegarty R., and Oddy V. H... 2020. A method for estimating the target for protein energy retention in sheep. J. Anim. Sci. 98:143. doi: 10.1093/jas/skaa278.260 [DOI] [Google Scholar]
- Dougherty, H.C., Evered M., Oltjen J.W. and Oddy V. H... 2021. How does fasting heat production vary relative to liveweight in sheep and cattle? Proc. 13th Recent Adv. in Anim. Nutr. Conf., 42–43. [Google Scholar]
- Dougherty, H. C., Evered M., Oltjen J. W., Hegarty R., Neutze S. A., and Oddy V. H... 2022a. Effects of dietary energy density and supplemental rumen undegradable protein on intake, viscera, and carcass composition of lambs recovering from nutritional restriction. J. Anim. Sci 100:1–16. doi: 10.1093/jas/skac158 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dougherty, H. C., Oddy V. H., Evered M., Clayton E. H., and Oltjen J. W... 2022b. Variation in mature body composition affects energy requirements and fat and lean deposition in sheep of different breeds and sex. Anim. – Sci. Proc. 13:494–495. doi: 10.1016/j.anscip.2022.07.206 [DOI] [Google Scholar]
- Dougherty, H. C., Evered M., Clayton E. H., Oltjen J. W., and Oddy V. H... 2022c. A revised model of heat production by sheep. Anim. Sci. Proc. 13:518–519. doi: 10.1016/j.anscip.2022.07.399 [DOI] [Google Scholar]
- Dougherty, H. C., Evered M., Clayton E. H., Oltjen J. W., and Oddy V. H... 2022d. Evaluation of a revised model of body composition in sheep. Anim. Sci. Proc. 13:561–562. doi: 10.1016/j.anscip.2022.07.433 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Early, R. J., McBride B. W., and Ball R... 1988. Phenyalanine metabolism in sheep infused with glucose plus insulin I. Effects of plasma phenylalanine concentration, entry rate and utilization by the hindlimb. Can. J. Anim. Sci. 68:711–719. doi: 10.4141/cjas88-080 [DOI] [Google Scholar]
- Eisemann, J. H., and Nienaber J. A... 1990. Tissue and whole-body oxygen uptake in fed and fasted steers. Br. J. Nutr. 64:399–411. doi: 10.1079/bjn19900041 [DOI] [PubMed] [Google Scholar]
- Ferrell, C. L. 1988. Contribution of visceral organs to animal energy expenditures. J. Anim. Sci. 66:23–24. doi: 10.1093/ansci/66.Supplement_3.23 [DOI] [Google Scholar]
- Ferrell, C. L., Crouse J. D., Field R. A., and Chant J. L... 1979. Effects of sex, diet, and stage of growth upon energy utilization by lambs. J. Anim. Sci. 49:790–801. doi: 10.2527/jas1979.493790x [DOI] [Google Scholar]
- Ferrell, C. L., Koong L. J., and Nienaber J. A... 1986. Effect of previous nutrition on body composition and maintenance energy costs of growing lambs. Br. J. Nutr. 56:595–605. doi: 10.1079/BJN19860140 [DOI] [PubMed] [Google Scholar]
- Freer, M., Dove H. and Nolan J.V... 2007. Nutrient requirements of domesticated ruminants. Collingwood, Victoria, Australia: CSIRO Publishing. [Google Scholar]
- Freer, M., Moore A.D. and Donelly J.R... 2012. The GRAZPLAN animal biology model for sheep and cattle and the GrazFeed decision support tool. CSIRO Plant Industry Technical Paper. CSIRO. GRAZPLAN: Decision Support Systems for Australian Grazing Enterprises (csiro.au) [accessed April 20, 2023] [Google Scholar]
- Freetly, H. C., Ferrell C. L., Jenkins T. G., and Goetsch A. L... 1995. Visceral oxygen consumption during chronic feed restriction and realimentation in sheep. J. Anim. Sci. 73:843–852. doi: 10.2527/1995.733843x [DOI] [PubMed] [Google Scholar]
- Gill, M., France J., Summers M., McBride B. W., and Milligan L. P... 1989. Mathematical integration of protein metabolism in growing lambs. J. Nutr. 119:1269–1286. doi: 10.1093/jn/119.9.1269 [DOI] [PubMed] [Google Scholar]
- Graham, N. M. C. 1964a. Energetic efficiency of fattening sheep I Utilization of low-fibre and high-fibre food mixtures. Aust. J. Agric. Res. 15:100–112. doi: 10.1071/AR9640100 [DOI] [Google Scholar]
- Graham, N. M. C. 1964b. Energetic efficiency of fattening sheep II. Effects of under-nutrition. Aust. J. Agric. Res. 15:113–126. doi: 10.1071/AR9640113 [DOI] [Google Scholar]
- Graham, N. M. C. 1964c. Utilization by fattening sheep of the energy and nitrogen in fresh herbage and in hay made from it. Aust. J. Agric. Res. 15:974–981. doi: 10.1071/AR9640974 [DOI] [Google Scholar]
- Graham, N. M. C. 1969. The net energy value of artificially dried subterranean clover harvested before flowering. Aust. J. Agric. Res. 20:365–373. doi: 10.1071/AR9690365 [DOI] [Google Scholar]
- Graham, N. M. C., Searle T. W., and Griffiths D. A... 1974. Basal metabolic rate in lambs and young sheep. Aust. J. Agric. Res. 25:957–971. doi: 10.1071/ar9740957 [DOI] [Google Scholar]
- Harris, P. M., Skene P. A., Buchan V., Milne E., Calder A. G., Anderson S. E., Connell A., and Lobley G. E... 1992. Effect of food intake on hind limb and whole body protein metabolism in growing lambs: chronic studies based on arteriovenous techniques. Br. J. Nutr. 68:389–407. doi: 10.1079/bjn19920097 [DOI] [PubMed] [Google Scholar]
- Hegarty, R. S., Neutze S. N., and Oddy V. H... 1999. Effects of protein and energy supply on the growth and carcass composition of lambs from differing nutritional histories. J. Agric. Sci. (Camb.) 132:361–375. doi: 10.1017/S0021859698006315 [DOI] [Google Scholar]
- Keogh, T. P., McGrath S. R., Allworth M. B., and Oddy V. H... 2023. Level of feeding and stage of maturity affects diet digestibility and protein and fat deposition in cross-bred lambs. J. Anim. Sci. 101:1–11. doi: 10.1093/jas/skad095 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lofgreen, G. P., and Garrett W. N... 1968. A system for expressing net energy requirements and feed values for growing and finishing beef cattle. J. Anim. Sci. 27:793–806. doi: 10.2527/jas1968.273793x [DOI] [Google Scholar]
- Marcondes, M. I., Tedeschi L. O., Valadares Filho S. C., and Gionbelli M. P... 2013. Predicting efficiency of use of metabolizable energy to net energy for gain and maintenance in Nellore cattle. J. Anim. Sci. 91:4887–4898. doi: 10.2527/jas.2011-4051 [DOI] [PubMed] [Google Scholar]
- Marston, H. R. 1948. Energy transactions in the sheep 1 the basal heat production and heat increment. Aust. J. Biol. Sci. 1:93–129. doi: 10.1071/BI9480093 [DOI] [Google Scholar]
- McBride, B. W., and Milligan L. P... 1985. Influence of feed intake and starvation on the magnitude of Na+, K+-ATPase (EC 3613)-dependent respiration in duodenal mucosa of sheep. Br. J. Nutr. 53:605–614. doi: 10.1079/bjn19850070 [DOI] [PubMed] [Google Scholar]
- Meyer, A. M., Vraspir R. A., Ellison M. J., and Cammack K. M... 2015. The relationship of residual feed intake and visceral organ size in growing lambs fed a concentrate- or forage-based diet. Livestock Sci. 176:85–90. doi: 10.1016/j.livsci.2015.03.019 [DOI] [Google Scholar]
- Minitab, LLC. 2022. Minitab. Retrieved from https://www.minitab.com [accessed March 20, 2023]
- Moriasi, D. N., Arnold J. G., Van Liew M. W., Bingner R. L., Harmel R. D., and Veith T. L... 2007. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 50:885–900. doi: 10.13031/2013.23153. [DOI] [Google Scholar]
- National Academies of Sciences, Engineering, and Medicine (NASEM). 2007. Nutrient requirements of small ruminants: sheep, goats, cervids, and new world camelids. Washington, DC, USA: National Academies Press. [Google Scholar]
- National Academies of Sciences, Engineering, and Medicine (NASEM). 2016. Nutrient requirements of beef cattle.’ 8th revised edn. Washington, DC, USA: National Academies Press. [Google Scholar]
- National Research Council (NRC). 1976. Nutrient requirements of beef cattle (6th ed.). Washington, DC: National Academy of Science. [Google Scholar]
- National Research Council (NRC). 1981. Nutritional energetics of domestic animals & glossary of energy terms. Second revised ed. Subcommittee on Biological Energy Committee on Animal Nutrition Board on Agriculture and Renewable Resources Commission on Natural Resources. Washington, DC: National Research Council. National Academy Press. [Google Scholar]
- Nelder, J. A., and Mead R... 1965. A simplex algorithm for function minimization. Comp. J. 7:308–313. doi: 10.1093/comjnl/7.4.308 [DOI] [Google Scholar]
- Oddy, V. H. 1993. Regulation of muscle protein metabolism in sheep and lambs: nutritional, endocrine and genetic aspects. Aust. J. Agric. Res. 44:901–913. doi: 10.1071/ar9930901 [DOI] [Google Scholar]
- Oddy, V. H., and Owens P. C... 1996. Insulin-like growth factor 1 inhibits degradation and improves retention of protein in hind limb muscle of lambs. Am. J. Physiol. 271:E973–E982. doi: 10.1152/ajpendo.1996.271.6.E973 [DOI] [PubMed] [Google Scholar]
- Oddy, V. H., Edwards S. R., Warren H. M., Speck P. A., Nicholls P. J., and Neutze S. A... 1997. Interrelationships between amino acid and glucose metabolism in lambs of different dietary history supplemented with rumen escape protein. J. Agric. Sci. (Camb.) 128:105–116. doi: 10.1017/S0021859696003917 [DOI] [Google Scholar]
- Oddy, V. H., Dougherty H. C., and Oltjen J. W... 2019. Integration of energy and protein transactions in the body to build new tools for predicting performance and body composition of ruminants. Anim. Prod. Sci 59:1970–1979. doi: 10.1071/an19229 [DOI] [Google Scholar]
- Oddy, V. H., Dougherty H. C., Evered M., and Oltjen J. W... 2021. Estimating visceral mass in a new method to predict body composition of sheep. Proc Australasian Assoc. Anim. Sci. http://www.animalscienceconference.com.au/wp-content/uploads/2021/01/2021AAAS_Dougherty_Holland.pdf [accessed March 11, 2023]
- Oddy V.H., Dougherty H.C., Evered M., Clayton E.H., and Oltjen J.W.. (2022). An alternative approach to estimation of energy transactions and body composition in sheep. Oral presentation given at the 7th EAAP International Symposium on Energy and Protein Metabolism and Nutrition. September 2022, Granada, Spain.
- Oltjen, J. W., Bywater A. C., Baldwin R. L., and Garrett W. N... 1986. Development of a dynamic model of beef cattle growth and composition. J. Anim. Sci. 62:86–97. doi: 10.2527/jas1986.62186x [DOI] [Google Scholar]
- Oltjen, J.W., Sainz R.D., Pleasants A.B., Soboleva T.K. and Oddy V.H... 2000. Second-generation dynamic cattle growth and composition models. In: McNamara J.P., France J., Beever D.E., editors, Modelling nutrient utilization in farm animals. Wallingford, Oxfordshire, UK: CAB International Publishing; p. 197–209. [Google Scholar]
- Oltjen, J.W., Sainz R.D, Pleasants A.B., Soboleva T.K. and Oddy V.H... 2006. Representation of fat and protein gain at low levels of growth and improved prediction of variable maintenance requirement in a ruminant growth and composition model. In: Kebreab E., Dijkstra J., Bannink A., Gerrits W.J.J., France J., editors, Nutrient digestion and utilization in farm animals: modelling approaches. Wallingford, Oxfordshire, UK: CAB International Publishing; p144–159. [Google Scholar]
- Ortigues, I., and Durand D... 1995. Adaptation of energy metabolism to undernutrition in ewes. Contribution of portal-drained viscera, liver and hindquarters. Br. J. Nutr. 73:209–226. doi: 10.1079/bjn19950024 [DOI] [PubMed] [Google Scholar]
- Owens, F. N., Gill D. R., Secrist D. S., and Coleman S. W... 1995. Review of some aspects of growth and development of feedlot cattle. J. Anim. Sci. 73:3152–3172. doi: 10.2527/1995.73103152x [DOI] [PubMed] [Google Scholar]
- R Core Team. 2023. R: A language and environment for statistical computing. R Foundation for Statistical Computing. Vienna, Austria. www.R-project.org [Google Scholar]
- Rattray, P. V., Garrett W. I. N., East N. E., and Hinman N... 1973. Net energy requirements of ewe lambs for maintenance, gain, and pregnancy and net energy values of feedstuffs for lambs. J. Anim. Sci. 37:853–857. doi: 10.2527/jas1973.373853x [DOI] [Google Scholar]
- Reynolds, C. K., Tyrrell H. F., and Reynolds P. J... 1991. Effects of diet forage-to-concentrate ratio and intake on energy metabolism in growing beef heifers: whole body energy and nitrogen balance and visceral heat production. J. Nutr. 121:994–1003. doi: 10.1093/jn/121.7.994 [DOI] [PubMed] [Google Scholar]
- Sainz, R. D., and Bentley B. E... 1997. Visceral organ mass and cellularity in growth-restricted and refed beef steers. J. Anim. Sci. 75:1229–1236. doi: 10.2527/1997.7551229x [DOI] [PubMed] [Google Scholar]
- Sainz, R. D., and Wolffe J. E... 1990. Development of a dynamic, mechanistic model of lamb metabolism and growth. Anim. Prod. 51:535–549. doi: 10.1017/S0003356100012575 [DOI] [Google Scholar]
- Searle, T. W., and Griffiths D. A... 1976. Differences in body composition between three breeds of sheep. Proc. Aust. Soc. Anim. Prod. 11:57–60. https://publications.csiro.au/rpr/pub?pid=procite:8d396ffc-fcf9-4dd1-867c-bac750d65d60 [Google Scholar]
- Soboleva, T. K., Oddy V. H., Pleasants A. B., Oltjen J. W., Ball A. J., and McCall D. G... 1999. A dynamical model of body composition in sheep. Proc. New Zealand Soc. Anim. Prod. 59:275–278. [Google Scholar]
- Sun, W., Goetsch A. L., Forster L. A., Galloway D. L., and Lewis P. K... 1994. Forage and splanchnic tissue mass in growing lambs: effects of dietary forage levels and source on splanchnic tissue mass in growing lambs. Br. J. Nutr. 71:141–151. doi: 10.1079/bjn19940122 [DOI] [PubMed] [Google Scholar]
- Tanner, M.A. 1996. Tools for statistical inference, 3rd ed. Springer-Verlag, New York, USA. [Google Scholar]
- Tedeschi, L. O. 2019. Relationships of retained energy and retained protein that influence the determination of cattle requirements of energy and protein using the California Net Energy System. Transl. Anim. Sci 3:1029–1039. doi: 10.1093/tas/txy120 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tedeschi, L. O. 2023. Review: harnessing extant energy and protein requirement modeling for sustainable beef production. Animal 17:1–14. doi: 10.1016/j.animal.2023.100835 [DOI] [PubMed] [Google Scholar]
- Turgeon, O. A.Jr, Brink D. R., Bartle S. J., Klopfenstein T. J., and Ferrell C. L... 1986. Effects of growth rate and compensatory growth on body composition in lambs 2: chemical and dissectible body composition. J. Anim. Sci. 63:770–780. doi: 10.2527/jas1986.633770x [DOI] [PubMed] [Google Scholar]
- Wainman, F. W., Blaxter K. L., and Pullar J. D... 1970. The nutritive value for ruminants of a complete processed diet based on barley straw. J. Agric. Sci. 74:311–314. doi: 10.1017/s0021859600022929 [DOI] [Google Scholar]
- Williams, C. B., and Jenkins T. G... 2003. A dynamic model of metabolizable energy utilization in growing and mature cattle I Metabolizable energy utilization for maintenance and support metabolism. J. Anim. Sci. 81:1371–1381. doi: 10.2527/2003.8161371x [DOI] [PubMed] [Google Scholar]