Hybrid QM/MM Methods For Studying Energy Transduction in Biomolecular Machines

Abstract

Hybrid quantum mechanical/molecular mechanical (QM/MM) methods have become an indispensable tool for the study of biomolecules. In this article, we briefly review the basic methodological details of QM/MM approaches and discuss their applications to various energy transduction problems in biomolecular machines, such as long-range proton transports, fast electron transfers and mechanochemical coupling. We highlight that for these applications it is particularly important to balance computational efficiency and accuracy. Using several recent examples, we illustrate the value and limitations of QM/MM methodologies for both ground and excited states, as well as strategies for calibrating them in specific applications. We conclude with brief comments on several areas that can benefit further efforts to make QM/MM analyses more quantitative and applicable to increasingly complex biological problems.

1. Introduction

One of the hallmarks of living systems is the efficient transduction of energy among different forms via biomolecular machines.^1,2 Remarkable examples include the conversion of light energy (or O₂ activation) into proton motive force by bacteriorhodopsin (cytochrome c oxidase), utilization of the proton gradient to synthesize ATP by the F₀F₁-ATPase and to transport small molecules across the membrane by various transporters, and driving the motion of biomolecular motors with the chemical energy of ATP hydrolysis. The definition of efficiency for these biomolecular machines is somewhat subtle,³ but generally the values are substantially higher compared to those of artificial machines. Therefore, uncovering the physical and chemical principles that govern the working mechanism of naturally evolved systems is not only of fundamental significance, but also valuable for providing guidance to the development of novel molecular machines at the nanoscale.^4,5

Since the ultimate driving force for most biomolecular machines involves chemical reactions, such as ATP hydrolysis, coupled proton-electron-transfers or electronic excitation, theoretical and computational analysis of bioenergy transduction necessarily involves treating chemical reactions and dissecting their coupling to other processes, such as protein conformational transitions or translocation of small molecules or ions. Therefore, compared to the problem of enzyme catalysis, which also involves chemical reactions in biomolecules, the topic of bioenergy transduction is arguably even more challenging as it requires methodologies that are able to bridge broader length and time scales. While striking the balance between computational accuracy and efficiency is relevant to most biophysical problems, its central role in the meaningful analysis of bioenergy transduction drives the development and integration of multi-scale computational methodologies, including semi-empirical quantum mechanical/molecular mechanical (QM/MM) methods,⁶ ab initio QM/MM approaches⁷ and more recently, machine learning (ML) techniques.

To illustrate the value and limitation of these methodologies, as well as strategies for properly calibrating them in specific systems, we will discuss several recent applications in the area of bioenergy transduction. Due to limited space, we will mainly focus on studies in our own labs, although complementary efforts by others will also be mentioned. The discussions will focus on steps that are most tightly coupled with the chemical reactions, while methodologies that tackle other steps such as large-scale conformational transitions can be found in recent reviews by others,^8,9 including general conceptual issues related to the efficiency of energy transduction.^4,10,11 We will end with a brief outlook that comments on future developments that will enable the analysis of increasingly complex bioenergy transduction problems.

2. Theory and Methods

To study biological processes driven by chemical reactions, the basic computational frame-work is the hybrid QM/MM approach^12,13 pioneered by Warshel, Levitt and Karplus, who were awarded the Nobel Prize in Chemistry for their efforts. At the conceptual level, the approach is intuitive: the reactive region of the system is treated at a QM level, while the environment is described with a more simplified MM model. Through the contributions of many researchers, the QM/MM approach has become an indispensable tool for the analysis of condensed phase problems,^14–16 especially biomolecules.¹⁷ Recent developments and applications, especially in chemical and enzymatic systems, have been summarized in excellent review articles;^7,18 some of the remaining challenges have also been discussed.¹⁹ In the following, we briefly touch upon several generally relevant methodological issues.

2.1. QM/MM Methods for Ground Electronic States

In the most standard scheme applied to biomolecules (Fig. 1), the QM/MM energy is given in the additive form,

$$E^{Tot}=\langle \Psi |{\widehat{H}}^{QM}+{\widehat{H}}_{\mathit{\text{elec}}}^{QM/MM}|\Psi \rangle +E_{vdW}^{QM/MM}+E_{\mathit{\text{bonded}}}^{QM/MM}+E^{MM},$$ (1)

which indicates that the QM and MM atoms interact through electrostatic, van der Waals and bonded terms; in most implementations, only the QM/MM electrostatic interaction (see below) is included in the self-consistent determination of the QM region wavefunction, Ψ (or the electron density), while the van der Waals and bonded terms are treated at the classical force field level. When the QM/MM partitioning is conducted across a covalent bond (e.g., between Cα and Cβ atoms of an amino acid), link atoms,^20,21 frozen orbitals²² or pseudo potentials²³ are required to properly treat the boundary QM atoms; care needs to be exercised to avoid artificial polarization of the QM atoms,^24,25 and it is generally advised against partitioning across highly polar covalent bonds.

Figure 1:

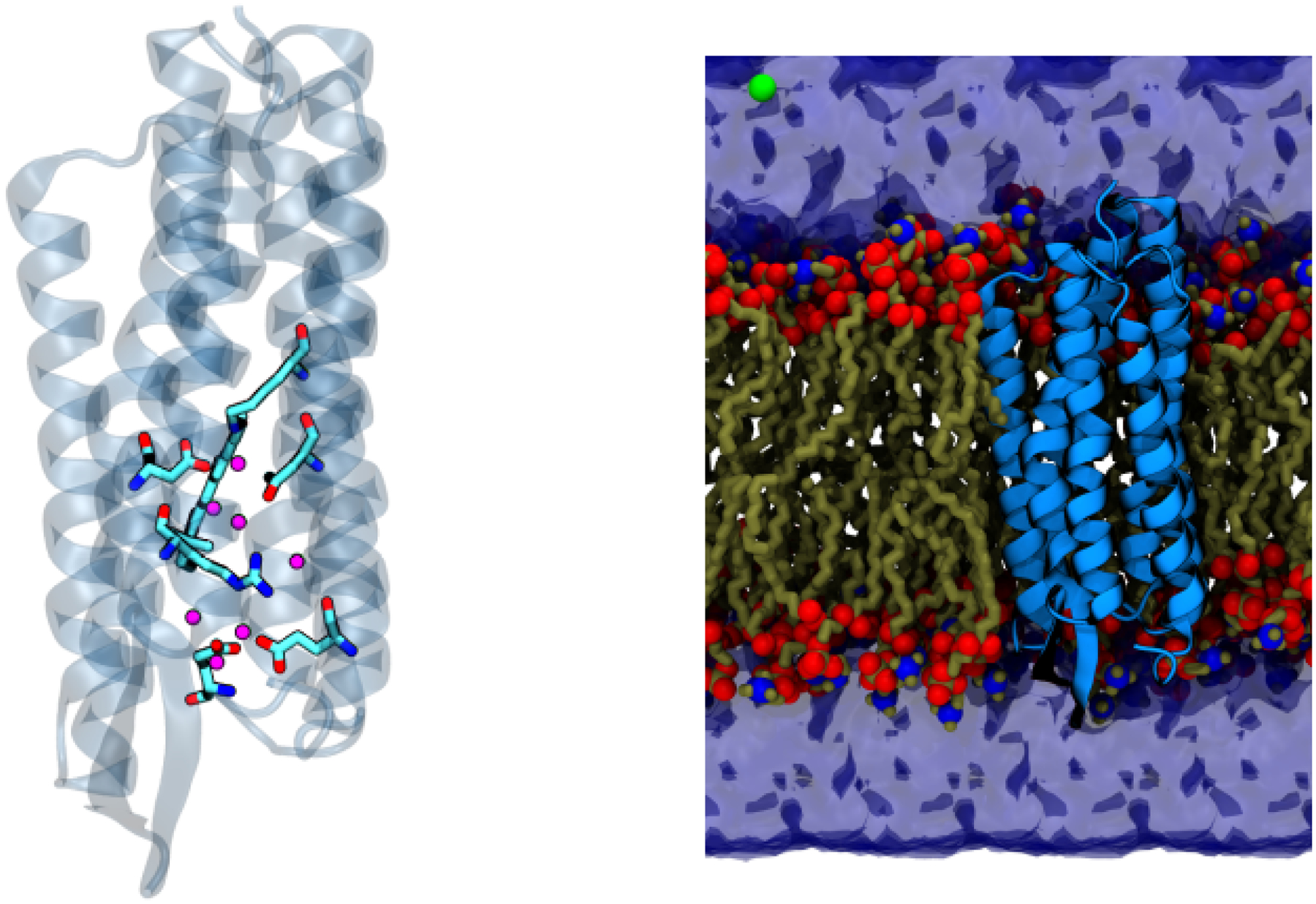
Illustration of a typical QM/MM set-up using the analysis of the O→bR transition in bacteriorhodopsin as an example. In the left panel, the QM region, which includes key amino acids and water molecules, is highlighted in the licorice form, while the rest of the MM protein environment is shown in transparent cartoon. As shown in the right panel, the entire protein is then embedded in a solvated lipid bilayer; the lipids, water molecules and salt ions are also treated at the MM level.

The proper QM level depends on the problem of interest. While ab initio or density functional theory (DFT) are generally more reliable than semi-empirical QM methods, they are computationally expensive. Even with modern hardwares, ab initio or DFT based QM/MM simulations are typically limited to tens to hundreds of picoseconds of sampling,²⁶ which are usually too short for a reliable computation of equilibrium (e.g., free energy) or dynamical properties. Therefore, carefully calibrated semi-empirical QM methods remain an attractive choice, especially for bioenergetics problems; in recent years, density functional tight binding models^6,27,28 have emerged as promising choices in many applications.

An issue that has attracted much debate in recent years concerns the appropriate size of the QM region;^29–34 with development of efficient algorithms and implementations on modern hardwares, it has become possible to conduct QM/MM simulations with hundreds or thousands of QM atoms,²⁶ or even with the entire system treated at the DFT³⁵ or DFTB³⁶ level. The computational cost associated with such large QM regions, however, limits the amount of conformational sampling. Therefore, depending on the properties of interest, it is important to choose the QM region to best balance computational cost and sampling efficiency. For example, for the analysis of reaction mechanism and free energy profiles, adequate sampling is essential; this is expected to be particularly important to systems involved in bioenergy transduction, as the driving chemical reactions often involve the migration of charged species (e.g., protons, electrons, metal ions) over a long distance, thus there are significant protein and solvent responses that need to be captured with extensive sampling. For properties that are particularly sensitive to electronic structure, such as NMR chemical shifts and hyperfine coupling constants, it is possible that large QM regions are required.^32,34,37

Regarding QM/MM interactions, in the simplest model, the electrostatic Hamiltonian $\left({\widehat{H}}_{\mathit{\text{elec}}}^{QM/MM}\right)$ involves Coulombic interactions between the QM atoms (nuclei and electrons) and fixed MM partial charges. At short QM-MM distances, however, the point charge models for the MM atoms may lead to overpolarization of the QM atoms. Thus a more physical model is to “blur” the MM charges as spherical Gaussians.^21,38

It is increasingly realized that it is valuable to explicitly include electronic polarization at the MM level. In recent years, substantial progress has been made in the systematic parameterization and validation of polarizable MM force field models for biomolecules,³⁹ including, for example, the CHARMM-Drude model,⁴⁰ AMEOBA,⁴¹ and SIBFA.⁴² Improvements in computational efficiency and implementation on GPUs have made it possible to conduct extensive molecular dynamics simulations for realistic biomolecules, including the ribosome.⁴³ The inclusion of electronic polarization is particularly relevant to a reliable treatment of bioenergy transduction, since many systems involve buried charges or ion-pairs; as shown in a recent analysis,⁴⁴ electronic polarization is critical to the description of the stabilization, conformational dynamics and hydration levels of these buried charges or dipoles. In this context, while charge-scaling has been advocated as an empirical approach for approximating the effect of electronic polarization,^45,46 such phenomenological model may not be able to capture both energetic and dynamic properties correctly,⁴⁷ thus including the MM polarization explicitly in QM/MM simulations is preferable.^48,49

2.2. QM/MM Methods for Excited Electronic States

Many bioenergy transduction processes are initiated by the absorption of photon, thus the description of electronically excited states is required. Often, ground state structures are QM/MM geometry optimized and the excited state can then be treated with a broad set of QM methods that include, for example, time-dependent DFT (TD-DFT) or post-Hartree-Fock methods. The typical errors for TD-DFT are in the range of 0.2–0.4 eV for singly excited states, strongly depending on the functional applied. Pure GGAs tend to have smaller errors, increasing with the amount of exact exchange. For example, an error of 0.26 eV was reported for B3LYP for a set of medium sized molecules of biological relevance;⁵⁰ since this behavior is often systematic, a simple shift in energies can help facilitate a comparison with experimental data. However, limitations of common functionals and the adiabatic linear-response approximations are well known, especially for charge-transfer and doubly excited states, which are not uncommon in biological systems.^51,52 For some problems, range-separated functionals (LC-DFT) provide major improvements, although not completely resolving the issues.^53,54

The absorption spectrum is better computed by sampling of the ground state potential energy surface and subsequent vertical excitation energy calculations, when nuclear quantum effects can be neglected. Here, methods with significantly reduced computational cost are needed, since convergence of the spectrum requires the calculation of hundreds or even thousands of snapshots. Semi-empirical methods are therefore suitable for these type of applications, however, the computational challenges put also strong constraints on the choice of methods, as discussed in detail for retinal proteins.⁵⁵ The Hartree-Fock based OM2 and OM3 methods within a MRCI implementation proved to be quite reliable, while the DFT based linear response TD-DFTB method was not able to treat these types of systems. They show the same failures as the GGA based TD-DFT methods. Long-range (LC) corrected DFT functionals have been shown to ameliorate the problems, and LC-TD-DFTB has been shown to be quite accurate for the calculation of absorption and fluorescence properties.^56,57 However, the typical TD-DFT problems discussed for retinal proteins and chlorophylls in detail, are not completely solved.⁵⁴

Since the ground and excited states usually feature rather different electronic distributions, polarization of the MM environment was found to make a non-negligible contribution to the excitation energy.^48,49,58 It is worth noting that in some cases, force fields have intrinsic limitations, such as for strong hydrogen-bonding interactions with the chromophore (see examples below), thus calling for large QM regions in QM/MM simulations.

2.3. Sampling Transitions and Dynamics Relevant to Chemistry in Biomolecules

For most problems in bioenergy transduction, the key quantity of interest is the underlying free energy profile, which can be used to compute rate constants with well-accepted theoretical models such as the transition state theory.⁵⁹ The rate constants can then be fed into kinetic network models for gaining further mechanistic insights,⁶⁰ such as dominant kinetic pathway(s) and the overall time-scale and efficiency of energy transduction; in this context, it is important to recall that rate constants depend exponentially on the free energy barrier, thus small errors in the computed barrier can lead to large errors in kinetics, hence effective computational techniques for adjusting computed rate constants based on experimental observables are highly valuable in this regard.^60,61 For the computation of free energy profiles, in principle the methodologies commonly used for classical simulations, such as metadynamics⁶² and finite-temperature string⁶³ methods, are readily adapted. The key difference lies in the choice of collective variables (CVs), which might take unique forms for chemical processes. For example, charge centroids based on either structural,⁶⁴ charge^65,66 or electron density⁶⁷ have been used to construct CVs for studying long-range proton transfers.

Since QM/MM computations are generally more expensive than classical simulations, it is worthwhile considering multi-level strategies. For example, semi-empirical QM methods are usually more reliable for structural properties than for energetics. Thus, one effective protocol⁶⁸ is to first sample the reaction pathway with, for example, DFTB/MM string simulations; with configurations from the optimized minimal free energy path as the initial guess, string calculations with a higher-level QM/MM potential are expected to converge more rapidly for more accurate energetics. Alternatively, configurations from semi-empirical QM/MM simulations can be used in conjunction with machine learning techniques to improve energetics; see below for further discussions.

A particularly interest topic concerns the direct simulation of sequential electron transfers (ETs) in proteins, for which two of us have developed the Fragment Orbital Tight Binding Density Functional Theory (FO-DFTB).^69,70 In this quantum-chemical calculation, the quantum region is divided into several fragments, with the general idea to reduce the computational cost as well as to allow for an easy and efficient parallelization. The fragments are defined in such a way that any conjugated π-electron systems are kept intact, so the electronic structure of the isolated fragments can be computed straightforwardly. For biological ET, the fragments may be side chains of aromatic amino acids, peptide bond moieties, or nucleic acid bases. Notably, while the electronic structure of a single fragment is calculated, the other fragments as well as the entire condensed phase environment is treated as point charges, so the fragment is polarized properly.

Next, the Hamiltonian (and overlap) matrices are set up in the basis of the computed fragment orbitals, and they are further used to propagate the electron density corresponding to the excess charge (electron or hole), by way of integrating a time-dependent Schrödinger equation. Effectively, the entire molecular system, with the exception of an excess electron or hole, is treated using a classical MM force field. Note that this also includes the ET-active fragments at any moment that they do not carry any excess charge. The actual propagation of the excess charge is performed in every step of the MD simulation, and proceeds as follows:

• The Hamiltonian (and overlap) matrices in the basis of frontier orbitals of the individual fragments are obtained with FO-DFTB/MM. Only the orbitals that play a role in the ET process need to be considered; in low-energy biological ET, these include typically one or few frontier orbitals. The diagonal elements, (“site energies” representing the ionization potentials for hole transfer or the electron affinities for excess electron transfer) as well as the off-diagonal elements (“electronic couplings”) were benchmarked, and high accuracy was observed although scaling is required in some cases.^71–74

• A time-dependent Schrödinger equation in the basis of the fragment molecular orbitals (FMOs) is set up, so that it can be integrated for the expansion coefficients of the individual FMOs. Since the problem at hand clearly possesses a semi-classical character, one of the many available non-adiabatic propagation schemes is used. Most common choices are the trajectory surface hopping and the mean-field Ehrenfest methods. We note that semi-classical non-adiabatic MD was pioneered^75,76 and first applied to charge separation in photosynthetic reaction center proteins⁷⁷ by Warshel et al., and our methodology follows the development of real-time time-dependent DFTB.⁷⁸

• The wave function of the excess electron is projected onto the atomic charges of the ET-active fragments, and their force-field charges are update accordingly. This procedure can be understood as an “on-the-fly” reparametrization of the force-field, driven by the electronic structure of the quantum region subject to the non-adiabatic propagation.

• Forces on the atoms are calculated using the force field including the updated charges. At this stage, the dynamics of the system is exclusively governed by the classical equations of motion. Nonetheless, such a scheme is capable of describing the dynamic relaxation of the system in response to any partial or complete electron transfers, which represents the microscopic mechanism of the reorganization processes in the phenomenological Marcus theory (see discussion below).

• For the purpose of analysis, the charge occupation (squared expansion coefficient) of each fragment is recorded along the trajectories being performed. This value ranges between 0 (neutral fragment) and 1 (fragment completely occupied by the hole or excess electron being transferred). After averaging over the ensemble of simulations, the time-dependent occupations can be fitted using a kinetic model⁷⁹ to obtain rate constants of the forward and backward ET events.

2.4. Computation of Experimental Observables

It is critical to compute experimental observables so that computational results can be validated and predictions tested. With QM/MM methods, a broad range of observables can in principle be computed,⁸⁰ ranging from various spectra through free energy relations to kinetic isotope effects.⁸¹ As mentioned above, computed properties such as rate constants, equilibrium constants and spectral densities can be fed into kinetic network models (either classical or quantum⁵⁹) for probing macroscopic features relevant to the energy transduction process. The convergence of those observables depends on the system and sometimes requires extensive sampling. For example, kinetic isotope effects can be computed with path-integral techniques,⁸² which may require the equivalence of multiple nanoseconds of sampling,^34,83 which is possible only with semi-empirical methods. The computation of infrared spectra,^84,85 especially multi-dimensional ones,⁸⁶ also requires extensive sampling.

For semi-empirical methods, the trade-off between computational efficiency and accuracy is a matter of concern, however, well calibrated semi-empirical methods have been shown to be very useful in interpreting and predicting spectral properies of complex systems. For example, the mid-IR C=O double bond vibration is highly sensitive to the hydrogen bonding environment, showing red-shifts up to 50 cm⁻¹ in strongly hydrogen bonded systems relative to the gas phase, and an reparametrized semi-empirical method has been shown to capture these shifts reliably,⁸⁷ being able to resolve details of water bridged hydrogen bonds between amino acids, which were experimentally difficult to determine. This helped to differentiate between various intermediate structures in the bR photocycle at different temperatures.^88,89

Another frequently computed property for energy transfer (e.g., light-harvesting) systems is the spectral density, which describes the coupling of the nuclear degrees of freedom to the electronic structure. In principle it can be computed from a time series of excitation energies along a classical MD trajectory. However, since classical force fields often do not capture the geometry of the chromophore reliably, spectral density computed using MD trajectories sampled with classical force fields often suffers from the “geometry mismatch” problem.⁹⁰ Accurate spectral densities compared to experimental data were obtained using a semi-empirical method specifically reparametrized for an accurate desription of vibrational frequencies.^90,91

2.5. Integration with Machine Learning

In recent years, machine learning (ML) has become an increasingly powerful tool in computational analysis of molecular systems.⁹² In the context of QM/MM simulations and bioenergy transduction, ML techniques are uniquely valuable in several areas (Fig. 2). First, ML techniques can be used to enhance the efficiency of free energy sampling, especially when multiple collective variables⁹³ are potentially important to describing the coupling between the reaction and environmental degrees of freedom.⁹⁴ Second, ML methods can be used to improve the accuracy of semi-empirical QM/MM simulations via iterative “Δ-learning”, in which configurations from “low-level” QM/MM (e.g., DFTB/MM) trajectories are used to learn the differences (Δ) from “high-level” QM/MM energies and forces; the differences are then used to either directly estimate correction of the free energy surface or re-sample the potential energy surface for improved free energies.^95,96 These “multi-level” free energy simulation methods have so far been applied to relatively simple solution reactions,⁹⁷ as learning the Δ reliably for realistic systems with a large QM region is, in fact, not straightforward and requires further developments. Finally, ML can also be used to learn other properties, such as electronic coupling elements⁹⁸ or vertical excitation energies⁹⁹ as functions of molecular configurations; training such ML models can substantially reduce the cost of electron transfer and spectra calculations.

Figure 2:

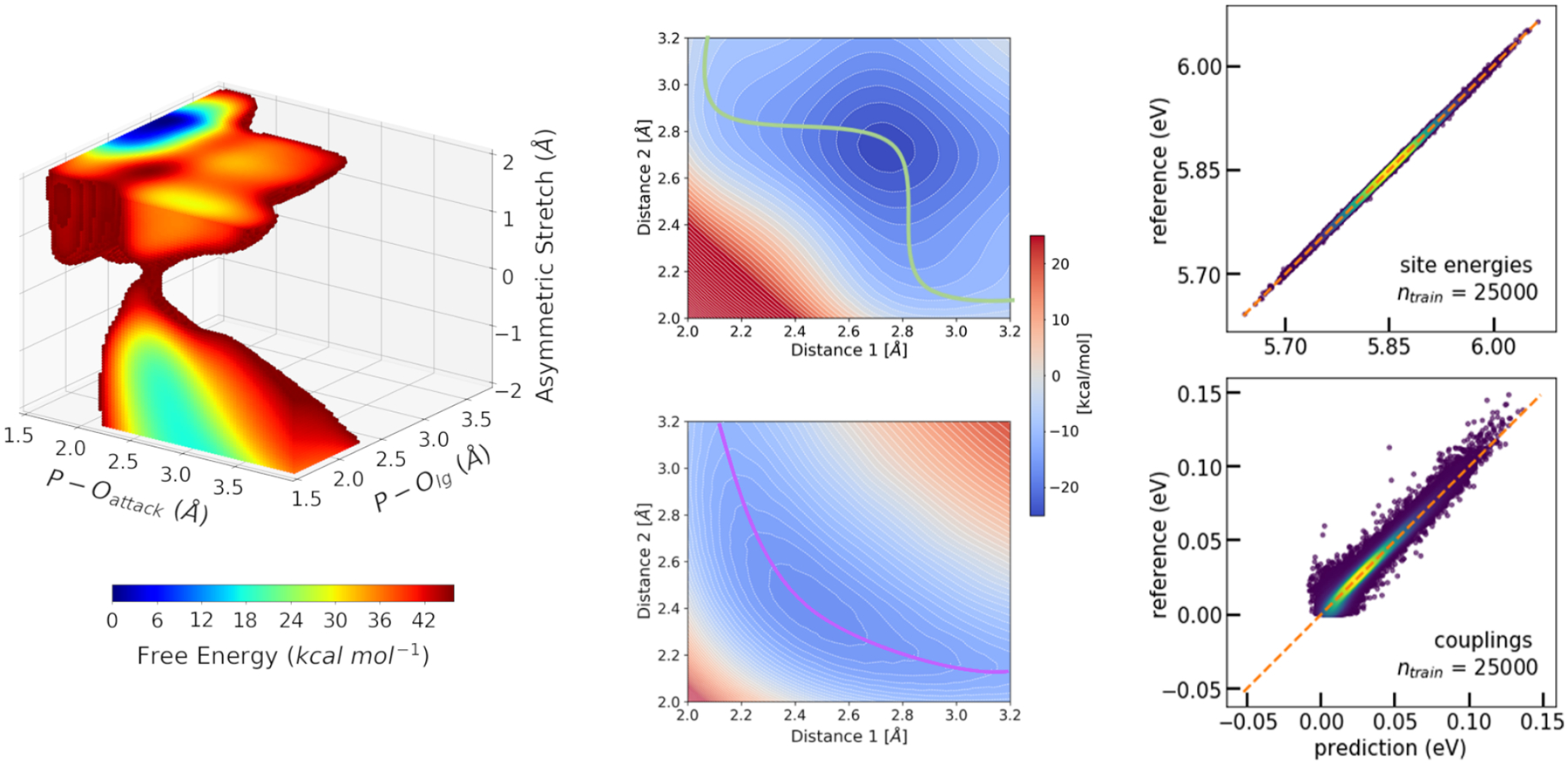
Machine learning (ML) techniques can be integrated with QM/MM simulations in diverse ways. Left: Reinforcement learning and other techniques can be used to accelerate QM/MM free energy simulations. The example shown here is the three-dimensional free energy surface for the hydrolysis of methyl phosphate in solution at the DFTB3/MM level.¹⁹ Middle: Neural networks using symmetry function representation of molecular structures are used in a Δ-ML scheme to correct the energies yielded by DFTB3. Here, the qualitatively wrong DFTB3 energy landscape of thiol–disulfide shuffling reaction (top) is corrected to agree with ab inition reference quantitatively (bottom).¹⁶⁹ Right: Kernel ridge regression combined with the Coulomb matrix representation was used to model the Hamiltonians describing ET processes in organic semiconductors. Shown is the accuracy of prediction vs. reference for electron transfer site energies (top) and couplings (bottom) for geometries taken from an MD simulation of crystalline anthracene.⁹⁸

3. Application and Case Studies

In this section, we discuss several recent applications to illustrate the value and limitations of QM/MM based simulations, including calibration of the methods in realistic applications for meaningful mechanistic insights. Due to the sampling requirement of these applications, we focus largely on DFTB/MM studies, although complementary efforts using other QM/MM methods are also mentioned for comparison.

3.1. Long-range Proton Transport in Proteins

3.1.1. Key Mechanistic Questions

Since the proton motive force plays key roles in bioenergetics, long-range proton transports coupled with either photon absorption or electron transfers are richly featured in bioenergy transductions. Representative examples include bacteriorhodopsin (bR), Complex I, Complex IV (cytochrome c oxidase) and the F₀F₁-ATPase. In terms of the key questions of common interest, these include: (1) What amino acids/co-factors are involved as the proton donor, acceptor and mediating groups? This is difficult to answer based on experiments alone because the positions of hydrogen atoms are usually not visible in crystal or EM structures; mutation experiments and spectroscopic data are potentially informative, although a molecular level interpretation is often not as straightforward as it may appear. An example that we’ll touch upon below concerns the proton storage group (PRG) in bR, which has attracted much attention in the past decades till very recently.¹⁰⁰ (2) Is there a single, dominant proton transfer pathway or many pathways are involved with similar fluxes? The typical approach for identifying potential proton transfer pathway(s) is to focus on water wires that mediate proton transfers via the canonical Grotthuss mechanism. As discussed in increasing number of studies,^101,102 however, water wires in static crystal structures in the absence of the excess proton may not represent the proton transfer pathway and very often multiple pathways may contribute. (3) Finally, arguably the most puzzling question is what controls the gating of proton transfers;¹⁰³ the timing and directionality of long-range proton transfers lie at the heart of the efficiency of bioenergy transduction, and understanding the underlying molecular mechanism requires going beyond structural models to evaluate how thermodynamics and kinetics of proton transfers are modulated by other events, such as reduction of nearby co-factors^104,105 and change in the local hydration level.^{101,106–108}

3.1.2. Model Validation

Proton transfer energetics depend critically on the pK_a values of the donor, acceptor and mediating group(s). Therefore, microscopic pK_a calculations are essential validations for both the enzyme model (e.g., titration state of key residues) and the computational (QM/MM) methodology.¹⁰⁹ The prediction of reliable microscopic pK_a values relies on an accurate treatment of both proton affinity of the relevant titratable group and its interaction with the protein environment while in different protonation states. Moreover, the responses of the protein and internal water molecules to the change of titration state also needs to be properly captured;¹¹⁰ these in general include both dipolar reorientations and electronic polarization, which requires extensive conformational sampling and treatment of electronic polarizability of the environment, respectively. In the study of cytochrome c oxidase, for example, DFTB/MM based thermodynamic integration simulations^111,112 were used to probe the microscopic pK_a value of the critical Glu286 residue, which was buried in a relatively hydrophobic internal cavity and thus featured a rather shifted experimental pK_a value of ~9.7. DFTB/MM free energy simulations with different enzyme models and approximate treatments of electronic polarization¹¹² found that reproducing the experimental pK_a value required penetration of water molecules into the cavity, which was coupled with the protonation of a propionate group of heme a₃. Therefore, in addition to serving as validation, microscopic pK_a calculations can potentially provide important mechanistic insights as well. Along this line, it is worth noting that microscopic pK_a calculations have also been used to calibrate reactive force field models (MS-EVB) for studying proton transfers in solution and proteins.¹¹³

3.1.3. Example: the O to bR Transition in Bacteriorhodopsin

One prototypical example of proton pumps is bacteriorhodopsin, whose photocycle features several proton transfer reactions coupled to conformational transitions. Some of the few last remaining challenges in the study of these complex processes were the atomic structure of the O state, especially with regard to the hydration of the active site, and the mechanism of the conversion to the ground state of bR, featuring a long-range proton transfer. Application of parallelized DFTB3/MM metadynamics protocols as well as other extended sampling methods made it possible to answer these questions with multi-dimensional free energy surfaces¹¹⁴ (Fig. 3).

Figure 3:

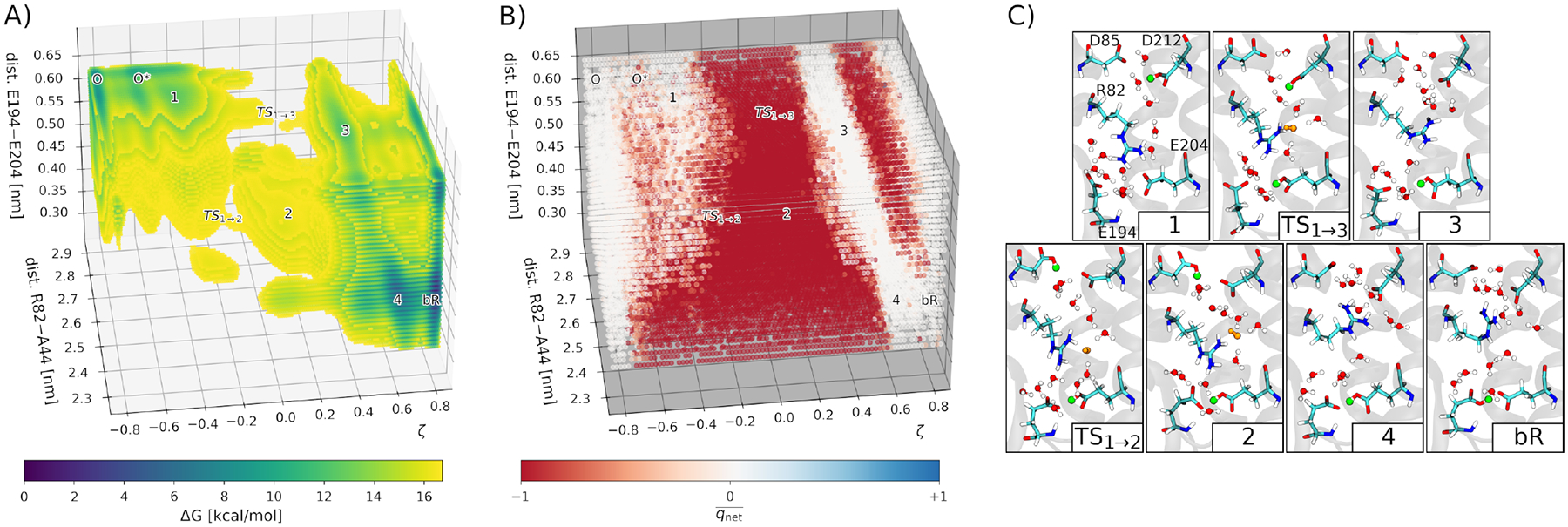
DFTB3/MM free energy simulations reveal a proton hole mechanism for the O→bR transition in bacteriorhodopsin,¹¹⁴ which involves a proton transfer from D85 to the PRG (E194, E204), mediated by D212, cavity water and R82. A: The 3D free energy surface from ~100 ns multi-walker metadynamics simulations. The relevant states are labeled. B: Net charge of QM water molecules. White: $\overline{q_{\text{net }}}=0$, neutral water; red: $\overline{q_{\text{net }}}=-1$, OH⁻; blue: $\overline{q_{\text{net }}}=+1$, H₃O⁺. C: Representative structures corresponding to the states identified in the free energy surface. Green: proton bound to an Asp or Glu; orange: charged water species (here, always OH⁻).

The thermodynamics and kinetics of the proton transfer was obtained in a good agreement with experimental estimates, which underscored the credibility of the methodology used. The reaction energy of −3.6 kcal/mol was consistent with the measure pK_a differences between D85 and the PRG. Concerning the kinetics, the obtained energy barrier translated into a time scale of ca. 0.6 ms, which is in the range of experimental estimates.

The study¹¹⁴ provided insight into the microscopic proton transfer mechanism and the key structural patterns, regarding especially charged amino acid side chains and water molecules, coupled to the actual proton transfer. The side chain of R82 sidechain switches between two possible distinct orientations to stabilize specific negatively charged amino acids: D85/D212 in the ground state bR, and PRG in the O state. Linked to that is the control of the hydration level of the active site by means of the motion of the R82 side chain and opening and closing of the PRG. The ground state bR features a low internal hydration level due to the closed PRG, and there is no continuous water wire because of the intervening R82 side chain. The latter feature helps prevent any wasteful back transfer of protons.¹⁰³ On the other hand, the O state has an elevated level of internal hydration, made possible by the open PRG; a continuous water wire is formed between D85 and the PRG, allowed by the reoriented side chain of R82. From a simple electrostatic perspective, the positive charge of R82 may also aid the generation and transfer of the hydroxide ion, which was observed in DFTB3/MM free energy simulations.¹¹⁴ The observation of the proton hole mechanism corroborates with the chloride pumping ability of the D85S mutant of bR,¹¹⁵ and with the similar mechanisms of bR and halorhodopsin, which feature conserved patterns of electrostatic interactions between the transferred anion and the protein’s amino acid side chains.¹¹⁶

3.1.4. Vibrational Spectra

Two examples concern vibrational bands in bacteriorhodopsin from FT-IR studies by Gerwert and co-workers.^117,118 The first example focused on the PRG (see Fig. 3C), whose identity has been debated for many years. Numerous crystal structure, including the very recent high-resolution crystal structures for multiple kinetic states,¹⁰⁰ revealed a pair of glutamate residues (Glu 194, Glu204) whose sidechains are extremely close to each other, with carboxylate oxygens merely separated by ~2.4 Å. Such unusual geometry together with mutation data suggested that the pair of glutamates are involved in storing the proton. The FT-IR study of Gerwert and co-workers observed a diffuse band around 2,000 cm⁻¹, which is commonly observed in protonated water clusters. Since a number of water molecules were observed near the pair of glutamates, it was initially suggested that the proton was in fact stored on these water molecules in the form of a “delocalized” proton. This interesting hypothesis stimulated a set of computational studies using different QM/MM methodologies and sizes of the QM region; nuclear quantum effects were also evaluated with ring-polymer molecular dynamics.⁸⁵ While it remains challenging to exactly match experimental line shape, the latest DFT/MM simulations¹¹⁹ continue to support the model⁸⁴ in which the excess proton is delocalized between the pair of glutamates, although nearby water molecules are clearly important to provide additional stabilizations.

Another unique infrared signature in bR was observed for a number of water molecules trapped between the protonated retinal Schiff base and deprotonated Asp96 in the N kinetic state.¹¹⁸ The vibrational peaks were observed around 2540–2775 cm⁻¹, which is substantially red-shifted compared to neutral water. DFTB3/MM simulations¹²⁰ were able to capture the key experimental observation (Fig. 5A) and highlighted how the unique environment of the water cluster led to its significant polarization and therefore dramatic red-shift of the collective O-H vibration. An interesting observation was that the computed line shape was sensitive to the number of water molecules in the “cavity”, since including a larger number of water molecules perturbs the hydrogen bonding network and thus the vibrational coupling between the strongly polarized water molecules. Therefore, by systematically comparing computed and measured vibrational spectra, one is potentially able to characterize the structure and composition of water molecules in protein internal cavities, which are difficult to accomplish otherwise, especially for transient kinetic states.

Figure 5:

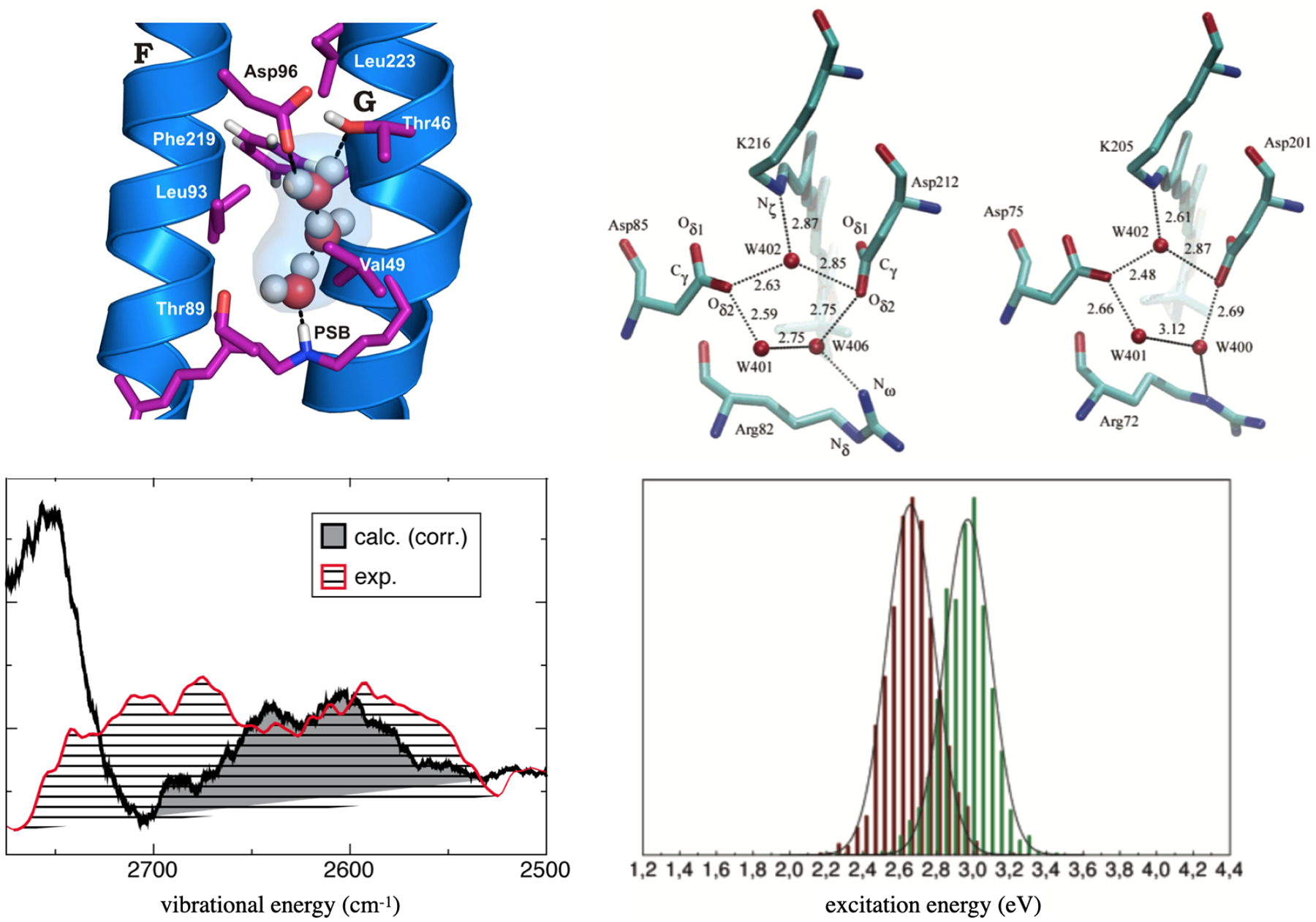
QM/MM calculations help explain shifts in vibrational and electronic spectra in retinal proteins. Left: A water cluster in the N state of bR has a unique local environment that leads to significant red-shifts of the computed (DFTB3/MM) vibrational spectra, in agreement with experimental observations.¹²⁰ Right: Difference in the hydrogen-bonding networks in the active sites of bR and ppR lead to significant shifts in the computed S0–S1 transitions: the histograms for bR (red) and ppR (green) are based on OM2/MRCI calculations sampled along ground state classical MD trajectories.¹³⁴

3.2. Fast Electron transfer

3.2.1. General Remarks

Of perhaps even more importance in bioenergetics are electron transfer (ET) processes as the primary “tool” of biological energy transduction. ET taking place between an electron donor and an acceptor in a complex molecular environment may be described with the Marcus theory.⁵⁹ For instance, Wu & van Voorhis developed a scheme based on constrained DFT the diabatic potential energy surfaces needed in the Marcus theory to express the reaction and reorganization energies.^121,122 The application of constrained DFT was crucial as it turned out to effectively avoid the over-delocalization problem of DFT.¹²³

Most biological ETs of interest, however, involve one or several electron relays, and a condition for the applicability of the Marcus theory is that any reorganization processes have finished completely before the subsequent ET event. Thus, the Marcus model works for slow hopping ET but not for fast ones, where “slow” means that the individual events are infrequent rather than that they would take a long time to complete. This was paraphrased by Troisi as a “speed limit” for hopping transfer.¹²⁴ It appears that numerous ET pathways in bioenergetics exceed this speed limit, and the temporal scales of the reorganization and of the (relatively fast, or frequent) ET itself overlap. On the same note, Matyushov et al. reasoned that the energy barriers to ET in proteins (as a representative of a complex molecular system) are not real equilibrium quantities; rather, they depend on the specific temporal scale of the ET reaction.¹²⁵ Such cases then need to be described by more flexible methodologies that do not imply any separation of temporal scales.

Biomolecular ET has been a frequent subject of computational studies, and the state of the art in 2015 was reviewed by Blumberger.¹²⁶ Fast ET has proven challenging to describe, but still it has been investigated using a few different approaches, usually employing more advanced versions of the traditional ET models. For example, the light-driven ET in multiheme cytochrome STC from S. oneidensis in aqueous solution occurs on a scale of several nanoseconds, and it was investigated by a combination of experimental and computational techniques.¹²⁷ This work used a non-ergodicity correction by Matyushov,¹²⁸ which removes the contribution of slow motions from the total reorganization energy. Also, the dynamics of ultrafast ET in flavodoxin protein was shown to depend on its coupling to environmental fluctuations.¹²⁹ This coupling reduces the reaction free energy as well as the reorganization energy. Most recently, the mechanism of the highly efficient ET supported by polymerized cytochrome OmcS in G. sulfurreducens was discovered.¹³⁰ The process takes place over micrometers, with elementary hopping on sub-nanosecond scale – hence the notion of “protein wire” – and accelerates upon cooling. On the other side of the spectrum of computational methods is the study of sub-picosecond ET in a rhenium complex coupled to the azurin protein from P. aeruginosa.¹³¹ Computationally expensive combination of surface hopping and hybrid-DFT based calculations of excited states were feasible given the short temporal scale to cover, making it possible to reveal the mechanism of the reaction.

By comparison, our FO-DFTB approach relies on the simultaneous propagation of the coupled electronic and nuclear degrees of freedom in a semi-classical fashion. This method does not involve any assumption on the relative rates of the ET reaction and the relaxation (reorganization) processes, making it possible to resolve any relevant temporal scales in an unbiased manner. The efficiency of the method makes it possible to explicitly describe ET processes on a nanosecond scale, as illustrated by the examples below.

3.2.2. Examples: Photolyases and Cryptochromes

We applied the FO-DFTB/MM methodology to investigate multi-step ETs in the proteins of the photolyase cryptochrome family (PCF), which are involved in DNA repair and in various signaling pathways. The part of the photoactivation process in E. coli DNA photolyase, which constitutes an ET along three conserved Trp side chains (ET from the protein surface to the FAD cofactor) was investigated in our first study.¹³² The ET was simulated on the naturally occurring temporal scales without introducing any system-specific parameters, and a kinetic analysis yielded rates in excellent agreement with experimental data. A detailed picture of the ET process emerged, and it became clear that the second ET step may occur before the structural relaxation following the first ET step has completed. This illustrates the flexibility of the non-adiabatic simulation approach, which is applicable even in this case for which the Marcus theory is not applicable, because of the non-equilibrium reaction conditions due to the overlapping temporal scales of the processes involved (ET itself, delocalization of charge, relaxation of protein, reorganization of solvent). As for the features of the ET in that protein and perhaps PCF in general, it was shown that it is the polarization of the solvent at the surface of the protein that makes the process exergonic and thus uni-directional.

Then, we investigated the interesting case of a class III cyclobutane pyrimidine dimer (CPD) photolyase from A. tumefaciens, which features not just one but two different, branching ET pathways containing a total of six Trp side chains, which were both found to play a role in the photoreduction of FAD.¹³³ We discovered an intriguing thermodynamic and kinetic competition between the two pathways: one pathway supports a faster ET while the other pathway stabilizes the final product better. This balance manifested itself in our simulations by the electron hole first transferring along the “fast” Trp triad, before a sequence of backward ET steps led to the transfer of the electron hole to the second pathway. The whole process occurred on a temporal scale of nanosecond, and was accompanied by complex repolarization of the environment (parts of the protein as well as, not least, water molecules), emphasizing the need for a multi-scale computational description (Fig. 4).

Figure 4:

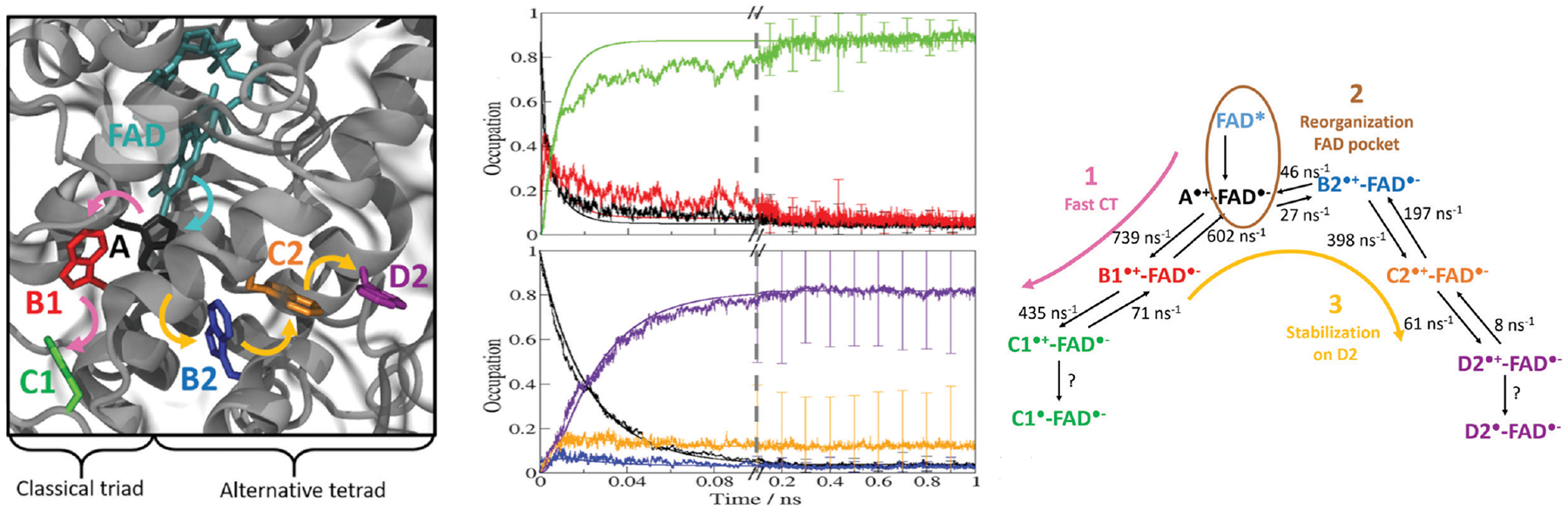
Multi-scale non-adiabatic semi-classical simulations of electron transfer in complex and bio-molecular systems involve a simultaneous propagation of the transferring electron and of the protein dynamics. By doing so, they provide atomic-level insight into the coupling of these processes. The example shown considers two different ET pathways in a photolyase protein PhrA.¹³³ Left: Active site of PhrA, showing the amino acid side chain participating in the branching electron transfer pathways. Center: Temporal course of the averaged occupation of the individual participating amino acid side chains by the transferring electron hole, along the two different pathways. Right: The kinetic scheme inferred from the temporal dependences of the occupations reveals a possible mechanism of the kinetic and thermodynamic control of the ET pathways in PhrA. All panels share the same color code to designate the different amino acid side chain considered as electron relays.

3.3. Electronic Excitation

3.3.1. The challenge of excited states in biomolecules

The computational determination of protein excited states is a significant challenge. The size of the chromophores requires approximate methods like time-dependent density functional theory (TD-DFT) or more approximate post-Hartree Fock methods like CC2 to be applied. In some cases, the determination of an optimized structure using QM/MM geometry minimization techniques may be sufficient when average and optimized structures agree sufficiently well. This is the case for many retinal proteins like bR or ppR, as shown by explicit calculations.¹³⁴ Here, the active site is characterized by a very stable and strongly hydrogen bonded structure. We note that force fields using fixed point charges, however, may have difficulties in describing strongly hydrogen bonded complexes, therefore equilibrating the protein structure using such force fields may lead to conformations that are not suitable for further QM/MM investigations; this problem was described recently for the ChR2 protein,¹³⁵ as well as for a Glucose binding protein.¹³⁶ Due to the long sampling times required, the system then requires using either a polarizable force field¹³⁶ or a semi-empirical QM/MM approach, which has been shown to retain the active site structure well.¹³⁵ In the latter case, however, a minimum energy structure may not be adequate, and absorption spectra have to be computed by sampling excited states along QM/MM MD trajectories.⁵⁴

All approximate quantum methods trade accuracy with computational efficiency, which is particularly challenging for electronically excited states as mentioned in Sect.2.2. We note, however, that the effects of approximations are already visible in the determination of the ground state structures of conjugated electronic systems,^54,55 where the bond-alternation (the difference of the bond-length of neighboring single and double bonds) is sensitive to the method applied. This is important since the ground state structure also determines the excited states properties, which calls for a careful choice of methods for both ground and excited states calculations. Similarly, torsional angles and planarity of the chromophore can be dependent on the approximation, which may also affect excited states properties.

The problems of TD-DFT for excited states are nowadays well known, as recently discussed for the case of chlorophylls.¹³⁷ Important to mention is the overestimation of excited states energies, which leads to a blue shift in the computed spectra and is pronounced for hybrid and long-range corrected functionals. This, however, is less problematic since a systematic blue-shift can be corrected when comparing to experimental data. More problematic is the inability of TD-DFT (or single reference methods in general) to describe doubly excited states, and the problems with describing charge transfer states,⁵² which have been seen for retinal proteins early on.^51,55 For retinal, this can result in a wrong dependence of excitation energies on the chromophore structure, but also on the influence of the protein electrostatic field. The development of long-range corrected (LC) TD-DFT methods could partially resolve many of the TD-DFT problems. However, LC-TD-DFT methods are far from being perfect for color-tuning studies in retinal proteins (see below), still underestimating the response to the protein electrostatic field. Similar effects have been reported for chlorophylls,⁵⁴ and it can be expected to hold for other color pigments as well.

3.3.2. Color tuning of excited states in biomolecules

Many photoactive biomolecules, like rhodopsins (Rh), green fluorescent proteins (GFP) or Blue light using FAD (BLUF) proteins contain one chromophore bound to a protein matrix. In contrast, light harvesting systems like the Fenna-Matthews-Olson complex (FMO) or light-harvesting complex II (LH2) contain several (chlorophyl) chromophors. The maximum absorption wave-length is determined by several factors, which are: (i) the geometrical and electronic features of the chromophore, (ii) the steric, electrostatic and hydrogen bonding interactions with the environment and (iii) a possible coupling between the chromophores within the protein complexes.

Due to their diverse molecular and electronic structure, the various chromophores have very different absorption maxima in gas phase, but also very different responses to steric and electrostatic interactions with their environments. A steric interaction with nearby protein groups can twist the often planar structure, thereby disturbing the conjugation of the delocalized electronic system. Through hydrogen bonding, as in the case of the retinal Schiff base in retinal proteins, the localization of charge on the chromophore can be strongly affected, leading to large color shifts. Electrostatic interactions with the environment can lead to a further color shift, when ground and excited states have different dipole moments. Polarizable residues, in particular in the immediate vicinity of the chromophore, can lead to a polarization-shift. Retinal proteins, for example, absorb in a range of 300–700 nm, which illustrates the immense tunability due to a very sensitive response to external electrostatic potentials^54,134, while it is much less for most other chromophores. For example, in Ref. 134, the color shift of 70 nm between bR and ppR (phoborhodopsin) has been investigated; it was found that the shift was partly due to the different hydrogen bonding networks around the retinal and partly due to the different electrostatic fields from the protein environment (Fig. 5). In multi-chromophoric systems like LH2, close-lying chromophores lead to a coupling of excited states, i.e., a delocalization of the excited states over several chromophores, which results in a red shift of about 50 nm in LH2.^54,138–140

The impact of polarization on retinal excited state properties has been emphasized by Warshel and coworkers early on¹⁴¹ and has then been investigated in detail using quantum mechanical and polarizable force field methods.^58,142 Including polarization allows to compute accurate absolute excitation energies, when a reliable and well calibrated ab initio method like SORCI is used for the QM region. This allowed to determine protonation states of protein side chains¹⁴³ and discriminate between different structural models proposed for early intermediates of the bR photocycle.^88,89 Several other implementations of QM/MM with polarizable force fields have been reported so far.^48,49 For chlorophylls¹⁴⁴ in LH2, interestingly, direct electrostatic interactions seem to cancel the polarization response, therefore it was suggested to rather neglect the direct electrostatic interaction when not including polarization.¹⁴⁵

3.4. Mechanochemical Coupling

3.4.1. Key Mechanistic Questions

Many bioenergy transduction processes in cells are driven by the binding and hydrolysis of NTP (e.g., ATP or GTP). While in many cases, large-scale conformational transitions have been established to be coupled directly to the binding of NTP and/or dissociation of hydrolysis products, it is an intrinsically interesting question how the hydrolysis of NTP is coupled with the conformational state of biomolecule. Indeed, if the coupling were weak, futile nucleotide hydrolysis would occur, leading to reduced thermodynamic efficiency of the energy transduction.¹⁴⁶ In addition to the more visible conformational transitions, other more subtle changes may make notable contributions to the chemical step. For example, an emerging theme in nucleic acid enzymes such as DNA polymerases and RNase H is that transient cation recruiting into the active site may play a major role in activating the chemical step.^147,148 For example, in the DNA polymerase η, time-resolved crystallography has captured the presence of the third Mg²⁺ ion during the nucleotide addition process.¹⁴⁹ Whether the third Mg²⁺ is essential to lowering the activation barrier of nucleotide addition or its main role is to stabilize the product has been debated. Nevertheless, the importance of such transiently recruited metal ion (i.e., not highly populated in the ground state structure) to the chemical activity has been well received.^150,151 After all, it is common to invoke change of protonation state of active site residues for efficient catalysis in enzymes, despite the fact that the concentration of protons is often substantially lower than those for common metal ions under physiological conditions.

In short, the key mechanistic questions commonly encountered in biomolecular machines using NTP as “fuels” include: (1) In what conformational state does the chemical step (e.g., ATP hydrolysis) occur? (2) What are the roles of the key regulatory events, which are likely local in nature, such as closure of the nucleotide binding pocket, reduction of the level of local hydration, and recruitment of additional metal ion(s)? (3) How are these local regulatory transitions coupled to the more global conformational transitions, so as to ensure a tight mechanochemical coupling and therefore a high thermodynamic efficiency of the bioenergy transduction process?

3.4.2. Model Validation

Since nucleotide hydrolysis is the driving reaction for many biomolecular machines, it is important to calibrate the QM/MM methodology for phosphoryl transfer chemistry.¹⁵² This has been a challenging task due to the highly charged nature of phosphates and existence of multiple competing mechanisms,^153,154 which place major demands in both computational accuracy and sampling efficiency. In addition to energetic properties, kinetic isotope effects are valuable for confirming that the nature of transition state is adequately captured.^83,153

3.4.3. Competing Pathways and Mechanochemical Coupling

To illustrate the value of QM/MM simulations to the analysis of chemical steps in biomolecular machines, we briefly discuss two recent examples (Fig. 6). The first is a classical biomolecular motor, myosin II, in which the hydrolysis of ATP requires closure of the active site, which in turn is coupled with the remarkable rotation of the converter domain more than 40 Å away.¹⁵⁵ Since our QM/MM analysis of myosin¹⁵⁶ has been summarized in several recent articles,^19,152 we only highlight two key points here. First, even with the crystal structure that features a fully closed active site (pre-powerstroke state), DFTB3/MM simulations were able to identify several reaction pathways for the hydrolysis of ATP that have rather similar rate-limiting free energy barriers. These pathways differ in terms of the mechanism through which the lytic water deprotonates to generate the strong nucleophile (OH⁻) and the routes that the ionized proton takes to reach the hydrolysis product, the inorganic phosphate and ADP. The observation highlights that even in enzyme active sites that have been “optimized” by evolution, competing pathways exist, thus it is essential to develop (almost) automated methodologies for the exploration of reaction pathways with little prior human biases. Along this line, the computational efficiency of DFTB3/MM approach was essential to the successful integration between metadynamics and finite temperature string methods for the exploration of alternative reaction mechanisms.¹⁵⁶

Figure 6:

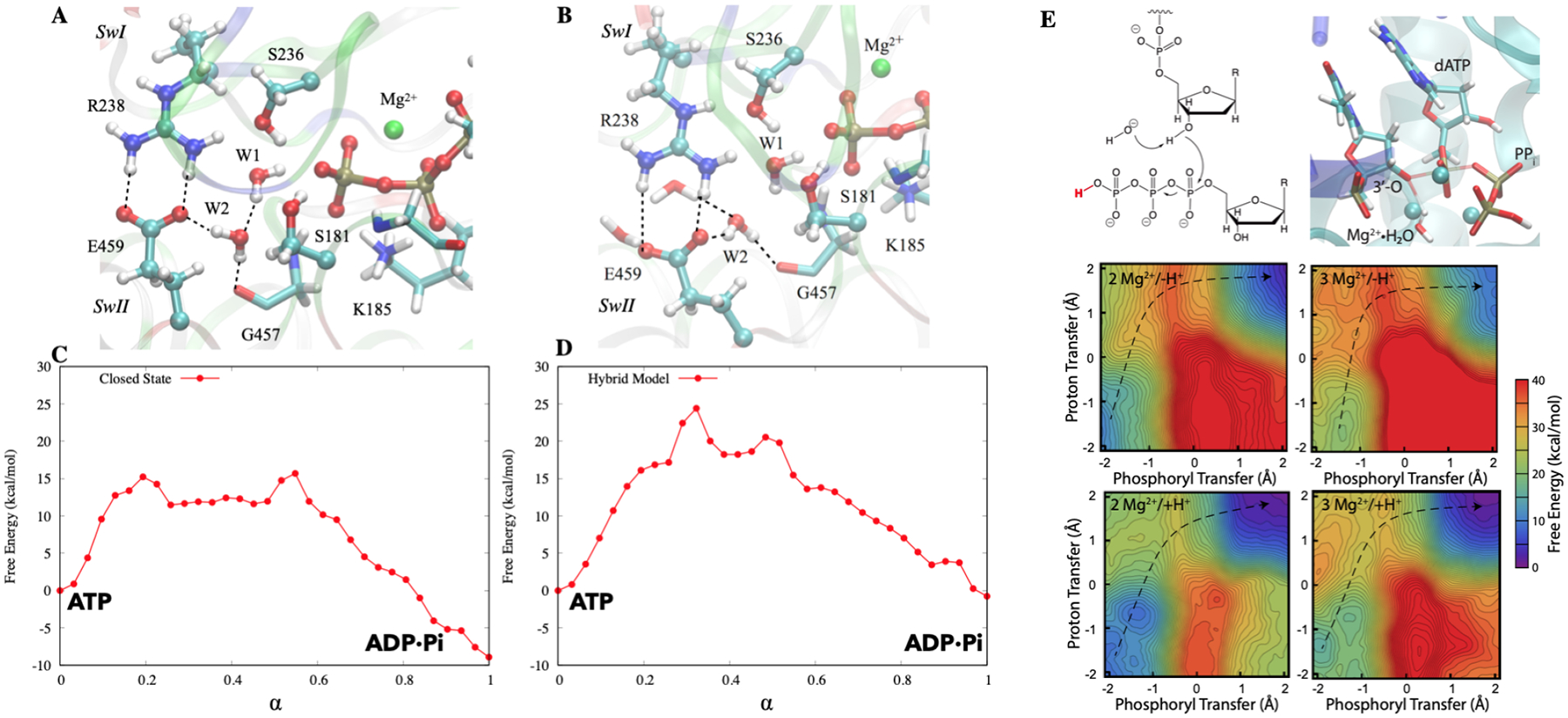
QM/MM studies of reaction mechanisms in biomolecular motors myosin¹⁵⁶ (A–D) and DNA polymerase η¹⁶⁰ (E). A. The pre-powerstroke state based on the crystal structure of the myosin motor domain complexed with ADP·vanadate (PDB code: 1VOM); B. A computational “hybrid” model, in which the active-site protein residues are restrained to adopt the structure of the pre-powerstroke state, while the rest adopts the post-rigor crystal structure (PDB code: 1FMW). C–D. Free energy profiles computed for the two structural models based on DFTB3/MM string calculations. Note that although the active-site structures are very similar in the two models, the hydrolysis free energy profiles are significantly different. E. Mechanism, transition state structure, and free-energy surfaces for a mechanism with a Mg²⁺-coordinated hydroxide as the base under 4 different conditions: 2 Mg²⁺ and deprotonated leaving group, 3 Mg²⁺ and deprotonated leaving group, 2 Mg²⁺ and protonated leaving group, 3 Mg²⁺ and protonated leaving group.

Another unique piece of insight was obtained by studying the hydrolysis energetics in an artificial “hybrid” construct that featured a closed active site in a post-rigor state of the myosin motor domain; this model was established to explicitly probe the coupling between ATP hydrolysis and distal conformational transitions. As shown in Fig. 6A–D, although the hybrid and pre-powerstroke active sites feature essentially the same set of first coordination shell interactions for the lytical water and the γ-phosphate, the computed free energy profiles differ significantly in terms of both the rate-limiting barrier height and the overall exergonicity; both quantities are less favorable by ~ 9 kcal/mol for the hybrid structural model. This result clearly underscores the notion that reaction free energy profiles in enzyme active sites are not solely determined by first-shell interactions. In particular, in the absence of conformational transitions beyond the active site, the reactive moieties and catalytic motifs (e.g., Switch II) in the hybrid model are surrounded by a cluster of water molecules, which are not observed in the pre-powerstroke state. As a result, the active site is less pre-organized in the hybrid model, leading to less favorable reaction energetics. This observation is reminiscent of the results from recent computational analysis of loop closure in triose phosphate isomerase;¹⁵⁷ it was found that the proton transfer energetics remained largely similar to the bulk values as far as a few water molecules were trapped in the active site, even with the “lid” loop adopting essentially the fully closed configuration. Evidently, establishing a well pre-organized active site for efficient catalysis requires conformational rearrangements beyond the nearest neighbors of the catalytic motifs, which together with cooperative conformational transitions form the basis of mechanochemical coupling in biomolecular machines.

As a second example, we briefly discuss DNA polymerase η, especially the role of the third Mg²⁺ ion in nucleotide addition. While energy transduction is not the primary function of DNA and RNA polymerases, they are no doubt sophisticated biomolecular machines in that their functional cycles involve complex and coordinated structural transitions at different spatial and temporal scales; the goal of many mechanistic studies is to establish the driving force and functional significance of these structural transitions.¹⁵⁸ For DNA polymerase η, a much debated issue in recent years concerns the role of the third Mg²⁺ ion identified in time-resolved crystallography studies;¹⁴⁹ a closely related question concerns the timing of the deprotonation of the 3’-OH in the terminal base, for which multiple mechanisms have been put forward.¹⁵⁹ To shed light onto these issues, we have conducted extensive free energy simulations using DFTB3/MM following model calibration, including microscopic pK_a calculations for both model compounds and enzyme active sites.¹⁶⁰ By systematically comparing free energy profiles for ten plausible mechanistic models, we found that the lowest activation barrier occurred for a reaction where a Mg²⁺-coordinated water deprotonates the nucleophilic 3’-OH in concert with the phosphoryl transfer step. The presence of a third Mg²⁺ in the active site was observed to indeed lower the activation barrier for the water-as-base mechanism, as did protonation of the pyrophosphate leaving group. This mechanistic model, which does not invoke any specific protein residue as the catalytic base to activate 3’-OH, is consistent with a recent study¹⁶¹ that systematically removed potential hydrogen-bonding partners of the 3’-OH; it was observed that no single or combined perturbations eliminated the catalytic activity; i.e., neither the proton acceptor nor the departure path of the nucleophile deprotonation is fixed. These observations supported a model in which the 3’-OH deprotonation does not require a specific general base and it is readily activated by the three Mg²⁺ ions with flexible proton exit routes.

DFT/MM simulations have also been employed to probe various mechanistic issues in related systems,^{94,159,162–167} sometimes reaching similar conclusions, such as the key features of ATP/GTP hydrolysis transition states in biomolecular motors^{162–164,167} and the role of the third Mg²⁺ ion in DNA polymerase η.¹⁶⁵ In other cases, different conclusions were drawn, such as the mechanism of 3’-OH deprotonation in DNA polymerase.¹⁵⁹ With substantial differences in the time scale of sampling and general computational accuracy between DFT/MM and DFTB/MM simulations, it remains difficult to resolve discrepancies based solely on computational results; as emphasized in many studies, it is imperative to view the computational results in the context of available experimental data, and only by combining information obtained from experiments with that obtained from simulation can we obtain microscopic answers to questions of chemical reactivity in complex settings.

4. Conclusions and Outlooks

In this review article, we have discussed QM/MM methods and their applications to various bioenergy transduction processes, such as long-range proton transport, fast electron transfers and nucleotide hydrolysis. These applications require balancing computational efficiency and accuracy for the system of interest, making semi-empirical QM/MM models particularly valuable, although calibration and comparison to higher-level QM/MM methods is indispensable. Looking forward, there are several areas that can benefit further efforts to make such QM/MM analyses more quantitative and applicable to increasingly complex problems.

First, further improvements in both semi-empirical and ab initio QM methods, especially for transition metal ions and non-covalent interactions, are of major significance, since many systems in bioenergetics involve metal co-factors and require treating a large number of atoms at the QM level for the description of long-range proton/electron transfers or mechanochemical coupling; further integration with machine learning techniques is likely required to reach quantitative accuracy for these challenging problems.

Second, for the MM region, it is important to further enhance not only the accuracy (e.g., an explicit consideration of electronic polarization) but also complexity that better represents the working environment of the biomolecular machine(s) under investigation. Examples for the latter includes representation of the transmembrane potential, pH gradient and molecular crowding. In other words, the general aim is to develop truly multi-scale computational models that enable the analysis of energy transduction under realistic cellular conditions.

Finally, while providing a better understanding of experimental observations remains a major goal for computational studies, we believe “blind” predictions will play an important role in critically evaluating different QM/MM methodologies, similar to such efforts in the areas of protein structure prediction (CASP, CAPRI) and ligand binding (SAMPLX). As QM/MM calculations become increasingly affordable and standardized, along with advances in high-throughput experiments¹⁶⁸ that are able to efficiently generate a large amount of data, the time might be ripe for initiating such efforts in the QM/MM community.