Improved 3D Markerless Mouse Pose Estimation Using Temporal Semi-Supervision

Abstract

Three-dimensional markerless pose estimation from multi-view video is emerging as an exciting method for quantifying the behavior of freely moving animals. Nevertheless, scientifically precise 3D animal pose estimation remains challenging, primarily due to a lack of large training and benchmark datasets and the immaturity of algorithms tailored to the demands of animal experiments and body plans. Existing techniques employ fully supervised convolutional neural networks (CNNs) trained to predict body keypoints in individual video frames, but this demands a large collection of labeled training samples to achieve desirable 3D tracking performance. Here, we introduce a semi-supervised learning strategy that incorporates unlabeled video frames via a simple temporal constraint applied during training. In freely moving mice, our new approach improves the current state-of-the-art performance of multi-view volumetric 3D pose estimation and further enhances the temporal stability and skeletal consistency of 3D tracking.

1. Introduction

In 3D pose estimation, the positions of user-defined body keypoints are inferred from images to reconstruct body kinematics (Desmarais, Mottet, Slangen, & Montesinos, 2021). Precise pose measurement is a long-standing computer vision research problem with a myriad of applications, including to human-computer interfaces, autonomous driving, virtual and artificial reality, and robotics (Sarafianos, Boteanu, Ionescu, & Kakadiaris, 2016). Specialized hardware and deep learning empowered algorithmic advances have inspired new developments in the field, with the ultimate goal to recover 3D body poses in natural, occlusive environments in real time. While most research and development have thus far focused on human body tracking, there has been a growing push in the biological research community to extend 3D human pose estimation techniques to animals. Precise quantification of animal movement is critical for understanding the neural basis of complex behaviors and neurological diseases (Marshall, Li, Wu, & Dunn, 2022). The latest generation of tools for animal behavior quantification ditch traditionally coarse and ad hoc measurements for 2D and 3D pose estimation with convolutional neural networks (CNNs) (Bala et al., 2020; Dunn et al., 2021; Gosztolai et al., 2021; Günel et al., 2019; Mathis et al., 2018; Pereira et al., 2019, 2022).

Nevertheless, the majority of state-of-the-art 3D animal pose estimation techniques are fully supervised, and their performance depends on large collections of 2D and 3D annotated training samples. Large-scale, well-curated animal 3D pose datasets are still rare, making it difficult to achieve consistent results on real-world data captured under varying experimental conditions. Marker-based motion capture techniques (Marshall et al., 2021; Mimica, Dunn, Tombaz, Bojja, & Whitlock, 2018) enable harvesting of precise and diverse 3D body pose measurements, but they are difficult to deploy in freely moving animals and can potentially perturb natural behaviors. Manual annotation of animal poses therefore often becomes mandatory. However, manual annotation is time-consuming, and it can become difficult for human annotators to precisely localize body landmark positions under nonideal lighting conditions or heavy (self-) occlusion of the body. Although the influence of label noise has not yet been closely examined for pose estimation, overfitting to these inherently ambiguous labels might adversely affect model performance, as it does in image classification (Patrini, Rozza, Krishna Menon, Nock, & Qu, 2017). In addition to issues with data scarcity, fully supervised training schemes are often limited by the quality of training data. Even when using hundreds of training samples, the performance of fully supervised 3D pose estimation models can be inconsistent (Wu et al., 2020), especially when deployed in new environments and subjects.

This label scarcity has become a major bottleneck in the current animal 3D pose estimation workflows, limiting model performance, generalization to different environments and species, and comprehensive performance analysis. In recent years, the success of semi-supervised (Berthelot et al., 2019) and unsupervised deep learning (T. Chen, Kornblith, Norouzi, & Hinton, 2020; He, Fan, Wu, Xie, & Girshick, 2020) methodologies has presented new possibilities for mitigating annotation burden. Rather than relying solely on task-relevant information provided by human supervision, these approaches exploit the abundant transferable features embedded in unlabeled data, resulting in robustness to annotation deprivation and better generalization capacity.

In this paper, we introduce a semi-supervised framework which seamlessly integrates with the current state-of-the-art 3D rodent pose estimation approach (Dunn et al., 2021) to enhance tracking performance in low annotation regimes. The core of our approach is additional regularization of body landmark localization using a Laplacian temporal prior. This encourages smoothness in 3D tracking trajectories without imposing hard constraints, while expanding supervisory signals to include both human-annotated labels and the implicit cues abundant in unlabeled video data. To further reduce reliance on large labeled datasets, we also emphasize a new set of evaluation protocols that operate on unlabeled frames, thus providing more comprehensive performance assessments for markerless 3D animal pose estimation algorithms. We have collected and validated our proposed method on a new multi-view video-based mouse behavior dataset with 2D and 3D pose annotations, which have released to the community. Compared to state-of-the-art approaches in both animal and human pose estimation, our method improves keypoint localization accuracy by 15 to 60% in low annotation regimes, achieves better tracking stability, and anatomical consistency, and is qualitatively more robust during identified difficult poses.

Our main contributions can be summarized as follows:

1. We introduce a state-of-the-art performing approach by leveraging temporal supervision in 3D mouse pose estimation.

2. We release a new multi-view 3D mouse pose dataset consisting of freely moving, naturalistic behaviors to the community.

3. We benchmark the performance of a broad range of contemporary pose estimation algorithms using the new dataset.

4. We designate a comprehensive set of evaluation metrics for performance assessment of animal pose estimation approaches.

2. Related Work

2.1. 3D Animal Pose Estimation

There are currently three primary categories of 3D animal pose estimation techniques. The first category encompasses multi-view approaches based on triangulation of 2D keypoint estimates (Bala et al., 2020; Günel et al., 2019; Karashchuk et al., 2021; Mathis et al., 2018). These are typically lightweight in terms of model training and inference and are improved by post hoc spatial-temporal filtering (Karashchuk et al., 2021) when measuring freely moving behavior, where occlusions are ubiquitous. The second category leverages multi-view geometric information during end-to-end training. Zimmermann et al. (Zimmermann, Schneider, Alyahyay, Brox, & Diester, 2020) and Dunn et al. (Dunn et al., 2021) use 3D CNNs to process volumetric image representations obtained via projective geometry, whereas Yao et al. (Yao, Jafarian, & Park, 2019) propose a self-supervised training scheme based on cross-view epipolar information. These techniques improve 3D tracking accuracy and consistency by exploiting multi-view features during training, although they are more computationally demanding. The third category comprises learned transformations of monocular 2D pose estimates into 3D space (Bolaños et al., 2021; Gosztolai et al., 2021). Monocular 3D pose estimation is an exciting and important advance in flexibility, but unavoidable 3D ambiguities currently limit its performance compared to multi-view techniques (Bolaños et al., 2021; Iskakov, Burkov, Lempitsky, & Malkov, 2019).

Despite the recent acceleration in method development, it remains challenging to build 3D animal pose estimation algorithms that achieve scientifically precise performance flexibly across diverse environments and species. Compared to humans, lab animals such as mice and rats are much smaller in scale, less articulated, and bear higher appearance similarities among different individuals (Moskvyak, Maire, Dayoub, & Baktashmotlagh, 2020), which limits the availability of discriminable features for body part tracking and annotation. Because of the drastic differences in animal body profiles across species, (e.g. cheetahs vs. flies), it is also difficult to leverage the universal skeleton models and large-scale pretraining datasets that power the impressive tracking performance in humans (Cao et al., 2019; Wu et al., 2020). It is imperative that we develop algorithms that more efficiently use the limited resources available for animals.

2.2. Semi-Supervised and Unsupervised Pose Estimation

Semi-supervised and unsupervised learning schemes reduce the reliance on laborious data annotation currently bottlenecking large-scale supervised training. These schemes learn from the implicit structure and distribution of unlabeled data and can utilize knowledge of universal principles, such as physics and geometry, to improve tracking performance.

Inspired by classic multi-view stereo 3D reconstruction, many works in 3D human pose estimation utilize annotation-free geometric supervision in the form of multi-view consistency (Iqbal, Molchanov, & Kautz, 2020; Kocabas, Karagoz, & Akbas, 2019; Rhodin, Spörri, et al., 2018; Wandt, Rudolph, Zell, Rhodin, & Rosenhahn, 2021), 3D-to-2D reprojection consistency (C.-H. Chen et al., 2019; Wandt & Rosenhahn, 2019), and geometry-aware 3D representation learning (Rhodin, Salzmann, & Fua, 2018). Training constraints with respect to consistent bone length, valid ranges of joint angles, and body symmetry (Dabral et al., 2018; Pavllo, Feichtenhofer, Grangier, & Auli, 2019; Spurr, Iqbal, Molchanov, Hilliges, & Kautz, 2020; Wu et al., 2020) can also encourage biomechanically-plausible tracking results. Exploiting temporal context is also effective, as we discuss in the next section. Appropriate use of these implicit supervision signals results in consistent and robust pose estimates using only a small fraction of the labeled data required for fully supervised approaches.

2.3. Temporal 3D Pose Estimation

The temporal nature of behavior provides information that can be harnessed to improve 3D pose estimation. Intuitively, movement progresses continuously through time in 3D space, providing a strong prior for future poses given their temporal history – body movement trajectories evolve smoothly and are bounded by plausible, physiological velocities. The spatial displacement between consecutive poses should therefore be small, exhibiting relative consistency or smoothness along the time dimension. Pose estimates from static, temporally isolated observations ignore these intuitive constraints.

Previous 3D pose estimation algorithms have incorporated temporal information in several different ways. Given a sequence of pose predictions, temporal consistency can be introduced as part of the post-processing optimization that refines initial 2D (prior to triangulation) or 3D keypoint estimates (Bala et al., 2020; Joska et al., 2021; Karashchuk et al., 2021; Zhang, Dunn, Marshall, Olveczky, & Linderman, 2021). Temporal consistency assumptions have also been used for filtering out invalid pseudolabels used for self-supervision (Mu, Qiu, Hager, & Yuille, 2020).

Another popular scheme for exploiting temporal information for 3D pose estimation is to build models that infer pose from spatiotemporal inputs, using either recurrent neural networks (Hossain & Little, 2018), temporal CNNs (Pavllo et al., 2019), or spatial-temporal graphical models (Wang, Yan, Xiong, & Lin, 2020). Hossain and Little (Hossain & Little, 2018) processed 2D pose sequences using layer-normalized LSTMs to produce temporally consistent 3D poses. Other works have used temporal CNNs for similar purposes (R. Liu et al., 2020; Pavllo et al., 2019). Temporal information can also be explicitly encoded and appended to model input using apparent motion estimations such as optical flow (X. Liu et al., 2021).

Other approaches incorporate temporal information as a form of regularization during training. By employing a temporal smoothness constraint, one enforces the assumption that joint positions should not displace significantly over short periods of time (Wang et al., 2020; Wu et al., 2020), encouraging learned temporal consistency in pose predictions. Critically, these temporal constraints can be applied to unlabeled video frames, providing an avenue for semi- and unsupervised learning. Chen et al. (L. Chen, Lin, Xie, Lin, & Xie, 2021) further exploited temporal consistency in hand pose estimates along both forward and backward video streaming directions to establish an effective self-supervised learning scheme. Our approach is most similar to Wu et al. (Wu et al., 2020), in that we incorporate a temporal smoothness constraint in the learning objective to support a semi-supervised scheme. But we employ this constraint with multi-view, volumetric 3D pose estimation during freely moving, naturalistic behavior, rather than during monocular 2D pose estimation in restrained animals.

2.4. Pose Evaluation Metrics

In this manuscript we also report a complementary set of performance metrics that provides more comprehensive benchmarks for sparsely labeled 3D animal pose data. The cornerstone metrics of the field are Euclidean distance errors relative to ground-truth 3D keypoints: mean per-joint position error (MPJPE), and, sometimes, PA-MPJPE, which evaluates MPJPE after rigid alignment of 3D predictions to ground-truth poses. Although these evaluation protocols convey an imperative assessment of a model’s landmark localization capability, they fall short for most markerless animal pose datasets, where 3D keypoint ground-truth is derived from noisy manual labeling only in a small subset of video frames.

Unlike in large-scale human benchmarks, in animals these position error metrics do not reflect the large extant diversity of possible poses and are prone to overestimating performance. Human3.6M (Ionescu, Papava, Olaru, & Sminchisescu, 2013) and HumanEva (Sigal, Balan, & Black, 2010) employ motion capture systems to acquire comprehensive ground-truth labels over hundreds of thousands of frames, spanning multiple human actors and dozens of action categories. Similar evaluation is nearly impossible for most markerless 3D animal pose datasets, where acquisition of 3D labels requires laborious human annotation.

Single-frame position errors over sparsely labeled recordings also ignore whether models capture the continuous and smooth nature of movement. Models with the same mean position error on a small subset of samples can diverge significantly, and pathologically, in unlabeled frames. We illustrate this in Fig.2 (a), which shows a set of synthetic movement trajectories. The three noisy traces all have the same average position error, yet represent distinct, and erroneous, movement patterns. The fidelity of predictions on unlabeled data can be captured using temporal metrics. For example, Pavllo et al. introduced the mean per-joint velocity error (MPJVE) to quantify the temporal consistency of predictions (Pavllo et al., 2019). Thus far, works in animal pose estimation have not incorporated quantitative temporal metrics, although some have presented qualitative evaluations of keypoint movement velocity (Karashchuk et al., 2021; Wu et al., 2020).

Fig. 2. Ambiguity in absolute position error analysis.

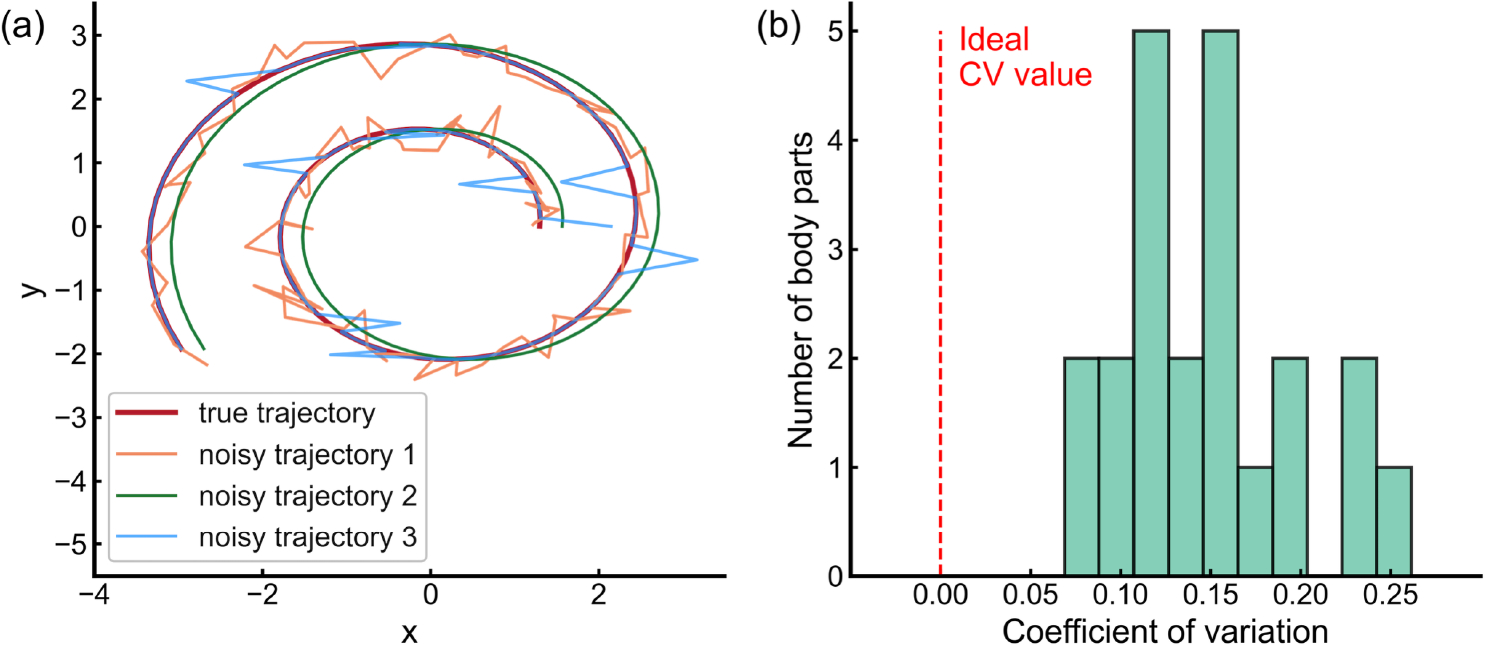
(a) In this simulated example, we present three noisy trajectories with the same absolute point position errors with respect the true spiral trajectory. (b) Histogram of body segment length variation in manually labeled mouse data. We compute the coefficient of variation (CV) for the lengths of 22 body segments. While CV values should ideally be close to 0, we instead observed notable amounts of length variation in all body segments. This illustrates the noise present in manually labeled 3D poses.

Finally, manually annotated 3D pose ground-truth is inherently noisy and exhibits substantial intra- and inter-labeler variability. We analyzed the coefficients of variation $(CV=\frac{\sigma }{\mu })$ (Reed, Lynn, & Meade, 2002), which measures the degree of data dispersion relative to its mean, for the lengths of 22 body segments connecting keypoints in our manually labeled mouse dataset (details in Section 4.1). Although the keypoints are intended to represent body joints, between which the lengths of body segments should remain constant, independent of pose, we found a 10% to 20% deviation in length for the majority of segments (Fig.2 (b)). This aleatoric uncertainty in the ground-truth labels will propagate to position errors.

Given these issues, we argue that it is important to establish more diverse evaluation protocols for markerless 3D animal pose estimation. These protocols should ideally capture temporal and anatomical variances in both labeled and unlabeled frames. In addition to our new semi-supervised training scheme, we introduce two new consistency metrics that resolve differences between models not captured by standard position errors, and these new metrics do not rely on large numbers of ground-truth annotations.

2.5. 3D Animal Pose Datasets and Benchmarks

Despite the critical importance of large-scale, high-quality datasets for developing 3D animal pose estimation algorithms (Jain et al., 2020), such resources are relatively uncommon compared to what is available for 3D human pose. Animal datasets are not easily applied across species, due to differences in body plans, and high-throughput marker-based motion capture techniques are challenging to implement in freely-moving, small-sized animals. Nevertheless, multiple 3D animal pose datasets have been released in recent years, including in dogs (Kearney, Li, Parsons, Kim, & Cosker, 2020), cheetahs (Joska et al., 2021), rats (Dunn et al., 2021; Marshall et al., 2021), flies (Günel et al., 2019), and monkeys (Bala et al., 2020). But in mice, by far the most commonly used mammalian model organism in biomedical research (Ellenbroek & Youn, 2016), large-scale pose datasets are still lacking. The LocoMouse dataset (Machado, Darmohray, Fayad, Marques, & Carey, 2015) contains annotated 3D keypoints in animals walking down a linear track. While being a valuable resource for developing gait tracking algorithms, the dataset does not represent the diversity of mouse poses composing the naturalistic behavioral repertoire. Several 3D mouse datasets also accompany published manuscripts (Zimmermann et al., 2020), but they are limited in the number of total annotated frames. Here we provide a new, much larger 3D mouse pose dataset consisting of 6.7 million frames with 310 annotated 3D poses (1860 annotated frames in 2D) on 5 mice engaging in freely moving, naturalistic behaviors, which we make publicly available as a resource for the community. We also utilize the scale of our dataset to benchmark a collection of popular 3D pose estimation algorithms and assess the impact of temporal constraints on performance, providing guidance on the development of suitable strategies for quantifying mouse behavior in three dimensions.

3. Methods

3.1. Volumetric Representation

Following recent computer stereo vision methods (Dunn et al., 2021; Iskakov et al., 2019; Kar, Häne, & Malik, 2017; Zimmermann et al., 2020), we construct a geometrically-aligned volumetric input $V_t$ from multi-view video frames at each timepoint $t$ and estimate 3D pose from them using a 3D CNN.

As memory limitations restrict the size of the 3D volume (64 × 64 × 64 voxels in our case), to increase its spatial resolution, we center the volume at the inferred 3D centroid of the animal. This centroid is inferred by triangulating 2D centroids detected in each camera view using a standard 2D UNet (Ronneberger, Fischer, & Brox, 2015), except with half the number of channels in each convolutional layer. For triangulation, we take the median of all pairwise triangulations across views. We then create an axis-aligned 3D grid cube centered at the 3D centroid position, which bounds the animal in 3D world space. We use $N=64$ voxels per grid cube side, resulting in an isometric spatial resolution of 1.875 mm per voxel.

Here, we briefly review the volume generation process. After initialization, 3D grids are populated with 2D image RGB pixel values from each camera using projective geometry. With known camera extrinsic (rotation matrix $R$, translation vector $t$) and intrinsic parameters $K$, a 2D image $ℱ$ can be unprojected along the viewing rays as they intersect with the 3D grid. In practice, rather than performing actual ray tracing, the center coordinates of each 3D voxel $X_{i,j,k}$ is projected onto the target 2D image plane by $K[R\mid t]X_{i,j,k}$ and the value of $X_{i,j,k}$ is set by bilinear sampling from the image at the projected point (Kar et al., 2017). The unprojected image volumes from different views are concatenated along the channel dimension, resulting in a $N\times N\times N\times \left(N_{\mathit{cam}}*C\right)$-sized volumetric input, where $C$ is the channel dimension size of each input view ($C=3$ for RGB images). While we sample directly from 3-channel RGB images to reduce memory footprint and computation costs, other approaches unproject features extracted by 2D CNNs (Iskakov et al., 2019; Tu, Wang, & Zeng, 2020; Zimmermann et al., 2020).

The unprojected image volumes are then processed by a 3D UNet (implementation details in Section 4.5), producing volumetric heatmaps associated with different keypoints. The differentiable expectation operation soft argmax (Nibali, He, Morgan, & Prendergast, 2018; Sun, Xiao, Wei, Liang, & Wei, 2018) is applied along spatial axes to infer the numerical coordinates of each keypoint.

3.2. Unsupervised Temporal Loss

At high frame rates, the per-frame velocity of animals is low and their overall movement trajectory should typically be smooth. We encode these assumptions as an unsupervised temporal smoothness loss ${ℒ}_T(\cdot )$ that can be easily integrated with heatmap-based pose estimation approaches.

Consider the inputs to the network to be a set of temporally consecutive chunks $𝒯$ where each chunk ${𝒯}_n$ consists of 3D volumetric representations constructed from $c$ adjacent timepoints

$${𝒯}_n=\left\{V_{t_i},\dots ,V_{t_{i+c-1}}\right\},$$

where $c$ specifies the time span covered by the unsupervised loss.

Given the 3D keypoint coordinates predicted by the 3D CNN $\left\{J_{t,j}\mid t_i\le t\le t_{i+c},1\le j\le N_J\}\right.$ from one temporal chunk ${𝒯}_n$, the temporal smoothness loss penalizes the keypoint-wise position divergence across consecutive frames, which is equivalent to constraining the movement velocity within the temporal window.

$${ℒ}_T\left(\left\{J_{t,j}\right\}\right)=\frac{1}{c}\sum _{t=t_i}^{t_{i+c-1}}\frac{1}{N_J}\sum _{j=1}^{N_J}d\left(J_{t,j},J_{t+1,j}\right)$$ (1)

where $N_J$ is the number of 3D keypoints and $d$ is the distance metric used for comparing displacement across timepoints.

This general formulation does not enforce limitations on the choice of distance metric, but empirically we found that L1 distance performed better than L2-norm Euclidean distance. Though it is difficult to give a theoretical explanation for this observation, the underlying reason could be similar to that for L1 total variation regularization in optical flow estimation. Formulating the smoothness constraint as a Laplacian prior allows discontinuity in the motion and is well known to be more robust to data outliers compared to quadratic regularizers (Wedel, Pock, Zach, Bischof, & Cremers, 2009). We have therefore used an L1 distance metric for all experiments presented in the later sections.

3.3. Supervised Pose Regression Loss

The unsupervised temporal loss on its own is insufficient and will result in mode degeneracy where the network learns to produce identical poses for all input samples. We therefore also include a standard supervised pose regression loss over a small set of labeled frames during training. Given the ground-truth and predicted 3D keypoint coordinates $J_t$ and ${\hat{J}}_t$, the supervised regression loss is defined as

$${ℒ}_S(J_t,{\hat{J}}_t)=\frac{1}{N_J}\sum _{j=1}^{N_J}d(J_{t,j},{\hat{J}}_{t,j})$$ (2)

We use L1 distance for computing the joint distances over L2 distance metric based on empirical results, which agrees with the results of Sun et al. on 3D human pose estimation (Sun et al., 2018).

4. Experiments

4.1. Dataset

For performance evaluation, we collected a total of five 1152 × 1024 pixels color video recordings from 6 synchronized cameras surrounding a cylindrical arena. We direct the reader to Appendix B and Supplementary Video 1 for more details on the 3D mouse pose dataset. Each set of recordings corresponds to a different mouse (M1, M2, M3, M4, M5). M1 and M2 were recorded for 3 minutes and M3, M4, M5 were recorded for 60 minutes. The number of manually annotated 3D ground-truth timepoints for 22 body keypoints is n = 81, 91, 48, 44 and 46 from each recording, respectively (486, 546, 288, 264, and 276 total annotated video frames). Out of the 22 keypoints, 3, 4, 6, 6, and 3 locate at the animal’s head, trunk, forelimbs, hindlimbs, and tail, respectively. Notice that the two keypoints at the middle and end of the tail were excluded from quantitative evaluations presented in this paper, as they were often cropped outside the bounds of the 3D grids. This results in a total of 20 body keypoints and 22 corresponding body segments used for analysis.

We allocated n = 172 from M1 and M2 for training and n = 48 from M3 for internal validation. We report all metrics using data from M4 and M5 (n = 90 labeled timepoints, plus unlabeled timepoints for additional temporal and anatomical consistency metrics), which were completely held out from training or model selection. We also simulated low annotation conditions by randomly selecting 5% (n = 8), 10% (n = 17) and 50% (n = 86) from the training samples and compared with the full annotation 100% condition.

4.2. Evaluation Metrics

4.2.1. Localization Accuracy

We adopt the three common protocols used in 3D human pose estimation for evaluating the landmark localization accuracy of different models.

• Protocol #1: Mean per-joint position error (MPJPE) evaluates the mean joint-wise 3D Euclidean distances between the prediction and ground truth keypoint positions. For $J$ keypoints,

  $$\mathrm{M}\mathrm{P}\mathrm{J}\mathrm{P}\mathrm{E}(\mathbf{s})=\frac{1}{J}\sum _j{\parallel {\mathbf{s}}_j-{\mathbf{s}}_j^{gt}\parallel }_2$$

• Protocol #2: Procrustes Analysis MPJPE (PA-MPJPE) reports the MPJPE values after rigidly aligning the landmark predictions (translation and rotation) with the ground-truth.

• Protocol #3: Normalized MPJPE (N-MPJPE) assesses the scale-insensitive MPJPE estimation errors by respectively normalizing the prediction and ground-truth landmarks by their norm (Rhodin, Spörri, et al., 2018).

4.2.2. Temporal Smoothness

The aforementioned single-frame evaluation metrics are inadequate for capturing the importance of temporal smoothness in videos. We therefore also report the mean per-joint velocity errors (MPJVE) proposed by Pavllo et al. (Pavllo et al., 2019). MPJVE is the mean absolute value of first-order derivative of predicted pose sequences. We used $T=10000$ continuous frames from recordings of mouse M5 for this evaluation.

$$\mathrm{M}\mathrm{P}\mathrm{J}\mathrm{V}\mathrm{E}(\mathbf{s})=\frac{1}{T\cdot j}\sum _j\sum _{t=1}^{T-1}|{\mathbf{s}}_{t,j}-{\mathbf{s}}_{t+1,j}|$$

4.2.3. Body Skeleton Consistency

Although not explicitly constrained during training, the anatomical consistency of predictions is an important component of model tracking performance. Inspired by the analysis by Karashchuk et al. (Karashchuk et al., 2021), we examined the mean and standard deviation of the estimated length of 22 body segments over 10000 continuous frames from M4 for this analysis.

4.3. Training Strategies

To evaluate the influence of temporal training, we designed four different model training schemes that were each applied to the 5%, 10%, 50% and 100% annotation conditions.

Baseline/DANNCE (Dunn et al., 2021)

We employ the multi-view volumetric method presented by Dunn et al. as the baseline comparison. All baseline models are trained solely with the supervised regression L1 loss over the labeled frames.

Baseline + smoothing.

No changes are made during the training; instead, the predictions from the baseline models are smoothed in time for each keypoint, with a set of different smoothing strategies.

Temporal baseline.

During training, each batch contains exactly one labeled sample with three additional unlabeled samples drawn from its local neighborhood. This scheme ensures a balance between supervised and unsupervised loss throughout the optimization. The models were then jointly trained with ${ℒ}_S$ and ${ℒ}_T$.

Temporal + extra.

In addition to the partially labeled training batches used in temporal baseline model training, the training set contains $N_u$ completely unlabeled, temporally consecutive chunks included only in the unsupervised temporal loss.

For experiments conducted under lower annotation conditions, 5%, 10% and 50%, we use respectively 95% $\left(N_u=163\right)$, 90% $\left(N_u=154\right)$ and 50% $\left(N_u=86\right)$ unlabeled chunks with respect to the entire training set. This aimed to match the number of samples used in the 100% baseline and temporal baseline models. For experiments using 100% of the training data, we add 20% $\left(N_u=34\right)$ extra unlabeled temporal chunks.

4.4. Comparison with state-of-the-art approaches

We compare the performance of our proposed approach against other contemporary animal and human pose estimation methods. Specifically, we have replicated and evaluated the following approaches on the mouse dataset:

2D animal pose estimation.

DeepLabCut (DLC) (Mathis et al., 2018) is a widely adopted toolbox for markerless pose estimation of animals, which expanded on the previous state-of-the-art method DeeperCut (Insafutdinov, Pishchulin, Andres, Andriluka, & Schiele, 2016). We followed the default architecture and training configurations using ResNet-50 as the backbone and optimized the network using sigmoid cross-entropy loss. Following the same practice by Mathis et al. (Mathis et al., 2018), the original frames were cropped around the mice instead of downsampling. 2D human pose estimation. We implemented the SimpleBaseline (Xiao et al., 2018) for its near state-of-the-art performance in 2D human pose estimation with simple architectural designs. This method leverages off-the-shelf object detectors to first locate the candidate subject(s) and performs pose estimation over the cropped and resized regions. Compared to DLC/DeeperCut, additional deconvolutional layers are added to the backbone network to generate higher-resolution heatmap outputs.

Multi-view 3D human pose estimation.

Learnable Triangulation (Iskakov et al., 2019) adopts a similar volumetric approach except that features extracted by a 2D backbone network, instead of raw pixel values, are used to construct the 3D inputs. Similar to SimpleBaseline, a 2D backbone network processes cropped and resized images, where the resulting multi-view features are unprojected on the-fly to construct the volumetric inputs in the end-to-end training.

Monocular 3D human pose estimation.

Pavllo et al. (Pavllo et al., 2019) presented a training scheme for sparsely labeled videos that also leveraged temporal semi-supervision. Instead of using a smoothness constraint, temporal convolutions are performed over sequences of predicted 2D poses obtained from off-the-shelf estimators to regress 3D poses, with additional supervision from a 3D-to-2D backprojection loss and a bone length consistency loss between predictions on labeled and unlabeled frames. Notice that we did not specifically train a 3D root joint trajectory model as in the original implementation but directly used the ground truth 3D animal centroids for convenience. Without easy access to off-the-shelf keypoint detectors for mice, we employed our best performing 2D model to obtain initial 2D pose estimates.

In addition to the aforementioned approaches, we have adapted a 2D variant of our proposed temporal constraint and applied it to the DLC architecture, similar to DeepGraphPose (Wu et al., 2020). Instead of using a final sigmoid activation and optimizing against target probability maps, we performed a soft argmax on the resulting 2D heatmaps and applied both a supervised regression loss and an unsupervised temporal loss as described in Section 3.2 and 3.3, except in the 2D pixel space.

For all approaches, ResNet-50 was used as the backbone network if not otherwise specified. The 2D mouse bounding boxes were computed from 2D projections of ground-truth 3D poses. For 2D approaches, the 2D poses were first estimated separately in each camera view and triangulated into 3D using the same median-based protocol as described in Section 3.1. The Protocol 1 MPJPE results were reported for each approach under different annotation conditions (5%, 10%, 50% and 100%).

4.5. Implementation Details

We implemented a standard 3D UNet (Ronneberger et al., 2015) with skip connections to perform our method’s 3D pose estimation. The number of feature channels is [64, 64, 128, 128, 256, 256, 512, 512, 256, 256, 128, 128, 64, 64] in the encoder-decoder architecture, followed by a final 1 × 1 × 1 convolution layer outputting one heatmap for each joint position. The encoder consists of four basic blocks with two 3 × 3 × 3 convolution layers with padding 1 and stride 1, one ReLU activation and one 2 × 2 × 2 max pooling for downsampling. The decoder consists three downsampling blocks, each with one 2 × 2 × 2 transpose convolution layer of stride 2 and two 3 × 3 × 3 convolution layers. The 3D keypoint coordinates were estimated by applying soft argmax (Sun et al., 2018) over the predicted heatmaps. We did not explore additional 3D CNN architectures, as this is not the focus of the paper, but we expect that the semi-supervised training strategy should generalize easily to different model architecture, as demonstrated for 2D in later sections (Section 1).

We trained all models using an Adam optimizer (${\beta }_1=0.9,{\beta }_2=0.999,ϵ=1e-7$) with a constant learning rate of 0.0001 for a maximum of 1200 epochs. We used a mini-batch size of 4. We did not use an early stopping for the training; instead, we used the model checkpoint with the best internal validation MPJPE value for evaluation on the test set.

Empirically, we found that a warm-start strategy that only incorporated the unsupervised loss during a later stage performed better for training the temporal+extra models. A similar strategy was also used by Xiong et al. (Xiong, Fan, Grauman, & Feichtenhofer, 2021). The temporal+extra models were only supervised by the pose regression loss during the first third of the training epochs, and the unsupervised temporal loss was added afterwards.

5. Results and Discussion

In this section, we quantitatively and qualitatively evaluate the performance gains of our semi-supervised approach.

5.1. Localization Accuracy

We first validated the performance of our semi-supervised approach across 5%, 10%, 50% and 100% annotation conditions using MPJPE and its two variants (Fig.3). Compared to fully supervised models, the temporal consistency constraint generally improved the keypoint localization accuracy, especially in the low annotation conditions. The temporal baseline models improved the MPJPE by 3.0% and 34.8% respectively using 5% and 10% of the training samples. With additional temporal supervision in “temporal+extra” models, our approach improved localization errors by 36.5% and 38.6% for the same low annotation condition.

Fig. 3. Qualitative comparison of landmark localization performance over different annotation conditions.

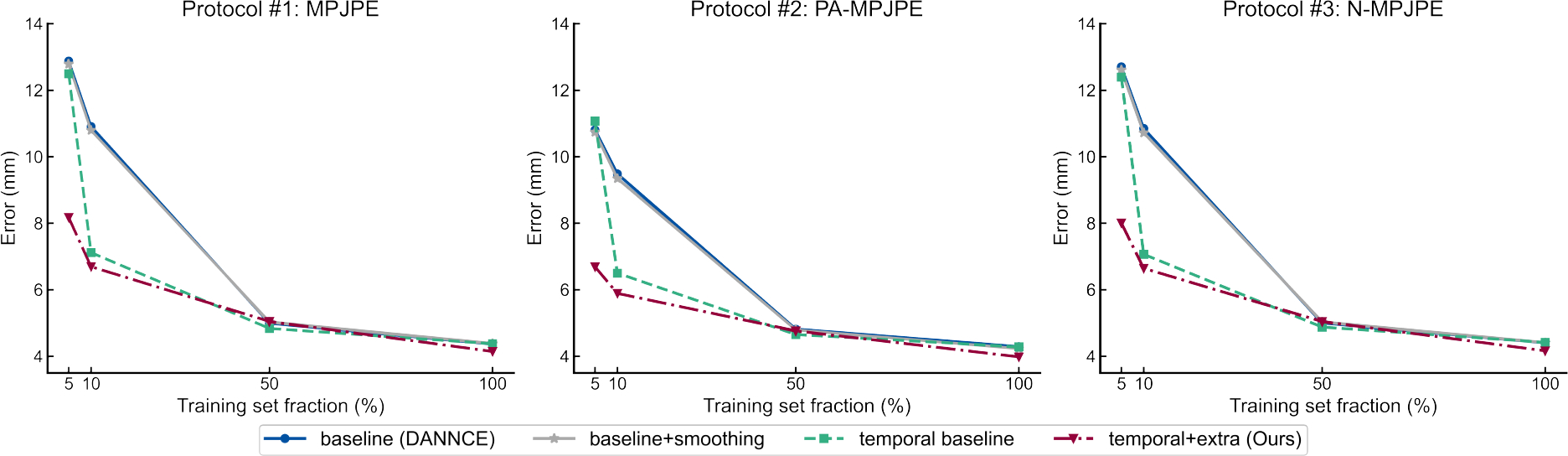
We randomly selected 5% (n = 8), 10% (n=17) and 50% (n=85) of the training set to simulate low annotation regimes. Temporal supervision generally improved performance on all three localization protocols compared to the baseline models, especially with limited access to the training data. Similar improvement cannot be achieved via post hoc smoothing of the predicted movement trajectories.

To confirm that this improvement in localization accuracy could not simply be obtained via post-processing, we tested deliberate smoothing of baseline model predictions using different smoothing methods and window sizes (the full comparisons are presented in Appendix A1). Despite the obvious decrease in trajectory oscillations from temporal smoothing (Appendix A Fig.7), no type of post hoc smoothing improved localization accuracy more than 1%. This suggests that the unsupervised temporal constraint encourages more selective and flexible adaptation of the spatio-temporal features, rather than naive filtering.

5.2. Temporal Smoothness

We first performed a qualitative examination of the movement trajectories of four different keypoint positions over 1000 frames (Fig.4 (a)). Given the same amount of labeled training data, the temporal approach produced noticeably smoother keypoint movement trajectories compared to baseline.

Fig. 4. Analysis of temporal smoothness.

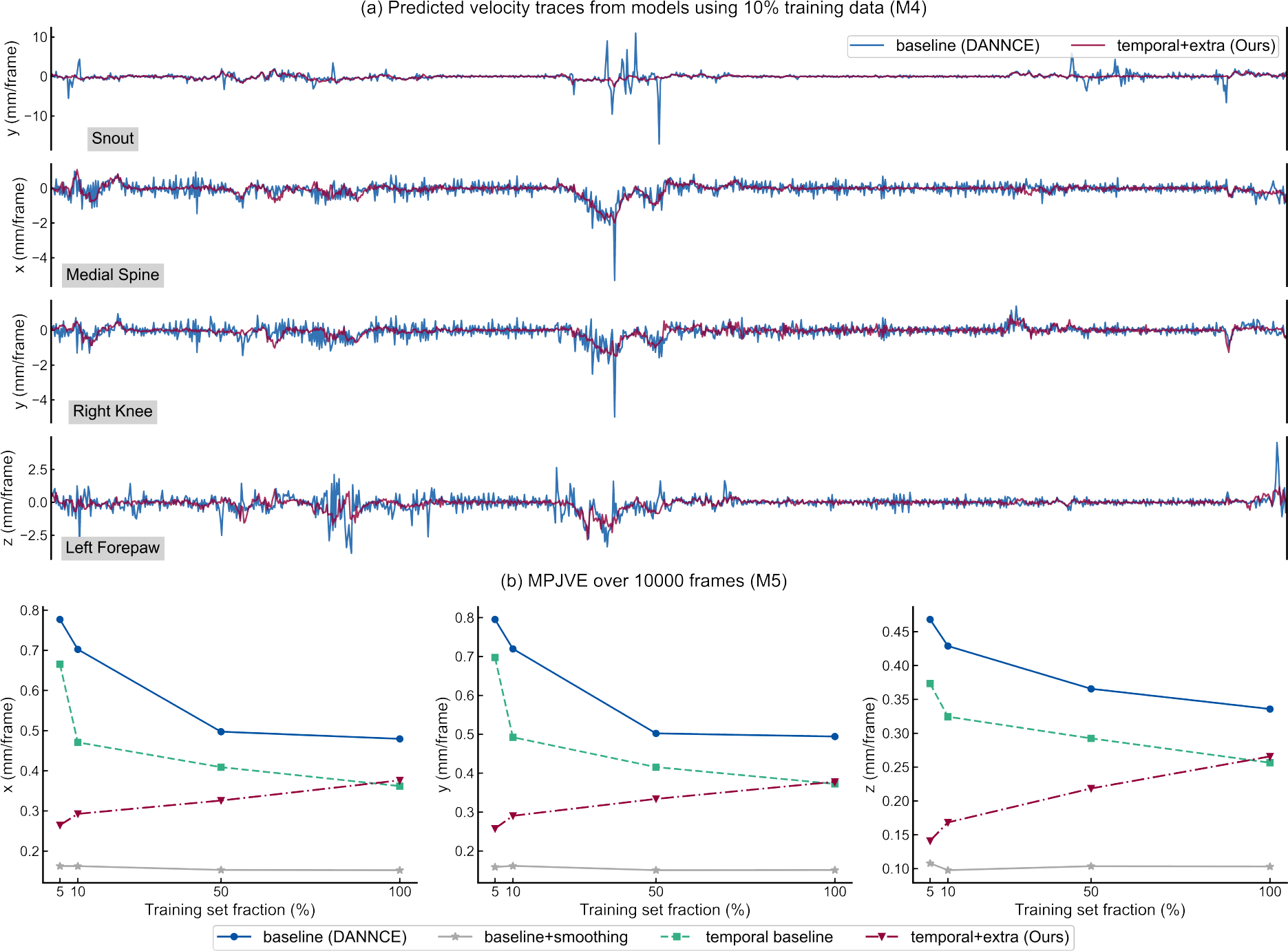
(a) Selected coordinate velocities of four different keypoint positions (snout, medial spine, right knee, left forehand) over 1000 consecutive frames from test mouse M4. (b) Quantitative MPJVE results across different training schemes over 10000 frames from test mouse M5. Our temporal models yield more stable movement trajectories than the baseline fully supervised models.

We then quantitatively evaluated MPJVE over a longer period of 10000 frames (Fig.4 (b)). The inclusion of temporal supervision improved MPJVE by 15.6%, 29.6%, 18.4% and 24.3% for each of the four annotation conditions and by 67.8%, 59.6%, 36.1% and 22.0% when additional unlabeled chunks were added. Post hoc temporal smoothing achieved superior trajectory smoothness as indicated by MPJVE (gray lines), but only resulted in marginal improvement in MPJPE. In the meanwhile, the temporal semi-supervised models improved both MPJVE and MPJPE when compared to the baseline models. This reiterates the importance of having a set of comprehensive and complementary performance metrics: MPJVE metric should not be interpreted alone but rather in concert with basic localization accuracy metrics.

5.3. Body Skeleton Consistency

We also quantitatively analyzed the length variations of different body segments of 10000 consecutive frames (Fig.5). For simplicity, we grouped the 22 body segments into four general categories: head, trunk, forelimb and hindlimb, and selected two from each category for presentation.

Fig. 5. Body segment length consistency.

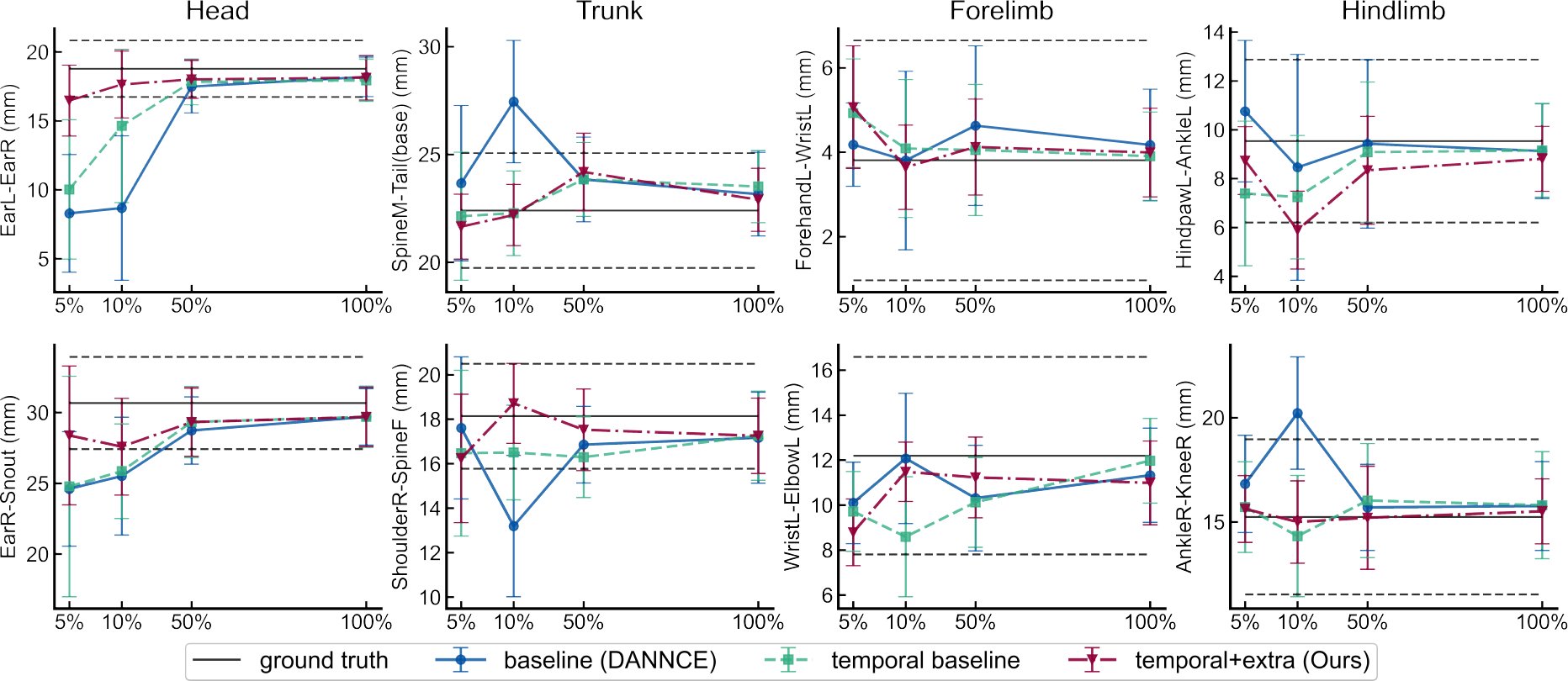
Plots reporting the statistics of eight different body segment lengths. The solid black horizontal line in each plot represents the mean body segment length computed from manually labeled ground-truth, and the horizontal dashed lines encompass corresponding standard deviations. Error bars are standard deviation.

While the fully supervised models struggled to preserve anatomical consistency in low annotation conditions, temporal semi-supervision helped to produce more consistent body structure. The temporal models exhibited less variability in predicted body segment lengths and more closely matched ground-truth average values, especially for the head and trunk. For body segments with higher coefficients of variation in the ground-truth data (forelimb, hindlimb), the addition of temporal supervision generally decreased such variability.

5.4. Qualitative Performance on Difficult Poses

In practice, we have identified that baseline models are prone to producing inaccurate keypoint predictions in low annotation regimes, especially for the limbs, when animals are in specific rearing poses. Aside from changes in appearance, such behaviors take place at lower frequencies than others and are thus underrepresented in labeled training data. We therefore also presented qualitative visualization results for one example sequence of rearing behavior frames.

While the baseline 10% model predicted malformed skeletons due to the limited label availability (Fig.6 blue bounding boxes), the addition of temporal supervision produced marked improvements in physical plausibility. With supervision from additional unlabeled temporal chunks, the “temporal+extra” model produced qualitatively better predictions, even when compared to the 100% baseline model. In cases where the fully supervised baseline model made inaccurate estimates of difficult hindlimb positions (Fig.6 red bounding box), the semi-supervised approach, with only 10% of the labeled data, better recovered the overall posture.

Fig. 6. Qualitative visualization on difficult rearing poses.

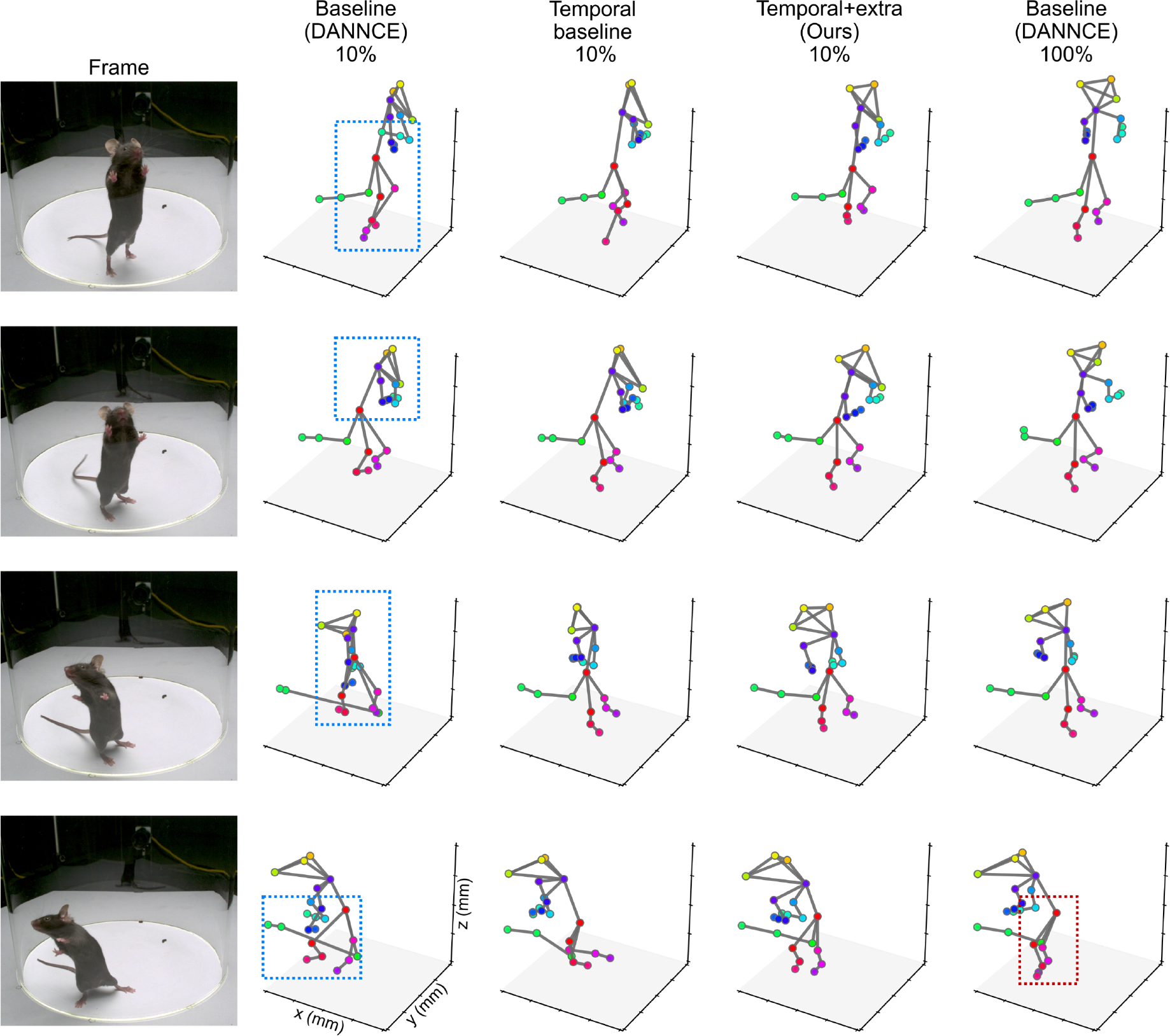
All 3D visualizations are plotted on the same spatial scale. With 10% of the training samples, the fully supervised baseline model consistently yields inaccurate predictions (blue bounding boxes). Even with 100% of the training samples, the model is still prone to making mistakes on limb landmarks (red bounding box). Many of these errors are corrected via temporal supervision when using just 10% of the labeled data, .

5.5. Quantitative Comparisons with Other Approaches

We quantitatively examined the proposed method’s performance against other widely-adopted animal and human pose estimation approaches, as summarized in Table.1.

Table 1. Quantitative comparison with other state-of-the-art 2D and 3D animal and human pose estimation methods.

We report the absolute 3D MPJPE in millimeters for each approach using four different fractions of training data.

Protocol 1 (absolute 3D MPJPE, mm)
	Training set fraction
	5%	10%	50%	100%
2D pose estimation methods (+ post hoc triangulation)
DLC† (Mathis et al., 2018)	11.0973	11.0512	9.8934	8.9060
SimpleBaseline† (Xiao, Wu, & Wei, 2018)	18.0990	14.6191	7.3636	5.9555
SimpleBaseline	18.5675	16.5800	8.3573	6.6957
DLC + soft argmax	11.0323	9.2244	6.3545	6.4739
DLC + 2D variant of our temporal constraint*	8.5432	9.1236	5.9526	6.0390
3D monocular pose estimation methods
Temporal Convolution* (Pavllo et al., 2019)	-	-	-	17.6337
3D multi-view pose estimation methods
Learnable Triangulation† (Iskakov et al., 2019)	18.7795	15.6614	8.9729	6.3177
DANNCE (Dunn et al., 2021)	12.8754	10.9085	4.9912	4.3614
Ours (temporal baseline)*	12.4940	7.1162	4.8347	4.3749
Ours (temporal + extra)*	8.1706	6.6927	5.0461	4.1409

The methods that use ground truth 2D bounding boxes during inference are masked by †.

The methods that use temporal information during training are masked by *.

For the monocular approach, the reported metric results are separately computed and averaged across all camera views.

Methods for post hoc triangulation of 2D poses.

Our proposed method consistently outperforms approaches that first independently estimate 2D pose in each camera view and reconstruct the 3D poses via post hoc triangulation. Compared to implicit optimization against heatmap targets, we observed that adapting existing 2D architectures to direct regression of keypoint coordinates effectively improved the overall metric performance (Table.1 “DLC + soft argmax”). While approaches like SimpleBaseline appeared sensitive to the quality of 2D bounding boxes, the soft argmax approach was able to operate robustly over full-sized images (i.e no cropping or resizing). Applying the 2D variant of our proposed temporal semi-supervision method further improved the performance under all annotation conditions, which implies that the temporal constraint behaves as a powerful prior for recovering plausible poses in both 2D and 3D.

The monocular 3D pose method.

Considering the inherent ambiguities in monocular 3D representations, it was expected that performance from monocular estimation cannot achieve scientific-level resolutions comparable to multi-view methods, even with 100% of training data and regularization from additional temporal information. These observations are consistent with what has been reported in previous literature (Bolaños et al., 2021; Iskakov et al., 2019).

Multi-view 3D pose estimation methods.

We did not observe particular advantages of using 3D volumes constructed from 2D features maps vs. raw pixel values. This likely implies that feature-based volumetric approaches require more accurate 2D feature extraction, via backbone networks pretrained on large-scale 2D pose datasets (Tu et al., 2020). For the human pose case, strong off-the-shelf 2D pose estimators already exist, whereas such options are limited for animal applications. Our results suggest that volume construction directly from pixels, i.e., the strategy used in our temporal semi-supervision method, is the more suitable choice for 3D animal pose estimation in cases where species-specific training data are scarce. This conclusion should nevertheless be re-evaluated in the future once larger 2D animal pose datasets become available.

6. Conclusion

In this paper, we present a state-of-the-art semi-supervised approach that exploits implicit temporal information to improve the precision and consistency of markerless 3D mouse pose estimation. The approach improves a suite of metrics, each providing a complementary measure of model performance, and the approach is particularly effective when the labeled data are scarce. Along with the newly released mouse pose dataset, these enhancements will facilitate ongoing efforts to measure freely moving animal behavior across different species and environments.

Fig. 1. Method Overview.

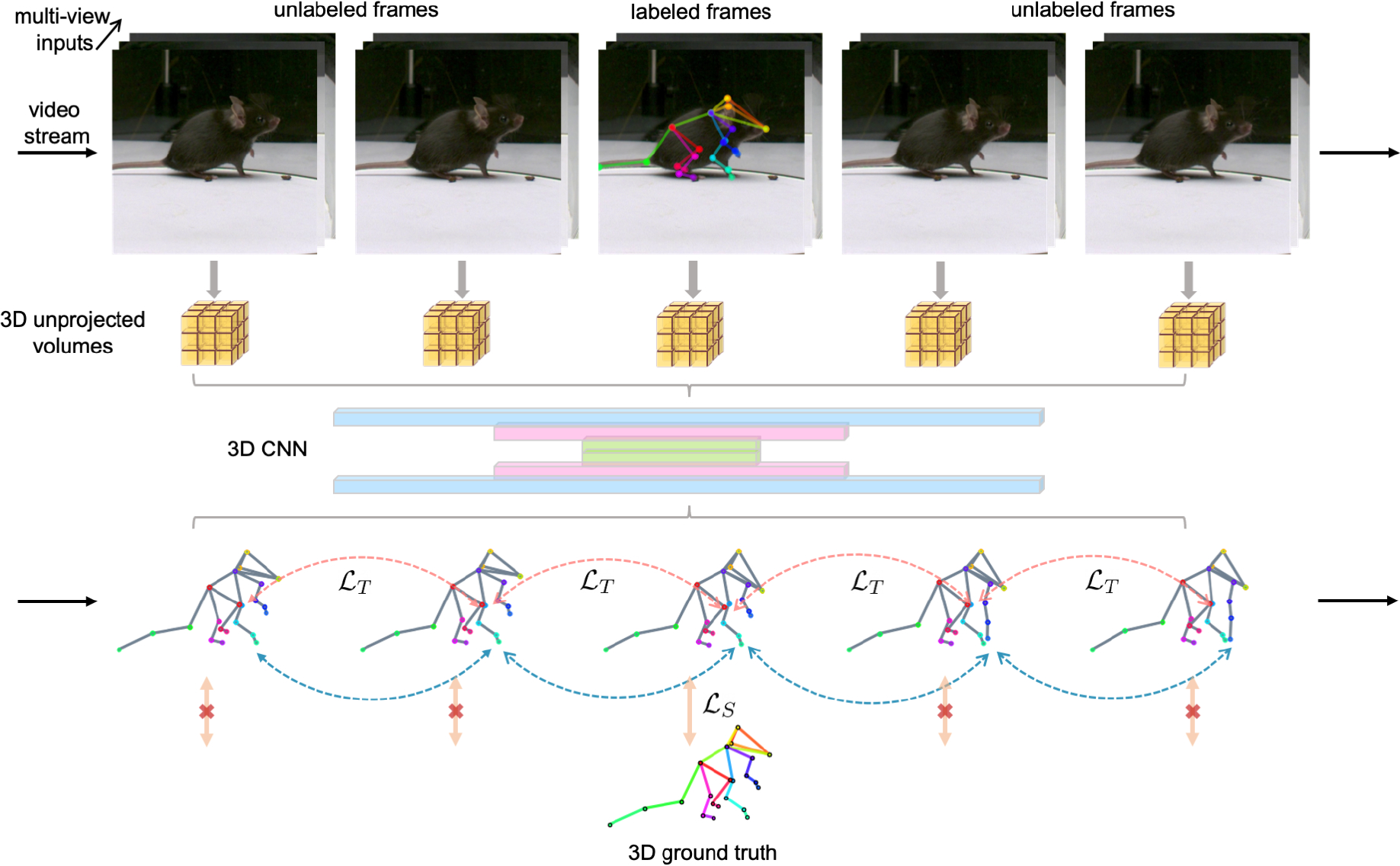
Our multi-view volumetric approach constructs a 3D image feature grid using projective geometry for each timepoint in videos. A 3D CNN (UNet) processes batches of temporally contiguous volumetric inputs and directly predicts 3D keypoint positions. We then combine a traditional supervised regression loss with an unsupervised temporal consistency loss for training. While the regression loss ${ℒ}_S$ is applied only on labeled video frames, which are sparsely distributed across video recordings, the unsupervised temporal loss ${ℒ}_T$ operates over both labeled and unlabeled frames.

Appendix A Additional Quantitative Results

We provide additional metric evaluation results using different smoothing strategies as discussed in section 5.1. We also qualitatively demonstrate the effects of such post hoc smoothing on the original trajectories.

Appendix B The Multi-View 3D Mouse Pose Dataset

We provide supplementary figures that demonstrate the released 3D mouse pose dataset.

Table A1. Complete localization metric comparison.

We recorded the changes in MPJPE, PA-MPJPE and N-MPJPE after applying 12 different post hoc smoothing strategies. We used either moving average smoothing (“MovAvg”) or Gaussian smoothing (“G”), with window size of 5, 10, 15, 20, 25 or 30 frames.

MP JPE (mm)		Baseline	MovAvg 5	MovAvg 10	MovAvg 15	MovAvg 20	MovAvg 25	MovAvg 30	G 5	G 10	G 15	G 20	G 25	G 30	Temp. baseline	Temp. +extra
	5%	12.8754	12.8332	12.8077	12.7994	12.7933	12.7887	12.7871	12.8399	12.8229	12.8106	12.8016	12.7949	12.7890	12.4940	8.1706
	10%	10.9085	10.8740	10.8511	10.8138	10.7925	10.7829	10.7826	10.8872	10.8613	10.8390	10.8204	10.8054	10.7938	7.1162	6.6927
	50%	4.9912	4.9704	4.9823	5.0063	5.0575	5.1187	5.1964	4.9767	4.9664	4.9677	4.9797	5.0021	5.0315	4.8347	50461
	100%	4.3614	4.3148	4.3371	4.3533	4.4126	4.4757	4.5646	4.3329	4.3129	4.3158	4.3301	4.3530	4.3832	4.3749	4.1409
PA-MP JPE (mm)		Baseline	MovAvg 5	MovAvg 10	MovAvg 15	MovAvg 20	MovAvg 25	MovAvg 30	G 5	G 10	G 15	G 20	G 25	G 30	Temp. baseline	Temp. +extra
	5%	10.8056	10.7785	10.7537	10.7461	10.7439	10.7363	10.7370	10.7846	10.7694	10.7569	10.7497	10.7444	10.7407	11.0714	6.6882
	10%	9 4846	9.4307	9 3968	9.3564	9.3382	9.3320	9.3324	9.4464	9.4162	9.3894	9.3688	9.3537	9.3436	6.4990	5.8894
	50%	4.8159	4.7846	4.7784	4.7839	4.8048	4.8404	4.8830	4.7971	4.7803	4.7736	4.7729	4.7797	4.7929	4.6510	4.7634
	100%	4.2863	4.2300	4.2188	4.2139	4.2360	4.2751	4.3181	4.2542	4.2240	4.2121	4.2098	4.2164	4.2291	4.2831	3.9797
N-MP JPE (mm)		Baseline	MovAvg 5	MovAvg 10	MovAvg 15	MovAvg 20	MovAvg 25	MovAvg 30	G 5	G 10	G 15	G 20	G 25	G 30	Temp. baseline	Temp. +extra
	5%	12.7044	12.6620	12.6374	12.6235	12.6153	12.6038	12.5988	12.6694	12.6513	12.6375	12.6271	12.6184	12.6104	12.3942	8.0054
	10%	10.8479	10.8082	10.7836	10.7430	10.7199	10.7043	10.6997	10.8236	10.7949	10.7704	10.7505	10.7338	10.7202	7.0648	6.6436
	50%	4.9995	4.9775	4.9898	5.0132	5.0582	5.1143	5.1836	4.9847	4.9750	4.9768	4.9879	5.0081	5.0339	4.8756	5.0439
	100%	4.3996	4.3548	4.3716	4.3836	4.4361	4.4924	4.5712	4.3731	4.3522	4.3529	4.3639	4.3833	4.4095	4.4150	4.1613

Fig. 7. Visualization of different smoothing strategies.

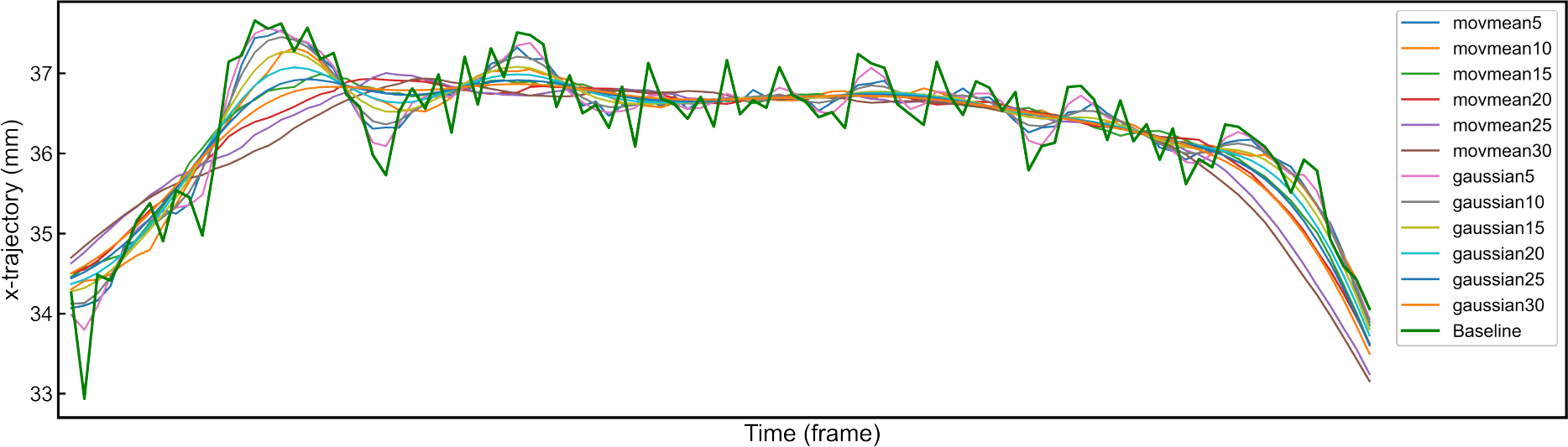
The thick green line corresponds to the original trajectory predicted by the 10% baseline model.

Fig. 8.

Multi-view captures from the released mouse dataset.

Fig. 9.

Multi-view captures from the released mouse dataset (overlaid with ground-truth annotations).

• Availability of data and materials:

The dataset is hosted using the Duke Research Data Repository and the detailed instructions for accessing the training dataset are available at https://github.com/tqxli/dannce-pytorch.