NON-UNIQUE GAMES OVER COMPACT GROUPS AND ORIENTATION ESTIMATION IN CRYO-EM

Abstract

Let $𝒢$ be a compact group and let $f_{ij}\in C\left(𝒢\right)$. We define the Non-Unique Games (NUG) problem as finding $g_1,\dots ,g_n\in 𝒢$ to minimize ${\sum }_{i,j=1}^n{f}_{ij}\left(g_i{g}_j^{-1}\right)$. We introduce a convex relaxation of the NUG problem to a semidefinite program (SDP) by taking the Fourier transform of $f_{ij}$ over $𝒢$. The NUG framework can be seen as a generalization of the little Grothendieck problem over the orthogonal group and the Unique Games problem and includes many practically relevant problems, such as the maximum likelihood estimator to registering bandlimited functions over the unit sphere in $d$-dimensions and orientation estimation of noisy cryo-Electron Microscopy (cryo-EM) projection images. We implement a SDP solver for the NUG cryo-EM problem using the alternating direction method of multipliers (ADMM). Numerical study with synthetic datasets indicate that while our ADMM solver is slower than existing methods, it can estimate the rotations more accurately, especially at low signal-to-noise ratio (SNR).

1. Introduction

We consider problems of the following form:

$$\begin{array}{ll}\underset{g_1,\dots ,g_n}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}& \sum _{i,j=1}^n{f}_{ij}\left(g_i{g}_j^{-1}\right)\\ \text{subject to}& g_i\in 𝒢,\end{array}$$ (1.1)

where $𝒢$ is a compact group and $f_{ij}:𝒢\to \mathbb{R}$ are suitable functions. We will refer to such problems as a Non-Unique Game (NUG) problem over $𝒢$.

Note that the solution to the NUG problem is not unique. If $g_1,\dots ,g_n$ is a solution to (1.1), then so is $g_{1}g,\dots ,g_{n}g$ for any $g\in 𝒢$. That is, we can solve (1.1) up to a global shift $g\in 𝒢$.

In many inverse problems, the goal is to estimate multiple group elements from information about group offsets, and can be formulated as (1.1). A simple example is angular synchronization [40], where one is tasked with estimating angles ${\left\{{\theta }_i\right\}}_i$ from information about their offsets ${\theta }_i-{\theta }_j$ mod $2\pi$. The problem of estimating the angles can then be formulated as an optimization problem depending on the offsets, and thus be written in the form of (1.1). In this case, $𝒢\cong SO\left(2\right)$.

One of the simplest instances of (1.1) is the Max-Cut problem, where the objective is to partition the vertices of a graph as to maximize the number of edges (the cut) between the two sets. In this case, $𝒢\cong {\mathbb{Z}}_2$, the group of two elements {±1}, and $f_{ij}$ is zero if $(i,j)$ is not an edge of the graph and

$$f_{ij}\left(1\right)=0\text{and}{f}_{ij}(-1)=-1\text{,}$$

if $(i,j)$ is an edge. In fact, we take a semidefinite programming based approach towards (1.1) that is inspired by — and can be seen as a generalization of — the semidefinite relaxation for the Max-Cut problem by Goemans and Williamson [21].

Another important source of inspiration is the semidefinite relaxation of $\mathrm{M}\mathrm{a}\mathrm{x}-2-\mathrm{L}\mathrm{i}\mathrm{n}\left({\mathbb{Z}}_L\right)$, proposed in [15], for the Unique Games problem, a central problem in theoretical computer science [26, 27]. Given integers $n$ and $L$, an Unique-Games instance is a system of linear equations over ${\mathbb{Z}}_L$ on $n$ variables ${\left\{x_i\right\}}_{i=1}^n$. Each equation constraints the difference of two variables. More precisely, for each $(i,j)$ in a subset of the pairs, we associate a constraint

$$x_i-x_j=b_{ij}\mathrm{m}\mathrm{o}\mathrm{d}L.$$

The objective is then to find ${\left\{x_i\right\}}_{i=1}^n$ in ${\mathbb{Z}}_L$ that satisfy as many equations as possible. This can be easily described within our framework by taking, for each constraint,

$$f_{ij}\left(g\right)=-{\delta }_{g\equiv b_{ij}},$$

and $f_{ij}=0$ for pairs not corresponding to constraints. The term ‘unique’ derives from the fact that the constraints have this special structure where the offset can only take one value to satisfy the constraint, and all other values have the same score. This motivated our choice of nomenclature for the framework treated in this paper. The semidefinite relaxation for the unique games problem proposed in [15] was investigated in [8] in the context of the signal alignment problem, where the $f_{ij}$ are not forced to have a special structure (but $𝒢\cong {\mathbb{Z}}_L$). The NUG framework presented in this paper can be seen as a generalization of the approach in [8] to other compact groups $𝒢$. We emphasize that, unlike [8] that was limited to the case of a finite cyclic group, here we consider compact groups that are possibly infinite and non-commutative.

Besides the signal alignment problem treated in [8] the semidefinite relaxation to the NUG problem we develop generalizes with other effective relaxations. When $𝒢\cong {\mathbb{Z}}_2$ it coincides with the semidefinite relaxations for Max-Cut [21], the little Grothendieck problem over ${\mathbb{Z}}_2$ [3, 32], recovery in the stochastic block model [2, 7], and Synchronization over ${\mathbb{Z}}_2$ [1, 7, 18]. When $𝒢\cong SO\left(2\right)$ and the functions $f_{ij}$ are linear with respect to the representation ${\rho }_1:SO\left(2\right)\to \mathbb{C}$ given by ${\rho }_1\left(\theta \right)=e^{i\theta }$, it coincides with the semidefinite relaxation for angular synchronization [40]. Similarly, when $𝒢\cong O\left(d\right)$ and the functions are linear with respect to the natural $d$-dimensional representation, then the NUG problem essentially coincides with the little Grothendieck problem over the orthogonal group [9, 31]. Other examples include the shape matching problem in computer graphics for which $𝒢$ is the permutation group (see [24, 16]). In addition, it has been shown in [13] that the formulation of NUG and the algorithms presented in this paper can be extended to simultaneous alignment and classification of a mixture of different signals.

1.1. Orientation estimation in cryo-Electron Microscopy.

A particularly important application of this framework is the orientation estimation problem in cryo-Electron Microscopy [39].

Cryo-EM is a technique used to determine the 3-dimensional structure of biological macromolecules. The molecules are rapidly frozen in a thin layer of ice and imaged with an electron microscope, which gives noisy 2-dimensional projections. One of the main difficulties with this imaging process is that these molecules are imaged at different unknown orientations in the sheet of ice and each molecule can only be imaged once (due to the destructive nature of the imaging process). More precisely, each measurement consists of a tomographic projection of a rotated (by an unknown rotation) copy of the molecule. The task is then to reconstruct the molecule density from many such noisy measurements. Although in principle it is possible to reconstruct the 3-dimensional density directly from the noisy images without estimation of the rotations [25], or by treating rotations as nuisance parameters [47, 6] here we consider the problem of estimating the rotations directly from the noisy images. In Section 2, we describe how this problem can be formulated in the form (1.1).

2. Multireference Alignment

In classical linear inverse problems, one is tasked with recovering an unknown element $x\in 𝒳$ from a noisy measurement of the form $𝒫\left(x\right)+ϵ$, where $ϵ$ represents the measurement error and $𝒫$ is a linear observation operator. There are, however, many problems where an additional difficulty is present; one class of such problems includes non-linear inverse problems in which an unknown transformation acts on $x$ prior to the linear measurement. Specifically, let $𝒳$ be a vector space and $𝒢$ be a group acting on $𝒳$. Suppose we have $n$ measurements of the form

$$y_i=𝒫\left(g_i\circ x\right)+{ϵ}_i,i=1,\dots ,n$$ (2.1)

where

• $x$ is a fixed but unknown element of $𝒳$,

• $g_1,\dots ,g_n$ are unknown elements of $𝒢$,

• $\circ$ is the action of $𝒢$ on $𝒳$,

• $𝒫:𝒳\to Y$ is a linear operator,

• $Y$ is the (finite-dimensional) measurement space,

• ${ϵ}_i$’s are independent noise terms.

If the $g_i$’s were known, then the task of recovering $x$ would reduce to a classical linear inverse problem, for which many effective techniques exist. While in many situations it is possible to estimate $x$ directly without estimating $g_1,\dots ,g_n$, or by treating these as nuisance parameters, here we focus on the problem of estimating the group elements $g_1,\dots ,g_n$.

There are several common approaches for inverse problems of the form (2.1). One is motivated by the observation that estimating $x$ knowing the $g_i$’s and estimating the $g_i$’s knowing $x$ are both considerably easier tasks. This suggests an alternating minimization approach where each estimation is updated iteratively. Besides a lack of theoretical guarantees, convergence may also depend on the initial guess. Another approach, which we refer to as pairwise comparisons [40], consists in determining, from pairs of observations $\left(y_i,y_j\right)$, the most likely value for $g_i{g}_j^{-1}$. Although the problem of estimating the $g_i$’s from these pairwise guesses is fairly well-understood [40, 10, 43] enjoying efficient algorithms and performance guarantees, this method suffers from loss of information as not all of the information of the problem is captured in this most likely value for $g_i{g}_j^{-1}$ and thus this approach tends to fail at low signal-to-noise-ratio.

In contrast, the Maximum Likelihood Estimator (MLE) leverages all information. Assuming that the ${ϵ}_i$’s are i.i.d. Gaussian, the MLE for the observation model (2.1) is given by the following optimization problem:

$$\begin{array}{cc}\underset{g_1,\dots ,g_n,x}{\text{minimize}}& \sum _{i=1}^n{‖y_i-𝒫\left(g_i\circ x\right)‖}_2^2\\ \text{subject}\text{ to}& g_i\in 𝒢\\ & x\in 𝒳\end{array}$$ (2.2)

We refer to (2.2) as the Multireference Alignment (MRA) problem. Let us denote the ground truth signal and group elements by $x^0$ and $g_1^0,\dots ,g_n^0$; the solution to the optimization problem by $x^{\mathrm{*}}$ and $g_1^{\mathrm{*}},\dots ,g_n^{\mathrm{*}}$, which we will also refer to as $x^{\mathrm{M}\mathrm{L}\mathrm{E}}$ and $g_1^{\mathrm{M}\mathrm{L}\mathrm{E}},\dots ,g_n^{\mathrm{M}\mathrm{L}\mathrm{E}}$. Unfortunately, the exponentially large search space and nonconvex nature of (2.2) often render it computationally intractable. However, for several problems of interest, we formulate (2.2) as an instance of an NUG for which we develop computationally tractable approximations.

Notice that although MLE typically enjoys several theoretical properties, their underlying technical conditions do not hold in this case. Specifically, the number of parameters to be estimated is not fixed but rather grows indefinitely with the sample size $n$: for each sample $y_i$ there is a group element $g_i$ that needs to be estimated. As a result, the MLE may not be consistent in this case. In other words, even in the limit $n\to \mathrm{\infty }$ the estimator $x^{\mathrm{M}\mathrm{L}\mathrm{E}}$ may not converge to the ground truth $x^0$. Similarly, the estimated group elements will not converge to their true values. A different version of MLE, not considered in this paper, in which the group elements are treated as nuisance parameters and are marginalized would enjoy the nice theoretical properties.

2.1. Registration of signals on the sphere.

Consider the problem of estimating a bandlimited signal on the circle $x:S^1\to \mathbb{C}$ from noisy rotated discrete sampled copies of it. In this problem, $𝒳=\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{n}{\left\{e^{\text{i}k\theta }\right\}}_{k=-t}^t$ is the space of bandlimited functions up to degree $t$ on $S^1,𝒢=SO\left(2\right)$ and the group action is

$$g\circ x=\sum _{k=-t}^t{\alpha }_k{e}^{\text{i}k\left(\theta -{\theta }_g\right)},$$

where $x={\sum }_{k=-t}^t{\alpha }_k{e}^{\text{i}k\theta }$ and we identified $g\in SO\left(2\right)$ with ${\theta }_g\in \left[\mathrm{0,2}\pi \right]$.

The measurements are of the form

$$y_i≔𝒫\left(g_i\circ x\right)+{ϵ}_i,i=1,\dots ,n$$

where

• $x\in 𝒳$,

• $g_i\in SO\left(2\right)$,

• $𝒫:𝒳\to {\mathbb{C}}^L$ samples the function at $L$ equally spaced points in $S^1$,

• ${ϵ}_i~𝒩\left(0,{\sigma }^2{I}_{L\times L}\right)(i=1,\dots ,n)$ are independent Gaussians.

Our objective is to estimate $g_1,\dots ,g_n$ and $x$. Since estimating $x$ knowing the group elements $g_i$ is considerably easier, we will focus on estimating $g_1,\dots ,g_n$. As shown below, this will essentially reduce to the problem of aligning (or registering) the observations $y_1,\dots ,y_n$.

In absence of noise, the problem of finding the $g_i$’s is trivial (cf. first column of Figure 2.1). With noise, if $x$ is known (as it is in some applications), then the problem of determining the $g_i$’s can be solved by matched filtering (cf. second column of Figure 2.1). However, $x$ is unknown in general. This, together with the high levels of noise, render the problem significantly more difficult (cf. last two columns of Figure 2.1).

Figure 2.1.

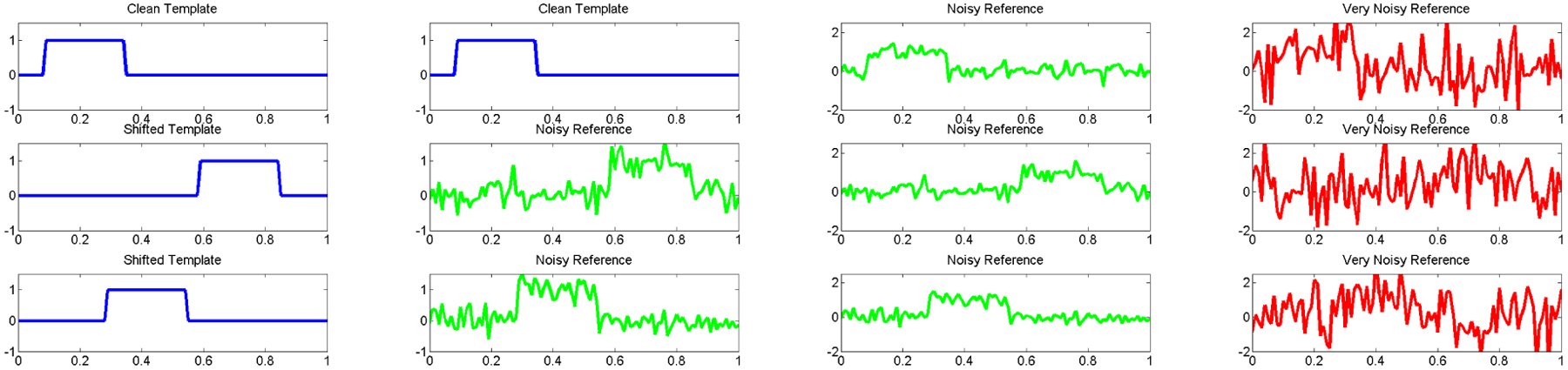
Illustration of the registration problem in $S^1$. The first column consists of a noiseless signal at three different shifts, the second column represents an instance for which the template $x$ is known and matched filtering is effective to estimate the shifts. However, in the examples we are interested in the template is unknown (last two columns) rendering the problem of estimating the shifts significantly harder.

We now define the problem of registration in $d$-dimensions in general. $𝒳=\mathrm{s}\mathrm{p}\mathrm{a}\mathrm{n}{\left\{p_k\right\}}_{k\in {𝒜}_t}$ is the space of bandlimited functions up to degree $t$ on $S^d$ where the $p_k$’s are orthonormal polynomials on $S^d,{𝒜}_t$ indexes all $p_k$ up to degree $t$ and $𝒢=SO(d+1)$.

The measurements are of the form

$$y_i≔𝒫\left(g_i\circ x\right)+{ϵ}_i,i=1,\dots ,n$$ (2.3)

where

• $x\in 𝒳,$

• $g_i\in SO(d+1)$,

• $𝒫:𝒳\to {\mathbb{C}}^L$ samples the function on $L$ points in $S^d$,

• ${ϵ}_i~𝒩\left(0,{\sigma }^2{I}_{L\times L}\right)(i=1,\dots ,n)$ are independent Gaussians.

Again, our objective is to estimate $g_1,\dots ,g_n$ and $x$. We would like the sampling operator $𝒫$ to be ‘uniform’. One possible sampling scheme is spherical designs surveyed in [11]. An illustration of signals on a sphere, sampled at such points, is provided in Figure 2.2.

Figure 2.2.

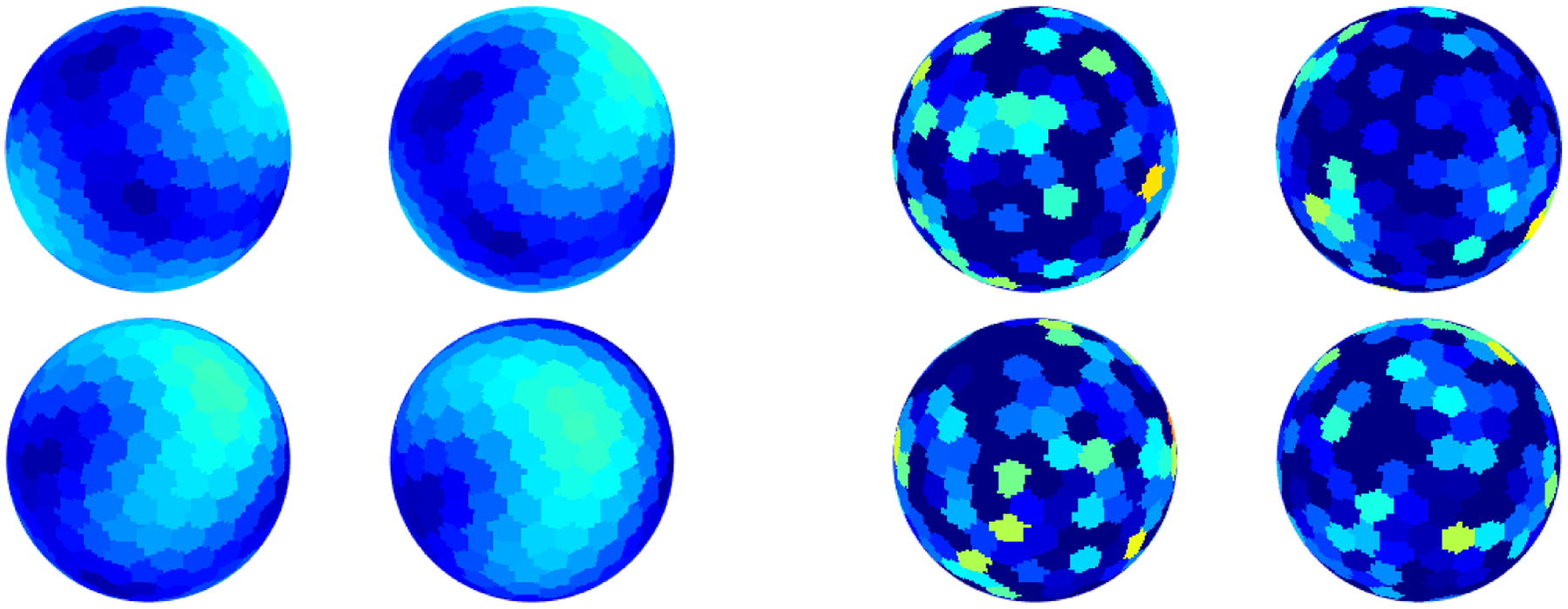
An illustration of registration in 2-dimensions. The left four spheres provide examples of clean signals $y_i$ and the right four spheres are of noisy observations. Note that the images are generated using a quantization of the sphere.

The MRA solution for registration in $d$-dimensions is given by

$$\begin{array}{ll}\underset{g_1,\dots ,g_n,x}{\text{minimize}}\hfill & \sum _{i=1}^n\parallel y_i-𝒫\left(g_i\circ x\right){\parallel }_2^2\hfill \\ \text{ subject }\text{to}\hfill & g_i\in SO\left(d+1\right)\hfill \\ \hfill & x\in 𝒳\hfill \end{array}$$ (2.4)

We now remove $x$ from (2.4). Let $𝒬:{\mathbb{C}}^L\to 𝒳$ be the adjoint of $𝒫.𝒬$ is also an approximate inverse of $𝒫$ (up to normalization), because points are sampled from a $t$-design which has the property of exactly integrating polynomials on the sphere. Then, ${∥y_i-𝒫\left(g_i\circ x\right)∥}_2^2\approx {∥𝒬\left(y_i\right)-g_i\circ x∥}_2^2$ (up to normalization), and the approximation error decreases as $L$ increases. Since $g_i$ preserves the norm $\parallel \cdot {\parallel }_2$, it follows that (2.4) is equivalent to

$$\begin{array}{cc}\underset{g_1,\dots ,g_n,x}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}& \sum _{i=1}^n{∥g_i^{-1}\circ 𝒬\left(y_i\right)-x∥}_2^2\hfill \\ \text{subject to}& g_i\in SO(d+1)\hfill \\ & x\in 𝒳.\hfill \end{array}$$ (2.5)

Since the minimizer $x$ with fixed $g_i$’s is the average, (2.5) is equivalent to

$$\begin{array}{ll}\underset{g_1,\dots ,g_n}{\text{minimize}}\hfill & \sum _{i,j=1}^n\parallel g_i^{-1}\circ 𝒬\left(y_i\right)-g_j^{-1}\circ 𝒬\left(y_j\right){\parallel }_2^2\hfill \\ \text{ subject}\text{ to}\hfill & g_i\in SO\left(d+1\right).\hfill \end{array}$$ (2.6)

Since $g_i$ preserves $\parallel \cdot {\parallel }_2$ norm, then (2.6) is equivalent to

$$\begin{array}{ll}\underset{g_1,\dots ,g_n}{\text{minimize}}\hfill & \sum _{i,j=1}^n\parallel 𝒬\left(y_i\right)-g_i{g}_j^{-1}\circ 𝒬\left(y_j\right){\parallel }_2^2\hfill \\ \text{ subject}\text{ to}\hfill & g_i\in SO\left(d+1\right).\hfill \end{array}$$ (2.7)

In summary, (2.4) can be approximated by (2.7), which is an instance of (1.1).

2.2. Orientation estimation in cryo-EM.

The task here is to reconstruct the molecule density from many noisy tomographic projection images (see the right column of Figure 1.1 for an idealized density and measurement dataset). We assume the molecule does not have any non-trivial point group symmetry. The linear inverse problem of recovering the molecule density given the rotations fits in the framework of classical computerized tomography for which effective methods exist. Thus, we focus on the non-linear inverse problem of estimating the unknown rotations and the underlying density.

Figure 1.1.

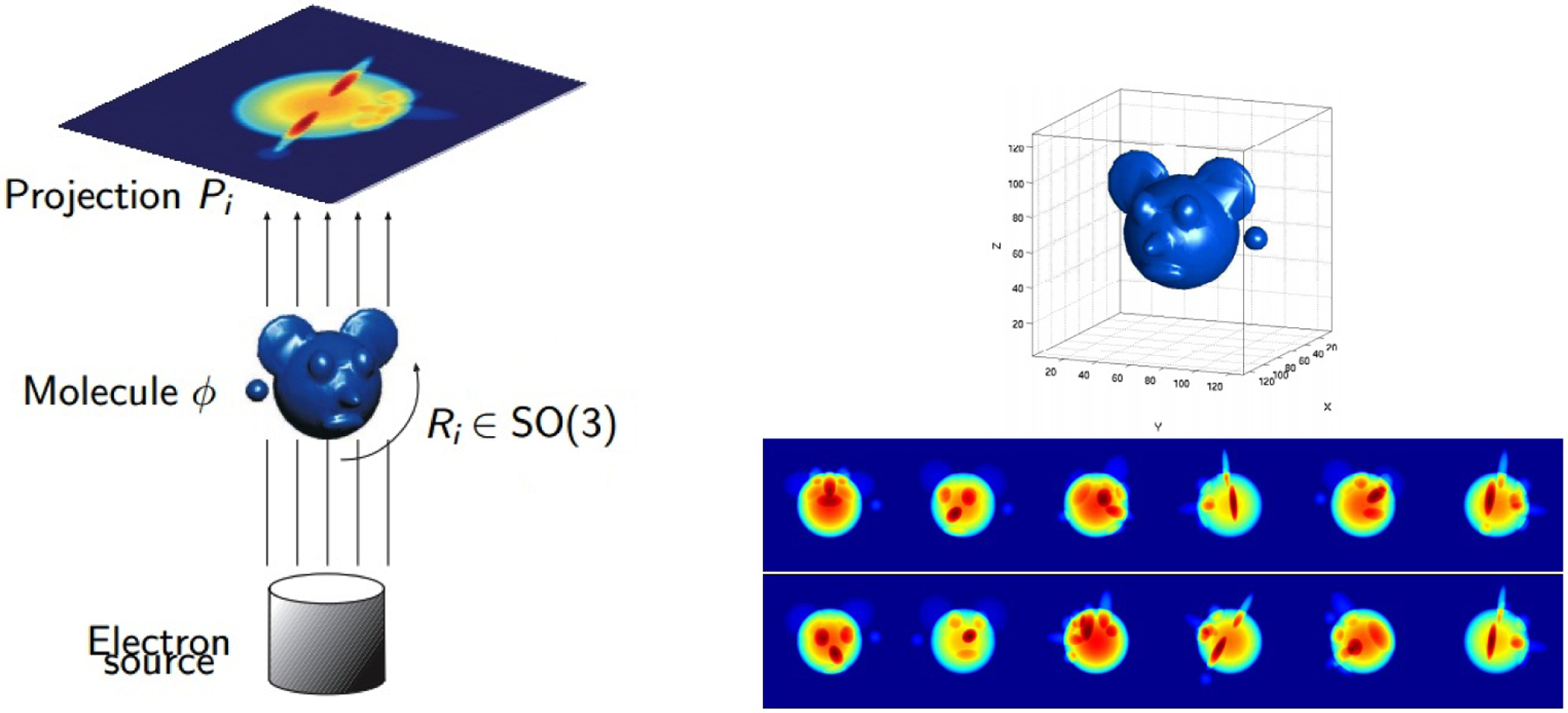
Illustration of the cryo-EM imaging process: A molecule is imaged after being frozen at a random (unknown) rotation and a tomographic 2-dimensional projection is captured. Given a number of tomographic projections taken at unknown rotations, we are interested in determining such rotations with the objective of reconstructing the molecule density. Images courtesy of Amit Singer and Yoel Shkolnisky [42].

An added difficulty is the high level of noise in the images. In fact, it is already non-trivial to distinguish whether a molecule is present in an image or if the image consists only of noise (see Figure 2.3 for a subset of an experimental dataset). On the other hand, these datasets consist of many projection images which renders reconstruction possible.

Figure 2.3.

Sample images from the E. coli 50S ribosomal subunit, generously provided by Dr. Fred Sigworth at the Yale Medical School.

We formulate the problem of orientation estimation in cryo-EM. Let $𝒳$ be the space of bandlimited functions that are also essentially compactly supported in ${\mathbb{R}}^3$ and $𝒢=SO\left(3\right)$. For perfectly centered images, and ignoring the effect of the microscope’s contrast transfer function, the measurements are of the form

$$I_i(x,y)≔𝒫\left(g_i\circ \varphi \right)+{ϵ}_i,i=1,\dots ,n$$ (2.8)

• $\varphi \in 𝒳,$

• $g_i\in SO\left(3\right)$,

• $𝒫\left(\varphi \right)$ samples ${\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}\varphi (x,y,z)dz(𝒫$ is called the discrete X-ray transform),

• ${ϵ}_i$’s are i.i.d Gaussians representing noise.

Our objective is to find $g_1,\dots ,g_n$ and $\varphi$.

The operator $𝒫$ in the orientation estimation problem is different than in the registration problem. Specifically, $𝒫$ is a composition of tomographic projection and sampling. To write the objective function for the orientation estimation problem, we will use the Fourier slice theorem [30].

The Fourier slice theorem states that the 2-dimensional Fourier transform of a tomographic projection of a molecular density $\varphi$ coincides with the restriction to a plane normal to the projection direction, a slice, of the 3-dimensional Fourier transform of the density $\varphi$. See Figure 2.4.

Figure 2.4.

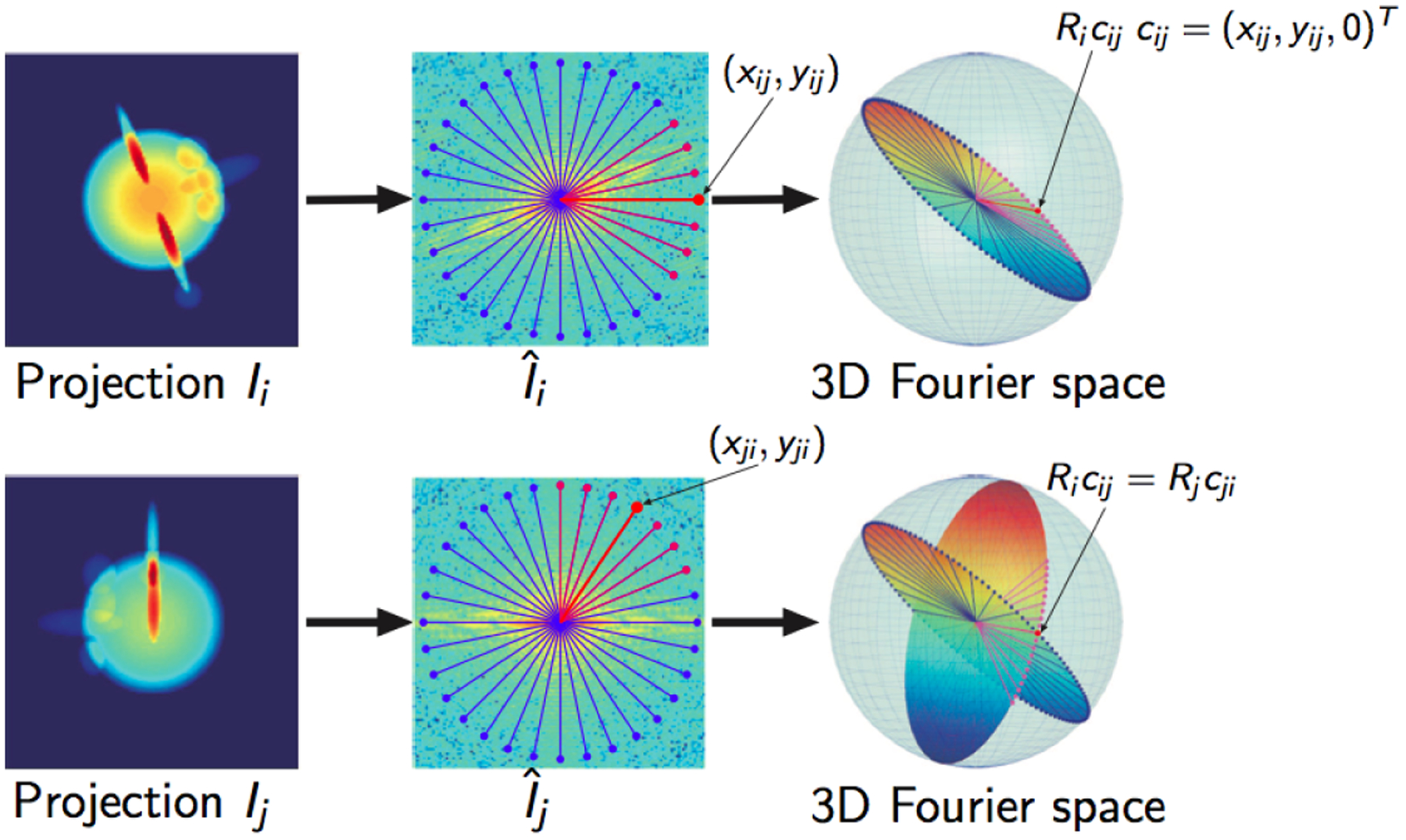
An illustration of the use of the Fourier slice theorem and the common lines approach to the orientation estimation problem in cryo-EM. Image courtesy of Amit Singer and Yoel Shkolnisky [42].

Let ${\widehat{I}}_i\left(r,\theta \right)$ be the Fourier transform of $I_i$ in polar coordinates. We identify ${\hat{I}}_i$ and ${\hat{I}}_j$ with the $xy$-plane in ${\mathbb{R}}^3$, and apply $g_i^{-1}$ and $g_j^{-1}$ to ${\hat{I}}_i$ and ${\hat{I}}_j$, respectively. Then, the directions of the lines of intersection on ${\hat{I}}_i$ and ${\hat{I}}_j$ are given, respectively, by unit vectors

$$c_{ij}\left(g_i{g}_j^{-1}\right)=\frac{g_i\left(g_i^{-1}\cdot {\overrightarrow{e}}_3\times g_j^{-1}\cdot {\overrightarrow{e}}_3\right)}{\parallel g_i(g_i^{-1}\cdot {\overrightarrow{e}}_3\times g_j^{-1}\cdot {\overrightarrow{e}}_3{\parallel }_2}=\frac{{\overrightarrow{e}}_3\times g_i{g}_j^{-1}\cdot {\overrightarrow{e}}_3}{\parallel {\overrightarrow{e}}_3\times g_i{g}_j^{-1}\cdot {\overrightarrow{e}}_3{\parallel }_2},$$ (2.9)

$$c_{ji}\left(g_i{g}_j^{-1}\right)=\frac{g_j\left(g_i^{-1}\cdot {\overrightarrow{e}}_3\times g_j^{-1}\cdot {\overrightarrow{e}}_3\right)}{\parallel g_j\left(g_i^{-1}\cdot {\overrightarrow{e}}_3\times g_j^{-1}\cdot {\overrightarrow{e}}_3\right)){\parallel }_2}=\frac{{\left(g_i{g}_j^{-1}\right)}^{-1}\cdot {\overrightarrow{e}}_3\times {\overrightarrow{e}}_3}{\parallel {\left(g_i{g}_j^{-1}\right)}^{-1}\cdot {\overrightarrow{e}}_3\times {\overrightarrow{e}}_3{\parallel }_2}.$$ (2.10)

where ${\overrightarrow{e}}_3≔(\mathrm{0,0},1{)}^T$. See [42] for details.

Since the noiseless images should agree on their common lines, we consider the following MRA-like cost function:

$$\begin{array}{ll}\underset{g_1,\dots ,g_n}{\text{minimize}}\hfill & \sum _{i,j=1}^n\parallel {\widehat{I}}_i\left(\cdot ,c_{ij}\left(g_i{g}_j^{-1}\right)\right)-{\widehat{I}}_j\left(\cdot ,c_{ji}\left(g_i{g}_j^{-1}\right)\right){\parallel }_2^2\hfill \\ \text{ subject to }\hfill & g_i\in SO\left(3\right),\hfill \end{array}$$ (2.11)

where, with a minor abuse of notation, we identify the vector $c_{ij}$ with the angle ${\theta }_{ij}$ of a common line in the Fourier transform of an image ${\hat{I}}_i$. Equation (2.11) is an instance of (1.1). Note that we could also use the $L_1$ norm or a weighted $L_2$ norm in the cost function.

Note that for $n=2$ images, there is always a degree of freedom along the line of intersection. In other words, we cannot recover the true orientation between ${\hat{I}}_1$ and ${\hat{I}}_2$. However, for $n\ge 3$, this degree of freedom is eliminated. It is also worth mentioning several important references in the context of angular reconstitution [22, 45]. In general, the measurement system suffers from a handedness ambiguity on the reconstruction (see, for example, [42]), this will be discussed in detail later in the paper.

3. Linearization via Fourier expansion

Let us consider the objective function in the general form

$$\sum _{i,j=1}^n{f}_{ij}\left(g_i{g}_j^{-1}\right).$$ (3.1)

Note that each $f_{ij}$ in (3.1) can be nonlinear and nonconvex. However, since $𝒢$ is compact (and since $f_{ij}\in C\left(𝒢\right)$), we can expand, each $f_{ij}$ in Fourier series. More precisely, given the unitary irreducible representations $\left\{{\rho }_k\right\}$ of $𝒢$, we can write

$$\begin{gathered} f_{ij}\left(g_i{g}_j^{-1}\right)=\sum _{k=0}^{\infty }{d}_k\text{tr}\left[{\widehat{f}}_{ij}\left(k\right){\rho }_k\left(g_i{g}_j^{-1}\right)\right] \\ =\sum _{k=0}^{\infty }{d}_k\text{tr}\left[{\widehat{f}}_{ij}\left(k\right){\rho }_k\left(g_i\right){\rho }_k^{\text{*}}\left(g_j\right)\right], \end{gathered}$$ (3.2)

where ${\hat{f}}_{ij}\left(k\right)$ are the Fourier coefficients of $f_{ij}$ and can be computed from $f_{ij}$ via the Fourier transform

$$\begin{gathered} {\widehat{f}}_{ij}\left(k\right)≔\underset{𝒢}{\int }{f}_{ij}\left(g\right){\rho }_k\left(g^{-1}\right)dg \\ =\underset{𝒢}{\int }{f}_{ij}\left(g\right){\rho }_k^{\text{*}}\left(g\right)dg. \end{gathered}$$ (3.3)

Above, $dg$ denotes the Haar measure on $𝒢$ and $d_k$ the dimension of the representation ${\rho }_k$. See [17] for an introduction to the representations of compact groups.

We express the objective function (3.1) as

$$\begin{gathered} \sum _{i,j=1}^n{f}_{ij}\left(g_i{g}_j^{-1}\right)=\sum _{i,j=1}^n\sum _{k=0}^{\infty }{d}_k\text{tr}\left[{\widehat{f}}_{ij}\left(k\right){\rho }_k\left(g_i\right){\rho }_k^{\text{*}}\left(g_j\right)\right] \\ =\sum _{k=0}^{\infty }\sum _{i,j=1}^n{d}_k\text{tr}\left[{\widehat{f}}_{ij}\left(k\right){\rho }_k\left(g_i\right){\rho }_k^{\text{*}}\left(g_j\right)\right], \end{gathered}$$

which is linear in ${\rho }_k\left(g_i\right){\rho }_k^{\mathrm{*}}\left(g_j\right)$. This motivates writing (1.1) as linear optimization over the variables

$$X^{\left(k\right)}≔\left[\begin{array}{c}{\rho }_k\left(g_1\right)\\ ⋮\\ {\rho }_k\left(g_n\right)\end{array}\right]{\left[\begin{array}{c}{\rho }_k\left(g_1\right)\\ ⋮\\ {\rho }_k\left(g_n\right)\end{array}\right]}^{\mathrm{*}}.$$

In other words,

$$\sum _{i,j=1}^n{f}_{ij}\left(g_i{g}_j^{-1}\right)=\sum _{k=0}^{\mathrm{\infty }}\text{tr}\left[C^{\left(k\right)}{X}^{\left(k\right)}\right],$$

where the coefficient matrices are given by

$$C^{\left(k\right)}≔d_k\left[\begin{array}{cccc}{\widehat{f}}_{11}\left(k\right)& {\widehat{f}}_{21}\left(k\right)& \cdots & {\widehat{f}}_{n1}\left(k\right)\\ {\widehat{f}}_{12}\left(k\right)& {\widehat{f}}_{22}\left(k\right)& \cdots & {\widehat{f}}_{n2}\left(k\right)\\ ⋮& ⋮& \ddots & ⋮\\ {\widehat{f}}_{1n}\left(k\right)& {\widehat{f}}_{2n}\left(k\right)& \cdots & {\widehat{f}}_{nn}\left(k\right)\end{array}\right].$$

We refer to the $d_k\times d_k$ block of $X^{\left(k\right)}$ corresponding to ${\rho }_k\left(g_i\right){\rho }_k^{\mathrm{*}}\left(g_j\right)={\rho }_k\left(g_i{g}_j^{-1}\right)$ as $X_{ij}^{\left(k\right)}$. We now turn our attention to constraints on the variables ${\left\{X^{\left(k\right)}\right\}}_{k=0}^{\mathrm{\infty }}$. It is easy to see that:

$$X^{\left(k\right)}⪰0,{\forall }_k$$ (3.4)

$$X_{ii}^{\left(k\right)}=I_{d_k\times d_k},{\forall }_{k,i},$$ (3.5)

$$\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left[X^{\left(k\right)}\right]=d_k,{\forall }_k,$$ (3.6)

$$X_{ij}^{\left(k\right)}\in \mathrm{I}\mathrm{m}\left({\rho }_k\right),{\forall }_{k,i,j}.$$ (3.7)

Constraints (3.4), (3.5) and (3.6) ensure $X^{\left(k\right)}$ is of the form

$$X^{\left(k\right)}=\left[\begin{array}{c}{X}_1^{\left(k\right)}\\ X_2^{\left(k\right)}\\ ⋮\\ X_n^{\left(k\right)}\end{array}\right]{\left[\begin{array}{c}{X}_1^{\left(k\right)}\\ X_2^{\left(k\right)}\\ ⋮\\ X_n^{\left(k\right)}\end{array}\right]}^{\mathrm{*}},$$

for some $X_i^{\left(k\right)}$ unitary $d_k\times d_k$ matrices. The constraint (3.7) attempts to ensure that $X_i^{\left(k\right)}$ is in the image of the representation of $𝒢$. Notably, none of these constraints ensures that, for different values of $k,X_{ij}^{\left(k\right)}$ correspond to the same group element $g_i{g}_j^{-1}$. Adding such a constraint would yield

$$\begin{array}{cc}\underset{X^{\left(k\right)}}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}& \sum _{k=0}^{\mathrm{\infty }}\mathrm{t}\mathrm{r}\left[C^{\left(k\right)}{X}^{\left(k\right)}\right]\hfill \\ \text{subject to}& X^{\left(k\right)}⪰0\hfill \\ & X_{ii}^{\left(k\right)}=I_{d_k\times d_k}\hfill \\ & \mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left[X^{\left(k\right)}\right]=d_k\hfill \\ & X_{ij}^{\left(k\right)}={\rho }_k\left(g_i{g}_j^{-1}\right),\hfill \end{array}$$ (3.8)

where $g_i$ and $g_j$ are elements of $𝒢$.

Unfortunately, both the rank constraint and the last constraint in (3.8) are, in general, nonconvex. We will relax (3.8) by dropping the rank requirement and replacing the last constraint by positivity constraints that couple different $X^{\left(k\right)}$’s. We achieve this by considering the Dirac delta funcion on $𝒢$. Notice that the Dirac delta funcion $\delta \left(g\right)$ on the identity $e\in 𝒢$ can be expanded as

$$\begin{gathered} \delta \left(g\right)=\sum _{k=0}^{\infty }{d}_k\text{tr}\left[\widehat{\delta }\left(k\right){\rho }_k\left(g\right)\right] \\ =\sum _{k=0}^{\infty }{d}_k\text{tr}\left[\left(\underset{𝒢}{\int }\delta \left(h\right){\rho }_k^{\text{*}}\left(h\right)dh\right){\rho }_k\left(g\right)\right] \\ =\sum _{k=0}^{\infty }{d}_k\text{tr}\left[{\rho }_k\left(g\right)\right]. \end{gathered}$$

If we replace $g$ with $g^{-1}\left(g_i{g}_j^{-1}\right)$, then we get

$$\begin{gathered} \delta \left(g^{-1}{g}_i{g}_j^{-1}\right)=\sum _{k=0}^{\infty }{d}_k\text{tr}\left[{\rho }_k\left(g^{-1}\right){\rho }_k\left(g_i{g}_j^{-1}\right)\right] \\ =\sum _{k=0}^{\infty }{d}_k\text{tr}\left[{\rho }_k^{\text{*}}\left(g\right)X_{ij}^{\left(k\right)}\right]. \end{gathered}$$

To arrive at a convex program, we consider the following convex constraints, that form a natural convex relaxation for Dirac deltas,

$$\sum _{k=0}^{\infty }{d}_k\text{tr}\left[{\rho }_k^{\text{*}}\left(g\right)X_{ij}^{\left(k\right)}\right]\ge 0\forall g\in 𝒢,$$ (3.9)

$$\underset{𝒢}{\int }\left(\sum _{k=0}^{\infty }{d}_k\text{tr}\left[{\rho }_k^{\text{*}}\left(g\right)X_{ij}^{\left(k\right)}\right]\right)dg=1.$$ (3.10)

This suggests relaxing (3.8) to

$$\begin{array}{ll}\underset{X^{\left(k\right)}}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}& \sum _{k=0}^{\mathrm{\infty }}\mathrm{t}\mathrm{r}\left[C^{\left(k\right)}{X}^{\left(k\right)}\right]\\ \text{subject to}& X^{\left(k\right)}⪰0\\ & X_{ii}^{\left(k\right)}=I_{d_k\times d_k}\\ & \sum _{k=0}^{\mathrm{\infty }}{d}_k\mathrm{t}\mathrm{r}\left[{\rho }_k^{\mathrm{*}}\left(g\right)X_{ij}^{\left(k\right)}\right]\ge 0\forall g\in 𝒢\\ & {\int }_{𝒢}\left(\sum _{k=0}^{\mathrm{\infty }}{d}_k\mathrm{t}\mathrm{r}\left[{\rho }_k^{\mathrm{*}}\left(g\right)X_{ij}^{\left(k\right)}\right]\right)dg=1.\end{array}$$ (3.11)

For a nontrivial irreducible representation ${\rho }_k$, we have ${\int }_{𝒢}{\rho }_k\left(g\right)dg=0$. This means that the integral constraint in (3.11) is equivalent to the constraint

$$X_{ij}^{\left(0\right)}=1,{\forall }_{i,j}.$$

Thus, we focus on the optimization problem

$$\begin{array}{cc}\underset{X^{\left(k\right)}}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}& \sum _{k=0}^{\mathrm{\infty }}\mathrm{t}\mathrm{r}\left[C^{\left(k\right)}{X}^{\left(k\right)}\right]\hfill \\ \text{subject to}& X^{\left(k\right)}⪰0\hfill \\ & X_{ii}^{\left(k\right)}=I_{d_k\times d_k}\hfill \\ & \sum _{k=0}^{\mathrm{\infty }}{d}_k\mathrm{t}\mathrm{r}\left[{\rho }_k^{\mathrm{*}}\left(g\right)X_{ij}^{\left(k\right)}\right]\ge 0\forall g\in 𝒢\hfill \\ & X_{ij}^{\left(0\right)}=1.\hfill \end{array}$$ (3.12)

When $𝒢$ is a finite group it has only a finite number of irreducible representations. This means that (3.12) is a semidefinite program and can be solved, to arbitrary precision, in polynomial time [46]. In fact, when $𝒢\cong {\mathbb{Z}}_L$, a suitable change of basis shows that (3.12) is equivalent to the semidefinite programming relaxation proposed in [8] for the signal alignment problem.

Unfortunately, many of the applications of interest involve infinite groups. This creates two obstacles to solving (3.12). One is due to the infinite sum in the objective function and the other due to the infinite number of positivity constraints. In the next section, we address these two obstacles for the groups $SO\left(2\right)$ and $SO\left(3\right)$.

4. Finite truncations for $\mathit{S}\mathit{O}\left(2\right)\mathbf{a}\mathbf{n}\mathbf{d}\mathit{S}\mathit{O}\left(3\right)$ via Fejér kernels

The objective of this section is to replace (3.12) by an optimization problem depending only in finitely many variables $X^{\left(k\right)}$. The objective function in (3.12) is converted from an infinite sum to a finite sum by truncating at degree $t$. That is, we fix a $t$ and set $C^{\left(k\right)}=0$ for $k>t$. This consists of truncating the Fourier series of ${\sum }_{i,j=1}^n{f}_{ij}\left(g_i{g}_j^{-1}\right)$. Unfortunately, constraint (3.9) given by

$$\sum _{k=0}^{\mathrm{\infty }}{d}_k\text{tr}\left[{\rho }_k^{\mathrm{*}}\left(g\right)X_{ij}^{\left(k\right)}\right]\ge 0\forall g\in 𝒢,$$

still involves infinitely many variables $X_{ij}^{\left(k\right)}$ and consists of infinitely many linear constraints.

We now address this issue for the groups $SO\left(2\right)$ and $SO\left(3\right)$.

4.1. Truncation for $SO\left(2\right)$.

Since we truncated the objective function at degree $t$, it is then natural to truncate the infinite sum in constraint (3.9) also at $t$. If we truncated below $t$, then some variables (such as $X^{\left(t\right)}$) are not constrained; and if we truncated above $t$, then some variables (such as $X^{(t+1)}$) do not affect the cost function. The irreducible representations of $SO\left(2\right)$ are $\left\{e^{\text{i}k\theta }\right\}$, and $d_k=1$ for all $k$. Let us identify $g\in SO\left(2\right)$ with ${\theta }_g\in \left[\mathrm{0,2}\pi \right]$. That straightforward truncation corresponds to approximating the Dirac delta with

$$\delta \left(g\right)\approx \sum _{k=-t}^t{e}^{\text{i}k{\theta }_g}.$$

This approximation is known as the Dirichlet kernel, which we denote as

$$D_t\left(\theta \right)≔\sum _{k=-t}^t{e}^{\text{i}k\theta }.$$

However, the Dirichlet kernel does not inherit all the desirable properties of the delta function. In fact, $D_t\left(\theta \right)$ is negative for some values of $\theta$.

Instead, we use the Fejér kernel, which is a non-negative kernel, to approximate the Dirac delta. The Fejér kernel is defined as

$$F_t\left(\theta \right)≔\frac{1}{t}\sum _{k=0}^{t-1}{D}_k=\sum _{k=-t}^t\left(1-\frac{\left|k\right|}{t}\right)e^{\text{i}k\theta },$$

which is the first-order Cesàro mean of the Dirichlet kernel.

This motivates us to replace constraint (3.9) with

$$\sum _{k=-t}^t\left(1-\frac{\left|k\right|}{t}\right)e^{-\text{i}k\theta }{X}_{ij}^{\left(k\right)}\ge 0\forall \theta \in \left[\mathrm{0,2}\pi \right],$$

where, for $k>0,X_{ij}^{(-k)}$ denotes ${\left[X_{ij}^{\left(k\right)}\right]}^{\mathrm{*}}$.

This suggests considering

$$\begin{array}{cc}\underset{X^{\left(k\right)}}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}& \sum _{k=0}^t\mathrm{t}\mathrm{r}\left[C^{\left(k\right)}{X}^{\left(k\right)}\right]\hfill \\ \text{subject to}& X^{\left(k\right)}⪰0\hfill \\ & X_{ii}^{\left(k\right)}=I_{d_k\times d_k}\hfill \\ & \sum _{k=-t}^t\left(1-\frac{\left|k\right|}{t}\right)e^{-\text{i}k\theta }{X}_{ij}^{\left(k\right)}\ge 0\forall \theta \in \left[\mathrm{0,2}\pi \right]\hfill \\ & X_{ij}^{\left(0\right)}=1,\hfill \end{array}$$

which only depends on the variables $X_{ij}^{\left(k\right)}$ for $k=0,\dots ,t$.

Unfortunately, the condition that the trigonometric polynomial ${\sum }_{k=-t}^t\left(1-\frac{\left|k\right|}{t}\right)e^{-\text{i}k\theta }{X}_{ij}^{\left(k\right)}$ is always non-negative, still involves an infinite number of linear in-equalities. Interestingly, due to the Fejér-Riesz factorization theorem (see [19]), this condition can be replaced by an equivalent condition involving a positive semidefinite matrix — it turns out that every nonnegative trigonometric polynomial is a square, meaning that the so called sum-of-squares relaxation [33, 34] is exact. However, while such a formulation would still be an SDP and thus solvable, up to arbitrary precision, in polynomial time, it would involve a positive semidefinite variable for every pair $(i,j)$, rendering it computationally challenging. For this reason we relax the non-negativity constraint by asking that ${\sum }_{k=-t}^t\left(1-\frac{\left|k\right|}{t}\right)e^{-\text{i}k\theta }{X}_{ij}^{\left(k\right)}$ is non-negative in a finite set ${\mathrm{\Omega }}_t\in SO\left(2\right)$. This yields the following optimization problem:

$$\begin{array}{cc}\underset{X^{\left(k\right)}}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}& \sum _{k=0}^t\mathrm{t}\mathrm{r}\left[C^{\left(k\right)}{X}^{\left(k\right)}\right]\hfill \\ \text{subject to}& X^{\left(k\right)}⪰0\hfill \\ & X_{ii}^{\left(k\right)}=I_{d_k\times d_k}\hfill \\ & \sum _{k=-t}^t\left(1-\frac{\left|k\right|}{t}\right)e^{-\text{i}k\theta }{X}_{ij}^{\left(k\right)}\ge 0\forall \theta \in {\mathrm{\Omega }}_t\hfill \\ & X_{ij}^{\left(0\right)}=1.\hfill \end{array}$$ (4.1)

4.2. Truncation for $SO\left(3\right)$.

The irreducible representations of $SO\left(3\right)$ are the Wigner-D matrices $\left\{W^{\left(k\right)}(\alpha ,\beta ,\gamma )\right\}$, and $d_k=2k+1$. See [48] for an introduction to Wigner-D matrices. Let us associate $g\in SO\left(3\right)$ with Euler $(Z-Y-Z)$ angle $(\alpha ,\beta ,\gamma )\in \left[\mathrm{0,2}\pi \right]\times [0,\pi ]\times \left[\mathrm{0,2}\pi \right]$. A straightforward truncation yields the approximation

$$\delta \left(g\right)\approx \sum _{k=0}^t\left(2k+1\right)\text{tr}\left[W^{\left(k\right)}\left(\alpha ,\beta ,\gamma \right)\right].$$

Observe that the operator tr is invariant under conjugation. Then $W^{\left(k\right)}$ can be decomposed as

$$W^{\left(k\right)}(\alpha ,\beta ,\gamma )=R{\mathrm{\Lambda }}^{\left(k\right)}\left(\theta \right)R^{\mathrm{*}}$$

with an $R$ such that

$${\mathrm{\Lambda }}^{\left(k\right)}\left(\theta \right)=\left[\begin{array}{ccccc}{e}^{-\text{i}k\theta }& & & & \\ & \ddots & & & \\ & & 1& & \\ & & & \ddots & \\ & & & & e^{\text{i}k\theta }\end{array}\right].$$

We can think of $R$ as a change of basis and ${\mathrm{\Lambda }}^{\left(k\right)}\left(\theta \right)$ as a rotation from $SO\left(2\right)$ under the basis $R$. It follows that

$$\text{tr}\left[W^{\left(k\right)}\left(\alpha ,\beta ,\gamma \right)\right]=\text{tr}\left[{\mathrm{\Lambda }}^{\left(k\right)}\left(\theta \right)\right]=\sum _{m=-k}^k{e}^{\text{i}m\theta }=D_k\left(\theta \right).$$

The relationship between $\theta$ and $\alpha ,\beta ,\gamma$ is

$$\theta =2\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{\beta }{2}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{\alpha +\gamma }{2}\right)\right].$$

This relationship can be obtained by directly evaluating $\mathrm{t}\mathrm{r}\left[W^{\left(1\right)}(\alpha ,\beta ,\gamma )\right]$ using the Wigner-d matrix $w^{\left(1\right)}$:

$$\begin{gathered} \text{tr}\left[W^{\left(1\right)}\left(\alpha ,\beta ,\gamma \right)\right]=\sum _{m=-1}^1{W}_{m,m}^{\left(1\right)}\left(\alpha ,\beta ,\gamma \right) \\ =\sum _{m=-1}^1{e}^{-\text{i}m\left(\alpha +\gamma \right)}{w}_{m,m}^{\left(1\right)}\left(\beta \right) \\ =\text{cos}\left(\beta \right)\left(1+\text{cos}\left(\alpha +\gamma \right)\right)+\text{cos}\left(\alpha +\gamma \right). \end{gathered}$$

See [48] also for an introduction to Wigner-d matrix. This straightforward truncation at $t$ yields

$$\delta \left(g\right)\approx \sum _{k=0}^t\left(2k+1\right)D_k\left(\theta \right),$$

which, again, inherits the undesirable property that this approximation can be negative for some $\theta$. Recall that we circumvented this property in the 1-dimension case by taking the first-order Cesàro mean of the Dirichlet kernel. In the 2-dimension case, we will need the second-order Cesàro mean. Notice that

$$D_k\left(\theta \right)=\frac{\text{sin}\left[\left(2k+1\right)\frac{\theta }{2}\right]}{\text{sin}\left(\frac{\theta }{2}\right)}.$$

Fejér proved that [4]

$$\sum _{k=0}^t\frac{(3{)}_{t-k}}{(t-k)!}\left(k+\frac{1}{2}\right)\mathrm{s}\mathrm{i}\mathrm{n}\left[(2k+1)\frac{\theta }{2}\right]\ge 0,0\le \theta \le \pi$$

where $\frac{(3{)}_{t-k}}{(t-k)!}=\frac{1}{2}(t-k+2)(t-k+1)$. It follows that

$$\begin{gathered} \sum _{k=0}^t\frac{{(3)}_{t-k}}{\left(t-k\right)!}\left(k+\frac{1}{2}\right)D_k\left(\theta \right) \\ =\sum _{k=0}^t\frac{{(3)}_{t-k}}{\left(t-k\right)!}\left(k+\frac{1}{2}\right)\frac{\text{sin}\left[\left(2k+1\right)\frac{\theta }{2}\right]}{\text{sin}\left(\frac{\theta }{2}\right)}\ge 0,-\pi \le 0\le \pi . \end{gathered}$$

Let us define

$$F_t\left(g\right)=F_t(\alpha ,\beta ,\gamma )≔\sum _{k=0}^t\frac{(3{)}_{t-k}}{(t-k)!}\left(k+\frac{1}{2}\right)\frac{\mathrm{s}\mathrm{i}\mathrm{n}\left[(2k+1)\frac{{\theta }_g}{2}\right]}{\mathrm{s}\mathrm{i}\mathrm{n}\left(\frac{{\theta }_g}{2}\right)}$$

where ${\theta }_g=2\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\left[\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{\beta }{2}\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(\frac{\alpha +\gamma }{2}\right)\right]$.

We replace constraint (3.9) with

$$F_t\left(\alpha ,\beta ,\gamma \right)\ge 0\forall \left(\alpha ,\beta ,\gamma \right)\in \left[\mathrm{0,2}\pi \right]\times \left[0,\pi \right]\times \left[\mathrm{0,2}\pi \right].$$

Secondly, we discretize the group $SO\left(3\right)$ to obtain a finite number of constraints. We consider a suitable finite subset ${\mathrm{\Omega }}_t\subset SO\left(3\right)$. In our implementation, we use a Hopf fibration [49] to discretize $SO\left(3\right)$. The quotient space $SO\left(3\right)/SO\left(2\right)$ is equivalent to $S^2$. We take a uniform discretization of $S^1\equiv SO\left(2\right)$ and a spherical design [11] of $S^2$. It is possible to find a spherical design on $S^2$ with $𝒪\left(r^2\right)$ points [11]. By [49], we use $𝒪\left(r\right)$ points to discretize $SO\left(2\right)$. The size of our $SO\left(3\right)$ discretization is $𝒪\left(r^3\right)$. So, we have to enforce $𝒪\left(r^3\right)$ inequality constraints. The choice of $r$ is up to the user to strike a balance between computational speed and accuracy. We can then relax the non-negativity constraint yielding the following semidefinite program¹:

$$\begin{array}{cc}\underset{X^{\left(k\right)}}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}& \sum _{k=0}^t\mathrm{t}\mathrm{r}\left[C^{\left(k\right)}{X}^{\left(k\right)}\right]\hfill \\ \text{subject to}& X^{\left(k\right)}⪰0\hfill \\ & X_{ii}^{\left(k\right)}=I_{d_k\times d_k}\hfill \\ & \sum _{k=0}^t\frac{(3{)}_{t-k}}{(t-k)!}\left(k+\frac{1}{2}\right)\mathrm{t}\mathrm{r}\left[{\left(W^{\left(k\right)}(\alpha ,\beta ,\gamma )\right)}^{\mathrm{*}}{X}_{ij}^{\left(k\right)}\right]\ge 0\forall (\alpha ,\beta ,\gamma )\in {\mathrm{\Omega }}_t\hfill \\ & X_{ij}^{\left(0\right)}=1.\hfill \end{array}$$ (4.2)

4.3. An additional constraint on $X^{\left(1\right)}$.

In this section, we discuss an additional constraint on $X^{\left(1\right)}$, which uses properties of quaternions to constrain each block $X_{ij}^{\left(1\right)}$ of $X^{\left(1\right)}$ in the convex hull of $SO\left(3\right)$ more directly.

We consider the standard rotation matrix $R$ and the unit quaternion $q=q_r+q_i\mathrm{i}+q_j\mathrm{j}+q_k\mathrm{k}$ which represent the same rotation as the block $X_{ij}^{\left(1\right)}$ (whose representation is associated with spherical harmonics), and we consider the outer product $Q_{ij}$ of the unit quaternion $q$

$$Q_{ij}=q^{T}q.$$ (4.3)

The standard rotation matrix $R$ is related to the block $X_{ij}^{\left(1\right)}$ by the formula

$$R^{\mathrm{*}}=M^{\mathrm{*}}\left(T^{\mathrm{*}}{X}_{ij}^{\left(1\right)}T\right)M,$$

where,

$$T≔\left[\begin{array}{ccc}-\frac{\mathrm{i}}{\sqrt{2}}& 0& \frac{1}{\sqrt{2}}\\ 0& 1& 0\\ -\frac{\mathrm{i}}{\sqrt{2}}& 0& -\frac{1}{\sqrt{2}}\end{array}\right],$$

and

$$M≔\left[\begin{array}{ccc}0& 1& 0\\ 0& 0& 1\\ -1& 0& 0\end{array}\right].$$

Indeed, one can verify that

$$T^{\mathrm{*}}{X}_{ij}^{\left(1\right)}T=\left[\begin{array}{ccc}R\left[22\right]& R\left[32\right]& -R\left[12\right]\\ R\left[23\right]& R\left[33\right]& -R\left[13\right]\\ -R\left[21\right]& -R\left[31\right]& R\left[11\right]\end{array}\right],$$

where,

$$R=\left[\begin{array}{lll}R\left[11\right]& R\left[12\right]& R\left[13\right]\\ R\left[21\right]& R\left[22\right]& R\left[23\right]\\ R\left[31\right]& R\left[32\right]& R\left[33\right]\end{array}\right],$$

and $M$ is used simply to rearrange the elements of $T^{\mathrm{*}}{X}_{ij}^{\left(1\right)}T$.

Next, $R$ is mapped to $Q_{ij}$ by Rodrigues’ rotation formula (see [37]):

$$Q_{ij}=ℛ\left(R\right)≔\frac{1}{4}\left[\begin{array}{cccc}1+R\left[11\right]+R\left[22\right]+R\left[33\right]& R\left[32\right]-R\left[23\right]& R\left[13\right]-R\left[31\right]& R\left[21\right]-R\left[12\right]\\ R\left[32\right]-R\left[23\right]& 1+R\left[11\right]-R\left[22\right]-R\left[33\right]& R\left[21\right]+R\left[12\right]& R\left[31\right]+R\left[13\right]\\ R\left[13\right]-R\left[31\right]& R\left[21\right]+R\left[12\right]& 1+R\left[22\right]-R\left[11\right]-R\left[33\right]& R\left[23\right]+R\left[32\right]\\ R\left[21\right]-R\left[12\right]& R\left[31\right]+R\left[13\right]& R\left[23\right]+R\left[32\right]& 1+R\left[33\right]-R\left[11\right]-R\left[22\right]\end{array}\right].$$

In summary, the mapping from $X_{ij}^{\left(1\right)}$ to $Q_{ij}$, which we denote by ${𝒜}_{E_q}$, is given by the formula:

$$Q_{ij}={𝒜}_{E_q}\left(X_{ij}^{\left(1\right)}\right)=ℛ\left(M^{\mathrm{*}}{T}^{\mathrm{*}}{X}_{ij}^{\left(1\right)}TM\right).$$

For each $Q_{ij}$, we wish to impose the constraints implied by Equation (4.3):

$$Q_{ij}⪰0,\mathrm{t}\mathrm{r}\left[Q_{ij}\right]=1,\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left[Q_{ij}\right]=1.$$

But since the constraint $\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{k}\left[Q_{ij}\right]=1$ is not convex, we will drop it, giving us the following SDP in place of (4.2):

$$\begin{array}{cc}\underset{X^{\left(k\right)}}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}& \sum _{k=0}^t\mathrm{t}\mathrm{r}\left[C^{\left(k\right)}{X}^{\left(k\right)}\right]\hfill \\ \text{subject to}& X^{\left(k\right)}⪰0\hfill \\ & X_{ii}^{\left(k\right)}=I_{d_k\times d_k}\hfill \\ & \sum _{k=0}^t\frac{(3{)}_{t-k}}{(t-k)!}\left(k+\frac{1}{2}\right)\mathrm{t}\mathrm{r}\left[{\left(W^{\left(k\right)}(\alpha ,\beta ,\gamma )\right)}^{\mathrm{*}}{X}_{ij}^{\left(k\right)}\right]\ge 0\forall (\alpha ,\beta ,\gamma )\in {\mathrm{\Omega }}_t\hfill \\ & X_{ij}^{\left(0\right)}=1\hfill \\ & Q_{ij}={𝒜}_{E_q}\left(X_{ij}^{\left(1\right)}\right),Q_{ij}⪰0,\mathrm{t}\mathrm{r}\left[Q_{ij}\right]=1.\hfill \end{array}$$ (4.4)

5. Applications

In this section, we consider the application of (4.1) to the problem of registration over the unit circle and the application of (4.4) to registration over the unit sphere and orientation estimation in cryo-EM. To solve the SDP for each problem, the only parameters we need to determine are the coefficient matrices $C^{\left(k\right)}$ and the truncation parameter $t$. The calculations of $C^{\left(k\right)}$ are detailed in the following pages. As for $t$, we experimented over a range of values for each problem, and chose a value that balances computational time with accuracy in the estimated rotations. The SDP outputs the relative transformations $g_{ij}=g_i{g}_j^{-1}$, while we need $g_1,\dots ,g_n$. For each problem, we describe a rounding procedure to recover $g_1,\dots ,g_n$ from the $g_{ij}$’s.

5.1. Registration in 1-dimension.

Recall that $𝒳$ is the space of bandlimited functions up to degree $t$ on $S^1$. That is, for $x\in 𝒳$, we can express

$$x\left(\omega \right)=\sum _{l=-t}^t{\alpha }_l{e}^{\text{i}l\omega }.$$

Again, the irreducible representations of $SO\left(2\right)$ are $\left\{e^{\text{i}k\theta }\right\}$, and $d_k=1$ for all $k$. Let us identify $g\in SO\left(2\right)$ with ${\theta }_g\in \left[\mathrm{0,2}\pi \right]$, then

$$g\cdot x\left(\omega \right)=\sum _{l=-t}^t{e}^{\text{i}l{\theta }_g}{\alpha }_l{e}^{\text{i}l\omega }.$$

Let $𝒫$ sample the underlying signal $x$ at $L=2t+1$ distinct points. This way, we can determine all the ${\alpha }_l$’s associated with $x$.

Since $y_i=𝒫\left(g_i\cdot x\right)+{ϵ}_i$, for the adjoint $𝒬$, we have

$$𝒬\left(y_i\right)\left(\omega \right)=\sum _{l=-t}^t{\alpha }_l^{\left(i\right)}{e}^{\text{i}l\omega }.$$

Let us identify $g_i{g}_j^{-1}$ with ${\theta }_{ij}\in \left[\mathrm{0,2}\pi \right]$. Then, we can express $f_{ij}$ in terms of ${\alpha }_l^{\left(i\right)},{\alpha }_l^{\left(j\right)}$ and ${\theta }_{ij}$:

$$\begin{gathered} f_{ij}\left(g_i{g}_j^{-1}\right)={\Vert 𝒬\left(y_i\right)-g_i{g}_j^{-1}\circ 𝒬\left(y_j\right)\Vert }_2^2 \\ =\underset{S^1}{\int }{\left|\sum _{l=-t}^t\left({\alpha }_l^{\left(i\right)}-{\alpha }_l^{\left(j\right)}{e}^{\text{i}l{\theta }_{ij}}\right)e^{\text{i}l\omega }\right|}^{2}d\omega \\ =\sum _{l=-t}^t{\left|{\alpha }_l^{\left(i\right)}-{\alpha }_l^{\left(j\right)}{e}^{\text{i}l{\theta }_{ij}}\right|}^2. \end{gathered}$$

The Fourier coefficients of $f_{ij}$ are

$$\begin{gathered} {\widehat{f}}_{ij}\left(k\right)={\int }_0^{2\pi }\sum _{l=-t}^t{\left|{\alpha }_l^{\left(i\right)}-{\alpha }_l^{\left(j\right)}{e}^{\text{i}l{\theta }_{ij}}\right|}^2{e}^{-\text{i}k{\theta }_{ij}}d{\theta }_{ij} \\ ={\int }_0^{2\pi }\sum _{l=-t}^t({\left|{\alpha }_l^{\left(i\right)}\right|}^2{e}^{-\text{i}k{\theta }_{ij}}+{\left|{\alpha }_l^{\left(j\right)}\right|}^2{e}^{-\text{i}k{\theta }_{ij}} \\ -{\alpha }_l^{\left(i\right)}\overline{{\alpha }_l^{\left(j\right)}}{e}^{\text{i}\left(-k-l\right){\theta }_{ij}}-\overline{{\alpha }_l^{\left(i\right)}}{\alpha }_l^{\left(j\right)}{e}^{\text{i}\left(-k+l\right){\theta }_{ij}})d{\theta }_{ij} \\ =2\pi \{\begin{array}{ll}{\sum }_{l=-t}^t\left({\left|{\alpha }_l^{\left(i\right)}\right|}^2+{\left|{\alpha }_l^{\left(j\right)}\right|}^2\right)-{\alpha }_0^{\left(i\right)}\overline{{\alpha }_0^{\left(j\right)}}-\overline{{\alpha }_0^{\left(i\right)}}{\alpha }_0^{\left(j\right)}\hfill & ,k=0\hfill \\ -{\alpha }_{-k}^{\left(i\right)}\overline{{\alpha }_{-k}^{\left(j\right)}}-\overline{{\alpha }_k^{\left(i\right)}}{\alpha }_k^{\left(j\right)}\hfill & ,k\ne 0\hfill \end{array} \end{gathered}$$

Note that we re-indexed the coefficients ${\hat{f}}_{ij}\left(k\right)\leftarrow {\hat{f}}_{ij}(k-(t+1\left)\right)$.

5.1.1. Rounding.

(4.1) gives us the $X^{\left(k\right)}$’s. From the $X^{\left(k\right)}$’s, we want to extract each ${\theta }_i\in \left[\mathrm{0,2}\pi \right]$ (up to a global transformation). Let us consider $X^{\left(1\right)}$. We want $X^{\left(1\right)}$ to be of the form

$$\left[\begin{array}{c}{e}^{\mathrm{i}{\theta }_1}\\ e^{\mathrm{i}{\theta }_2}\\ ⋮\\ e^{\mathrm{i}{\theta }_n}\end{array}\right]{\left[\begin{array}{c}{e}^{\mathrm{i}{\theta }_1}\\ e^{\mathrm{i}{\theta }_2}\\ ⋮\\ e^{\mathrm{i}{\theta }_n}\end{array}\right]}^{\mathrm{*}}.$$

Although $X^{\left(1\right)}$ is not guaranteed to be rank 1, we will simply take the top eigenvector of $X^{\left(1\right)}$ as our estimate of $e^{\mathrm{i}{\theta }_1},\dots ,e^{\mathrm{i}{\theta }_n}$. And from $e^{\mathrm{i}{\theta }_1},\dots ,e^{\mathrm{i}{\theta }_n}$, we can recover ${\theta }_1,\dots ,{\theta }_n$. See [40] for the reasoning behind this approach. In practice, we find using the top eigenvector of $X^{\left(1\right)}$ is a sufficient estimate of ${\theta }_1,\dots ,{\theta }_n$. We do not need to run additional comparisons against $X^{\left(2\right)},\dots ,X^{\left(t\right)}$.

5.2. Registration in 2-dimension.

Recall that $𝒳$ is the space of bandlimited functions up to degree $t$ on $S^2$. That is, for $x\in 𝒳$, we can express

$$x\left(\omega \right)=\sum _{l=0}^t\sum _{m=-l}^l{\alpha }_{l,m}{Y}_{l,m}\left(\omega \right),$$

where $\left\{Y_{lm}\right\}$ are the spherical harmonics. Again, the irreducible representations of $SO\left(3\right)$ are the Wigner D-matrices $\left\{W^{\left(k\right)}(\alpha ,\beta ,\gamma )\right\}$, and $d_k=2k+1$. Let us associate $g\in SO\left(3\right)$ with Euler (Z-Y-Z) angle $(\alpha ,\beta ,\gamma )\in \left[\mathrm{0,2}\pi \right]\times [0,\pi ]\times \left[\mathrm{0,2}\pi \right]$, then

$$g\cdot x\left(\omega \right)=\sum _{l=0}^t\sum _{m,m^{\prime }=-l}^l{W}_{m,m^{\prime }}^{\left(l\right)}\left(\alpha ,\beta ,\gamma \right){\alpha }_{l,m^{\prime }}{Y}_{l,m}\left(\omega \right).$$

Let $𝒫$ sample the underlying signal $x$ at $L=(t+1{)}^2$ points. This way, we can determine all the ${\alpha }_{lm}$’s associated with $x$.

Again, for the adjoint $𝒬$ we have

$$𝒬\left(y_i\right)\left(\omega \right)=\sum _{l=0}^t\sum _{m=-l}^l{\alpha }_{l,m}^{\left(i\right)}{Y}_{l,m}\left(\omega \right).$$

Let us identify $g_i{g}_j^{-1}\in SO\left(3\right)$ with Euler (Z-Y-Z) angle $\left({\alpha }_{ij},{\beta }_{ij},{\gamma }_{ij}\right)\in \left[\mathrm{0,2}\pi \right]\times [0,\pi ]\times \left[\mathrm{0,2}\pi \right]$. Then, we can express $f_{ij}$ in terms of ${\alpha }_{l,m}^{\left(i\right)},{\alpha }_{l,m}^{\left(j\right)}$ and $\left({\alpha }_{ij},{\beta }_{ij},{\gamma }_{ij}\right)$:

$$\begin{gathered} f_{ij}\left(g_i{g}_j^{-1}\right)=\parallel 𝒬\left(y_i\right)-g_i{g}_j^{-1}\circ 𝒬\left(y_j\right){\parallel }_2^2 \\ =\sum _{l=0}^t\sum _{m=-l}^l\left({\left|{\alpha }_{l,m}^{\left(i\right)}\right|}^2+{\left|{\alpha }_{l,m}^{\left(j\right)}\right|}^2\right) \\ -\sum _{l=0}^t\sum _{m,m^{\prime }=-l}^l{\alpha }_{l,m}^{\left(i\right)}\overline{W_{m,m^{\prime }}^{\left(l\right)}}\left({\alpha }_{ij},{\beta }_{ij},{\gamma }_{ij}\right)\overline{{\alpha }_{l,m^{\prime }}^{\left(j\right)}} \\ -\sum _{l=0}^t\sum _{m,m^{\prime }=-l}^l\overline{{\alpha }_{l,m}^{\left(i\right)}}{W}_{m,m^{\prime }}^{\left(l\right)}\left({\alpha }_{ij},{\beta }_{ij},{\gamma }_{ij}\right){\alpha }_{l,m^{\prime }}^{\left(j\right)}. \end{gathered}$$

The Fourier coefficients are given by

$${\widehat{f}}_{ij}\left(k\right)={\int }_{SO\left(3\right)}{f}_{ij}\left(g\right){\left(W^{\left(k\right)}\left(\alpha ,\beta ,\gamma \right)\right)}^{\text{*}}dg=\frac{8{\pi }^2}{2k+1}\{\begin{array}{ll}{\sum }_{l=0}^t{\sum }_{m=-l}^l\left({\left|{\alpha }_{lm}^{\left(i\right)}\right|}^2+{\left|{\alpha }_{lm}^{\left(j\right)}\right|}^2\right)-{\alpha }_{00}^{\left(i\right)}\overline{{\alpha }_{00}^{\left(j\right)}}-\overline{{\alpha }_{00}^{\left(i\right)}}{\alpha }_{00}^{\left(j\right)}\hfill & ,k=0\hfill \\ {\left(-{(-1)}^{m-m^{\prime }}{\alpha }_{k,-m^{\prime }}^{\left(i\right)}\overline{{\alpha }_{k,-m}^{\left(j\right)}}-\overline{{\alpha }_{k,m^{\prime }}^{\left(i\right)}}{\alpha }_{k,m}^{\left(j\right)}\right)}_{m,m^{\prime }=-k}^k\hfill & ,k\ne 0\hfill \end{array}$$

Here, we used the orthogonality relationship

$${\int }_{SO\left(3\right)}\stackrel{-}{W_{m_1,m_2}^{\left(k\right)}}\left(\alpha ,\beta ,\gamma \right)W_{m_1^{\prime },m_2^{\prime }}^{\left(k^{\prime }\right)}\left(\alpha ,\beta ,\gamma \right)dg=\frac{8{\pi }^2}{2k+1}{\delta }_{k,k^{\prime }}{\delta }_{m_1,m_1^{\prime }}{\delta }_{m_2,m_2^{\prime }},$$

and the property

$$W_{m,m^{\prime }}^{\left(k\right)}(\alpha ,\beta ,\gamma )=(-1{)}^{m-m^{\prime }}\stackrel{-}{W_{-m,-m^{\prime }}^{\left(k\right)}}\left(\alpha ,\beta ,\gamma \right).$$

5.2.1. Rounding.

Again, (4.4) gives us the $X^{\left(k\right)}$’s. From the $X^{\left(k\right)}$’s, we want to extract each $(\alpha ,\beta ,\gamma )\in \left[\mathrm{0,2}\pi \right]\times [0,\pi ]\times \left[\mathrm{0,2}\pi \right]$ (up to a global transformation). Let us consider $X^{\left(1\right)}$. We want $X^{\left(1\right)}$ to be of the form

$$\left[\begin{array}{c}{W}^{\left(1\right)}\left({\alpha }_1,{\beta }_1,{\gamma }_1\right)\\ W^{\left(1\right)}\left({\alpha }_2,{\beta }_2,{\gamma }_2\right)\\ ⋮\\ W^{\left(1\right)}\left({\alpha }_n,{\beta }_n,{\gamma }_n\right)\end{array}\right]{\left[\begin{array}{c}{W}^{\left(1\right)}\left({\alpha }_1,{\beta }_1,{\gamma }_1\right)\\ W^{\left(1\right)}\left({\alpha }_2,{\beta }_2,{\gamma }_2\right)\\ ⋮\\ W^{\left(1\right)}\left({\alpha }_n,{\beta }_n,{\gamma }_n\right)\end{array}\right]}^{\mathrm{*}},$$

where each $W^{\left(1\right)}\left({\alpha }_i,{\beta }_i,{\gamma }_i\right)$ is a 3 × 3 matrix. Similarly, $X^{\left(1\right)}$ is not guaranteed to be rank 3, but we will simply take the top 3 eigenvector of $X^{\left(1\right)}$ as our estimate of $W^{\left(1\right)}\left({\alpha }_1,{\beta }_1,{\gamma }_1\right),\dots ,W^{\left(1\right)}\left({\alpha }_n,{\beta }_n,{\gamma }_n\right)$. And from $W^{\left(1\right)}\left({\alpha }_1,{\beta }_1,{\gamma }_1\right),\dots ,W^{\left(1\right)}\left({\alpha }_n,{\beta }_n,{\gamma }_n\right)$, we can recover $\left({\alpha }_1,{\beta }_1,{\gamma }_1\right),\dots ,\left({\alpha }_n,{\beta }_n,{\gamma }_n\right)$.

5.3. Orientation estimation in cryo-EM.

We refer to [50] to expand the objective function. We emphasize that the theory holds for arbitrary basis on the space containing the ${\hat{I}}_i$’s. We choose to construct the $C^{\left(k\right)}$’s using coefficients and parameters from the Fourier-Bessel expansion. Projection ${\hat{I}}_i$ can be expanded via Fourier-Bessel series as

$${\widehat{I}}_i\left(r,\theta \right)=\sum _{k=-\infty }^{\infty }\sum _{q=1}^{\infty }{\alpha }_{kq}^{\left(i\right)}{\psi }_{kq}^{\left(c\right)}\left(r,\theta \right),$$

where

$${\psi }_{kq}^{\left(c\right)}(r,\theta )=\left\{\begin{array}{ll}{N}_{kq}{J}_k\left(R_{kq}\frac{r}{c}\right)e^{ik\theta }& ,r\le c,\\ 0& ,r>c.\end{array}\right.$$

The parameters above are defined as follows:

• $c$ is the radius of the disc containing the support of ${\hat{I}}_i$,

• $J_k$ is the Bessel function of integer order $k$,

• $R_{kq}$ is the $q^{\text{th}}$ root of $J_k$,

• $N_{kq}=\frac{1}{c\sqrt{\pi }\left|J_{k+1}\left(R_{kq}\right)\right|}$ is a normalization factor.

To avoid aliasing, we truncate the Fourier-Bessel expansion as follows.

$${\widehat{I}}_i\left(r,\theta \right)\approx \sum _{k=-k_{\text{max}}}^{k_{\text{max}}}\sum _{q=1}^{p_k}{\alpha }_{kq}^{\left(i\right)}{\psi }_{kq}^{\left(c\right)}\left(r,\theta \right).$$

See [50] for a discussion on $k_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and $p_k$. For the purpose of this section, let us assume we have $\left\{{\alpha }_{kq}^{\left(i\right)}:-k_{\mathrm{m}\mathrm{a}\mathrm{x}}\le k\le k_{\mathrm{m}\mathrm{a}\mathrm{x}},1\le q\le p_k\right\}$ for each ${\hat{I}}_i$. (These can be computed from the Cartesian grid sampled images.)

We shall determine the relationship between ${\hat{I}}_i\left(r,{\theta }_i\right)$ and ${\hat{I}}_j\left(r,{\theta }_j\right)$, and the lines of intersection between $g_i^{-1}\cdot {\hat{I}}_i$ and $g_j^{-1}\cdot {\hat{I}}_j$ embedded in ${\mathbb{R}}^3$. Recall from (2.9) and (2.10) that the directions of the lines of intersection between $g_i^{-1}\cdot {\hat{I}}_i$ and $g_j^{-1}\cdot {\hat{I}}_j$ are given, respectively, by unit vectors

$$c_{ij}\left(g_i{g}_j^{-1}\right)=\frac{{\overrightarrow{e}}_3\times g_i{g}_j^{-1}\cdot {\overrightarrow{e}}_3}{\parallel {\overrightarrow{e}}_3\times g_i{g}_j^{-1}\cdot {\overrightarrow{e}}_3{\parallel }_2},$$

$$c_{ji}\left(g_i{g}_j^{-1}\right)=\frac{{\left(g_i{g}_j^{-1}\right)}^{-1}\cdot {\overrightarrow{e}}_3\times {\overrightarrow{e}}_3}{\parallel {\left(g_i{g}_j^{-1}\right)}^{-1}\cdot {\overrightarrow{e}}_3\times {\overrightarrow{e}}_3{\parallel }_2}.$$

Let us associate $g_i{g}_j^{-1}\in SO\left(3\right)$ with Euler (Z-Y-Z) angle $\left({\alpha }_{ij},{\beta }_{ij},{\gamma }_{ij}\right)\in \left[\mathrm{0,2}\pi \right]\times [0,\pi ]\times \left[\mathrm{0,2}\pi \right]$. Then

$${\overrightarrow{e}}_3\times g_i{g}_j^{-1}\cdot {\overrightarrow{e}}_3=\left[\begin{array}{c}\text{sin}{\gamma }_{ij}\text{sin}{\beta }_{ij}\\ -\text{cos}{\gamma }_{ij}\text{sin}{\beta }_{ij}\\ 0\end{array}\right],$$

$${\left(g_i{g}_j^{-1}\right)}^{-1}\cdot {\overrightarrow{e}}_3\times {\overrightarrow{e}}_3=\left[\begin{array}{c}-\text{sin}{\alpha }_{ij}\text{sin}{\beta }_{ij}\\ -\text{cos}{\alpha }_{ij}\text{sin}{\beta }_{ij}\\ 0\end{array}\right],$$

under the rotation matrix $R_Z\left({\gamma }_{ij}\right)R_Y\left({\beta }_{ij}\right)R_Z\left({\alpha }_{ij}\right)$. The directions of the lines of intersection in ${\hat{I}}_i$ and ${\hat{I}}_j$ under $g_i{g}_j^{-1}$ are in the directions, respectively,

$${\theta }_i=\text{arctan}\left(\text{sin}{\gamma }_{ij},-\text{cos}{\gamma }_{ij}\right)={\gamma }_{ij}-\frac{\pi }{2},$$

$$\begin{array}{rr}& {\theta }_j=\text{arctan}\left(-\text{sin}{\alpha }_{ij},-\text{cos}{\alpha }_{ij}\right)=-{\alpha }_{ij}-\frac{\pi }{2}.\end{array}$$

We express the $f_{ij}$’s in terms of ${\alpha }_{kq}^{\left(i\right)},{\alpha }_{kq}^{\left(j\right)}$, and ${\theta }_i$ and ${\theta }_j$:

$$\begin{gathered} f_{ij}\left({\theta }_i,{\theta }_j\right)≔f_{ij}\left(g_i{g}_j^{-1}\right) \\ =\parallel \sum _{k=-k_{\text{max}}}^{k_{\text{max}}}\sum _{q=1}^{p_k}\left({\alpha }_{kq}^{\left(i\right)}{\psi }_{kq}^{\left(c\right)}\left(r,{\theta }_i\right)-{\alpha }_{kq}^{\left(j\right)}{\psi }_{kq}^{\left(c\right)}\left(r,{\theta }_j\right)\right){\parallel }_{L^2}^2 \\ =\sum _{k,k^{\prime },q,q^{\prime }}c{N}_{kq}{N}_{k^{\prime }{q}^{\prime }}\left({\alpha }_{kq}^{\left(i\right)}{e}^{\text{i}k{\theta }_i}-{\alpha }_{kq}^{\left(j\right)}{e}^{\text{i}k{\theta }_j}\right){\left({\alpha }_{k^{\prime }{q}^{\prime }}^{\left(i\right)}{e}^{\text{i}{k}^{\prime }{\theta }_i}-{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(j\right)}{e}^{\text{i}{k}^{\prime }{\theta }_j}\right)}^{\text{*}} \\ \cdot {\int }_0^1{J}_k\left(R_{kq}r\right)J_{k^{\prime }}\left(R_{k^{\prime }{q}^{\prime }}r\right)dr. \end{gathered}$$

For each $k,k^{\prime },q,q^{\prime }$, we approximate the integral

$${\int }_0^1{J}_k\left(R_{kq}r\right)J_{k^{\prime }}\left(R_{k^{\prime }{q}^{\prime }}r\right)dr$$

with a Gaussian quadrature.

Using the approximation above, we have

$$\begin{gathered} f_{ij}\left({\theta }_i,{\theta }_j\right)\approx \sum _{k,q,k^{\prime },q^{\prime }}{b}_{k,q,k^{\prime },q^{\prime }}({\alpha }_{kq}^{\left(i\right)}\overline{{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(i\right)}}{e}^{\text{i}\left(k-k^{\prime }\right){\theta }_i}+{\alpha }_{kq}^{\left(j\right)}\overline{{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(j\right)}}{e}^{\text{i}\left(k-k^{\prime }\right){\theta }_j} \\ -{\alpha }_{kq}^{\left(i\right)}\overline{{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(j\right)}}{e}^{\text{i}\left(k{\theta }_i-k^{\prime }{\theta }_j\right)}-{\alpha }_{kq}^{\left(j\right)}\overline{{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(i\right)}}{e}^{\text{i}\left(k{\theta }_j-k^{\prime }{\theta }_i\right)}), \end{gathered}$$

where

$$b_{k,q,k^{\prime },q^{\prime }}=c{N}_{kq}{N}_{k^{\prime }{q}^{\prime }}\sum _i{w}_i{J}_k\left(R_{kq}{r}_i\right)J_{k^{\prime }}\left(R_{k^{\prime }{q}^{\prime }}{r}_i\right).$$

In terms of the Euler (Z-Y-Z) angles,

$$\begin{gathered} f_{ij}\left({\alpha }_{ij},{\gamma }_{ij}\right)≔f_{ij}\left({\theta }_i,{\theta }_j\right) \\ \approx \sum _{k,q,k^{\prime },q^{\prime }}{b}_{k,q,k^{\prime },q^{\prime }}{e}^{-\text{i}\frac{\pi }{2}\left(k-k^{\prime }\right)}({\alpha }_{kq}^{\left(i\right)}\overline{{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(i\right)}}{e}^{\text{i}\left(k-k^{\prime }\right){\gamma }_{ij}}+{\alpha }_{kq}^{\left(j\right)}\overline{{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(j\right)}}{e}^{-\text{i}\left(k-k^{\prime }\right){\alpha }_{ij}} \\ -{\alpha }_{kq}^{\left(i\right)}\overline{{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(j\right)}}{e}^{\text{i}k{\gamma }_{ij}+\text{i}{k}^{\prime }{\alpha }_{ij}}-{\alpha }_{kq}^{\left(j\right)}\overline{{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(i\right)}}{e}^{-\text{i}k{\alpha }_{ij}-\text{i}{k}^{\prime }{\gamma }_{ij}}). \end{gathered}$$

The Fourier coefficients are given by

$$\begin{gathered} {\widehat{f}}_{ij}\left(k\right)={\int }_{SO\left(3\right)}{f}_{ij}\left(\alpha ,\gamma \right){\left(W^{\left(k\right)}\left(\alpha ,\beta ,\gamma \right)\right)}^{\text{*}}dg \\ ={\int }_0^{2\pi }{\int }_0^{2\pi }{f}_{ij}\left(\alpha ,\gamma \right)\left({\int }_0^{\pi }{W}^{\left(k\right)}\left(-\gamma +\pi ,\beta ,-\alpha +\pi \right)\text{sin}\beta d\beta \right)d\alpha d\gamma . \end{gathered}$$

Note that

$${\left({\int }_0^{\pi }{W}^{\left(k\right)}(\alpha ,\beta ,\gamma )\mathrm{s}\mathrm{i}\mathrm{n}\beta d\beta \right)}_{m,m^{\prime }}={\int }_0^{\pi }{e}^{\text{i}m\alpha }{w}_{m,m^{\prime }}^{\left(k\right)}\left(\beta \right)e^{\text{i}{m}^{\prime }\gamma }\mathrm{s}\mathrm{i}\mathrm{n}\beta d\beta ,$$

where $w^{\left(k\right)}$ is the Wigner $d$-matrix. Let us define

$$\begin{gathered} H_k\left(m,m^{\prime }\right)≔(-1{)}^{m+m^{\prime }}{\int }_0^{\pi }{w}_{m,m^{\prime }}^{\left(k\right)}(\beta )\mathrm{s}\mathrm{i}\mathrm{n}\beta d\beta \\ =(-1{)}^{m+m^{\prime }}{\int }_0^{\pi }{\mathrm{i}}^{m-m^{\prime }}\sum _{l=-k}^k{w}_{l,m}^{\left(k\right)}(\pi /2)e^{-\text{i}l\beta }{w}_{l,m^{\prime }}^{\left(k\right)}(\pi /2)\mathrm{s}\mathrm{i}\mathrm{n}\beta d\beta \\ =(-1{)}^{m+m^{\prime }}{\mathrm{i}}^{m-m^{\prime }}\left[2w_{0,m}^{\left(k\right)}(\pi /2)w_{0,m^{\prime }}^{\left(k\right)}(\pi /2)\right. \\ -\frac{\text{i}\pi }{2}{w}_{1,m}^{\left(k\right)}(\pi /2\left)w_{1,m^{\prime }}^{\left(k\right)}\right(\pi /2)+\frac{\text{i}\pi }{2}{w}_{-1,m}^{\left(k\right)}(\pi /2\left)w_{-1,m^{\prime }}^{\left(k\right)}\right(\pi /2) \\ \left.+\sum _{\left|l\right|\ge 2}^k\left(\frac{1+e^{-\text{i}l\pi }}{1-l^2}\right)w_{l,m}^{\left(k\right)}(\pi /2)w_{l,m^{\prime }}^{\left(k\right)}(\pi /2)\right]. \end{gathered}$$

The ${\left(m,m^{\prime }\right)}^{th}$ entry of ${\hat{f}}_{ij}\left(k\right)$ is approximated by

$$\begin{gathered} {\left({\widehat{f}}_{ij}\left(k\right)\right)}_{m,m^{\prime }}=H_k\left(m,m^{\prime }\right){\int }_0^{2\pi }{\int }_0^{2\pi }{f}_{ij}\left(\alpha ,\gamma \right)e^{-\text{i}m\gamma }{e}^{-\text{i}{m}^{\prime }\alpha }d\alpha d\gamma \\ =4{\pi }^2{H}_k\left(m,m^{\prime }\right)\sum _{k,q,k^{\prime },q^{\prime }}{b}_{k,q,k^{\prime },q^{\prime }}({\alpha }_{kq}^{\left(i\right)}\overline{{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(i\right)}}{\delta }_{\left\{m=k-k^{\prime }\right\}}{\delta }_{\left\{m^{\prime }=0\right\}} \\ +{\alpha }_{kq}^{\left(j\right)}\overline{{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(j\right)}}{\delta }_{\left\{m=0\right\}}{\delta }_{\left\{m^{\prime }=k^{\prime }-k\right\}}-{\alpha }_{kq}^{\left(i\right)}\overline{{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(j\right)}}{\delta }_{\left\{m=k\right\}}{\delta }_{\left\{m^{\prime }=k^{\prime }\right\}} \\ -{\alpha }_{kq}^{\left(j\right)}\overline{{\alpha }_{k^{\prime }{q}^{\prime }}^{\left(i\right)}}{\delta }_{\left\{m=-k^{\prime }\right\}}{\delta }_{\left\{m^{\prime }=-k\right\}}). \end{gathered}$$

Here, $\delta$ is the Kronecker delta and $b_{k,q,k^{\prime },q^{\prime }}$ absorbed $e^{-\mathrm{i}\frac{\pi }{2}\left(k-k^{\prime }\right)}$.

5.3.1. Handedness ambiguity in cryo-EM.

There exists one additional issue specifically for the cryo-EM problem arising from the handedness ambiguity. Suppose an image was projected from some molecular density $\varphi$ and orientation $R$. Let $J$ be the reflection operator across the imaging plane. The molecular density $J\varphi$ under orientation $JR{J}^{\mathrm{*}}$ would produce the same projection. In other words, the set of projection images can belong to different molecular densities $\varphi$ and $J\varphi$ under different rotations.

We will formalize and deal with the handedness ambiguity in terms of the Wigner D-matrices. Recall that the Wigner D-matrix $W^{\left(k\right)}\left(g\right)$ corresponding to $(\alpha ,\beta ,\gamma )\in SO\left(3\right)$ is

$$W^{\left(k\right)}\left(g\right)={\left[e^{\text{i}m\alpha }{w}_{m,m^{\prime }}^{\left(k\right)}\left(\beta \right)e^{\text{i}m\gamma }\right]}_{m,m^{\prime }=-k}^k.$$

Let $J^{\left(k\right)}$ be the following $(2k+1)\times (2k+1)$ diagonal matrix:

$$J^{\left(k\right)}≔\left[\begin{array}{lllll}\ddots & & & & \\ & -1& & & \\ & & 1& & \\ & & & -1& \\ & & & & \ddots \end{array}\right].$$

(The diagonal alternates between +1 and −1.) Due to the handedness ambiguity, if ${\left\{W^{\left(k\right)}\left(g_i\right)W^{\left(k\right)}\left(g_j^{-1}\right)\right\}}_k$ is a solution to (4.4), then ${\left\{J^{\left(k\right)}{W}^{\left(k\right)}\left(g_i\right)W^{\left(k\right)}\left(g_j^{-1}\right)J^{\left(k\right)}\right\}}_k$ is also a valid solution to (4.4). In fact, for any $h\in \left[\mathrm{0,1}\right]$,

$${\left\{h{W}^{\left(k\right)}\left(g_i\right)W^{\left(k\right)}\left(g_j^{-1}\right)+(1-h)J^{\left(k\right)}{W}^{\left(k\right)}\left(g_i\right)W^{\left(k\right)}\left(g_j^{-1}\right)J^{\left(k\right)}\right\}}_k$$

is a valid solution to (4.4).

Let us remove this extra degree of freedom $h$. Observe that for $h=\frac{1}{2}$,

$$\frac{1}{2}{W}^{\left(k\right)}\left(g\right)+\frac{1}{2}{J}^{\left(k\right)}{W}^{\left(k\right)}\left(g\right)J^{\left(k\right)}=\left\{\begin{array}{ll}{e}^{\text{i}m\alpha }{w}_{m,m^{\prime }}^{\left(k\right)}\left(\beta \right)e^{\text{i}{m}^{\prime }\gamma },& m+m^{\prime }\equiv 0\mathrm{m}\mathrm{o}\mathrm{d}2,\\ 0,& \text{otherwise.}\end{array}\right.$$

I.e., the odd-indexed entries are 0. For example, in the case of $k=1$,

$$\frac{1}{2}{W}^{\left(1\right)}\left(g\right)+\frac{1}{2}{J}^{\left(1\right)}{W}^{\left(1\right)}\left(g\right)J^{\left(1\right)}=\left[\begin{array}{ccc}{e}^{-\text{i}\alpha }{w}_{-1,-1}^{\left(1\right)}\left(\beta \right)e^{-\text{i}\gamma }& 0& e^{-\text{i}\alpha }{w}_{-1,1}^{\left(1\right)}\left(\beta \right)e^{\text{i}\gamma }\\ 0& w_{0,0}^{\left(1\right)}\left(\beta \right)& 0\\ e^{\text{i}\alpha }{w}_{1,-1}^{\left(1\right)}\left(\beta \right)e^{-\text{i}\gamma }& 0& e^{\text{i}\alpha }{w}_{1,1}^{\left(1\right)}\left(\beta \right)e^{\text{i}\gamma }\end{array}\right],$$

and in the case of $k=2$,

$$\frac{1}{2}{W}^{\left(2\right)}\left(g\right)+\frac{1}{2}{J}^{\left(2\right)}{W}^{\left(2\right)}\left(g\right)J^{\left(2\right)}=\left[\begin{array}{ccccc}{e}^{-2\text{i}\alpha }{w}_{-2,-2}^{\left(2\right)}\left(\beta \right)e^{-2\text{i}\gamma }& 0& e^{-2\text{i}\alpha }{w}_{-\mathrm{2,0}}^{\left(2\right)}\left(\beta \right)& 0& e^{-2\text{i}\alpha }{w}_{-\mathrm{2,2}}^{\left(2\right)}\left(\beta \right)e^{2\text{i}\gamma }\\ 0& e^{-\text{i}\alpha }{w}_{-1,-1}^{\left(2\right)}\left(\beta \right)e^{-\text{i}\gamma }& 0& e^{-\text{i}\alpha }{w}_{-\mathrm{1,1}}^{\left(2\right)}\left(\beta \right)e^{\text{i}\gamma }& 0\\ w_{0,-2}^{\left(2\right)}\left(\beta \right)e^{-2\text{i}\gamma }& 0& w_{\mathrm{0,0}}^{\left(2\right)}\left(\beta \right)& 0& w_{\mathrm{0,2}}^{\left(2\right)}\left(\beta \right)e^{2\text{i}\gamma }\\ 0& e^{\text{i}\alpha }{w}_{1,-1}^{\left(2\right)}\left(\beta \right)e^{-\text{i}\gamma }& 0& e^{\text{i}\alpha }{w}_{\mathrm{1,1}}^{\left(2\right)}\left(\beta \right)e^{\text{i}\gamma }& 0\\ e^{2\text{i}\alpha }{w}_{2,-2}^{\left(2\right)}\left(\beta \right)e^{-2\text{i}\gamma }& 0& e^{2\text{i}\alpha }{w}_{\mathrm{2,0}}^{\left(2\right)}\left(\beta \right)& 0& e^{2\text{i}\alpha }{w}_{\mathrm{2,2}}^{\left(2\right)}\left(\beta \right)e^{2\text{i}\gamma }\end{array}\right].$$

We constrain the odd-indexed entries of $X_{ij}^{\left(k\right)}$’s to be 0 so that the SDP finds the solution with $h=\frac{1}{2}$. Note that, in practice, we do not explicitly add this constraint. Instead, we permute $X_{ij}^{\left(k\right)}$ into two disjoint diagonal blocks. For example, in the case of $k=1$,

$$\frac{1}{2}{W}^{\left(1\right)}\left(g\right)+\frac{1}{2}{J}^{\left(1\right)}{W}^{\left(1\right)}\left(g\right)J^{\left(1\right)}=\left[\begin{array}{cc}{w}_{0,0}^{\left(1\right)}\left(\beta \right)0& 0\\ 0& e^{-\text{i}\alpha }{w}_{-1,-1}^{\left(1\right)}\left(\beta \right)e^{-\text{i}\gamma }& e^{-\text{i}\alpha }{w}_{-1,1}^{\left(1\right)}\left(\beta \right)e^{\text{i}\gamma }\\ 0& e^{\text{i}\alpha }{w}_{1,-1}^{\left(1\right)}\left(\beta \right)e^{-\text{i}\gamma }& e^{\text{i}\alpha }{w}_{1,1}^{\left(1\right)}\left(\beta \right)e^{\text{i}\gamma }\end{array}\right],$$

and in the case of $k=2$,

$$\frac{1}{2}{W}^{\left(2\right)}\left(g\right)+\frac{1}{2}{J}^{\left(2\right)}{W}^{\left(2\right)}\left(g\right)J^{\left(2\right)}=\left[\begin{array}{cccc}{e}^{-\text{i}\alpha }{w}_{-1,-1}^{\left(2\right)}\left(\beta \right)e^{-\text{i}\gamma }{e}^{-\text{i}\alpha }{w}_{-1,1}^{\left(2\right)}\left(\beta \right)e^{\text{i}\gamma }& 0& 0& 0\\ e^{\text{i}\alpha }{w}_{1,-1}^{\left(2\right)}\left(\beta \right)e^{-\text{i}\gamma }& e^{\text{i}\alpha }{w}_{1,1}^{\left(2\right)}\left(\beta \right)e^{\text{i}\gamma }& 0& 0& 0\\ 0& 0& e^{-2\text{i}\alpha }{w}_{-2,-2}^{\left(2\right)}\left(\beta \right)e^{-2\text{i}\gamma }& e^{-2\text{i}\alpha }{w}_{-2,0}^{\left(2\right)}\left(\beta \right)& e^{-2\text{i}\alpha }{w}_{-2,2}^{\left(2\right)}\left(\beta \right)e^{2\text{i}\gamma }\\ 0& 0& w_{0,-2}^{\left(2\right)}\left(\beta \right)e^{-2\text{i}\gamma }& w_{0,0}^{\left(2\right)}\left(\beta \right)& w_{0,2}^{\left(2\right)}\left(\beta \right)e^{2\text{i}\gamma }\\ 0& 0& e^{2\text{i}\alpha }{w}_{2,-2}^{\left(2\right)}\left(\beta \right)e^{-2\text{i}\gamma }& e^{2\text{i}\alpha }{w}_{2,0}^{\left(2\right)}\left(\beta \right)& e^{2\text{i}\alpha }{w}_{2,2}^{\left(2\right)}\left(\beta \right)e^{2\text{i}\gamma }\end{array}\right].$$

We can conjugate each $X_{ij}^{\left(k\right)}$ in (4.4) by a permutation and get

$$X_{ij}^{\left(k\right)}=\left[\begin{array}{cc}{X}_{ij}^{(k,0)}& 0\\ 0& X_{ij}^{(k,1)}\end{array}\right].$$

Similarly, we can conjugate $X^{\left(k\right)}$ by a permutation and get

$$X^{\left(k\right)}=\left[\begin{array}{cc}{X}^{(k,0)}& 0\\ 0& X^{(k,1)}\end{array}\right],$$

where

$$X^{(k,0)}=\left[\begin{array}{ccc}{X}_{11}^{(k,0)}& \cdots & X_{1n}^{(k,0)}\\ ⋮& \ddots & ⋮\\ X_{n1}^{(k,0)}& \cdots & X_{nn}^{(k,0)}\end{array}\right],X^{(k,1)}=\left[\begin{array}{ccc}{X}_{11}^{(k,1)}& \cdots & X_{1n}^{(k,1)}\\ ⋮& \ddots & ⋮\\ X_{n1}^{(k,1)}& \cdots & X_{nn}^{(k,1)}\end{array}\right].$$

Let us denote the above permutation as ${\mathrm{\Pi }}_k$. The objective function in (4.4) is preserved if we conjugate both the $C^{\left(k\right)}$’s and the $X^{\left(k\right)}$’s by ${\mathrm{\Pi }}_k$. I.e.,

$$\text{tr}\left[C^{\left(k\right)}{X}^{\left(k\right)}\right]=\text{tr}\left[{\mathrm{\Pi }}_k{C}^{\left(k\right)}{\mathrm{\Pi }}_k^T{\mathrm{\Pi }}_k{X}^{\left(k\right)}{\mathrm{\Pi }}_k^T\right]=\text{tr}\left[C^{\left(k,0\right)}{X}^{\left(k,0\right)}\right]+\text{tr}\left[C^{\left(k,1\right)}{X}^{\left(k,1\right)}\right],$$

where $C^{(k,0)}$ and $C^{(k,1)}$ are blocks corresponding to $X^{(k,0)}$ and $X^{(k,1)}$, respectively. We apply the same permutation to the $X^{\left(k\right)}$’s in the constraints of (4.4) and reduce (4.4) to

$$\begin{array}{ll}\underset{X^{\left(k,0\right)},X^{\left(k,1\right)}}{\text{minimize}}\hfill & \sum _{k=0}^t\text{tr}\left[C^{\left(k,0\right)}{X}^{\left(k,0\right)}\right]+\text{tr}\left[C^{\left(k,1\right)}{X}^{\left(k,1\right)}\right]\hfill \\ \text{subject }\text{to}\hfill & X^{\left(k,0\right)}\underset{\_}{\succ }0,X^{\left(k,1\right)}\underset{\_}{\succ }0\hfill \\ \hfill & X_{ii}^{\left(k,0\right)}=I_{k\times k},X_{ii}^{\left(k,1\right)}=I_{\left(k+1\right)\times \left(k+1\right)}\hfill \\ \hfill & \sum _{k=0}^t\frac{{(3)}_{t-k}}{\left(t-k\right)!}\left(k+\frac{1}{2}\right)\left(\text{tr}\left[{\left(W^{\left(k,0\right)}\left(\alpha ,\beta ,\gamma \right)\right)}^{\text{*}}{X}_{ij}^{\left(k,0\right)}\right]\right.\hfill \\ \hfill & \left.+\text{tr}\left[{\left(W^{\left(k,1\right)}\left(\alpha ,\beta ,\gamma \right)\right)}^{\text{*}}{X}_{ij}^{\left(k,1\right)}\right]\right)\ge 0\forall \left(\alpha ,\beta ,\gamma \right)\in {\mathrm{\Omega }}_t\hfill \\ \hfill & X_{ij}^{\left(0,1\right)}=1\hfill \\ \hfill & Q_{ij}={𝒜}_{E_q}\left(X_{ij}^{\left(1,0\right)},X_{ij}^{\left(1,1\right)}\right),Q_{ij}\underset{\_}{\succ }0,\text{ tr}\left[Q_{ij}\right]=1,\hfill \end{array}$$ (5.1)

where ${𝒜}_{E_q}$ defines the linear relationship between $Q_{ij}$ and $\left(X^{\left(\mathrm{1,0}\right)},X^{\left(\mathrm{1,1}\right)}\right)$ as

$$\begin{array}{l}{Y}^{\left(ij\right)}={\left[\begin{array}{ccc}-\frac{\text{i}}{\sqrt{2}}& 0& \frac{1}{\sqrt{2}}\\ 0& 1& 0\\ -\frac{\text{i}}{\sqrt{2}}& 0& -\frac{1}{\sqrt{2}}\end{array}\right]}^{\text{*}}\left[\begin{array}{ccc}{X}_{ij}^{\left(1,1\right)}\left(1,1\right)& 0& X_{ij}^{\left(1,1\right)}\left(1,2\right)\\ 0& X_{ij}^{\left(1,0\right)}& 0\\ X_{ij}^{\left(1,1\right)}\left(2,1\right)& 0& X_{ij}^{\left(1,1\right)}\left(2,2\right)\end{array}\right]\left[\begin{array}{ccc}-\frac{\text{i}}{\sqrt{2}}& 0& \frac{1}{\sqrt{2}}\\ 0& 1& 0\\ -\frac{\text{i}}{\sqrt{2}}& 0& -\frac{1}{\sqrt{2}}\end{array}\right],\end{array}$$

$$\begin{array}{l}{Q}_{ij}=\frac{1}{4}\left[\begin{array}{cccc}1+Y_{11}^{\left(ij\right)}+Y_{22}^{\left(ij\right)}+Y_{33}^{\left(ij\right)}& 0& 0& -\left(Y_{31}^{\left(ij\right)}-Y_{13}^{\left(ij\right)}\right)\\ 0& 1-Y_{11}^{\left(ij\right)}-Y_{22}^{\left(ij\right)}+Y_{33}^{\left(ij\right)}& -\left(Y_{31}^{\left(ij\right)}+Y_{13}^{\left(ij\right)}\right)& 0\\ 0& -\left(Y_{31}^{\left(ij\right)}+Y_{13}^{\left(ij\right)}\right)& 1+Y_{11}^{\left(ij\right)}-Y_{22}^{\left(ij\right)}-Y_{33}^{\left(ij\right)}& 0\\ -\left(Y_{31}^{\left(ij\right)}-Y_{13}^{\left(ij\right)}\right)& 0& 0& 1-Y_{11}^{\left(ij\right)}+Y_{22}^{\left(ij\right)}-Y_{33}^{\left(ij\right)}\end{array}\right].\end{array}$$

5.3.2. Rounding.

(5.1) gives us the $X^{(k,0)}$’s and the $X^{(k,1)}$’s. We aggregate $X^{\left(\mathrm{1,0}\right)}$ and $X^{\left(\mathrm{1,1}\right)}$ into the $3n\times 3n$ matrix $X^{\left(1\right)}$. From the $X^{\left(1\right)}$’s, we build the synchronization matrix $S$ described in [39] and apply the cryo_syncrotations function on $S$ from the ASPIRE software package [5] to recover $\left({\alpha }_1,{\beta }_1,{\gamma }_1\right),\dots ,\left({\alpha }_n,{\beta }_n,{\gamma }_n\right)$. Note that we do not truncate the eigenvectors and eigenvalues from $X^{\left(1\right)}$.

6. Implementation and results for synthetic cryo-EM datasets

In this section, we give a brief history of methods used for determining orientations of cryo-EM projection images, and where we stand against the current state-of-the-art.

In 1986, Vainshtein and Goncharov developed a common-lines based method for ab-initio modeling in cryo-EM [45]. In 1987, M. Van Heel also independently discovered the same method, and coined it angular reconstitution [22]. Recall that by the Fourier slice theorem, two cryo-EM projection images (in Fourier space) must intersect along a common line. Given three cryo-EM images from different viewing directions, their common lines must uniquely determine their relative orientations up to handedness. (See Figure 6.1.) The orientations of the rest of the images are determined by common lines with the first three images. This is angular reconstitution in a nutshell.

Figure 6.1.

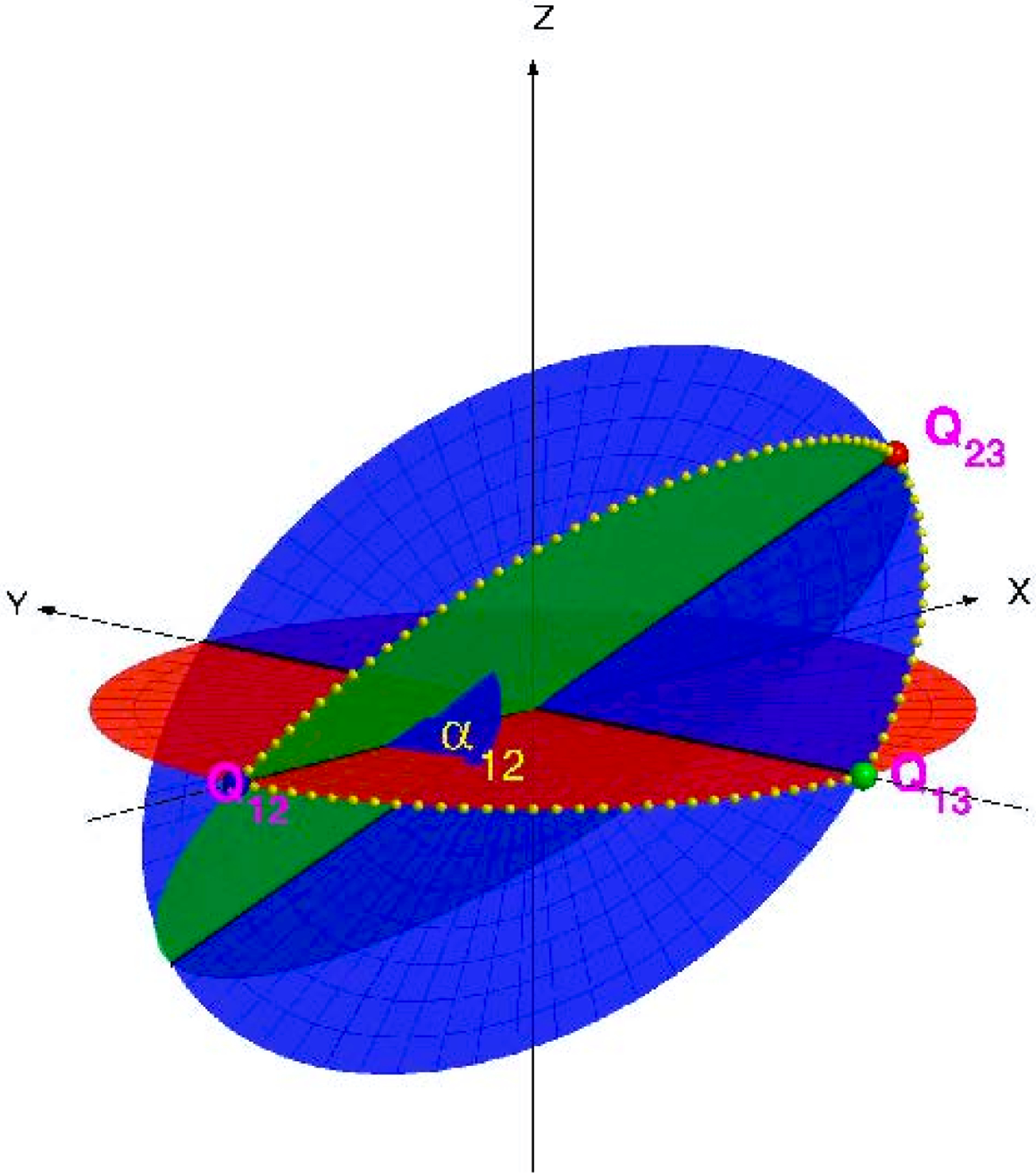
Three cryo-EM images uniquely determine their orientations up to handedness. Image courtesy of Singer et al. [41].

In 1992, Farrow and Ottensmeyer expanded upon angular reconstitution by developing a method to sequentially add images via least squares [20]. One major drawback in sequentially assigning orientations of cryo-EM images is the propagation of error due to false common line detection. In 1996, Penczek, Zhu, and Frank tried to circumvent the issue via brute-force search for a global energy minimizer [35]. However, the search space is simply too big for that method to be applicable. In 2006, Mallick et al. introduced a Bayesian method in which common lines between pairs of images are determined by their common lines with different projection triplets [29]. In the method by Mallick et al., at least seven common lines must be correctly and simultaneously determined, which can be problematic. In 2010, Singer et al. lowered the requirement to that only two common lines need to be correctly and simultaneously determined [41]. In 2011, Singer and Shkolnisky built upon [41] by adding a global consistency condition among the orientations [39]. This method is called synchronization, and it is regarded as the current state-of-the-art.

Note that all avaible methods for orientation determination, including the NUG approach proposed in this paper, cannot be directly applied to raw experimental images. We will explain the factors preventing us from doing so in the next subsection. We therefore numerically validate and evaluate the method using synthetic data.

6.1. Shifts, CTF and contrast.

In comparison to the simplistic forward model (2.8), there are three major imperfections in the experimental cryo-EM datasets. First, the images are not centered, and the common lines will not correspond exactly even under their true orientations. Second, the images are subject to the contrast transfer function (CTF) of the electron microscope. A CTF, as a function of radial frequency, is shown in Figure 6.2. Making matters mathematically more challenging, a CTF is typically estimated per micrograph and each micrograph would have a different CTF. Thus, all images from the same micrograph are typically assigned the same CTF. We also say those images belong to the same defocus group. However, as shown in Table 2 of Section 6.4, shifts and CTFs are not detrimental to NUG’s performance. This brings us to the third obstacle, which does prevent us from directly applying NUG on raw experimental images. The ice layer in which the molecules are frozen is not uniform. It can be thicker/thinner where different projections are taken, and this effect is equivalent to scaling the projections by a factor $\gamma >0$. So, various projections have various contrasts. Those effects are typically mitigated in class averages. Class averages are formed by in-plane aligning and averaging raw images that are estimated to have similar viewing directions. It is possible to apply NUG on class averages instead of the original raw experimental images. However, the quality of the results then depends crucially on the specific class averaging procedure being used and does not provide much insight into the performance of NUG itself.

Figure 6.2.

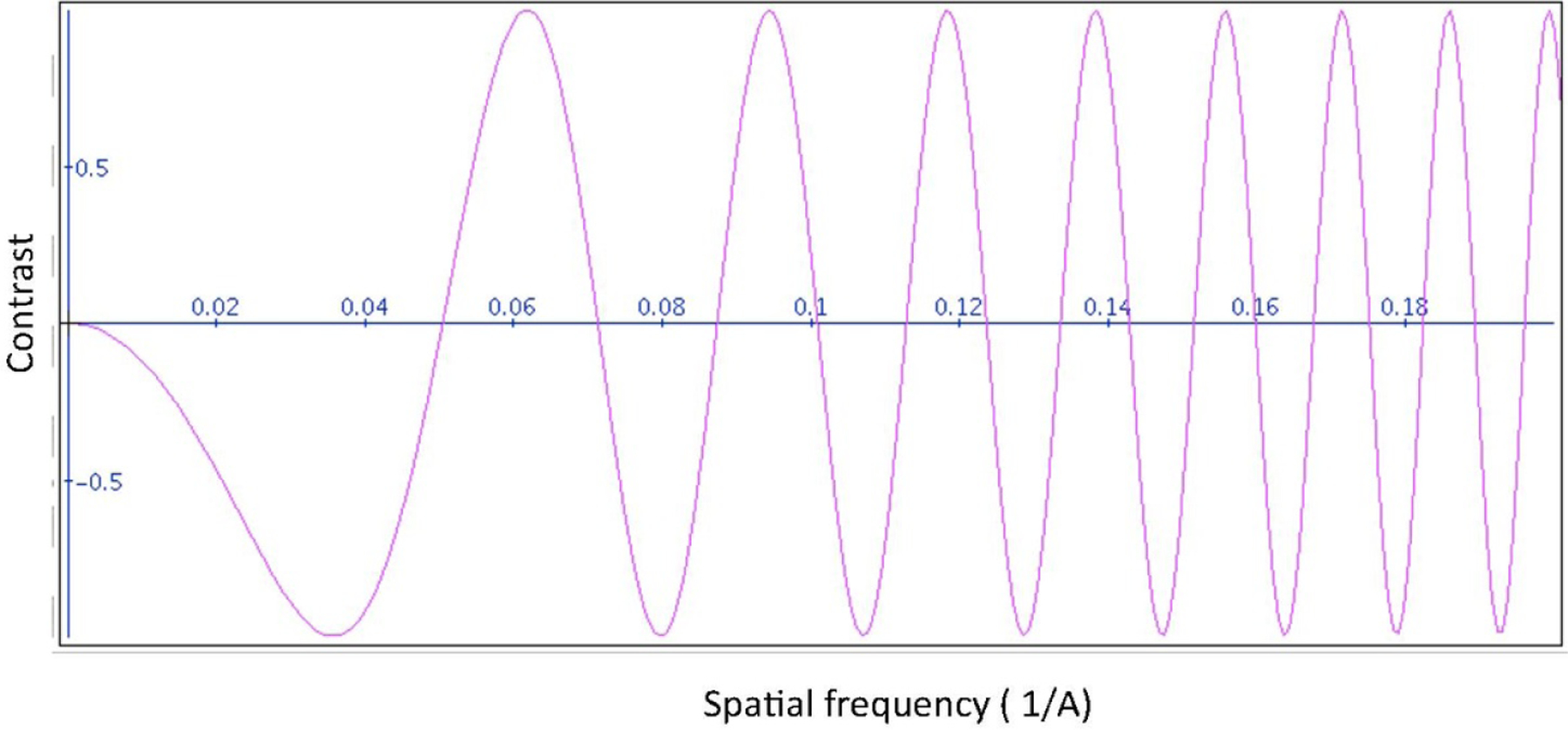
Example created by Jiang and Chiu available at http://jiang.bio.purdue.edu/software/ctf/ctfapplet.html

Table 2.

Effects of shifts, CTFs and contrast on the MSE (defined in (6.8)) of the NUG SDP cryo-EM. Shifts are sampled from $𝒰(-\mathrm{5,5})$, CTFs are drawn uniformly from 4 defocus groups and contrasts are sampled from $𝒰\left(\mathrm{0.5,1.5}\right)$. We used 500 simulated projections of size 64 × 64.

SNR	benchmark	CTF	CTF and shifts	CTF and contrast
1/4	0.0285	0.0381	0.3382	0.7342
1/8	0.0333	0.1450	0.5741	> 2.0
1/16	0.0698	0.7631	1.3391	> 2.0
1/32	0.4387	1.9199	> 2.0	> 2.0
1/64	1.8587	> 2.0	> 2.0	> 2.0

6.2. ADMM implementation.

There are two parts that are particularly challenging for obtaining a numerical solution to the NUG SDP (4.4) and (5.1):

• implementing a SDP solver that is scalable to real-world problems such as orientation estimation in cryo-EM,

• computing the coefficient matrix for generic objective function $f_{ij}$’s.

For the cryo-EM problem, the NUG SDP is simply too big to iterate on solvers based on techniques like interior point methods. Interior point methods are known for their accuracy. However, their accuracy is achieved at the expense of computational complexity. In essence, interior point methods solve a system of linear equations that attempts to satisfy both primal and dual feasibilities [14]. That is, solvers based on interior point methods have to invert a matrix that contains both primal and dual variables. The number and size of the signals coupled with the number of inequality constraints in (4.4) and (5.1) make this inversion impractical. Instead, we use the alternating direction method of multipliers, or ADMM. As the name suggests, ADMM alternates between the primal and the different sets of dual variables. More importantly, the steps in ADMM are linear, with the exception of an eigendecomposition on the primal variable. In practice, the eigendecomposition on the primal variable is manageable.

In general, it is not possible to obtain a closed-form expression for the coefficient matrices $C^{\left(k\right)}$’s. Sometimes, we need to employ numerical integration schemes over the group $𝒢$ to find the $C^{\left(k\right)}$’s.

6.2.1. The alternating direction method of multipliers.

In short, ADMM solves the augmented Lagrangian via iterative partial updating. We solve an unconstrained optimization problem over the objective variable, and enforce the constraints via dual variables. We will express the NUG SDP in a more general form, and derive ADMM updates in the more general setting. (4.4) and (5.1) are SDPs of the following form:

$$\begin{array}{cc}\underset{X}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}& ⟨C,X⟩\hfill \\ \text{subject to}& X⪰0\hfill \\ & {𝒜}_E\left(X\right)=b_E\hfill \\ & {𝒜}_I\left(X\right)\ge b_I.\hfill \end{array}$$ (6.1)

We can think of $C$ and $X$ as the following block matrices:

$$C=\left[\begin{array}{cccc}{C}^{\left(0\right)}& & & \\ & C^{\left(1\right)}& & \\ & & \ddots & \\ & & & C^{\left(t\right)}\end{array}\right],X=\left[\begin{array}{llll}{X}^{\left(0\right)}& & & \\ & X^{\left(1\right)}& & \\ & & \ddots & \\ & & & X^{\left(t\right)}\end{array}\right].$$

Note that going from (4.4) and (5.1) to (6.1), we used the fact that

$$\mathrm{t}\mathrm{r}\left[C^{\left(k\right)}{X}^{\left(k\right)}\right]=⟨C^{\left(k\right)},X^{\left(k\right)}⟩$$

because the $C^{\left(k\right)}$’s are Hermitian. ${𝒜}_E$ and ${𝒜}_I$ are linear operators that encapsulate the equality and inequality constraints, respectively. For example, we can think of $𝒜$ as

$$𝒜\left(X\right)=\left[\begin{array}{c}⟨A_I^{\left(1\right)},X⟩\\ ⋮\\ ⟨A_I^{\left(m\right)},X⟩\\ ⋮\end{array}\right],$$

where, for the constraint ${\sum }_{k=0}^t{b}_k\mathrm{t}\mathrm{r}\left[{\rho }_k^{\mathrm{*}}\left(g_m\right)X_{ij}^{\left(k\right)}\right],A_I^{\left(m\right)}$ is the matrix containing $b_k{\rho }_k\left(g_m\right)$ at the position of $X_{ij}^{\left(k\right)}$ and 0 everywhere else.

More concretely, $𝒜\left(X\right)=b$ is equivalent to $A\mathrm{v}\mathrm{e}\mathrm{c}\left(X\right)=b$, where

$$A={\left[\begin{array}{llll}\mathrm{v}\mathrm{e}\mathrm{c}\left(A^{\left(1\right)}\right)& \cdots & \mathrm{v}\mathrm{e}\mathrm{c}\left(A^{\left(m\right)}\right)& \cdots \end{array}\right]}^T$$

and vec vectorizes the matrix $A^{\left(m\right)}$ along the columns. The adjoint operator of $𝒜$ is given by

$${𝒜}^{\mathrm{*}}\left(z\right)=\text{mat}\left(A^{T}z\right),$$

where mat is the reverse operator of vec. Furthermore, we can verify

• $⟨𝒜\left(X\right),z⟩=⟨A\mathrm{v}\mathrm{e}\mathrm{c}\left(X\right),z⟩=⟨\mathrm{m}\mathrm{a}\mathrm{t}\left(A^{T}z\right),X⟩=⟨{𝒜}^{\mathrm{*}}\left(z\right),X⟩$,

• $\left(𝒜{𝒜}^{\mathrm{*}}\right)\left(z\right)=𝒜\left({𝒜}^{\mathrm{*}}\left(z\right)\right)=\left(A{A}^T\right)z,$

• $\left({𝒜}^{\mathrm{*}}𝒜\right)\left(z\right)={𝒜}^{\mathrm{*}}\left(𝒜\right(X\left)\right)=\mathrm{m}\mathrm{a}\mathrm{t}\left(\left(A^{T}A\right)\mathrm{v}\mathrm{e}\mathrm{c}\left(X\right)\right)$.

Now, we describe the ADMM solver outlined in [44] for SDP (6.1). ADMM is essentially a series of partial iterative updates based on the augmented Lagrangian. So, we will define the dual variables and write out the augmented Lagrangian. Then, we derive the updates by setting the gradient of the augmented Lagrangian, with respect to specific variables, to 0.

The dual variables corresponding to (6.1) are

$$\begin{array}{lll}-X\underset{\_}{\prec }0\hfill & \leftrightarrow \hfill & \hfill S\underset{\_}{\succ }0\\ b_E-{𝒜}_E\left(X\right)=0\hfill & \leftrightarrow \hfill & \hfill y_E\\ b_I-{𝒜}_I\left(X\right)\le 0\hfill & \leftrightarrow \hfill & \hfill y_I\ge 0.\end{array}$$

The Lagrangian for (6.1) is

$$L\left(X,S,y_E,y_I\right)≔-⟨\left(b_E,b_I\right),\left(y_E,y_I\right)⟩+⟨X,S+{𝒜}_E^{\mathrm{*}}\left(y_E\right)+{𝒜}_I^{\mathrm{*}}\left(y_I\right)-C⟩.$$ (6.2)

The motivation for defining (6.2) is so that the primal variable $X$ satisfies the constraints using the dual variables via

$$\underset{S⪰0,y_E,y_I\ge b_I}{\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}\underset{X}{\mathrm{m}\mathrm{a}\mathrm{x}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}}L\left(X,S,y_E,y_I\right).$$ (6.3)

Notice that (6.3) is an unconstrained optimization problem over $X$. If $X$ is not PSD, then there exists $S⪰0$ such that $L\left(X,S,y_E,y_I\right)=-\mathrm{\infty }$. Thus, due to the inner maximization over $X,$ (6.3) produces a solution satisfying $X⪰0$. The equality and inequality constraints are enforced in a similar manner. The maximizing $X$ must satisfy

$${\nabla }_{X}L=0\iff S+{𝒜}_E^{\mathrm{*}}\left(y_E\right)+{𝒜}_I^{\mathrm{*}}\left(y_I\right)=C.$$

In fact, this gives us the dual problem to (6.1)

$$\begin{array}{ll}\underset{S,y_E,y_I}{\text{minimize}}\hfill & {\delta }_{\underset{\_}{\prec }0}\left(S\right)+{\delta }_{\le 0}\left(y_I\right)-\langle \left(b_E,b_I\right),\left(y_E,y_I\right)\rangle \hfill \\ \text{subject }\text{to}\hfill & S+{𝒜}_E^{\text{*}}\left(y_E\right)+{𝒜}_I^{\text{*}}\left(y_I\right)=C.\hfill \end{array}$$

The augmented Lagrangian is the Lagrangian with the dual variables regularized by the Frobenius norm:

$$\begin{gathered} L_{\rho }\left(X,S,y_E,y_I\right)≔-\langle \left(b_E,b_I\right),\left(y_E,y_I\right)\rangle +\langle X,S+{𝒜}_E^{\text{*}}\left(y_E\right)+{𝒜}_I^{\text{*}}\left(y_I\right)-C\rangle \\ +\frac{\rho }{2}\parallel S+{𝒜}_E^{\text{*}}\left(y_E\right)+{𝒜}_I^{\text{*}}\left(y_I\right)-C{\parallel }_{\text{Fro }}^2. \end{gathered}$$ (6.4)

This regularization term is crucial for numerical convergence of the solver.

The updates for the dual variables are given by their individual optimality conditions.

• Solving $0={\nabla }_S{L}_{\rho }$ for $S$ and applying the PSD projection, we get

  $$S^{(k+1)}={\left[C-{𝒜}_E^{\mathrm{*}}\left(y_E^{\left(k\right)}\right)-{𝒜}_I^{\mathrm{*}}\left(y_I^{\left(k\right)}\right)-\frac{1}{\rho }{X}^{\left(k\right)}\right]}_{⪰0}.$$
• Solving $0={\nabla }_{y_E}{L}_{\rho }$ for $y_E$, we get

  $$y_E^{(k+1)}={\left({𝒜}_E{𝒜}_E^{\mathrm{*}}\right)}^{-1}\left(\frac{1}{\rho }\left(b_E-{𝒜}_E\left(X^{\left(k\right)}\right)\right)-{𝒜}_E\left({𝒜}_I^{\mathrm{*}}\left(y_I^{\left(k\right)}\right)+S^{\left(k\right)}-C\right)\right).$$

  Note that for the NUG SDP, ${𝒜}_E{𝒜}_E^{\mathrm{*}}=ℐ$ because each equality constraint is on a single entry in $X$. So, this update simplifies to

  $$y_E^{(k+1)}=\frac{1}{\rho }\left(b_E-{𝒜}_E\left(X^{\left(k\right)}\right)\right)-{𝒜}_E\left({𝒜}_I^{\mathrm{*}}\left(y_I^{\left(k\right)}\right)+S^{\left(k\right)}-C\right).$$
• Note that if we solve $0={\nabla }_{y_I}{L}_{\rho }$ for $y_I$, we will have to invert the operator ${𝒜}_I{𝒜}_I^{\mathrm{*}}$, and this is extremely computationally challenging. Instead, we add an additional regularization term $\frac{\rho }{2}{∥y_I-y_I^{\left(k\right)}∥}_{\lambda ℐ-{𝒜}_I{𝒜}_I^{\mathrm{*}}}^2$, where $\lambda$ is the largest eigenvalue of ${𝒜}_I{𝒜}_I^{\mathrm{*}}$ and $y_I^{\left(k\right)}$ is the element from the previous $y_I$-update. Solving $0={\nabla }_{y_I}\left[L_{\rho }+\frac{\rho }{2}{∥y_I-y_I^{\left(k\right)}∥}_{\lambda ℐ-{𝒜}_I{𝒜}_I^{\mathrm{*}}}^2\right]$ for $y_I$ and applying the the nonnegativity projection, we get

  $$y_I^{\left(k+1\right)}={\left[\frac{1}{\rho \lambda }\left(b_I-{𝒜}_I\left(X^{\left(k\right)}\right)\right)+\frac{1}{\lambda }{𝒜}_I\left(C-{𝒜}_E^{\text{*}}\left(y_E^{\left(k\right)}\right)-{𝒜}_I^{\text{*}}\left(y_I^{\left(k\right)}\right)-S^{\left(k\right)}\right)+y_I^{\left(k\right)}\right]}_{\ge 0}.$$

The update for the primal variable is simply a gradient descent given by

$$X^{(k+1)}=X^{\left(k\right)}+\rho \left(S^{\left(k\right)}+{𝒜}_E^{\mathrm{*}}\left(y_E^{\left(k\right)}\right)+{𝒜}_I^{\mathrm{*}}\left(y_I^{\left(k\right)}\right)-C\right).$$

We initialize the variables as the following:

• $X^{\left(0\right)}=I$,

• $y_I^{\left(0\right)}=0$,

• $S^{\left(0\right)}=0$,

• $y_E^{\left(0\right)}=\frac{1}{2}{𝒜}_E\left(C-{𝒜}_I^{\mathrm{*}}\left(y_I^{\left(0\right)}\right)-S^{\left(0\right)}\right)$.

We apply the updates in the following order:

1. $S^{(k+1)}={\left[C-{𝒜}_E^{\mathrm{*}}\left(y_E^{\left(k\right)}\right)-{𝒜}_I^{\mathrm{*}}\left(y_I^{\left(k\right)}\right)-\frac{1}{\rho }{X}^{\left(k\right)}\right]}_{⪰0},$

2. $y_E^{(k+1/2)}={𝒜}_E\left(C-{𝒜}_I^{\mathrm{*}}\left(y_I^{\left(k\right)}\right)-S^{(k+1)}\right),$

3. $y_I^{(k+1)}=\left[\frac{1}{\rho \lambda }\left(b_I-{𝒜}_I\left(X^{\left(k\right)}\right)\right)\right.{\left.+\frac{1}{\lambda }{𝒜}_I\left(C-{𝒜}_E^{\mathrm{*}}\left(y_E^{(k+1/2)}\right)-{𝒜}_I^{\mathrm{*}}\left(y_I^{\left(k\right)}\right)-S^{(k+1)}\right)+y_I^{\left(k\right)}\right]}_{\ge 0},$

4. $y_E^{(k+1)}={𝒜}_E\left(C-{𝒜}_I^{\mathrm{*}}\left(y_I^{(k+1)}\right)-S^{(k+1)}\right),$

5. $X^{(k+1)}=X^{\left(k\right)}+\rho \left(S^{(k+1)}+{𝒜}_E^{\mathrm{*}}\left(y_E^{(k+1)}\right)+{𝒜}_I^{\mathrm{*}}\left(y_I^{(k+1)}\right)-C\right).$

Note that we updated $y_E$ twice, which guarantees the solver’s convergence to the optimizer [44].

6.2.2. Fourier coefficients for bandlimited functions on $\mathit{S}\mathit{O}\left(3\right)$.

The coefficient matrix in (3.12) is composed of

$${\widehat{f}}_{ij}\left(k\right)={\int }_{𝒢}{f}_{ij}\left(g\right){\rho }_k^{\text{*}}\left(g\right)dg.$$

We obtained closed-form expressions for the registration problem (2.4) under the assumption that the noise in the underlying signal is Gaussian. For the cryo-EM problem (2.11), we require a single approximation of an integral using Gaussian quadrature. However, this is not always the case. For example, the noise in the cryo-EM projections is better modeled by the Poisson distribution [36]. We describe the numerical integration scheme in [28] that can be used to obtain the desired Fourier coefficients ${\hat{f}}_{ij}\left(k\right)$. We need to make the assumption that $f_{ij}$’s are bandlimited by $T$. The method described in [28] has a better computational complexity than straight forward numerical integration. We will define the quadrature, and then outline the evaluation over the quadrature.

For function $f$ with bandlimit $T$, we have the equality

$$\widehat{f}\left(k\right)=\frac{1}{{(2T)}^2}\sum _{j_1=0}^{2T-1}\sum _{j_2=0}^{2T-1}\sum _{l=0}^{2T-1}{b}_T\left(l\right)f\left({\alpha }_{j_1},{\beta }_l,{\gamma }_{j_2}\right){\rho }_k^{\text{*}}\left({\alpha }_{j_1},{\beta }_l,{\gamma }_{j_2}\right),$$ (6.5)

where

$$b_T\left(l\right)=\frac{2}{T}\text{sin}\left[\frac{\pi \left(2l+1\right)}{4T}\right]\sum _{m=0}^{T-1}\frac{1}{2m+1}\text{sin}\left[\frac{\pi \left(2l+1\right)\left(2m+1\right)}{4T}\right],$$

and

$${\alpha }_{j_1}=\frac{2\pi j_1}{2T},{\beta }_l=\frac{\pi (2l+1)}{4T},{\gamma }_{j_2}=\frac{2\pi j_2}{2T},0\le j_1,j_2,l<2T.$$

Recall that

$${\left[{\rho }_k(\alpha ,\beta ,\gamma )\right]}_{m,m^{\prime }}=e^{\text{i}m\alpha }{w}_{m,m^{\prime }}^{\left(k\right)}\left(\beta \right)e^{\text{i}{m}^{\prime }\gamma }.$$

We can re-write the entries in (6.5) as

$${[\widehat{f}\left(k\right)]}_{m,m^{\prime }}=\frac{1}{{(2T)}^2}\sum _{l=0}^{2T-1}{b}_T\left(l\right)w_{m^{\prime },m}^{\left(k\right)}\left({\beta }_l\right)\sum _{j_2=0}^{2T-1}{e}^{-\text{i}m{\gamma }_{j_2}}\sum _{j_1=0}^{2T-1}{e}^{-\text{i}{m}^{\prime }{\alpha }_{j_1}}f\left({\alpha }_{j_1},{\beta }_l,{\gamma }_{j_2}\right).$$ (6.6)

By rearranging the terms in (6.6), it becomes obvious that we should compute $\hat{f}\left(k\right)$ in the following order:

1. for all $0\le j_2,l<2T$ and $-T\le m^{\prime }\le T$, compute

   $$S_1\left(l,j_2,m^{\prime }\right)=\frac{1}{2T}\sum _{j_1=0}^{2T-1}{e}^{-\text{i}{m}^{\prime }{\alpha }_{j_1}}f\left({\alpha }_{j_1},{\beta }_l,{\gamma }_{j_2}\right),$$
2. for all $0\le l<2T$ and $-T\le m^{\prime },m\le T$, compute

   $$S_2\left(l,m^{\prime },m\right)=\frac{1}{2T}\sum _{j_2=0}^{2T-1}{e}^{-\text{i}m{\gamma }_{j_2}}{S}_1\left(l,j_2,m^{\prime }\right),$$
3. for all $-T\le m^{\prime },m\le T$, compute

   $${[\widehat{f}\left(k\right)]}_{m,m^{\prime }}=\sum _{l=0}^{2T-1}{b}_T\left(l\right)w_{m^{\prime },m}^{\left(k\right)}\left({\beta }_l\right)S_2\left(l,m^{\prime },m\right).$$

The complexity to compute $\left[\hat{f}\right(k){]}_{m,m^{\prime }}$ for all $m,m^{\prime }$ and $k$ is $𝒪\left(T^4\right)$; and the complexity of the straight-forward evaluation in (6.5) is $𝒪\left(T^6\right)$ [28].

6.2.3. Simplification for cryo-EM.

Recall that the objective function for cryo-EM does not depend on $\beta$. I.e.,

$$f\left(\alpha ,\gamma \right)=f\left(\alpha ,{\beta }_1,\gamma \right)=f\left(\alpha ,{\beta }_2,\gamma \right).$$

(6.6) reduces to

$${[\widehat{f}\left(k\right)]}_{m,m^{\prime }}=\left(\sum _{l=0}^{2T-1}{b}_T\left(l\right)w_{m^{\prime },m}^{\left(k\right)}\left({\beta }_l\right)\right)\left(\frac{1}{{(2T)}^2}\sum _{j_2=0}^{2T-1}{e}^{-\text{i}m{\gamma }_{j_2}}\sum _{j_1=0}^{2T-1}{e}^{-\text{i}{m}^{\prime }{\alpha }_{j_1}}f\left({\alpha }_{j_1},{\gamma }_{j_2}\right)\right).$$ (6.7)

We compute (6.7) in the following order:

1. compute

   $$B_T\left(k\right)=\sum _{l=0}^{2T-1}{b}_T\left(l\right)w_{m^{\prime },m}^{\left(k\right)}\left({\beta }_l\right),$$
2. for all $0\le j_2<2T$ and $-T\le m^{\prime }\le T$, compute

   $$S_1\left(j_2,m^{\prime }\right)=\frac{1}{2T}\sum _{j_1=0}^{2T-1}{e}^{-\text{i}{m}^{\prime }{\alpha }_{j_1}}f\left({\alpha }_{j_1},{\gamma }_{j_2}\right),$$
3. for all $-T\le m^{\prime },m\le T$, compute

   $$S_2\left(m^{\prime },m\right)=\frac{1}{2T}\sum _{j_2=0}^{2T-1}{e}^{-\text{i}m{\gamma }_{j_2}}{S}_1\left(j_2,m^{\prime }\right),$$
4. for all $-T\le m^{\prime },m\le T$, compute

   $${[\widehat{f}\left(k\right)]}_{m,m^{\prime }}=B_T\left(k\right)S_2\left(m^{\prime },m\right).$$

The complexity to compute $\left[\hat{f}\right(k){]}_{m,m^{\prime }}$ for all $m,m^{\prime }$ and $k$ is $𝒪\left(T^3\right)$.

6.3. Rotation MSE and FSC resolution.

We assess the performance of orientation estimation method using the mean squared error (MSE), defined as follows:

$$\text{MSE}≔\frac{1}{n}\sum _{i=1}^n\parallel {\widehat{R}}_i-R_i{\parallel }_{\text{Fro}}^2.$$ (6.8)

Here $R_i$ are the true rotations (which are known in the simulation setting) and ${\hat{R}}_i$ are the estimated rotations (note that we previously used the hat notation for the Fourier transform, but here it is used for estimators). Since the estimation is up to a global rotation and possibly handedness, the two sets of rotations are aligned prior to computing the MSE.

In addition, we will include the Fourier Shell Correlation (FSC) of the reconstructed structure against the known structure. We reconstruct the 3-dimensional structure (in Fourier space) using the estimated orientations to get $\hat{\varphi }$, and compare it against the known structure $\varphi$ (in Fourier space). For each spatial frequency $r_k$, we calculate the FSC

$$\text{FSC}\left(r_k\right)≔\frac{\sum _{\parallel v{\parallel }_2=r_k}\widehat{\varphi }\left(v\right){\varphi }^{\text{*}}\left(v\right)}{{\sum _{\parallel v{\parallel }_2=r_k}\left|\widehat{\varphi }\left(v\right)\right|}^2\sum _{\parallel v{\parallel }_2=r_k}{\left|\varphi \left(v\right)\right|}^2}.$$

We derive the resolution (in Angstroms) by interpolating the FSC until we reach an $r_k$ yielding $\mathrm{F}\mathrm{S}\mathrm{C}\left(r_k\right)\le 0.5$. See [23] for a discussion on the FSC and the cutoff value.

Note that the rotation MSE is the most direct assessment of orientation estimation methods. After all, the stated objective of orientation estimation in cryo-EM is to estimate the orientations. In addition, the quality of the 3-dimensional reconstruction depends on several other factors such as the signal-to-noise ratio of the images, the number of images, the distribution of the viewing directions and the CTF of the images. We focus on the rotation MSE because the other factors mentioned are independent of the algorithm being used.

6.4. Simulated data.

With the ASPIRE software package in [5], we generate a set of 100 and a set of 500 projection images of size 129 × 129 from the Plasmodium falciparum $80S$ ribosome (see https://www.ebi.ac.uk/pdbe/emdb/empiar/entry/10028/.) We add Gaussian noise to the simulated projections, and then apply a circular mask to zero out the noise outside of the radius. Table 1 shows a comparison of NUG and the synchronization method for different noise levels. In particular, the estimation error of NUG at SNR=1/64 with 500 images is sufficiently low (MSE=0.05) to result in a meaningful 3-D ab-initio model (with ¡ 30 Angstrom resolution). Numerical experiments were conducted on a cluster of Intel(R) Xeon(R) CPU E7–8880v3 @ 2.30GHz totaling 144 cores and 792GB of RAM. The synchronization method is roughly two orders of magnitude faster than NUG, but NUG gives more accurate estimates at low SNR.

Table 1.

The resolutions shown are in Angstroms. At high SNR, synchronization is accurate to more decimal places. This is not surprising since we have compromised on various truncations and discretizations for computational speed, etc. However, as the noise increases, we see NUG outperforming synchronization.

100 images	SNR	NUG MSE	sync. MSE	NUG res	sync res
	1/1	0.0153	1.2759e-04	24.6	20.8
	1/2	0.0155	1.3593e-04	21.5	20.3
	1/4	0.0174	3.6615e-04	27.0	22.4
	1/8	0.0192	0.0037	28.7	25.8
	1/16	0.0227	0.0300	29.8	30.9
	1/32	0.0298	0.1572	35.6	45.8
	1/64	0.1559	2.7818	45.3	174.1
	1/128	2.1239	4.1492	97.9	175.3
500 images	SNR	NUG MSE	sync. MSE	NUG res	sync res
	1/1	0.0125	4.1412e-05	18.1	14.6
	1/2	0.0130	5.1825e-05	20.8	18.2
	1/4	0.0134	1.5268e-04	21.7	17.0
	1/8	0.0143	0.0018	16.4	18.1
	1/16	0.0175	0.0189	20.8	17.7
	1/32	0.0195	0.1559	24.6	30.7
	1/64	0.0460	2.2496	29.3	71.1
	1/128	1.6060	3.1661	64.2	107.6

To put the numbers in Table 1 into perspective, a MSE of 0.1, for example, can be regarded as small enough in one instance to lead to a good reconstruction, but too large in another. The 3-dimensional reconstruction from 100 images at low SNR (e.g., SNR=1/128) looks bad even if one uses the true orientations (i.e., MSE=0). On the other hand, the 3-dimensional reconstruction from 500 images at moderate SNR (e.g., SNR=1/32) would look very decent at MSE=0.1. The latter case is shown in Figure 7 in [39], where SNR=1/32 and the MSE is slightly above 0.1. The resolution measure quantifies the quality of the 3-D ab-initio model. An idea about the quality of 3-dimensional reconstruction with respect to the MSE can also be obtained from Table 3 and Figure 8 in [42]. We would like to point out that for the same computational cost, synchronization can process more images than NUG, and therefore may yield better 3-dimensional reconstructions. However, beyond the theoretical importance, NUG still might be useful in situations in which the number of images is limited (e.g., when there are only a handful number of class averages or in electron tomography).

We also illustrate the effects of contrast, CTF and shifts on the performance of NUG in the numerical experiment reported in Table 2. In this numerical experiment, phase flipping was applied to correct for the phases of the CTF but not their magnitudes. As for shifts, we simply ignore it in the NUG SDP. In the future, we can expand (4.4) to include shifts to improve upon our estimates. Please see Section 6.1 for a discussion on the effects of contrast, CTF and shifts.

The distribution for the contrast was based on the following numerical experiment. We used the publicly available experimental dataset EMPIAR-10028 found here: https://www.ebi.ac.uk/pdbe/emdb/empiar/entry/10028/. Using the known 3-dimensional structure of the molecule, we construct 10,000 simulated clean projections of size 64 × 64 at different orientations sampled uniformly over $SO\left(3\right)$. For each image $\hat{I}$ in the experimental dataset, we solve for $\gamma$ in

$$\underset{\gamma ,I_i}{\text{minimize}}\parallel \gamma \widehat{I}-I_i{\parallel }_{\text{Fro }}^2,$$

where $I_i$’s are simulated projections generated from the known structure. Figure 6.3 shows the empirical distribution of $\gamma$.

Figure 6.3.

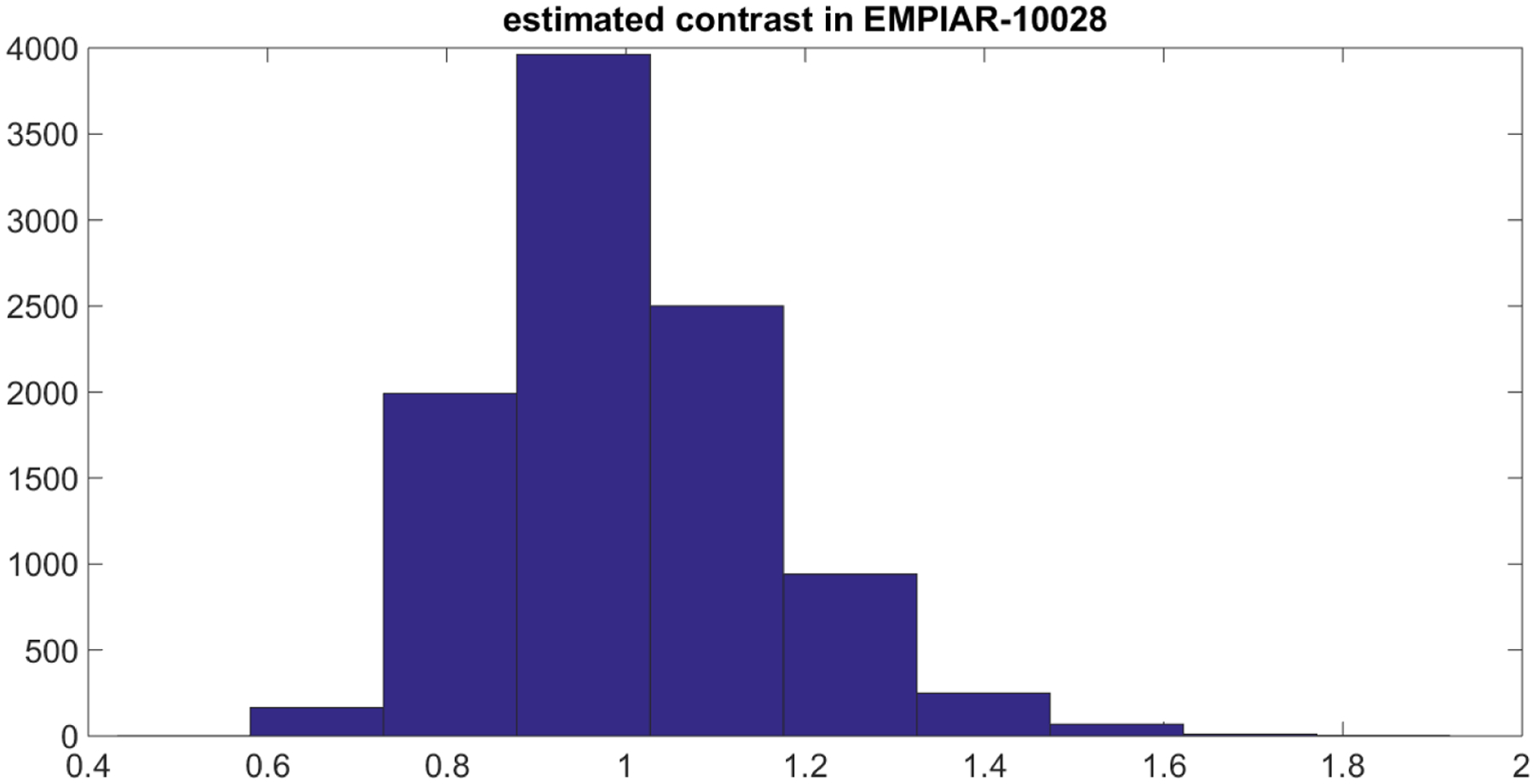
Distribution of contrast in the experimental dataset EMPIAR-10028.

7. Summary

The NUG problem consists in the minimization of the sum of pairwise cost functions defined over the ratio between group elements, for arbitrary compact groups. This corresponds to the simultaneous multi-alignment of many datapoints (e.g. signals, images, or molecule densities) with respect to transformations given by an action of the corresponding group. We presented a methodology to solve this problem involving a relaxation of the problem to an SDP and an implementation of an ADMM algorithm to solve the resulting SDP.

In this paper we focused mainly in the context of alignment over $SO\left(2\right)$ and $SO\left(3\right)$. A notable example is that of finding a consistent set of pairwise rotations of many different functions defined on a sphere which globally minimize the disagreement between pairs of functions.

The NUG problem arises in cryo-EM, where the task is to recover the relative orientations of many noisy 2-dimensional projections images of a 3-dimensional object, each obtained from a different unknown viewing direction. Once good alignments are estimated, the 3-dimensional object can be reconstructed using standard tomography algorithms. In this paper we formulate the problem of image alignment in cryo-EM as an instance of NUG, and demonstrate the applicability to simulated datasets.

The computational and numerical considerations require truncations of the both the cost functions and group representations; a general approach is proposed as part of the formulation as an SDP, and additional methods particularly developed for the case of $SO\left(3\right)$, and to the special properties of the cryo-EM problem, are presented.

It is noteworthy that, compared to previous work on related alignment problems, the formulation of the problem as an SDP can provide a certificate for optimality in some cases. Specifically, whenever the solution of the SDP also satisfies the nonconvex constraints that have been relaxed, it serves as a certificate that optimality has been achieved. In numerical work not reported in this paper we have numerically observed optimality of NUG SDP for some instances of MRA, but not for estimation of orientations in cryo-EM. Better theoretical understanding of when NUG SDP achieves optimality is an interesting open problem. In the context of cryo-EM, like other common-line based approaches, it does not require an initial guess. These properties make NUG a candidate for future work on robust ab initio alignment which would provide an initialization for other refinement algorithms.