A Structural-based Machine Learning Method to Classify Binding Affinities between TCR and peptide-MHC Complexes

Abstract

The activation of T cells is triggered by the interactions of T cell receptors (TCRs) with their epitopes, which are peptides presented by major histocompatibility complex (MHC) on the surfaces of antigen presenting cells (APC). While each TCR can only recognize a specific subset from a large repertoire of peptide-MHC (pMHC) complexes, it is very often that peptides in this subset share little sequence similarity. This is known as the specificity and cross-reactivity of T cells, respectively. The binding affinities between different types of TCRs and pMHC are the major driving force to shape this specificity and cross-reactivity in T cell recognition. The binding affinities, furthermore, are determined by the sequence and structural properties at the interfaces between TCRs and pMHC. Fortunately, a wealth of data on binding and structures of TCR-pMHC interactions becomes publicly accessible in online resources, which offers us the opportunity to develop a random forest classifier for predicting the binding affinities between TCR and pMHC based on the structure of their complexes. Specifically, the structure and sequence of a given complex were projected onto a high-dimensional feature space as the input of the classifier, which was then trained by a large-scale benchmark dataset. Based on the cross-validation results, we found that our machine learning model can predict if the binding affinity of a given TCR-pMHC complex is stronger or weaker than a predefined threshold with an overall accuracy approximately around 75%. The significance of our prediction was estimated by statistical analysis. Moreover, more than 60% of binding affinities in the ATLAS database can be successfully classified into groups within the range of 2kcal/mol. Additionally, we show that TCR-pMHC complexes with strong binding affinity prefer hydrophobic interactions between amino acids with large aromatic rings instead of electrostatic interactions. Our results therefore provide insights to design engineered TCRs which enhance the specificity for their targeted epitopes. Taken together, this method can serve as a useful addition to a suite of existing approaches which study binding between TCR and pMHC.

Introduction

As the onset of cell-mediated adaptive immunity, protein fragments from foreign pathogens are captured by major histocompatibility complex (MHC) using the peptide binding groove in-between their α₁ and α₂ helices [1]. These peptide-MHC complexes (pMHC) are expressed on the surfaces of antigen presenting cells (APC), which then migrate through blood vessels into the lymph nodes where they encounter naive T cells to activate immune responses [2]. The activation of T cells is initiated by the recognition between pMHC and T cell receptors (TCRs), which consists of two subunits, known as α chain and β chain, respectively [3]. During development of T cells, they go through a selection process in the thymus to ensure that their TCRs might only respond to specific subsets of pMHC but not others [4]. The binding affinities between different types of TCRs and pMHC are the major driving force to shape this specificity in T cell recognition [5]. For instance, T cell activation requires a threshold that determines the minimal level of binding between TCR and pMHC [6]. It has been demonstrated that a relatively low affinity threshold plays a positive role in maintaining a high degree of specificity in TCR-pMHC interactions [7]. On the other side of specificity, it is common that the same TCR can recognize two or more peptides which sequences share little similarity [8]. This cross-reactivity is resulted from the fact that the number of possible antigens is more than the number of distinct TCRs in an individual by orders of magnitude [9]. Recent experimental evidences suggest that the structural plasticity of TCRs can explain the ability of their cross-reaction with different peptides: a TCR can adopt various conformations to interact with corresponding ligands [10]. One of these examples is the binding of 2C TCR to two of its ligands SIY/K^b and QL9/L^d [11]. Above information indicates that the functions of TCRs in adaptive immune responses, which are characterize by their specificity and cross-reactivity, are rooted in structural properties of complexes formed between TCR and pMHC and their associated binding affinities [12].

Unfortunately, different from antibodies, which are secreted proteins involved in humoral immune responses, surface-bound TCRs are difficult to express in soluble form at relatively high concentrations [13]. Moreover, TCRs have considerably lower binding affinities for their ligands pMHC than the analogous interactions between antigens and antibodies. These factors make the studies of interactions between TCRs and pMHC practically much more challenging. Nevertheless, remarkable progresses have been made to reveal the binding properties of TCR-pMHC complexes and their impacts on T cell specificity by various experimental techniques. Specifically, a wealth of data on binding parameters has been accumulated and becomes publicly accessible in online resources such as the Immune Epitope Database (IEDB) [14] and the AntiJen Database [15]. These data suggest that the recognition of pMHC by wildtype TCRs can be characterized by slow association rates and intermediate dissociation rates, which gives the range of binding affinity between 1 and 100 μM [16]. In parallel, more and more structures of TCR-pMHC complexes have been solved and become available in the Protein Data Bank (PDB). The information of TCR-pMHC complex structures and their corresponding binding affinities have been linked together in a recently developed database, called ATLAS [17]. This database, as a comprehensive training set, offers an opportunity to computationally model or predict binding affinities between TCRs and pMHC based on the structure of their complexes. In order to compensate the time-consuming and labor-intensive experimental approaches, a large variety of computational methods have been utilized to study the functions of TCR-pMHC interactions. For instance, the binding affinity of peptides bound to MHC was estimated by the average score of configurations from molecular dynamics (MD) simulations [18]. The structures of TCR-pMHC complexes can be computationally constructed by a comparative modeling pipeline [19]. A computational framework was further developed to predict cross-reactive peptides by scoring the structural models of TCR-pMHC complexes [20]. In addition to these models, the new advancements in machine-learning algorithms have gained increasing attention from the field of computational biology [21, 22]. The application of these algorithms to study protein-protein interactions and predict binding affinities has achieved a big success [23]. For an example, antigen specificity of single T cells has been predicted by deep learning algorithm based on their TCR CDR3 regions[24]. More recently, a logistic regression model, called PRIME, was trained to recognize immunogenic epitopes [25].

In this article, a machine-leaning-based method is designed to predict the binding affinities of a TCR-pMHC complex. The prerequisite is that the pMHC can be recognized by the TCR, i.e., we have already known that these two proteins can bind to each other. The task of current study is to evaluate the strength of their binding. In detail, random forest algorithm was applied to estimate if the interaction of a specific TCR-pMHC complex is stronger than certain threshold, or further classify its binding affinity into specific range. All the structures and binding affinities of wildtype and mutated TCR-pMHC complexes in the ATLAS database are used as the training set. A high-dimensional feature space was constructed as the input of the random forest classifier. The feature space incorporates both structure and sequence information at the binding interfaces between TCR and pMHC. Based on the cross-validation results, we found that our machine learning model can predict if the binding affinity of a given TCR-pMHC complex is stronger or weaker than a predefined threshold with an overall accuracy approximately around 75%. The significance of our prediction was estimated by statistical analysis. Moreover, more than 60% of binding affinities in the ATLAS database can be successfully classified into groups within the range of 2kcal/mol. The feature space further provides insights to the preferential combinations of intermolecular residue pairs at specific locations of binding interfaces on a systematic level. In summary, our computational modeling study can serve as a useful addition to a suite of existing approaches which measure affinities of binding between TCR and pMHC. The method can also help engineering TCRs by designing residues on binding interfaces to enhance their specificity for targeted epitopes.

Materials and Methods

Constructing a high-dimensional feature space of TCR-pMHC binding interfaces

The binding interface of each TCR-pMHC complex was transformed into a high-dimensional feature space. The feature space integrates both structural and sequence information of residues at the binding interfaces on both TCR and pMHC. Specifically, three complementarity-determining regions (CDR), called CDR1, CDR2 and CDR3, are evolved in TCRs in order to recognize these pMHC from the large repertoire of peptides and the highly polymorphic MHC. The secondary structures of these three regions are mostly loops. While CDR1 and CDR2 loops are germline derived, the hypervariable CDR3 loop is directly involved in peptide binding (Figure 1a) [26]. On the other hand, in addition to the intermolecular interactions between peptides and TCRs, there are still a remarkable number of residues in MHC involved in TCR recognition. Almost all these residues are located in their α₁ and α₂ helices (Figure 1a). Based on these pieces of structural information, we divide the binding interface of a TCR-pMHC complex into four compartments (Figure 1a). The first compartment contains all intermolecular contacts between residues from the hypervariable loop of TCR (both α and β chains) and residues from the peptide. This compartment is denoted as ‘HP’ in the following context. The second compartment contains all intermolecular contacts between residues from the germline loops of TCR and residues from the α₁ and α₂ helices of MHC. This compartment is denoted as ‘GM’. The third compartment contains all intermolecular contacts between residues from the hypervariable loop of TCR and residues from the α₁ and α₂ helices of MHC. This compartment is denoted as ‘HM’. Finally, the last compartment contains all intermolecular contacts between residues from the germline loops and residues from the peptide. This compartment is denoted as ‘GP’.

Figure 1:

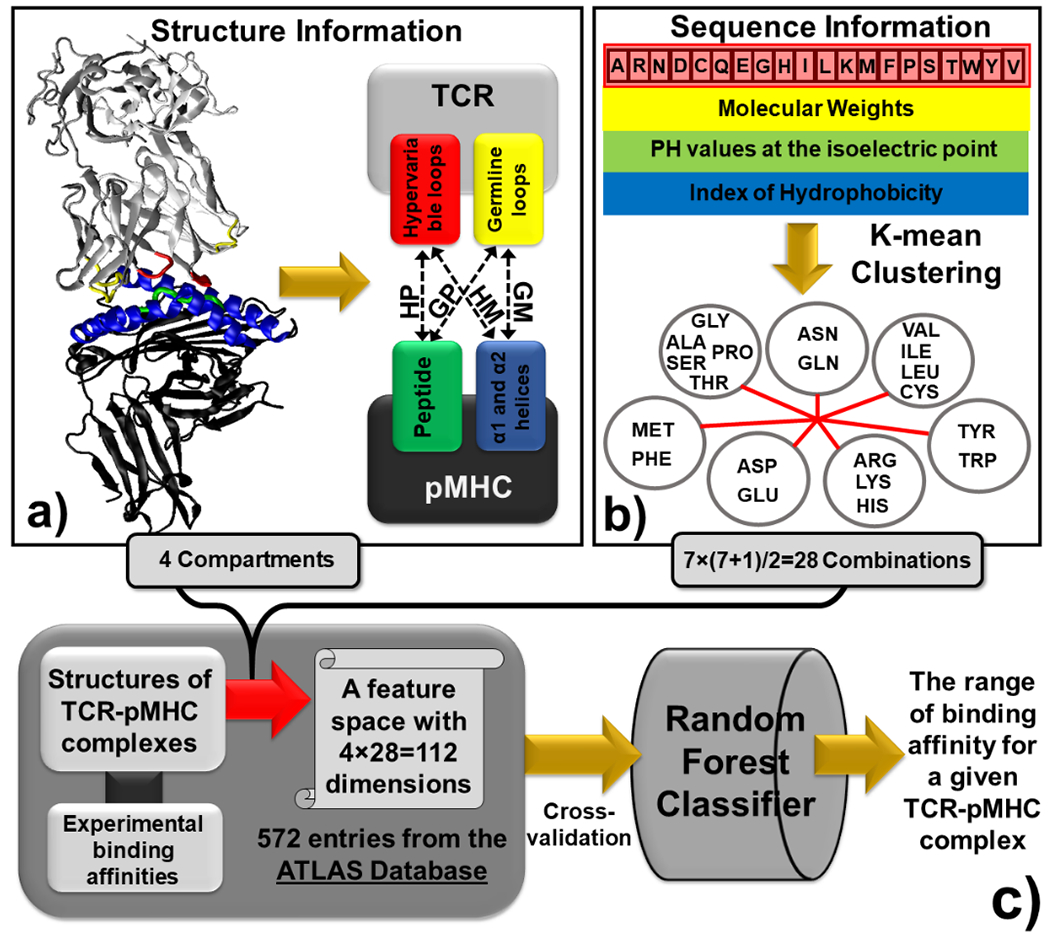
The binding interfaces between TCRs and pMHC are represented by vectors in a high-dimensional feature space. We first divided the structure of a binding interface into four compartments (a). The information of primary sequence at binding interfaces was further integrated into the feature space by coarse-graining the 20 types of amino acids into 7 groups based on the three physicochemical properties (b). Based on the construction of the feature space, all TCR-pMHC complexes in the ATLAS database were used as the benchmark to train a random forest classifier, so that the range of binding affinity for a specific TCR-pMHC complex can be predicted (c).

The information of primary sequence at binding interfaces is further reflected by distinguishing the type of residue combinations for all pairs of intermolecular contacts. In order to reduce the dimensionality of the feature space, the 20 types of amino acids are coarse-grained into 7 groups. In detail, three physicochemical properties were considered in order to cluster the 20 amino acids types into 7 representative groups based on their similarity. The first property used to calibrate similarity among among amino acids is their molecular weights. The pH value at the isoelectric point which identifies if an amino acid is positively or negatively charged is used as the second property. Finally, the Kyte and Doolittle index [27] which characterizes the hydrophobicity and polarity of each amino acid is used as the third property. Specific values of these three properties are summarized in Supplemental Table S1 for all 20 amino acids. For each property, its values for all 20 types of amino acids were further rescaled by calculating the z-scores, so that the weights between different properties can be balanced. Calculated z-scores were used as input vectors to cluster amino acids into 7 groups by k-mean clustering algorithm [28]. The clustering result is shown in Figure 1b. The figure indicates that positively charged, negatively charged and non-charged polar amino acids are fallen into different groups, while groups of hydrophobic amino acids are identified by their size. Given the 7 groups of amino acids, there are 7×(7+1)/2=28 possible combinations for any pairs of intermolecular contacts. If the intermolecular interactions are further divided into 4 above-mentioned compartments, the total dimensions of the feature space become 4×28=112 (Figure 1c). These 112 degrees of freedom represent the basic structural and sequence properties of binding interfaces between TCR and pMHC.

Implementing the ATLAS database as a benchmark dataset for training and testing

The information about the structures and binding affinities of all TCR-pMHC complexes used for training and testing in this study was derived from the ATLAS database. It is a manually curated repository not only for binding between wild-type TCRs and pMHC, but also for binding which contains mutants in TCRs, antigen peptides, or MHC. The data of TCR-pMHC interactions collected in the database are either from human or from mouse. Moreover, both class I and class II MHC, with 28 different types of alleles, are included in the database. The binding affinities were all experimentally measured by isothermal titration calorimetry (ITC) [29] or surface plasmon resonance (SPR) [30]. In parallel, the 3D structures were all derived from the PDB for wild-type TCR-pMHC complexes. For mutant, structural models were computationally built by Rosetta [31] based on the template of their corresponding wild-type complexes in the PDB. The fixed-backbone design option in Rosetta was adopted during the model construction. The current database contains a total number of 694 entries. All these data can be downloaded at http://atlas.wenglab.org/web/. However, the information of binding affinities for some entries is missing due to either undetectable or unreliable measurements. For an example, the dissociation constant of interaction between TCR 1G4 with a mutation Y31D and MHC HLA-A*02:01 with tumor epitope NY-ESO (157-165) is shown as higher than 240 μM in the ATLAS database, which is unusable in our follow-up analysis. These entries with either no or ambiguous binding affinity therefore were removed while we constructed our benchmark set for binding affinity classification. Consequently, the final dataset contains 572 entries, which consists of 83 experimentally derived structures and 489 computationally constructed models of TCR-pMHC complexes. Each entry is represented by a structure model and its corresponding binding affinity.

For each entry in the dataset, all interfacial residue pairs between TCR and pMHC were projected onto the feature space which was described in the last section. Specifically, for a given TCR-pMHC complex, an interfacial residue pair is defined by the following two criteria: 1) one residue in the pair comes from TCR and the other comes from agent peptide or MHC; 2) after all distances of side-chains atoms between two residues in the pair are calculated, at least one distance among these inter-residue atomic pairs should be smaller than the predefined distance cutoff. Although previous studies used 4 Angstrom as the distance cutoff to define the intermolecular contacts between atoms in TCR-pMHC complexes [32], a slightly larger value (5 Angstrom) was adopted in current model to take account of longer-range biophysical effects such as electrostatic interactions at the interface between TCR and pMHC. It is worth mentioning that the determination of this distance cutoff, either 4 Angstrom or 5 Angstrom, is rather empirical. A more comprehensive study in the future should explore multiple definitions of residue contacts at TCR-pMHC complexes and how these different definitions affect classification of binding affinities.

For a given pair of interacting residues which meets the above two criteria, their sequence information is designated by the 7 coarse-grained groups. We further record if the residue in the pair from TCR is located in the hypervariable loops or in the germline loops. Similarly, we also record if the residue from pMHC is located in the agent peptide or in α₁ and α₂ helices of MHC. As a result, any interfacial residue pair belongs to one of the 112 categories. After all interfacial residue pairs in a specific TCR-pMHC complex are identified, a vector with 112 dimensions can be constructed. The value of each dimension in the vector indicates the number of interfacial residue pairs that fall into the corresponding category. The binding interface of each TCR-pMHC complex is thus represented by a specific vector in the feature space. Each vector is further paired with its experimentally measured value of binding affinity. Finally, all vectors were normalized before feeding into the machine-learning classifier. In summary, our benchmark dataset consists of 572 vectors, as shown in Figure 1c. The 112 dimensions in each vector store the structural and sequence information at the binding interface of a specific complex, while an additional dimension in the vector is used for its binding affinity.

Applying a random-forest-based classifier to predict TCR-pMHC binding affinities

The range of binding affinities for all TCR-pMHC complexes in our dataset was classified by a machine learning algorithm, given the fact that the number of entries in the dataset is not large enough for more powerful deep-learning methods. Among all different machine-learning-based models, we chose random forest as the algorithm for classification. Random forest is an algorithm that tends to have low risk of data overfitting and is designed for high-dimensional datasets. Moreover, comparing with other machine learning models including neural networks, it is not only more suitable for tabular data such as the vectors used in this study, but also have much less tunable parameters during training.

In detail, the random forest classifier implemented in this study is based on the growth of many single decision trees [33]. The maximal number of trees that are allowed to grow equals 500. Each single decision tree in the forest was built by using a combination of randomly selected features. The total number of input features for a data point equals 112, as described above. On the other hand, the overall distribution of binding affinities for all TCR-pMHC complexes in the dataset is divided into several predefined ranges, corresponding to the classes as the output of a decision tree. These classes are reflected by the leaf nodes of decision trees. After formatting the inputs and outputs, each decision tree was then trained on a different sample of data points, which are entries randomly selected from the dataset by bootstrapping. Following the tree construction, the class of a new data point can be predicted as follows. The new data point entering the forest will be traversed through all trees from the root to one of their leaf nodes, from which the class of the data point can be determined. The class estimated from each individual tree is usually different from each other. Our classifier chooses the class which has the most votes over all the trees in the forest as the final output.

In order to calibrate the performance of classification results, cross-validation was applied to the benchmark derived from the ATLAS database. In order to avoid the potential over-fitting, the leave-one-out strategy was adopted. In practical, the cross-validation procedure consists of multiple runs of training. During each run of the leave-one-out training, one entry of TCR-pMHC complex was selected from the dataset as the testing set, while the remaining 571 complexes were considered as the training set. Each complex in the training set were assigned into specific class based on what predefined range its binding affinity is fallen into. The vectors in the 112-dimensional feature space for all complexes in the training set were used as inputs to build the decision trees in random forest, while the classes of their associated binding affinities were used as outputs. After training, the vector of selected testing entry was fed into the classifier as input for prediction. The predicted class was compared with the real binding affinity. After above training and testing procedure was gone through all entries, the overall accuracy of the classification was calculated by counting the number of complexes which classes of binding affinity were correctly predicted.

The classification program is accessible at: https://github.com/wujah/RFATLAS/. This package contains an executable file predicting the range of binding affinity for all TCR-pMHC complexes in our benchmark dataset. All source codes used to compile the executable file are also available. The source codes were written in FORTRAN 77, consisting of a main program and a subroutine of random forest classifier. All input parameters are included in two files. The first file provided the index of 7 coarse-grained groups for all 20 amino acids based on the k-mean clustering results. The second file stores the list of all interfacial residue pairs for all 572 entries in the dataset. The information about the type of each amino acid in each pair and which compartment it belongs to are also provided. Finally, a sample output file which records the prediction result of each entry and the calculated accuracy from the overall cross-validation is also presented. The classifier works on a Linux platform and can be freely downloaded for all academic users.

Results

The experimentally measured dissociation constants of interactions between TCR and pMHC span a wide spectrum with several orders of magnitude. For instance, the interaction with the strongest binding affinity found in the ATLAS database is formed between TCR 1G4 and the NY-ESO-1(157-165) tumor-associated peptide presented by the class I MHC HLA-A*0201 [34]. The measured dissociation constant equals 26 pM, corresponding to the binding free energy of −14.44 kcal/mol. On the other hand, the weakest binding affinities found in the ATLAS database are in the scale of millimolar (mM). One example is the complex formed between TCR A6 and the Tax peptide presented by the class I MHC HLA-A*0201 with a mutation L98A in the β chain of TCR and a mutation Y8A in the peptide [35]. The measured dissociation constant equals 1.4 mM, corresponding to the binding free energy of −3.88 kcal/mol. The statistical distribution of binding affinities for all 572 TCR-pMHC complexes in our benchmark dataset was plotted as histogram in Figure 2a with an average value of −6.9 kcal/mol. The figure shows that binding affinities of most entries (around 70%) in the dataset are between −5.5 and −7.5 kcal/mol. This is well compatible with previous observation that TCR-pMHC binding affinities are ranged from 1 to 100 μM. Moreover, there is a long tail on the left side of the distribution, indicating that binding affinities for a small portion of complexes are lower than −10 kcal/mol.

Figure 2:

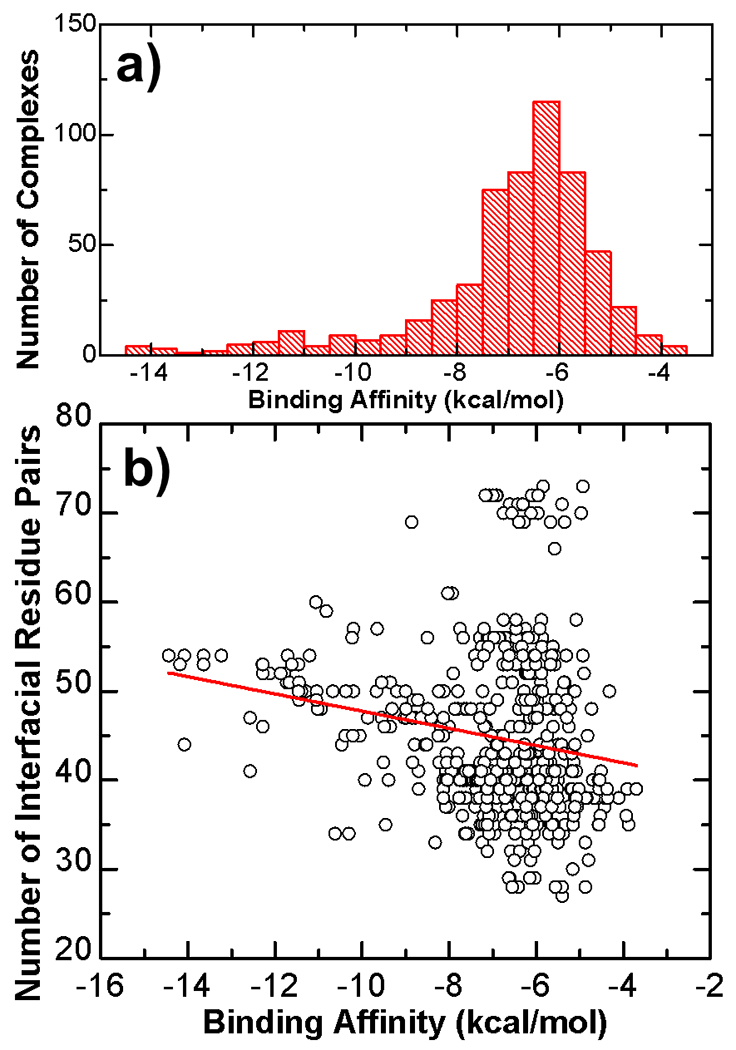
The statistical distribution of binding affinities for all 572 TCR-pMHC complexes in our benchmark dataset was plotted as histogram in (a). The average biding affinity equals −6.9 kcal/mol. Moreover, while binding affinities of around 70% entries are between −5.5 and −7.5 kcal/mol, there is a long tail on the left side of the distribution, indicating that binding affinities for a small portion of complexes are lower than −10 kcal/mol. Additionally, we also plotted the number of interfacial residue pairs for all complexes in the dataset against their corresponding values of binding affinity in (b). As labeled by the red line, there is a weak negative correlation between binding affinities and number of interfacial residue pairs. The Pearson correlation coefficient equals −0.19.

In order to link binding affinities to the structural information at the interface between TCRs and pMHC on a systematic level, we plotted the number of interfacial residue pairs for all complexes in the dataset against their corresponding values of binding affinity, as shown in Figure 2b. Each black open circle in the figure represents a specific TCR-pMHC interaction. Its binding affinity is indexed by the x-axis, while the number of interfacial residue pairs in the structure of its complex is indexed by the y-axis. Overall, there is a weak negative correlation between binding affinities and number of interfacial residue pairs. As labeled by the red line in the figure, the Pearson correlation coefficient (PCC) is −0.19. This result suggests that in general, if there are fewer interacting residues at the binding interface between TCR and pMHC, the binding affinity of the complex will be weaker. This conclusion is consistent to our intuition. However, it is impossible to predict binding affinity purely based on the number of interactions at TCR-pMHC binding interfaces due to their weak correlation. For an example, although the interaction between TCR 2B4 and the moth cytochrome c peptide (MCC88–103) presented by the class II MHC I-Ek has the moderate binding affinity of −6.9 kcal/mol, the structure of its complex (PDB id 3QIB) contains 72 interfacial residue pairs, which is the highest level in the dataset. On the other hand, for the interaction which has the strongest binding affinity in the dataset (−14.44 kcal/mol) as we described in the last paragraph, the structure of its complex (PDB id 2P5E) only contains 44 interfacial residue pairs. The difference in these two systems suggests that additional strategies based on more complicated features in the structures of TCR-pMHC complexes are necessary to predict their binding affinities.

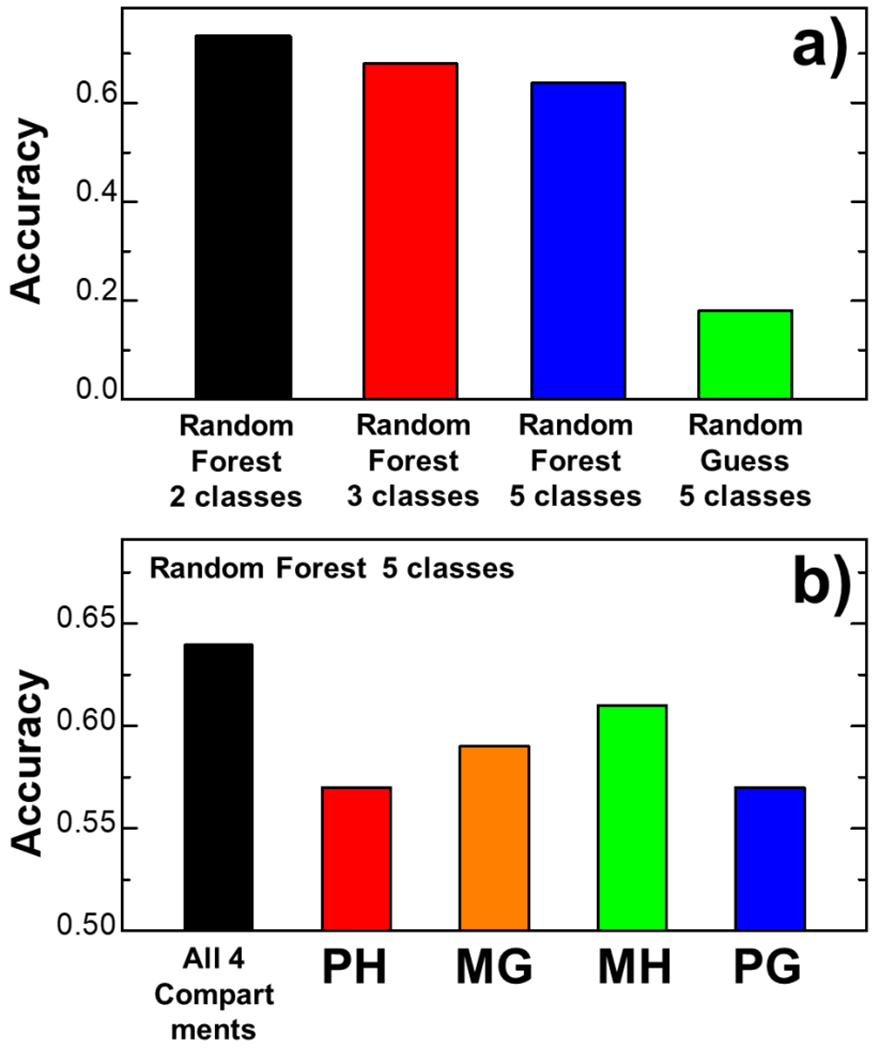
We therefore constructed a high-dimensional feature space to incorporate both structural and sequence information at binding interfaces between TCR and pMHC. Each complex in the dataset is then represented by a vector in the feature space. We fed these vectors into random forest classifier as inputs. On the other hand, all complexes were grouped into different classes based on the range of their binding affinities. More details about the construction of feature space and algorithm of random forest classification have been described in the Materials and Methods. We assume that these structural and sequence features can help the machine learning model correctly predict what range of binding affinity a specific TCR-pMHC complex belongs to. We first divided all complexes into two classes. Specifically, any complex which binding affinity is stronger than a predefined threshold is in one class, while any complex which binding affinity is weaker than the threshold is in the other class. The threshold was set to −6.45 kcal/mol so that the number of complexes in one class almost equals the other. Based on the leave-on-out cross-validation, the random forest classifier successfully recognized the class of 420 complexes out of 572 entries in the benchmark set, corresponding to an overall accuracy of 0.734. The accuracy is defined by calculating the ratio between the number of correct predictions for complexes which binding affinities are either higher or lower than the threshold versus the total number of entries in the dataset. The results are shown by the red bar in Figure 3a.

Figure 3:

We first divided all complexes into two classes. The results from our cross-validation test for different classifiers are summarized in (a). The red bar shows accuracy of the classification results using the inputs with 112 dimensions. The black bar shows the results purely based on random guessing. The blue, green and yellow bars show three additional models with the same random-forest classification algorithm and cross-validation process, but different dimensions of inputs. We further adjusted the threshold of binding affinity into different values. Under each threshold value, we calculated sensitivity, specificity, precision and overall accuracy, which are illustrated in (b). Finally, the correlation between true positive rate and false positive rate under different threshold values was plotted as a receiver operating characteristic (ROC) curve in (c). The data points in the ROC curve are consistently higher than the line of no-discrimination (the dashed diagonal representing random guess), indicating the good quality of our classification results on a statistical level.

The machine learning method was compared with a control model to test the significance of our classification results. In the control model, predictions were made purely by random guessing. Each TCR-pMHC complex was randomly assigned either higher or lower than the threshold of binding affinity with equal probabilities. The result can be directly evaluated by checking whether the randomly assigned class of a given complex is consistent to its real binding affinity. Predictions were carried out for all complexes in the benchmark. This process was then repeated 100 times. shown by the black bar in Figure 3a, the average accuracy of this random guessing model is 0.47. The much higher accuracy of our machine learning method confirms its power in predicting whether the binding affinity of an interaction between a specific TCR and its corresponding antigen is higher or lower than a predefined threshold. We further applied three additional models with the same random-forest classification algorithm and cross-validation process, but different inputs. The first one used the total number of interfacial residue pairs in each complex. The results of this classifier are shown by the blue bar in Figure 3a. The overall accuracy is 0.55, only slightly better than random guessing. This confirms that it is not possible to predict binding affinity only based on the number of interactions between TCRs and pMHC. The inputs of the second classifier have 4 dimensions, corresponds to the numbers of interfacial residue pairs in four different compartments. The inputs of the third classifier have 28 dimensions, corresponding to all possible combinations of an interfacial residue pair. While the second classifier only captures the structural information at binding interface, the third classifier only captures the sequence information. The results of these two classifiers are shown by the green and blue bars in Figure 3a. The overall accuracies are 0.67 and 0.71, respectively. Therefore, the classifier combines both structural and sequence information achieved the highest accuracy in predicting ranges of binding affinity between TCRs and pMHC.

In order to evaluate the performance of the classification method on a systematical level, we further adjusted the threshold of binding affinity into different values. Specifically, the threshold was raised from the lowest value (−12cal/mol) to the highest value (−4cal/mol). For each threshold value, leave-one-out cross-validation was carried out for all 572 entries. After the cross-validation, we calculated sensitivity, specificity, precision and overall accuracy of predictions under different values of threshold. Sensitivity is defined as the percentage of correct predictions among all complexes in the dataset which binding affinities are lower than the threshold. Specificity is defined as the percentage of correct predictions among all complexes in the dataset which binding affinities are higher than the threshold. Precision is defined by calculating the ratio between the number of complexes that are correctly predicted to be lower than the threshold versus the total number of predictions that are reported to be lower than the threshold. Figure 3b plots the calculated results as a function of threshold values. The x-axis in the figure is the change of threshold, while the sensitivity, specificity, precision and overall accuracy were plotted as black, green, blue and red curves along the y-axis, respectively. The figure shows that the sensitivity and precision increase from low level to 1, while the specificity decreases to 0 along with the raise of threshold from the lowest to the highest value. When the threshold equals −6.5kcal/mol, corresponding to the above-mentioned situation in which two classes are equally divided, the system achieves the optimal performance in which specificity, precision, sensitivity and accuracy are all higher than 70%.

Further analysis has been carried out to test the classification results. In detail, after cross-validation was performed to all complexes in the benchmark for a given threshold, we also investigated the correlation between true positive rate (TPR) and false positive rate (FPR) from the classification results. The TPR is equivalent to sensitivity, based on the definition. The FPR, on the other hand, is defined as the ratio between the total number of false positive predictions versus the total number of complexes that were predicted as higher than the threshold, whereas a false positive prediction corresponds to a wrongly classified complex which real binding affinity is lower than the threshold. TPR and FPR were collectively changed under different values of threshold, leading into a collection of points as shown in Figure 3c. Statistically, these points form a receiver operating characteristic (ROC) curve [36, 37]. We compared it with the dashed diagonal which is known as the line of no-discrimination indicating that the test is completely based on random guess. Figure 3c shows that the TPRs under all different values of threshold are consistently higher than the FPRs. For instance, we obtained a TPR of 0.75 when FPR equals 0.3. Therefore, the ROC curve represents the good quality of our classification data on a systematical level.

In order to further evaluate the predictive power of our approach and rule out the potential issue of over-fitting during cross-validation of machine learning, an independent dataset was constructed to test the model. Specifically, the new testing dataset consists of a total number of 42 entries which are not included in the ATLAS database. It contains 10 different alleles of MHC. The structures of these TCR-pMHC complexes were downloaded from PDB and corresponding experimental binding affinities were collected from the relevant literatures. Using above optimized threshold (−6.5kcal/mol), the 42 entries can be divided into two classes with equal amount. The random forest classifier was then applied to recognize each entry in the dataset. In detail, all 572 complexes from the ATLAS database were used as training set. After training, all 42 entries from the new independent dataset were fed into the classifier as inputs for prediction. Consequently, our random forest classifier successfully recognized the class of 26 complexes out of these 42 entries, corresponding to an overall accuracy of 62%. The result of this independent evaluation is comparable to the accuracy from cross-validation, indicating that our method can really be applied to predict if the binding affinity of a newly discovered TCR-pMHC complex is stronger or weaker than a predefined threshold. Detailed information of all TCR-pMHC complexes in the testing dataset, including their PDB id, experimentally measured binding affinities, and our prediction results for each entry can be found in Supplemental Table S2.

In addition to predict whether the binding affinity of a complex is stronger or weaker than a threshold, we further tested if our method is capable to produce more detailed classification. Specifically, we first divided all complexes into three classes. Any complex which binding affinity is stronger than −8 kcal/mol is in the first class labeled as “strong interactions”. On the other side, any complex which binding affinity is weaker than −6 kcal/mol is in the second class labeled as “weak interactions”. Finally, any complex which binding affinity is in between of −6 and −8 kcal/mol is in the third class labeled as “moderate interactions”. Based on the leave-on-out cross-validation, the random forest classifier successfully recognized the class of 389 complexes out of 572 entries in the benchmark set, corresponding to an overall accuracy of 0.68. The accuracy is defined by calculating the ratio between the number of correct predictions versus the total number of entries in the dataset, whereas a correct prediction is defined as a complex which predicted class is consistent to the range of its real binding affinity. The results are shown by the red bar in Figure 4a. Comparing with the study in which complexes were classified into two groups (the black bar in Figure 4a), the accuracy is only slightly lower.

Figure 4:

In addition to predict whether the binding affinity of a complex is stronger or weaker than a threshold, we further tested if our method is capable to produce more detailed classification. The results are summarized (a). The overall accuracy of the cross-validation results in which complexes were classified into two, three and five groups are shown by the black red and blue bars, respectively. The green bar represents the control study in which predictions were made purely by random guessing. Moreover, in order to test which compartment makes more contributions to binding affinity, we designed four random forest classifiers. Each classifier uses the 28 combinations of interfacial residue pairs in one of the four compartments as inputs, whereas the outputs fell into five classes. The accuracy of the cross-validation results is plotted in (b) for each classifier which compartment is indexed at the bottom.

Secondly, the binding affinities of complexes in the benchmark were divided into five classes with an interval of 2 kcal/mol. In detail, complexes which binding affinities are weaker than −6 kcal/mol belong to the first class; complexes which binding affinities are between −6 and −8 kcal/mol belong to the second class; complexes which binding affinities are between −8 and −10 kcal/mol belong to the third class; complexes which binding affinities are between −10 and −12 kcal/mol belong to the fourth class. Finally, complexes which binding affinities are stronger than −12 kcal/mol belong to the fifth class. Based on the leave-on-out cross-validation, the random forest classifier successfully recognized the class of 366 complexes out of 572 entries in the benchmark set, corresponding to an overall accuracy of 0.64, as shown by the blue bar in Figure 4a. To evaluate the significance of this classification results, a control study was carried out in which predictions were made purely by random guessing. All TCR-pMHC complexes were randomly assigned to one of the five classes with equal probabilities. We then checked whether the randomly assigned class of a given complex is consistent to the range of its real binding affinity. This process was then repeated 100 times. shown by the green bar in Figure 4a, the average accuracy of this random guessing model is 0.18. The much higher accuracy of our random forest classifier confirms its power in predicting the relative ranges of binding affinity for interactions between specific TCRs and their corresponding antigens within a resolution of 2 kcal/mol.

We divided the binding interface between TCR and pMHC into four compartments based on their structural properties. In order to test which compartment makes more contributions to binding affinity, we designed four random forest classifiers. Each classifier uses the 28 combinations of interfacial residue pairs in one of the four compartments as inputs. The outputs fell into five classes, based on the range of binding affinity as described in the last paragraph. The results from cross-validation are summarized in Figure 4b. The figure shows that if we only used the interfacial residue pairs between the hypervariable loops in TCRs and the antigen peptides as inputs (the compartment “HP”), the random forest classifier successfully recognized the class of 326 complexes out of 572 entries in the benchmark set, corresponding to an overall accuracy of 0.57. This is represented by the red bar in Figure 4b. Similarly, when we only used the interfacial residue pairs in the other three compartments “MG”, “MH” and “PG”, the random forest classifiers successfully recognized the class of 337, 349, and 326 complexes out of 572 entries in the benchmark set, respectively. This corresponds to the overall accuracies of 0.59, 0.61 and 0.57, represented by the orange, green and blue bars in the figure. In comparison, as we mentioned above, if the interfacial residues pairs from all four compartment were fed into one classifier, we can successfully achieve an overall accuracy of 0.64, represented by the black bar in Figure 4b. These testing results suggest that while interactions from all compartments of binding interface contribute to binding affinity, the interfacial residue pairs between the hypervariable loops in TCR and the α₁/α₂ helices in MHC are more sensitive to the stability of TCR-pMHC complexes.

Finally, average profiles of the feature space were plotted in Figure 5. The combinations between all 7 coarse-grained groups of amino acids are indexed along the x-axis, whereas the y-axis represents the probability for a pair of groups appearing at the specific compartment of binding interfaces. The profiles of probabilities for all combinations of residues between hypervariable loops and antigen peptides, corresponding to the compartment of “PH”, are shown in Figure 5a. Similarly, the profiles of probabilities for all combinations of interfacial residue pairs in the compartments of “MG”, “MH”, and “PG” are shown in Figure 5b, 5c and 5d, respectively. The correspondence between the 20 amino acids and the 7 coarse-grained groups is listed on the right side of the figure. The black squares indicate the probabilities of interfacial residue pairs averaged over all TCR-pMHC complexes in the weak binding class which affinities are higher than the threshold −6.45 kcal/mol, while the red circles indicate the probabilities averaged over all complexes in the strong binding class which affinities are lower than the threshold. The blue triangles correspond to the differences between these two probabilities for a specific combination of interfacial reside pairs.

Figure 5:

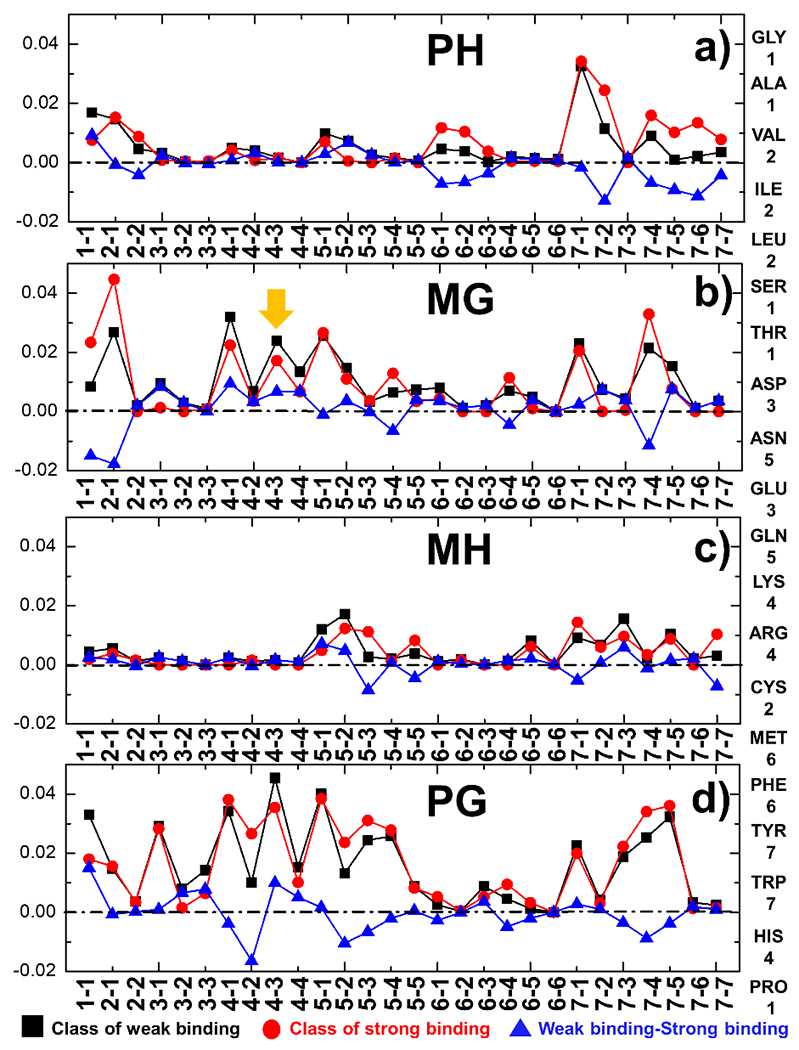
The profiles of probabilities for all 28 combinations of interfacial residue pairs from the compartments “PH”, “”MG”, “MH”, and “PG” are shown in (a), (b), (c) and (d), respectively. The combinations between all 7 coarse-grained groups of amino acids are indexed along the x-axis. The relations between the 20 amino acids and the 7 coarse-grained groups that they belong to are listed on the right-hand side. The black squares and red circles indicate the probabilities of interfacial residue pairs averaged over all TCR-pMHC complexes in the classes which affinities are higher and lower than the threshold (−6.45 kcal/mol), respectively. Finally, the blue triangles correspond to the differences of probability between these two classes for a specific combination of residue pairs.

The profiles shown in Figure 5 can provide some insights on the mechanisms underlying the binding between TCRs and pMHC. For instance, the right side of Figure 5a indicates that residues in the 7^th coarse-grained group are more likely to form interactions between hypervariable loops and antigen peptides in the TCR-pMHC complexes with strong binding affinities. The 7^th coarse-grained group contains amino acids which side-chains have large aromatic rings, such as Tyrosine and Tryptophan. One of such examples is the complex formed between human TCR B7 and the viral peptide TAX presented by class I MHC HLA-A*0201 [38]. The structure of the complex is shown in Figure 6a, in which TCR, peptide and MHC are plotted with carton representation in grey, green and black, respectively. The PDB id of the complex is 1BD2 and its experimentally measured binding affinity is −8.01 kcal/mol. The binding interface of the complex is further highlighted in Figure 6b, whereas all side-chain atoms of residues in the peptide are shown and the hypervariable loops of TCR are colored in red. The figure indicates that a Tyrosine is located in the middle of the peptide. This residue forms a contact with another Tyrosine from one of the hypervariable loops in TCR.

Figure 6:

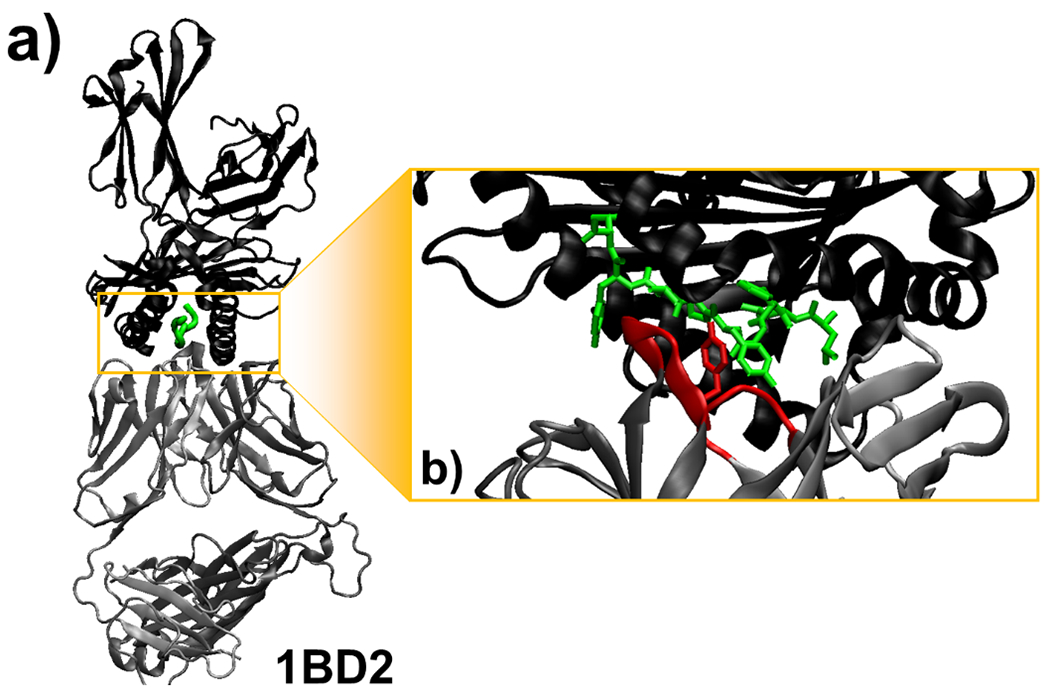
We found that residues which side-chains have large aromatic rings are more likely to form interactions between hypervariable loops and antigen peptides in the TCR-pMHC complexes with strong binding affinities. One example is the complex formed between human TCR B7 and the viral peptide TAX presented by class I MHC HLA-A*0201, which structure is shown (a). In the complex (PDB id 1BD2), TCR, peptide and MHC are plotted with carton representation in grey, green and black, respectively. The binding interface of the complex is further highlighted in (b), where a Tyrosine in the middle of the peptide forms a contact with another Tyrosine from one of the hypervariable loops in TCR which are colored in red.

On the other hand, the electrostatic interactions between positively charged and negatively charged residues are less frequently observed in the complexes with strong binding affinity than in the complexes with weak binding affinity. The positively charged amino acids, aspartic acid and glutamic acid, belong to the 3^rd coarse-grained group, while the negatively charged amino acids belong to the 4^th coarse-grained group. For instance, Figure 5b suggests that the probability of interactions between these two groups is lower for the complexes with strong binding affinities between their MHC and germline loops, which is marked by the orange arrow. Taken together, our study revealed that instead of electrostatic interactions, TCR-pMHC complexes with strong binding affinity prefer hydrophobic interactions between amino acids with large aromatic rings. This is consistent to the previous observation, which found the enrichment of hydrophobic/aromatic amino acids in the center of antigen peptides [39]. A more recent study also confirmed that aromatic and hydrophobic sidechains are more prevalent than charged sidechains in epitope residues that directly interact with the TCR [25]. The underlying mechanism can be described as follows. The electrostatic interactions depend highly on angles and distances. During the formation of TCR-pMHC complex, removal of these interactions from bulk water to binding interfaces is energetically expensive. In contrast, burial of a hydrophobic and aromatic residue from bulk water to binding interfaces is always favorable, and thus can contribute more to binding affinity. Similar mechanisms have also been proposed previously [12].

Concluding Discussions

The activities of T cells in the adaptive immune system highly depend on how their TCRs recognize the corresponding targets from a large repertoire of pMHC complexes [40]. On the other side of this specificity is the cross-reactivity of TCRs, in which a large number of peptides with little sequence similarity can be shared by the same TCRs. Both specificity and cross-reactivity are shaped by the binding affinities of different TCRs-pMHC complexes. The binding affinities, furthermore, are determined by the sequence and structural properties at the interfaces between TCRs and pMHC. While more and more structures of TCR-pMHC complexes have been deposited in PDB, a wealth of data on binding affinity has been measured by various experimental techniques. This enabled us to develop a random forest classifier for predicting the binding affinities between TCR and pMHC based on the structure of their complexes. Specifically, the structure and sequence of a given complex were projected onto a high-dimensional feature space as the input of the classifier, which was then trained by all the available entries in the ATLAS database. Based on the cross-validation and the further prediction on a new independent dataset, we found that our method can successfully recognize whether the binding affinity of a given TCR-pMHC complex is stronger than the predetermined threshold. Moreover, we can classify the binding affinities of all TCR-pMHC complexes into groups within the range of 2kcal/mol with an overall accuracy approximately around 64%.

Our study divides the binding interface of a TCR-pMHC complex into four structurally distinguishable regions: 1) between hypervariable loops from TCR and peptides; 2) between germline loops from TCR and α₁/α₂ helices from MHC; 3) between hypervariable loops from TCR and α₁/α₂ helices from MHC; and 4) between germline loops from TCR and peptides. Although hypervariable loops are directly involved in peptide recognition, we found that residue pairs from all these four regions of binding interface contribute to binding affinity. It is consistent to previous studies. For instance, in the complex of A6 TCR, the peptide Tax_11-19, and the class I MHC HLA-A2, the specificity is contributed by not only the interfaces between CDR3α loop and the peptide, but also the key electrostatic interactions formed between CDR3α loop and α₁ helix in MHC [41]. While current efforts of engineering the binding affinity of TCR-pMHC interactions mainly focus on the interface between hypervariable loops and peptides, our study suggests that residues from other regions of the interface can also potentially be taken into account. Moreover, we show that TCR-pMHC complexes with strong binding affinity prefer hydrophobic interactions between amino acids with large aromatic rings instead of electrostatic interactions. Our results therefore provide insights to design engineered TCRs which enhance the specificity for their targeted epitopes. Taken together, this method can serve as a useful addition to a suite of existing approaches which study binding between TCR and pMHC.

We showed that a threshold of −6.45 kcal/mol can divide the affinities of TCR-pMHC complexes in the ATLAS database into two groups with equal amount. We also showed that the cross-validation of our machine learning classification achieved the optimal performance when the threshold equals a very close value (−6.5 kcal/mol). This binding free energy corresponds to an equilibrium constant in the scale of ~10μM. It is widely accepted that a pMHC which binds to TCR with an equilibrium constant lower than 10μM is regarded as a strong agonist. For instance, the best anti-pathogen TCRs interact with foreign-peptide presenting MHC with dissociation constants in the range of 0.1–10 μM [42]. On the other hand, a pMHC which binds to TCR with an equilibrium constant higher than 10μM is regarded as a weak agonist. For instance, TCRs isolated from anticancer and autoimmune T-cells react weakly with self-peptide presenting pMHC in the range of 20–500 μM [43]. Moreover, a recent study showed there is an affinity threshold around 10μM for maximal anti-tumoral activity and autoreactivity which is necessary for the immune system to avoid self-damage [44]. These experimental works reflect the biological relevance of the threshold in our machine learning classifier, although it was assigned computationally.

Additionally, we also classified TCR-pMHC complexes into five groups based on their binding affinities with an interval of 2kcal/mol. Similar to our classification, previous studies also defined five categories based on the relationship between T cell activities and TCR affinities: no activity; antagonist/weak agonist; agonist, strong agonist and cross-reactive [45], although there is no clear boundary between different categories. This suggests that our predictions on the brief range of binding affinity for a specific interaction between TCR pMHC could provide potential insights to T cell activities. While our study is the first trial to predict binding affinities of TCR-pMHC interactions, it has much room for improvements. One possibility is to use the smaller free energy interval so that binding affinity can be predicted with higher resolution, considering that the 2 kcal/mol interval used in current study is equivalent to a 30-fold variation in dissociation constant. However, smaller intervals in binding affinity indicate that the dataset needs to be divided into more classes and there will be fewer entries in each class. The lack of enough datapoints during training could affect the performance of classification. We expect that this situation will be improved in the future, when more experimental data will be accumulated in the database. An alternative strategy is to use more advanced computational models such as deep learning, which has recently gained increasing attention in the field of bioinformatics [46, 47].

It is worth mentioning that the prediction of our machine learning classifier could also be affected by the inconsistency in the ATLAS database in which experimental data were collected from different literatures. It was well documented that different value of binding affinity can be derived for the same protein-protein interactions by using different measuring techniques, or by the same technique but under different experimental conditions [48]. For an example, the complex between TCR A6 and the Tax peptide presented by the class I MHC HLA-A*0201 with an E166A mutation, the measured dissociation constant in one study equals 1.9 mM, corresponding to the binding free energy of −3.69 kcal/mol [35]. In another study, however, the measured dissociation constant for the same complex with the same mutation equals 4.0 μM, corresponding to the binding free energy of −7.36 kcal/mol [49]. Both entries are presented in the ATLAS database. These different affinities of the same TCR-pMHC complexes can cause ambiguous signals to the classifier, increase the noise during training and thus reduce the prediction accuracy. A more careful curation of the database, including the removal of these ambiguous items, will be necessary to improve the performance our machine learning classifier in the future.

Another factor which could potentially affect the performance of our model is the usage of distance cutoff which defines an interfacial residue pair between TCR and pMHC. As we mentioned in the Methods, this distance cutoff was adopted empirically, while only one value was assigned to determine all intermolecular interactions. In reality, the effective distance range of interactions between proteins highly depends on their biophysical properties. For instance, hydrogen bonds normally have a distance cutoff of 3.5 Angstrom, while the range of electrostatic interactions are usually much longer. An upgraded version of our classifier will envision the integration of various physics-based interactions, including hydrogen bonds, salt bridges, and hydrophobic effect, into the feature space. We should also use different distance cutoffs to determine these interactions corresponding to their specific categories.