Abstract
Spatial skill is highly related to success in math and science (e.g., Casey, Nuttall, Pezaris, & Benbow, 1995). However, little work has investigated the cognitive pathways by which the relation between spatial skill and math achievement emerges. We hypothesized that spatial skill plays a crucial role in the development of numerical reasoning by helping children to create a spatially meaningful, powerful numerical representation—the linear number line. In turn, a strong linear number representation improves other aspects of numerical knowledge such as arithmetic estimation. We tested this hypothesis using 2 longitudinal data sets. First, we found that children’s spatial skill (i.e., mental transformation ability) at the beginning of 1st and 2nd grades predicted improvement in linear number line knowledge over the course of the school year. Second, we found that children’s spatial skill at age 5 years predicted their performance on an approximate symbolic calculation task at age 8 and that this relation was mediated by children’s linear number line knowledge at age 6. The results are consistent with the hypothesis that spatial skill can improve children’s development of numerical knowledge by helping them to acquire a linear spatial representation of numbers.
Keywords: number line, spatial skill, math development
Previous research has established that spatial skill is related to achievement in math and science (Casey, Nuttall, Pezaris, & Benbow, 1995; Shea, Lubinski, & Benbow, 2001; Wai, Lubinski, & Benbow, 2009; Webb, Lubinski, & Benbow, 2007). This relation is evident across a variety of spatial tasks (Delgado & Prieto, 2004; Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Guay & McDaniel, 1977) and mathematical domains (Battista, 1990; Kyttälä & Lehto, 2008; Tolar, Lederberg, & Fletcher, 2009) and has been shown to emerge early in development (de Hevia & Spelke, 2010; Kyttälä, Aunio, Lehto, Van Luit, & Hautamäki, 2003). However, little work has investigated the various underlying pathways by which spatial skill can improve mathematics early in development. We hypothesized that spatial skill plays a crucial role in the development of numerical reasoning by helping children to create a spatially meaningful, powerful numerical representation: the linear number line.
Relations Between Spatial Skill and Math Achievement
Positive relations between spatial skill and math achievement have been reported across a variety of ages and tasks. For example, preschoolers’ spatial skill, as measured by their ability to reproduce geometric designs and perform a spatial scanning task, is positively correlated with their adaptive strategy use in an arithmetic task (Geary & Burlingham-Dubree, 1989). Early elementary school students’ visuomotor skill (coordinating visual perception and motor planning, differentiating between similar figures, and recalling previously observed images) correlates with their math achievement both concurrently and predictively (Kulp, 1999; Kurdek & Sinclair, 2001; Lachance & Mazzocco, 2006). Adolescents’ spatial–mechanical reasoning is correlated with their performance on a math test measuring fractions, number sense, measurement, geometry, and data representation (Casey, Nuttall, & Pezaris, 2001). Similarly, controlling for verbal ability, mental rotation ability among college students and high-ability middle-school students predicts performance on the math portion of the Scholastic Aptitude Test (SAT-M; Casey et al., 1995). Further, individuals with high spatial ability are more likely to earn college and graduate degrees and enter fields involving engineering, computer science, and mathematics (Humphreys, Lubinski, & Yao, 1993; Shea et al., 2001; Wai et al., 2009; Webb et al, 2007).
These studies provide strong evidence for a link between spatial skill and math achievement. However, in investigating this relation, studies have typically used composite scores encompassing a variety of math and spatial tasks (e.g., Casey et al, 2001; Kurdek & Sinclair, 2001; Wai et al, 2009). Although a few studies have investigated this relation in more detail (e.g., showing that adults’ mental rotation ability is related to their ability to solve mathematical word problems; Johnson, 1984), on the whole, little research to date has investigated whether specific components of spatial skills are related to specific components of math skills (see Mix & Cheng, in press, for a recent review). It is especially difficult to examine specific components of spatial skills that might be related to math achievement since researchers have not agreed upon a typology of spatial skills (see Uttal et al., 2012). Linn and Petersen (1985) have proposed a three-component model of spatial skills: mental rotation (mentally rotating a 2–D or 3–D object), spatial perception (determining spatial relations with respect to the orientation of one’s own body while ignoring distracting information; e.g., rod and frame test, water level test), and spatial visualization (processing multistep manipulations of spatial information; e.g., paper-folding test, embedded figures test). However, others have argued that this typology is too vague and that the spatial visualization category is used as a catchall for a variety of tasks that may not be conceptually related (e.g., Voyer, Voyer, & Bryden, 1995). Although the question of whether certain components of spatial skills relate differentially to math achievement is theoretically important, in the current work we focus on why spatial skill might be related to math achievement and for which domains or components of math achievement this relation holds.
One possibility is that spatial skill is primarily important for achievement in math and science domains that are ostensibly spatial, such as geometry and engineering, where reasoning about spatial relations is prevalent and the representation of problems and concepts often requires creating, maintaining, and performing transformations on 2–D or 3–D visuospatial models. For instance, spatial visualization predicts success in geometry problem solving in high school (Battista, 1990) as well as on measures that incorporate geometry as part of a larger battery of math tasks (Casey et al., 2001; Kurdek & Sinclair, 2001; Lachance & Mazzocco, 2006). Nevertheless, the fact that spatial skill predicts performance on broad measures of math achievement, such as the SAT-M as well as word problems (Casey et al., 1995; Delgado & Prieto, 2004; Hegarty & Kozhevnikov, 1999; Johnson, 1984; Kyttälä & Lehto, 2008), suggests that spatial processing might be implicated in other domains of mathematics beyond those that are ostensibly spatial.
A second less direct possibility is that spatial skill may enhance the numerical representations that are important in many mathematical tasks, even those that may not appear ostensibly spatial. We explore this second possibility and in doing so provide a mechanism through which spatial skill may improve numerical aspects of math performance. Specifically, we hypothesize that spatial skill plays a role in the numerical development of early elementary school children by helping them form a powerful representation of numbers—the mental number line. The number line representation, in turn, is related to other aspects of numerical knowledge such as approximate calculation and estimation (e.g., Booth & Siegler, 2008). Thus, we propose that one mechanism linking spatial skill with math achievement is the acquisition of a spatial, linear number line representation.
Associations Between Numbers and Space: The Number Line Representation
Evidence from a variety of sources suggests that humans are predisposed to associate numbers with space (e.g., Dehaene, Bossini, & Giraux, 1993; de Hevia & Spelke, 2010; Pinel, Piazza, Le Bihan, & Dehaene, 2004). Viewing numerically small (e.g., 2, 3, 4) versus large (e.g., 7, 8, 9) numbers causes implicit spatial biases in adults’ motor responses, where individuals respond faster to large numbers with their right hand and faster to small numbers with their left hand (what is termed the spatial numeric association of response codes, or the SNARC effect; Dehaene et al., 1993; Fias & Fischer, 2005). The SNARC effect suggests that participants are imagining numbers along a number line where small numbers are placed on the left and large numbers on the right. Similarly, individuals with hemispatial neglect, who make systematic errors when asked to bisect a physical line (i.e., individuals with left-side neglect err to the right of the midpoint), make equivalent errors when asked to bisect an abstract numerical interval without calculating (Zorzi, Priftis, & Umiltà, 2002). For example, an individual with left-side neglect might guess that 17 is the midpoint between 11 and 19, erring to the “right,” assuming a left-to-right mental number line. These results provide convergent evidence that humans’ internal representation of numbers is spatial in nature.
Formal schooling does not appear to be a prerequisite for the ability to associate numbers with space, as infants can associate increasing numbers of dots with increasing line lengths (but cannot associate increasing numbers of dots with decreasing line lengths; de Hevia & Spelke, 2010), and adults from nonnumerate cultures are able to order nonsymbolic numbers (sets of dots) along a linear number line (Dehaene, Izard, Spelke, & Pica, 2008). Indeed, the brain regions involved in numerical representations in the intraparietal sulcus overlap with areas involved in discriminating spatial dimensions such as size and length, suggesting underlying representations of space and number that share cortical regions (Pinel et al., 2004). While it is not yet known whether these findings represent a unified phenomenon or multiple distinct ways in which spatial and numerical representations can be linked, they indicate that humans are predisposed to associate numbers with space.
Importantly, this predisposition to associate space and numbers is culturally codified through the linear number line representation of Arabic numerals. Although children may intuitively associate numerical and spatial representations, they do not represent numbers linearly right away; rather, children’s understanding of the number line undergoes an important developmental shift, becoming increasingly linear over developmental time. While some investigators posit that young children’s intuitive representation of numbers is logarithmic, meaning that smaller numbers are more distinguishable from each other than are larger numbers (Booth & Siegler, 2006; Siegler & Booth, 2004; Siegler & Opfer, 2003), others posit that all age groups use a proportional strategy in estimating the location of numbers but that older children respond more linearly because they have more accurate knowledge of the end point of the number line (Barth & Paladino, 2011). Although there is disagreement about the mechanism explaining the shift toward greater linearity, researchers agree that children’s responses become increasingly linear over time. Further, Siegler and Ramani (2008) have suggested that exposure to relevant cultural representations—such as rulers, number lines, and linear numerical board games—promotes the shift toward a more linear representation of the Arabic numerals.
Relations Between Linear Number Line Knowledge and Math Achievement
One well-established method of measuring the linearity of children’s mental number line involves showing children a picture of a number line with only the end points labeled (e.g., 0 and 100) and asking them to show where other numbers would go on the number line (Siegler & Opfer, 2003). Using this measure, by first grade children typically represent the numbers 1–10 in a linear fashion but represent the numbers 0–100 logarithmically (Berteletti, Lucangeli, Piazza, Dehaene, & Zorzi, 2010; Siegler & Booth, 2004). By second grade, most children represent 0–100 linearly but continue to represent 0–1,000 logarithmically until fourth grade (Booth & Siegler, 2006; Siegler & Booth, 2004). As children develop a linear number line representation, they do not lose the logarithmic representation; rather, they continue to deploy the logarithmic representation in less familiar situations such as those involving higher numbers (Thompson & Siegler, 2010). Further, the linear number line representation extends only to Arabic numerals; even educated adults are unable to represent nonsymbolic number representations (such as dot arrays) in a linear fashion and continue to represent nonsymbolic numbers logarithmically throughout life (Dehaene et al., 2008).
The ability to correctly create and interpret symbolic linear number lines is related to other formal mathematics skills involving categorizing and recalling numbers, approximate calculation, and symbolic estimation (Booth & Siegler, 2008; Laski & Siegler, 2007; Siegler & Ramani, 2008, 2009; Thompson & Siegler, 2010). Children who perform linearly on a number line task also perform linearly on other nonspatial, symbolic numerical estimation tasks, such as categorizing which numbers are “small,” “medium,” or “big” (Laski & Siegler, 2007; Thompson & Siegler, 2010). This suggests that performance on the number line task is indicative of a mental representation of Arabic numerals as equidistant from each other, which can be observed across a variety of approximation tasks.
Importantly, activating or improving children’s linear number representation leads to broad improvements in numerical reasoning. Showing first graders correct magnitude representations of addends (e.g., showing number line bars representing “36” and “48” while solving the problem 36 + 48) improves children’s accuracy on an approximate symbolic addition task (Booth & Siegler, 2008). Similarly, when low-income preschool children are given experience playing a linear numerical board game, their ability to space the numbers linearly on a number line improves, and this knowledge generalizes to improvements in the ability to compare numerical magnitudes (e.g., “Which is more, 3 or 6?”; Siegler & Ramani, 2009). Taken together, the existing research suggests that these experiences help linearize children’s representation of the magnitudes of the Arabic numerals. The beneficial effects of this increased numerical precision are most frequently reported on tasks involving approximate symbolic magnitudes (e.g., Booth & Siegler, 2008; Siegler & Ramani, 2009), although it is possible that the benefits extend to exact numerical tasks as well.
The Present Study: Linking Spatial Skill, Linear Number Line Knowledge, and Math
In light of the literature just outlined, we propose that individual differences in spatial ability influence how quickly children develop a linear mental representation of Arabic numerals and that this representation in turn helps children succeed on symbolic numerical tasks, even when those tasks do not require explicit spatial representations. We have chosen to assess spatial skill by measuring mental transformation ability using a test of mental rotation ability in Study 1 (Thurstone, 1938) and a test of mental rotation and mental translation ability in Study 2 (Levine, Huttenlocher, Taylor, & Langrock, 1999). We chose mental transformation because this skill, particularly mental rotation, has received the most attention in previous research on the relation between math and spatial skill (e.g., Humphreys, Lubinski, & Yao, 1993; Wai et al, 2009) and has been shown to be related to a variety of spatial tasks (e.g., Vandenberg & Kuse, 1978). However, we are not theoretically committed to mental transformation as the specific or only spatial skill that is related to children’s linear number line representations. Rather, we have chosen this measure as indicative of children’s general spatial skill level. The question of which components of spatial skill are most important for the development of linear number line knowledge remains an open and important question but is not addressed in the current studies.
Our first hypothesis was that children’s initial spatial skill would predict improvement over time on a number line task. At least one previous study has shown that children’s visuospatial ability in kindergarten and first grade is correlated contemporaneously with their accuracy on a number line task (Geary et al., 2007); we sought to extend this finding by showing that first and second graders’ spatial skill predicts improvement in number line knowledge over the course of the school year. Our second hypothesis was that children’s initial spatial skill would predict their later performance on a numerical task that is not ostensibly spatial (i.e., a task where the presentation and response formats do not contain meaningful spatial representations) and that their development of a linear number line representation would account for (mediate) this relation. We used an approximate symbolic calculation task as our nonspatial numerical task, since this type of approximate task has been previously shown to be related to number line knowledge (e.g., Booth & Siegler, 2008; Siegler & Ramani, 2009). Finally, given that the linear number line representation is specific to Arabic numerals, we predicted that symbolic number line knowledge would mediate the relation between spatial skill and an approximate symbolic calculation task involving Arabic numerals but not an approximate nonsymbolic calculation task involving dot arrays.1
Study 1
Method
Participants.
This study was conducted as part of a larger longitudinal study of social and cognitive development, in which we explored the relation between teachers’ attitudes and students’ achievement (Beilock, Gunderson, Ramirez, & Levine, 2010). First- and second-grade students were recruited from five public schools in a large urban school district. One hundred sixty-two students (87 girls, 75 boys) participated in the study. From this sample, 10 were excluded (6 girls, 4 boys) because they did not complete the tasks or left the school before the study was complete. The remaining sample of 152 students included 87 first graders (44 girls, 43 boys) and 65 second graders (37 girls, 28 boys). Children’s average age at the time of the first session was 7.1 years (SD = 0.6) and at the time of the second session was 7.6 years (SD = 0.6). Parent reports of race/ethnicity (N = 142) indicated that students were 39% African American, 38% Hispanic, 13% white, 5% Asian, and 6% other or multiple races. Average annual family income was $37,743 (SD = $26,671, N = 134).
Measures and procedure.
Students’ number line knowledge, spatial skill, and math and reading achievement were assessed in a one-on-one session with an experimenter during the first 3 months of the school year. Students’ number line knowledge was assessed again 6 months later, during the last 2 months of the school year. The average time between sessions was 0.50 years (SD = 0.02), and the range was from 0.47 to 0.55 years (173–201 days).
Number line knowledge.
Number line knowledge was assessed using the 0–1,000 number line task (Siegler & Booth, 2004). Children were shown a piece of paper with a horizontal line that was 25 cm long, labeled 0 at the left side and 1,000 at the right side. The experimenter explained the number line by saying, “This number line goes from 0 at this end to 1,000 at this end. If this is 0 and this is 1,000 where would you put N?” The experimenter then held up a card displaying an Arabic numeral, and children responded by drawing a hatch mark through the number line to show the position of that number. The numbers presented were chosen to oversample the lower end of the number line, where discrepancies between logarithmic and linear representations are greatest. At the beginning of the year, the numbers presented were 4, 6, 18, 71, 230, and 780. At the end of the year, the numbers presented were 2, 6, 25, 86, 390, and 810. The numbers were presented in a fixed pseudorandom order. Children were given a new number line for each trial, so that they could not see their previous responses when making each judgment. The number line task was scored by converting children’s responses to the equivalent numerical value and then finding the percentage of variance explained (R2) by the best fitting linear model relating their responses to the number requested. If between one and three trials of the number line task were not completed due to experimenter error or the child’s refusal to complete the item, the child’s data were analyzed using the linear R2 based on the remaining trials. This was the case for two children at the beginning of the year and three children at the end of the year.
Our decision to use linear R2 as our measure of number line performance rather than another commonly used measure, percent absolute error (e.g., Siegler & Booth, 2004), was theoretically motivated. Specifically, we hypothesized that spatial skill would relate most strongly to the linearity of children’s performance, since linearity itself is the meaningful spatial component of number line performance. Thus, we used the measure of number line performance that best captures the linearity of children’s number line estimates, the linear R2.
Spatial skill.
Spatial skill was assessed using the mental rotation subtest of Thurstone’s Primary Mental Abilities Test (Thurstone, 1938; Thurstone & Thurstone, 1949). In this task, children saw a square with a piece missing and were asked to choose which of four shapes would fit together with the first shape to make a square (see Figure 1). The task involves forming and maintaining a visual representation of each shape and mentally rotating the shapes to determine which shape would fit together with the first one. Children completed eight items (shortened from the original 16-item test due to time constraints).
Figure 1.
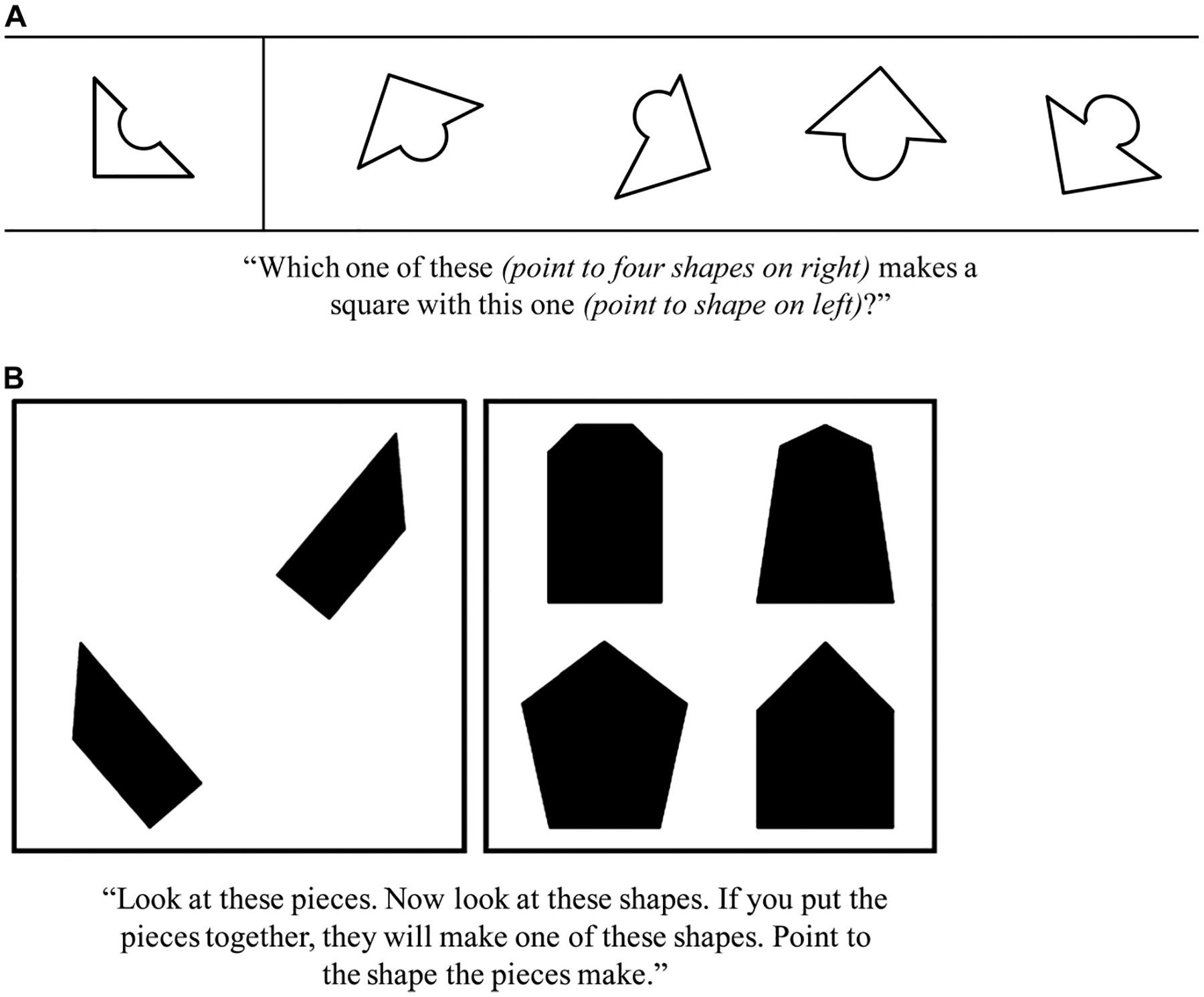
A: Illustration of the type of items used on the Thurstone mental rotation task (Study 1). B: A sample item from the children’s mental transformation task (Study 2).
Math achievement.
Students’ math achievement was assessed using the Applied Problems subtest of the nationally normed Woodcock-Johnson III Tests of Achievement (Woodcock, McGrew, & Mather, 2001). This task requires students to solve orally presented word problems that involve identifying information relevant to the problem, choosing an appropriate procedure to solve the problem, and carrying out that procedure (typically arithmetic calculations). The problems are ordered by increasing level of difficulty. For example, some of the early problems require children to solve single-digit arithmetic problems and identify the correct time on a clock, while later problems require children to solve two-digit arithmetic problems, perform monetary calculations, and understand simple fractions. Children are given paper and pencil at any point in the test if they request them and are offered paper and pencil starting at Item 30 (a problem appropriate for the beginning of third grade). The task is normed for kindergarten through adulthood. Testing continued until both a basal (six items in a row correct) and ceiling (six items in a row incorrect) were established. Due to experimenter error, some students completed between three and five items for the basal or ceiling; these students were scored as if they had completed the full basal or ceiling. Students’ W scores, which transform their raw scores into a Rasch-scaled score with equal intervals, were used for all analyses involving the Applied Problems test (a score of 500 is the approximate average performance of a 10-year-old; McGrew & Woodcock, 2001; Woodcock, 1999). The W scores are measured on a norm-referenced, equal-interval scale, meaning that a score difference of 10 units represents the same amount of growth regardless of where on the scale it falls. Given that our research questions involved development and individual differences, we felt that it was appropriate to use these developmentally meaningful scaled scores when possible.
Reading achievement.
Students’ reading achievement was assessed using the Letter–Word Identification subtest of the Woodcock-Johnson III Tests of Achievement, a decoding task. This task requires students to recognize letters and read words of increasing difficulty. It is administered using the basal and ceiling procedure described earlier. Students’ W scores were used for all analyses involving the Letter–Word Identification test.
Results
Descriptive statistics.
The mean scores on the number line, mental rotation, math, and reading tasks are reported in Table 1. The percentage of variance explained by the linear function on the number line task increased significantly from the beginning (M = 0.55, SD = 0.19) to the end (M = 0.59, SD = 0.19) of the year, t(151) = 2.27, p < .05. On the mental rotation task, children were well above the chance level of 25%, averaging 4.6 correct out of 8 (57.5%), t(151) = 20.0, p < .001. The range of scores spanned the full range of the eight-item task, from 0 to 8 correct.2
Table 1.
Means (Standard Deviations) and Ranges of Assessments Used in Study 1 (N = 152)
| Assessment point and task | M (SD) | Range |
|---|---|---|
| Beginning-of-year scores | ||
| Number line knowledge (0–1,000 number line linear R2) | 0.55 (0.19) | 0.00–0.98 |
| Spatial skill (Thurstone mental rotation; items correct of eight) | 4.62 (1.62) | 0–8 |
| Math achievement (WJ-III Applied Problems W score) | 451.4 (18.1) | 409.0–490.0 |
| Reading achievement (WJ-III Letter–Word Identification W score) | 437.4 (34.0) | 348.0–501.0 |
| End-of-year score | ||
| Number line knowledge (0–1,000 number line linear R2) | 0.59 (0.19) | 0.00–0.99 |
Note. WJ-III = Woodcock-Johnson III Tests of Achievement.
Children’s scores on the math and reading tasks also varied widely. Although the W scores for the math and reading tasks were used for all analyses, we also measured children’s grade-equivalent scores, representing the grade level at which children performed, to understand how our sample performed relative to national norms. We found that, on average, our sample was performing at or above grade level on both math and reading. While the average grade level of the sample was 1.43 (SD = 0.50), the average math grade-equivalent score was 1.62 (SD = 0.89), and the average reading grade-equivalent score was 2.18 (SD = 0.87). There was also wide variation in students’ grade-equivalent scores, ranging from kindergarten to third- and fourth-grade levels on the math and reading tasks, respectively.
The first-order correlations between the tasks are reported in Table 2. All measures were significantly but moderately intercorrelated. None of the measures were so highly correlated as to raise concerns regarding collinearity (all rs < .70). The correlation between math and reading achievement was particularly high, r(150) = 0.63, p < .001, which likely reflects the fact that our measure of general math achievement, the Woodcock-Johnson Applied Problems test, primarily involves orally presented word problems.
Table 2.
Correlations Between Tasks in Study 1 (N = 152)
| Assessment point and task | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Beginning-of-year scores | ||||
| 1. Number line knowledge (0–1,000 number line linear R2)a | — | |||
| 2. Spatial skill (Thurstone mental rotation; items correct of eight) | .25** | — | ||
| 3. Math achievement (WJ-III Applied Problems W score) | .23** | .20* | — | |
| 4. Reading achievement (WJ-III Letter-Word Identification W score) | .24** | .17* | .63*** | — |
| End-of-year score | ||||
| 5. Number line knowledge (0–1,000 number line linear R2)a | .32*** | .27** | .38*** | .22** |
Note. WJ-III = Woodcock-Johnson III Tests of Achievement.
These variables have been transformed using an arcsine transformation {2 × asin[sqrt(x)]}.
p < .05.
p < .01.
p < .001.
Relation between spatial skill and number line knowledge.
Our main question was whether children’s initial spatial skill, as measured by the mental rotation task, predicted improvement in number line knowledge over the course of the school year. To investigate this question, we conducted a series of simultaneous regression models predicting children’s end-of-year number line knowledge controlling for their beginning-of-year number line knowledge (see Table 3).3 In Model 1, we found that children’s beginning-of-year number line knowledge was a significant predictor of their end-of-year number line knowledge (β = .32, t = 4.09, p < .001), accounting for 10% of the variance. Next, we tested our main hypothesis by asking whether children’s initial spatial skill, as measured by the mental rotation task, was a significant predictor of their end-of-year number line knowledge even after controlling for their beginning-of-year number line knowledge (Model 2). We found that, controlling for initial number line knowledge, children’s initial spatial skill significantly predicted their end-of-year number line knowledge (β = .20, t = 2.57, p = .01), accounting for an additional 4% of the variance. In other words, among children who started the year with the same level of number line knowledge, those with greater spatial skill showed greater improvement on the linear number line over the course of the school year.
Table 3.
Regression Models Predicting End-of-Year Number Line Knowledge From Beginning-of-Year Scores (Study 1)
| End-of-year number line linear R2 (0–1,000)a | ||||
|---|---|---|---|---|
| Measure | Model 1 | Model 2 | Model 3 | Model 4 |
| Number line linear R2 (0–1,000)a | .32*** | .27** | .21** | .22** |
| Spatial skill | .20* | .16* | .16* | |
| Math achievement | .30*** | .34*** | ||
| Reading achievement | −.07 | |||
| R2 (%) | 10.0 | 13.9 | 22.0 | 22.3 |
| F | 16.7*** | 12.0*** | 13.9*** | 10.5*** |
| F dfs | (1, 150) | (2, 149) | (3, 148) | (4, 147) |
These variables have been transformed using an arcsine transformation {2 × asin[sqrt(x)]}. Parameter estimates are standardized.
p < .05.
p < .01.
p < .001.
We were also interested in determining whether the relation between initial spatial skill and improvement in number line knowledge could be accounted for by other aspects of children’s initial knowledge, specifically math and reading achievement. In Model 3, we found that children’s conventional math knowledge, as assessed by the Woodcock-Johnson III Applied Problems, was a significant predictor of end-of-year number line knowledge controlling for beginning-of-year number line knowledge and spatial skill (β = .30, t = 3.92, p < .001). However, even when children’s conventional math knowledge and beginning-of-year number line knowledge were accounted for, children’s spatial skill remained a significant predictor of children’s end-of-year number line knowledge (β = .16, t = 2.08, p < .05). Finally, in Model 4, we asked whether children’s verbal skills could account for the relation between spatial skill and growth in number line knowledge. While verbal skills were not a significant predictor of end-of-year number line knowledge controlling for children’s beginning-of-year number line knowledge, spatial skill, and math knowledge (β = −.07, t = −0.74, ns), spatial skill remained a significant predictor of end-of-year number line knowledge (β = .16, t = 2.10, p < .05).
Discussion
Children’s initial spatial skill predicted their end-of-year number line knowledge, even after their initial levels of number line knowledge and conventional math and reading achievement were taken into account. This suggests that spatial skill that is involved in representing, maintaining, and transforming visual representations may facilitate the formation of children’s linear representation of the number line.
However, it is possible that since the number line task is itself spatial in its presentation and response formats, this result may be limited to improvement in the procedural aspects of performing the number line task and not generalize to real conceptual math development. Therefore, in Study 2 we asked whether early spatial skill predicts later performance on a measure of numerical knowledge that is not ostensibly spatial (approximate symbolic calculation) and whether this relation is mediated (or accounted for) by number line knowledge.
Study 2
Method
Participants.
This research was conducted as part of a longitudinal study of child language and mathematical development (Gunderson & Levine, 2011). Forty-two children (26 male, 16 female) participated in this study. They were drawn from a larger sample of 63 children who were selected to be representative of the demographics of Chicago in terms of race/ethnicity and income levels. All children were being raised as monolingual English speakers. From the original sample, eight were excluded because they left the study before it was completed, and 13 were excluded because they did not complete one or more of the tasks that were needed for this study. Parent reports of race/ethnicity indicated that 62% of the children in this study were white, 17% African American, 12% Hispanic, and 10% other or multiple races. Average annual family income was $60,119 (SD = $30,559). The average level of education of the primary caregiver was 15.8 years (SD = 1.9), where 16 years is equivalent to a 4-year college degree.
Measures.
Experimenters visited each child at home and administered four tasks during three or four sessions when the child was between ages 5 and 8 years. The data for this study were gathered in the context of 2-hr sessions consisting of observations and videotaping of naturalistic parent–child interactions and the administration of a variety of cognitive and language tasks.
Spatial skill.
Spatial skill was assessed at age 5.4 (SD = 0.2), when children were in preschool or kindergarten, using the children’s mental transformation task (CMTT; Levine et al., 1999). This task requires children to choose which shape would be made by moving two separate pieces together (see Figure 1). For younger children, the CMTT is more appropriate than the Thurstone mental rotation task used in Study 1, but otherwise it is similar in content and presentation format. Both tasks require children to visualize two pieces moving together to form a single piece, and both tasks also involve a multiple-choice response. Half of the items on the CMTT require mental rotation, and half of the items require mental translation (i.e., mentally moving the pieces without rotating them, a simpler task). Children completed 22 items in one of two forms (Forms A and B) and orders (forward and backward). Form and order were counterbalanced across children. Since children’s performance on the rotation items was highly correlated with their performance on the translation items, r(40) = 0.61, p < .001, and the results reported later did not differ for the rotation versus translation items, we combined these items to form a total spatial skill score.
Vocabulary.
Children’s vocabulary knowledge was measured at age 6.2 (SD = 0.6), when they were in kindergarten, using the Peabody Picture Vocabulary Test–Third Edition (PPVT-III; Dunn & Dunn, 1997). The PPVT-III is a widely used, nationally normed test of vocabulary knowledge. The PPVT-III requires children to choose one of four pictures that matches an orally presented word. Standardized scores based on age were used for all analyses.
Number line knowledge.
Number line knowledge was assessed at age 6.3 (SD = 0.4), when children were in kindergarten, using the 0–100 number line task (Siegler & Opfer, 2003). Since the children in Study 2 were younger at the time of the number line task than those in Study 1, we felt that the 0–100 number range would be a more age-appropriate measure for this sample (as opposed to the 0–1,000 number range used in Study 1), based on data collected by Siegler and Booth (2004). The task was presented as described in Study 1, with the exception that the target numbers were printed in a circle at the top center of the sheet instead of shown on a separate card. The target numbers were 2, 8, 11, 15, 17, 33, 49, 66, 72, and 87. As in Study 1, the percentage of variance (R2) explained by the best fitting linear function was used as our measure of number line knowledge.
Approximate symbolic calculation.
Approximate symbolic calculation skill was assessed at age 8.0 (SD = 0.4), when children were in second grade, using a computerized task in which number symbols were presented and then hidden, and children indicated which side of the screen had a larger total (see Figure 2, Panel A). The task required children to add and subtract approximate symbolic quantities (adapted from Gilmore, McCarthy, & Spelke, 2007). For example, children saw one character (“Sarah”) receive a bag of cookies labeled “20” and then receive a second bag labeled “16.” Then Sarah’s bags were occluded, and a second character (“John”) received a bag labeled “45.” The child’s task was to determine which character had more cookies in total. Children completed eight addition and eight subtraction problems. The numbers presented ranged from 6 to 51, and the ratios for comparison were either 2:3 or 4:5. Refusal to respond to an item was counted as an incorrect response (this occurred on only one item for one participant).
Figure 2.
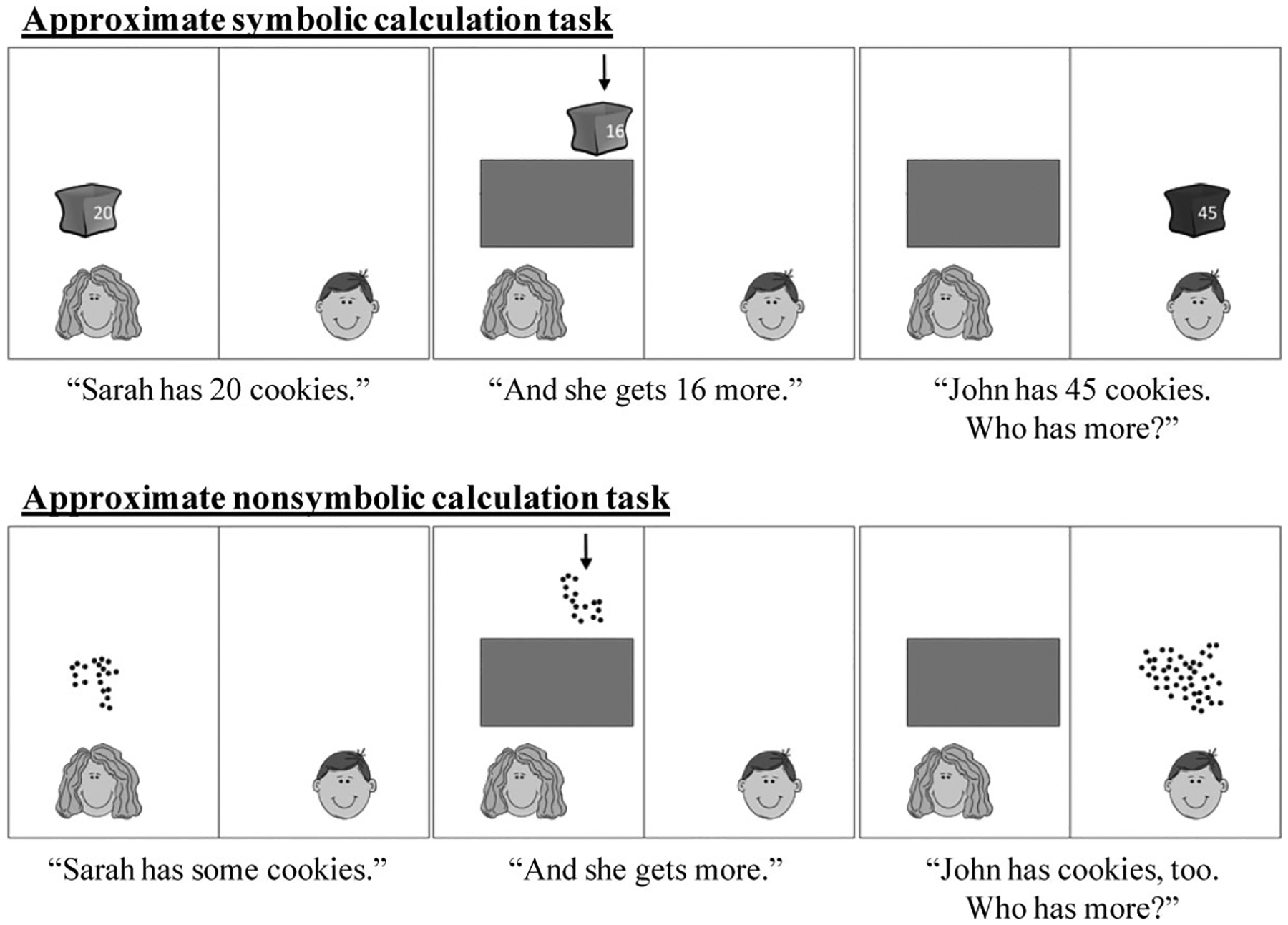
Graphic depiction of the approximate symbolic and nonsymbolic calculation tasks (adapted from “Symbolic Arithmetic Knowledge Without Instruction,” by C. K. Gilmore, S. E. McCarthy, and E. S. Spelke, 2007, Nature, 447, p. 589. Copyright 2007 by Nature Publishing Group). Images are presented sequentially, and children must respond by saying whether Sarah or John has more cookies.
Approximate nonsymbolic calculation.
Approximate nonsymbolic calculation skill was assessed at age 8.0 (SD = 0.4), when children were in second grade, using a procedure that closely paralleled the approximate symbolic calculation task. However, the quantities to be calculated and compared were represented as clusters of a certain number of dots, instead of as Arabic numerals (similar to the nonsymbolic addition task used by Barth et al., 2006). Clusters of dots were presented and then hidden on the computerized display, and children indicated which side of the screen had a larger total (see Figure 2, Panel B). The dot clusters were labeled as some cookies, and no number words were used during the task. The set sizes and ratios were the same as in the approximate symbolic calculation task. Refusal to respond to an item was counted as incorrect (this occurred once each for two participants). The approximate nonsymbolic calculation task always preceded the approximate symbolic calculation task.
Results
Descriptive statistics.
The mean, standard deviation, and range of scores on each task are reported in Table 4. As in Study 1, there was a great deal of variability in children’s performance on all tasks. On the spatial skill task (CMTT), children performed significantly above chance on average (M = 58.0%, SD = 19.4%, relative to a chance level of 25%), t(41) = 11.1, p < .001. Scores varied from 18% to 95% correct. On the vocabulary task, children on average scored above the national norms (M = 108.4, SD = 15.9, relative to the national norm of 100 and SD of 15), with children’s scores varying from 3 standard deviations below to 3 standard deviations above the mean. Similarly, on the number line task children’s average performance was a linear R2 of 57%, with scores ranging from 0% to 96%. On the approximate symbolic calculation task, average scores were significantly above chance(83.5% correct, SD = 13.4%, relative to a chance level of 50%), t(41) = 16.14, p < .001, and again performance ranged from chance level (50%) to a perfect score (100%). Consistent with previous research, children’s performance was significantly better on the items with a wider ratio (2:3 ratio; M = 86.6%, SD = 14.4%) than on the items with a narrower ratio (4:5 ratio; M = 80.4%, SD = 17.1%), t(41) = 2.44, p < .05 (Gilmore et al., 2007). On the approximate nonsymbolic calculation task, average scores were significantly above chance (M = 78.1%, SD = 8.5%, relative to a chance level of 50%), t(41) = 21.35, p < .001, while performance ranged from 56% to 94% correct. Finally, as in the approximate symbolic calculation task, performance on the approximate nonsymbolic calculation task also was better on the items with a wider ratio (2:3 ratio; M = 83.0%, SD = 13.8%) than on the items with a narrower ratio (4:5 ratio; M = 73.2%, SD =12.5%), t(41) = 3.18, p < .01.4
Table 4.
Means (Standard Deviations) and Ranges of Assessments Used in Study 2 (N = 42)
| Task | M (SD) | Range |
|---|---|---|
| Spatial skill (CMTT, items correct of 22; chance = 25%) | 12.8 (4.26) | 4–21 |
| Vocabulary (PPVT-III standardized score) | 108.4 (15.9) | 56–44 |
| Number line knowledge (0–100 number line linear R2) | 0.57 (0.30) | 0.00–0.96 |
| Approximate symbolic calculation (items correct of 16; chance = 50%) | 13.4 (2.15) | 8–16 |
| Approximate nonsymbolic calculation (items correct of 16; chance = 50%) | 12.5 (1.37) | 9–15 |
Note. CMTT = children’s mental transformation task; PPVT-III = Peabody Picture Vocabulary Test–Third Edition.
The tasks measuring spatial skill, vocabulary, and approximate symbolic calculation were significantly but moderately intercorrelated, but none were so highly correlated as to raise concerns regarding collinearity (all rs < .70; see Table 5). Children’s performance on the approximate nonsymbolic calculation task was not significantly correlated with their performance on the other measures.
Table 5.
Correlations Between Tasks in Study 2 (N = 42)
| Task | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| 1. Spatial skill (CMTT; items correct of 22) | — | |||
| 2. Vocabulary (PPVT-III standardized score) | .43** | — | ||
| 3. Number line knowledge (0–100 number line linear R2)a | .49** | .46** | — | |
| 4. Approximate symbolic calculation (items correct of 16) | .47** | .46** | .66*** | — |
| 5. Approximate nonsymbolic calculation (items correct of 16) | .10 | −.11 | .14 | .05 |
Note. CMTT = children’s mental transformation task; PPVT-III = Peabody Picture Vocabulary Test–Third Edition.
These variables have been transformed using an arcsine transformation {2 × asin[sqrt(x)]}.
p < .01.
p < .001.
Relations between spatial skill, number line, and approximate symbolic calculation.
Our main question was whether children’s early spatial skill (at age 5) predicted their later mathematical knowledge assessed using a numerical task that was not ostensibly spatial (the approximate symbolic calculation task at age 8) and, if so, whether this relation was mediated (or accounted for) by children’s linear number line knowledge at an intermediate time point (at age 6). To test our mediation hypothesis, we conducted a series of simultaneous regression models based on the procedure recommended by Baron and Kenny (1986; see Figure 3). In order to reduce the possibility that general cognitive development was the reason for the potentially mediating effect of number line knowledge at age 6, we controlled for children’s vocabulary knowledge at age 6 in all models. Vocabulary knowledge serves as a good proxy for general cognitive skill, as it is typically one of the measures most highly correlated with general intelligence (e.g., Horn & Cattell, 1966; Lynn & Mulhern, 1991).
Figure 3.
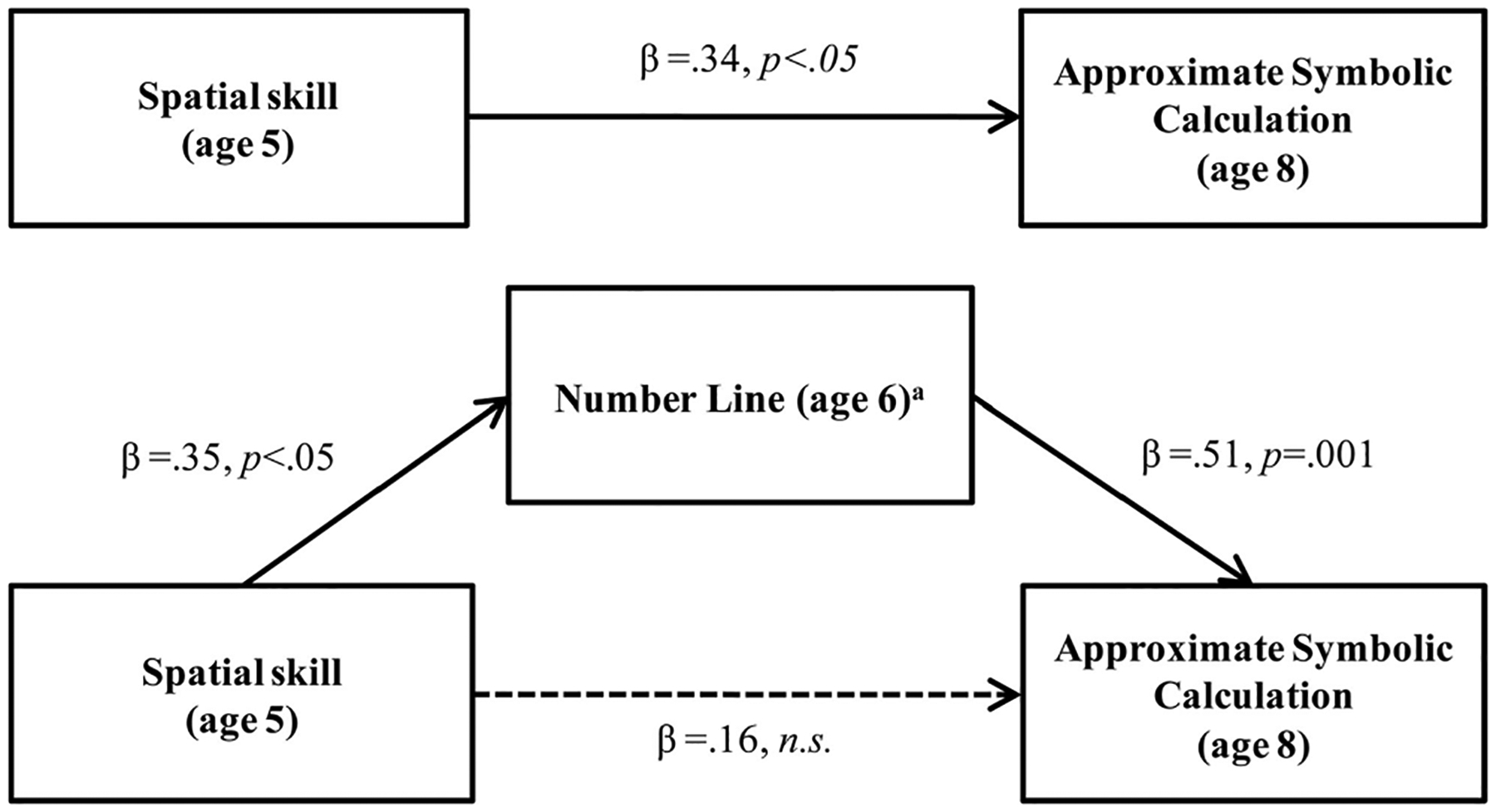
Study 2 mediation analysis based on series of regression models (N = 42). All models control for vocabulary knowledge at age 6. a This variable has been transformed using an arcsine transformation {2 × asin[sqrt(x)]}.
First, we conducted a regression model predicting our dependent variable, children’s approximate symbolic calculation score at age 8, using spatial skill at age 5 (our independent variable of interest) as well as vocabulary knowledge at age 6 (our control variable) as predictors (see Table 6, Model 5). We found that both children’s spatial skill (β = .34, t = 2.27, p < .05) and vocabulary knowledge (β = .32, t = 2.13, p < .05) were significant predictors of their approximate symbolic calculation score. Second, we asked whether children’s spatial skill at age 5 and vocabulary knowledge at age 6 predicted their number line knowledge at age 6 (our proposed mediator). Again, both spatial skill (β = .35, t = 2.40, p < .05) and vocabulary knowledge (β = .31, t = 2.10, p < .05) were significant predictors of children’s number line knowledge (see Table 6, Model 8). Third, we asked whether children’s number line and vocabulary knowledge at age 6 predicted their approximate symbolic calculation score at age 8. In this case, number line knowledge was a significant predictor of later approximate symbolic calculation (β = .57, t = 4.30, p < .001), while vocabulary knowledge was not (β = .20, t = 1.51, p > .10; see Table 6, Model 6).
Table 6.
Regression Models Predicting Approximate Symbolic Calculation Skill and Number Line Knowledge From Measures of Spatial Skill, Number Line Knowledge, and Vocabulary in Study 2 (N = 42)
| Approximate symbolic calculation | Number line linear R2 (0–100)a | |||
|---|---|---|---|---|
| Measure | Model 5 | Model 6 | Model 7 | Model 8 |
| Spatial skill | .34* | .16 | .35* | |
| Number line linear R2 (0–100)a | .57*** | .51** | ||
| Vocabulary knowledge | .32* | .20 | .16 | .31* |
| R2 (%) | 30.4 | 46.5 | 48.2 | 31.4 |
| F | 8.5** | 17.0*** | 11.8*** | 8.9** |
| F dfs | (2, 39) | (2, 39) | (3, 38) | (2, 39) |
Note. Parameter estimates are standardized for all data.
These variables have been transformed using an arcsine transformation {2 × asin[sqrt(x)]}.
p < .05.
p < .01.
p < .001.
Finally, we tested the mediation hypothesis by asking whether the relation between spatial skill and approximate symbolic calculation score was reduced when our proposed mediator, number line knowledge, was controlled. To do so, we regressed spatial skill, number line knowledge, and vocabulary knowledge (as a control variable) on approximate symbolic calculation score. We found that number line knowledge remained a significant predictor of approximate symbolic calculation score (β = .51, t = 3.62, p = .001), while neither spatial skill (β = .16, t = 1.13, p = .27) nor vocabulary knowledge (β = .16, t = 1.15, p = .26) were significant predictors (see Table 6, Model 7). This series of regression models satisfies the requirements to establish that number line knowledge mediates the relation between spatial skill and approximate symbolic calculation (Baron & Kenny, 1986). In addition, we used bias-corrected bootstrapping to determine whether there was a significant indirect effect of spatial skill on approximate symbolic calculation via the mediator of the number line (Preacher & Hayes, 2008). The resulting 95% confidence interval for the indirect effect was 0.015 to 0.237. Because this interval does not include zero, we can say with 95% confidence that the indirect (mediation) effect is greater than zero.
Relations between spatial skill, number line, and approximate nonsymbolic calculation.
To further investigate the specificity of these results, we examined whether children’s early spatial skill or number line knowledge predicted their performance on the approximate nonsymbolic calculation task at age 8. In a simultaneous regression including spatial skill at age 5 and vocabulary at age 6 as predictors of approximate nonsymbolic calculation at age 8, neither spatial skill (β = .18, t = 1.01, p = .32) nor vocabulary (β = −.18, t = −1.05, p = .30) were significant predictors. Similarly, in a simultaneous regression including number line knowledge and vocabulary as predictors of approximate nonsymbolic calculation, neither number line knowledge (β = .25, t = 1.41, p = .17) nor vocabulary (β = −.22, t = −1.26, p = .22) were significant predictors.
Discussion
In Study 2, we showed that children’s spatial skill at age 5 predicted their performance on an ostensibly nonspatial numerical task, approximate symbolic calculation, at age 8. Further, this relation was mediated by their performance on a task assessing number line knowledge at age 6. Importantly, these effects held even after controlling for children’s vocabulary knowledge at age 6, indicating that general cognitive development did not explain the relations. These results were also specific to an approximate symbolic calculation task; no relation was found between spatial skill or number line knowledge and an approximate nonsymbolic calculation task. These results are consistent with a causal model in which spatial skill facilitates improvement in linear symbolic number representations, which in turn improves children’s numerical knowledge even on an ostensibly nonspatial numerical task.
General Discussion
Results from two longitudinal studies converge to reveal a significant relationship between spatial skill, number line knowledge, and approximate symbolic calculation skill. In Study 1, we showed that first- and second-grade children’s initial level of spatial skill predicted improvement on a linear number line task, over and above their initial reading and math achievement. This suggests that spatial skill may help facilitate children’s development of a linear, spatial numerical representation. In Study 2, we asked whether the relation between children’s spatial skill and number line performance reflected specific and localized knowledge (perhaps because the number line task involves spatial representations in its presentation and response formats) or whether the improvement on the number line that was attributable to spatial skill would also extend to improvement on an ostensibly nonspatial numerical task—approximate symbolic calculation. We found that children’s spatial skill at age 5 predicted their number line knowledge at age 6, which in turn predicted their performance on an approximate symbolic calculation task at age 8 (controlling for vocabulary knowledge). In addition, children’s number line knowledge mediated the relation between spatial skill and later approximate symbolic calculation skill. Taken together, these studies suggest that spatial skill exerts a positive influence on children’s early numerical development by improving the linearity of their number line representation.
Importantly, the relation between early spatial skill and later numerical knowledge extended to a symbolic numerical task but not to a nonsymbolic numerical task. This pattern of data supports our assertion that the linear number line accounts for the relation between spatial skill and later symbolic numerical knowledge because the linear number line is a spatialized representation of symbolic numbers. Our findings are also consistent with previous research showing that children’s performance on symbolic and nonsymbolic numerical estimation tasks were not correlated and that only performance on a symbolic numerical estimation task (and not on a nonsymbolic task) was related to other mathematical skills such as symbolic calculation (Holloway & Ansari, 2009). Further, the specificity of this finding helps to eliminate alternative explanations for the relation between spatial skill and approximate symbolic calculation, such as the possibility that spatial skill is simply correlated with performance on any type of numerical task.
Further, the fact that spatial skill predicted an approximate symbolic calculation task, mediated by number line knowledge, is likely due to the fact that this outcome task was approximate in nature. Understanding the linear number line involves increasing the precision of one’s representation of symbolic quantities, and many previous studies have shown that number line knowledge generalizes to other symbolic number tasks that involve approximation (Booth & Siegler, 2008; Laski & Siegler, 2007; Thompson & Siegler, 2010). The question of whether number line knowledge also generalizes to exact symbolic numerical tasks, and thus whether spatial skill can impact these types of tasks via understanding of the number line, remains open.
While these results are consistent with the hypothesis that spatial skill helps children to develop number line knowledge, it is important to keep in mind the correlational nature of the data. We attempted to control for general cognitive ability in order to eliminate one major alternative explanation for the relation between spatial skill and number line knowledge, using prior math and reading achievement (Study 1) and vocabulary knowledge (Study 2) as control variables. Nevertheless, it is possible that an unmeasured factor could account for the relations found. For example, the central executive component of working memory is related to number line performance at the ages studied, over and above IQ (Geary, Hoard, Nugent, & Byrd-Craven, 2008). Thus, it is possible that some form of central executive processing may contribute to the relations we found between tasks. In interpreting our results, it is also important to keep in mind the small sample size in Study 2 (N = 42). Future work will help extend the generalizability of our results.
Although further studies are needed to substantiate the causal nature of our findings, there are several reasons to believe that spatial skill may positively affect children’s development of linear number line knowledge. One possibility is that children with stronger spatial skill may more readily translate their conceptual knowledge of the linear relations between numbers (e.g., understanding that the distance between 0 and 10 is the same as the distance between 10 and 20) into a corresponding linear spatial representation. Another possibility is that when children are exposed to linear number line representations as part of their formal schooling, those with stronger spatial skill are better able to remember the layout of the number line. Children with strong spatial skill may also reinforce their number line knowledge by mentally calling upon this spatial representation even when doing nonspatial symbolic numerical tasks. It is possible that one or more of these mechanisms may explain the relations we have found between spatial skill and number line knowledge. Future work using experimental techniques is important for substantiating our hypothesized causal chain linking spatial skill, number line knowledge, and symbolic numerical knowledge and for determining the specific mechanisms that underlie these relations.
These results suggest that improving children’s spatial thinking at a young age may not only help foster skills specific to spatial reasoning but also improve symbolic numerical representations. This is important since spatial thinking is malleable and can be positively influenced by early spatial experiences (e.g., Baenninger & Newcombe, 1989; Huttenlocher, Levine, & Vevea, 1998; Levine, Ratliff, Huttenlocher, & Cannon, 2011; Pruden, Levine, & Huttenlocher, 2011; Uttal et al., 2012). Thus, improving children’s spatial skill may have positive impacts on their future success in science, technology, engineering, or mathematics (STEM) disciplines not only by improving spatial thinking but also by enhancing the numerical skills that are critical for achievement in all STEM fields.
Acknowledgments
This research was supported by National Institute of Child Health and Human Development Grant P01HD040605 to Susan C. Levine; by National Science Foundation Science of Learning Center Award SBE 0541957, the Spatial Intelligence and Learning Center (SILC), to Susan C. Levine and Sian L. Beilock; by National Science Foundation CAREER DRL-0746970 to Sian L. Beilock; and by National Center for Education Research Grant R305C050076 to Elizabeth A. Gunderson and Gerardo Ramirez.
Footnotes
Although we predicted that number line knowledge would not mediate the relation between spatial skill and approximate nonsymbolic calculation, it was possible that we would find a direct relation between spatial skill and approximate nonsymbolic calculation. Indeed, prior research has suggested that there are links between nonsymbolic number representations and spatial representations (e.g., Dehaene, Bossini, & Giraux, 1993; de Hevia & Spelke, 2010; Pinel, Piazza, Le Bihan, & Dehaene, 2004). However, to our knowledge studies have not shown early spatial skills to predict later nonsymbolic numerical processing ability. Thus, we did not have specific predictions regarding whether spatial skills would be directly related to a nonsymbolic numerical task.
Since gender differences are often reported on tasks assessing spatial skills (e.g., Voyer, Voyer, & Bryden, 1995) and have previously been reported on the number line task (Thompson & Opfer, 2008), we examined whether gender differences were observed on any of our measures. Boys performed marginally better than girls on the end-of-year number line task (arcsine-transformed), t(150) = 1.88, p = .06. No significant gender differences were found on any other measure. Further, controlling for gender in regression Models 1–4 (reported later) did not alter the significance of the results.
Number line knowledge was measured as the percentage of variance explained (R2) by the best fitting linear model. Since this is a proportion, the R2 value was transformed using the arcsine transformation {2 × asin[sqrt(x)]} in order to correct for nonnormality. All models were checked for violations of regression assumptions, and none were found.
We examined whether gender differences were observed on any of our measures. Boys performed significantly better than girls on the number line task (arcsine-transformed), t(40) = 3.24, p <.01, and on the approximate symbolic calculation task, t(40) = 5.59, p < .001. No significant gender differences were found on any other measure. Further, controlling for gender in the regression models reported later did not alter the pattern of results (all results reported as statistically significant remained significant at p < .05).
References
- Baenninger M, & Newcombe N (1989). The role of experience in spatial test performance: A meta-analysis. Sex Roles, 20, 327–344. doi: 10.1007/BF00287729 [DOI] [Google Scholar]
- Baron RM, & Kenny DA (1986). The moderator-mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology, 51, 1173–1182. doi: 10.1037/0022-3514.51.6.1173 [DOI] [PubMed] [Google Scholar]
- Barth H, La Mont K, Lipton J, Dehaene S, Kanwisher N, & Spelke ES (2006). Non-symbolic arithmetic in adults and young children. Cognition, 98, 199–222. doi: 10.1016/j.cognition.2004.09.011 [DOI] [PubMed] [Google Scholar]
- Barth HC, & Paladino AM (2011). The development of numerical estimation: Evidence against a representational shift. Developmental Science, 14, 125–135. doi: 10.1111/j.1467-7687.2010.00962.x [DOI] [PubMed] [Google Scholar]
- Battista MT (1990). Spatial visualization and gender differences in high school geometry. Journal for Research in Mathematics Education, 21, 47–60. doi: 10.2307/749456 [DOI] [Google Scholar]
- Beilock SL, Gunderson EA, Ramirez G, & Levine SC (2010). Female teachers’ math anxiety affects girls’ math achievement. PNAS Proceedings of the National Academy of Sciences, USA, 107, 1860–1863. doi: 10.1073/pnas.0910967107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berteletti I, Lucangeli D, Piazza M, Dehaene S, & Zorzi M (2010). Numerical estimation in preschoolers. Developmental Psychology, 46, 545–551. doi: 10.1037/a0017887 [DOI] [PubMed] [Google Scholar]
- Booth JL, & Siegler RS (2006). Developmental and individual differences in pure numerical estimation. Developmental Psychology, 189–201. doi: 10.1037/0012-1649.41.6.189 [DOI] [PubMed] [Google Scholar]
- Booth JL, & Siegler RS (2008). Numerical magnitude representations influence arithmetic learning. Child Development, 79, 1016–1031. doi: 10.1111/j.1467-8624.2008.01173.x [DOI] [PubMed] [Google Scholar]
- Casey MB, Nuttall RL, & Pezaris E (2001). Spatial-mechanical reasoning skills versus mathematics self-confidence as mediators of gender differences on mathematics subtests using cross-national gender-based items. Journal for Research in Mathematics Education, 32, 28–57. doi: 10.2307/749620 [DOI] [Google Scholar]
- Casey MB, Nuttall R, Pezaris E, & Benbow CP (1995). The influence of spatial ability on gender differences in mathematics college entrance test scores across diverse samples. Developmental Psychology, 31, 697–705. doi: 10.1037/0012-1649.31.4.697 [DOI] [PubMed] [Google Scholar]
- Dehaene S, Bossini S, & Giraux P (1993). The mental representation of parity and number magnitude. Journal of Experimental Psychology: General, 122, 371–396. doi: 10.1037/0096-3445.122.3.371 [DOI] [Google Scholar]
- Dehaene S, Izard V, Spelke E, & Pica P (2008, May 30). Log or linear? Distinct intuitions of the number scale in Western and Amazonian indigene cultures. Science, 320, 1217–1220. doi: 10.1126/science.1156540 [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Hevia MD, & Spelke ES (2010). Number-space mapping in human infants. Psychological Science, 21, 653–660. doi: 10.1177/0956797610366091 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delgado AR, & Prieto G (2004). Cognitive mediators and sex-related differences in mathematics. Intelligence, 32, 25–32. doi: 10.1016/S0160-2896(03)00061-8 [DOI] [Google Scholar]
- Dunn LM, & Dunn LM (1997). Peabody Picture Vocabulary Test (3rd ed.). Circle Pines, MN: American Guidance Service. [Google Scholar]
- Fias W, & Fischer MH (2005). Spatial representation of numbers. In Campbell J (Ed.), Handbook of mathematical cognition (pp. 43–54). New York, NY: Psychology Press. [Google Scholar]
- Geary DC, & Burlingham-Dubree M (1989). External validation of the strategy choice model for addition. Journal of Experimental Child Psychology, 47, 175–192. doi: 10.1016/0022-0965(89)90028-3 [DOI] [Google Scholar]
- Geary DC, Hoard MK, Byrd-Craven J, Nugent L, & Numtee C (2007). Cognitive mechanisms underlying achievement deficits in children with mathematical learning disability. Child Development, 78, 1343–1359. doi: 10.1111/j.1467-8624.2007.01069.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geary DC, Hoard MK, Nugent L, & Byrd-Craven J (2008). Development of number line representations in children with mathematical learning disability. Developmental Neuropsychology, 33, 277–299. doi: 10.1080/87565640801982361 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilmore CK, McCarthy SE, & Spelke ES (2007, May 31). Symbolic arithmetic knowledge without instruction. Nature, 447, 589–591. doi: 10.1038/nature05850 [DOI] [PubMed] [Google Scholar]
- Guay RB, & McDaniel ED (1977).) The relationship between mathematics achievement and spatial abilities among elementary school children. Journal for Research in Mathematics Education, 8, 211–215. doi: 10.2307/748522 [DOI] [Google Scholar]
- Gunderson EA, & Levine SC (2011). Some types of parent number talk count more than others: Relations between parents’ input and children’s cardinal-number knowledge. Developmental Science, 14, 1021–1032. doi: 10.1111/j.1467-7687.2011.01050.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hegarty M, & Kozhevnikov M (1999). Types of visual-spatial representations and mathematical problem solving. Journal of Educational Psychology, 91, 684–689. doi: 10.1037/0022-0663.91.4.684 [DOI] [Google Scholar]
- Holloway ID, & Ansari D (2009). Mapping numerical magnitudes onto symbols: The numerical distance effect and individual differences in children’s math achievement. Journal of Experimental Child Psychology, 103, 17–29. doi: 10.1016/j.jecp.2008.04.001 [DOI] [PubMed] [Google Scholar]
- Horn JL, & Cattell RB (1966). Refinement and test of the theory of fluid and crystallized general intelligence. Journal of Educational Psychology, 57, 253–270. doi: 10.1037/h0023816 [DOI] [PubMed] [Google Scholar]
- Humphreys LG, Lubinski D, & Yao G (1993). Utility of predicting group membership and the role of spatial visualization in becoming an engineer, physical scientist, or artist. Journal of Applied Psychology, 78, 250–261. doi: 10.1037/0021-9010.78.2.250 [DOI] [PubMed] [Google Scholar]
- Huttenlocher J, Levine S, & Vevea J (1998). Environmental input and cognitive growth: A study using time-period comparisons. Child Development, 69, 1012–1029. doi: 10.2307/1132360 [DOI] [PubMed] [Google Scholar]
- Johnson ES (1984). Sex differences in problem solving. Journal of Educational Psychology, 76, 1359–1371. doi: 10.1037/0022-0663.76.6.1359 [DOI] [Google Scholar]
- Kulp MT (1999). Relationship between visual motor integration skill and academic performance in kindergarten through third grade. Optometry and Vision Science, 76, 159–163. [DOI] [PubMed] [Google Scholar]
- Kurdek LA, & Sinclair RJ (2001). Predicting reading and mathematics achievement in fourth-grade children from kindergarten readiness scores. Journal of Educational Psychology, 93, 451–455. doi: 10.1037/0022-0663.93.3.451 [DOI] [Google Scholar]
- Kyttälä M, Aunio P, Lehto JE, Van Luit JEH, & Hautamäki J (2003). Visuospatial working memory and early numeracy. Educational and Child Psychology, 20(3), 65–76. [Google Scholar]
- Kyttälä M, & Lehto J (2008). Some factors underlying mathematical performance: The role of visuospatial working memory and non-verbal intelligence. European Journal of Psychology of Education, 23, 77–94. doi: 10.1007/BF03173141 [DOI] [Google Scholar]
- Lachance JA, & Mazzocco MMM (2006). A longitudinal analysis of sex differences in math and spatial skills in primary school age children. Learning and Individual Differences, 16, 195–216. doi: 10.1016/j.lindif.2005.12.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laski EV, & Siegler RS (2007). Is 27 a big number? Correlational and causal connections among numerical categorization, number line estimation, and numerical magnitude comparison. Child Development, 78, 1723–1743. doi: 10.1111/j.1467-8624.2007.01087.x [DOI] [PubMed] [Google Scholar]
- Levine SC, Huttenlocher J, Taylor A, & Langrock A (1999). Early sex differences in spatial skill. Developmental Psychology, 35, 940–949. doi: 10.1037/0012-1649.35.4.940 [DOI] [PubMed] [Google Scholar]
- Levine SC, Ratliff KR, Huttenlocher J, & Cannon J (2011). Early puzzle play: A predictor of preschoolers’ spatial transformation skill. Developmental Psychology. Advance online publication. doi: 10.1037/a0025913 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Linn MC, & Petersen AC (1985). Emergence and characterization of sex differences in spatial ability: A meta-analysis. Child Development, 56, 1479–1498. doi: 10.2307/1130467 [DOI] [PubMed] [Google Scholar]
- Lynn R, & Mulhern G (1991). A comparison of sex differences on the Scottish and American standardisation samples of the WISC-R. Personality and Individual Differences, 12, 1179–1182. doi: 10.1016/0191-8869(91)90082-M [DOI] [Google Scholar]
- McGrew KS, & Woodcock RW (2001). Technical manual: Woodcock-Johnson III. Itasca, IL: Riverside. [Google Scholar]
- Mix KS, & Cheng YL (in press). Space and math: The developmental and educational implications. In Benson JB (Ed.), Advances in child development and behavior (Vol. 42). New York, NY: Elsevier. [DOI] [PubMed] [Google Scholar]
- Pinel P, Piazza M, Le Bihan D, & Dehaene S (2004). Distributed and overlapping cerebral representations of number, size, and luminance during comparative judgments. Neuron, 41, 983–993. doi: 10.1016/S0896-6273(04)00107-2 [DOI] [PubMed] [Google Scholar]
- Preacher KJ, & Hayes AF (2008). Asymptotic and resampling strategies for assessing and comparing indirect effects in multiple mediator models. Behavior Research Methods, 40, 879–891. doi: 10.3758/BRM.40.3.879 [DOI] [PubMed] [Google Scholar]
- Pruden SM, Levine SC, & Huttenlocher J (2011). Children’s spatial thinking: Does talk about the spatial world matter? Developmental Science, 14, 1417–1430. doi: 10.1111/j.1467-7687.2011.01088.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shea DL, Lubinski D, & Benbow CP (2001). Importance of assessing spatial ability in intellectually talented young adolescents: A 20-year longitudinal study. Journal of Educational Psychology, 93, 604–614. doi: 10.1037/0022-0663.93.3.604 [DOI] [Google Scholar]
- Siegler RS, & Booth JL (2004). Development of numerical estimation in young children. Child Development, 75, 428–444. doi: 10.1111/j.1467-8624.2004.00684.x [DOI] [PubMed] [Google Scholar]
- Siegler RS, & Opfer JE (2003). The development of numerical estimation: Evidence for multiple representations of numerical quantity. Psychological Science, 14, 237–243. doi: 10.1111/1467-9280.02438 [DOI] [PubMed] [Google Scholar]
- Siegler RS, & Ramani GB (2008). Playing linear numerical board games promotes low-income children’s numerical development. Developmental Science, 11, 655–661. doi: 10.1111/j.1467-7687.2008.00714.x [DOI] [PubMed] [Google Scholar]
- Siegler RS, & Ramani GB (2009). Playing linear number board games—But not circular ones—Improves low-income preschoolers’ numerical understanding. Journal of Educational Psychology, 101, 545–560. doi: 10.1037/a0014239 [DOI] [Google Scholar]
- Thompson CA, & Opfer JE (2008). Costs and benefits of representational change: Effect of context on age and sex differences in magnitude estimation. Journal of Experimental Child Psychology, 101, 20–51. doi: 10.1016/j.jecp.2008.02.003 [DOI] [PubMed] [Google Scholar]
- Thompson CA, & Siegler RS (2010). Linear numerical-magnitude representations aid children’s memory for numbers. Psychological Science, 21, 1274–1281. doi: 10.1177/0956797610378309 [DOI] [PubMed] [Google Scholar]
- Thurstone LL (1938). Primary mental abilities. Chicago, IL: University of Chicago Press. [Google Scholar]
- Thurstone LL, & Thurstone LG (1949). Examiner manual for the SRA Primary Mental Abilities Test. Chicago, IL: Science Research. [Google Scholar]
- Tolar TD, Lederberg AR, & Fletcher JM (2009). A structural model of algebra achievement: Computational fluency and spatial visualisation as mediators of the effect of working memory on algebra achievement. Educational Psychology, 29, 239–266. doi: 10.1080/01443410802708903 [DOI] [Google Scholar]
- Uttal DH, Meadow NG, Tipton E, Hand LL, Alden AR, Warren C, & Newcombe NS (2012). The malleability of spatial skills: A meta-analysis of training studies. Manuscript submitted for publication. [DOI] [PubMed] [Google Scholar]
- Vandenberg SG, & Kuse AR (1978). Mental rotations, a group test of three-dimensional spatial visualization. Perceptual and Motor Skills, 47, 599–604. doi: 10.2466/pms.1978.47.2.599 [DOI] [PubMed] [Google Scholar]
- Voyer D, Voyer S, & Bryden MP (1995). Magnitude of sex differences in spatial abilities: A meta-analysis and consideration of critical variables. Psychological Bulletin, 117, 250–270. doi: 10.1037/0033-2909.117.2.250 [DOI] [PubMed] [Google Scholar]
- Wai J, Lubinski D, & Benbow CP (2009). Spatial ability for STEM domains: Aligning over 50 years of cumulative psychological knowledge solidifies its importance. Journal of Educational Psychology, 101, 817–835. doi: 10.1037/a0016127 [DOI] [Google Scholar]
- Webb RM, Lubinski D, & Benbow CP (2007). Spatial ability: A neglected dimension in talent searches for intellectually precocious youth. Journal of Educational Psychology, 99, 397–420. doi: 10.1037/0022-0663.99.2.397 [DOI] [Google Scholar]
- Woodcock RW (1999). What can Rasch-based scores convey about a person’s test performance? In Embretson SE & Hershberger SL (Eds.), The new rules of measurement: What every psychologist and educator should know (pp. 105–127). Mahwah, NJ: Erlbaum. [Google Scholar]
- Woodcock RW, McGrew KS, & Mather N (2001). Woodcock-Johnson III Tests of Achievement. Itasca, IL: Riverside. [Google Scholar]
- Zorzi M, Priftis K, & Umiltà C (2002, May 9). Brain damage: Neglect disrupts the mental number line. Nature, 417, 138–139. doi: 10.1038/417138a [DOI] [PubMed] [Google Scholar]


