Electrical 180° switching of Néel vector in spin-splitting antiferromagnet

Abstract

Antiferromagnetic spintronics have attracted wide attention due to its great potential in constructing ultradense and ultrafast antiferromagnetic memory that suits modern high-performance information technology. The electrical 180° switching of Néel vector is a long-term goal for developing electrical-controllable antiferromagnetic memory with opposite Néel vectors as binary “0” and “1.” However, the state-of-art antiferromagnetic switching mechanisms have long been limited for 90° or 120° switching of Néel vector, which unavoidably require multiple writing channels that contradict ultradense integration. Here, we propose a deterministic switching mechanism based on spin-orbit torque with asymmetric energy barrier and experimentally achieve electrical 180° switching of spin-splitting antiferromagnet Mn₅Si₃. Such a 180° switching is read out by the Néel vector–induced anomalous Hall effect. On the basis of our writing and readout methods, we fabricate an antiferromagnet device with electrical-controllable high- and low-resistance states that accomplishes robust write and read cycles. Besides fundamental advance, our work promotes practical spin-splitting antiferromagnetic devices based on spin-splitting antiferromagnet.

The electrical 180° switching and detection of the Néel vector in spin-splitting antiferromagnet Mn₅Si₃ is achieved.

INTRODUCTION

One of the most well-known applications of spintronics is the electrical-controllable nonvolatile magnetic random-access memory (MRAM), where the information states “1” and “0” are stored by the up and down directions of the order parameter in ferromagnet (FM), i.e., the magnetic moment (1–3). For the original MRAM, the electrical read is based on tunneling magnetoresistance (4–6) (TMR), and the electrical write is realized by applying current along single channel to switch the magnetic moment due to spin transfer torques (7, 8). Over the past decades, although many emerging effects such as spin-orbit torques (SOTs) switching (9, 10) have improved the performance of MRAM, intrinsic large stray fields and gigahertz dynamics of FM fundamentally limit MRAM from achieving future breakthroughs in high-density integration and high-speed operation (11, 12). Besides, a very small magnetic field may be able to switch the direction of magnetic moment in MRAM, challenging its data storage stability (11, 12). Supreme to FM counterparts, antiferromagnet (AFM) exhibits tremendous potential for building ultradense and ultrafast AFM-RAM with high immunity to magnetic field disturbance thanks to their intrinsic advantages of zero stray field, terahertz dynamics, and compensated moment (13–17). With TMR predicted (18, 19) and found (20, 21) recently in many AFMs, the long-desired electrical-controllable AFM-RAM becomes possible as long as the electrical switching of the AFM order parameter (i.e., the Néel vector) can be achieved.

However, the state-of-art reorientation of Néel vectors are all in-plane 90° or 120° switching by SOTs, which inevitably require multiple writing channels, leading to huge integration difficulties for AFM-RAM (13, 22–24). Similar to FM MRAM, practical AFM-RAM undoubtably needs electrical current along single writing channel to switch the Néel vector back and forth, which generates high and low resistance to represent binary “1” and “0” (11). An ideal solution is the 180° switching of Néel vectors back and forth (n₊ ↔ n₋) in AFMs by electrical current with opposite polarities along single writing channel. Moreover, 180° switching is truly needed to generate substantial antiferromagnetic TMR (18, 19). Therefore, electrical 180° switching of Néel vector is very important but remains unveiled.

The core difficulty of electrical 180° switching of Néel vector lies in equal energy barriers for n₊ → n₋ and n₋ → n₊, defined by uniaxial magnetic anisotropy. In this case, if SOTs drive the Néel vector to rotate from n₊ to n₋ by overcoming the energy barrier for n₊ → n₋, it can also continuously drive the Néel vector to rotate from n₋ to n₊ (23), which makes the 180° switching of Néel vector nondeterministic. That is why the more promising 180° switching of Néel vector remains unrealized for a long time since the first discovery of 90° switching of Néel vector in 2016 (13). Note that the 180° switching of CuMnAs by staggered spin-orbit fields is actually due to antiferromagnetic domain wall motion instead of the most desired deterministic 180° switching of Néel vector (25). Besides, the 180° switching of perpendicular cluster magnetic octuple has been achieved in noncollinear AFM (ncAFM) Mn₃Sn, but it is fundamentally different from 180° switching of Néel vector as the order parameter in collinear AFM (cAFM) (26, 27). Another important difficulty is to read out the 180° switching of Néel vector. Antiferromagnetic anisotropic magnetoresistance has been widely adopted, but it cannot read out 180° switching (13, 22–24). Harmonic measurements need specific sublattice symmetry breaking, which is not general and is hard to implement (25). Fortunately, the 180° switching of Néel vector may be feasibly read out by the anomalous Hall effect (AHE) (28–31) in some recently found special cAFMs with spin-splitting band structure (32–37), also termed as altermagnets (38, 39). Moreover, their spin-splitting band structure and related properties, such as unconventional spin current generation (40–42) and piezomagnetism (37), can all be manipulated through 180° switching of the Néel vector, which makes it very promising to investigate the electrical 180° switching of Néel vector in spin-splitting AFM.

Here, we achieve deterministic electrical 180° switching of the Néel vector in spin-splitting AFM Mn₅Si₃ films based on SOTs with asymmetric switching barrier that can be easily generalized to other AFM materials. We prove theoretically and experimentally that 180° switching of the Néel vector indeed tunes the spin-splitting bands and flips the anomalous Hall conductivity (AHC), which can be used as an unconventional electrical readout approach of 180° switching. With these write and read methods ready, we successfully fabricate an AFM device with high and low resistance that realizes robust write and readout cycles, paving the way for the long-desired electrical-controllable AFM-RAM.

RESULTS

Spin splitting manipulated by reversing the Néel vector

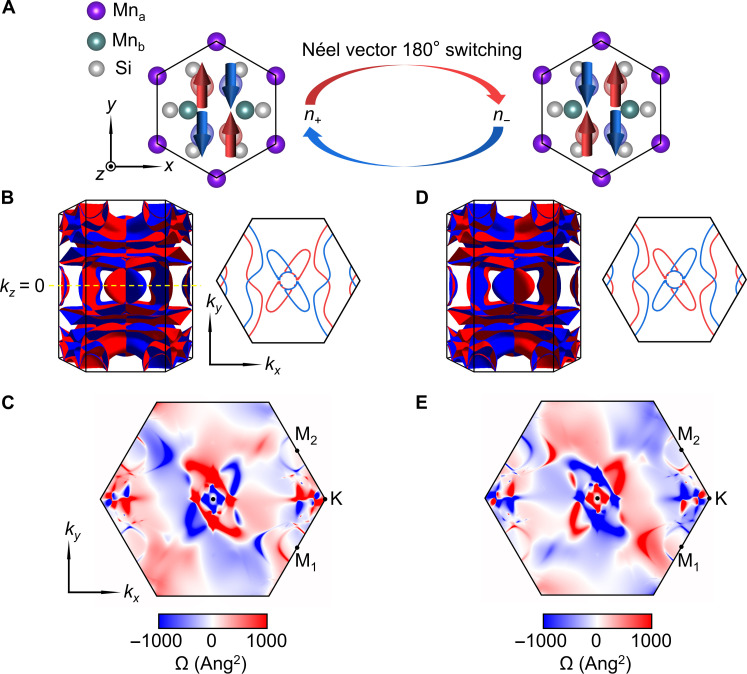
We start with introducing basic crystal structure and magnetic phase characteristics of Mn₅Si₃. The space group of Mn₅Si₃ at room temperature is P6₃/mcm with the unit cell composing of four Mn_a and six Mn_b atoms at two inequivalent Wyckoff positions and six Si atoms (Fig. 1A) (43–45). As temperature decreases, Mn₅Si₃ undergoes a magnetic phase transition from paramagnetic to cAFM and then to ncAFM. In the cAFM phase, the G-type AFM ordering occurs on two-thirds of Mn_b atoms, where adjacent magnetic Mn_b atoms have opposite spin orientations to form the Néel vector (Fig. 1A and fig. S1 for other perspectives) (43–47). The PT symmetry is broken in cAFM Mn₅Si₃ thin film (29), and, hence, its energy state at a generic momentum is spin-polarized, i.e., $E_k^{\uparrow }\ne E_k^{\downarrow }$ , because of the exchange coupling between itinerant electrons and local magnetic moments. Moreover, the states at mirror symmetry–related momenta must have contrasting spin polarizations to form the C-paired spin-momentum locking, further suppressing spin-flipping (37), which is confirmed by our first-principles calculations as shown in Fig. 1B. These unique features provide possibilities for the existence of AHE in cAFM Mn₅Si₃ thin film (29).

Fig. 1. Spin-splitting band and Berry curvature in Mn₅Si₃ of opposite Néel vectors.

(A) Crystal and magnetic structure of G-type cAFM Mn₅Si₃ with opposite magnetization density represented by red and blue isosurfaces. (B and D) Fermi surface and its contour plot in the k_z = 0 plane. (C and E) Berry curvature in the k_z = 0 plane. When the Néel vector is 180°-switched, both spin-splitting band and Berry curvature are flipped.

Next, it is demonstrated that through reversing the Néel vector, we can manipulate spin-resolved and Berry curvature–dependent phenomena, which, in turn, serve as potential readout approach of 180° Néel vector switching in cAFM Mn₅Si₃. Although spin-orbit coupling has negligible effect on the band structure (fig. S1), it can break the strict SU (2) symmetry and, hence, induce nonzero Berry curvature for spin-splitting bands of cAFM Mn₅Si₃ with C-paired spin-momentum locking as presented in Fig. 1C. When the Néel vector n is switched 180° from n₊ to n_–, equivalent to the time-reversal operation, the spin orientations will be reversed (Fig. 1A). Accordingly, both spin splitting (Fig. 1B) and Berry curvature (Fig. 1C) at (k_x, k_y) will switch their signs at the T-paired momentum (−k_x, −k_y), as displayed in Fig. 1 (D and E, respectively). Therefore, through 180° Néel vector switching, we can control the spin-splitting bands and Berry curvature and, hence, manipulate all spin-resolved and Berry curvature–dependent phenomena such as AHE. Correspondingly, AHE may serve as a potential readout method of 180° Néel vector switching.

Demonstration of AHE as a readout method

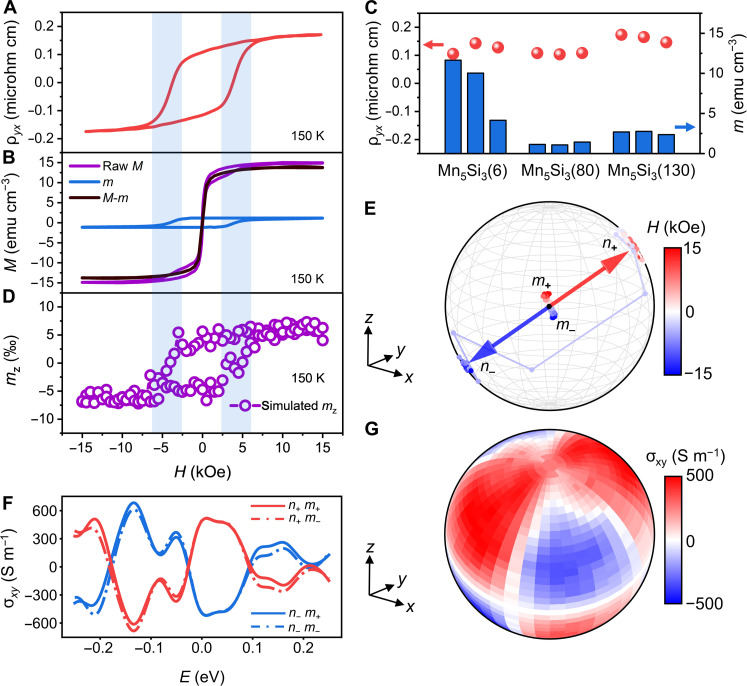
As expected, AHE is observed distinctly in the cAFM temperature range (60 to 230 K) of sputtered Mn₅Si₃(0001) thin films (fig. S2 and text S1) by Hall resistivity measurements (fig. S3) and polar magneto-optical Kerr effect measurements (fig. S4). Typical hysteresis of Hall resistivity ρ_yx under out-of-plane magnetic field at 150 K is shown in Fig. 2A, exhibiting a nonvolatile characteristic. Notably, the corresponding hysteresis of magnetization M in Fig. 2B exhibits two abrupt changes around zero field and 4 kOe: The one around zero field (black line) is due to the net moment from unavoidable local defects in the sputtering process, which does not contribute to ρ_yx near zero field and can be markedly suppressed (fig. S5 and text S2). The other around 4 kOe (blue line) has consistent coercive field H_c with that of the ρ_yx hysteresis, which can be more clearly illustrated by similar peak locations in field-derivative hysteresis of both ρ_yx and M around 4 kOe (fig. S3 and text S1). The net moment around 4 kOe, denoted to be m, most likely originates from the relativistic Dzyaloshinskii-Moriya interaction (DMI) due to interfacial symmetry breaking (48).

Fig. 2. Electrical detection of the Néel vector of Mn₅Si₃ by the AHE.

(A) Hysteresis of Hall resistivity ρ_yx and (B) magnetization M under out-of-plane magnetic field at 150 K, within the cAFM phase of Mn₅Si₃. M can be decomposed into DMI-induced m as blue line and defect-induced M-m as black line. (C) Comparison between ρ_yx and m of Mn₅Si₃ thin films with different thickness at 150 K. The numbers in parentheses indicate the thickness of the film in nanometer. (D) Simulated hysteresis of out-of-plane net moment m_z under out-of-plane magnetic field at 150 K. (E) Simulated trajectories of 180° switching of Néel vector n and net moment m by out-of-plane magnetic field from 15 kOe to −15 kOe at 150 K. m and n are defined on the basis of the AFM sublattice of Mn₅Si₃ and averaged over all of simulation cells (Materials and Methods). (F) Calculated σ_xy near the Fermi level for the Néel vector along n₊ or n₋ with net moment along m₊ or m₋ at 150 K. (G) Calculated σ_xy at the Fermi level for n along any direction at 150 K.

A natural question is that whether the AHE is simply due to this net moment m. The answer is that AHE comes from Néel vector–dependent Berry curvature instead of m. First, the measured m can be as small as ~1 emu cm⁻³, corresponding to only 2.5 mμ_B per magnetic Mn_b atom, which can hardly induce the measured large ρ_yx of 0.17 microhm cm with comparable magnitude to typical FMs (49, 50). m varies for samples of different thicknesses, but ρ_yx almost remains unchanged, which further rules out that ρ_yx comes from m (Fig. 2C, fig. S6, and text S2). Moreover, the coercive field of AHE markedly decreases when the width of the Hall bar is reduced below 500 nm, which is quite different from FMs (fig. S7 and text S2). Besides, ρ_yx has opposite temperature dependence compared to longitudinal resistivity ρ_xx (inset of fig. S3), which excludes out extrinsic mechanisms and indicates intrinsic mechanism (49, 50). Hence, the experimentally observed AHE should be attributed to the intrinsic Néel vector–dependent Berry curvature as indicated by first-principles calculations in Fig. 1. Note that there is no detectable net moment m in a previous result on cAFM Mn₅Si₃ thin film, which may be due to different deposition methods and substrates (29). It is worth emphasizing that it is impossible to measure AHE with absolutely zero net moment because both Hall vector and magnetization follow the same symmetry rules (31, 49, 50).

We further performed a systematic theoretical study through atomic spin simulations and first-principles calculations (Materials and Methods) to explicitly explain why the AHE indeed arises from n-dependent Berry curvature instead of the negligible net moment m. We first demonstrate that the 180° switching of m by reversing magnetic field will simultaneously drive the Néel order n to reverse, which provides prerequisites for n-dependent AHE measured by sweeping magnetic field. It is investigated from the responses of m and n to external magnetic field by simulations, considering the realistic crystal and magnetic structure of cAFM Mn₅Si₃ with all of the parameters extracted from first-principles calculations (figs. S8 and S9 and text S3). The simulated magnetic hysteresis is shown in Fig. 2D, where the coercive field and the magnitude of simulated m match very well with experimental m in Fig. 2B (text S3). Figure 2E presents the simulated trajectories of both m and n when sweeping the out-of-plane magnetic field H from 15 to −15 kOe, where the 180° switching of m from m₊ to m₋ by H drives the 180° switching of n from n₊ to n₋ simultaneously. This process only requires overcoming the magnetic anisotropy energy (MAE) because m and n remain the same chirality with unchanged DMI energy. The reverse of m can also be achieved without reversing n by only switching the tilting direction of cAFM moment, which does not overcome the MAE but changes the chirality between m and n, and thus increases DMI energy. However, this scenario can be excluded for cAFM Mn₅Si₃ because simply reversing m without reversing n cannot bring about the measured AHE, as we discussed in the previous paragraph. In addition, first-principles calculations also reveal that MAE is one order of magnitude smaller than DMI energy (text S3), further illustrating that the reverse of m and n will appear simultaneously in cAFM Mn₅Si₃.

With m and n reverse at the same time demonstrated, we move on to demonstrate that it is the reverse of n instead of m that determines the AHE by first-principles calculations. The dependence of AHC σ_xy on both m and n in cAFM Mn₅Si₃ is calculated at 150 K, as shown in Fig. 2F. σ_xy at the Fermi level is calculated to be approximately 400 S m⁻¹, matching the experimentally obtained σ_xy of around 300 S m⁻¹. Notably, σ_xy values for n₊ with m₊ or m₋ are almost the same, but both are opposite to those for n₋ with m₊ or m₋. Thus, the influence of m on σ_xy is negligible, and the sign reversal of σ_xy is determined by the 180° switching of n, consistent with aforementioned experimental results. Moreover, σ_xy at the Fermi level for n along any direction is calculated and presented as a spherical image in Fig. 2G. It turns out that σ_xy always reverses once n is 180° switched, irrespective of any specific direction n aligning. As a result, both our experimental and theoretical results reveal that the sign of σ_xy is uniquely determined by the direction of n, and thus, the AHE can serve as a reliable readout method for 180° switching of n in cAFM Mn₅Si₃.

Asymmetric energy barrier mechanism for electrical 180° switching of Néel vector

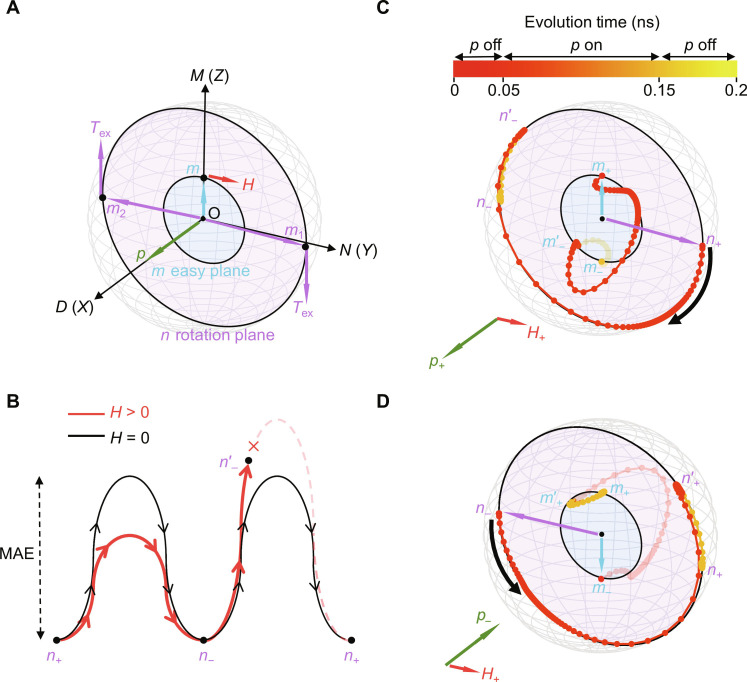
After solving the problem of reading the 180° switching of Néel vector, the remaining question is how to realize the deterministic electrical 180° switching of Néel vector, i.e., the information write process. There are three basic requirements in general: (i) Both n₊ and n₋ should be stable with minimum energy to realize binary information states “0” and “1”; (ii) n needs to be driven into motion electrically; (iii) transition from n₊ to n₋ and its time-reversal counterpart from n₋ to n₊ must have unequal energy barriers to achieve the deterministic switching. The requirement (i) is naturally satisfied in cAFMs since both n₊ and n₋ are stable along the easy axis due to MAE, and thus, we will focus on how to fulfill requirements (ii) and (iii) in the following.

According to the definition of m and n, they are always perpendicular to each other in canted AFMs, and a strong DMI vector d enforces a fixed chirality between m and n as demonstrated above in cAFM Mn₅Si₃. Without losing the generality, we start by assuming d to be perpendicular to the plane of m and n, which forms an orthogonal coordinate system as presented in Fig. 3A. To achieve requirement (ii), n needs to be driven into rotation along the n × p direction through the AFM exchange torque induced by the spin polarization p, which can be usually generated from the spin Hall effect of heavy metals such as Pt adjacent to Mn₅Si₃. We first consider p perpendicular to the plane of m and n, i.e., along d, and n will roughly rotate circularly in this plane (Fig. 3A) for this scenario. However, because of equal transition barriers of n₊ to n₋ and n₋ to n₊ (H = 0 case of Fig. 3B), n will rotate continuously driven by p and, lastly, nondeterministically relaxes to n₊ or n₋ after p is withdrawn. To address this issue, we propose to construct asymmetric switching barriers through a fixed magnetic field H acting on nonzero m as shown in Fig. 3B (H > 0 case), and the asymmetry will be maximized when H is perpendicular to m as shown in Fig. 3A. In this case, through choosing a positive p with suitable magnitude, n can rotate from n₊ to n₋ through the lower barrier but cannot further climb over the higher barrier from n₋ to n₊ and thus stays at the intermediate state n'_–. When p is withdrawn, n will naturally stabilize as n₋. Similarly, by applying another p with opposite direction, n can switch from n₋ back to n₊ through the same lower energy barrier. Thus, the desired deterministic 180° switching between n₊ and n₋ can be electrically realized by damping-like SOT with a tiny external magnetic field.

Fig. 3. Mechanism for 180° switching of the Néel vector by SOT.

(A) Schematic of n rotation driven by exchange torques T_ex with p along +X and n along +Y. n can be simplified as (m₁ − m₂)/2 for cAFM Mn₅Si₃ with four sublattices where m₁ = m₃ and m₂ = m₄ (Materials and Methods). Damping-like SOT shares the same direction for m₁ and m₂ on opposite AFM sublattice as T_DL ~ m₁ × (p × m₁) ~ m₂ × (p × m₂). Hence, T_DL pulls m₁ and m₂ toward the direction of p, bringing about exchange torques T_ex ~ m₁ × H_ex ~ m₂ × H_ex due to the AFM exchange field H_ex, which alters on m₁ and m₂ to drive both m₁ and m₂ to rotate coherently. The rotation of n is accompanied by the motion of m, which is favorite by magnetic field H along +Y. (B) Schematic of energy barriers for the transition from n₊ to n₋ and n₋ to n₊. Without H, these two energy barriers are the same, determined by MAE. With nonzero H such as H > 0, the degeneracy between them cannot be maintained. (C) Simulated switching trajectories of m and n for positive p₊ and positive H₊ as well as (D) negative p₋ and positive H₊. m is magnified 10 times for better visualization. The color of trajectories indicates the evolution time, where p is added from 0.05 ns to 0.15 ns.

This SOT mechanism with asymmetric energy barrier for 180° switching between n₊ and n₋ can further be confirmed explicitly by atomic spin simulations. Under a positive p, n will rotate clockwise accompanied by m moving toward the hemisphere favored by positive H and then settles at an intermediate state n'_– (Fig. 3C). After SOT is turned off, n will naturally relax to the local energy minimum n₋ to achieve the deterministic 180° switching from n₊ to n₋ (fig. S10 for other perspectives). Similarly, n will switch back to n₊ from n₋ deterministically with a reversing p through anticlockwise rotation (Fig. 3D). Reversing the direction of H also gives rise to deterministic 180° switching with reversing switching polarity (fig. S11). The same conclusion can be drawn through similar mechanisms for arbitrary orientations of p and H revealed by atomic spin simulations, even when d is not perpendicular to m and n (text S4 and figs. S12 and S13). Note that this mechanism is not restricted to Mn₅Si₃ but can be easily generalized to other AFMs with tiny intrinsic net moment.

Experimental demonstration of electrical 180° switching of the Néel vector

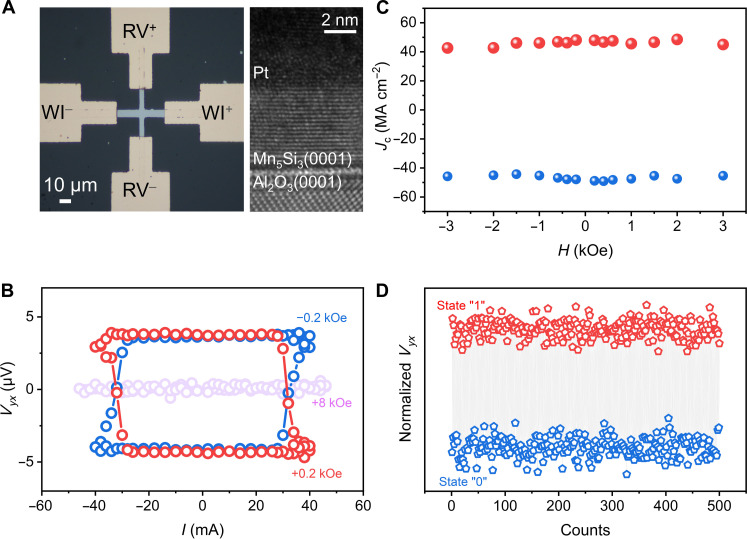
We carried out SOT switching experiments on Mn₅Si₃(0001)/Pt crossbars of 6 μm by 4 μm (Fig. 4A) based on the mechanism above, where Pt serves as the spin source. Electrical pulses of different magnitude were introduced into the write channel WI⁺-WI⁻ with an assistant field H along the same direction, and the Hall voltage was collected simultaneously along RI⁺-RI⁻ to read the direction of n through AHE. As expected, 180° switching of n in cAFM Mn₅Si₃ are observed under various temperatures (fig. S14), and the results at 180 K are representatively presented in Fig. 4B. The largest switching ratio reaches 41%, and such an incomplete switching is most likely due to the existence of microscopical multidomain and local defects pinning (fig. S15). Opposite switching polarity can be observed if the polarity of current pulse or H is reversed, consistent with aforementioned theoretical results and matching basic symmetry requirements for deterministic SOT switching (9, 10). No switching can be observed with a high H of 8 kOe, which confines the direction of m and thus also confines the direction of n, further verifying that the change of Hall voltage is due to the switching of n instead of thermal artifacts. Moreover, AHE can also be observed in the temperature range of ncAFM Mn₅Si₃ (below 60 K), but electrical 180° switching cannot be achieved, further demonstrating that it is n that can be switched electrically (fig. S16).

Fig. 4. Electrical 180° switching of the Néel vector of Mn₅Si₃.

(A) Optical microscopy and transmission electron microscopy image of Mn₅Si₃(0001)/Pt crossbars for electrical switching. WI⁺ and WI⁻ denote the write channel where the electrical pulse I is added, and RV⁺ and RV⁻ denote the read channel where the Hall voltage V_yx is collected. (B) Hall voltage V_yx as a function of electrical pulse I for different H of −0.2, 0.2, and 8 kOe at 180 K. (C) Critical switching current density J_c under different assistant field H at 180 K. (D) Continuous cycling between high V_yx (state “1”) and low V_yx (state “0”) by 180° switching of n for 500 electrical pulses at 180 K.

We now show that the 180° SOT switching of n in cAFM Mn₅Si₃ is fundamentally different from FMs and ncAFMs such as Mn₃Sn (26, 27, 51–55). In FMs, the assistant field H can effectively assist the SOT to overcome MAE for switching, as characterized by a linear decrease of the critical switching current density J_c with increasing H (44). In contrast, for cAFM Mn₅Si₃, H only eliminates the degeneracy of energy barriers between n₊ to n₋ and n₋ to n₊ but barely helps n to overcome MAE. That is because it is the large AFM exchange energy that determines the tilting of n toward p as a prerequisite to obtain nonzero AFM exchange torque for overcoming MAE, where AFM exchange energy is much larger than the Zeeman energy induced by H acting on the negligible m. Thus, J_c should be very insensitive to H for cAFM Mn₅Si₃. As presented in Fig. 4C and fig. S17, we carried out SOT switching measurements under different assistant field H, and the experimentally extracted J_c (text S5) remains almost unchanged with the increase of H for cAFM Mn₅Si₃. Besides, unlike uniaxial Néel vector n as order parameter perpendicular to m in cAFM Mn₅Si₃, cluster magnetic octuple as the order parameter with complex magnetic anisotropy in ncAFM Mn₃Sn is parallel to its intrinsic m, leading to different dynamic behaviors under p and H of specific symmetry (26, 27, 51–53).

To investigate the efficiency for 180° switching of n in cAFM Mn₅Si₃, we calculate the ratio of AHE coercivity to critical switching current density μ₀H_c/J_c as a figure of merit (52). For the averaged J_c of 49 MA cm⁻² at 180 K (fig. S15), it turns out to be about 5 mT cm² MA⁻¹, which is five times higher than traditional ferromagnetic systems such as Pt/Co/AlO_x of approximately 1 mT cm² MA⁻¹ (52, 56), indicating that the 180° SOT switching of n in cAFM Mn₅Si₃ shows high efficiency. Moreover, we test the endurance for 180° switching of n by applying electrical pulses with opposite directions alternately. The Hall voltage can be switched between high and low values corresponding to information states between “0” and “1” (Fig. 4D), which is reversible and reproducible. The device does not show degradation after 500 cycles, manifesting its robustness. As a result, spin-splitting Mn₅Si₃ shows unique advantages to construct electrical-controllable AFM-RAM with low power consumption, high reliability, and exceptional abundance in addition to its intrinsic high density and high speed.

DISCUSSION

We achieve electrical 180° switching of the Néel vector in spin-splitting cAFM Mn₅Si₃. The demonstration of electrical 180° switching of the Néel vector involves two steps. One is to prove that it is the 180° switching of the Néel vector instead of net moment that tunes the spin-splitting band structure and brings about opposite AHC, which makes AHE as a unique readout method of 180° switching of Néel vector. It is supported by both systematic theoretical calculations and several control experiments including thickness-dependent and channel width–dependent measurements. The other is to design SOT switching mechanism with asymmetric energy barriers between n₊ and n₋. It is experimentally implemented and confirmed by realizing current and assistant field polarity–dependent 180° Néel vector switching and further verified by assistant field magnitude-dependent measurements and nonswitching of ncAFM Mn₅Si₃. On the basis of electrical 180° switching and electrical readout of the Néel vector in Mn₅Si₃, electrical-controllable AFM devices with “0” and “1” resistance states were fabricated, which show high efficiency and high reproducibility. Our results establish the groundwork for practical applications of spin-splitting AFMs in next-generation information technology and serve as the basis of exploring other intriguing properties in spin-splitting AFMs arising from interactions among different degrees of freedom such as spin, valley, and charge.

MATERIALS AND METHODS

Sample preparation

Six nanometers of Mn₅Si₃(0001) films was grown on Al₂O₃(0001) substrates by cosputtering of Mn and Si at 465°C with a rate of 0.4 Å s⁻¹ under a base pressure below 5 × 10⁻⁸ torr, followed by annealing at 600°C for 2 hours. After that, 10-nm Pt was deposited in situ by magnetron sputtering at room temperature. Crossbars (6 μm by 4 μm) for SOT switching measurements were patterned using optical lithography combined with Ar ion milling. Then, Cr(10 nm)/Cu(70 nm) electrode was electron beam (e-beam)–evaporated for wire bonding. For room temperature and low-temperature x-ray diffraction (XRD) measurements, Mn₅Si₃(0001) films (80 nm) were prepared to obtain diffraction peaks with substantial intensity for precisely determining the lattice parameter. Besides, Mn₅Si₃(0001) films (130 nm) were grown for control measurements. For size-dependent measurements of the AHE, e-beam lithography was used to fabricate crossbars with width varying from 100 nm to 5 μm. All of the samples were kept in a glove box with O₂ and H₂O < 0.01 parts per million to prevent degradation or oxidation.

Characterizations

Cross-sectional transmission electron microscopy (TEM) images for Mn₅Si₃(6 nm)/Pt(10 nm) were collected at room temperature using a commercial TEM system (JEM-2100F). Magnetic hysteresis curves were collected in commercial superconducting quantum interference device (SQUID; Quantum Design), where the diamagnetic contribution of Al₂O₃(0001) substrate was subtracted. Magnetization-temperature curves were also collected from SQUID without subtracting diamagnetic contribution of Al₂O₃(0001) substrate. θ-2θ XRD measurement at room temperature was carried out at Rigaku SmartLab. In situ θ-2θ XRD at low temperatures was performed at BL02U2 Beamline from Shanghai Synchrotron Radiation Facility. Atomic force microscopy images were collected at Bruker Dimension FastScan.

Transport measurements

ρ_xx and ρ_yx of Mn₅Si₃ films were measured using a standard four-terminal method in commercial Physical Property Measurement System (Quantum Design). Ordinary Hall resistivity that is linear to magnetic field was subtracted from ρ_yx. For SOT switching measurements, writing pulses (1 ms) within the range of 46 mA were added in the WI⁺-WI⁻ channel with an assistant field H applied along the WI⁺-WI⁻ channel, followed by waiting for 10 s before collecting the Hall voltage in the RV⁺-RV⁻ channel by a nanovoltmeter with a base current of 2 mA (Fig. 4A).

Time-resolved reflectivity measurements

Time-resolved reflectivity measurements were carried out by a Ti:sapphire oscillator (center wavelength of 800 nm, repetition rate of 80 MHz, and pulse width of 20 fs) in a typical wavelength-degenerate pump-probe setup. Both the pump and probe beams were linearly polarized in a cross-polarization configuration to block the pump scattering. The pump beam was focused to 30 μm on the sample with a fixed fluence at 35.4 μJ/cm². The focal spot size and fluence of the probe beam were about 2 and 40 times smaller than those of the pump beam, respectively. The intensity of the pump beam was modulated by an optical chopper at 3 kHz to facilitate lock-in detection. The reflectivity signal was detected by a balanced detector to suppress laser power fluctuations. The sample was kept in a cryostat under vacuum of better than 1 × 10⁻³ mbar during experiments.

Magneto-optical Kerr effect measurements

The polar magneto-optical Kerr effect measurements were carried out using a power-stabilized 633-nm HeNe laser. After transmitting through a linear polarizer, the light (25 μW) was focused to an ~1-μm spot on the sample by a 40× reflective objective at normal incidence to avoid the large backgrounds that occur when a typical lens is used. The sample was mounted in the vacuum chamber of an optical superconducting magnet system with the magnetic field applied perpendicular to the sample plane (Faraday geometry). The reflected beam was modulated at ~50 kHz by a photoelastic modulator, split by a Wollaston prism and detected using a balanced photodiode with a standard optical bridge arrangement. The resulting 50- and 100-kHz modulations detected by lock-in amplifiers then correspond to the ellipticity and rotation angle of the beam, respectively. We additionally modulated the intensity of the beam with a lower-frequency (~1319 Hz) chopper to measure the dc signal for normalization using a third lock-in amplifier. The background from the optic window and a linear background were subtracted.

First-principles calculations

First-principles calculations were performed on the basis of density functional theory (DFT) (57) as implemented in Vienna ab initio simulation package (58). Exchange-correlation interaction was described by the Perdew-Burke-Ernzerhof parametrization of generalized gradient approximation (59). We also used Perdew-Wang (60) and local density approximation exchange-correlation functional, where similar results were obtained. Structures were relaxed until the force on each atom is less than 0.01 eV/Å. The cutoff energy and electronic iteration convergence criterion were set to 400 and 10⁻⁵ eV, respectively. To model the Brillouin zone, a Monkhorst-Pack (MP) k-grid mesh (61) of 7 × 7 × 9 was used. For MAE calculations, self-consistent charge density was read to get a converged result. Four-states method was used to evaluate the strength of DMI. Berry curvature and AHC were calculated on the basis of ab initio tight-binding models with all parameters extracted from first-principles calculations using the FPLO software (62).

Atomic spin simulations of magnetic hysteresis

We carried out atomic spin simulations on VAMPIRE software (63), which can define specific lattice parameters a and c consistent with our hexagonal cAFM phase Mn₅Si₃ thin film of 6.902 and 4.795 Å, respectively. Discretized 50 × 50 × 10 units cells in the x-y-z direction were used to model the Mn₅Si₃ thin film. The Hamiltonian of the system at 0 K can be written as following

$$H_{\text{total}}=\sum _{<\mathit{ip},\mathit{jq}>}{J}_{\mathit{ip},\mathit{jq}}{m}_{\mathit{ip}}·m_{\mathit{jq}}+\sum _{<\mathit{ip},\mathit{jq}>}{d}_{\mathit{ip},\mathit{jq}}·(m_{\mathit{ip}}\times m_{\mathit{jq}})-K\sum _{\mathit{ip}}{(k·m_{\mathit{ip}})}^2+H_{\mathrm{Z}}$$

Here, i and j denote unit cell and p and q represent sublattice (p, q = 1, 2, 3, 4). H_total is the total Hamiltonian, and m_ip (m_jq) is the unit magnetic moment at sublattice Mn_p (Mn_q) of unit cell i (j) with the magnitude of 2.4 μ_B. J_ip,jq, d_ip,jq, and K are the exchange interaction constant, the DMI vector, and the uniaxial anisotropy constant, respectively. H_Z is the Zeeman energy under magnetic field, equaling $-{\mathrm{\mu }}_0{m}_s{\sum }_{\mathit{ip}}{m}_{\mathit{ip}}·H$ , where μ₀, m_s, and H are the vacuum permeability, the saturation magnetization of magnetic Mn atom, and the external field, respectively. k is the direction of easy axis, which was set to be (1,1,1) direction in the cartesian coordinate system with the uniaxial anisotropy constant K of 0.1 meV from DFT estimations (text S3). Four exchange interactions were considered, namely J₁ = −12.23 meV, J₂ = −2.16 meV, J₃ = 3.98 meV, and J₄ = 2.89 meV (fig. S8A) with magnitude consistent with former DFT calculation results (64, 65). Note that J₄ interaction was set to be ferromagnetic to eliminate the 𝓉𝒯 symmetry for consistency with experimentally measured nonzero σ_xy (text S3). The DMI vector was set along x axis with a magnitude of 1.35 meV from DFT calculations and the experimentally measured out-of-plane AHE-related net moment m (text S2). These settings of basic material parameters give a simulated magnetic hysteresis that is analogous with SQUID-derived m under 150 K (Fig. 2C and text S2), illustrating that these parameters are suitable for modeling the magnetic switching behavior of cAFM Mn₅Si₃. Specifically speaking, the Landau-lifshitz-Gilbert (LLG) equation for each magnetic Mn atom is written as

$$\frac{d{m}_{\mathit{ip}}}{\mathit{dt}}=-\mid \mathrm{\gamma }\mid m_{\mathit{ip}}\times H_{\text{eff},\mathit{ip}}+\mathrm{\alpha }{m}_{\mathit{ip}}\times \frac{d{m}_{\mathit{ip}}}{\mathit{dt}}$$

where H_eff,ip is the effective magnetic field acting on the magnetic Mn atom at sublattice p of unit cell i. $H_{\text{eff},\mathit{ip}}=-\frac{\mathrm{\partial }{H}_{\text{total}}}{\mathrm{\partial }{m}_{\mathit{ip}}}+H_{\text{th}.\mathit{ip}}$ , where H_th,ip is the Gaussian stochastic magnetic field to describe the effect of finite temperature (66). γ and α are the gyromagnetic ratio of the electron and the Gilbert damping coefficient, equaling 176 s⁻¹ T⁻¹ and 0.1, respectively. A fine iteration time step Δt of 0.1 fs was used to precisely capture the dynamics of atomic magnetic moments. First, the system was initialized with random orientations of atomic magnetic moments and then relaxed into a perfect G-type AFM ordering at 0 K (fig. S8B). After applying negative magnetic field, each atomic magnetic moment can be switched by 180° (fig. S8C). The simulated m and n for each unit cell should be defined as m = (m₁ + m₂ + m₃ + m₄)/4 and n = (m₁ − m₂ + m₃ − m₄)/4, which further equaling (m₁ + m₂)/2 and (m₁ − m₂)/2 because m₁ = m₃ and m₂ = m₄ due to J₃. Thus, the 180° switching of each atomic magnetic moment is consistent with the 180° switching of m and n. Then, the hysteresis was simulated at 150 K (Fig. 2D), and 180° switching of m and n can also be observed (Fig. 2E), where m and n on all of unit cells were averaged.

Atomic spin simulations of SOT switching

To understand the mechanism for SOT 180° switching of the Néel vector n of cAFM Mn₅Si₃, we consider the damping-like effective field H_DL of the spin polarization p generated by the spin Hall effect of Pt. Then, the LLG equation under SOT can be written as

$$\begin{array}{cc}\hfill \frac{d{m}_{\mathit{ip}}}{\mathit{dt}}& =-\mid \mathrm{\gamma }\mid m_{\mathit{ip}}\times H_{\text{eff},\mathit{ip}}+\mathrm{\alpha }{m}_{\mathit{ip}}\times \frac{d{m}_{\mathit{ip}}}{\mathit{dt}}+{\mathrm{\xi }}_{\text{DL}}{m}_{\mathit{ip}}\times (p\times m_{\mathit{ip}})\hfill \\ & \mathbf{=}-\mid \mathrm{\gamma }\mid m_{\mathit{ip}}\times H_{\text{eff},\mathit{ip}}+\mathrm{\alpha }{m}_{\mathit{ip}}\times \frac{d{m}_{\mathit{ip}}}{\mathit{dt}}+\mid \mathrm{\gamma }\mid m_{\mathit{ip}}\times H_{\text{DL},\mathit{ip}}\hfill \end{array}$$

where H_DL,ip is the damping-like effective field of SOT acting on the magnetic Mn atom at sublattice p (p = 1, 2, 3, 4) of unit cell i. p is the unit vector for the spin polarization. ξ_DL is the magnitude of damping-like SOT, which has linear relationship with the magnitude of H_DL,ip and current density J (text S3). Note that for the simulation of SOT switching, 5 × 5 × 5 unit cells were used to save calculation time, which gives consistent results with that of 50 × 50 × 10 unit cells. In analogous to the simulations for magnetic hysteresis, the system was initialized with random orientations of atomic magnetic moments and relaxed into G-type AFM ordering before adding a 0.1-ns-long electrical pulse with transverse p under assistant field H. The magnitude of assistant field H was fixed at 10 kOe. This magnitude of H is reasonable because the simulations of SOT switching were carried out at 0 K, and the coercive field of simulated magnetic hysteresis at 0 K is around 150 kOe. It means that H of no more than 10% of the coercive field can assist the deterministic 180° switching of n, consistent with experimental results. m and n on all of unit cells were averaged to plot trajectories of m and n under p. The settings of pulse lengths and random seeds do not influence simulation results, proving their reliability (text S6). The influence of field-like SOTs was also investigated by adding field-like effective field H_FL as a term of ∣γ∣m_ip × H_FL,ip. It turns out that H_FL has a negative influence on SOT switching, which increases the critical switching current density (text S7).

Supplementary Materials

This PDF file includes:

Texts S1 to S7

Figs. S1 to S20

Legend for movie S1

References

Other Supplementary Material for this manuscript includes the following:

Movie S1