A Deep Learning Framework for Prostate Localization in Cone Beam CT Guided Radiotherapy

Abstract

Purpose:

To develop a deep learning-based model for prostate planning target volume (PTV) localization on cone-beam CT (CBCT) to improve the workflow of CBCT-guided patient setup.

Methods:

A two-step task-based residual network (T²RN) is proposed to automatically identify inherent landmarks in prostate PTV. The input to the T²RN is the pre-treatment CBCT images of the patient, and the output is the deep learning-identified landmarks in the PTV. To ensure robust PTV localization, the T²RN model is trained by using over thousand sets of CT images with labeled landmarks, each of the CTs corresponds to a different scenario of patient position and/or anatomy distribution generated by synthetically changing the planning CT (pCT) image. The changes, including translation, rotation, and deformation, represent vast possible clinical situations of anatomy variations during a course of radiation therapy (RT). The trained patient-specific T²RN model is tested by using 240 CBCTs from six patients. The testing CBCTs consists of 120 original CBCTs and 120 synthetic CBCTs. The synthetic CBCTs are generated by applying rotation/translation transformations to each of the original CBCT.

Results:

The systematic/random setup errors between the model prediction and the reference are found to be less than 0.25/2.46 mm and 0.14/1.41° in translation and rotation dimensions, respectively. Pearson’s correlation coefficient between model prediction and the reference is higher than 0.94 in translation and rotation dimensions. The Bland-Altman plots show good agreement between the two techniques.

Conclusions:

A novel T²RN deep learning technique is established to localize the prostate PTV for RT patient setup. Our results show that highly accurate marker-less prostate setup is achievable by leveraging the state-of-the-art deep learning strategy.

1. INTRODUCTION

Management of inter- and intra-fraction organ motion is one of the most challenging and important issues for the success of prostate RT ¹. Image-guidance is essential to ensure accurate beam targeting to fully exploit the potential of modern RT ². Clinically, on-board CBCT is commonly used for image-guided RT (IGRT) of prostate cancer ^3–9. In reality, prostate patient setup using CBCT is complicated by the inherent low image contrast of the prostate in addition to the substantial prostate motion ^10–13. Fiducial markers (FMs) are often implanted into the prostate target or adjacent normal tissue to facilitate image guided patient setup ¹⁴, which is invasive and may introduce bleeding, infection and discomfort to the patient.

Several studies focus on precise prostate localization prior to treatment^14–25. Among all prostate localization methods, daily X-ray imaging is the most widely used tool for improving the setup accuracy in intensity-modulated radiotherapy (IMRT), stereotactic body radiotherapy (SBRT) and proton therapy². The X-ray guided prostate localization methods fall into two major categories depending on whether the prostate is detected in a 2D X-ray projection-domain or in a 3D CT/CBCT image-domain.

The X-ray projection-domain method estimates the prostate position from 2D kilo-voltage (KV)/megavoltage (MV) images to guide the setup^{11, 26–29} whereby bony anatomy or implanted fiducial markers (FMs) serve as imaging surrogates for the prostate. These methods improve the setup accuracy to a certain extent, with different drawbacks in practical implementations. For bony anatomy alignment^30–34, planar X-ray projection images of the pelvis are obtained in orthogonal views. Automatic or manual registration is then applied to match of the bony anatomy between digitally reconstructed radiographs and the planar X-ray projection images. A major drawback with this approach is that the correlation of the bony pelvis anatomy and the prostate position is weak³⁵ because independent inter-fractional motion exists between the bony anatomy and the prostate. The FMs method is thus currently commonly used to overcome the disadvantages of the bony anatomy alignment. With this approach FMs (small pieces of biologically inert material) are implanted into the prostate before simulation imaging to serve as prostate surrogates. Due to the high image contrast of the FMs in the X-ray projection images, these images can be used to identify the FMs in different views and localize the prostate position in these views. Alignment of the FMs localized at planning and prior to treatment is then used to identify and correct prostate target setup errors. However, the FM method has the following drawbacks: (1) implanting FMs into the prostate is an invasive procedure; (2) FMs insertion cannot be performed for all prostate cancer patients due to contraindications; (3) FM migration occurs sometimes between simulation and treatment; (4) dose perturbations due to the composition of the FMs are introduced, particularly for particle beams, and (5) FMs implantation introduces additional treatment cost.³⁶.

With 3D pre-treatment imaging, pre-treatment 3D images of the prostate are directly matched to the planning CT to obtain a corrective displacement^{3–9, 37}. On-board cone-beam computed tomography (CT) (CBCT) is widely available on C-arm medical linear accelerators and in combination with automatic and/or manual registration can be used for quick prostate repositiong³⁸. However, in contrast to other anatomical sites, such as brain and lung, performing this process automatically and accurately is complicated by two factors: (1) the inherently low image contrast of the prostate and (2) substantial daily prostate position changes and some prostate deformations because of absence or presence of bladder/rectal filling and/or bowel gas during treatment^{10, 39}. As a result of image content changes, accurate correspondence between a planning CT (pCT) and a CBCT acquired at a different time does not exist. Thus registration methods depending on image intensity matching of corresponding regions might be inadequate in dealing with prostate CT-to-CBCT registration. The required further manual intervention for correcting the registration errors is thus becoming a barrier to quick and accurate on-line marker-less prostate localization. Therefore, there is an urgent need for fully automatic accurate marker-less x-ray image-guidance for prostate radiation therapy.

To address this need, we propose an approach different from the techniques²⁶ summarized above. In this work, we use deep convolutional neural network model pre-trained specifically for each patient to automatically detect prostate landmarks within the PTV in the daily CBCT scans for this patient. These landmarks serve as a surrogate for the prostate PTV and thus the deep learning model learns multiple levels of representations that enable detection of the low contrast prostate without implanted fiducials. The setup errors between the pCT and the CBCT are obtained by aligning the corresponding prostate landmarks, which are generated from the deep learning model^40–42. To mitigate the challenge of gathering large amount of annotated training data needed for robust clinical performance, we propose a novel patient-specific DL model training strategy based on synthetically generated patient images without relying on the acquisition of a large amount of clinically annotated CT images. To alleviate the adverse effects of anatomical changes and image artifacts, we introduce two-step task-based residual network (T²RN) to localize the prostate PTV in CBCT for accurate prostate patient setup.

2. METHODS AND MATERIALS

To obtain a reliable DL model for prostate PTV localization, three tasks, including construction of neural network, collection of annotated training datasets, and testing of the trained model, must be accomplished. In the following, we will first construct the T²RN model for the detection/tracking of a set of landmarks pre-identified in the PTV of pCT images. Instead of experimentally collecting a large amount of training images and manually annotating the landmarks for model training, we generate the training CT images corresponding to different scenarios of patient position and/or anatomy distribution by changing the pCT image. For each synthetically generated training CT, the landmarks pre-identified on pCT are mapped onto the corresponding synthetic pCT and serve as the annotation. The synthetic pCTs with annotations are then used to train a patient-specific PTV localization network. In the final step, the model is validated on independent CBCTs from patients who underwent prostate RT. The following provides more detailed description of the tasks.

Deep learning model

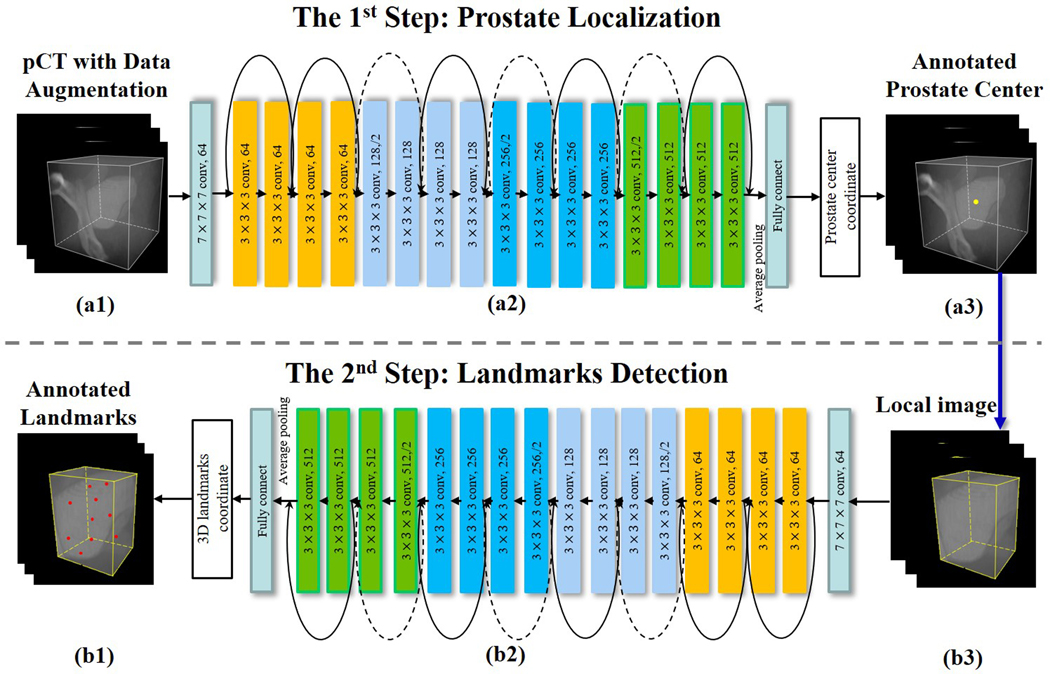
In the T²RN framework shown in Fig. 1, each step focuses on a specific task. Given the pCT or CBCT [Fig. 1(a1)], we first train a Res-net [Fig. 1(a2)] to predict the coordinates of the center of prostate PTV [Fig. 1(a3)]. The Res-net includes 17 convolutional layers, 2 pooling layers, and 1 fully connected layer. The parameter setting is specified in Fig. 1. For brevity, the normalization layers and the activation function are not shown. Besides, 8 shortcut connections are introduced to address the degradation problem of the convolutional stacked layers⁴³. At the end of the network, the coordinates of the PTV center are outputted from the fully connected layer. Based on the coordinates of the center of PTV, we extract a cropped image encompassing the prostate PTV [Fig. 1(b3)], the aim of the second step is to train a Res-net [Fig. 1(b2)] to provide the coordinates of the inherent landmarks identified manually on the PTV [Fig. 1(b1)]. The architecture of the Res-net here is similar to that of the first step, which uses the 3D images as input and outputs the coordinates of landmarks. The difference between the two Res-nets is in the sizes of input and output. Note that, the output data in the first step are the coordinates of the center of the prostate PTV with three parameters. Assuming that we detect N landmarks in the second step, the size of the output is 3×N in this step.

Figure 1.

Network architecture of the proposed T²RN for prostate setup. (a) the 1^st step for prostate center localization. (b) the 2^nd step for landmarks detection. Abbreviation: pCT = planning computed tomography, T²RN = Two-step Task-based Residual Network.

The two-step network is optimized using Adam algorithm. Here we set the initial learning rate at 10⁻² and slowly decrease it to 10⁻⁶. 100 epochs are used to train the model. To accelerate the training processing, in the first step, the entire pCT is cropped into a region of interest (ROI) according to the prostate position in the pCT image.

Generation of annotated dataset

Training of the T²RN model requires a large amount of annotated datasets. Instead of collecting the training datasets clinically and manually labeling the same sets of landmarks in all training and validation datasets, which may be practically impossible, we propose a patient specific data synthesis method by introducing physically practical changes in the pCT image. In this approach, an annotated training dataset corresponding to a specific scenario of patient position and/or anatomy distribution is generated by translating/rotating/deforming the pCT with a transformation matrix. Specifically, we randomly translate the pCT using uniformly distributed shifts from −35 mm to 35 mm in Anterior-Posterior (A-P), Left-Right (L-R), or Superior-Inferior (S-I) direction. Rotated CT images with uniformly distributed random angles from −10° to 10° in yaw, pitch, or roll direction are also generated. Additionally, deformation of the pCT image is also introduced, which is achieved by using an existing B-spline based deformable model ⁴⁴. Finally, these CT images are filtered by using a variety of Gaussian to reflect possible inter-fractional changes in the image content. The filtering is done probabilistically with a standard deviation of the Gaussian distribution selected randomly from 0.1 to 8.

For a given patient, ten landmarks were automatically selected in the PTV as the annotations. We aim to maximize the distance between each of the landmarks so that the landmarks can cover the whole prostate. The strategy of the landmark selection is shown in Equation 1:

$$\stackrel{⃑}{x^{\mathrm{*}}}=\arg min\left(-\sum _{i=1}^n\sum _{j=1}^n{‖x_i-x_j‖}_2\right)/n^2$$

$$\stackrel{⃑}{\text{S.t.}x}\in b$$ (1)

Here $\stackrel{⃑}{\mathit{x}}$ is the vectorized coordinate of the landmarks with each entry denoted by${\mathit{x}}_{\mathit{i}}$ where $\mathit{i}$ indicates the i^th landmarks’ coordinate.$\mathit{n}$ indicates the number of selected landmarks. $\mathit{b}$ indicates the boundary of the prostate. The objective function is solved using the generalized pattern search algorithm. With a known transformation field, the landmarks in the pCT are mapped automatically to the corresponding synthetic CT images to generate the annotations. These landmarks as whole can be considered as a surrogate of the prostate PTV. The original pCT, augmented CT images and the corresponding landmarks are then applied to train the T²RN model. We divide all the synthetic data into training datasets (1102 images) and the validation datasets (123 images). The model is further tested using datasets of over 200 clinically acquired CBCT images for six patients (see next section for details).

Test of the T²RN model

The trained patient-specific deep learning model is tested by using the setup CBCT images of six prostate patients. For prostate localization, each of these patients had four FMs implanted in the prostate. For each patient, 20 CBCT fractions were acquired during the course of the patient’s RT by using on-board imaging (OBI) system of a Varian TrueBeam® linear accelerator. To better assess the spatial invariance of the proposed model, we synthetically created additional CBCTs for each clinically acquired CBCT by applying rotation/translation transformations. 120 original CBCTs and the 120 created CBCTs with FMs were included for quantitative analysis. To mitigate any influence of the implanted fiducials in the DL model, all FMs in the pCT and CBCT are identified and replaced with adjacent soft tissue using the interpolation algorithm during the process of model training. In the quantitative analysis with FMs, the imperfect FMs removal method may influence the DL performance. Thus, we added an extra patient without FMs to investigate the effect of FMs residual on the proposed model.

The translational and rotational setup errors of prostate PTV are evaluated quantitatively in the testing CBCT images. Suppose that the N landmarks are spatially characterized by ${\overrightarrow{L}}_{pCT}\left(i\right)$ and ${\overrightarrow{L}}_{CBCT}\left(i\right),i=1, 2,3,\dots ,N$ in the pCT and CBCT, respectively. Then the couch translation and rotation can be determined by

$$min\sum _{i=1}^N{\left|R{\overrightarrow{L}}_{CBCT}\left(i\right)+T-{\overrightarrow{L}}_{pCT}\left(i\right)\right|}^2,\left(2\right)$$ (2)

where $R$ denotes the rotation matrix in the direction of yaw, pitch, and roll, and $T$ represents the translation matrix in A-P, L-R, and S-I directions. To evaluate the accuracy of the model prediction, we use the results obtained by using fiducial-based method as the reference.

The Pearson’s correlation coefficient (CC) is used to measure the correlation in the couch shifts between the model prediction and the reference ⁴⁵. The Bland-Altman plots calculate the mean difference of the couch shifts between the two technique and estimate the 95% confidence interval (CI) of the agreement limits ⁴⁶. The group systematic error (M), systematic error (∑), and random error (σ) for the proposed method are calculated ⁴⁷.

3. RESULTS

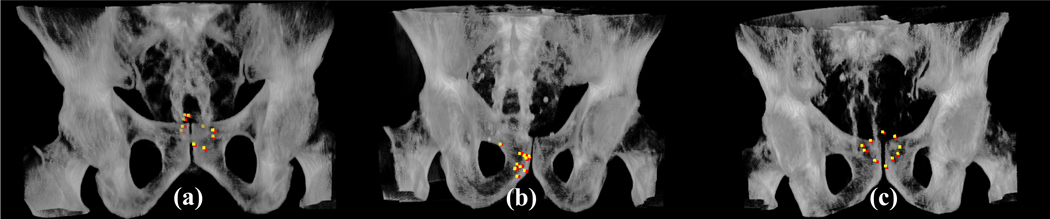
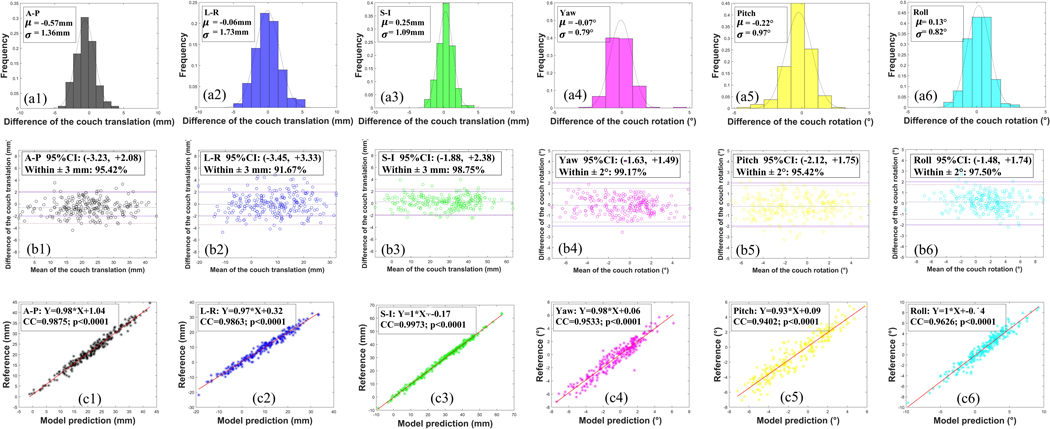
In Figure 2 we show the volume rendering images of the CBCT images of the three examples together with the predicted landmarks of the T²RN model. It is seen that the positions of the predicted landmarks (colored in yellow) are very close to the reference (colored in red). The couch shifts are determined by the positions of the landmarks. The quantitative differences of the couch shifts between the model prediction and the reference are plotted in Fig. 3 for the 240 CBCTs. Figure 4 (a), (b) and (c) show the histograms of the errors, Bland-Altman analysis, and CC between the two approaches, respectively. A quantitative analysis of figure 3 and 4 is summarized in Table 1. From these results the following observations are made. First, the Bland-Altman analysis shows that the proportion of the testing fractions within a predefined clinically accepted tolerance (±3mm/±2º) ⁴⁸ is higher than 91% and 95% in translation and rotation dimensions, respectively. Second, there are strong correlations (all > 0.94) in the couch shifts between model prediction and the reference.

Figure 2.

Examples of the 3D landmarks estimated from the proposed T²RN model (colored in yellow) and their corresponding reference (colored in red) in the 3D rendering. The columns (a), (b) and (c) show the results in three patients, respectively.

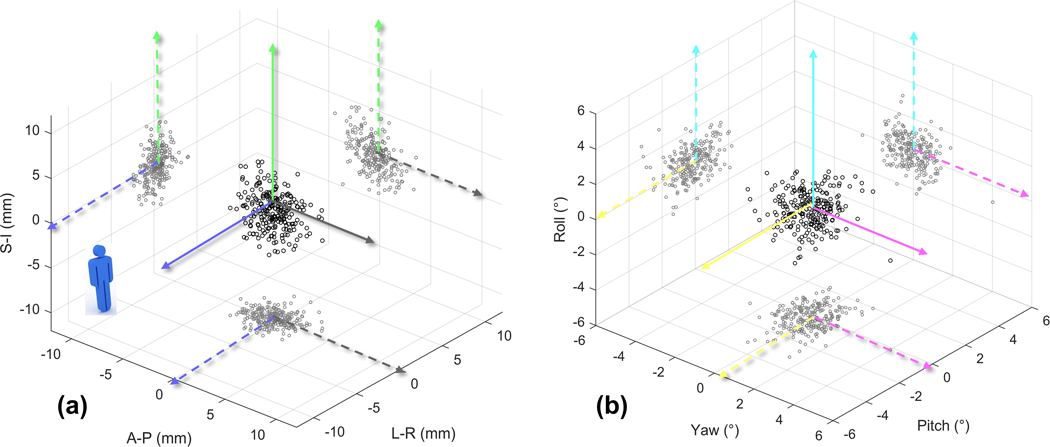
Figure 3.

The difference of couch shifts between the model prediction and the reference on the 240 CBCT scans of different treatment fractions of six patients. (a) and (b) are the results in translation and rotation dimensions, respectively.

Figure 4.

Analysis of the difference of couch shifts between the model prediction and the reference on the 240 CBCT scans of different treatment fractions of six patients. The first row shows the histograms of the difference. The second row shows the Bland-Altman analysis with the predefined clinically accepted tolerance (solid line) and the 95% confidence interval (dot-dash line). The third row shows the CC. (1–6) show the results in the direction of A-P, L-R, S-I, yaw, pitch, and roll, respectively. Abbreviation: A-P = anterior-posterior, L-R = left-right, S-I = superior-inferior.

Table 1.

Summary of the setup errors on the 240 CBCT scans of different treatment fractions of six patients. Both translational and rotational errors are presented. For each catalog, we calculate the ensemble mean ± SD, 95% CI, the proportion of the testing fractions within a predefined clinically accepted tolerance (±3mm/±2º), and CC.

	Translation			Rotation
	A-P	L-R	S-I	Yaw	Pitch	Roll
Ensemble Mean ± SD (mm/°)	−0.57 ± 1.36	−0.06 ± 1.73	0.25 ± 1.09	−0.07 ± 0.79	−0.18 ± 0.99	0.13 ± 0.82
[5th, 95th] (mm/°)	[−3.23, 2.08]	[−3.45, 3.33]	[−1.88, 2.38]	[−1.63, 1.49]	[−2.12, 1.75]	[−1.48, 1.74]
Within 3mm/2° (%)	95.42	91.67	98.75	99.17	95.42	97.50
Correlation Coefficient	0.99	0.99	0.99	0.95	0.94	0.96

Table 2 analyzes the inter-observer variability (group systematic error M, systematic error ∑, and random error σ) in the couch shifts between the model prediction and the reference. Overall, the systematic/random setup errors between the T²RN model prediction and the reference are less than 0.25/2.46 mm and 0.14/1.41° in translation and rotation dimensions, respectively. These results suggest that the proposed T²RN model can achieve high accuracy in the patient setup without relying on the FMs.

Table 2.

Analysis of the inter-observer variability in the setup errors. We calculate Mean ± St. Dev of the difference for each patient in translation and the rotation dimensions. The combinations of these values give the inter-observer variability (group systematic error M, systematic error ∑, and random error σ) for a population of the prostate setup.

		Translation			Rotation
		A-P (mm)	L-R (mm)	S-I (mm)	Yaw (°)	Pitch (°)	Roll (°)
Mean ± St. Dev.	Patient 1	−0.43±1.56	0.18±1.95	0.07±1.35	−0.13±0.88	−0.15±1.15	0.16±0.88
	Patient 2	−0.55±1.32	−0.09±1.86	0.48±1.24	−0.13±0.96	−0.15±0.76	0.10±0.82
	Patient 3	−0.69±1.31	0.06±1.63	0.35±0.92	−0.06±0.77	−0.24±0.91	0.17±0.79
	Patient 4	−0.45±1.20	−0.13±1.59	0.17±0.91	−0.08±0.71	−0.22±1.02	0.17±0.71
	Patient 5	−0.62±1.22	−0.24±2.00	0.31±0.97	−0.10±0.72	−0.10±1.11	0.08±0.89
	Patient 6	−0.71±1.55	−0.15±1.33	0.15±1.07	−0.07±0.72	−0.24±0.97	0.11±0.87
Group systematic error (M)		−0.57	−0.06	0.25	−0.07	−0.18	0.13
Systematic error (∑)		0.16	0.25	0.18	0.10	0.14	0.07
Random error (σ)		1.93	2.46	1.54	1.13	1.41	1.17

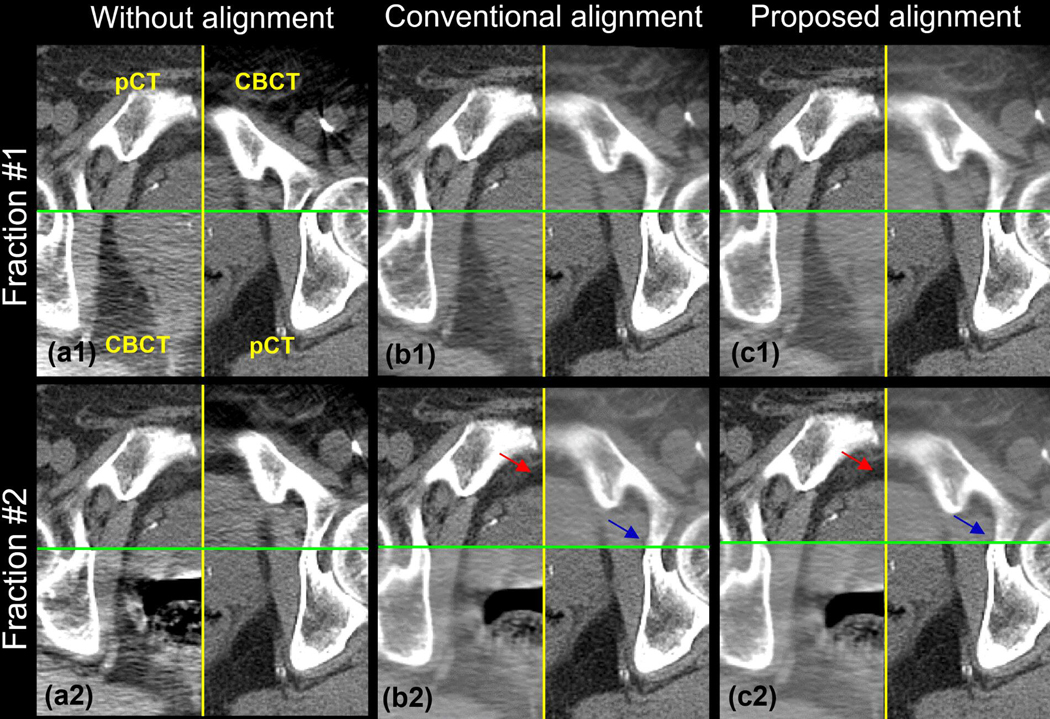
To further evaluate the efficient of the proposed method, we add an experiment for the patient without the fiducial markers. We compare the result of the proposed process with the conventional rigid alignment process from Simple ITK, a widely used registration toolkit. Figure 1 shows the checkerboard of FMs-free images without (a), with the conventional (b), and with the proposed (c) prostate alignment. Row 1 and 2 show the result of fraction #1 and #2, respectively. The relative motion between bony anatomy and prostate in fraction #1 is small, while fraction #2 is large. The prostate and the bone in figure 1(b1) and 1(c1) can match the conventional and the proposed alignment well. However, in figure 1(b2) [red arrow], the prostate is mismatched using the conventional alignment method due to the large relative motion between the bone and the prostate. Instead, the bony anatomy is matched well with the conventional method, pointed at the blue arrow. In figure 1(c2), the prostate matches well [red arrow] with the proposed method suggesting that our approach can detect the prostate itself without the FMs.

4. DISCUSSION

Internal organ movement is one of the most challenging issues in prostate RT. Prostate localization is commonly achieved by using implanted FMs, especially in modern prostate SBRT. In this work, we investigate a novel deep learning strategy of prostate target localization on CBCT. The approach utilizes the prior information and helps to localize prostate PTV with high accuracy and efficiency.

Different from the population-based DL model, we propose a patient-specific DL model to localize the prostate PTV. The novelties of our method include: 1) we develop a T²RN deep learning architecture for landmark detection in the PTV. With the advantage of deep feature extraction using the Resnet, the proposed network can detect the landmarks accurately, even if there are no FMs implantation; and 2) Instead of acquiring a large annotated clinical dataset, we propose a personalized pCT augmentation method to generate a large amount of annotated pCT, making the DL modeling clinically practical.

CBCT artifacts may result in prostate localization inaccuracy. Similarity between the pCT and CBCT is essential for model prediction because the deep learning model is trained using the pCT dataset. CBCT with severe scatter, metal, and motion artifacts may lead to inaccurate tumor localization but we expect the performance of our strategy to improve as recently, significant advances in CBCT artifact removal have been achieved ^{49, 50} and in this study, the proposed method has already produced accurate prostate localizations in 240 CBCT images. However, the quality of CBCT images vary with different IGRT systems. Thus, in future we plan to evaluate the method on more CBCT images acquired on different IGRT platforms.

Insufficient training images may also influence the results. In this paper, we applied 1102 images reflecting different clinical situations for model training. The results are found to be clinically acceptable. Effectively enlarging the training dataset using the augmentation method is critically important for improving the accuracy of PTV localization and avoiding the overfitting.

Although the proposed framework produces accurate results for prostate positioning, refinements can be made in the future. Firstly, in this study, the landmarks in the prostate are selected somewhat randomly and all the landmarks are treated equally. To further improve the performance of the proposed method, the landmarks can be assigned with different weightings in the training process because different landmarks may influence the accuracy of prostate localization differently. Secondly, we adopt two 3D convolutional neural networks in the T²RN, which is computationally intensive. The efficiency can be improved in the training step by balancing network width, depth, and resolution ⁵¹.

5. CONCLUSION

In this paper we reported on an accurate marker-less prostate PTV localization technique based on deep learning. This work represents the first attempt to apply deep learning to CBCT-guided RT. The use of a patient-specific data synthesis method mitigates the need for a vast amount of patient images for the model training, which makes the proposed approach a clinically practical solution. Evaluation of the proposed technique to clinical prostate IGRT cases strongly suggest that highly accurate prostate tracking in CBCT images is readily achievable using the proposed deep learning model. Hence our approach has the potential to eliminate the need for implanted fiducials.

We emphasize that the proposed method is quite general and can be easily extended to the localization of targets in other anatomical regions such as head and neck, brain, liver, lung, brain, and spine. The proposed strategy should also be directly applicable to other image-guided interventions that require fusion of 3D pre- and intra-interventional imaging.

Figure 5.

The checkerboard of the FMs-free images without (a), with the conventional (b), and with the proposed (c) prostate alignment. Row 1 and 2 shows the result of the fraction #1 and #2, respectively. The relative motion between bony anatomy and prostate in fraction #1 is small, while fraction #2 is large.