A metabolic modeling platform for the Computation Of Microbial Ecosystems in Time and Space (COMETS)

Abstract

Genome-scale stoichiometric modeling of metabolism has become a standard systems biology tool for modeling cellular physiology and growth. Extensions of this approach are emerging as a valuable avenue for predicting, understanding and designing microbial communities. Computation of microbial ecosystems in time and space (COMETS) extends dynamic flux balance analysis to generate simulations of multiple microbial species in molecularly complex and spatially structured environments. Here we describe how to best use and apply the most recent version of COMETS, which incorporates a more accurate biophysical model of microbial biomass expansion upon growth, evolutionary dynamics and extracellular enzyme activity modules. In addition to a command-line option, COMETS includes user-friendly Python and MATLAB interfaces compatible with the well-established COBRA models and methods, as well as comprehensive documentation and tutorials. This protocol provides a detailed guideline for installing, testing and applying COMETS to different scenarios, generating simulations that take from a few minutes to several days to run, with broad applicability to microbial communities across biomes and scales.

Introduction

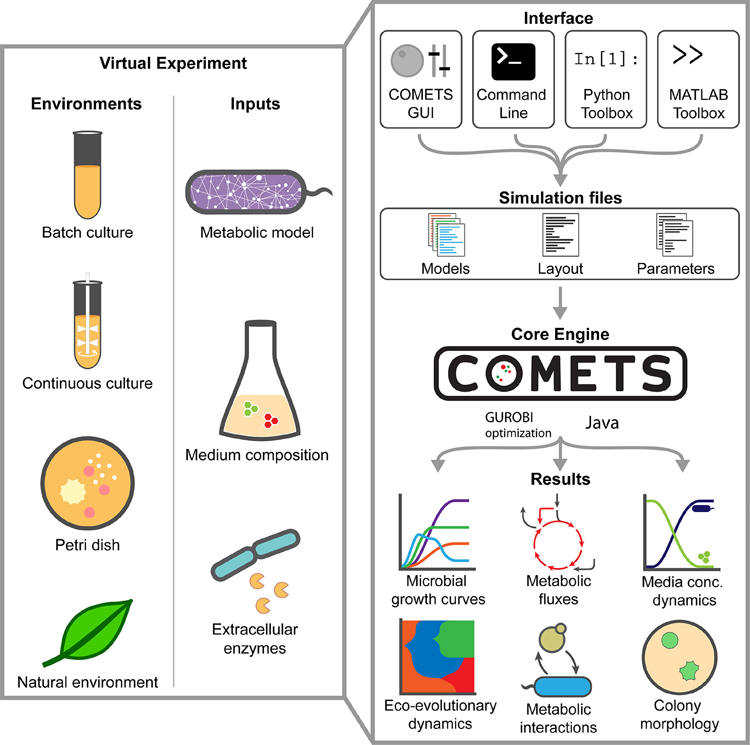
Microbial communities, from the simplest synthetically constructed^1–6 to the most complex naturally occurring ones^7–10, have substantial impact on multiple aspects of human life, and have therefore become a key focus of interdisciplinary research in different fields, including microbial ecology and evolution^11,12, human health^10,13–15, biogeochemistry^7,9,16–18 and metabolic engineering^19,20. These communities may involve extensive interactions of different microbial species with each other, and with the surrounding environment^11,21–24. Often, short-term metabolic strategies employed by individual organisms can have long-term effects on environmental structure and composition, leading to complex processes and cycles that span multiple spatial and temporal scales. An emerging challenge in systems biology is the development of quantitative predictive frameworks that can help understand, control and design microbial communities across these different scales—a task with a myriad of practical implications^11,25–27. This protocol describes computation of microbial ecosystems in time and space (COMETS)²⁸, a multiscale, open-access, collaborative platform for predicting the complex emergent properties that result from intracellular metabolism of individual species, and ensuing microbe–microbe and microbe–environment interactions (http://runcomets.org, Fig. 1 and Table 1).

Figure 1. Overview of the COMETS platform.

Virtual experiments in COMETS combine a variety of environments and biochemical inputs. These combinations can be quickly generated using one of the provided interfaces, which feed into the COMETS core engine. The engine simulates the spatio-temporal dynamics of the ecosystem and outputs microbial biomass information, metabolic fluxes, and media concentration over time. Downstream analysis, either within the toolboxes or with the user’s software of choice, can then be applied to further visualize and characterize the results.

Table 1:

List of key COMETS capabilities and application examples.

General category	Specific category	Capability	Example rationale
Spatial capabilities	Biomass motion	Linear diffusion	Run-and-tumble motion
		Non-linear diffusion dependent on local properties, deterministic or stochastic	Metabolite lubrication, surfactant secretion in the environment, cooperative motion
		Convective (pushing) motion, deterministic or stochastic	Colony growth via pushing forces, non-motile motion
		Impenetrable barriers	Barriers such as rocks or beads
		Model mixing or enforced non-overlap	Cells can swim into the same general space, or create layered biofilms which prevents penetration by other cell types
	Metabolite motion	Linear diffusion	Normal property of chemicals
		Impenetrable barriers	Barriers such as rocks or beads
Biological capabilities	Cell growth and death	Growth rate via flux-balance analysis with or without pFBA secondary optimization	Optimal metabolic growth with or without minimized sum of absolute values of all fluxes
		Standard FBA, Monod, or Hill uptake rates	Linear, saturating, or cooperative uptake mechanisms
		Lag phases via activation rate	Variable time to exit from stationary state
		Fixed, species-specific death rates	Cell death, proportional to population size
		Gene cost	Size of the genome represents an energy cost that is applied to lower the biomass growth rate.
		Light absorption	Simulation of photosynthetic organisms
	Stochastic changes	Evolution by generation of related models with altered flux bounds	Mutations arising during ecosystem lifetime
		Stochastic fluctuations (Gaussian or demographic)	Random fluctuations in growth rate due to environmental or demographic fluctuations
Environmental capabilities	Metabolite sources and sinks	Fixed local concentration of a given metabolite	Buffered source of a metabolite, such as oxygen at an air/liquid interface
		Fixed local environmental metabolite replenishment rate	Spatially structured: interaction of community with nutrient-producing host cells Spatially unstructured: Chemostat
		Constant dilution rates (for all biomass and environmental metabolites)	Simulation of bioreactor in chemostat mode
		Time-dependent variation on the abundance of a given extracellular metabolite, according to a predefined function	Periodic availability of light for day-night cycles
	Bottlenecks	Abrupt dilution events of biomass followed by replenishment of nutrients	Batch transfer experiments or seasonality
Other		Extracellular enzyme costly secretion and activity	Secretion of cellulase and cellulolytic activity by diffusing enzymes in the environment
		Capacity to handle many (>>100) stoichiometric models	Simulations of complex communities/microbiomes

Applications and alternative methods

In recent years, genome-scale stoichiometric models of metabolism (such as flux balance analysis, FBA) have made it possible to produce testable predictions of all metabolic rates (or fluxes) in individual organisms, based on the knowledge of their genomes, and on simplifying assumptions (steady state and optimality) that do not require the knowledge of thousands of kinetic parameters necessary for kinetic models^29–32. Manually curated and automatically constructed genome-scale stoichiometric models are now available for hundreds of prokaryotic and eukaryotic organisms, from a growing number of resources^33–37. Genome-scale metabolic modeling and flux balance methods can be expanded from individual microbes to multispecies communities, through a variety of approaches that are still the subject of active research³⁸. Some of these approaches assume specific community- level optimization or balanced growth across organisms to predict ecosystem-level fluxes at steady state^39–41. Another class of approaches (Table 2), including the one at the core of COMETS, has instead taken advantage of an iterative dynamical variant of FBA known as dynamic flux balance analysis (dFBA)^42–45. In dFBA, intracellular metabolism is still assumed to be at steady state, but the abundance of the different species and of environmental metabolites are treated as dynamical variables. Thus, dFBA has in principle the capacity to predict both population dynamics and ecological interactions as emergent properties that arise purely from the physiology of their constituent species^{28,43,46–48}. The landscape of opportunities in this arena has been also largely catalyzed by the availability of an increasing number of models for hundreds of different species, based on manual reconstructions and automated computational pipelines^49,50.

Table 2.

Comparison of COMETS capabilities with previous version and other dynamic FBA based software packages. The black checkmark labels a fully functional capability. The blue checkmark labels a limited capability, one that requires additional programming/script writing.

	COMETS v.128	COMETS v.2 (this work)	BacArena101	Matnet114	3DdFBA115	Spatial dFBA lab42	IndiMesh116
Multiple genotypes	✓	✓	✓	✓	✗	✓	✓
Diffusive bacterial / metabolite spread	✓	✓	✓	✓	✓	✓	✓
Convective and/or collective bacterial spread	✗	✓	✓	✓	✓	✓	✓
Chemotaxis	✗	✗	✓	✓	✗	✓	✓
Spatially-varying diffusion	✗	✓	✓	✗	✗	✗	✓
Evolution	✗	✓	✗	✗	✗	✗	✗
Extracellular enzymes	✗	✓	✗	✗	✗	✓	✗
Approachable toolboxes	✗	✓	✓	✓	✗	✗	✗
GUI	✓	✓	✗	✗	✗	✗	✗
Population-based or agent-based	population	population	agent	agent	population	population	agent

In addition to being dynamic systems, naturally occurring communities typically occupy heterogeneous, structured environments, rather than well-mixed bioreactors. Spatial structure can have major consequences on interspecies interactions, and on community structure and function, both at the microscopic scale (e.g., the structure of a biofilm⁵¹), and at macroscopic ones (e.g., the distribution of colonies on a Petri dish⁵²). COMETS was initially developed as a spatially structured simulation engine²⁸, making an important step towards realistic modeling of microbial communities. In parallel, other studies have also implemented different versions of spatially explicit dFBA, often taking different approaches that are tailored for different applications (Table 2).

COMETS was first developed as a flexible tool for research on natural and synthetic microbial communities²⁸. Nontrivial predictions about the taxonomic distribution and functional role of different species in a three-species artificial consortium were successfully tested experimentally²⁸, paving the way for a number of follow-up studies. Since then, several works have used COMETS to address disparate scientific questions on microbial metabolism and microbiomes such as identifying ecological interactions among microbes^21,53,54, studying the evolution of mutualism^55,56, eco-evolutionary dynamics⁵⁷, microbial community engineering⁵⁸, gut microbiome function⁵⁹ and spatial distribution of colonies on a surface⁵². COMETS is being further developed as a free open-access software platform for predictive modeling of microbes, microbial communities and complex cellular populations. COMETS could become a practical computational tool for research on microbial communities across a large range of disciplines, including microbiology, synthetic biology, metabolic engineering and biophysics. We envisage that it will continue to grow as a community effort, for which different research teams will be able to add their own modules, and benefit from the collective effort of everyone else.

With the inclusion of a user-friendly graphical interface and versatile scripting toolboxes (e.g., Python and MATLAB, Fig. 1), our aim is to make COMETS accessible to a wide range of computational and experimental researchers as well as educators and students. For instance, students can use COMETS to simulate ‘experiments’ and learn-by-doing core concepts in biology such as those related to microbial growth, competition for resources, metabolic exchange and evolution (Table 1). By integrating the scripting toolboxes with the widely used FBA software COBRA⁶⁰, we have enabled a seamless workflow from building COBRA metabolic networks to running COMETS simulations, which greatly simplifies the process of testing predictive metabolic reconstructions. An online, hands- on tutorial is also available (https://segrelab.github.io/comets-manual/), and is regularly updated as new functionalities are added to COMETS.

Development of the protocol

We describe below some of the key mathematical and computational components underlying the COMETS framework. Each subsection is a brief summary, for which additional details are provided in related references and in Supplementary Discussion 1.

Flux balance analysis.

FBA is a constraint-based computational method used to predict the function or phenotype of an organism by simulating its metabolism^31,32,60. The network of metabolic chemical reactions of an organism is represented by the stoichiometric matrix S. In this matrix, rows represent metabolites and columns represent reactions; Sij represents the moles of metabolite i consumed (Sij < 0) or produced (Sij > 0) by reaction j. FBA, like many other stoichiometry-based models of metabolism, relies on the assumption that cellular metabolism is at steady state. This assumption should be thought of as pertaining to a population of cells over a certain period of time, such that, on average, the concentrations of metabolites inside cellular biomass do not change in time.

To predict a specific set of reaction fluxes for a given metabolic network, FBA searches the feasible space for a point (or set of points) that maximizes (or minimizes) a given objective function, represented in the form of a linear combination of the flux variables. Usually, this objective function is the production of a set of molecules (building blocks, energy and redox currency) that metabolism needs to provide in precise proportions as required by other cellular processes (synthesis of macromolecules, membranes, DNA replication, transcription, etc.) to generate new biomass⁶¹. The use of linear objective functions makes it possible to solve this mathematical problem through well- established efficient linear programming algorithms, available through a number of libraries. A typical FBA optimization for a genome-scale model, on a standard laptop computer, takes on the order of a few milliseconds. Biologically, the search for a set of fluxes that optimizes a given objective implies the hypothesis that an organism has evolved to be able to regulate its metabolic fluxes to approach that optimum under a set of environmental conditions. In other words, the model assumes an ‘optimal regulation’. This assumption is partly justified by evolution^62,63, but it does not necessarily hold in all conditions^62,64,65,66. COMETS can accommodate arbitrary objective functions, in addition to maximization of biomass production. Moreover, it supports multiple objectives optimized iteratively, including the minimization of the sum of the absolute values of fluxes (also known as parsimonious FBA)⁶⁶.

Dynamic flux balance analysis (dFBA).

dFBA^28,43 is an iterative extension of FBA that explicitly includes the dynamics of the organisms as they grow, and the effects of their growth on the environment. dFBA produces piecewise-linear approximations of the microbial growth curve (i.e., biomass as a function of time), and of the environmental abundance of metabolites, that can change due to external factors, or through uptake/ secretion fluxes. In dFBA, the uptake rate of a resource into the cell has to be estimated at each time point on the basis of the environmental concentration of that resource, using a Michaelis–Menten equation. Notably, in dFBA, while extracellular metabolites can dynamically change, intracellular ones are still assumed to be at steady state (through fast equilibration).

Boundary conditions for environmental metabolites and physical barriers.

All simulations begin with an initial metabolite environment, which may vary across space. Metabolites can also be set to change in predefined ways during the simulation. In a first modality, a metabolite can be assigned the static property, which causes it to begin each time step at the defined value. Second, the refresh property can be used to add (or remove) a constant amount of metabolite to a spatial location per hour, divided equally among the time steps. Third, metabolite abundances can be set to vary periodically using defined wave functions. Finally, all metabolites can be set to dilute proportionally. Propagation of biomass or nutrients into certain lattice locations can be prevented by the placement of barriers. Barriers act as reflective boundaries for diffusion and biomass motion calculations.

Spatial structure and dynamics.

The classical implementation of dFBA described above (which can be implemented in COMETS) corresponds to a well-mixed system, in which all microbes and metabolites are uniformly distributed and have access to each other in proportion to their concentration. In addition to this dynamic behavior in time, COMETS is able to take into account the spatial structure of microbial colonies and communities, simulating arbitrary 2D spatial structures (a 3D version is in principle available, but has not been thoroughly tested yet). Spatial structure in COMETS is implemented as a 2D grid of cubic ‘boxes’ with a given dimension and volume. Inside each of these ‘boxes’, a well-mixed scenario is assumed. The biomass of different species and the environmental metabolites can propagate from a given box to neighboring boxes on the basis of physics laws of convection–diffusion, as described in detail below.

Biomass propagation.

The core of the COMETS method is the simulation of the growth and propagation of the biomass present in the system. The simulations are performed by numerically solving the partial-differential equations that govern the dynamics of the system^67–73. The dynamical variable of biomass (formally biomass density) is spatially continuous. Although the natural unit of biomass is a single cell of an organism, we implemented the biomass dynamics as a locally averaged continuous quantity. This makes it possible to simulate macroscopic systems on the order of centimeters and larger. An individual cell-based methodology^74,75 would significantly hinder the extent of both size and time of the simulations.

Demographic and growth noise.

Two types of stochastic noise are implemented in COMETS. Demographic noise is a consequence of sampling in finite populations, and can be introduced in COMETS by adding a stochastic term⁷⁶. Additionally, growth rate noise consists of a simple broadening of the growth rate with a Gaussian noise term. It is introduced to take into account other stochastic effects, such as fluctuation of the nutrient availability and cellular properties.

Extracellular reactions.

COMETS includes the capability to simulate reactions happening in the extracellular environment, without association to a specific organism. Users can implement either elementary reactions of arbitrary order based on mass-action kinetics, or enzyme-catalyzed reactions obeying Michaelis–Menten kinetics, e.g., for the simulation of extracellular enzymes.

Random mutation.

In addition to capturing ecological dynamics, COMETS has the capability of generating mutated organisms during a simulation, making it possible to study evolutionary dynamics. Given the total population growth NG and mutation rate μ, COMETS stochastically samples a number from a Poisson distribution with mean NGμ (or a binomial if populations contain less than ten cell divisions). The resulting mutants—new stoichiometric models with modified stoichiometry based on a set of rules (see below)—are then placed randomly in spatial grid boxes containing biomass of the ancestor. The new mutant populations are also mutable with the same mutation rates as the ancestor, allowing the accumulation of mutations in time.

Numerical integration of spatiotemporal equations.

The method used for numerical integration of the partial differential equations in COMETS depends on the type of equation, i.e., the type of model of spatiotemporal propagation, that is being solved. The three different models for propagation of biomass, i.e., the simple diffusion, propagation by pushing and nonlinear cooperative diffusion, cannot be optimally solved by a single method.

For the simple (linear) diffusion model of biomass propagation, the user can choose between two implemented numerical methods for its solution. One is using an alternating direction implicit scheme with a central difference formulation²⁸, and the other is an eight-point integration scheme. The other two models of biomass propagation, i.e., the model of convection (pushing) and the nonlinear diffusion, due to the presence of the nonlinear terms, are solved by implementing the predictor–corrector Adams–Bashforth–Moulton scheme^77,78. The diffusion of the media is solved by the standard implicit method, the same as for the linear diffusion of the biomass.

Overview of the procedures

The seven procedures in this protocol describe in detail how to get started with COMETS simulations, presenting representative test cases, from the simplest to the more sophisticated. For each procedure, we provide a full step-by-step description of how to implement simulations and interpret the results. The procedures also illustrate the use of specific interfaces for the different scenarios, but each procedure can be performed using any of the available interfaces.

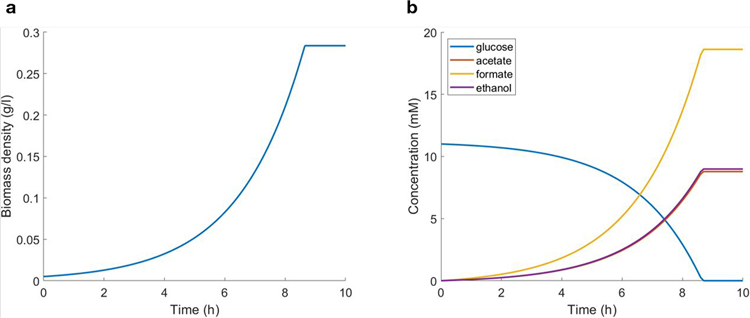
Procedure 1: growth of bacteria in well-mixed conditions

One of the first successful simulations of the time-dependent dynamics of bacterial metabolism was the classical study of Escherichia coli batch culture by Varma and Palsson^43,79. Here we reproduce one of the results in the study, the anaerobic fermentation in minimal media with glucose as the only carbon source using the core model of E. coli⁸⁰. This model consists only of a small but key subset of the reactions present in the metabolic network of E. coli. However, it is sufficiently complex to reproduce some of the fundamental metabolic activities in a bacterial cell, such as glycolysis, the tricarboxylic acid cycle and the pentose phosphate shunt. The spatial layout in this elementary case consists of a single grid point of 1 cm³ of volume, thus modeling well-mixed, i.e., nonspatially structured, conditions. We seeded the batch culture with 5 × 10⁻⁶ g of E. coli biomass. The initial composition of the substrate was 11 mM of glucose and unlimited amounts of ammonia and phosphate. The nutrient uptake was modeled with the standard Michaelis–Menten kinetics^43,81,82, using the typical Monod parameters for anaerobic uptake of glucose by E. coli.

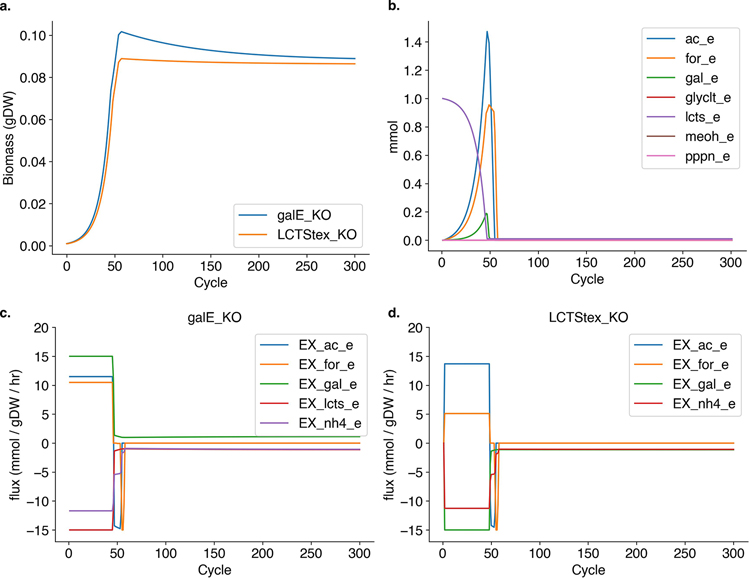
Procedure 2: cross-feeding in a chemostat

COMETS provides the functionality to run simulations in a chemostat. In this procedure, we illustrate how to use the Python toolbox to generate a chemostat simulation by manually assigning the initial metabolite concentrations, the metabolite inflow rate, metabolite dilution rate and model death rate. We simulate a chemostat with lactose as the sole carbon resource and two strains of E. coli: one that is deficient in the ability to uptake lactose, and one that is deficient in the ability to metabolize galactose. The strain that is unable to metabolize lactose can only grow by cross-feeding galactose produced as a byproduct when the other strain metabolizes lactose, and therefore this procedure also highlights how emergent interstrain interactions can occur in COMETS. For this procedure, we use the iJO1366 model provided as part of COBRApy⁸³.

Procedure 3: periodic environments and light absorption; modeling the diurnal cycle using the MATLAB toolbox

COMETS can simulate periodically changing environments, where the periodic function can be either a step function, a sine function or a half sine function (shown below). The most obvious use case for this functionality is to study how the metabolism of photosynthetic organisms changes during the day/night cycle with varying sunlight (photons) and how this affects the microbes. Here we simulate one such experiment with a genome-scale model of Prochlorococcus⁸⁴, the most abundant marine photoautotroph.

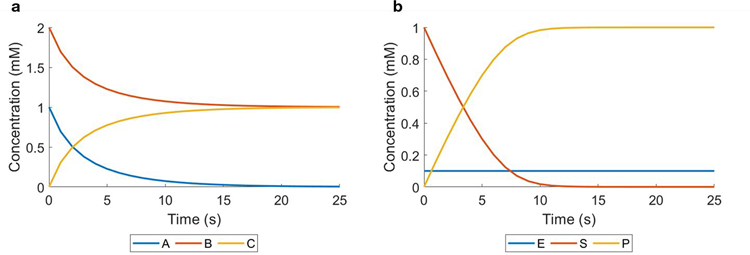
Procedure 4: simulations including extracellular reactions

This protocol demonstrates the capacity of COMETS to simulate reactions involving extracellular metabolites using the MATLAB toolbox. In the first case, a simple binding reaction is defined with the form A + B → C. In the second case, an enzyme, E, catalyzes the conversion of F → G. Extracellular reactions are present in some microbial communities owing to the activity of secreted extracellular enzymes^85–88. The example presented here simulates an extracellular reaction showing the role of extracellular cellulase in the degradation of cellulose.

Procedure 5: simulating evolutionary processes in microbial populations

COMETS is able to perform simulations that include the appearance of mutants containing reaction deletions and additions. In this procedure, we perform a serial transfer experiment starting with a clonal E. coli population, and simulate the random appearance of reaction deletion mutants.

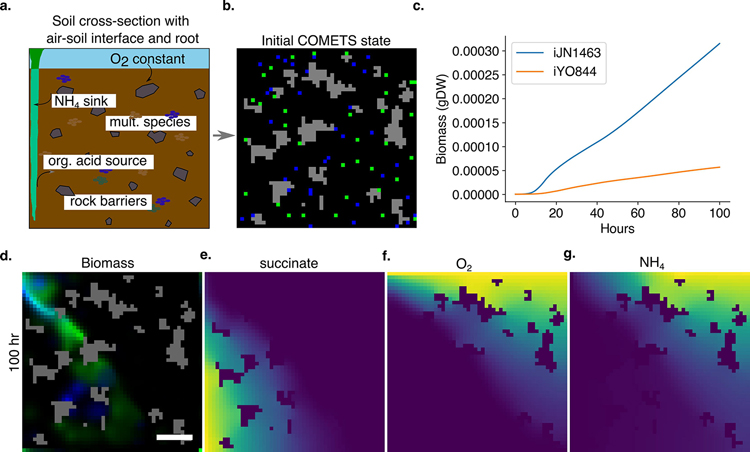
Procedure 6: microbial growth in natural environments; soil–air interface simulation

Using the functionality of COMETS, one can design simulations that go beyond in silico corollaries of laboratory experiments to make predictions for environments mimicking natural ecosystems, which is a necessary step for understanding natural ecology from first principles. In this example, we consider a spatially structured simulation of a soil environment. We use source-and-sink functions to model how a root provides organic acids to the environment while removing ammonia⁸⁹. While we restrict the root functionality to a source/sink, one could use functionality demonstrated in Procedure 4, secretion of extracellular enzymes, to generate feedback loops between microbe-produced metabolites and root exudation. We use fixed metabolite concentrations to mimic the largely unchanging air interface above a root, which generates an oxygen gradient. Additionally, since soil is characterized by strong spatial structure with many impenetrable barriers that localize interactions⁹⁰, we place ‘rock’ barriers throughout the simulation area. A more complex simulation could use varying diffusion constants for metabolites. Similarly, we use standard diffusion of biomass, but this could be changed to use pushing force or nonlinear diffusion for a potentially increased realism.

Procedure 7: demographic noise and cooperative biomass propagation

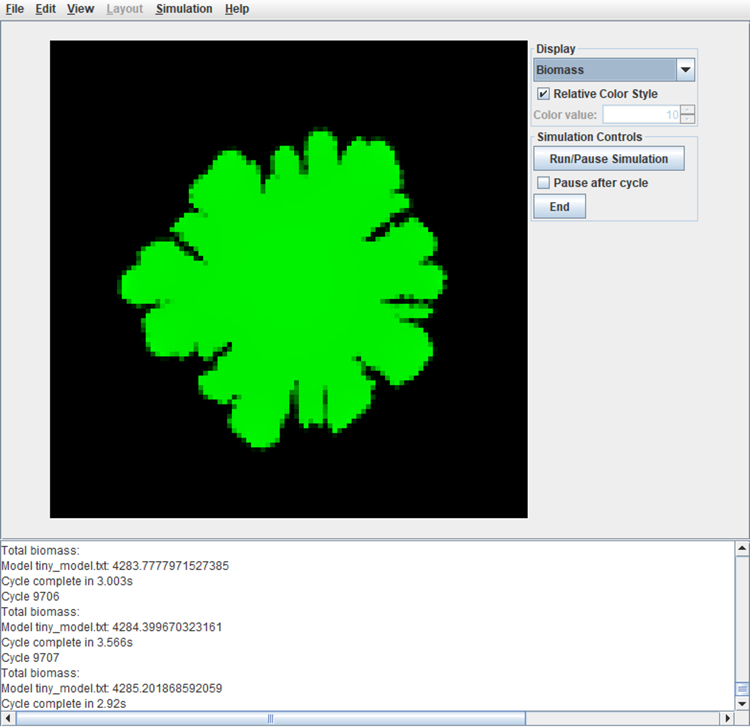
This protocol illustrates two biological features modeled in COMETS: demographic noise and cooperative biomass propagation. We use the model of cooperative propagation of bacteria to simulate the spread of the bacterial biomass, and the formation of branched (dendritic) morphology⁹¹. We illustrate the role of demographic noise by showing the formation of single-strain sectors in a population consisting of a mix of two metabolically identical strains. In this procedure, we start with the initial population of the colony consisting of two metabolically identical strains. We provide two alternative options for the simulation: one with all of the biomass being mobile and spreading, and another with only the portion of the biomass with growth rate above a threshold spreading. In the second case, the presence of demographic noise leads to formation of sectors populated by a single strain. This genetic demixing has been observed in experiments and studied theoretically⁹². This procedure also provides an example of visualization of the biomass, the growth rate and the spatial profile of glucose concentration, as well as visualization of the dynamics of colony formation shown in Extended Data Videos 1 and 2.

Limitations

Some fundamental limitations of COMETS are inherited from the basic limitations of the stoichiometric modeling and FBA methodology. For example, one limitation inherent to FBA, which is propagated to COMETS, is the lack of explicit gene regulation^93–96. Some approaches previously developed to cope with this limitation (such as rFBA⁹⁷, caFBA⁹⁸, GIMME⁹⁹) can in principle be added to COMETS, but are not part of the current release. However, classical FBA perturbations, such as deletion of specific genes or blockage of specific reactions, can be easily implemented in COMETS, by setting appropriate constraints.

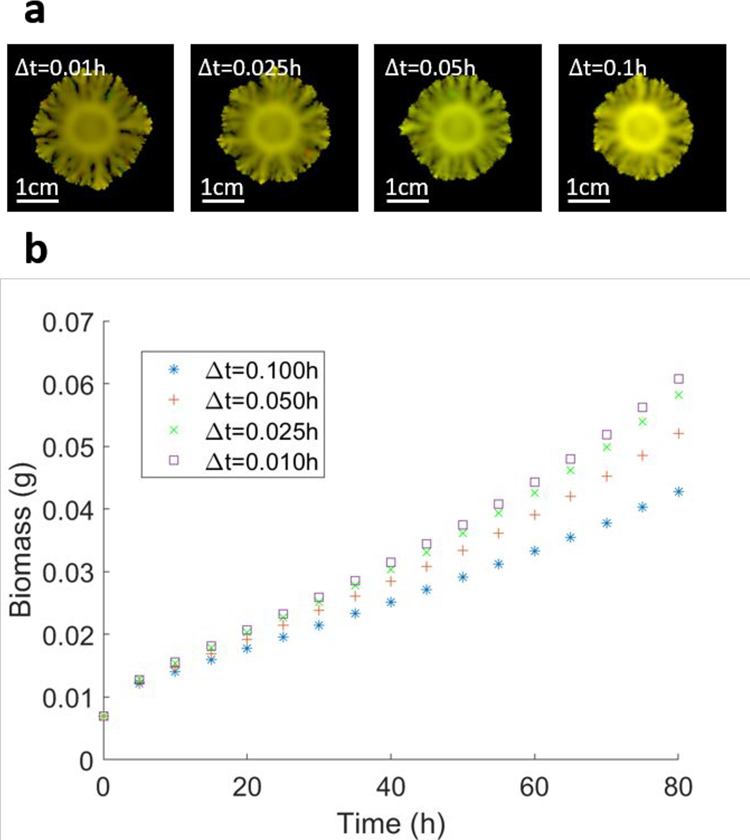
Other limitations of COMETS specifically arise from the complexity of numerical integration of the convection–diffusion equations. Internally, the COMETS engine uses a fixed time-step integration rather than a variable time-step integrator such as in DFBAlab⁴². This requires users to choose a time step that is small enough to avoid numerical errors and instabilities that can propagate in growth and spatial solutions. This sometimes requires the choice of very small time steps (<1 h for the branching colony in Procedure 7), which can result in long simulation times for complex layouts.

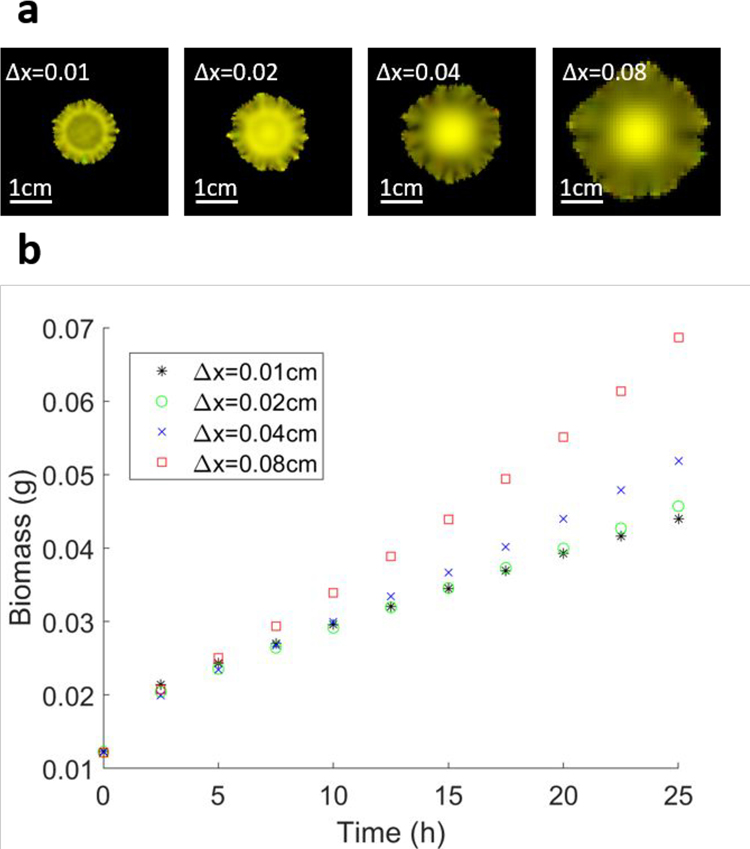
Regardless of the numerical instabilities that can be eliminated by setting a proper time step and spatial grid spacing, the precision of COMETS predictions will always be limited, due to the discrete nature of the integrating scheme, as would be the case in any numerical simulation. The user must therefore define the acceptable tolerance for the numerical error in the simulation. Users are encouraged to estimate the values of the time step and spatial grid spacing, given their preferred tolerance for the numerical error. The standard way of doing this is to perform several simulations of the identical system, but with a varying simulation time step, and/or spatial grid spacing. Extended Data Fig. 1 illustrates such estimation of the numerical errors due to a finite size of the time step, performed for the case study in Procedure 7. Extended Data Fig. 1b shows that the results of the simulations converge with an asymptotically vanishing difference as we lower the size of the simulation time step. The decision of what represents an acceptable time step of course depends on the choice of the tolerance for this difference. The images in Extended Data Fig. 1a, however, show that the morphology of the final state does not change much, so if there is no requirement for highly accurate numerical results, but only a qualitative estimate of the morphology, one can speed up the simulations considerably by setting a fairly high value for the time step, in the order of several tens of minutes. Extended Data Fig. 2 illustrates the estimation of the effect of finite spatial grid spacing on the outcome of the simulation. The same system is simulated on four different grids, with all the other parameters kept at the same values. In this case, too, one can choose the spatial grid resolution on the basis of the error tolerance. In this case, however, the final morphology depends more strongly on the choice of the grid spacing.

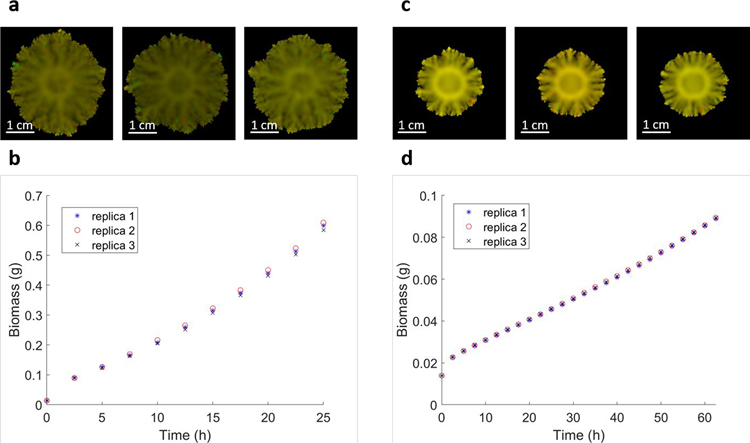
Another important limitation that users should be aware of is that, by design, COMETS takes a population-level approach, rather than an individual-based approach. In other words, FBA, as computed per model at each coordinate in space, is meant to estimate the average metabolic behavior of the population of cells present in a box at those coordinates. This approximation, which is a natural extension of the steady state nature of FBA, implies that COMETS is currently not ideal for studying phenotypic cell-to-cell variability in a population. For simulations of single-cell dynamics in continuous space that rely on gene networks instead of genome-scale models, a good alternative is the gro platform¹⁰⁰, which simulates individual cell dynamics using finite state machines. For single-cell dynamics that use genome-scale models in a lattice, a good alternative is BacArena¹⁰¹. Notably, however, by using appropriate statistical calculations, COMETS can be used to model some important aspects of microbial dynamics that depend on the discrete nature of cellular populations, including demographic noise (see Procedure 7) and evolutionary dynamics stemming from genetic variations (see Procedure 5). In this case, the simulation is stochastic, which will necessarily result in statistical differences between random replicas of the same system. The amplitude of the stochastic term will determine the number of replicas needed to obtain a statistically well-sampled ensemble of runs. Extended Data Fig. 3 shows the results of such an ensemble of three runs, for two different amplitudes of the stochastic term. Again, as in the case of the variability of the results due to finite time step size, here we see that it is the tolerance of the error due to finite sampling of random replicas that will determine how many replicas are needed to obtain accurate averaged results. Clearly, as illustrated in Extended Data Fig. 3a,c, here too the morphologies of the simulated colonies are very similar, so one may get an acceptable result with a single run. However, we see that the relative error is much larger for a larger amplitude of the stochastic term σ = 0.01, shown in Extended Data Fig. 3b, than the one with smaller amplitude σ = 0.001, shown in Extended Data Fig. 3d.

A last important caveat for COMETS users interested in applying this framework to the simulation of real ecosystems is that these may involve organisms for which genome-scale reconstructions have limited or untested accuracy, or are unavailable altogether. For natural communities, it is furthermore often very challenging to obtain detailed information on the molecular composition of the environment, and the spatially dependent abundance of different metabolites. Overall, it is not clear upfront how the accuracy of COMETS simulations will depend on such missing data, partly because high uncertainty exists on how communities respond to disturbances in the first place^102,103. We anticipate that future studies with COMETS or other computational platforms for microbial ecology will gradually shed light on these questions: on the one hand, it will be possible to use synthetic communities under well-controlled environments^104,105 to establish datasets against which COMETS simulations could be tested, e.g., asking whether the observed effects of removal of individual species from the community are recapitulated by simulations; on the other hand, one could think of COMETS as a computational laboratory to explore questions that may not be easily answerable experimentally, such as assays under large combinatorial environmental compositions or upon systematic removal of many individual or sets of species. This last kind of use of COMETS may not be able to provide accurate quantitative predictions of the detailed behavior of individual organisms, but may help reveal general principles and statistical behavior of communities. In general, it will be crucial for COMETS users to carefully balance the capacity to generate simulations of increasingly complex communities and environments, with the need for subjecting any conclusion to sensitivity analyses and experimental testing.

Finally, while we have incorporated many biological processes into the COMETS engine, there is a long list of important biological processes that can impact microbial growth, many of which can be incorporated in future versions or extensions of COMETS. These include chemotaxis, toxin release and sensitivity, quorum sensing and other kinds of signaling processes.

Experimental design considerations

To optimally employ COMETS for their own specific applications, users should first determine whether genome-scale metabolic reconstructions of suitable quality for the organisms of interest are available. The process of creating a new genome-scale metabolic model from the sequenced genome of an organism has its own protocols⁴⁹, and is not discussed here in further detail. A number of approaches for the automated reconstruction and gap filling of stoichiometric models are now available, though one should consider enhancing such gap-filled models with further testing or manual curation^33–37. No less important is to have a good understanding of the molecular composition of the environments or growth media of interest.

With the exception of some specific, nondefault settings (e.g., demographic noise), COMETS is deterministic and, therefore, replicates are not required. However, it is possible to use replicates as a way of assessing the impact of uncertainty due to limited biological knowledge. For example, one may generate sensitivity analyses by repeating simulations that use different perturbed versions of a model, different genome-scale reconstructions of the same strain from different gap-filling algorithms, or different possible values of uptake kinetic parameters (V_max and K_M), if the actual values are unknown.

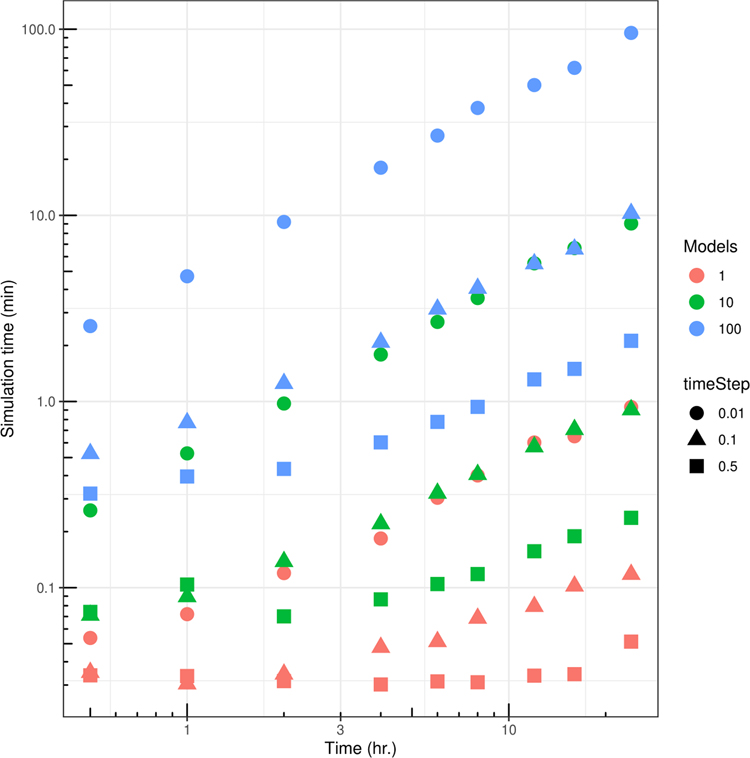
As for wetlab experiments, appropriate controls are just as important for COMETS in silico experiments. The specific controls will depend upon the study, but typical controls will include monoculture simulations alongside multispecies experiments, and nonspatial simulations alongside spatial experiments. For example, the user may want to test the scaling of the computational resources requirements, as well as the results, with the number of models involved in the simulation. Extended Data Fig. 4 shows an example of such a study of the scaling performed with 1, 10 and 100 identical strains of E. coli.

Finally, it is recommended that the user estimates the magnitude of the potential errors in a simulation, due to the finite size of the time step and spatial grid size used for the numerical integration procedure. In particular, one can estimate the numerical errors of the type described in ‘Limitations’, as shown in Extended Data Figs. 1–3. COMETS will let the user know if the time step is too big to guarantee correct numerical integration of the biomass propagation equation or the media diffusion equation (see Troubleshooting table).

Table 3.

Troubleshooting

Step	Problem	Possible reasons	Possible solution
Attempting to create a model file from a cobra file in the Matlab toolbox. Many steps, e.g.: Procedure 1, Step 5.	initCobraToolbox() or any Cobra command not found.	The Cobra toolbox was not installed, or the path to it was not added to MATLAB.	Install Cobra and add the path. See the installation instructions in the EQUIPMENT SETUP section.
Attempting to start a COMETS simulation or the COMETS gui. Many steps, e.g.: Procedure #1, Step 13.	COMETS fails to launch.	Java is not installed.	Install Java from https://www.oracle.com/technetwork/java/javase/downloads/index.html.
		32-bit version of Java is also installed.	Check and make sure 64-bit Java has priority in the Path environment variable, putting it before the 32-bit version.
		The COMETS_HOME environment variable is not set.	Windows: Set the environment variable COMETS_HOME. Unix: Add the line: export COMETS_HOME=[path to COMETS] to either .bashrc (Linux) or .bash_profile (Mac). Matlab toolbox: Check and make sure COMETS_HOME and GUROBI_HOME variables are set in Matlab (i.e. getenv(‘COMETS_HOME’ or getenv(‘GUROBI_HOME’). This is done by running the toolbox command testCOMETS(). For Mac operating systems, a manual setting may be needed. Instructions are provided in a Supplementary Discussion 5: Setting the environmental variables in Mac OS X.
	COMETS starts, but the output is not as expected, or an error message is printed on the console.	COMETS was not started with the proper Java command.	Run the help option: comets_scr -h A detailed help information on how to run COMETS will be printed on the console.
Attempting to start a COMETS simulation from the command line or using a toolbox. Many steps.	COMETS fails to launch. “Comets usage:...” or “COMETS requires at least one argument...” message is printed.	Wrong usage syntax. Wrong list of arguments.	Follow the instructions in the “Comets usage:” message.
	COMETS launches but halts upon loading a model, a parameters file, or a layout file, with a “classnotfound” error.	Java class libraries are not in the path.	Make sure installed libraries are in the expected path downstream from COMETS_HOME. If you are running a cloned version of the github version, make sure you download and install all dependencies.
Attempting to start the COMETS GUI. Procedure #1, Step 13.	GUI launched on a remote system does not show up.	X11 forwarding is not enabled.	When connecting to the remote Linux system via ssh, use the -Y option: ssh -Y remote_address.
Attempting to start COMETS simulation from the command line or load layout or model file in GUI. Many steps: Example step: Procedure #1, Step 14.	Layout or model file fails to load.	Wrong syntax or inconsistent input.	Check the error message on the COMETS console, or in the standard error file, for syntax errors. Check the consistency of the numbers of reactions and metabolites in the model file.
		Gurobi class not found.	Install Gurobi, obtain a license. Check if the GUROBI_HOME environment variable is set.
Attempting to run a COMETS simulation with the Python toolbox. Many steps. See for example Supplementary Discussion 2, Software architecture and the basics of COMETS.	Initial test of a model after load fails.	The optimizer is not installed or the optimizer license was not installed.	Install Gurobi from gurobi.com. Check the OPTIMIZER block in the model file. Install license.
	“Error occurred while loading parameter file” message is printed.	Parameter file names do not match.	Check the parameter file name(s).
	“Parsing error in parameter file” message.	Parameter file keyword or value is wrong.	Check the parameter file(s).
	The propagation of biomass or media is numerically unstable.	Poor choice of time and spatial steps parameters values.	Change the time step to a lower value, or set a coarser spatial grid.
	Error in starting script mode. “Error running script file” message printed.	Error in the script file syntax.	Check the script file. Check the names of the parameters and layout files.
Attempting to create a comets.comets() object in the Python toolbox. Procedure #2, Step 15.	Warning or Error about COMETS_HOME or COMETS_GUROBI_HOME environmental variables not being found.	The variables are not set, or are not visible in the python environment.	Set these variables correctly and try again. Example code follows, although the specific directory will depend on the system. import os os.environ[“COMETS_HOME”] = “/home/jeremy/comets” os.environ[“COMETS_GUROBI_HOME”] = “/opt/gurobi900/linux64”
Procedure #7, Step 2.	Model does not grow/uptake the metabolites provided in the media.	COMETS can only set model bounds dynamically at a given exchange reaction if they are within the bounds specified in the loaded model.	Make sure that the model loaded into COMETS has the relevant exchange reactions with widely open bounds (e.g. −1000, 1000). In the Python toolbox, this can be accomplished with the model.open_exchanges() function.
Any run with larger than 1×1 spatial grid. Many steps: Example step: Procedure #7, Step 5.	A warning message is printed on the console output: Warning: Negative biomass at X,Y, reduce the time step.	The time step is too big to guarantee correct numerical integration of the biomass propagation equation.	Set the timeStep parameter to a smaller value.
	A warning message is printed on the console output: Unstable diffusion constants. Try setting the time step below <Δt> seconds.	The time step is too big to guarantee correct numerical integration of the media diffusion equation. COMETS lets the user know that the timeStep parameter is larger than the time step given by the stability criteria Δt<Δx2/D, where Δx is the size of the spatial grid spacing and D is the diffusion constant.	Set the timeStep parameter to a smaller value or set the numDiffPerStep parameter to a higher value.
Running a COMETS simulation. Many steps, e.g. Procedure 6, step 20.	COMETS simulation stops after 1 timestep with zero biomass.	Initial biomass has not been set and therefore defaults to 0 initial biomass.	Change initial biomass. In the Python toolbox, model.initial_pop = [x, y, biomass] In the MATLAB toolbox, setInitialPop(world, ‘1×1’, 5e-6);
Python toolbox: running simulation, e.g. Procedure 6, Step 20.	“Done” is not printed and an error is given about trying to load the totalBiomass file	If the computer’s language uses commas for decimal separation, this can cause Java to write files with commas instead of periods, which the pandas package (that the Python toolbox uses to load .csvs) will misinterpret	Set the language of the computer to use periods for decimals places, or manually load the results files in python
Python toolbox: running simulation, e.g. Procedure 6, step 20.	Data are in an unexpected format	Potentially due to the computer’s default language (see row above)	Users might want to use the delete_files = False argument within the run() method, which will result in the models, parameters and layout files built by cometspy being written in the current folder, allowing the user to examine them manually for errors.
Running a COMETS simulation, e.g. Procedure 2, Step 16.	“Done” is not printed and an error not related to totalBiomass is given	Common reasons for this are that models did not have their initial_pop set, or the locations in initial_pop are outside the range in layout.grid. Additionally, issues like the gurobi license being expired or not found will cause an error, as will the inability of COMETS to detect any of its dependencies.	Read the error closely and fix the relevant step. For example, setting model.initial_pop to be within range of layout.grid, or updating the GUROBI license.
Plotting media data, e.g. Procedure 2, Step 18.	An error message occurred when trying to access the media DataFrame	Media information was likely not saved in the simulation, or not saved at the specified time step.	Set the parameters values as desired, e.g. params.set_param(“writeMediaLog”,True) params.set_param(“mediaLogRate”, 1)
Visualizing biomass results data. Many steps in Procedures using the Python toolbox.	In the Python toolbox, models grow with identical rates when they are expected not to.	The models have different ID variables. If models have the same ID, the last COMETS model in the layout will be used for all models.	Make unique model names. E.g. Ecoli1.id = ‘e_coli_core_1’ Ecoli2.id = ‘e_coli_core_2’
Attempting to create a video. Procedure #7, Step 6.	The application convert not found.	The ImageMagic application is not installed.	Install ImageMagic from https://imagemagick.org.

Software modes and user experience

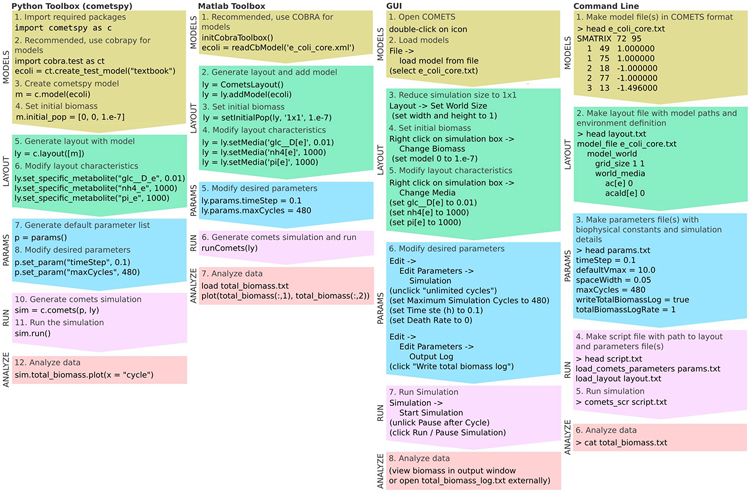
COMETS can be utilized in several different modes, requiring different levels of expertise. The workflow for all modes is described in the flowcharts in Fig. 2. To run COMETS in its most elementary form, the expertise required is a general familiarity with the simulated biological processes and basic computational skills. At this level, the user can easily utilize the graphical user interface (GUI) or manually write text input files to run simple COMETS simulations. This approach may be appropriate for introducing COMETS to undergraduate students in classes on biology and related disciplines.

Figure 2.

Basic workflows. Flowchart showing a typical workflow for the four interfaces for COMETS, with sufficient code / steps to run an introductory (i.e. “hello world”-like) simulation of anaerobic batch culture growth of the E. coli core model.

A slightly more advanced level is required to use the MATLAB or the Python toolbox to prepare and run the models and layouts, given available stoichiometric models in other standard formats such as SBML and/or .mat (also used in COBRA). Using these toolboxes requires a basic knowledge of MATLAB or Python, depending on the toolbox of choice. These interfaces allow the user to create advanced environments and settings in an efficient and intuitive manner. The layout and model files created by these toolboxes are then, under the hood, provided as input files to the core COMETS software as illustrated in Fig. 1. Using these toolboxes, however, greatly expands the possibilities of interaction with COMETS. For example, one can easily run simulations in a loop that changes environmental conditions in each loop, and plot and analyze the results in a fully customized way. These modes of running COMETS, in addition to being relevant for a number of research applications, could be used in educational settings, e.g., for teaching systems biology in graduate student classes. Users comfortable with command line applications and scripting can run COMETS using a command line approach, which can facilitate use in a high-performance computing facility.

Finally, the most advanced level of expertise is the development of custom COMETS features, which requires knowledge of the Java programming language, and version control systems Git and GitHub. In this case, a desirable skill is familiarity with one of the integrated development environments such as Eclipse. This level of expertise is required if the user would like to develop novel capabilities, which are beyond the scope of this protocol.

Graphical user interface.

The basic level of expertise required to run COMETS with the GUI is the ability to download the installer from the COMETS website, download and install Java and Gurobi, and obtain and install the Gurobi license. The installation instructions for obtaining Gurobi license require the ability to open a command line terminal and run a single command line. The COMETS installer provides an option for creating a desktop shortcut. This in practice means that the user is required to only be able to navigate the COMETS GUI. Downloading a layout and model files, editing the run parameters, running the simulations, etc. are all based on a standard windows GUI and do not require any specialized computational skills. The GUI, however, currently only supports the very basic COMETS capabilities, with limited access to only a subset of the modeling parameters, and it can only save the layout images. Any visualization of the results, such as the plot of biomass versus time, requires knowledge of some of the standard plotting and data manipulation software such as MATLAB or R. This level of expertise would be typical for a high-school or undergraduate biology student. The GUI should therefore be used only as an educational tool or an introduction to COMETS for novice users. The full simulation capabilities of COMETS are accessed through the MATLAB and Python toolboxes, and/or direct manipulation of the input files.

cometspy: COMETS Python toolbox.

cometspy is a Python package able to set up and run COMETS simulations using a previously installed COMETS program. It integrates with existing Python scientific computing and visualization packages (scipy, matplotlib, etc.) and offers full compatibility with established software packages for constraint-based modeling methods in the field such as COBRApy⁶⁰. cometspy is fully documented, and information on any class or method can be retrieved using help(), often including example code. This documentation is available at https://cometspy.readthedocs.io/.

More details on the basics of the use of this toolbox can be found in Supplementary Discussion 2, including an explanation of all spatial settings found in Supplementary Discussion 3.

We recommend the usage of the COMETS Python toolbox in the context of Jupyter (https://jupyter.org/), and we provide Jupyter notebooks for all the procedures presented here, although of course other platforms can also be used (e.g., IPython). A benefit of using the cometspy package is that COMETS models can be easily generated by supplying a cobrapy model as the first step, therefore facilitating usage by existing cobrapy users.

COMETS MATLAB toolbox.

The COMETS MATLAB toolbox is a collection of classes and functions intended to facilitate the processes involved in creating layouts for simulations, and includes utilities to execute COMETS within scripts from the command line and to parse output files. The MATLAB toolbox uses metabolic models in the format of the COBRA toolbox for MATLAB⁶⁰. The user of this toolbox needs to be familiar with the basics of using MATLAB. A knowledge of the COBRA Toolbox is desired but not necessary. More details on the basics of the use of this toolbox can be found in Supplementary Discussion 2

Command line use.

This level of expertise will be required from users that plan to perform a large ‘production’ level of sets of simulations most likely on a computational cluster. This requires knowledge of the Linux operating system, and remote connection software to a computational cluster, such as ssh, Putty or MobaXterm. Skills in submitting and deleting jobs on a queue scheduler such as qsub are required. More details on the basics of the command line use of COMETS can be found in Supplementary Discussion 2.

Optimizers.

A central computational part of the FBA method as implemented in COMETS is the optimization of the objective function in each genome-scale metabolic network. COMETS currently supports two optimizers that perform this task. The optimizer is defined at the model level, and the user can choose one of them for each model. The currently supported optimizers are Gurobi and the GNU Linear Programming Package (glpk). Gurobi is a commercial software package that can be accessed at https://www.gurobi.com/. Users with academic affiliation can obtain a free academic license. Gurobi is set as the default optimizer in COMETS. The optimized glpk is a free, open-source alternative that can be accessed at https://www.gnu.org/software/glpk/.

Parallelized dFBA.

The simulation algorithm implemented in COMETS at each time step performs a single FBA optimization for each model present at the spatial grid point. We have implemented an option to run these optimizations in parallel on a multicore CPU. This provides substantial improvement in performance when computations are run on high-performance computers. The algorithm can compute the FBA calculation for several spatial grid points in parallel. The parallelization is implemented by a multithreading algorithm, and accessed through the parameter numRunThreads (Supplementary Table 1).

COMETS inputs.

There are three types of input: models, parameters and layout. All three types of input are stored in text files with a specific COMETS format. At the basic level, the simulation parameters, models and layouts are loaded into the core COMETS from input text files. Models contain the stoichiometric metabolic reconstructions for organisms to be used, and some model- specific COMETS parameters such as model propagation constants and type of optimizer. The layout contains information about the environment, including the media and spatial structure at each location in space, and the possible presence of extracellular enzymatic reactions. Finally, the para- meters input file contains a comprehensive set of parameters that can be specified and can be found in Supplementary Table 1 and in the online documentation. The parameters files can also be loaded from the GUI. Some of the key simulation parameters can be set directly in the GUI. If a parameter is not listed in the input file, it is assigned the default value.

COMETS outputs.

A COMETS simulation can produce several types of quantitative outputs at all, or at selected, time steps. Output files can be written in a MATLAB.mat binary format, as MATLAB.m scripts containing variable definitions, or as tab-separated files. When using the Python toolbox, these files will be automatically read and stored by the comets object within the Python environment, facilitating downstream analyses.

The most basic outputs of comets are ‘total biomass’, ‘biomass’, ‘media’ and ‘fluxes’, although for specific functionalities additional output types can be produced. The ‘total biomass’ consists of a table containing the iteration number in the first column, and the total biomass of each model present in the simulation in the successive columns. The ‘biomass’ output contains detailed information about the spatial distribution of biomass for each model and each simulation grid box. The ‘media’ output consists of the detailed information of the amount of extracellular metabolites/nutrients on the spatial grid. Alternatively, one can select specific metabolites to track using the specificMedia parameter set, which returns a tab-separated file. Finally, the ‘fluxes’ output contains the collection of all fluxes, including the exchange fluxes, recorded for each model at each time point, and at each grid point of the spatial layout. The detailed description of the format of the output files is in Supplementary Discussion 4.

Online documentation and tutorial. The documentation for COMETS and for its Python and MATLAB toolboxes is available at https://segrelab.github.io/comets-manual. The documentation is structured as a tutorial and contains examples other than those shown in this protocol. Raw documentation files are stored at https://github.com/segrelab/comets-manual. The COMETS Protocols GitHub repository (https://github.com/segrelab/COMETS_Protocols) also contains all input files and jupyter notebooks for all the procedures from this manuscript, as well as additional examples presented in the online manual.

Materials

Equipment

Recommended hardware:

• A computer with a 64-bit processor and either Linux, Windows or MacOS system. Memory recommendation is 8Gb or higher. A multicore processor is recommended to run multithreaded simulation of a large spatial layout grid, but not strictly necessary.

• Java, including Java Development Kit. Version 8 or higher is recommended.

• Gurobi Optimizer (recommended; free academic license available). Alternatively, the GNU Linear Programming Kit (GLPK) can be used as an open source, optimizer.

• Python (recommended > 3.4) is required to use the Python toolkit. Additionally, COBRApy⁸³ is recommended to facilitate model creation.

• MATLAB and Cobra Toolbox⁶⁰ are required to use the MATLAB toolbox.

One of the following operating systems:

• Microsoft Windows 10 (We tested COMETS on Home, version 10.0.18362).

• Linux (We tested COMETS on Ubuntu 20.04.1 LTS and 18.04)

• MacOS X (We tested COMETS on Catalina 10.15.5 and El Capitan Version 10.11.6)

We have tested COMETS on the listed versions of the operating systems, but we anticipate that COMETS will work on most versions of these systems.

Equipment setup

Java.

COMETS is written in the Java programming language. Installed Java 64-bit platform is a prerequisite for running COMETS. The minimum required version of 64-bit Java is 1.8. Java can be downloaded and installed from https://www.java.com/. The Java Development Kit can be downloaded and installed from https://www.oracle.com/technetwork/java/javase/downloads/index.html

Gurobi.

The primary and default optimization software in COMETS is Gurobi. The package can be downloaded and installed from http://www.gurobi.com/. The installation of Gurobi requires obtaining a license from http://www.gurobi.com/downloads/licenses/license-center. Academic users that will use COMETS on an individual basis may obtain a free academic license. When the installation of Gurobi is finished, it is very important to have the environment variable GUROBI_HOME set to the directory where Gurobi was installed. In Windows, this variable is set automatically during the installation process. In Linux and MacOS, however, depending on the system, sometimes this is not the case. It is therefore important to make sure that a line such as the following example:

export GUROBI_HOME=/usr/gurobi/gurobi902/linux64/ 

is included in the user’s .bashrc file in Linux, or the corresponding file for an alternative shell. The version name and number in gurobi902 should be set to the one installed. Here, we use Gurobi version 9.0.2 (i.e., ‘gurobi902’) as a representative example version of Gurobi, but we anticipate that the following steps will continue to be valid for subsequent implementations.

In MacOS, the line:

export GUROBI_HOME=/Library/gurobi902/mac64/ 

should be included in the .bash_profile file in older versions of MacOS, or .zshrc in the latest version of MacOS. The version name and number in gurobi902 should be set to the one installed. It is important to source these files before attempting to run COMETS. The easiest way to do that is to close the terminal and open another one.

Also, the COMETS installer will add lines:

export COMETS_HOME=/home/username/comets 
export PATH=$PATH:$COMETS_HOME 
export GUROBI_COMETS_HOME=$(echo $(ls -d /usr/gurobi/gurobi*/linux64)|awk 
{‘print $NF’}) 
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$GUROBI_COMETS_HOME/lib/ 

in the.bashrc file in Linux, and

export COMETS_HOME=/home/username/comets 
export PATH=$PATH:$COMETS_HOME 
export GUROBI_COMETS_HOME=$(echo $(ls -d /Library/gurobi*/mac64)|awk {‘print $NF’}) 
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$GUROBI_COMETS_HOME/lib/ 

in the .bash_profile file in older versions of MacOS, and .zshrc in the latest version of MacOS, where username is replaced with the specific one for the user. This should make Gurobi libraries available to COMETS. More information can be found in the Troubleshooting table.

In Windows, the Gurobi installer adds the GUROBI_HOME environment variable automatically. In Windows, this variable can be set in the Control Panel.

More information can be found in the manual: https://segrelab.github.io/comets-manual.

GLPK.

The installer for the alternative optimizer used by COMETS can be found here: https://www.gnu.org/software/glpk/. This is an open-source package. The details on how to install it can be found in the COMETS manual: https://segrelab.github.io/comets-manual.

COMETS.

There are two ways to install COMETS: (i) using the COMETS installer and (ii) unpacking the comets_2.10.0.tar.gz file. The easiest way is to use the installer, especially recommended for individual use on a laptop or desktop. The installer can be downloaded from https://www.runcomets.org. The users are required to register, after which they can obtain the installer appropriate for their system. If the download is interrupted with ‘Google Drive can’t scan this file for viruses’ or similar message, click on the ‘Download anyway’ button. The installer guides the user through a standard GUI installation procedure that includes accepting the license agreement, choosing the directory where COMETS will be installed (the default directory is recommended), the option to create a desktop shortcut, etc. The installer is available for the Windows (comets_windows-x64_2_10_0.exe), MacOS (comets_macos_2_10_0.dmg) and Linux (comets_unix_2_10_0.sh) systems. The installer is invoked either by a double-click on their icon (Windows, MacOS), or running them from a command line (Windows, Linux). If the installer cannot be started in Linux, the following command should be executed before running it:

chmod a+x comets_unix_2_10_0.sh 

In MacOS, if the system does not allow the application to be installed, holding the command button and clicking on the installer, or going to the apple menu → System Preferences → Security & Privacy → General → Open Anyway, will solve this problem. If another window with security warning opens up, clicking on Open Anyway will allow the installation.

The installer will install the GUI version and a shortcut to it on the desktop. Also, the installer will add the script comets_scr to the user’s PATH variable, so COMETS can be started in all three systems from a command line by:

comets_scr comets_script where comets_script contains description of the input files:

load_comets_parameters global_params.txt 
load_package_parameters package_params.txt 
load_layout layout.txt 

As mentioned above, the COMETS installer will add the lines such as:

export COMETS_HOME=/home/username/comets 
export PATH=$PATH:$COMETS_HOME 
export GUROBI_COMETS_HOME=$(echo $(ls -d /usr/gurobi/gurobi*/linux64)|awk {‘print $NF’}) 
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$GUROBI_COMETS_HOME/lib/ 

in the .bashrc file in Linux, and the lines:

export COMETS_HOME=/home/username/comets 
export PATH=$PATH:$COMETS_HOME 
export GUROBI_COMETS_HOME=$(echo $(ls -d /Library/gurobi*/mac64)|awk {‘print $NF’}) 
export LD_LIBRARY_PATH=$LD_LIBRARY_PATH:$GUROBI_COMETS_HOME/lib/ 

in the .bash_profile file in older versions of MacOS, and .zshrc in latest versions of MacOS, where username is replaced with the specific one for the user. In order to source the above lines, the user in Linux or MacOS should open a new terminal, or source the .bashrc, .bash_profile or .zshrc files by the dot command: . ~/.bashrc

If the user chooses to install COMETS or Gurobi in directories other than the default ones, then the lines above should be edited accordingly.

In Windows the user may first want to check if COMETS_HOME and GUROBI_HOME are properly set, and otherwise proceed to set them. The installer will set these variables automascally. However, if this for some reason is not done, the user should set them by going to Start and/or the Windows search bar and search for “Edit environment variables for your account.” Alternatively search for “Control Panel”, open it and click on System and Security-> System->Advanced system sexngs-> Environment Variables. When the “Environment Variables” window opens, check if COMETS_HOME and/or GUROBI_HOME are listed under “User variables for <your username>“. If they are not listed, click on the “New” button and enter as “Variable name” COMETS_HOME, and as “Variable value” the path where COMETS was installed, typically: C:\Program Files\comets. Finish by clicking on the “OK” button. Similarly, repeat the same procedure for GUROBI_HOME if needed.

In addition to the GUI installer, we provide the comets_2.10.0.tar.gz file for custom installation, typically on a Linux system. The file should be unpacked in the directory where COMETS will be installed with:

tar -xzvf comets_2.10.0.tar.gz ./ 

This will create the comets installation directory. In this case, the user should add the above lines to the .bashrc file manually.

COMETS can easily be uninstalled by running the uninstaller that can be found in the directory where COMETS was installed. In Windows it can also be uninstalled from the Control Panel.

For more information, the user can consult the manual: https://segrelab.github.io/comets-manual.

COMETS MATLAB Toolbox.

The prerequisite for this toolbox is to have MATLAB installed from https://www.mathworks.com. The COMETS toolbox for MATLAB can be downloaded from https://github.com/segrelab/comets-toolbox. The user may download the toolbox as an archive from the GitHub repository, or execute the following command from the command line (the folder ./comets-toolbox will be created in the working directory):

git clone https://github.com/segrelab/comets-toolbox.git comets-toolbox 

A prerequisite to install the toolbox this way is to have installed git which can be found here: https://git-scm.com/. Once git is installed, the user can download the toolbox either using the command line above, or by using the GitHub Desktop application that can be obtained here: https://desktop.github.com/.

Once this folder has been created, run the following commands in MATLAB to add the toolbox and its subfolders to the MATLAB path:

addpath(genpath(“comets-toolbox”),”-end”); 
savepath(); 

where comets-toolbox is the full path to the directory where the toolbox was installed. On a Windows system, for example, this path may be:

C:\Users\username\comets-toolbox 

where username is replaced with the specific one for the user.

Alternatively, the code can be downloaded as a .zip file by clicking on the green “Code” button at the repository. Then it needs to be extracted by right click→Extract all or using the unzip command:

unzip comets-toolbox-master.zip 

and run the addpath and savepath commands as above, with the path to the directory comets-toolbox-master.

In addition, this toolbox requires the installation of the COBRA toolbox, available at https://opencobra.github.io/ ⁶⁰. Many functions of the COMETS toolbox will not work before loading the COBRA toolbox using the initCobraToolbox() command. The detailed instructions for installing the COBRA toolbox can be found here: https://opencobra.github.io/cobratoolbox/stable/installation.html. A prerequisite to install the COBRA toolbox is to have installed git which can be found here: https://git-scm.com/. Once git is installed, the toolbox can be installed by running:

git clone --depthti1 https://github.com/opencobra/cobratoolbox.git
cobratoolbox

As mentioned above, the package can be fetched by using GitHub Desktop: https://desktop.github.com/. Once this folder has been created, run the following commands in MATLAB to add the toolbox and its subfolders to the MATLAB path:

addpath(genpath(“cobratoolbox”),”-end”); 
savepath(); 

where cobratoolbox is the full path to the directory where the toolbox was installed. On a Windows system, for example, this path may be:

C:\Users\username\cobratoolbox 

where username is replaced with the one specific for the user.

A general overview of the structure of the toolbox and instructions on how to use it can be found in the Supplementary Discussion 2.

COMETS Python Toolbox.

We recommend installing Python (version >= 3.6) using the Anaconda distribution which can be installed from https://www.anaconda.com/products/individual. Anaconda will conveniently install the jupyter notebook, which is how we have provided our protocols. Alternatively, Python can be installed from https://www.python.org/. Note that if the downloaded installer does not run in Linux or MacOS, execute the following command line:

chmod a+x Anaconda3-X.sh 

where X is replaced with the specific version name and number.

The COMETS Python toolbox (cometspy) is available from the package manager PyPI using the pip command. In Linux systems, the pip command is usually installed through available repositories (e.g. sudo apt-get install python3-pip in Debian-based distributions). If Python has been installed through Anaconda pip will have been installed during this installation.

Once pip is installed, cometspy can be installed by running the command line:

pip3 install cometspy

If this command does not run, close the terminal and open another one, then run it again.

In Windows this is best done by going to the start menu, and running “Anaconda Powershell Prompt”. The above command can be run from the Anaconda Powershell.

General overview of the structure of the toolbox and instructions on how to use it can be found in the Supplementary Discussion 2.

Open source development.

COMETS (https://www.runcomets.org) is an open source code and it is available at https://github.com/segrelab/comets. The code is distributed under the GNU General Public License Version 3. The Matlab toolbox is available at https://github.com/segrelab/comets-toolbox, distributed under the GNU General Public License Version 3. The COMETS Python toolbox is available at https://github.com/segrelab/cometspy, distributed under the GNU General Public License Version 3. Interested developers can contribute to the growing COMETS community and collaboration is facilitated by a public forum at https://gitter.im/segrelab/comets. Contributors, as well as users, should follow the license requirements, the contributing guidelines and the code of conduct found in the GitHub repository. For further information about the code, both users and contributors can contact the development team at comets@bu.edu.

Procedure 1: Growth of bacteria in well mixed conditions using the MATLAB toolbox and COMETS GUI

setup: 30 min - 1hr, simulation: 1–5 min

Download the protocol files

• 1
  Download the protocol files from https://github.com/segrelab/COMETS_Protocols/. The files can be downloaded either as a single zip file, or using the GitHub Desktop application. If downloaded as a zip file, it needs to be extracted in Windows by right clicking on the file, clicking on “Extract all”. This will create a directory COMETS_Protocols-master. In Linux and Mac OS it can be unzipped by the command line:

  unzip COMETS_Protocols-master.zip
  

• 2
  Navigate to the working directory as follows:

  cd COMETS_Protocols-master/COMETS_Protocols-master/COMETS_Protocols/COMETS_example_Ecoli_CoreModel_WellMixed/Matlab/Create_layout_MATLAB_toolbox/
  

Create the COMETS format input files

• 3The E. coli core model used in this simulation can be downloaded from the BIGG Models database: http://bigg.ucsd.edu/models/e_coli_core. For this example, download the uncompressed e_coli_core.xml SBML file, and move it to the working directory.

  : The availability of a stoichiometric model is a prerequisite for any COMETS simulation.

• 4
  To create COMETS format input files, follow the MATLAB script:

  COMETS_example_Ecoli_CoreModel_WellMixed/Create_layout_MATLAB_toolbox/create_comets_model_and_layout.m.
  

  The file can be opened and run in MATLAB, or each step can be entered at the MATLAB command line, as follows.

• 5
  Assuming the COBRA toolbox has been initialized with:

  >>initCobraToolbox()
  

  use the Cobra function readCbModel to read the SBML model file, as follows:

  >> ecoli = readCbModel(‘e_coli_core.xml’); 
  

  This creates a MATLAB structure ecoli that contains the E. coli core model:

  S: [72×95 double]
  mets: {72×1 cell} 
  b: [72×1 double] 
  csense: [72×1 char] 
  rxns: {95×1 cell}
  lb: [95×1 double]
  ub: [95×1 double]
  c: [95×1 double] 
  osenseStr: ‘max’
  genes: {137×1 cell} 
  rules: {95×1 cell} 
  geneNames: {137×1 cell} 
  compNames: {2×1 cell} 
  comps: {2×1 cell} 
  proteins: {137×1 cell} 
  metFormulas: {72×1 cell} 
  metNames: {72×1 cell} 
  metHMDBID: {72×1 cell } 
  metKEGGID: {72×1 cell } 
  metChEBIID: {72×1 cell} 
  metMetaNetXID: {72×1 cell} 
  rxnNames: {95×1 cell}
  rxnECNumbers: {95×1 cell}
  rxnKEGGID: {95×1 cell}
  rxnMetaNetXID: {95×1 cell}
  rxnSBOTerms: {95×1 cell}
  subSystems: {95×1 cell}
  description: ‘e_coli_core’
  modelVersion: [1×1 struct] 
  modelName: ‘Escherichia coli str. K-12 substr. MG1655’
  modelID: ‘e_coli_core’
  . . .
  

  Optionally, change the name/descripson of the model file, as follows. This will be the name of the COMETS format input model file.

  >> ecoli.description=’e_coli_core’; 
  

  ? TROUBLESHOOTING

• 6
  Use the COMETS MATLAB toolbox commands as follows to create an empty COMETS layout and add the model to it:

  >> world = CometsLayout();
  >> world = world.addModel(ecoli);
  

  This creates a default COMETS simulation spatial layout structure with one model in it:

  models: {[1×1 struct]} 
  xdim: 1 
  ydim: 1 
  mets: {20×1 cell} 
  media_amt: [20×1 double]
  params: [1×1 CometsParams] 
  diffusion_constants: [20×2 double] 
  global_media_refresh: [20×1 double] 
  media_refresh: [20×1 double] 
  global_static_media: [20×2 double] 
  static_media: [20×1 double] 
  initial_media: 0 
  barrier: 0 
  initial_pop: 1.0000e-06 
  external_rxns: [0×0 table] 
  external_rxn_mets: [0×0 table] 
  

  Here the layout is populated with the metabolites world.mets that are exchanged by the model, as follows:

  >> world.mets 
  {‘ac[e]’ } 
  {‘acald[e]’ } 
  {‘akg[e]’ } 
  {‘co2[e]’ } 
  {‘etoh[e]’ } 
  {‘for[e]’ } 
  {‘fru[e]’ } 
  {‘fum[e]’ } 
  {‘glc__D[e]’ } 
  {‘gln__L[e]’ } 
  {‘glu__L[e]’ } 
  {‘h2o[e]’ } 
  {‘h[e]’ } 
  {‘lac__D[e]’ } 
  {‘mal__L[e]’ } 
  {‘nh4[e]’ } 
  {‘o2[e]’ } 
  {‘pi[e]’ } 
  {‘pyr[e]’ } 
  {‘succ[e]’ } 
  

• 7
  Set the dimensions of the simulation grid to 1×1, i.e. a trivial grid consisting of a single point. This corresponds to spatially homogeneous (i.e. well-mixed) conditions.

  >> x = 1; 
  >> y = 1; 
  >> world = world.setDims(x,y); 
  

• 8
  Set the amounts of the metabolites in the media to 0.011 mmol for glucose, and 1000 mmol for ammonia, phosphate, water and hydrogen as follows. The amount for oxygen is set to zero to simulate anaerobic conditions.

  >> world = world.setMedia(‘glc__D[e]’,0.011); 
  >> world = world.setMedia(‘nh4[e]’,1000); 
  >> world = world.setMedia(‘pi[e]’,1000); 
  >> world = world.setMedia(‘h2o[e]’,1000); 
  >> world = world.setMedia(‘h[e]’,1000); 
  >> world = world.setMedia(‘o2[e]’,0); 
  

  : Setting the correct amount of nutrients for the organism will have a strong impact on the final result.

• 9
  Set the initial population to 5·10⁻⁶ grams as follows:

  >> world = setInitialPop(world, ‘1×1’, 5e-6);
  

  : The initial population must be set.

• 10
  Finally, write the layout and model files as follows:

  >> writeCometsLayout(world,’./’,’Ecoli_batch_layout.txt’,0);
  

  The last parameter with value 0 specifies that no parameters will be included in the layout file. We will create separate parameters files manually in Step 12, to better illustrate their structure.

  The outcomes of the procedure are the layout file Ecoli_batch_layout.txt and the model file e_coli_core_txt.

  The COMETS format layout file Ecoli_batch_layout.txt consists of the following fields relevant for this simulation:

  model_file e_coli_core.txt 
  model_world 
  grid_size 1 1 
     world_media 
        ac[e] 0 
        acald[e] 0 
        akg[e] 0 
        co2[e] 0 
        etoh[e] 0 
        for[e] 0 
        fru[e] 0
        fum[e] 0 
        glc__D[e] 0.011 
        gln__L[e] 0 
        glu__L[e] 0 
        h2o[e] 1000 
        h[e] 1000 
        lac__D[e] 0 
        mal__L[e] 0 
        nh4[e] 1000 
        o2[e] 0 
        pi[e] 1000 
        pyr[e] 0 
        succ[e] 0 
        ... 
          // 
          // 
         initial_pop 
       0 0 5.000000e-06 
     // 
  

  The COMETS format model file e_coli_core.txt consists of the following fields:

  SMATRIX 72 95 
  1 49 1.000000 
  ... 
  // 
  BOUNDS −1000 1000 
  1 −1000.000000 1000.000000 
  ... 
  // 
  OBJECTIVE 
  13 
  // 
  METABOLITE_NAMES 
  13dpg[c] 
  ... 
  // 
  REACTION_NAMES 
  ACALD 
  ... 
  // 
  EXCHANGE_REACTIONS 
  20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 
  // 
  OBJECTIVE_STYLE 
  MAX_OBJECTIVE_MIN_TOTAL 
  // 
  

• 11
  Copy the layout and model files to the working directory where we will run COMETS, as follows:

  cp e_coli_core.txt ../COMETS_simulation_Ecoli_core 
  cp Ecoli_batch_layout.txt ../COMETS_simulation_Ecoli_core 
  

• 12Create the parameters files. In addition to the required layout and model files, as described in steps 4–11 above, this Procedure uses the optional parameters files. These files are loaded to COMETS ater the layout. The parameters are typically classified in two files: global parameters file, defining the total number of simulation steps and output files, and package parameters file with parameters that define the dFBA specific simulation parameters such as the size of the spatial grid box and the sme step. In the global parameters, by default output files are saved in the current working directory due to the prefix “./”. This can be removed or a full path can be used to specify a different output directory.
  The global parameters file global_params.txt contains:

  maxCycles = 1000 
  pauseonstep = false 
  writeFluxLog = false 
  FluxLogName = ./flux.m 
  FluxLogRate = 10 
  writeMediaLog = true 
  MediaLogName = ./media.m 
  MediaLogRate = 10 
  writeBiomassLog = false 
  BiomassLogName = ./biomass.txt 
  BiomassLogRate = 1 
  writeTotalBiomassLog = true 
  totalBiomassLogRate = 1 
  TotalbiomassLogName = ./total_biomass.txt 
  useLogNameTimeStamp = false 
  

  The FBA package parameters file package_params.txt contains:

  numDiffPerStep = 10 
  numRunThreads = 1 
  exchangestyle = Monod Style 
  defaultVmax = 18.5 
  defaultKm = 0.000015 
  defaultHill = 1 
  timeStep = 0.01 
  deathRate = 0.0 
  spaceWidth = 1.0 
  maxSpaceBiomass = 10 
  minSpaceBiomass = 1e-11 
  showCycleTime = true 
  showCycleCount = true 
  

  : The parameter exchangestyle must be set to Monod Style in order to simulate the nutrient uptake with the Michaelis-Menten kinetics. The parameters defaultVmax, defaultKm and defaultHill must be set here.

Run the COMETS simulation

• 13Run COMETS from the graphical user interface (GUI). We start the program by running COMETS from the installed shortcut icon in Windows, Mac OS or Linux.
  Once COMETS has started, the user will see the window of the COMETS application such as the one shown in Extended Data Figure 5.

  ? TROUBLESHOOTING 
  

• 14
  Load the layout file from Step 11 by clicking on the ‘Load layout file’ button.

  ? TROUBLESHOOTING 
  

• 15
  When the layout is loaded, load both of the parameters files from Step 12:

  global_params.txt and package_params.txt, from the File tab:
        File->LoadParametersFile. 
  

• 16To start the simulation, click on the Run/Pause Simulation button at the Simulation tab. To run the simulation continuously, uncheck the Pause after cycle field.

Analyse the simulation results

• 17Visualize the results. The COMETS run above produces the total_biomass.txt and media.m output files. Visualize the time dynamics of the bacterial biomass production with the following MATLAB script that produces Fig. 3a: COMETS_protocols/COMETS_example_Ecoli_CoreModel_WellMixed/Matlab/COMETS_simulation_Ecoli_core/PlotTotalBiomass.m

Figure 3. Growth of E. coli (core model) batch culture in minimal medium, with glucose as the only carbon source.

These figures show results obtained from the simulation described in Procedure 1. a) Plot of biomass vs. time. b) Plot of the key metabolites vs. time. The biomass growth stops when the glucose is completely depleted. The production of the typical products of fermentation also coincides with the growth of the biomass.

%Load the biomass output
load ‘total_biomass.txt’
%The timestep (in hours) is defined in the package_params.txt file
timeStep=0.01; 
%Spatial grid point volume in litres
volume=1e-3;
%Plot the biomass density (in g/l) as a function of time (in hours) biomass_plot = plot(timeStep*total_biomass(:,1),total_biomass(:,2)/volume) 
set(gca,’FontName’,’Helvetica’); 
set(gca,’FontSize’,15); 
set(biomass_plot,’LineWidth’,2); 
xlabel ‘Time [h]’
ylabel ‘Biomass density [g/l]’ 
print(‘Ecoli_core_batch_biomass’,’-dpng’)

Produce the expected results shown in Fig. 3b using the following MATLAB script for visualization of the relevant metabolites: COMETS_protocols/COMETS_example_Ecoli_CoreModel_WellMixed/Matlab/COMETS_simulation_Ecoli_core/PlotMedia.m.

%Load the media output
%It contains the metabolite names in the string array media_names
media
%Choose the metabolites to be plotted
%Here we choose glucose, acetate, formate and ethanol
metabolites_to_plot = [9 1 6 5];
metabolites_names = [“glucose” “acetate” “formate” “ethanol”];
%The time step (in hours) is defined in the package_params.txt file
timeStep=0.01;
%Spatial grid point volume in litres
volume=1e-3;
%Media write step
mediaLogRate = 10;
%Number of simulation steps
maxCycles = 1000;
%Number of media write steps
total_write_steps = maxCycles/mediaLogRate;
%Line styles for the plot
lines_vec = {‘-’, ‘--’, ‘:’, ‘−.’};
for j=1:length(metabolites_to_plot) 
for i=0:total_write_steps
varname=genvarname([‘media_’,num2str(i*mediaLogRate)]); 
var=eval(varname); 
metabolite_variable=var(metabolites_to_plot(j)); 
metabolite=full(metabolite_variable{1});
metabolite_density(i+1,metabolites_to_plot(j))=metabolite/volume; 
time(i+1)=timeStep*mediaLogRate*i;
end
metabolites_plot=plot(time,metabolite_density(:,metabolites_to_plot(j))
,’LineStyle’,lines_vec{j}) 
set(metabolites_plot,’LineWidth’,2);
hold on
end
set(gca,’FontName’,’Helvetica’); 
set(gca,’FontSize’,15);
xlabel ‘Time (h)’
ylabel ‘Concentration (mM)’ 
legend(metabolites_names,’Location’,’northwest’); 
print(‘Ecoli_core_batch_metabolites’,’-dpng’)

Set the indices of the metabolites to be plotted metabolites_to_plot = [9 1 6 5] according to the world.mets list in Step 6, or alternatively set it by searching the list for the metabolite names with metabolites_to_plot = [strmatch(media_names,’glc D[e]’) strmatch(media_names,’ac[e]’) strmatch(media_names,’for[e]’) strmatch(media_names,’etoh[e]’)]. The output file media.m contains the array media_names. The names of the metabolites in this file are the same as the ones in the input layout file.

Procedure 2: Simulating cross-feeding in a chemostat

setup: 30 min- 1hr, simulation: 1–5 min

Import required packages

• 1
  Open the file COMETS_protocols\COMETS_example_Chemostat\chemostat_notebook.ipynb in Jupyter. Load the cobra.test module which gives access to the iJO1366 model used in this procedure. Load the cometspy package and alias it as “c”. Also load the plotting package matplotlib to make subplots later during analysis, as follows:

  # Start by loading the dependencies
  import cobra.test 
  import cometspy as c
  from matplotlib import pyplot as plt 
  import pandas as pd
  

Create the models

• 2
  Create the cobrapy models. cometspy is designed to take cobrapy models as inputs when generating COMETS models. Therefore, first create the cobrapy models using cobrapy’s included iJO1366 model. This procedure asks whether an E. coli model which cannot uptake lactose can be supported in a chemostat only supplied lactose, when another strain is present which can metabolise lactose but which cannot metabolise the galactose monomer. Create these strains using cobrapy’s knock_out() methods, as follows:

  # Load the E. coli iJO1366 model
  E_no_galE = cobra.test.create_test_model(“ecoli”)
  # copy it
  E_no_LCTStex = E_no_galE.copy()
  # Perform galE KO in the first model
  E_no_galE.genes.b0759.knock_out() # cannot metabolize galactose
  # Perform LCTStex reaction KO in the second model
  E_no_LCTStex.reactions.LCTStex.knock_out() # cannot uptake lactose
  

• 3
  Assign IDs. COMETS requires each model to have a unique ID. Assign these within the cobra model. Then, the ids will get propagated to the COMETS model, along with all reactions, metabolites, reaction boundaries, and the objective. Recall that in COMETS each model is optimized independently using this objective; there is no multi-strain objective. Note that gene-protein-reaction information is not currently used by COMETS. Convert a cobra model to a COMETS model by providing the cobra model to the model object constructor of the cometspy package, as follows:

  # Create the medium for COBRAPy growth tests 
  # change the ids of the models
  E_no_galE.id = “galE_KO” 
  E_no_LCTStex.id = “LCTStex_KO”
  # make COMETS models from the cobrapy models 
  galE_comets = c.model(E_no_galE) 
  lcts_comets = c.model(E_no_LCTStex)
  

• 4
  Initialize the biomass. COMETS models must have an initial biomass. This is done by changing the initial_pop attribute, which is a list of sublists, as follows. Each sublist has three values: the x location, the y location, and population size in grams dry weight. Note that for non-spatial simulations, the location is at x=y=0. In spatial simulations, biomass can be placed at multiple locations by using multiple sublists.

  initial_pop = 1.e-3 # gDW
  galE_comets.initial_pop = [0,0,initial_pop] # x, y, gDW
  lcts_comets.initial_pop = [0,0,initial_pop] # x, y, gDW
  

  : Models must have positive initial_pop for a simulation to run.

• 5
  Open the exchange reactions. In COMETS simulations, metabolite concentrations should determine exchange bounds (in contrast to cobra, where exchange bounds determine metabolite concentrations). Therefore, open all exchanges using the open_exchanges method of the COMETS model objects (default lower_bound = −1000, upper_bound = 1000), as follows:

  galE_comets.open_exchanges()
  lcts_comets.open_exchanges()
  

• 6
  Set the optimization method. For this Procedure, parsimonious flux-balance analysis will be used, which does two optimizations: first, maximizing biomass, and subsequently, minimizing total flux. This is useful to a) prevent models from inefficiently using metabolites, and b) reduces the solution space to make the simulations more reproducible. Set Parsimonious FBA by changing the obj_style attribute of the COMETS models as follows:

  galE_comets.obj_style = “MAX_OBJECTIVE_MIN_TOTAL” # default FBA option is “MAXIMIZE_OBJECTIVE_FLUX”
  lcts_comets.obj_style = “MAX_OBJECTIVE_MIN_TOTAL”
  Create the layout
  

• 7
  Load the models into a required COMETS object, the layout, by giving a list of COMETS models to the layout constructor, as follows:

  layout = c.layout([galE_comets, lcts_comets]) 
  

  : Note that by default, a layout has a grid attribute of (1,1), meaning that unless otherwise specified COMETS simulations run on a 1×1 lattice grid, i.e. in a well-mixed environment. Changing the grid attribute converts the simulation from a well-mixed environment to a spatial environment, and is done in Procedure 6. This procedure will not change the grid, and therefore will be a well-mixed simulation.

• 8
  Next, specify the metabolites in this layout. Set the initial metabolite amounts using the set_specific_metabolite method of class layout, by using the metabolite name and the initial amount as arguments. For this Procedure, the initial amounts will be equal to the reservoir amounts, which is 1000mmol for all unlimited metabolites, and 1mmol for lactose. To simplify setting these amounts, place the names of the unlimited metabolites into a list. Then, iterate through this list using a loop and assign each one an initial value of 1000. Finally, set the initial value of lcts_e (the name of the metabolite lactose) to 1, as follows:

  unlimited_mets = [‘ca2_e’, ‘cl_e’, ‘co2_e’, ‘cobalt2_e’, ‘cu2_e’, ‘fe2_e’, ‘fe3_e’,’h_e’, ‘h2o_e’, ‘k_e’, ‘mg2_e’, ‘mn2_e’, ‘mobd_e’, ‘na1_e’, ‘nh4_e’, ‘ni2_e’,’o2_e’, ‘pi_e’, ‘sel_e’, ‘slnt_e’, ‘so4_e’, ‘tungs_e’, ‘zn2_e’] 
  for met in unlimited_mets:
  layout.set_specific_metabolite(met, 1000.) 
  layout.set_specific_metabolite(“lcts_e”, 1.)
  

  : Layouts must have metabolites for models to be able to grow.

• 9
  Chemostats require metabolites to be “refreshed,” i.e. added to the simulation, at every time step. Use the set_specific_refresh method of class layout as follows to achieve this, which takes the metabolite name and the refresh rate (mmol / hour / box) as arguments. Given a dilution rate of 0.1 (per hour), this is a refresh rate of 100. mmol / hour / box for the unlimited metabolites, and 0.1 mmol / hour / box for lactose. Within COMETS, this amount will be divided equally among the time steps, to simulate the continuous in-flow of a chemostat.

  dilution_rate = 0.1 # / hr for met in unlimited_mets:
  layout.set_specific_refresh(met, 1000. * dilution_rate) # 100 mmol / hour
  layout.set_specific_refresh(“lcts_e”, 1. * dilution_rate) # 0.1 mmol / hour
  

  : This refresh is what creates the constant inflow of the chemostat.

Create the params

• 10
  At this point, the layout is complete. The other required COMETS object is the params object, which contains both biophysical parameters and simulation metadata, such as which results to log. First, generate a params object. As a note, all parameters are stored in an attribute called all_params within params, which can be modified directly. Here, use the set_param method to directly change specific parameter values as follows:

  params = c.params()
  

• 11
  Chemostats also have outflow. Set the outflow rate for metabolites using the “metaboliteDilutionRate” parameter, and the outflow rate for biomass using the “deathRate” parameter, as follows. These values determine loss rate of metabolites (biomass) from the system, as a proportion lost per hour. In a chemostat these are both equal to the dilution rate and represent outflow. Specifically, during a COMETS simulation, each time step, metabolite abundances and biomasses will be subtracted according to these rates, for example for a metabolite: metaboliteDilutionRate * timeStep * [metabolite abundance] will be subtracted every time step. deathRate also uses this approach. By default, both of these parameters have value 0, as in a flask.

  params.set_param(“deathRate”, dilution_rate)
  params.set_param(“metaboliteDilutionRate”, dilution_rate) 
  

  : These dilution rates are what create the outflow of the chemostat.

• 12
  By default in COMETS, metabolite exchange reaction boundaries (i.e. uptake rates) are set by Michaelis-Menten kinetics, in which the maximum uptake of a metabolite is: max_uptake = vmax * [metabolite] / (km + [metabolite]). Here, the [metabolite] is the metabolite concentration in molar units. It is calculated from the amount of metabolite in the lattice box in mmol, divided by the cube of the lattice box spaceWidth. The spaceWidth by default is 0.02cm and can be changed using the params method set_param(“spaceWidth”, <length in cm>). The vmax by default = 10 mmol / gDW / hr, and the km by default = 0.01. Change all of these parameters to create a 0.1×0.1×0.1cm box, vmax = 15, and km = 0.0001, as follows:

  params.set_param(“spaceWidth”, 0.1) 
  params.set_param(“defaultVmax”, 15.) 
  params.set_param(“defaultKm”, 0.0001) 
  

• 13
  Next, set the timeStep parameter (units of hours) to 0.1, the maxSpaceBiomass parameter to 10. (which is arbitrarily larger than the default of 0.1 gDW), and the maxCycles parameter (the total number of cycles) to 300. Note that, in order to see all possible parameters which can be altered with set_param, run the show_params method of the params object (i.e. params.show_params())

  params.set_param(“timeStep”, 0.1) # hours 
  params.set_param(“maxSpaceBiomass”, 10.) 
  params.set_param(“maxCycles”, 300) 
  

• 14
  By default, COMETS logs the total biomass of all models, summed over space (if doing a spatial simulation). COMETS does not log media or flux information by default, because this data can quickly become very large. In this Procedure, however, it is important to examine the media and also the species’ fluxes. This is done in two steps: First, specify that the parameters writeFluxLog and writeMediaLog are True, and second set the log rate (in cycles) to 1, as follows:

  params.set_param(“writeFluxLog”, True) 
  params.set_param(“writeMediaLog”, True) 
  params.set_param(“FluxLogRate”, 1)
  params.set_param(“MediaLogRate”, 1) 
  

  : If these are not set, media and flux data will not be saved.

Create the comets object and run the simulation

• 15
  At this point the two objects required to begin a COMETS simulation have been created: the layout and the params. The layout has in it the media information, the two models, and model attributes including initial_pop. The params has the dilution information, timing information, and which extra data to log. The penultimate step to running the simulation is to provide these objects to the constructor of the comets object. Arbitrarily, call the comets object sim, as follows:

  sim = c.comets(layout, params)
  ? TROUBLESHOOTING
  

• 16
  Next, run the simulation using the run method of the comets object, as follows. Warning: this will take 1–5 minutes depending on the system.

  sim.run()
  ? TROUBLESHOOTING
  

Analyze the simulation results

• 17
  First examine the total_biomass, which is always recorded, and contains the amount of biomass of each model over time. This data is stored in the total_biomass attribute of the comets object and is a pandas.DataFrame object, with one column containing the time in cycles, and the other columns containing biomass data. This object has a plot method which is used here to show the biomasses over time, as follows (Fig. 4). Also set the ylabel using matplotlib as follows, which will be done with every subsequent step. Note that the LCTStex_KO model grows despite lacking the ability to uptake lactose, the only carbon source.

  sim.total_biomass.plot(x = “cycle”)
  plt.ylabel(“biomass (gDW)”)
  

• 18
  Next, examine the media. The amount of every metabolite at every location and time recorded can be accessed in the pandas DataFrame media in the comets object (e.g. sim.media). However, typically only a few metabolites are of interest. cometspy provides a helper function get_metabolite_time_series which returns only metabolites which ever have non-zero values, summed over space. Additionally, an upper_threshold argument can be provided; any metabolite which ever exceeded this threshold is not returned. This is useful to remove metabolites present in unlimited amounts from the analysis. The function get_metabolite_time_series returns the data as a pandas DataFrame with one column called “cycle,” the other columns being the metabolite names, and the values being their amount in mmol at that cycle. This data can be plotted just like the total_biomass (Fig. 3).

  media = sim.get_metabolite_time_series(upper_threshold = 900.) 
  media.plot(x = “cycle”)
  plt.ylabel(“mmol”)
  ? TROUBLESHOOTING
  

• 19
  The metabolite analysis showed that galactose increased in the environment, then reduced to near-zero. This suggests that, as hypothesized, the LCTStex_KO strain is consuming galactose. To test this, examine the fluxes of the models. The fluxes of each species are kept in species-specific pandas DataFrames, which are stored in the fluxes_by_species dictionary attribute of the comets object. The keys to this dictionary are the model ids, and the values are the flux DataFrames. cometspy also has a helper method called get_species_exchange_fluxes which returns only the fluxes of exchange reactions of a given species. For this Procedure, use this helper function to retrieve flux data showing what the models take up and secrete. Use the optional argument threshold to determine the minimum absolute value of flux an exchange reaction achieved to only retain significant exchange fluxes (i.e. to exclude small-magnitude fluxes of trace minerals), as follows:

  LCTStex_KO_flux = sim.get_species_exchange_fluxes(“LCTStex_KO”, threshold = 5.)
  galE_KO_flux = sim.get_species_exchange_fluxes(“galE_KO”, threshold = 5.)
  

• 20
  Furthermore, fluxes of some metabolites such as O₂ are often large in magnitude, but for this Procedure are not relevant. Therefore, use the drop method of pandas DataFrames to remove these fluxes, as follows:

  ignoreable_exchanges = [“EX_o2_e”, “EX_h_e”, “EX_h2o_e”, “EX_co2_e”] LCTStex_KO_flux = LCTStex_KO_flux.drop(ignoreable_exchanges, axis = 1) galE_KO_flux = galE_KO_flux.drop(ignoreable_exchanges, axis = 1)
  

• 21
  Finally, plot the remaining exchange flux time series (Fig. 4). Plot each flux dataframe in a different subplot, which are created using the plotting package matplotlib. This is done by creating the subplots with matplotlib, and then specifying which subplot to use for each plot with the ax argument, as follows:

  plt.rcParams[“figure.figsize”] = (10,5) fig, ax = plt.subplots(1,2)
  galE_KO_flux.plot(x = “cycle”, ax = ax[0], title = “galE_KO”) 
  LCTStex_KO_flux.plot(x = “cycle”, ax = ax[1], title = “LCTStex_KO”)
  

Figure 4. Chemostat simulation of cross-feeding E. coli strains grown on lactose.

Results from a chemostat simulation (Procedure 2), prepared with the Python toolbox, in which one strain unable to break down lactose (LCTStex_KO) receives galactose from a different strain (galE_KO) that can break lactose into glucose and galactose, but is unable to metabolize galactose. The medium environment was composed of a constant supply of lactose (lcts_e), ammonia, and trace nutrients. Galactose (gal_e) was not supplied externally but started being available in the environment as galE_KO grew. a) Biomass of the two strains over time (cycle indicates the current time step). b) Amounts of the key metabolites over time (ac_e = acetate, for_e = formate, gal_e = galactose, glyclt_e = glycolate, lcts_e = lactose, meoh_e = methanol, pppn_e = phenylpropanoate). Note that it is typical for limiting nutrients (here, lactose and galactose) to have near-zero concentrations in a chemostat. c) Fluxes of relevant exchange reactions in galE_KO, and d) LCTStex_KO (the prefix “EX_” indicates an exchange reaction, and the metabolites being exchanged with the environment are: ac_e = acetate, for_e = formate, gal_e = galactose, lcts_e = lactose, nh4_e = ammonia). Negative flux represents uptake, while positive flux is excretion.

Procedure 3: Periodic environments and light absorption; modelling the diurnal cycle using the Matlab toolbox

setup: 15 min; simulation: 1–5 min

Import the models and medium conditions, defining light and light absorption parameters and initialize the COMETS layout

• 1
  Assuming that COBRA Toolbox is initialized in Matlab, open the file COMETS_protocols\COMETS_example_Diurnal_cycle\Matlab\diurnal_cycle_tutorial.mlx in Matlab and load the Prochlorococcus model iSO595⁸⁴, as follows:

  % Load Prochlorococcus genome-scale model
  model_fn = ‘iSO595v6.mat’;
  model = readCbModel(model_fn); 
  

• 2
  Define parameters related to light absorption and use these to calculate a model-specific absorption coefficient, as follows:

  % The ratio of chlorophyll is extracted from the model biomass-function
  ci_dvchla = 0.0163 % g / gDW (Partensky 1993 / Casey 2016)
  ci_dvchlb = 0.0013 % g / gDW (Partensky 1993 / Casey 2016)
  absorption_dvchla_680 = 0.0184; % m^2 mg^-1 (Bricaud et al., 2004)
  absorption_dvchlb_680 = 0.0018; % m^2 mg^-1 (Bricaud et al., 2004)
  absorption_water_680 = 0.465; % m^−1 (Pope and Fry, 1997)
  wavelength = 680;% nm
  

  : In this Procedure we assume a monochromatic light source at 680 nm, but it is possible to extend these calculations to a light source with a spectral distribution. All parameters are acquired from the literature ^106–111.

• 3
  Calculate the packaging effect, as follows. This is taking into account that the light-absorbing pigments are not dissolved in the media, but contained within discrete cells ¹¹². The packaging effect approaches 0 asymptotically for large cells. Depending on the accuracy needed in the calculation, the packaging effect can be assumed to be close to 1 for very small cells, such as Prochlorococcus ¹¹².

  diameter = 0.6; % um (Morel et al., 1993)
  n_dash = 13.77*1e-3; % imaginary part of refractive index at 675 nm (Stramski et al. 2001)
  size_parameter_alpha = diameter*1e3*pi/wavelength; % A variable describing the size ratio between the cell size and wavelength rho_dash = 4*size_parameter_alpha*n_dash;
  Q_a = 1+(2*exp(−rho_dash)/rho_dash)+2*(exp(−rho_dash)-1)/rho_dash^2; packaging_effect = 1.5*Q_a/rho_dash; 
  % Calculate the Prochlorococcus specific biomass absorption coefficient in units m2/ g DW biomass
  absorption_biomass = packaging_effect*(ci_dvchla*1e3*absorption_dvchla_680+ci_dvchlb*1e3*absorption_dvchlb_680); 
  

  : Setting the correct parameters is critical for the outcome of the simulation.

• 4
  Set the calculated absorption rate as a model parameter for the exchange reaction of light, as follows. LightEX is the exchange reaction for photons in the model.

  absorption_matrix = zeros(1,2);
  absorption_matrix(1) = absorption_water_680;
  absorption_matrix(2) = absorption_biomass;
  model = setLight(model, {‘LightEX’}, absorption_matrix);
  

• 5
  Create the layout using the function CometsLayout() from the COMETS toolbox and define parameters such as filenames for media and biomass log files, number of iterations, time-step etc., as follows:

  % Make layout with the COMETS 
  toolbox layout = CometsLayout();
  layout = layout.addModel(model); 
  % We use a single cell as the model layout, and set initial amount of cells to 1e-7 g
  layout = setInitialPop(layout, ‘1×1’, 1e-7); 
  % Set simulation parameters
  layout.params.writeMediaLog = true;
  layout.params.mediaLogName = [pwd ‘/mediaLog.m’];
  layout.params.writeBiomassLog = true; 
  layout.params.biomassLogName = [pwd ‘/biomassLog.m’];
  layout.params.maxCycles = 480; 
  layout.params.timeStep = 0.1; 
  layout.params.defaultDiffConst = 0; 
  layout.params.objectiveStyle = ‘MAX_OBJECTIVE_MIN_TOTAL’; 
  

• 6
  Define the concentration of each metabolite in the growth medium as follows:

  % Define medium
  layout = layout.setMedia(‘Ammonia[e]’, 1000); % 1 mmol 
  layout = layout.setMedia(‘HCO3[e]’, 1000);
  layout = layout.setMedia(‘CO2[e]’, 1000); layout = layout.setMedia(‘H[e]’, 1000);
  layout = layout.setMedia(‘Orthophosphate[e]’, 1000); 
  layout = layout.setMedia(‘H2O[e]’, 1000);
  layout = layout.setMedia(‘Cadmium[e]’, 1000);
  layout = layout.setMedia(‘Calcium_cation[e]’, 1000);
  layout = layout.setMedia(‘Chloride_ion[e]’, 1000); 
  layout = layout.setMedia(‘Cobalt_ion[e]’, 1000); 
  layout = layout.setMedia(‘Copper[e]’, 1000);
  layout = layout.setMedia(‘Fe2[e]’, 1000);
  layout = layout.setMedia(‘Magnesium_cation[e]’, 1000); 
  layout = layout.setMedia(‘Molybdenum[e]’, 1000); 
  layout = layout.setMedia(‘K[e]’, 1000);
  layout = layout.setMedia(‘Selenate[e]’, 1000); 
  layout = layout.setMedia(‘Sodium_cation[e]’, 1000);
  layout = layout.setMedia(‘Strontium_cation[e]’, 1000); 
  layout = layout.setMedia(‘Sulfate[e]’, 1000);
  layout = layout.setMedia(‘Zn2[e]’, 1000);
  layout = layout.setMedia(‘Hydrogen_sulfide[e]’,1000); 
  

  : In this Procedure we set the concentration of all essential metabolites except photons to 1000 mmol because we want the growth to be only limited by the available light.

• 7
  Define light conditions. The light flux (irradiation) should be defined with an amplitude given in mmol photons per second per square meter. Then, the Beer-Lambert law is used in COMETS to predict the number of absorbed photons (in mmol). To model natural light conditions we use the periodic function called half sin which is equal to

  $$max\left(f\right(t),0)$$

  where

  $$f\left(t\right)=Asin(\omega t+\varphi )+C.$$
  Here A is the amplitude, $\mathrm{\omega }$ the angular frequency

  $$\omega =2\pi /T,$$
  T the period, $\mathrm{\phi }$ the phase and C the offset. In this example we define global light conditions, but when running a simulation with one or more spatial dimensions it is possible to set different light conditions in each grid cell by using the function setDetailedPeriodicMedia. In this Procedure we define the period to 24 hours with an amplitude of 0.04 mmol photons per meter squared per second, as follows.

  % Set light conditions by defining parameters
  amplitude = 0.04; % mmol photons / m^2 / s
  function_name = ‘half_sin’;
  period = 24; % In hours
  phase = 0;
  offset = 0;
  photon_metabolite_id = ‘Photon[e]’;
  % Set globally changing light conditions
  layout = layout.setGlobalPeriodicMedia(photon_metabolite_id, function_name, amplitude, period,phase,offset); 
  

  : Setting the correct parameters is critical for the outcome of the simulation.

Run the COMETS simulation

• 8
  Run Comets by using the function runComets() in the Comets toolbox. If you want to run this layout in the Comets GUI export the layout and model by using the function createCometsFiles(layout, pwd) and import the layout in the GUI.

  % Run comets and produce the output files mediaLog.m and biomassLog.m runComets(layout)
  ? TROUBLESHOOTING
  

Load and plot the results

• 9
  Load the results, i.e. the biomass and media log files as follows:

  media = parseMediaLog(‘mediaLog.m’); 
  biomass = parseBiomassLog(‘biomassLog.m’); 
  

Analyse the simulation results

• 10
  Plot the output, e.g. the biomass and the light intensity as follows. Plot the media components by using the function plotMediaTimecourse(). The result is shown in Fig. 5.

  % Plot the light intensity
  f = figure(‘Name’, ‘Biomass and Light’);
  time = biomass.t*layout.params.timeStep;
  photon = media(strcmp(‘Photon[e]’, media.metname),:);
  p = plot(time, photon.amt, ‘color’,’b’, ‘linewidth”,2, ‘DisplayName’, ‘Photon[e]’); 
  legend(‘Location’,’northeast’)
  ylabel(‘Light flux [mmol photons m^{−2} s^{−1}]’);
  ylim([0 0.045]); 
  % Plot the biomass in the same figure
  yyaxis right
  p1 = plot(time, biomass.biomass, ‘color’, ‘r’, ‘linewidth’, 2, ‘DisplayName’, ‘Biomass’); 
  xlabel(‘Time (h)’);
  ylabel(‘Biomass [g DW]’);
  ax = gca;
  ax.YAxis(2).Color = ‘k’;
  ylim([1e-7 1.16e-7]); 
  

Figure 5. Simulations of the diurnal cycle of the marine photoautotrophic bacteria Prochlorococcus.

In this dynamic simulation of Prochlorococcus (Procedure 3), the organism is placed in an environment with a periodic light cycle, replicating the day-night alternation of sunlight. The growth of the biomass occurs only during daytime.

Procedure 4: Simulations including extracellular reactions

setup: 30 min, simulation 1–2 min

Create the COMETS input files

• 1Open the file
  COMETS_protocols\COMETS_example_Extracellular_Reactions\Matlab\rxn_demo_combined.mlx in Matlab. The first step is to load a model and create a layout, as follows. Set the initial population as a single grid point, i.e. a spatially homogeneous system, as follows.

  load(‘Scerevisiae_iMM904.mat’); %as ‘model’ 
  layout = createLayout(model);
  layout = setInitialPop(layout,’1×1’); 
  

  : For the purposes of this example we will not be concerned with the metabolites used by the metabolic model, but this step is included because attempting to execute COMETS without any biomass will return a warning instead of completing the simulation.

• 2
  Add a simple extracellular reaction of the form A+B, with a reaction rate k=0.5s⁻¹, as follows:

  layout = addExternalReaction(layout,’reaction1’,{‘A’ ‘B’ ‘C’},... 
  [−1 −1 1],’k’,0.2);
  layout = setMedia(layout,’A’,1); 
  layout = setMedia(layout,’B’,2); 
  

• 3
  Add an enzyme-catalyzed reaction of the form F, catalyzed by the enzyme E, with turnover rate 20s⁻¹ and KM=0.01mmol, as follows:

  layout = addExternalReaction(layout,’enz_reaction’,{‘F’ ‘G’},... [−1 1],’enzyme’,’E’,’kcat’,2,’km’,0.25);
  layout = setMedia(layout,’F’,1); layout = setMedia(layout,’E’,0.1); 
  

  Setting these parameters correctly is critical for the outcome of the simulation.

  At this point, the extracellular reaction information is included in the COMETS layout file, in blocks with the following format:

  REACTANTS
              rxnIdx metIdx order k  //elemental rxn 
              rxnIdx metIdx km       //enzyme catalyzed
        ENZYMES
              rxnIdx metIdx kcat 
        PRODUCTS
              rxnIdx metIdx stoich
        //
  

  Each reactant or product in a given reaction should appear on its own line, using the same integer rxnIdx per extracellular reaction. The metIdx field corresponds to a metabolite’s position in the world_media block. The system determines whether a reaction is elemental or enzymatic based on the presence of an entry in the ENZYMES block. In the case of elemental reactions, only the first entry for the rate constant k is used.

  The REACTIONS block in the comets_layout.txt file generated by the runComets command contains the following:

  reactions
        reactants
              1 15 1 2.000000e-01
              1 16 1 2.000000e-01
              2 19 2.500000e-01
        enzymes
              2 18 2
        products
              1 17 1
              2 20 1
  //
  

  The first column under each heading denotes the ID of the reaction each metabolite is participating in. The second column is the index of the metabolite in the WORLD_MEDIA list (the values here are not 1–6 because the media also contains exchange metabolites from the metabolic model that was included at the start of the script).

  Under the reactants heading, the subsequent columns differ for mass-balance and enzymatic reactions. For mass-balance reaction 1, the third value is the stoichiometry of the reactant and the fourth value is the reaction rate constant (which is the same for all reactants). For enzymatic reaction two, the third value is the turnover rate and there is no fourth value (it is assumed that the stoichiometry of the substrate in an enzymatic reaction is always 1).

  The enzymes heading only includes a row for the enzymatic reaction. The values here are the reaction number, the index of the metabolite that acts as the enzyme, and the millimolar half-saturation concentration.

  The products heading contains values for the reaction number, the index of the produced metabolite, and the product’s stoichiometry.

Run the COMETS simulation

• 4
  Set a few parameters and execute the simulation as follows:

  layout.params.timeStep = 1/3600; %timestep = 1 second
  layout.params.writeMediaLog = 1;
  layout.params.maxCycles = 25;
  runComets(layout)
  ? TROUBLESHOOTING
  

Analyse the simulation results

• 5
  Load the results and plot the data as follows:

  media = parseMediaLog(layout.params.mediaLogName,{‘A’ ‘B’ ‘C’ ‘E’... ‘F’ ‘G’});
  plotMediaTimecourse(media,{‘A’ ‘B’ ‘C’});
  title(‘A + B -> C’); 
  plotMediaTimecourse(media,{‘E’ ‘F’ ‘G’});
  title(‘Enzymatic: F -> G’); 
  

  The figures produced by the plotMediaTimecourse function should appear as in Fig. 6.

Figure 6. Media concentrations over time during simulations demonstrating extracellular reactions.

Demonstration of how extracellular reactions, happening in the environment, independent of any specific organism, can be implemented in COMETS (Procedure 4). a) Environmental metabolite changes for a simple bimolecular reaction of the form A+B→C, with rate ν=νmax·[A]·[B] where νmax = 0.2 s⁻¹mM⁻¹.

b) An environmental enzyme-catalyzed reaction of the form E+S→E+P, with rate according to the Michaelis-Menten equation ν=νmax·[E]·[S]/(KM+[S]), where vmax = 2 s⁻¹, KM = 0.25 mM. The enzyme E is not associated with any specific organism, and is present in the environment at a constant concentration [E]= 0.1 mM.

Procedure 5: Simulating evolutionary processes in microbial populations

setup: 30 min- 1hr, simulation: 5min-indefinite

Load the model

• 1
  Open the file COMETS_protocols\COMETS_example_Evolution\Python\P5_evolution-checkpoint.ipynbin Jupyter. Import the necessary libraries and load the E. coli model as follows:

  import cometspy as c
  import cobra.test
  import os
  import pandas as pd
  import matplotlib.pyplot as plt
  # load model
  wt = cobra.test.create_test_model(“ecoli”)
  

• 2
  Remove the bounds for all exchange reactions in the model to allow them to be controlled dynamically by COMETS as follows:

  # Remove bounds from exchange reactions
  for i in wt.reactions:
      if ‘EX_’ in i.id:
          i.lower_bound =−1000.0
  

Set up the layout

• 3
  Create a well-mixed environment with a glucose minimal media. Here, we use the add_typical_trace_metabolites method to add trace metabolites (ions, metals etc) in unlimited amounts (static flag), as follows:

  # generate layout
  test_tube = c.layout()
  test_tube.set_specific_metabolite(‘glc D_e’, 0.0001)
  test_tube.add_typical_trace_metabolites(amount=1000)
  # add model
  wt = c.model(wt)
  wt.initial_pop = [0, 0, 1e-7]
  test_tube.add_model(wt)
  

Set up simulation parameters

• 4
  Create a params object, and modify the needed parameters as follows. The simulation in this Procedure consists of 10 days of experiment, with a 1:2 transfer every 3h. The mutation rate will be 10⁻⁸ deletion events per reaction and generation. The cellSize parameter sets the amount of biomass that appears when a mutant occurs (i.e., one mutant cell appears).

  # Load parameters and layout from file
  evo_params = c.params()
  # Set relevant parameters
  evo_params.set_param(‘timeStep’, 0.1)    # hours
  evo_params.set_param(‘maxCycles’, 2400)
  evo_params.set_param(‘batchDilution’, True)
  evo_params.set_param(‘dilFactor’, 0.5)
  evo_params.set_param(‘dilTime’, 3)       # hours
  evo_params.set_param(‘evolution’, True)
  evo_params.set_param(‘mutRate’, 1e-8)    # /generation /reaction
  evo_params.set_param(‘cellSize’, 1e-10)
  evo_params.set_param(‘minSpaceBiomass’, 1e-11)
  evo_params.set_param(‘BiomassLogRate’, 1)
  

  : Simulations including evolution are very sensitive to parameters such as mutRate (and addRate if additions are modeled) and cellSize (the dry weight of one cell in grams). The parameter cellSize is critical because in order to perform simulations, COMETS computes the number of single cells in the amount of biomass of each population, and samples the resulting number of cells according to mutRate to decide the number of mutations to perform.

Run the simulation

• 5
  Create the COMETS object using the above layout and parameters, and run the simulation, as follows:

  # create comets object from the loaded parameters and layout
  evo_simulation = c.comets(test_tube, evo_params)
  # run comets simulation
  evo_simulation.run()
  ? TROUBLESHOOTING
  

Analyse the simulation results

• 6
  Plot the population dynamics of all species over time (color coded) using standard Python plotting tools, as follows:

  fig, ax = plt.subplots(figsize=(15, 5))
  for key, grp in evo_simulation.biomass.groupby([‘species’]):
      ax = grp.plot(ax=ax, kind=‘line’, x=‘cycle’, y=‘biomass’)
  ax.get_legend().remove()
  plt.yscale(‘log’)
  plt.ylabel(“Biomass (gr.)”)
  

• 7
  Visualize the genotypes. In order to analyze the results, it is also helpful to visualize the genotypes data frame, which contains all the mutants that ever appeared during the simulation, as follows:

  evo_simulation.genotypes
  

  The data frame contains three columns: The ancestor, the mutation (reaction number in the model), and the name of the resulting genotype, which is assigned as a random string as its “Species name” when the mutant is born. This data, together with the population dynamics (Step 6), represent a detailed picture of all the evolution happening within a simulation, and can be used in downstream analysis to address specific questions (e.g. reconstruct the phylogeny of a simulation). The results of a sample simulation are shown in Fig. 7. Note that, given that mutation and population dynamics are random processes, the specific results of each simulation will vary.

  	Ancestor	Mutation	Species
  0	NO_ANCESTOR	NO_MUY	iJO1366.cmd
  1	iJO1366.cmd	del_1618	ff37d064-b32a-4a4f-9990-adee15665d20
  3	iJO1366.cmd	del_524	41cfb561-75b1-4941-84bc-992de5b45a3c
  4	iJO1366.cmd	del_594	8a41bfd2-1c58-4d8c-b08d-064f031706aa
  ...	...	...	...
  92	iJO1366.cmd	del_1338	d519772d-ebe5-4697-a4a6-5ecde288bd11
  93	iJO1366.cmd	del_1026	25bb819f-5b79-459c-9fdf-921b9a018b4
  94	iJO1366.cmd	del_2556	c9435324-61c8-416b-a1cb-c29dc1c76c21
  95	iJO1366.cmd	del_1757	73450a19-50ca-4b53-ad2c-ed32573c9270
  96	iJO1366.cmd	del_1772	691548f9-5765-4259-bd89-1f6b4e94b69

Figure 7. Simulation of evolutionary processes.

In this simulation exemplifying an evolutionary process (Procedure 5), an Escherichia coli model was seeded in 1μL of glucose minimal medium (0.1mM) and transferred every 3 hours to a fresh medium using a dilution factor of 1:2 during 10 days. Mutations (in the form of reaction knock-outs) were allowed to happen in this population at a rate of 10⁻⁸ knock-outs appearing per gene and generation. The gray line represents the ancestor, which remains at high density, and other colors are used to represent different mutations that appear, persist during variable periods and extinguish stochastically.

Procedure 6: Microbial growth in natural environments; soil-air interface simulation

setup: 30 min- 1hr, simulation: 3–6 hr

Prepare models and determine initial locations of biomass and rock barriers

• 1
  Open the file COMETS_Protocols\COMETS_protocols\COMETS_example_Soil\soilexample.ipynb in Jupyter. Import the necessary libraries as follows:

  import cobra 
  import sys
  import copy
  import numpy as np
  from matplotlib import pyplot as plt 
  import cometspy as c
  

• 2
  For the strain models, use the two ubiquitous, well-curated soil bacteria available in the BiGG database: Pseudomonas putida (model iJN1463) and Bacillus subtilis (model iYO844). Put those files into a subdirectory from the working directory called “models”. First, load these COBRApy models by name, as follows:

  model_dir = “./models” # model location
  iJN = cobra.io.read_sbml_model(model_dir + ‘/iJN1463.xml’) 
  iYO = cobra.io.read_sbml_model(model_dir + ‘/iYO844.xml’)
  

• 3
  Recall that when a cometspy model is created from a COBRApy model, all reactions, metabolites, the objective function, and reaction bounds are propagated to the cometspy model. The Bacillus model (iYO844) had positive lower bounds on the biomass function. Change this using COBRApy as follows.

  iYO.reactions.get_by_id(‘BIOMASS_BS_10’).bounds = (0., 1000.)
  

• 4
  Convert the cobrapy models to cometspy models, as follows:

  iJN_comets = c.model(iJN)
  iYO_comets = c.model(iYO)
  

• 5
  Open exchange reactions (default bounds = (−1000., 1000.)) so that extracellular metabolite concentrations and Michaelis-Menten kinetics control uptake bounds.

  iJN_comets.open_exchanges()
  iYO_comets.open_exchanges()
  

  : Often Cobra models are saved with media definitions. If we do not open exchanges, these media definitions will overrule the media we specify in the layout.

• 6
  Import the helper functions. Typically in a cometspy workflow all model attributes, including the required initial_pop attribute, would be set before moving onto the layout. However, this Procedure also introduces the concept of impenetrable barriers, which are conceptualized as “rocks.” Since biomass cannot be located within an impenetrable rock, first it is necessary to create the rocks. The first step is to import two helper functions from the cometspy.utils module as follows:

  from cometspy.utils import grow_rocks, pick_random_locations
  

• 7
  Use a grid size of (50, 50) for the simulation, meaning the simulation will occur on a lattice of size 50 × 50 in units of boxes. Use the helper function grow_rocks to choose the locations of the impenetrable barriers (Fig. 8a). This function returns a list of (x,y) locations. It takes in as arguments the number of rocks desired (n), the x and y range over which barriers can exist, and the mean size (in number of boxes) that a rock should have (mean_size), as follows:

  grid_size = 50
  n_rocks = 30
  # note: to get the exact same locations as shown below, uncomment the following two lines
  #import random
  #random.seed(2)
  rock_locs = grow_rocks(n = n_rocks, xrange = [2,grid_size-2],yrange = [2,grid_size-2],mean_size = 10)
  

  : Note that grow_rocks is a useful helper function but in practice any method of generating a list of (x,y) locations can be used to determine barrier locations. When using grow_rocks for this simulation, reduce the xrange and yrange, so that rocks are not on edges.

• 8
  Determine the initial locations for each model using the pick_random_locations helper function (imported in Step 6), as follows. This function returns n randomly-chosen locations within the specified xrange and yrange, while not choosing from an optional list of locations called forbidden_locs. Because biomass should not overlap with rocks, or with other biomass, use the rock_locs as the first list of forbidden_locs, then add to this list the intended biomass locations as they are generated.

  forbidden_locs = copy.deepcopy(rock_locs) n_founders = 35
  # determine iJN locations
  iJN_locs = pick_random_locations(n = n_founders,
                    xrange = [1,grid_size], yrange = [1,grid_size],
                    forbidden_locs = forbidden_locs)
  # add the iJN locations to the forbidden_locs
  forbidden_locs.extend(iJN_locs)
  # determine iYO locations
  iYO_locs = pick_random_locations(n_founders, [1,grid_size],[1,grid_size], forbidden_locs) 
  

  : Using the forbidden_locs argument is critical to ensuring biomass does not overlap initially, or overlap with rocks.

• 9
  Visualize the initial locations. It is helpful to visualize the initial locations, so that the locations can be re-randomized if desired. Do this by creating a 3D numpy array and altering the value of occupied locations to 1, as follows. Use a different z-axis layer for each species, and for rocks, create gray points by setting all three levels of the z-axis to the same value. Finally, plot using matplotlib (Fig. 8b).

  initial_image = np.zeros((grid_size,grid_size,3))
  for rock in rock_locs:
      initial_image[rock[0],rock[1],0:3] = 0.5
  for loc in iJN_locs:
      initial_image[loc[0],loc[1],1] = 1
  for loc in iYO_locs:
      initial_image[loc[0],loc[1],2] = 1
  plt.imshow(initial_image)
  

• 10
  Finalize the models by setting their essential initial_pop. Recall from Procedure 2 that initial_pop is a list of lists. Each sublist has three values: the x location (an integer), the y location (integer), and the amount of biomass (a float, units of grams dry weight). Typically the authors use list comprehensions to create initial_pop from a list of locations, however for clarity here the more verbose “for loop” method is used. Set the amount of biomass to 1.e-8 for each location, as follows:

  # iJN
  iJN_initial_pop = [] 
  for loc in iJN_locs:
        iJN_initial_pop.append([loc[0], loc[1], 1.e-8]) 
  iJN_comets.initial_pop = iJN_initial_pop
  # iYO
  iYO_initial_pop = [] 
  for loc in iYO_locs:
        iYO_initial_pop.append([loc[0], loc[1], 1.e-8]) 
  iYO_comets.initial_pop = iYO_initial_pop
  

Figure 8. Soil-air interface simulation.

A two-species community colonizes a soil microhabitat (Procedure 6). a) Schematic detailing common features of a soil microhabitat, which are set in COMETS using simple commands to specify metabolite concentrations, and different ways of maintaining or supplementing those concentrations, in specific spatial locations. b) The initial state of the COMETS simulation, showing impenetrable barriers (gray) and the founder locations of the iJN1463 model (green) and the iYO844 model (blue). c) Time series showing biomass of the two models over time, integrated over the whole spatially structured environment. d) Snapshots of biomass and three key metabolites (f) succinate, f) O2, g) NH4) from 100 hours into the simulation. In the biomass snapshot, green is the iJN1463 model and blue is the iYO844 model. In e-g, the color scale denotes relative metabolite concentration, with bright yellow the maximum and dull purple the minimum. The scale bar shows 2mm.

Create the layout

• 11
  At this point the models are complete. Following the typical workflow, next create the required layout object with a list of the models as the constructor’s argument, as follows:

  layout = c.layout([iJN_comets, iYO_comets])
  

• 12
  Change grid to create the 50×50 box layout as described in step 7, as follows. Spatial simulations are created by making the grid attribute of the layout object greater than (1,1) in either the x or y directions.

  layout.grid = [grid_size,grid_size]
  

• 13
  Set the barriers. Add impenetrable barriers to the layout using the add_barriers method, which takes in a list of tuples of x,y locations, as follows. These were created in Step 7 using the grow_rocks utility function.

  layout.add_barriers(rock_locs) 
  

• 14
  First populate the entire simulation with trace metabolites which are essential to growth but are not carbon or nitrogen sources. Use set_specific_metabolite to do this as follows, which sets the amount in mmol in every box in the lattice to the second argument (here, 1000.). These metabolites should remain fixed and unlimited. Therefore, set the third argument of set_specific_metabolite to True, which means at the beginning of each time step the metabolite amounts will return to 1000. To make this easier, use a loop that iterates through each metabolite.

  abundant_trace_metabolites = [‘ca2_e’, ‘cl_e’, ‘co2_e’, ‘cobalt2_e’, ‘cu2_e’, ‘fe2_e’, ‘fe3_e’,
  ‘h_e’, ‘hco3_e’, ‘k_e’, ‘mg2_e’, ‘mn2_e’, ‘mobd_e’, ‘na1_e’, ‘ni2_e’, ‘pi_e’, ‘sel_e’, ‘so3_e’, ‘so4_e’, ‘tungs_e’, ‘zn2_e’]
  for met in abundant_trace_metabolites:
        layout.set_specific_metabolite(met, 1000.,static= True)
  

• 15
  Next, populate the entire latice with a much smaller initial abundance of nitrogen and oxygen, as follows:

  layout.set_specific_metabolite(‘nh4_e’,0.000001
  layout.set_specific_metabolite(‘o2_e’, 0.00001)
  

• 16
  Create the air-soil interface. The air-soil interface will supply two things. First, oxygen, which will be kept at a fixed abundance per box. Second, ammonia, which will be added in a small amount per-hour, mimicking decomposition. To set a fixed abundance per box in a specific location, use the method set_specific_static_at_location, as follows, which takes as arguments the metabolite name, a tuple containing the x,y location, and the amount in mmol. To set a metabolite to be added at a constant amount per-hour in a specific location, use the method set_specific_refresh_at_location, as follows, which takes as arguments the metabolite name, a tuple containing the x,y location, and the rate of addition (mmol / hour). This rate is achieved by adding a fixed amount of the metabolite per-time-step. For simplicity, use a loop that iterates through each horizontal location and run the methods just described for each location.

  # create the air-soil interface
  for x in range(grid_size):
  layout.set_specific_static_at_location(‘o2_e’, (0,x), .00001) # top
  layout.set_specific_refresh_at_location(‘nh4_e’, (0,x), 0.000001) 
  

• 17
  To mimic continuous oxygen diffusion down through the substrate, set a fixed abundance of zero oxygen per box along the bottom of the lattice, as follows. This causes all oxygen which reaches the bottom of the lattice to be removed from the system.

  for x in range(grid_size): layout.set_specific_static_at_location(‘o2_e’, (grid_size-1,x), 0.) # bottom
  

• 18
  The ‘root’ will do two things: remove all ammonia which reaches it from the system and supply a steady addition of consumable carbon sources. Similar to when the air-soil interface was created, use ‘static’ values to cause the removal of ammonia, and ‘refresh’ values to cause the steady addition of carbon, as follows:

  for x in range(grid_size):
        # removal of nh4
        layout.set_specific_static_at_location(‘nh4_e’, (x,0), 0.0)
        # addition of carbon sources
        layout.set_specific_refresh_at_location(‘cit_e’, (x,0), .000001)
        layout.set_specific_refresh_at_location(‘meoh_e’, (x,0), .000001)
        layout.set_specific_refresh_at_location(‘succ_e’, (x,0), .000001)
  

Set up the simulation parameters

• 19
  The layout is now complete, having initialized it with the models, creating a two-dimensional grid, and altering the metabolite addition and removal to mimic both the air-soil interface and a root. Following the standard workflow, the next step is to create the params object, as follows. Set the timeStep to 0.1 hours and the spaceWidth to 1/50 (cm, to make a 1cm×1cm simulation). Set a positive death rate, which means that biomass which cannot grow as fast as the specified rate will eventually go locally extinct. Set the biomass diffusion constant (flowDiffRate) to 1/1000 of the metabolite diffusion constant (defaultDiffConst). Also set the logging parameters so that spatially-explicit metabolite and biomass data is saved. To use three CPUs, set numRunThreads to 3. Finally, reduce the default km (defaultKm) so that Michaelis-Menten kinetics are often near-maximum.

  params = c.params() 
  params.set_param(‘timeStep’, 0.1) 
  params.set_param(‘spaceWidth’, 1/50.) 
  params.set_param(‘maxCycles’, 1000)
  params.set_param(‘maxSpaceBiomass’, 10) 
  params.set_param(‘flowDiffRate’, 1.e-9) 
  params.set_param(‘defaultDiffConst’, 1.e-6)
  params.set_param(‘deathRate’, 0.00005) # die at rate of 0.5/10000 per hour
  params.set_param(‘writeBiomassLog’, True) 
  params.set_param(‘BiomassLogRate’, 100) 
  params.set_param(‘writeMediaLog’, True) 
  params.set_param(‘MediaLogRate’, 100)
  params.set_param(‘numRunThreads’, 3)
  params.set_param(‘defaultKm’, 0.000001)
  

Run the simulation

• 20
  Finally, create the comets simulation object and initialize it with the layout and params, then run, as follows. This simulation will take multiple hours. Therefore, it useful to not have COMETS delete simulation files (as it does by default). Do this with the optional . run() argument delete_files = False, as follows:

  sim = c.comets(layout, params) 
  sim.run(delete_files = False) 
  ? TROUBLESHOOTING
  

Analyze the simulation results

• 21
  Analyze the total biomass of each model through time (Fig. 8c) with the plot method of the total_biomass simulation object, as follows:

  sim.total_biomass.plot(x = “cycle”)
  

• 22
  Visualize the biomass at the end of the simulation using the helper function get_biomass_image to get numpy arrays of each model at the specified cycle, then put these together into a single numpy array which can be plotted with the matplotlib method imshow, as follows. Also, add the rocks to this image (Fig. 8d).

  im = sim.get_biomass_image(‘iJN1463’, params.all_params[‘maxCycles’])
  im2 = sim.get_biomass_image(‘iYO844’,params.all_params[‘maxCycles’]) 
  final = np.zeros((grid_size,grid_size,3))
  final[:,:,1] = im / np.max(im)
  final[:,:,2] = im2 / np.max(im2) 
  for rock in rock_locs:
        final[rock[0]-1,rock[1]-1,0:3] = 0.4
  fig, ax = plt.subplots(figsize = (3.1, 3.1))
  ax.imshow(final) 
  plt.imshow(final) 
  

• 23
  Visualize critical metabolite concentrations at the end of the simulation using a similar helper function, get_metabolite_image, as follows (Fig. 8e–g).

  fig, ax = plt.subplots(1,3) 
  ax[0].imshow(sim.get_metabolite_image(“succ_e”,1000)) 
  ax[1].imshow(sim.get_metabolite_image(“o2_e”,1000)) 
  ax[2].imshow(sim.get_metabolite_image(“nh4_e”,1000)) 
  

Procedure 7: Demographic noise and cooperative biomass propagation

setup: 30min-1hr, simulation: 3–4 days

Create the COMETS input files

• 1
  Prepare the stoichiometric model for this protocol in the same way as in Procedure 1, using COMETS_protocols\COMETS_example_DemographicNoiseCooperativePropagation_TwoStrains\e_core_model.txt. The difference in this case, is that this file, in addition to the required metabolic model fields, contains the fields for the cooperative propagation model, and the demographic noise, as follows:

  convNonlinDiffZero 0.0
  //
  convNonlinDiffN 6000e-6
  //
  convNonlinDiffExponent 1.0
  //
  convNonlinDiffHillN 1.0
  //
  convNonlinDiffHillK 0.0
  //
  noiseVariance 0.0
  //
  neutralDrift true
  //
  neutralDriftSigma 0.001
  //
  

  The cooperative propagation model and the demographic noise are introduced in the “Development of the Protocol” section, and described in detail in the Supplementary Discussion 1: Detailed information on the development of the protocol.

  There are two possible options in this step, by setting the following parameter.

  Option A:

  convNonlinDiffHillK 0.0
  

  Option B:

  convNonlinDiffHillK 0.01
  

  These two options will result in: A) spatially mixed population of the two strains, B) spatial demixing of the two strains.

• 2Prepare the following layout file COMETS_protocols/COMETS_example_DemographicNoiseCooperativePropagation_TwoStrains/circular.txt, which consists of a 400×400 grid initially uniformly populated with the nutrients and inoculated with initial biomass of two identical E. coli strains in the center, simulating an initial drop.
  This layout file contains a block with the definition of two models, grid size and nutrients concentrations:

  model_file e_coli_core.txt e_coli_core.txt 
      model_world
         grid_size 400 400 
         world_media 
         ac[e] 0.0
         acald[e] 0
         akg[e] 0
         co2[e] 0
         etoh[e] 0
         for[e] 0
         fru[e] 0
         fum[e] 0
         glc__D[e] 5.5e-6 
         gln__L[e] 0
         glu__L[e] 0
         h2o[e] 1000
         h[e] 1000
         lac__D[e] 0
         mal__L[e] 0
         nh4[e] 1000
         o2[e] 1000.0
         pi[e] 1000
         pyr[e] 0
         succ[e] 0
      //
  

  The next block is statically fixing the concentrations of the media. The first line corresponds to the global setting of the fixed media, by specifying two numbers for each metabolite. The first number, 0 by default, is a flag that if set to 1, sets the media to a static value given by the second number. Following the global static media line, we specify static media as a list of x and y coordinates, followed by a list of static flags and an abundance value for each metabolite.

  static_media 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
      0    0        0    0.000000e+00 ... 1    5.5e-6  … 0.000000e+00
      0    1        0    0.000000e+00 ... 1    5.5e-6  … 0.000000e+00
      ...
      398   399     0    0.000000e+00 ... 1    5.5e-6  … 0.000000e+00
      399   399     0    0.000000e+00 ... 1    5.5e-6  … 0.000000e+00
  

  In this case we do not set a global static value for any of the nutrients. We fix only the value of glucose at the edges of the simulated space.

  The last block in this file, defines the initial population of the two organisms in the layout:

       initial_pop
     151 191 0.619774e-06 0.619774e-06
     151 192 0.619650e-06 0.619650e-06
     ...
     249 208 0.617671e-06 0.617671e-06
     249 209 0.617547e-06 0.617547e-06
     //
  //
  

  The population in this case is initialized as a centered circle with a radius of 50 grid points (simulated 5 mm), populated with a Gaussian with a prefactor of 1e-6 g biomass and width (standard deviation) of 50 grid points (5 mm).

• 3
  Prepare the following file COMETS_protocols/COMETS_example_DemographicNoiseCooperativePropagation_TwoStrains/global_params.txt, which contains the rate and name of saving the snapshot images of the colony during the simulation, as follows:

  maxCycles = 2000
  pauseonstep = false
  pixelScale = 5
  saveslideshow = true
  slideshowExt = png
  slideshowColorRelative = false
  slideshowRate = 100
  slideshowLayer = 20
  slideshowName = ./images/image
  writeFluxLog = true
  FluxLogName = ./flux.txt
  FluxLogRate = 500
  writeMediaLog = true
  MediaLogName = ./media.txt
  MediaLogRate = 500
  writeBiomassLog = true
  BiomassLogName = ./biomass.txt
  BiomassLogRate = 500
  writeTotalBiomassLog = true
  totalBiomassLogRate = 1
  TotalbiomassLogName = ./total_biomass.txt
  useLogNameTimeStamp = false
  

• 4
  Set the simulation parameters in the package parameters file as follows, most notably the propagation mode of the colony set to biomassmotionstyle = ConvNonlin Diffusion 2D

  biomassmotionstyle = ConvNonlin Diffusion 2D
  defaultdiffconst = 6.0E-6
  exchangestyle = Monod Style
  defaultVmax = 18.5
  defaultKm = 0.000015
  defaultHill = 1
  

  : Setting the correct values of the parameters is critical for obtaining the correct outcome.

Run the COMETS simulation

• 5
  Submit the simulation files prepared in steps 1–4 and run it in a cluster queuing system, using the Grid Engine User command provided on the computational cluster. For example:

  qsub -pe omp 10 -l h_rt=24:00:00 qscript
  

  Where qscript is the bash script to be submitted:

  #!/bin/bash -l
  module load gurobi/9.0.0
  comets_scr comets_script
  

  Here the second line loads the gurobi optimizer module. The specific name and version of the optimizer should be set to the one installed on the user’s system.

  The output of this run consists of a collection of figures representing the 2D morphology of the single species bacterial colony with examples for the two options shown in Fig. 9a and 9b.

  ? TROUBLESHOOTING
  

Figure 9. A variety of morphologies simulated by COMETS.

Snapshot at time 50 hours of COMETS simulations of bacterial colonies with different morphologies, implemented using the ConvNonLinDiff 2D biomass propagation model in the presence of demographic noise (Procedure 7): a) Colony of two identical strains of E. coli (labeled individually as green and red). In this case all bacterial biomass is assumed to be motile, regardless of whether or not there is growth at a given spatial location. In this case, the two strains mix, visible as yellow regions. b) Same system as panel a, except that in this case only the portions of the colony that are actively growing are assumed to be motile. In this case, the two strains are genetically demixed, forming sectors of red and green color. c) Visualization of the regions of active growth, achieved by plotting the sum of the growth rates of the two strains at individual spatial locations, for the system shown in panel a; d) Visualization of the amount of glucose left on the plate, highlighting the depletion in the area where the colony grew. The scale bar shows 1cm.

Analyze the simulation results

• 6
  With the collection of images from Step 5 in the directory images/, create a gif format video of the growth of the colonies, with the additional step:

  convert image_*.png movie.gif
  

  or any protocol of choice for creation of movies from collection of png images. The convert command is part of the ImageMagick program. Install it for Linux, Mac OS X or Windows, by following the instructions in https://imagemagick.org/script/download.php.
  The videos are shown in Extended Data Videos 1 and 2.

  ? TROUBLESHOOTING
  

• 7
  Further analyze and visualize the data in the media.m and fluxes.m files. Here we provide examples of visualization of the biomass growth rate and the glucose spatial profiles in Figs. 9c and 9d. The figures were obtained by running the MATLAB script RateandNutrientImage.m. In order to manage the memory needed to run the script, prepare the flux and metabolite output file in a way to contain only the results at the desired time step 2000 using the command line, as follows:

  cat fluxes.m |grep {2000} >fluxes_atTime2000.m
  

  and

  cat media.m |grep _2000{9} >media_glucose_atTime2000.m
  

Timing

A typical time to prepare and run a COMETS simulation is from 30 minutes to a few hours. This time however may vary depending on the complexity and size of the simulation layout grid, the number of models present in the simulation, the size of the S matrix in each model, and certainly the speed and number of available CPUs. The preparation of the input files (in MATLAB and Python) takes no more than 30 minutes. The simulation of a small model such as one consisting only of the core E. coli metabolism, for about 1000 time steps, in a layout consisting of a single grid point will take a few minutes. A single FBA calculation on the E. coli core model takes less than 0.02 seconds on a typical laptop PC. A simulation of a 400 by 400 grid layout, with several models consisting of a few thousands of reactions and metabolites, parallelized over 10 CPUs, can take several days. A simulation including evolution, for example, can run indefinitely, as long as the experimenter wants.

Troubleshooting

Troubleshooting advice can be found in Table 3.

Anticipated Results

Procedure 1:

In this first protocol we reproduced a classic FBA result, simulation of the dynamics of the core E. coli metabolism^43,79. In this simplest case, we created a batch culture of E. coli, supplied with minimal media in homogeneous, or well mixed, conditions. This simulation is an example of a dFBA run, in its original form. The results are shown in Fig. 3. As mentioned above, Fig. 3a shows the growth of the E. coli biomass, while Fig. 3b shows the concentrations of glucose and the three products of glucose fermentation. The growth period of the biomass, as well as the secretion of the metabolic products, coincide with the depletion period of glucose.

Procedure 2:

Fluxes of both strains should go through three different phases as the conditions equilibrate (Fig. 4c,d). The galE_KO strain should take up lactose (negative flux) and secrete galactose (positive flux) throughout the simulation (Fig. 4c). Early on when metabolites are in abundance, uptake should be near the maximum (vmax = 15) due to the Michaelis-Menten uptake kinetics. The LCTStex_KO strain should take up galactose throughout the simulation (Fig. 4d). These flux results confirm the hypothesis that a strain unable to take up lactose can cross-feed off of a different strain able to take up lactose, but unable to metabolize galactose, in a lactose chemostat. As a result, both strains survive at very similar densities (Fig. 4a). This is to be expected, because lactose molecules consist of a monomer of glucose bound to a monomer of galactose, each of which can be converted to biomass with similar efficiency. Since the galE_KO strain can only metabolize the glucose portion, and the LCTStex_KO therefore has access only to the galactose portion, both strains reach similar density. Additionally, the growth-limiting metabolites (lactose and galactose), as is typical in a chemostat, are in very low concentrations once equilibrium is reached (Fig. 4b).

Procedure 3:

In this protocol we implemented the possibility to simulate periodic changes in the environment. Here we implemented half sine function as a model for the day/night changes in the diel cycle of a photosynthetic organism. More generally, the periodic function can be either a step function, a sine function or a half sine function. We simulate one such experiment with a genome-scale model of Prochlorococcus^110,112, one of the most abundant marine photoautotrophs. The result is shown in Fig. 5. The biomass growth follows this light cycle with periods of growth and resting in a simulation of the day/night periodicity.

Procedure 4:

In this protocol we introduced a method for modeling the secretion and catalytic functions of extracellular enzymes. This new capability of COMETS simulates the costly production and secretion of enzymes by the cell. The secreted enzymes are free to diffuse into the environment. Figure 6 illustrates two cases. In the first case, shown in Fig. 6a, a simple reaction is defined with the form A+B→C. In the second case, shown in Fig. 6b, an enzyme, E, catalyzes the conversion of F→G. Here we used the Scerevisiae_iMM904.mat¹¹³ stoichiometric model. The two panels show the difference of the outcome when an extracellular enzyme is involved in the reaction, and when it is not.

Procedure 5:

COMETS includes the ability to simulate evolutionary processes through the generation of metabolic mutants that have gained or lost novel reactions. In Fig. 7 we illustrate a small example of such a simulation. We start with a clonal population of E. coli and grow them in batch culture in minimal glucose. Over the course of the growth cycle new mutants arise (in this example through loss of function mutations (reaction deletions). Most of these mutants are lost due to drift during passaging, but some are able to increase in frequency due to either drift or a modest reduction in genome-size (and associated genome-size cost).

Procedure 6:

The source and sink dynamics coupled with microbial metabolism should generate gradients in metabolite concentration and biomass (Fig. 8d). In this simulation, we set up source/sink metabolite pools along opposite axes: the “root,” at the left-side, produced nutritious organic acids and removed ammonia, while the “air,” at the top-side, provided a constant concentration of oxygen and nitrogen. Therefore, growth tends to be concentrated in the quadrant closest to the root and the air, as the soil bacterial models require both organic acids and oxygen to grow (Fig. 8d). Furthermore, as time progresses, strong gradients become established due to the interaction between the nutrient source/sink pools and bacterial metabolism.

Procedure 7:

In this simulation we included two biological properties modeled in COMETS: demographic noise and cooperative biomass propagation. We simulated a colony of two metabolically identical strains of E. coli. The morphology of the growth front of a colony of E. coli in this case is dendritic, due to the presence of growth instabilities in the model of cooperative biomass propagation⁹¹. The cooperative propagation is the result of the fact that the diffusivity of the biomass is not a constant, but a linear function of the biomass. The two strains propagate as one compound population as shown on Fig. 9a. The presence of demographic noise however, for certain values of the simulation parameters, will cause the genetic demixing⁹² of the two populations, as shown in Fig. 9b. The reason for this phenomenon is that due to the noise, each of the populations has a finite probability to die off at a given spatial point. In spatially well mixed conditions this would lead to genetic drift and fixation of the entire population to one of the strains. In spatially inhomogeneous conditions, a population fixed locally to one of the strains will continue to propagate as a single strain, if the remixing due to lateral diffusion is low enough so it does not prevent the formation of demixed sectors, as shown in Fig. 9b.

Extended Data

Extended Data Figure 1.

Sensitivity of the simulation results depending on the value of the finite time step. Starting with a simulation identical to the one in Procedure 7, we repeated it with four different values of the time step: a) images of the final colony morphologies, b) plot of the total biomass change with time, illustrating the magnitude of the error due to the finite time step size. The simulation time step size should be chosen such that final simulation result is within the tolerated error.

Extended Data Figure 2.

Sensitivity of the simulation results depending on the value of the finite spatial grid size. Starting with a simulation identical to the one in Procedure 7, we repeated it with four different values of the grid size: a) images of the final colony morphologies, b) plot of the total biomass change with time, illustrating the magnitude of the error due to the finite grid size. The simulation finite spatial grid size should be chosen such that the final simulation result is within the tolerated error.

Extended Data Figure 3.

Sensitivity of the simulation results depending on the value of the amplitude of the demographic noise. Starting with a simulation identical to the one in Procedure 7, we repeated it with two different magnitudes of the noise amplitude $\sigma$: a) images of three replicas of a colony simulation and b) plot of the total biomass change with time of the three replicas simulations with $\sigma =0.01$; c) images of three replicas of a colony simulation and d) plot of the total biomass change with time of the three replicas simulations with $\sigma =0.01$. A finalized result of a simulation study in presence of noise should be averaged over several replicas of the stochastic simulation. The change of the noise amplitude however may have a significant effect of the growth rate and the final morphology. The value of the noise amplitude should be chosen to best represent an experimental result.

Extended Data Figure 4.

We performed a 24hr batch culture run similar to Procedure 1, with either 1, 10 or 100 models (the E. coli model iJO1366 was used in all instances). The settings were identical to Procedure 1 in the main text. We tested three timesteps, 0.01 hr. (circles), 0.1 hr. (triangles) and 0.5 hr. (squares). The x axis shows simulated time (i.e. number of simulation steps × timeStep, in hr); the y axis shows elapsed simulation time (the time taken by the computer to run the program) in min. Simulations were performed in Python using cometspy in a personal laptop running linux (Intel Core i7–10610U CPU at 1.80GHz × 4 cores, 15.3 GiB memory).

Extended Data Figure 5.

The Graphical User Interface of COMETS. COMETS simulations can be started from the GUI by loading a previously prepared layout, models and parameters files. It is meant mostly as a training tool with limited functionality. Future development of COMETS will focus on the development of a comprehensive GUI.

Extended Data Video 1.

Branching colony of two identical strains of E. coli. Procedure 7, growth regime without genetic demixing.

NIHMS1948756-video-Extended_Data_Video_1.gif ^{(16.4MB, gif)}

Extended Data Video 2.

Branching colony of two identical strains of E. coli. Procedure 7, growth regime with genetic demixing.

NIHMS1948756-video-Extended_Data_Video_2.gif ^{(14.9MB, gif)}

Supplementary Material

Supplement Discussions

Supplementary Table 1: Table of COMETS input parameters, with units, default value and a short definition.

Supplementary Discussion 1: Detailed information on the development of the protocol

Supplementary Discussion 2: Software architecture and the basics of using COMETS

Supplementary Discussion 3: Spatial settings in the cometspy toolbox

Supplementary Discussion 4: Detailed structure of the Output Files

Supplementary Discussion 5: Setting the environmental variables in Mac OS X

Data availability

The COMETS Protocols GitHub repository (https://github.com/segrelab/COMETS_Protocols) contains all input files and jupyter notebooks from which one can reproduce the results presented in this protocol. The data is distributed under the Creative Commons CC0 1.0 Universal license.