MetaNO: How to Transfer Your Knowledge on Learning Hidden Physics

Abstract

Gradient-based meta-learning methods have primarily been applied to classical machine learning tasks such as image classification. Recently, PDE-solving deep learning methods, such as neural operators, are starting to make an important impact on learning and predicting the response of a complex physical system directly from observational data. Taking the material modeling problems for example, the neural operator approach learns a surrogate mapping from the loading field to the corresponding material response field, which can be seen as learning the solution operator of a hidden PDE. The microstructure and mechanical parameters of each material specimen correspond to the (possibly heterogeneous) parameter field in this hidden PDE. Due to the limitation on experimental measurement techniques, the data acquisition for each material specimen is commonly challenging and costly. This fact calls for the utilization and transfer of existing knowledge to new and unseen material specimens, which corresponds to sampling efficient learning of the solution operator of a hidden PDE with a different parameter field. Herein, we propose a novel meta-learning approach for neural operators, which can be seen as transferring the knowledge of solution operators between governing (unknown) PDEs with varying parameter fields. Our approach is a provably universal solution operator for multiple PDE solving tasks, with a key theoretical observation that underlying parameter fields can be captured in the first layer of neural operator models, in contrast to typical final-layer transfer in existing meta-learning methods. As applications, we demonstrate the efficacy of our proposed approach on PDE-based datasets and a real-world material modeling problem, illustrating that our method can handle complex and nonlinear physical response learning tasks while greatly improving the sampling efficiency in unseen tasks.

1. Introduction

Few-shot learning is an important problem in machine learning, where new tasks are learned with a very limited number of labelled datapoints [1]. In recent years, significant progress has been made on few-shot learning using meta-learning approaches [2–12]. Broadly speaking, given a family of tasks, some of which are used for training and others for testing, meta-learning approaches aim to learn a shared multi-task representation that can generalize across the different training tasks, and result in fast adaptation to new and unseen testing tasks. Meta-learning learning algorithms have been successfully applied to conventional machine learning problems such as image classification, function regression, and reinforcement learning, but studies on few-shot learning approaches for complex physical system modeling problems have been limited. The call of developing a few-shot learning approach for complex physical system modeling problems, such as to learn the material response model from experimental measurements, is just as acute, while the typical understanding of how multi-task learning should be applied on this scenario is still nascent.

As a motivating example, we consider the scenario of new material discovery in the lab environment, where the material model is built based on experimental measurements of its responses subject to different loadings. Since the physical properties (such as the mechanical and structural parameters) in different material specimens vary, the model learnt from experimental measurements on one specimen would have large generalization errors on other specimens. As a result, the data-driven model has to be trained repeatedly with a large number of material specimens, which makes the learning process inefficient. Furthermore, experimental measurement acquisition of these specimens is often challenging and expensive. In some problems, a large amount of measurements are not even feasible. For example, in the design and testing of biosynthetic tissues, performing repeated loading would potentially induce the cross-linking and permanent set phenomenon, which notoriously alter the tissue durability [13]. As a result, it is critical to learn the physical response model of a new specimen with sample size as small as possible. Furthermore, since many characterization methods to obtain underlying material mechanistic and structural properties would require the use of destructive methods [14, 15], in practice many physical properties are not measured and can only be treated as hidden and unknown variables. Hence, we likely only have limited access to the measurements on the complex system responses caused by the change of these physical properties.

Supervised operator learning methods are typically used to address this class of problems. They take a number of observations on the loading field as input, and try to predict the corresponding physical system response field as output, corresponding to one underlying PDE (as one task). Herein, we consider the meta-learning of multiple complex physical systems (as tasks), such that all these tasks are governed by a common PDE with different (hidden) physical property or parameter fields. Formally, assume that we have a distribution $p\left(𝒯\right)$ over tasks, each task ${𝒯}^{\eta }~p\left(𝒯\right)$ corresponds to a hidden physical property field $b^{\eta }\left(x\right)\in ℬ\left({ℝ}^{d_b}\right)$ that contains the task-specific mechanistic and structural information in our material modeling example. On task ${𝒯}^{\eta }$, we have a number of observations on the loading field $g_i^{\eta }\left(x\right)\in 𝒜\left({ℝ}^{d_g}\right)$ and the corresponding physical system response field $u_i^{\eta }\left(x\right)\in 𝒰\left({ℝ}^{d_u}\right)$ according to a hidden parameter field $b^{\eta }\left(x\right)$. Here, $i$ is the sample index, $ℬ,𝒜$ and $𝒰$ are Banach spaces of function taking values in ${ℝ}^{d_b},{ℝ}^{d_g}$ and ${ℝ}^{d_u}$, respectively. For task ${𝒯}^{\eta }$, our modeling goal is to learn the solution operator ${𝒢}_{b^{\eta }}^{\eta }:𝒜\to 𝒰$, such that the learnt model can predict the corresponding physical response field $u\left(x\right)$ for any loading field $g\left(x\right)$¹. Without transfer learning, one needs to learn a surrogate solution operator for each task only based on the data pairs on this task, and repeat the training for every task. The learning procedure would require a relatively large amount of observation pairs and training time for each task. Therefore, this physical-based modeling scenario raises a key question: Given data from a number of parametric PDE solving (training) tasks with different unknown parameters, how can one efficiently learn an accurate surrogate solution operator for a test task with new and unknown parameters, with few data on this task² ?

To address this question, we introduce MetaNO, a novel meta-learning approach for transferring knowledge between neural operators, which can be seen as transferring the knowledge of solution operators between governing (potentially unknown) PDEs with varying hidden parameter fields. Our main contributions are:

• MetaNO is the first neural-operator-based meta-learning approach for multiple tasks, which not only preserves the generalizability to different resolutions and input functions from the integral neural operator architecture, but also improves sampling efficiency on new tasks – for comparable accuracy, MetaNO saves the number of measurements required by ~90%.

• With rigorous operator approximation analysis, we made the key observation that the hidden parameter field can be captured by adapting the first layer of the neural operator model. Therefore, our MetaNO is substantially different from existed popular meta-learning approaches [5, 10], since the later typically rely on the adaptation of their last layers [12]. By construction, MetaNO serves as a provably universal solution operator for multiple PDE solving tasks.

• On synthetic, benchmark, and real-world biological tissue datasets, the proposed method consistently outperforms existing non-meta transfer-learning baselines and other gradient-based meta-learning methods.

2. Background and Related Work

2.1. Hidden Physics Learning with Neural Networks

For many decades, physics-based PDEs have been commonly employed for predicting and monitoring complex system responses. Then traditional numerical methods were developed to solve these PDEs and provide predictions for desired system responses. However, three fundamental challenges usually present. First, the choice of governing PDE laws is often determined a priori and free parameters are often tuned to obtain agreement with experimental data, which makes the rigorous calibration and validation process challenging. Second, traditional numerical methods are solved for specific boundary and initial conditions, as well as loading or source terms. Therefore, they are not generalizable for other operating conditions and hence not effective for real-time prediction. Third, complex PDE systems such as turbulence flows and heterogeneous materials modeling problems usually require a very fine discretization, and are therefore very time-consuming for traditional solvers.

To provide an efficient surrogate model for physical responses, machine learning methods may hold the key. Recently, there has been significant progress in the development of deep neural networks (NNs) for learning the hidden physics of a complex system [17–25]. Among these methods, the neural operators show particular promises in resolving the above challenges, which aim to learn mappings between inputs of a dynamical system and its state, so that the network can serve as a surrogate for a solution operator [26–34].

Comparing with classical NNs, most notable advantages of neural operators are resolution independence and generalizability to different input instances. Moreover, comparing with the classical PDE modeling approaches, neural operators require only data with no knowledge of the underlying PDE. All these advantages make neural operators promising tools to PDE learning tasks. Examples include modeling the unknown physics law of real-world problems [35, 36] and providing efficient solution operator for PDEs [26–28, 37, 38]. On the other hand, data in scientific applications are often scarce and incomplete. Utilization of other relevant data sources could alleviate such a problem, yet no existing work have addressed the transferability of neural operators. Through the meta-learning techniques, our work fulfills the demand of such a transfer setting, with the same type of PDE system but different (hidden) physical properties.

2.2. Base Model: Integral Neural Operators

We briefly introduce the integral neural operator model, which will be utilized as the base model of this work. The integral neural operators, first proposed in [26] and further developed in [27–29, 39] comprises of three building blocks. First, the input function, $g\left(x\right)\in 𝒜$, is lifted to a higher dimensional representation via $h\left(x,0\right)=𝒫\left[g\right]\left(x\right):=P\left(x\right){[x,g\left(x\right)]}^T+p\left(x\right).P\left(x\right)\in {ℝ}^{\left(s+d_g\right)\times d_h}$ and $p\left(x\right)\in {ℝ}^{d_h}$ define an affine pointwise mapping, which are often taken as constant parameters, i.e., $P\left(x\right)\equiv P$ and $p\left(x\right)\equiv p$. Then, the feature vector function $h\left(x,0\right)$ goes through an iterative layer block where the layer update is defined via the action of the sum of a local linear operator, a nonlocal integral kernel operator, and a bias function: $h\left(\cdot ,l+1\right)={𝒥}_{l+1}\left[h\left(\cdot ,l\right)\right]$. Here, $h\left(\cdot ,l\right),l\in \left\{0,\cdots ,L\right\}$, is a sequence of functions representing values of the network at each hidden layer, taking values in ${ℝ}^{d_h}.{𝒥}_1,\cdots ,{𝒥}_L$ are nonlinear operator layers. In this work, we employ the implicit Fourier neural operator (IFNO) as the base model³ and take the iterative layers as ${𝒥}_1=\cdots ={𝒥}_L=𝒥$, where

$$h\left(x,l+1\right)=𝒥\left[h\left(x,l\right)\right]:=h\left(x,l\right)+\frac{1}{L}\sigma \left(Wh\left(x,l\right)+{ℱ}^{-1}\left[ℱ\right[\kappa \left(\cdot ;v\right)\left]\cdot ℱ\right[h\left(\cdot ,l\right)]]\left(x\right)+c\left(x\right)\right).$$ (2.1)

$ℱ$ and ${ℱ}^{-1}$ denote the Fourier transform and its inverse, respectively. $c\in {ℝ}^{d_h}$ defines a constant bias, $W\in {ℝ}^{d_h\times d_h}$ is the weight matrix, and $ℱ\left[\kappa \left(\cdot ;v\right)\right]:=R$ is a circulant matrix that depends on the convolution kernel $\kappa .\sigma$ is an activation function, which is often taken to be the popular rectified linear unit (ReLU) function. Finally, the output $\mathit{u}(\cdot )\in 𝒰$ is obtained through a projection layer, by mapping the last hidden layer representation $h\left(\cdot ,L\right)$ onto $𝒰$ as: $u\left(x\right)=𝒬\left[h\left(\cdot ,L\right)\right]\left(x\right):=Q_2\left(x\right)\sigma \left(Q_{1}h\left(x,L\right)+q_1\left(x\right)\right)+q_2\left(x\right).Q_1\left(x\right)\in {ℝ}^{d_Q\times d_h},Q_2\left(x\right)\in {ℝ}^{d_u\times d_Q},q_1\left(x\right)\in {ℝ}^{d_Q}$ and $q_2\left(x\right)\in {ℝ}^{d_u}$ are appropriately sized matrices and vectors that are part of the parameter set that we aim to learn, which are often taken as constant parameters and will be denoted as $Q_1,Q_2,q_1$ and $q_2$, respectively. In the following, we denote the set of trainable parameters in the lifting layer as ${\theta }_P$, the set from the iterative layer block as ${\theta }_I$, and the set in the projection layer as ${\theta }_Q$.

The neural operator can be employed to learn an approximation for the solution operator, $𝒢$. Given $𝒟:={\left\{\left(g_i,u_i\right)\right\}}_{i=1}^N$, a labelled (context) set of observations, where the input $\left\{g_i\right\}\subset 𝒜$ is a set of independent and identically distributed (i.i.d.) random fields from a known probability distribution $\mu$ on $𝒜$, and $u_i\left(x\right)\in 𝒰$ is the observed but possibly noisy corresponding solution. Let $\Omega \subset {ℝ}^s$ be the domain of interest, we assume that all observations can be modeled with a parametric PDE form:

$${𝒦}_{b\left(x\right)}\left[u_i\right]\left(x\right)=g_i\left(x\right),x\in \Omega .$$ (2.2)

${𝒦}_b$ is the operator representing the possibly unknown governing law, e.g., balance laws. Then, the system response can be learnt by constructing a surrogate solution operator of (2.2): $\widetilde{𝒢}\left[g;\theta \right]\left(x\right):={𝒬}_{{\theta }_Q}\circ {\left({𝒥}_{{\theta }_I}\right)}^L\circ {𝒫}_{{\theta }_P}\left[g\right]\left(x\right)\approx u\left(x\right)$, where parameter set $\theta =\left[{\theta }_P,{\theta }_I,{\theta }_Q\right]$ is obtained by solving the optimization problem:

$$\underset{\theta \in \Theta }{\text{min }}{ℒ}_{𝒟}\left(\theta \right):=\underset{\theta \in \Theta }{\text{min }}\sum _{i=1}^N\left[C\left(\widetilde{𝒢}\left[g_i;\theta \right],u_i\right)\right].$$ (2.3)

Here $C$ denotes a properly defined cost functional which is often taken as the relative mean square error.

2.3. Gradient-Based Meta-Learning Methods

Traditionally, machine learning models are designed to address one single task by learning from the dataset corresponding to such a task. Hence, its efficacy relies on the quality and abundance of available data. To improve the learning efficacy in the small data regime, a significant body of work has tackled the challenge of few-shot learning using transfer-learning or meta-learning approaches, with the basic idea of utilizing prior knowledge gained from related (source) tasks to improve the learning performance on the target task. Among these two types of approaches, the basic idea of transfer-learning is to train a model from the source task and then refine the pre-trained model in the target task [40]. In comparison, meta-learning approaches aim to learn a generalizable representations that shared across the different training tasks, which can accelerate learning of test tasks [5, 41]. One of highly successful meta-learning algorithms is Model Agnostic Meta-Learning (MAML) [5], which led to the development of a series of related gradient-based meta-learning (GBML) methods [7, 9, 10, 42]. Almost-No-Inner-Loop algorithm (ANIL) [10] modifies MAML by freezing the final layer representation during local adaptation. Recently, theoretical analysis [12] found that the driving force causing MAML and ANIL to recover the general representation is the adaptation of the final layer of their models, which harnesses the underlying task diversity to improve the representation in all directions of interest.

Beyond applications such as image classification and reinforcement learning, a few approaches have studied hidden-physics learning under meta [43–46] or even transfer setting [47, 48]. Among these meta-learning works, [43, 44] are designed for specific physical applications, while [45, 46] focus on on dynamics forecasting by learning the temporal evolution information directly [45] or learning time-invariant features [46]. Hence, none of these works have provided a generic approach nor theoretical understanding on how to transfer the multi-task knowledge between a series of complex physical systems, such that all these tasks are governed by a common parametric PDE with different physical parameters.

3. Meta-Learnt Neural Operator

To transfer the multi-task knowledge between a series of complex systems governed by different hidden physical parameters, we proposed to leverage the integral neural operator with a meta-learning setting. Before elaborating our novel meta-learnt neural operator architecture, MetaNO, we formally state the transfer-learning problem setting for PDE with different parameters.

Assume that we have a set of training tasks $\left\{{𝒯}^{\eta }\right\}$ such that ${𝒯}^{\eta }~p\left(𝒯\right)$, and for each training task we have a set of observations of loading field/respond field data pairs ${𝒟}^{\eta }:={\left\{\left(g_i^{\eta }\left(x\right),u_i^{\eta }\left(x\right)\right)\right\}}_{i=1}^{N^{\eta }}$. Each task can be modeled with a parametric PDE form

$${𝒦}_{b^{\eta }\left(x\right)}\left[u_i^{\eta }\right]\left(x\right)=g_i^{\eta }\left(x\right),x\in \Omega ,$$ (3.1)

where $b^{\eta }\left(x\right)$ is the hidden task-specific physical parameter field for the common governing law. Given a new and unseen test task, ${𝒯}^{\text{test }}$, and a (usually small) context set of labelled samples ${𝒟}^{\text{test }}:={\left\{\left(g_i^{\text{test }}\left(x\right),u_i^{\text{test }}\left(x\right)\right)\right\}}_{i=1}^{N^{\text{test }}}$ on it, our goal is to obtain the approximated solution operator model on the test task as $\widetilde{𝒢}\left[g;{\theta }^{\text{test }}\right]$. To provide a quantitative metric of the performance for each method, we reserve a separate set of labelled samples on the test task as the target set, and measure averaged relative errors of $u$ on this set. In the few-shot learning context, we are particularly interested in the small-sample scenario where $N^{\text{test }}\ll N^{\eta }$.

3.1. A Novel Meta-Learnt Neural Operator Architecture

We now propose MetaNO, which applies task-wise adaptation only to the first layer, i.e., the lifting layer, with the full algorithm outlined in Algorithm 1. We point out that MetaNO is substantially different from existed popular meta-learning approaches such as MAML and ANIL, since the later rely on the adaptation of their last layer, as shown in [12]. This property makes MetaNO more suitable for PDE solving tasks as will be discussed in theoretical analysis below and confirmed in empirical evaluations of Section 4.

Algorithm 1.

MetaNO

Meta-Train Phase:

Input: a batch ${\left\{{𝒯}^{\eta }\right\}}_{\eta =1}^H$ of training tasks and labelled data pairs ${𝒟}^{\eta }:={\left\{\left(g_i^{\eta }\left(x\right),u_i^{\eta }\left(x\right)\right)\right\}}_{i=1}^{N^{\eta }}$ on each task.

Output: common parameters ${\theta }_I^{*}$ and ${\theta }_Q^{*}$ across all tasks.

1. Initialize ${\theta }_I,{\theta }_Q$, and ${\left\{{\theta }_P^{\eta }\right\}}_{\eta =1}^H$.

2. Solve for $\left[{\left\{{\theta }_P^{\eta ,*}\right\}}_{\eta =1}^H,{\theta }_I^{*},{\theta }_Q^{*}\right]$ from the optimization problem in (3.2).

Meta-Test Phase:

Input: a test task ${𝒯}^{\text{test }}$ and few labelled data pairs ${𝒟}^{\text{test }}:={\left\{\left(g_i^{\text{test }}\left(x\right),u_i^{\text{test }}\left(x\right)\right)\right\}}_{i=1}^{N^{\text{test }}}$ on it.

Output: the task-wise parameter ${\theta }_P^{\text{test,* }}$ and the corresponding surrogate PDE solution operator $\widetilde{𝒢}\left[g;\left[{\theta }_P^{\text{test}*,},{\theta }_I^{*},{\theta }_Q^{*}\right]\right]\left(x\right)$ for the test task.

3. Solve for the lift layer parameter ${\theta }_P^{\text{test},*}$ from the optimization problem in (3.3).

4. (For cases with large $N^{\mathit{\text{test }}}$ and/or small $N^{\eta }$), fine tune all parameters on the test task.

Similar as in other meta-learning approaches [49–52], the MetaNO algorithm consists of two phases: 1) a meta-train phase which learns shared iterative layers parameters ${\theta }_I$ and projection layer parameters ${\theta }_P$ from training tasks; 2) a meta-test phase which transfers the learned knowledge and rapidly learning surrogate solution operators for unseen test tasks with unknown physical parameter field, where only a few labelled samples are provided. In the meta-train phase, a batch ${\left\{{𝒯}^{\eta }\right\}}_{\eta =1}^H$ of $H$ tasks is drawn from the training tasks set, with a context set of $N^{\eta }$ numbers of labelled loading field/response field data pairs, ${𝒟}^{\eta }:={\left\{\left(g_i^{\eta }\left(x\right),u_i^{\eta }\left(x\right)\right)\right\}}_{i=1}^{N^{\eta }}$, provided on each task. Then, we seek the common iterative $\left({\theta }_I\right)$ and projection $\left({\theta }_Q\right)$ parameters, and the task-wise lifting parameters ${\theta }_P^{\eta }$ by solving the optimization problem:

$$\left[{\left\{{\theta }_P^{\eta ,*}\right\}}_{\eta =1}^H,{\theta }_I^{*},{\theta }_Q^{*}\right]=\underset{\left\{{\left\{{\theta }_P^{\eta }\right\}}_{\eta =1}^H,{\theta }_I,{\theta }_Q\right\}}{\text{argmin}}\sum _{\eta =1}^H{ℒ}_{{𝒟}^{\eta }}\left(\left[{\theta }_P^{\eta },{\theta }_I,{\theta }_Q\right]\right).$$ (3.2)

Then, in the meta-test phase, we adapt the knowledge to a new and unseen test task ${𝒯}^{\text{test }}$, with limited data on the context set ${𝒟}^{\text{test }}:={\left\{\left(g_i^{\text{test }}\left(x\right),u_i^{\text{test }}\left(x\right)\right)\right\}}_{i=1}^{N^{\text{test }}}$ on this task. In particular, we fix the common parameters ${\theta }_I^{*}$ and ${\theta }_Q^{*}$, then solve for the task-wise parameter ${\theta }_P^{\text{test }}$ via:

$${\theta }_P^{\text{test },*}=\underset{{\theta }_P^{\text{test }}}{\text{argmin }}{ℒ}_{{𝒟}^{\text{test }}}\left(\left[{\theta }_P^{\text{test }},{\theta }_I^{*},{\theta }_Q^{*}\right]\right).$$ (3.3)

One can then fine tune all test task parameters $\left[{\theta }_P^{\text{test }},{\theta }_I,{\theta }_Q\right]$ for further improvements. Finally, the surrogate PDE solution operator on the test task is obtained as:

$$\widetilde{𝒢}\left[g;\left[{\theta }_P^{\text{test },*},{\theta }_I^{*},{\theta }_Q^{*}\right]\right]\left(x\right):={𝒬}_{{\theta }_Q^{*}}\circ {\left({𝒥}_{{\theta }_I^{*}}\right)}^L\circ {𝒫}_{{\theta }_P^{\text{test },*}}\left[g\right]\left(x\right).$$

and will be evaluated on a reserved target data set on the test task.

3.2. Universal Solution Operator

To see the inspiration of the proposed architecture, without loss of generality, we assume that the underlying task parameter field $b^{\eta }\left(x\right)$, modeling the physical property field, is normalized and satisfying ${\Vert b^{\eta }\left(x\right)-\overline{b}\left(x\right)\Vert }_{L^2\left(\text{Ω}\right)}\le 1$ for all $\eta \in \left\{1,\cdots ,H\right\}$, where $\overline{b}:={\mathbb{E}}_{{𝒯}^{\eta }~p\left(𝒯\right)}\left[b^{\eta }\right]$. Denoting ${ℱ}_u\left[b\right]:={𝒦}_b\left[u\right]$ as a function from physical parameter fields $ℬ$ to loading fields $𝒜$, we take the Fréchet derivative of $ℱ$ with respect to $b-\overline{b}$ and obtain:

$${𝒦}_{b^{\eta }}\left[u\right]={ℱ}_u\left[\overline{b}\left]+D{ℱ}_u\right[\overline{b}\right]\left(b^{\eta }-\overline{b}\right)+o\left({\Vert b^{\eta }-\overline{b}\Vert }_{L^2\left(\Omega \right)}\right).$$

Substituting the above formulation into (3.1) yields:

$${ℱ}_{u_i^{\eta }}\left[\overline{b}\right]+D{ℱ}_{u_i^{\eta }}\left[\overline{b}\right]\left(b^{\eta }-\overline{b}\right)\approx g_i^{\eta }.$$

Denoting $F_1\left[b^{\eta }\right]:=\left[1,b^{\eta }-\overline{b}\right]$ and $F_2\left[u_i^{\eta }\right]:=\left[{ℱ}_{u_i^{\eta }}\left[\overline{b}\right],D{ℱ}_{u_i^{\eta }}\left[\overline{b}\right]\right]$, we can reformulate (3.1) into a more generic form:

$$F_1\left[b^{\eta }\right]\left(x\right)\cdot F_2\left[u_i^{\eta }\right]\left(x\right)=g_i^{\eta }\left(x\right),x\in \Omega .$$

Note that this parametric PDE form is very general and applicable to many science and engineering applications – besides our motivating example on material modeling, other examples include the monitoring of tissue degeneration problems [13], the detection of subsurface flows [53], the nondestructive inspection in aviation [54], and the prediction of concrete structures deterioration [55], etc.

In the following, we show that MetaNOs are universal solution operators for the multi-task PDE solving problem in (3.4), in the sense that they can approximate a fixed point method to a desired accuracy. For simplicity, we consider a $1D$ domain $\Omega \subset ℝ$, and scalar-valued functions $F_1\left[b^{\eta }\right],F_2\left[u_i^{\eta }\right]$. These functions are assumed to be sufficiently smooth and measured at uniformly distributed nodes $\chi :=\left\{x_1,x_2,\dots ,x_M\right\}$, with $F_1\left[b^{\eta }\right]\left(x_j\right)\ne 0$ for all $\eta$ and $j$. Then, (3.4) can be formulated as an implicit system of equations:

$$\mathscr{H}\left(U_i^{\eta ,*};{\tilde{G}}_i^{\eta }\right):=\left[\begin{array}{c}{F}_2\left[u_i^{\eta }\right]\left(x_1\right)-g_i^{\eta }\left(x_1\right)/F_1\left[b^{\eta }\right]\left(x_1\right)\\ ⋮\\ F_2\left[u_i^{\eta }\right]\left(x_M\right)-g_i^{\eta }\left(x_M\right)/F_1\left[b^{\eta }\right]\left(x_M\right)\end{array}\right]=\mathbf{0},$$ (3.5)

where $U_i^{\eta ,*}:=\left[u_i^{\eta }\left(x_1\right),\dots ,u_i^{\eta }\left(x_M\right)\right]$ is the solution we seek, ${\tilde{G}}_i^{\eta }:=\left[g_i^{\eta }\left(x_1\right)/F_1\left[b^{\eta }\right]\left(x_1\right),\dots ,g_i^{\eta }\left(x_M\right)/F_1\left[b^{\eta }\right]\left(x_M\right)\right]$ is the reparameterized loading vector, and $G_i^{\eta }:=\left[g_i^{\eta }\left(x_1\right),g_i^{\eta }\left(x_2\right),\dots ,g_i^{\eta }\left(x_M\right)\right]$ is the original loading vector. Here, we notice that all task-specific information is encoded in ${\tilde{G}}_i^{\eta }$ and can be captured in the lifting layer parameter. Therefore, when seeing (3.5) as an implicit problem of $U_i^{\eta ,*}$ and ${\tilde{G}}_i^{\eta }$, it is actually independent of the task parameter field $b^{\eta }$, i.e., this problem is task-independent. In the following, we refer to (3.5) without the task index, as $\mathscr{H}\left(U^{*};\tilde{G}\right)$, for notation simplicity.

To solve for $U^{*}$ from the nonlinear system $\mathscr{H}\left(U^{*};\tilde{G}\right)=0$, a popular approach would be to use fixed-point iteration methods such as the Newton-Raphson method. With an initial guess of the solution (denoted as $U^0$), the process is repeated to produce successively better approximations to the roots of (3.5), from the solution of iteration $l$ (denoted as $U^l)$ to that of $l+1$ (denoted as $U^{l+1})$ as:

$$U^{l+1}=U^l-{\left(\nabla \mathscr{H}\left(U^l;\tilde{G}\right)\right)}^{-1}\mathscr{H}\left(U^l;\tilde{G}\right):=U^l+ℛ\left(U^l,\tilde{G}\right),$$ (3.6)

until a sufficiently precise value is reached. In the following, we show that as long as Assumptions 1 and 2 hold, i.e., there exists a converging fixed point method, then MetaNO can be seen as an resemblance of the fixed point method in (3.6) and hence acts as an universal approximator of the solution operator for (3.4).

Assumption 1. There exists a fixed point equation, $U=U+ℛ\left(U,\tilde{G}\right)$ for the implicit of problem (3.5), such that $ℛ:{ℝ}^{2M}\mapsto {ℝ}^M$ is a continuous function satisfying $ℛ\left(U,\tilde{G}\right)=0$ and $\parallel ℛ\left(\hat{U},\tilde{G}\right)-ℛ\left(\tilde{U},\tilde{G}\right){\parallel }_{l^2\left({ℝ}^M\right)}\le m\parallel \hat{U}-\tilde{U}{\parallel }_{l^2\left({ℝ}^M\right)}$ for any two vectors $\hat{U},\tilde{U}\in {ℝ}^M$. Here, $m\ge 0$ is a constant independent of $\tilde{G}$.

Assumption 2. With the initial guess $U^0:=\left[x_1,\cdots ,x_M\right]$, the fixed-point iteration $U^{l+1}=U^l+ℛ\left(U^l,\tilde{G}\right)$ $\left(l=0,1,\dots \right)$ converges, i.e., for any given $\epsilon >0$, there exists an integer $L$ such that

$${\Vert U^l-U^{*}\Vert }_{l^2\left({ℝ}^M\right)}\le \epsilon ,\forall l>L,$$

for all possible input instances $\tilde{G}\in {ℝ}^M$ and their corresponding solutions $U^{*}$.

Intuitively, Assumptions 1 and 2 ensure the hidden PDEs to be numerically solvable with a converging iterative solver, which is a typical required condition of numerical PDE solving problems. Then, we have our universal approximation theorem as below. The main result of this theorem is to show that for any desired accuracy $\epsilon >0$, one can find a sufficiently large $L>0$ and sets of parameters ${\theta }^{\eta }=\left\{{\theta }_P^{\eta },{\theta }_I,{\theta }_Q\right\}$, such that the resultant MetaNO model acts as a fixed point method with the desired prediction for all tasks and samples.

Theorem 1 (Universal approximation). Given Assumptions 1–2, let the activation function $\sigma$ for all iterative kernel integration layers be the ReLU function, and the activation function in the projection layer be the identity function. Then for any $\epsilon >0$, there exist sufficiently large layer number $L>0$ and feature dimension number $d_h>0$, such that one can find a parameter set for the multi-task problem, ${\theta }^{\eta }=\left[{\theta }_P^{\eta },{\theta }_I,{\theta }_Q\right]$, such that the corresponding MetaNO model satisfies

$$\Vert {𝒬}_{{\theta }_Q}\circ {\left({𝒥}_{{\theta }_I}\right)}^L\circ {𝒫}_{{\theta }_P^{\eta }}\left({\left[U^0,G^{\eta }\right]}^{\text{T}}\right)-U^{\eta ,\text{*}}\Vert \le \epsilon ,$$

for all loading instance ${\mathit{G}}^{\eta }\in {\mathbb{R}}^M$ and tasks.

We now provide the detailed proof for Theorem 1, based on Assumptions 1 and 2. Intuitively, these assumptions mean the underlying implicit problem is solvable with a converging fixed point method. This condition is a basic requirement by numerical PDEs, and it generally holds true in many applications governed by nonlinear and complex PDEs, such as in our three experiments.

Here, we prove that the MetaNO is universal, i.e., given a fixed point method satisfying Assumptions 1 and 2, one can find parameter sets ${\theta }^{\eta }$ whose output approximates ${\mathit{U}}^{\eta ,*}$ to a desired accuracy, $\epsilon >0$, for all $\eta =1,\cdots ,H$ tasks. For the task-wise parameters, with a slight abuse of notation, we denote $P^{\eta }\in {ℝ}^{d_{h}M\times \left(d_g+s\right)M}$ as the collection of the pointwise weight matrices at each discretization point in $\chi$ for the $\eta$-th task, and ${\mathit{p}}^{\eta }\in {\mathbb{R}}^{d_{h}M}$ for the bias in the lifting layer. Then, for the parameters shared among all tasks, in the iterative layer we denote $C=\left[c\left(x_1\right),\cdots ,c\left(x_M\right)\right]\in {ℝ}^{d_{h}M}$ as the collection of pointwise bias vectors $c\left(x_i\right),W\in {ℝ}^{d_h\times d_h}$ for the local linear transformation, and $R=ℱ\left[\kappa \right(\cdot ;\mathit{v}\left)\right]\in {\mathbb{C}}^{d_h\times d_h\times M}\in {\mathbb{C}}^{d_h\times d_h\times M}$ for the Fourier coefficients of the kernel $\kappa$. For simplicity, here we have assumed that the Fourier coefficient is not truncated, and all available frequencies are used. Then, for the projection layer we seek $Q_1\in {\mathbb{R}}^{d_{Q}M\times d_{h}M}$, $Q_2\in {\mathbb{R}}^{d_{u}M\times d_{Q}M},{\mathit{q}}_1\in {\mathbb{R}}^{d_{Q}M}$ and ${\mathit{q}}_2\in {\mathbb{R}}^{d_{u}M}$. For the simplicity of notation, in this section we organize the feature vector $\mathit{H}\in {\mathbb{R}}^{d_{h}M}$ in a way such that the components corresponding to each discretization point are adjacent, i.e., $H=\left[H\left(x_1\right),\cdots ,H\left(x_M\right)\right]$ and $H\left(x_i\right)\in {ℝ}^{d_h}$.

We point out that under this circumstance, the (discretized) iterative layer can be written as

$$\begin{gathered} 𝒥\left[H\left(l\right)\right]=H\left(l\right)+\frac{1}{L}\sigma \left(\tilde{W}H\left(l\right)+\text{Re}\left({ℱ}_{\Delta x}^{-1}\left(R\cdot {ℱ}_{\Delta x}\left(H\left(l\right)\right)\right)\right)+C\right) \\ =H\left(l\right)+\frac{1}{L}\sigma \left(VH\left(l\right)+C\right), \end{gathered}$$

with

$$V:=\text{Re }\left[\begin{array}{cccc}\sum _{n=0}^{M-1}{R}_{n+1}+W& \sum _{n=0}^{M-1}{R}_{n+1}\text{exp}\left(\frac{2i\pi \Delta xn}{M}\right)& \cdots & \sum _{n=0}^{M-1}{R}_{n+1}\text{exp}\left(\frac{2i\pi \left(M-1\right)\Delta xn}{M}\right)\\ \sum _{n=0}^{M-1}{R}_{n+1}\text{exp}\left(\frac{2i\pi \Delta xn}{M}\right)& \sum _{n=0}^{M-1}{R}_{n+1}+W& \cdots & \sum _{n=0}^{M-1}{R}_{n+1}\text{exp}\left(\frac{2i\pi \left(M-2\right)\Delta xn}{M}\right)\\ ⋮& ⋮& \ddots & ⋮\\ \sum _{n=0}^{M-1}{R}_{n+1}\text{exp}\left(\frac{2i\pi \left(M-1\right)\Delta xn}{M}\right)& \sum _{n=0}^{M-1}{R}_{n+1}\text{exp}\left(\frac{2i\pi \left(M-2\right)\Delta xn}{M}\right)& \cdots & \sum _{n=0}^{M-1}{R}_{n+1}+W\end{array}\right].$$

Here, $R\in {ℂ}^{M\times d_h\times d_h}$ with $R_i\in {ℂ}^{d_h\times d_h}$ being the component associated with each discretization point $x_i\in \chi ,V\in {ℝ}^{d_{h}M\times d_{h}M},C\in {ℝ}^{d_{h}M},\tilde{W}:=W\oplus W\oplus \cdots \oplus W$ is a $d_{h}M\times d_{h}M$ block diagonal matrix formed by $W\in {ℝ}^{d_h\times d_h},{ℱ}_{\Delta x}$ and ${ℱ}_{\Delta x}^{-1}$ denote the discrete Fourier transform and its inverse, respectively. By further taking $R_2=\cdots =R_M=W=0$, a $d_h\times d_h$ matrix with all its elements being zero, it suffices to show the universal approximation property for an iterative layer as follows:

$$𝒥\left(H\left(l\right)\right):=H\left(l\right)+\frac{1}{L}\sigma \left(\tilde{V}H\left(l\right)+C\right)$$

where $\tilde{V}:=1_{\left[M,M\right]}\otimes V$ with $V\in {ℝ}^{d_h\times d_h}$ and $1_{\left[m,n\right]}$ being an $m$ by $n$ all-ones matrix.

For the proof of this main theorem, we need the following approximation property of a shallow neural network, with its detailed proof provided in [39]:

Lemma 1. Given a continuous function $𝒯:{ℝ}^{2M}\mapsto {ℝ}^M$, and a non-polynomial and continuous activation function $\sigma$, for any constant $\hat{\epsilon }>0$ there exists a shallow neural network model $\widehat{𝒯}:=S\sigma \left(BX+A\right)$ such that

$${\Vert 𝒯\left(X\right)-\stackrel{\text{ˆ}}{𝒯}\left(X\right)\Vert }_{l^2\left({ℝ}^M\right)}\le \hat{\epsilon },\forall X\in {ℝ}^{2M},$$

for sufficiently large feature dimension $\hat{d}>0$. Here, $S\in {ℝ}^{M\times \hat{d}M},B\in {ℝ}^{\hat{d}M\times 2M}$, and $A\in {ℝ}^{\hat{d}M}$ are matrices/vectors which are independent of $X$.

We now proceed to the proof of Theorem 1:

Proof. Since all $U^{\eta ,*}$ satisfies Assumptions 1–2, for any $\epsilon >0$, we first pick a sufficiently large integer $L$ such that the $L$-th layer iteration result of this fixed point formulation satisfies ${\Vert U^L-U^{\eta ,*}\Vert }_{l^2\left({ℝ}^M\right)}\le \frac{\epsilon }{2}$ for all tasks. By taking $\hat{\epsilon }:=\frac{m\epsilon }{2{(1+m)}^L}$ in Lemma 1, there exists a sufficiently large feature dimension $\hat{d}$ and one can find $S\in {ℝ}^{M\times \hat{d}M},B\in {ℝ}^{\hat{d}M\times 2M}$, and $A\in {ℝ}^{\hat{d}M}$, such that $\widehat{ℛ}\left(U^{\eta },{\tilde{G}}^{\eta }\right):=S\sigma \left(B{\left[U^{\eta },{\tilde{G}}^{\eta }\right]}^{\text{T}}+A\right)$ satisfies

$${\Vert ℛ\left(U^{\eta },{\tilde{G}}^{\eta }\right)-\widehat{ℛ}\left(U^{\eta },{\tilde{G}}^{\eta }\right)\Vert }_{l^2\left({ℝ}^M\right)}={\Vert ℛ\left(U^{\eta },{\tilde{G}}^{\eta }\right)-S\sigma \left(B{\left[U^{\eta },{\tilde{G}}^{\eta }\right]}^{\text{T}}+A\right)\Vert }_{l^2\left({ℝ}^M\right)}\le \hat{\epsilon }=\frac{m\epsilon }{2{(1+m)}^L},$$

where $m$ is the contraction parameter of $ℛ$, as defined in Assumption 1. By this construction, we know that $S$ has independent rows. Denoting $\tilde{d}:=\hat{d}+1>0$, there exists the right inverse of $S$, which we denote as $S^{+}\in {ℝ}^{\left(\tilde{d}-1\right)M\times M}$, such that

$$S{S}^{+}=I_M,S^{+}S:={\tilde{I}}_{\left(\tilde{d}-1\right)M},$$

where $I_M$ is the $M$ by $M$ identity matrix, ${\tilde{I}}_{\left(\tilde{d}-1\right)M}$ is a $\left(\tilde{d}-1\right)M$ by $\left(\tilde{d}-1\right)M$ block matrix with each of its element being either 1 or 0. Hence, for any vector $Z\in ℝ\left(\tilde{d}-1\right)M$, we have $\sigma \left({\tilde{I}}_{\left(\tilde{d}-1\right)M}Z\right)={\tilde{I}}_{\left(\tilde{d}-1\right)M}\sigma \left(Z\right)$. Moreover, we note that $S$ has a very special structure: from the $\left(\left(i-1\right)\left(\tilde{d}-1\right)+1\right)$-th to the $\left(i\left(\tilde{d}-1\right)\right)$-th column of $S$, all nonzero elements are on its $i$-th row. Correspondingly, we can also choose $S^{+}$ to have a special structure: from the $\left(\left(i-1\right)\left(\tilde{d}-1\right)+1\right)$-th to the $\left(i\left(\tilde{d}-1\right)\right)$-th row of $S^{+}$, all nonzero elements are on its $i$-th column. Hence, when multiplying $S^{+}$ with $U$, there will be no entanglement between different components of $U$. That means, $S^{+}$ can be seen as a pointwise weight function.

We now construct the parameters of MetaNO as follows. In this construction, we choose the feature dimension as $d_h:=\tilde{d}M$. With the input $\left[U^0,G^{\eta }\right]\in {ℝ}^{2M}$, for the lift layer we set

$$P^{\eta }:=1_{[M,1]}\otimes \left[\begin{array}{cc}{S}^{+}& \mathbf{0}\\ \mathbf{0}& D^{\eta }\end{array}\right]={\underset{\text{repeated for }M\text{ times}}{\underbrace{\left[\begin{array}{ccccccc}{S}^{+}& \mathbf{0}& S^{+}& \mathbf{0}& \cdots & S^{+}& \mathbf{0}\\ \mathbf{0}& D^{\eta }& \mathbf{0}& D^{\eta }& \cdots & \mathbf{0}& D^{\eta }\end{array}\right]}}}^T\in {ℝ}^{d_{h}M\times 2M},$$

and $p^{\eta }:=\mathbf{0}\in {ℝ}^{d_{h}M}$. Here, $D^{\eta }:=\text{diag}\left[1/F_1\left[b^{\eta }\right]\left(x_1\right),\cdots ,1/F_1\left[b^{\eta }\right]\left(x_M\right)\right]$. As such, the initial layer of feature is then given by

$$H\left(0\right)=P^{\eta }\left({\left[U^0,G^{\eta }\right]}^{\text{T}}\right)=1_{\left[M,1\right]}\otimes {\left[S^{+}{U}^0,D^{\eta }{G}^{\eta }\right]}^{\text{T}}=1_{\left[M,1\right]}\otimes {\left[S^{+}{U}^0,{\tilde{G}}^{\eta }\right]}^{\text{T}}\in {ℝ}^{dM}.$$

Here, we point out that $P^{\eta }$ and $p^{\eta }$ can be seen as pointwise weight and bias functions, respectively.

Next we construct the shared iterative layer $𝒥$, by setting

$$V:=\left[\begin{array}{c}{\tilde{I}}_{\left(\tilde{d}-1\right)M}B/M\\ 0\end{array}\right]\left[\begin{array}{cc}LS& \mathbf{0}\\ \mathbf{0}& L{I}_M\end{array}\right],\tilde{V}:={\mathbf{1}}_{\left[M,M\right]}\otimes V,\text{ and }C:={\mathbf{1}}_{\left[M,1\right]}\otimes \left[\begin{array}{c}L{\tilde{I}}_{\left(\tilde{d}-1\right)M}A\\ \mathbf{0}\end{array}\right].$$

Note that $\tilde{V}$ is independent of $\eta$, and falls into the formulation of $V$, by letting $R_1=V$ and $R_2=R_2=\cdots =R_M=W=0$. For the $l+1$-th layer of feature vector, we then arrive at

$$H\left(l+1\right)=H\left(l\right)+\frac{1}{L}\sigma \left(\tilde{V}H\left(l\right)+\mathit{C}\right)=H\left(l\right)+\left(I_M\otimes \left[\begin{array}{cc}{S}^{+}S& \mathbf{0}\\ \mathbf{0}& I_M\end{array}\right]\right)\sigma \left(\left(1_{\left[M,1\right]}\otimes \left[\begin{array}{c}B/M\\ \mathbf{0}\end{array}\right]\right)\left(1_{\left[1,M\right]}\otimes \left[\begin{array}{cc}S& \mathbf{0}\\ \mathbf{0}& I_M\end{array}\right]\right)H\left(l\right)+1_{\left[M,1\right]}\otimes \left[\begin{array}{c}A\\ \mathbf{0}\end{array}\right]\right),$$

where $H\left(l\right)={\left[{\hat{h}}_1^l,{\hat{h}}_2^l,\dots ,{\hat{h}}_{2M-1}^l,{\hat{h}}_{2M}^l\right]}^{\text{T}}$ denotes the (spatially discretized) hidden layer feature at the $l-$th iterative layer of the IFNO. Subsequently, we note that the second part of the feature vector, ${\hat{h}}_{2j}^l\in {ℝ}^M$, satisfies

$${\hat{h}}_{2j}^{l+1}={\hat{h}}_{2j}^l=\cdots ={\hat{h}}_{2j}^0={\tilde{G}}^{\eta },\forall l=0,\cdots ,L-1,\forall j=1,\cdots ,M$$

Hence, the first part of the feature vector, ${\hat{h}}_{2j-1}^l\in {ℝ}^{\left(\tilde{d}-1\right)M}$, satisfies the following iterative rule:

$${\hat{h}}_{2j-1}^{l+1}={\hat{h}}_{2j-1}^l+S^{+}S\sigma \left(B{\left[S{\hat{h}}_{2j-1}^l,{\tilde{G}}^{\eta }\right]}^{\text{T}}+A\right),\forall l=0,\cdots ,L-1,\forall j=1,\cdots ,M,$$

and

$${\hat{h}}_1^{l+1}={\hat{h}}_3^{l+1}=\cdots ={\hat{h}}_{2M-1}^{l+1}.$$

Finally, for the projection layer $𝒬$, we set the activation function in the projection layer as the identity function, $Q_1:=I_{d_{h}M}$ (the identity matrix of size $d_{h}M$), $Q_2:=\left[S,0\right]\in {ℝ}^{M\times d_{h}M},q_1:=0\in {ℝ}^{d_{h}M}$, and $q_2:=0\in {ℝ}^M$. Denoting the output $U^{\eta }:={𝒬}_{{\theta }_Q}\circ {\left({𝒥}_{{\theta }_I}\right)}^L\circ {𝒫}_{{\theta }_P^{\eta }}\left({\left[U^0,G^{\eta }\right]}^{\text{T}}\right)$, we now show that $U^{\eta }$ can approximate $U^{\eta ,*}$ with a desired accuracy $\epsilon$:

$$\begin{gathered} \Vert {\mathit{U}}^{\eta }-{\mathit{U}}^{\eta ,*}\Vert \le {\Vert {\mathit{U}}^{\eta }-{\mathit{U}}^L\Vert }_{l^2\left({ℝ}^M\right)}+{\Vert {\mathit{U}}^L-{\mathit{U}}^{\eta ,*}\Vert }_{l^2\left({ℝ}^M\right)} \\ \le {\Vert S{\hat{\mathit{h}}}_1^L-{\mathit{U}}^L\Vert }_{l^2\left({ℝ}^M\right)}+\frac{\epsilon }{2}\left(\mathit{\text{ by Assumption }}\mathit{2}\right) \\ \le {\Vert S{\hat{\mathit{h}}}_1^{L-1}-{\mathit{U}}^{L-1}\Vert }_{l^2\left({ℝ}^M\right)}+{\Vert \widehat{ℛ}\left(S{\hat{\mathit{h}}}_1^{L-1},\tilde{\mathit{G}}\right)-ℛ\left({\mathit{U}}^{L-1},\tilde{\mathit{G}}\right)\Vert }_{l^2\left({ℝ}^M\right)}+\frac{\epsilon }{2} \\ \le {\Vert S{\hat{\mathit{h}}}_1^{L-1}-{\mathit{U}}^{L-1}\Vert }_{l^2\left({ℝ}^M\right)}+{\Vert \widehat{ℛ}\left(S{\hat{\mathit{h}}}_1^{L-1},\tilde{\mathit{G}}b\right)-ℛ\left(S{\hat{\mathit{h}}}_1^{L-1},\tilde{\mathit{G}}b\right)\Vert }_{l^2\left({ℝ}^M\right)} \\ +{\Vert ℛ\left(S{\hat{\mathit{h}}}_1^{L-1},\tilde{G}b\right)-ℛ\left({\mathit{U}}^{L-1},\tilde{G}b\right)\Vert }_{l^2\left({ℝ}^M\right)}+\frac{\epsilon }{2} \\ \le \left(1+m\right){\Vert S{\hat{\mathit{h}}}_1^{L-1}-{\mathit{U}}^{L-1}\Vert }_{l^2\left({ℝ}^M\right)}+\frac{m\epsilon }{2{(1+m)}^L}+\frac{\epsilon }{2}\left(\mathit{\text{ by Lemma }}\mathit{1}\mathit{\text{ and Assumption }}\mathit{1}\right) \\ \le \frac{m\epsilon }{2{(1+m)}^L}\left(1+\left(1+m\right)+{(1+m)}^2+\cdots +{(1+m)}^{L-1}\right)+\frac{\epsilon }{2} \\ \le \frac{\epsilon }{2}+\frac{\epsilon }{2}=\epsilon . \end{gathered}$$

4. Empirical Evaluation

In this section, we demonstrate the empirical effectiveness of the proposed MetaNO approach. Specifically, we conduct experiments on a synthetic dataset from a nonlinear PDE solving problem, a benchmark dataset of heterogeneous materials subject to large deformation, and a real-world dataset from biological tissue mechanical testing. We compare the proposed method against competitive GBML methods as well as two non-meta transfer-learning baselines. All of the experiments are implemented using PyTorch with Adam optimizer, and performed on a workstation with two 2.2 $\text{GHz}$ 24-core CPUs and eight NVIDIA Tesla T4 GPUs. For a fair comparison, for each algorithm, we tune the hyperparameters, including the learning rate from {0.1, 0.01, 0.001, 0.0001, 0.00001, 0.000001}, the decay rate from {0.5, 0.7, 0.9}, the weight decay parameter from {0.01, 0.001, 0.0001, 0.00001, 0.000001}, and the inner loop learning rate for the baseline GBML methods (MAML and ANIL) from {0.01, 0.001, 0.0001, 0.00001, 0.000001}, to minimize the error on a separate validation dataset. In all experiments we decrease the learning rate with a ratio of learning rate decay rate every 100 epochs. A detailed description of each baseline method is provided in Appendix A.

In all experiments, we considered the averaged relative error, ${\Vert u_{i,\mathit{\text{pred}}}-u_i\Vert }_{L^2\left(\Omega \right)}/{\Vert u_i\Vert }_{L^2\left(\Omega \right)}$, as the error metric. We repeat each experiment for 5 times, and report the averaged relative errors and their standard errors.

4.1. Example 1: Synthetic Data Sets and Ablation Study

We first consider the PDE-solution-finding problem of the Holzapfel-Gasser-Odgen (HGO) model [56], which describes the deformation of hyperelastic, anisotropic, and fiber-reinforced materials. In this example, the goal is to find its displacement field $u:{[0,1]}^2\to {ℝ}^2$ under different boundary loadings. The specimen is assumed to be subject to a uniaxial tension $T_y\left(x\right)$ on the top edge (see Figure 2(a)). Therefore, we take the input function $g\left(x\right)$ as the padded traction loading field, and the output function as the corresponding displacement field.

Figure 2:

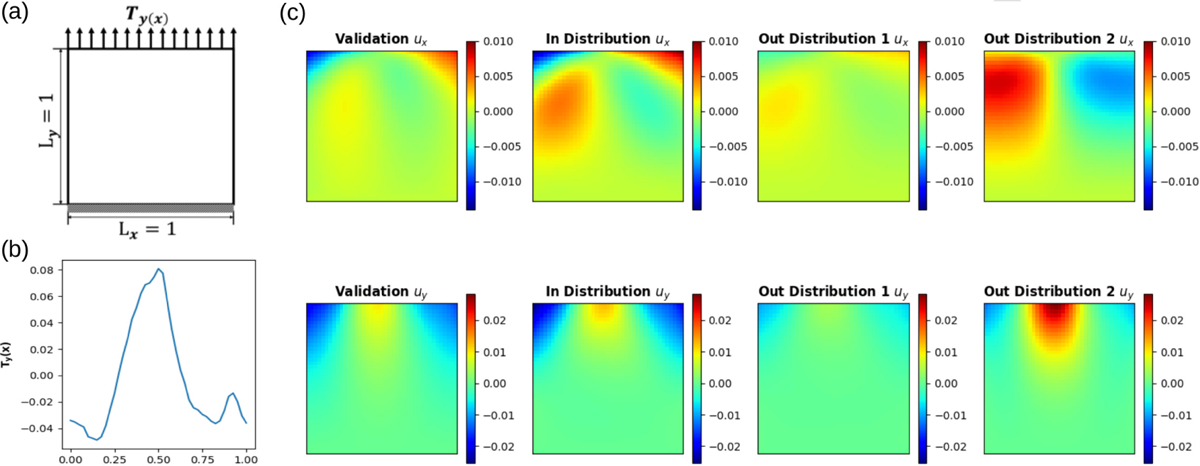
Problem setup of example 1: the synthetic data sets. (a) A unit square specimen subject to uniaxial tension with Neumann-type boundary condition. (b) & (c) Visualization of an instances of the loading field $T_y\left(x\right)$, and the corresponding ground-truth solutions $u^{\eta }\left(x\right)$ from the in-distribution and out-of-distribution tasks, showing the solution diversity across different tasks, due to the change of underlying hidden material parameter set. □

Data Generation.

To generate training and test samples, the Holzapfel-Gasser-Odgen (HGO) model [56] was employed to describe the constitutive behavior of the material in this example, with its strain energy density function given as:

$$\eta =\frac{E}{4\left(1+\nu \right)}\left({\overline{I}}_1-2\right)-\frac{E}{2\left(1+\nu \right)}\text{ln}\left(J\right)+\frac{k_1}{2k_2}\left(\text{ exp }\left(k_2{\langle S\left(\alpha \right)\rangle }^2\right)+\text{ exp }\left(k_2{\langle S\left(-\alpha \right)\rangle }^2\right)-2\right)+\frac{E}{6\left(1-2\nu \right)}\left(\frac{J^2-1}{2}-\text{ ln }J\right).$$

Here, 〈⋅〉 denotes the Macaulay bracket, and the fiber strain of the two fiber groups is defined as:

$$S\left(\alpha \right)=\frac{{\overline{I}}_4\left(\alpha \right)-1+\left|{\overline{I}}_4\left(\alpha \right)-1\right|}{2}.$$

where $k_1$ and $k_2$ are fiber modulus and the exponential coefficient, respectively, $E$ is the Young's modulus for the non-fibrous ground matrix, and $\nu$ is the Poisson ratio. Moreover, ${\overline{I}}_1=\text{tr}\left(C\right)$ is the is the first invariant of the right Cauchy-Green tensor $C=F^{T}F,F$ is the deformation gradient, and $J$ is related with $F$ such that $J=\text{det}F$. For the fiber group with angle direction $\alpha$ from the reference direction, ${\overline{I}}_4\left(\alpha \right)=n^T\left(\alpha \right)Cn\left(\alpha \right)$ is the fourth invariant of the right Cauchy-Green tensor $C$, where $n\left(\alpha \right)={[\text{cos}\left(\alpha \right),\text{sin}\left(\alpha \right)]}^T$. To generate samples for different specimens, different specimens (tasks) correspond to different material parameter sets, $\left\{k_1,k_2,E,\nu ,\alpha \right\}$.

To investigate the performance of MetaNO in few-shot learning, we generate 59 training, 1 validation tasks, and 5 in-distribution (ID) test tasks by sampling different physical parameters $k_1,k_2,E,\nu ,\alpha$ from the same uniform distribution. To further evaluate the generalizability when the physical parameters of test tasks are outside the training regime, we also generate 2 out-of-distribution (OOD) test tasks with physical parameters from different distributions. For the training tasks, the validation task, and the in-distribution (ID) test task, their physical parameters are sampled from: $k_1,k_2~𝒰\left[0.1,1\left],E~𝒰\right[0.55,1.5\right]$, $\nu ~𝒰\left[0.01,0.49\right]$, and $\alpha ~𝒰\left[\pi /10,\pi /2\right]$. For the two out-of-distribution (OOD) test tasks, we sample their parameters following $k_1,k_2~𝒰[1,1.9\left],E~𝒰\right[1.5,2\left]\cup 𝒰\right[0.5,0.55\left],\nu ~𝒰\right[0.01,0.49]$⁴, and $\alpha ~𝒰\left[\pi /2,3\pi /4]\cup [0,\pi /10\right]$. To generate the high-fidelity (ground-truth) dataset, we sampled 500 different vertical traction conditions $T_y\left(x\right)$ on the top edge from a random field, following the algorithm in [36, 58]. $T_y\left(x\right)$ is taken as the restriction of a $2\text{D}$ random field, $\varphi \left(x\right)={ℱ}^{-1}\left({\gamma }^{1/2}ℱ\left(\Gamma \right)\right)\left(x\right)$, on the top edge. Here, $\Gamma \left(x\right)$ is a Gaussian white noise random field on ${ℝ}^2,\gamma ={\left(w_1^2+w_2^2\right)}^{-\frac{5}{4}}$ represents a correlation function, and $w_1,w_2$ are the wave numbers on $x$ and $y$ directions, respectively. Then, for each sampled traction loading, we solved the displacement field on the entire domain by minimizing potential energy using the finite element method implemented in FEniCS [59]. In particular, the displacement filed was approximated by continuous piecewise linear finite elements with triangular mesh, and the grid size was taken as 0.025. The finite element solution was interpolated onto $\chi$, a structured 41 × 41 grid which will be employed as the discretization in our neural operators. The distribution of training and ID/OOD tasks are demonstrated in Figure 3, where one can see that the first OOD task (denoted as “OOD Task1”) corresponds to a stiffer material sample and smaller deformation for each given loading, while the second OOD task (denoted as “OOD Task2”) generates a softer material sample and larger deformation. For each training task, we generate 500 data pairs ${𝒟}^{\eta }:={\left\{\left(g_i^{\eta },u_i^{\eta }\right)\right\}}_{i=1}^{500}$, by sampling the vertical traction loading from a Gaussian random field. Then, the corresponding ground-truth displacement field is obtained using the finite element method implemented in FEniCS [59]. For test tasks, we train with $N^{\text{test }}=\left\{2,4,8,12,20,100,300\right\}$ numbers of labelled data pairs (the context set), and evaluate the model on a reserved dataset with 200 data pairs (the target set) on each test task. An 8-layer IFNO is employed as the base model.

Figure 3:

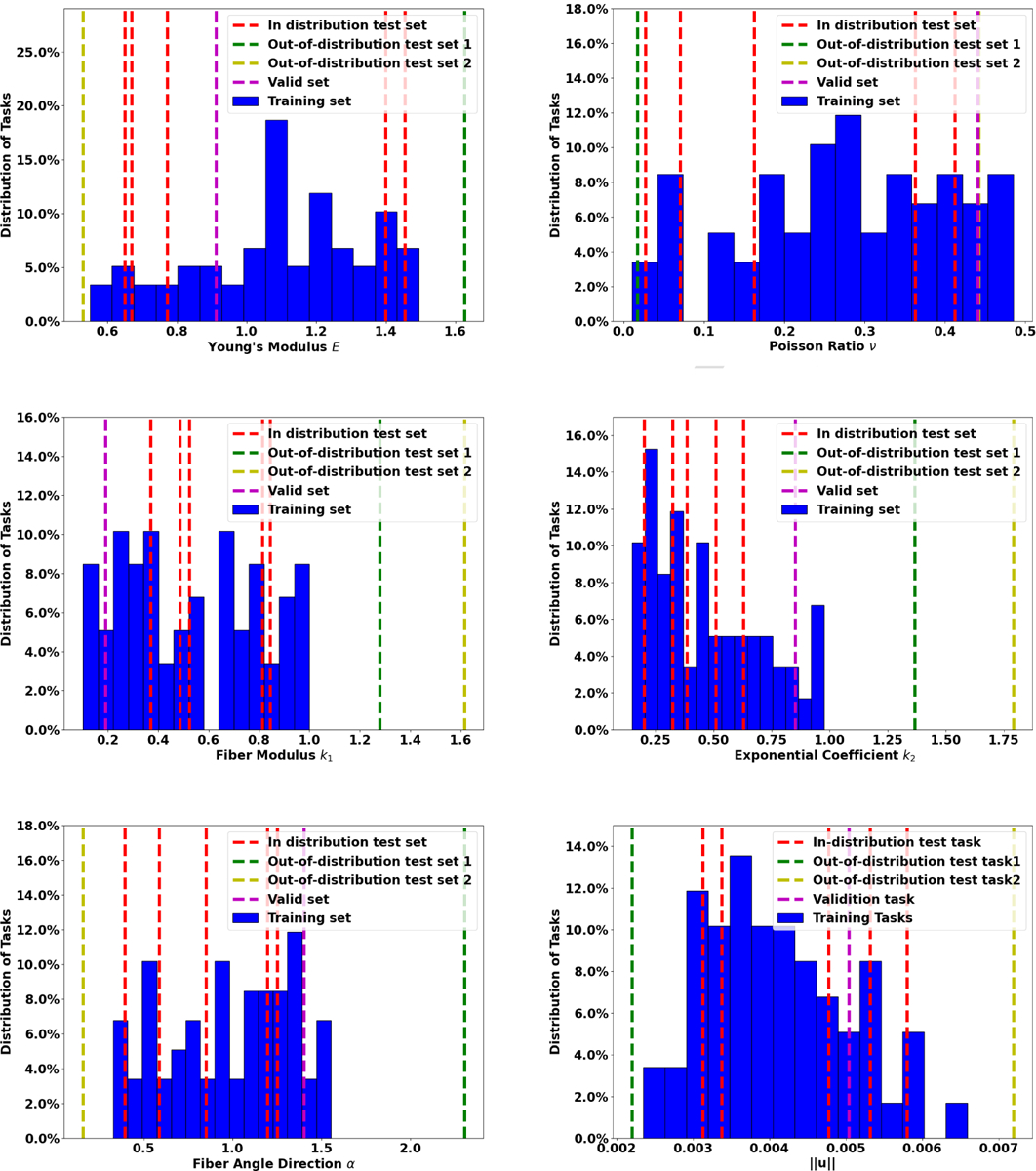
Distribution of physical parameters of different tasks in example 1, and the resultant magnitude of material response, ${\Vert u^{\eta }\left(x\right)\Vert }_{L^2\left(\Omega \right)}$, on an exemplar loading instance shown in Figure 2(b).

Ablation Study.

We first conduct an ablation study on 4 variants of the proposed algorithm: 1) to use the full meta-train and meta-test phases as in Algorithm 1 (denotes as “MetaNO”); 2) to perform steps 1–3 of Algorithm 1, such that only the lifting layer is adapted in the meta-test phase (denotes as “MetaNO-”); 3) to apply task-wise adaptation only to the iterative layers instead of the lift layer in both meta-train and meta-test phases (denoted as “MetaMid”); 4) to apply task-wise adaptation only to the projection layer instead of the lift layer in both meta-train and meta-test phases (denoted as “MetaLast”). We study if the successful “adapting last layers” strategy of MAML and ANIL in image classification problems would apply for our PDE solving problem. Besides these four settings, we also report the few-shot learning results with five baseline methods: 1) Learn a neural operator model only based on the context data set of the test task (denoted as “Single”); 2) Pretrain a neural operator model based on all training task data sets, then fine-tune it based on the context test task data set (denoted as “Pretrain1”); 3) Pretrain a single neural operator model based on the context data set of one training task, then fine-tune it based on the context test task data set (denoted as “Pretrain2”); To remove the possible dependency on the pre-training task, in this baseline we randomly select five training tasks for the purpose of pretraining and report the averaged results. 4) MAML, and 5) ANIL. For all experiments we use the full context data set on each training task $\left(N^{\eta }=500\right)$.

As shown in Figure 4, MetaNO- and MetaNO are both able to quickly adapt with few data pairs – to achieve a test error below 5%, “Single” and the two transfer-learning baselines (“Pretrain1”, “Pretrain2”) require 100+ data pairs, while MetaNO- and MetaNO requires only 4 data pairs. On the other hand, MetaMid, MetaLast, MAML and ANIL have similar performance. They all require 100 data pairs to achieve a < 5% test error. In particular, when using only 4 data pairs on the target task, “MetaNO-” has $2.91\text{\%}\pm 0.90\text{\%}$ relative test error, while “MetaMid” and “MetaLast” have $58.41\text{\%}\pm 9.92\text{\%}$ and $43.99\text{\%}\pm 11.36\text{\%}$ relative test errors, respectively. This observation verifies our finding on the multi-task parametric PDE solution operator learning problem, where one should adapt the first layer, not the middle layers or the last ones. A detailed comparison on the computational time and test errors of these “MetaNO-” and “MetaNO” is provided in Table 1. Herein, the total time of MetaNO- includes the Meta-Train Phase (Steps 1 and 2) and the step of solving for ${\theta }_P^{\mathit{\text{test}}}$ in the Meta-Test Phase (Step 3) of Algorithm 1, and the total time of MetaNO includes all steps of both the Meta-Train and Meta-Test Phases (Steps 1–4). Since the Meta-Train Phase took the majority of training time (45612 seconds), although “MetaNO” requires an additional fine-tuning step, its computational cost is of a similar scale as “MetaNO-”. When comparing the test errors, we can see that the additional fine-tune step only improves the performance in the larger-sample regime (when $N^{\text{test }}\ge 100$). This fact shows that when given sufficient training context sets, adapting the first layer can capture the underlying task diversity so further fine-tuning may not be needed, especially in the small data regime.

Figure 4:

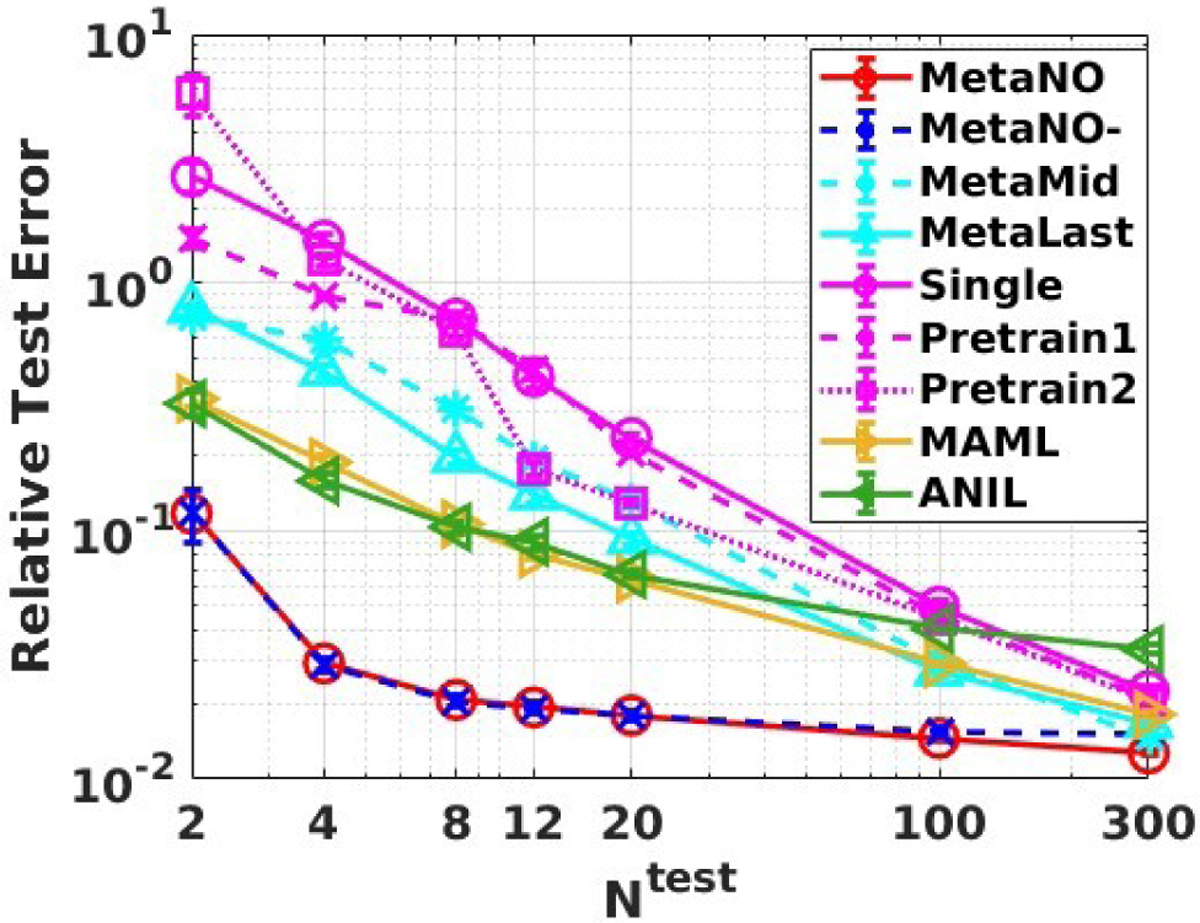
Results of the ablation study on example 1: the synthetic data set. Comparison on test errors in the in-distribution test, when using the full context set $\left(N^{\eta }=500\right)$ on training tasks and different sizes of context set $\left(N^{\text{test }}\right)$ on test tasks.

Table 1:

A comparison of the computational costs (in seconds) and test errors (in relative $L^2$ norm) of MetaNO and MetaNO-, in the ablation study on example 1. Here, the total time of MetaNO- includes the Meta-Train Phase (Steps 1 and 2) and the step of solving for ${\theta }_P^{\text{test }}$ in the Meta-Test Phase (Step 3), and the total time of MetaNO includes all steps of both the Meta-Train and Meta-Test Phases (Steps 1–4).

			MetaNO-		MetaNO
N test	Step 3	Step 4	Total Time	Test Error	Total Time	Test Error
2	24	25	45636	11.70%±14.01%	45661	11.72%±14.02%
4	48	49	45660	2.91%±0.90%	45709	2.93%±0.90%
8	93	98	45705	2.07%±0.53%	45803	2.08%±0.53%
12	141	147	45753	1.94%±0.56%	45900	1.92%±0.55%
20	223	247	45835	1.82%±0.41%	46082	1.80%±0.39%
100	976	1025	46588	1.56%±0.35%	47613	1.46%±0.26%
300	2116	2282	47728	1.53%±0.34%	50010	1.27%±0.15%

Effect of Varying Training Context Set Sizes.

In this study, we investigate the effect of different training task context sizes $N^{\eta }=\left\{50,100,200,500\right\}$ on four meta-learnt models: MetaNO, MetaNO-, MAML, and ANIL. The comparison on test errors are demonstrated in the top plot of Figure 5. Here, MetaNO- and MetaNO did not have any inner loop updates. All parameters from all training tasks are optimized together. In MAML and ANIL we use half of the context set for inner loop updates (support set) and the other half for outer loop updates (target set). One can see that when $N^{\text{test }}\le 20$, MetaNO- and MetaNO have similar performance and consistently beat MAML and ANIL for both context set sizes. With the increase of $N^{\text{test }}$, the fine-tuning strategy on the test context set becomes more helpful where we see MetaNO becomes more accurate than MetaNO- and MAML beats ANIL. Such effect is more evident on small training context set cases. Perhaps unsurprisingly, with the training task context size varying from 50 to 500, all methods have improved performance with decreasing relative test errors (with the same colors for the same methods across different context dataset). In addition, as the context set size in the test task grows, fine-tuning will gradually have better performance as MetaNO and MAML beats MetaNO- and ANIL, respectively. Overall, in all combinations of $N^{\eta }$ and $N^{\text{test }}$, MetaNO achieves the best performance among all models.

Figure 5:

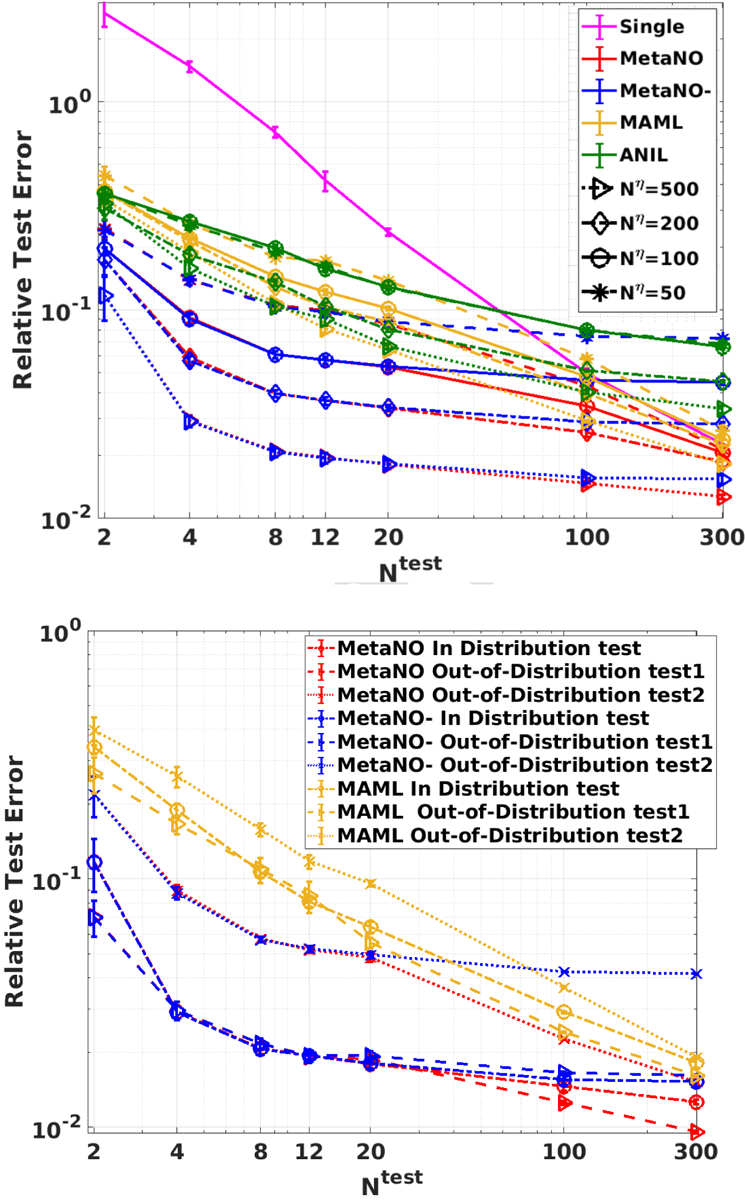
Results on on example 1: the synthetic data set. Top: The relative test error results showing the effect of varying training task context set sizes $N^{\eta }\in \left\{50,100,200,500\right\}$. Bottom: The relative error of MetaNO and MAML in in-distribution and out-of distribution tests.

In-Distribution and Out-Of-Distribution Tests.

On bottom Figure 5, we demonstrate the relative test error of MetaNO against MAML in both ID and OOD tasks. We can see that test errors of these 3 tasks are in a similar scale as the error on training tasks. The error from OOD task1 is comparable to the averaged ID test task error, while the error from OOD task2 is much larger, as expected by the data property: due to the fact that the solutions in OOD task1 generally have smaller magnitude and hence its solution operator lies more in a linear regime, which makes the solution operator learning task easier. probably due to the fact that the solutions in OOD task1 generally have smaller magnitude and hence its solution operator lies more in a linear regime, which makes the solution operator learning task easier. In all three cases, MetaNO outperforms MAML, hence validating the good generalization performance of MetaNO.

4.2. Example 2: Benchmark Mechanical MNIST Datasets

We further test MetaNO and five baseline methods on benchmark Mechanical MNIST [60]. Mechanical MNIST is a benchmark dataset of heterogeneous material undergoing large deformation, modeled by the Neo-Hookean material with a varying modulus converted from the MNIST bitmap images [60]. It contains 70,000 heterogeneous material specimens, and each specimen is governed by the Neo-Hookean material with a varying modulus converted from the MNIST bitmap images. On each specimen, we have 32 loading/response data pairs on a structured 27 by 27 grid, under the uniaxial extension, shear, equibiaxial extension, and confined compression load scenarios, respectively⁵.

Data Generation and Settings.

Here in, we randomly select one specimen corresponding to hand-written number 0 and 2 – 9 respectively as training tasks. Then, among the specimens corresponding to 1, we randomly select six specimens: one for validation and the rest five as the test tasks. Visualization of the ground-truth solutions corresponding to one common loading from different tasks is provided in Figure 6(a), together with the underlying (hidden) microstructure pattern which determines the parameter set $b^{\eta }$. On the meta-train phase, we use the full context data set of all 32 samples for each training task. On the meta-test phase, we reserve 20 data pairs on the test task as the target set for evaluation, then train each model under the few-shot learning setting with $N^{\text{test }}=\left\{2,4,8,12\right\}$ labelled data pairs as the context set. All approaches are developed based on an 32-layer IFNO model.

Figure 6:

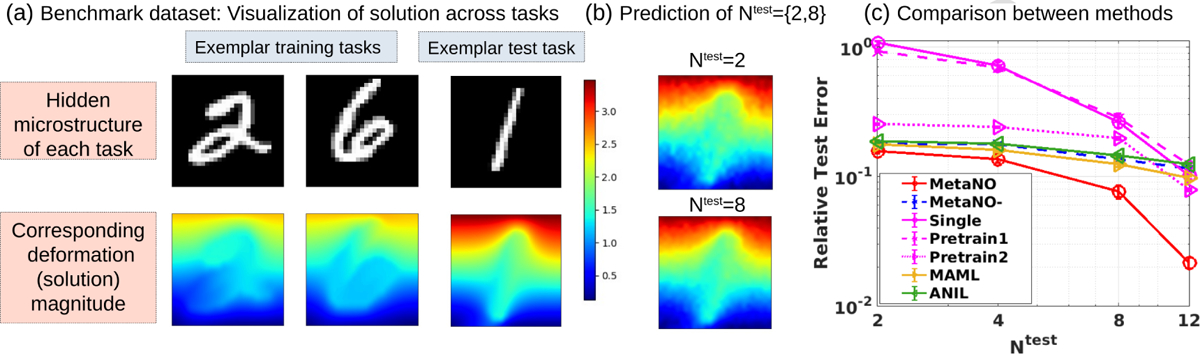
Results on example 2: the benchmark (Mechanical MNIST [60]) dataset. (a) The visualization of different tasks, their underlying microstructure field $b^{\eta }$, and the corresponding ground-truth solution. (b) Prediction results based on few samples $(N^{\text{test }}=2$ and $N^{\text{test }}=8)$ on a test task. (c) Comparison of MetaNO and five baseline methods.

Results.

Besides the diversity of tasks as seen in Figure 6(a), notice that we also have a small number of training tasks $\left(H=9\right)$, and a relatively small training context set size $\left(N^{\eta }=32\right)$. All these facts make the transfer learning on this benchmark dataset challenging. We present the results in Figure 6(b) and (c). The neural operator model learned by MetaNO again outperforms the baseline single/transfer learning models and the state-of-the-art GBML models. Our MetaNO model achieves 15% error when using only 2 labelled data pair on the test task, while the Single model has high errors due to overfitting. This fact highlights the importance of learning across multi-tasks: when the total number of measurements on each specimen is limited, it is necessary to transfer the knowledge across specimens. Moreover, while MetaNO-, MAML, and ANIL all have a similar performance in this example, the fine-tuning step in MetaNO seems to substantially improve the accuracy, especially when $N^{\text{test }}$ gets larger. This observation is consistent with previous finding on varying training task context sizes.

4.3. Example 3: Application on Real-World Data Sets

We now take a step further to demonstrate the performance of our method on a real-world physical response dataset, which is not generated by solving PDEs. We consider the problem of learning the mechanical response of multiple biological tissue specimens from DIC displacement tracking measurements. We measure the biaxial loading of tricuspid valve anterior leaflet (TVAL) specimens from a porcine heart, such that each specimen (as a task) corresponds to a different region of the leaflet. Due to material heterogeneity of biological tissues, these specimens contain different mechanical and structural properties. However, these properties are generally not observable without damaging the tissue. Therefore, this example provides a proof-of-principle demonstration that how MetaNO applies to learning tasks where the governing equations and physical properties are both unknown, and the dataset has unavoidable measurement noise.

Data Generation.

We now briefly provide the data generation procedure for the tricuspid valve anterior leaflet (TVAL) response modeling example. To generate the data, we firstly followed the established biaxial testing procedure, including acquisition of a healthy porcine heart and retrieval of the TVAL [61, 62]. Then, we sectioned the leaflet tissue and applied a speckling pattern to the tissue surface using an airbrush and black paint [63–65]. The painted specimen was then mounted to a biaxial testing device (BioTester, CellScale, Waterloo, ON, Canada). To generate samples for each specimen, we performed 7 protocols of displacement-controlled testing to target various biaxial stresses: $P_{11}:P_{22}=\left\{1:1,1:0.66,1:0.33,0.66:1,0.33:1,0.05:1,1:0.1\right\}$. Here, $P_{11}$ and $P_{22}$ denote the first Piola-Kirchhoff stresses in the $x$- and $y$-directions, respectively. Each stress ratio was performed for three loading/unloading cycles. Throughout the test, images of the specimen were captured by a CCD camera, and the load cell readings and actuator displacements were recorded at 5 Hz. After testing, the acquired images were analyzed using the digital image correlation (DIC) module of the BioTester’s software. The pixel coordinate locations of the DIC-tracked grid were then exported and extrapolated to a 21 by 21 uniform grid. In this example, we have the DIC measurements on 16 specimens, with 500 data pairs of loadings and material responses from the 7 protocols on each specimen. These specimens are divided into three groups: 12 for the purpose of meta-train, 1 for validation, and 3 for test. This reflects a common challenge in scientific applications, we not only have limited samples per task, the number of available training tasks is also limited. To demonstrate the diversity of these specimens due to the material heterogeneity in biological tissues, in Figure 7 we plot the processed displacement field of two exemplar training specimens and the validation and test specimens. For each model, the results are reported as the average of all 3 test tasks.

Figure 7:

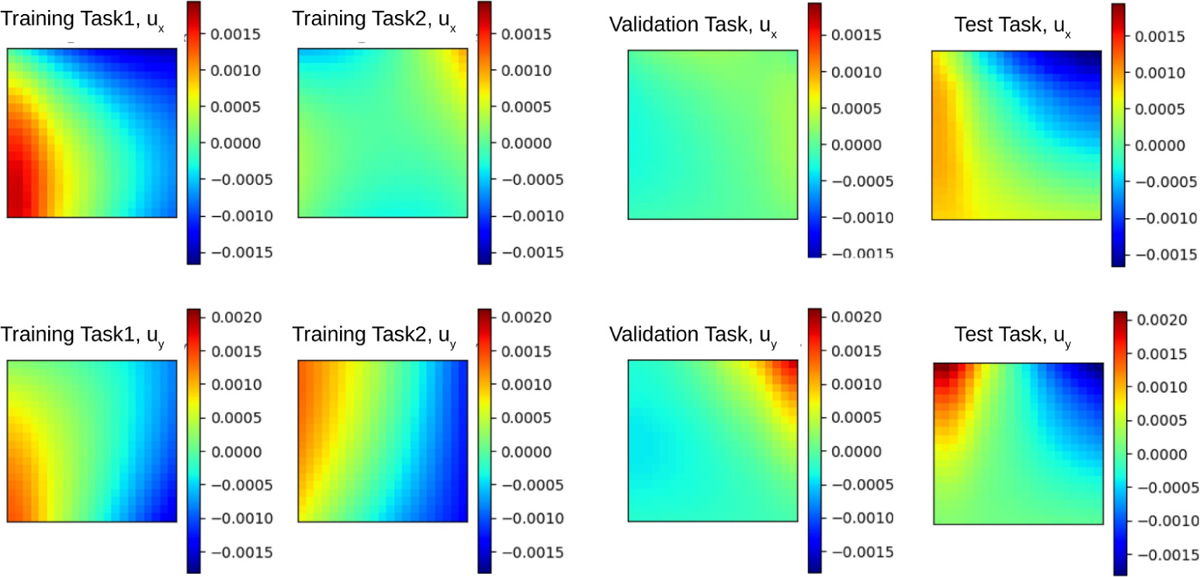
Visualization of the processed dataset in example 3: learning the biological tissue responses. Subject to the same loading instance, different columns show the corresponding ground-truth solutions $u^{\eta }\left(x\right)$ from different tasks, showing the solution diversity across different tasks due to the change of underlying hidden material parameter field.

Results.

Herein, we aim to model the tissue response by learning a neural operator mapping the boundary displacement loading to the interior displacement field on each tissue specimen. We use 13 specimens for training and validation with context size $N^{\eta }=500$, and provide the test results as the average on the rest 3 specimens. With a 4-layer IFNO as the base model, we train each model based on $N^{\text{test }}\in \left[2,300\right]$ samples, and then evaluate the performance on another 200 samples. The results are provided in Figure 8. MetaNO performs the best among all the methods across all $N^{\text{test }}$, beating MAML and ANIL by a significant margin. Interestingly, MAML and ANIL did not even beat the “Pretrain1” method, possibly due to the low efficacy of the adapting last layers strategy and the small number of training tasks.

Figure 8:

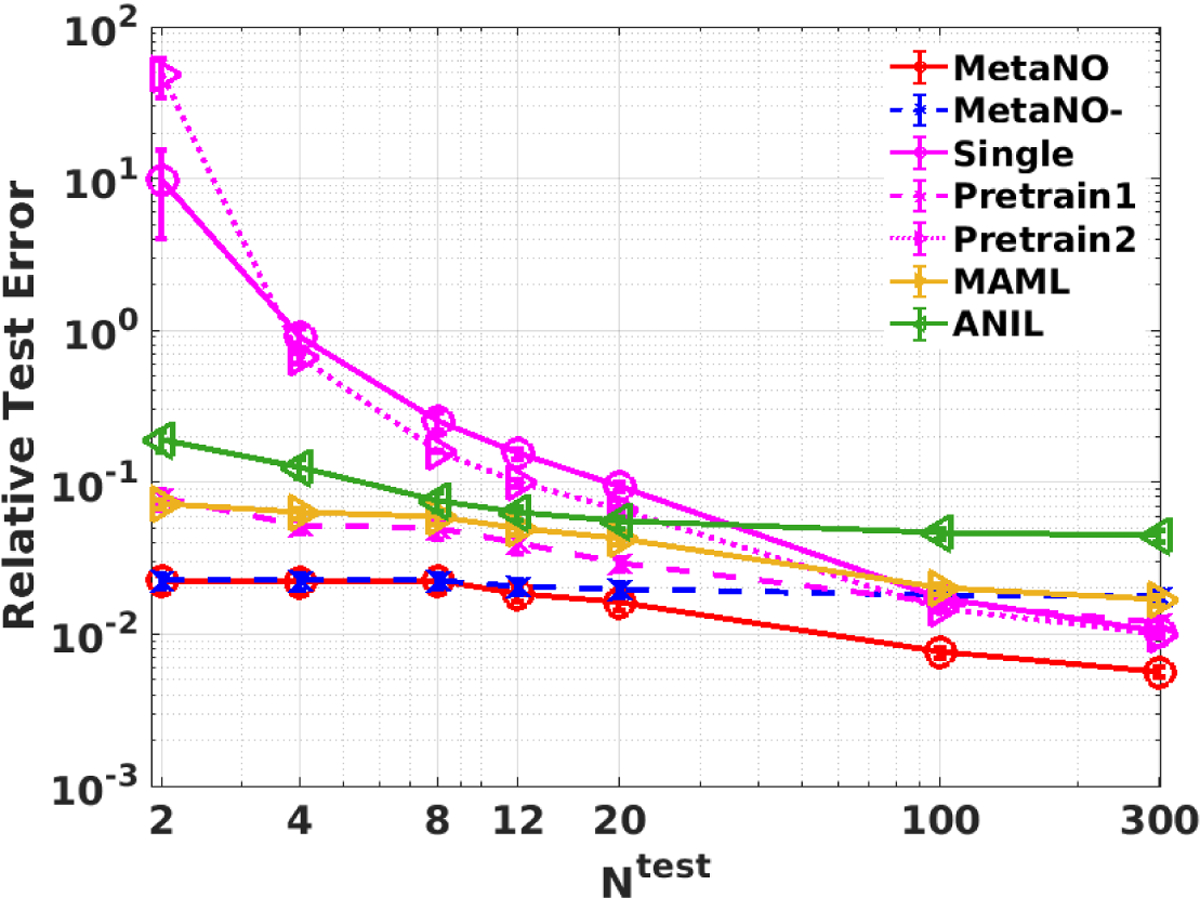
Comparison of MetaNO and five baseline methods in example 3: learning the biological tissue responses. This example features measurement noise and a small number of available tasks.

5. Summary and Future Directions

In this paper we propose MetaNO, the first neural-operator-based meta-learning approach that is designed to achieve good transferability in learning complex physical system responses. In particular, we focus on the scenario that the physical responses of different systems can be modeled by a common parametric PDE, and the behavior of each system (specimen) is governed by a different underlying parameter field. Then, based on the observed data from several known systems, the goal is to efficiently learn a surrogate model, which acts as the surrogate solution operator for the hidden PDE, for a new and unseen system. Comparing with existed transfer-learning techniques, our MetaNO features a novel first layer adaption architecture, which is theoretically motivated and shown to be a universal solution operator for multiple parametric PDE solving tasks. We demonstrate the effectiveness of our proposed MetaNO algorithm on various synthetic, benchmark, and real-world datasets, showing promises with significant improvement in sample efficiency over baseline methods.

Although in this paper we focus on material modeling problems in experiments, the proposed approach is a machine learning model that can handle different PDEs with heterogeneous coefficients, which is common in physics problems and not limited in material modeling. For example, another suitable example is climate modeling, where cities responses, temperature exposures, and impacts are all heterogeneous, resulting in different parameters in the PDE model. Here we choose material as the application mainly due to the availability of data. For future work, we will investigate the applicability of the proposed approach to other scientific domains. Moreover, we point out that the universal approximator property of MetaNO relies on the assumption that all systems are governed by a common parametric PDE. As such, a set of common characteristic solution operator features can be obtained from the training tasks in the form of the common layer parameters, and then can be utilized to accelerate the learning efficacy in the test task. Therefore, we anticipate the method to suffer from performance deterioration when handling the transferability between different types of PDEs, e.g., when all training tasks are solving diffusion problems but the test task is on an advection problem. It would be an interesting future direction of extending MetaNO to handle such a challenging scenario. In this paper, we employed the implicit Fourier neural operator [39] as the base model. As another natural extension, one might consider the proposed meta-learning approach based on other types of neural operators and neural networks, such as the graph neural operators [26, 29] and the general graph neural networks [66, 67]. As such, the model will be capable to handle measurements from unstructured grid points and domains, which be valuable for applications with complex and possibly evolving domain geometries.

Figure 1:

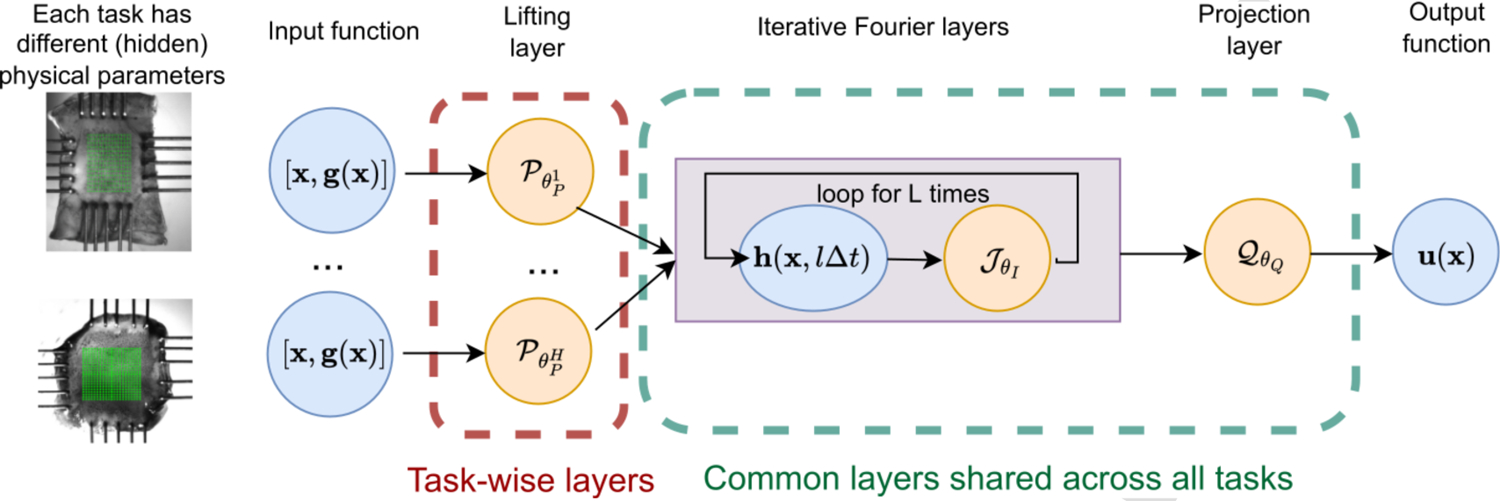
The architecture of MetaNO based on an integral neural operator model.

Appendix A. Formulation of Baseline Methods

In this section, we discuss each baseline methods in details and how they are used in our experiments. A meta-learning baseline in our problem setting would be to apply MAML and ANIL to a neural operator architecture. Here we formally state the implementation of ANIL and MAML for the problem described above, and they will serve as the baselinebaseline meta-based methods in our empirical experiments.

MAML.

The MAML algorithm proposed in [5] aims to find an initialization, $\tilde{\theta }$, across all tasks, so that new tasks can be learnt with very few gradient updates and examples. First, a batch ${\left\{{𝒯}^{\eta }\right\}}_{\eta =1}^H$ of $H$ tasks are drawn from the training task set. For each task ${𝒯}^{\eta }$, the context set of loading field/response field data pairs ${𝒟}^{\eta }$ is split to a support set of samples, ${𝒮}^{\eta }$, which will be used for inner loop updates, and a target set of samples, ${𝒵}^{\eta }$, for outer loop updates. Then, for the inner loop, let ${\theta }^{\eta ,0}:=\tilde{\theta }$ and ${\theta }^{\eta ,i}$ be the task-wise parameter after $i$-th gradient update. During each inner loop update, the task-wise parameter is updated via

$${\theta }^{\eta ,i}={\theta }^{\eta ,i-1}-\alpha {\nabla }_{{\theta }^{\eta ,i-1}}{ℒ}_{{𝒮}^{\eta }}\left({\theta }^{\eta ,i-1}\right),\text{ for }\eta =1,\cdots ,H,$$ (A.1)

where ${ℒ}_{{𝒮}^{\eta }}\left({\theta }^{\eta ,i-1}\right)$ is the loss on the support set of the $\eta$-th task, and $\alpha$ is the step size. After $m$ inner loop updates, the initial parameter $\tilde{\theta }$ is updated with a fixed step size $\beta$:

$$\tilde{\theta }\leftarrow \tilde{\theta }-\beta {\nabla }_{\tilde{\theta }}{ℒ}_{\text{meta }}\left(\tilde{\theta }\right),\text{ where the meta-loss }{ℒ}_{\text{meta }}\left(\tilde{\theta }\right):=\sum _{\eta =1}^H{ℒ}_{{𝒵}^{\eta }}\left({\theta }^{\eta ,m}\right).$$ (A.2)

Then, on the test task, ${𝒯}^{\text{test }}$, an inner loop adaptation is performed based on few labelled samples ${𝒟}^{\text{test }}$ until convergence, and the approximated solution operator model is obtained on the test task as $\widetilde{𝒢}\left[g;{\theta }^{\text{test }}\right]$.

ANIL.

In [10], ANIL was proposed as a modified version of MAML with inner loop updates only for the final layer. The inner loop update formulation of (A.1) is modified as

$${\theta }_Q^{\eta ,i}={\theta }_Q^{\eta ,i-1}-\alpha {\nabla }_{{\theta }_Q^{\eta ,i-1}}{ℒ}_{{𝒮}^{\eta }}\left({\theta }_Q^{\eta ,i-1}\right),\text{ for }\eta =1,\cdots ,H,$$ (A.3)

where ${\theta }_Q^{\eta ,i}$ is the task-wise parameter on the final (projection) layer after $i$th gradient update. Then, the same outer loop updates are performed following (A.2).

Single/Pretrain1/Pretrain2.

We also implemented 3 non-meta-learning baseline approaches.

• Single: Learn a neural operator model only based on the context data set of the test task.

• Pretrain1: Pretrain a neural operator model based on all training task data sets, then fine-tune it based on the context test task data set.

• Pretrain2: Pretrain a single neural operator model based on the context data set of one training task, then fine-tune it based on the context test task data set. To remove the possible dependency on the pre-training task, in this baseline we randomly select five training tasks for the purpose of pretraining and report the averaged results.

Appendix B. Training Details

In the following we briefly describe the hyperparameter settings employed in running of each algorithm. The code and the processed datasets will be publicly released at Github for readers to reproduce the experimental results.

Appendix B.1. Example 1: Synthetic Data Sets

Base model:

As the base model for all algorithms, we construct an architecture for IFNO [39] as follows. First, the input loading field instance $g\left(x\right)\in 𝒜$ is lifted to a higher dimensional representation via lift layer $𝒫\left[g\right]\left(x\right)$, which is parameterized as a 1-layer feed forward linear layer with width $\left(3,32\right)$. Then for the iterative layer in (2.1), we implement ${ℱ}^{-1}\left[ℱ\right[\kappa \left(\cdot ;v\right)\left]\cdot ℱ\right[h\left(\cdot ,l\right)]]\left(x\right)$ with $2\text{D}$ fast Fourier transform (FFT) with input channel and output channel widths both set as 32 and the truncated Fourier modes set as 8. The local linear transformation parameter, $W$, is parameterized as a 1-layer feed forward network with width (32,32). In the projection layer, a 2-layer feed forward network with width (32,128,2) is employed. To accelerate the training procedure, we apply the shallow-to-deep training technique to initialize the optimization problem. In particular, we start from the NN model with depth $L=1$, train until the loss function reaches a plateau, then use the resultant parameters to initialize the parameters for the next depth, with $L=2,L=4$, and $L=8$. In the synthetic experiments, we set the layer depth as $L=8$.

MetaNO:

During the meta-train phase, we train for the task-wise parameters ${\theta }_P^{\eta }$ and the common parameters ${\theta }_I$ and ${\theta }_Q$ on all 59 training tasks, with the context set of 500 samples on each task. After meta-train phase, we load ${\theta }_I$ and ${\theta }_Q$ and the averaged ${\theta }_P^{\eta }$ among all 59 tasks as initialization, then tune the hyperparameters based on the validation task. In particular, the 500 samples on the validation task is split into two parts: 300 samples are reserved for the purpose of training (as the context set) and the rest 200 samples are used for evaluation (as the target set). Then we train for the lift layer on the validation task, and tune the learning rate, the decay rate, and the weight decay parameter for different context set sizes $\left(N^{\text{test }}\right)$, to minimize the loss on the target set. Based on the chosen hyperparameters, we perform the test on the test task by training for the lift layer on different numbers of samples on its context set, then evaluate and report the performance based on its target set. We repeat the procedure on the test task with selected hyperparameters with different 5 random seeds, and calculate means and standard errors for the resultant test errors on target set.

MAML&ANIL:

For MAML and ANIL, we use the same architecture as the base model, and also split the training tasks for the purpose of training (59 tasks) and validation (1 task) as in MetaNO. During the meta-train phase, for each task we randomly split the available 500 samples to two sets: 250 samples in the support set used for inner loop updates, and the rest in the target set for outer loop updates. During the inner loop update, we train for the task-wise parameter with one epoch, following the standard settings of MAML and ANIL [5, 10]. Then, the model hyperparameters, including the learning rate, weight decay, decay rate, and inner loop learning rate, are tuned. In the meta-test phase, we load the initial parameter and train for all parameters (in MAML) or the last-layer parameters (in ANIL) until the optimization algorithm converges. Similar as in MetaNO, we first tune the hyperparameters on the validation task, then evaluate the performance on the test task.

Appendix B.2. Example 2: Mechanical MNIST

Base model:

As the base model for all algorithms, we construct two IFNO architectures, for the prediction of $u_x$ and $u_y$, the displacement fields in the $x$- and $y$-directions, respectively. On each architecture, the input loading field instance $g\left(x\right)\in 𝒜$ is mapped to a higher dimensional representation via a lifting layer $𝒫\left[g\right]\left(x\right)$ parameterized as a 1-layer feed forward linear layer with width (4,64). Then for the iterative layer in (2.1), we set the number of truncated Fourier mode as 13, and parameterize the local linear transformation parameter, $W$, as a 1-layer feed forward network with width (64,64). In the projection layer, a 2-layer feed forward network with width (64,128,1) is employed. In this example we also apply the shallow-to-deep technique to accelerate the training, and set the layer depth as $L=32$.

MetaNO:

During the meta-train phase, we train for the task-wise parameters ${\theta }_P^{\eta }$ and the common parameters ${\theta }_I$ and ${\theta }_Q$ on all 9 training tasks, with the context set of 32 samples on each task. After the meta-train phase, we load ${\theta }_I$ and ${\theta }_Q$ and the averaged ${\theta }_P^{\eta }$ among all 9 tasks as initialization, then train ${\theta }_P$ on the validation task. In particular, the 32 samples on the validation task is split into two parts: 12 samples are reserved for the purpose of training (as the context set) and the rest 20 samples are used for the purpose of evaluation (as the target set). Then we train the lift layer on the validation task, and tune the learning rate, the decay rate, and the weight decay parameter for different context set sizes $\left(N^{\text{test }}\right)$, to minimize the loss on the target set. Based on the chosen hyperparameters, we perform the meta-test phase on the test task by training for the lift layer on different numbers of samples on its context set, then evaluate and report the performance based on its target set. We repeat the procedure with different 5 random seeds on each of the 5 test tasks, and calculate means and standard errors for the resultant test errors on the target set.

MAML&ANIL:

For MAML and ANIL, we use the same architecture as the base model. During the meta-train phase, for each task we randomly split the available 32 samples to two sets: 16 samples in the support set used for inner loop updates, and the rest in the target set for outer loop updates. During the inner loop update, we also follow the standard settings of MAML and ANIL [5, 10], and tune the hyperparameters following the same procedure as elaborated above for Example 1.

Appendix B.3. Example 3: Experimental Measurements on Biological Tissues

Base model:

As the base model, we first construct the lifting layer as a 1-layer feed forward linear layer with width (4,16). Then for the iterative layer in we keep 8 truncated Fourier modes and parameterize the local linear transformation parameter, $W$, a 1-layer feed forward network with width (16,16). In the projection layer, a 2-layer feed forward network with width (16,64,1) is employed. We construct two 4-layer IFNO architectures, for the prediction of $u_x$ and $u_y$, the displacement fields in the $x$ - and $y$-directions, respectively.

MetaNO:

During the meta-train phase, we train for the task-wise parameters ${\theta }_P^{\eta }$ and the common parameters ${\theta }_I$ and ${\theta }_Q$ on all 12 tasks, with the context set of 500 samples on each task. After meta-train phase, we load ${\theta }_I$ and ${\theta }_Q$ and the averaged ${\theta }_P^{\eta }$ among all 12 tasks as initialization, then tune the hyperparameters based on the validation task. In particular, the 500 samples on the validation task is divided into two parts: 300 samples are reserved for the purpose of training (as the context set) and the rest 200 samples are used for evaluation (as the target set). Based on the chosen hyperparameters, we perform the test on the test tasks by training for the lift layer on different numbers of samples on its context set, then evaluate the performance based on its target set.

MAML&ANIL:

For MAML and ANIL, we use the same architecture as the base model, and also split the training tasks for the purpose of training and validation as in MetaNO. During the meta-train phase, for each task we randomly split the available 500 samples to two sets: 250 samples in the support set used for inner loop updates, and the rest in the target set for outer loop updates. During the inner loop update, we train for the task-wise parameter with one epoch, following the standard settings of MAML and ANIL [5,10].