Abstract
Lactobacillus casei ASCC 292 was grown in the presence of six prebiotics, namely, sorbitol, mannitol, maltodextrin, high-amylose maize, fructooligosaccharide (FOS), and inulin, in order to determine the combination of probiotic and prebiotics that would remove the highest level of cholesterol. A first-order model showed that the combination of L. casei ASCC 292, FOS, and maltodextrin was the most efficient for the removal of cholesterol, and the optimum experimental region was developed by using the steepest ascent. This led to the middle points of probiotic (1.70% [wt/vol]), FOS (4.80% [wt/vol]), and maltodextrin (6.80% [wt/vol]) for the development of a central composite design for optimization. Perturbation plot, response surface, and coefficient estimates showed that all three factors had significant quadratic effects on cholesterol removal, with FOS showing the most conspicuous quadratic change. A second-order polynomial regression model estimated that the optimum condition of the factors for cholesterol removal by L. casei ASCC 292 is 1.71% (wt/vol) probiotic, 4.95% (wt/vol) FOS, and 6.62% (wt/vol) maltodextrin. Validation experiments showed that the predicted optimum conditions were more efficient than the high and low levels of the factors and the center points. A response surface method proved reliable for developing the model, optimizing factors, and analyzing interaction effects. Analyses of growth, substrate utilization, growth yield, mean doubling time, and short-chain fatty acid (SCFA) production by the use of quadratic models indicated that cholesterol removal was growth associated. The concentration of L. casei ASCC 292 had the most significant quadratic effect on all responses studied, except for substrate utilization and SCFA production, which were significantly (P < 0.05) influenced by the interactions between the probiotic and both prebiotics, indicating that they were closely associated with the uptake of prebiotics.
A probiotic is defined as a “live microbial supplement that beneficially affects the host by improving its intestinal microbial balance” (11). Over the years, lactobacilli have been associated with improvements in lactose intolerance, increases in natural resistance to infectious disease in the gastrointestinal tract, the suppression of cancer, improved digestion, and reductions in cholesterol levels in the serum (12). Studies have shown that a small reduction in serum cholesterol of 1% may reduce the risk of coronary heart disease by 2 to 3% (17). We have previously shown that cholesterol is removed by strains of lactobacilli in laboratory media (16). Various in vivo studies have reported that some lactobacilli can lower total cholesterol and low-density lipoprotein cholesterol levels (1, 23). A prebiotic is a food ingredient that is neither hydrolyzed nor absorbed in the upper part of the gastrointestinal tract and that is selectively used as a substrate for beneficial bacteria in the colon (5). Most widely researched prebiotics fall into the group of oligosaccharides, especially oligofructose (19). Feeding rats a diet supplemented with oligofructose lowered concentrations of very-low-density lipoprotein, triacylglycerol, and phospholipids in plasma (21) and reduced postprandial triglyceridemia (14).
Another approach to gut microflora management is the use of synbiotics, for which probiotics and prebiotics are used in combination. The concept of synbiotics has been widely studied, mostly to improve the survivability of probiotics in both in vitro and in vivo experiments (5, 7) and to modulate colonic microbial populations in animal models (10, 12). However, to our knowledge, there is no information on suitable combinations of probiotics and prebiotics specifically targeting the removal of cholesterol for in vitro models, although a limited number of studies have addressed the use of prebiotics or synbiotics to reduce serum cholesterol and to regulate hepatic lipogenesis and lipid metabolism (14, 25). Yet all of these studies involved in vivo experiments, in which the true interaction patterns of synbiotics which reduce cholesterol are poorly understood.
The response surface method (RSM) is a statistical and mathematical method that involves main and interaction effects to account for curvature, to improve optimal process settings, and to troubleshoot process problems and weak points (18). It has been successfully utilized to optimize compositions of microbiological media, conditions of enzyme hydrolysis, and parameters for food preservation and fermentation processes (15). Previous studies have used conventional methods (such as one factor at one time) to evaluate the in vitro performance of probiotics and/or prebiotics in the removal of cholesterol. These methods, however, require a large number of experiments to describe the effect of individual factors and are time-consuming. Besides, no established statistical method has been introduced to distinguish the interaction effects from the main effects. Furthermore, up to now, there has been no reported study on the use of RSM to remove or reduce cholesterol by the use of either in vitro experiments or animal models. Thus, the aims of this study were to optimize cholesterol removal by Lactobacillus casei ASCC 292 in the presence of fructooligosaccharide (FOS) and maltodextrin through the response surface approach. This information will provide a better understanding of the interactions involved in cholesterol reduction for in vivo experiments.
MATERIALS AND METHODS
Bacteria and medium preparation.
L. casei ASCC 292 is a human-derived strain obtained from the Australia Starter Culture Collection Center (ASCC; Werribee, Australia). The organism was grown in sterile de Mann, Rogosa, Sharpe (MRS) broth from a 1% inoculum with a 20-h incubation at 37°C and was transferred successively three times in MRS broth prior to use. At the end of the fermentation period, the culture was centrifuged and the cell pellet was washed twice with distilled water. The supernatant was discarded, and 0.1 M phosphate buffer (pH 6.8) containing 2.0% (wt/vol) food-grade cryoprotectant Unipectin RS 150 (Savannah Bio Systems, Balwyn East, Australia) was added. The mixture was vortexed and freeze-dried at −18°C for 48 h.
Six types of commercially available prebiotics were used, including sorbitol (Sigma Chemical Co., St. Louis, Mo.), mannitol (Sigma), maltodextrin (Grain Processing Corp., Muscatine, Iowa), high-amylose maize (Starch Australasia Ltd., Lane Cove, New South Wales, Australia), inulin (Orafti Pty. Ltd., Tienen, Belgium), and FOS (Orafti). High-amylose maize contained >70% amylose and 32.5% total dietary fiber. The inulin used was Raftiline ST, with a purity of 92% and an average degree of polymerization of 10. The FOS used was Raftilose P95, with a purity of 95% and an average degree of polymerization of 4.
All prebiotics and freeze-dried cells of L. casei ASCC 292 were used at concentrations as indicated in the experimental design explained below (Table 1). Prebiotic media were inoculated with freeze-dried cells of L. casei ASCC 292 at appropriate levels, as described in the experimental design.
TABLE 1.
Treatment combinations and responses for screening experiments
| Standard order | Coded factor levela
|
Amt of cholesterol removed (μg/ml) (Y)b | ||||||
|---|---|---|---|---|---|---|---|---|
| Probiotic (X1) | Sorbitol (X2) | Mannitol (X3) | Maltodextrin (X4) | High-amylose maize (X5) | Inulin (X6) | FOS (X7) | ||
| 1 | −1 | −1 | −1 | −1 | −1 | 1 | 1 | 28.44 |
| 2 | 1 | −1 | −1 | −1 | −1 | −1 | −1 | 36.10 |
| 3 | −1 | 1 | −1 | −1 | −1 | −1 | −1 | 22.11 |
| 4 | 1 | 1 | −1 | −1 | −1 | 1 | 1 | 39.32 |
| 5 | −1 | −1 | 1 | −1 | −1 | −1 | 1 | 26.62 |
| 6 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 39.17 |
| 7 | −1 | 1 | 1 | −1 | −1 | 1 | −1 | 20.75 |
| 8 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | 39.74 |
| 9 | −1 | −1 | −1 | 1 | −1 | −1 | −1 | 18.76 |
| 10 | 1 | −1 | −1 | 1 | −1 | 1 | 1 | 39.79 |
| 11 | −1 | 1 | −1 | 1 | −1 | 1 | 1 | 27.82 |
| 12 | 1 | 1 | −1 | 1 | −1 | −1 | −1 | 36.46 |
| 13 | −1 | −1 | 1 | 1 | −1 | 1 | −1 | 17.96 |
| 14 | 1 | −1 | 1 | 1 | −1 | −1 | 1 | 39.64 |
| 15 | −1 | 1 | 1 | 1 | −1 | −1 | 1 | 23.91 |
| 16 | 1 | 1 | 1 | 1 | −1 | 1 | −1 | 31.62 |
| 17 | −1 | −1 | −1 | −1 | 1 | 1 | −1 | 19.28 |
| 18 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 38.47 |
| 19 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | 25.89 |
| 20 | 1 | 1 | −1 | −1 | 1 | 1 | −1 | 34.53 |
| 21 | −1 | −1 | 1 | −1 | 1 | −1 | −1 | 18.80 |
| 22 | 1 | −1 | 1 | −1 | 1 | 1 | 1 | 40.06 |
| 23 | −1 | 1 | 1 | −1 | 1 | 1 | 1 | 28.91 |
| 24 | 1 | 1 | 1 | −1 | 1 | −1 | −1 | 36.72 |
| 25 | −1 | −1 | −1 | 1 | 1 | −1 | 1 | 24.62 |
| 26 | 1 | −1 | −1 | 1 | 1 | 1 | −1 | 33.65 |
| 27 | −1 | 1 | −1 | 1 | 1 | 1 | −1 | 19.58 |
| 28 | 1 | 1 | −1 | 1 | 1 | −1 | 1 | 39.16 |
| 29 | −1 | −1 | 1 | 1 | 1 | 1 | 1 | 24.33 |
| 30 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | 31.15 |
| 31 | −1 | 1 | 1 | 1 | 1 | −1 | −1 | 18.23 |
| 32 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 37.29 |
| 33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 31.67 |
| 34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 27.92 |
| 35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 27.40 |
| 36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 30.94 |
| 37 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 32.08 |
Concentrations: probiotic, 0.10 to 0.30% (wt/vol); sorbitol, 0.50 to 1.50% (wt/vol); mannitol, 0.50 to 1.50% (wt/vol); maltodextrin, 0.50 to 1.50% (wt/vol); high-amylose maize, 0.50 to 1.50% (wt/vol); inulin, 0.50 to 1.50% (wt/vol); FOS, 0.50 to 1.50% (wt/vol).
All factorial points are means of duplicate values.
Cholesterol removal.
Freshly prepared media containing prebiotics were added to water-soluble filter-sterilized cholesterol (polyoxyethanyl-cholesteryl sebacate) at a final concentration of 70 to 100 μg/ml, inoculated with appropriate levels of freeze-dried L. casei ASCC 292 (Table 1), and incubated anaerobically at 37°C for 24 h. After the incubation period, the cells were centrifuged and the remaining cholesterol concentration in the spent broth was determined by the o-phthalaldehyde colorimetric method as described previously (22).
Growth of L. casei ASCC 292 in the presence of prebiotics.
The growth of L. casei was determined by the plate count method. Bacilli generally divide in one plane and can produce chains of cells due to the failure to separate completely. Thus, at the end of the fermentation time, fermentation broth containing probiotic cultures was sonicated for 5 s to disrupt clumps of lactobacilli (3) before serial dilutions were performed. MRS agar was used for plating, and the plates were incubated anaerobically at 37°C for 24 h. Growth was calculated in log10 CFU (CFU per milliliter) and expressed as the percent difference between initial growth values obtained at time zero and values obtained at the end of the incubation period.
Mean doubling time.
The mean doubling time was calculated as described previously (24). The specific growth rate (μ) of the cultures was obtained by use of the following equation: μ = (ln X2 − ln X1)/(t2 − t1), where X2 and X1 are the cell densities at times t2 and t1, respectively. The mean doubling time (Td) was calculated as follows: Td = ln 2/μ, expressed in minutes.
Utilization of substrate and growth yield.
The utilization of substrate was determined as the difference between the initial concentrations of prebiotics and their final concentrations after the incubation period. Broths containing L. casei ASCC 292 were centrifuged at 2,714 × g at 4°C for 15 min, and the supernatants were used to determine the concentrations of residual prebiotics. Since both substrates are oligosaccharides, their residual concentrations were determined by colorimetry after hexose hydrolysis with phenol-sulfuric acid (9). Utilization of the substrate was expressed as a percentage (initial concentration over final concentration). The growth yield was expressed as growth per gram of substrate utilized. Growth was obtained by the pour plate method described above and expressed as the difference between the initial log10 CFU values per milliliter at time zero and the values at the end of the incubation period.
SCFA determination.
The fermentation of prebiotics was determined by measuring short-chain fatty acids (SCFA) as the end products of fermentation by high-performance liquid chromatography (Varian Australia Pty. Ltd., Mulgrave, Australia). At the end of the incubation period, fermentation broths containing L. casei ASCC 292 and prebiotics were centrifuged at 2,714 × g at 4°C for 15 min, and the supernatants were prepared for high-performance liquid chromatography by a previously described method (8). SCFA were expressed as the total acetic, butyric, and propionic acids.
Experimental design and statistical analyses.
Screening experiments to select prebiotics were performed with seven independent factors, namely, L. casei ASCC 292 (X1), sorbitol (X2), mannitol (X3), maltodextrin (X4), high-amylose maize (X5), inulin (X6), and FOS (X7), by use of a two-level partial factorial design (27-22) resulting in 64 experimental runs (including duplicates) and 5 middle-point runs (Table 1). A first-order empirical equation was used to exclude insignificant factors and to generate the steepest ascent, which led to optimization by a rotatable central composite design (CCD). The treatment combinations were allocated into two blocks, and all experiments were performed in 2 days. The first block, representing the first day of the experiment, contained the factorial runs accompanied by four center runs. The second block, representing the second day of the experiment, contained the axial runs accompanied by two center runs. These modeling and statistical analyses were performed by the use of Design Expert, version 5.07, software (Stat-Ease Corp., Minneapolis, Minn.).
RESULTS AND DISCUSSION
Screening of prebiotics and steepest ascent.
Response surfaces are often influenced by various factors. The primary purpose of screening experiments is to select important main effects from less important ones. In this study, screening was used to generate a first-degree equation and to test the significance of factors. The complete replication of a 27 factorial design would involve 128 experimental runs. However, only 7 degrees of freedom would be needed to estimate main effects and 21 degrees of freedom would estimate two-factor interaction effects, while the remaining 99 degrees of freedom would estimate error and/or three- or higher-factor interaction effects (6). Thus, a partial two-level factorial design (27-22) was applied for this study. Partial factorial designs are capable of identifying important factors and determining interaction effects between factors, using a smaller number of experimental runs than a full factorial design without a loss of information on main factor effects and their interactions (18). Results from the two-level partial factorial design are shown in Table 1, while analysis of variance (ANOVA) results for evaluations of the first-order model are shown in Table 2. ANOVA showed that the model used was suitable, with only 4.63% total variation that was not explained by the model, and the lack-of-fit test was insignificant. The first-order model generated for screening was linear, with the presence of curvature being insignificant. The removal of cholesterol was significantly influenced by the concentrations of probiotic (X1), maltodextrin (X4), and FOS (X7), while the other prebiotics were found to have insignificant influences. Thus, only these three factors were used for further optimization experiments. From this first-order model, the following first-order equation (coded term) was generated to determine the response of cholesterol removal (Y) to the probiotic (X1), FOS (X2), and maltodextrin (X3) factors:
 |
(1) |
From the equation and coefficient estimates, the probiotic level (X1) produced the largest effect and was used as the fundamental scale for the next step, steepest ascent. This determined the path of steepest ascent, and movement was generated along that path until no improvement occurred. The steepest ascent design was based on increases of 0.50% (wt/vol) of the concentration for X1. This produced five design units (0.50/0.10 = 5). Thus, the movement for X2 was 2.51 design units [(3.58/7.13) × 5 = 2.51] and that for X3 was 3.85 design units [(5.49/7.13) × 5 = 3.85]. Steepest ascent coordinates were generated and are shown in Table 3. Steepest ascent coordinates showed that the removal of cholesterol decreased after the fourth step, with the highest value being 55.16 μg/ml, from the combination of probiotic (1.70% [wt/vol]), FOS (4.78% [wt/vol]), and maltodextrin (6.79% [wt/vol]). This combination was used as the middle point for optimization experiments.
TABLE 2.
ANOVA and coefficient estimates for evaluation of the first-order model
| Source of variation or factor | Sum of squares or coefficient estimate | DFa | Mean square or standard error | F or t value | P value |
|---|---|---|---|---|---|
| Sources of variation | |||||
| Modelb | 6,354.22 | 9 | 706.02 | 132.88 | 0.0001 |
| Curvature | 0.31 | 1 | 0.31 | 0.058 | 0.8099 |
| Residual | 308.17 | 58 | 5.31 | ||
| Lack of fit | 153.00 | 22 | 6.95 | 1.61 | 0.0988 |
| Pure error | 155.17 | 36 | 4.31 | ||
| Correlation total | 6,662.70 | 68 | |||
| Factors | |||||
| Probiotic (X1) | 7.13 | 1 | 0.29 | 24.73 | 0.0001c |
| Maltodextrin (X4) | 5.49 | 1 | 0.29 | 19.05 | 0.0001c |
| FOS (X7) | 3.58 | 1 | 0.29 | 12.41 | 0.0001c |
DF, degrees of freedom.
R2 = 0.9537.
Significant at an alpha level of 0.05.
TABLE 3.
Steepest ascent coordination path for all chosen factors at coded and natural levels
| Step | Coded factor
|
Natural factora (% [wt/vol])
|
Amt of cholesterol removed (μg/ml) | ||||
|---|---|---|---|---|---|---|---|
| ξ1 | ξ4 | ξ7 | X1 | X2 | X3 | ||
| Base | 0 | 0 | 0 | 0.20 | 1.00 | 1.00 | 25.61 |
| Δ | 5 | 3.85 | 2.51 | (5)(0.1) = 0.5 | (2.51)(0.50) = 1.26 | (3.85)(0.50) = 1.93 | |
| Base + Δ | 5 | 3.85 | 2.51 | 0.70 | 2.26 | 2.93 | 37.66 |
| Base + 2Δ | 10 | 7.70 | 5.02 | 1.20 | 3.52 | 4.86 | 50.31 |
| Base + 3Δ | 15 | 11.55 | 7.53 | 1.70 | 4.78 | 6.79 | 55.16 |
| Base + 4Δ | 20 | 15.40 | 10.04 | 2.20 | 6.04 | 8.72 | 51.88 |
| Base + 5Δ | 25 | 19.25 | 12.55 | 2.70 | 7.30 | 10.65 | 47.24 |
X1, probiotic; X2, FOS; X3, maltodextrin.
Optimization of cholesterol removal.
The optimization of cholesterol removal was performed by CCD with the fixed middle point of probiotic (1.70% [wt/vol]), FOS (4.80% [wt/vol]), and maltodextrin (6.80% [wt/vol]) and with an α value of ±1.682 to produce design rotatability (2). The design matrix for CCD and the experimental responses are shown in Table 4, while adequacy and fitness were evaluated by ANOVA and calculations of regression coefficients (Table 5). The ANOVA results indicated that the quadratic regression to produce the second-order model was significant. The lack-of-fit test was insignificant, and only 4.60% of the total variation was not explained by the model. This suggested that the model accurately represents the data in the experimental region. This also indicated that second-order terms were sufficient and higher-order terms were not necessary. Probiotic, maltodextrin, and FOS levels were significant for the removal of cholesterol. It must be noted that the t value of the quadratic term of FOS (X22) was higher than others (Table 5), indicating that the second-order regression of FOS was the strongest effect. The intercept c is the estimated response at the center point, with the coded values of X1, X2, and X3 set to 0.
TABLE 4.
CCD combination matrix using coded levels and responses
| Standard run | Blocka | Probiotic (X1) | FOS (X2) | Maltodextrin (X3) | Responsesb
|
|||||
|---|---|---|---|---|---|---|---|---|---|---|
| Amt of cholesterol removed (μg/ml) | Growth (%) | Substrate utilization (%) | Yield (% growth/g of substrate utilized) | Mean doubling time (min) | SCFA (mM) | |||||
| 1 | 1 | −1 | −1 | −1 | 14.30 | 7.38 | 40.32 | 47.98 | 244.86 | 86.93 |
| 2 | 1 | 1 | −1 | −1 | 29.77 | 19.61 | 28.67 | 19.88 | 218.99 | 29.72 |
| 3 | 1 | −1 | 1 | −1 | 29.84 | 16.25 | 53.24 | 36.37 | 265.36 | 103.15 |
| 4 | 1 | 1 | 1 | −1 | 32.42 | 27.79 | 50.56 | 34.80 | 188.54 | 50.77 |
| 5 | 1 | −1 | −1 | 1 | 29.84 | 27.65 | 49.39 | 41.30 | 247.70 | 74.91 |
| 6 | 1 | 1 | −1 | 1 | 27.58 | 15.22 | 30.74 | 23.78 | 214.76 | 45.67 |
| 7 | 1 | −1 | 1 | 1 | 29.77 | 21.62 | 51.37 | 35.75 | 265.37 | 71.93 |
| 8 | 1 | 1 | 1 | 1 | 16.33 | 9.94 | 52.63 | 36.56 | 215.11 | 81.23 |
| 9 | 1 | 0 | 0 | 0 | 48.98 | 43.46 | 50.38 | 60.93 | 242.68 | 60.10 |
| 10 | 1 | 0 | 0 | 0 | 45.39 | 43.03 | 59.20 | 58.02 | 246.22 | 66.44 |
| 11 | 1 | 0 | 0 | 0 | 49.53 | 47.53 | 53.22 | 63.69 | 246.13 | 67.80 |
| 12 | 1 | 0 | 0 | 0 | 45.78 | 40.42 | 53.43 | 60.27 | 242.06 | 66.36 |
| 13 | 2 | −1.682 | 0 | 0 | 44.61 | 30.96 | 51.85 | 44.04 | 265.78 | 98.70 |
| 14 | 2 | 1.682 | 0 | 0 | 43.28 | 29.52 | 50.39 | 43.21 | 196.65 | 39.42 |
| 15 | 2 | 0 | −1.682 | 0 | 33.20 | 27.80 | 33.36 | 38.44 | 242.94 | 33.27 |
| 16 | 2 | 0 | 1.682 | 0 | 35.17 | 28.29 | 64.63 | 23.95 | 243.23 | 60.58 |
| 17 | 2 | 0 | 0 | −1.682 | 43.05 | 29.06 | 22.37 | 62.66 | 243.34 | 41.73 |
| 18 | 2 | 0 | 0 | 1.682 | 39.77 | 28.42 | 34.66 | 85.15 | 243.12 | 50.66 |
| 19 | 2 | 0 | 0 | 0 | 50.78 | 48.11 | 50.57 | 64.53 | 242.41 | 59.61 |
| 20 | 2 | 0 | 0 | 0 | 52.50 | 56.06 | 51.12 | 65.65 | 244.81 | 63.79 |
1, first day of experiment; 2, second day of experiment.
All factorial and axial points are means of duplicates.
TABLE 5.
ANOVA of the second-order model and coefficient estimates for the response factor Y0 and factors X1, X2, and X3a
| Source of variation or factor | Sum of squares or coefficient estimate | DF | Mean square or standard error | F or t value | P value |
|---|---|---|---|---|---|
| Sources of variation | |||||
| Modelb | 1,778.16 | 9 | 197.57 | 20.76 | 0.0001 |
| Residual | 82.18 | 5 | 16.44 | ||
| Lack of Fit | 70.47 | 5 | 14.09 | 3.71 | 0.1140 |
| Pure error | 15.19 | 4 | 3.80 | ||
| Total | 1,860.34 | 14 | 214.01 | ||
| Factorc | |||||
| Intercept | c = 50.61 | 1 | 1.27 | ||
| X1 | c1 = 0.0081 | 1 | 0.83 | 0.0096 | 0.0003d |
| X2 | c2 = 0.75 | 1 | 0.83 | 0.89 | 0.0001d |
| X3 | c3 = −0.61 | 1 | 0.83 | −0.73 | 0.0001d |
| X12 | c11 = −4.65 | 1 | 0.81 | −5.72 | 0.0003d |
| X22 | c22 = −8.10 | 1 | 0.81 | −9.96 | 0.0001d |
| X32 | c33 = −5.55 | 1 | 0.81 | −6.82 | 0.0001d |
| X1X2 | c12 = −3.01 | 1 | 1.09 | −2.76 | 0.0222d |
| X1X3 | c13 = −4.22 | 1 | 1.09 | −3.87 | 0.0038d |
| X2X3 | c23 = −3.69 | 1 | 1.09 | −3.38 | 0.0081d |
Y0 = 50.61 + 0.0081X1 + 0.75X2 − 0.61X3 − 4.65X12 − 8.10X22 −5.55X32 − 3.01X1X2 − 4.22X1X3 − 3.69X2X3.
R2 = 0.9540.
X1, probiotic; X2, FOS; X3, maltodextrin.
Significant at an alpha value of 0.05.
The effect of each factor was further assessed by the use of perturbation plots to show how the response changes as each factor moves from the chosen reference point, with all other factors held constant at reference values (20). For this study, as one particular chosen factor was assessed, the other factors were held constant at the optimum point. We defined the response surface model, as obtained from Tables 5 and 6, as  = f(X1, X2, X3), with X*1, X*2, and X*3 as the optimum points of the factors, which in our experiments would be 0.018, 0.062, and −0.081. Thus, the perturbation effect of X1 was defined as follows:
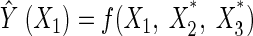 |
(2) |
Similarly, the perturbation effects of X2 and X3 would be:
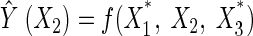 |
(3) |
 |
(4) |
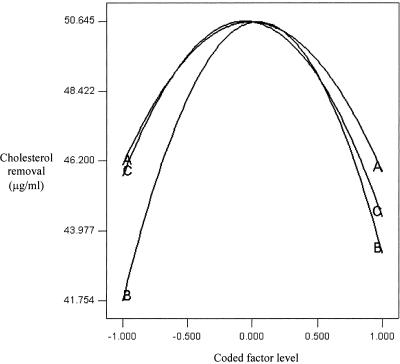
Perturbation effect curves were produced with the vertical axis representing Ŷ(Xj) and the horizontal axis representing Xj. In this study, all Xj values have common coded levels, and thus the horizontal axis represents the common coded levels. By overlying all of the perturbation curves, we obtained a perturbation plot (20). Figure 1 shows the perturbation plot of the factors used in this study. Although all factors showed significant quadratic effects, the curve with the most prominent change was the perturbation curve of FOS compared to those of the other factors fixed at their maximum levels. Thus, we believe that FOS was the most significant factor that contributed to the removal of cholesterol and had the most pronounced quadratic effect. The probiotic showed the least prominent change compared to the other two factors, but it still showed a significant quadratic effect.
TABLE 6.
Regression coefficients of the second-order equation for the five responsesa
| Coefficient | Value for indicated response
|
||||
|---|---|---|---|---|---|
| Y1 | Y2 | Y3 | Y4 | Y5 | |
| c | 47.96 | 52.58 | 64.12 | 244.81 | 62.07 |
| c1 | −0.20 | −2.50b | −3.50 | −22.12b | −16.78b |
| c2 | 0.48 | 8.15b | −1.01 | 0.63 | 8.48 |
| c3 | 0.17 | 2.34b | 2.65 | 1.82 | 1.33 |
| c11 | −7.93b | −0.12 | −9.75b | −5.93b | 5.04b |
| c22 | −8.71b | −0.88 | −14.14b | −1.74 | −2.79 |
| c33 | −8.46b | −8.12b | 0.96 | −1.69 | −3.04 |
| c12 | 0.0079 | 3.61b | 5.61 | −8.53b | 5.42b |
| c13 | −5.99b | −0.38 | 1.62 | 2.44 | 11.21b |
| c23 | −3.54b | −1.37 | 0.49 | 3.50 | −0.59 |
| R2 | 0.9794 | 0.9437 | 0.9064 | 0.9682 | 0.9551 |
| P value | 0.0001 | 0.0001 | 0.0012 | 0.0001 | 0.0001 |
Y = c + c1X1 + c2X2 + c3X3 + c11X12 + c22X22 + c33X32 + c12X1X2 + c13X1X3 + c23X2X3. Y1 = growth (%), Y2 = substrate utilization (%), Y3 = yield (% growth per gram of substrate utilized), Y4 = mean doubling time (minutes), and Y5 = SCFA (mM).
Significant at an alpha level of 0.05.
FIG. 1.
Perturbation plot of probiotic (A), FOS (B), and maltodextrin (C).
The best explanatory equation to fit the second-order model and subsequently produce the response surface was expressed as follows:
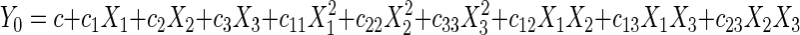 |
(5) |
where c…c23 are regression coefficients and X1, X2, and X3 are the coded independent factors. In this case, the second-order regression model involved three factors, thus producing three linear, three quadratic, and three interaction terms. The response surface was generated (Fig. 2) based on the following second-order equation:
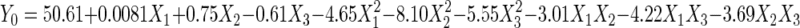 |
(6) |
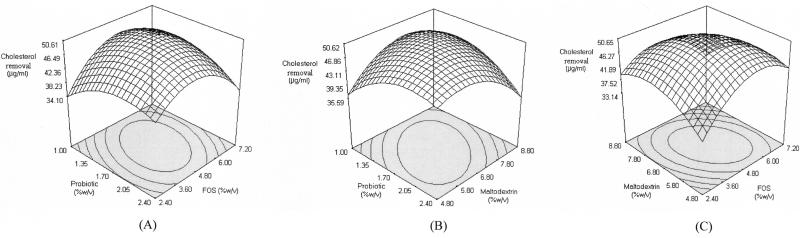
FIG. 2.
Response surface for cholesterol removal from the effects of probiotic and FOS at 6.64% (wt/vol) maltodextrin (A), probiotic and maltodextrin at 4.95% (wt/vol) FOS (B), and FOS and maltodextrin at 1.71% (wt/vol) probiotic (C).
An optimum point was produced, with optimum cholesterol removal obtained at 50.66 μg/ml. The combination that produced the optimum point was (X1, X2, X3) = (0.018, 0.062, −0.081). The original levels that correlated with those coded values were found to be probiotic at 1.71% (wt/vol), FOS at 4.95% (wt/vol), and maltodextrin at 6.64% (wt/vol). From the coefficient estimates (Table 5), all interaction terms were found to be significant. It must be noted that the coefficient estimates of the interaction terms (X1, X3) and (X2, X3) had negative signs (X13 = −4.22, and X23 = −3.69). These negative signs may imply that for an increase in the response, the coded levels of (X1, X3) and (X2, X3) must have different signs, i.e., one must be larger than zero and the other must be lower than zero (20). From the three-dimensional plot of probiotic and maltodextrin (Fig. 2B), we found that when the optimum point was achieved, the coded levels of X1 and X3 were 1.71 and −0.081, respectively. The same applied for maltodextrin and FOS interactions (Fig. 2C), with the optimum being achieved at 0.062 and −0.081 for X2 and X3, respectively. However, it must be noted that the interaction of X1 and X2 also showed a negative sign, but the response surface showed that the optimum was achieved when X1 = 0.018 and X2 = 0.062, which would produce a positive sign instead. This may be due to other terms that dominate this particular interaction term (20). Considering that the lack-of-fit test was insignificant, other higher terms would not have contributed to this, and thus we postulate that the linear term might have played a role.
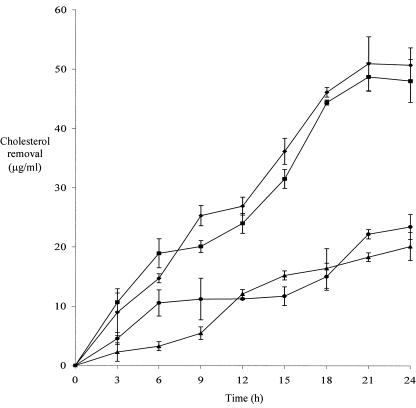
All of these predictions by the regression model were further ascertained by a validation experiment. We compared the cholesterol removal patterns over a 24-h period by using four different media: the optimum medium (1.71% [wt/vol] probiotic, 4.95% [wt/vol] FOS, and 6.64% [wt/vol] maltodextrin), the center-point medium (1.70% [wt/vol] probiotic, 4.80% [wt/vol] FOS, and 6.80% [wt/vol] maltodextrin), the high-point medium (2.40% [wt/vol] probiotic, 7.20% [wt/vol] FOS, and 8.80% [wt/vol] maltodextrin), and the low-point medium (1.00% [wt/vol] probiotic, 2.40% [wt/vol] FOS, and 4.80% [wt/vol] maltodextrin). The cholesterol removal curves are shown in Fig. 3. Although the exact cholesterol removal quantities were different from the predictions, the patterns were in tandem with the predictions by the model. The highest levels of cholesterol were removed from the optimum medium and the center-point medium. The smallest amounts of cholesterol were removed from both the high-point and low-point media, as supported by the response surface of cholesterol removal (Fig. 2). All of these data indicated that the model produced was reliable to optimize in vitro cholesterol removal that may be used to benefit human physiological health.
FIG. 3.
Cholesterol removal by L. casei ASCC 292 in optimum (♦), center-point (▪), high-point (•), and low-point (▴) media used for validation experiments. The factors used in combination for the optimum medium were probiotic (1.71% [wt/vol]), FOS (4.95% [wt/vol]), and maltodextrin (6.64% [wt/vol]). The combination used for the center-point medium was probiotic (1.70% [wt/vol]), FOS (4.80% [wt/vol]), and maltodextrin (6.80% [wt/vol]). The combination used for the high-point medium was probiotic (2.40% [wt/vol]), FOS (7.20% [wt/vol]), and maltodextrin (8.80% [wt/vol]). The combination used for the low-point medium was probiotic (1.00% [wt/vol]), FOS (2.40% [wt/vol]), and maltodextrin (4.80% [wt/vol]). Error bars represent standard errors of the means. N = 2 replicates, N = 3 sets of data/replicate, and n = 6 total observations.
Growth, substrate utilization, and end product of fermentation of prebiotics.
We further studied the growth, substrate utilization, growth yield, mean doubling time, and end product of fermentation of prebiotics for the experimental regions used to obtain the optimum removal of cholesterol. Statistical analyses with coefficient estimates and the significance of each response model are presented in Table 6.
The response surface of growth (Y1) was generated based on the coded factor equation by use of the coefficients shown in Table 6. The growth increased with increasing probiotic levels from 1.00 to 1.69% (wt/vol). Further increases in the concentrations of probiotic beyond 1.69% (wt/vol) generated decreases in growth. Similarly, increments in FOS and maltodextrin concentrations from 2.40 to 4.86% (wt/vol) and 4.80 to 6.82% (wt/vol), respectively, increased the growth, but further increases in the prebiotic concentrations generated decreases in growth. All factors studied showed significant quadratic effects, as shown by the P values of the coefficient estimates. Other than the main quadratic effects, the interaction between the probiotic and maltodextrin produced the strongest influence on growth, while the interaction between the probiotic and FOS was insignificant. The response surface of growth showed similar patterns with the response surface of the removal of cholesterol, indicating a strong correlation between the removal of cholesterol and growth. We have previously shown that in vitro cholesterol assimilation is growth associated (16). Knowing this, it would be beneficial to maintain or improve the viability of Lactobacillus acidophilus ASCC 292 in in vivo models in order to favor cholesterol removal as well.
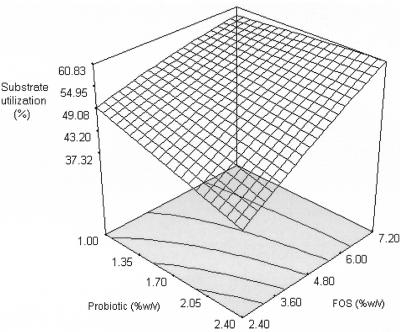
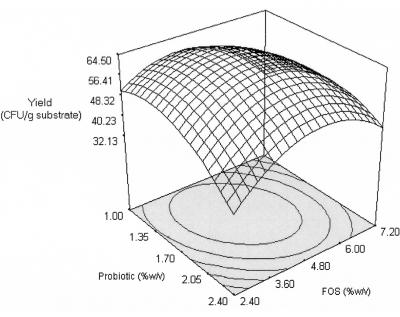
The response surfaces of substrate utilization (Y2) and growth yield (Y3) are shown in Fig. 4 and 5 and were generated based on the second-order coefficients (Table 6). Only maltodextrin produced a significant quadratic effect; the substrate utilization increased with increasing maltodextrin concentrations from 4.80 to 6.56% (wt/vol), but a further increase produced a decrease in substrate utilization. A maltodextrin-like oligosaccharide was reported to have a lower rate of fermentation than FOS and was more fermentable in the distal part of the large intestine (10). The probiotic and FOS did not produce a significant quadratic effect, but they showed significant linear correlations (Fig. 4). The interaction effects showed that only the interaction between probiotic and FOS was significant. At a higher FOS concentration (7.20% [wt/vol]), substrate utilization increased with increasing concentrations of probiotic (1.00 to 2.40% [wt/vol]). In contrast, at a low FOS concentration (2.40% [wt/vol]), substrate utilization decreased with increasing concentrations of the probiotic. This may be due to competition for the substrate with increasing cell numbers at low substrate levels. It must be noted that substrate utilization increased with increasing probiotic and FOS concentrations, despite a decrease in growth and cholesterol removal for these experimental regions. Thus, cholesterol removal may be growth associated, but both cholesterol removal and growth were not influenced solely by the utilization of FOS. This was supported by the lower growth yield at these regions (Fig. 5). Although maltodextrin did not show an overall significant interaction effect with the probiotic or FOS, it generated a significant main quadratic effect. Our results indicated that interactions between the probiotic and maltodextrin might have a stronger influence on growth and cholesterol removal at regions that were not contributed by an interaction of the probiotic and FOS. It appears that maltodextrin served as an alternative substrate when FOS was insufficient to increase the growth and subsequent removal of cholesterol. This is important for synbiotic preparation as an in vivo adjunct; FOS may be used solely or used at low concentrations coupled with maltodextrin.
FIG. 4.
Response surface for substrate utilization (%) from the effects of probiotic and FOS at 6.64% (wt/vol) maltodextrin.
FIG. 5.
Response surface for growth yield from the effects of probiotic and FOS at 6.64% (wt/vol) maltodextrin.
The mean doubling time was used as a measure of the effectiveness of a specific carbon source in modulating the growth rate (4). For this study, the quadratic model for the mean doubling time (Y4) was generated by using the coefficients shown in Table 6. The mean doubling time decreased minimally at a low FOS level (2.40% [wt/vol]) compared to the prominent changes at a higher FOS level (7.20% [wt/vol]). It must be noted that substrate utilization increased with increasing probiotic concentrations at the higher FOS level (Fig. 4), thus resulting in a decrease in the mean doubling time. This indicated that the fermentation of FOS was more effective at the higher FOS concentration. However, the mean doubling time was found to be lowest for the combinations of 2.40% (wt/vol) probiotic and 2.40% (wt/vol) FOS and of 2.40% (wt/vol) probiotic and 4.80% (wt/vol) maltodextrin, despite the lowest substrate utilization, growth, and removal of cholesterol for those regions. Considering that the concentration of probiotic was at its highest but the FOS and maltodextrin concentrations were at their lowest, it appears logical that the growth would be faster (shorter mean doubling time) but that, overall, the percentage of growth would be small compared to that at lower probiotic concentrations or higher prebiotic concentrations. Thus, although cholesterol removal was found to be lower, there is a possibility that cholesterol removal was faster in these regions before cholesterol-removing activities reached a plateau. Further studies would be needed to confirm these phenomena.
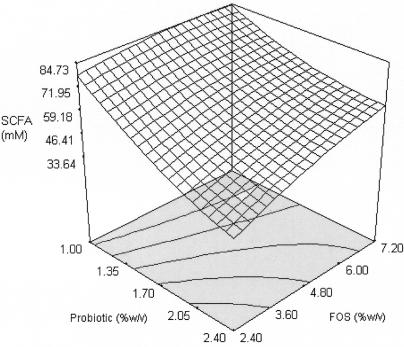
The major products of the metabolism of prebiotics are SCFA, carbon dioxide, hydrogen, and bacterial cell mass (7). Although much work has been done on SCFA production and the significance of the individual fatty acids, no particular pattern of SCFA production from prebiotic fermentation has yet emerged. The amount of SCFA (Y5) was obtained as a total of individual fatty acids, namely, acetic, butyric, and propionic acids. Only the probiotic produced significant quadratic effects on SCFA production, as did interactions between (X1, X2) and (X1, X3). The response surface (Fig. 6) generated from the second-order coefficients (Table 6) showed a close correlation with substrate utilization (Fig. 4). This indicated that the production of SCFA from the fermentation of FOS was closely associated with the uptake of the substrate. However, it must be noted that increasing the concentration of probiotic at a higher level of FOS (7.20% [wt/vol]) generated a decrease in SCFA production but increased substrate utilization. The hydrolysis of FOS was repressed by the products of the hydrolysis (13). Thus, we postulate that an increase in substrate utilization in the experimental regions would generate higher concentrations of hydrolysis products and subsequently repress further SCFA production.
FIG. 6.
Response surface for SCFA production from the effects of probiotic and FOS at 6.64% (wt/vol) maltodextrin.
Conclusions.
The optimal cholesterol removal from different media was 50.66 μg/ml in the presence of 1.71% (wt/vol) probiotic, 4.95% (wt/vol) FOS, and 6.64% (wt/vol) maltodextrin. The validation experiment showed that RSM was reliable for developing a model, optimizing factors, and analyzing interaction effects. Analyses of growth, substrate utilization, yields, mean doubling times, and the production of SCFA showed that cholesterol removal was growth associated. FOS was the preferred substrate for growth, cholesterol removal, and the production of SCFA, while maltodextrin was alternatively used for these purposes when FOS was insufficient. The information gathered in this study will benefit the development of a synbiotic product that will particularly target cholesterol removal. In vivo experiments are required to ascertain the cholesterol-lowering capacity of L. acidophilus ASCC 292 in the presence of prebiotics.
REFERENCES
- 1.Anderson, J. W., and S. E. Gilliland. 1999. Effect of fermented milk (yoghurt) containing Lactobacillus acidophilus L1 on serum cholesterol in hypercholesterolemic humans. J. Am. Coll. Nutr. 18:43-50. [DOI] [PubMed] [Google Scholar]
- 2.Araujo, P. W., and R. G. Brereton. 1996. Experimental design II: optimization. Trends Anal. Chem. 15:63-70. [Google Scholar]
- 3.Bermudez, L., C. B. Inderlied, P. Kolonoski, M. Wu, P. Aralar, and S. L. Young. 2001. Telithromycin is active against Mycobacterium avium in mice despite lacking significant activity in standard in vitro and macrophage assays and is associated with low frequency of resistance during treatment. Antimicrob. Agents Chemother. 45:2210-2214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bruno, F. A., W. E. V. Lankaputhra, and N. P. Shah. 2002. Growth, viability and activity of Bifidobacterium spp. in skim milk containing prebiotics. J. Food Sci. 67:2740-2744. [Google Scholar]
- 5.Collins, M. D., and G. R. Gibson 1999. Probiotics, prebiotics and synbiotics: approaches for modulating the microbial ecology of the gut. Am. J. Clin. Nutr. 69:1052S-1057S. [DOI] [PubMed] [Google Scholar]
- 6.Cox, D. R., and N. Reid. 2000. The theory of the design of experiments. Chapman and Hall, London, United Kingdom.
- 7.Cummings, J. H., G. T. Macfarlane, and H. N. Englyst. 2001. Prebiotic digestion and fermentation. Am. J. Clin. Nutr. 73:415S-420S. [DOI] [PubMed] [Google Scholar]
- 8.Dubey, U. K., and V. V. Mistry. 1996. Effect of bifidogenic factors on growth characteristics of bifidobacteria in infant formulas. J. Dairy Sci. 79:1156-1163. [DOI] [PubMed] [Google Scholar]
- 9.Dubois, M., K. A. Gilles, J. K. Hamilton, P. A. Rebers, and A. Smith. 1956. Colorimetric method for determination of sugars and related substances. Anal. Chem. 28:350-356. [Google Scholar]
- 10.Flickinger, E. A., B. W. Wolf, K. A. Garleb, J. Chow, G. J. Leyer, P. W. Johns, and G. C. Fahey. 2000. Glucose-based oligosaccharides exhibit different in vitro fermentation patterns and affect in vivo apparent nutrient digestibility and microbial populations in dogs. J. Nutr. 130:1267-1273. [DOI] [PubMed] [Google Scholar]
- 11.Fuller, R. 1992. Probiotics: the scientific basis. Chapman and Hall, London, United Kingdom.
- 12.Gibson, G. R., and M. B. Roberfroid. 1995. Dietary modulation of the human colonic microbiota: introducing the concept of prebiotics. J. Nutr. 125:1401-1412. [DOI] [PubMed] [Google Scholar]
- 13.Kaplan, H., and W. Hutkins. 2003. Metabolism of fructooligosaccharides by Lactobacillus paracasei 1195. Appl. Environ. Microbiol. 69:2217-2222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kok, N., and A. Delzenne. 1998. Oligofructose modulates lipid metabolism alterations induced by a fat-rich diet in rats. J. Appl. Toxicol. 18:47-53. [DOI] [PubMed] [Google Scholar]
- 15.Lee, S. L., and W. C. Chen. 1997. Optimization of medium composition for the production of glucosyltransferase by Aspergillus niger with response surface methodology. Enzyme Microb. Tech. 21:436-440. [Google Scholar]
- 16.Liong, M. T., and N. P. Shah. 2005. Acid and bile tolerance and cholesterol removal ability of lactobacilli strains. J. Dairy Sci. 88:55-66. [DOI] [PubMed] [Google Scholar]
- 17.Manson, J. E., H. Tosteson, P. M. Ridker, S. Satterfield, P. Herbert, and G. T. O'Conner. 1992. The primary prevention of myocardial infarction. N. Engl. J. Med. 326:1406-1416. [DOI] [PubMed] [Google Scholar]
- 18.Montgomery, D. C. 1996. Design and analysis of experiments. John Wiley and Sons, New York, N.Y.
- 19.Niness, K. R. 1999. Nutritional and health benefits of inulin and oligofructose. J. Nutr. 129:1402S-1406S. [DOI] [PubMed] [Google Scholar]
- 20.Oh, S., S. Rheem, J. Sim, S. Kim, and Y. Baek. 1995. Optimizing conditions for the growth of Lactobacillus casei YIT 9018 in tryptone-yeast extract-glucose medium by using response surface methodology. Appl. Environ. Microbiol. 61:3809-3814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Robertfroid, M. B., and N. Delzenne. 1998. Dietary fructans. Annu. Rev. Nutr. 18:117-143. [DOI] [PubMed] [Google Scholar]
- 22.Rudel, L. L., and M. D. Morris. 1973. Determination of cholesterol using o-phthalaldehyde. J. Lipid Res. 14:364-366. [PubMed] [Google Scholar]
- 23.Sanders, M. E. 2000. Considerations for use of probiotic bacteria to modulate human health. J. Nutr. 130:384S-390S. [DOI] [PubMed] [Google Scholar]
- 24.Shin, H. S., J. H. Lee, J. J. Pestka, and Z. Ustunol. 2000. Growth and viability of commercial Bifidobacterium spp. in skim milk containing oligosaccharides and inulin. J. Food Sci. 65:884-887. [Google Scholar]
- 25.Suskovic, J., B. Kos, J. Goreta, and S. Matosic. 2001. Role of lactic acid bacteria and bifidobacteria in synbiotic effect. Food Technol. Biotechnol. 39:227-235. [Google Scholar]