Patient-Specific Three-Dimensional Ultrasound Derived Computational Modeling of the Mitral Valve

Abstract

Several new techniques to repair the mitral valve affected by functional mitral regurgitation are in development. However, due to the heterogeneity of valve lesions between patients, predicting the outcomes of novel treatment approaches is challenging. We present a patient-specific, 3D ultrasound-derived computational model of the mitral valve for procedure planning that faithfully mimics the pathological valve dynamics. 3D ultrasound images were obtained in three pigs induced with heart failure and developing functional mitral regurgitation. For each case, images were segmented, and finite element model of mitral valve was constructed. Annular and papillary muscle dynamics were extracted and imposed as kinematic boundary conditions, and the chordae were pre-strained to induce valve tethering. Valve closure was simulated by applying physiologic transvalvular pressure on the leaflets. Agreement between simulation results and truth datasets was excellent, with accurate location of regurgitation jets and coaptation defects. Inclusion of kinematic patient-specific boundary conditions was necessary to achieve these results, whereas use of idealized boundary conditions deviated from the truth dataset. Due to the impact of boundary conditions on the model, the effect of repair strategies on valve closure varied as well, indicating that our approach of using patient-specific boundary conditions for mitral valve modeling is valid.

1. Introduction

Computational models of heart valves can be powerful tools in testing the safety and efficacy of new surgical techniques and interventional devices, prior to their application in human patients [21]. Since new techniques or devices can impact the valve function and tissue mechanics in unforeseen ways, certain risks exist in their application in humans. Animal models fill this gap quite well, however, they do not capture the heterogeneity of the valve lesions seen in human patients, and are challenging to use when biomechanical insights are needed [34]. Computational modeling fills this gap, as patient-specific valve geometries can be constructed from clinical imaging modalities, and the hypothetical effects of different repair strategies on the valve function and mechanics can be investigated. In theory, these benefits are well known, but computational modeling to date has largely been isolated to idealized geometries, due to the complexity of segmenting and reconstructing geometries from clinically used, proprietary imaging modalities [1]. Computed tomography (CT) imaging has been used by others in developing models [9, 20, 22], but this is rarely used in clinical workflow when repairing most heart valves [8]. Ultrasound imaging is used in every heart valve procedure and provides the best platform for any patient-specific computational modeling strategies [29].

Recently, interest in developing computational models of the mitral valve (MV), the left-sided atrioventricular valve, has emerged [4], as several new techniques to repair or replace the diseased mitral valve are in development [15, 37]. The mitral valve has a complex geometry, with several dynamic components, all of which work in synchrony for optimal valve function [18]. Dysfunction of the mitral valve includes disruption of the physiological geometry and dynamism of one or more of these components, and thus significant heterogeneity exists between patients [14]. Especially in functional mitral regurgitation (FMR), which is seen in patients with heart failure from different types of cardiomyopathies, the distortion and extent of geometric changes to the mitral valve vary significantly between patients [11, 35]. Large animal models of FMR have been reported extensively [13, 39], including our group [19, 30], but none capture the valve geometry or disease severity that is seen in human patients [17]. Thus, computational modeling can fill a significant gap.

Numerical simulation of the MV structure based on patient-specific imaging data has been attempted previously, to define the native mechanics of the valve [36], understand its physiology and pathology [24], and investigate the impact of novel treatment strategies [38]. All of these models were focused on healthy valves and did not mimic disease conditions that new therapies would be used to ameliorate. Till date, only a few models were created to investigate the mechanics of the MV in the presence of FMR. Pham et al. [22] and Kong et al. [9] presented detailed MV model with realistic chordae locations created using CT data. While CT provides good quality images, it is rarely used to depict the MV kinematics due to radiation exposure, and dynamic multiphase images are rarely available [8]. In the acquired CT data, the authors were not able to detect all the chordae or the accurate chordal length, so a complete patient-specific chordal distribution was not achieved. Choi et al. [2] reported a model from echocardiographic data and used this model to simulate the outcomes of annuloplasty repair, but the model lacked patient-specific motion of papillary muscles (PMs) and any one-to-one comparison to truth datasets. Rego et al. [25] also used echocardiographic images to reconstruct just the valve leaflets, which oversimplified the geometry of the valve. Due to lack of chordae, no patient-specific motion of papillary muscles (PMs) could be included in this model.

In this study, we present a modeling approach to create a patient-specific mitral valve model from 3D echocardiography. This approach addresses the limitations that were present in FMR models created by other research groups. In particular, we (1) used 3D ultrasound data, which is a clinical standard for MV imaging, (2) included geometric model of the leaflets on a patient-specific basis, and chordae tendineae distribution from human anatomical studies, (3) prescribed patient-specific kinematic boundary conditions, i.e., systolic motion of mitral annulus and papillary muscles, and (4) performed one-to-one comparison of simulation results to the truth datasets. To indicate the impact of patient-specific motion of annulus and PMs on FMR modeling, we evaluated the outcomes of systolic function simulation given different boundary conditions, i.e., with and without motion of mitral annulus and PMs. In addition, to emphasize this impact and to justify modeling contribution, we present simulations of the MV systolic function after MitraClip implantation, which is the only medical device approved for the repair of FMR.

2. Materials and Methods

A. Swine model of functional mitral regurgitation

The animal procedures were performed in the AAALAC accredited facility, per the regulations of the United States Department of Agriculture (USDA) and National Institutes of Health (NIH) guidelines for use of animals in research. Three swine were purchased from a USDA certified vendor (Valley Brook Farms, GA), transported to our lab, and quarantined for 3–5 days. The procedures were performed in a cardiac catheterization lab dedicated for animal use only (Phillips Allura, Phillips Healthcare). The pigs were fasted overnight, and on the procedure day, sedated with Telazol (2–8.8 mg/kg, intramuscular (IM)), intubated, and then mechanically ventilated in supine position with 1–2% isoflurane mixed in 100% oxygen. An auricular vein catheter was placed, and Cefazolin (antibiotic, 22–25 mg/kg, intravenous (IV)), Rimadyl (analgesic, 2 mg/kg, IM), and Buprenex (analgesic, 0.0075–0.01 mg/kg, IM) were injected. A continuous drip of Amiodarone (anti-arrhythmic, 0.5 mg/min, IV) was maintained to reduce the risk of arrhythmias during the procedure. A small left thoracotomy was performed to tunnel an ultrasound probe (Z6Ms, Siemens Healthineers, WA) placed in a sterile cover, onto the surface of the left atrium to image the entire left heart. Baseline transesophageal echocardiography was performed to obtain 2D and 3D images and color Doppler data on the MV (Siemens SC2000 Prime, Siemens Healthineers, WA). A femoral arterial and venous sheath were placed, to gain access to the vasculature. A 6 Fr pigtail catheter was advanced through the arterial sheath into the left ventricle, and a ventriculogram was performed to obtain cardiac function. The catheter was then removed and exchanged with a 6 or 7 Fr hockey stick catheter, to engage the left coronary ostium and to map the left coronary arterial system. The left circumflex artery was identified, and a 0.014” guidewire was advanced through the catheter into the main stem of the artery. A balloon was inflated just after the first obtuse marginal branch artery to block all blood flow. Through the central lumen of this catheter, 100%, 200-proof, ethanol was injected into the vascular volume downstream of this balloon to coagulate it. Ethanol coagulates blood within 5–10 minutes of mixing, causing a clot to form that cannot be resolved. This results in a posterolateral myocardial infarction that spans 30–40% of the entire left ventricular myocardial mass. Ultrasound imaging was repeated, and the catheters were removed. Incisions then were closed, and animals were recovered from surgery.

Between 2.5–3 months after this infarction procedure, animals were prepared as described above, and repeat echocardiographic imaging of the left side of the heart was performed. Extensive details of this swine model of heart failure and FMR were reported in earlier studies from our group [19, 30].

B. Computational model development

Image segmentation:

Post-infarction 3D echocardiographic images were segmented using semi-automated methods in a proprietary software (Siemens AutoValve, Siemens Healthineers, WA). In each time frame from end-diastole to peak systole, automated segmentation enabled identification of major landmarks of the MV: the annulus, free margin of the leaflets, the leaflet surfaces, and the PMs. In most cases, some degree of manual correction of the valve geometry was needed, following which the 3D segmented model was exported as a stereolithographic (STL) image.

Model adjustments:

The semi-automated segmentation process was fast and the exported STL model was accurate but had some limitations. Firstly, a uniform thickness was applied onto the model by the software, which modified the leaflet geometry to a certain extent. Secondly, the surface nodes on the exported mesh were irregularly arranged, which would not yield a good quality mesh for computational purposes. For this reason, a custom MATLAB (MathWorks, MA) code was developed, into which the STL model was read, and the-mid surfaces of the leaflets from the model were calculated to create a good quality mesh.

After the end-diastolic geometry of the MV was segmented (Figure 1a and Figure 1b) and the STL file was exported, the model was positioned in the 3D Cartesian coordinate system such that the z-axis would go through the LV apex and the MV centroid, and x- and y-axes would be perpendicular to the MV annular plane (Figure 1c). The oriented model was then imported into MATLAB as a point cloud (Figure 1d) and the mid-surfaces of the leaflets were calculated. To achieve this, the 3D point cloud was sliced into radial planes, rotated uniformly around the z-axis. The number of planes was chosen according to the MV geometry, and 9 or 18 planes were sufficient to obtain adequate spatial resolution. Each created plane had two sets of points, describing the positions of anterior leaflet (AL) and posterior leaflet (PL) in the specific plane. To calculate the curves depicting the mid-surfaces of the leaflets, a polynomial was fitted to each set of points. Each curve was then resampled to 32 points, uniformly distributed along the length of the leaflets in the radial direction, thus creating a new 3D point cloud, organized in 32 parallels. For each parallel, the coordinates of consisting points were approximated with a 3D closed spline and up-sampled to 300 points, uniformly distributed along the circumference of the MV (Figure 1e). Finally, the created points were meshed using triangular shell elements (Figure 1f). Regionally varying thickness was assigned to the leaflets, as suggested by Kunzelman et al. [10], with mean values of 1.32±0.11 mm for the AL and 1.22±0.03 mm for the PL. Density for the MV leaflets was assumed to be 10.4 g/cm³, which is ten times higher than the real density, thus accounting the inertial effects of the blood volume spanned and moved by the MV during its closure. Such volume is about ten times larger than the volume of the MV leaflets [33].

Figure 1.

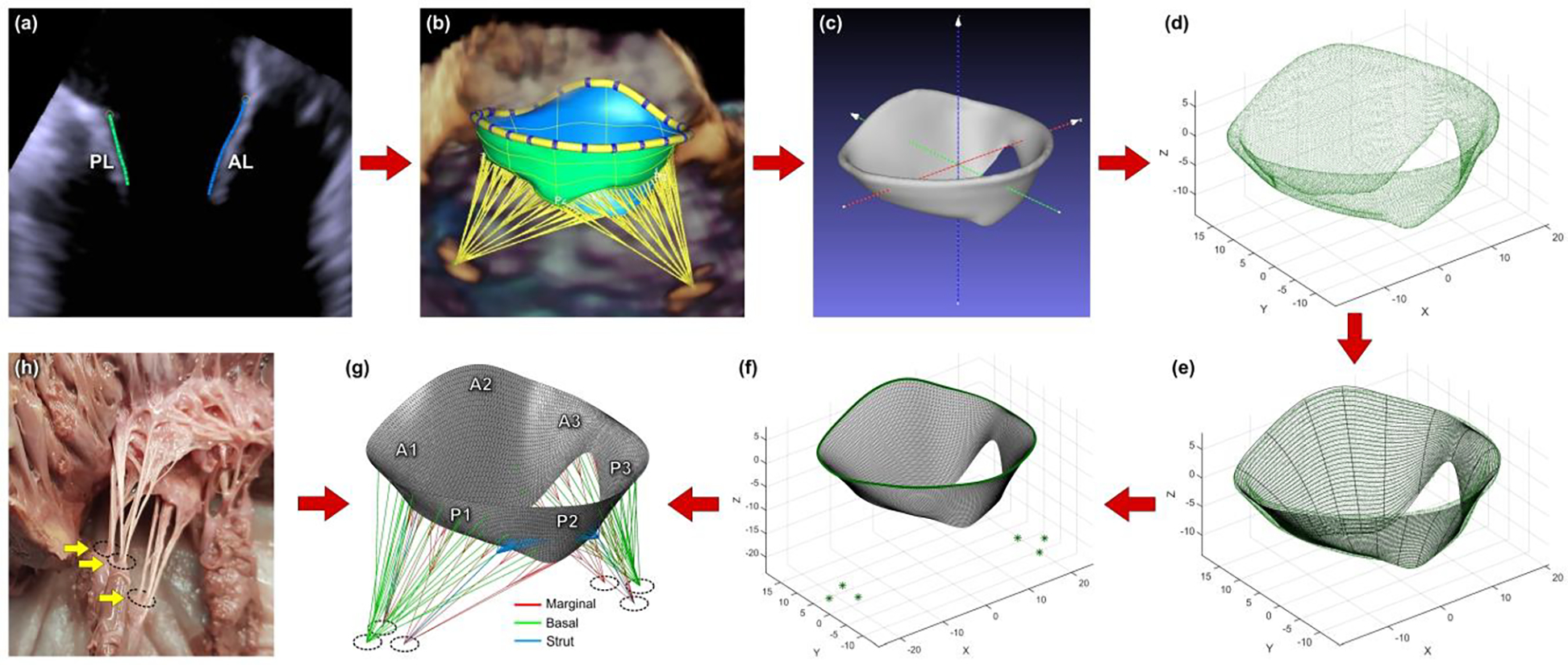
Steps for creating a patient-specific mitral valve computational model: (a) MV leaflets segmented in Siemens AutoValve; (b) complete geometry of the valve ready to be exported as STL model; (c) model positioned in the 3D Cartesian coordinate system; (d) model imported into MATLAB as a point cloud; e) mid-surface of the leaflets approximated with splines; (f) mesh created using triangular shell elements; (g) finished finite element model with chordae tendineae; (h) ex vivo mitral valve specimen showing chordae emerging from three papillary muscle heads.

Chordae tendineae:

The MV model was completed by creating a network of 22 marginal, 6 strut, and 22 basal branched chordae (Figure 1g). The chordal distribution pattern developed by the Biomechanics Group in DEIB, Politecnico di Milano (Italy) [32] was adapted, while chordal insertion points on the PMs were determined in accordance with ex vivo findings in cadaver hearts. Each PM was subdivided into three regions, representing individual PM heads, with marginal, strut, and basal chordae emerging from these heads, as seen in the ex vivo MV specimens (Figure 1h). The chordae were modeled as truss elements with constant cross-sectional area values of 0.40 mm², 1.15 mm², and 0.79 mm² for marginal, strut, and basal chordae, respectively.

C. Mechanical properties

The mechanical behavior of the leaflets was assumed nonlinear and anisotropic because of the high concentration of collagen fibers in the leaflets [3], which leads to a higher stiffness along the fiber direction. In addition, as the MV model was described by shell elements, a plane stress assumption was made, meaning that all stresses were applied in a single plane while stress in the thickness direction was disregarded from the calculations $\left({\mathrm{\sigma }}_{33}=0\right)$. The stress-strain behavior of the leaflets was described using hyperelastic strain energy density function, proposed by Lee et al. [12]:

$$\Psi \left(I_1,I_4\right)=c_0\left(I_1-3\right)+c_1\left(\left(1-\beta \right)e^{[c_2{\left(I_1-3\right)}^2]}+\beta e^{[c_3{\left(I_4-1\right)}^2]}-1\right),$$

where $\mathrm{\beta }$ is a constitutive material parameter ranging from 0 to 1 and related to the level of material anisotropy, and ${\mathrm{c}}_0,{\mathrm{c}}_1,{\mathrm{c}}_2,{\mathrm{c}}_3$ are the remaining material parameters. The strain invariant ${\mathrm{I}}_1$ is used to describe the matrix material, and the invariant ${\mathrm{I}}_4$ is used to characterize the properties of the collagen and elastin fibers. The material parameters for the hyperelastic strain energy density function were identified by curve fitting to the experimental data published by May-Newman and Yin [16] of biaxial tensile test on the porcine MV leaflets. Stress-stretch curve fitting to the reported experimental data using a nonlinear least square method was performed in MATLAB, and the material parameters were calculated (Table 1). The strain energy density function was implemented in a user-defined subroutine within Abaqus, in which the derivatives of strain energy $\mathrm{\Psi }$ with respect to the invariants ${\mathrm{I}}_1$ and ${\mathrm{I}}_4$ are evaluated and the components of the Cauchy stress tensor $\mathbf{\sigma }$ are returned as an output.

Table 1.

Material parameters for the MV leaflets tissue.

	c0	c1	c2	c3	β
Anterior leaflet	0.826·10–3	0.048·10–3	25.5	32.5	0.195
Posterior leaflet	0.248·10–3	0.415·10–3	10.15	17.973	0.044

The mechanical behavior of the chordae tendineae was assumed nonlinear and isotropic, because the chordae are mainly composed of collagen fibers aligned in the longitudinal direction [27], thus making them both stiff and robust. The chordae were modeled to undergo only uniaxial tension and the incompressible behavior was assumed since no volumetric data was defined. For the mechanical behavior of the chordae, the 3rd order Ogden hyperelastic model was chosen from the Abaqus material model library. The constitutive material parameters for this model were computed in Abaqus by curve fitting to the uniaxial test data on porcine marginal, strut, and basal chordae reported by Pokutta-Paskaleva et al. [23].

D. Boundary conditions

End-diastole was chosen as the initial state for the simulation. In general, it can be assumed that at this time point, the chordae are straightened, while the whole model is approximately unloaded since the transvalvular pressure acting on the leaflets can be considered to be zero. However, in the FMR state, the PM locations are displaced, imposing pre-strains on the chordae. To mimic this, the chordae were divided into groups according to their type (marginal, strut, basal), origin (anteroposterior and posteromedial papillary muscles), and insertion site (AL, PL), and each group was pre-strained by displacing its origin along the z-axis further from the annular plane (Figure 2a). To obtain leaflet concavity toward the LA, which is characteristic to FMR, the largest pre-strains were imposed on the strut chordae, while the basal chordae experienced the smallest pre-strains. The maximum pre-strains induced on the chordae in each created model was 0.118±0.004. By including these pre-strains, we were able to simulate the FMR-imposed restricted motion of the leaflets and obtain a realistic systolic configuration of the valve.

Figure 2.

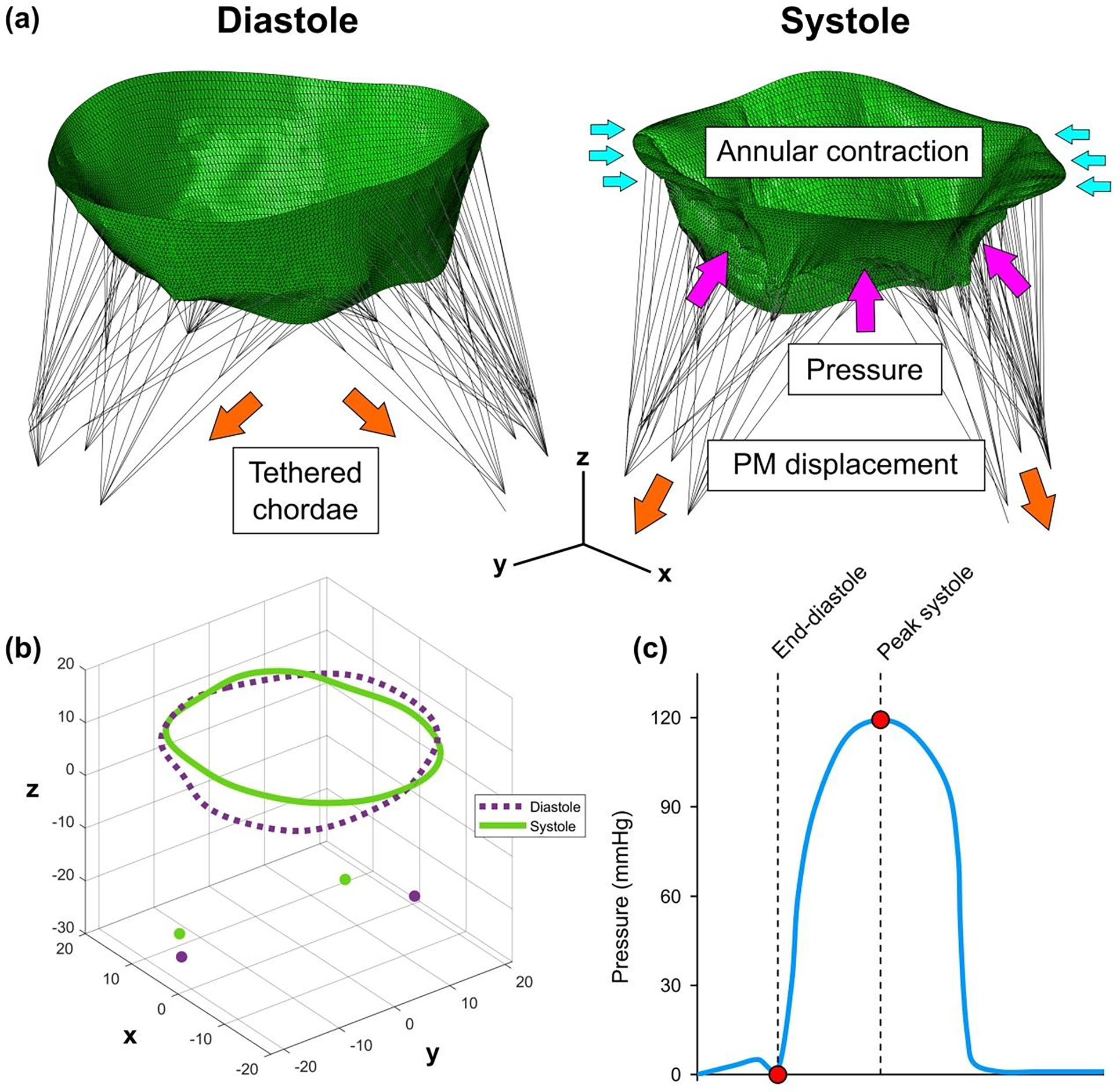
(a) Mitral valve model showing pre-strained chordae and boundary conditions. (b) Patient-specific systolic and diastolic configuration of mitral annulus and papillary muscle tips. (c) Time-dependent physiologic transvalvular pressure curve with end-diastole and peak systole highlighted as a time frame for the valve closure simulation.

To include patient-specific kinematic boundary conditions, the peak systolic geometry of the MV was segmented in Siemens AutoValve and exported as the STL model, similarly as the end-diastolic geometry. After positioning peak systolic model in the coordinate system used for the end-diastolic configuration, the systolic positions of the MV annulus and PMs were identified. By subtracting the diastolic coordinates from the systolic ones, the nodal displacements of the annulus and PMs were calculated. The annular contraction and the movement of the PMs were modeled by applying the calculated displacements to the nodes of the annulus and the PM heads (Figure 2b).

The impact of such patient-specific kinematic boundary conditions was investigated by running four simulations with different boundary conditions for each model: (1) dynamic annular and PMs motion, (2) without PMs motion, (3) without annular motion, and (4) without annular and PMs motion.

MV closure was simulated by applying time-dependent physiologic transvalvular pressure with a maximum value of 120 mmHg on the ventricular surface of the leaflets (Figure 2c). To capture the contact of the leaflets, a general contact algorithm available in Abaqus with a scale penalty method and a friction coefficient of 0.05 was set between the atrial surface of the leaflets.

E. Simulation

Because of the different heart rates in the obtained data sets, the time intervals between end-diastole and peak systole were different for every analyzed case. To simplify time incrementation of the analysis and processing of the results, these time frames were scaled to 0.25 s each. Automatic time incrementation with the maximum allowed time increment of 5·10⁻⁷ s was specified for all simulations. Each finite element model was prepared for the analysis and the simulations of the MV systolic function were run in Abaqus/Explicit. The following parameters were calculated in peak systole to quantitatively evaluate the mitral valve function in the presence of FMR: stress and strain distribution on the leaflets, tension forces in the chordae tendineae, and reaction forces acting on the PMs.

F. Modeling contribution

The modeling contribution was justified by running simulations of the MV systolic function after MitraClip implantation for case 1 with different boundary conditions, i.e., with and without motion of mitral annulus and PMs. The arms of MitraClip were modeled as two 9×5 mm rigid rectangular plates. The device was positioned in systole, and angular displacement was prescribed to the plates to draw them together and grasp the leaflets. For each simulation, two devices were deployed to assure the elimination of regurgitant gaps.

3. Results

A. Model validation and impact of boundary conditions

Validation of the created models was done by comparing the computed systolic surfaces of the MV with ultrasound data. Figure 3 depicts anteroposterior cross-sectional view of each computational model in systole superimposed to corresponding echocardiographic image. In addition, this figure also shows the agreement between modeling results and imaging data given different boundary conditions.

Figure 3.

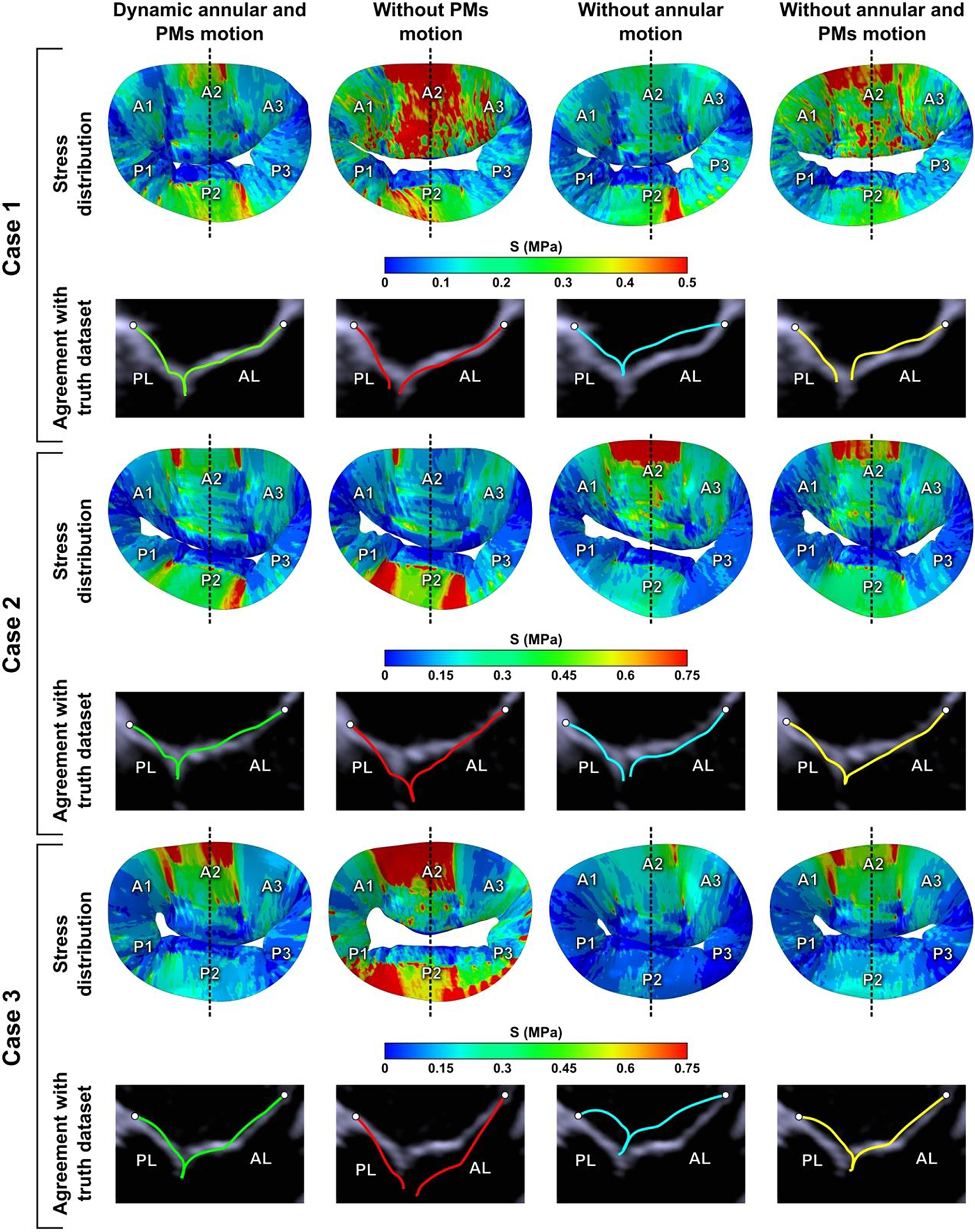
Impact of boundary conditions on stress distribution across the leaflets in peak systole and comparison of anteroposterior cross-sectional views of simulation results and echocardiographic images given different boundary conditions.

Good agreement between computational results and echocardiographic images in systole for each investigated case was observed only when patient-specific motion of mitral annulus and PMs was imposed as a boundary condition, thus indicating the fidelity of the computational models. However, in all other cases, i.e., when no annular or PM motion was included, corroboration between models and ultrasound data was weak, meaning that boundary conditions had a major impact on systolic leaflet configuration. Moreover, boundary conditions strongly impacted stress distribution on the leaflets as well: different high stress concentration areas and their locations on the leaflets were observed after each simulation with different boundary conditions prescribed (Figure 3).

To determine the congruence of regurgitant gap formation, further validation was done by comparing computational results (only models with patient-specific boundary conditions were used) to the 3D color Doppler echocardiographic images (Figure 4). A similar formation of regurgitant gaps both in models and echocardiographic images was observed. Such morphological congruence enhances the fidelity of the computational models and the modeling approach itself.

Figure 4.

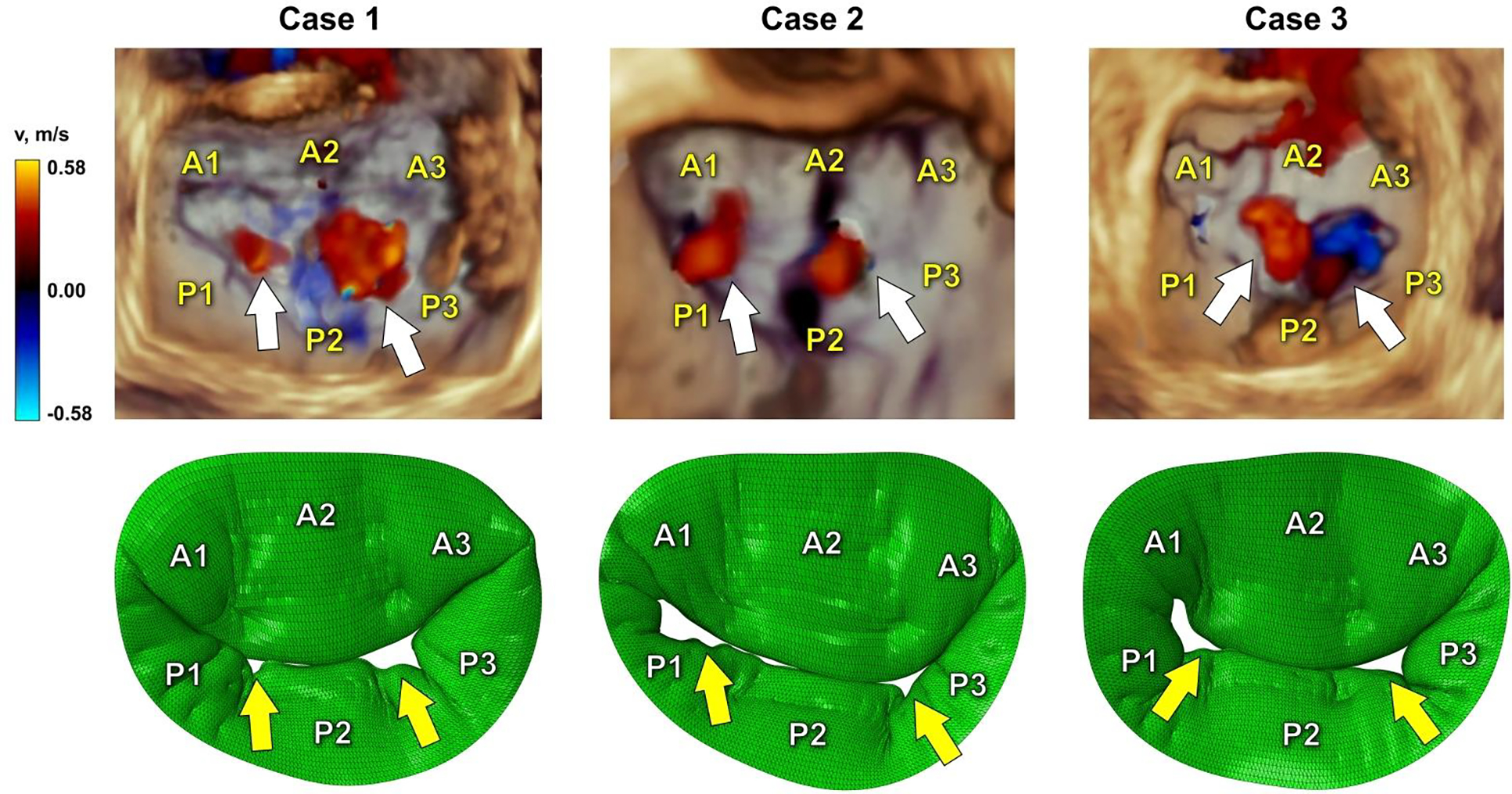
Comparison of 3D color Doppler ultrasound data and simulation results in systole. White arrows indicate regurgitant gaps in echocardiographic images, while yellow arrows show the formation of regurgitant gaps in computational models.

B. Mitral valve function in swine model of heart failure

At 2.5–3 months after the infarction, all three pigs had FMR. In cases 1 and 2, moderate FMR was observed, while in case 3 mild FMR was seen in the echocardiographic images. In cases 1 and 3, a larger regurgitant jet was noticed in A3-P3 region, while in A1-P1 region a small jet was observed. On the contrary, in case 2, a small jet was seen in A3-P3 region, while a larger jet was observed in A1-P1 region. Mitral valve function and dynamics measured in each model in diastole and systole are summarized here and tabulated in Table 2 and Table 3. The obtained values were compared with the echocardiographic measurements made in our lab [19] and the porcine data found in the literature [5].

Table 2.

Geometric parameters of the MV models and their comparison with echocardiographic measurements in diastole.

	Case 1	Case 2	Case 3	Mean±SD	Echo measurements (FMR) [5, 19]	Echo measurements (Control) [5, 19]
Annular area (mm2)	1242.0	1026.0	982.4	1083.4±139.0	-	-
Annular perimeter (mm)	127.9	117.3	113.2	119.5±7.6	-	-
AP diameter (mm)	33.5	33.9	32.0	33.1±1.0	-	-
IC diameter (mm)	42.7	39.7	41.2	41.2±1.5	-	-
A2 length (mm)	21.9	22.4	22.3	22.2±0.3	22.7±2.4	20.5±2.3
P2 length (mm)	11.7	13.2	13.0	12.6±0.8	14.7±1.8	14.0±1.5
AL area (mm2)	860.3	761.5	812.3	811.4±49.4	-	-
PL area (mm2)	497.6	513.1	488.6	499.8±12.4	-	-
Total leaflet area (mm2)	1357.9	1274.6	1300.9	1311.1±42.6	1254.8±91.6	1041.7±102.6
AL tenting angle (deg)	51.7	56.3	48.2	52.0±4.1	58.3±6.3	73.1±7.8
PL tenting angle (deg)	64.7	72.1	74.9	70.6±5.2	87.5±14.2	95.7±13.9
PM distance (mm)	46.3	40.0	37.7	41.3±4.4	39.4±5.8	28.0±4.7

AP diameter – anteroposterior diameter; IC diameter – intercommissural diameter; PM distance – interpapillary distance

Table 3.

Geometric parameters of the MV models and their comparison with echocardiographic measurements in systole.

	Case 1	Case 2	Case 3	Mean±SD	Echo measurements (FMR) [5, 19]	Echo measurements (Control) [5, 19]
Annular area (mm2)	994.8	871.9	895.8	920.8±65.2	1065.2±77.0	891.9±86.2
Annular perimeter (mm)	114.9	108.3	108.9	110.7±3.7	119.0±4.3	108.8±5.0
AP diameter (mm)	31.8	29.1	30.2	30.4±1.4	32.2±1.4	29.3±2.1
IC diameter (mm)	40.3	37.9	38.3	38.8±1.3	39.8±1.8	35.8±1.7
A2-P2 tenting height (mm)	10.4	12.2	11.5	11.4±0.9	10.1±1.5	6.9±1.1
A2-P2 tenting area (mm2)	166.1	177.1	174.3	172.5±5.7	235.2±18.5	109.4±18.0
AL tenting angle (deg)	24.8	29.6	27.9	27.5±2.4	23.7±4.1	22.4±4.7
PL tenting angle (deg)	48.4	57.8	53.7	53.3±4.7	46.7±4.4	31.2±5.7
AL excursion angle (deg)	26.9	26.6	20.2	24.6±3.8	34.7±4.4	50.7±5.9
PL excursion angle (deg)	16.4	14.3	21.2	17.3±3.6	40.8±17.0	64.5±11.0
PM distance (mm)	38.7	39.4	35.2	37.8±2.2	38.0±7.4	22.6±3.9

AP diameter – anteroposterior diameter; IC diameter – intercommissural diameter; PM distance – interpapillary distance

Data from computational models:

In diastole, the annular area for each case was 1242.0 mm², 1026.0 mm², and 982.4 mm², and the annular perimeter was 127.9 mm, 117.3 mm, and 113.2 mm. These parameters decreased to 994.8 mm², 871.9 mm², and 895.8 mm², and 114.9 mm, 108.3 mm, and 108.9 mm in systole due to the contraction of the annulus. The anteroposterior (AP) and inter-commissural (IC) diameters also decreased in systole due to annular contraction: AP diameter in each model changed from 33.5 mm, 33.9 mm, and 32.0 mm to 31.8 mm, 29.1 mm, and 30.2 mm; and IC diameter decreased from 42.7 mm, 39.7 mm, and 41.2 mm to 40.3 mm, 37.9 mm, and 38.3 mm. The radial lengths of A2 and P2 segments were measured in diastole, and the values of 21.9 mm, 22.4 mm, and 22.3 mm for the A2, and 11.7 mm, 13.2 mm, and 13.0 mm for the P2 were obtained. The AL surface area in diastole in each model was 860.3 mm², 761.5 mm², and 812.3 mm², while for the PL the leaflet surface area was 497.6 mm², 513.1 mm², and 488.6 mm².

In all computational models, the reduced mobility of the leaflets was observed during systole, with the small excursion angles of 26.9°, 26.6°, and 20.2° for the AL, and 16.4°, 14.3°, and 21.2° for the PL. Because of such reduced mobility, the large tenting height of 10.4 mm, 12.2 mm, and 11.5 mm appeared in each model. In addition, the increased tenting area of 166.1 mm², 177.1 mm², and 174.3 mm² was calculated in systole.

Since each PM was subdivided into three regions, representing the PM heads, the interpapillary distance was calculated by averaging the distances between the corresponding PM heads. In diastole, the interpapillary distance was calculated to be 46.3 mm, 40.0 mm, and 37.7 mm, and in systole it decreased to 38.7 mm, 39.4 mm, and 35.2 mm for each case.

Data from echocardiographic images:

To justify the eligibility of the computed MV systolic configuration, the AL and PL excursion angles, tenting height, and tenting area were also measured in the echocardiographic images (Table 4). For each case, slightly higher values of the excursion angle were obtained: 27.1°, 29.0°, and 21.0° for the AL, and 18.0°, 16.7°, and 24.8° for the PL. Because of that, the values of tenting height and tenting area were a little lower: 10.2 mm, 11.3 mm, and 11.1 mm, and 162.7 mm², 163.9 mm², and 167.8 mm².

Table 4.

Tenting parameters measured in the echocardiographic images.

	Case 1		Case 2		Case 3
	Diastole	Systole	Diastole	Systole	Diastole	Systole
A2-P2 tenting height (mm)	-	10.2	-	11.3	-	11.1
A2-P2 tenting area (mm2)	-	162.7	-	163.9	-	167.8
AL tenting angle (deg)	51.8	24.7	56.7	27.8	48.5	27.6
PL tenting angle (deg)	64.8	46.8	72.4	55.7	75.9	51.1
AL excursion angle (deg)	27.1		28.9		21.0
PL excursion angle (deg)	18.0		16.7		24.8

C. Simulation results

The systolic configuration of each MV model is shown in Figure 3 and the computed parameters are presented in Table 5.

Table 5.

Simulation results in peak systole.

	Case 1		Case 2		Case 3
	AL	PL	AL	PL	AL	PL
Maximum principal stress (MPa)	0.74	2.15	5.36	2.83	2.65	0.75
Maximum principal strain	0.36	0.44	0.39	0.45	0.38	0.43
Maximum marginal chordal force (N)	0.65		1.17		0.86
Maximum strut chordal force (N)	2.87		6.66		5.11
Maximum basal chordal force (N)	0.65		0.39		0.57
Average marginal chordal force (N)	0.12		0.13		0.13
Average strut chordal force (N)	0.32		0.55		0.44
Average basal chordal force (N)	0.09		0.12		0.17
APM force (N)	11.33		15.66		14.06
PPM force (N)	10.79		16.75		15.94

APM force – total reaction force on anteroposterior papillary muscle; PPM force – total reaction force on posteromedial papillary muscle

Stress and strain distribution:

In each model, the highest stress region occurred on the AL, with peak values of 0.74 MPa, 5.36 MPa, and 2.65 MPa, while the maximum stresses on the PL were 2.15 MPa, 2.83 MPa, and 0.75 MPa. On both leaflets, these peak stresses were observed near the strut chordae insertion regions due to the pre-strain imposed on these chordae. The analysis of strain distribution gave the opposite results in terms of the peak region location: the highest strains of 0.44, 0.45, and 0.43 were observed on the PL, and on the AL peak strains were lower, reaching 0.36, 0.39, and 0.38. However, the highest strain values were still observed near the strut chordae insertion regions.

Tension and reaction forces:

The computation of systolic chordal tension forces showed the highest values of 0.65 N, 1.17 N, and 0.86 N in marginal, 2.87 N, 6.66 N, and 5.11 N in strut, and 0.65 N, 0.39 N, and 0.57 N in basal chordae. The highest average values of 0.32 N, 0.55 N, and 0.46 N were also seen in strut chordae. Average tension forces acting in marginal and basal chordae were lower: 0.12 N, 0.13 N, and 0.13 N for marginal, and 0.09 N, 0.12 N, and 0.17 N for basal chordae. Total reaction forces acting on the anteroposterior PM were calculated to be 11.33 N, 15.66 N, and 14.06 N, while on the posteromedial PM such forces reached 10.79 N, 16.75 N, and 15.94 N for each computational model.

Simulation of MitraClip implantation:

Systolic configurations of post-MitraClip models with stress distribution on the leaflets are shown in Figure 5. In the MV model with patient-specific boundary conditions, both regurgitant gaps were largely eliminated and coaptation of the leaflets increased. Whereas in models without fully defined patient-specific boundary conditions, larger post-repair regurgitant gaps were observed. In addition, larger high stress concentration areas were evident in models with no annular or PMs motion, in particular, on the posterior leaflet.

Figure 5.

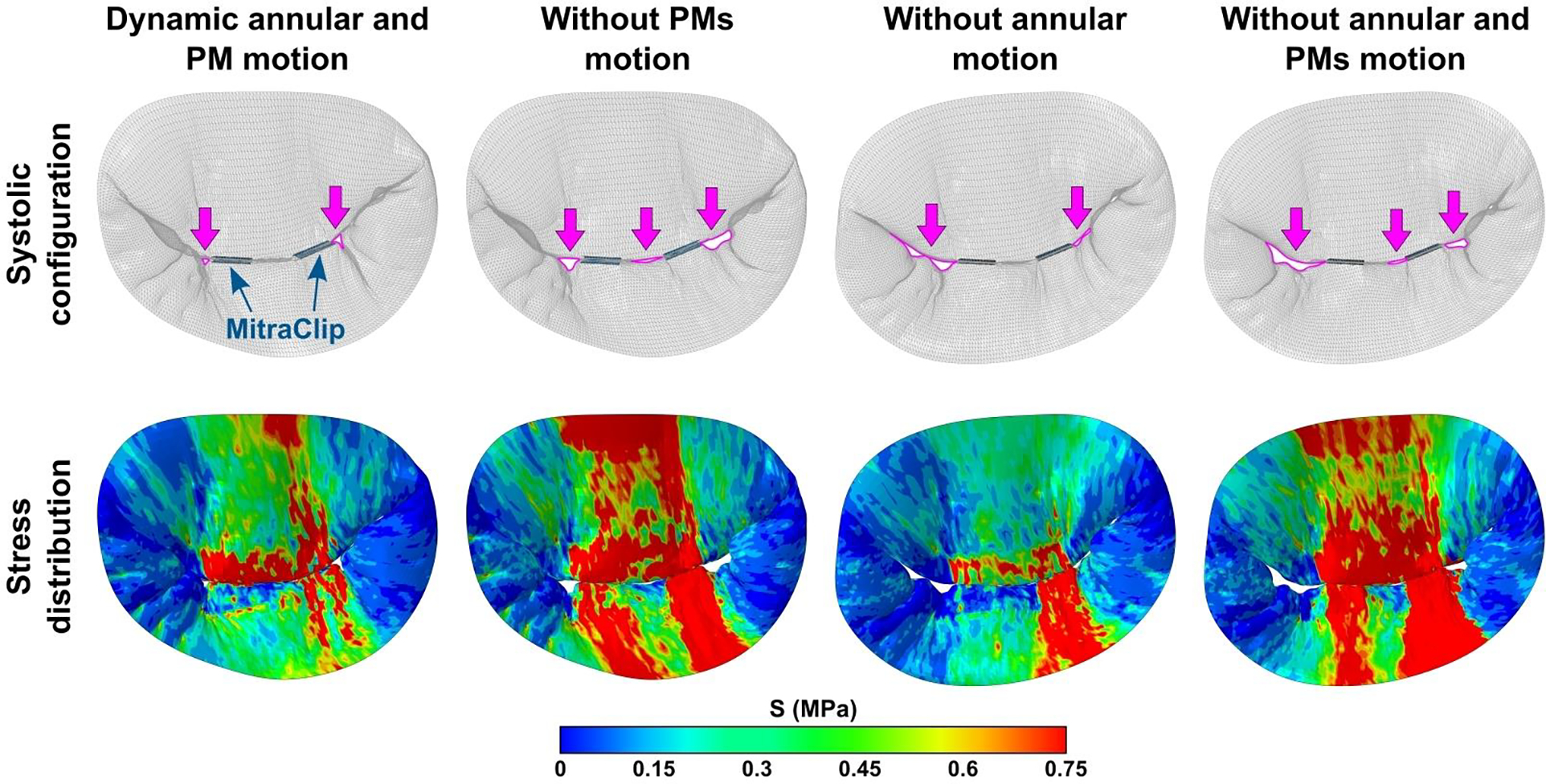
Systolic configuration of the MV leaflets and leaflet stress distribution after FMR repair using MitraClip for case 1 with and without patient-specific kinematic boundary conditions. Residual regurgitant gaps are marked in magenta.

4. Discussion

In this study, we presented a modeling approach of the MV and developed three computational models, each representing patient-specific MV affected by FMR: echocardiographic images showed moderate FMR in cases 1 and 2, and mild FMR in case 3. Based on our experience with large animal models and ex vivo bench experiments, the following alterations caused by the presence of FMR were expected to be seen during the simulation of the MV systolic function: annular dilation, excess leaflet tethering, reduced leaflet mobility, increased interpapillary distance, restricted PM motion, increased leaflet stresses and chordal tension forces.

The geometric parameters measured in each computational MV model were compared with the echocardiographic measurements made in our lab of healthy (control group) and FMR affected valves (Table 2 and Table 3) [19]. The geometric parameters describing the annulus of the MV, including annular area, AP diameter, and IC diameter, were higher than the ones in the control group, showing the annular dilation. Similarly, the leaflet area increase, if compared to the control group, was observed. This was caused by the impact of the systolic traction on the leaflets related to ventricular distortion. Both annular geometric parameters and leaflet area values had a good agreement with the FMR measurements.

In terms of the MV tenting parameters, both AL and PL tenting angles were lower than in the control group during diastole and higher during systole. For this reason, both AL and PL excursion angles were significantly lower than the ones measured in the control group, showing the reduced mobility of both leaflets. Because of that, a substantial increase in tenting height and tenting area were observed, leading to the formation of the regurgitant gap.

Besides the measurements in the computational model, the tenting parameters were also measured in the corresponding echocardiographic images. In each case, slightly higher values of excursion angle and slightly lower ones of tenting height and tenting area were measured, meaning that the leaflet coaptation point in each computational model was a little lower than it appears in the echocardiographic images. However, this difference was very small (0.52±0.35 mm). Its occurrence might be related to the fact that the chordae were pre-strained in groups rather than individually.

According to study by Jensen et al. [5], in healthy condition the interpapillary distance changes from 28.0±4.7 mm in diastole to 22.6±3.9 mm in systole, while in FMR cases the significant increase in this distance and the restriction of the PM motion can be seen, with interpapillary distance of 39.4±5.8 mm in diastole and 38.0±7.4 mm in systole. In addition, the study done in our lab [7] shows that shortening of the interpapillary distance from diastole to systole is larger in mild FMR cases and decreases if FMR is moderate/severe, thus indicating the increased restriction of the PM motion. In the present study, the increased interpapillary distance was observed in all cases, while the restriction of the PM motion was clearly visible in cases 2 and 3, with the shortening of interpapillary distance from diastole to systole of 0.6 mm and 2.2 mm, respectively.

The evaluation of stress distribution on the leaflets in each model showed the high stress concentration areas near the strut chordae insertion regions. According to the data from the literature for human valves, in healthy state the systolic stress values usually do not exceed 0.5 MPa [26, 28, 31]. In each model, higher peak stresses were observed on both leaflets, thus indicating the leaflet tethering due to the pre-strained chordae. In terms of chordal tension forces, while the average values in marginal, strut and basal chordae were in the same range as the ones reported in the literature for the porcine valves [6, 40], the peak force values were significantly higher. The highest tension forces occurred in strut chordae, which experienced the largest pre-strains. Some high force values were noticed in marginal and basal chordae as well, which also originate from the pre-straining of the chordae.

Finally, to justify modeling contribution, we presented simulations of MitraClip implantation for FMR repair. Our computational model produced realistic and reasonable results, indicating that MitraClip deployment reduces FMR and restores leaflet coaptation. However, such outcomes were observed only in the MV model with patient-specific kinematic boundary conditions, while models with no annular or PMs motion demonstrated larger residual FMR. Therefore, we want to emphasize the importance of patient-specific boundary conditions since the exclusion of annular or PMs motion from the simulations impacts both post-repair leaflet configuration and leaflet stress distribution.

Some limitations of the presented modeling approach should be highlighted. Firstly, it should be noted that although the reconstruction of the MV geometry was based on echocardiographic images, the regionally varying thickness was assigned to the leaflets according to the measurements reported by Kunzelman et al. [10]. This assumption was made because there is no possibility to measure leaflet thickness directly in the echocardiographic images, as the image resolution is probably within the range of the measurement error. Another important limitation is related to the chordae tendineae, which cannot be seen in the echocardiographic images. A chordal layout scheme developed by the Biomechanics Group in DEIB, Politecnico di Milano [32] in accordance with ex vivo findings and indications by the clinicians was adapted to create a branched network of chordae. While thickness of the leaflets and configuration of the chordae tendineae might have a significant impact on the function of the whole valvular structure, none of these limitations can be avoided if geometry reconstruction is done from echocardiographic images.

In summary, we presented a 3D ultrasound-derived FMR modeling approach, which allowed to obtain a realistic systolic configuration of the MV and provided quantitative evaluation of MV function in the presence of FMR. In addition, we presented simulations of MitraClip implantation for FMR repair, demonstrating realistic and reasonable post-repair results. Therefore, our study suggests that such models may be used to virtually implement various FMR repair techniques, allowing to predict post-repair outcomes and optimize FMR repair at a patient-specific level.