Spatial Patterning of Micromotor Aggregation and Flux

Abstract

Using a spatially varying light pattern with light activated semi-conductor based magnetic TiO₂ micromotors, we study the difference in micromotor flux between illuminated and non-illuminated regions in the presence and absence of an applied magnetic field. We find that the magnetic field enhances the flux of the motors which we attribute to a straightening of the micromotor trajectories which decreases the time they spend in the illuminated region. We also demonstrate spatially patterned light-induced aggregation of the micromotors and study its time evolution at various micromotor concentrations. Although light induced aggregation has been observed previously, spatial patterning of aggregation demonstrates a further means of control which could be relevant to swarm control or self-assembly applications. Overall, these results draw attention to the effect of trajectory shape on the flux of active colloids as well as the concentration dependence of aggregation and its time dependence within a spatially patterned region, which is not only pertinent to self-assembly and swarm control, but also provides insight into the behavior of active matter systems with spatially varying activity levels.

Graphical Abstract

Applying a spatial pattern of light, we observe assembly of active light-driven micromotors within the illuminated region as well as a negative flux of motors out of the region, which was enhanced with the application of a magnetic field.

Introduction

Collections of active particles, such as chemically fueled artificial motors or bacteria, can display intriguing phenomena such as swarming^[1,2], directional rectification^[3], motility induced phase separation^[4], and powered motion of microgears^[5]. Such collections of out-of-equilibrium active units constitute “active matter” systems which also include many natural systems such as schools of fish or bacteria colonies^[6,7]. The ability of active particles to display such behavior is a consequence of their out of equilibrium nature that is distinct from a collection of passive particles which are in thermal equilibrium. There has been a great amount of interest in understanding these active matter systems, particularly to develop theories to explain their behavior in ways analogous to that of statistical mechanics or thermodynamics of equilibrium systems^[8], although much work still remains to be done.

Active micromotors have also been employed as microrobots for carrying out tasks at the microscale, such as micromanipulation, and show promise for a wide variety of future applications such as microsurgery, targeted drug delivery, or sensing^[9]. Swarms of active microrobot particles have been of interest for their ability to accomplish tasks that are not possible with individual microrobots^[10]. Magnetic microparticle swarms have been shown to move through channel openings more efficiently than individual units^[11], and change shape based on certain input control parameters^[12].

Light active micromotors and bacteria have been used to create spatially varying patterns of density from dense collections of active units due to a flux in or out of illuminated regions^[13–16]. For example, phototaxis of light active micromotors was used to gather micromotors into spatial patterns. In other work, the activity level of light powered bacteria was controlled by the application of a spatial varying light intensity, resulting in a flux of the bacteria from regions of high activity to low activity. This phenomenon was utilized to demonstrate “painting” by light powered bacteria in which the distribution of bacteria density was controlled to create various patterns^[14]. In similar studies, dynamic and static patterned stripes of light were also used to collect bacteria in specified regions^[16]. It was found that the bacteria density varied inversely with their speed, a result that agreed with theoretical predictions for run and tumble bacteria^[4]. Although these results demonstrated highly controlled density variation of very dense collections of active run and tumble bacteria, the effect of the persistence of the individual active particle trajectories has not yet been investigated. Tuning this parameter can shed light on the behavior of active matter systems and how it effects their flux from active regions to inactive regions.

Active particles have also been found to form aggregates with each other or with passive particles and assemble into crystal structures due to attractive phoretic-based forces^[17,18]. Spatial patterning of these self-attracting aggregates could be important for future applications in swarm control, self-assembly, or microfabrication.

In this study we use patterned light and an externally applied magnetic field to study the flux of active semi-conductor micromotors from illuminated, active, regions to dark, inactive regions. We vary the persistence length (the distance that the micromotor travels before it reorients appreciably) of the micromotor trajectories by the application of a magnetic field which acts to straighten the micromotors trajectories. We find that this results in a greater flux of micromotors away from the illuminated region and into the non-illuminated regions compared to the cases in which no field was applied. We attribute this to the greater distance that the micromotors with more persistent trajectories can travel, which leads to a lower amount of time that they spend in the illuminated region. This results in a more effective flux transfer from illuminated to dark regions. We also induce spatially controlled attractive aggregation of light active TiO₂ micromotors by applying a spatially varying light pattern. We study the affect of micromotor concentration on both the aggregation and flux. Overall, this work presents a novel study of the effects of magnetic field on the aggregation and flux of active particles as well as demon-strating spatial patterning of their attractive aggregation. These results are relevant to swarm control of micromotors and provide insight into the behavior of active matter systems with spatially varying activity levels.

Results and Discussion

Micromotor Motion

We utilized TiO₂ microspheres (1–2 μm in diameter) as the base of micromotors which are coated in a hemispherical layer of nickel/iron alloy, platinum, and silver to make them magnetic and self-phoretically active. Details of the fabrication and other experimental procedures are given in the Experimental section. The Ni/Fe alloy was used to make the micromotors magnetic, while the Pt layer was applied due to its known ability as an optimal metal to enhance the light activity level of TiO₂ micromotors. The Ag layer was placed atop the Pt layer to reduce the creation of oxygen bubbles due to the catalytic properties of Pt with hydrogen peroxide, and also to mitigate self-phoretic motion of the micromotors without applied light. Electrons in the TiO₂ semiconductor-based micromotors are excited into the conduction band when exposed to UV light, creating a flow of current and a self-produced electric field which results in a self-electrophoretic mobility of the micromotors^[19] (Fig. 1(E)). Although, due to their small size, we do not directly observe the direction of motion of the micromotors relative to their metal cap, previous work with light-active TiO₂ micromotors has found that they move in the direction away from the metal coating^[19,20]. We also observe this to be the case with larger, ~ 5–8 μm diameter TiO₂ micromotors. The micromotors were observed on a glass slide under a microscope and a digital micromirror device (DMD) was used to shine UV light (365 nm) onto the slide from below, as shown in the schematic of the experimental setup in Fig. 1(A). A permanent magnetic placed on the stage of the microscope supplied magnetic fields for applying a magnetic torque to the micromotors and negligible magnetic forces. In the absence of applied light, the TiO₂ micromotors appear to only undergo Brownian motion. Fig. 1(D) shows example trajectories in the cases of no applied light (left most panel), applied light (middle panel), and applied light and magnetic field (right panel). Application of UV light causes them to become active and undergo either persistent Brownian motion, circular, or helical trajectories.

Figure 1.

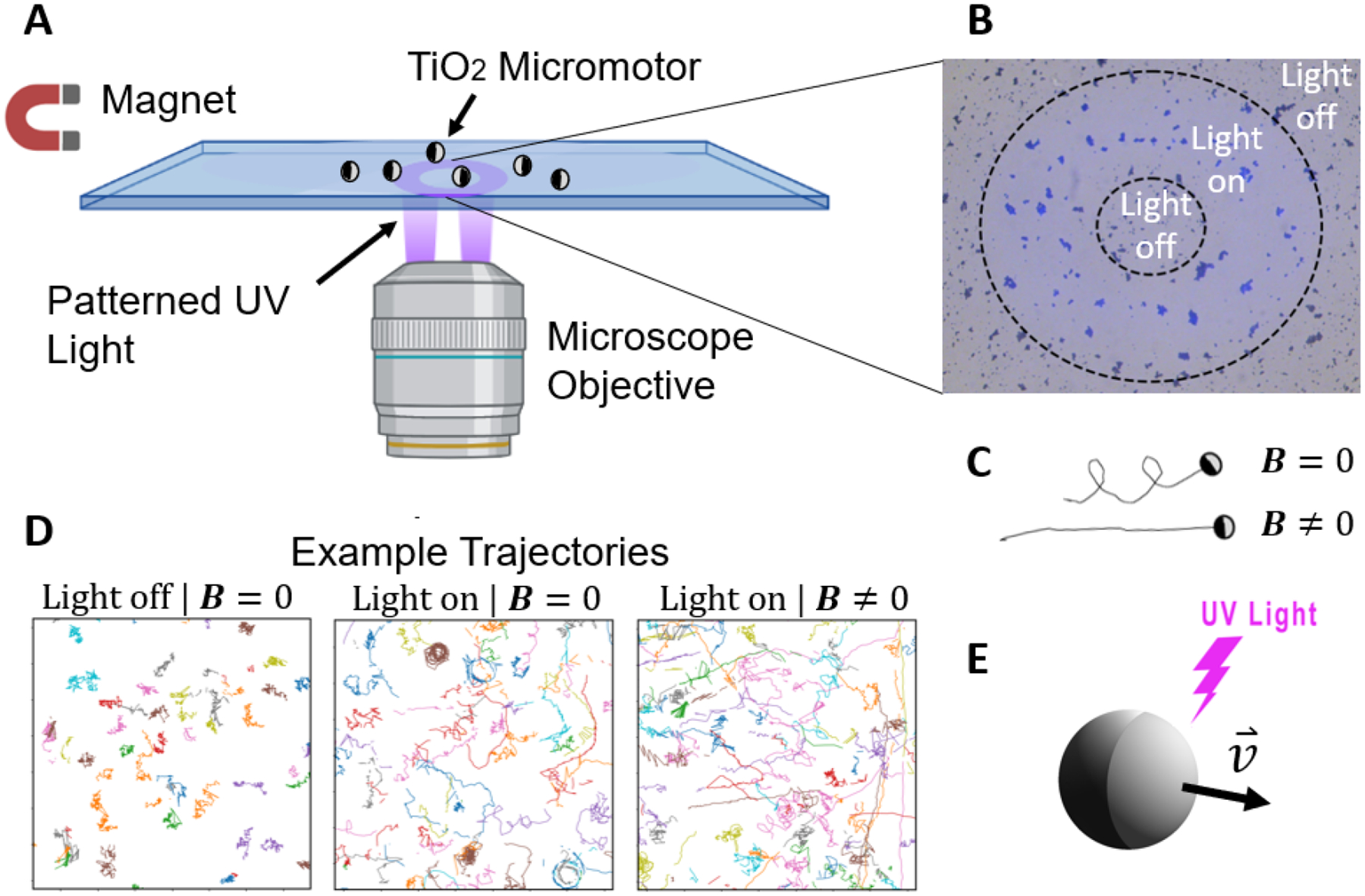
(A): Schematic of the experimental setup. (B): An image of the annulus light pattern used in the experiments. The dashed lines were added as a visual aid to help identify the regions. (C): Sketches showing an example of the longer persistence length of a micromotor in the presence of a magnetic field compared to one with no magnetic field. (D): Trajectories of the micromotors without light (left), with light (middle), and with light and a magnetic field (right). All trajectories were over a 10 second duration and the figure dimensions shown are 50 × 50 μm. (E): A schematic showing a light-active micromotor moving with applied UV light.

In the presence of a magnetic field, the micromotors tend to move more persistently (Fig. 1C,D), thereby having a greater displacement in a given time period. We find that the micromotors do not move in a single direction, as would be expected if their direction of motion was parallel to their magnetic moment, but rather in a wide range of directions. We attribute this variation to differences in the magnetic coatings on the micromotors. The glancing angle magnetic coating on the polydisperse and densely distributed TiO₂ microspheres may have resulted in some shielding others from the metal vapor, and hence in a variation of coatings on each micromotor. Another possible explanation for their differences in direction of motion is that individual micromotors that clump together into clusters can lead to the aggregate possessing a direction of propagation that is non-parallel to its magnetic moment. This randomization of their directionality makes them well suited as a model 2D active system with tunable persistence length.

Micromotor Flux

We applied UV light in a pattern of an annulus (Fig. 1(B)) in order to achieve spatially varying activity levels of TiO₂ micromotors. Therefore, micromotors outside this region are inactive while those inside are active. Fig. 2 shows a schematic of the regions. Inside the illuminated annulus region the micromotors actively move while at the center and outer regions they are inactive. The spatial variation in velocity results in a tendency for the micromotors to move preferentially from the region that is illuminated by light (inside the annulus) to the regions that are not illuminated (the center and outer regions). The measured number of micromotors/aggregates that crossed from one region to another after a 71 second time period is shown for the case in which a magnetic field was applied, which counts both individual micromotors as well as aggregates. As one can see, there is a net flux from the illuminated region to the central and outer regions. We measured the number of micromotors/aggregates that move from one region to another as a function of time for three different micromotor concentrations with and without a magnetic field applied and the results are shown in Fig. 3. the y-axis shows the difference between the number of micromotors/aggregates that enter a region, N₊, with the number that leave a region, N₋. A positive value indicates a net flux into the region while a negative value indicates that more micromotors/aggregates exited the region than entered. The sum of all three data points at any given time is zero. The blue data correspond to the outer region, the green to the center region, and the orange to the illuminated annulus. As can be seen from the plots, there tends to be a net flux out of the illuminated region and into the outer non-illuminated region, although it is enhanced in the cases with a magnetic field applied. The net flux into the center region is not prominent in the absence of a magnetic field, but is clearly positive with the field applied, except in the lowest density case with low statistics. Although the aggregates could influence the flux by acting as sort of micromotor sinks which reduces the number of motors that can leave the region, there was no significant difference in cluster formation with or without a magnetic field applied and we observe an increase in flux with the field on even in the lowest density case in which few to no clusters formed (Fig. 3(E–F).

Figure 2.

A sketch of the annulus light pattern showing the active motors inside the annulus and the inactive motors at the center and in the outer region. The numbers shown are the measured total flux of micromotors from each region to the other over a 71 second time period with a magnetic field applied at a micromotor concentration of around 0.016 per μm². The diameters of the inner and outer regions of the annulus are approximately 90 μm and 280 μm, respectively.

Figure 3.

The net micromotor flux as a function of time since the light was turned on in cases with no magnetic field (left panels) and with a magnetic field applied (right panels). The blue, green, and orange data correspond to the net flux of micromotors in/out of the outer region, center, and illuminated annulus regions, respectively. (A,B): At high micromotor concentration. (C,D): At intermediate micromotor concentration. (E,F): At low micromotor concentration. The micromotor concentrations were approximately 0.016, 0.008, and 0.001 motors per μm². Images showing examples of the three different concentrations are given in the SI. Videos of all six experiments are also provided in the SI.

We attribute the enhanced flux when a magnetic field is applied to be due to the straightening of the micromotor’s trajectories. A longer time is taken for a micromotor with a curved trajectory to move through the illuminated region compared to one with a straight-line trajectory at the same speed. The longer time results in a lower rate of micromotors exiting the region and hence a reduced total flux. Overall, these results demonstrate that the persistence length of active micromotor trajectories can be used a means to alter the net flux of the micromotors between regions of varying activity levels.

In the highest density case (Fig. 3(A,B)), the flux appears to reach a steady state after approximately 30 seconds. One would expect steady state to be reached once all of the micromotors have had sufficient time to move out of the illuminated region. Since there is a large variation in micromotor speed, this time is not easily estimated. However, a time of around 30 seconds to move approximately 100 μm, the width of the annulus, implies a speed of around 4 μm/s which is similar to a typical micromotor speed. A histogram of the micromotor speeds inside the illuminated region within 10 seconds of the light being turned on is given in Fig. S4 of the SI. The individual active motors have speeds up to 25 μm/s or so and the aggregates up to 15 μm/s, with the majority of faster micromotors/aggregates observed soon after the light is turned on and less fast ones observed later. Note that a fraction of the micromotors respond weakly or not at all to the applied light and therefore do not possess a well-defined velocity but rather exhibit a diffusive like motion until they join an aggregate. Alternatively, steady state may be reached once the very large aggregates form and therefore eliminate smaller aggregates and individual motors in the illuminated region, suppressing the flux out of the region. This also could explain why steady state appears to be reached faster in the high density case compared to the lower density cases which produce smaller aggregates, as will be discussed in the next section.

In general, the steady state density of a collection of active Brownian colloids within two regions of varying activity levels is expected to be inversely proportional to the difference in velocity of the micromotors in the two regions^[4,15,21]. The total flux of micromotors from when the light was turned on to when steady-state was reached would also be expected to reflect this relation. However, in our system the micromotor speeds are equal with and without a magnetic field applied (see Fig. S4) and yet the total flux at steady state is unequal (Fig. 3(A) and Fig. 3(B)). The reason for this discrepancy could be due to several factors. First, considering our micromotors as active Brownian colloids may not be valid. For example, the active micromotors that have linear trajectories do not reorient since their direction of motion is fixed by the magnetic field. Additionally, the aggregates may absorb more of the motors that do not move linearly (and therefore that take longer to leave the illuminated region). Although, as mentioned above, we do not observe any noticeable difference in aggregate size between the cases in which the magnetic field was on or off, only a small difference may be needed to produce the measured difference in total flux.

The net positive flux of micromotors into the central region demonstrates a means to collect micromotors into a specified region of space. One can imagine utilizing this as a means of swarm control. We also note that imposing spatially varying activity levels such as this could be used to separate micromotors based on speed or persistence length. For example, micromotors that respond most strongly to light and/or move with a more linear trajectory will tend to leave regions that are illuminated by light sooner than slower micromotors or ones with less persistent trajectories.

Patterned Aggregation

We observe that the micromotors are attracted to one another and tend to form aggregates under UV light. Video S1 of the supporting information and Fig. 4 shows the formation of aggregates of the micromotors in the region where the light was applied for the case of micromotor concentration of around 0.016 micromotors per μm². Figure 4(A–C) shows frames of the video right before the light was applied (A), right before the light was turned off (B), and 10 seconds after the light was turned off (C). As can be seen from Fig. 4(B), clusters form inside the illuminated annulus. These clusters also move, with smaller clusters at early times having speeds up to ~ 15μm/s and larger clusters later on moving more slowly, as mentioned in the previous section. No magnetic field was applied in this experiment. As can be seen in Video S1, the micromotors tend to collide which results in the formation of clumps, and these clumps will also collide and form larger aggregates. Such light-induced aggregation has been shown previously with TiO₂ active/passive mixtures as well as hematite-infused polymeric particles and has been explained by a phoretic attraction^[17,18].

Figure 4.

(A-C): Images showing the micromotors right before the light was applied (A), right before it was turned off (B), and 10 seconds after it was turned off (C). The dashed lines in (B) are a visual aid to help better distinguish the illuminated region. The micromotors inside the illuminated region increase their speed and collide, forming aggregates. (D): A plot of the number of micromotor clusters within various size ranges inside the annulus region as a function of time. The vertical dashed lines correspond to when the light was turned on and the micromotors began to aggregate (at 5 seconds) and when it was turned off and the aggregates dissolved (76 seconds). (E): A color bar plot of the number of clusters as a function of their size within the illuminated region. The blue colored data correspond to times just after the light was applied and the green colored data correspond to later times up to the moment the light was turned off.

The attractive interaction that results in cluster formation is eliminated upon turning off the light causing many of the micromotors to break off of the aggregates. The reason the aggregates do not completely dissolve is likely the result of attractive magnetic interactions. Indeed, even before the light was applied one can see that there is some aggregation in the sample in Fig. 4(A). The dissolution occurred more rapidly when using a higher light intensity (see Vid. S4) and faster than expected for a diffusive process, therefore there could be a repulsive component to the dissolution as well, but further investigation will be needed to characterize this. We measured the size distribution of the clusters in the annulus region as a function of time (see Fig. 4(D)). The vertical dashed lines correspond to the times at which the light was turned on (5 seconds) and later turned off (71 seconds). As can be seen from the figure, the number of large clusters of sizes between 54 to 162 μm² increase over time until the light is turned off. The rate of increase appears to decrease with time which can be explained by a depletion of micromotors available to combine with the already formed aggregates. There is a large decrease in the number of aggregates with sizes between 2–6 μm² and 6–18 μm². This decrease is partly due to the flux of micromotors out of the illuminated region and also partly due to the formation of larger clusters which attract and combine with individual motors and smaller clusters. Once the light is turned off, the number density of the clusters tends to return to the values prior to turning on the light, especially the individual micromotors/small clusters in the 2–6 μm² range which quickly break off from the perimeter of the larger clusters. The partial dissolution of the clusters happens relatively quickly, in about 10–20 seconds, as can be seen from the figure.

As an additional means of displaying the cluster size distribution, we also measured the number of clusters within the illuminated annulus region as a function of their size and plot the result in Fig. 4(E). The blue colored data correspond to times just after the light was turned on while the green colored data correspond to later times up to the moment the light was turned off. As can be seen from the figure, when the light was first applied, the size distribution peaks around 2 μm² which corresponds to the size of an individual TiO₂ micromotor. There is a decline in the number of clusters with increasing area above this. After the light had been applied, the distribution flattens considerably. There is a depletion of clusters in sizes up to approximately 20–30 μm² compared to the initial distribution, and an increase in the number of cluster sizes above that value. The depletion of the smaller sizes is due to flux and the formation of larger aggregates, as mentioned above, and the increase in number of aggregates above 20–30 μm² corresponds to the increase in the red data points in Fig. 4(D).

We also measured the cluster sizes as a function of time in the samples with lower micromotor concentrations. We find that fewer large clusters form upon application of the light at the lower micromotor concentrations. We plot the number of clusters within various cluster size ranges as a function of time for all three micromotor concentrations studied in Fig. 5. The results shown are for videos without a magnetic field applied. We saw no significant difference in results between the magnetic field on and off cases (see Fig. S1). We also show images of the sample before the light was applied and immediately after it was turned off in Fig. S3 of the SI. At lower concentrations of micromotors, the cluster formation is decreased. The lowest concentration of around 0.001 micromotors per μm² shows no aggregate formation which is due to the long mean free path between the micromotors leading to few or no collisions. In addition to a reduction in collision rate of the micromotors at the lower concentrations, there are also initially fewer/smaller magnetically attracted aggregates which likely reduces the attractive phoretic forces produced by the aggregates once the light is applied.

Figure 5.

Plots of the number of micromotor clusters within various size ranges inside the annulus region as a function of time for the three micromotor concentrations studied.The micromotor concentrations were approximately 0.016, 0.008, and 0.001 motors per μm².

Conclusion

We have demonstrated the ability to control the spatial distribution and clustering of micromotors by the use of magnetic fields and a spatially varying light pattern. We have shown that light-active micromotors can be made to preferentially travel from illuminated regions to non-illuminated regions and we amplify this effect by employing magnetic fields which increases the tendency for the micromotors to move persistently, and hence travel farther in a given amount of time. Controlling the micromotor flux in this manner could be a useful strategy for swarm control or for separating micromotors based on their degree of light responsiveness or persistence length. We have also demonstrated clustering of the micromotors in the light pattern due to light-induced attractive interactions. One can imagine that such patterning could possibly be useful in assembling microstructures on demand in microfabrication applications.

We believe that the application of stronger magnetic fields would result in an even more enhanced flux of micromotors due to an increase in linearity of the trajectories of micromotors with large active torques that otherwise overcome the applied magnetic torques. Because we chose a light pattern that was rotationally symmetric, the direction of motion of the micromotors should not effect their flux. However, their aggregation could be influenced by their relative directionality^[17]. Therefore creating micromotors that all move in one direction could alter the clustering behavior. This, and studying the effects of various field strengths, could make for interesting future studies.

Overall, the ability to spatially and reversibly control cluster formation and micromotor flux using patterned light may find use in areas such as self-assembly or swarm control applications as well as shedding light on the behavior of active matter systems with spatially varying activity.

Experimental

Fabrication of TiO₂ micromotors

TiO₂ microparticles were fabricated based on the procedure given in^[19]. First, a 1/40 ratio of tetrabutyl titanate (Sigma #244112) to ethanol was mixed in 1.5 mL vials and allowed to sit for one day. Then, the vial was centrifuged in a microcentrifuge (Eppendorf 5415 D) at 7000 rpm for 1 minute followed by the removal of the supernatant. The microparticles were rinsed a total of three times in ethanol and three times in DI water. The concentrated particles were then pipetted into a glass vial and placed on a hot plate at approximately 90 degrees Celsius to evaporate the liquid. The glass vial containing dry TiO₂ particles was then placed in a furnace at 400 degrees Celsius for two hours in order to form the anatase phase which was confirmed with X-ray diffraction (see Supporting Information Figure S5). A small amount of ethanol was then added to the glass vial to suspend the TiO₂ particles and this was then pipetted onto a glass slide. The ethanol was allowed to evaporate and layers of a nickel/iron alloy (20 nm) at a glancing angle of 70 degrees followed by platinum (20 nm) at normal incidence and then silver (20 nm) also at normal incidence were coated on the surface with e-beam deposition. Previous experiments have demonstrated that platinum is optimal for micromotor speed^[20] and a bimetallic coating has also shown to enhance the mobility of light active micromotors^[22]. Therefore, in order to maximize the surface contact between the TiO₂ and Pt layer, we deposited a layer of Ni/Fe at a glancing angle to make them magnetic while also providing surface contact between the TiO₂ and the following Pt layer. The Ag layer was deposited directly over the Pt layer which provided a bimetallic coating while also reducing the catalytic decomposition of hydrogen peroxide. This was important to minimize the production of oxygen bubbles, which could disturb the system, and also to reduce any self-phoretic motion from the chemical catalysis.

Procedures

The micromotors were removed from the glass surface with a wet piece of lens paper and suspended in a vial with DI water. The vial was then sonicated for approximately 3 minutes. Then the desired amount of the water containing the suspended micromotors was pipetted into a separate vial and 10 μL of 30% hydrogen peroxide was added followed by DI water to make a final volume of 110 μL. This solution was mixed with pipetting action and 70 μL was then pipetted onto a glass cover slide for observation under an inverted microscope (Zeiss Axiovert 200). A 20x objective was used for the experiments. Videos were recorded with an Amscope camera at around 13.6 frames per second.

To apply a magnetic field, a cylindrical neodymium magnetic (length 1 cm, diameter 0.4 cm) was placed 3 cm from the center of the slide, resulting a field strength of approximately 0.7 mT at the center. This field strength was sufficient to produce the desired straightening of the micromotor’s trajectories. Placing the magnetic closer to the sample would result in a stronger magnetic field strength but also would increase the magnetic gradient, therefore making the field less uniform. The magnetic gradient was found to be approximately 0.05 T/m, therefore the field was quite uniform over the region of interest. We estimate that such a gradient resulted in a magnetic force on the micromotors of approximately 10⁻¹⁶ N which would result in negligible displacements compared those produced by Brownian and active forces. This is supported by our observations that the micromotors that are not active do not move appreciably in any one direction.

Videos were taken very soon after placing the magnet near the sample. Videos taken with and without a magnetic field applied were captured on the same sample, typically about a minute apart. The cover slide was moved between each application of light in order to maintain the same initial state.

Light Source

The UV light was supplied by a DMD system (Mightex Polygon 1000) which shines 365 nm light in a binary fashion (each micromirror set to either on or off). Software enables a pattern within the rectangular region to be drawn which corresponds to the location where the light is applied. The light intensity setting can be varied from 0–1000 in the software. We used a setting of 50 which gave approximately 20 mW/cm² light intensity. We found that using the high intensity setting of our light source (approximately 25 times greater) caused light leakage into the central region which resulted in cluster formation in the center as well (see Vid. S4), which is why we used a lower light intensity in the experiments shown here. However, at the higher intensity the cluster dissolution is more pronounced once the light is turned off.

Video Analysis

Videos were analyzed using python and the micromotors were tracked with the Trackpy^[23] particle tracking package. Average micromotor velocities were found by first smoothing the x and y coordinate data using a rolling window size of 3 frames. Then, the time derivative was evaluated to obtain the x and y velocities at each frame and from this the speed was computed. This was averaged over time to determine the mean speed for each micromotor.

Cluster area size was determined by first converting the image into a binary intensity by zeroing all pixel values below a threshold value (one standard deviation plus the mean) and setting all pixels to 1 that were above this threshold. All groups of connected pixels were found and their size determined using the ndimage package from the scipy library.