Abstract
Metabolomics as a research field and a set of techniques is to study the entire small molecules in biological samples. Metabolomics is emerging as a powerful tool generally for precision medicine. Particularly, integration of microbiome and metabolome has revealed the mechanism and functionality of microbiome in human health and disease. However, metabolomics data are very complicated. Preprocessing/pretreating and normalizing procedures on metabolomics data are usually required before statistical analysis. In this review article, we comprehensively review various methods that are used to preprocess and pretreat metabolomics data, including MS-based data and NMR -based data preprocessing, dealing with zero and/or missing values and detecting outliers, data normalization, data centering and scaling, data transformation. We discuss the advantages and limitations of each method. The choice for a suitable preprocessing method is determined by the biological hypothesis, the characteristics of the data set, and the selected statistical data analysis method. We then provide the perspective of their applications in the microbiome and metabolome research.
Key words: Data centering and scaling, Data normalization, Data transformation, Missing values, MS-Based data preprocessing, NMR Data preprocessing, Outliers, Preprocessing/pretreatment
Introduction
Metabolomics can be defined as a research field and a set of techniques to study the entire set of small molecules in a biological sample. Currently, metabolomic technologies go well beyond the scope of standard clinical chemistry techniques and are playing an important role in precision medicine due to its capability of precise analysis of hundreds to thousands of metabolites. In microbiome research, there is a trend to integrate the microbiome and metabolome to discover mechanism and functionality of microbiome in healthy status and disease development. However, statistical analysis of metabolomics data is very challenging, not only because the metabolomics as a research field is very complicated, but also due to the complexity of metabolomics data. Before the statistical analysis, metabolomics data are usually required to be pretreated and normalized.
Metabolites as chemical entities can be analyzed using standard chemical analysis tools, such as mass spectrometry (MS) and nuclear magnetic resonance (NMR) spectroscopy. Since the 1980s MS techniques are synergistically combined with gas chromatography (GC) or liquid chromatography (LC), producing two new powerful techniques, called gas chromatography–MS (GC–MS) and liquid chromatography-MS (LC–MS). Currently compared to NMR spectroscopy GC–MS, LC–MS techniques are the most commonly used analytical platforms in metabolomics. For the capabilities of MS-based and NMR-based analytic platforms for generating metabolic profiling datasets and the advantages and disadvantages of MS-based and NMR-based methods, the interested reader is referred to Chapter 2 (Section 2.4.2) of book.1 In this review article, we are interested in the methods of pretreating and normalizing metabolomics data for statistical analysis. Before performing a statistical analysis of metabolomics data, we must perform several preprocessing and pretreatment steps on the metabolomics data regardless of which platforms have been used to collect them.
Preprocessing and pretreatment
In our recent book An Integrated Analysis of Microbiomes and Metabolomics,1 we described several processing steps for metabolomics data analysis and then briefly introduced data preprocessing for two platforms of metabolomics data generating: preprocessing for MS-Based data and preprocessing for 1H NMR data.
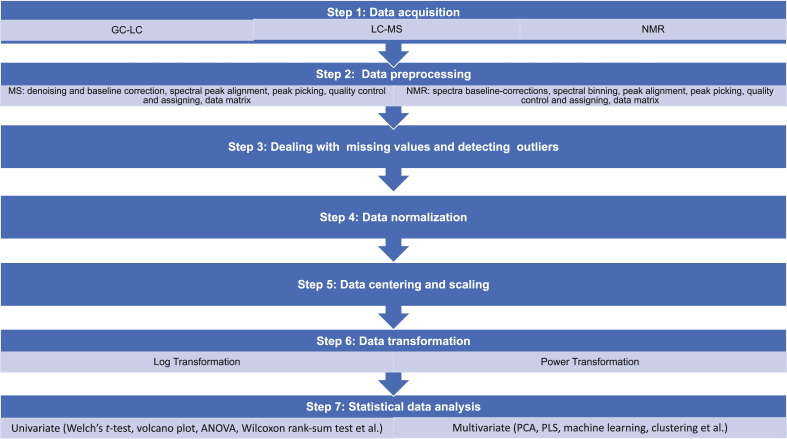
Generally seven data processing steps could be taken from data acquisition to statistical analysis although in practice not all these steps must be implemented in order1 (Fig. 1).
Figure 1.
Seven general data processing steps in metabolomics data analysis. The schematic summarizes general data processing steps from data acquisition to statistical analysis in metabolomics study. Among these seven steps, Steps 2 to 6 are considered as data preprocessing and pretreatment. The data preprocessing procedures (Step 2) in MS and NMR are similar but have slightly different terms due to their data generation platforms.
The terms “data preprocessing” and “data pretreatment” have not been used consistently in metabolomics literature. Narrowly “data preprocessing” refers to data processing before data collection, including baseline correction, phasing, peak alignment, binning (spectral bins), and noise filtering. Sometime “variable scaling” and “normalization” are also assigned into “data preprocessing” steps. Usually “normalization” and “data pretreatment” are used as two separate data-processing steps, while both “centering and scaling” and “data transformation” are considered as a “data pretreatment”. Sometimes, “data pretreatment” also include the “missing value estimation/imputation” and “noise filtering”.
Broadly, we can consider all data processing steps before statistical data analysis as data preprocessing/pretreatment.2 The goals of data preprocessing/pretreatment1 are 1) to correct for or minimize instrumental artifacts and irrelevant biological variability to enhance the signal-to-noise ratio (SNR); and 2) to appropriately transform the data into interpretable spectral profiles through centering and scaling data and reducing its dimensionality.3
Here, we focus on data preprocessing and pretreatment. For statistical analysis, the interested reader is referred to Chapters 5 and 6 of Statistical Data Analysis of Microbiomes and Metabolomics.4 Bijlsma et al5 and Karaman6 have discussed a general strategy for preprocessing and pretreatment for statistical analysis. Particularly, Yang et al7 have proposed a strategy to deal with the missing values and to reduce mask effects from high variation of abundant metabolites. In this review article, we provide an overall preprocessing and pretreatment procedures and normalization methods before performing statistical analysis. The remaining of this article is organized in this way: We first present data preprocessing. Then we describe how to deal with zero and/or missing values and detect outliers. Next we focus on introducing data normalization methods. Followed that we investigate data centering and scaling, and data transformation, respectively. Finally we briefly summarize this review and provide some perspectives.
Data preprocessing
Preprocessing metabolomics data is challenging. As we described above, although in general, for all the platforms used to generate the data, data preprocessing/pretreatment aim to correct for or minimize instrumental artifacts and irrelevant biological variability as well as to appropriately transform the data into interpretable spectral profiles, preprocessing (or pretreating) metabolomics data is platform-specific in terms of their measurements. Due to their different data recording, the necessary steps prior to statistical analyses are different.8 For example, for NMR data, when performing comparisons of spectra heavy shifts or displacement of signals can occur along the axis of a 1H NMR spectrum due to pH and other factors. Thus, for NMR data it is crucial to apply an appropriate data preprocessing to ensure that statistical analysis can systematically compare the signals across the spectra so that any differences in signal intensity among groups of samples can be detected. Several data preprocessing options can be performed8 including 1) binning the data (aka. ‘bucket’): adding the signal up over small chemical shift intervals; 2) applying a peak fitting based on a spectral database; and 3) working on the whole spectrum to evaluate and remove those unstable and/or uninformative spectral regions and in particular the water region and the signal-free high- and low-frequency extremities so that a smaller number of variables (metabolites) can be kept for statistical analysis.
For LC-MS data, big challenges come from variations in retention times (RTs). Thus, to overcome this challenge, the LC-MS-based approaches are required to develop at a time where detection of chromatographic peaks by ultraviolet (UV) or flame ionization detector (FID) is the norm.8 Like LC–MS data preprocessing, application of an MS-based profiling approach results in outputs consisting a three-dimensional (3D) table. Thus, the preprocessing of GC–MS data aims to detect peaks via deconvolution and peak integration to produce a two-dimensional (2D) table (intensity for each sample of ‘features’ corresponding to {RT/m/z} pairs) for statistical analysis.8 However, the metabolite identification approaches between GC–MS and LC-MS metabolomic data are inherently different.
With GC–MS method, reproducible mass spectra can be obtained and very large databases can be consulted to identify the metabolites based on characteristic recognizable fragment ions. Therefore, the central efforts of process are towards the automation and the accuracy and the peak identification, integration and annotation. For example, for MS-based analysis, data preprocessing generally includes denoising and baseline (background) correction, spectral peak alignment, peak picking (detection), quality control and assigning data matrix; for NMR-based analysis, the main data preprocessing includes baseline corrections, spectral binning, peak alignment, peak detection, and quality control and assigning data matrix (see Fig. 1).
In summary, although the general preprocessing/pretreatment strategy still aims to make the data comparable across samples regardless of instrumental variability, the strategies used in MS-based methods are radically different from those used in NMR-based method. The approaches used in GC–MS and LC-MS metabolomic data are also different. For the details on general preprocessing/pretreatment strategy to be used in GC–MS and LC-MS-based as well as NMR -based metabolomic data, the interested reader is referred to these publications.3,5,6,8
MS-based data preprocessing
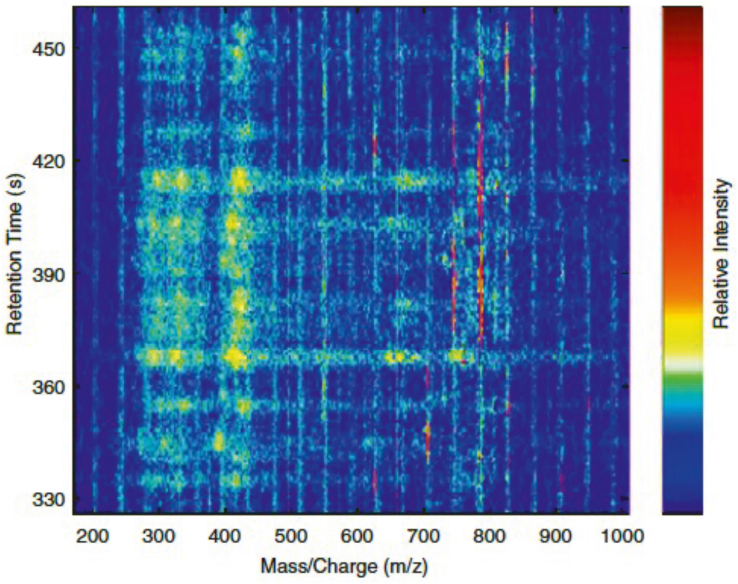
MS-based analysis measures mass-to-charge ratios (m/z). When MS is combined with GC or LC, the raw GC/LC -MS data have three measured variables: m/z, chromatographic retention time (RT) and intensity count which consists of a 3 dimensions (3D) data structure (see Fig. 2, which was modified from Karaman (2017) 6).
Figure 2.
Visualized LC-MS profile in a 3D data structure. This schematic visualized representation of blood serum LC-MS profile in a specific retention time interval. A 3 dimensions (3D) data structure represents three measured variables: mass/charge (m/z), chromatographic retention time (RT) and relative intensity counts.
A 2D data structure of features table (also called feature quantification matrix) is generated through by peak picking to remove the spectral noise and irrelevant biological variability, e.g., column material, contaminants. The 2D data structure of features table collects samples by metabolites of quantified data (see Table 1). This matrix contains all the quantified metabolic features from the analyzed samples with the rows corresponding to the samples and the columns to a list of variables (peak areas/intensities) characterized by m/z and retention time in minutes or scan number (m/z-RT pairs). That is, the raw GC–MS data contains m/z value on the x-axis and retention time on the y-axis.
Table 1.
A data matrix generated by a metabolomics platform.
| … | ||||
|---|---|---|---|---|
| … | … | … | ||
MS data preprocessing can be divided into (1) denoising and baseline correction, (2) alignment across all samples, (3) peak picking, (4) merging the peaks, and (5) creating a data matrix.9 We describe each of these steps below:
-
(1)
Performing denoising and baseline (background) correction9 to minimize the influence of noise introduced by variations in instrumental conditions. This is typically done through various denoising techniques10 and automatically using numerous types of polynomial fitting, such as asymmetric least squares (ALS)11 with B-splines, B-splines with penalization (i.e., P-splines)12 and an orthogonal basis of the background spectra.13
-
(2)
Performing peak alignment to group detected peaks across the samples regarding a m/z and a RT window and to integrate the grouped peaks into peak height or peak area.6 Alignment aims to correct the distortions of the RT caused by column aging, temperature changes or sometimes unknown deviations in instrumental conditions.9 RT axis could shift across the samples and specifically in a long experimental run6 that are generally associated with changes in the stationary phase of the chromato-graphic column.14 Generally we can peak alignment either before or after peak detection.15 For alignment, usually some compounds (peaks) are used as retention time standards (internal standard).5 For the most commonly used alignment techniques and methods, the interested reader is referred to the review article.16
-
(3)
Performing peak picking/detection to detect each measured ion in a sample and to assign it to a feature (m/z-RT pair) after rejecting all peaks that are below the arbitrary area threshold.5,6 First, find all local maxima and the associated peak endpoints (i.e., local minima) for each peak, and then calculate a signal-to-noise ratio (SNR). Next, check the alignment, the picked peaks and perform quality control (data cleanup) to remove those peaks that do not represent the compounds, such as typically all peaks with m/z < 300 and with scan numbers <200 will be removed5 and keep those peaks that all local maxima (i.e., peaks) with SNR above the threshold.9
-
(4)
Performing automated peak matching based on the spectral signature to merge peaks.
-
(5)
Finally, performing assignment to construct data matrix. That is, assigning the integrated peak height or peak area into a feature in a data matrix/data table for further (pre-)processing and pretreatment. The data matrix consists of annotated features (metabolites) with (relative) abundances with sample in each row, and each scan number in each column.
NMR -based data preprocessing
Similar to MS-based analysis, NMR-based analysis generates a 2D structure of feature data matrix with the samples in the rows and the spectral data points in the columns.
Also similar to MS-based analysis, the NMR-based analysis (e.g., 1H NMR analysis) requires to perform data preprocessing to mitigate non-biologically relevant effects. The following data preprocessing steps could be performed:
-
(1)
Performing baseline correction to remove or minimize baseline low frequency artifacts and experimental and instrumental variation among samples on the spectra (this step is also applied to GC/LC-MS-based analysis).2,15 The techniques used for baseline correction include robust baseline estimation,17 polynomial fitting, least-squares polynomial curve fitting,18 asymmetric least squares.19,20
-
(2)
Performing peak binning (bucketing) to reduce the number of continuous variables. NMR records spectra as continuous variables. Binning spectra is to first divide the spectrum into a desired number of bins (like histograms), and then sum all the spectral measurements inside each bin as area under the curve (i.e., one single value) to form new spectra with fewer variables.2,6 Although binning can reduce the number of variables, improve the implicit smoothing of the spectra and potentially can correct small peak shifts on the raw spectra or misalignments on the aligned spectra; binning takes the risk to remove real information of data or produce false information, resulting in less precise subsequent statistical analysis if it is used inappropriately.2 Thus, the feature (peak) detected have poor performance by binning-based methods than by peak-based methods,15 especially performance is even poor when spectral unalignment is significant, or using the same spectral bin to capture multiple peaks from different metabolites.
-
(3)
Performing peak alignment to align metabolite signals across runs. Like in MS-based analysis, in NMR-based analysis, spectrum peaks can be shifted and are observed in parts per million (ppm) axis which is caused by various variations such as instrumental, experimental or even over samples (e.g., different chemical environment of the sample like ionic strength, pH, or protein content).15 Metabolite signals can be aligned by several approaches. Among them, the simplest peak alignment is to divide the spectra into a number of local windows to match the shifted peaks across spectra. More robust peak alignment is to optimize correlation warping, which uses section length and flexibility parameters to control how spectra can be warped towards a reference spectrum.2,21 Other alignment algorithms include fast Fourier transform cross-correlation,22 e.g., the very fast icoshift alignment,23 and recursive segment-wise peak alignment for metabolic biomarker recovery.24 Like in MS-based analysis, most alignment algorithms in 1H NMR analysis require a reference spectrum. We can randomly select a reference spectrum, or we can use a sample spectrum that is the closest to the rest of the sample spectra, and we even can create a reference spectrum using the mean or median spectrum from the entire sample set or the quality control samples.6
-
(4)
Finally, performing quality control and assigning data matrix as in GC/LC-MS-based analysis after peak alignment and peak detection. Many pre-processing methods have been developed. These have been reviewed (through 2015) by Alonso et al15 The R package PepsNMR (or Packaged Extensive Preprocessing Strategy for NMR data) for 1H NMR metabolomic data pre-processing was introduced by Martin et al3 to provide an exhaustive and flexible workflow to deal with typical features of raw 1H NMR data and to cover the preprocessing and pretreatment steps.
In summary the preprocessing by either MS or NMR constructs a data matrix containing the relative abundances of a set of mass spectra for a group of samples or subjects under different conditions (e.g., disease vs treatment). The metabolomics data matrix are typically constructed in such a way that each row of the data matrix represents the subject and each column represents the mass spectra (metabolite intensities or metabolite relative abundances, peak or peak intensities). This data format is the same or similar as that are used in other ‘omics’ studies such as microbiome data matrix. We can further perform preprocessing and pretreatment steps and statistical data analysis on this data matrix.
Dealing with zero values and outliers
Both zero values and outliers challenge metabolomics data processing and statistical data analysis, but it is not easy to deal with.
The sources of zeros
Zero values could be caused by both biological and technical resources.5,25 We can categorize zero values in metabolomics into four sources: (1) structural zeros, (2) sampling zeros, (3) below the limit of detection (LOD), and (4) automatically transformed zeroes from the negative values. The first three kinds of zeros are the primary sources.
(1) Structural zeros are referred to those specific peaks that are not presented in sample/chromatogram for genuine biological reasons. (2) Sampling zeros are referred to those peaks that present in samples but are missed by peak picking. In the metabolomics data sets regardless which methods are used to generate, it is often that compounds in certain samples cannot be identified/quantified, occurring missing values in some of the samples. Here, the missing values occur due to sampling. For example, GC/LC-MS analyses utilize chromatographic separation prior to MS and thus require a complex deconvolution step to transform these 3D data matrices into lists of 2D matrix, which frequently contains missing values in the samples. (3) Some intensities or abundances are below the detection limit of the mass spectrometer.5 For example, generally the badly shaped peaks and peaks with low intensity cannot be detected during the peak picking process. (4) There is still another source of zero values that is the negative values resulted from metabolomics measurements. These negative values are usually considered as spectral artifacts or noise, therefore are transformed automatically into zeros.26 In summary, both technical errors and biological factors, or a mixture of the two may cause missing value data.25 The zero and/or missing values pose a big challenging in data processing and downstream statistical data analysis of metabolomics data. High percentage of zeros could affect the correlation between variables and deteriorate the statistical analysis.
The approaches of dealing with zeros
It should be recognized that there is no general strategy for dealing zeros because in practice identifying different sources of zeros is difficult.27 However, a large percentage of zeros poses a major challenge for statistical analysis and misleads the analysis results. Thus, in metabolomics study, researchers usually propose some practical methods to handle zero values. Typically there are three approaches to deal with the zero values present in the samples. We describe them below.
-
(1)
One simple way is to remove the zero values based on a threshold such as the ‘80% rule’28 or ‘modified 80% rule’.7 By applying the ‘80% rule’, a metabolite is kept for data analysis if it has a non-zero value for at least 80% samples, while the modified’80% rule’ considers that the missing values occur due to below the detect limitation in one specific class. Thus the ‘80% rule’ is modified to keep a metabolite for data analysis if it has a non-zero value for at least 80% in the samples of any one class. This approach will significantly reduce the number of zeros and facilitate statistical analysis. But it ignores the fact that the zero values could be caused by different sources and especially a large proportion of zeros in a study may be missing values.
-
(2)
Another approach is to impute the missing values based on imputation options such as mean, minimum, half of the minimum of non-missing values or zero.26 We summarize the imputation methods used for missing metabolomics data in Table 2.
Table 2.
Imputation methods for missing metabolomics data.
| Method | Definition |
|---|---|
| An arbitrary small value | Replacing the missing values with an arbitrary small value. |
| Zero29 | Replacing the missing values with zeros. |
| HM (Half of the Minimum)30,31 | Replacing missing value with half of the minimum of non-missing values in that variable (metabolite/peak). |
| Mean31,32 | Replacing missing value with the mean of the non-missing values across all samples for that variable (metabolite/peak). |
| Median32 | Replacing missing value with the median of the non-missing values across all samples for that variable (metabolite/peak). |
| kNN(k-nearest neighbors)31, 32, 33 |
|
| RF (random forest)35 |
|
| SVD (singular value decomposition)31,36,37 |
|
| QRILC (quantile regression imputation of left-censored data)39 |
|
| BPCA30,31,40,41 |
|
| PPCA37 |
|
| MI42 |
|
| EM and MCMC43 |
|
However, it was shown that the choice of imputation methods influences normalization and statistical analysis results.44
(3) More convincing strategy is based on missing data estimation algorithms (or types) to choose different methods to handle missing values. Generally, there are three types of missing values45: missing completely at random (MCAR), missing at random (MAR) and missing not at random (MNAR). Specifically, for metabolomics data, if the missing values are due to random errors and stochastic fluctuations in the data acquisition process, incomplete derivatization or ionization, then they are MCAR38; if the missing values are caused by other observed variables in suboptimal data preprocessing such as inaccurate peak detection and deconvolution of co-eluting compounds, then they are MAR.38 The censored missing values due to limits of quantification (LOQ) are considered as MNAR.46 For example, the missing values that often occur due to LOQ when using MS technique to identify the targeted panel of bile acids are belong to MNAR.38 However, the challenge is that missing data often do not occur randomly but rather as a function of (at least) peak abundance (signal intensity) and mass-to-charge ratio (m/z value)25 and even they occur randomly, it is difficult to differentiate MCAR from MAR data.47 In practice, the even more challenge is that the important biological information is potentially embedded in the peaks with missing values.25 In summary, it is still difficult to discern sampling zeros from biological zeros or zero values that is truly physically or biologically absent in sample based on missingness algorithms. Thus this approach also cannot provide guidelines for imputation.
In a recent survey of 47 cohort representatives from the Consortium of Metabolomics Studies (COMETS),48 eighty five percentage of studies reported that had missing values in metabolomics data, which is due to the LOD/quantification of the platform, low abundance, and rare metabolites and co-elution issues and failed quality control (QC). In most studies, the missing values were imputed most commonly by a fraction of the lowest values or by zero or by the minimum value or KNN. Most studies excluded metabolites with a percent of missingness above a certain threshold (e.g., median 50%; range 5%–90%).
However, there are no agreement on which imputation method is the optimal missing value estimation approach. For example, Hrydziuszko and Viant25 found that the k-nearest neighbor imputation method (kNN) is optimal for direct infusion mass spectrometry datasets among eight compared imputation methods they conducted (see Table 2). Gromski et al34 compared five methods for substituting missing values: zero, mean, median, k-nearest neighbors (kNN) and random forest (RF) imputation (see Table 2) on GC/MS metabolomics data in terms of unsupervised and supervised learning analyses and biological interpretation. They demonstrated that RF performed best and kNN second in both principal components-linear discriminant analysis (PC-LDA) and partial least squares-discriminant analysis (PLS-DA) supervised methods. While Wei et al38 also comprehensively compared eight imputation methods for different missing data estimation algorithms using four metabolomics datasets. They demonstrated that RF had the best performance for MCAR/MAR data and QRILC favored the left-censored MNAR data (see Table 2).
Based on above discussion on dealing with missing values in metabolomics data, the overall take-home message is: (1) Different sources of missing values in metabolomics data need different ways to deal with. (2) For a given missing metabolomic data, particular caution needs to be taken in choosing an appropriate imputation method. Because missing data may actually represent the true biological differences between groups and hence using an inappropriate method to estimate missing value may not only fail to detect significant peaks, but instead introduce further bias if the method used results in non-significant peaks as significant difference between groups.25 And (3) currently a comprehensive and systematic evaluation of different methods for handling missing values using different sources of metabolomics data is still needed.
Detecting outliers
Related to dealing with missing values is the detection and handling of possible outliers (i.e., extreme metabolite value) within the metabolomics data. Several methods have been developed so far, including: (1) Usually checking the respective peak areas and the (relative) ratio of the mean and median of the distribution. The median is considered more robust with respect to outliers in unimodal distributions.32 (2) Predominantly utilizing principal component analysis (PCA) to identify outliers followed by principal component partial R-square (PC-PR2) and analysis of variance (ANOVA) in a survey of above cited COMETS.48
Recently two specifically designed algorithms for the identification of outliers for metabolomic data have been proposed: (1) Cellwise outlier diagnostics using robust pairwise log ratios (cell-rPLR)49 was proposed for use when the measured values are not directly comparable due to the small size effect. This method is useful for biomarker identification, particularly in the presence of cellwise outliers. (2) Kernel weight function-based biomarker identification technique was proposed for missing data imputation method to handle missing values and outliers.50 Basically this technique uses the group-wise robust singular value decomposition, t-test, fold-change analysis, and SVM-based feature selection approaches to identify biomarker correctly by imputing missing values and solving outliers problem simultaneously. The goal is to improve the accuracy of imputation and the accuracy of biomarker identification deteriorated by outliers.
Data normalization
Followed by preprocessing and dealing with zeros and outliers, we typically perform two groups of methods towards statistical analysis of metabolomics data51: The first group of methods is to remove unwanted sample-to-sample variation, and the second group of methods is to adjust the variance of the different metabolites to reduce sample heteroscedasticity. We typically refer the first group of methods as data normalization and include centering, scaling and log transformations into the second group of methods. Because the first group of methods is generally performed on rows while the second group of methods on columns, thus in terms of data structure of metabolomics data matrix, they are also referred to as row-wise normalization and column-wise normalization,52 which are usually performed sequentially.
Here, we treat centering, scaling and log transformations as the different processing steps and reserve the name of normalization for row (sample)-wise normalization which include normalizing to total spectral area, normalizing to a reference sample, and normalizing to a reference feature/metabolite-based approaches. Normalization as well as centering, scaling and log/power transformations belong to preprocessing/pretreatment methods, and are performed prior to statistical data analysis of metabolites. Their overall goal is to allow the same variable (metabolite) within an array of different spectra comparable26 and thus to improve the reliability and interpretability of downstream statistical analysis.
A normalization step has been considered as be necessary due to both biological factors and technical reasons. For example, unspecific variations of the overall concentrations of samples, and a different number of scans or different devices that are used to record spectra could have the absolute signal intensities of peaks.53
Most common sample-based normalization methods scale the spectra to the same virtual overall concentration to account for different dilutions of samples. The goal of sample-based normalization is to make samples comparable to each other by removing or minimizing the unwanted systematic errors/biases and experimental variance,54 or specifically, to reduce systematic variation or bias in the data due to instrumental or sampling problems (e.g., sources of experimental variation, sample inhomogeneity, differences in sample preparation, ion suppression), or to separate biological variation from variations introduced in the experimental process.52 Mathematically, the normalized intensities of metabolite peaks represent the fraction of initial intensities of metabolite peaks over the summation of the integrated intensities with an appropriate power for all the spectral regions.53
This section focuses on the topic of normalization, the topics of centering, scaling and log/power transformations will be covered in next sections.
Constant sum normalization (CSN)
CSN (or total spectral area normalization or integral normalization) normalizes the spectra to a constant sum (i.e., total spectral area) by dividing each signal metabolite intensity or each bin (if normalization is operated after binning or bucketing) of a spectrum by the total peak areas. That is, transform every single metabolite into a fraction of the total intensity of the “spectrum”. For metabolic profiling of biofluids in 1H NMR metabolomics, the default standard normalization is integral normalization (also refers to CSN),55 normalizing the individual spectra to the same total integral intensity over the whole profile.53,56 CSN assumes that the total peak area of a spectrum is constant across the samples, i.e., the total profile is directly proportional to the total concentration of the sample. For example, the integral normalization assumes that the total integrals of spectra is a function of the overall concentrations (dilution) of samples.53 Although this approach has been widely used in both NMR and MS data as well as in other “omics” (e.g., transcriptomics, proteomics); however, this kind of normalization has the weaknesses: (1) Is not robust and inaccurate due to its above assumption.53,55 (2) It could result in incorrectly normalized data/scaled spectra due to being strongly influenced by very large signals or massive amounts of single metabolites in samples.53,57
Probabilistic quotient normalization (PQN)
PQN method53 was proposed to normalize spectra on the basis of the most probable dilutions, which estimates and utilizes a most probable quotient between the signals of the corresponding spectrum and of a reference spectrum as the normalization factor. PQN assumes that concentrations of a majority of metabolites remain unchanged across the samples and hence the changes in the concentrations of single metabolites only influence parts of the spectra, whereas changes of the overall concentration of a sample influence the complete spectrum.53 PQN uses a reference spectrum to calculate the quotients, which makes it differentiate from integral normalization, which uses the total integral as marker of the sample concentration. PQN method has the strengths, including: (1) It is more exact and more robust than the integral normalization.53 (2) It is flexible to choose the reference spectrum from either a single spectrum of the study, a “golden” reference spectrum from a database, or a median or mean spectrum of all spectra in the study or in a subset of the study53 although the most robust reference spectrum is the median spectrum of control samples. (3) It reduces some outlier effects of the CSN method because of using a median as a reference. (4) It can provide adequate normalization for most clinical metabolomics.53 And (5) particularly it was showed that PQN along with the Variance Stabilization Normalization (VSN), the log transformation are the three best methods among those 16 compared methods of normalization, scaling and transformation in terms of the partial least squares discriminant analysis (PLS-DA) and the area under the curve values (AUCs).58
However, PQN also has the weaknesses, including: (1) The results in differential metabolites analysis using PQN could be false positives. (2) It is not adequate to use PQN to normalize the data when the number of variables (metabolites) is greater than the number of samples (e.g., when the number of metabolites is greater than half of the number of samples).59
PQN can be implemented in MetaboAnalyst60,61 and other examples of using PQN are available from these studies.62, 63, 64
Quantile normalization (QN)
Quantile Normalization65 was originally proposed for multiple high-density oligonucleotide array. QN employs a nonparametric approach to normalize measured intensities from a single fluorophore to a common distribution. It assumes that the distribution of metabolite abundances in different samples is similar, and two distributions can be considered to identify in statistics properties by adjusting their distributions.
QN normalizes the data through the following five steps.
Step 1: Lists and assigns each of sample to a column and metabolites to a row. Step 2: Sorts each column by intensity from lowest to highest. Step 3: Calculates the arithmetical mean of each row according to sorted rank. Step 4: Substitutes the mean value for each intensity value in the row. Step 5: Restores the original order of the assigned mean values to find the normalized relative intensity/abundance for a given metabolite.
QN method has the strengths, including: (1) It was demonstrated as the best method for reducing variability compared to other normalization methods (e.g., central tendency, linear regression, locally weighted regression, cyclic loess, contrast-based methods) in proteomics and microarray data65,66 and the best method for removing bias between samples, and accurately reproducing fold changes in NMR-based metabolomics data.67 (2) It was also showed that QN reached the highest AUC values in all runs in a comparative study and outperformed the widely used variable scaling methods, as well as was the only method that performed consistently well in all tests.67 And (3) specifically compared to 1-norm and 2-norm normalization methods,68 QN had the most obvious ability to differentiate grouping memberships in principal component analysis (PCA), reduced the variances and no outlier was detected in the box plot, and showed the largest minimization of systematic errors by Q–Q plot from human LC-MS-based metabolomics data.69
However, the main weakness of QN method is that it only has a moderate quality of classification result for small data sets and thus QN method was recommended for use in large dataset with sizes of samples.67
Vector length normalization (VLN)
In mathematics, a norm is a function from a real or complex vector space to the nonnegative real numbers. It commutes with scaling by calculating the distance from the origin. In general, absolute-value norm (1-norm) and the Euclidean norm (2-norm) are commonly used. The absolute-value norm is a norm on the one-dimensional vector space. To obtain a vector of norm 1, multiply any nonzero vector by the inverse of its norm. However, by far the most commonly used norm is the Euclidean norm, a norm on the n-dimensional Euclidean space. The Euclidean norm is the Euclidean distance of a vector from the origin, which is calculated by the ordinary distance from the origin to the point X based on the Pythagorean theorem. The Euclidean norm sets the Euclidean distance in the multidimensional space to be constant.
VLN method70 treats the spectra as vectors and a total vector length as constraint. It sets the lengths of the vectors to 1 to adjust different concentrations. VLN is to normalize the data set by scaling each sample-vector to unit vector norm. VLN assumes that the concentration of a sample determines the length of the corresponding vector, whereas the content of a sample determines the direction of the vector. The absolute-value norm (1-norm) is to divide each variable (metabolite) by the sum of the absolute value of all variables (metabolites) for a given sample to return a vector with unit area.68 As a row-wise normalization, the Euclidean norm unifies the influence of each sample. The Euclidean norm (2-norm) is to divide each variable (metabolite) by the sum of the squared value of all variables (metabolites) for a given sample to return a vector with unit length.68 We can geometrically interpret the Euclidean norm as a projection of the samples x to a hypersphere.70 Because the length of the sample vector is scaled to one, the ratios between variables (metabolites) do not change. Thus the effect of vector normalization is closely related to correlation analysis, which leads to project the highly correlated samples close to each other.70 VLN method has been used in metabolite fingerprinting70 and the normalization effects of 1-norm and 2-norm methods were evaluated with NMR-based metabolomics data68 and LC-MS-based metabolomic data.69
The Euclidean norm has the strengths, including: (1) It was evaluated that the Euclidean norm has better classification effect than absolute-value norm in separation of group membership based on PCA.68,69 (2) It can achieve better results of separation than unit variance scaling (as a column-wise normalization, it unifies the influence of each variable) based on PCA. However, VLN methods also have the weaknesses. Particularly, one study using human LC-MS-based metabolomics data69 showed that compared to QN, both absolute-value norm and Euclidean norm were less obviously able to differentiate groups in PCA, to reduce the variances and to detect outliers in the box plot, and had the less minimization of systematic errors by Q–Q plot.69
Internal standard Normalization (ISN)
ISN is to divide the concentration of each metabolite by the concentration of an internal reference metabolite. Creatinine normalization (CN) method is a special case of the ISN method, adopting from the field of clinical chemistry.71 In metabolomics, CN was proposed in early publications.72 CN is to divide the concentration of the metabolite by the urinary creatinine (UCr) concentration obtained in the same urine sample,73 resulting the concentration of target analyte per milligram of creatinine. The goal of CN is to adjust for the variation of spot urine samples in dilution effects, sample volume and the rate of urine production by normalizing analyte quantification for specimen concentration in a ratio format.
CN is based on the assumption that creatinine is excreted into urine at a normal and constant rate in healthy individuals (creatinine clearance), and thus creatinine can be used as an indicator of the concentration of urine.53,74,75 For NMR, spectra of urine creatinine concentration (peak area) is often used as reference to adjust for urine analyte concentration72,73,76 and hence to correct for the variability observed in individual sample volumes.57
However, using urinary creatinine as a normalization factor has the weaknesses, including: (1) Biologically, CN lies on the assumption that constant excretion of creatine into urine and thus the concentration of creatine is directly related to the urine concentration.77 This may not be true because in many diseases (e.g., kidney disease), the renal function and glomerular filtration are affected, and impacts urinary creatinine concentration. Thus, UCr levels cannot be completely attributable to variations in urine concentration.73 The biological challenges of using creatinine normalization lies on the factor that changes of the concentrations of creatinine are caused by metabolomic responses.78,79 (2) Actually, adjusting for urine concentration is similar to quantify a source of random noise across all samples, likely adjusting for other factors that might be specific to a group of subjects (e.g., renal function or reduced muscle mass).73 Thus using urine concentration as normalization factor leads to inaccurate correction.80 And (3) It in practice has both technical and biological challenges.53
Other normalization methods
Combining different approaches of normalization is more adequate for most matrices commonly encountered in clinical metabolomics.81 Several normalization methods have been developed that can be combinedly used in metabolomics data, including: (1) MS Total Useful Signal (MSTUS)57 and normalization factor for each individual molecular species (NOMIS)82 for LC/MS based metabolomics data. (2) Histogram matching (HM) normalization,83 group aggregating normalization,59 maximum superposition normalization algorithm (MaSNAl),84 time-domain algorithm85 and subspace time-domain algorithm86 for NMR-based metabolomics data.
Other normalization methods that were originally developed in other fields, such as microarray experiments, have been also adopted to normalize metabolomics data. For example: (1) Cubic-spline normalization87 from DNA microarray experiments. (2) Cyclic loess normalization88,89 from microarray experiments. (3) Non-linear baseline normalization,90 contrast normalization 91from oligonucleotide arrays. And (4) linear baseline normalization65,92 from oligonucleotide array.
Data centering and scaling
To analyze metabolomics data appropriately, three categories of pretreatment usually also be performed: (1) centering, (2) scaling, and (3) transformation. The goals of data centering, scaling and transformations are to reduce the impact of very large feature values and to make all features more comparable or normally distributed.52
Mean centering
Mean centering and unit variance scaling are the two traditional scaling methods that can be used for pretreating metabolomics data. Mean-centering or unit variance scaling93 is used to remove the overall offset among other benefits such as reducing rank of the model, increasing data fitting and avoiding numerical problems.94 Let be each value of the data, be the mean of the , be the number of data points, and present the data after centering, then the (mean) centering is defined as:
| (1) |
Mean centering is just to subtract the mean value from each measured metabolite. The aim of centering is to convert all the metabolite concentrations to fluctuate around zero instead of around the mean of them. The effect of centering is to correct for the differences between high and low abundant metabolites, allowing the data analysis to focus on the mean of the metabolite concentrations, i.e., the differences of the data and instead of the similarities in the data. However, the disadvantage of centering is that: (1) It is not always sufficient to remove the biases when data is heteroscedastic.95 And (2) it could result in a parsimonious model.
Scaling
Scaling is usually conducted after replacing missing values. Scaling is to divide each variable by a scaling factor. In other words, scaling is to time each variable by a scaling weight (the reciprocal of its scaling factor). Scaling aims to adjust for the fold change differences between the different metabolites; it converts the data into differences in concentration relative to the scaling factor. Scaling is applied in metabolomics data for several reasons including to adjust scale differences, accommodate for heteroscedasticity, and allow for different sizes of subsets of data.94 Different variables could have a different scaling factor, which are named as different scaling methods. Based on whether using a data dispersion or a size measure as scaling factor, we can divide scaling into two subclasses: dispersion-based scaling and average-based scaling methods (See Table 3). Unit variance scaling,96 pareto scaling,97,98 range scaling,28 and vast scaling belong to the former category, while level scaling and linear baseline scaling belong to the latter category. We summarize their definitions in Table 3 and describe them separately.Where, present the data after centering, is the estimated standard deviation, is the number of data points, and denotes the each value of the data and is the mean of . are the intensities of the baseline spectrum and is the trimmed mean intensity. and are the mean and standard deviation of the variable for the jth class, respectively, and c is the total number of classes.
Table 3.
Definitions of scaling methods.
Unit variance scaling
Unit variance scaling (aka unit scaling or autoscaling) is a commonly used scaling or standardization method. It uses the standard deviation(σ) as the scaling factor (the scaling weight is the reciprocal of its standard deviation ) to convert the data to be analyzed on the basis of correlations instead of covariances, which is similar to centering95,96(see Table 3). In metabolomics, the goal of unit variance scaling is to convert metabolites into correlations of metabolites. Unit variance scaling has been considered as the probably most reliable scaling method.100 After unit variance scaling, all metabolites are equally weighted and hence having equal potential to influence the model. In other words, after performing unit variance scaling, the data will be allowed for better recognition,95 and hence leading to favor systematic changes with small variance and avoiding the domination by a few high-intensity variables in the final solution.94
However, like centering, unit variance scaling: (1) Does not provide the prior information about variable importance99 or confounds the potential useful information embedded in peak height, resulting in diminishing the mask effect of the abundant metabolites.7 (2) It tends to inflate the importance of small metabolites and because small metabolites are more likely to contain measurement errors and thus inflate the measurement errors.95 And (3) should not be used for the data with poor signal-to-noise ratio (i.e., noisy) because of its equally weighting all metabolites.9
Pareto scaling
Pareto scaling uses the square root of the standard deviation () as the scaling factor (see Table 3), which provides an intermediate scaling effect between the no scaling and unit variance scaling. Comparing to unit variance, pareto scaling is closer to the original measurement because it divides the centering value by instead of σ. The goal of pareto scaling is to reduce the relative importance of large values, while keeping data structure partially intact. Due to using the square root of the standard deviation of the data as scaling factor, compared to unit variance scaling, pareto scaling method can reduce more the large fold changes in metabolite signals, but leaves the extremely large fold changes unchanged.67 Pareto scaling can be used to improve the pattern recognition for metabolomics data via tailoring sensitivity reduction.7,101 However, pareto scaling is sensitive to large fold changes.95
Range scaling
Range scaling uses the difference of maximum between minimum (i.e., the biological range) as scaling factors (see Table 3). The goal of range scaling is to make metabolites be compared relative to the biological response range. Range scaling equally weights importance of all metabolites. It can be used to fuse MS-based metabolomics data.28 However, range scaling not only could result in the inflation of the measurement errors, as in the case of autoscaling,95 but also is sensitive to outliers because the biological range is estimated by only two values (the maximum and minimum values), which does not adjust for smaller and larger values of the data.
Variable stability (VAST) scaling
In the fields of metabolomics and proteomics, one common problem is to deal with the mask effect of the abundant metabolites. Unit variance scaling prefers to systematic changes with small variance and is vulnerable to diminish the mask effect of the abundant metabolites such as in peak height and peak multiplicities. VAST scaling99 was proposed to weight each variable according to a metric of its stability (see Table 3). The stable variables are the variables that do not have strong variation. VAST scaling uses the coefficient of variation (cv = , where the mean of each variable is calculated on the uncentred dataset) as the stability parameter or scaling factor. In other words, VAST uses as the scaling weight.
VAST scaling sequentially applies mean-centering and unit variance scaling (autoscaling); i.e., first puts each variable on ‘a level footing’, and then scaling by the coefficient of variation (1/CV) to incorporate stability.99 Thus, we can consider VAST scaling as an extension of unit variance scaling with one step further by actually down weighting unstable variables.99 Vast scaling puts a higher weight to the variables (metabolites) with a small relative standard deviation(σ) through using the coefficient of variation (cv). Thus by using VAST scaling the metabolites with a small relative σ are higher important, while those metabolites with a large relative σ are getting less important95; allowing us focus on the less fluctuated metabolites. VAST has been used to identify biomarkers for the NMR-based metabolomics data102 and has been shown that it improved the class distinction and predictive power of partial least squares discriminant analysis (PLS-DA) models.99 However, VAST scaling is not effective for the metabolites with large variations.
X-VAST scaling
Above we reviewed that unit variance scaling favors systematic changes with small variance but confounds the potential useful information embedded in peak height and peak multiplicities. In order to diminish the adverse effects, VAST scaling assigns a weight according to its stability to each variable (metabolite) and orthogonal signal correction (OSC)103 was proposed to extract the components with the maximum variance orthogonal to response. However how to reduce the mask effect in analysis of metabolomics data remains unsolved. The ‘x-VAST’ method7 was developed to as a part of pretreatment strategy to amend the measurement deviation enlargement. This pretreatment strategy consists of three steps:
Step 1: Uses a ‘modified 80%’ rule to reduce effect of missing values (i.e., the artificial cutoffs from the peak alignment). The ‘80% rule’ developed by Smilde et al28 is to keep a variable when this variable has a non-zero value for at least 80% of all samples. However, when this rule is implemented, some perfect differential metabolites will be lost due to their concentrations below the detect limitation in one specific class. The ‘modified 80% rule’ uses the class information as the supervisor to keep a variable if this variable has a non-zero value for at least 80% in the samples of any one class.
Step 2: Uses unit-variance and Pareto scaling methods to reduce the mask effect from the abundant metabolites.
Step 3: Uses stability information of the variables deduced from intensity information and the class information to assign suitable weights to the variables and hence to fix the adverse effect of scaling.
However, the strategy of excluding zeros at any missingness threshold is arbitrary.104
Level scaling
Average-based scaling method uses average as scaling factors, resulting the values that are changes in percentages compared to the mean concentration. One average-based scaling method is level scaling, which uses the mean concentration (i.e., the average value of each metabolite) as the scaling factor (see Table 3). Level scaling converts the metabolite concentrations to represent changes in percentage of metabolite concentrations compared to the mean concentration of the metabolite. Level scaling focuses on relative changes and hence is suitable for identifying relatively abundant biomarkers. It has been used in LC-MS study of urinary nucleosides.105 However, level scaling has the weaknesses: It is prone to inflate the measurement errors.95
Linear baseline scaling
In the metabolomics literature, linear baseline scaling (LBS) has been used,65 which normalizes each sample spectrum to the baseline. Usually, the spectrum having the median of the median intensities is chosen as a baseline spectrum.65 LBS assumes that there exists a constant linear relationship between each metabolite of a given spectrum and the baseline. However, the assumption of a linear correlation between spectra has been considered as an oversimplification.67
Data transformation
Following data scaling it is often necessary to adjust the variance of the data by using transformation. The variance of non-induced biological variation often correlates with the corresponding mean abundance of metabolites, which leads to considerable heteroscedasticity in the data, and impacts subsequent data analysis. Three overlapped goals of transformations95 are: (1) to correct for heteroscedasticity,106 (2) to convert multiplicative relations into additive relations, and (3) to make skewed distributions (more) symmetric. Both log and power transformations reduce large values relatively more than the small values. Generally the log and the power transformations, and variance stabilization normalization (VSN)107,108 are the three usually used transformations in metabolomics to reduce heteroscedasticity.
Log transformation
The log transformation has two most common applications: (1) to reduce the skewness of the data and (2) reduce the variability due to the outliers with the common belief that the log transformation is able to make data conform more closely to the normal distribution.109,110 Log transformation is defined as:
| (9) |
By default the natural logarithm is used. The general form of log transformation with adding the shift parameter --log (x, base) computes logarithms with any desired based. In metabolomics studies the base 2 log transformation is commonly used. The normal distribution is widely used for analysis of continuous outcomes. However, in practice such a well-shaped symmetric distribution rarely exists. Almost all data in real studies are skewed to some extent. When the data is not normally distributed, the log transformation is used as a common remedy to deal with the skewed data. The underlying assumption of the log transformation is that the transformed data have a distribution equal or close to the normal distribution.110
The log transformation has been reported as a powerful tool to convert right-skewed metabolomics data to be symmetric, to adjust heteroscedasticity and to transform the relationship of metabolites from multiplication to addition.95,111 It was shown that the log transformation along with PQN and Variance Stabilization Normalization (VSN), are the three best methods among those 16 compared methods of normalization, scaling and transformation in terms of the partial least squares discriminant analysis (PLS-DA) and the area under the curve values (AUCs).58 Although log transformation make multiplicative models additive to facilitate the data analysis and can perfectly remove heteroscedasticity if the relative standard deviation is constant106; however, log transformation has three main drawbacks: (1) It is unable to deal with the value zero because log zero is undefined. (2) It has limited effect on values with a large relative standard deviation, which unfortunately is usually the case when the metabolites have a relatively low concentration. And (3) It has the tendency to inflate the variance of values near zero112 although it can reduce the large variance for large values.
Specifically, using simulation and real data, Feng et al109,110 showed that the log transformation is often misused:
-
•
Log transformation usually only can remove or reduce skewness of the original data that follows a log-normal distribution or approximately so. Instead, in some cases it actually makes the distribution more skewed than the original data.
-
•
It is not generally true that the log transformation can reduce variability of data especially if the data includes outliers. In fact, whether the log transformation reduces such variability depends on the magnitude of the mean of the observations — the larger the mean the smaller the variability.
-
•
It is difficult to interpret model estimates from log transformed data because the results obtained from standard statistical tests on log-transformed data are often not relevant to the original, non-transformed data. To have straightforward biological interpretation, usually the obtained model estimates from fitting the transformed data are required to translate back to the original scale through exponentiation.113 However, since no inverse function can map back exp (E (log X)) to the original scale in a meaningful fashion, it was advised that all interpretations should focus on the transformed scale once data are log-transformed.110
-
•
Fundamentally statistical hypothesis testing of equality of (arithmetic) means of two samples is different from testing equality of (geometric) means of two samples after log transformation of right-skewed data. These two hypothesis tests are equivalent if and only if the two samples have equivalent standard deviations.
-
•
Log transformation with adding the shift parameter not only cannot help reducing the variability, but also can be quite problematic to test the equality of means of two samples using log transformation when there are values close to 0 in the samples.
Power transformation
Tukey (1957)114 is often credited with introducing a family of power transformations such that the transformed values are a monotonic function of the observations over some admissible range115 which is defined as:
| (10) |
for . This family was modified by Box and Cox (1964)116 to take the form of the Box–Cox transformation:
| (11) |
Power transformation is a parametric transformation method used to stabilize variance, make the data more normal distribution-like. We can see the log transformation embodies a family of power transformations. Mathematically many other transformations, including square root transformation (), inverse transformation, arcsine transformation belong to family of power transformations.
The strengths of power transformation lies on the factor that: (1) It does not have above three problems of log transformation. (2) Furthermore it also has positive effects on heteroscedasticity.117 (3) For metabolomics data, it was shown that power transformation outperforms log transformation in terms of reducing the heteroscedasticity and has the potential to further improve performance95 if a different power would be used.116 (4) Although the power transformation was not able to completely remove the heteroscedasticity of metabolites, it really can reduce the heteroscedasticity. However, power transformation has the weakness: it is unable to make multiplicative effects additive.
The log transformation was able to remove heteroscedasticity only for the metabolites with high concentrations; whereas for low abundant metabolites the log transformation inflated the heteroscedasticity. Based on these arguments, we prefer to use power transformation over log transformation to deal with skewed metabolomics data. For example, it was shown that the square root transformation is robust with the error variance than the log transformation and is able to handle zero values and has fewer problems for very small values in the data.95,118 Additionally, we suggest using a distribution-free method, such as the generalized estimating equations (GEE)110,119 to model the metabolomics data if metabolites are skewed rather than trying to find an appropriate transformation. GEE is tolerant of distribution assumption, providing valid inference regardless of the distribution of the data.
Variance stabilization normalization (VSN)
VSN is a non-linear transformation approach that reduces heteroscedasticity. Actually this approach is a hybrid of sample-wise normalization and a scaling procedure because it both reduces the sample-to-sample variation and adjusts the variance of different metabolites.67,77 This approach was originally developed for the analysis of DNA microarray data with different solutions,107,108,112,120 which was reviewed by Kohl et al67. It was then adopted for analysis of NMR-based metabolomics data.67,77
VSN approach combines normalization with stabilization of the metabolite variances aiming to keep the variance constant over the whole data range.77 VSN assumes that a metabolite variance depends on the mean of that metabolite via a quadratic function, while for those values that approach to the lower limit of detection, their variances stay constant without decreasing any more, and thus the coefficient of variation increases.67
VSN uses the transformation of inverse hyperbolic sine to address this assumption. It approaches the logarithm for large values to remove heteroscedasticity, while approaches linear transformation for small intensities to leave the variance unchanged. For example, the version of the R package “vsn” is implemented in107 via the following two steps:
Step 1: Corrects or reduces the sample-to-sample variation by linearly mapping the each sample concentration to a reference sample (i.e., the first sample in the data set).
Step 2: Adjusts the variance through an inverse hyperbolic sine transformation. Because VSN combines variance stabilization with between-sample normalization,67 this approach has the strengths: (1) Like PQN,53 VSN is robust and has a good performance in classification of metabolomics data such as reported in the principal component analysis(PCA),51 as well as reported in terms of the partial least squares discriminant analysis (PLS-DA) and the area under the curve values (AUCs).58,67,77,121 (2) The VSN, the Log Transformation and the PQN were identified as three best methods that had the best normalization performance, among those 16 compared methods of normalization, scaling and transformation (AUCs).58
Conclusion and perspective
Different preprocessing and pretreatment methods are used to address different issues of the metabolomics data and they are performed during different stages of data processing. Each preprocessing and pretreatment method has its own advantages and disadvantages. The choice for a suitable preprocessing or pretreatment method is determined by the biological question to be answered, the characteristics of the data set and the statistical data analysis method to be selected.
In this review, we divide the data processing from data acquisition to statistical analysis into seven steps: (1) Data acquisition, (2) Data preprocessing, (3) Dealing with missing values and detecting outliers, (4) Data normalization, (5) Data centering and scaling, and (6) Data transformation, and (7) Statistical data analysis.
Although preprocesses for MS-based data and NMR-based data have slightly different, basically a preprocessing strategy involves five steps: denoising and baseline correction, peak alignment, peak picking, peak matching, and construction of data matrix. It is common that missing values occur in processing metabolomics data sets and regardless of missing values occur from structure, sampling or below the detection limit of the machine, the zeros pose a big challenge for downstream statistical analysis. Many methods have been proposed to deal with the missing values. Related to dealing with missing values is to detect and handle outliers. Several methods have been developed so far.
Normalization is a general class of pretreatment methods aiming to remove unwanted sample-to-sample variation. Choosing an appropriate normalization method is very important topic and has been widely discussed in metabolomics. Overall probabilistic quotient normalization and quantile normalization have been evaluated as outperformed and more appropriate than other normalization methods for metabolomics data. Centering and scaling is another general class of pretreatment methods aiming to adjust the variance of the different metabolites to reduce heteroscedasticity. Different scaling methods have their own merits and drawbacks and are suitable for different data sets. Mean centering aims to convert all the metabolite concentrations to fluctuate around zero. Scaling aims to convert the data into differences in concentration relative to the scaling factor. Two scaling approaches are available: dispersion-based scaling and average-based scaling.
Data transformation is also an important topic in metabolomics and other research fields. Data transformation is to correct for heteroscedasticity, to convert multiplicative relations into additive relations, and to make skewed distributions more symmetric. Although the log transformation is the most commonly used than power transformations and variance stabilization normalization for correcting heteroscedasticity and reducing skewness. However, its appropriateness lies on log normal assumption, which is not always true in both real and simulation data. Additionally, log zero is undefined and the log transformation approach is challenging to handle very small values. Thus, a power transformation such as the square root transformation and variance stabilization normalization (VSN) are recommended. VSN combines normalization with stabilization, is a non-linear transformation approach that reduces heteroscedasticity.
Pretreating and normalizing metabolomics data is an important and challenging topic for statistical analysis of metabolomics data in biomedical research and especially in integration of metabolomics data and microbiome data. The integration of metabolomics data sets and microbiome data sets with appropriate pretreating and normalizing methods is still at an early stage compared with individual pretreating and normalizing methods proposed for each of metabolomics and microbiome, and accounting for heteroscedasticity between metabolomics and microbiome (and other omics) data sets represents a critical challenge for integration multiple omics research.
The integration of metabolomics study to complement microbiome study may open new possibility for investigating the functional roles of microbiome, although further research is needed to formally establish an appropriate paradigm. The research so far points to an associative relationship between metabolites and microbiome, but whether this link could be used as predictive pathway or even as a causative relationship is still unclear. More specifically, the lack of clarity into which microbial features and or composition of microbial communities are associated with which metabolites in individual study need to be addressed. An outstanding limitation in this field is the lack of standard or robust procedures to pretreat and normalize metabolomics and microbiome data respectively and then integrate them into one data set for statistical analysis and modeling. Therefore, most findings of the metabolites on the role to microbiome are limited to identify the metabolites that are associated with the changes of microbiome diversity and composition. Thus most of the existing data on integration of metabolomics and microbiome studies are derived from small cross-sectional studies with limited information on causality. As such, this represents an important area for future research because changes and/or diversity in the microbiota may relate to changes and/or diversity in metabolites but the microbiome taxonomic diversity does not necessarily indicate the association with the diversity at the functional level. In conclusion, although numerous unanswered questions remained on a standard procedure for pretreating and normalizing metabolomics data and integrating metabolomics data into microbiome study, the integration of metabolomics and microbiome brings a new research era for microbiome research.
Conflict of interests
The contents do not represent the views of the United States Department of Veterans Affairs or the United States Government. The study sponsor plays no role in the study design in the collection, analysis, and interpretation of data. And the authors declare no competing interests in this work.
Funding
This project was supported by the Crohn's & Colitis Foundation Senior Research Award (No. 902766 to J.S.); The National Institute of Diabetes and Digestive and Kidney Diseases (No. R01DK105118-01 and R01DK114126 to J.S.); United States Department of Defense Congressionally Directed Medical Research Programs (No. BC191198 to J.S.); VA Merit Award BX-19-00 to J.S.
Footnotes
Peer review under responsibility of Chongqing Medical University.
Contributor Information
Jun Sun, Email: Junsun7@uic.edu.
Yinglin Xia, Email: yxia@uic.edu.
References
- 1.Xia Y., Sun J. American Chemical Society; 2022. An Integrated Analysis of Microbiomes and Metabolomics. [Google Scholar]
- 2.Liland K.H. Multivariate methods in metabolomics – from pre-processing to dimension reduction and statistical analysis. TrAC, Trends Anal Chem. 2011;30(6):827–841. [Google Scholar]
- 3.Martin M., Legat B., Leenders J., et al. PepsNMR for 1H NMR metabolomic data pre-processing. Anal Chim Acta. 2018;1019:1–13. doi: 10.1016/j.aca.2018.02.067. [DOI] [PubMed] [Google Scholar]
- 4.Xia Y., Sun J. American Chemical Society; 2022. Statistical Data Analysis of Microbiomes and Metabolomics. [Google Scholar]
- 5.Bijlsma S., Bobeldijk I., Verheij E.R., et al. Large-scale human metabolomics studies: a strategy for data (pre-) processing and validation. Anal Chem. 2006;78(2):567–574. doi: 10.1021/ac051495j. [DOI] [PubMed] [Google Scholar]
- 6.Karaman I. In: Metabolomics: From Fundamentals to Clinical Applications. Sussulini A., editor. Springer International Publishing; Cham: 2017. Preprocessing and pretreatment of metabolomics data for statistical analysis; pp. 145–161. [Google Scholar]
- 7.Yang J., Zhao X., Lu X., Lin X., Xu G. A data preprocessing strategy for metabolomics to reduce the mask effect in data analysis. Front Mol Biosci. 2015;2:4. doi: 10.3389/fmolb.2015.00004. 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Defernez M., Le Gall G. In: Rolin D., editor. vol. 67. Academic Press; 2013. Chapter eleven - strategies for data handling and statistical analysis in metabolomics studies; pp. 493–555. (Advances in Botanical Research). [Google Scholar]
- 9.Smolinska A., Hauschild A.-C., Fijten R., Dallinga J., Baumbach J., Van Schooten F. Current breathomics—a review on data pre-processing techniques and machine learning in metabolomics breath analysis. J Breath Res. 2014;8(2) doi: 10.1088/1752-7155/8/2/027105. [DOI] [PubMed] [Google Scholar]
- 10.Trygg J., Gabrielsson J., Lundstedt T. Data preprocessing: Background estimation, Denoising, and Preprocessing. Comprehensive Chemometrics. 2009 doi: 10.1016/B978-044452701-1.00097-1. Corpus ID: 59884452. [DOI] [Google Scholar]
- 11.Eilers P.H. A perfect smoother. Anal Chem. 2003;75(14):3631–3636. doi: 10.1021/ac034173t. [DOI] [PubMed] [Google Scholar]
- 12.Eilers P.H., Marx B.D. Flexible smoothing with B-splines and penalties. Stat Sci. 1996;11(2):89–121. [Google Scholar]
- 13.Xu Z., Sun X., Harrington PdB. Baseline correction method using an orthogonal basis for gas chromatography/mass spectrometry data. Anal Chem. 2011;83(19):7464–7471. doi: 10.1021/ac2016745. [DOI] [PubMed] [Google Scholar]
- 14.Burton L., Ivosev G., Tate S., Impey G., Wingate J., Bonner R. Instrumental and experimental effects in LC–MS-based metabolomics. J Chromatogr B. 2008;871(2):227–235. doi: 10.1016/j.jchromb.2008.04.044. [DOI] [PubMed] [Google Scholar]
- 15.Alonso A., Marsal S., Julià A. Analytical methods in untargeted metabolomics: state of the art in 2015. Front Bioeng Biotechnol. 2015;3:23. doi: 10.3389/fbioe.2015.00023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jellema R.H., Folch-Fortuny A., Hendriks M.M. 2020. Variable Shift and Alignment. [Google Scholar]
- 17.Ruckstuhl A.F., Jacobson M.P., Field R.W., Dodd J.A. Baseline subtraction using robust local regression estimation. J Quant Spectrosc Radiat Transf. 2001;68(2):179–193. [Google Scholar]
- 18.Lieber C.A., Mahadevan-Jansen A. Automated method for subtraction of fluorescence from biological Raman spectra. Appl Spectrosc. 2003;57(11):1363–1367. doi: 10.1366/000370203322554518. [DOI] [PubMed] [Google Scholar]
- 19.Eilers P.H., Boelens H.F. Baseline correction with asymmetric least squares smoothing. Leiden University Medical Centre Report. 2005;1(1):5. [Google Scholar]
- 20.Eilers P.H. Parametric time warping. Anal Chem. 2004;76(2):404–411. doi: 10.1021/ac034800e. [DOI] [PubMed] [Google Scholar]
- 21.Nielsen N.-P.V., Carstensen J.M., Smedsgaard J. Aligning of single and multiple wavelength chromatographic profiles for chemometric data analysis using correlation optimised warping. J Chromatogr A. 1998;805(1–2):17–35. [Google Scholar]
- 22.Wong J.W., Durante C., Cartwright H.M. Application of fast Fourier transform cross-correlation for the alignment of large chromatographic and spectral datasets. Anal Chem. 2005;77(17):5655–5661. doi: 10.1021/ac050619p. [DOI] [PubMed] [Google Scholar]
- 23.Savorani F., Tomasi G., Engelsen S.B. icoshift: a versatile tool for the rapid alignment of 1D NMR spectra. J Magn Reson. 2010;202(2):190–202. doi: 10.1016/j.jmr.2009.11.012. [DOI] [PubMed] [Google Scholar]
- 24.Veselkov K.A., Lindon J.C., Ebbels T.M., et al. Recursive segment-wise peak alignment of biological 1H NMR spectra for improved metabolic biomarker recovery. Anal Chem. 2009;81(1):56–66. doi: 10.1021/ac8011544. [DOI] [PubMed] [Google Scholar]
- 25.Hrydziuszko O., Viant M.R. Missing values in mass spectrometry based metabolomics: an undervalued step in the data processing pipeline. Metabolomics. 2012;8(1):161–174. [Google Scholar]
- 26.Gaude E., Chignola F., Spiliotopoulos D., et al. muma, an R package for metabolomics univariate and multivariate statistical analysis. Current Metabolomics. 2013;1(2):180–189. [Google Scholar]
- 27.Martín-Fernández J.A., Palarea-Albaladejo J., Olea R.A. Dealing with zeros. Compositional data analysis: Theory and applications. 2011:43–58. [Google Scholar]
- 28.Smilde A.K., van der Werf M.J., Bijlsma S., van der Werff-van der Vat B.J., Jellema R.H. Fusion of mass spectrometry-based metabolomics data. Anal Chem. 2005;77(20):6729–6736. doi: 10.1021/ac051080y. [DOI] [PubMed] [Google Scholar]
- 29.Steuer R. Review: on the analysis and interpretation of correlations in metabolomic data. Briefings Bioinf. 2006;7(2):151–158. doi: 10.1093/bib/bbl009. [DOI] [PubMed] [Google Scholar]
- 30.Xia J., Psychogios N., Young N., Wishart D.S. MetaboAnalyst: a web server for metabolomic data analysis and interpretation. Nucleic Acids Res. 2009;37(Web Server issue):W652–W660. doi: 10.1093/nar/gkp356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Xia J., Sinelnikov I.V., Han B., Wishart D.S. MetaboAnalyst 3.0--making metabolomics more meaningful. Nucleic Acids Res. 2015;43(W1):W251–W257. doi: 10.1093/nar/gkv380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Steuer R., Morgenthal K., Weckwerth W., Selbig J. Metabolomics. Springer; 2007. A gentle guide to the analysis of metabolomic data; pp. 105–126. [DOI] [PubMed] [Google Scholar]
- 33.Troyanskaya O., Cantor M., Sherlock G., et al. Missing value estimation methods for DNA microarrays. Bioinformatics. 2001;17(6):520–525. doi: 10.1093/bioinformatics/17.6.520. [DOI] [PubMed] [Google Scholar]
- 34.Gromski P.S., Xu Y., Kotze H.L., et al. Influence of missing values substitutes on multivariate analysis of metabolomics data. Metabolites. 2014;4(2):433–452. doi: 10.3390/metabo4020433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Stekhoven D.J., Bühlmann P. MissForest—non-parametric missing value imputation for mixed-type data. Bioinformatics. 2012;28(1):112–118. doi: 10.1093/bioinformatics/btr597. [DOI] [PubMed] [Google Scholar]
- 36.Hastie T., Tibshirani R., Sherlock G., Eisen M., Brown P., Botstein D. 1999. Imputing Missing Data for Gene Expression Arrays. [Google Scholar]
- 37.Stacklies W., Redestig H., Scholz M., Walther D., Selbig J. pcaMethods—a bioconductor package providing PCA methods for incomplete data. Bioinformatics. 2007;23(9):1164–1167. doi: 10.1093/bioinformatics/btm069. [DOI] [PubMed] [Google Scholar]
- 38.Wei R., Wang J., Su M., et al. Missing value imputation approach for mass spectrometry-based metabolomics data. Sci Rep. 2018;8(1):663. doi: 10.1038/s41598-017-19120-0. 663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lazar C. vol. 2. 2015. imputeLCMD: A Collection of Methods for Left-Censored Missing Data Imputation. R package, version. [Google Scholar]
- 40.Oba S., Sato M.A., Takemasa I., Monden M., Matsubara K.I., Ishii S. A Bayesian missing value estimation method for gene expression profile data. Bioinformatics. 2003;19(16):2088–2096. doi: 10.1093/bioinformatics/btg287. [DOI] [PubMed] [Google Scholar]
- 41.Steinfath M., Groth D., Lisec J., Selbig J. Metabolite profile analysis: from raw data to regression and classification. Physiol Plantarum. 2008;132(2):150–161. doi: 10.1111/j.1399-3054.2007.01006.x. [DOI] [PubMed] [Google Scholar]
- 42.Buuren Sv, Groothuis-Oudshoorn K. mice: multivariate imputation by chained equations in R. J Stat Software. 2010:1–68. [Google Scholar]
- 43.Lin T.H. A comparison of multiple imputation with EM algorithm and MCMC method for quality of life missing data. Qual Quantity. 2010;44(2):277–287. [Google Scholar]
- 44.Costea P.I., Zeller G., Sunagawa S., Bork P. A fair comparison. Nat Methods. 2014;11(4):359. doi: 10.1038/nmeth.2897. 359. [DOI] [PubMed] [Google Scholar]
- 45.Little R.J., Rubin D.B. vol. 793. John Wiley & Sons; 2019. (Statistical Analysis with Missing Data). [Google Scholar]
- 46.Karpievitch Y.V., Dabney A.R., Smith R.D. Normalization and missing value imputation for label-free LC-MS analysis. BMC Bioinf. 2012;13(16):S5. doi: 10.1186/1471-2105-13-S16-S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Lazar C., Gatto L., Ferro M., Bruley C., Burger T. Accounting for the multiple natures of missing values in label-free quantitative proteomics data sets to compare imputation strategies. J Proteome Res. 2016;15(4):1116–1125. doi: 10.1021/acs.jproteome.5b00981. [DOI] [PubMed] [Google Scholar]
- 48.Playdon M.C., Joshi A.D., Tabung F.K., et al. Metabolomics analytics workflow for epidemiological research: perspectives from the consortium of metabolomics studies (COMETS) Metabolites. 2019;9(7):145. doi: 10.3390/metabo9070145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Walach J., Filzmoser P., Kouřil Š., Friedecký D., Adam T. Cellwise outlier detection and biomarker identification in metabolomics based on pairwise log ratios. J Chemometr. 2020;34(1):e3182. doi: 10.1002/cem.3182. e3182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kumar N., Hoque M.A., Sugimoto M. Kernel weighted least square approach for imputing missing values of metabolomics data. Sci Rep. 2021;11(1) doi: 10.1038/s41598-021-90654-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zhang S., Zheng C., Lanza I.R., Nair K.S., Raftery D., Vitek O. Interdependence of signal processing and analysis of urine 1H NMR spectra for metabolic profiling. Anal Chem. 2009;81(15):6080–6088. doi: 10.1021/ac900424c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Xia J., Mandal R., Sinelnikov I.V., Broadhurst D., Wishart D.S. MetaboAnalyst 2.0—a comprehensive server for metabolomic data analysis. Nucleic Acids Res. 2012;40(W1):W127–W133. doi: 10.1093/nar/gks374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Dieterle F., Ross A., Schlotterbeck G., Senn H. Probabilistic quotient normalization as robust method to account for dilution of complex biological mixtures. Application in 1H NMR metabonomics. Anal Chem. 2006;78(13):4281–4290. doi: 10.1021/ac051632c. [DOI] [PubMed] [Google Scholar]
- 54.Zacharias H., Altenbuchinger M., Gronwald W. 2018. Data Normalization in NMR-Based Metabolomics. [Google Scholar]
- 55.Craig A., Cloarec O., Holmes E., Nicholson J.K., Lindon J.C. Scaling and normalization effects in NMR spectroscopic metabonomic data sets. Anal Chem. 2006;78(7):2262–2267. doi: 10.1021/ac0519312. [DOI] [PubMed] [Google Scholar]
- 56.Spraul M., Neidig P., Klauck U., et al. Automatic reduction of NMR spectroscopic data for statistical and pattern recognition classification of samples. J Pharmaceut Biomed Anal. 1994;12(10):1215–1225. doi: 10.1016/0731-7085(94)00073-5. [DOI] [PubMed] [Google Scholar]
- 57.Warrack B.M., Hnatyshyn S., Ott K.-H., et al. Normalization strategies for metabonomic analysis of urine samples. J Chromatogr B. 2009;877(5):547–552. doi: 10.1016/j.jchromb.2009.01.007. [DOI] [PubMed] [Google Scholar]
- 58.Li B., Tang J., Yang Q., et al. Performance evaluation and online realization of data-driven normalization methods used in LC/MS based untargeted metabolomics analysis. Sci Rep. 2016;6(1) doi: 10.1038/srep38881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Dong J., Cheng K.-K., Xu J., Chen Z., Griffin J.L. Group aggregating normalization method for the preprocessing of NMR-based metabolomic data. Chemometr Intell Lab Syst. 2011;108(2):123–132. [Google Scholar]
- 60.Xia J., Wishart D.S. Web-based inference of biological patterns, functions and pathways from metabolomic data using MetaboAnalyst. Nat Protoc. 2011;6(6):743–760. doi: 10.1038/nprot.2011.319. [DOI] [PubMed] [Google Scholar]
- 61.Chong J., Wishart D.S., Xia J. Using MetaboAnalyst 4.0 for comprehensive and integrative metabolomics data analysis. Current Protocols in Bioinformatics. 2019;68(1):e86. doi: 10.1002/cpbi.86. [DOI] [PubMed] [Google Scholar]
- 62.De Filippis F., Pellegrini N., Vannini L., et al. High-level adherence to a Mediterranean diet beneficially impacts the gut microbiota and associated metabolome. Gut. 2016;65(11):1812–1821. doi: 10.1136/gutjnl-2015-309957. [DOI] [PubMed] [Google Scholar]
- 63.Rocha C.M., Barros A.S., Goodfellow B.J., et al. NMR metabolomics of human lung tumours reveals distinct metabolic signatures for adenocarcinoma and squamous cell carcinoma. Carcinogenesis. 2014;36(1):68–75. doi: 10.1093/carcin/bgu226. [DOI] [PubMed] [Google Scholar]
- 64.O'Keefe S.J.D., Li J.V., Lahti L., et al. Fat, fibre and cancer risk in African Americans and rural Africans. Nat Commun. 2015;6(1):6342. doi: 10.1038/ncomms7342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Bolstad B.M., Irizarry R.A., Åstrand M., Speed T.P. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics. 2003;19(2):185–193. doi: 10.1093/bioinformatics/19.2.185. [DOI] [PubMed] [Google Scholar]
- 66.Callister S.J., Barry R.C., Adkins J.N., et al. Normalization approaches for removing systematic biases associated with mass spectrometry and label-free proteomics. J Proteome Res. 2006;5(2):277–286. doi: 10.1021/pr050300l. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Kohl S.M., Klein M.S., Hochrein J., Oefner P.J., Spang R., Gronwald W. State-of-the art data normalization methods improve NMR-based metabolomic analysis. Metabolomics : Official journal of the Metabolomic Society. 2012;8(Suppl 1):146–160. doi: 10.1007/s11306-011-0350-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Wen J., Xiao X., Dong J., Chen Z., Dai X. Paper Presented at: 2007 1st International Conference on Bioinformatics and Biomedical Engineering. 2007. Data normalization for diabetes II metabonomics analysis. [Google Scholar]
- 69.Lee J., Park J., Lim M.S., et al. Quantile normalization approach for liquid chromatography–mass spectrometry-based metabolomic data from healthy human volunteers. Anal Sci. 2012;28(8):801–805. doi: 10.2116/analsci.28.801. [DOI] [PubMed] [Google Scholar]
- 70.Scholz M., Gatzek S., Sterling A., Fiehn O., Selbig J. Metabolite fingerprinting: detecting biological features by independent component analysis. Bioinformatics. 2004;20(15):2447–2454. doi: 10.1093/bioinformatics/bth270. [DOI] [PubMed] [Google Scholar]
- 71.Jatlow P., McKee S., O'Malley S.S. Correction of urine cotinine concentrations for creatinine excretion: is it useful? Clin Chem. 2003;49(11):1932–1934. doi: 10.1373/clinchem.2003.023374. [DOI] [PubMed] [Google Scholar]
- 72.Holmes E., Foxall P., Nicholson J., et al. Automatic data reduction and pattern recognition methods for analysis of 1H NMR spectra of human urine from normal and pathological states. Anal Biochem. 1994;220:284–296. doi: 10.1006/abio.1994.1339. [DOI] [PubMed] [Google Scholar]
- 73.Wagner B.D., Accurso F.J., Laguna T.A. The applicability of urinary creatinine as a method of specimen normalization in the cystic fibrosis population. J Cyst Fibros : official journal of the European Cystic Fibrosis Society. 2010;9(3):212–216. doi: 10.1016/j.jcf.2010.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Heavner D.L., Morgan W.T., Sears S.B., Richardson J.D., Byrd G.D., Ogden M.W. Effect of creatinine and specific gravity normalization techniques on xenobiotic biomarkers in smokers' spot and 24-h urines. J Pharmaceut Biomed Anal. 2006;40(4):928–942. doi: 10.1016/j.jpba.2005.08.008. [DOI] [PubMed] [Google Scholar]
- 75.Suwazono Y., Åkesson A., Alfvén T., Järup L., Vahter M. Creatinine versus specific gravity-adjusted urinary cadmium concentrations. Biomarkers. 2005;10(2–3):117–126. doi: 10.1080/13547500500159001. [DOI] [PubMed] [Google Scholar]
- 76.Fauler G., Leis H., Huber E., et al. Determination of homovanillic acid and vanillylmandelic acid in neuroblastoma screening by stable isotope dilution GC-MS. J Mass Spectrom. 1997;32(5):507–514. doi: 10.1002/(SICI)1096-9888(199705)32:5<507::AID-JMS503>3.0.CO;2-9. [DOI] [PubMed] [Google Scholar]
- 77.Saccenti E. Correlation patterns in experimental data are affected by normalization procedures: consequences for data analysis and network inference. J Proteome Res. 2017;16(2):619–634. doi: 10.1021/acs.jproteome.6b00704. [DOI] [PubMed] [Google Scholar]
- 78.Shockcor J.P., Holmes E. Metabonomic applications in toxicity screening and disease diagnosis. Curr Top Med Chem. 2002;2(1):35–51. doi: 10.2174/1568026023394498. [DOI] [PubMed] [Google Scholar]
- 79.Beckwith-Hall B., Nicholson J., Nicholls A., et al. Nuclear magnetic resonance spectroscopic and principal components analysis investigations into biochemical effects of three model hepatotoxins. Chem Res Toxicol. 1998;11(4):260–272. doi: 10.1021/tx9700679. [DOI] [PubMed] [Google Scholar]
- 80.Kohler I., Verhoeven A., Derks R.J., Giera M. Analytical pitfalls and challenges in clinical metabolomics. Bioanalysis. 2016;8(14):1509–1532. doi: 10.4155/bio-2016-0090. [DOI] [PubMed] [Google Scholar]
- 81.Chen Y., Shen G., Zhang R., et al. Combination of injection volume calibration by creatinine and MS signals' normalization to overcome urine variability in LC-MS-based metabolomics studies. Anal Chem. 2013;85(16):7659–7665. doi: 10.1021/ac401400b. [DOI] [PubMed] [Google Scholar]
- 82.Sysi-Aho M., Katajamaa M., Yetukuri L., Orešič M. Normalization method for metabolomics data using optimal selection of multiple internal standards. BMC Bioinf. 2007;8(1):93. doi: 10.1186/1471-2105-8-93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Torgrip R.J.O., Åberg K.M., Alm E., Schuppe-Koistinen I., Lindberg J. A note on normalization of biofluid 1D 1H-NMR data. Metabolomics. 2008;4(2):114–121. [Google Scholar]
- 84.Romano R., Lamanna R., Santini M.T., Indovina P.L. A new algorithm for NMR spectral normalization. J Magn Reson. 1999;138(1):115–122. doi: 10.1006/jmre.1999.1708. [DOI] [PubMed] [Google Scholar]
- 85.Romano R., Santini M.T., Indovina P.L. A time-domain algorithm for NMR spectral normalization. J Magn Reson. 2000;146(1):89–99. doi: 10.1006/jmre.2000.2102. [DOI] [PubMed] [Google Scholar]
- 86.Lemmerling P., Vanhamme L., Romano R., Van Huffel S. A subspace time-domain algorithm for automated NMR spectral normalization. J Magn Reson. 2002;157(2):190–199. doi: 10.1006/jmre.2002.2598. [DOI] [PubMed] [Google Scholar]
- 87.Workman C., Jensen L.J., Jarmer H., et al. A new non-linear normalization method for reducing variability in DNA microarray experiments. Genome Biol. 2002;3(9):0041. doi: 10.1186/gb-2002-3-9-research0048. research0048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Cleveland W.S., Devlin S.J. Locally weighted regression: an approach to regression analysis by local fitting. J Am Stat Assoc. 1988;83(403):596–610. [Google Scholar]
- 89.Dudoit S., Yang Y.H., Callow M.J., Speed T.P. Statistical methods for identifying differentially expressed genes in replicated cDNA microarray experiments. Stat Sin. 2002:111–139. [Google Scholar]
- 90.Li C., Hung Wong W. Model-based analysis of oligonucleotide arrays: model validation, design issues and standard error application. Genome Biol. 2001;2(8):0031. doi: 10.1186/gb-2001-2-8-research0032. research0032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Åstrand M. Contrast normalization of oligonucleotide arrays. J Comput Biol. 2003;10(1):95–102. doi: 10.1089/106652703763255697. [DOI] [PubMed] [Google Scholar]
- 92.Park T., Yi S.-G., Kang S.-H., Lee S., Lee Y.-S., Simon R. Evaluation of normalization methods for microarray data. BMC Bioinf. 2003;4(1):33. doi: 10.1186/1471-2105-4-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Martens H., Naes T. Wiley; Chichester, UK: 1989. Multivariate Calibration. [Google Scholar]
- 94.Bro R., Smilde A.K. Centering and scaling in component analysis. J Chemometr. 2003;17(1):16–33. [Google Scholar]
- 95.van den Berg R.A., Hoefsloot H.C., Westerhuis J.A., Smilde A.K., van der Werf M.J. Centering, scaling, and transformations: improving the biological information content of metabolomics data. BMC Genom. 2006;7(1):142. doi: 10.1186/1471-2164-7-142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Jackson J., Edward A. John Willey Sons. Inc; New York: 1991. User's Guide to Principal Components; p. 40. [Google Scholar]
- 97.Erikson L., Johansson E., Kettaneh-Wold N., Wold S. Umetrics AB; Sweden: 1999. Introduction to Multi-And Megavariate Data Analysis Using Projection Methods (PCA & PLS) Umea. [Google Scholar]
- 98.Wold S., Johansson E., Cocchi M. ESCOM; Leiden, Holland: 1993. 3D QSAR in Drug Design: Theory, Methods and Applications; pp. 523–550. [Google Scholar]
- 99.Keun H.C., Ebbels T.M.D., Antti H., et al. Improved analysis of multivariate data by variable stability scaling: application to NMR-based metabolic profiling. Anal Chim Acta. 2003;490(1):265–276. [Google Scholar]
- 100.Goodacre R., Broadhurst D., Smilde A.K., et al. Proposed minimum reporting standards for data analysis in metabolomics. Metabolomics. 2007;3(3):231–241. [Google Scholar]
- 101.Yan Z., Yan R. Tailored sensitivity reduction improves pattern recognition and information recovery with a higher tolerance to varied sample concentration for targeted urinary metabolomics. J Chromatogr A. 2016;1443:101–110. doi: 10.1016/j.chroma.2016.03.023. [DOI] [PubMed] [Google Scholar]
- 102.Giskeødegård G.F., Grinde M.T., Sitter B., et al. Multivariate modeling and prediction of breast cancer prognostic factors using MR metabolomics. J Proteome Res. 2010;9(2):972–979. doi: 10.1021/pr9008783. [DOI] [PubMed] [Google Scholar]
- 103.Wold S., Antti H., Lindgren F., Öhman J. Orthogonal signal correction of near-infrared spectra. Chemometr Intell Lab Syst. 1998;44(1):175–185. [Google Scholar]
- 104.Arioli A., Dagliati A., Geary B., et al. OptiMissP: a dashboard to assess missingness in proteomic data-independent acquisition mass spectrometry. PLoS One. 2021;16(4) doi: 10.1371/journal.pone.0249771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Struck W., Siluk D., Yumba-Mpanga A., Markuszewski M., Kaliszan R., Markuszewski M.J. Liquid chromatography tandem mass spectrometry study of urinary nucleosides as potential cancer markers. J Chromatogr A. 2013;1283:122–131. doi: 10.1016/j.chroma.2013.01.111. [DOI] [PubMed] [Google Scholar]
- 106.Kvalheim O.M., Brakstad F., Liang Y. Preprocessing of analytical profiles in the presence of homoscedastic or heteroscedastic noise. Anal Chem. 1994;66(1):43–51. [Google Scholar]
- 107.Huber W., Von Heydebreck A., Sültmann H., Poustka A., Vingron M. Variance stabilization applied to microarray data calibration and to the quantification of differential expression. Bioinformatics. 2002;18(suppl_1):S96–S104. doi: 10.1093/bioinformatics/18.suppl_1.s96. [DOI] [PubMed] [Google Scholar]
- 108.Parsons H.M., Ludwig C., Günther U.L., Viant M.R. Improved classification accuracy in 1- and 2-dimensional NMR metabolomics data using the variance stabilising generalised logarithm transformation. BMC Bioinf. 2007;8(1):234. doi: 10.1186/1471-2105-8-234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Feng C., Wang H., Lu N., et al. Log-transformation and its implications for data analysis. Shanghai archives of psychiatry. 2014;26(2):105–109. doi: 10.3969/j.issn.1002-0829.2014.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Feng C., Wang H., Lu N., Tu X.M. Log transformation: application and interpretation in biomedical research. Stat Med. 2013;32(2):230–239. doi: 10.1002/sim.5486. [DOI] [PubMed] [Google Scholar]
- 111.De Livera A.M., Dias D.A., De Souza D., et al. Normalizing and integrating metabolomics data. Anal Chem. 2012;84(24):10768–10776. doi: 10.1021/ac302748b. [DOI] [PubMed] [Google Scholar]
- 112.Durbin B.P., Hardin J.S., Hawkins D.M., Rocke D.M. A variance-stabilizing transformation for gene-expression microarray data. Bioinformatics. 2002;18(suppl_1):S105–S110. doi: 10.1093/bioinformatics/18.suppl_1.s105. [DOI] [PubMed] [Google Scholar]
- 113.Bland J.M., Altman D.G. Transformations, means, and confidence intervals. BMJ Br Med J (Clin Res Ed) 1996;312(7038):1079. doi: 10.1136/bmj.312.7038.1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Tukey J.W. On the comparative anatomy of transformations. Ann Math Stat. 1957:602–632. [Google Scholar]
- 115.Sakia R.M. The Box-Cox transformation technique: a review. J Roy Stat Soc: Series D (The Statistician) 1992;41(2):169–178. [Google Scholar]
- 116.Box G.E., Cox D.R. An analysis of transformations. J Roy Stat Soc B. 1964;26(2):211–243. [Google Scholar]
- 117.Box G.E., Hill W.J. Correcting inhomogeneity of variance with power transformation weighting. Technometrics. 1974;16(3):385–389. [Google Scholar]
- 118.Waaijenborg S., Korobko O., Willems van Dijk K., et al. Fusing metabolomics data sets with heterogeneous measurement errors. PLoS One. 2018;13(4) doi: 10.1371/journal.pone.0195939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Liang K.-Y., Zeger S.L. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73(1):13–22. [Google Scholar]
- 120.Anderle M., Roy S., Lin H., Becker C., Joho K. Quantifying reproducibility for differential proteomics: noise analysis for protein liquid chromatography-mass spectrometry of human serum. Bioinformatics. 2004;20(18):3575–3582. doi: 10.1093/bioinformatics/bth446. [DOI] [PubMed] [Google Scholar]
- 121.Välikangas T., Suomi T., Elo L.L. A systematic evaluation of normalization methods in quantitative label-free proteomics. Briefings Bioinf. 2016;19(1):1–11. doi: 10.1093/bib/bbw095. [DOI] [PMC free article] [PubMed] [Google Scholar]