The missing hydrogen ion, part-1: Historical precedents vs. fundamental concepts

Abstract

The purpose of this review and commentary was to provide an historical and evidence-based account of organic acids and the biochemical and organic chemistry evidence for why cells do not produce metabolites that are acids. The scientific study of acids has a long history dating to the 16^th and 17^th centuries, and the definition of an acid was proposed in 1884 as a molecule that when in an aqueous solution releases a hydrogen ion (H⁺). There are three common ionizable functional groups for molecules classified as acids: 1) the carboxyl group, 2) the phosphoryl group and 3) the amine group. The propensity by which a cation will associate or dissociate with a negatively charged atom is quantified by the equilibrium constant (K_eq) of the dissociation constant (K_d) of the ionization (K_eq ​= ​K_d), which for lactic acid (HLa) vs. lactate (La^-) is expressed as: $K_{eq}=K_d=\raisebox{1ex}{$\left[H^{+}\right]\left[{La}^{-}\right]$}\!\left/ \!\raisebox{-1ex}{$\left[HLa\right]$}\right.=$ 4 677.351 4 (ionic strength ​= ​0.01 Mol⋅L^-1, T ​= ​25 ​°C). The negative log₁₀ of the dissociation pK_d reveals the pH at which half of the molecules are ionized, which for HLa ​= ​3.67. Thus, knowing the pK_d and the pH of the solution at question will reveal the extent of the ionization vs. acidification of molecules that are classified as acids.

List of abbreviations

$H^{+}$

Hydrogen ion, which is a hydrogen atom that is missing its single electron (also termed a proton)

$K_{eq}$

Equilibrium constant

$K_d$

Dissociation constant

HLa

Lactic acid

La^-

Lactate

HNO₃

Nitric acid

H₂SO₄

Sulphuric acid

HA

Acid

B

Base

BH⁺

Protonated base

$A^{-}$

Ionized (deprotonated) acid

H₃O⁺

Hydronium ion

∼H⁺

Fractional H⁺ release

H₂O

Water

OH^-

Hydroxyl ion

$K_w$

Ion product of water

pH

Measurement scale of acidity-alkalinity, ranging from 1 to 14

HPO₄^2-

Hydrogen phosphate, also known as inorganic phosphate (HPi)

H₂PO₄^1-

Di-hydrogen phosphate

-HCOO^1-

Carboxyl functional group

-HPO₄^2-

Phosphoryl functional group

-NH₂

Amine functional group

Na⁺

Sodium ion

K⁺

Potassium ion

Ca²⁺

Calcium ion

Mg²⁺

Magnesium ion

1. Introduction

There has been a historical acceptance of the cellular production of acid molecules (molecules that release a hydrogen ion (H⁺) in aqueous solution) within living systems. However, as will be explained throughout this three-part series, this historical perspective, as with all topics, has needed considerable refinement based on a progressive improved understanding of acid-base chemistry and its involvement in cellular metabolic biochemistry. This improvement is needed as the prior historical interpretations developed over time, with a foundation formed over decades, perhaps centuries. During such times, science was a concept early in its development, and human decisions were based more on inference and convenience than evidential proof.

For example, the basic structural chemistry of acid molecules was researched and refined during the period from 1754 to 1923.¹ The isolation and structure of many acids were also known as early as the late 18th century, where lactic acid was isolated, and its structure deduced as early as 1780.² The problem with this very early work was that at that time there was insufficient knowledge of the more detailed chemistry of biological acids and bases and their functions in biological system. Of even greater importance was the lack of understanding of the organic chemistry of the atomic changes that occur during chemical reactions and how such reactions occurred to balance atoms, electrons and resultant charges between substrates and products. Such historically simplistic views of acid-base chemistry led to researchers measuring what they thought was lactic acid, but which we now know was the negatively charged base, lactate. Consequently, during this early research, and for many decades to follow, researchers erroneously stated they measured lactic acid instead of lactate.

The perception that acid molecules are produced and therefore exist in living tissues were notable as early as the late 19^th century, and based on the understanding at that time of the process of fermentation (the chemical breakdown of carbohydrate molecules in the absence of oxygen).³ In short, the inferential logic (not evidence-based deduction) was that if fermentation resulted in acidosis, which in turn caused food to taste sour, then sour milk was caused by the production of an acid and as sour milk contains lactic acid (lactate), it is the production of lactic acid (lactate) that causes milk to become sour.² Consequently, the later discovery of lactic acid (lactate) in skeletal muscle following intense contractions was then interpreted to cause the acidosis that was seen during intense exercise.^2,3

Such views gained further acceptance and relevance to skeletal muscle metabolism based on the research of Hill^4,5 and Meyerhoff.^6,7 Both scientists were awarded a Nobel Prize in 1922 for their independent contributions to elucidating how cells can release energy from reactions that do not rely on oxygen, and during such conditions produce lactic acid (lactate) which was associated with a decline in cellular and blood pH (acidosis); lactic acidosis.

Since the 1930s, decades of research ensued to reveal a temporal and energy demand association between cellular and systemic acidosis and increases in cellular or blood lactic acid (lactate).8, 9, 10, 11, 12, 13 Such research was originally interpreted to reinforce the lactic acidosis construct, with subsequent acceptance by mainstream basic, applied and clinical scientists, even though such acceptance is based on two cardinal sins for what not to do in science. These are to: a) interpret association (or correlation) as cause-and-effect, and b) build acceptance of new knowledge on inference and not evidence-based deduction.¹⁴ Regardless, most people, across all levels of education in the clinical sciences, sports medicine and health sciences (minimal to highly educated), are aware of the molecule lactic acid (lactate) and use its increased production to explain the acidosis of intense exercise and many disease processes (e.g., heart disease, heart failure, peripheral vascular disease, blood poisoning [sepsis], etc.), sore muscles, failing muscle contraction and faltering sports performance. In addition, another widely held view is that other molecules of ‘acidic nature’ produced by the liver (two of the ketone bodies; β-hydroxybutyrate, acetoacetate) explained the acidosis of starvation and/or cellular carbohydrate depletion, in addition to diabetic and alcoholic keto-acidosis.15, 16, 17, 18

Despite these historical precedents, we must ask the questions: Do cells produce metabolic acid molecules, and do they alter cellular and systemic acid-base balance? Based on an analysis of the last 100 years of research of acid-base chemistry, molecule and cation pH dependent dissociation constants, organic chemistry, and cellular biochemistry, the answer to both questions is an emphatic NO. This answer opposes past and even currently accepted understandings of the metabolic cause (as distinct from nutritional or renal causes) of cellular and systemic acidosis. Why is there a discrepancy?

This is the first of a three-part series that is written for all teachers, scientists and students of the biological sciences that has an overarching purpose of providing the background knowledge and evidence for why cells do not produce metabolic acids. In addition, during the third and final part, the series uses core concepts from the historical and philosophical development of science to foster an understanding of why the human pursuit of science can frequently develop and support incorrect paradigms. Each part of the series will pose pertinent questions, where each question is followed by the authors’ interpretation of a conventional explanation (current view), and then, where necessary, a summary of empirical evidence that leads to what will be argued to be a more accurate (scientifically supported by empirical evidence) answer.

In Part-1 of the series, the questions will initially focus on content essential to understand the fundamental principles of acid-base chemistry. The expanded purpose of this first manuscript is to provide pertinent questions concerning the chemistry and physiology of organic acids, and the related fundamental principles of acid-base chemistry. Part-2 will extend the questions to present evidence of the biochemistry of acidosis, with key emphasis on the results from organic and computational chemistry for why cells are incapable of producing metabolic acids, and why the acidosis that does occur can be explained by other sources of H⁺ release. Part-3 will explain the historical development of science and the key features revealed from scientific philosophy for how science is, compared to how science should, be conducted. Part-3 will also provide other examples of topics from within exercise physiology, sports medicine and the health sciences that have been challengend and refined or replaced with more evidence-based understanding. Such content further emphasizes the need for scientists to be self-aware of the need for careful critical evaluation of data interpretation and the dissemination of these findings.

The final product of all parts will be a synopsis of the human pursuit of science. This will reveal the fragility and vulnerability of its pursuit, and further detail the flaws of human behaviour that can too easily divert a subset of intended research inquiry to a path disconnected from the truth and consequently more aligned to convention, conformity, and convenience (pseudoscience).

2. Question 1: What has been the historical evolution of the understanding and definition of acids?

Current View: The prevailing definition of an acid is that it is a molecule that when dissolved in water will release a H⁺ and lower pH below 7.0.

Evidence: Prior to the 17^th century it was known that certain liquids could cause harm to materials (living tissues and inanimate objects) that they contacted. When referring to fruits or liquids, a common observation was that sour tasting substances (‘acere’; Greek for sour tasting) had added corrosive properties. The English words ‘acid’ and ‘acetic’ are both derived from ‘acere’.¹

There is a long history of scientific progress and improved understanding of acid molecules in nature. As early as 1754, it was proposed that bases react with acids where the final product (the prior acid) was a bitter tasting acid salt.¹⁹ In 1776, LaVoisier formed a new theory of acids based on his work with nitric acid (HNO₃) and sulphuric acid (H₂SO₄). As both acids had a central atom attached to multiple oxygen atoms, LaVoisier theorized that acids contained oxygen atoms, and it was the oxygen atom that made solutions of molecules so volatile/reactive/corrosive. Interestingly, the Greek derivation of the word oxygen combines acid (oxys) and engender or formation (geinomai).¹

After added scientific contributions about the relevance of acids that do not contain oxygen, and the interpretation that acids were dependent on a peculiar arrangement of atoms, in 1838, Liebig deduced that acids were hydrogen containing compounds where the hydrogen can be replaced by a metal (e.g., for biological applications this would mean either sodium, potassium or magnesium). This ‘hydrogen theory of acids’ was refined in 1884 by Arrhenius and Ostwald, where an acid is a substance that when released in water, has a volatile H⁺ released (dissociated or deprotonated) to cause an increase in free H⁺.¹ This theory later became referred to as the Arrhenius theory, possibly because of the senior role Arrhenius played in the original concept and theory development. The Arrhenius theory and definition of an acid is pertinent to the biological understanding of acidosis, but it was not chemically complete. Further theories were also developed based on the constraint of the Arrhenius model to aqueous solutions (numerous acids do not release a H⁺ in liquids other than water). In 1923 Bronsted and Lowry developed their theory of conjugate acid-base reactions, where the deprotonation (dissociation) of an acid (HA) was connected to the protonation (association) of a base (B to BH⁺) and formation of an ionized acid (A^-) (technically no longer an acid). A chemical depiction of such conjugate acid-base pairs is presented in Equation (1).

$$HA+B\to B{H}^{+}+A^{-}$$ (Equation 1)

As water can act as an acid and a base (it is amphoteric), Equation (2) from Question 3 presents how one molecule of water can dissociate, acting as an acid, forming a hydroxyl group (OH^-), and the other can accept the H⁺, acting as a base, forming the hydronium ion (H₃O⁺). Interestingly, given the role of the H₃O⁺ functioning as H⁺ activity, this ionization reaction meets both definitions of an Arrhenius acid and a Bronsten-Lowry conjugate acid-base reaction.

It is important to note that the Bronsted-Lowry model of conjugate acid-base pairs was instrumental in the further mathematical explanation of acid-base reactions that do not release H⁺ (conjugate acid-base chemistry), and the added importance of bases that buffer H⁺ dissociation. The relevance of conjugate acid-base chemistry was further emphasized through the ability to now mathematically express H⁺ dissociation (release) and association (attachment), as presented and discussed in more detail in Question 3.¹

In 1923 Lewis proposed that constraining the definition of an acid to the requirement of H⁺ dissociation was too limiting to acid-base chemistry. Instead, viewing the movement of electrons was the important feature to define acids and bases. The Lewis theory proposed that; an acid has the capacity to gain an electron pair, while a base can donate an electron pair. Added theories of acids and bases were also proposed during this era of chemistry,¹ however, the Arrhenius and Bronsted-Lowry theories have remained core to contemporary acid-base chemistry and its computational expression.

Answer: Despite there being on-going refinement to the definition of an acid, to current time the most accepted and pertinent definition is the Arrhenius definition as nearly all chemical reactions in biological systems occur in an aqueous environment; an acid is a substance that when dissolved in water releases a H⁺(dissociates). As such, when concerned with acid-base chemistry in biological systems, an acid is a molecule that when dissolved in a water solution results in the fractional (∼) (in regard to the total number of acid molecules) release of H⁺ (∼H⁺) that increases the H⁺ concentration ([H⁺] or [H₃O⁺]; see Questions 2 and 3) and therefore, by definition, has the capability to lower pH, or if starting in pure water, decrease pH below 7.0 (pH ​= ​-log [H+]) (see Question 2).

3. Question 2: What is the origin and mathematical derivation of the pH scale?

Current View: The pH scale is derived from the mathematical adjustment of the molarity of water (55.5 Mol⋅L^-1), revealing that the ion product of water ([H⁺] x [OH^-]) is equal to 10^-14 Mol⋅L^-1. When the [H⁺] ​= ​[OH^-], such as at neutral acidity, this then corrects to 10^-7 Mol⋅L^-1. When this number is further corrected to positive units by -Log₁₀ transformation, the pH is derived as follows; pH ​= ​-Log₁₀[H⁺], which at neutral acidity ​= ​7, with a pH range from 0 to 14.

Evidence: Based on the answer to question 1, Arrhenius provided the theory of acids most pertinent to biochemistry as well as the focus on the resulting increase in free H⁺, or the increase in the [H⁺], or more accurately, the increase in the concentration of the hydronium ion ([H₃O⁺]). This approach, when combined with the computational structure of the Bronsted-Lowry theory, directly led to the focus, definitions, and mathematical computation of the [H⁺] and the pH unit and scale.¹ Such mathematical presentation and explanation for the derivation of the pH scale are presented in most textbooks of biochemistry,²⁰ as well as here in equations (Equation 2), (Equation 3), (Equation 4), (Equation 5), (Equation 6), (Equation 7), (Equation 8), (Equation 9), (Equation 10)).

It is best to detail the ion constant of water as an introduction to the pH scale. Though, for reflection, it is important to note that we routinely use water in everyday life, and such routine use can fuel the perception that it is simply a liquid that comes from the clouds, or from a tap, that serves our needs. However, the reality is that water has its own complex chemistry that make it an essential ingredient for the chemistry of life on earth.

Water is close to a pure substance (H₂O), with only small amounts of ionic components due to a low propensity to dissociate into positively and negatively charged compounds (H₃O⁺ and hydroxyl ions (OH^-), which as previously explained are referred to as the hydronium ion and hydroxyl ion, respectively. As previously identified, historically, quantitative chemists have referred to H₃O⁺ simply as a H⁺ or proton, yet subsequent chemical discovery has revealed that it is more accurate to represent the dissociation of the positively charged H⁺ in water dissociation as H₃O⁺ (Equation (2)). Nevertheless, the computational representation of water dissociation to follow will refer to the H⁺ to be consistent with past research and computational formulae. Where you see a H⁺ symbol, simply remember that in aqueous solutions this is really H₃O⁺.

$${2H}_{2}O\to H_{2}O+H^{+}+O{H}^{-}\to H_3{O}^{+}+O{H}^{-}$$ (Equation 2)

The dissociation of water is shown in Equation (2) and can be expressed as a routine equilibrium constant (K_eq) as shown in Equation (3).

$$K_{eq}=\raisebox{1ex}{$\left[H^{+}\right]\left[{OH}^{-}\right]$}\!\left/ \!\raisebox{-1ex}{$\left[H_{2}O\right]$}\right.$$ (Equation 3)

Pure water at 25 ​°C has a molarity of 55.5 Mol⋅L^-1, which can be incorporated into equation (3) to form Equation (4).

$$K_{eq}=\raisebox{1ex}{$\left[H^{+}\right]\left[{OH}^{-}\right]$}\!\left/ \!\raisebox{-1ex}{$\left[55\right]$}\right.$$ (Equation 4)

Equation (4) can be re-arranged to form Equation (5).

$$K_{eq}\left[55\right]=\left[H^{+}\right]\left[{OH}^{-}\right]$$ (Equation 5)

The value of K_eq for water is known to be 1.8 x 10^-16 Mol⋅L^-1, so equation (5) can be expressed as Equation (6) to reveal the ion product of water (K_w).

$$\left[1.8\times {10}^{-16}\right]\times 55.5={10}^{-14}=\left[H^{+}\right]\left[{OH}^{-}\right]=K_w=ionproductofwater$$ (Equation 6)

At neutral pH (7.0), the [H⁺] ​= ​[OH^-], so equation (6) can be re-expressed as Equation (7).

$${\left[H^{+}\right]}^2={10}^{-14}$$ (Equation 7)

The [H⁺] can now be solved as presented in Equation (8).

$$\left[H^{+}\right]=\sqrt{{10}^{-14}}={10}^{-7}$$ (Equation 8)

Thus, for water at neutral pH, the derivation formula for pH is presented in Equation (9).

$$pH=-{\log }_{10}\left[H^{+}\right]{=-{\log }_{10}10}^{-7}=7.0$$ (Equation 9)

Aqueous solutions with a pH lower than 7.0 are acidic, with the strength of the acidity expressed by the extent to which the pH is lower than 7.0. Aqueous solutions with a pH greater than 7.0 are referred to as basic (or alkaline).

Answer: The derivation of the pH scale is consistent with the Common View and required no correction or refinement.

4. Question 3: What are common acid chemical structures or functional groups in biological systems?

Common View: The main acidic function groups in biological systems are the carboxyl group (-HCOO^-) and phosphoryl (-HPO₄^2-) groups and can be found in many of the molecules involved in the reactions of cytosolic and mitochondrial metabolism (catabolism and anabolism).

Evidence: The body produces many acid and base functional groups, though as will be clarified throughout this manuscript, the so-called ‘acid functional groups’ are not produced as acids in biological systems. The details of these differences will be explained in the evidence and answer that pertains to Question 5. Furthermore, the important feature of such molecules and their functional groups is not whether they are acidic, but whether they can be vulnerable (altered) by pH dependent changes in ionization through the removal (dissociation) or attachment (association) of a cation, of which the H⁺ is the most influential (see Questions 4 and 5).

There are three common ionizable functional groups in biological systems: 1) the carboxyl group (-HCOO^-), 2) the phosphoryl group (-HPO₄^2-) and 3) the amine group (-NH₂) (Fig. 1). Examples of metabolites containing one or more of these groups are presented in Table 1 along with added data pertinent to further questions that follow. Carboxyl groups are present in all amino acids, most molecules of phase 2 of glycolysis, all molecules of the Kreb's cycle (tricarboxylic acid [TCA] cycle) and all fatty acids. Phosphoryl groups are plentiful in molecules of cellular energy metabolism and each of deoxyribonucleic acid and ribonucleic acid. Interestingly, the phosphate molecule (hydrogen phosphate [HPi]; HPO₄^2-), which is core to this functional group, is cleaved from ATP during ATP hydrolysis which fuels cellular work; the increase in the HPi concentration during more intense skeletal muscle contractions²¹ is a good example. Amine groups are present in all amino acids (and therefore are plentiful in all proteins) and some of the nucleotides (e.g., guanine, adenine, and cytosine) and intermediary molecules of cellular energy catabolism (e.g., creatine). The amine groups have relevance to ionization because amine groups cannot be further catabolized in the body (are biochemically inert) and when released from amino acids or other amine containing molecules, the amine groups eventually form ammonia (liver and peripheral tissues) which is then capable for pH dependent ionization (though functions as a H⁺ acceptor [base] across the physiological pH range).

Fig. 1.

Structures of the three most common ionizable chemical functional groups within biological systems. Note that the bold hydrogen atoms are those able to undergo pH dependent association and dissociation (see Question 5). The carboxyl and phosphoryl functional groups can function as acids or acid bases, whereas the amine groups are relevant when expressed as ammonia. Ammonia is not acidic but is involved in H⁺ association during decreasing physiological pH conditions.

Table 1.

Examples of metabolites from lipid and carbohydrate oxidation in cells, along with their chemical structure and -log₁₀ of their dissociation constants (pK_d) at temperature ​= ​25 ​°C and ionic strength ​= ​0.1 Mol⋅L^-1.^a Source: https://chemicalize.com/welcome.

Name	Structure	pKd1	pKd2	pKd3
3-phosphoglycerate		3.84
Pyruvate		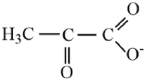2.93
Lactate		3.67
Citrate		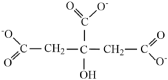3.05	4.67	5.39
Succinate		3.55	5.69
Oxaloacetate		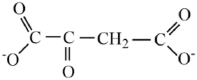2.41	3.58
Palmitate		4.95
Glutamate		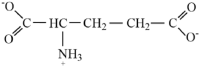1.88
α-ketoglutarate		2.66
β-hydroxybutyrate		4.41
Acetoacetate		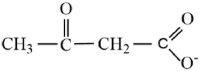4.02
Alanine		2.47
Arginine		2.41
Methionine		2.53

^aSee Questions 5 and 6 for the explanation and discussion of dissociation constants.

Answer: The Common View is correct in that there are two main acidic functional groups in biological systems; the carboxyl group (-HCOO^-) and phosphoryl (-HPO₄^2-) groups, which are presented here in their ionized (non-acidic) form. However, what is more important is the realization that these functional groups are not produced in their acidic structure (see Part-2 of this series). This means that once produced they are exposed to pH dependent cation association, of which the H⁺ is the main cation (see Question 5). In this regard, the added chemical functional group of importance to comprehensively understand cellular and systemic pH dependent ionization is the amine group (-NH₂) which during physiological pH conditions a large proportion of free amine groups will acquire a H⁺, forming ammonia (NH₃).

5. Question 4: How is the propensity for H⁺ association or dissociation quantified?

Common View: The extent to which an ionizable molecule (acid or base) can have H⁺ association of dissociation is quantified by the -Log₁₀ of the K_eq (pK_a) in association with the pH of the solution it is dissolved in.

Evidence: The propensity by which a cation will associate or dissociate with a negatively charged atom is best understood and quantified from an altered expression of the K_eq (Equation (3)). As an example, the ionization of lactic acid to lactate is represented in Equation (10) and then re-expressed mathematically at concentration equilibriums in Equation (11) to reveal the equilibrium constant (K_eq), also referred to as the dissociation constant (K_d), for this ionization.

$$HLa\to {La}^{-}+H^{+}$$ (Equation 10)

$$K_{eq}=K_d=\raisebox{1ex}{$\left[H^{+}\right]\left[{La}^{-}\right]$}\!\left/ \!\raisebox{-1ex}{$\left[HLa\right]$}\right.$$ (Equation 11)

When there is a large dissociation (see Equation (11)) there is a large numerator and a small denominator and therefore the K_d would be very large for strong acids. In fact, the K_d for lactic acid is extremely large at 4 677.351(1/3)4. To adjust the value down and based on Question 2 to eventually reference the K_d to the pH scale, by convention you compute the Log₁₀ of the K_eq (Log₁₀K_eq), which has been defined as the pK_a, or acid dissociation constant (pK_d; Equation (12)). The pK_d for lactic acid ​= ​3.67 (Table 1). The term pK_a is outdated as it implies the molecule it is referenced to is an acid, which of course this three-part series attempts to prove that in biological systems it is not. Thus, convention for biological systems should transition to simply referring to the constant as what it is; a dissociation constant (pK_d).

$${\mathsf{p}K}_a={pK}_d={\mathsf{Log}}_{10}\left(\raisebox{1ex}{$\left[H^{+}\right]\left[{La}^{-}\right]$}\!\left/ \!\raisebox{-1ex}{$HLa$}\right.\right)$$ (Equation 12)

Thus, if an acid metabolite was produced in a cell, or any other biological solution (which we present an evidence-based interpretation that it is not), there would be a large H⁺ dissociation. It is this construct that has fuelled the disciplines of acid-base chemistry, physiology, and biochemistry for the last 100 years. However, if biological systems (e.g., cells) do not produce metabolic acids but instead produce anions (acid functional groups devoid of a H⁺), which this manuscript series provides proof for, then these molecules would incur a very low H⁺ association. Consequently, given that the pK_d of an ionizable group from a specific molecule represents the pH at which half of all the molecules have this ionizable group dissociated, the pK_d value further informs you of the extent to which these molecules are or are not protonated when referenced to the cellular or tissue pH of interest (normally pH ​= ​7.0). For pH values more than 2 units on either side of the pK_d there is near complete association or dissociation for lower vs. higher pH values, respectively. This profile is non-linear (sigmoidal) for pH as shown in Fig. 2 for the pH dependent change in the concentrations of lactic acid (HLa) vs. lactate (La^-) across the entire pH range for an assumed muscle lactate concentration of 0.001 Mol⋅L^-1 (1 ​mmol ​L^-1).²²

Fig. 2.

The pH dependent dissociation of lactic acid (HLa) (•) to lactate (La-) (o) during changes in pH across the entire pH range. The negative log of the dissociation constant (pK_d) value is identified based on an ionic strength ​= ​0.01 Mol⋅L^-1 and temperature ​= ​25 ​°C. Shaded area ​= ​muscle cellular physiological pH range. Note the lactate concentration of 0.001 Mol⋅L^-1 (1 ​mmol ​L^-1) was chosen as it represents the resting condition for skeletal muscle.

Answer: Yes, the most accurate measure of the propensity by which a metabolite categorized as an acid will undergo H⁺ association of dissociation is the pK_d. The expression pK_d is preferred to pK_a as the latter assumes that the molecule is an acid, which in biological systems it is not as is explained in detail in Part-2.

6. Question 5: What determines the pK_d of an acid functional group within a molecule?

Common View: There really is no common view for the answer to this question within the sports medicine and health sciences as such content is not taught in the general epistemological foundation of the disciplines. Nevertheless, general and organic chemistry reveal that the factors influential to this chemical behaviour comprise the variability in the atomic and charge structure surrounding the functional groups within different molecules and the concentration of each of the competing cations.

Evidence:Table 1 presented the pK_d values for some of the metabolites of glycolysis and the TCA cycle. Note that despite all containing one or more carboxyl or phosphoryl groups, the pK_d values for one or multiple ionizable oxygen atoms within or between molecules are all different, even for the same functional group.

For H⁺ dissociation (a H⁺ leaving an acid functional group), which is exemplified by the placement of an acid solution in water, the extent of H⁺ dissociation depends on the pK_d value; the lower the pK_d value below 7.0, the greater the dissociation for a given pH between the pK_d of the acid and the higher pH of the solution the acid is added to.

The reason for the variability in the pK_d values can be explained by the variability in the affinity of the H⁺ to the negative charge of the ionizable oxygen atom(s). Before explanations are provided, think of this scenario as a jigsaw puzzle, with one open piece remaining (the chemical functional group) and a series shapes (the cations) that are left. The cations need the correct geometry and size to fit the remaining space, though unlike a jigsaw puzzle, there is no need for the space to be filled. In other words, the chemical puzzle may be complete without all the pieces in their place!

The variability in the affinity of the H⁺ to the negativity of the functional group is due to a combination of factors. First, the localized atomic and charge environments around the ionizable oxygen atom are slightly different for different functional groups in different molecules. These in turn influence the propensity to which a cation will bind to the negatively charged atom. In addition to this, the H⁺ is not the only cation of influence in biological fluids. Other cations such as sodium (Na⁺), potassium (K⁺), calcium (Ca²⁺), magnesium (Mg²⁺), etc., all have different propensities for competing with H⁺ for the negativity of the functional group.22, 23, 24 Finally, these propensities are all different because of the differences in the atomic size of the cations, their extent of positivity, and their respective concentrations.

Given that the H⁺ is the smallest of all the cations, it is no surprise that data from research of the competitive cation association to molecules from substrates and products of cellular metabolism reveal a preference for pH dependent H⁺ association (despite the extremely low [H⁺]), but more importantly, that at pH ​= ​7.0, specific molecules have minimal cation association (remain negatively charged).22, 23, 24 For example, for lactate in solution at pH ​= ​7.0, there is only 0.062% of the lactate molecules that ionically interact with a cation, and the majority of the association is for H⁺ not Na⁺, Mg²⁺, or K⁺.²² Thus, it is wrong to simply assume that the negatively charged ionic form of an acid molecule will automatically associate with a cation to balance charge.

A better example to document this is for HPO₄^2- (Fig. 3, Fig. 4) that has three of the four oxygen atoms that can be ionized with pK_d values of 11.59, 6.75 and 1.99, respectively. If you are understanding these concepts, then you should have interpreted this data to reveal that for the initial ionizable oxygen atom (pK_d ​= ​11.59), the higher the pH is above 11.59 the greater the proportion of inorganic phosphate that has a PO₄^3- structure (Fig. 4). Yet of course, this is non-physiological. For conditions close to pH ​= ​8, the inorganic phosphate structure HPO₄^2- predominates. When pH ​= ​6.75 there are equal proportions of H₂PO₄^- and HPO₄^2-. The second ionizable oxygen atom is interesting because as cellular pH lowers below 7.0 there is an increasing proportion of these molecules that become protonated (there is H⁺ association), which is another way to define how inorganic phosphate is a H⁺ buffer during intense muscle contractions. Robergs et al.,²² and Robergs25, 26, 27 provide added evidence on how lowering cellular pH causes added H⁺ association to HPO₄^2-, forming dihydrogen phosphate (H₂PO₄^-). This in turn increases the H⁺ release from reactions that involve HPi as a substrate (the phosphorylase reaction of glycogenolysis, as well as the glyceraldehyde-3-phosphate dehydrogenase reaction of glycolysis) due to there now being two H⁺ released during phosphate transfer. Such realities complicate the role of HPO₄^2- as a H⁺ buffer during extreme conditions of cellular metabolic acidosis. The third ionizable oxygen atom (pK_d ​= ​1.99) has such a low pK_d that it is only during non-physiological extremes of acidosis that there would be H⁺ association.

Fig. 3.

Inorganic phosphate with the three ionizable oxygen atoms identified, along with their negative log of the dissociation constant (pK_d) values.

Fig. 4.

The change in the concentrations of the different forms of inorganic phosphate during changes in pH across the entire pH range. Shaded area ​= ​muscle cellular physiological pH range. Data referenced to the peak muscle Pi concentration that can occur during intense exercise to contractile failure (0.04 Mol⋅L^-1).

Answer: The advanced understanding of the pH dependent functions of metabolites in cellular metabolism should be taught to all students and practitioners involved in the sports medicine, clinical and health sciences. Such knowledge provides the foundation for understanding atomic changes during chemical reactions, which in turn informs an advanced understanding of the roles of molecules classified as acids or bases in cellular metabolism. The geometry of the atomic structure and charge distribution surrounding functional groups classified as acidic, in combination with the concentration of competing cations all influence the pH dependent extent to which these functional groups gain or lose a H⁺ once they are produced, where production occurs in their ionized, not acidic, form (see Part 2).

7. Conclusion

This initial manuscript of the three-part series revealed the following facts;

• (1)Acids were known of as early as the 17^th century and the recognition that in aqueous solutions acids released a H⁺ was proposed in 1884. Such a H⁺ definition has remained pertinent to current time.
• (2)Based on the above, when concerned with acid-base chemistry, an acid is a molecule that when dissolved in a water solution results in the fractional (in regard to the total number of acid molecules) release of H⁺ that increases the [H⁺] ([H₃O⁺]) and therefore by definition has the capability to lower pH (pH ​= ​-log₁₀[H⁺]).
• (3)In biological context, there are three common ionizable functional groups of molecules classified as acids; 1) the carboxyl group, 2) the phosphoryl group and 3) the amine group.
• (4)The propensity by which a cation (e.g., H⁺). will associate or dissociate with a negatively charged atom is best understood and quantified from an altered expression of the K_eq (= K_d) of the ionization, where the negative log of the dissociation constant, - log₁₀K_eq ​= ​pK_d. The pK_d reveals the pH at which half of the molecules are ionized. The pK_d for HLa ↔ La^- ​= ​3.67 (ionic strength ​= ​0.01 Mol⋅L^-1, T ​= ​25 ​°C). Thus, knowing the pK_d and the pH of the solution at question will allow calculation of the proportionality of the ionized (dissociated) vs. protonated (associated) structure of the molecule.

Part-2 of this series will expand on this content to reveal evidence from organic chemistry of chemical reactions in cells, and their related computational chemistry (applications of the pK_d values) within the physiological pH range, that establish why cells do not produce metabolic acids. Cellular metabolism releases H⁺ from certain reactions based on covalent modification of substrates to products, with added pH dependent H⁺ exchange (association and dissociation) occurring due to differences in the pK_d of products compared to substrates.

Submission statement

All authors have read and agree with the manuscript content. In addition, while this manuscript is being reviewed for this journal, the manuscript will not be submitted elsewhere for review and publication.

Authors’ contributions

Robergs conceived the idea and researched the prior research evidence, wrote the manuscript and developed all tables and figures. Siegler, Torrens and O'Malley assisted in researching the prior research evidence, provided interpretations, assisted in the writing of the manuscript and completed proof reading and manuscript editing prior to submission.

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.