Research Advances in Machine Learning Techniques in Gas Hydrate Applications

Abstract

The complex modeling accuracy of gas hydrate models has been recently improved owing to the existence of data for machine learning tools. In this review, we discuss most of the machine learning tools used in various hydrate-related areas such as phase behavior predictions, hydrate kinetics, CO₂ capture, and gas hydrate natural distribution and saturation. The performance comparison between machine learning and conventional gas hydrate models is also discussed in detail. This review shows that machine learning methods have improved hydrate phase property predictions and could be adopted in current and new gas hydrate simulation software for better and more accurate results.

1. Introduction

Gas hydrates are ice-like solid compounds that are formed by the combination of guest (mostly gas) and water molecules at high pressures and low-temperature conditions.¹⁻³ The formation of gas hydrate in oil and gas pipelines is unwanted due to its ability to plug the flow lines, leading to economic and operational losses.⁴ On the other hand, gas hydrate formation has useful applications in CO₂ capture and sequestration, energy supply, water desalination, and gas separation and transportation.⁵ The application of gas hydrate technologies lies deeply in the understanding of the experimental thermodynamics and kinetics of gas hydrate formation. Despite the success of several experimental data works on gas hydrate, the area of modeling lacks equal success due to the stochastic nature of hydrate formations.

Several methods and models have been reported in literature for calculating/predicting the equilibrium conditions of gas hydrate formation.^3,6 Carson and Katz⁷ established a set of vapor–solid coefficients to calculate the hydrate stability conditions for some pure gases. Also, the use of a statistical thermodynamics approach for the prediction of hydrate phase behavior conditions was presented by Waals and Platteeuw.⁸ Such phase behavior models have been modified in literature to predict the effect of additives on gas hydrate phase behavior.⁹⁻¹¹

Hydrate formation kinetics modeling needs to be studied just like its thermodynamic behavior. There is extensive experimental work¹²⁻¹⁶ available in literature for predicting the thermodynamic conditions of the hydrate formation with and without inhibitors. In contrast, there are no sufficient studies on kinetic gas hydrate models in literature. The existing hydrate kinetic models are incomplete and have poor prediction accuracies. This is because gas hydrate nucleation is probabilistic in nature and depends on the sample water history and cannot be predicted certainly.¹⁷⁻²⁰ Therefore, the most available kinetic models and studies related to hydrate formation focus on the hydrate growth rate. Also, the prediction of the gas hydrate distribution in natural gas hydrate sediments has gained much attention owing to its methane production potential. In such modeling studies, the hydrate saturation, sediment porosity, permeability, and rock compressive and tensile strength are predicted.

The recent focus on artificial intelligence methods (AIs) to solve scientific problems has assisted in improving the prediction of gas hydrate formation behavior in various areas. The broad employment of AIs for solving nonlinear complex problems without prior knowledge gives AIs an advantage over conventional models for many chemical applications. Apart from the variety of experimental and modeling studies on hydrate thermodynamics, kinetics, exploration, and production, several review papers have focused on providing state-of-the-art knowledge on hydrate research progress. Such hydrate modeling reviews have paved the way to fill and improve many empirical gas hydrate behavior predictive models such as the Peng²¹ and the van der Waals²² models, among others.

However, no review paper in the open literature focuses on the use of machine learning in gas hydrate behavior modeling despite the active involvement of machine learning in gas hydrate applications in recent times. This work therefore presents a comprehensive review of machine learning applications in the gas hydrate. Thus, in this work, the reported literature on gas hydrate application prediction using machine learning methods is reviewed to provide a clear understanding of its performance by summarizing all the data with a detailed discussion of errors and suggesting prospects for continuous discoveries. The main novelty of this work in gas hydrate application lies in the ability to use the findings in this work to develop gas hydrate mitigation or promotional additives for CO₂ capture and storage, desalination, and flow assurance operations.

2. Machine Learning Models Used for Gas-Hydrate-Related Studies

This section provides a basic overview of the machine learning models in gas hydrate applications. The commonly used machine learning models in gas hydrate applications are shown in Figure 1.

Figure 1.

Gas hydrate empirical and machine learning models.

The most used machine learning model for gas-hydrate-related modeling is the artificial neural network (ANN). The ANN method uses functions to simulate human brain behavior to predict scientific processes.²³ Typically, ANN models operate under hidden, input, and output layers that are designed to produce the right results.²³ ANN models are able to solve nonlinear functions with multiple output and input variables. It also predicts patterns in noisy data with good accuracy.²⁴ Aside from ANN, the group method of the data handling (GMDH) neural network has also been used for hydrate modeling.²⁵ The GMDH is similar to ANN but designed for nonlinear patterns among data outputs and inputs using quadratic polynomials.²⁵ GMDH has advantages in predicting and simulating complex system scenarios.

Vladimir and Alexey in 1964 proposed the support vector regression (SVR) machine learning model based on statistical learning theory.²⁶ This method has also found relevance in gas-hydrate-related modeling techniques. The merits of the SVR in hydrate modeling reside in its ability to deal with overfitting, unlike ANN. A modified version of the SVR used in hydrate modeling is the least square support vector regression (LSSVR). The LSSVR can model complex systems with huge data sets and a higher convergence rate than the SVR.

Fuzzy logic (FL) is another method that uses the classical fuzzy sets mathematical theory.^27,28 Fuzzy logic uses membership functions (MFs) to evolve between real-world and fuzzy models. pimf, zmf, and smf are the common MFs.²⁹ FL has been used for gas hydrate modeling in different systems. In nonlinear complex arbitrary functions, the use of FL could yield good modeling accuracy.

The combination of ANN and Takagi–Sugeno-type fuzzy systems, known as the adaptive neuro-fuzzy inference system (ANFIS), is commonly used for hydrate formation behavior modeling.³⁰ The ANFIS model exhibits good prediction performance in complicated nonlinear systems.³⁰ This advantage also encourages its application in gas-hydrate-based studies. Another used machine learning algorithm in the hydrate community is random forest (RF). The RF algorithm predictions result from each tree in the decision trees.³¹ Its advantages are based on its simplicity of implementation in parallel, fast training, and prediction. The RF and k-nearest neighbors (KNN) have been widely applied in gas hydrate systems with promising efficiencies.

Some other researchers have used the nonlinear autoregressive models with exogenous inputs (NARX neural network) to predict gas hydrate phase behavior. Though NARX is known as a good algorithm for time series data,³² its ability to deal with unilinear data and patterns promotes its application in gas hydrate studies. Deep neural network techniques such as the feedforward neural networks have been used for gas hydrate modeling in our modeling framework. The hybrid of the artificial neural network (HFGA) and the extra trees approach have also been proven as good algorithms for predicting the hydrate dissociation pressure with and without inhibitors.

2.1. Mathematics Fundamentals of Gas Hydrate Machine Learning Techniques

2.1.1. Support Vector Regression (SVR)

Support vector regression (SVR) is a robust mathematical tool used to solve nonprobabilistic problems ranging from nonlinear function approximation to pattern classification.³³ Basically, SVR attempts to nonlinearly project the input spectra to a higher/infinite dimension by further locating the optimum hyperplane with a minimum distance from actual data. Due to the algorithm’s limitation to small data, an upgraded version of the model (LSSVR) was developed.

A typical SVR algorithm for nonlinear regression models for a given data set {(xi yi), i = 1, 2, ..., N}, is expressed as:

1

The structural risk function used in SVR is

2

The loss function in eq 2 is

3

By substituting eq 3 into eq 2 and introducing relaxation variables ξ and ξ*, the objective function can be obtained as:

4

5

Equation 4 introduces the Lagrange function. Dual processing is performed, which yields the following.

6

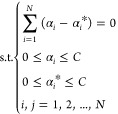7

Using eqs 6 and 7, the SVR model can be obtained.

8

For the inner-product problem, there are four types of common kernel functions: linear kernel function, polynomial kernel function, radial basis function (RBF) kernel function, and sigmoid kernel function. Among them, the RBF kernel function has better performance and more applications.³⁴ Therefore, in this paper, the internal product problem is replaced by the RBF function, whose expression is as follows:

9

Eventually, the SVR model becomes the following.

10

where ε is the loss factor; ξ and ξ* are the relaxation variables; C denotes the penalty factor; α_i – α^*_i are the Lagrange multiplier pairs for each sample; and γ is the width parameter of the kernel function.

2.1.2. ANN

Among all the ANN models, the multilayer perceptron and the radial basis function network are used in gas-hydrate-related machine learning models. In this section, we will focus more on the mathematical formulation of these models.^35,36

2.1.2.1. Multilayer Perceptron (MLP)

This is a feed-forward artificial neural network model. In the feed-forward neural networks, the movement is only possible in the forward direction.³⁷ A typical MLP consists of many layers of nodes in a directed graph, with each layer connected to the next one, which can be represented mathematically as:

11

The equation is the transfer function in a neural network. This linear weight sum would be a threshold at some value, so that the output of the neuron would be either 1 or 0. The multilayer perceptron networks are suitable for the discovery of complex nonlinear models. On the possibility of approximating any regular function with a sum of sigmoid, it is power-based. MLP utilizes a supervised learning technique called back-propagation for training the network. This requires a known desired output for each input value to calculate the loss function gradient.

2.1.2.2. Radial Basis Function Network

RBFs are developed on the basis of localized basis functions and an iterative function approximation. In RBF networks, the supervised training algorithm is utilized.³⁸ The primary advantage of the RBF network over other FFNNs is its easy design. This is due to the fact that the RBF network has only three layers, namely, the input layer, the hidden layer, and the output layer. Considering x as the input vector, the output of RBF ANN, ϕ, can be expressed by:

12

in which N and a_i stand for the number of hidden neurons and the weight of neuron i in the output neuron; c_i denotes the center vector for neuron i; and ρ(∥x – c_i∥) is the RBF. A typical neuron i could be represented by the following equations:

13

14

where x_j and w_ij denote the input signals and the neuron’s synaptic weights, respectively, and r_i, b_i, y_i, and f are the linear combiner output, bias term, output signal of the neuron, and activation function, respectively. The authors of refs (38 and 39) used the back-propagation algorithm to minimize the mean squared error (MSE) of the input and output variables. Also depending on the type of model development, the RBFs might need several hidden layers and a transfer function.

2.1.3. ANFIS

The fuzzy set theory was introduced in 1965. ANFIS used fuzzy logic theory to formulate the mapping of the input and output layers. Neural networks are used to regulate the mapping parameters by leaning functions.⁴⁰ A fuzzy set A in X which is referred to as the universe of discourse is defined as a set of ordered pairs:

15

where μ_A(x) is called membership function (MF) for the fuzzy set A which ranges between 0 and 1.

16

where R_j is the rule label; A_ji is the antecedent fuzzy set; y = f_j(X) is a crisp function which is usually a polynomial function of input variables; and N is the total number of fuzzy if–then rules. When f(X) is a first-order polynomial, it is called a first-order Sugeno fuzzy model and is defined as:

17

The output of each rule is a linear combination of input variables plus a constant term, and the weighted average of each rule output produces the final output given by:

18

where W_j is the firing strength of R_j, defined as:

19

where T denotes a T-norm operator of minimum or product. The fuzzy reasoning is solved by using a rule based on Sugeno’s type fuzzy. However, some authors^30,41 use fuzzy rules in Takagi–Sugeno systems.

2.1.4. XGBoost (eXtreme Gradient Boosting) Boosting

Boosting is a type of additive modeling that employs a series of several learning models as one powerful model. By adding these models together, a stronger predictive model is formed.⁴² The XGBoost algorithm employs the first and second derivatives of the loss function to quickly converge to global optimality quickly. It also improves the performance of the model. The objective function minimized by XGBoost is as follows:

20

21

where f_k is the k^th tree and l is a differentiable convex loss function that measures the difference between the prediction ŷ_i and target y_i. The second term Ω reduces overfitting by penalizing the complexity of the model in terms of the number of leaves in tree T and the vector of scores on leaves w. λ′ is a regularized parameter, and γ′ is the learning rate, whose values lie between 0 and 1. Since a tree ensemble model includes functions as parameters, it cannot be optimized using traditional optimization methods in Euclidean space and is therefore trained in an additive manner. The objective function to be minimized is then given by:

22

where ŷ^t_i is the prediction of the i^th instance at the t^th iteration, and k is the total number of predictions. Therefore, the loss function is represented as the sum of the loss functions for the prediction until the t-1st iteration and a tree structure that, when added at the t^th iteration, most improves the model as per eq 22. Accordingly, the objective function can be optimized by using the second-order Taylor approximation of the loss function (instead of first-order in general gradient boosting) which is given by:

23

where and 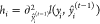represent the first and second derivatives of each sample. The sum of loss values determines the loss function in eq 23 for each data sample corresponding to every leaf node. Assuming that the loss function is the mean square error function for regression problems and removing the constants, the objective function can be written for regression tree-based problems as:

24

where I_j represents all the data samples in the leaf node. During the process of building a tree, a particular node split will be carried out only if there is an improvement in the performance of the model as evaluated by this objective function.

2.1.5. Random Forest (RF)

Random forest was proposed by Breiman⁴³ as a bagging algorithm in ensemble learning. RF is similar to a decision tree but differs from the standard trees. In the RF model, there is a random selection of a part of the data from the original data set and construction of a subdata set of the same length and size as the original data set. However, the data in the subdata set can be repeated. After that, the subdata set can be used to build a subdecision tree; a part of the result features obtained can be selected by each decision tree; and finally the optimal result features can be selected from the randomly selected part of the result features.

The RF for regression is formed by growing trees depending on a random vector, and its predictor is formed by taking the average over k of the growing trees. The mathematical model of RF is as follows:

25

where g_i(x) represents the value of each base learner. The model is not determined by specific eigenvalues or combinations of features, and the final prediction results are averaged, giving the overall model results in generalization performance and decreasing the average error of the model results.

2.1.6. Group Method of Data Handling

The relationship between the inputs and the output of a multiple-input single-output network can be estimated by the Volterra–Kolmogorov–Gabor (VKG) polynomial.

26

where X = (x₁, x₂, ..., x_M) is the vector of input variables; a is the vector of weight coefficients; and ŷ_n is the predicted output. The general equation in the form of VKG can be simplified to a partial quadratic polynomial consisting of only two variables:

27

28

In order to determine the “best fit” values, the value e should be minimized, or in other words, the partial derivatives of eq 28 with respect to each constant a_i are taken and set to zero:

29

Solving eq 29 leads to a system of equations that are solved by a training set of data:

30

31

32

33

34

35

2.1.7. Deep Neural Networks

The DNN framework is one of the machine learning methods used for gas hydrate phase behavior prediction. A DNN is a collection of nested compositional functions. The algorithm recursively performs linear transformations to the inputs and output layers as well as nonlinear transformations to the hidden layers. DNN can accurately learn without any rules. Also, DNN models can determine flaws in data training and accurately correct them. The feed forward neural network is mostly adopted for prediction.^44,45

Suppose 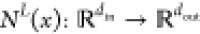is an l layer of NN or an l – 1 hidden layer NN, with N_l neurons in the lth layer (N_o = d_in, N_L = d_out). Let us denote the weight matrix and bias vector in the lth layer by 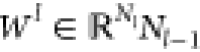and 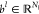, respectively. Given a nonlinear activation function σ, which is applied element-wise, the FNN is recursively defined as follows;

Input layer:

36

Hidden layers:

37

Output layer:

38

Because there is no universal rule for selecting the most suitable activation function, researchers mostly use a trial-and-error strategy. The commonly used activation functions, such as the logistic sigmoid, tanh, relu, Leaky relu, elu, and selu, were for studying gas hydrate systems. The training process requires a search for good weights and biases through the minimization of the loss function. The loss function is defined as the sum of error squares and is written as follows:

39

For hydrate-related studies, the RMSprop algorithm is one of the five methods adopted for predictions. This algorithm was introduced by Geoff Hinton and uses an adaptive learning rate framework. Adadelta and RMSprop were independently developed for about the same period but independently to resolve issues relating to rapidly declining learning rates. A closer look at the initial updating vector between RMSprop and Adadelta conclusively shows similarities in their initial updating vector. Mathematically, the RMSprop algorithm can be written as follows:

40

41

The second algorithm used for hydrate-related studies is Adagrad. Adagrad is a gradient-based optimization algorithm that can adapt the learning rate alongside the parameters.⁴⁶ This algorithm performs a small update with low learning rates, whereas a high learning rate will have much larger updates. These updates are associated with infrequent features. This algorithm is ideal for working with sparse data. The algorithm is expressed mathematically as:

42

43

Adadelta, which is the third algorithm adopted for hydrate-related studies, is a modification that slows down the aggressive nature of the Adagrad algorithm. This monotonically decreased the learning rate. Adadelta simply restricts the window of accumulated past gradients to a specific size instead of gathering all past squared gradients:⁴⁷

44

45

46

47

The adaptive moment estimation (Adam) algorithm is another approach for computing adaptive learning rates for parameters. Adam has also been used in hydrate-related studies. Adam preserves an exponentially decaying average of past squared gradients (v_t) similar to Adadelta and RMSprop. This method utilizes some properties of the momentum algorithm by preserving the exponential decay of past gradients. The method prefers the use of the minima error on a flat surface.⁴⁸ Mathematically, Adam can be written as follows:

48

49

m_t and v_t are estimates of the gradients’ first (mean) and second (uncentered) moments, respectively.

The biases can be corrected in the first and second estimates of the moments with the following formulas:

50

51

Then these corrections are employed to update the parameters

52

For all of the algorithms, the loss functions will be determined by the values of w and input variables. The weights are represented by the w vector, and the input vectors are represented by the x vector. The losses for all of the training data were calculated, and the total losses are used for the predictions.

3. Gas-Hydrate-Related Machine Learning Data Processing

The quality of data and its processing or treatment process are very important to any machine learning model. Most often poor machine learning predictions are a result of poor data representation, lack of enough data, and incorrect or an absence of data processing. The data used in gas-hydrate-related machine learning modeling are mostly gathered from experimental articles in literature,⁴⁹ field flow assurance data,⁵⁰ field reservoir rock properties data,⁵¹ and experimental procedures by others.^50,52 Data from literature is commonly used for the prediction of gas hydrate phase behavior conditions. This is because such data are easy to correlate from different data or experimental sources, thus allowing hydrate phase behavior prediction using machine learning techniques. However, there is little work done on predicting hydrate phase behavior in the presence of additives due to a lack of experimental data in the literature. Recently, Bavoh et al.⁵³ developed a deep learning model for predicting the methane hydrate phase boundary behavior in ionic liquids. Gas hydrate kinetics behavior is poorly modeled using machine learning using poor data. Also, the lack of experimental data and access to field data is a challenging fact that hinders the modeling of other gas hydrate applications using machine learning methods.

From all the data sources, the input and output variables used to well represent hydrate modeling are shown in Figure 2. Hydrate equilibrium pressure and temperature are the output variables predicted using machine learning models for phase behavior studies. When the prediction output variable is pressure, temperature becomes one of the input variables, and vice versa. For the pure gas phase, the gas composition, molecular weight of the gas molecules, or specific gravity of the gas molecules are considered input variables. Since hydrate phase behavior could be affected by the type of hydrate structure formed, the gas composition data could be further clustered or grouped to cover the hydrate study form. For example, methane and ethane composition would be summed up as one variable since they both form sI hydrates. In systems with an oil phase, the gas–oil ratio or oil gravity is also considered input variables. Similarly, systems with inhibitors or promoters also include the inhibitor type (molecular weight, density, or chemical details) and concentration in the water phase as input variables. The number of input variables for predicting hydrate properties is decided by the researchers but has to be as well minimized as possible and has a direct relationship to the output variable.^30,41,50,53

Figure 2.

Gas hydrate application machine learning modeling input and output variables.

In kinetics prediction systems, the hydrate growth rate is predicted as output variables with temperature, pressure, and inhibitor concentration as input variables. In practical systems, other kinetics factors such as moles consumed, reactor size, volume, and stirring speed could be considered to give better prediction representation and accuracy. Hydrate rock properties such as water saturation, hydrate saturation, rock tensile strength, pore size, acoustic velocity, and resistivity are also used as input variables for predicting the gas hydrate distribution in hydrate sediments.

Getting data sources and relevant variable representation of output value prediction is not enough for an accurate machine learning prediction. Aside from these features, having adequate data size is very important for accurate machine learning performances. The data size used by most researchers in developing machine learning models in the gas hydrate applications is summarized in Figure 3. As shown in Figure 3, 45% of the authors used a data size below 500, while 13% used a data size between 500 and 1000 and about 42% data above 1000. In terms of model performance by data size, about 42% of the models developed using data above 1000 points show an acceptable representation. It is evident that about 45% of the machine learning models developed in the field of gas hydrates are biased or limited in data size acceptability.

Figure 3.

Data size used by researchers for developing machine learning models in gas hydrate applications.

Data processing for machine learning mode development data normalization is very important to prevent truncation errors. As shown in literature, data normalization is not often conducted by all authors. Some authors have stayed silent about their data normalization process. However, normalization according to Yarveicy et al.³⁸ is conducted for all the model variables between −1.0 and +1.0. This has proven to yield an equivariance for each input and output.⁵⁴ Also, outlier detection is mostly conducted to treat or fine-tune the data set for accurate model development. Outlier detection further helps to identify data that far differ from the primary population data. This also helps to minimize the models and deal with possible experimental errors that might have occurred during the hydrate studies’ experimentation. The Leverage method with a William plot statistical approach is adopted by researchers to remove outliers from hydrate data used for machine learning model development.^43,49,55 Bavoh et al.⁵³ proved that the Mahalanobis distances, Jackknife distances, and T² outliers’ analysis methods can effectively improve data quality. On the other hand, the absence of outlier detection or analysis in a hydrate-based machine learning model is potentially suspected to have reliability issues. Some authors are either silent on their outlier detection method or do not even undertake it. Mohammadi et al.⁵⁶ agreed that when the average absolute relative deviation (AARD%) of the experimental data is less than 3% outlier detection analysis could be neglected.

The choice of optimization algorithm and activation function is key to achieving an improved machine learning prediction.⁵⁷ Ideally, the choice of algorithms and activation function for gas hydrate application machine learning modeling is supposed to be done based on convincing reasons such as the type and nature of the data.⁵³ Contrarily, the choice of machine learning models for hydrate property predictions is based on a trial-and-error method. The models or algorithms are selected randomly and tested with the data to confirm that the models fit better with the data. Although there are other models that are modifications of existing ones, these modified models are also not developed based on the hydrate data type and nature. They are developed as novel models used to fit the hydrate data.

The data used to develop the models are usually divided into training, validation, and testing. In a broader context, the validation and testing data are considered together. The training data sets are mostly a percentage of the data set used to train the model, and the remaining percentage of data is used for validation and testing. The percentage of data used for training the models in gas-hydrate-related machine-learning models is dependent on the data size. As shown in Figure 4, about 50% to 98% of the data are used to train the machine learning models for gas hydrate properties predictions. When a huge size is used, the training percentages are higher than models built with smaller data sizes. About 38% of the authors used 80–85% of their data for training, while 33% used 70–75% and 20% used 90–98%. However, 14% of authors used 50–58% and 60–69% data for training their models (Figure 4). However, using data percentages above 70% is highly recommended for an effective model performance.

Figure 4.

Percentage of data used for training the models in gas-hydrate-related machine learning models.

4. Machine Learning in Gas Hydrate Applications

The application of machine learning in gas-hydrate-related fields is mainly focused on hydrate phase behavior equilibrium data predictions. Though current empirical models have proven to be very effective in predicting the hydrate phase behavior conditions, they fail in systems involving high pressure and mixed gases. However, the use of the machine learning approach has been proven to be effective in such difficult systems. Very few studies have used machine learning to predict the kinetics of hydrate formation. This could be due to the complex nature of hydrate kinetics due to its probabilistic behavior. The current phase behavior studies mainly focus on the hydrate inhibition effect in various systems such as salts, alcohol, and ionic liquids. The use of machine learning in predicting hydrate formation risk for a practical field operation has also been tested in the literature with some success and challenges. Studies on hydrate promotional effects in CO₂ have also been studied using machine learning approaches. However, the prediction of the hydrate phase behavior of natural gas systems with additives is also well explored to cover several relevant hydrate formers. Some authors have also used machine learning approaches in methane hydrate sediment studies to aid in hydrate reserve estimations, exploration, and production. Particular attention is mostly given to the predictions of the hydrate saturation with the sediments. The use of machine learning to predict methanol concentration has also been studied to prevent overuse and ensure the correct and needed dosage for field problems. The following subsections discuss in detail all of the gas-hydrate-related areas where machine learning methods have been used or applied.

4.1. Hydrate Phase Behavior Prediction

The prediction of hydrate phase behavior without additives using machine learning methods is very promising and has shown much improvement for complex natural gas systems containing H₂S and CO₂. Table 1 shows the machine learning-assisted hydrate phase behavior predicted systems. The prediction of hydrate phase behaviors is mostly focused on natural gas systems with high H₂S and CO₂ content and a few mixed gases. Generally, the use of empirical models to predict the hydrate formation conditions of pure gas systems such as CO₂, CH₄, C₂H₆, etc., is very accurate. This is the main reason most studies are focused on natural gas systems with high levels of H₂S and CO₂.

Table 1. Summary of Machine Learning Techniques Used for Gas Hydrate Phase Behaviour Studies^a,bu,v,w.

Gas	Machine learning model	Inputs	Outputs	R2	AARD %	RMSE	Remarks	ref
Natural gas (γ = 0.6 and 0.7)	ANFIS	Pi, Pf, and γ	Ti	0.9994	0.129	0.525	ANFIS, LSSVM, and RBF ANN models show good prediction with LSSVM exhibiting the best.	(38)
	LSSVM			0.9998	0.058	0.255
	RBF-ANN			0.9998	0.062	0.27
Sweet and sour gas	ANN	SI = C1, C2, C3, C4, and N2; SII = C5 + NHF	T	0.9882	0.2137	0.6065	ANN can predict the hydrate formation temperature of sour natural gas at high H2S concentrations	(61)
C1, Natural gas and crude oil, model oil, condensate, or kerosene (hydrocarbon phase)c	SVC and ANN	WC, GOR, SFV, γo, IFT, V, (HVF), HFa, Fa	(PoF) (“No Plug’ (0) or “Plug” (1))	0.827			SVC with RBF kernel and neural network predicts hydrate plug and formation conditions efficiently	(50)
				0.905
				0.975
				0.991
				0.969
		WC, GOR, SFV, γo, IFT, V, and TPWHD	HVF	0.92	0.018	0.0009
Natural gas_1d	(RF)	Ic, P, γ	T	94.35			XGBoost outperforms RF and ET in hydrate phase behavior prediction	(42)
	(ET)	Ic, P, γ	T	94.08
	(XGBoost)	Ic, P, γ	T	98.06
Natural gas	ANN	Pd	HF	90			ANN predicts hydrate formation averagely well with both single and multiple inputs	(62)
		P, T, Ic		92
Natural gas	NNARX	P, T, Ic	hydrate formation	90			NNARX predicts hydrate formation.	(54)
Natural gas		Mwr and P	T	99.9		0.04	GA-SVM model best predicts the stability of hydrate formation conditions	(73)
Natural gas		T and Mwr	P	0.98666	7.01949	1.2207	DNN model could supplant traditional models in terms of thermodynamic predictions.	(71)
C1e	AdaBoost-CART	Zi, Ic, and P	T	0.9994	0.04	NS	AdaBoost-CART provides more reliable HDT prediction	(63)
C2		Zi, Ic, and P	T	0.9977	0.05	NS
C3		Zi, Ic, and P	T	0.9982	0.04	NS
i-C4		Zi, Ic, and P	T	0.9978	0.23	NS
H2S		Zi, Ic, and P	T	0.9934	0.16	NS
N2		Zi, Ic, and P	T	0.9993	0.09	NS
Mixed gas		Zi, Ic, and P	T	0.998	0.03	NS
C1	ANFIS	Zi, Ic, and P	T	0.9865	0.55	NS
C2		Zi, Ic, and P	T	0.9197	1.1	NS
C3		Zi, Ic, and P	T	0.9881	0.33	NS
i-C4		Zi, Ic, and P	T	0.9983	0.13	NS
H2S		Zi, Ic, and P	T	0.9638	0.51	NS
N2		Zi, Ic, and P	T	0.9998	0.04	NS
Mixed gas		Zi, Ic, and P	T	0.8812	0.91	NS
C1	ANN	Zi, Ic, and P	T	0.7617	0.86	NS
C2		Zi, Ic, and P	T	0.9827	0.31	NS
C3		Zi, Ic, and P	T	0.948	0.23	NS
i-C4		Zi, Ic, and P	T	0.988	0.12	NS
H2S		Zi, Ic, and P	T	0.9785	0.33	NS
N2		Zi, Ic, and P	T	0.994	0.21	NS
Mixed gas		Zi,	T	0.8551	1.37	NS
H2f	ANN	Ic, T	P	NS	NS	NS	ANN algorithm is a useful tool to model hydrate systems	(74)
Methane, tert-butylamine		Ic, T	P	NS	NS	NS
Natural gas_2g	LSSVM	Zi, Ic, and P	T	92.4	0.61	NS	Extra Trees and LSSVM models predict hydrate phase equilibria accurately	(59)
	Extra Trees	Zi, Ic, and P	T	97.46	0.35	NS
Natural gas	GA-LSSVM	P, γ	T	99.97	0.136428	0.52785	LSSVM approach for estimating hydrate formation temperature	(68)
CO2h	GA-LSSVM	Ic and T	P	1	2.7	0.04	The model has good predictions but fails relatively in N2 + THF, CH4 + 1,4-dioxane, and H2 + acetone clathrate hydrate systems	(69)
CO2I		Ic and T	P	0.999	4	0.07
CO2j		Ic and T	P	0.996	46	0.22
H2j		Ic and T	P	0.999	0.2	0.01
H2I		Ic and T	P	1	29	15.13
C1h		Ic and T	P	0.995	18	19
C1I		Ic and T	P	0.999	10	24
C1j		Ic and T	P	0.994	133	27
N2h		Ic and T	P	0.999	2.4	2.3
N2I		Ic and T	P	1	6.9	2
N2j		Ic and T	P	0.999	74	3.89
Natural gas	PNN	γC1+C2, γC3+C4+N2, γC5+, γH2S, γCO2, P	T	97.49	0.3187	1.1862	Predicts well for sour gases	(55)
Natural gas	LSSVM	γC1+C2, γC3+C4+N2, γC5+, γCO2, γH2S, γ, P	T	0.9823	0.2177	0.8667	LSSVM accurately predicts hydrate phase behavior epecially in the case of sour gases with high H2S	(75)
CO2k	TOKM	Ic and T	P	0.8728	18.8876	0.438	ANFIS method performed the best in predicting hydrate equilibrium conditions among these methods	(64)
CO2l		Ic and T	P	0.8751	5.2883	0.427
CO2I	ANFIS	Ic and T	P	0.9916	3.825	0.08
CO2k		Ic and T	P	0.9952	2.926	0.08408
CO2l		Ic and T	P	0.9833	4.1091	0.1385
CO2I	ANN	Ic and T	P	0.9766	7.6639	0.1581
CO2k		Ic and T	P	0.894	23.152	0.4243
CO2l		Ic and T	P	0.9468	9.7663	0.2887
CO2I	HFGA	Ic and T	P	0.9867	4.31	0.1004
CO2k		Ic and T	P	0.9801	5.7074	0.1664
CO2l		Ic and T	P	0.9735	6.2658	0.17913
C2SG	LSSVM	T, PV	P	1	1.2	0.007	LSSVM models can predict the hydrate phase equilibrium data in porous media systems	(56)
CH4MS		T, PV	P	1	0.7	0.096
CH4PG		T, PV	P	0.99	6.6	0.379
CH4SG		T, PV	P	1	1	0.069
CO2PG		T, PV	P	0.991	3	0.113
CO2SG		T, PV	P	1	0.7	0.021
C1m	MLP	P	T	0.694	1.442	4.965	GBR gives the best predictions for the methane hydrate phase boundary conditions	(70)
	k-NN	P	T	0.863	0.632	3.366
	SVR	P	T	0.938	0.644	2.362
	RF	P	T	0.995	0.143	0.67
	GBR	P	T	0.999	0.039	0.144
Natural gas (sour gas)	ANN	γC1+C2, γC3+C4+N2, γC5+, γCO2, γH2S, γ, P	T	0.9882	0.2137	0.6065	ANN model hydrate phase behavior predictions are accurate	(61)
Natural gass	ANN	T and γ	P	NS	4	NS	ANN accuracy estimates hydrate dissociation pressures of natural gases in inhibitors	(76)
Natural gas	ANN	T and γ	P	0.991	4.8091	NS	ANFIS model outperforms the ANN model in hydrate phase boundary prediction	(65)
	ANFIS	T and γ	P	0.9789	2.7003	NS
CO2 and CH4	LSSVM	P and γ	T	131	NS	0.524	GPR provides better predictions than LSSVM and ANN models	(58)
	ANN	P and γ	T	95.8	NS	0.03
	GPR	P and γ	T	96.71	NS	0.023
Mixed gas system	ANN	T and γ	P	0.99	7.881	0.218	Predicts gas hydrate phase behavior accurately	(66)
	ANFiS	T and γ	P	0.985	0.709	0.085
Natural gas_3	ANN	Zi, T, and P	Pc	NS	2.896	NS	ANN improves the prediction accuracy of the van der Waals–Platteeuw thermodynamic model	(72)
Natural gas_4		Zi, T, and P	Pc	NS	3.126	NS
Natural gas_5		Zi, T, and P	Pc	NS	3.014	NS
Natural gas_6		Zi, T, and P	Pc	NS	3.217	NS
Natural gas_7		Zi, T, and P	Pc	NS	3.834	NS
Natural gas_8		Zi, T, and P	Pc	NS	2.967	NS
Natural gas_9		Zi, T, and P	Pc	NS	3.748	NS
Natural gas_10		Zi, T, and P	Pc	NS	3.897	NS
Natural gas_11		Zi, T, and P	Pc	NS	2.782	NS
Natural gas_12		Zi, T, and P	Pc	NS	2.667	NS
Natural gas_13		Zi, T, and P	Pc	NS	3.783	NS
Natural gas_14		Zi, T, and P	Pc	NS	3.126	NS
Natural gas_15		Zi, T, and P	Pc	NS	3.283	NS
Natural gas_16		Zi, T, and P	Pc	NS	3.721	NS
Natural gas_17		Zi, T, and P	Pc	NS	2.327	NS
Natural gas_18		Zi, T, and P	Pc	NS	2.102	NS
Natural gas_19		Zi, T, and P	Pc	NS	3.273	NS
Natural gas_20		Zi, T, and P	Pc	NS	2.651	NS
Natural gas_21		Zi, T, and P	Pc	NS	3.236	NS
Natural gas_22		Zi, T, and P	Pc	NS	3.123	NS
Natural gas_23		Zi, T, and P	Pc	NS	1.789	NS
Natural gas_24		Zi, T, and P	Pc	NS	2.875	NS
Natural gas_25		Zi, T, and P	Pc	NS	3.138	NS
Natural gas_26		Zi, T, and P	Pc	NS	3.247	NS
Natural gas_27		Zi, T, and P	Pc	NS	2.917	NS
Natural gas_28		Zi, T, and P	Pc	NS	3.674	NS
Natural gas_29		Zi, T, and P	Pc	NS	2.67	NS
Natural gas_30	ANN	Zi, T, and P	Pc	NS	2.571	NS	ANN improves the prediction accuracy of the van der Waals–Platteeuw thermodynamic model	(72)
Natural gas_31		Zi, T, and P	Pc	NS	2.832	NS
Natural gas_32		Zi, T, and P	Pc	NS	3.328	NS
Natural gas_33		Zi, T, and P	Pc	NS	2.897	NS
Natural gas_34		Zi, T, and P	Pc	NS	2.671	NS
Natural gas_35		Zi, T, and P	Pc	NS	3.127	NS
Natural gas_36		Zi, T, and P	Pc	NS	3.782	NS
C1n	LSSVM	γ, P, and Ic	T	0.9888	0.29	NS	LSSVM models predict hydrate phase behavior accurately especially for C1, C2, C3, i-C4, CO2, H2S, N2, and natural gas	(77)
C2o		γ, P, and Ic	T	0.9747	0.44	NS
C3o		γ, P, and Ic	T	0.961	0.29	NS
i-C4o		γ, P, and Ic	T	0.9866	0.2	NS
CO2p		γ, P, and Ic	T	0.9746	0.76	NS
H2Sq		γ, P, and Ic	T	0.9743	0.46	NS
N2q		γ, P, and Ic	T	0.9993	0.07	NS
Natural gasr		γ, P, and Ic	T	0.9533	0.51	NS
Natural gas (sour gas)	ANN	P and γ	T	NS	NS	0.0312	ANN predicts hydrate phase behavior conditions	(67)
		P and γ	T	NS	NS	1.3213
		P and γ	T	NS	NS	0.7529
		P and γ	T	NS	NS	1.2469
Natural gas	ANN	P and γ	T	0.9941	3.035	NS	Predicts gas hydrate phase behavior accurately	(78)

^aRBF (radial basis functional), P_i (Initial pressure), P_f (final pressure), γ (gas gravity), T_i (Initial temperature), T (temperature), P (pressure), NHF (nonhydrate formers), C₁ (Methane), C₂ (Ethane), C₃ (Propane), C₄ (Butane), C₅ (Propane), WC (water cut), GOR (gas-oil ratio), SFV (superficial fluid velocity), γ_o (oil specific gravity), IFT (interfacial tension), V (viscosity), HVF (hydrate volume fraction), HFa (hydrate interparticle cohesive force), Fa (interparticle cohesive force), PoF (Probability of failure), TPWHD (time of operating within hydrate domain), HVF (Hydrate volume fraction), RF (Random Forest), ET (Tremely randomized trees), XGBoost (Extreme Gradient Boosting), HF (hydrate formation), I_c (quality of the inhibitor/inhibitor concentration), P_d (differential pressure), NNARX (Neural Network Auto-Regressive X), GA-SVM (Hybrid genetic algorithm–support vector machine), M_wr (relative molecular weight), DNN (Deep nueral network), Zi (gas composition), H₂ (Hydrogen), Extra Trees (Extremely Randomized Trees), TOKM (The ordinary kriging method), ANFIS (Adaptive neurofuzzy interference system), ANN (artificial neural network), HFGA (Hybrid of Fuzzy logic and Genetic Algorithm), PNN (polynomial neural network), NMS (Nelder–Mead simplest), PV (pore size), SG (silica gel), MS (mesoporous silica), PG (porous glass), Pc (pressure correction), MLP (multiple linear regression), k-NN (k-Nearest Neighbor), SVR (Support Vector Regression), RF (Random Forest), GBR (Gradient Boosting Regression), BR (Bayesian Regulation back-propagation), tirmf (triangular-shaped), gaussmf (Gaussian curve), gbellmf (generalized bell-shaped), RPROP (resilient back-propagation), R_hg (Hydrate growth rate), ST (surface tension), GHBS (gas hydrate-bearing sediment), HSTS (Hydrate sediments tensile strength), HSSS (hydrate sediments shear strength), Vs (shear wave velocity), GR (Gamma-ray), ρ (density), Vp (porosity), RL (resistivity logs), LR (leak rate), WS (wind speed), WD (wind direction), GDSC (gas dispersion spatial concentration), R (resistivity), AV (acoustic velocity), HS (gas hydrate saturation by the chloride concentration), DS (Dry Saturated), IWS (Initial water saturation), GHF (Gas hydrate formation), GWD (Gas to water displacement), NS (Not stated).

^bNatural gas_1 (CO₂, CH₄, C₂H₆, C₃H₈, n-C₄H₁₀, i-C₄H₁₀, N₂), Natural gas_2 (C₁, C₂, C₃, i-C₄, n-C₄, i-C₅, n-C₅, n-C₆, n-C₇, n-C₈, CO₂, H₂S, N₂, H₂), Natural gas_3 (CH₄ + C₂H₆ + C₃H₈), Natural gas_4 (CH₄ + C₂H₆ + C₃H₈ + N₂), Natural gas_5 (CH₄ + C₂H₆ + C₃H₈ + CO₂), Natural gas_6 (CH₄ + C₂H₆ + C₃H₈ + H₂S), Natural gas_7 (CH₄ + C₂H₆ + C₃H₈ + i-C₄H₁₀), Natural gas_8 (CH₄ + C₂H₆ + C₃H₈ + n-C₄H₁₀), Natural gas_9 (CH₄ + C₂H₆ + C₃H₈ + CO₂ + H₂S), Natural gas_10 (CH₄ + C₂H₆ + C₃H₈ + CO₂ + i-C₄H₁₀), Natural gas_11 (CH₄ + C₂H₆ + C₃H₈ + CO₂ + n-C₄H₁₀), Natural gas_12 (CH₄ + C₂H₆ + C₃H₈ + i-C₄H₁₀ + H₂S), Natural gas_13 (CH₄ + C₂H₆+ C₃H₈+ i-C₄H₁₀+ n-C₄H₁₀), Natural gas_14 (CH₄ + C₂H₆ + C₃H₈ + N₂+ CO₂), Natural gas_15 (CH₄ + C₂H₆ + C₃H₈ + N₂ + H₂S), Natural gas_16 (CH₄ + C₂H₆ + C₃H₈ + N₂ + i-C₄H₁₀), Natural gas_17 (CH₄ + C₂H₆ + C₃H₈ + N₂ + n-C₄H₁₀), Natural gas_18 (CH₄ + C₂H₆ + C₃H₈ + n-C₄H₁₀ + H₂S), Natural gas_19 (CH₄ + C₂H₆ + C₃H₈ + CO₂ + i-C₄H₁₀ + H₂S), Natural gas_20 (CH₄ + C₂H₆ + C₃H₈ + CO₂ + i-C₄H₁₀ + n-C₄H₁₀), Natural gas_21 (CH₄ + C₂H₆ + C₃H₈ + CO₂ + n-C₄H₁₀ + H₂S), Natural gas_22 (CH₄ + C₂H₆ + C₃H₈ + i-C₄H₁₀ + n-C₄H₁₀ + H₂S), Natural gas_23 (CH₄ + C₂H₆ + C₃H₈ + N₂ + CO₂ + H₂S), Natural gas_24 (CH₄ + C₂H₆ + C₃H₈ + N₂ + CO₂ + i-C₄H₁₀), Natural gas_25 (CH₄ + C₂H₆ + C₃H₈ + N₂ + CO₂ + n-C₄H₁₀), Natural gas_26 (CH₄ + C₂H₆ + C₃H₈ + N₂ + i-C₄H₁₀ + H₂S), Natural gas_27 (CH₄ + C₂H₆ + C₃H₈ + N₂ + i-C₄H₁₀ + n-C₄H₁₀), Natural gas_28 (CH₄ + C₂H₆ + C₃H₈ + N₂ + i-C₄H₁₀ + H₂S), Natural gas_29 (CH₄ + C₂H₆ + C₃H₈ + CO₂ + i-C₄H₁₀ + n-C₄H₁₀ + H₂S), Natural gas_30 (CH₄ + C₂H₆ + C₃H₈ + N₂ + CO₂ + i-C₄H₁₀ + H₂S), Natural gas_31 (CH₄ + C₂H₆ + C₃H₈ + N₂ + CO₂ + i-C₄H₁₀ + n-C₄H₁₀), Natural gas_32 (CH₄ + C₂H₆ + C₃H₈ + N₂ + CO₂ + n-C₄H₁₀ + H₂S), Natural gas_33 (CH₄ + C₂H₆ + C₃H₈ + N₂ + i-C₄H₁₀ + n-C₄H₁₀ + H₂S), Natural gas_34 (CH₄ + C₂H₆ + C₃H₈ + N₂ + CO₂ + i-C₄H₁₀ + n-C₄H₁₀ + H₂S), Natural gas_35 (CH₄ + C₂H₆ + C₃H₈ + N₂ + CO₂ + i-C₄H₁₀ + n-C₄H₁₀ + C₅₊), Natural gas_36 (CH₄ + C₂H₆ + C₃H₈ + N₂ + CO₂ + i-C₄H₁₀ + n-C₄H₁₀ + H₂S + C₅).

^c(NaCl).

^d(NaCl, KCl, CaCl₂, MgCl₂ (25.75 wt %).

^e(NaCl, KCl, CaCl₂, MgCl₂, MeOH, EG, DEG, TEG, 1-propanol, and 2-propanol).

^f(tert-Butylamine).

^g(NaCl, KCl, CaCl₂, MgCl₂, MeOH, EG).

^h(1,4-Dioxane).

^I(acetine).

^j(THF).

^k(TBAB).

^l(TBAC).

^m(NaCl, CaCl₂, KCl, MgCl₂).

ⁿ(NaCl, KCl, MeOH, TEG, CaCl₂, DEG, EG, 1-propanol, 2-propanol, MgCl₂).

^o(NaCl, KCl, MeOH, TEG, CaCl₂).

^p(NaCl, KCl, MeOH, CaCl₂, EG, Glycerol, MgCl₂).

^q(NaCl, KCl, MeOH, EG).

^r(NaCl, KCl, MeOH, CaCl₂, EG, MgCl₂).

^s(MeOH, EtOH, EG, DEG, TEG, salt).

^u(Data were estimated via interpolated to 1400).

^v((Trees = 200) (Depth = 10) (Properties = 219)).

^w(Maximum trials = 50).

A study by Yarveicy³⁸ shows that ANFIS, LSSVM, and RBF ANN models show good prediction, with LSSVM exhibiting the best. In their study, the RMSE of the LSSVM model was about 50% less than ANFIS and 5% less than the RBF ANN model. This indicates that the LSSVM model efficiently predicts natural gas hydrate formation conditions without sour constituents and the presence of inhibitors. Contrarily, Suresh⁵⁸ showed that GPR provides better predictions than LSSVM and ANN models for pure hydrates of CH₄ and CO₂ systems. The performance of the LSSVM model in predicting natural gas hydrate formation conditions decreases 3–15 times in the presence of inhibitors, CO₂, and H₂S based on AARD evaluation.^59,60 For the same inhibitors and natural gas systems, the use of the extra trees model works better with about 50% error reduction compared with the LSSVM model.⁵⁹ Using the findings of Yarveicy³⁸ as the basis, LSSVM model performance in predicting CO₂ hydrate phase behavior in porous media has an increasing error margin of 12–20 times for silica gel and mesoporous silica, and 52–113 times in porous glass systems. The high error margins, especially in porous media, were due to the use of fewer data points in the model training and testing.⁵⁶

The predictions of natural gas phase behavior with ANN have been reported to depend on the input variables, the algorithm, and the transfer function used. The use of ANN with the Levenberg–Marquardt algorithm and tangent sigmoid predicts natural gas hydrate phase behavior (both sweet and sour gas systems) with RMSE of 0.6065 and AARD of 0.2137%.⁶¹ ANN also predicts hydrate formation on average well with both single and multiple inputs. This implies that the use of critical input variables will perform very well in ANN prediction. This is highly recommended compared to using more variables that have a weak impact on the hydrate formation conditions.⁶² ANN with the hyperbolic tangent sigmoid function predicts hydrate phase boundary conditions in the same range as ANFIS (Gaussian MF).⁶³ However, in the CO₂ gas hydrate system ANFIS performs better than ANN.⁶⁴ Mehrizadeh⁶⁵ also confirms the performance of ANFIS over ANN. In his models, the Levenberg–Marguardt algorithm was used for the ANN, and the first-order Takagi-Sugeno inference system was used for the ANFIS model. In natural gas systems with inhibitors, the ANN model performance reduces. According to Qin,⁵⁰ the performance of ANN in predicting hydrate formation conditions is 0.92 based on R² evaluations, while Soroush⁶¹ reported 0.998. Also, in the mixed gas systems, ANFIS (with tirmf, gaussmf, and gbellmf algorithms) shows better prediction performance than ANN (with the Bayesian regulation backpropagation algorithm) with a tangent sigmoid transfer function.⁶⁶ In sour natural gas systems, the use of ANN with Levenberg–Marquardt algorithms performs better in predicting the hydrate phase boundary conditions compared with the gradient descent with momentum, scaled conjugate gradient, and one-step secant backpropagation algorithms. The model prediction performance of ANN with Levenberg–Marquardt algorithms reduces by 24, 42, and 40 times, respectively, for the scaled conjugate gradient, gradient descent with momentum, and one-step secant backpropagation algorithms.⁶⁷ The choice of the algorithm and transfer function affects the model performance. These algorithms and transfer function selections must be selected carefully by considering the type of data and variable inputs for the phase behavior prediction.

Aside from the LSSVM and ANN, several machine learning models are able to hydrate phase boundary conditions efficiently. SVC with RBF kernel predicts formation conditions efficiently compared with ANN.⁵⁰ AdaBoost-CART provides more reliable HDT prediction than ANFIS and ANN. The hydrate phase behavior prediction error of ANFIS and ANN decreases by 5 times when replaced with AdaBoost-CART.⁶³ GA-LSSVM model is a modification of the LSSVM and has been used for hydrate phase boundary prediction using gas gravity and pressure as inputs.⁶⁸ Its predictions are relatively good, with an AARD of about 0.5%. However, the model performance is relatively poor in N₂ + THF, CH₄ + 1,4-dioxane, and H₂ + acetone clathrate hydrates systems.⁶⁹ The use of ANN and ANFIS still outperforms some hybrid machine learning algorithms such as TOKM and HFGA.⁶⁴ GBR gives the best prediction for predicting the methane hydrate phase boundary conditions than MLP, k-NN, SVR, and RF algorithms.⁷⁰ A study by Suresh⁵⁸ also confirmed that GPR has good hydrate phase behavior prediction accuracy than ANN and LSSVM. RF and ET have similar prediction accuracy, but XGBoost outperforms both RF and ET in hydrate phase behavior prediction.⁴² The use of PNN, DNN, with ReLU activation function and NNARX has also proven efficient in predicting gas hydrate phase boundary conditions.^54,55,71

The use of machine learning in hydrate phase behavior predictions is used as an algorithm to optimize or assist the prediction accuracy of the existing hydrate thermodynamic models. Among the machine learning models, ANN has proven to improve the prediction accuracy of the van der Waals–Platteeuw thermodynamic model.⁷² Such practices are good and recommended since they can be empirically explained in terms of hydrate structural and molecular level inclusive perspective. This is very useful for the statistical modeling of complex gas hydrate guest molecules and inhibitor systems.

4.2. Hydrate Kinetics Prediction

The prediction of gas hydrate kinetics is a complex phenomenon to determine due to the stochastic nature of hydrate formation. Empirically, hydrate kinetics modeling is still not well established; in addition, the existing kinetics models are limited with high errors. Hence, the use of artificial intelligence might provide a better prediction accuracy. With the increase in the use of AI and machine learning techniques in gas hydrate applications, very few studies have been conducted on the kinetics of hydrate formation. Table 2 summarizes the details of machine learning techniques on gas hydrate kinetics. ANN and ANFIS models have been used to predict the kinetics of pure methane hydrates and natural gas hydrates. ANFIS prediction of the interfacial tension of SDS surfactant-based systems near the ethylene hydrate formation region was conducted by Zare.⁸⁰ The study showed that the prediction of the SDS interfacial tension was relatively good, with an AARD of 1.2%. Also, Foroozesh⁷⁹ predicted the methane hydrate formation rate using the ANN model. The model prediction was relatively poor with about 13.86% AARD. The poor performance of the model could be due to the limited number of data used in the model training and testing. The core parameters of gas hydrate formation kinetics are the induction time, rate, and moles of guest uptake. Out of these, only one attempt has been made so far on the rate of the hydrate formation, with none reported in the open literature on hydrate formation induction time and guest molecule uptake. The main challenges faced with the hydrate kinetics machine learning modeling is the availability of data. Gas hydrate kinetics are reactor dependent, and thus using different data for different reactors will result in wrong comparison and data standardization. Aside from the need for large data sets, the use of stochastic machine learning algorithms could prove better prediction accuracy. Also, machine learning algorithms can be employed as tools to optimize, assist, and/or enhance the prediction accuracies of the existing gas hydrate empirical kinetic models.

Table 2. Summary of Machine Learning Techniques Used for Gas Hydrate Kinetics Studies.

Gas	Machine learning model	Inputs	Outputs	R2	AARD %	RMSE	Remarks	ref
Methane	ANN	T and P	Rhg	NS	13.86	NS	ANN modeled hydrate growth rate with high sensitivity to temperature difference driving force	(79)
Natural gasa	ANFIS	P, T, and Ic	ST	0.9977	1.1998	NS	ANFIS prediction of the interfacial tension of SDS surfactant-based systems near the ethylene hydrate formation region was accurate	(80)

^a(SDS/ethylene).

4.3. Natural Gas Hydrate and CO₂ Capture

Natural gas hydrates are a potential source of energy that could replace fossil fuels. The use of machine learning methods in natural methane hydrates is focused on natural gas hydrate saturation distribution, tensile and shear strength, and hydrate morphology (see Table 3). The use of new NN and CNN was used to predict the tensile and shear strength of gas hydrate stability.⁵¹ The proposed new NN reduced the error of the CNN by 38 times. A gas hydrate morphology and saturation prediction behavior were proposed by You.⁸¹ Their findings suggest that machine learning techniques using the LSTM method perform better than LSF in the predictions of the shear wave velocity and hydrate morphologies. Li⁸² demonstrated the performance of using RNN with the Adam transfer function to predict gas hydrate saturation. In a distinguishing attempt, Kim⁸³ suggested that RF outperforms CNN and SVR in predicting water, gas, and GH saturation hydrate saturation reservoirs. These studies are geologically related and need many images or logging data to increase their performance. The use of machine learning in hydrate saturation prediction can be used to estimate hydrate reserves, deposition, and production technologies.

Table 3. Summary of Machine Learning Techniques Used for Gas Hydrate Sediment Saturation and Related Studies.

Gas	Machine learning model	Inputs	Outputs	R2	AARD %	RMSE	Remarks	ref
GHBS samples from the Nankai Trough in Japan	ANN	NS	HSTS and HSSS	0.9958	NS	0.0013	The new NN structure outperformed the CNN in the estimation of the tensile and shear strength	(51)
			HSTS and HSSS	0.9297		0.05
Morphology and saturation of Alaminos Canyon (Block 21)	LSTM and LSF	GR, ρ, Vp, RL	Vs	0.876	1.5634	0.0114	The LSTM method performs better than LSF in the predictions of the shear wave velocity and the hydrate morphologies	(81)
GHBS saturation in the Shenhu area, South China Sea (SH7)	RNN	R and AV	HS	0.7085	NS	0.1208	This method has a higher accuracy prediction of gas hydrate saturation than traditional machine learning methods	(82)
GHBS saturation, Korean East Sea region	RF	CT Scan (DS, IWS, GHF, and GWD)	HS	NS	NS	27	The RF best predicts the performance for water, gas, and GH saturation in the samples among the three methods. The CNN and SVR also exhibit sufficient performances	(83)
	SVR	CT Scan (DS, IWS, GHF, and GWD)	HS			1088.5
	CNN	CT Scan (DS, IWS, GHF, and GWD)	HS			434

In the area of hydrate-based carbon capture, the application of machine learning is much less. Ahmadi⁶⁴ used ANFIS, TOKM, ANN, and HFGA to predict the phase behavior of different porous media systems in the presence of inhibitors. The porous media that the models covered were silica gel, porous glass, and mesoporous silica. ANFIS was the best in determining the hydrate formation conditions of CO₂ hydrates in porous media. Data scarcity for porous media system variability is a main challenge for conducting effective machine learning related studies in hydrate-based CO₂ capture technologies. However, it is recommended that the best machine learning models be evaluated for such applications.

5. Machine Learning in Hydrate Field Data Prediction

The emergence of the fourth world industrialization (Industry 4.0) has increased the use of machines in the oil and gas industries. Though most hydrate-related studies are based on empirical or laboratory data, the main goal is to achieve a machine learning algorithm that can be applied to practical field activities. In this section, the use of gas hydrate field data for machine learning models is discussed to provide state-of-the-art knowledge and advance machine learning in gas hydrate applications. For hydrate predictions, just like other predictive models in drilling, fracturing, and shale studies, ANN models are mostly used.⁸⁴⁻⁸⁸ An ANN and SVR machine learning model was developed by Qin⁵⁰ using field data from a dry tree facility in the Gulf of Mexico. The models were programmed to predict or detect gas hydrate formation plugs and the formation conditions. The use of machine learning was argued as a good tool that could serve as a roadmap to hydrate risk detection and management systems. However, there are no findings in the literature to confirm if these models are currently used in the field during pipeline operations. GHBS samples from the Nankai Trough of Japan were used to develop a machine learning model for the estimation of hydrate reservoirs’ tensile and shear strength.⁵¹ GHBS data from the Korean East Sea region, Shenhu area, South China Sea (SH7), and Alaminos Canyon (Block 21) are practical field data used to develop machine learning models for predicting hydrate sediments, gas hydrate saturation, and morphologies.⁸¹⁻⁸³ In areas such as Ulleung Basin, Korea, Mackenzie Delta (Canada), and on the Alaska north slope (USA), reservoir data have been used to develop machine learning models to characterize gas hydrate reservoirs and determine and estimate the hydrate rocks’ mineral compositions.⁴³

6. Comparison between Conventional and Machine Learning Models

The performance of machine learning models is best proven when compared to that of existing hydrate models. In this context, the comparison of machine learning models’ performance to conventional models is solely limited to gas hydrate thermodynamics. The other aspect of gas hydrate application is lacking in machine learning studies, and thus their comparison with existing models is rare in the literature. Generally, most of the machine learning models show better predictions and could supplant traditional models and correlations in terms of thermodynamic predictions. Most of the conventional models used for comparison are mostly Bahadori and Vuthaluru⁸⁹ correlation; Berge⁹⁰ correlation; Motiee⁹¹ correlation; Towler and Mokhatab⁹² correlation; Hammerschmidt⁹³ correlation; and Sun and Chen,⁹⁴ Baillie and Wichert,⁹⁵ and van der Waals²² methods. Aside from the van der Waals–Platteeuw (vdWP) method, which is more accurate but rarely used, the other correlations are very old, though they have been used in gas hydrate simulation software (Hydrate Plus software).

A machine learning multilayer perceptron neural network that uses the ReLU activation function reduced errors of hydrate phase behavior predictions of multiphase and CSMHYD software by 50%.⁷¹ The comparison of LSSVM to traditional correlations shows the great capability of LSSVM.⁶⁸ Specifically for the modeling of gas systems containing H₂S, LSSVM performed better than the Berg correlation, Motiee correlation, Towler and Mokhatab correlation, and the Baillie and Wichert models.⁷⁵ The hybrid group method of data handling (GMDH), ANFIS, and ANN also outperforms these same traditional correlations.^55,61,80,96 Contrarily, van der Waals–Platteeuw (vdWP) models and HFGA are in the same range of performance for CO₂ hydrate systems with promoters such as acetone, TBAB, and TBAC. However, the van der Waals–Platteeuw (vdWP) EOS model outperforms ANN and Ordinary Kriging models by 112% and 215%, respectively, but the adaptive neuro-fuzzy interference system (ANFIS) performs better than the thermodynamics-based approach of van der Waals–Platteeuw (vdWP) by 26%.⁶⁴ The machine learning performance with conventional hydrate models suggests that the incorporation of machine learning models into commercial simulation software will reduce the calculation stress while maintaining accuracy.

7. Recommendations and Prospects

An emphasis has been placed on ensuring that the developed model can successfully predict multicomponent equilibria. Machine learning models could be used to develop novel gas hydrate additives for application in gas hydrate research areas such as flow assurance, CO₂ capture, desalination, etc., where the search for novel additives is needed, especially in the areas of finding the best deep eutectic solvent or ionic liquid cation and anion combinations. Future studies should focus on generating suitable kinetics and natural gas hydrate reservoir data efficiently and proper machine learning modeling. The efficient machine learning models should be incorporated into existing gas-hydrate-related software for accurate predictions. The use of gas hydrate application field data for machine learning models will provide suitable and practical results for industrial use. Also, machine learning algorithms should be used for optimizing the modeling parameters of the existing empirical models for improved accuracy. Machine learning models for predicting gas hydrate kinetics and thermodynamic behavior in the presence of novel additives are highly recommended. Classification models for differentiating the various hydrate structures and textures and predicting the guest molecules are needed for an in-depth scientific knowledge of hydrate detection. The use of AI in methane hydrate production and exploration is at an early stage and needs further research to guide its production processes and environmental impact.

The generalization of machine learning models for gas hydrate applications is an important area that needs research attention. The existing models in the literature are focused on specific systems or components. Such models must have the ability to predict several hydrate properties from different gas systems, chemical additives, and kinetic systems. Also, the developing hydrate-based machine learning models with engineering features will provide safe hydrate plug-free flow assurance operations. Such inclusions could consider engineering features that enhance, promote, or necessitate hydrate formation. Such models could be accomplished by developing semisupervised and reinforced learning in gas hydrate application predictions.

8. Conclusions

In this study, the use of machine learning models in gas hydrate applications has been reviewed to establish the successes and state-of-the-art knowledge of its progress. The main contribution of this work lies in outlining critical areas where machine learning models could help make gas hydrate technology achievable. The use of machine learning models to predict the hydrate phase behavior conditions (with and without inhibitors) is the most applied and successful breakthrough in the use of machine learning in gas hydrates. Both hybrid and traditional models have been proven to effectively predict hydrate properties for both classification and regression analysis. The use of machine learning models to improve the predictions of existing gas hydrate models is a novel innovation that could be adopted and incorporated into current gas hydrate software for efficient predictions. The successful machine learning models in gas hydrate applications are rigorous and relatively well validated to show positive improvement in hydrate phase behavior prediction. Despite the relevance of machine learning in gas hydrate applications, several green gas hydrate areas have received little attention in terms of AI applications. Such areas are the kinetics of gas hydrates, hydrate separation methods, desalination, additive development, and hydrate-bearing sediment applications.

The authors declare no competing financial interest.