Emerging BaZrS₃ and Ba(Zr,Ti)S₃ Chalcogenide Perovskite Solar Cells: A Numerical Approach Toward Device Engineering and Unlocking Efficiency

Abstract

BaZrS₃ chalcogenide perovskites have emerged as a promising absorber due to their exceptional properties. However, there are no experimental reports on the applicability of BaZrS₃ in photovoltaics. Thus, theoretical knowledge of device structure engineering is essential for its successful fabrication. In this regard, we have proposed various BaZrS₃ device configurations by altering 12 electron transport layers (ETLs) in combination with 13 hole transport layers (HTLs) using SCAPS-1D, wherein a total of 782 devices are simulated by tuning the thickness, carrier concentration, and defect density of BaZrS₃, ETLs, and HTLs. Interestingly, the absorber’s thickness optimization enhanced the absorption in the device by 2.31 times, elevating the generation rate of charge carriers, while the increase in its carrier concentration boosted the built-in potential from 0.8 to 1.68 V, reducing the accumulation of charge carriers at the interfaces. Notably, on further optimization of ETL and HTL combinations, the best power conversion efficiency (PCE) of 28.08% is achieved for FTO/ZrS₂/BaZrS₃/SnS/Au, occurring due to the suppressed barrier height of 0.1 eV at the ZrS₂/BaZrS₃ interface and degenerate behavior of SnS, which increased charge carrier transportation and conductivity of the devices. Upon optimizing the work function, an ohmic contact is achieved for Pt, boosting the PCE to 28.17%. Finally, the impact of Ti alloying on BaZrS₃ properties is examined on the champion FTO/ZrS₂/BaZrS₃/SnS/Pt device where the maximum PCE of 32.58% is obtained for Ba(Zr_0.96,Ti_0.04)S₃ at a thickness of 700 nm due to extended absorption in the NIR region. Thus, this work opens doors to researchers for the experimental realization of high PCE in BaZrS₃ devices.

1. Introduction

With the increase in global energy demand, extensive efforts have been made to address the depletion of fossil fuels like coal, oil, and natural gas. Thus, the quest for enduring eco-friendly energy solutions to meet the escalating demand has become crucial. Amidst these pursuits, solar energy conversion employing photovoltaic (PV) technology is a sustainable and environmentally conscious approach to generating electricity.¹ Over the past decade, lead halide perovskites (MAPbX₃ where X = I, Br, Cl) have revolutionized the development of PV materials. They demonstrated a power conversion efficiency (PCE) of 3.8% in 2009² by using liquid electrolytes as a hole transport layer (HTL).³ The PCE was improved to 9.7% in 2012 by replacing the HTL with the solid-state spiro-OMeTAD. Within a few years, the lead halide perovskites emerged as a promising optoelectronic material with its unpreceded rate of increase in PCE up to 26.1% in 2023.⁴ Despite the enhanced performance, the toxicity of lead and instability of halides in humidity, heat, and light hinder their pace of commercialization. As a result, researchers have been exploring lead-free perovskite materials to address these environmental concerns. Various materials are being developed as alternatives to lead-based perovskites. To be specific, perovskites based on tin (Sn) and germanium (Ge) such as MASnI₃, CsSnI₃, FASnI₃, CsGeI₃, MAGeI₃, FAGeI₃, and CsSn_0.5Ge_0.5I₃have emerged as promising alternatives due to their similar isoelectronic (s²p²) configuration, high carrier mobility, nontoxicity, and narrow band gaps. Although there are some challenges when it comes to stability, such as Sn²⁺ and Ge²⁺ ions being easily oxidized and converting to Sn⁴⁺ and Ge⁴⁺ when exposed to ambient atmosphere, the high cost and lack of Ge in the earth’s crust also limit its applicability.⁵ Certainly, researchers have found some alternative solutions. For instance, they have introduced trivalent cations like Bi³⁺ and Sb³⁺ instead of Pb²⁺ ions. However, the PCE achieved is still much lower than lead halide perovskites due to their low-dimensional structure, which results in unfavorable optoelectronic properties. To overcome these challenges, halide double perovskites (HDPs) have been developed with a structure similar to A₂B⁺B³⁺X₆, replacing Pb²⁺ with eco-friendly Bi³⁺ while maintaining a three-dimensional (3D) structure. This innovative solution involves replacing two Pb²⁺ ions with one B⁺ ion and one B³⁺ ion.⁶ Some notable examples of these HDPs are Cs₂AgBiBr₆, Cs₂NaBiCl₆, (CH₃NH₃)₂AgBiBr₆, and (CH₃NH₃)₂KBiCl₆, which have recently emerged as highly promising materials. While HDPs have great potential, their efficiency is limited by large charge carrier effective masses, high band gap (>2 eV), and weak charge carrier transport capabilities. Research has been focused on exploring antimony-based perovskite materials (such as Cs₂SbCuCl₆, Cs₄SbCuCl₁₂, Cs₂SbAgCl₆, Cs₂SbAgI₆, and Cs₂SbAgBr₆) as they offer unique attributes like stability at high temperatures and exceptional charge carrier conductivity. However, their wide band gaps, high binding energies, and high carrier effective mass limit their performance.⁷ Apart from perovskites, researchers are also exploring other light absorbers such as ternary II–IV–N₂ nitrides (ZnSnN₂),^8,9 binary halides (InI¹⁰ and BiI₃¹¹), AbZ₂ chalcogenides (AgBiS₂,¹² NaBiS₂,¹³ and NaSbS₂¹⁴), Bi-based chalcohalides (BiOI,¹⁵ BiSI,¹⁶ Bi₁₉S₂₇Br₃, and Bi₁₃S₁₈I₂), Sb-based chalcohalides (SbSI,^18,19 SbSeI,²⁰ and SbBiISI²¹), Pb-based chalcohalides (Pb₄S₃Br₂²² and Pb₂SbS₂I₃²³), Ag-based chalcohalides (Ag₃BiI_6–2xS_x),²⁴ Sn-based chalcohalides (Sn₂SbS₂I₃),²⁵ hybrid organic–inorganic metal chalcogenides (MASbSI₂²⁶ and MA₃Bi₂I_9–2xS_x²⁷), I₂–II–IV–VI₄ semiconductors (Cu₂BaSnSe₄,²⁸ Cu₂SrSnS₄²⁹), and II–V semiconductors (Zn₃P₂).³⁰⁻³² Despite their promise, these emerging absorbers have exhibited PCEs below 8%. Therefore, we are urged to discover new materials that can retain the extraordinary properties of lead halide perovskites while overcoming the aforementioned limitations.

In this concern, chalcogenide perovskites emerged as an alternative novel material due to their nontoxicity and high stability. They grabbed the limelight in 2015 when Sun et al. theoretically screened 18 ABX₃ (A = Ba, Sr, Ca; B = Ti, Zr, Hf; X = S, Se) compounds to be promising for optoelectronic applications.³³ Among them, BaZrS₃ is considered to be ideal from the standpoint of the direct band gap of 1.7 eV,³⁴ high absorption coefficient >10⁵ cm^–1 at photon energy larger than 1.97 eV (<700 nm),³⁵ elevated carrier mobility of 30 cm²/(V s) with p-type conductivity,³⁶ and exceptional stability toward moisture, light, and temperature.³⁷ Prior research indicates that the performance of BaZrS₃ can be improved further by alloying with both titanium (Ti) and selenium (Se). So far, Ti alloying has proven to be more productive due to its effective band gap reduction with less atom %. Specifically, Meng et al. reported that the band gap obtained for 0.1 atom % Ti alloying can only be accomplished at 1 atom % of Se alloying.³⁸ However, no experimental reports related to the applicability of BaZrS₃ and Ba(Zr,Ti)S₃ in PV exist due to its challenging synthesis temperatures exceeding 900 °C, limiting its feasibility and exploration of chalcogenide perovskites.³⁹

Nevertheless, recent advancements have resulted in a reduction in the operating temperature required to synthesize BaZrS₃. For example, Comparotto et al. reported the synthesis of BaZrS₃ thin films, employing a sputter-sulfurization approach with a process temperature below 600 °C.⁴⁰ Similarly, Nag et al. detailed their work on BaZrS₃ nanocrystals (powder) synthesis at 600 °C, followed by the formulation of an ink and film-coating process, while Yu et al. demonstrated the synthesis of BaZrS₃ thin films at an even lower temperature of 500 °C by modifying the chemical reaction pathway.⁴¹ Interestingly, Yang et al. and Zilevu et al. reported colloidal synthesis of BaZrS₃ nanopowders at an impressive temperature below 350 °C, underscoring the potential of solution-based processing of BaZrS₃.^42,112 Most recently, in 2023, Vincent et al. introduced a groundbreaking approach for the solution processing of direct BaZrS₃ thin films. This method involves heat treatment of precursor thin films in a sulfur-containing atmosphere at modest temperatures ranging from 500 to 575 °C.⁴³ These reports are a major accomplishment in producing BaZrS₃. They used processing temperatures similar to those of traditional absorbers, which is a significant advancement. These developments have opened new opportunities for creating effective BaZrS₃ devices. Therefore, to predict the device performance, we utilized a solar cell capacitance simulator in a one dimension (SCAPS-1D) theoretical tool to study the influence of each layer’s parameters, interfacial defects, stability, and band alignment of the device by saving the time and cost before investing into fabrication.⁴⁴ Moreover, SCAPS-1D is a highly reliable software as the simulation results are consistent with the experimental work.⁴⁵

Researchers recently employed BaZrS₃ and Ba(Zr,Ti)S₃ as absorbers in thin-film devices and studied their influence using SCAPS-1D.^37,46,47 However, a comprehensive study on the device engineering and properties of BaZrS₃ and Ba(Zr,Ti)S₃ is scarce, creating more room to discover and understand the potential of these absorbers in thin-film devices. Also, choosing the right electron transport layers (ETLs) and HTLs is crucial in creating efficient devices. ETLs are particularly important as they help extract and transfer photogenerated electrons while blocking holes. An ideal ETL should possess several vital attributes, including a wide band gap that facilitates high light transmission, perfect energy levels, cost-effectiveness, high electron mobility for efficient electron injection and transport, and photochemical and thermal stability. Organic materials and polymers are lead halide perovskites, the most widely used ETLs. However, these materials tend to be expensive and less stable. Interestingly, inorganic ETLs are a promising alternative due to their high stability, easy preparation process, cost-effectiveness, and excellent electronic properties.^48,49 Considering these advantages, we have carefully curated a list of 12 promising inorganic ETLs, including Bi₂S₃,^50,51 ZrS₂,^52,53 SnS₂,⁵⁴ In₂S₃,⁵⁵ ZnS,⁵⁵ Zn₂SnO₄,⁵⁶ BaSnO₃,⁵⁷ Al₂O₃,^58,59 WO₃,⁵⁸ TiO₂,⁶⁰ ZnO,⁶⁰ and SnO₂⁶⁰ for our simulation. On the other hand, the choice of HTLs significantly affects the device’s performance, durability, and production cost. While small-molecule HTLs can enhance the device’s performance, they often suffer from stability issues. In contrast, polymeric HTLs offer stability at high temperatures and compatibility with other materials, but their poor optoelectronic properties hinder efficiency. Additionally, commonly used organic HTLs like Spiro-MeOTAD are expensive and unstable in ambient conditions. Interestingly, inorganic HTLs offer numerous advantages, such as outstanding stability, high hole mobility, low cost, and easy preparation techniques, and have proven to be promising for achieving stable and efficient device performance.^6,61 In this context, we have selected 13 HTLs, including MoS₂,⁶² CuO,⁶³ Cu₂S,⁶⁴ FeS₂,⁶⁵ Sb₂S₃,⁶⁶ SnS,⁶⁷ Cu₃BiS₃,⁶⁸ Cu₂SnS₃,⁶⁹ CuSbS₂,⁷⁰ Cu₂BaSnS₄,⁷¹ CuInGaS₂,⁷² Cu₂ZnSnS₄,⁷³ and Cu₂ZnSn_1–xGe_xS₄.⁷³ Thus, our work embarks on modeling 782 thin-film devices employing BaZrS₃ as the absorber, varying 13 HTLs and 12 ETLs to elucidate an ideal device structure. The material properties have been studied extensively by varying the thickness, carrier concentration, and defect density of each ETL with 13 HTLs to investigate their suitability for emerging BaZrS₃-based devices. Moreover, the role of back contacts is meticulously examined by tuning the metal electrode work functions. Furthermore, we studied the influence of Ti alloying, with its concentration ranging from 1 to 4 atom % in the BaZrS₃ absorber for the device that attained the highest PCE.⁷⁴ To this end, an array of analyses, including current density–voltage (J–V), capacitance–voltage (C–V), quantum efficiency (QE), electric field distributions, generation profiles, and recombination profiles, have been utilized to gain a broader knowledge of the functioning of devices. On top of that, the role of band alignment between the absorber and transporting layers was also examined using the energy band diagram extracted from SCAPS-1D. Thus, we firmly believe that our work creates a significant impact among researchers worldwide by providing a better direction for understanding the performance of BaZrS₃ and Ba(Zr,Ti)S₃ and facilitates the research community in selecting cost-effective and efficient devices for commercialization as the wheel of development rolls on.

2. Computational Strategy and Device Description

One-dimensional Solar Cell Capacitance Simulator (SCAPS-1D) is a well-known software program developed by Mark Burgelmann at the University of Ghent in Belgium to predict the device performance concerning the characteristics of each layer and interface. This software offers numerous advantages, such as conducting performance analysis at up to seven levels to perform comprehensive and batch analyses.⁷⁵ The theoretical calculation relies on three fundamental equations, namely, Poisson’s equation, the carrier continuity equation, and the drift-diffusion equation, which are as follows⁷⁶

1

2

3

where q is the charge of electrons (C), p is the concentration of holes (cm^–3), ε is the dielectric constant, n is the concentration of electrons (cm^–3), φ is the electric potential (V), R is the carrier recombination rate (cm^–3 s^–1), G is the carrier generation rate (cm^–3 s^–1), J_p is the current density of holes (mA/cm²), J_n is the current density of electrons (mA/cm²). D_n and D_p refer to coefficients of electrons and hole diffusion (cm²/s), respectively, while μ_n and μ_p are the mobilities of electrons and holes (cm²/(V s)).^76,77

In this work, we initially designed a base device with superstrate configuration FTO/SnO₂/BaZrS₃/Cu₂S/Au, as shown in Figure 1a, using SCAPS-1D (version 3.3.10). The light enters through fluorine-doped tin oxide (FTO) and gets transmitted through the SnO₂ ETL to the absorber. Due to the p–n junction’s built-in potential, charge carriers are generated, separated, and collected at the respective contacts.⁷⁸ A summary of the simulation’s initial device parameters for FTO, SnO₂, BaZrS₃, and Cu₂S is shown in Table 1. All of the analyses were performed under AM 1.5G (100 W cm^–2, one sun) spectral irradiance, and the operational temperature of devices was maintained at 300 K.

Figure 1.

(a) Initial device structure and (b) J–V characteristics of the emerging BaZrS₃ chalcogenide perovskite device.

Table 1. SCAPS-1D Input Parameters of the Initial Device Structure.

parameter	FTO	SnO2	BaZrS3	Cu2S
thickness (nm)	10	30	500	50
band gap Eg (eV)	3.50	3.50	1.70	1.21
affinity χ (eV)	4.00	4.00	4.10	4.45
dielectric permittivity εr	9.0	9.0	9.6	30
conduction band effective density of states NC (cm–3)	2.2 × 1018	2.20 × 1017	2.2 × 1018	1.00 × 1019
valence band effective density of states NV (cm–3)	1.8 × 1019	2.20 × 1016	1.8 × 1019	6.15 × 1019
electron thermal velocity (cm/s)	1 × 107	1 × 107	1 × 107	1 × 107
hole thermal velocity (cm/s)	1 × 107	1 × 107	1 × 107	1 × 107
electron mobility (cm2/(V s))	2 × 101	2.00 × 1001	1.10 × 10–02	5.00 × 101
hole mobility (cm2/(V s))	1 × 101	1.00 × 1001	3.90 × 10–02	4.00 × 100
donor density ND (cm–3)	1 × 1018	1 × 1018	0	0
acceptor density NA (cm–3)	0	0	1 × 1015	7 × 1016
defect density NT (cm–3)	1 × 1015	1 × 1015	1 × 1010	1 × 1013
references	(79)	(80)	(46,47)	(81)

To begin with, the initial device performance (Section 3.1) is represented in the J–V curve (Figure 1b). After that, the influence of varying the thickness, carrier concentration, and defect density of ETL, absorber, and HTL is studied and reported in Section 3.2. The corresponding device parameters, such as open-circuit voltage (V_oc), short-circuit current density (J_sc), fill factor (FF), and PCE, are obtained. After optimizing each layer in the initial device, the impact of different ETLs and HTLs on the device’s PCE is explained in Section 3.3. A schematic representation of energy band diagrams and the 156 devices that achieved the highest PCE for each ETL and HTL combination is shown in Figure 4 and Table 2, respectively. In addition, the influence of metal contacts with different work functions is studied in Section 3.4. Then, the effect of Ti alloying for the device with the highest PCE is briefly investigated in Section 3.5. Finally, devices with the highest PCE are selected from the simulations above, and their performances are investigated by varying series resistance (R_S), shunt resistance (R_Sh), and working temperature from 1 to 10 Ω cm², 10 to 10⁷ Ω cm², and 300 to 400 K, respectively (Section 3.6). Subsequently, the material properties are elucidated using J–V, C–V, QE, electric field distributions, generation profiles, and recombination profiles from SCAPS-1D.

Figure 4.

Schematic representation of energy-level diagram for different ETLs, HTLs, and BaZrS₃ chalcogenide perovskite absorbers.

Table 2. Influence of Metal Work Function on PV Parameters.

metal contacts	work function (eV)	Voc (V)	Jsc (mA/cm2)	FF (%)	PCE (%)
Cu/Mo	4.6	0.87	23.81	73.14	15.16
Ag	4.7	0.88	26.22	70.81	16.36
Fe	4.8	0.94	29.55	74.73	20.78
Cu-doped C	5.0	1.11	29.74	81.95	27.09
Au	5.1	1.17	29.74	80.42	28.08
W	5.2	1.18	29.74	80.16	28.17
Ni	5.5	1.18	29.74	80.15	28.17
Pd	5.6	1.18	29.74	80.15	28.17
Pt	5.7	1.18	29.74	80.15	28.17

3. Results and Discussion

3.1. Initial Device Performance

To acquire a suitable device configuration for enhanced performance of chalcogenide perovskites, we designed a base device structure (FTO/SnO₂/BaZrS₃/Cu₂S/Au) as illustrated in Figure 1a. The simulations were performed according to the parameters listed in Table 1, and the resulting J–V characteristics of the initial device and its respective PV parameters are provided in Figure 1b. Afterward, ETL, absorber, and HTL properties were optimized to enhance performance by varying their thickness, carrier concentration, and defect density. The results of the simulations are shown in Section 3.2.

3.2. Optimization of ETL, Absorber, and HTL Parameters

To begin with, SnO₂ ETL was optimized by varying the parameters such as thickness, carrier concentration, and defect density. However, no significant changes in the PV parameters were observed with the ETL optimization, as shown in Figure S1. Interestingly, significant improvements in the device performance have been achieved by optimizing the absorber and HTL, which are comprehensively discussed in the following sections.

3.2.1. Impact of Absorbers Thickness, Carrier Concentration, and Defect Density

In this study, we varied the absorber thickness from 100 to 2000 nm. Figure 2a demonstrates that the V_oc reaches an optimum value of 1.37 V at 1000 nm and remains insignificant with an increase in thickness beyond 1000 nm. In contrast, the J_sc surges from 13.90 to 21.95 mA/cm² as the thickness increases from 100 to 2000 nm. This increase in J_sc is attributed to the enhanced spectral response at longer wavelengths.⁸² Conversely, the V_oc saturates as the absorber becomes thick enough to absorb almost all incident light. This saturation could be linked to nonradiative losses associated with point defects, carrier lifetime, and interface recombination.⁸³ Examining Figure 2b, we observe that the FF increases from 48.64 to 79.12% as the thickness increases from 100 to 1000 nm and then diminishes. Conversely, the PCE experiences a substantial increase from 7.96 to 24.43% as the thickness increases from 100 to 2000 nm. Notably, the PCE increases by three times when the thickness extends from 100 to 1000 nm, while it improves by 0.94 times when the thickness is doubled from 1000 to 2000 nm. FF is the ratio of the maximum power output (P_max) to the product of J_sc and 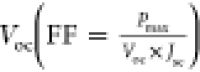, while PCE is the ratio of P_max to incident power of light i.e., 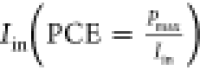.⁸³ The increased J_sc and V_oc at an optimum thickness result in higher FF. However, charge carrier depletion accelerates at an absorber thickness beyond 1000 nm, and the series resistance increases, leading to a subtle decrease in the fill factor.⁸⁴ Furthermore, the PCE of the device is influenced by both light absorption and carrier transport. When the absorber is thin, it absorbs a small portion of light and then transmits the unreflected remaining incident light, resulting in major absorption in the HTL. Subsequently, charge carriers accumulate near the back contact, enhancing recombination in the device. When the thickness increases, more light is absorbed in the absorber layer, reducing the buildup of charge carriers in the back contact.⁸² This behavior is documented in Figure 2c, illustrating the charge carrier generation rate at two distinct thicknesses, 100 and 1000 nm. At 100 nm, the generation rate is higher in the HTL region than in the absorber region, indicating a large accumulation of charge carriers, while at 1000 nm, it is more prominent in the absorber region, revealing increased photon absorption in the absorber, resulting in enhanced device performance.⁸⁵ Additionally, QE measurements in Figure 2d show that the integral area of QE absorption increases from 27.2 to 62.9% when the thickness increases from 100 to 1000 nm, whereas it improves by only 1% with further increments to 2000 nm. Considering the device’s generation rate, QE measurements, and manufacturing cost, 1000 nm is the optimum thickness.

Figure 2.

Changes in (a) V_oc, J_sc, (b) FF, PCE, (c) generation rate, and (d) QE as a function of absorber thickness. Changes in (e) V_oc, J_sc (f) FF, PCE, and (g) Mott–Schottky as a function of the absorber carrier concentration. Changes in (h) V_oc, J_sc (i) FF, PCE, and (j) recombination rate as a function of absorber defect density.

Higher carrier concentration can lead to Auger recombination and hinder hole transportation from the absorber to the HTL due to increased recombination rate and impurity scattering in the absorber.⁸⁶ To investigate this, we conducted simulations with carrier concentrations ranging from 10¹² to 10¹⁷ cm^–3, as shown in Figure 2e,f. It can be noted that J_sc decreases with increasing carrier concentration, which can be attributed to the reduction in the diffusion length of minority carriers and the depletion width.⁶ Conversely, V_oc and FF remain relatively stable from 10¹² to 10¹⁴ cm^–3 and increase beyond 10¹⁴ cm^–3. The increase in V_oc originates from the elevating built-in potential (V_bi) at the interfaces for higher carrier concentrations, which is evident in Figure 2g, where V_bi increases from 0.80 to 1.68 V when the carrier concentration is varied from 10¹² to 10¹⁷ cm^–3. This subsequently improves the separation and collection of charge carriers at the respective contacts without recombination. However, the increase in FF is linked to the reduction in series resistance in the absorber layer.⁸⁷ Overall, when the carrier concentration is increased from 10¹² to 10¹⁷ cm^–3, PCE is enhanced from 22.85 to 24.27% due to the increase in V_oc and FF, while the decrease in J_sc does not affect the device performance. However, Meng et al. reported that only a weakly p-type BaZrS₃ film is possible under stoichiometric (S-rich/Zr-poor) conditions. Based on this understanding, we performed further simulations by selecting a carrier concentration of 10¹⁵ cm^–3 instead of 10¹⁷ cm^–3, even though the latter achieved a higher efficiency.³⁷

Defects play a significant role in regulating interfacial recombination, carrier lifetime, and material doping levels. They can arise from uncoordinated atoms, nonstoichiometry, etc., and are predominantly found at the interface, surface, or grain boundaries. Bulk defects, such as interstitial and vacancy defects, and Schottky and Frenkel defects, also adversely affect the absorber’s properties.³⁷ Therefore, the influence of defect density is studied and reported in Figure 2h,i. As the defect density increases, a decrease in all of the PV parameters is observed. This can be attributed to the increased recombination rate (Figure 2g) at higher defect densities.⁸⁸ Thus, a defect density of 10¹² cm^–3 is selected as an optimum value for the BaZrS₃ absorber. Generally, BaZrS₃ synthesized under S-rich/Zr-poor conditions is identified to be defect-tolerant owing to its high formation energy, which surpasses deep-level defects, revealing the possibility of achieving lower defect density experimentally.³⁸

3.2.2. Impact of HTL Thickness, Carrier Concentration, and Defect Density

The thickness of the HTL is varied from 10 to 100 nm (Figure 3a,b), where a slight decrease in V_oc from 1.13 to 1.06 V is observed, indicating a surging probability of recombination with HTL thickness.⁸² In contrast, J_sc improves from 22.01 to 27.22 mA/cm² with increasing HTL thickness due to the enhanced light absorption in the device.⁸⁹ This can also be witnessed in Figure 3c, where the absorption increases from 54 to 61% when the HTL thickness is extended from 10 to 100 nm. In addition, FF improves marginally from 79.02 to 81.56%, resulting from the enriched charge transportation from the absorber.⁹⁰ As a result, PCE increases from 19.81 to 23.60%, primarily driven by increased J_sc and FF. Generally, the HTL should be thicker than the ETL to ensure an equal number of charge carriers reach the terminals simultaneously, minimizing the likelihood of recombination. Additionally, a thicker HTL creates room for more photons to be absorbed.⁶ Based on these considerations, an optimal thickness of 100 nm is selected for further optimization.

Figure 3.

Changes in (a) V_oc, J_sc, (b) FF, PCE, and (c) QE as a function of HTL thickness. Changes in (d) V_oc, J_sc (e) FF, PCE, and (f) electric field (E) along the HTL region as a function of HTL carrier concentration. Changes in (g) V_oc, J_sc (h) FF, and PCE as a function of HTL defect density.

We varied the carrier concentration from 10¹² to 10²⁰ cm^–3, as displayed in Figure 3d,e. It can be observed that all of the PV parameters exhibit insignificant changes until a concentration of 10¹⁵ cm^–3. This indicates that the carrier concentration of the HTL does not influence the PV parameters when it is lower than that of the absorber. However, when the carrier concentration exceeds 10¹⁵ cm^–3, the variation in J_sc remains insignificant, while V_oc demonstrates an increase from 1.01 to 1.16 V, which together with the improvement in the FF from 77.61 to 82.21%, enhances the PCE from 21.35 to 26.10%. This elevation in PCE is attributed to the upward shift in energy bands that occurs with an increase in the carrier concentration. Consequently, a strong built-in electrical field is formed at the interface, as displayed in Figure 3f. This intense electric field promotes the transportation of holes from BaZrS₃ to the back contact through Cu₂S by raising the charge transport velocity and conductivity⁹¹ while restricting the flow of minority carriers, thereby reducing the carrier recombination rate. Overall, it is evident that the carrier concentration of the HTL must be higher than that of the absorber to achieve high device performance. As a result, a carrier concentration of 10²⁰ cm^–3 is selected for further studies.

Defects create additional nonradiative recombination pathways, converting light into heat instead of electricity. In particular, the recombination centers trap the photogenerated carriers before they can reach the terminals of the device, thus reducing the carrier’s lifetime.⁹² Therefore, it is crucial to minimize defects to enhance the performance of devices. To analyze the influence of defect density, we varied the defect density of the HTL from 10¹² to 10²⁰ cm^–3, as displayed in Figure 3g,h. There was a noticeable reduction in the V_oc, J_sc, FF, and PCE from 1.19 to 0.91 V, 27.22 to 21.40 mA/cm², 81.46 to 76.58%, and 26.46 to 15.02%, respectively. This significant decrease in the PV parameters can be attributed to decreased carrier diffusion length at higher defect densities, resulting in an increased recombination rate at the BaZrS₃/Cu₂S interface.⁹³ Therefore, a HTL defect density of 10¹² cm^–3 is required for highly efficient chalcogenide perovskite devices.

3.3. Influence of Different ETL and HTL

We systematically examined 12 ETLs (Bi₂S₃,^50,51 ZrS₂,^52,53 SnS₂,⁵⁴ In₂S₃,⁵⁵ ZnS,⁵⁵ Zn₂SnO₄,⁵⁶ BaSnO₃,⁵⁷ Al₂O₃,^58,59 WO₃,⁵⁸ TiO₂,⁶⁰ ZnO,⁶⁰ SnO₂⁶⁰) and 13 HTLs (MoS₂,⁶² CuO,⁶³ Cu₂S,⁶⁴ FeS₂,⁶⁵ Sb₂S₃,⁶⁶ SnS,⁶⁷ Cu₃BiS₃,⁶⁸ Cu₂SnS₃,⁶⁹ CuSbS₂,⁷⁰ Cu₂BaSnS₄,⁷¹ CuInGaS₂,⁷² Cu₂ZnSnS₄,⁷³ Cu₂ZnSn_1–xGe_xS₄⁷³) to identify suitable transport layers for emerging BaZrS₃ chalcogenide perovskite devices (Figure 4) and their simulation parameters are given in Table S1. As previously discussed, we initially optimized SnO₂ (ETL), BaZrS₃ (absorber), and Cu₂S (HTL) in our base device by varying the thickness, carrier concentration, and defect density. We altered the ETL and changed the abovementioned parameters in this optimized configuration. Then, while keeping the optimized ETL and absorber, we varied 13 HTLs and optimized their parameters to determine the most suitable device structure. We applied this approach to all of the remaining ETLs and HTLs, resulting in 782 devices (Table S1). Among them, 156 devices demonstrated the highest PCE for each ETL and HTL combination (Table S2). Interestingly, 139 devices showed a PCE > 20%, and 50 devices exhibited a PCE over 25%. Notably, 10 of these devices displayed an impressive PCE above 27%. To be specific, the devices that are represented as SC11, SC24, SC37, SC50, SC63, SC76, SC89, SC102, and SC128 in Table S2 demonstrated efficiencies of 27.34, 27.44, 27.44, 27.35, 27.43, 27.44, 27.35, 27.34, and 27.47%, respectively, and the highest PCE of 28.08% was accomplished for the champion device SC141 with structure ZrS₂/BaZrS₃/SnS. Figure 5 displays the QE of the aforementioned 10 devices with PCE greater than 27% in the wavelength range of 300–900 nm. An average QE > 70% was obtained for all device structures, wherein the highest QE of 76.23% was achieved for the champion SC141, which reveals that the light absorption in this device is considerably increased. The generated charge carriers are efficiently separated and collected at the contacts with less recombination due to the proper band alignment at the ZrS₂/BaZrS₃ and BaZrS₃/SnS interface, leading to its superior device performance.

Figure 5.

QE measurements of 10 devices obtained a PCE of >27%. (a) SC11, (b) SC24, (c) SC37, (d) SC50, (e) SC63, (f) SC76, (g) SC89, (h) SC102, (i) SC128, and (j) SC141.

The critical factor behind the device’s overall performance is the band alignment between the absorber, ETL, and HTL. This alignment guarantees the effective separation and transportation of charge carriers. Conversely, any disparity in energy band positioning could lead to elevated carrier recombination and increased interface resistance. To understand the obtained PCE as a function of their energy band alignment, we selected three devices among 156 devices, demonstrating low (In₂S₃/BaZrS₃/Cu₂SnS₃, 15.96%), intermediate (TiO₂/BaZrS₃/Cu₂BaSnS₄, 21.30%), and high (ZrS₂/BaZrS₃/SnS, 28.08%) PCEs, and their corresponding energy band diagrams were extracted from SCAPS-1D (Figure 6b–d) to perform a comparative analysis. It can be seen in Figure 6b that a spike-like barrier is observed at the BaZrS₃/In₂S₃ and In₂S₃/FTO interface, respectively. This leads to the accumulation of electrons at both interfaces, which impedes flow to the front contact, resulting in high interface recombination.⁹⁴ Considering the Cu₂SnS₃/BaZrS₃ interface, a VBO of 0.2 eV indicates a smaller barrier for holes. However, a cliff at the CBO reveals that most holes will be collected in the HTL instead of blocking the electrons, leading to high recombination at the interface.⁹⁵ A similar kind of alignment is observed for TiO₂/BaZrS₃/Cu₂BaSnS₄ (Figure 6c) with a difference that the CBO is comparatively low at the TiO₂/BaZrS₃ interface, reducing the accumulation of electrons and leading to improved PCE. Interestingly, for ZrS₂/BaZrS₃/SnS devices (Figure 6d), we can see that the cliff-like barrier at ZrS₂/BaZrS₃ is reduced to 0.1 eV. Also, the barrier height at the ZrS₂/FTO interface is minute, which minimizes the electron accumulation in the ETL and facilitates the transportation of electrons to the front contact. In addition, CBO at the BaZrS₃/SnS interface is high (0.3 eV), which blocks the flow of electrons to SnS, preventing the recombination at the interface. However, we can see that VBO at the BaZrS₃/SnS interface is 0.6 eV, which is comparatively larger than the VBO of Cu₂SnS₃ (0.2 eV) and Cu₂BaSnS₄ (0.1 eV)-based devices used for the comparison. Nevertheless, SnS portrays degenerate behavior, i.e., the quasi-hole Fermi level is within the valence band. This implies that the conductivity is substantial at the BaZrS₃/SnS interface, which enhances the flow of holes from the absorber to HTL, irrespective of the large barrier.⁹⁶ Consequently, it enhances the collection of holes at the back contact. Thus, the high conductivity of SnS, in combination with less barrier for electrons at the ETL/absorber interface and high barrier for electrons at the HTL/absorber interface, resulted in the highest PCE of the ZrS₂/BaZrS₃/SnS device. Hence, achieving a suitable alignment enhances charge separation and transport, reduces recombination losses, and boosts device efficiency, which underscores the importance of understanding band alignment to craft high-performance devices.

Figure 6.

(a) Histogram of PCE for 156 devices detailed in Table S2. Energy band diagram for device structures, (b) In₂S₃/BaZrS₃/Cu₂SnS₃, (c) TiO₂/BaZrS₃/Cu₂BaSnS₄, and (d) ZrS₂/BaZrS₃/SnS.

3.4. Influence of Different Metal Contacts

To study the influence of metal contacts on the high-performing device ZrS₂/BaZrS₃/SnS (PCE 28.08%), we varied different metal contacts, namely, Cu/Mo, Ag, Fe, Cu-doped C, Au, W, Ni, Pd, and Pt with work functions of 4.6, 4.7, 4.8, 5.0, 5.1, 5.2, 5.5, 5.6, and 5.7 eV, respectively. As displayed in Figure 7a,b, when the work function is low (4.6), the Fermi level of the metal contact approaches the conduction band of the HTL, leading to a significant barrier for hole transfer from the HTL to the metal contact. In addition, due to a low barrier (1.1 eV) for electrons, there is easy transfer between the conduction band of the HTL and the metal contact, leading to increased recombination in devices. Interestingly, a higher metal work function induces an inverse bending of the energy bands, facilitating the transfer of photogenerated holes to the metal contacts while creating a Schottky barrier (2.2 eV) for electron transfer.⁹⁷ This behavior is observed in Pt contacts, where the metal’s Fermi level moves toward the valence band of the HTL, resulting in effortless hole transportation and improved device performance. However, the PCE of devices with Ni, Pd, and Pt metal contacts remains constant (Table 2). This phenomenon is attributed to the saturation of the V_bi when the metal work function increased beyond 5.2 eV, primarily caused by increased ohmic resistance at the HTL/metal contact interface.¹⁰⁰ Consequently, we achieved the highest PCE of 28.17% with the ZrS₂/BaZrS₃/SnS/Pt device structure.

Figure 7.

Influence of (a) lowest and (b) highest metal work functions in the device performance.

3.5. Investigating the Influence of Ti Alloying in the BaZrS₃ Absorber

Alloying is a widely employed technique to attain the desired optoelectronic properties that enhance the device’s overall performance. Thus, alloying BaZrS₃ with a suitable metal can further enhance its optical properties. Notably, the band gap of BaZrS₃ (1.7 eV) is slightly larger than the optimal band gap for single-junction devices, as governed by the Shockley–Quiesser limit.^38,98 To reduce BaZrS₃’s band gap through alloying, Ti and Se are ideal choices due to their favorable energy states, atomic size, and electronegativity. In a first-principles study, Meng et al. demonstrated that Ti alloying lowers the conduction band edge, making Ti suitable for facilitating the n-type character in BaZrS₃, while Se alloying raises the valence band edge, making it ideal for lowering the band gap and enabling p-type doping by shallowing the acceptors.³⁸ However, Se alloying exhibits a bowling effect, familiar in anion alloying, and requires approximately 1 atom % of Se to achieve the same band gap reduction, which is significantly higher than the 0.1 atom % estimated for Ti.³⁸ Considering these factors, we focused on Ti alloying for our study. The alloying process was performed on the best device structure, incorporating ZrS₂ as the ETL, SnS as the HTL, and Ba(Zr_(1–x)Ti_x)S₃ as an absorber with x values ranging from 0.01 to 0.04. This small concentration of alloying effectively reduced the band gap from 1.71 to 1.51 eV and resulted in a performance boost.⁷⁴ Therefore, we investigated the influence of alloying with four different concentrations: Ba(Zr_0.99,Ti_0.01)S₃ (Device T1), Ba(Zr_0.98,Ti_0.02)S₃ (Device T2), Ba(Zr_0.97,Ti_0.03)S₃ (Device T3), and Ba(Zr_0.96,Ti_0.04)S₃ (Device T4) on the PCE as shown in the following subsections.

3.5.1. Impact of Ti Alloying in Absorbers Thickness, Carrier Concentration, and Defect Density

The thickness of the absorber is varied from 100 to 1000 nm to study its influence on the PV parameters for devices T1, T2, T3, and T4 (Figure S2). A modest increase in V_oc is noticed due to improved quasi-Fermi-level splitting, while a significant increase in J_sc values results from increased absorption.⁹⁹ Conversely, a subtle reduction in FF is linked to increased internal resistance associated with thickness. Notably, the PCE demonstrates an initial increase with thickness up to 700 nm, followed by a marginal decline. This dip aligns with increased recombination rates at higher thicknesses due to the extended travel path for photogenerated charge carriers.⁹³ Interestingly, for absorber thickness ranging from 100 to 700 nm, devices TI, T2, T3, and T4 exhibit escalated PCEs from 26.64 to 30.20%, 27.20 to 31.43%, 27.53 to 32.09%, and 27.59 to 32.57%, respectively. This trend is further confirmed by QE measurements (Figure 8a–d). The QE drops for devices with less thickness, while a consistent spectral response occurs from 348 to 763 nm, 358 to 790 nm, 355 to 808 nm, and 350 to 840 nm, accompanied by an absorption increase of 79.02, 82.14, 83.85, and 85.24% for devices T1, T2, T3, and T4, respectively. Notably, a reduced band gap expands the absorption range into the NIR range (750–840 nm), fostering increased absorption and boosting performance.

Figure 8.

Changes in the QE % for devices (a) T1, (b) T2, (c) T3, and (d) T4 as a function of absorber thickness.

Analyzing the impact of carrier concentration (10¹² to 10²⁰ cm^–3) on devices T1, T2, T3, and T4 (Figure S3) unveils a clear trend. It can be observed that J_sc and PCE remain stable until 10¹⁴ cm^–3, beyond which a slight decrease occurs. The root cause of this behavior is the escalated recombination rate observed at higher carrier concentrations (Figure 9a–d). Within 10¹² to 10¹⁴ cm^–3, recombination in the HTL region remains the same, attributing to the unaltered device performance. However, beyond 10¹⁴ cm^–3, recombination in the HTL region increases significantly, resulting in a rapid decrease in J_sc and PCE. While a slight increase in V_oc and FF with higher carrier concentration may occur due to elevated electric fields at the interfaces, this can also intensify the possibility of recombination.⁸⁷ Thus, increasing the carrier concentration of the absorber beyond an optimum value led to a dramatic increase in HTL recombination, adversely affecting the device performance. Therefore, an optimal carrier concentration of 10¹⁴ cm^–3 is chosen for further simulations.

Figure 9.

Changes in the recombination rate at the HTL/absorber region in (a) T1, (b) T2, (c) T3, and (d) T4 as a function of the absorber carrier concentration.

Likewise, the influence of defect density for the devices T1, T2, T3, and T4 is analyzed by varying it from 10¹² to 10²⁰ cm^–3. A steep increase in the V_oc is observed for unknown reasons, while J_sc, FF, and PCE decrease (Figure S4) with defect density. This is attributed to higher defects acting as traps for photogenerated charge carriers, hindering their separation as they have lower diffusion lengths and carrier lifetime.⁹³ As a result, a high PCE is observed at 10¹² cm^–3, chosen as the optimal defect density for further studies.

3.5.2. Output Performance of BaZrS₃ and Ba(Zr_0.96,Ti_0.04)S₃ Devices

The J–V characteristics of devices utilizing BaZrS₃ and Ba(Zr_0.96,Ti_0.04)S₃ (T4) are shown in Figure 10a. Strikingly, the Ba(Zr,Ti)S₃ absorber yields a higher PCE of 32.58% compared to that of BaZrS₃ (PCE of 28.17%). This enhancement is primarily attributed to the improved J_sc arising from more light absorption as it has a lower band gap of 1.51 eV in Ba(Zr,Ti)S₃ than 1.7 eV in BaZrS₃. Additionally, optimal band alignment contributes to reduced recombination at the interface. Moreover, the low band gap of Ba(Zr,Ti)S₃ enables it to absorb a large fraction of solar spectrum incident upon it, resulting in a high PCE.

Figure 10.

Changes in the (a) J–V curve and (b) QE measurements as a function of band gap in BaZrS₃ and Ba(Zr,Ti)S₃ devices.

The obtained QE plots for BaZrS₃ and Ba(Zr,Ti)S₃ are displayed in Figure 10b. It can be noticed that the absorption edge is at 729 nm for BaZrS₃ and 858 nm for Ba(Zr,Ti)S₃. This is due to alloying, which shifts the absorption to the NIR region as it has a lower band gap. This increased absorption from 76 to 85% in the NIR region contributes to the enhancement in the PCE in association with an increase in J_sc, significantly impacting the device performance.

Furthermore, the improvement in PCE can be justified by calculating the lattice mismatch. In general, the lattice mismatch between layers and surface roughness causes interfacial defects, which act as recombination centers and negatively impact the performance of the devices. Additionally, it affects the symmetry at the ETL/absorber and absorber/HTL interfaces, causing dislocations, point defects, and lattice inhomogeneities.⁴⁶ Therefore, we assessed the lattice mismatch (δ) between the transport layers and the absorber for device structures that achieved the best PCE of 32.58% (FTO/ZrS₂/Ba(Zr_0.96,Ti_0.04)S₃/SnS/Pt) and 28.17% (FTO/ZrS₂/BaZrS₃/SnS/Pt) using the formula

4

Here, “a_s” represents the lattice constant of the substrate, while “a_e” stands for the lattice constant of the epitaxial layer.⁹³

Table 3 displays the lattice constants^46,100,101 and compares the δ values for BaZrS₃ and Ba(Zr_0.96Ti_0.04)S₃ absorbers concerning the ETL and HTL layers. The ZrS₂/BaZrS₃ and BaZrS₃/SnS interface exhibits δ values of 19.17 and 55.09%, respectively. On the other hand, slightly lesser δ values of 19.08 and 45.60% are observed for the ZrS₂/Ba(Zr_0.96, Ti_0.04)S₃ and Ba(Zr_0.96, Ti_0.04)S₃/SnS interface, respectively. It is evident that the reduction in mismatch is closely linked to the concentration of Ti alloying at the Zr site.⁴⁶ This reduces the carrier recombination rate and minimizes the occurrence of dislocation or defects at the Ba(Zr_0.96Ti0.04)S₃ interface, leading to enhanced performance.

Table 3. Lattice Mismatch of BaZrS₃ and Ba(Zr_0.96Ti_0.04)S₃ with ETL and HTL.

	lattice parameters (Å)			lattice mismatch (%)
layers	a	b	c	ETL/absorber	absorber/HTL
BaZrS3	7.06	9.98	7.02	19.17	55.09
Ba(Zr0.96Ti0.04)S3	7.05	9.90	7.02	19.08	45.60
ZrS2 (ETL)	3.65		5.80
SnS (HTL)	3.64	11.21	3.99

3.6. Influence of R_s, R_sh, and Working Temperature

Parasitic resistances, such as R_S and R_Sh, play a significant role in the PV performance of the device. These resistances dictate the characteristics of J–V curves and reflect the considerable loss mechanisms within the device. In general, devices should exhibit low R_S and high R_Sh values. However, in practical applications, R_S depends on the contacts between charge transfer layers (ETL and HTL) and the metal contact layer, which affects charge transfer. Likewise, R_Sh may be reduced due to factors like morphologies or unavoidable leakage currents.⁴⁶ Hence, this section explores the influence of varying R_S and R_Sh of the final device T4 (FTO/ZrS₂/Ba(Zr_0.96,Ti0_.04)S₃/SnS/Pt).

Initially, the R_S of the device is varied from 1 to 10 Ω cm², as displayed in Figure 11a,b. It can be noticed that V_oc and J_sc remain unaltered across the entire range. However, a decrease in FF is evident, dropping from 84.94 to 70.52%, with an increase in R_S attributed to the substantial power loss within the device. Since power loss is directly proportional to R_S, increasing R_S leads to higher power loss, impacting FF. Consequently, the PCE of the device reduced from 32.58 to 27.05%. This underscores the importance of maintaining a low R_S of 1 Ω cm² for efficient device functioning. Thereafter, we varied the R_Sh from 10 to 10⁷ Ω cm² to study its influence on the performance of the devices (Figure 11c,d). The findings reveal a slight increase in V_oc up to 10³ Ω cm²; after that, it remains unchanged. Likewise, J_sc remains constant. On the other hand, when the R_Sh is increased from 10 to 10⁷ Ω cm², an increase in FF and PCE from 25 to 84.94% and 2.60 to 32.58% is observed. Therefore, with higher values of R_Sh, the device shows improved performance.^37,46

Figure 11.

Changes in the PV parameters as a function of (a, b) R_S, (c, d) R_Sh, and (e, f) working temperature.

The impact of temperature has been investigated by varying it from 300 to 400 K. Figure 11e,f illustrates the changes in the PV parameters as a function of temperature. The J_sc and V_oc remain unaltered throughout the entire range, whereas the FF and PCE experience a slight decrease from 84.94 to 82.95% and 32.58 to 31.79%, respectively. This can be attributed to the increased R_S and charge carrier recombination within the layers at elevated temperatures. Yet, it is noteworthy that the PCE dropped by just 0.8%, underscoring the stability of Ba(Zr,Ti)S₃ compared with lead halide perovskites. Therefore, these findings highlight the potential of Ba(Zr,Ti)S₃ as a stable PV device.^37,47

4. Comparison of SCAPS-1D Results with BaZrS₃ and Ba(Zr,Ti)S₃ Chalcogenide Perovskite Devices in the Literature

Table 4 summarizes theoretical works on chalcogenide perovskite absorbers (BaZrS₃, BaZrSe₃, Ba(Zr,Ti)S₃) using SCAPS-1D. Notably, the highest PCE of 30% emerged from the (a-Si/Ba(Zr_0.95,Ti_0.05)S₃/CdS/i-ZnO/AZO) device. However, its inclusion of CdS has a buffer layer containing the toxic element Cd, which limits its commercialization due to environmental toxicity concerns.¹⁰² Following closely, the (FTO/TiO₂/BaZrSe₃/Spiro-OMeTAD/Au) device achieved the second highest PCE of 25% by employing Spiro-OMeTAD. Although it is a prominently used HTL, its stability and high cost remain a major barrier.⁵² Nevertheless, so far in the literature, only oxide ETLs have been studied for BaZrS₃-based chalcogenide perovskites, which sets the research gap. In recent years, sulfide ETLs emerged as a promising material owing to their exceptional photoelectric properties stemming from the valence electron shell structure within the 3d orbitals. Compared with oxide ETLs, metal sulfides offer many compelling advantages. To begin with, metal sulfides exhibit exceptional electron transport mobility, which serves as a catalyst for efficient charge extraction and transportation, effectively mitigating the risk of charge accumulation and recombination at the ETL/absorber interface. Moreover, they can be synthesized using low-temperature methods, underscoring their energy efficiency and compatibility with flexible substrates. Furthermore, metal sulfides distinguish themselves as wide band gap materials without oxygen vacancies, enhancing the device’s optical stability. Indeed, the substantial binding energy between metal sulfides and absorbers can effectively eliminate the ionic migration within the absorber, offering the pathway to elevate the overall performance and durability of devices.^48,,104

Table 4. Summary of BaZrS₃ and Ba(Zr,Ti)S₃ Chalcogenide Perovskite Devices Reported in the Literature.

device structure	VOC (V)	JSC (mA/cm2)	FF (%)	PCE (%)	ref
FTO/TiO2/BaZrS3/Spiro-OMeTAD/Au	1.21	16.54	86.26	17.29	(88)
FTO/TiO2/BaZrS3/Cu2O/Au	1.16	12.24	87.13	12.42	(46)
FTO/TiO2/BaZrS3/CuSbS2/W	1.00	22.57	73.7	17.13	(105)
FTO/TiO2/BaZrS3/Spiro-OMeTAD/Au	0.70	22.00	79.40	12.12	(106)
AZO/i-ZnO/CdS/BaZrS3/a-Si	1.31	19.08	78.88	19.72	(37)
FTO/TiO2/BaZrSe3/Spiro-OMeTAD/Au	0.72	46.65	77.32	25.84	(106)
FTO/TiO2/Ba(Zr0.87,Ti0.12)S3/Cu2O/back contact	1.09	26.57	85.78	24.86	(107)
AZO/i-ZnO/CdS/Ba(Zr0.95,Ti0.05)S3/a-Si	1.26	27.06	88.47	30.06	(37)
FTO/ZrS2/BaZrS3/SnS/Pt	1.18	29.74	80.15	28.17	this work
FTO/ZrS2/Ba(Zr0.96,Ti0.04)S3/SnS/Pt	1.18	32.26	84.94	32.58	this work

To date, various sulfide ETLs such as MoS₂, WS₂, TiS₂, TaS₂, SnS₂, SnS, In₂S₃, Bi₂S₃, ZnS, and Sb₂S₃ have been investigated for lead halide perovskites, revealing their dominant characteristics over oxides.¹⁰⁴ Hence, it is interesting to investigate the suitability of new sulfide ETLs. In this concern, we have meticulously selected ZrS₂ ETL and examined its applicability for emerging BaZrS₃ chalcogenide perovskite devices, which creates opportunities for experimental scientists to explore the effectiveness of novel ZrS₂ ETLs in practice. Hence, we have performed comprehensive device engineering and accomplished PCEs of 32.58% (FTO/ZrS₂/Ba(Zr_0.96,Ti_0.04)S₃/SnS/Pt) and 28.17% (FTO/ZrS₂/BaZrS₃/SnS/Pt) which is the highest among the reported works. Thus, we firmly believe that our work will ignite the interest in the scientific community and provide a roadmap for experimentalists to fabricate highly efficient BaZrS₃ and Ba(Zr,Ti)S₃ chalcogenide perovskite devices.

4.1. Experimental Suggestions to Improve the Device Performance in Practice Based on Simulation Outcomes

Our study employed SCAPS-1D theoretical simulation to identify the most suitable device configuration for the new BaZrS₃ device. We propose the most effective device configurations of ZrS₂/BaZrS₃/SnS and ZrS₂/Ba(Zr,Ti)S₃/SnS, which offer impressive PCE of 28.17 and 32.58%, respectively. The optimization of essential parameters such as thickness, carrier concentration, and defect density of the ETL, absorber, and HTL are the key factors that led to high PCE values. However, it is essential to note that practical guidance for the successful fabrication of the devices is still necessary. In view of this, we have outlined various strategies to optimize the key parameters experimentally.

To start with, we found that ZrS₂, a transition-metal dichalcogenide semiconductor (TMDS), performs best when its influential parameters, such as carrier concentration (10¹⁹ cm^–3) and defect density (10¹⁶ cm^–3), are within the optimal range. Substitutional and chemical doping can increase the carrier concentration. External dopants like transition metals and halogens can replace metal or chalcogen sites in substitutional doping to boost the carrier concentration. Chemical doping, on the other hand, involves the adsorption of dopants onto the semiconductor surface without altering its structure. This process stimulates the surface charge transfer between the dopants and TMDS, improving carrier concentration and charge transfer properties. It is noteworthy that annealing with continuous electron beam irradiation has been explored as an alternative technique to improve the carrier concentration.⁵² ZrS₂ is generally prone to sulfur defects, which can be rectified by a sulfur vapor annealing process to minimize defects and improve crystallinity.¹⁰⁸

As stated in Section 3.2, the BaZrS₃ absorber showed its best performance at an optimum thickness of 1000 nm. This can be achieved using various techniques such as vapor deposition, sputtering, and electrodeposition, which allow for better control over factors like film thickness, composition, purity, and uniformity by changing deposition conditions such as time, temperature, pressure, and potential.¹⁰⁹ The film thickness can be increased by repeating the deposition time and annealing steps. Furthermore, Meng et al. reported that BaZrS₃ and Ba(Zr,Ti)S₃ films synthesized under S-rich/Zr-poor conditions exhibit strong p-type behavior with an optimum carrier concentration of 10¹⁵ cm^–3 and surpass the deep-level defects due to their high formation energy that results in lower defect density. However, films synthesized under S-poor/Zr-rich conditions possess n-type behavior with a high carrier concentration of >10¹⁷ cm^–3, making them unsuitable for the absorber. Thus, it is necessary to adjust the elemental composition while synthesizing BaZrS₃ and Ba(Zr,Ti)S₃ films to obtain an optimum carrier concentration and reduce the formation of deep-level defects.³⁸

Interestingly, the highest PCEs of 28.17 and 32.58% were achieved with SnS as the HTL, indicating its suitability and appropriate band alignment with the absorber. However, the formation of impurity phases such as Sn₂S₃ and SnS₂ in SnS remains a significant drawback. To overcome this, Steinmann et al. reported that annealing SnS for 1 h under vacuum conditions (15 m Torr) at 500 °C or in an Ar or H₂ gas atmosphere at ambient temperature prevents the formation of impurity phases.¹¹⁰ Moreover, introducing Sn excess composition (Sn_1.05S) during the synthesis process significantly reduces the formation of Sn₂S₃ without additional thermal processing.¹¹¹ In summary, the methods and strategies proposed have the potential to significantly benefit the PV community by enabling them to fabricate highly efficient BaZrS₃-based devices as technology advances.

5. Conclusions

In this work, we have comprehensively shed light on the device engineering of BaZrS₃ solar cells using SCAPS-1D numerical simulation. Initially, we optimized each layer (FTO/SnO₂/BaZrS₃/Cu₂S/Au) of the base device structure by varying its thickness, carrier concentration, and defect density. Thereafter, we altered the ETL and optimized it by keeping other layers constant. In the next step, by keeping the optimized conditions of ETL and absorber, we varied 13 HTLs and optimized it. This stepwise process was adopted to find the suitable device structure for the BaZrS₃ absorber. We modeled 782 devices by this approach, and 156 devices showed the best PCE for each ETL and HTL combination. Interestingly, the FTO/ZrS₂/BaZrS₃/SnS/Pt device demonstrated the highest PCE of 28.08%. This rotational selection of ETLs and HTLs resulted in the efficient collection of electrons and holes and gave desirable band offset, restricting the interfacial recombination and ideal band alignment, resulting in enhanced performance. Furthermore, the PCE of the device was enhanced to 28.17% after optimizing the metal contacts. In addition, the performance of BaZrS₃ was further improved by Ti alloying with 4 atom % and achieved a maximum theoretical PCE of 32.58% due to its extended absorption to the NIR region and less lattice mismatch compared with BaZrS₃. Our study provides a guiding rule for understanding the material properties and selecting cost-effective and efficient pin structures.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c06627.

• Changes in the PV parameters as a function of ETL thickness, carrier concentration, and defect density; changes in the PV parameters for devices TI, T2, T3, and T4 as a function of absorber thickness, carrier concentration, and defect density; simulation parameters for 12 ETLs and 13 HTLs; simulation parameters for devices TI, T2, T3, and T4; and device engineering of 782 chalcogenide perovskite devices (PDF)

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

The authors declare no competing financial interest.