Exploring protein–ligand binding affinity prediction with electron density-based geometric deep learning

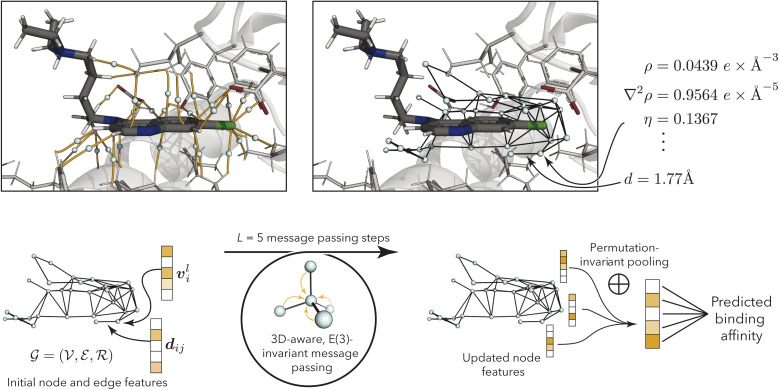
Abstract

Rational structure-based drug design relies on accurate predictions of protein–ligand binding affinity from structural molecular information. Although deep learning-based methods for predicting binding affinity have shown promise in computational drug design, certain approaches have faced criticism for their potential to inadequately capture the fundamental physical interactions between ligands and their macromolecular targets or for being susceptible to dataset biases. Herein, we propose to include bond-critical points based on the electron density of a protein–ligand complex as a fundamental physical representation of protein–ligand interactions. Employing a geometric deep learning model, we explore the usefulness of these bond-critical points to predict absolute binding affinities of protein–ligand complexes, benchmark model performance against existing methods, and provide a critical analysis of this new approach. The models achieved root-mean-squared errors of 1.4–1.8 log units on the PDBbind dataset, and 1.0–1.7 log units on the PDE10A dataset, not indicating significant advantages over benchmark methods, and thus rendering the utility of electron density for deep learning models context-dependent. The relationship between intermolecular electron density and corresponding binding affinity was analyzed, and Pearson correlation coefficients r > 0.7 were obtained for several macromolecular targets.

A deep learning approach centered on electron density is suggested for predicting the binding affility between proteins and ligands. The approach is thoroughly assessed using various pertinent benchmarks.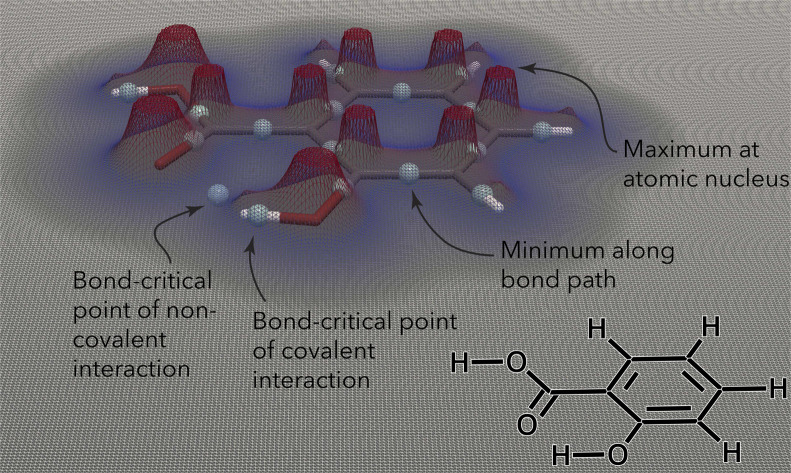

Introduction

A key requirement for most drug candidates is a high binding affinity of the investigated ligand to its desired biological target.¹ However, the experimental determination of binding affinity can be time- and resource-intensive, often requiring synthesis of the ligand and a suitable experimental assay. Aiming to limit the number of laboratory experiments and enable more rapid ligand design, several computational approaches have been developed for in silico binding affinity prediction.² Structure-based deep learning has received particular attention for this specific task,^3–5 as well as for binding site identification,^6,7 molecular docking,^8,9 and de novo molecular design.¹⁰

Although different deep learning-based techniques for predicting binding affinity have achieved success in computational drug design studies,^11,12 certain deep learning models have been criticized for specific challenges regarding their generalization abilities and their potential to adequately capture the fundamental physical principles governing intermolecular interactions.^2,13–15 Much simpler methods such as nearest-neighbor analysis or prediction of random values have been shown to achieve a similar predictive performance.¹⁶ Furthermore, existing datasets such as PDBbind^17,18 commonly used for model development have been criticized as biased because similar prediction accuracies were achieved irrespective of whether the whole protein–ligand complex, only the protein, or only the ligand was considered.^2,19,20 This potential bias in dataset composition makes it challenging to meaningfully assess and compare model performance.^2,16,19,20 As a potential remedy to the challenge of learning underlying dataset biases rather than meaningfully capturing physical interactions, Rognan and coworkers suggested to consider “only noncovalent interactions while omitting their protein and ligand atomic environments”.²

In addition to geometric deep learning approaches,^5,23–26 also simulation-based approaches (e.g., free energy perturbation,^27,28 MM/PBSA^29–31) are frequently used for binding affinity prediction. While simulation-based methods are, by design, rooted in physical principles, deep-learning methods often incur lower computational cost for predictions and can leverage pre-existing data. Herein, we combine a commonly used simulation technique, the Quantum Theory of Atoms in Molecules (QTAIM),³² with geometric deep learning neural networks.

The QTAIM analyzes the topology of the electron density surrounding a molecular geometry.³² The electron density is highest at the nuclei, decreases as one moves away from a nucleus, and eventually increases again as another nucleus is approached (Fig. 1). The QTAIM partitions the electron density in three-dimensional (3D) space into atomic basins, the boundaries between which are surfaces of zero flux of the gradient vector of the electron density. A bond path is formed between two interacting nuclei, following the line along which the electron density is maximal relative to its local surroundings. The point along this line with the lowest electron density (i.e., the point at which the bond path crosses the zero-flux interatomic surface) is termed a “bond-critical point” (BCP).^32,34 A range of quantum-mechanical (QM) properties (Table 1) can be evaluated at BCPs and have been connected to physically observable quantities.^{32,34,41–43}

Fig. 1. Contour plot of the electron density (at z = 0, in plane with the phenyl ring) surrounding the salicylic acid molecule. The electron density reveals local maxima at the atomic nuclei and decreases as one moves away from the nuclei. The point with the lowest electron density along a bond path (either covalent or noncovalent) is termed a “bond-critical point”. Figure inspired by ref. 21 and created using ParaView.²².

Quantum-mechanical properties at bond-critical points (BCPs) and their chemical interpretation.

Property	Formula	Interpretation	Ref.
Electron density	ρ	Bond order/strength of interaction	33 and 34
Laplacian	∇2ρ	Covalent character of interaction	34
Electron localization function	ELF	Degree of electron localization	35 and 36
Localized orbital locator	t σ	Degree of electron localization	37
Reduced density gradient	RDG	Homogeneity of electron density & type of interactions	38
sign (λ2)ρ	sign (λ2)ρ	Strength & type of interactionsa	38
Gradient norm	|∇ρ|	Magnitude of the gradient	39
Bond ellipticity	ε	Cylindrical symmetry and π-character of interaction	34
ETA index	η	Type of interaction	40

^a λ ₂ denotes the second-largest eigenvalue of the electron density's Hessian matrix.

Herein, we investigate the hypothesis that an electron density-based, interaction-centric view of protein–ligand complexes may be exploited with geometric deep learning to predict binding affinities. Our objective is to evaluate whether this approach offers advantages in comparison to established methods for predicting binding affinity. Choosing a molecular representation directly rooted in the electron density is motivated by the following three considerations: First, the electron density surrounding a molecule is uniquely mapped to all observable properties of that molecule.²¹ Second, the electron density is a fundamental description of physical and chemical phenomena.³² By providing deep learning models with a molecular description that is more closely connected to the observed phenomenon itself than commonly used model concepts (such as atomic nuclei as points in space), we hypothesized that the experimentally measured binding affinity might potentially be more accurately predicted. Third, the electron density and other derived properties at intermolecular BCPs were successfully employed in previous quantitative structure–activity relationship (QSAR) studies.^{32,34,41–48}While the idea of combining QM with machine learning (ML) is not new (e.g., ML to predict QM-calculated properties,^49–54 or QM-calculated features being used as ML inputs,^55–59) this work represents, to the best or our knowledge, the first combination of BCPs with 3D-aware neural networks. Previous studies on BCP-based QSAR models mainly relied on aggregated information or scalar descriptors of structural information.^{41–43,60,61} For example, a recent study showcased a strong correlation (r = 0.891) between the sum of the electron density at BCPs and experimental protein–ligand binding affinity for 34 D2-dopamine receptor inhibitors.⁴³ The authors argued that this relationship depends on e.g., the number of rotatable bonds in the series of ligands, as a low number of rotatable bonds may indicate that entropic effects (which cannot be captured by the static picture of a QTAIM analysis) can be neglected or are very similar across the set of ligands.⁴³

This current study offers two key contributions: First, we investigated whether specific quantum mechanical (QM) properties and their spatial distribution can be utilized to predict binding affinity. We employed 3D message-passing neural networks (MPNNs) for this analysis. An automated Python-based pipeline was created to prepare protein structures, perform QM calculations, and conduct electron density analysis for this research. We conducted a comprehensive evaluation of the suggested method and discovered that, for two extensive data sets, the selected representation did not appear to offer any discernible advantages over established methods in the specific cases we examined. Our intention in sharing these findings is to offer valuable insights for future research directions that concentrate on the utilization of electron density-based descriptors for predicting protein–ligand binding affinity. Second, we analyzed the correlation between the sum of the electron density at BPCs and the measured binding affinities across two large-scale datasets of protein–ligand binding complexes (i.e., PDBBind^17,18 and PDE10A⁶²).

Data compilation & processing

We performed our analysis using two datasets of protein–ligand complex structures: the commonly used PDBbind (version 2019) dataset^17,18 (as prepared in ref. 2) and a recently released collection of PDE10A inhibitors⁶² originating from a former discovery project at Roche. In addition to consistently measured binding affinities, crystal structures, and expert-curated docking poses, the PDE10A dataset contributes dataset splits inspired by real-world drug discovery programs. These splitting strategies include temporal splits and splits according to binding mode, enabling a thorough investigation of a model's ability to extrapolate to unseen types of interactions.⁶² The PDE10A dataset may help address some of the shortcomings and biases previously identified in using the PDBbind dataset to assess model performance. These shortcomings include similar performance when using ligand-only or protein-only representations and a failure of PDBbind-trained models to meaningfully capture physical interactions.² In keeping with previous work⁶³ and to reduce computational cost, we removed protein residues in which all atoms are farther away than 6 Å from the ligand (see details in Section S1†).

QM & QTAIM calculations

While previous QTAIM studies of biomolecular systems have used density functional theory (DFT) to obtain electron densities for a few dozen structures,^43,66 such an approach is challenging to apply to tens of thousands of protein–ligand complexes, each consisting of hundreds to thousands of atoms. Accordingly, the semiempirical method GFN2-xTB^67–70 (version 6.4.1) was used for QM calculations using Analytical Linearized Poisson–Boltzmann (ALPB) implicit water solvent.^71,72 GFN2-xTB has been successfully used in several biological applications,^63,73 though the considerable speed-up with respect to DFT comes at the expense of lower accuracy.⁷⁴ However, it has been observed that the electron density shows little sensitivity to the electronic structure method being used for computation and that key features are well preserved between different methods.^38,75,76 In a preliminary study, we benchmarked GFN2-xTB against two DFT approaches, ωB97X-D/def2-QZVP^77,78 and B3LYP-D3/6-31G*,^79,80 calculated using Psi4 (ref. 81) (version 1.7). While we observed some discrepancies (Section S2†), the overall acceptable performance and dramatic speedup (5–6 or 3 orders of magnitude, respectively [Table S1†]) of GFN2-xTB versus ωB97X-D/def2-QZVP or B3LYP-D3/6-31G*, respectively, suggested GFN2-xTB as a suitable choice given the need for computational efficiency in such a large-scale investigation.

Following QM calculations, Multiwfn³⁹ (version 3.8(dev), 03/2023) was used to find BCPs and compute their QM properties (Table 1) based on the wavefunction files obtained from the GFN2-xTB calculation. RDKit⁸² (version 2021.09.4) was used for general molecular processing tasks. At the end of this pipeline, 14 181 (out of 14 215) and 1162 (out of 1162) successfully processed graphs were obtained for PDBbind and PDE10A, respectively (Section S1†).

Molecular representation

While we primarily investigated the usefulness of BCP-based, interaction-centric graphs (Fig. 2), we additionally investigated a related graph setup based on nucleus-critical points (NCPs). Although this approach deviates slightly from the recommendation of Rognan and coworkers² to use interaction-centric molecular representations, it appears as a natural alternative to BCP-based graphs for the use of MPNNs in the context of the QTAIM. Both graphs consist of nodes, edges, and node positional information 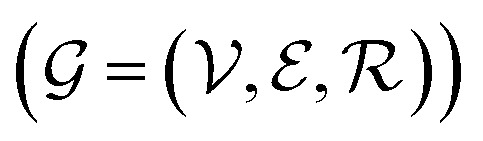and were constructed as follows.

Fig. 2. (Top left) bond-critical points (teal) in the binding pocket (PDB ID: 1CET⁶⁴), connecting protein and ligand atoms via bond-critical paths (orange). Atoms are shows in black (carbon in ligand), gray (carbon in protein), white (hydrogen), blue (nitrogen), red (oxygen), and green (chlorine). The figure was generated using PyMol.⁶⁵ (Top right) Resulting bond-critical point graph with example annotations using quantum-mechanical properties (see Table 1) and node-to-node distances. For clarity, only edges between nodes within 3 Å are shown, while the discussed models use a 6 Å cutoff. (Bottom) model overview, processing node and edge features via geometry-aware E(3)-invariant message-passing to predict protein–ligand binding affinity.

BCP graphs

The nodes in the graph correspond to BCPs, and edges 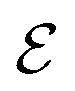were added between any pair of nodes within 6 Å (similar to previous studies^83,84). Initial node features v⁰_i were the QM properties at the respective BCP (see details in Section S3†). Optionally, the identities of atoms connected by the BCP were added. Node-to-node distances d_ij described via a sinusoidal and cosinusoidal encoding (similar to other 3D-tasks^85,86) were used as edge features e_ij.

NCP graphs

Nodes 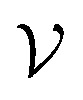were placed at NCPs (atomic nuclei) that participate in interactions between the protein and ligand (as identified by the presence of intermolecular BCPs). Initial node features v⁰_i for NCPs were obtained from their QM properties (Table 1) and (optionally) atomic identities. Intermolecular edges were added between interacting NCPs (one on the protein side and one on the ligand side) and featurized using Fourier-like encoded distances and QM properties of the corresponding BCP. Additional intramolecular edges were introduced between all NCPs of the ligand and featurized using their respective BCPs for covalent bonds (if present). See Section S3† for full details.

Extreme QM values of individual BCPs or NCPs rendered common input normalization strategies unsuitable, prompting the use of a custom scaling method (Section S3†).

Model architecture & training

3D-MPNNs based on the EGNN architecture,^85,91 which had previously shown good performance in several other 3D-based prediction tasks,^55,86 were used to operate on the BCP-/NCP-based graphs. Initial node features were based on QM properties at the BCPs (for BCP-based graphs) or at the NCPs (for NCP-based graphs), respectively, and optionally combined with atom types. QM properties were transformed using multi-layer perceptrons (MLPs). Atom types were embedded using MLPs. For BCP-based graphs with atom types, the atom embeddings of both connected atoms were summed to achieve permutation invariance to the neighbor ordering. The transformed QM properties and atom embeddings were concatenated (in cases where both were present) to obtain initial node features v₀^l. Node features v_i^l in layer l were iteratively updated via the message-passing scheme

m_ij = ϕ_e(v_i^l,v_j^l,e_i^j) 1

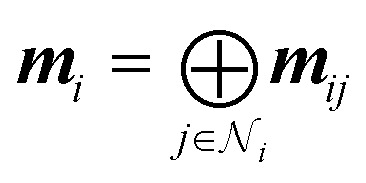2

v_i^l+1 = ϕ_h(v_i^l,m_i) 3

where the non-linear transformations on edge and node features, ϕ_e and ϕ_h, were described with SiLU-activated MLPs.⁹² Edge messages m_ij were obtained from the features of a pair of connected nodes and their (Fourier-encoded) distance e_ij (eqn (1)), achieving E(3)-invariance (to translation, rotation, and inversion of the input). Incoming edges to one node were mean-aggregated (eqn (2)), and the node's features were updated based on the aggregated message m_i and the previous node features v_i^l (eqn (3)). After five message-passing steps, the node features from each step were concatenated and transformed again using a SiLU-activated MLP ϕ_f to obtain final node-level features V_i:

V_i = ϕ_f(concat_l=0^l=5(v_i^l)). 4

The final node-level features V_i were mean-pooled (achieving permutation invariance) as preliminary experiments did not indicate a benefit from using sum or multi-headed attention pooling (not shown). The predicted binding affinity was obtained using another MLP. In line with previous work,⁸⁶ models were trained for 1000 epochs to minimize the mean squared error (MSE) loss using the Adam optimizer⁹³ with an initial learning rate of 10⁻⁴, a learning rate decay factor of 0.7, and a patience of 20 epochs. Combinations of the hyperparameters batch size (∈ {16, 32, 64, 128}), kernel dimension (∈ {16, 32, 64, 128}), and MLP dimension (∈ {128, 256, 512}) were screened, and the configuration with the lowest root mean squared error (RMSE) on the validation set was used for testing. Models were built and trained using PyTorch⁹⁴ (version 1.9.1), and PyTorch Geometric⁹⁵ (version 2.0.3). Code for structure preparation, QM/QTAIM calculations, and model training is available at https://github.com/ETHmodlab/bcpaff (resp. https://doi.org/10.5281/zenodo.8097403).

Benchmarks

One recently published benchmark model was selected for each dataset. For the PDBbind dataset, we used the “merged protein, ligand and interaction graph”,² a 3D-aware MPNN model that has shown strong performance on the PDBbind dataset and has undergone careful evaluation. This model uses pseudoatoms to represent protein–ligand interactions. For the PDE10A dataset, we used the 2D3D hybrid model which has previously performed well on this dataset.⁶² The 2D3D hybrid constitutes an ensemble model combining predictions from the RF-PLP^88,89 (3D, protein–ligand structure-based) and AttentiveFP⁹⁰ (2D, ligand-based) approaches.

Electron density-based models can predict binding affinity but show greater errors than benchmark models

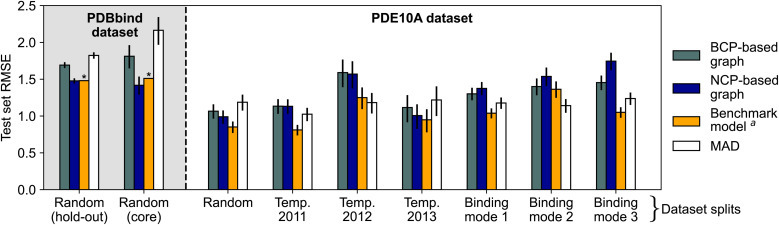
Initial experiments suggested that using all the available QM properties (Table 1) as node features might be beneficial for model performance (see Section S4.4† for statistical analysis). Unless otherwise specified, all discussed models used the entire range of QM properties given in Table 1. Model performance is shown in Fig. 3 (Section S4†). These models were trained using only QM properties without access to atomic identities, providing the desired “interaction-centric view”. These electron density-based models (both BCP-/NCP-based graphs) achieved root-mean-squared errors (RMSEs) of 1.4–1.8 log units on the PDBbind dataset, and 1.0–1.7 log units on the PDE10A dataset, not outperforming the benchmark models. This finding suggests that the proposed electron density-based representation did not improve on existing methods for the prediction of absolute protein–ligand binding affinities. Particularly for the non-random splits of the PDE10A dataset, these deep-learning models even failed to outperform the mean absolute deviation (MAD) baseline model, which predicts the arithmetic mean of the training and validation sets for all compounds in the test set. This apparent failure to outperform the MAD highlights the more challenging extrapolation task in these cases. The errors on the random split of the PDE10A dataset were generally lower than those on the PDBbind dataset (∼1 log unit vs. ∼1.5–1.7 log units), which is potentially due to consistently measured binding affinities and the presence of only a single protein target across the entire dataset. However, also the MAD was lower for the PDE10A dataset than for the PDBbind dataset, indicating a higher bar for non-trivial performance. While the PDBbind-trained BCP/NCP models achieved Pearson correlation coefficients r in the range of 0.45–0.76, the PDE10A-trained models achieved r > 0.5 only for the random and the temporal 2013 (NCP model only) splits, while showing very poor or no correlation to experimental values for other dataset splits (Section S4†). For the BCP models trained on binding mode splits, the predicted values were contained within a small range of values around the mean (Fig. S6†), mirroring previous observations.² While the NCP-based models showed significantly lower test set errors than the BCP-based models for the PDBbind dataset (Section S4.3† for statistical analysis), this trend was less pronounced or even reversed for the individual splits of the PDE10A dataset. Specifically, when considering the splits by binding mode, which necessitate more complex generalization across various interaction types, the incorporation of NCPs resulted in a rise in test set error. This suggests that this approach struggles with poor generalizability in such cases.

Fig. 3. Test set root-mean-squared error (RMSE) of electron density-based deep learning models for PDBbind (shaded background) and PDE10A (white background) with different data splitting strategies. Binding modes 1, 2, and 3 refer to the aminohetaryl-C1-amide, C1-hetaryl-alkyl-C2-hetaryl, and aryl-C1-amide-C2-hetaryl splits, respectively. Models trained using QM properties as initial node features. Error bars show 95% confidence intervals.⁸⁷ Model performance for PDBbind is reported for the 2019 hold-out test set and the 2016 core set (ignoring complexes for which processing failed, see Section S1†). ^a Benchmark models are the “merged protein, ligand and interaction graph²” model for PDBbind and the 2D3D hybrid model (ensemble of RF-PLP^88,89 and AttentiveFP⁹⁰) for PDE10A.⁶² * No 95% confidence interval available for benchmark model.².

In order to more closely assess the predictive performance of the proposed representation, we additionally analyzed BCP/NCP-based models trained on the PDBbind dataset to make predictions for the CASF-2013 (ref. 96 and 97) and CASF-2016 (ref. 98) challenges, respectively. For model training, only structures that were not part of the test sets (CASF-2013 and CASF-2016) were incorporated, in adherence to an established splitting strategy.⁹⁹ (see Section S1.3† for details). With Pearson correlation coefficients of 0.552 and 0.591, and RMSE values of ∼1.9 and ∼1.8 for the CASF-2013 and CASF-2016 benchmark sets respectively, the BCP-based models did not exhibit any advantages in comparison to other benchmark models when considering these metrics (see details in Section S4.1.3†). A somewhat different scenario emerged for the models based on NCP descriptors, as they ranked center-field among the benchmark methods in terms of Pearson correlation coefficients and RMSE (see details in Section S4.1.3†). The finding that the NCP-based models showed higher correlations and lower RMSEs than the BCP-based models is in line with the findings for the test and core sets of PDBbind. This outcome reinforces the notion that, for the PDBbind dataset, details about the atomic characteristics of interacting atoms offer advantages in conjunction with interaction-centric information provided by the BCPs. However, no such pattern was identified for the PDE10A dataset splits, underscoring the possibility of a dataset bias. Overall, no substantial advantages were identified concerning scoring performance when compared to the best benchmark model that was examined (GraphscoreDTA⁹⁹).

Furthermore, we explored the approach of training the PDBbind-based models exclusively on the refined set and then making predictions for the test and core sets. In both BCP- and NCP-based models, there were moderate increases in prediction errors observed on the core set (RMSEs increasing from ∼1.8 to ∼2.1 log units, and from ∼1.4 to ∼1.6 log units, respectively [Section S4.1.2†]), suggesting that the larger amount of training data available in the PDBbind general set had a small positive impact on modeling performance. Similar trends were observed for the test set predictions (see details in Section S4.1.2†).

Based on these results, our initial hypothesis regarding the use of electron density-based graphs for binding affinity prediction via MPNNs was rejected. There are several potential explanations for this outcome, offering insights into why our deep models trained on electron density-based graphs did not provide more accurate binding affinity predictions than benchmark models.

Firstly, the (calculated) electron density was obtained by inputting atomic coordinates into the QM method of choice (i.e., GFN2-xTB). The output, in terms of BCP-/NCP-based graphs annotated with QM properties, was thus mapped 1 : 1 to the initial atomic coordinates. Accordingly, much of the information contained in the BCP-centric view was already implicitly contained in the atomic coordinates, lacking only the information contributed by the data GFN2-xTB was fitted to. Owing to this lack of additional information, a BCP-centric view may not exhibit an advantage over more traditional atom position-based views, and the results of this study do not indicate that this alternative molecular representation renders the prediction task more feasible.

Secondly, although a generally acceptable agreement with more accurate QM calculations was confirmed (Section S2†), the lower accuracy of GFN2-xTB (compared to e.g., DFT) may still contribute to the limited predictive accuracy of the deep-learning models. A similar effect was observed when using electron densities calculated with DFTB+¹⁰⁰ as an alternative semiempirical method (Section S4.2.1† for details). Given the substantial computational cost associated with running higher-accuracy QM calculations for thousands of protein–ligand interactions (Table S1†), one might consider turning towards recently developed ML-based methods that predict the electron density at a fraction of the cost of first-principles methods.^101–109 In addition to the epistemological problem associated with stacking multiple models on top of one another, making existing approaches compatible with commonly used BCP/NCP calculation software^39,110,111 is not straight-forward.

Thirdly, when considering BCP-based representations (without access to ligand coordinates), evaluating the inherent strain in the ligand within a bound conformation may pose greater challenges than with alternative methods. Ligand strain, which refers to the energy penalty associated with a ligand potentially having to deviate from a more stable solution-phase conformation to fit into the binding pocket, can considerably impact the measured binding affinity.^112,113 This hypothesis was tested by visualizing absolute per-structure model errors against ligand strain energies calculated for structures from the PDBbind dataset¹¹³ (Fig. S6 and S7†). Based on the lack of correlation (slope = −0.028 ± 0.010 log units kcal⁻¹ mol and −0.008 ± 0.022 log units kcal⁻¹ mol for the test and core sets, BCP-based models) between ligand strain and model error, we rejected the hypothesis that poorly capturing ligand strain is a key driver behind the unsatisfactory model performance.

Fourthly, “a more precise chemical description of the protein–ligand complex does not generally lead to a more accurate prediction of binding affinity”.¹¹⁴ Potential challenges associated with the use of a more precise description lie in the difficulty of extracting information from such a representation, and in additional modeling assumptions required to produce the representation, such as protonation states and the choice of method for electron density calculation.¹¹⁴

Finally, an inherent limitation of many current deep learning-based binding affinity prediction methods lies in their focus on fixed atom positions (respectively fixed BCP/NCP positions, as in the present study). This view fails to capture the relevance of entropic contributions and the dynamic process of protein–ligand binding.^115–118 It has previously been argued that descriptors that remain relatively constant during the binding event (such as atomic identities) may alleviate the restrictions from this focus on the bound state to an extent.¹¹⁴ Accordingly, the strong dependence of BCP-based graphs on the underlying molecular structure⁴² may contribute to their inability to capture the dynamic binding process. This strong dependence of BCPs on the molecular structure may also amplify the effects of e.g., incorrectly assigned atom positions or protonation states.⁵² Other potentially contributing factors include the free energy of protein–ligand proton transfer or solvation effects.¹¹⁹

Using atom identities instead of quantum-mechanical properties achieves similar performance

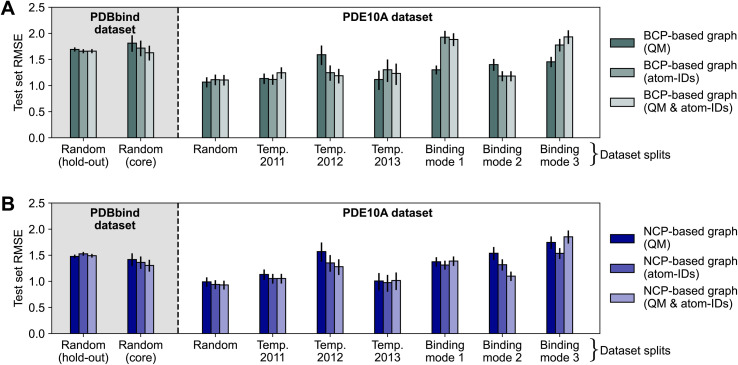
To assess the impact of using atom identities in the initial node features (as is typically done in structure-based deep learning methods for binding affinity prediction^3,4), we compared the test set errors of models trained using only QM properties to those of models trained using only atom types or a combination of both. This approach moves away from a purely interaction-focused view, as it directly includes information about the chemical composition of the protein and ligand, respectively. Fig. 4 shows the effect of varying node features on the performance of deep learning models. The effect of modifying the node features was limited, resulting in mostly overlapping 95% confidence intervals for RMSE estimates. For the “binding mode 1” and “binding mode 3” splits of the PDE10A dataset, the models trained on BCP-based graphs with QM features (Fig. 4A) performed significantly better (Section S4.3† for statistical analysis) than models trained using only atom types or a combination of QM features and atom types, with RMSE values differing by up to 0.6 log units. While one might hypothesize that using atom types instead of QM properties could be detrimental for BCP-based graphs (essentially placing pseudo-atoms at the BCP locations but not using their respective QM properties), this effect was not observed in other dataset splits. Because the binding mode splits require the model to make more challenging extrapolations than a random split, the increasing error when going from QM properties to atom types to a combination of both could be related to the models overfitting to this information. For NCP-based graphs (Fig. 4B), for which an augmentation with atom types appears more natural than for BCP-based graphs (as NCPs correspond to positions of atomic nuclei), minor improvements were observed for individual data splitting strategies (binding modes 2 and 3), though no decisive impact was measured.

Fig. 4. Impact of varying node features on model performance of message-passing deep learning models trained on BCP-based graphs (A) and NCP-based graphs (B), respectively. Results reported as test set root-mean-squared error (RMSE) for the PDBbind (shaded background) and PDE10A (white background) datasets with different data splitting strategies. Error bars show 95% confidence intervals.⁸⁷ Model performance for PDBbind is reported for the 2019 hold-out test set and the 2016 core set.

Intermolecular electron density correlates with binding affinity for some, but not all, protein targets

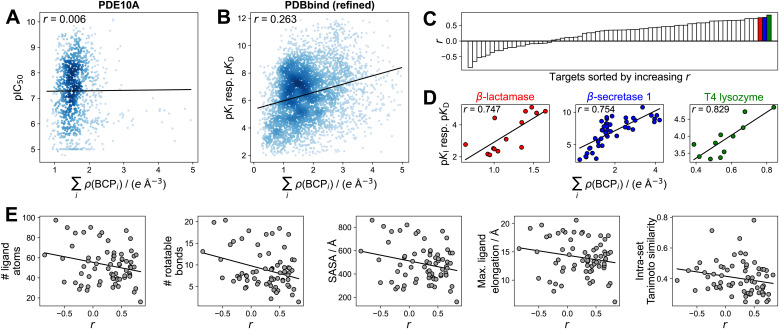
To gain additional insights into the utility of electron density for binding affinity prediction, we turned to a simpler method, foregoing ML techniques. We pursued a previously used approach^43,48 of assessing the correlation between the sum of electron density at intermolecular BCPs on the one hand, and the binding affinity on the other hand (Section S5†). Focusing this analysis on the PDBbind refined set and the PDE10A dataset was motivated by the goal of using high-quality structures and binding affinity measurements and ensuring comparability between individual binding affinity measurements (e.g., not comparing IC50 values to pK_I or pK_D values as present in the PDBbind general set). While a previous study⁴³ used molecular dynamics-refined docking structures, we directly used crystal structures for the PDBbind dataset. We found no correlation (r = 0.006) or extremely limited correlation (r = 0.263) between the sum of electron density at intermolecular BCPs and binding affinity when looking at the PDE10A and PDBbind datasets, respectively (Fig. 5A and B), indicating that no such general trend exists when comparing these large sets of different protein–ligand interactions. This observation may be related to very different entropic contributions to protein–ligand binding across the datasets. When analyzing protein-specific correlations in the PDBbind dataset (Fig. 5C), large differences in correlations were observed for different proteins. In this more detailed view, individual proteins emerged for which good correlations (r > 0.7) were observed (Fig. 5D). The three top-scoring protein targets featured sets of ligands with both a wide range of affinity values (8 log units for β-secretase 1) and with narrow ranges (1.5 log units for T4 lysozyme, 3 log units for β-lactamase). These ranges were also reflected in the respective ranges of electron densities. An additional analysis using a very simple measure, such as the number of ligand atoms instead of the sum of electron density, is shown in Table S15.† For T4 lysozyme, the intermolecular electron density and number of intermolecular BCPs showed a substantially better correlation with binding affinity than the number of ligand atoms, though less pronounced trends were observed for the other protein targets. This result suggests that for these targets, the connection between intermolecular electron density and binding affinity is at least partly driven by ligand size.

Fig. 5. Correlation between the sum of electron density at intermolecular BCPs and binding affinity, expressed as Pearson's correlation coefficient r. (A) PDE10A dataset. (B) PDBbind (refined) dataset. Complexes with ∑_iρ(BCP_i) > 5 e Å⁻³ not shown in (A and B). (C) Protein targets (grouped by Uniprot-ID and protein name) sorted by increasing correlation. Only protein targets with at least 10 ligands shown. See Fig. S9† for complete labels. (D) Correlation analysis for the three highest-correlated protein targets (β-lactamase (Uniprot-ID P00811), β-secretase 1 (Uniprot-ID P56817), T4 lyzozyme (Uniprot-ID P00720)). (E) Average structural properties of ligands per protein target from the PDBbind (refined) set, indicating limited predictive value for the correlation r between ∑_iρ(BCP_i) and binding affinity. SASA = solvent-accessible surface area. Intra-set Tanimoto similarity measured by mean pairwise Tanimoto similarity of Morgan fingerprints (radius 2, 2048 bit).¹²⁰ Solid black lines in panels (A, B, D, and E) indicate least-squares fit.

Aiming to analyze to what degree the observed trends were affected by the accuracy of the semiempirical GFN2-xTB method, electron densities at the B3LYP-D3/6-31G* level of theory^79,80 (analogous to a previous study⁴³) were computed for three sets of ligands binding to different protein targets (Section S5†). These targets included a set of two high-correlation protein targets with medium-to-high affinity ranges (β-lactamase and β-secretase 1) and one low-correlation target (acetylcholine-binding protein) from the PDBbind refined set. This analysis revealed that the correlations identified using GFN2-xTB were also identified using B3LYP-D3/6-31G*, showing only minor deviations (Δr < 0.05).

To understand the impact of previously suggested⁴³ structural factors that may contribute to the differing correlations between sets of ligands, we assessed the average number of atoms, number of rotatable bonds, solvent-accessible surface area (SASA), spatial dimensions, and mean pairwise ligand similarity for each set of ligands binding to one protein target (Fig. 5E). This analysis indicated a rather weak trend of smaller and more rigid ligands showing better correlations. Groups of ligands with higher mean pairwise similarity between them showed a slight tendency to have poorer correlation between electron density and binding affinity. While such weak trends were observed, none of the investigated properties fully rationalized the vastly different correlations observed between the electron density at intermolecular BCPs and the measured binding affinity, suggesting that more detailed studies on the applicability of simple correlation-based QTAIM approaches are warranted.

Conclusion

Herein, we explored the use of a QM-based, interaction-centric descriptor of protein–ligand complexes, focusing on the electron density as a fundamental physical description of molecular systems. To this end, a computational pipeline was introduced that enables the large-scale computation of QM properties and the extraction of BCPs for protein–ligand complexes. Training geometric deep learning models on BCP-based descriptors does not seem to alleviate the “frustration to predict binding affinities from protein–ligand structures with deep neural networks”.² The lack of competitive predictive performance of electron density-based deep neural networks may be driven by insufficient accuracy of the chosen QM method, the already implicitly-contained information in atom center-based representations, and the inability to account for entropic contributions in protein–ligand binding.

The findings regarding the correlation of the electron density at intermolecular BCPs with the binding affinity may help focus future QTAIM analyses on protein targets for which informative results can be obtained. Certain groups of ligands that bind to the same target show better correlations than others. However, the specific structural features of ligands and protein pockets that drive the utility of electron density as a predictor of binding affinity remain currently unclear.

To complement the incomplete picture emerging from the static view provided by a QTAIM analysis, a molecular dynamics (MD) approach might be suitable. Such an approach could use the ensemble of BCPs sampled from an MD trajectory of a protein–ligand complex, aiming to capture a physically more meaningful representation of the binding event. Specifics of the graph-construction process (“through-time” edges or other aggregation strategies) and whether such a strategy potentially provides benefits over a corresponding atom-centered view remain as questions for future work. An opportunity lies in the exploration of predicted (rather than calculated) electron densities using deep models trained on ab initio calculations.

Author contributions

C. I.: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing – original draft. K. A.: formal analysis, investigation, methodology, writing – review & editing. S. R.: formal analysis, investigation, methodology, supervision, writing – review & editing. G. S.: formal analysis, investigation, methodology, supervision, funding acquisition, project administration, writing – review & editing.

Conflicts of interest

G. S. declares a potential financial conflict of interest as co-founder of https://insili.com/ GmbH, Zurich, and in his role as a scientific consultant to the pharmaceutical industry.