SUMMARY
Changes in an animal’s behavior and internal state are accompanied by widespread changes in activity across its brain. However, how neurons across the brain encode behavior and how this is impacted by state is poorly understood. We recorded brain-wide activity and the diverse motor programs of freely-moving C. elegans and built probabilistic models that explain how each neuron encodes quantitative behavioral features. By determining the identities of the recorded neurons, we created an atlas of how the defined neuron classes in the C. elegans connectome encode behavior. Many neuron classes have conjunctive representations of multiple behaviors. Moreover, while many neurons encode current motor actions, others integrate recent actions. Changes in behavioral state are accompanied by widespread changes in how neurons encode behavior, and we identify these flexible nodes in the connectome. Our results provide a global map of how the cell types across an animal’s brain encode its behavior.
INTRODUCTION
Animals generate diverse behavioral outputs that vary depending on their environment, context, and internal state. The neural circuits that control these behaviors are distributed across the brain. However, it is challenging to record activity across the brain of a freely-moving animal and relate brain-wide activity to comprehensive behavioral information. For this reason, it has remained unclear how neurons and circuits across entire nervous systems represent an animal’s varied behavioral repertoire and how this flexibly changes depending on context or state.
Recent studies suggest that internal states and moment-by-moment behaviors are associated with widespread changes in neural activity1–7. Behavioral states, like quiet versus active wakefulness, and homeostatic states, like thirst, are associated with activity changes in many brain regions1,7,8. In addition, instantaneous motor actions are associated with altered neural activity across many brain regions5,7. However, our understanding of how global dynamics spanning many brain regions encodes behavior remains limited. In mammals, representations of motor actions are found in cortex, cerebellum, spinal cord, and more. Given the vast number of cell types involved and their broad spatial distributions, characterizing this entire system is not yet tractable.
The C. elegans nervous system consists of 302 neurons with known connectivity9–13. C. elegans generates a well-defined repertoire of motor programs: locomotion, feeding, head oscillations, defecation, egg-laying, and postural changes. C. elegans express different behaviors as they switch behavioral states14,15. For example, animals enter sleep-like states during development and after intense stress16,17, awake animals exhibit different foraging states like roaming versus dwelling18–21, and aversive stimuli induce sustained states of increased arousal22,23. In C. elegans, it may be feasible to decipher how behavior is encoded across an entire nervous system and how this can flexibly change across behavioral states.
Previous studies identified some C. elegans neurons that reliably encode specific behaviors. The neurons AVA, AIB, and RIM encode backwards motion; AVB, RIB, AIY and RID encode forwards motion; SMD encodes head curvature; and HSN encodes egg-laying24–31. In addition, corollary discharge signals from RIM and RIA propagate information about motor state to other neurons32–34. Proprioceptive responses to postural changes have also been observed in a handful of neurons35–37. Large-scale recordings suggest that there are widespread activity changes related to behavior. Brain-wide recordings in immobilized animals identified population activity patterns associated with fictive locomotion25,26. In moving animals, velocity and curvature can be decoded from population activity3. While this suggests that many neurons carry behavioral information, we still lack an understanding of how quantitative behavioral features are encoded by most C. elegans neurons.
Here, we elucidate how neurons across the C. elegans brain encode the animal’s behavior. We developed technologies to record high-fidelity brain-wide activity and the diverse motor programs of >60 freely-moving animals. We then devised a probabilistic encoding model that fits most recorded neurons, providing an interpretable description of how each neuron encodes behavior. By also determining neural identity in 40 of these datasets, we created an atlas of how most C. elegans neuron classes encode behavior. This revealed the encoding properties of all recorded neurons and showed that ~30% of the neurons flexibly change how they encode behavior in a state-dependent manner. Our results reveal how activity across the defined cell types of an animal’s brain encodes its behavior.
RESULTS
Technologies to record brain-wide activity and behavior
We built a microscopy platform for brain-wide calcium imaging in freely-moving animals and wrote software to automate processing of these recordings. We constructed a transgenic C. elegans strain that expresses NLS-GCaMP7f and NLS-mNeptune2.5 in all neurons. Recording nuclear-localized GCaMP makes it feasible to record brain-wide activity, though this approach misses local calcium signals in neurites34. Transgenic animals’ behavior was normal, based on assays for chemotaxis and learning (Fig. S1A). Animals were recorded on a microscope with two light paths 38,39. The lower light path is coupled to a spinning disk confocal for volumetric imaging of fluorescence in the head. The upper light path has a near-infrared (NIR) brightfield configuration to capture images for behavior quantification (Movie S1). To allow for closed-loop animal tracking, the location of the worm’s head is identified in real time with a deep neural network40 and input into a PID controller that moves the microscope stage to keep the animal centered.
We wrote software to automatically extract calcium traces from these videos (Fig. 1D). First, a 3D U-Net41 uses the time-invariant mNeptune2.5 to locate and segment all neurons in all timepoints. We then register images from different timepoints to one another and use clustering to link neurons’ identities over time (see Methods). To test whether this accurately tracks neurons, we recorded a control strain expressing NLS-GFP at different levels in different neurons (Peat-4::NLS-GFP), along with pan-neuronal NLS-mNeptune2.5 (Fig. S1B). Mistakes in linking neurons’ identities would be obvious here, since GFP levels would fluctuate in a neural trace if timepoints were sampled from different neurons. This analysis showed that neural traces were correctly sampled from individual neurons in 99.7% of the frames. We estimated motion artifacts by recording a strain with pan-neuronal NLS-GFP and NLS-mNeptune2.5 (Fig. 1E–G; Fig. S1C). Fluorescent signals were far more narrowly distributed for GFP compared to GCaMP7f, suggesting that motion artifacts are negligible (Fig. 1F). Nevertheless, we used the GFP datasets to control for any such artifacts in all analyses below (see Methods). Compared to previous imaging systems38, there was an order of magnitude increase in SNR of the GCaMP traces from this platform (likely due to 3D U-Net segmentation; see Methods).
Figure 1. A probabilistic encoder model reveals how neurons across the C. elegans brain represent behavior.
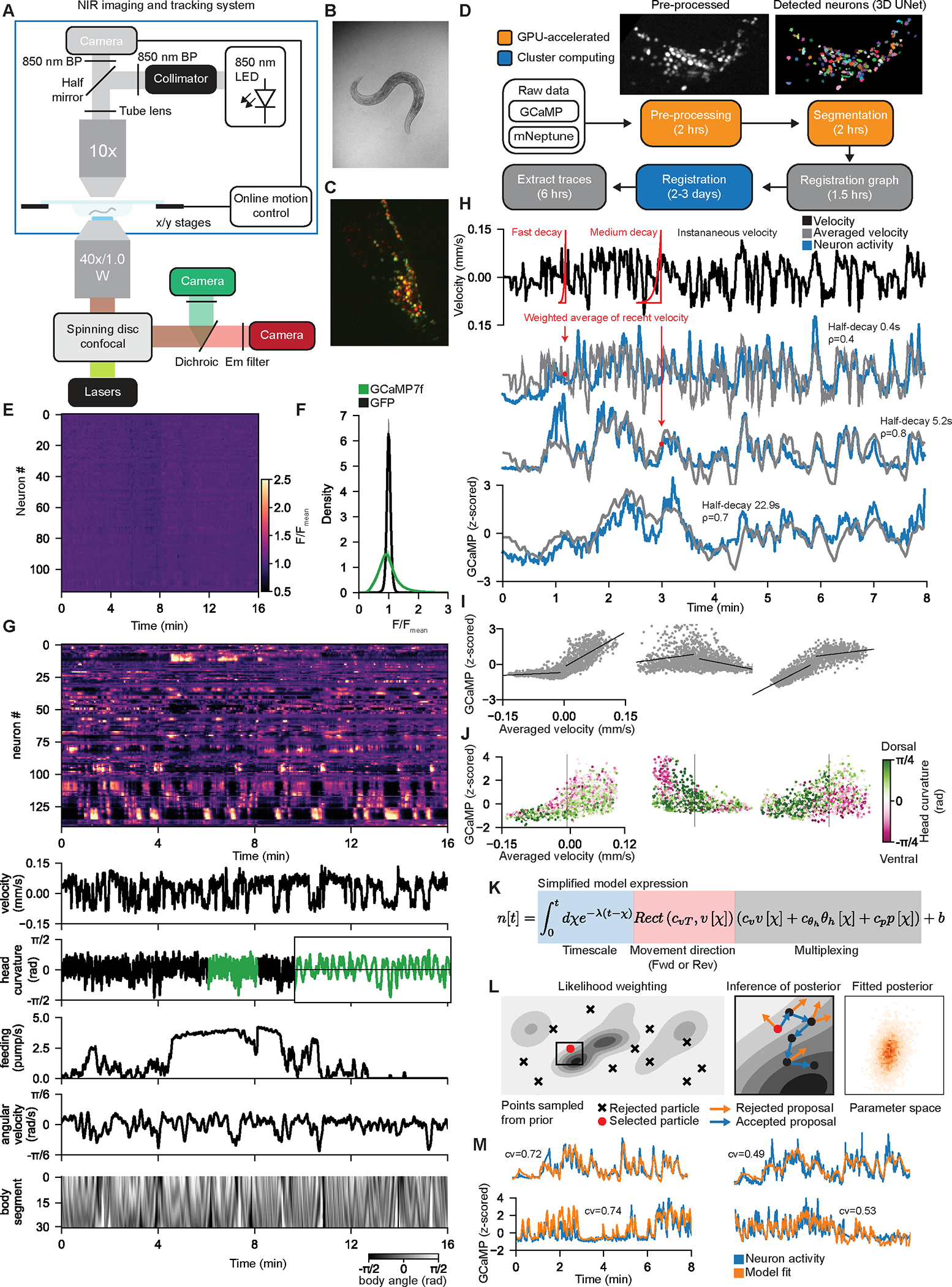
(A) Light path of the microscope. Top: behavioral data are collected in NIR brightfield. Images (panel B) are processed by the online tracking system, which sends commands to the stage to cancel out the motion. Bottom: spinning disk confocal for imaging head fluorescence.
(B-C) Example images from the two light paths in (A). Panel (C) is a maximum intensity projection.
(D) Software pipeline to extract GCaMP signals from the confocal volumes. See Methods.
(E) Heatmap of neural traces collected from a pan-neuronal GFP control animal. Data are shown using same color scale as GCaMP data in (G).
(F) Comparison of signal variation in all neurons from GFP and GCaMP recordings.
(G) Example dataset, with GCaMP data and behavioral features. GCaMP data displayed on same color scale as (E). Body segment is a vector of body angles from head to tail. Inset (green) shows a zoomed region to illustrate fast head oscillations.
(H) Three example neurons from one animal that encode velocity over different timescales. Each neuron (blue) is correlated with an exponentially-weighted (red kernels) moving average (gray) of the animal’s recent velocity, over different timescales. Inset shows half-decay times of exponentials and correlations of neurons to gray traces.
(I) Example tuning scatterplots for three neurons (different from those in H) showing how their activity relates to velocity. Dots are individual timepoints.
(J) Example tuning scatterplots for three neurons that combine information about head curvature (color) and velocity (x-axis). Dots are individual timepoints. For each neuron, the red and green dots separate from one another only for negative or positive velocity values.
(K) Simplified expression of the deterministic component of CePNEM. Here, we represent the effect of timescale via an integral, whereas Equation 1 in the text represents timescale via recursion.
(L) Left and Middle: Fitting procedure. Likelihood weighting selects a particle with the best fit to the data and uses it to initialize a Monte Carlo process that infers the posterior distribution (see Methods for details). Gray shading indicates model likelihood. Right: example posterior distribution for a neural trace, shown for two model parameters for illustrative purposes.
(M) Example neural traces and median of all posterior CePNEM fits for that neuron. Inset cross-validation (cv) scores are pseudo-R2 scores on withheld testing data (see Methods).
We also wrote software that extracts behavioral variables from the brightfield images: velocity, body posture, feeding (or pharyngeal pumping), angular velocity, and head curvature (bending of the head, associated with steering). Animals did not exhibit egg-laying or defecation in these recording conditions. Together, these advances permit us to quantify brain-wide calcium signals and a diverse list of behavioral variables from freely-moving C. elegans.
A probabilistic neural encoding model reveals how C. elegans neurons encode behavior
We recorded brain-wide activity and behavior from 14 animals as they explored sparse food over 16 minutes (data available at www.wormwideweb.org). We obtained data from 143 ± 12 head neurons per animal (example in Fig. 1G). 94.7% of the recorded neurons exhibited clear dynamics and could be classified as active (see Methods). Our goal was to build models of how each neuron “encodes” or “represents” the animal’s behavior, in other words how its activity is quantitatively associated with behavioral features. Our initial efforts revealed three features of neural encoding that we describe here. We systematically identify neurons with these features below (Fig. 2).
Figure 2. Varied representations of behavior across the C. elegans brain.
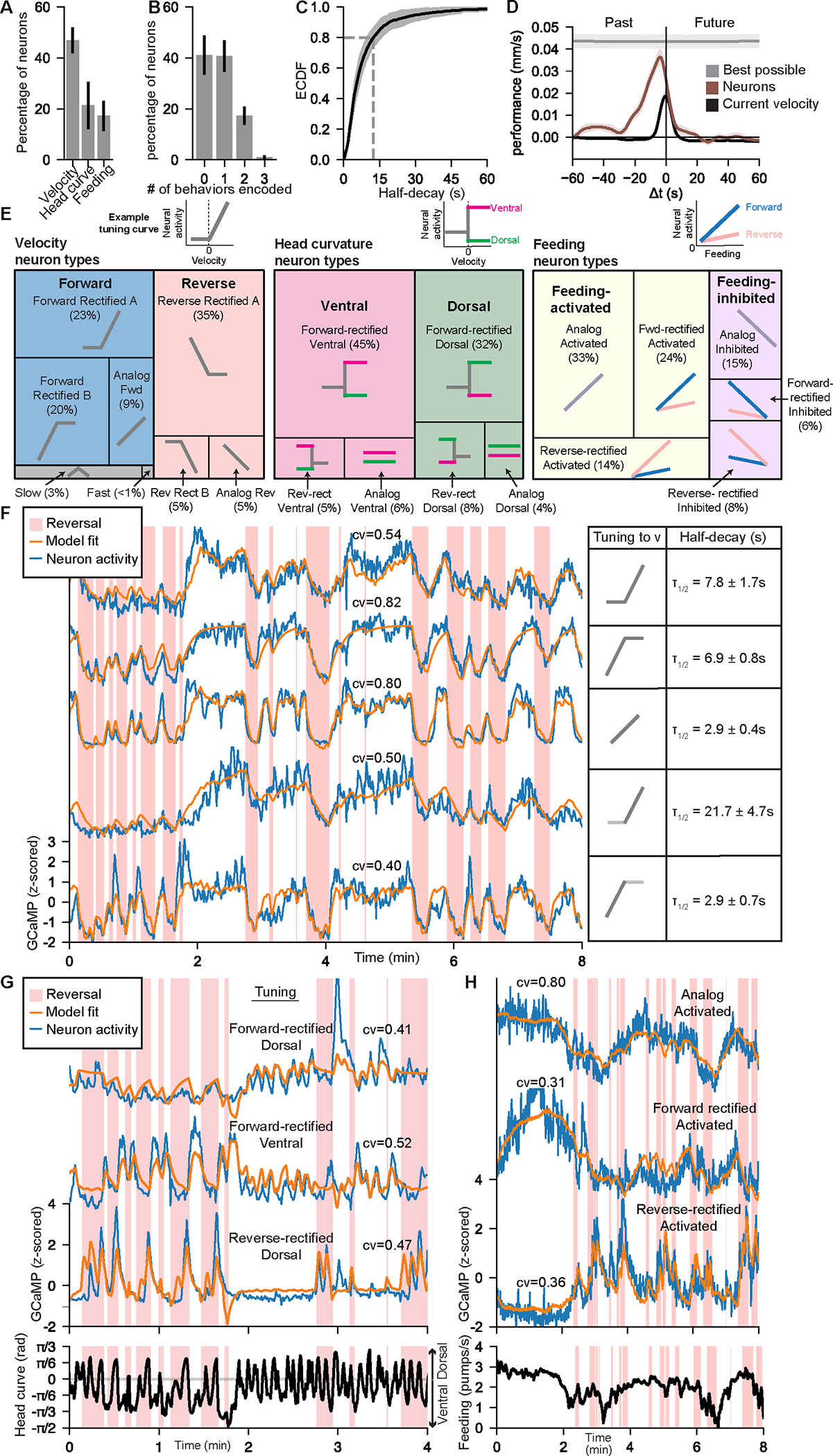
(A) Fraction of neurons per animal that encode indicated behaviors. If a neuron encoded >1 behavior, it is represented in multiple categories. Error bars show standard deviation between animals.
(B) Fraction of neurons per animal that encode 0, 1, 2, or 3 of the behaviors. Error bars show standard deviation between animals.
(C) ECDF of the median model half-decay time for neurons that encode at least one behavior. Shading shows standard deviation between animals.
(D) Performance of linear decoders that predict velocity at times offset from current neural activity (brown). Performance is the difference in error between the actual decoders and control scrambled decoders. Predicted velocity values were averaged over a 10-sec sliding window centered Δ𝑡 seconds from the current time. Decoders trained to make this prediction based on current velocity (black) or velocity values at all times (gray) are also shown. Shading shows standard deviation across animals.
(E) Distributions of how neurons encode the indicated behaviors. Neurons were categorized based on their tuning curves to each behavior (see Methods). Example tuning curves are shown above and prototypical tuning curves for each category are shown.
(F) Five example neurons that encode forward locomotion, together with CePNEM-derived tuning curves for each neuron, and the mean and standard deviation of each neuron’s half-decay time.
(G) Three example neurons that encode head curvature in conjunction with movement direction, together with CePNEM-derived tuning parameters.
(H) Three example neurons that encode feeding information, together with CePNEM-derived tuning parameters.
First, neurons encoded behavior over a wide range of timescales. For example, the activity of individual neurons that encode velocity was precisely correlated with an exponentially weighted average of the animal’s recent velocity. The decays of the exponentials, which determine how much a given neuron’s activity weighs past versus present velocity, varied widely across neurons (range of half-decay: 0.9 – 31.7 sec; GCaMP7f half-decay is <1 sec42,43). Fig. 1H illustrates this by showing correlations between individual neurons’ activities and velocity that has been convolved with exponential filters with varying decay times (see also Fig. S1D–E). We also observed a broad range of timescales for neurons that encode other behaviors (see below). This suggests that C. elegans neurons differ in how much they reflect the animal’s past versus present behavior.
Second, neurons reflected individual behaviors in a heterogeneous fashion. For example, for neurons that encode velocity, this encoding can be captured by a tuning curve that relates the neuron’s activity to velocity. Some neurons displayed analog tuning, but others displayed “rectification”, where the slopes of their tuning curves during reverse and forward velocity differed (Fig. 1I). While many neurons were more active during forward or reverse movement, others encoded slow locomotion regardless of movement direction (Fig. 1I, middle). This suggests that neurons that encode velocity can represent overall speed, movement direction, or finely tuned aspects of forward or reverse movement.
Third, many neurons conjunctively represented multiple motor programs. For example, most neurons whose activities were correlated with oscillatory head bending showed different tunings to head curvature during forwards versus reverse movement (Fig. 1J). Similarly, many neurons conjunctively represented the animal’s velocity and feeding rate. This suggests that many C. elegans neurons encode multiple motor programs in combination.
Based on these observations, we constructed an encoding model that uses behavioral features to predict each neuron’s activity (Equation 1; Fig. 1K). This model provides a quantitative explanation of how each neuron’s activity is related to behavior. The relationship between activity and behavior for a given neuron could be due to that neuron causally influencing behavior or, alternatively, due to the neuron receiving proprioceptive or corollary discharge signals. In contrast to decoding analyses3, which reveal the presence of behavioral information in groups of neurons, an encoding model can provide precise information about how each neuron’s dynamics relate to behavior. Each neuron’s activity was modeled as a weighted average of the animal’s recent behavior with a single decay parameter , allowing for different timescale encoding. Neurons can additively weigh multiple behavioral predictor terms (based on coefficients , and ), which can interact with the animal’s movement direction parameterized by . This allows for rectified and non-rectified tunings to behavior, as well as conjunctive encoding of multiple behaviors. We compared the goodness of fit of this full model to partial models with parameters deleted (and to a linear model) and found that deletion of any parameter significantly increased model error (Fig. S1F–G).
The model parameters are interpretable, describing how each neuron encodes each behavioral feature. However, because the model is fit on a finite amount of data, these parameters have a level of uncertainty that is important to estimate. Therefore, we determined the posterior distribution of all model parameters that were consistent with our recorded data, where consistency was defined as likelihood in the context of a Gaussian process residual model parameterized by , and (see Methods). This allowed us to quantify our uncertainty in each model parameter and perform meaningful statistical analyses. The posterior distribution was determined using a custom inference algorithm implemented with the probabilistic programming system Gen44 (Fig. 1L). We confirmed the validity of this approach using simulation-based calibration, a technique that ensures that approximations from such inference algorithms are sufficiently accurate (Fig. S2A)45.
Equation 1: The C. elegans Probabilistic Neural Encoding Model (CePNEM) expression
| Parameter | Meaning |
|---|---|
| Observed velocity, head curvature, and pumping rate | |
| Modeled neural activity. | |
| Locomotion direction rectification term with different values based on forwards versus reverse movement. | |
| Locomotion direction rectification parameter. | |
| Velocity, head curvature, and feeding parameters. | |
| Exponentially weighted moving average (EWMA) timescale parameter. | |
| Baseline activity parameter. | |
| Initial condition parameter. | |
| White noise parameter. | |
| Autocorrelative residual parameter. | |
| Autocorrelative residual timescale parameter. | |
| Gaussian process. | |
| Gaussian process kernels. |
We fit this model (The C. elegans Probabilistic Neural Encoding Model, or CePNEM) on all neurons and found significant encoding of at least one behavioral feature in 83 ± 10 out of 143 neurons per animal (examples in Fig. 1M and Fig. S2B; see also Fig. S2C and Methods for statistics). To ensure that these results were not due to motion artifacts, we applied the model to animals expressing pan-neuronal GFP and found that only 2.1% of GFP neurons significantly encoded behavior (versus 58.6% in GCaMP datasets; Fig. S2D). We were also concerned whether the model could potentially explain neural activity via overfitting and tested this using two approaches. First, we tested whether neural activity from one animal could be explained using behavioral features from other animals. However, only 2.7% of neurons encoded this incorrect behavior (Fig. S2D). Second, we performed 5-fold cross-validation across recorded neurons and found a high level of performance on withheld testing data (Fig. S2E).
There were active neurons with calcium dynamics not well fit by CePNEM (see Fig. S2F). However, it was ambiguous whether these neurons encoded behavior in a manner not captured by CePNEM or whether their activity was related to other ongoing sensory or internal variables. To distinguish between these possibilities, we examined the model residuals, i.e. the neural activity unexplained by CePNEM. We attempted to decode behavioral features using all neurons’ model residuals and, as a control, the original neural activity traces. Decoding from the full neural traces was successful, but decoding from the residuals was close to chance (Fig. S2G). This suggests that neural variance unexplained by CePNEM is unrelated to the overt behaviors quantified here. These residuals may be related to sensory inputs, internal states, or behaviors that we were unable to detect. Decoding of specific behavior features was also most successful from neurons that CePNEM suggested encode those features (Fig. S2H). Thus, CePNEM determines the encoding features of neurons in a manner that is concordant with decoding analyses.
Diverse representations of behavior across the C. elegans brain
We used the CePNEM results to analyze how the neurons across each animal’s brain encode its behavior. Among the recorded neurons, encoding of velocity was most prevalent, followed by head curvature and feeding (Fig. 2A). 58.6% of recorded neurons encoded at least one behavior (Fig. 2B), with approximately one third of these conjunctively encoding multiple behaviors (Fig. 2B). Most neurons primarily encoded current behavior, but a sizeable subset weighed past behavior (Fig. 2C). Long timescale encoding was especially prominent among forward-active velocity neurons (Fig. S2I–J). This suggested that current neural activity may contain information about past velocity. Indeed, we were able to train a linear decoder to predict past velocity up to at least 20 sec prior based on current neural activity (Fig. 2D; black line shows this was not due to current velocity predicting past velocity). A similar decoder could predict past head bending behavior, albeit less robustly (Fig. S2K). However, we were not able to predict future velocity or head bending from current neural activity (Fig. 2D, S2K).
We analyzed how each behavior was represented across the full set of neurons, first focusing on velocity. Using the CePNEM fits, we determined the shapes of each neuron’s tuning curve to velocity (see Methods). There were eight ways that a neuron could be tuned to velocity (Fig. 2E; examples in Fig. 2F). Most neurons (83%) exhibited rectified tunings, in which the encoding of forward and reverse speed differed. A smaller set of neurons represented analog velocity and others encoded slow locomotion. To highlight how CePNEM accurately captures the dynamics of neurons with different tunings, Fig. 2F shows five neurons with higher activity during forward movement, but with different dynamics. The CePNEM fits to each neuron reveal how they encode velocity with different tunings and timescales.
Among the neurons that encoded head curvature, many did so in a manner that depended on locomotion direction (Fig. 2E). Thus, we categorized these neurons based on both their head curvature tuning and velocity tuning. Most neurons only displayed head curvature-associated activity changes during forward or reverse movement, with more neurons in the forward-rectified group (Fig. 2E; examples in Fig. 2G). These results indicate that the network that controls head steering is broadly impacted by the animal’s movement direction, which could relate to the fact that steering behavior must be controlled differently during forward versus reverse movement (see also Fig. S2L). In addition to these neurons that encode the animal’s acute head curvature, a smaller group of neurons encoded angular velocity (Fig. S2M).
Neural representations of the animal’s feeding rates were also diverse (Fig. 2E; examples in Fig. 2H). Many neurons displayed analog tuning to feeding rates; others encoded feeding in conjunction with movement direction. Neurons could be positively or negatively correlated with feeding.
The above analyses suggest a surprising amount of heterogeneity in how C. elegans neurons encode behavior. To obtain a more global view of these representations, we embedded the neurons into a two-dimensional UMAP subspace where proximity between neurons indicates how similarly they encode behavior (Fig. 3A; see Fig. S3A–D for related analyses). This analysis could reveal clusters of cells that encode behavior the same way or, alternatively, the neurons could be evenly distributed if the representations were more heterogeneous. We found that the neurons were diffusely distributed, with no evident clustering (Fig. 3A). However, neurons’ localization still depended on their encoding (Fig. 3B–E). For example, encoding of velocity was graded along one axis, and encoding of feeding was graded along the other. The continuous distribution of neurons was especially evident when examining neurons with related tuning curves (Fig. 3F). Other standard clustering approaches also suggested that the neurons were not clusterable into discrete groups based on their encoding (Fig. S3E). These results suggest that in general the C. elegans neurons represent behavior along a continuum.
Figure 3. Global analysis of how neurons encode behavior in the C. elegans nervous system.
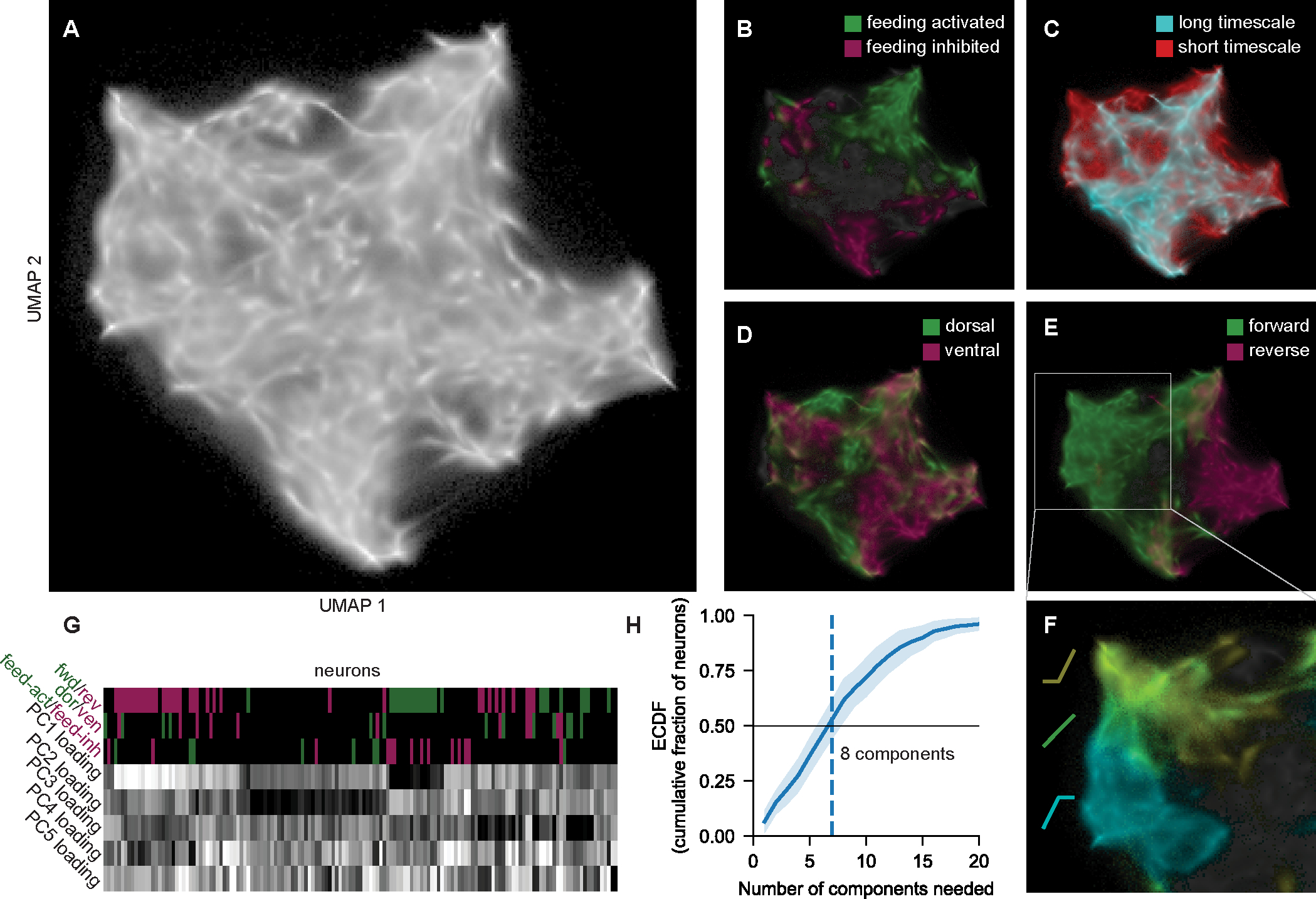
(A) UMAP embedding of all neurons in 14 animals, where proximity indicates encoding similarity (see Methods). Here, we projected all points from each neuron’s CePNEM posterior. Fig. S3D shows only one dot per neuron.
(B-E) UMAP space where neurons are colored by their behavioral encodings. Long versus short timescale is split at half-decay time of 20 sec.
(F) Zoomed portion of UMAP space, where neurons are color-coded by their velocity tuning curves.
(G) Example animal, showing neurons’ tuning to behavior and loadings onto the top five PCs. Neurons are hierarchically clustered by their PC loadings.
(H) Number of PCs needed to explain 75% of the variance in a given neuron, averaged across neurons in 14 animals. Data are means and standard deviation across animals.
See also Figure S3.
How do these diverse representations of behavior arise? C. elegans neural activity can be decomposed into different modes of dynamics shared by the neurons26, identifiable through Principal Component Analysis (PCA). In our data, the first three PCs explained 42% of the variance in neural activity, and 18 PCs were required to explain 75% of the variance (Fig. S3F). Single neurons were almost exclusively described as complex mixtures of PCs rather than single PCs (Fig. 3G–H). The weights of the PCs on different neurons were diverse, and hierarchical clustering of these data revealed little structure. However, as expected, the loadings were still predictive of the neuron’s encoding type (Fig. 3G). Overall, these results suggest that there are many ongoing modes of dynamics shared among neurons, which relate to their distinct representations of behavior.
An atlas of how the defined neuron classes in the C. elegans connectome encode behavior
We next sought to map these diverse representations of behavior onto the defined cell types of the C. elegans connectome. Thus, we collected additional datasets in which we determined neural identity using NeuroPAL46, a transgene in which three fluorescent proteins are expressed under well-defined genetic drivers. This makes it possible to determine neural identity based on neuron position and multi-spectral fluorescence. We crossed the pan-neuronal NLS-GCaMP7f transgene to NeuroPAL (using otIs670, a low brightness NeuroPAL integrant). Data were collected as above, except animals were immobilized by cooling47 after each freely-moving recording. We then collected multi-spectral NeuroPAL fluorescence (Fig. S4A) and registered those images to the freely-moving images.
We collected data from 40 NeuroPAL/GCaMP7f animals. Compared to the above datasets, a similar number of neurons encoded behavior (52.0%, compared to 58.6%); behavioral parameters and other metrics of neural activity were also mostly similar (Fig. S4B–E; Fig. S3B; though NeuroPAL animals reversed more frequently and had a slight ventral bias). Across recordings, we obtained data from 78 of the 80 neuron classes in the head. While most neuron classes are single left/right pairs, 13 classes consist of 2–3 pairs of neurons in 4- or 6-fold symmetric arrangements. In these cases, we separately analyzed each neuron pair. Left/right pairs were pooled for all neuron classes except four that displayed asymmetric activities (ASE, SAAD, IL1, IL2; see Methods). We generated CePNEM fits for all of these neurons to reveal how they encode behavior (Fig. 4A; Table S1; Fig. S4F–H). The encoding properties of the neuron classes determined via CePNEM predicted their activity changes in event-triggered averages aligned to key behaviors (Fig. S4G). For well-studied neurons, our results provided a clear match to previous work: AVB, RIB, AIY, and RID encoded forward movement; AVA, RIM, and AIB encoded reverse movement; and SMDD and SMDV encoded dorsal and ventral head curvature, respectively24–30.
Figure 4. An atlas of how the different C. elegans neuron classes encode behavior.
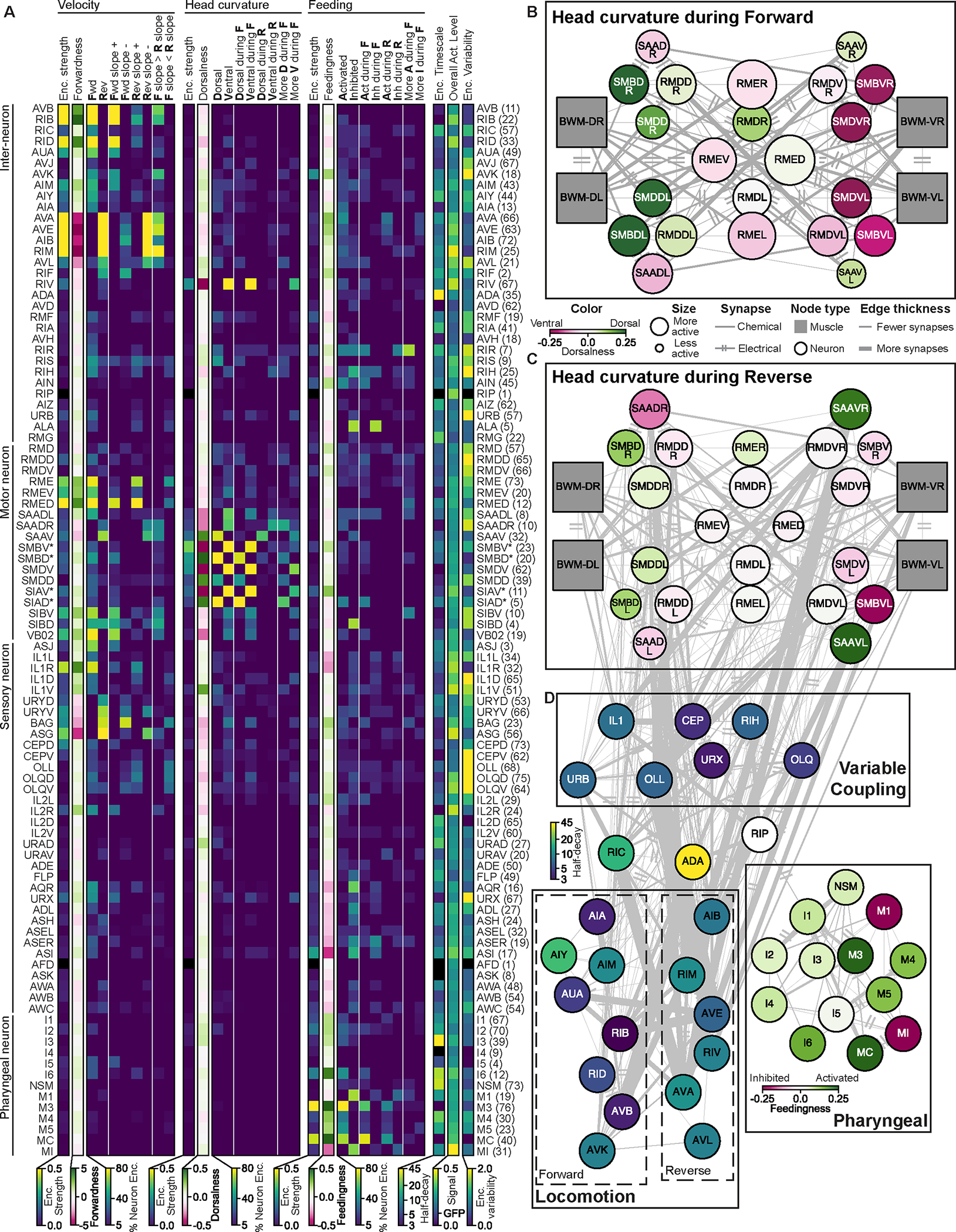
(A) An atlas of how the indicated neuron classes encode behavior, derived from analysis of fit CePNEM models. Columns show:
• Encoding strength: approximate variance in neural activity explained by each behavioral variable.
• Forwardness, Dorsalness, and Feedingness: slope of the tuning to each behavior.
• Enc. timescale: median half-decay time
• Overall act. level: standard deviation of the calcium traces when normalized as F/Fmean.
• Enc. Variability: how differently the neuron class encoded behavior across recordings. Other columns show the fraction of recorded neurons that significantly encoded behaviors:
• Fwd, Rev, Dorsal, Ventral, Activated, and Inhibited: neurons with that overall tuning to behavior.
• Fwd slope −, Fwd slope +, Rev slope −, and Rev slope +: neurons with that slope in their velocity tuning curves during the specified movement direction.
• F slope > R slope and F slope < R slope: neurons displaying rectification in their velocity tuning curves.
• Dorsal during F, Ventral during F, Dorsal during R, Ventral during R, Act during F, Inh during F, Act during R, and Inh during R: neurons with that tuning to behavior during the specified movement direction (Forward or Reverse).
• More D during F, More V during F, More A during F, and More I during F: neurons with different tunings to behavior during forward versus reverse.
Parenthesis on right indicates the number of CePNEM fits per neuron class (first and second halves of videos, which have different model fits, are counted separately).
(B-C) Circuit diagram of neurons that innervate head muscles with overlaid behavioral encodings during forward (B) and reverse (C) movement. Edge thickness indicates number of synapses between neurons. Left/right neurons shown separately, because one of these pairs (SAAD) exhibited asymmetric activity, suggesting an asymmetry in this circuit.
(D) Circuit diagrams of behavioral circuits.
See also Figures S4, Figure S5, and Table S1.
This analysis revealed many features of how the C. elegans nervous system is organized to control behavior. Among the velocity-encoding neurons, those that encode forward movement displayed a wide range of tunings to velocity and included many neurons not previously implicated (AIM, AUA, and others). The reverse neurons were more uniform in their tunings to velocity, but several also represented head curvature, suggesting that they may control turning during reversals. Neural representations of velocity also spanned multiple timescales. For example, RIC, ADA, AVK, AIM, and AIY integrated the animal’s recent velocity over tens of seconds. We silenced some neurons that encoded velocity (AIM, RIC, AUA, AVL, RIF) and found that this specifically altered animals’ velocity (Fig. S4I). In addition, we optogenetically stimulated ASG sensory neurons, which encoded reverse movement, and found that this triggered reversals (Fig. S4I). Thus, results from the neuron atlas can predict causal effects on behavior.
These data also revealed neural dynamics in the circuit that controls head steering. The neuron classes in this network are often 4-fold symmetric, consisting of separate neuron pairs that innervate the ventral and dorsal head muscles. These opposing dorsal and ventral neurons were functionally antagonistic in our analysis (Fig. 4A–C). We found that the neural control of head steering is different during forward versus reverse motion (Fig. 4B–C). Some neurons that encode head curvature are more active during forward (RMED/V) or reverse (SAAV) movement. Others have more robust tuning to head curvature during forward movement (SMDD/V, SMBD/V). In addition, RMDD was more active during dorsal head bending during forwards motion, but preferred ventral head bending during reverse movement. The forward-rectified tuning of SMD was previously described and matches our results25. Our data now show that this entire network shifts its functional properties depending on movement direction. This suggests that the network functions differently while animals steer forwards towards a target compared to when they back away from one. We ablated some neurons that jointly encoded movement direction and head curvature (SAA, SMB) and found that this altered animal’s head bending and velocity (Fig. S4I).
Most neurons that encoded feeding were in the pharyngeal nervous system, but several extrapharyngeal neurons also encoded feeding, including AIN, ASI, and AVK. Neurons within the pharyngeal system encoded feeding with both positive (I6, M3, M4, etc) and negative (M1, MI) relationships. Optogenetically silencing neurons that encoded feeding (M4, MC) specifically inhibited feeding behavior (Fig. S4I).
Finally, we observed that many neurons (OLL, OLQ, IL1, RIH, URB, others) had tunings to different motor programs that were variable across animals (Fig. 4D). To directly examine this, we computed a variability index that describes how dissimilar each neuron class’s encoding of behavior was across all datasets (Fig. 4A; see Methods). While many neuron classes had invariant representations of behavior across animals (AVA, AIM, many others), others had high variability (Fig. 4A; Fig. S5A). NeuroPAL labeling and registration procedures for the neurons with high variability were determined with equal confidence to the other neuron classes, suggesting that identification errors are unlikely to explain these observations (Fig. S5B–D). Further supporting this, these neurons also changed encoding over the course of continuous recordings (see below). The ability of models trained on one set of animals to generalize to other animals inversely scaled with the neuron class’s variability index (Fig. S5E). For neurons with high variability, it is informative to look at the range of possible encodings reported in Fig. 4A rather than just the encoding strength metric. Overall, these datasets provide a functional map of how most neuron classes in the C. elegans nervous system encode the animal’s behavior.
Different encoding features are localized to distinct regions of the connectome
We next examined how these representations of behavior relate to connectivity in the C. elegans connectome. We first examined whether synaptically connected neurons had similar dynamics. Indeed, connected neurons – especially those connected through electrical synapses – were more highly correlated than neurons that were not synaptically connected (Fig. 5A). In addition, neurons were more strongly correlated (either positively or negatively) to their synaptic input and output neurons, compared to random controls (Fig. 5B).
Figure 5. Neural encoding features map onto different regions of the connectome.
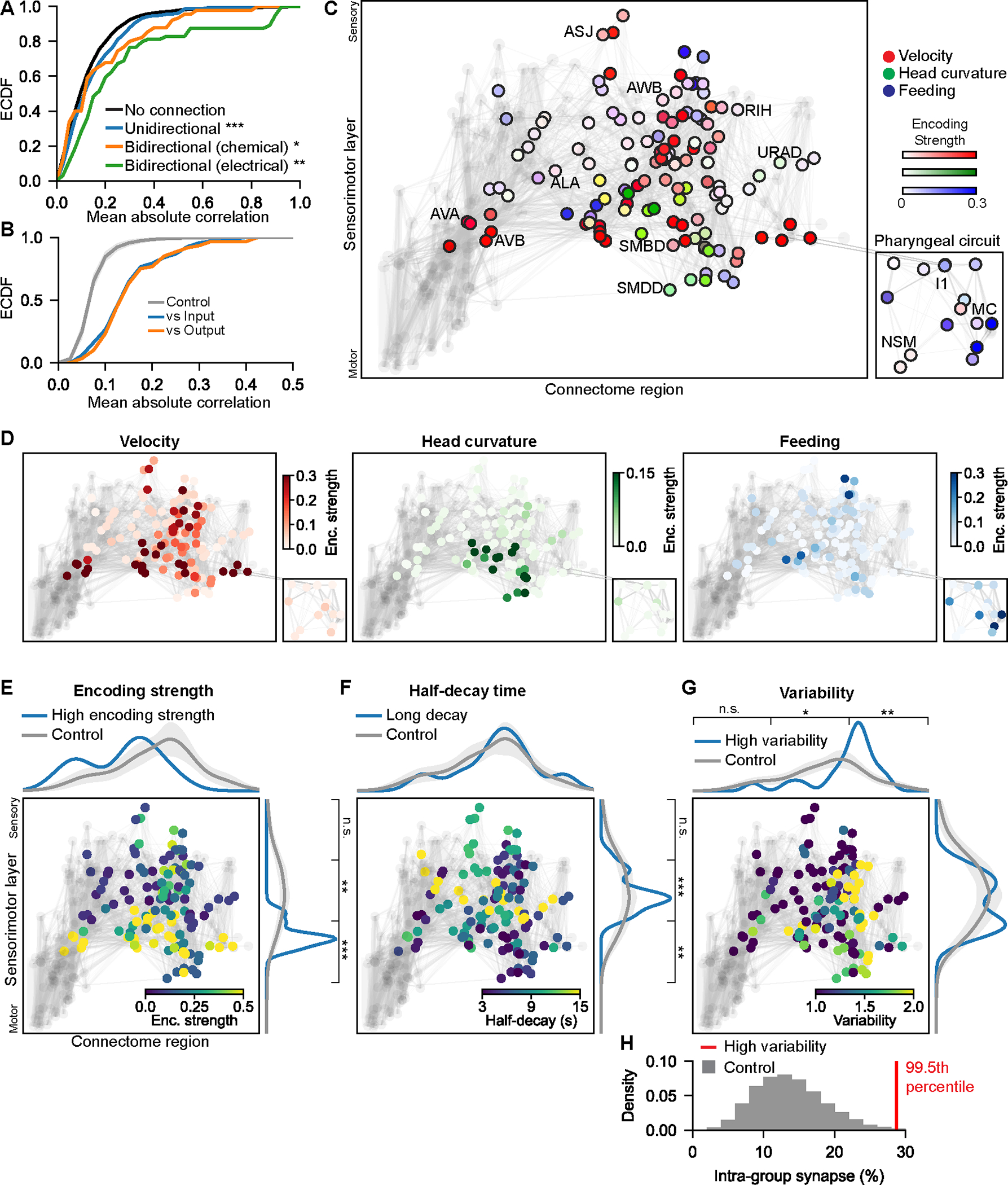
(A) Cumulative distribution of the correlation coefficients of activities of pairs of neurons connected in different ways. Left/right pairs were merged for this analysis, so it only considers relationships between different neuron classes. *p<0.05 **p<0.005 ***p<0.0005, Mann-Whitney U-test.
(B) Median correlation coefficients between each neuron and its synaptic inputs (blue) or outputs (orange). Control (gray) shows randomly selected neurons of equal group size.
(C) Neurons (circles) and connections (gray lines) in the C. elegans connectome, with behavior encoding information. Connectome region (x-axis): neurons with similar wiring are adjacent on this axis, computed as the second eigenvector of the laplacian of the connectome graph. Sensorimotor layer (y-axis): neurons arranged from sensory to motor (see Methods). Some neurons are labeled to provide rough orientation to the layout.
(D) Same as in (C), but one behavior per plot.
(E-G) Distribution of encoding features in the connectome, arranged as in (C). Marginal distributions (blue) show values of each behavioral feature along each axis. Gray control lines show how behavioral features are distributed when randomly shuffled. *p< 0.05 **p<0.005, ***p<0.0005, one sample Z-test for proportion.
(H) The number of synapses connecting the neurons with high variability (see Methods) is shown as a red line. Gray shows the number of synapses connecting random neuron groups. Inset shows rank of the true value in this shuffle distribution.
This raised the possibility that local communities of neurons in the connectome may encode related behavioral information. To examine this, we determined the localization of behavioral information in the connectome. We examined localization with respect to whether neurons are connected to one another, and whether neurons are closer to sensory versus motor layers (x- and y-axes of the Fig. 5C–G). Velocity information was widespread, whereas head curvature and feeding were located in more restricted connectomic regions (Fig. 5C–D). In general, behavioral information was most prominent at lower sensorimotor layers, closer to motor output (Fig. 5E). Neurons with long timescale information were located at middle sensorimotor layers, primarily in interneurons that innervated premotor and motor neurons (Fig. 5F). The neurons with variable encoding across animals were largely localized in one synaptic community (Fig. 5G–H), suggesting that they comprise an interconnected circuit that exhibits variable coupling. Together, these observations suggest that different features of behavior encoding are located in different regions of the C. elegans connectome.
The encoding of behavior is dynamic in many neurons
We noted that the encoding properties of some neurons appeared to change over time in a single recording. Therefore, we analyzed our data to determine whether neural representations of behavior dynamically change. We fit two CePNEM models trained on the first and second halves of the same neural trace and used the Gen statistical framework to test whether the model parameters significantly changed between time segments (see Methods; and Fig. S6A–B). Based on this test, ~31% of neurons that encoded behavior changed that encoding over the course of our continuous recordings. A similar fraction (24%) of neurons changed encoding in the NeuroPAL strain. These identified neurons substantially overlapped with those that variably encode behavior between animals (Fig. 6A; Fig. S6C) and were densely interconnected (Fig. 6B; see also Fig. S6D). Neurons changed encoding in different ways: some changed which behaviors they encoded; others showed gains or losses of encoding; and others showed subtle changes in tuning (Fig. 6C; examples in Fig. 6D–E). This suggests that some neurons in the C. elegans connectome are variably coupled to behavioral circuits and remap how they couple to these circuits over time.
Figure 6. Neural representations of behavior dynamically change over time.
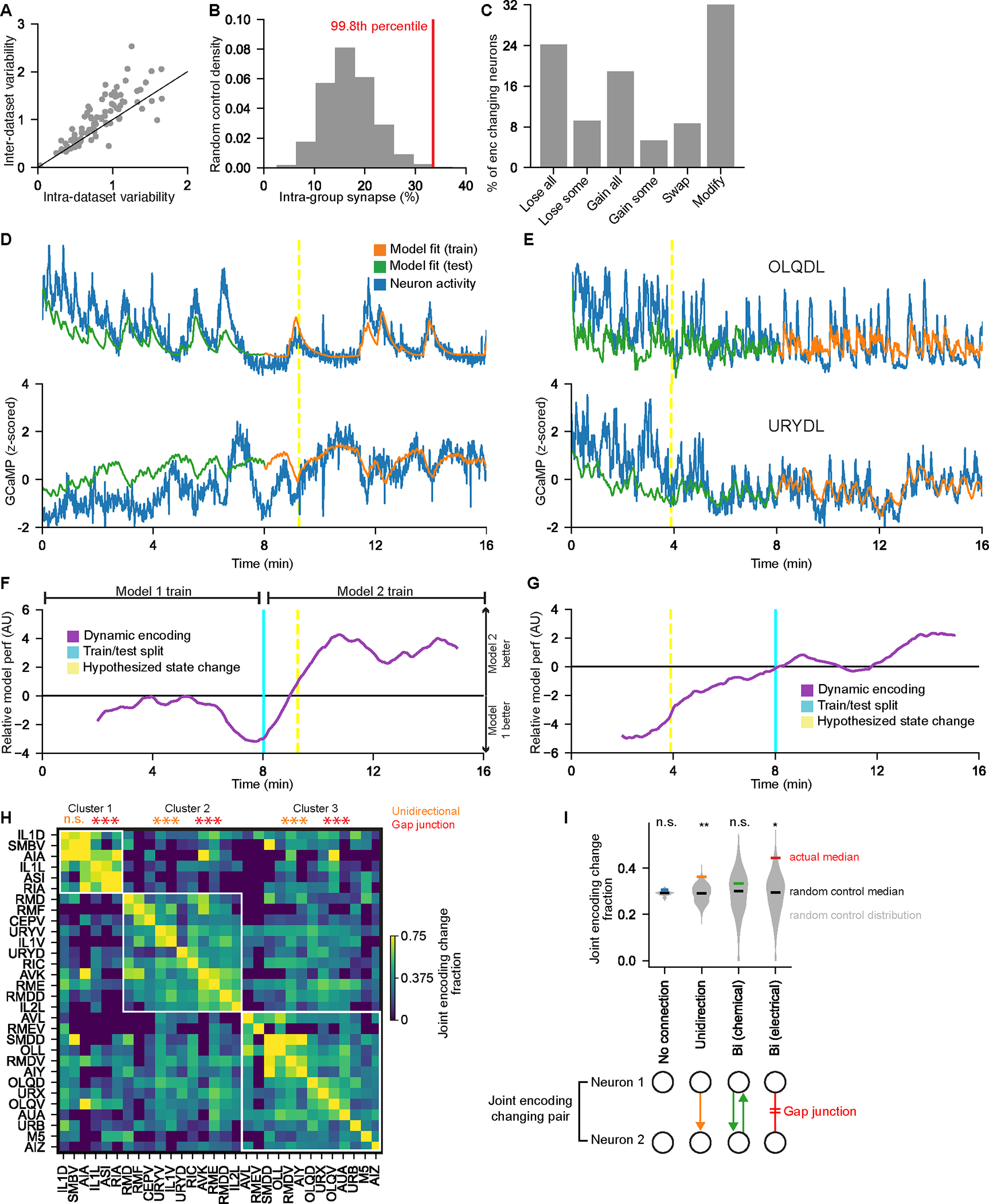
(A) Analysis of inter- versus intra-dataset encoding variability. Each dot is a neuron class.
(B) For the group of neurons that frequently change encoding, red line shows percent of synapses onto these neurons that come from neurons within the group. Gray controls are the same values for random groups of neurons of similar size. Inset percentile shows rank of true number.
(C) How neurons changed encoding across SWF415 animals. Categories are: “lose all” (lost tuning to behavior), “lose some” (lost tuning to one or more behavior), “gain all”, “gain some”, “swap” (both gained and lost tuning to behaviors), and “modify” (encode the same behavior(s), but differently).
(D) Two example neurons with CePNEM fits, showing a change in neural encoding of behavior. Yellow dashed lines indicate times when neurons across the full dataset displayed a sudden shift in encoding (see (F)).
(E) Example neurons OLQDL and URYDL, depicted as in (D).
(F) Data from same animal as (D) showing a sharp change in neural encoding of behavior. We fit CePNEM models to the first and second halves of the recording (Model 1 and Model 2). We then computed the difference between the errors of the two median model fits and smoothened with a 200-timepoint moving average. This was then averaged across encoding changing neurons. A sudden change (yellow line) indicates a sudden shift in behavior encoding across neurons.
(G) Data from the same animal as (E) showing a sudden change in neural encoding, displayed as in (F).
(H) Fraction of times that neuron classes changed encoding at the same moment, relative to their encoding changes overall. Rows were clustered and white outlines depict main clusters. **p<0.005, empirical p-value that clustering would perform as well during random shuffles. Within each cluster, the neurons were more likely to have unidirectional synapses and/or gap junctions with one another compared to random shuffles, as indicated. ***p<0.0005, empirical p-value.
(I) Neuron pairs with unidirectional synapses or electrical synapses were more likely to change encoding together, compared to random shuffles (gray distributions). *p<0.05, **p<0.005, empirical p-value.
See also Figure S6.
We next sought to understand the temporal structure of these encoding changes. For instance, individual neurons could remap independently or in a synchronized manner. We developed a metric to identify when an encoding change took place based on the difference between the errors of models trained on different time regions of the same trace (Fig. 6F–G; controls in Fig. S6E–F). We observed sharp changes (yellow lines) where many neurons simultaneously changed encoding in many datasets (Fig. 6F–G), although in some datasets there were gradual shifts (Fig. S6G–H). Certain neuron classes were more likely to change encoding at the same time as one another such that they could be grouped into clusters (Fig. 6H). The neurons that remapped their encoding at the same time were more likely to be synaptically connected, especially via gap junctions (Fig. 6I). Moreover, the number of neurons that changed encoding was positively correlated with the degree of behavioral change across the hypothesized moment of the change (Fig. S6I). Therefore, at times there is a coordinated remapping where many neurons change how they represent behavior.
The encoding of behavior is influenced by the behavioral state of the animal
We next tested whether changes in the animal’s behavioral state could elicit these synchronous encoding changes. Behavioral states are persistent changes in behavior that outlast the sensory stimuli that initiate them48,49. Previous work has shown that aversive stimuli can induce this type of response in C. elegans22,23,50. Therefore, we recorded 30 datasets where we delivered a sudden, noxious heat stimulus to animals part way through the recording (19 of these datasets had NeuroPAL labels). For stimulation, we heated the agar around the worm’s head by 10°C for 1 second (Fig. 7A; temperature decayed to baseline within 3 seconds). This elicited an immediate avoidance (reversal) behavior and reduction in feeding (Fig. 7B). Animals continued to exhibit reduced feeding and increased reversals for minutes after the stimulus, revealing a persistent behavioral state change (Fig. 7B). However, behavior reverted to normal within an hour and animal viability was not adversely impacted by the stimulus (Fig. S7A–B).
Figure 7. Behavioral state changes cause a widespread remapping of how neurons encode behavior.
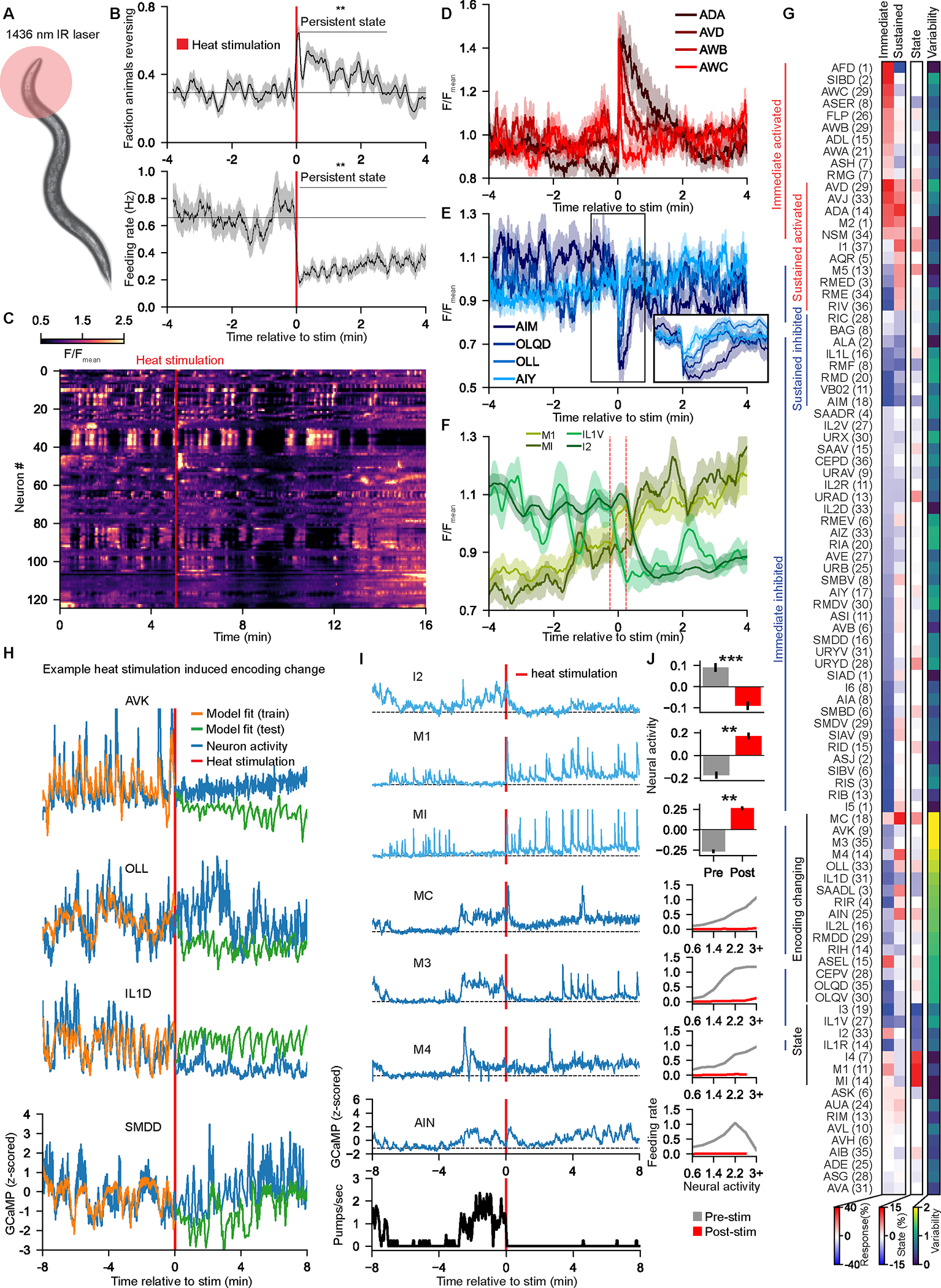
(A) Illustrative cartoon: a 1436nm IR laser transiently increases the temperature around the animal’s head by 10°C for 1 sec.
(B) Event-triggered averages of behavior of 32 animals in response to the heat stimulus. **p<0.05, Wilcoxon signed rank test, pre- versus post-stimulus.
(C) Neural data from an animal that received a heat stimulus (red line).
(D-F) Event-triggered averages of neural activity aligned to the heat stimulus for some neurons with (D) excitatory or (E) inhibitory responses to the stimulus, or (F) persistent activity changes. ETAs in (F) are smoothed over 30 seconds; dashed lines indicate where the stim is within the moving average window.
(G) Responses of different neuron classes to the heat stimulus (n=19 animals):
• Immediate (<4 seconds) and sustained (15–30 seconds) GCaMP responses
• Persistent activity changes. See Methods.
• Encoding variability pre- vs post-stimulus. See Methods.
(H) Example neurons that showed abrupt changes in their behavior encoding immediately after the stimulus.
(I) Example dataset. Light blue neurons had persistent activity changes. Dark blue neurons changed encoding after the stimulus.
(J) Top three plots: Average activity, computed as , before and after the heat stimulus. Error bars show SEM across animals. **p<0.005, ***p<0.0005, Wilcoxon signed rank test. Bottom four plots: tuning curves to feeding behavior for each neuron class (pre- versus post-heat-stimulus data). Data are pooled across 19 animals.
See also Figure S7.
We measured brain-wide responses during this behavioral state change (Fig. 7C–G). Several neurons displayed transient responses to the sensory stimulus, including thermosensory neurons AFD, AWC, FLP, and others (Fig. 7D–E; see also Fig. S7C–D)51,52. Other neurons displayed minutes-long responses to the stimulus. We also identified some neurons with persistent changes in activity that lasted for the rest of the recordings after the stimulus (Fig. 7F). Finally, we found that 35% of the neurons that encoded behavior changed encoding time-locked to the heat stimulus (compared to 24% in animals without any stimulus; p<0.05, Mann-Whitney U-Test; Fig. S7E; examples in Fig. 7H). The neurons that changed encoding were stereotyped across animals, especially the neurons related to feeding, which is the behavior most robustly altered by the heat stimulus (Fig. S7F; see also Fig. S7G–H). Thus, inducing a behavioral state change elicits a reliable shift in the network that remaps the relationship between neural activity and behavior.
We examined how these activity changes related to the behavioral changes that comprise the aversive behavioral state, focusing on the robust suppression of feeding. Three neurons that encoded feeding showed persistent activity changes that paralleled the state: I2 activity persistently decreased and MI and M1 activity increased. In addition, four feeding neurons showed a change in encoding after the heat stimulus. These neurons, MC, M3, M4, and AIN, had correlated activity bouts aligned with bouts of feeding prior to the heat stimulus (Fig. 7I–J). After the stimulus, activity bouts still occurred in these neurons, but this was not accompanied by feeding. Notably, at baseline, MI and M1 activity were highest during pauses in feeding (Fig. 7I–J). This suggests that MI and M1 might inhibit feeding and that the state-dependent increase in MI and M1 activity might suppress feeding normally elicited by MC/M3/M4/AIN. Overall, these results show how changes in behavioral state are accompanied by persistent activity changes and alterations in how neural activity is functionally coupled to behavior.
DISCUSSION
Animals must adapt their behavior to a constantly changing environment. How neurons represent these behaviors and how these representations flexibly change in the context of the whole nervous system was unknown. To address this question, we developed technologies to acquire high quality brain-wide activity and behavioral data. Using the probabilistic encoder model CePNEM, we constructed a brain-wide map of how each neuron encodes behavior. By also determining the ground-truth identity of these neurons, we overlaid this map upon the physical wiring diagram. Behavioral information is richly expressed across the brain in many different forms – with distinct tunings, timescales, and levels of flexibility – that map onto the defined neuron classes of the C. elegans connectome.
Previous work showed that animal behaviors are accompanied by widespread changes in activity across the brain, resulting in a low-dimensional neural space53. Here we found that an extra layer of complexity emerged when we determined each neuron’s encoding of behavior. Representations were complex and diverse, and this heterogeneity could be largely explained by four motifs: varying timescales, non-linear tunings to behavior, conjunctive representations of multiple motor programs, and different levels of flexibility. Having many different forms of behavior representation present may confer the nervous system with computational flexibility. Depending on the context, the brain may be able to combine different representations to construct new coordinated behaviors. We did not distinguish whether a given neuron’s encoding of behavior reflected the neuron causally driving behavior versus receiving a corollary discharge or proprioceptive signal related to behavior32–37. Future work separating these classes of signals across the C. elegans network should reveal the full set of causal interactions between neurons and behavior.
While many neurons encoded current behavior, others integrated recent motor actions with varying timescales. This allows the brain to encode the animal’s locomotion state of the recent past. Combining representations with different timescales could allow the animal’s nervous system to perform computations that relate past and present behavior. We also observed that the dynamics of the nervous system can change over longer time courses. In particular, many neurons flexibly remapped their relationships to behavior over minutes. These changes may be triggered by changes in neuromodulation or other state-dependent shifts in circuit function. This remapping may then change sensorimotor responses and the generation of behavior.
Our results here reveal how neurons across the C. elegans nervous system encode the animal’s behavior. Under the environmental conditions explored here, we observed that ~30% of the worm’s nervous system can flexibly remap. Future studies conducted in a wider range of contexts will reveal whether this comprises the core flexible neurons in the connectome or, alternatively, whether the neurons that remap differ depending on context or state.
LIMITATIONS OF THE STUDY
We wish to highlight three limitations of our study. First, our neural recordings were performed using nuclear-localized GCaMP. While this makes brain-wide recordings feasible, the spatial and temporal resolution of this imaging is more limited than other approaches. Second, some recorded neurons were not well fit by CePNEM. Our results suggest that these neurons may carry sensory, internal, or behavioral information not studied here, but additional work will be necessary to resolve this. Finally, we examined animals under a limited set of environmental conditions. Future recordings in different contexts may identify other types of behavior encoding not yet revealed in our recordings.
STAR METHODS
RESOURCE AVAILABILITY
Lead Contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the lead contact, Steven Flavell (flavell@mit.edu).
Materials Availability
All plasmids, strains, and other reagents generated in this study are freely available upon request. The key strains SWF415 and SWF702 are openly available through the Caenorhabditis Genetics Center (CGC).
Data and Code Availability
Data: All brain-wide recordings and accompanying behavioral data are freely available in a browsable and downloadable format at www.wormwideweb.org. The data files have also been deposited at Zenodo and Github and are publicly available as of the date of publication. DOIs are listed in the key resources table.
Code: All original code has been deposited at Github and Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the Lead Contact upon request.
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Bacterial and Virus Strains | ||
| E. coli: Strain OP50 | Caenorhabditis Genetics Center (CGC) | OP50 |
| Chemicals, Peptides, and Recombinant Proteins | ||
| Rhodamine 110 | Millipore Sigma |
Cat#83695 |
| Rhodamine B | Millipore Sigma |
Cat#83689 |
| Deposited Data | ||
| Original code and data related to recording and analyzing neural activity and behavior | This paper | Data: https://doi.org/10.5281/zenodo.8150515 and www.wormwideweb.org Code: https://doi.org/10.5281/zenodo.8151918 and https://github.com/flavell-lab/AtanasKim-Cell2023 |
| Experimental Models: Organisms/Strains | ||
| C. elegans: flvIsl 7[tag-168: :NLS-GCaMP7F, gcy-28.d::NLS-tag-RFPt, ceh-36:NLS-tag-RFPt, inx-1::tag-RFPt, mod-1 ::tag-RFPt, tph-1 (short)::NLS-tag-RFPt, gcy-5::NLS-tag-RFPt, gcy-7::NLS-tag-RFPt]; flvIs18[tag-168: :NLS-mNeptune2.5]; lite-1(ce314); gur-3(ok2245) | This paper | SWF415 |
| C. elegans: flvIs17; otIs670 [low-brightness NeuroPAL]; lite-1(ce314); gur-3(ok2245) | This paper | SWF702 |
| C. elegans: flvEx450[eat-4::NLS-GFP, tag-168: :NLS-mNeptune2.5]; lite-1(ce314); gur-3(ok2245) | This paper | SWF360 |
| C. elegans: flvEx451[tag-168::NLS-GFP, tag-168::NLS-mNeptune2.5]; lite-1(ce314); gur-3(ok2245) | This paper | SWF467 |
| C. elegans: flvEx207[nlp-70::HisCl1, elt-2::nGFP] | This paper | SWF515 |
| C. elegans: flvEx301[tbh-1:: TeTx: :sl2-mCherry, elt-2::nGFP] | This paper | SWF688 |
| C. elegans: flvEx481[flp-8::inv[unc-103-sl2-GFP], ceh-6::cre, myo-2::mChrimson] | This paper | SWF996 |
| C. elegans: flvEx482[unc-25::inv[unc-103-sl2-GFP], flp-22::cre, myo-2::mChrimson] | This paper | SWF997 |
| C. elegans: kyEx4268 [mod-1::nCre, myo-2::mCherry]; kyEx4499 [odr-2(2b)::inv[TeTx::sl2GFP], myo-3::mCherry] | This paper | SWF703 |
| C. elegans: leIs4207 [Plad-2::CED-3 (p15), Punc-42::CED-3 (p17), Plad-2::GFP, Pmyo-2::mCherry] | This paper | UL4207 |
| C. elegans: leIs4230 [Pflp-12s::CED-3 (p15), Pflp-12s::CED-3 (p17), Pflp-12s::GFP, Pmyo-2::mCherry] | This paper | UL4230 |
| C. elegans: flvEx485[gcy-21::Chrimson-t2a-mScarlett, elt-2::nGFP] | This paper | SWF1000 |
| C. elegans: flvEx502[ceh-28::GtACR2-t2a-GFP, myo-2::mCherry] | This paper | SWF1026 |
| C. elegans: flvEx499[ceh-19::inv[GtACR2-sl2-GFP], ins-10::nCre, myo-2::mCherry] | This paper | SWF1023 |
| Recombinant DNA | ||
| pSF300 [tag-168 ::NLS-GCaMP7F] | This paper | pSF300 |
| pSF301[tag-168::NLS-mNeptune2.5] | This paper | pSF301 |
| pSF302[tag-168::NLS-GFP] | This paper | pSF302 |
| pSF303 [tag-168::NLS-tag-RFPt] | This paper | pSF303 |
| Software and Algorithms | ||
| NIS-Elements (v4.51.01) | Nikon | https://www.nikoninstruments.com/products/software |
| Other | ||
| Zyla 4.2 Plus sCMOS camera | Andor | N/A |
| Ti-E Inverted Microscope | Nikon | N/A |
EXPERIMENTAL MODEL AND STUDY PARTICIPANT DETAILS
C. elegans
C. elegans Bristol strain N2 was used as wild-type. All transgenic and mutant strains used in this study are listed in the Key Resources Table. One day-old adult hermaphrodite animals were used for experiments, after growth on nematode growth medium (NGM) supplemented with OP50. For crosses, animals were genotyped by PCR. For making transgenic animals, DNA was injected into the gonads of young adult hermaphrodites.
METHOD DETAILS
Transgenic animals
Four transgenic strains were used for large-scale recordings in this study, as described in the text. The first (SWF415) contained two integrated transgenes: (1) flvIs17: tag-168::NLS-GCaMP7f, along with NLS-TagRFP-T expressed under the followed promoters: gcy-28.d, ceh-36, inx-1, mod-1, tph-1(short), gcy-5, gcy-7; and (2) flvIs18: tag-168::NLS-mNeptune2.5. The second strain we recorded (SWF702) contained two integrated transgenes: (1) flvIs17: described above; and (2) otIs670: low-brightness NeuroPAL (Yemini et al., 2021). Strains were backcrossed 5 generations after integration events. The third and fourth strains are non-integrated transgenic strains expressing NLS-GFP and NLS-mNeptune2.5 in defined neurons, listed in the Key Resources Table (SWF360 and SWF467).
We also generated strains for neural activation and silencing. The promoters used for cell-specific expression were as follows: RIC (Ptbh-1), AIM (Pnlp-70), AUA (Pflp-8+Pceh-6; intersectional Cre/Lox), AVL (Punc-25+Pflp-22; intersectional Cre/Lox), RIF (Podr-2b+Pmod-1; intersectional Cre/Lox), SAA (Plad-2+Punc-42; split Caspase), SMB (Pflp-12, 350bp), ASG (Pgcy-21), M4 (Pceh-28), MC (Pceh-19+Pins-10; intersectional Cre/Lox). The split caspase plasmids have been previously described54. For Cre/Lox intersection expression, we used the inverted/floxed plasmid design that has been previously described18. All promoters, including Cre/Lox intersectional combinations, were validated via co-expression of fluorophores (which were co-expressed via sl2 or t2a in each strain). Cell ablation lines were confirmed by loss of co-expressed GFP signal in the ablated cells.
Recordings of neural activity and behavior
Microscope
Animals were recorded under a dual light-path microscope that is similar though not identical to one that we have previously described20. The light path used to image GCaMP, mNeptune, and the fluorophores in NeuroPAL at single cell resolution is an Andor spinning disk confocal system with Nikon ECLIPSE Ti microscope. Light supplied from a 150 mW 488 nm laser, 50 mW 560 nm laser, 100 mW 405 nm laser, or 140 mW 637 nm laser passes through a 5000 rpm Yokogawa CSU-X1 spinning disk unit with a Borealis upgrade (with a dual-camera configuration). A 40x water immersion objective (CFI APO LWD 40X WI 1.15 NA LAMBDA S, Nikon) with an objective piezo (P-726 PIFOC, Physik Instrumente (PI)) was used to image the volume of the worm’s head (a Newport NP0140SG objective piezo was used in a subset of the recordings). A custom quad dichroic mirror directed light emitted from the specimen to two separate sCMOS cameras (Zyla 4.2 PLUS sCMOS, Andor), which had in-line emission filters (525/50 for GcaMP/GFP, and 610 longpass for mNeptune2.5; NeuroPAL filters described below). Data was collected at 3 × 3 binning in a 322 × 210 region of interest in the center of the field of view, with 80 z planes collected at a spacing of 0.54 um. This resulted in a volume rate of 1.7 Hz (1.4 Hz for the datasets acquired with the Newport piezo).
The light path used to image behavior was in a reflected brightfield (NIR) configuration. Light supplied by an 850-nm LED (M850L3, Thorlabs) was collimated and passed through an 850/10 bandpass filter (FBH850–10, Thorlabs). Illumination light was reflected towards the sample by a half mirror and was focused on the sample through a 10x objective (CFI Plan Fluor 10x, Nikon). The image from the sample passed through the half mirror and was filtered by another 850-nm bandpass filter of the same model. The image was captured by a CMOS camera (BFS-U3–28S5M-C, FLIR).
A closed-loop tracking system was implemented in the following fashion. The NIR brightfield images were analyzed at a rate of 40 Hz to determine the location of the worm’s head. To determine this location, the image at each time point is cropped and then analyzed via a custom-trained network with transfer learning using DeepLabCut40 that identified the location of three key points in the worm’s head (nose, metacorpus of pharynx, and grinder of pharynx). The tracking target was determined to be halfway between the metacorpus and grinder (central location of neuronal cell bodies). Given the target location and the error, the PID controller configured in disturbance rejection sends velocity commands to the stage to cancel out the motion at an update rate of 40 Hz. This permitted stable tracking of the C. elegans head.
Mounting and recording
L4 worms were picked 18–22 hours before the imaging experiment to a new NGM agar plate seeded with OP50 to ensure that we recorded one day-old adult animals. A concentrated OP50 culture to be used in the mounting buffer for the worm was inoculated 18h before the experiment and cultured in a 37C shaking incubator. After 18h of incubation, 1mL of the OP50 culture was pelleted, then resuspended in 40uL of M9. This was used as the mounting buffer. Before each recording, we made a thin, flat agar pad (2.5cm × 1.8cm × 0.8mm) with NGM containing 2% agar. On the 4 corners of the agar pad, we placed a single layer of microbeads with a diameter of 80um to alleviate the pressure of the coverslip on the worm. Then a worm was picked to the middle of the agar pad, and 9.5uL of the mounting buffer was added on top of the animal. Finally, a glass coverslip (#1.5) was added on top of the worm. This caused the mounting buffer to spread evenly across the slide. We waited for 5 minutes after mounting the animal before imaging.
Procedure for NeuroPAL imaging
For NeuroPAL recordings, animals were imaged as described above, but they were subsequently immobilized by cooling, after which multi-spectral information was captured. The slide was mounted back on the confocal with a thermoelectric cooling element attached to it, set to cool the agar temperature to 4°C 55. A closed-loop temperature controller (TEC200C, Thorlabs) with a micro-thermistor (SC30F103A, Amphenol) embedded in the agar kept the agar temperature at the 1 °C set point. Once the temperature reached the set point, we waited 5 minutes for the worm to be fully immobilized before imaging. Details on exactly which multi-spectral images were collected are in the NeuroPAL annotation section below.
Heat stimulation
For experiments involving heat stimulation, animals were recorded using the procedure described above, but were stimulated with a 1436-nm 500-mW laser (BL1436-PAG500, Thorlabs) a single time during the recording. The laser was controlled by a driver (LDC220C, Thorlabs) and cooled by the built-in TEC and a temperature controller (TED200C, Thorlabs). The light emitted by the laser fiber was collimated by a collimator (CFC8-C, Thorlabs) and expanded to be about 600 um at the sample plane. The laser light was fed into the NIR brightfield path via a dichroic with 1180-nm cutoff (DMSP1180R, Thorlabs). We determined the amplitude and kinetics of the heat stimulus in calibration experiments where temperature was determined based on the relative intensities of rhodamine 110 (temperature-insensitive) and rhodamine B (temperature-sensitive). This procedure was necessary because the thermistor size was considerably larger than the 1436-nm illumination spot, so it could not provide a precise measurement of temperature within the spot. Slides exactly matching our worm imaging slides were prepared with dyes added (and without worms). Dyes were suspended in water at 500mg/L and diluted into both agar and mounting buffer at a 1:100 dilution (final concentration of 5mg/L). Rhodamine 110 was imaged using a 510/20 bandpass filter and rhodamine B was imaged with a 610LP filter. We recorded data using the confocal light path during a calibration procedure where a heating element ramped the temperature of the entire agar pad from room temp to >50°C. Temperature was simultaneously recorded via a thermistor embedded on the surface of the agar, approximating the position of the worm. Fluorescence was also recorded at the same time, at the precise position where the worm’s head is imaged. This yielded a calibration curve that mapped the ratio of Rhodamine B/Rhodamine 110 intensity at the site of the worm’s head onto precise temperatures. Slides were then stimulated with the 1436-nm laser using identical setting to the experiments with animals. The response profile of the ratio of the fluorescent dyes was then converted to temperature. We quantitatively characterized the change in temperature, noting the mean temperature over the first second of stimulation (set to be exactly 10.0°C) and its decay (0.39 sec exponential decay rate, such that it returns to baseline within 3 sec).
Extraction of behavioral parameters from NIR videos
We quantified behavioral parameters of recorded animals by analyzing the NIR brightfield recordings. All of these behaviors are initially computed at the NIR frame rate of 20Hz, and then transformed into the confocal time frame using camera timestamps, averaging together all of the NIR data corresponding to each confocal frame.
Velocity
First, we read out the (x,y) position of the stage (in mm) as it tracks the worm. To account for any delay between the worm’s motion and stage tracking, at each time point we added the distance from the center of the image (corresponding to the stage position) to the position of the metacorpus of pharynx (detected from our neural network used in tracking). This then gave us the position of the metacorpus over time. To decrease the noise level (eg: from neural network and stage jitter), we then applied a Group-Sparse Total-Variation Denoising algorithm to the metacorpus position. Differentiating the metacorpus position then gives us a movement vector of the animal.
Because this movement vector was computed from the location of the metacorpus, it contains two components of movement: the animal’s velocity in its direction of motion, and oscillations of the animal’s head perpendicular to that direction. To filter out these oscillations, we projected the movement vector onto the animal’s facing direction, i.e. the vector from the grinder of the pharynx to its metacorpus (computed from the stage-tracking neural network output). The result of this projection is a signed scalar, which is reported as the animal’s velocity.
Worm spline and body angle
To generate curvature variables, we trained a 2D U-Net to detect the worm from the NIR images. Specifically, this network performs semantic segmentation to mark the pixels that correspond to the worm. To ensure consistent results if the worm intersects itself (for instance, during an omega-turn), we use information from worm postures at recent timepoints to compute where a self-intersection occurred, and mask it out. Next, we compute the medial axis of the segmented and masked image and fit a spline to it. Since the tracking neural network was more accurate at detecting the exact position of the worm’s nose, we set the first point of the spline to the point closest to the tracking neural network’s nose position. We next compute a set of points along the worm’s spline with consistent spacing (8.85 μm along the spline) across time points, with the first point at the first position on the spline. Body angles are computed as the angles that vectors between adjacent points make with the x-axis; for example, the first body angle would be the angle that the vector between the first and second point makes with the x-axis, the second body angle would be , and so on.
Head curvature
Head curvature is computed as the angle between the points 1, 5, and 8 (ie: the angle between and ). These points are 0 μm, 35.4 μm, and 61.9 μm along the worm’s spline, respectively.
Angular velocity
Angular velocity is computed as smoothed , which is computed with a linear Savitzky-Golay filter with a width of 300 time points (15 seconds) centered on the current time point.
Body curvature
Body curvature is computed as the standard deviation of for between 1 and 31 (ie: going up to 265 μm along the worm’s spline). This value was selected such that this length of the animal would almost never be cropped out of the NIR camera’s field of view. To ensure that these angles are continuous in , they may each have added or subtracted as appropriate.
Feeding (pumping rate)
Pumping rate was manually annotated using Datavyu, by counting each pumping stroke while watching videos slowed down the 25% of their real-time speeds. The rate is then filtered via a moving average with a width of 80 time points (4 seconds) to smoothen the trace into a pumping rate rather than individual pumping strokes.
Extraction of normalized GCaMP traces from confocal images
We developed the Automatic Neuron Tracking System for Unconstrained Nematodes (ANTSUN) software pipeline to extract neural activity (normalized GCaMP) from the confocal data consisting of a time series of z-stacks of two channels (TagRFP-T or mNeptune2.5 for the marker channel and gCaMP7f for the neural activity channel). Each processing step is outlined below.
Pre-processing
The raw images first go through several pre-processing steps before registration and trace extraction. For datasets with a gap in the middle, all of the following processing is done separately and independently on each half of the dataset.
Shear correction
Shear correction is performed on the marker channel, and the same parameters are also used to transform the activity channel. Since the images in a z-stack are acquired over time, there exists some translation across the images within the same z-stack, causing some shearing. To resolve this, we wrote a custom GPU accelerated version of the FFT based subpixel alignment algorithm 56. Using the alignment algorithm, each successive image pair is aligned with x/y-axis translations.
Image cropping
We crop the z-stacks to remove the irrelevant non-neuron pixels. For each z-stack in the time series, the shear-corrected stack is first binarized by thresholding intensity. Using principal component analysis on the binarized worm pixels, the rotation angle about the z-axis is determined. Then the stack is rotated about the z-axis with the determined angle to align the worm’s head. Then the 3D bounding box is determined using the list of worm pixels after the rotation. Finally, the rotated z-stack is cropped using the determined 3D bounding box. Similar to shear correction, this procedure is first done on the marker channel, and the same parameters are then applied to the activity channel.
Image filtering using total variation minimization
To filter out noise on the marker channel images, we wrote a custom GPU accelerated version of the total variation minimization filtering method, commonly known as the ROF model 57. This method excels at filtering out noise while preserving the sharp edges in the images. Note that the activity channel is kept unfiltered for GCaMP extraction.
Registering volumes across time points
To match the neurons across the time series, we register the processed z-stacks across time points. However, simply registering all time points to a single fixed time point is intractable because of the high amount of both global and small-scale deformations. To resolve this, we compute a similarity metric across all possible time point pairs that reports the similarity of worm postures. We then use this metric to construct a registration graph where nodes are timepoints and edges are added between timepoints with high posture similarity. The graph is constrained to be fully connected with an average connectedness of 10. Therefore, it is possible to fully link each time point to every other time point. Using this graph, we register strategically chosen pairs of z-stacks from different time points (i.e. the ones with edges). The details of the procedure are outlined below.
Posture similarity determination
For each z-stack, we first find the anterior tip of the animal using a custom trained 2D U-Net, which outputs the probability map of the anterior tip given a maximum intensity projection of the z-stack. We then fit a spline across the centerline of the neuron pixels beginning at the determined anterior tip, which is the centroid of the U-Net prediction. Using the spline, we compare across time points pairs to determine the similarity.
Image registration graph construction
Next, we construct a graph of registration problems, with time points as vertices. For each time point, an edge is added to the graph between that time point and each of the ten time points with highest similarity to it. The graph is then checked for being connected.
Image registration
For each registration problem from the graph, we perform a series of registrations that align the volumes, iteratively in multiple steps in increasing complexity: Euler (rotation and translation), affine (linear deformation), and B-spline (non-linear deformation). In particular, the B-spline registration is performed in four scales, decreasing from global (the control points are farther apart) to local (the control points are placed closer together) registration. The image registrations and transformations are performed using elastix on OpenMind, a high-performance computing cluster. They are performed on the mNeptune2.5 marker channel.
Channel alignment registration
To align the two cameras used to acquire the marker and the activity channels, we perform Euler (translation and rotation) registration across the two channels over all time points. Then we average the determined transformation parameters from the different time points and apply across all time points.
Neuron ROI determination
To segment out the pixels and find the neuron ROIs, we first use a custom trained 3D U-Net. The instance segmentation results from the U-Net are further refined with the watershed algorithm.
Simultaneous semantic and instance segmentation with 3D U-Net
We trained a 3D U-Net to simultaneously perform semantic and instance segmentation of the neuronal ROIs in the z-stacks of the unfiltered marker images. To achieve instance segmentation, we labeled and assigned high weights to the boundary pixels of the neurons, which guides the network to learn to segment out the boundaries and separate out neighboring neurons. Given a z-stack, the network outputs the probability of each pixel being a neuron. We threshold and binarize this probability volume to mark pixels that are neurons.
Instance segmentation refinement
To refine the instance segmentation results from the 3D U-Net, we perform instance segmentation using the watershed algorithm. This generates, for each time point, a set of ROIs in the marker image corresponding to distinct neurons.
Neural trace extraction
ROI Similarity Matrix
To link neurons over time, we first create a symmetric similarity matrix, where is the number of total ROIs detected by our instance segmentation algorithm across all time points. Thus, for each index in this matrix, we can define the corresponding time point and the corresponding ROI from that time point. This matrix is sparse, as its th entry is nonzero only if there was a registration between and that maps the ROI to . In the case of such a registration existing, the th entry of the matrix is set to a heuristic intended to estimate confidence that the ROIs and are actually the same neuron at different timepoints. This heuristic includes information about the quality of the registration mapping to (computed using Normalized Correlation Coefficient), the fractional volume of overlap between the registration-mapped and (i.e. position similarity), the difference in marker expression between and (i.e. similarity of mNeptune expression), and the fractional difference in volume between and (i.e. size similarity of ROIs). The diagonal of the matrix is additionally set to a nonzero value.
Clustering the Similarity Matrix
Next, we cluster the rows of this similarity matrix using a custom clustering method; each resulting cluster then corresponds to a neuron. First, we construct a distance matrix between rows of the similarity matrix using L2 Euclidean distance. Next, we apply minimum linkage hierarchical clustering to this distance matrix, except that after a merge is proposed, the resulting cluster is checked for ROIs belonging to the same time point. If too many ROIs in the resulting cluster belong to the same time point, that would signify an incorrect merge, since neurons should not have multiple different ROIs at the same time point. Thus, if that happens, the algorithm does not apply that merge, and continues with the next-best merge. This continues until the algorithm’s next best merge reaches a merge quality threshold, at which point it is terminated, and the clusters are returned. These clusters define the grouping of ROIs into neurons.
Linking multiple datasets
For datasets that were recorded with a gap in the middle, the above process was performed separately on each half of the data. Then, the above process was repeated to link the two halves of the data together, except that only two edges that must connect to the other half of the data are added to the registration graph per time point, and the clustering algorithm does not merge clusters beyond size 2.
Trace extraction
Next, neural traces are extracted from each ROI in each time point belonging to that neuron’s cluster. Specifically, we obtain the mean of the pixels in the ROI at that time point. This is done in both the marker and activity channels. They are then put through the following series of processing steps:
Background-subtraction, using the median background per channel per time point.
Deletion of neurons with too low of signal in the activity channel (mean activity lower than the background – this was not done in the SWF360 control dataset due to the presence of GFP-negative neurons in that strain), or too few ROIs corresponding to them (less than half of the total number of time points).
Correction to account for laser intensity changing halfway through our recording sessions (done separately on each channel based on intensity calibration measurements taken at various values of laser power).
Linear interpolation to any time point that lacked an ROI in the cluster.
Division of the activity channel traces by the marker channel traces, to filter out various types of motion artifacts. These divided traces are the neural activity traces.
Bleach correction
We then compute the mean neural activity (averaged across all neurons) over the entire time range, and fit a one-parameter exponential bleaching model to it. The bleaching model was initialized such that it had value equal to the median neural activity value at the median time point, and it was fit using log-MSE error to the averaged neural activity value. A small number of datasets with very high bleaching (determined using the exponential decay parameter of the bleaching model) were excluded from all analysis. Each neural activity trace is then divided by the best-fit bleaching curve; the resulting traces are referred to as . In our SWF360 analysis, we refer directly to ; the trace heatmaps shown in this paper are ; we also display z-scored neural activity in many figure panels, as indicated; and the CePNEM models are fit by z-scoring each neuron separately.
Controls to test whether neurons are correctly linked over time
We ran a control to test whether neurons were being mismatched by our registration process. We did this by processing data from our SWF360 strain that expresses GFP at different levels in different neurons (eat-4::NLS-GFP). The recording was made with a gap and was processed identically to GCaMP datasets with gaps in the middle, thus also serving as a test of inter-gap registration. This SWF360 recording allows us to detect errors in neuron registration, since GFP-negative neuron could briefly become GFP-positive or vice versa. We quantified this by setting a threshold of median to call a neuron a GFP neuron. This threshold resulted in of neurons being quantified as containing GFP, which is about what was expected for the promotors expressed. Then, for each neuron, we quantified the number of time points such that the neuron’s activity at that time point differed from its median by more than 1.5, and exactly one of [the neuron’s activity at that time point] and [its median activity] was larger than 1.5. These time points represent mismatches, since they correspond to GFP-negative neurons that were mismatched to GFP-positive neurons (if the neuron’s activity increased at the time point) or vice versa (if its activity decreased). We then computed an error rate of as an estimate of the mis-registration rate of our pipeline. The term corrects for the fact that mis-registration errors that send GFP-negative to other GFP-negative neurons, or GFP-positive to other GFP-positive neurons, would otherwise not be detected by this analysis. This error rate came out to 0.3%, so we conclude that artifacts resulting from mismatched neurons are a negligible component of our data.
Annotation of neural identities using NeuroPAL
NeuroPAL images and annotation procedure
The identities of neurons were determined via NeuroPAL using the following procedure. We obtained a series of images from each recorded animal, while the animal was immobilized after the freely-moving GCaMP recording (recording and immobilization procedures described above):
(1–3) Spectrally isolated images of mTagBFP2, CyOFP1, and mNeptune2.5. We excited CyOFP1 using the 488nm laser at 32% intensity under a 585/40 bandpass filter. mNeptune2.5 was recorded next using a 637nm laser at 48% intensity under a 655LP-TRF filter, in order to not contaminate this recording with TagRFP-T emission. Finally, mTagBFP2 was isolated using a 405nm laser at 27% intensity under a 447/60 bandpass filter.
(4) An image with TagRFP-T, CyOFP1, and mNeptune2.5 (all of the “red” markers) in one channel, and gCaMP7f in the other channel. As described below, this image was used for neuron segmentation and registration with both the freely moving recording and individually isolated marker images. We excited TagRFP-T and mNeptune2.5 via 561nm laser at 15% intensity and CyOFP1 and gCaMP7f via 488nm laser at 17% intensity. TagRFP-T, mNeptune2.5, and CyOFP1 were imaged with a 570LP.
All isolated images were recorded for 60 timepoints. We increased the signal to noise ratio for each of the images by first registering all timepoints within a recording to one another and then averaging the transformed images. Finally, we created the composite, 3-dimensional RGB image by setting the mTagBFP2 image to blue, CyOFP1 image to green, and mNeptune2.5 image to red as done by Yemini et al. (2021) and manually adjusting the intensity of each channel to optimally match their manual.
The neuron segmentation U-Net was run on the “all red” image and we then determined the identities of U-Net identified neurons using the NeuroPAL instructions. The landmarks in the NeuroPAL atlas were identified first and the identities of the remaining neurons were subsequently determined by comparing the individual channel intensities, overall coloring, and relative positioning of the cells. In some cases, neuronal identities could not be determined with certainty due a number of factors including: unexpectedly dim expression of one or more fluorophores, unexpected expression of a fluorophore in cells not stated to express a given marker, and extra cells in a region expressing similar intensities when no other cells are expected. Rarely, multiple cells were labeled as potential candidates for a given neuron and the most likely candidate (based on position, coloring, and marker intensity) was used for analysis. If a cell was not bright enough to be distinguished from its neighbors or was undetected by the neuron segmentation U-Net, we left it unlabeled.
Finally, the neural identity labels from the RGB image were mapped back to the GCaMP traces from the freely-moving animal by first registering each fluorophore-isolated image to the image containing all of the red markers. The “all red” image was then registered back to the freely moving recording, permitting mapping of neuronal labels back to GCaMP traces.
Determination of left/right asymmetry
To determine which neuron classes had left/right asymmetry, we computed the mean correlation between the left and right neurons in each neuron class over all datasets where both the left and right neurons in that neuron class were detected. We included our heat-stimulus datasets in this analysis, but for those datasets the correlation was only computed using the pre-stim data; for our baseline datasets, the entire time series was used. For a neuron to be marked as having left/right asymmetry, we required that (i) we recorded at least five animals where both the left and right neurons of the pair were detected, (ii) the left and right neurons had a mean correlation averaged across animals of <0.2, and (iii) the neuron had a mean signal value (averaged across animals) of at least 0.25. The signal value threshold was intended to exclude inactive neurons with low correlation values due to noise. This analysis resulted in the neurons ASE, IL1, IL2, and SAAD showing left/right asymmetry.
C. elegans Probabilistic Neural Encoding Model (CePNEM)
CePNEM Residual Model
The CePNEM model uses a Gaussian process residual model adding together a white-noise kernel and a squared exponential kernel. The white-noise kernel is intended to capture measurement noise in our neural data, which is expected to be independent between time points, while the squared exponential kernel is intended to capture variance in neural activity unrelated to behavior, which may have a slower timescale. The squared-exponential residual term is critically important, as otherwise the model will be forced to try to explain all autocorrelation in neural activity with behavioral information, resulting in severe overfitting.
The white-noise kernel has standard deviation and thus its covariance matrix is . The squared-exponential kernel has standard deviation and length scale , giving a covariance matrix defined by . The full residual model is then the Gaussian process model with kernel , which is then added to the timeseries of the rest of the model fit to generate the likelihood of a given neural activity trace under CePNEM.
CePNEM Prior Distributions
Here is the normal distribution with mean and standard deviation . Since the neural traces being fit are all z-scored, the priors on the behavioral parameters are also standardized. The prior on the moving average term was based on preliminary data from fitting previous, conventional versions of our model. The priors on the residual terms were intended to be wide enough to accommodate both neurons that are well-explained by behaviors (in which case, the model would assign them a low residual value), and neurons that contain little to no information about behaviors (in which case, the model would assign them a high residual value).
Fitting procedure
Overview of fitting approach
Let N be a neural trace from an animal, B be the behaviors of that animal, and be the model parameters that we are trying to fit. Then the goal our model fitting procedure is to estimate the probability distribution of model parameters given our observations, namely . Our model defines the likelihood – that is, the likelihood of observing a set of neural data given a set of model parameters and behavioral data. Our prior distributions define ; in this case, our prior distributions on model parameters are independent of the animal’s behaviors, so . Therefore, by Bayes’ rule,
Unfortunately, is difficult to compute. Crucially, however, it does not depend on the model parameters . This means that by comparing the value of for different values of , we can make meaningful insights into the distribution of . In particular, we can define a Markov chain that defines a sequence of , where is a stochastic “proposal function” of . The idea is that the proposal function can be biased to walk toward regions in parameter space with higher likelihood. Indeed, there are a family of algorithms, such as Metropolis-Hastings58 and Hamiltonian Monte Carlo59 that define such proposal functions. In particular, the proposal functions defined by these algorithms have the property that, in the limit of generating an infinitely long Markov chain, sampling from the chain is equivalent to sampling from the true posterior distribution .
Model fitting procedure
Of course, in practice, we do not have computational resources for an infinitely long chain, so it is necessary to ensure that the chain can replicate the posterior distribution in a manageable amount of time. This in turn requires custom inference algorithms, moving beyond the generic MCMC and variational inference algorithms provided with probabilistic programming platforms such as Stan and Pyro. Accordingly, we used the Gen probabilistic programming platform44, and its inference meta-programming functionality60, to express a suitable custom inference algorithm.
We fit our models using a mixture of Metropolis-Hastings (MH) and Hamiltonian Monte Carlo (HMC) steps with adaptive proposals, embedded within a resample-move sequential Monte Carlo (SMC) scheme55 with one particle. The HMC step uses gradient information and tries to move the chain towards regions of higher likelihood. The other MH steps are intended to help the chain get out of local optima by using information about the structure of the model, so the Markov chain can better explore the full parameter space. Specifically, one iteration of our fitting algorithm involves the following steps (here is once again the normal distribution, and is drawn uniformly at random from the set {−1,1}), and is the current iteration of the algorithm:
MH proposal
MH proposal:
MH proposal:
HMC proposal on parameters with
MH proposal:
- MH proposal (note that the instances of are drawn independently):
After each iteration of the algorithm, the proposal distribution parameters for each proposal are updated as follows: If the respective proposal was accepted, its parameter is multiplied by 1.1; otherwise, it is divided by 1.1. (They are all initialized to 1.) This adaptive, heuristic choice of proposal distribution aims to encourage proposals that are accepted roughly half the time. Although repeated iteration of these adaptive proposals does not guarantee convergence via the usual MCMC convergence theory, these adaptive proposals remain valid target-preserving MCMC rejuvenation kernels for use within resample-move SMC. To construct the posterior samples used in our analysis, we run this fitting procedure for 11,000 iterations, and discard the first 1,000 (including the initialization point). The remaining 10,001 points are treated as approximate samples from the posterior distribution and are referred to as particles elsewhere in the paper. Our control experiments, including simulation-based calibration (detailed below), suggest that this approach results in good quality approximations.
Model initialization
Despite our efforts to use MH proposal steps to prevent the model fitting procedure from falling into local optima, we found that the algorithm still occasionally got stuck, preventing it from finding a good approximation to the true posterior. To remedy this, we added a likelihood weighting initialization step consisting of sampling 100,000 points from the prior distribution of model parameters and selecting the point with the highest likelihood under our model, given the neural and behavioral data to be fit. This point is then used to initialize the resample-move SMC scheme described above.
Simulation-based calibration
To ensure that our fitting process gave a calibrated description of the true model posterior, we performed simulation-based calibration41. In this procedure, we generated 4,000 sample traces from the model distribution using the prior distribution for . 500 traces were generated using each of eight total values of : two 800-time-point subsegments from each of four animals (two SWF415, and two SWF702 animals). We then ran our model fitting procedure on each sample (three of the 4,000 traces timed out and were discarded). After fitting, we then compared the sampled posterior distribution from our inference algorithm to the ground-truth parameter values using a rank test with 128 bins. If our inference process was giving unbiased estimates of the posterior distribution, then across all of our traces, the distribution of these ranks should be the uniform distribution. Gen automated the implementation of this simulation-based calibration procedure.
We used a χ2 test to differentiate the observed ranks from the uniform distribution, and found that 9 of the 10 model parameters passed the test at p=0.05. The final parameter, the EWMA decay constant , seemed to have a minor bias towards larger values, meaning that our fitting algorithm is prone to occasionally overestimate this parameter. However, we quantified an upper bound on the degree of this overestimation by computing the maximum deviation of the CDF of the observed rank distribution for , compared with the predicted CDF from the uniform distribution, and found a value of 3.5%. This means that the fits of at most 3.5% of encoding neurons will be affected by this minor bias, which is less than an average of 4 per animal. Thus, we do not believe this minor bias will substantially affect the results described in this paper.
Controls
GFP Control
We wanted to ensure that we would not spuriously detect motion artifacts as encodings of behavior. To do this, we used our pan-neuronal GFP control line SWF467, which by definition should not have any neurons that encode behavior. We fit our GFP datasets with CePNEM and applied the same encoding analysis to this strain and found that only 2.1% of neurons showed behavioral encoding, compared with 58.6% in the SWF415 strain, suggesting that the majority (>95%) of our detected encodings are not motion artifacts. We also used the GFP recordings to determine which neurons displayed low or no neural dynamics in a given recording. We defined a neuron with low or no dynamics to be one whose signal variation, defined as where is un-normalized ratiometric fluorescence, was less than the 99th percentile of the signal variations of GFP neurons. For this analysis only (and not any other analyses in this paper), we fit a per-neuron bleaching model to each GCaMP neuron when computing its signal variation and used this corrected F, in order to ensure that apparently-active neurons were not due to GCaMP neurons having worse-quality bleach correction than the GFP controls.
Based on this analysis, 5.3% of the neurons were inactive across our recordings. The fraction of inactive neurons here appears to be lower than in some prior brain-wide recordings.3,26 This may be related to experimental conditions (immobilized versus freely-moving; off-food versus on-food) or differences in the SNR of the recordings, which determines the minimal neural signal that can be resolved from motion and data extraction artifacts.
Scrambled Control
We furthermore wanted to ensure that the model would not overfit to spurious correlations between neural activity and behavior. To accomplish this, we fit 11 SWF415 animals with CePNEM, but replaced the behaviors , and with spurious behaviors from other recorded animals, which should result in few neurons showing behavioral encoding. The spurious behaviors were generated as follows: we first assign pairs of datasets to minimize the behavioral correlation across the datasets within a given pair. To do this, we compute correlation across all possible behavior and dataset combinations. After that, we determine the pairing such that it minimizes the maximum absolute cross-correlation value across all pairings. To penalize high correlation values, we raised the correlations to the power of 4.
When we analyzed the CePNEM model results, we found that only 2.7% of neurons detected as having behavioral encoding, suggesting that the vast majority (>95%) of our detected encodings are not due to overfitting.
Median model fits
For display purposes, or analyses where it was necessary to represent a neuron with a single model, we computed the median model by computing for each set of parameters in the neuron’s posterior distribution, and then defining . This is what is meant by “median CePNEM fit” unless otherwise noted.
Validation metrics and analyses
Cross-validation (cv) score
The cross-validation pseudo-R2 metric, named ‘cross-validation score’ or simply ‘ score’ in the text, is defined by
Here is the mean squared error between data vectors and is the evaluation of the median CePNEM model fit over the ith training data split evaluated on the corresponding testing data is the mean neuron activity over the ith training data split, and is the observed neuron activity vector on the testing data . This metric is an approximation of the variance of the neural activity explainable by the model on the testing data.
Since CePNEM contains a Gaussian process residual model, it can only be trained over continuous data. Additionally, the presence of this Gaussian process residual model could cause the mathematical properties of the model to change slightly based on the length of training data. Thus, we structured our five-fold training/testing splits such that each training data split consisted of 8 minutes of continuous data, exactly as the model was fit in the rest of the paper. These training splits were uniformly tiled along the 16-minute recordings. The testing splits were then constructed such that they were equal length (20% of full dataset), each time point in the recording was included in exactly one of the testing splits, and each testing split was near (but not overlapping with) its corresponding training split.
We only computed the cross-validation score in situations where it would be reasonable to expect our model to cross-validate. In particular, since there is no expectation of our behavior-based model to cross-validate for neurons that don’t encode behavior, we ran it only on neurons that encoded behavior in both of the original 8-minute CePNEM fits in the dataset. Additionally, we excluded train/test splits where the training data did not contain feeding information while the testing data did, since in such splits there would be no way for any model to be able to constrain a feeding parameter in the training data (feeding was episodic in these datasets, giving rise to the necessity of imposing this constraint).
Bayesian Generalization Index (BGI)
We also computed a separate metric, which we call the Bayesian generalization index, to assess performance of the full CePNEM model, including the residual model, to generalize to withheld testing data. To compute it, each dataset was split in half temporally, and for each neuron, CePNEM models were fit on each half of the data (the training data). Each of those training models was then evaluated on the other half of the data (the testing data) as follows.
First, 500 training samples were drawn from the CePNEM posterior distribution from the training model. Each sample (a 10-vector of all CePNEM parameters) was then evaluated on the testing data using CePNEM likelihood to compute a training array of test-time scores.
Similarly, 500 control samples were drawn from the set of all CePNEM posteriors from all neurons in our 14 SWF415 baseline datasets. This was done instead of sampling from the model prior to ensure that high BGI values were specifically learned from the training data, rather than being generally learned properties that apply across neurons. Each of the 10 model parameters was drawn independently. Each of these control samples was then evaluated with CePNEM on the testing data to compute a control array of test-time scores.
The Bayesian generalization index for the given CePNEM training fit was then computed as
Here and are randomly sampled from the respective distributions of test-time scores. In this manner, if the BGI is very close to 1, it means that it is extremely unlikely for a randomly-sampled model set of model parameters to be able to match the performance of any of the training model parameters on the testing data. On the other hand, a BGI of 0 means that the training model did not outperform the control model, either because CePNEM failed to constrain the training posterior distributions, or because a substantial portion of them failed to generalize to the testing data. Negative BGI values indicate overfitting, where the model performs worse on the testing data than simply randomly sampled model parameters.
We computed this index over all neurons in all SWF415 datasets. Note that unlike the cross-validation score, we included non-encoding neurons in this analysis because we would expect them to generalize to the testing data through their CePNEM residual parameters, which are included in the BGI computation (though we note that they did perform worse on average than the encoding neurons). We observed that 91% of neurons had positive BGI values, and 48% of neurons had BGI values above 0.9, indicating a high level of model generalization. The results were very similar between SWF415 and NeuroPAL strains.
Comparison with simpler models
MSE model fits
For some analyses (in particular model degradation analyses where fitting many different models with probabilistic inference would be extremely computationally expensive), we found it useful to fit our model in a more conventional manner, simply trying to minimize the mean-squared error (MSE) between the model fit and neural activity rather than using Gen to compute the posterior. For these fits, we deleted the residual component of our model and instead simply fit by trying to minimize the MSE between it and the observed neural activity, set , and ignored the first 50 time points after each recording began for the MSE calculation (so for datasets with a gap in the middle, we would ignore the first 50 time points, as well as time points 801:850). We used L-BFGS for local optimization and MLSL-LDS for global optimization, and performed these fits using the NLopt Julia package.
Model degradation analysis
We tested how each component in the model affects the performance by quantifying the increase in error, compared to the full model, when removing the following component individually: each predictor (velocity, head curvature, feeding), the velocity non-linearity, removing the EWMA, and all non-linear features (resulting in a fully linear model). The models were fitted using our MSE fitting technique with L2 regularization. Out of the 14 pan-neuronal GCaMP baseline datasets, 5 were excluded from this analysis due to low variance in the pumping rate. 3 datasets were used to optimize the regularization parameter, and the remaining 6 datasets were used to compute the increase in error. Models were fit with 5-fold cross-validation set, splitting each dataset into 5 equal length time segments. The error was computed as the mean test time error of the cross-validation splits. For each degraded model type, neurons encoding the removed feature were selected for analysis. For example, degraded model without velocity was tested on the neurons with velocity encoding. The increase in error was computed by comparing the error in degraded model to the error of the full model. Finally, we used the Wilcoxon signed rank test for statistical significance.
Comparing exponentially-weighted moving average (EWMA) to other filtering methods
In Fig. S1D, alternative smoothing methods were evaluated to compare against the EWMA in the model. The alternatives were: optimal Gaussian kernel (Gaussian smoothing), optimal shift (shifting to maximize the absolute correlation), and optimal lowpass filter. For each method, including the EWMA, gradient descent was used to minimize the error (MSE) between the neural trace and the transformed velocity in order to find optimal filtered versions of velocity for each metho. This was repeated across all recorded neurons for the analysis in Fig. S1E. As is shown, EWMA performed the best.
Statistical tests to determine encoding properties of neurons
Summary of statistical approach
Our strategy for determining whether neurons encode a particular behavioral feature (for example, whether the neuron encoded ventral head curvature during forward locomotion) is briefly summarized here. More details are provided below.
-
We first convert the CePNEM parameters into a space where the encoding of the neuron to that behavioral feature can be quantified for each point in the posterior.
(‘Deconvolved activity matrix’ section below)
Compute an empirical p-value based on the fraction of points in the posterior with sufficiently strong encoding of the behavioral feature. “Sufficiently strong” means exceeding two thresholds that were defined based on GFP and wrong-behavior controls. (‘Statistical encoding tests’ section below).
Multiple-hypothesis correct these p-values across different types of tunings to each behavior, across neurons, and/or across time ranges, as appropriate for the analysis in question.
Deconvolved activity matrix
In order to be able to make statistical assertions about the neural encoding of behavior based on the posterior distributions from CePNEM fits, we first needed to transform model parameters into a more intuitive space. To accomplish this, for each neuron, we constructed a 10001 × 4 × 2 × 2 deconvolved activity matrix constructed as follows: corresponds to the modeled activity of the nth particle from that neuron’s CePNEM fit at velocity , head curvature , and pumping rate Here, where is the animal’s head curvature (dorsal is positive) and is the animal’s pumping rate over the course of the recording, we have:
For this calculation, the EWMA and residual components are excluded from the modeled activity; the idea is that this matrix contains information about the neuron’s activity at high and low values of each behavior, so we can now run analyses on this matrix and not have to take into account the actual behavior of the animal. In particular, many simple combinations of entries in this matrix have intuitive meanings:
- The slope of the neuron’s tuning to velocity during forward locomotion is
- The slope of the neuron’s tuning to velocity during reverse locomotion is
- The neuron’s deconvolved forwardness (overall slope of the neuron’s tuning to velocity) is
- The rectification of the neuron’s tuning to velocity (difference between forward and reverse slopes) is
- The slope of the neuron’s tuning to head curvature during forward locomotion (positive means dorsal during forward) is
- The slope of the neuron’s tuning to head curvature during reverse locomotion (positive means dorsal during reverse) is
- The neuron’s deconvolved dorsalness (overall slope of the neuron’s tuning to head curvature) is
- The rectification of the neuron’s tuning to head curvature with respect to locomotion direction (positive means the neuron is more dorsal during forward; negative means the neuron is more ventral during forward) is
The neuron’s tuning to feeding follows the same pattern as its tuning to head curvature.
Importantly, the linear structure of the multiplexing component of CePNEM implies that the value of the unset parameters in the expressions above do not change the value of those expressions. For head curvature, since worms can lay on either side, we manually checked the location of the animal’s vulva from the NIR recordings of each animal and flipped dorsal/ventral labels as appropriate.
Statistical encoding tests
With the intuition derived from the deconvolved activity matrix, for each particle in the posterior distribution of the neuron, we can ask whether that particle satisfies a certain property. For example, to categorize a particle as representing forward locomotion, we would check whether that particle had a sufficiently large deconvolved forwardness value. Specifically, we would check whether its deconvolved forwardness value was at least , where (here and is the un-normalized ratiometric fluorescence of the neuron in question), and (here is the standard deviation of the model fit corresponding to that particle with and is the standard deviation of the model fit corresponding to that particle). The number 0.125 was selected based on its ability to filter out the small amount of motion artifacts observed in our three GFP control datasets (see Methods section on that control above). Specifically, we chose a value that filtered out almost all of the motion artifacts (leaving only 2.1% of GFP neurons showing false behavioral encoding), while removing as few true encodings from our GCaMP data as possible. Similarly, the number 0.25 was selected based on its ability to filter out extremely weak correlations between neural activity and behavior, which was measured by our controls attempting to fit neurons with behaviors from different animals (after the correction, only 2.7% of such neurons showed behavioral encoding). The term is a correction for the fact that neurons with large values will have higher values in . If the particle’s deconvolved forwardness value was at least , it would be classified as representing forward locomotion.
By the same token, we would classify a particle as representing reverse locomotion if its deconvolved reverseness (negative forwardness) value was at least , we would classify a particle as representing more dorsal information during forward locomotion if its rectification to head curvature with respect to locomotion direction was at least , and so on.
Now that we can classify particles, we can create empirical p-values for neurons based on the fraction of their particles that share a category. For example, if 98% of particles for a neuron are classified as representing forward locomotion, then that neuron’s p-value for forward locomotion would be 0.02. We can then construct a list of such p values computed for each neuron in an animal that was fit with CePNEM and use Benjamini-Hochberg correction with FDR=0.05 to get a list of forward-encoding neurons in that animal. We can similarly get a list of reversal neurons, dorsally-rectified head curvature neurons, neurons activated by feeding during forward locomotion (i.e. have a positive slope to feeding during forward locomotion), and so on.
To construct larger categories, such as neurons with any behavioral encoding, or neurons with head curvature encoding, another multiple hypothesis correction step is necessary. For this step, we first use Bonferroni correction on opposing categories where it is impossible for a neuron to have both categories (for instance, dorsal and ventral tuning), followed by a Benjamini-Hochberg correction step on the Bonferroni-corrected p-values. We then proceed with the inter-neuron Benjamini-Hochberg correction, as before.
A neuron is categorized as encoding head curvature if it expresses statistically significant information about any of the four head curvature categories outlined above, in either direction; feeding encoding is computed similarly. A neuron is categorized as encoding velocity if it either expresses statistically significant information about any of the four velocity categories, or if it expresses statistically significant information about any of the rectified categories, since rectification of head curvature or feeding based on forward/reverse locomotion state is a form of velocity information. A neuron is categorized as encoding if it has statistically significant information in any of the tests. Note that for datasets without any feeding information (defined as the 25th and 75th percentile of feeding in that dataset being the same, causing ), neurons cannot encode feeding information, so feeding is not included in the multiple-hypothesis correction to check whether a neuron encoded any behavior.
Time ranges
One final note is that all neurons are fit twice – once over the first half of the data, and once over the second half. Thus, for consistency between all our datasets, we fit all of our SWF415 and NeuroPAL datasets in this manner.
For Figure 2A, the encoding statistics are computed on a per-neuron basis, with an additional Benjamini-Hochberg correction step to account for the fact that each neuron got two chances to qualify as encoding. Time ranges with insufficient feeding variance (this time, defined as the difference between the 25th and 75th percentile of feeding being at most 0.5) are excluded from feeding analysis. To avoid different behaviors having different amounts of available data, animals that never had sufficient feeding variance are excluded from Figure 2A entirely. For Figure 2B, the same analysis is used, and there is an additional multiple-hypothesis step across the three behaviors. For Figures 2C and S2I–J, all time ranges are used. Fits on different time ranges from the same animal are added to the CDF independently of each other, but only encoding neurons are included. For example, a neuron that encoded behavior in both time ranges would have its EWMA timescale from both fits added to the CDF, while a neuron that only encoded behavior once would have that EWMA timescale added. In Figure S2I–J, only neurons that statistically significantly encoded the appropriate behavior are included
Neuron Subcategorization
We next sought to combine various pieces of information from our encoding analysis together to generate a holistic view of how a given neuron is tuned to a given behavioral parameter (Figure 2E). To accomplish this, we sorted neurons as follows (this analysis is done independently on each time range):
If the neuron had a different sign to its tuning to behavior during forward and reverse (eg: a slow neuron that has a positive slope in its tuning to velocity during reversal, but a negative slope during forward locomotion), then the neuron was categorized as such. In Figures 2G–2I, these neurons would appear in the bins (+,−) and (−,+); for head curvature, they would be (D,V) or (V,D).
Otherwise, if the neuron has rectified tuning to the behavior (depending on the behavior, one of the following categories: forward slope > reverse slope, reverse slope < forward slope, more dorsal during forward, more ventral during more activated during forward, more activated during forward, or more inhibited during forward), it will be placed in one of the four rectified bins (+,0), (−,0), (0, −), or (0,+), depending on the sign of the rectification and sign of the slopes of the neural tuning to behavior.
Otherwise, if the neuron had the same slope during both forward and reverse movement, it will be classified in one of the two analog bins (+,+) or (−,−) depending on the sign of that slope. Notably, it would be placed in a rectified bin (and not an analog bin) if it had rectified information, even if it had the same slope during both forward and reverse locomotion.
If none of the above were true, the neuron lacked statistical significance in at least two of the three parameters (forward slope, reversal slope, rectification) with respect to the behavior in question, and it will be excluded from Figure 2E.
Methods to determine encodings of neuron classes across recordings
Hierarchical model to fit neuron classes recorded across multiple animals
Neuron classes that were detected in multiple animals had multiple CePNEM fits. To attain a more accurate depiction of the neuron across datasets, we used a hierarchical model that takes into account the parameters and uncertainty of each CePNEM fit to compute the global mean and variability between datasets. The global mean provides the best overall model to the neuron class, while the variability (see below for further details) provides a description of how reliably the neuron encodes behavior.
Specifically, if the neuron was detected n times, with CePNEM posteriors corresponding to each model fit , the hierarchical model fits maximum a posteriori (MAP) estimates of vectors of parameters , where . Here corresponds to the global mean parameters for the neuron taking into account its data across observations, corresponds to the global variability, and corresponds to a point estimate for the parameters of the neuron in each observation. The rough form of the hierarchical model is that come from a distribution determined by and , but simultaneously come from the distributions , so they are fit in such a way as to maximize the likelihood under both of these distributions.
More specifically, the parameters and are comprised of a 5-vector , where and are analogous to their respective CePNEM parameters, is a spherical-coordinate transform of . The variability is comprised of a 4-vector . The reason for the spherical transform is that some neural variability could be simply a result of different normalization in different animals, which is difficult to perfectly correct for; in spherical coordinates, all of that possibly-spurious variability is encapsulated in one parameter , rather than being spread across multiple parameters.
The likelihood function of the hierarchical model then specifies the distribution of the given and . Specifically, for the non-angle parameters, model assumes the normal distributions for . Meanwhile, the angular parameters are determined by a von Mises-Fisher distribution: for .
Finally, to ensure that the carry information about the actual CePNEM fits, the posterior distributions are first approximated by fitting them with a multivariate-normal distribution . This approximation was necessary in order to make the problem of fitting the hierarchical model computationally tractable. We verified using manual examination of Q-Q plots that the posteriors were well approximated by multivariate-normal distributions, though the approximation was not perfect. After this approximation, the parameters are transformed back to Cartesian coordinates and then the likelihood of these parameters under the multivariate-normal approximation is computed: . The other five CePNEM parameters are not of biological interest and are not included in the hierarchical model.
The priors for the hierarchical model are as follows (the priors for the mean values were created by examining the full set of CePNEM parameter values, after fitting):
Cartesian average
The hierarchical model was designed to compute neural variability, but we also found that it provided a useful method of measuring mean neural parameters across animals. However, for neurons with high variability, simply using as the mean parameters is not the correct metric since the spherical coordinates prevent it from properly canceling out opposing tunings (rather, it would instead try to pick an angle in between and keep the same ). Thus, we decided to instead convert all the of the model back into Cartesian coordinates and average them to produce , the Cartesian average model parameters of the neuron under the hierarchical model. This is what is being plotted in Figure S5E.
Forwardness, Dorsalness, and Feedingness
The forwardness metric for a neuron class is computed as signal, where is the deconvolved forwardness of the Cartesian average of the hierarchical model fit to that neuron class (see “Deconvolved activity matrix” and “Hierarchical model” methods sections above for more details; the behavior values used in the deconvolved forwardness computation were constructed by appending together all of the behaviors for the neuron class), is the standard deviation of the model fit corresponding to with is the standard deviation of the model fit corresponding to , and signal as before. This ratio is intended to correct for the fact that the model parameters need to be larger (resulting in larger deconvolved forwardness values) for the same neural response size if the neuron has a long EWMA decay. Dorsalness and feedingness are computed in a similar fashion.
Encoding strength and relative encoding strength
Encoding strength is a metric designed to approximate the information content a neuron contains about each behavior, given its CePNEM model fits. It is computed on each particle of the CePNEM posterior by generating three model traces , and , each of which is identical to the full model except that the behavior is set to 0 for model . Thus, the MSE between and provides a metric of how important behavior was for the neuron. We compute the relative encoding strength of a neuron to behavior as the ratio
For neuron classes labeled with NeuroPAL (eg: in Figures 4 and 5), instead of taking the median over parameters from the posterior distribution, we used one set of parameters which was the Cartesian average of the hierarchical model fit for that neuron, and we used behaviors constructed by appending together the behaviors from all observations of that neuron class. Then we define the encoding strength of the neuron to behavior as , where was the full model fit.
Analyses of dynamic encoding of behavior
Statistical tests to examine dynamic changes in neural encoding.
To determine whether a given neuron in a recording changed how it encoded behavior, we used the following procedure. First, we fit two CePNEM models to compare against each other. For baseline datasets without any stimulation (both SWF415 and NeuroPAL), we split the dataset in half and used fits from each half – the same fits used in the encoding analysis. For the NeuroPAL heat-stimulation datasets, we took one fit from the timepoints up until just before the stimulation (799 or 800 timepoints), and another fit from the 800 time point block (stim+10) to (stim+809). For the SWF415 heat-stimulation datasets, we took one fit from the timepoints up until just before the stimulation, and another fit from the 400 timepoint block (stim+10) to (stim+409) for heat-stimulation datasets without a gap in the middle, or alternatively (stim+10) to 800 for datasets with such a gap. Note that almost all of the heat-stim analysis uses the NeuroPAL datasets rather than the SWF415 ones, because the longer durations and equal time lengths of the pre-stim and post-stim data allow for much more powerful analysis.
Next, we computed deconvolved activity matrices as defined above on each of the CePNEM fit posteriors. We ran the same procedure used to detect encoding, but this time instead of computing metrics on individual particles, we computed those metrics on differences between the deconvolved activity matrices for all possible pairs of particles from each of the two model fits, which was a total of slightly more than 108 such differences per neuron. We used our residual threshold as before, but is set to 0 for this test because it is not well-defined when considering multiple model fits. Neurons that passed our encoding test at using the differences between the deconvolved activity matrices for behaviors other than feeding (there were too few datasets with enough feeding variance in both time ranges to make a meaningful statistical comparison), and encoded behavior (using our standard behavior encoding test) in at least one time range were added to the list of encoding changing neuron candidates. Additionally, we checked whether the EWMA parameter changed by computing differences between all possible values of in the two model fits, and asking whether that was greater than 0. This comparison was Benjamini-Hochberg corrected over all neurons, and neurons that passed the test at and also encoded behavior (using our standard behavior encoding test) in both time ranges were added to the list of encoding changing neuron candidates.
Variability index
To compute the variability index of labeled neurons, we fit our hierarchical model (see above) on all CePNEM fits for that neuron, and then computed the variability index as , where is a function that computes the circular standard deviation from the von Mises-Fisher concentration parameter . Note that variability in the EWMA parameter is not included as this parameter is not meaningful if the neuron lacked behavioral information. Furthermore, variability in encoding strength is also not included as this can include variability related to data normalization differences between animals.
Inter-dataset variability
To compute the inter-dataset variability, first the set of model parameters of the neuron within the same animal are transformed into Cartesian coordinates (because normalization is the same within the same animal, we can use the scaling information), averaged together, and projected back into spherical coordinates to produce a per-animal model estimate . Then is computed as the standard deviation of the component of the , and is estimated by fitting a von Mises-Fisher distribution to the angular parameters of the . Variability is then computed as above.
Intra-dataset variability
To compute the intra-dataset variability, first the set of model parameters corresponding to different observations of the neuron in the same animal in the same time range are averaged together as with inter-dataset variability. This results in a set of averaged model parameters and , where is the animal number, corresponding to the CePNEM fits in the first and second halves of the recording. We then compute
Here is the value of the parameter or vector of parameters in the averaged model parameters , transforming coordinates as appropriate. This represents a distance in model parameter space between the two CePNEM fits in the same animal; the normalization by serves to ensure that differences in normalization do not result in different animals being weighted differently, similarly to how wasn’t included in the variability index. The intra-dataset variability can then be computed as , where the division by transforms distance into standard deviation.
Amount of encoding change (Figure S7G)
The amount of encoding change of a neuron in an animal is defined as 0 if that neuron did not exhibit an encoding change in that animal, and the variability index of a hierarchical model fit on data from only that animal (for Figure S7G, pre-stim and post-stim data) if that neuron did exhibit an encoding change. It is computed separately for different components of neuron pairs, and in Figure S7G it is averaged over all detections of the given neuron.
Feeding decoder analysis for encoding change (Figure 7I–J)
In order to detect encoding changes in the feeding circuit triggered by the heat stimulus, we needed to develop a different approach. This is because the animal doesn’t feed after the heat stimulation, so the CePNEM post-stim feeding parameters for each neuron will not be possible to constrain, resulting in it being impossible to statistically demonstrate a difference when compared with the pre-stim condition. Thus, instead of using the CePNEM encoder model, we compared the performance of decoder models on the pre-stim and post-stim data to determine if an encoding change was taking place for a given neuron class.
More specifically, for each neuron class, we trained a linear decoder model to predict feeding behavior from neural activity. Each model was trained on detections of its neuron class in the 21 baseline NeuroPAL animals, with the neural activity and feeding behavior being appended together for the training. The neural activity was normalized as , where was the 10th percentile of the raw (ratiometric) fluorescence in each animal.
After training, we determined the set of neuron classes where the decoder analysis succeeded. This was determined based on the MSE of the predicted feeding rate in the training data (compared to the actual feeding rate) being at least 0.0075 better than the MSE of the null model (which is given a constant vector as neural activity). We also only considered neurons that had at least 3 detections in both the baseline and heat-stim datasets. This yielded a set of neurons that are almost exactly the same as the feeding-encoding neurons from CePNEM: AIN, AQR, I2, I3, I6, IL2L, M1, M3, M4, M5, MC, MI, RIH, RIR, RMG, and SIBV. For this set of neurons, we then evaluated the performance difference of the trained model and the null model on each heat stimulus dataset, evaluating the pre-stim and post-stim halves of each dataset separately. We then ran a Wilcoxon rank-sum test on this paired data to identify neuron classes where the decoder performed significantly worse on post-heat-stim data. Benjamini-Hochberg multiple-hypothesis correction was applied across the list of neurons subject to this analysis.
Modified intra-dataset variability (Figure 7G)
In Figure 7G, we also made a modification to the intra-dataset variability index (see above) to account for CePNEM’s inability to resolve feeding information post-stim (which would erroneously lead to neurons with feeding encoding changes having low variability). Specifically, we defined the modified intra-dataset variability of a neuron to be
Here is the intra-dataset variability index for the neuron and is the mean performance (measured as MSE of the training model minus MSE of the null model) of the feeding decoder for that neuron evaluated on the x-stim data. Thus, if the decoder performs better on the pre-stim data and degrades on the post-stim data, it will result in an increase to the modified intra-dataset variability index for that neuron.
Connectome analysis
Connectomes used
For all quantitative analysis, the two adult datasets from Witvliet et al. 2021 were averaged. Self-looping edges and single-synapse edges were excluded. For the pharyngeal circuit analysis, the connectome from the original White et al. 1986 was used, as the Witvliet connectome only covers the head ganglion. For the 2D embedding of the connectome (the sensorimotor layer and the graph eigenvector; see below), the White et al. 1986 connectome was used to replicate the embedding previously used in the field61. On Fig. 4 (B,C,D), the Witvliet connectome was used for visualization.
2D embedding of the connectome
The 2D embedding of the connectome was performed by determining the sensorimotor layer (referred to as processing depth in the original paper) for each neuron and the 2nd eigenvector of the Laplacian of the graph. See the Supporting Text S1 in Varshney et al.61 for the exact methods used in determining those values.
Connectome localization analysis
In Fig. 5 (E,F,G), the marginal distribution (kernel density estimation using KernelDensity.jl) of the group of neurons of interest (top 15th percentile of the feature of interest, which was either (i) high encoding strength, (ii) long decay, or (iii) high variability) was compared to the marginal distribution of the random control group (shuffling the features across the neurons that were recorded). One-proportion z-test was used in each trisected segment, along the sensorimotor layer axis of the connectome region axis. All selected neuron distributions (blue lines) were significantly different from the random control distributions (overall, without trisecting) at *p<0.05. Mann-Whitney U test. For the localization in the connectome region axis (Fig. 5G), further testing was done to show that the high variability group of neurons were interconnected above chance. For that test, the variability values were shuffled across the recorded neurons and the intra-group synapse fraction was computed in the same way for these random shuffles (Fig. 5H). The random sampling was repeated 100,000 times. Then the p-value was empirically determined by computing the percentile of the actual intra-group synapse fraction among the random control samples.
Connectivity vs joint encoding change analysis
To assess the relationship between the connectivity type and joint encoding probability for neuron pairs (Fig. 6I), a random shuffling test was used. Among the joint encoding neurons shown in Fig. 6H, we iterate through all possible pairs (other than self-pairing). For each pair of neurons, we record the type of the connection (no connection, unidirectional chemical, bidirectional chemical, bidirectional electrical/gap junction) and the joint encoding change probability. For control, we shuffle the neuron assignments on the joint encoding change matrix and repeat the analysis (1000 random samples). Finally, the actual value was compared to the random shuffled distribution for each connection type to empirically compute p-value.
Handling of left/right bilateral pairs
For the neuron classes with bilateral pairing (left/right), the left/right pairs were merged for all quantitative analysis, except for the group of neurons with bilateral asymmetry in encoding (ASE, SAAD, IL1, IL2). Analysis of relationships between connectivity and correlation (or other aspects of encoding) were then conducted on merged neuron classes. The purpose of this merging was to prevent the special case of left/right connectivity and correlation from dominating our analyses of connectome trends. Left/right pairs are typically well connected and strongly correlated, so including them in these analyses would have resulted in there being strong relationships between connectivity and activity, even if these were only found in the left/right pairs. Excluding them allowed us to ask whether connections between neuron classes were associated with trends in neural activity and behavior encoding.
For visualization (2D embedding of the connectome), left/right pairs were kept separate and not merged.
Other analysis methods applied to neural recordings
Decoding behavior from neural activity
Full activity, current behavior
We trained L1-regularized linear decoder models to predict the worm’s current velocity, head curvature, feeding rate, angular velocity, and body curvature based on its current (z-scored) neural activity. To set the regularization parameter, we withheld three datasets that were randomly selected from the set of datasets with feeding standard deviation of at least 0.5. The other eleven datasets were used to evaluate decoder performance. The decoders were evaluated using five-fold cross-validation splits. All behaviors were z-scored for the decoder, and the decoder accuracy is reported as one minus the MSE between the decoder’s prediction and actual behavior, evaluated on the test-time data.
Model residuals, current behavior
We computed model residuals for each neuron by taking that neuron’s activity and subtracting the modeled (computed based off of the median of all posterior CePNEM parameters for that neuron), and then z-scoring the resulting residual trace. We then trained separate decoder models using the same procedure as above, except using the model residuals instead of neural activity. We regularized these decoders separately using the same three set-aside datasets.
Decoding past and future behavior (Figures 2D, S2K)
The following outlines the decoder method for predicting past (retrospective) or future behavior (prospective). For predicting head curvature and velocity, the same method was used; for ease of explanation, in this description we focus on velocity. We trained linear decoder models to predict the average velocity of the worm at various temporal shifts, based on the worm’s current (z-scored) neural activity; only neurons that encoded velocity (or head curvature, for the head curvature prediction) were included. The models were trained on data from all 14 SWF415 animals. A separate model was trained for each time point. The average velocity was computed in the window spanning where is the difference between the time point to be predicted and the current time ( is current; positive values indicate future values of behavior while negative values indicate past values). This approximately corresponds to a 10-sec time window. Velocity across the full 1600 time points was z-scored before being averaged. Each dataset was split into 5 segments for cross-validation, with 100-timepoint gaps in between to prevent the training time information from spilling over to the test time segment. The models were regularized using an elastic net (L1 and L2).
As a control, separate models were trained that attempted to predict shifted velocity, which should scramble the relationship between neural activity and behavior. Velocity was circularly shifted by an amount between 125 and 600 time points, and, additionally, shifts that would result in a correlation of greater than 0.2 with actual velocity were discarded. 50 such decoders were trained, each using a different, randomly-selected shift. The performance of the decoder trained to predict averaged velocity time points into the past was then defined as the difference between the cost (square root of MSE) of that decoder and the average cost of each of the 50 decoders trained on shifted velocity.
To ensure that decoder performance based on neural activity with was actually a representation of historical velocity information, and not simply due to the autocorrelative nature of velocity, a separate family of decoders were trained that was given the worm’s current (z-scored) velocity as input instead of neural activity. The error of those decoders to their shifted controls is also displayed in Figure 2D. Finally, to estimate the maximum possible performance of these decoder models, separate “perfect” decoders were trained that were given the worm’s (z-scored) velocity at time points for each value of , and were then subjected to the same shift test.
Constructing low-dimensional embeddings of neurons via UMAP
We wanted to use CePNEM to construct a low-dimensional UMAP space where any neuron from any animal could be embedded. To accomplish this, we took the three modeled behaviors from 12 SWF415 animals and appended them, so as to have a wide range of possible behavioral dynamics. Then, we took 4,004 median CePNEM fits (sampled from 4004 neurons across 14 SWF415 animals) and extrapolated them over the appended behavioral data, to estimate what the neuron would have done under our model over a wide range of behaviors. We then ran UMAP on the resulting 4004 × 19200 matrix to define a two-dimensional embedding space. Finally, we projected all posterior CePNEM fits from each neuron into this UMAP space to create the point cloud shown in Figure 3A. We also projected subsets of neurons based on encoding type (Figures 3B–3F), identity (Figure 5E), and dataset (Figure S3); to do this, we simply run the same projection procedure on all posterior CePNEM fits from each neuron in the subset in question (i.e. the UMAP space was the same for all embeddings shown in the paper).
Neural trace reconstruction using principal component analysis
To determine the number of principal components needed to reconstruct each neuron, PCA was performed first on all neurons in each dataset. Neurons without high enough SNR were excluded from the analysis. We determined the SNR cutoff based on our GFP datasets. Specifically, a given neuron needed to have signal standard deviation higher than , where is the GFP signal standard deviation and is the required fraction of variance explained. To reconstruct the neurons, each neuron’s loadings were sorted by absolute value. Then we increase the number of principal components used to reconstruct until the required variance explained is met. In each dataset, this process is repeated for all neurons with high enough SNR.
Neural trace clustering analysis
To estimate the optimal number of clusters in the neural traces (Fig. S4A), we first mean center neuron. Then k-means clustering is performed on each dataset with varying number of clusters, k, ranging from 2 to 10. For each k, we compute the Calinski-Harabasz index. We repeat this on all SWF415 datasets.
State neuron detection analysis (Figure 7F–G)
For detecting state neurons whose persistent activity changes are aligned to the heat-induced state change, we needed to find neurons with activity changes that were approximately time-locked to the heat stimulus, rather than neurons that simply have very slowly varying activity. To accomplish this, we trained decoder models to decode the indicator function of a time point from neural activity, and then asked whether the neuron was able to decode better when was the time of the heat-stim, when compared to other control values of . Neurons where the heat-stim decoder outperformed all of the other decoders were considered to have time-locked state responses to the stimulus. Time points that were too close to the beginning or end of the recording, or too close to the heat-stim were excluded from the controls.
The average persistent change in activity in response to the heat stimulus metric displayed in the Figure 7G heatmap was computed as the average difference between mean pre-stim and post-stim neural activity . When the neuron statistically failed to have time-locked responses to the stim in a dataset, the difference was entered into the average as 0 for that dataset in order to filter out responses that were not time-locked to the stimulus.
Behavioral analyses during cellular perturbations
For behavioral analysis in animals that had single neuron classes chronically silenced or ablated, we (i) recorded animal speed on multi-worm trackers, as previously described62, (ii) recorded head curvature behaviors on high-resolution single worm trackers, as previously described63, and (iii) quantified pharyngeal pumping manually. For single neuron manipulations that involved optogenetic activation or silencing, we used the same methods for behavioral quantification, but delivered blue (250 uW/mm2) or red (700 uW/mm2) wavelength light at defined times, as described in the figures and figure legends.
List of key software packages used
Gen.jl, PyPlot.jl, PyCall.jl, HDF5.jl, ProgressMeter.jl, Distributions.jl, Images.jl, Nlopt.jl, DelimitedFiles.jl, NaNMath.jl, Clustering.jl, DataStructures.jl, Interpolations.jl, MultivariateStats.jl, Optim.jl, TotalVariation.jl, UMAP.jl, Lasso.jl, VideoIO.jl, Impute.jl, JLD2.jl, JSON.jl LsqFit.jl, MLBase.jl, ImageTransformations.jl, HypothesisTests.jl, MultipleTesting.jl, GLM.jl, GLMNet.jl, ForwardDiff.jl, FFTW.jl, Distances.jl, DSP.jl, CoordinateTransformations.jl, Combinatorics.jl, Colors.jl, ColorTypes.jl, Cairo.jl, CUDA.jl, KernelDensity.jl
QUANTIFICATION AND STATISTICAL ANALYSIS
All statistical methods used in the paper are described in the figure legends and, where indicated, additional details are provided in the Method Details. Definitions of sample size, measures of center and dispersion, and precision measures are also indicated in figure legends. Statistics were computed using Julia, MATLAB, and GraphPad Prism. Non-parametric statistics were exclusively used in the study. When appropriate, corrections for multiple comparisons were implemented via Benjamini-Hochberg or Bonferroni correction, as indicated in the figure legends.
Supplementary Material
Supplemental Figure 1. Behavioral assays, GFP control recordings, and evaluation of model parameters, Related to Figure 1.
(A) Salt learning assay for N2 control animals, compared to pan-neuronal GCaMP7f animals. Naïve refers to animals grown on 0 mM NaCl; conditioned (‘cond’) refers to animals grown under the same conditions but exposed to 50mM NaCl with food for one hour prior to assay, which causes animals to prefer higher salt concentrations. Chemotaxis was measured on a plate with a 0mM to 50mM NaCl gradient with sorbitol added to ensure uniform osmolarity. Positive values correspond to chemotaxis directed toward high NaCl. Data are shown as means and standard deviation across plates. n=12–13 chemotaxis plates per group for naïve and n=4–6 plates per group for conditioned. n.s. not significant, Mann-Whitney U-Test.
(B) Un-normalized F heatmap of neural traces collected and extracted from a control animal expressing eat-4::NLS-GFP. Since GFP is expressed only in a fraction of cells in this strain, perfect neural identity mapping would result in a set of bright horizontal lines (GFP-positive neurons) and a set of dark horizontal lines (GFP-negative neurons), while a registration mismatch would appear as a bright spot in the trace of an otherwise GFP-negative neuron, or a dark spot in the trace of an otherwise GFP-positive neuron. Note that there are very few instances of registration mismatches visible in the traces. As described in the main text, we estimate the number of neuron identification errors to be 0.3% of frames (see Methods).
(C) Heatmap of neural traces collected and extracted from three GFP control animals.
(D) Analysis of which velocity filtering method best matches neural dynamics. An example neuron that encodes behavior with a long timescale value according to CePNEM (blue; same for all four traces) and different processed versions of velocity (gray). Velocity was processed in different ways and the match to neural activity was evaluated. Average performance across all neurons is in panel (E). For each method of processing velocity, the optimal fit to the neuron was taken by minimizing the error (MSE) using gradient descent. The different methods of processing velocity were: (1) EWMA: exponentially-weighted average of recently velocity; (2) Optimal Shift: time-lagged shift in velocity; (3) Optimal Gaussian kernel: gaussian averaging of velocity at each time point; (4) Optimal lowpass filter: velocity filtered based on frequency. The alternative smoothing methods were evaluated to compare against the EWMA used in the model.
(E) Average fit of how velocity filtered in the indicated ways (see panel (D) legend for more description) matches neural activity, quantified as mean square error (lower is better). This was averaged across all recorded neurons. ***p<0.0005, Wilcoxon signed rank test.
(F) Degradation analysis on each model parameter, comparing the percentage that the error (as measured by cross-validated mean-squared error when fitting the model with MSE optimization – see Methods) increases when the model is refit with that parameter removed. Wilcoxon signed rank test (comparing the full model and the partial model) resulted in p-value below 0.0005 for all shown parameters. For reference, black line shows the error increase for a model with no behavioral parameters (just an offset parameter so that the model would guess each neuron’s mean activity).
(G) Degradation analysis using same procedure as in (F), but plotting a different outcome. For “behavior” predictor terms (left): for each neuron the three degraded models were fit (lacking each predictor term) and the predictor term whose deletion caused the greatest increase in error was determined. The fraction of neurons that had each parameter as their most important predictor term is displayed. For “non-linearity” terms (right): the same procedure was conducted, except the degraded models lacked one or both model non-linearities. Model lacking both non-linearities was the fully “linear” model. The analysis was done on the encoding neurons and averaged across datasets.
Supplemental Figure 2. Controls for model fitting, decoding analyses, and analyses of neurons’ timescales, Related to Figure 1.
(A) Simulation-based calibration results for CePNEM. Simulation-based calibration was performed by simulating 1997 neurons from CePNEM using behaviors from 4 different animals and fitting them each twice, on different time ranges. For each model parameter, the ground-truth parameter was ranked within the fitted posterior. If model fitting is perfectly calibrated, the ground-truth parameter’s rank should be the uniform distribution. Therefore, for each parameter, we performed a χ2 test to distinguish their distribution from the uniform distribution with p=0.05. All parameters passed this test, except for the timescale parameter , which has a very small calibration artifact predicted to impact <4 neurons per dataset. See Methods.
(B) A series of CePNEM model fits to various neurons, showing the model’s ability to fit a wide variety of neural tunings to behavior. The model was fit on the first half of the dataset, and tested on the second half, revealing that these neurons have robust tunings to behavior across time that is well-explained by CePNEM. The inset cross-validation (cv) indicates the goodness-of-fit of the model on testing data (see Methods for additional details).
(C) The fraction of neurons with encoding vs the fraction of active neurons (the signal value above the GFP threshold). Each dot is a dataset. The fractions are computed by averaging across two time segments in each dataset. The tight clustering of dots indicates that datasets were roughly consistent, according to these basic metrics.
(D) Controls comparing the percentage of neurons that were detected as encoding behavior using real GCaMP traces with the same animal’s behavior, using the same GCaMP traces but attempting to fit with a different animal’s behavior (essentially a scramble control; ‘wrong behavior’), and using GFP datasets. See Methods for statistical methods used to determine if a given neuron significantly encodes a behavior.
(E) Cumulative distribution of cross-validation scores across neurons in continuous SWF415 recordings (see Methods). Its intuitive meaning is that a value of zero indicates that the fit CePNEM model fails to generalize to the testing data, whereas a value of +1 indicates that the model perfectly explains neural activity on withheld testing data. 96% of neurons had a positive cross-validation score.
(F) Distribution of overall neuron signals (as a metric for overall activity levels) across all neurons in three categories: GFP control neurons, encoding neurons (GCaMP neurons that significantly encoded at least one behavior based on CePNEM), and non-encoding neurons (GCaMP neurons that did not significantly encode any behaviors according to CePNEM). Neuron signal here is defined as where is the un-normalized ratiometric fluorescence of the neuron in question. It provides a measure of overall level of dynamics exhibited by the neuron. Note that non-encoding neurons still exhibited robust dynamics, for the most part exceeding the negative control GFP neurons.
(G) Linear, L1-regularized decoder models were trained to predict various behaviors (velocity, head curvature, feeding, angular velocity, and curvature, respectively) from 11 animals from either neurons (blue) or CePNEM model residuals (orange). Decoding accuracy was assessed as 1 – MSE (decoded behavior, true behavior), averaged over five 80/20 cross-validation splits (see Methods). Note that the decoder models do much worse when trained on CePNEM model residuals than when trained on the full neural data, suggesting that the model can explain most neural variance overtly related to behavior.
(H) An analysis of decoding accuracy from specific subsets of neurons. Linear, L1-regularized decoder models were trained to predict the behavioral parameters listed on the x-axis. For each behavioral parameter we compared decoder accuracy when the model was trained on (i) the neurons that encoded that behavioral feature according to CePNEM (e.g. for forward speed, the full set of neurons that had significant information about forward speed; shown as red lines); versus (ii) random subsets of neurons equal in size to group (i) selected from the neurons that did not encode that behavioral feature (gray distributions). *p<0.05, **p<0.005, empirical p-values based on rank of red lines in respective gray distributions.
(I) Mean ECDF of the model half-decay time of all neurons demonstrated to encode forward locomotion, contrasted with the ECDF of neurons demonstrated to encode reverse locomotion, in 14 animals. The shaded regions represent the standard deviation between animals. The median fraction (across animals) of forward neurons with long timescales (half-decay τ1/2 > 20𝑠) was 0.12, compared with only 0.03 for reversal neurons; this difference was statistically significant (p = 0.029) under a Mann-Whitney U-Test.
(J) Mean ECDF of model half-decay time of all neurons that encode the indicated behaviors. Data are shown as in panel (H).
(K) Performance of a decoder trained to predict past and future head curvature of animals based on current population neural activity. Models were trained and data are displayed as in Fig. 2D, except these models were trained to predict head curvature rather than velocity. See Fig. 2D legend for additional details.
(L) Violin plots showing distribution of head curvature angles (in radians) during forward and reverse movement. Note that the distributions are similar, suggesting that the widespread differences in neural encoding of head curvature during forward versus reverse movement is not due to animals exhibiting different head angles based on their movement direction.
(M) A neuron that encodes angular velocity (defined as longer-timescale head curvature; due to the higher frequency nature of head curvature oscillations, longer-timescale is defined here as at least 5 seconds). This neuron has a half-decay of τ1/2 = 9.5 ± 1.3 seconds and is multiplexed with velocity as well.
Supplemental Figure 3. Additional analyses of UMAP projections, Related to Figure 3.
(A) Projections of all neurons from each of four different SWF415 animals into the same UMAP space (built from full population of animals; same as in Fig. 3A). Observe that the overall structure is very similar, suggesting that the locations of neurons in UMAP space are similar across datasets.
(B) Projections of all neurons from each of two different NeuroPAL animals into the UMAP space. These neurons also fill in a similar pattern to that of the SWF415 animals, suggesting that the overall neural encodings of the two strains are similar.
(C) Projections of all neurons from each of two different GFP control animals into the UMAP space. These neurons fail to fill most of the space, which is consistent with the non-encoding nature of neurons in this control strain.
(D) Projections of all neurons from 14 different SWF415 animals into the UMAP space, taking the median of each neuron’s posterior point cloud in the UMAP space. Note that the medians fill out the same space as when projecting the full posteriors (as in Fig. 3), suggesting the continuity of the UMAP space is not merely an artifact of parameter uncertainty.
(E) An analysis of clusterability of all neurons that encode behavior. For each dataset, we attempted to cluster all neurons that encode behavior using a similarity metric based on the difference of the neurons’ GCaMP traces. To determine the optimal number of clusters, we computed the Calinski-Harabasz index over varying number of clusters when performing k-means clustering on the neural traces. Clustering was done on a per dataset basis on all SWF415 datasets, and the mean and standard error values are plotted. Note that the optimal number of clusters in this analysis is 2, which is the minimum number that can be assessed with this metric. This suggests that there is not a larger set of discrete subgroups of neurons that are separable from one another.
(F) Cumulative variance explained by the top 20 PCs, averaged over 14 animals. The shaded region is the standard deviation across animals.
Supplemental Figure 4, Analysis of NeuroPAL recordings and effects of perturbing neural activity, Related to Figure 4.
(A) A RGB composite image of one of the NeuroPAL animals that we recorded. The composite was constructed by combining images of NLS-mTagBFP2 (shown in blue), NLS-cyOFP2 (shown in green), and NLS-mNeptune2.5 (shown in red). Using this composite image, we were able to label a large number of neurons in this animal. Neural identity was determined while making use of all 3D information, but for display purposes here we show a maximum intensity projection of a subset of the z-slices from the recording. Therefore, this image does not show all the neurons in the head (a maximum intensity projection of all z-slices is too dense with neurons to show for display purposes here).
(B) Comparison of behavioral parameters during recordings of brain-wide GCaMP7f in animals without NeuroPAL (SWF415, labeled “415”) and with NeuroPAL (SWF702, labeled “NP”). Four behavioral metrics are shown. n=14 and 21 animals for SWF415 and SWF702, respectively. *p<0.05 ***p<0.0005, Mann-Whitney U-Test.
(C) Average overall neural signal across recordings of animals expressing pan-neural GFP (green), pan-neural GCaMP (blue) and pan-neural GCaMP with NeuroPAL transgene (orange). Overall neural signal here is defined as where is the un-normalized ratiometric fluorescence.
(D) A comparison of how much variance in neural activity is explained by different number of principal components in pan-neural GCaMP strains without NeuroPAL (blue, SWF415) and with NeuroPAL (orange, SWF702).
(E) Distribution of cross-validation scores (see Methods for quantitative details) for pan-neural GCaMP strain without NeuroPAL (blue) and with NeuroPAL (orange).
(F) UMAP plot showing the posterior distributions of the CePNEM model fits for various neurons; each neuron is plotted in a different color. The same set of time points from the same animal were used for each neuron’s fit. This plot shows a subset of neurons with largely non-overlapping tunings, just to illustrate how neurons map onto the UMAP space described in Fig. 3.
(G) Event-triggered averages showing average neural activity of the indicated neuron classes aligned to key behaviors, as indicated in the column labels. Data are pooled across all instances of recordings of the neuron classes for the behaviors indicated. Note that event-triggered averages in general are noisier for feeding due to a lower number of events where feeding suddenly started or stopped (compared to forward/reverse and dorsal/ventral transitions). The shading indicates the standard error across the recorded animals.
(H) Table of the signal values of the neuron classes identified in NeuroPAL. For each neuron class, dot is the median level of overall activity (‘signal’) for the neuron across all recorded instances, quantified as in Fig. 4A. The line denotes the 25th - 75th percentile range. The neurons are ordered by the median signals. The dashed green line indicates the boundary below which neurons are likely to be inactive, determined based on the signal values in the GFP control datasets.
(I) Effects of perturbing the indicated neurons on the animal’s behavioral output. For all perturbations, we quantified forward speed (shown as means ± standard error of the mean (SEM)), reverse speed (means ± SEM), median head curvature during dorsal and ventral head bends (box plots showing 25th and 75th percentiles and medians as red lines; separate boxes for dorsal and ventral bending), frequency of head bending (plotted as distribution of intervals between head swings), and feeding rates (means ± SEM). Neuron inactivation methods were: (1) RIC: tetanus toxin (TeTx) expression; (2) AIM: chemogenetic silencing using the Histamine-gated chloride channel (HisCl); (3) AUA: chronic silencing via expression of leaky potassium channel unc-103(gf); (4) RIF: chronic silencing via unc-103(gf); (5) AVL: chronic silencing via unc-103(gf); (6) SAA: neuron ablation via split caspase expression; (7) SMB: neuron ablation via split caspase expression; (8) MC: optogenetic inactivation via GtACR2; (9) M4: optogenetic inactivation via GtACR2; (10) ASG: optogenetic activation via Chrimson. All promoters were single cell-specific, either through highly specific single-cell promoters or intersectional Cre/Lox promoters. Details of promoters used are in Method Details under the Transgenic Animals section. *p<0.05, **p<0.01, ***p<0.001, ****p<0.0001, Bonferroni-corrected Mann-Whitney test. n.s., not significant.
Supplemental Figure 5, Analysis of variable encoding neurons, Related to Figure 4.
(A) Locations of different neuron classes in UMAP space, showing results for multiple recordings of each neuron. The UMAP space is the same as is shown in Fig. 3, where distance between neurons is proportional to the difference in how they encode behavior. Here, each colored dot depicts how the indicated neuron class encoded behavior in a single recording. Two types of neurons are shown: (1) Low variability neurons that have consistent encoding of behavior according to CePNEM: RIM, RIB, MC, IL2D; and (2) High variability neurons that have variable encoding across animals according to CePNEM: URX, OLQD. Note that the dots for the variable neurons are more distributed in this space than the dots for the low variability neurons. Only six neuron classes are shown to prevent the plot from being overcrowded.
(B) Scatter plot of labeling confidence (a qualitative metric determined by person scoring, reflecting their confidence that the neuron is correctly identified based on position and multi-spectral fluorescence; the higher the better; note that neurons with sufficiently low confidence were entirely excluded from all analyses in the paper, and this plot only shows values above this threshold) and encoding variability (lower value means more consistency). There is no evident relationship between these values, suggesting that labeling error does not introduce encoding variability.
(C) Scatter plot of GCaMP ROI match score (the higher the better in terms of confidence that NeuroPAL ROI was confidently mapped to a GCaMP ROI; see Methods) and encoding variability shows no relationship. This suggests that the process that matches the NeuroPAL ROI to the GCaMP ROI does not introduce encoding variability.
(D) Examples of a variable coupling neuron (OLQD from 3 animals shown). On the left column, the NeuroPAL fluorescence images with OLQD labeled show consistent color combination and location of this neuron class. On the right column, the corresponding neural traces (blue) are shown along with CePNEM fits (orange), and a written description of the encoding properties. Note that the neurons of the same class from different animals encode different sets of behaviors.
(E) Performance of CePNEM model across different animals, for neuron classes with different levels of variable encoding. In this analysis, the optimal CePNEM model parameters learned from 21 animals’ neural and behavioral data was determined (using a hierarchical Bayesian approach; see Methods). These model parameters were then used to predict neural activity in three additional animals shown here (animals 22–24). This analysis is shown for three categories of neurons: (1) neurons with low variability according to CePNEM: RIB, ASG, and SMDV; (2) neurons with moderate variability according to CePNEM: AUA, CEPD, and URYV; and (3) neurons with high variability according to CePNEM: URX, IL1D, and OLQD. The Variability Index for each neuron is displayed by the neuron’s name. Note that the level of variability in neural encoding, determined by our analysis, scales with the ability of models to successfully predict neural activity across different animals, as expected.
Supplemental Figure 6, Analysis of dynamic encoding neurons, Related to Figure 6.
(A) An analysis of what fraction of neurons were detected as changing encoding in our GCaMP datasets and simulated datasets. Simulated datasets are labeled ‘SBC’ for simulation-based calibrations. These are neurons simulated from the CePNEM model, where ground-truth parameters were set to not have any encoding changes.
(B) Scatterplot of datasets showing that extent of photobleaching is not correlated with detection of encoding changes. Each dot is a SWF415 dataset.
(C) Scatterplot depicting each neuron class’s likelihood of changing encoding in a single continuous recording (x-axis) versus its variability overall across all animals (y-axis). Each dot is a single neuron class. Note the positive trend (p<0.05, conditional independence test). The box highlights neurons that are variable both across and within animals.
(D) The frequency of neurons changing encoding in single recordings, separating neurons based on whether they are sensory, inter-, or motor neurons. No major difference was observed between these three groups, and this remains true when variability index is used instead of encoding change fraction.
(E) The same dataset in Fig. 6F but also plotting the relative model performance averaged over the static encoding neurons. Note that the black line does not show the sudden changes in value seen for the purple line.
(F) Same as (E), but for the dataset in Fig. 6G.
(G) An example dataset that shows a less synchronized encoding change, displayed in the same manner as in (E-F).
(H) Two example encoding changing neurons from the animal in (G), one with an abrupt encoding change at approximately 12 minutes, and another neuron that appears to have a slowly-increasing gain to its behavioral encoding over the last ~10 minutes of the recording.
(I) A plot of the fraction of encoding neurons that exhibited encoding change in a dataset, compared with the behavioral difference between the first and second half of that dataset. Behavioral variability was computed as the sum of the absolute values of the differences (across the two time segments) of the following behavioral parameters (each such parameter was normalized to the standard deviation of that behavior across all 14 SWF415 datasets): median of reverse velocity, median of forward velocity, 25th percentile of head curvature, 75th percentile of head curvature, 25th percentile of feeding rate, and 75th percentile of feeding rate. This value provides a general description of how much the distributions of behavioral parameters changed across the two halves of the recording. Observe that datasets with large behavioral changes tend to have more encoding changes, suggesting that the neural flexibility may be related to the observed behavior changing.
Supplemental Figure 7, Analysis of stimulus-induced encoding changes, Related to Figure 7.
(A) Experiments to examine the impact of the heat stimulation on the behavior and health of the animals. Animals subjected to the heat stimulation did not display a significant difference (p = 0.62 in a Mann-Whitney U-Test computed over 10 animals) in their exploratory behavior (computed as counting the number of squares each animal entered on an assay plate) relative to mock-stimulated animals (animals that were mounted on imaging slides, but not given the thermal stimulus). Behavior was quantified one hour after the heat stimulation.
(B) The heat stimulation did not kill any animals (all animals were alive 2 days after the stimulation).
(C) Connectome localization of neurons that exhibit sensory responses to the thermal stimulus. Neurons in red generated transient (<4sec) excitatory responses to the heat stimulus and neurons in blue generated transient inhibitory responses. Layout of connectome is the same as in Fig. 5C–F (see that legend for further details). Marginal distributions show the enrichment of each group of neurons along the two axes, relative to a random shuffle control (gray). *p< 0.05 **p<0.005, one sample Z-test for proportion on the excitatory responses; the inhibitory responses were not significant.
(D) Connectome localization of neurons that exhibit long-lasting (15–30sec) excitatory (red) or inhibitory (blue) responses to the thermal stimulus. Data are displayed as in panel (C); there was not a significant enrichment of these neurons in any sensorimotor layer.
(E) A comparison of the relative model performance averaged across all 11 SWF415 animals that underwent a heat shock (top) with the same metric computed over 4 animals that were not stimulated (bottom). Note that the baseline animals do not have a sharp change in relative model performance at the train/test split, suggesting that the encoding changes in the heat-stimulation datasets are a direct result of the stimulation.
(F) Fraction of times that each neuron class changed encoding after the heat stimulus. More specifically, the fraction of times that decoders trained on baseline data to predict feeding from the given neuron’s activity performed better on the pre-stim data than the post-stim data (see Methods). Note that the neurons have degradations in performance well above what would be expected by chance (50%); this indicates that the neurons changed encoding after the heat stimulus. *p<0.05, **p<0.005, ***p<0.0005, Wilcoxon signed rank test comparing pre-stimulus vs post-stimulus performance of the decoders across animals, as an indicator of whether these encoding changes were reliable across animals. The neurons shown here encoded feeding prior to the heat stimulus. p-values for encoding change were Benjamini-Hochberg corrected over all neurons where the decoder succeeded at predicting feeding in the baseline data (see Methods for additional details).
(G) Average amount of encoding change between pre-stim and post-stim CePNEM fits across heat-stimulated animals. Insets display the fraction of times that the indicated neurons changed encoding at all after the heat stimulus. Neurons shown here encoded either velocity or head curvature prior to the heat stimulus (the neurons that encoded feeding prior to the stimulus are analyzed in panel F; different statistical methods needed to be used for these two categories, since feeding was strongly suppressed post-heat-stim; see Methods for details). (*)p<0.1, *p<0.05, **p<0.005, p-value based on rank of actual magnitude of encoding change across animals (red) to level expected by chance (grey distribution), as an indication of whether the reliability of encoding change was greater than expected by chance. The p-values were Benjamini-Hochberg corrected over this set of neurons.
(H) A plot that relates each neuron class’s variability in encoding of behavior within heat stimulation datasets (y-axis) to its variability within baseline spontaneous behavior datasets (x-axis). See Methods for additional detail on how intra-dataset variability was computed based on encoding in the first versus second halves of the recordings. Black line is the identity line and each dot is a neuron class. Note the positive trend.
Movie S1. Example video of baseline recording conditions, Related to Figure 1. An excerpt from an example neural/behavioral dataset, showing the NIR behavioral recording. Raw video data is shown with overlaid information: (i) blue, orange, and green dots are the identified targets for worm tracking that were determined during live recording, which allowed us to locate the worm’s head and keep the animal centered in view; (ii) black line shows a spline fit to the animal’s centerline; (iii) upper left shows time and values of three ongoing behavioral parameters: velocity, head curvature, and feeding rate.
ACKNOWLEDGMENTS
We thank Drew Robson, Jennifer Li, Qiang Liu, Shay Stern, Andrew Gordus, Brady Weissbourd, Nate Cermak, Robert Yang, Quilee Simeon, Cori Bargmann, and members of the Flavell lab for comments on the manuscript; Drew Robson and Jennifer Li for spline fitting code; Span Spanbauer for modeling insights; Martin Chalfie and Andrew Fire for reagents; and Ian Hope for discussions. N.C. acknowledges funding from EPSRC (EP/J004057/1). V.K.M. acknowledges funding from DARPA (030523-00001); the Singapore DSTA/MIT SCC collaboration; the Aphorism Foundation; and the Siegel Family Foundation. S.W.F. acknowledges funding from NIH (NS104892, NS131457, GM135413); NSF (Award #1845663); McKnight Foundation; Alfred P. Sloan Foundation; The Picower Institute for Learning & Memory; and The JPB Foundation.
INCLUSION AND DIVERSITY
One or more of the authors of this paper self-identifies as an underrepresented ethnic minority in their field of research or within their geographical location. One or more of the authors of this paper self-identifies as a gender minority in their field of research. One or more of the authors of this paper received support from a program designed to increase minority representation in their field of research.
Footnotes
DECLARATION OF INTERESTS
The authors declare no competing interests.
REFERENCES
- 1.Allen WE, Chen MZ, Pichamoorthy N, Tien RH, Pachitariu M, Luo L, and Deisseroth K (2019). Thirst regulates motivated behavior through modulation of brainwide neural population dynamics. Science 364, 253. 10.1126/science.aav3932. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Brezovec LE, Berger AB, Druckmann S, and Clandinin TR (2022). Mapping the Neural Dynamics of Locomotion across the Drosophila Brain. 2022.03.20.485047. 10.1101/2022.03.20.485047. [DOI] [PubMed] [Google Scholar]
- 3.Hallinen KM, Dempsey R, Scholz M, Yu X, Linder A, Randi F, Sharma AK, Shaevitz JW, and Leifer AM (2021). Decoding locomotion from population neural activity in moving C. elegans. Elife 10, e66135. 10.7554/eLife.66135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Marques JC, Li M, Schaak D, Robson DN, and Li JM (2020). Internal state dynamics shape brainwide activity and foraging behaviour. Nature 577, 239–243. 10.1038/s41586-019-1858-z. [DOI] [PubMed] [Google Scholar]
- 5.Musall S, Kaufman MT, Juavinett AL, Gluf S, and Churchland AK (2019). Single-trial neural dynamics are dominated by richly varied movements. Nat Neurosci 22, 1677–1686. 10.1038/s41593-019-0502-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Schaffer ES, Mishra N, Whiteway MR, Li W, Vancura MB, Freedman J, Patel KB, Voleti V, Paninski L, Hillman EMC, et al. (2021). Flygenvectors: The spatial and temporal structure of neural activity across the fly brain. 2021.09.25.461804. 10.1101/2021.09.25.461804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Stringer C, Pachitariu M, Steinmetz N, Reddy CB, Carandini M, and Harris KD (2019). Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, 255. 10.1126/science.aav7893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Niell CM, and Stryker MP (2010). Modulation of visual responses by behavioral state in mouse visual cortex. Neuron 65, 472–479. 10.1016/j.neuron.2010.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cook SJ, Jarrell TA, Brittin CA, Wang Y, Bloniarz AE, Yakovlev MA, Nguyen KCQ, Tang LT-H, Bayer EA, Duerr JS, et al. (2019). Whole-animal connectomes of both Caenorhabditis elegans sexes. Nature 571, 63–71. 10.1038/s41586-019-1352-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.White JG, Southgate E, Thomson JN, and Brenner S (1986). The structure of the nervous system of the nematode Caenorhabditis elegans. Philos. Trans. R. Soc. Lond., B, Biol. Sci. 314, 1–340. [DOI] [PubMed] [Google Scholar]
- 11.Witvliet D, Mulcahy B, Mitchell JK, Meirovitch Y, Berger DR, Wu Y, Liu Y, Koh WX, Parvathala R, Holmyard D, et al. (2021). Connectomes across development reveal principles of brain maturation. Nature 596, 257–261. 10.1038/s41586-021-03778-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Brittin CA, Cook SJ, Hall DH, Emmons SW, and Cohen N (2021). A multi-scale brain map derived from whole-brain volumetric reconstructions. Nature 591, 105–110. 10.1038/s41586-021-03284-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Moyle MW, Barnes KM, Kuchroo M, Gonopolskiy A, Duncan LH, Sengupta T, Shao L, Guo M, Santella A, Christensen R, et al. (2021). Structural and developmental principles of neuropil assembly in C. elegans. Nature 591, 99–104. 10.1038/s41586-020-03169-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Flavell SW, Raizen DM, and You Y-J (2020). Behavioral States. Genetics 216, 315–332. 10.1534/genetics.120.303539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Flavell SW, and Gordus A (2022). Dynamic functional connectivity in the static connectome of Caenorhabditis elegans. Curr Opin Neurobiol 73, 102515. 10.1016/j.conb.2021.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Raizen DM, Zimmerman JE, Maycock MH, Ta UD, You Y, Sundaram MV, and Pack AI (2008). Lethargus is a Caenorhabditis elegans sleep-like state. Nature 451, 569–572. 10.1038/nature06535. [DOI] [PubMed] [Google Scholar]
- 17.Van Buskirk C, and Sternberg PW (2007). Epidermal growth factor signaling induces behavioral quiescence in Caenorhabditis elegans. Nat Neurosci 10, 1300–1307. 10.1038/nn1981. [DOI] [PubMed] [Google Scholar]
- 18.Flavell SW, Pokala N, Macosko EZ, Albrecht DR, Larsch J, and Bargmann CI (2013). Serotonin and the neuropeptide PDF initiate and extend opposing behavioral states in C. elegans. Cell 154, 1023–1035. 10.1016/j.cell.2013.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fujiwara M, Sengupta P, and McIntire SL (2002). Regulation of body size and behavioral state of C. elegans by sensory perception and the EGL-4 cGMP-dependent protein kinase. Neuron 36, 1091–1102. [DOI] [PubMed] [Google Scholar]
- 20.Ji N, Madan GK, Fabre GI, Dayan A, Baker CM, Kramer TS, Nwabudike I, and Flavell SW (2021). A neural circuit for flexible control of persistent behavioral states. Elife 10, e62889. 10.7554/eLife.62889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dag U, Nwabudike I, Kang D, Gomes MA, Kim J, Atanas AA, Bueno E, Estrem C, Pugliese S, Wang Z, et al. (2023). Dissecting the functional organization of the C. elegans serotonergic system at whole-brain scale. Cell 186, 2574–2592.e20. 10.1016/j.cell.2023.04.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ardiel EL, Yu AJ, Giles AC, and Rankin CH (2017). Habituation as an adaptive shift in response strategy mediated by neuropeptides. NPJ Sci Learn 2, 9. 10.1038/s41539-017-0011-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chew YL, Tanizawa Y, Cho Y, Zhao B, Yu AJ, Ardiel EL, Rabinowitch I, Bai J, Rankin CH, Lu H, et al. (2018). An Afferent Neuropeptide System Transmits Mechanosensory Signals Triggering Sensitization and Arousal in C. elegans. Neuron 99, 1233–1246.e6. 10.1016/j.neuron.2018.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gordus A, Pokala N, Levy S, Flavell SW, and Bargmann CI (2015). Feedback from network states generates variability in a probabilistic olfactory circuit. Cell 161, 215–227. 10.1016/j.cell.2015.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kaplan HS, Salazar Thula O, Khoss N, and Zimmer M (2020). Nested Neuronal Dynamics Orchestrate a Behavioral Hierarchy across Timescales. Neuron 105, 562–576.e9. 10.1016/j.neuron.2019.10.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kato S, Kaplan HS, Schrödel T, Skora S, Lindsay TH, Yemini E, Lockery S, and Zimmer M (2015). Global brain dynamics embed the motor command sequence of Caenorhabditis elegans. Cell 163, 656–669. 10.1016/j.cell.2015.09.034. [DOI] [PubMed] [Google Scholar]
- 27.Li Z, Liu J, Zheng M, and Xu XZS (2014). Encoding of both analog- and digital-like behavioral outputs by one C. elegans interneuron. Cell 159, 751–765. 10.1016/j.cell.2014.09.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lim MA, Chitturi J, Laskova V, Meng J, Findeis D, Wiekenberg A, Mulcahy B, Luo L, Li Y, Lu Y, et al. (2016). Neuroendocrine modulation sustains the C. elegans forward motor state. Elife 5, e19887. 10.7554/eLife.19887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Luo L, Wen Q, Ren J, Hendricks M, Gershow M, Qin Y, Greenwood J, Soucy ER, Klein M, Smith-Parker HK, et al. (2014). Dynamic encoding of perception, memory, and movement in a C. elegans chemotaxis circuit. Neuron 82, 1115–1128. 10.1016/j.neuron.2014.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Roberts WM, Augustine SB, Lawton KJ, Lindsay TH, Thiele TR, Izquierdo EJ, Faumont S, Lindsay RA, Britton MC, Pokala N, et al. (2016). A stochastic neuronal model predicts random search behaviors at multiple spatial scales in C. elegans. Elife 5, e12572. 10.7554/eLife.12572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zhang M, Chung SH, Fang-Yen C, Craig C, Kerr RA, Suzuki H, Samuel ADT, Mazur E, and Schafer WR (2008). A self-regulating feed-forward circuit controlling C. elegans egg-laying behavior. Curr Biol 18, 1445–1455. 10.1016/j.cub.2008.08.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ji N, Venkatachalam V, Rodgers HD, Hung W, Kawano T, Clark CM, Lim M, Alkema MJ, Zhen M, and Samuel AD (2021). Corollary discharge promotes a sustained motor state in a neural circuit for navigation. Elife 10, e68848. 10.7554/eLife.68848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Riedl J, Fieseler C, and Zimmer M (2022). Tyraminergic corollary discharge filters reafferent perception in a chemosensory neuron. Curr Biol 32, 3048–3058.e6. 10.1016/j.cub.2022.05.051. [DOI] [PubMed] [Google Scholar]
- 34.Hendricks M, Ha H, Maffey N, and Zhang Y (2012). Compartmentalized calcium dynamics in a C. elegans interneuron encode head movement. Nature 487, 99–103. 10.1038/nature11081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Xu T, Huo J, Shao S, Po M, Kawano T, Lu Y, Wu M, Zhen M, and Wen Q (2018). Descending pathway facilitates undulatory wave propagation in Caenorhabditis elegans through gap junctions. Proc Natl Acad Sci U S A 115, E4493–E4502. 10.1073/pnas.1717022115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Yeon J, Kim J, Kim D-Y, Kim H, Kim J, Du EJ, Kang K, Lim H-H, Moon D, and Kim K (2018). A sensory-motor neuron type mediates proprioceptive coordination of steering in C. elegans via two TRPC channels. PLoS Biol 16, e2004929. 10.1371/journal.pbio.2004929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Denham JE, Ranner T, and Cohen N (2018). Signatures of proprioceptive control in Caenorhabditis elegans locomotion. Philos Trans R Soc Lond B Biol Sci 373, 20180208. 10.1098/rstb.2018.0208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nguyen JP, Shipley FB, Linder AN, Plummer GS, Liu M, Setru SU, Shaevitz JW, and Leifer AM (2016). Whole-brain calcium imaging with cellular resolution in freely behaving Caenorhabditis elegans. Proc. Natl. Acad. Sci. U.S.A. 113, E1074–1081. 10.1073/pnas.1507110112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Venkatachalam V, Ji N, Wang X, Clark C, Mitchell JK, Klein M, Tabone CJ, Florman J, Ji H, Greenwood J, et al. (2016). Pan-neuronal imaging in roaming Caenorhabditis elegans. Proc. Natl. Acad. Sci. U.S.A. 113, E1082–1088. 10.1073/pnas.1507109113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mathis A, Mamidanna P, Cury KM, Abe T, Murthy VN, Mathis MW, and Bethge M (2018). DeepLabCut: markerless pose estimation of user-defined body parts with deep learning. Nat Neurosci 21, 1281–1289. 10.1038/s41593-018-0209-y. [DOI] [PubMed] [Google Scholar]
- 41.Wolny A, Cerrone L, Vijayan A, Tofanelli R, Barro AV, Louveaux M, Wenzl C, Strauss S, Wilson-Sánchez D, Lymbouridou R, et al. (2020). Accurate and versatile 3D segmentation of plant tissues at cellular resolution. Elife 9, e57613. 10.7554/eLife.57613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dana H, Sun Y, Mohar B, Hulse BK, Kerlin AM, Hasseman JP, Tsegaye G, Tsang A, Wong A, Patel R, et al. (2019). High-performance calcium sensors for imaging activity in neuronal populations and microcompartments. Nat Methods 16, 649–657. 10.1038/s41592-019-0435-6. [DOI] [PubMed] [Google Scholar]
- 43.Wei Z, Lin B-J, Chen T-W, Daie K, Svoboda K, and Druckmann S (2020). A comparison of neuronal population dynamics measured with calcium imaging and electrophysiology. PLoS Comput Biol 16, e1008198. 10.1371/journal.pcbi.1008198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Cusumano-Towner MF, Saad FA, Lew AK, and Mansinghka VK (2019). Gen: a general-purpose probabilistic programming system with programmable inference. In Proceedings of the 40th ACM SIGPLAN Conference on Programming Language Design and Implementation PLDI 2019. (Association for Computing Machinery; ), pp. 221–236. 10.1145/3314221.3314642. [DOI] [Google Scholar]
- 45.Talts S, Betancourt M, Simpson D, Vehtari A, and Gelman A (2020). Validating Bayesian Inference Algorithms with Simulation-Based Calibration. 10.48550/arXiv.1804.06788. [DOI] [Google Scholar]
- 46.Yemini E, Lin A, Nejatbakhsh A, Varol E, Sun R, Mena GE, Samuel ADT, Paninski L, Venkatachalam V, and Hobert O (2021). NeuroPAL: A Multicolor Atlas for Whole-Brain Neuronal Identification in C. elegans. Cell 184, 272–288.e11. 10.1016/j.cell.2020.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wang YL, Grooms NWF, Jaklitsch EL, Schulting LG, and Chung SH (2023). High-throughput submicron-resolution microscopy of Caenorhabditis elegans populations under strong immobilization by cooling cultivation plates. iScience 26, 105999. 10.1016/j.isci.2023.105999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Anderson DJ, and Adolphs R (2014). A framework for studying emotions across species. Cell 157, 187–200. 10.1016/j.cell.2014.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Flavell SW, Gogolla N, Lovett-Barron M, and Zelikowsky M (2022). The emergence and influence of internal states. Neuron 110, 2545–2570. 10.1016/j.neuron.2022.04.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Byrne Rodgers J, and Ryu WS (2020). Targeted thermal stimulation and high-content phenotyping reveal that the C. elegans escape response integrates current behavioral state and past experience. PLoS One 15, e0229399. 10.1371/journal.pone.0229399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kotera I, Tran NA, Fu D, Kim JH, Byrne Rodgers J, and Ryu WS (2016). Pan-neuronal screening in Caenorhabditis elegans reveals asymmetric dynamics of AWC neurons is critical for thermal avoidance behavior. Elife 5, e19021. 10.7554/eLife.19021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Goodman MB, and Sengupta P (2019). How Caenorhabditis elegans Senses Mechanical Stress, Temperature, and Other Physical Stimuli. Genetics 212, 25–51. 10.1534/genetics.118.300241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Urai AE, Doiron B, Leifer AM, and Churchland AK (2022). Large-scale neural recordings call for new insights to link brain and behavior. Nat Neurosci 25, 11–19. 10.1038/s41593-021-00980-9. [DOI] [PubMed] [Google Scholar]
- 54.Chelur DS, and Chalfie M (2007). Targeted cell killing by reconstituted caspases. Proc Natl Acad Sci U S A 104, 2283–2288. 10.1073/pnas.0610877104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wang YL, Jaklitsch EL, Grooms NWF, Schulting LG, and Chung SH (2022). High-throughput submicron-resolution microscopy of entire C. elegans populations under strong immobilization by cooling cultivation plates. 2021.12.09.471981. 10.1101/2021.12.09.471981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Guizar-Sicairos M, Thurman ST, and Fienup JR (2008). Efficient subpixel image registration algorithms. Opt Lett 33, 156–158. 10.1364/ol.33.000156. [DOI] [PubMed] [Google Scholar]
- 57.Rudin LI, Osher S, and Fatemi E (1992). Nonlinear total variation based noise removal algorithms. Physica D: Nonlinear Phenomena 60, 259–268. 10.1016/0167-2789(92)90242-F. [DOI] [Google Scholar]
- 58.Hastings WK (1970). Monte Carlo Sampling Methods Using Markov Chains and Their Applications. Biometrika 57, 97–109. 10.2307/2334940. [DOI] [Google Scholar]
- 59.Neal RM (2011). MCMC using Hamiltonian dynamics 10.1201/b10905. [DOI] [Google Scholar]
- 60.Mansinghka VK, Schaechtle U, Handa S, Radul A, Chen Y, and Rinard M (2018). Probabilistic programming with programmable inference. In Proceedings of the 39th ACM SIGPLAN Conference on Programming Language Design and Implementation, pp. 603–616. 10.1145/3192366.3192409. [DOI] [Google Scholar]
- 61.Varshney LR, Chen BL, Paniagua E, Hall DH, and Chklovskii DB (2011). Structural properties of the Caenorhabditis elegans neuronal network. PLoS Comput Biol 7, e1001066. 10.1371/journal.pcbi.1001066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Rhoades JL, Nelson JC, Nwabudike I, Yu SK, McLachlan IG, Madan GK, Abebe E, Powers JR, Colón-Ramos DA, and Flavell SW (2019). ASICs Mediate Food Responses in an Enteric Serotonergic Neuron that Controls Foraging Behaviors. Cell 176, 85–97.e14. 10.1016/j.cell.2018.11.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Cermak N, Yu SK, Clark R, Huang Y-C, Baskoylu SN, and Flavell SW (2020). Whole-organism behavioral profiling reveals a role for dopamine in state-dependent motor program coupling in C. elegans. Elife 9, e57093. 10.7554/eLife.57093. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental Figure 1. Behavioral assays, GFP control recordings, and evaluation of model parameters, Related to Figure 1.
(A) Salt learning assay for N2 control animals, compared to pan-neuronal GCaMP7f animals. Naïve refers to animals grown on 0 mM NaCl; conditioned (‘cond’) refers to animals grown under the same conditions but exposed to 50mM NaCl with food for one hour prior to assay, which causes animals to prefer higher salt concentrations. Chemotaxis was measured on a plate with a 0mM to 50mM NaCl gradient with sorbitol added to ensure uniform osmolarity. Positive values correspond to chemotaxis directed toward high NaCl. Data are shown as means and standard deviation across plates. n=12–13 chemotaxis plates per group for naïve and n=4–6 plates per group for conditioned. n.s. not significant, Mann-Whitney U-Test.
(B) Un-normalized F heatmap of neural traces collected and extracted from a control animal expressing eat-4::NLS-GFP. Since GFP is expressed only in a fraction of cells in this strain, perfect neural identity mapping would result in a set of bright horizontal lines (GFP-positive neurons) and a set of dark horizontal lines (GFP-negative neurons), while a registration mismatch would appear as a bright spot in the trace of an otherwise GFP-negative neuron, or a dark spot in the trace of an otherwise GFP-positive neuron. Note that there are very few instances of registration mismatches visible in the traces. As described in the main text, we estimate the number of neuron identification errors to be 0.3% of frames (see Methods).
(C) Heatmap of neural traces collected and extracted from three GFP control animals.
(D) Analysis of which velocity filtering method best matches neural dynamics. An example neuron that encodes behavior with a long timescale value according to CePNEM (blue; same for all four traces) and different processed versions of velocity (gray). Velocity was processed in different ways and the match to neural activity was evaluated. Average performance across all neurons is in panel (E). For each method of processing velocity, the optimal fit to the neuron was taken by minimizing the error (MSE) using gradient descent. The different methods of processing velocity were: (1) EWMA: exponentially-weighted average of recently velocity; (2) Optimal Shift: time-lagged shift in velocity; (3) Optimal Gaussian kernel: gaussian averaging of velocity at each time point; (4) Optimal lowpass filter: velocity filtered based on frequency. The alternative smoothing methods were evaluated to compare against the EWMA used in the model.
(E) Average fit of how velocity filtered in the indicated ways (see panel (D) legend for more description) matches neural activity, quantified as mean square error (lower is better). This was averaged across all recorded neurons. ***p<0.0005, Wilcoxon signed rank test.
(F) Degradation analysis on each model parameter, comparing the percentage that the error (as measured by cross-validated mean-squared error when fitting the model with MSE optimization – see Methods) increases when the model is refit with that parameter removed. Wilcoxon signed rank test (comparing the full model and the partial model) resulted in p-value below 0.0005 for all shown parameters. For reference, black line shows the error increase for a model with no behavioral parameters (just an offset parameter so that the model would guess each neuron’s mean activity).
(G) Degradation analysis using same procedure as in (F), but plotting a different outcome. For “behavior” predictor terms (left): for each neuron the three degraded models were fit (lacking each predictor term) and the predictor term whose deletion caused the greatest increase in error was determined. The fraction of neurons that had each parameter as their most important predictor term is displayed. For “non-linearity” terms (right): the same procedure was conducted, except the degraded models lacked one or both model non-linearities. Model lacking both non-linearities was the fully “linear” model. The analysis was done on the encoding neurons and averaged across datasets.
Supplemental Figure 2. Controls for model fitting, decoding analyses, and analyses of neurons’ timescales, Related to Figure 1.
(A) Simulation-based calibration results for CePNEM. Simulation-based calibration was performed by simulating 1997 neurons from CePNEM using behaviors from 4 different animals and fitting them each twice, on different time ranges. For each model parameter, the ground-truth parameter was ranked within the fitted posterior. If model fitting is perfectly calibrated, the ground-truth parameter’s rank should be the uniform distribution. Therefore, for each parameter, we performed a χ2 test to distinguish their distribution from the uniform distribution with p=0.05. All parameters passed this test, except for the timescale parameter , which has a very small calibration artifact predicted to impact <4 neurons per dataset. See Methods.
(B) A series of CePNEM model fits to various neurons, showing the model’s ability to fit a wide variety of neural tunings to behavior. The model was fit on the first half of the dataset, and tested on the second half, revealing that these neurons have robust tunings to behavior across time that is well-explained by CePNEM. The inset cross-validation (cv) indicates the goodness-of-fit of the model on testing data (see Methods for additional details).
(C) The fraction of neurons with encoding vs the fraction of active neurons (the signal value above the GFP threshold). Each dot is a dataset. The fractions are computed by averaging across two time segments in each dataset. The tight clustering of dots indicates that datasets were roughly consistent, according to these basic metrics.
(D) Controls comparing the percentage of neurons that were detected as encoding behavior using real GCaMP traces with the same animal’s behavior, using the same GCaMP traces but attempting to fit with a different animal’s behavior (essentially a scramble control; ‘wrong behavior’), and using GFP datasets. See Methods for statistical methods used to determine if a given neuron significantly encodes a behavior.
(E) Cumulative distribution of cross-validation scores across neurons in continuous SWF415 recordings (see Methods). Its intuitive meaning is that a value of zero indicates that the fit CePNEM model fails to generalize to the testing data, whereas a value of +1 indicates that the model perfectly explains neural activity on withheld testing data. 96% of neurons had a positive cross-validation score.
(F) Distribution of overall neuron signals (as a metric for overall activity levels) across all neurons in three categories: GFP control neurons, encoding neurons (GCaMP neurons that significantly encoded at least one behavior based on CePNEM), and non-encoding neurons (GCaMP neurons that did not significantly encode any behaviors according to CePNEM). Neuron signal here is defined as where is the un-normalized ratiometric fluorescence of the neuron in question. It provides a measure of overall level of dynamics exhibited by the neuron. Note that non-encoding neurons still exhibited robust dynamics, for the most part exceeding the negative control GFP neurons.
(G) Linear, L1-regularized decoder models were trained to predict various behaviors (velocity, head curvature, feeding, angular velocity, and curvature, respectively) from 11 animals from either neurons (blue) or CePNEM model residuals (orange). Decoding accuracy was assessed as 1 – MSE (decoded behavior, true behavior), averaged over five 80/20 cross-validation splits (see Methods). Note that the decoder models do much worse when trained on CePNEM model residuals than when trained on the full neural data, suggesting that the model can explain most neural variance overtly related to behavior.
(H) An analysis of decoding accuracy from specific subsets of neurons. Linear, L1-regularized decoder models were trained to predict the behavioral parameters listed on the x-axis. For each behavioral parameter we compared decoder accuracy when the model was trained on (i) the neurons that encoded that behavioral feature according to CePNEM (e.g. for forward speed, the full set of neurons that had significant information about forward speed; shown as red lines); versus (ii) random subsets of neurons equal in size to group (i) selected from the neurons that did not encode that behavioral feature (gray distributions). *p<0.05, **p<0.005, empirical p-values based on rank of red lines in respective gray distributions.
(I) Mean ECDF of the model half-decay time of all neurons demonstrated to encode forward locomotion, contrasted with the ECDF of neurons demonstrated to encode reverse locomotion, in 14 animals. The shaded regions represent the standard deviation between animals. The median fraction (across animals) of forward neurons with long timescales (half-decay τ1/2 > 20𝑠) was 0.12, compared with only 0.03 for reversal neurons; this difference was statistically significant (p = 0.029) under a Mann-Whitney U-Test.
(J) Mean ECDF of model half-decay time of all neurons that encode the indicated behaviors. Data are shown as in panel (H).
(K) Performance of a decoder trained to predict past and future head curvature of animals based on current population neural activity. Models were trained and data are displayed as in Fig. 2D, except these models were trained to predict head curvature rather than velocity. See Fig. 2D legend for additional details.
(L) Violin plots showing distribution of head curvature angles (in radians) during forward and reverse movement. Note that the distributions are similar, suggesting that the widespread differences in neural encoding of head curvature during forward versus reverse movement is not due to animals exhibiting different head angles based on their movement direction.
(M) A neuron that encodes angular velocity (defined as longer-timescale head curvature; due to the higher frequency nature of head curvature oscillations, longer-timescale is defined here as at least 5 seconds). This neuron has a half-decay of τ1/2 = 9.5 ± 1.3 seconds and is multiplexed with velocity as well.
Supplemental Figure 3. Additional analyses of UMAP projections, Related to Figure 3.
(A) Projections of all neurons from each of four different SWF415 animals into the same UMAP space (built from full population of animals; same as in Fig. 3A). Observe that the overall structure is very similar, suggesting that the locations of neurons in UMAP space are similar across datasets.
(B) Projections of all neurons from each of two different NeuroPAL animals into the UMAP space. These neurons also fill in a similar pattern to that of the SWF415 animals, suggesting that the overall neural encodings of the two strains are similar.
(C) Projections of all neurons from each of two different GFP control animals into the UMAP space. These neurons fail to fill most of the space, which is consistent with the non-encoding nature of neurons in this control strain.
(D) Projections of all neurons from 14 different SWF415 animals into the UMAP space, taking the median of each neuron’s posterior point cloud in the UMAP space. Note that the medians fill out the same space as when projecting the full posteriors (as in Fig. 3), suggesting the continuity of the UMAP space is not merely an artifact of parameter uncertainty.
(E) An analysis of clusterability of all neurons that encode behavior. For each dataset, we attempted to cluster all neurons that encode behavior using a similarity metric based on the difference of the neurons’ GCaMP traces. To determine the optimal number of clusters, we computed the Calinski-Harabasz index over varying number of clusters when performing k-means clustering on the neural traces. Clustering was done on a per dataset basis on all SWF415 datasets, and the mean and standard error values are plotted. Note that the optimal number of clusters in this analysis is 2, which is the minimum number that can be assessed with this metric. This suggests that there is not a larger set of discrete subgroups of neurons that are separable from one another.
(F) Cumulative variance explained by the top 20 PCs, averaged over 14 animals. The shaded region is the standard deviation across animals.
Supplemental Figure 4, Analysis of NeuroPAL recordings and effects of perturbing neural activity, Related to Figure 4.
(A) A RGB composite image of one of the NeuroPAL animals that we recorded. The composite was constructed by combining images of NLS-mTagBFP2 (shown in blue), NLS-cyOFP2 (shown in green), and NLS-mNeptune2.5 (shown in red). Using this composite image, we were able to label a large number of neurons in this animal. Neural identity was determined while making use of all 3D information, but for display purposes here we show a maximum intensity projection of a subset of the z-slices from the recording. Therefore, this image does not show all the neurons in the head (a maximum intensity projection of all z-slices is too dense with neurons to show for display purposes here).
(B) Comparison of behavioral parameters during recordings of brain-wide GCaMP7f in animals without NeuroPAL (SWF415, labeled “415”) and with NeuroPAL (SWF702, labeled “NP”). Four behavioral metrics are shown. n=14 and 21 animals for SWF415 and SWF702, respectively. *p<0.05 ***p<0.0005, Mann-Whitney U-Test.
(C) Average overall neural signal across recordings of animals expressing pan-neural GFP (green), pan-neural GCaMP (blue) and pan-neural GCaMP with NeuroPAL transgene (orange). Overall neural signal here is defined as where is the un-normalized ratiometric fluorescence.
(D) A comparison of how much variance in neural activity is explained by different number of principal components in pan-neural GCaMP strains without NeuroPAL (blue, SWF415) and with NeuroPAL (orange, SWF702).
(E) Distribution of cross-validation scores (see Methods for quantitative details) for pan-neural GCaMP strain without NeuroPAL (blue) and with NeuroPAL (orange).
(F) UMAP plot showing the posterior distributions of the CePNEM model fits for various neurons; each neuron is plotted in a different color. The same set of time points from the same animal were used for each neuron’s fit. This plot shows a subset of neurons with largely non-overlapping tunings, just to illustrate how neurons map onto the UMAP space described in Fig. 3.
(G) Event-triggered averages showing average neural activity of the indicated neuron classes aligned to key behaviors, as indicated in the column labels. Data are pooled across all instances of recordings of the neuron classes for the behaviors indicated. Note that event-triggered averages in general are noisier for feeding due to a lower number of events where feeding suddenly started or stopped (compared to forward/reverse and dorsal/ventral transitions). The shading indicates the standard error across the recorded animals.
(H) Table of the signal values of the neuron classes identified in NeuroPAL. For each neuron class, dot is the median level of overall activity (‘signal’) for the neuron across all recorded instances, quantified as in Fig. 4A. The line denotes the 25th - 75th percentile range. The neurons are ordered by the median signals. The dashed green line indicates the boundary below which neurons are likely to be inactive, determined based on the signal values in the GFP control datasets.
(I) Effects of perturbing the indicated neurons on the animal’s behavioral output. For all perturbations, we quantified forward speed (shown as means ± standard error of the mean (SEM)), reverse speed (means ± SEM), median head curvature during dorsal and ventral head bends (box plots showing 25th and 75th percentiles and medians as red lines; separate boxes for dorsal and ventral bending), frequency of head bending (plotted as distribution of intervals between head swings), and feeding rates (means ± SEM). Neuron inactivation methods were: (1) RIC: tetanus toxin (TeTx) expression; (2) AIM: chemogenetic silencing using the Histamine-gated chloride channel (HisCl); (3) AUA: chronic silencing via expression of leaky potassium channel unc-103(gf); (4) RIF: chronic silencing via unc-103(gf); (5) AVL: chronic silencing via unc-103(gf); (6) SAA: neuron ablation via split caspase expression; (7) SMB: neuron ablation via split caspase expression; (8) MC: optogenetic inactivation via GtACR2; (9) M4: optogenetic inactivation via GtACR2; (10) ASG: optogenetic activation via Chrimson. All promoters were single cell-specific, either through highly specific single-cell promoters or intersectional Cre/Lox promoters. Details of promoters used are in Method Details under the Transgenic Animals section. *p<0.05, **p<0.01, ***p<0.001, ****p<0.0001, Bonferroni-corrected Mann-Whitney test. n.s., not significant.
Supplemental Figure 5, Analysis of variable encoding neurons, Related to Figure 4.
(A) Locations of different neuron classes in UMAP space, showing results for multiple recordings of each neuron. The UMAP space is the same as is shown in Fig. 3, where distance between neurons is proportional to the difference in how they encode behavior. Here, each colored dot depicts how the indicated neuron class encoded behavior in a single recording. Two types of neurons are shown: (1) Low variability neurons that have consistent encoding of behavior according to CePNEM: RIM, RIB, MC, IL2D; and (2) High variability neurons that have variable encoding across animals according to CePNEM: URX, OLQD. Note that the dots for the variable neurons are more distributed in this space than the dots for the low variability neurons. Only six neuron classes are shown to prevent the plot from being overcrowded.
(B) Scatter plot of labeling confidence (a qualitative metric determined by person scoring, reflecting their confidence that the neuron is correctly identified based on position and multi-spectral fluorescence; the higher the better; note that neurons with sufficiently low confidence were entirely excluded from all analyses in the paper, and this plot only shows values above this threshold) and encoding variability (lower value means more consistency). There is no evident relationship between these values, suggesting that labeling error does not introduce encoding variability.
(C) Scatter plot of GCaMP ROI match score (the higher the better in terms of confidence that NeuroPAL ROI was confidently mapped to a GCaMP ROI; see Methods) and encoding variability shows no relationship. This suggests that the process that matches the NeuroPAL ROI to the GCaMP ROI does not introduce encoding variability.
(D) Examples of a variable coupling neuron (OLQD from 3 animals shown). On the left column, the NeuroPAL fluorescence images with OLQD labeled show consistent color combination and location of this neuron class. On the right column, the corresponding neural traces (blue) are shown along with CePNEM fits (orange), and a written description of the encoding properties. Note that the neurons of the same class from different animals encode different sets of behaviors.
(E) Performance of CePNEM model across different animals, for neuron classes with different levels of variable encoding. In this analysis, the optimal CePNEM model parameters learned from 21 animals’ neural and behavioral data was determined (using a hierarchical Bayesian approach; see Methods). These model parameters were then used to predict neural activity in three additional animals shown here (animals 22–24). This analysis is shown for three categories of neurons: (1) neurons with low variability according to CePNEM: RIB, ASG, and SMDV; (2) neurons with moderate variability according to CePNEM: AUA, CEPD, and URYV; and (3) neurons with high variability according to CePNEM: URX, IL1D, and OLQD. The Variability Index for each neuron is displayed by the neuron’s name. Note that the level of variability in neural encoding, determined by our analysis, scales with the ability of models to successfully predict neural activity across different animals, as expected.
Supplemental Figure 6, Analysis of dynamic encoding neurons, Related to Figure 6.
(A) An analysis of what fraction of neurons were detected as changing encoding in our GCaMP datasets and simulated datasets. Simulated datasets are labeled ‘SBC’ for simulation-based calibrations. These are neurons simulated from the CePNEM model, where ground-truth parameters were set to not have any encoding changes.
(B) Scatterplot of datasets showing that extent of photobleaching is not correlated with detection of encoding changes. Each dot is a SWF415 dataset.
(C) Scatterplot depicting each neuron class’s likelihood of changing encoding in a single continuous recording (x-axis) versus its variability overall across all animals (y-axis). Each dot is a single neuron class. Note the positive trend (p<0.05, conditional independence test). The box highlights neurons that are variable both across and within animals.
(D) The frequency of neurons changing encoding in single recordings, separating neurons based on whether they are sensory, inter-, or motor neurons. No major difference was observed between these three groups, and this remains true when variability index is used instead of encoding change fraction.
(E) The same dataset in Fig. 6F but also plotting the relative model performance averaged over the static encoding neurons. Note that the black line does not show the sudden changes in value seen for the purple line.
(F) Same as (E), but for the dataset in Fig. 6G.
(G) An example dataset that shows a less synchronized encoding change, displayed in the same manner as in (E-F).
(H) Two example encoding changing neurons from the animal in (G), one with an abrupt encoding change at approximately 12 minutes, and another neuron that appears to have a slowly-increasing gain to its behavioral encoding over the last ~10 minutes of the recording.
(I) A plot of the fraction of encoding neurons that exhibited encoding change in a dataset, compared with the behavioral difference between the first and second half of that dataset. Behavioral variability was computed as the sum of the absolute values of the differences (across the two time segments) of the following behavioral parameters (each such parameter was normalized to the standard deviation of that behavior across all 14 SWF415 datasets): median of reverse velocity, median of forward velocity, 25th percentile of head curvature, 75th percentile of head curvature, 25th percentile of feeding rate, and 75th percentile of feeding rate. This value provides a general description of how much the distributions of behavioral parameters changed across the two halves of the recording. Observe that datasets with large behavioral changes tend to have more encoding changes, suggesting that the neural flexibility may be related to the observed behavior changing.
Supplemental Figure 7, Analysis of stimulus-induced encoding changes, Related to Figure 7.
(A) Experiments to examine the impact of the heat stimulation on the behavior and health of the animals. Animals subjected to the heat stimulation did not display a significant difference (p = 0.62 in a Mann-Whitney U-Test computed over 10 animals) in their exploratory behavior (computed as counting the number of squares each animal entered on an assay plate) relative to mock-stimulated animals (animals that were mounted on imaging slides, but not given the thermal stimulus). Behavior was quantified one hour after the heat stimulation.
(B) The heat stimulation did not kill any animals (all animals were alive 2 days after the stimulation).
(C) Connectome localization of neurons that exhibit sensory responses to the thermal stimulus. Neurons in red generated transient (<4sec) excitatory responses to the heat stimulus and neurons in blue generated transient inhibitory responses. Layout of connectome is the same as in Fig. 5C–F (see that legend for further details). Marginal distributions show the enrichment of each group of neurons along the two axes, relative to a random shuffle control (gray). *p< 0.05 **p<0.005, one sample Z-test for proportion on the excitatory responses; the inhibitory responses were not significant.
(D) Connectome localization of neurons that exhibit long-lasting (15–30sec) excitatory (red) or inhibitory (blue) responses to the thermal stimulus. Data are displayed as in panel (C); there was not a significant enrichment of these neurons in any sensorimotor layer.
(E) A comparison of the relative model performance averaged across all 11 SWF415 animals that underwent a heat shock (top) with the same metric computed over 4 animals that were not stimulated (bottom). Note that the baseline animals do not have a sharp change in relative model performance at the train/test split, suggesting that the encoding changes in the heat-stimulation datasets are a direct result of the stimulation.
(F) Fraction of times that each neuron class changed encoding after the heat stimulus. More specifically, the fraction of times that decoders trained on baseline data to predict feeding from the given neuron’s activity performed better on the pre-stim data than the post-stim data (see Methods). Note that the neurons have degradations in performance well above what would be expected by chance (50%); this indicates that the neurons changed encoding after the heat stimulus. *p<0.05, **p<0.005, ***p<0.0005, Wilcoxon signed rank test comparing pre-stimulus vs post-stimulus performance of the decoders across animals, as an indicator of whether these encoding changes were reliable across animals. The neurons shown here encoded feeding prior to the heat stimulus. p-values for encoding change were Benjamini-Hochberg corrected over all neurons where the decoder succeeded at predicting feeding in the baseline data (see Methods for additional details).
(G) Average amount of encoding change between pre-stim and post-stim CePNEM fits across heat-stimulated animals. Insets display the fraction of times that the indicated neurons changed encoding at all after the heat stimulus. Neurons shown here encoded either velocity or head curvature prior to the heat stimulus (the neurons that encoded feeding prior to the stimulus are analyzed in panel F; different statistical methods needed to be used for these two categories, since feeding was strongly suppressed post-heat-stim; see Methods for details). (*)p<0.1, *p<0.05, **p<0.005, p-value based on rank of actual magnitude of encoding change across animals (red) to level expected by chance (grey distribution), as an indication of whether the reliability of encoding change was greater than expected by chance. The p-values were Benjamini-Hochberg corrected over this set of neurons.
(H) A plot that relates each neuron class’s variability in encoding of behavior within heat stimulation datasets (y-axis) to its variability within baseline spontaneous behavior datasets (x-axis). See Methods for additional detail on how intra-dataset variability was computed based on encoding in the first versus second halves of the recordings. Black line is the identity line and each dot is a neuron class. Note the positive trend.
Movie S1. Example video of baseline recording conditions, Related to Figure 1. An excerpt from an example neural/behavioral dataset, showing the NIR behavioral recording. Raw video data is shown with overlaid information: (i) blue, orange, and green dots are the identified targets for worm tracking that were determined during live recording, which allowed us to locate the worm’s head and keep the animal centered in view; (ii) black line shows a spline fit to the animal’s centerline; (iii) upper left shows time and values of three ongoing behavioral parameters: velocity, head curvature, and feeding rate.
Data Availability Statement
Data: All brain-wide recordings and accompanying behavioral data are freely available in a browsable and downloadable format at www.wormwideweb.org. The data files have also been deposited at Zenodo and Github and are publicly available as of the date of publication. DOIs are listed in the key resources table.
Code: All original code has been deposited at Github and Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the Lead Contact upon request.
KEY RESOURCES TABLE.
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Bacterial and Virus Strains | ||
| E. coli: Strain OP50 | Caenorhabditis Genetics Center (CGC) | OP50 |
| Chemicals, Peptides, and Recombinant Proteins | ||
| Rhodamine 110 | Millipore Sigma |
Cat#83695 |
| Rhodamine B | Millipore Sigma |
Cat#83689 |
| Deposited Data | ||
| Original code and data related to recording and analyzing neural activity and behavior | This paper | Data: https://doi.org/10.5281/zenodo.8150515 and www.wormwideweb.org Code: https://doi.org/10.5281/zenodo.8151918 and https://github.com/flavell-lab/AtanasKim-Cell2023 |
| Experimental Models: Organisms/Strains | ||
| C. elegans: flvIsl 7[tag-168: :NLS-GCaMP7F, gcy-28.d::NLS-tag-RFPt, ceh-36:NLS-tag-RFPt, inx-1::tag-RFPt, mod-1 ::tag-RFPt, tph-1 (short)::NLS-tag-RFPt, gcy-5::NLS-tag-RFPt, gcy-7::NLS-tag-RFPt]; flvIs18[tag-168: :NLS-mNeptune2.5]; lite-1(ce314); gur-3(ok2245) | This paper | SWF415 |
| C. elegans: flvIs17; otIs670 [low-brightness NeuroPAL]; lite-1(ce314); gur-3(ok2245) | This paper | SWF702 |
| C. elegans: flvEx450[eat-4::NLS-GFP, tag-168: :NLS-mNeptune2.5]; lite-1(ce314); gur-3(ok2245) | This paper | SWF360 |
| C. elegans: flvEx451[tag-168::NLS-GFP, tag-168::NLS-mNeptune2.5]; lite-1(ce314); gur-3(ok2245) | This paper | SWF467 |
| C. elegans: flvEx207[nlp-70::HisCl1, elt-2::nGFP] | This paper | SWF515 |
| C. elegans: flvEx301[tbh-1:: TeTx: :sl2-mCherry, elt-2::nGFP] | This paper | SWF688 |
| C. elegans: flvEx481[flp-8::inv[unc-103-sl2-GFP], ceh-6::cre, myo-2::mChrimson] | This paper | SWF996 |
| C. elegans: flvEx482[unc-25::inv[unc-103-sl2-GFP], flp-22::cre, myo-2::mChrimson] | This paper | SWF997 |
| C. elegans: kyEx4268 [mod-1::nCre, myo-2::mCherry]; kyEx4499 [odr-2(2b)::inv[TeTx::sl2GFP], myo-3::mCherry] | This paper | SWF703 |
| C. elegans: leIs4207 [Plad-2::CED-3 (p15), Punc-42::CED-3 (p17), Plad-2::GFP, Pmyo-2::mCherry] | This paper | UL4207 |
| C. elegans: leIs4230 [Pflp-12s::CED-3 (p15), Pflp-12s::CED-3 (p17), Pflp-12s::GFP, Pmyo-2::mCherry] | This paper | UL4230 |
| C. elegans: flvEx485[gcy-21::Chrimson-t2a-mScarlett, elt-2::nGFP] | This paper | SWF1000 |
| C. elegans: flvEx502[ceh-28::GtACR2-t2a-GFP, myo-2::mCherry] | This paper | SWF1026 |
| C. elegans: flvEx499[ceh-19::inv[GtACR2-sl2-GFP], ins-10::nCre, myo-2::mCherry] | This paper | SWF1023 |
| Recombinant DNA | ||
| pSF300 [tag-168 ::NLS-GCaMP7F] | This paper | pSF300 |
| pSF301[tag-168::NLS-mNeptune2.5] | This paper | pSF301 |
| pSF302[tag-168::NLS-GFP] | This paper | pSF302 |
| pSF303 [tag-168::NLS-tag-RFPt] | This paper | pSF303 |
| Software and Algorithms | ||
| NIS-Elements (v4.51.01) | Nikon | https://www.nikoninstruments.com/products/software |
| Other | ||
| Zyla 4.2 Plus sCMOS camera | Andor | N/A |
| Ti-E Inverted Microscope | Nikon | N/A |


