Performance of Linear Mixed Models in Estimating Structural Rates of Glaucoma Progression Using Varied Random Effect Distributions

Abstract

Purpose

To compare how linear mixed models (LMMs) using Gaussian, Student t, and log-gamma (LG) random effect distributions estimate rates of structural loss in a glaucomatous population using OCT and to compare model performance to ordinary least squares (OLS) regression.

Design

Retrospective cohort study.

Subjects

Patients in the Bascom Palmer Glaucoma Repository (BPGR).

Methods

Eyes with ≥ 5 reliable peripapillary retinal nerve fiber layer (RNFL) OCT tests over ≥ 2 years were identified from the BPGR. Retinal nerve fiber layer thickness values from each reliable test (signal strength ≥ 7/10) and associated time points were collected. Data were modeled using OLS regression as well as LMMs using different random effect distributions. Predictive modeling involved constructing LMMs with (n – 1) tests to predict the RNFL thickness of subsequent tests. A total of 1200 simulated eyes of different baseline RNFL thickness values and progression rates were developed to evaluate the likelihood of declared progression and predicted rates.

Main Outcome Measures

Model fit assessed by Watanabe–Akaike information criterion (WAIC) and mean absolute error (MAE) when predicting future RNFL thickness values; log-rank test and median time to progression with simulated eyes.

Results

A total of 35 862 OCT scans from 5766 eyes of 3491 subjects were included. The mean follow-up period was 7.0 ± 2.3 years, with an average of 6.2 ± 1.4 tests per eye. The Student t model produced the lowest WAIC. In predictive models, all LMMs demonstrated a significant reduction in MAE when estimating future RNFL thickness values compared with OLS (P < 0.001). Gaussian and Student t models were similar and significantly better than the LG model in estimating future RNFL thickness values (P < 0.001). Simulated eyes confirmed LMM performance in declaring progression sooner than OLS regression among moderate and fast progressors (P < 0.01).

Conclusions

LMMs outperformed conventional approaches for estimating rates of OCT RNFL thickness loss in a glaucomatous population. The Student t model provides the best model fit for estimating rates of change in RNFL thickness, although the use of the Gaussian or Student t distribution in models led to similar improvements in accurately estimating RNFL loss.

Financial Disclosure(s)

Proprietary or commercial disclosure may be found in the Footnotes and Disclosures at the end of this article.

Accurate detection of disease progression is essential in managing glaucoma and preventing visual disability. Although standard automated perimetry (SAP) has traditionally been utilized to assess functional vision loss in glaucoma, changes in the retinal nerve fiber layer (RNFL), as measured with OCT, provide valuable objective data in evaluating structural loss due to glaucoma. Accurate assessments of change in RNFL thickness provide guidance in identifying eyes with glaucomatous progression, which can then be treated appropriately. Given that SAP test variability can be high among glaucoma patients,¹ trending structural OCT data may be beneficial.

Rates of changes have typically been estimated using ordinary least squares (OLS) regression, which is applied to summary metrics such as average RNFL thickness. However, OLS can be highly imprecise in the presence of a few measurements, which often occur in clinical practice. Commercially available progression software typically requires 5 tests before any analysis is provided due to this imprecision. With a typical frequency of OCT testing completed once or twice yearly,² a substantial amount of time would be required before the availability of OLS-based analyses for clinical use.

Linear mixed models (LMMs) have been applied in estimating rates of change in glaucoma, primarily due to their ability to utilize correlated patient data in the overall population. These rates have been shown to be more precise using various modalities such as SAP and scanning laser ophthalmoscopy,^3,4 as data regarding the overall population are able to guide eye-level estimates. Individual estimates are improved by “borrowing strength” from population trends when fewer data points are available for a particular eye. As more measurements are available, estimates will rely primarily on the individual’s data, and the need to rely on population data decreases. Linear mixed model estimates consist of fixed effects, which are the population averages, and random effects, which are eye-specific deviations from the overall population means.

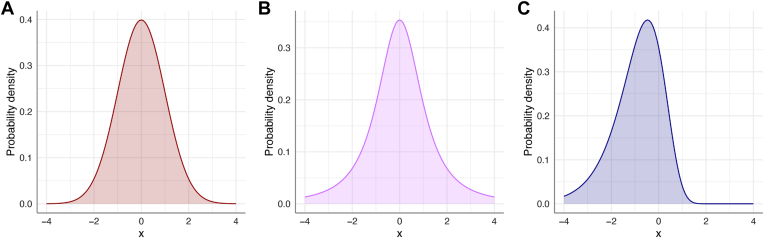
The traditional LMM estimates random effects using a Gaussian distribution, leading to the assumption of a normal distribution of rates of change in the population. However, prior work has demonstrated that only a small percentage of patients with glaucoma have moderate or fast progression as assessed by SAP, leading to a left-skewed distribution.^5,6 In addition, the shrinkage of estimates toward the population mean may attenuate more extreme values. Recent work has evaluated SAP metrics using the Gaussian LMM as well as models utilizing alternative random effects distributions, such as the Student t distribution and left-skewed log-gamma (LG) distribution (Fig 1).⁷ Prior work had suggested that the LG distribution may be more appropriate, as the majority of eyes have rates of change close to 0, whereas a minority have more extreme values.⁸ These analyses demonstrated that the LG model provided the best fit for SAP data.

Figure 1.

(A) Gaussian, (B) Student t, and (C) log-gamma probability density distributions. The x-axis consists of arbitrary units, whereas the y-axis indicates the probability density. The Student t distribution has thicker tails than the Gaussian, whereas the log-gamma distribution features a left-skewed distribution.

However, an analogous analysis of OCT data has not been completed. Although LMMs have been commonly used with OCT data,9, 10, 11 improved performance compared with traditional OLS has not been clearly demonstrated. It is unknown if the LG model would be beneficial when assessing glaucomatous progression with OCT data. The purpose of this work was to compare LMM performance with OLS predictions, as well as the accuracy of Gaussian, Student t, and LG LMMs in estimating rates of change in OCT RNFL thickness.

Methods

The University of Miami institutional review board approved this study and granted a waiver of informed consent given the retrospective nature of this work. The study adhered to the Declaration of Helsinki and the Health Insurance Portability and Accountability Act.

Data Collection

The Bascom Palmer Glaucoma Repository contains demographic and ophthalmic data of eyes with or suspected of glaucoma examined at the clinical sites of the Bascom Palmer Eye Institute (Miami, FL), identified using International Classification of Diseases codes (Table S1, available at www.ophthalmologyscience.org) from the Epic electronic health record (Epic Systems). The large Hispanic and Black populations in South Florida contribute to the diversity of this database. Glaucoma type was determined by the International Classification of Diseases coding at the time of the first visit in this analysis. Normal tension glaucoma was classified as primary open-angle glaucoma, whereas pigmentary and pseudoexfoliative glaucomas were classified as secondary open-angle glaucomas. For eyes that met inclusion criteria, we identified any instance of key ocular diagnoses that would substantially confound testing. These diagnoses included exudative macular degeneration, retinal detachment, uveitis, retinal vascular occlusions, proliferative diabetic retinopathy, and nonglaucomatous optic neuropathy (see Table S2, available at www.ophthalmologyscience.org, for the complete list). These exclusions mirror those utilized by a similar electronic health record database analysis.¹² Any testing after the first instance of any of these diagnoses was excluded. In addition, eyes that underwent glaucoma procedures (trabeculectomy, aqueous shunt insertion, cyclophotocoagulation, laser iridotomy, or microinvasive glaucoma surgeries—identified by Current Procedural Terminology codes 66170, 66172, 0192T, 66183, 66180, 66179, 66710, 66711, 66761, 65855, 65820, 66174, 65865, 66991, 66989, 66987, 66988, 0474T, 0449T, and 0450T) were identified. OCT tests after any of these procedures were eliminated due to the potential impact of surgical intervention on the rate of change of RNFL thickness.

OCT data from the Zeiss Cirrus system were extracted from Zeiss Forum (Carl Zeiss Meditech). All data between April 2008 and February 2022 were collected. Any scans with RNFL thickness values < 30 μm or > 130 μm were excluded due to likely artifacts as previously completed.¹² All scans were required to have signal strength ≥ 7/10 and a baseline RNFL thickness ≥ 38 μm to allow for longitudinal trend given the “floor” effect.¹³ If multiple scans were completed on 1 day, an averaged RNFL thickness value was utilized. Eyes included in this study were required to have ≥ 5 reliable tests over ≥ 2 years of follow-up.

Bayesian Modeling

Bayesian LMMs were constructed. The construction of these models has been discussed fully in our prior publication.⁷ In short, Bayesian statistics utilizes probabilities to gauge the true rate of progression. The prior distribution represents an initial belief in the probability of an event, which is then combined with the observed data to compute a posterior distribution. The model construction of the Gaussian, Student t, and LG distributions followed the same construction completed in our prior work. A random-intercept and random-slope Bayesian model was used to estimate OCT RNFL thickness as follows:

$${\mathrm{Y}}_{\text{it}}={\mathrm{\beta }}_0+{\mathrm{\beta }}_{0\mathrm{i}}+({\mathrm{\beta }}_1+{\mathrm{\beta }}_{1\mathrm{i}})\ast {\mathrm{x}}_{\text{it}}+{\mathrm{\epsilon }}_{\text{it}}$$

where Y_it represents OCT RNFL thickness at time t of eye i, β₀ represents the fixed intercept for the population, β₁ represents the fixed slope for the population, and β_0i and β_1i represent eye-specific random intercepts and slopes. The prior distributions for β₀, β₁, and the error term (ε_it) were normally distributed for all 3 LMMs, but the prior distributions of the random effects were either Gaussian, Student t, or LG. Random effects were placed at the eye level. A more complex model with the eye nested within the patient did not provide additional improvement in estimates, so the simpler model was described. All analyses were completed using R 4.2.0 (R Foundation for Statistical Computing). The brms package was used to model the Gaussian and Student t LMMs, whereas the prior distribution for the LG model was directly coded into Stan (Stan Development Team) using the rstan package. Further details regarding model construction can be obtained from our prior work.⁷

Data Analysis

Ordinary least squares regression was completed using standard linear regression for each eye. Linear mixed models calculations were completed on the University of Miami Institute for Data Science and Computing Triton supercomputer. Posterior distribution estimates of model parameters were obtained with 4 chains each running 8000 iterations (burn-in of 1000 iterations). Model convergence was confirmed using autocorrelation diagnostics. Bayesian LMMs were compared using the Watanabe–Akaike information criterion, a metric that reflects the fit of a Bayesian model to the data; lower values indicate a better fit. Mean posterior estimated intercepts and slopes were estimated for each eye by adding the fixed and random components of each draw and averaging these values for all draws corresponding to each eye. Eyes were defined as progressors if the 1-sided Bayesian P value < 0.05 (i.e., the posterior probability that an eye-specific slope was < 0 had to be < 0.05). Ordinary least squares progressors were defined as those with a statistically significant negative rate of change (P < 0.05, 1-sided).

For predictive modeling, OLS and Bayesian models were constructed using different numbers of OCTs and assessing their ability to predict future RNFL values. For example, a model using the OCT RNFL thickness values from the first 3 tests was constructed. This model was then used to predict the RNFL thickness of the fourth, fifth, sixth, seventh, and eighth tests. This process was repeated using the first 4 OCTs to predict the RNFL thickness of the fifth, sixth, seventh, and eighth OCT tests, and so on, up to a model that used the first 7 OCTs to predict the RNFL thickness of the eighth test. The mean absolute error (MAE) of all Bayesian models and the OLS were compared for each predicted test. Bootstrapped 95% confidence intervals were calculated for MAE for each model and at each OCT using 200 bootstrap samples. In addition to confidence intervals, we performed statistical comparisons using ANOVA and Tukey’s honest significant difference test for pairwise comparisons.

Simulations

Simulated eyes with different baseline RNFL thickness values and rates of change were created and analyzed with the LMMs as well as OLS regression. The goal of these simulations was to evaluate the ability of the different LMMs to accurately estimate rates of change among different clinical scenarios, particularly moderate and fast progressors, which may be more prone to shrinkage toward the overall population mean. A major advantage to simulations is their known ground truth (i.e., a predefined rate of change), thereby allowing the assessment of the accuracy of model estimates. In contrast, the true rates of change in observed clinical cohorts are unknown. Simulations allow for a larger number of fast progressors to be evaluated, which are typically infrequent in an observed population. Simulations were completed in a similar fashion as previously described.⁷ Briefly, data from the Bascom Palmer Glaucoma Repository were split at the patient level, with 80% used for model training and 20% used to create a distribution of residuals. A total of 12 different settings were utilized, which were created from 3 baseline thickness categories (i.e., intercept) and 4 progressor categories (i.e., slope). The 3 baseline thickness categories were labeled “thick,” “moderate,” and “thin,” and corresponded to thickness values between 90 to 110 μm, 70 to 90 μm, and 50 to 70 μm, respectively. The rate categories were defined as nonprogressor (0 μm/year), slow (0 to –1 μm/year), moderate (–1 to –2 μm/year), and fast (–2 to –3 μm/year) based on previously defined cutoff values.¹²

A total of 100 simulated eyes were generated for each setting, with the intercept and slope of each eye randomly generated from the noted range of values. Time points used in this analysis were the mean times for the first 8 visits in the study population (0, 1.2, 2.6, 3.9, 5.1, 6.2, 7.1, and 8.1 years). Estimated RNFL thickness at the 8 time points was calculated using linear regression with the intercept and slope of the simulated eye. Noise was added to the estimated RNFL thickness at each time point by sampling the residual distribution corresponding to the estimated RNFL thickness value. Residual distributions were binned in increments of 5 μm between 50 μm and 110 μm. Residuals corresponding to RNFL thickness values < 50 μm or > 110 μm were included in the first and last bins, respectively. The smallest bin contained 88 residuals for sampling. The aim of the addition of noise was to generate simulations mimicking eyes observed in clinical practice. Additional details regarding this methodology can be reviewed in prior publications.^1,7,14

Simulation Analysis

The LMMs trained on 80% of the data set as well as OLS regression estimated the intercept and slopes of all 1200 eyes. Model performance was assessed by evaluating the cumulative rates of glaucoma progression among all models as well as the overall bias of slope estimates. Bias is defined as the difference between the predicted and true values of a variable. Cumulative rates of glaucoma progression were assessed among the models, with P value cutoffs adjusted accordingly for a 5% false-positive rate for each model. The log-rank test was used to compare the different curves. Median time to progression was calculated for each of the progressor groups for OLS and each model. Bias values were pooled across the different intercept groups and compared at each time point by the progressor group using ANOVA and Tukey’s honest significant difference test for pairwise comparisons.

Results

This analysis evaluated a total of 35 862 OCT tests from 5766 eyes of 3491 subjects (Table 3). The mean age of subjects was 65.9 ± 12.7 years, with female subjects comprising 61.8% of the study cohort. A total of 16.2% subjects self-identified as Black. The mean follow-up period was 7.0 ± 2.3 years, with a mean of 6.2 ± 1.4 OCT tests per eye. The average baseline RNFL thickness was 81.8 ± 13.5 μm, which ranged from 40.2 to 129.3 μm. Most eyes were glaucoma suspects or diagnosed with open-angle glaucomas (91.7%) at the initial visit, whereas chronic angle-closure glaucoma only accounted for 5% of eyes. A total of 672 eyes (11.2%) underwent glaucoma procedures during follow-up; all OCT tests following these procedures were excluded.

Table 3.

Demographics and Clinical Characteristics at Baseline of the Subjects and Eyes Included in the Study

Characteristic	n = 5766 Eyes of 3491 Patients
Baseline age, yrs
Mean ± SD	65.9 ± 12.7
Sex, female (%)	2158 (61.8)
Self-identified race, (%)
Black	564 (16.2)
Eye-specific characteristics
Glaucoma type
Suspect	2730 (47.3%)
POAG	2298 (39.9%)
SOAG	261 (4.5%)
CACG	287 (5.0%)
Other	190 (3.3%)
Number of OCT tests, n	35 862
Follow-up time, yrs
Mean ± SD	7.0 ± 2.3
Median (IQR)	6.7 (5.1–8.6)
Number of OCT tests per eye, n
Mean ± SD	6.2 ± 1.4
Median (IQR)	6.0 (5.0–7.0)
Baseline OCT RNFL thickness, μm
Mean ± SD	81.8 ± 13.5
Median (IQR)	82.6 (72.7–91.1)
Number of eyes that underwent cataract extraction during follow-up	798 (13.8%)
Number of eyes that underwent glaucoma surgery during follow-up	672 (11.7%)

CACG = chronic angle-closure glaucoma; IQR = interquartile range; POAG = primary open-angle glaucoma; RNFL = retinal nerve fiber layer; SD = standard deviation; SOAG = secondary open-angle glaucoma.

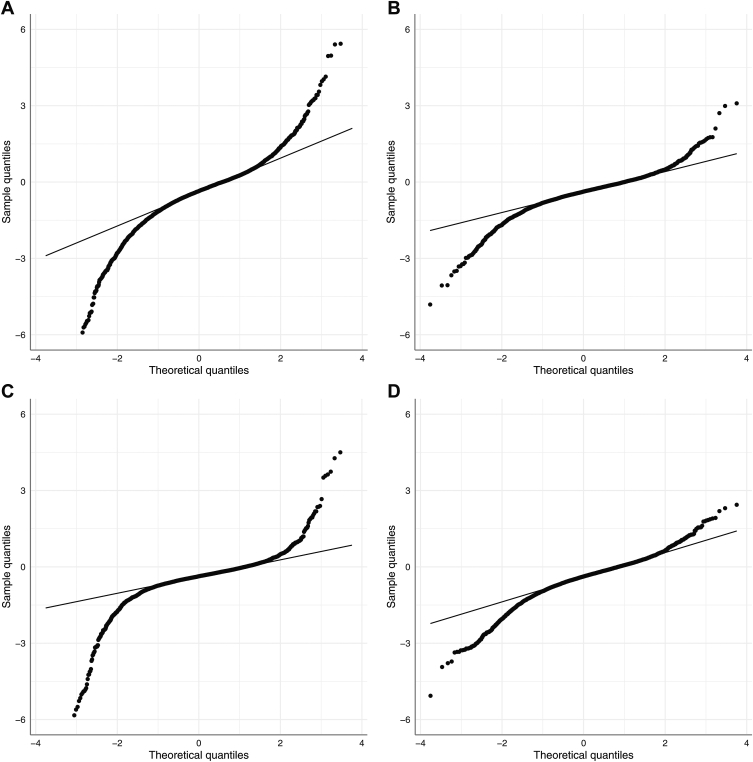
The distributions of slopes from OLS and the different LMMs are displayed in Figure 2. The Gaussian model demonstrated more shrinkage to the population mean, whereas the Student t and LG distributions had slightly more extreme slope estimates. Table 4 contains different model parameters from the 3 LMMs, including eye-specific slopes and the Watanabe–Akaike information criterion value of each model. The Watanabe–Akaike information criterion was lowest for the Student t LMM, indicating that this model provided the best overall fit for OCT data.

Figure 2.

Quantile–quantile plots describing the distributions of the estimated slopes from (A) ordinary least squares regression and posterior estimated slopes from the (B) Gaussian, (C) Student t, and (D) log-gamma Bayesian linear mixed models. Ordinary least squares and Student’s t models demonstrated a greater range of slopes with more positive and negative extreme values, whereas the Gaussian model demonstrated a more normal distribution with shrinkage toward the mean. The log-gamma model demonstrated more extreme negative values, reflecting a left-skewed distribution.

Table 4.

Bayesian Linear Mixed Model Characteristics using Varied Random Effect Distributions

	Population Intercept (ß0), μm	Population Slope (ß1), μm/yr	Eye-Specific Slopes, μm/yr	WAIC
Gaussian	81.54 ± 0.18	–0.42 ± 0.01	–0.38 (–0.67, –0.12) [–4.81, 3.09]	195 418
Student t	81.71 ± 0.18	–0.39 ± 0.01	–0.37 (–0.60, –0.16) [–9.04, 7.42]	193 774
Log-gamma	81.42 ± 0.01	–0.59 ± 0.01	–0.38 (–0.73, –0.08) [–5.07, 2.44]	198 213

Data are displayed as mean ± standard error or as median (interquartile range) [Range].

Eye-specific slopes are estimates derived from the posterior distributions and include both fixed and random effect components.

The boldface value indicates the lowest WAIC, demonstrating best model fit.

WAIC = Watanabe–Akaike information criterion.

The distribution of rates of all eyes and progressors is presented in Tables 5 and 6. As expected, the LG model led to more negative estimates. The Gaussian, Student t, and LG LMMs estimated a slope of ≤ –1 μm/year or faster for 573 eyes (9.9%), 456 eyes (7.9%), and 821 eyes (14.2%), respectively (Table 5). When evaluating those eyes identified as progressors by each model or OLS regression (Table 6), the Student t distribution identified the greatest number of progressors, with most of these eyes identified as slow progressors with rates between 0 and –1 μm/year. However, the Student t model allowed for faster progressors to have significantly extreme slope values when warranted (Fig 2 and “eye-specific slopes” in Table 4).

Table 5.

Distribution of Slopes Estimated by Ordinary Least Square (OLS) Regression and Bayesian Linear Mixed Models of All Eyes

	0 to –1 μm/yr	–1 to –2 μm/yr	< –2 μm/yr
OLS	2983 (51.7%)	841 (14.6%)	303 (5.3%)
Gaussian	4286 (74.3%)	502 (8.7%)	71 (1.2%)
Student t	4570 (79.3%)	363 (6.3%)	93 (1.6%)
Log-gamma	3800 (65.9%)	679 (11.8%)	142 (2.5%)

Data are presented as n (%). Slopes of the Bayesian models are estimates derived from the posterior distributions.

OLS = ordinary least squares.

Table 6.

Distribution of Slopes Estimated by OLS Regression and Bayesian Linear Mixed Models of Eyes Identified as Progressors

	Number of Progressors	Mean Slope, μm/yr	0 to –1 μm/yr	–1 to –2 μm/yr	< –2 μm/yr
OLS	1142 (19.8%)	–1.42 ± 1.03	482 (42.2%)	445 (39.0%)	215 (18.8%)
Gaussian	1388 (24.1%)	–1.05 ± 0.50	815 (58.7%)	502 (36.2%)	71 (5.1%)
Student t	1501 (26.0%)	–1.01 ± 0.76	1046 (69.7%)	362 (24.1%)	93 (6.2%)
Log-gamma	1391 (24.1%)	–1.21 ± 0.59	634 (45.6%)	615 (44.2%)	142 (10.2%)

Data are presented as n (%) or mean ± standard deviation. Percentages listed in the first column are with respect to all eyes in the analysis, whereas those listed in subsequent columns are with respect to only progressors. Slopes of the Bayesian models are estimates derived from the posterior distributions.

OLS = ordinary least squares.

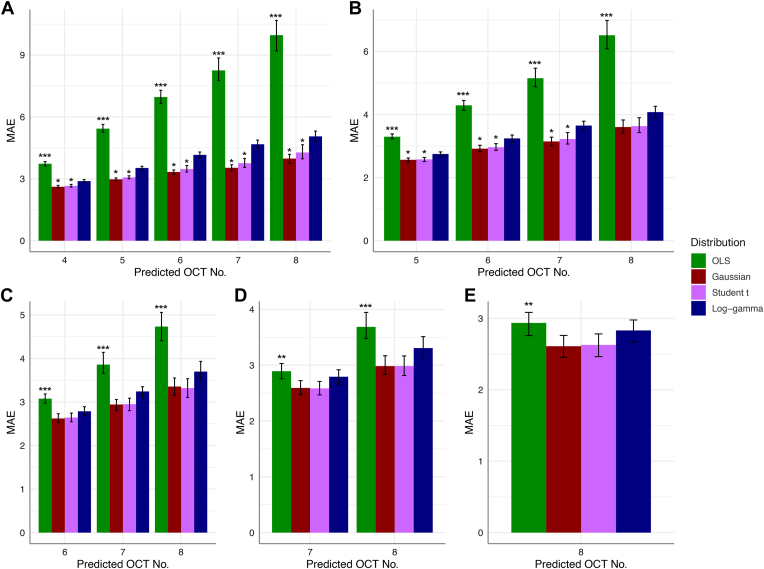
When evaluating predictive modeling data, all LMMs had significantly lower MAE than OLS regression (Fig 3) until LMMs utilized 6 OCT tests (P < 0.001 for all comparisons between each LMM and OLS utilizing 3–5 OCT tests). When using 6 OCT tests, OLS MAE for the seventh and eighth tests remained significantly higher than those of the Gaussian and Student t models but not the LG MAE. When using 7 OCT tests to predict the eighth test, OLS MAE remained significantly higher than those of the Gaussian and Student t models (P = 0.027 and P = 0.041, respectively) but not the LG MAE (P = 0.819).

Figure 3.

Mean absolute error (MAE) of ordinary least squares (OLS) regression and Bayesian linear mixed models (LMMs) in predicting retinal nerve fiber layer thickness of subsequent OCT tests. Mean absolute error values for the models constructed using the first (A) 3, (B) 4, (C) 5, (D) 6, and (E) 7 OCTs of eyes are shown. The x-axis represents the predicted OCT test. Error bars represent bootstrapped 95% confidence intervals. Three asterisks (∗∗∗) above the OLS estimate indicate the statistical significance of OLS MAE compared with those of all 3 LMMs, whereas 2 asterisks (∗∗) above the OLS estimate indicate the statistical significance of OLS MAE compared with only the Gaussian and Student t estimates. One asterisk (∗) above the Gaussian or Student t estimate indicates statistical significance compared with the LG estimate.

When comparing MAEs among the different LMMs, Gaussian and Student t MAEs were persistently lower than those of the LG model when only a few tests were utilized (Fig 3). When evaluating the model that used 3 OCTs, MAE from the LG model was consistently worse (P < 0.001 vs. Gaussian and P < 0.001 vs. Student t). When evaluating the model that used 4 OCTs, the MAEs of the LG model were significantly lower than those of the Gaussian and Student t models for the fifth (P = 0.002 and 0.005, respectively), sixth (P = 0.003 and 0.016, respectively), and seventh tests (P = 0.003 and 0.018, respectively). When predicting the eighth OCT RNFL value, the differences were nonsignificant (P = 0.139 and P = 0.182, respectively). The MAEs of the Gaussian and Student t models did not significantly differ from each other (P > 0.05).

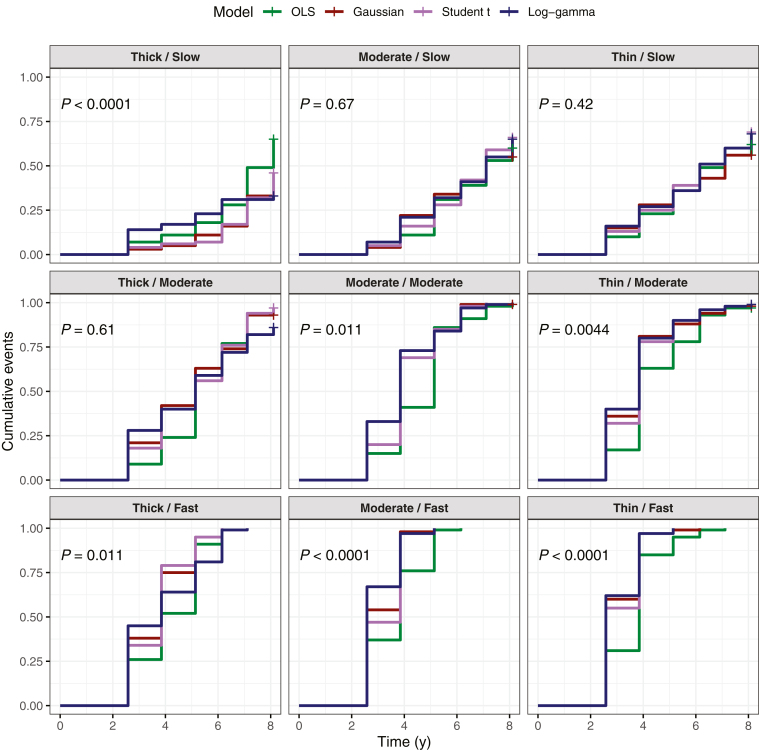
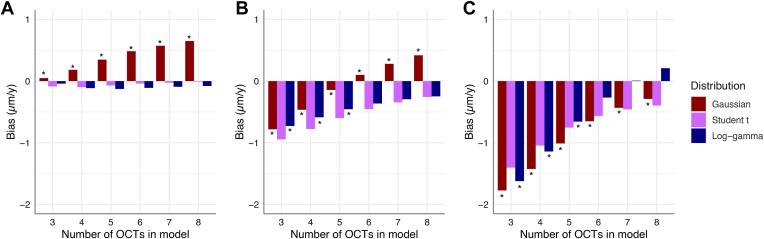
Simulations confirmed that LMMs performed better than OLS in declaring progression sooner among simulated moderate and fast progressors. Except for the thick baseline/moderate progressor setting, OLS was significantly slower in identifying progression among these simulated eyes (Fig 4). There were no significant differences between the 3 LMMs (P > 0.05). Among moderate progressors, bias was higher with Student t estimates, whereas Student t estimates had the lowest bias for fast progressors (Fig 5). No one LMM demonstrated consistently lower bias values. The median time to progression was lower among LMMs for moderate and fast progressors compared with OLS (Table 7).

Figure 4.

Cumulative event curves indicating the probability of declaring glaucomatous progression among simulated eyes under different simulation settings with OCT data (indicated by panel title). The first term refers to the baseline retinal nerve fiber layer thickness category (intercept), and the second term refers to the progressor class (slope). P values indicate comparison of the different models using the log-rank test. OLS = ordinary least squares.

Figure 5.

Comparison of bias estimates of the 3 linear mixed models by the number of OCT tests used to estimate the slope in the models. Data are grouped by progressor class: (A) slow, (B) moderate, and (C) fast. The asterisk (∗) indicates a statistically significant difference between the Student t model and the respective model.

Table 7.

Median Time to Progression (in years) among Different Progressor Groups as Assessed by OLS Regression and Linear Mixed Models

	Slow (0 to –1 μm/y)	Moderate (–1 to –2 μm/yr)	Fast (–2 to –3 μm/yr)
OLS	7.1	5.1	3.9
Gaussian	7.1	3.9	2.6
Student t	7.1	3.9	3.9
Log-gamma	8.1	3.9	2.6

The third through eighth tests occurred at 2.6, 3.9, 5.1, 6.2, 7.1, and 8.1 years, respectively.

OLS = ordinary least squares.

Discussion

In this analysis, we demonstrated that LMMs significantly outperform OLS regression in predicting future OCT RNFL thickness values and that the Student t LMM seems to provide the best fit for this population of over 5500 eyes. Both Student t and Gaussian LMMs had significantly lower MAEs compared with the LG LMM, indicating better overall prediction. Simulations confirmed faster declaration of progression with LMMs compared with OLS among moderate or fast progressors. This study suggests that the LMM approach is superior to traditional OLS regression when estimating future RNFL thickness or declaring progression in a glaucomatous population.

Our results confirm the value of LMMs compared with OLS, particularly when few tests are available (Fig 3). The MAE values of all LMMs were substantially lower than that of OLS regression when only 3 or 4 OCT tests were utilized in modeling. Although the benefit of the LMM methodology is gradually attenuated with additional tests, MAE values from OLS regression remained significantly worse. Precise assessments with fewer tests are clinically meaningful, given the biannual or annual frequency of OCT testing observed in clinical practice.

With respect to model fit, the Student t distribution seems to be superior in modeling the random effects among these eyes. We believe this finding is likely due to its flexibility with respect to permitting more extreme positive and negative slopes. Thus, this distribution performs better than the Gaussian distribution in modeling fast progressors. However, in contrast to SAP mean deviation, the distribution of rates of change in RNFL thickness is not as left-skewed, leading to reduced benefit of the LG LMM. In addition, RNFL thickness can be impacted by retinal changes such as hyaloid traction or temporary epiretinal membrane formation, which can transiently impact RNFL thickness. Wu et al¹⁵ recently identified various factors such as Black race that may be associated with greater RNFL thickness variability. Increased variability may lead to some positive slopes in population-level data, which the Student t distribution could handle better than the LG distribution, although these are not clinically meaningful in the assessment of glaucoma. Similarly, the Student t distribution is able to handle more extreme negative estimates than the Gaussian distribution, likely leading to a superior fit with the Student t LMM. Although the Student t LMM technically provided the best fit, predictive modeling demonstrated similar MAE values for the Student t and Gaussian distribution. The MAE from the LG model was persistently higher, indicating poorer performance.

Simulation results confirmed that LMM outperforms OLS regression in the most important clinical scenarios, namely moderate or fast progressors. All LMMs significantly outperform OLS regression when only 3 or 4 OCT tests are available among fast progressors, a scenario in which rapid detection of progression is crucial. The bias of LMM estimates for simulated eyes have statistically significant differences as noted in Figure 5, although the clinical significance of these differences would seem to be minimal. The Student t LMM features the lowest bias with the use of fewer OCT tests among fast progressors, whereas the Student t LMM has slightly higher values for moderate progressors. Collectively, we believe the simulation data confirm the strength of the LMM approach compared with OLS but do not clearly indicate the superiority of one LMM distribution over others. Given the noninferior performance of the Gaussian LMM when compared with the Student t LMM, we believe it is reasonable to model longitudinal OCT data with Gaussian LMMs, which have been used extensively in glaucoma research thus far.^11,15, 16, 17 Our work seems to demonstrate that although their estimates may shrink estimates toward the population mean, this change does not seem to negatively impact their predictive value nor their ability to declare progression with fewer tests.

These results with longitudinal OCT data stand in contrast to our prior analysis using longitudinal SAP data, in which the LG LMM was noted to provide the best fit.⁷ We believe that this is due to inherent differences between SAP and OCT data. Prior work had suggested that the LG distribution was more appropriate for SAP data, whereas the Gaussian distribution was more appropriate for OCT data.⁸ In addition, the SAP mean deviation metric is measured on a logarithmic scale, whereas RNFL thickness is measured on a linear scale. Early disease is often characterized by minimal change on SAP testing but notable changes on OCT testing, referred to as preperimetric glaucoma.¹⁸ The left-skewed distribution of SAP mean deviation rates may be due to many eyes having rates close to 0 due to early disease. In contrast, the distribution of rates of OCT RNFL thickness was likely less left-skewed per this analysis, perhaps due to the more linear relationship between disease progression and structural rate of change.

Limitations of this work include the use of retrospective data and the assumption of linear rates of change over time. Although we accounted for surgical interventions, we did not have access to data regarding the augmentation of medical therapy between OCT tests, which could affect rates of change. As noted in Table 3, this study cohort had a mixture of open-angle and closed-angle glaucomas, which may progress at different rates. However, only 5% of eyes in our cohort had chronic angle-closure glaucoma, of which only 54 of these eyes had cataract surgery during the study period, constituting < 1% of the entire cohort. We believe these findings are unlikely to alter the comparison of rates assessed by LMMs in this analysis. In addition, these data are drawn from 1 institutional database using the Zeiss Cirrus OCT platform, which may limit our conclusions. The prediction of individual slopes from LMM estimates relies on the concept that the individual shares characteristics with the population used to derive the prior probabilities in the Bayesian framework and, therefore, estimation of the individual slope can benefit from such prior knowledge. As such, a model derived from one population may not necessarily be applicable to individuals from other populations. Further studies are needed in this regard. As done in our prior work, we assumed a constant correlation between intercept and slope, which may not necessarily occur in clinical practice due to more intensive treatment for patients with advanced disease. Finally, other empirical distributions could be considered in addition to the 3 evaluated here, but the Gaussian, Student t, and LG distributions were chosen given clinical knowledge regarding OCT rates of change.

In summary, we have confirmed in this work that linear mixed modeling significantly improves future predictions of OCT RNFL thickness values compared with OLS regression. We also demonstrated that the LMM utilizing the Student t distribution technically provides the best model fit for OCT RNFL data. However, the Gaussian LMM performs as well as the Student t LMM in estimating future RNFL thickness values in predictive modeling. Both Student t and Gaussian LMMs are reasonable options for analyzing structural glaucoma data. These findings substantiate the application of linear mixed modeling to longitudinal OCT data among glaucomatous populations.

Manuscript no. XOPS-D-23-00235R1.