Abstract
Background and Objective
Computational models of the cardiovascular system allow for a detailed and quantitative investigation of both physiological and pathological conditions, thanks to their ability to combine clinical—possibly patient-specific—data with physical knowledge of the processes underlying the heart function. These models have been increasingly employed in clinical practice to understand pathological mechanisms and their progression, design medical devices, support clinicians in improving therapies. Hinging upon a long-year experience in cardiovascular modeling, we have recently constructed a computational multi-physics and multi-scale integrated model of the heart for the investigation of its physiological function, the analysis of pathological conditions, and to support clinicians in both diagnosis and treatment planning. This narrative review aims to systematically discuss the role that such model had in addressing specific clinical questions, and how further impact of computational models on clinical practice are envisaged.
Methods
We developed computational models of the physical processes encompassed by the heart function (electrophysiology, electrical activation, force generation, mechanics, blood flow dynamics, valve dynamics, myocardial perfusion) and of their inherently strong coupling. To solve the equations of such models, we devised advanced numerical methods, implemented in a flexible and highly efficient software library. We also developed computational procedures for clinical data post-processing—like the reconstruction of the heart geometry and motion from diagnostic images—and for their integration into computational models.
Key Content and Findings
Our integrated computational model of the heart function provides non-invasive measures of indicators characterizing the heart function and dysfunctions, and sheds light on its underlying processes and their coupling. Moreover, thanks to the close collaboration with several clinical partners, we addressed specific clinical questions on pathological conditions, such as arrhythmias, ventricular dyssynchrony, hypertrophic cardiomyopathy, degeneration of prosthetic valves, and the way coronavirus disease 2019 (COVID-19) infection may affect the cardiac function. In multiple cases, we were also able to provide quantitative indications for treatment.
Conclusions
Computational models provide a quantitative and detailed tool to support clinicians in patient care, which can enhance the assessment of cardiac diseases, the prediction of the development of pathological conditions, and the planning of treatments and follow-up tests.
Keywords: Computational cardiology, image-based reconstruction procedures, multi-physics, ablation, cardiac valve diseases
Introduction
This narrative review aims at discussing the benefits and challenges that the integration of computational methods and clinical observations provides to the investigation of cardiac and vascular pathophysiology. Specifically, we illustrate how innovative computational methodologies can have an impact on clinical practice, both in the present day and in the near future. The discussion is enriched with some specific applications addressed by our group in collaboration with hospital centers in our area empowered by our integrated virtual model of the heart.
This latter is a comprehensive computational model of the human heart, capable of describing all the main physiological processes (electrophysiology, contractile force generation, passive and active mechanics, blood dynamics, valve dynamics, myocardial perfusion) in a multi-physics integrated framework, and coupling them to the rest of the cardiovascular system. Exploiting both the descriptive and predictive power of computational models, we managed to reproduce virtually both the physiological heart function and the effects of some pathological conditions, by which we could address clinical questions of interest.
Background
Diagnostic tools, such as the electrocardiogram (ECG), cardiac and arterial echocolordoppler, coronary computed tomography (CT), magnetic resonance imaging (MRI), provide important measures of several specific features of the cardiac function (1-5). Various measurements made with different modalities need to be combined to provide a more comprehensive view, albeit still partial. Physical knowledge may enable these gaps to be filled, through models that can represent the behavior and dynamics of quantities of interest, such as the transmembrane potential, the blood velocity and pressure, or cardiac muscle displacement (6). This has become particularly relevant in recent years, due to the increasingly complex and rich data available from diagnostic tests and to the need to exploit such data in the most effective way. Indeed, also regulators encourage computational trials in the development of treatment protocols and in the design of medical devices (7-9), thanks to: (I) the reduced costs of numerical simulations with respect to those of extensive experimental campaigns and (II) the non-invasiveness of computational models, which is particularly important when children medical care and treatment are entailed.
Fostered by this interest, several research groups at the intersection of the medical, bioengineering, mathematical and scientific computing fields have been developing computational methods and procedures for the in-silico reproduction of the cardiovascular system and its analysis. In the last decade, detailed models have been introduced for the description of specific components of the heart function, such as electrophysiology (10-19), ion dynamics in the cardiomyocytes (20-23), contraction and mechanical behavior of the cardiac tissue (24-34), blood flow (35-48), valve dynamics (49-66), and cardiac perfusion (67-73). Special efforts have been made to integrate all these components into a single computational model. A first example of multi-physics computational heart model was proposed by the UT-Heart team (74) (ut-heart.com) with clinical investigations, e.g., in double-outlet right ventricle (75) and cardiac resynchronization therapy (CRT) (76). Very few other groups have succeeded in introducing models that couple the electromechanics of the cardiac muscle with the 3D distribution of blood flow and pressure, focusing, e.g., on the systolic phase (77), on the assessment of a left ventricular assist device (LVAD) (78), or on the computational efficiency of the solution of the equations pertaining to the model (79).
Rationale and knowledge gap
In our group we have created an integrated simulator of the cardiac function, encompassing the several physical processes occurring in the heart, from cell-scale myocyte force generation (80) to organ-scale motion and blood flow (81,82), from the microseconds of electrical pulse propagation to the timespan of a whole heartbeat (www.iheart.polimi.it). This simulator was then used to address specific questions arising at different stages of the clinical practice: in the investigation of the physiological behavior of a normal heart, in the diagnostics of pathologies and the assessment of their severity, in decision making and treatment planning, and in the prediction of the insurgence of complications after a device implantation.
The main features of our integrated cardiocirculatory model are listed below:
A detailed description of the physical processes entailed in the cardiac function, by means of state-of-the-art computational models of electrophysiology, force generation, myocardium mechanics, blood flow dynamics, valve dynamics, and myocardial perfusion;
The merging of the abovementioned models into a single integrated model accounting for the strict coupling between all the functions of the heart, using mathematically rigorous coupling strategies;
An accurate resolution of the abovementioned models, employing state-of-the-art numerical methods, implemented in efficient software libraries and often validated against actual clinical data;
The analysis of diagnostic imaging and other clinical data and the extraction of anatomical and functional information that is integrated into our computational models, by means of innovative image processing tools.
Objective
This narrative review aims to demonstrate the advantages and challenges of using computational models in the clinical diagnosis and treatment of the cardiovascular system. Our discussion is accompanied by relevant clinical examples investigated by means of our simulator.
The characteristics of computational models can be exploited in two directions. First, their descriptive power can be used for an in-depth investigation of the physiological processes entailed in the cardiac function and its pathologies, as well as to uncover relations between clinical indicators, or even to bring forth new quantities of interest to be investigated. Second, the predictive power of physics-based models can be exploited in scenario analysis to stratify patients, compare different treatment strategies, or to anticipate the development of future pathological conditions.
The computational models that we discuss were mainly developed on data coming from adult human heart observations and measurements, but their high flexibility allows them to be employed also in the pediatric context. Indeed, the same physical laws that we included in our models govern the blood flow, the electric signal propagation and the contraction of the heart in the general sense. An example of this wide applicability will be discussed in the case of an investigation of cardiovascular effect of coronavirus disease 2019 (COVID-19) on children (see Part V in “Illustrative applications” and the following discussion). We present this article in accordance with the Narrative Review reporting checklist (available at https://tp.amegroups.com/article/view/10.21037/tp-23-184/rc).
Methods
We report clinical applications of our computational methods and discuss the corresponding results with references to other computational studies in the main journals of the bioengineering and numerical modeling literature, in the last decade. A more structured description of the search strategy is provided in Table 1.
Table 1. The search strategy summary.
| Items | Specification |
|---|---|
| Date of search | 31 January 2023 |
| Databases and other sources searched | Google Scholar |
| Search terms used | Cardiac modeling, computational hemodynamics, cardiac valves, electrophysiology, heart multi-physics, patient-specific simulation |
| Timeframe | 2013–2023 |
| Inclusion criteria | We considered papers describing computational models used in the fields of bioengineering and medical research on the heart and cardiovascular system. We focused on works with direct clinical applications and published in the last decade |
| Selection process | No selection process on human subjects was required: all quantitative and subject-specific information was retrieved from published works |
Illustrative applications
In what follows we briefly discuss some studies as paradigmatic examples of clinical applications of our computational models.
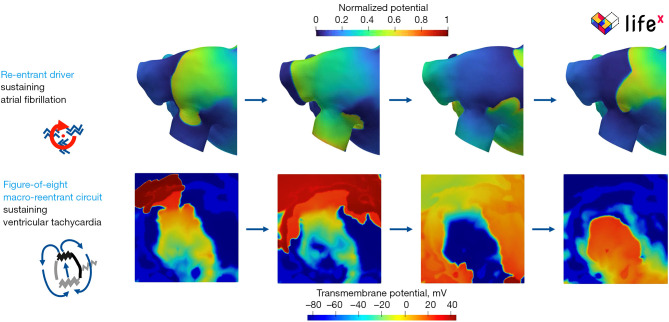
Atrial fibrillation (AF), the arrhythmia with the highest worldwide incidence, is an electrical dysfunction characterized by a progression of episodes with irregular rhythm and, in most cases, high heart rate and reduced contraction. These expose the patient to numerous complications, such as thrombo-embolic risk or heart failure. AF represents a very challenging pathology, resulting from dysfunctionalities of ionic species at the cellular level combined with signal conduction abnormalities in myocardial tissue architecture. Moreover, there is not yet a complete picture of its etiopathology and, consequently, the optimal treatments tailored for the individual patient remains an open challenge. In this context, computational models along with advanced electroanatomical mapping systems and clinical images with increasing high resolution are rapidly advancing research in this area. Specifically, computational models have the ability to simulate the induction and sustainment of AF episodes (18) (Figure 1) and to provide a framework for linking arrhythmic propensity to biomarkers computed from electroanatomical maps (19,85,86) or imaging (87,88).
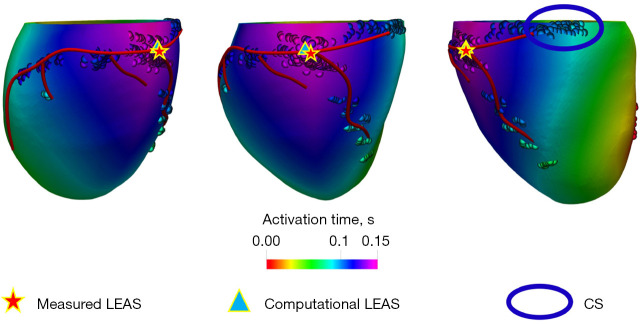
Another pathological condition of the cardiac electrophysiological function is the left bundle branch block (LBBB), which induces an asynchronous contraction of the ventricles, possibly impairing the pumping function of the heart. To assess the severity of the condition and to plan the device implantation for CRT, invasive measures of the activation map are currently performed on the patients, by means of catheterization of the ventricles and the epicardial coronary veins. In studies of Stella et al. and Vergara et al. (89,90), a computational model was employed with the aim of reducing the invasiveness of such measurements. The left ventricle geometry of different patients was reconstructed from MRI, and the personalization of the electrophysiological model was based only on the activation map measures acquired on the septum and in the proximal portion of the epicardial veins. Distal measures in the veins were used only for cross-validation. The computational model effectively predicted the region of latest activation, as well as the latest activation time (see Figure 2).
Figure 1.
Numerical prediction of arrhythmogenic propensity in atria (18) and ventricles (83,84): numerical simulations on patient-specific geometries allow to accurately identify re-entrant distributions of transmembrane potential characterizing atrial fibrillation (above) and ventricular tachycardia (below). Credits: S. Pagani.
Figure 2.
Computed (continuous map) and measured activation times. The measured and computational LEAS, and the calibrating data at CS are highlighted. LEAS, latest electrical activation segment; CS, coronary sinus. Credits: S. Stella.
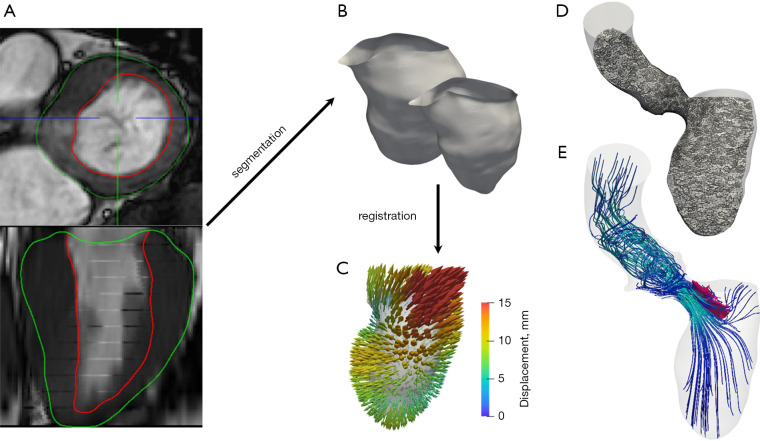
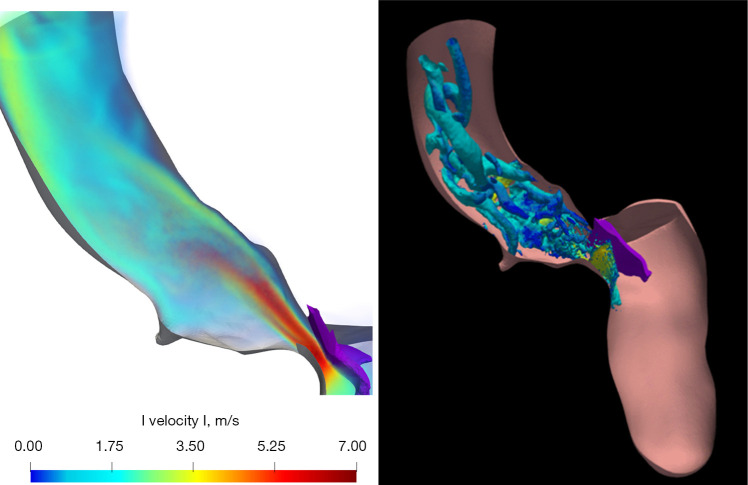
We investigated the effects of hypertrophic cardiomyopathy (HCM) on the blood flow, in patient-specific scenarios, to assess the severity of the HCM-induced obstruction and provide clinical indications for its treatment (45,60). Starting from kinetic MRI (cine-MRI) data, we developed an image-processing procedure to reconstruct the anatomy and motion of the left ventricle of HCM patients (see Figure 3). In the case of systolic anterior motion (SAM) of the mitral valve, we also reconstructed the shape and displacement of the anterior leaflet of the valve. Then, we simulated the blood flow induced by the patient-specific anomalous heart contraction, evaluated the pressure and stress exerted by the flow on the endocardium, described the turbulent structures developing in the aorta (see Figure 4), and proposed a synthetic indicator to identify the most suitable region for surgical intervention by septal myectomy, which is the mostly advised treatment for obstructive HCM according to clinical guidelines (91,92).
Figure 3.
General image-based computational procedure for patient-specific simulations. From diagnostic imaging data (A), segmentation yields anatomical surfaces (B) possibly for different times of the heartbeat. Registration algorithms are used to reconstruct displacement fields (C) with respect to a reference configuration. A computational mesh of the patient’s anatomy is generated (D) and used to perform numerical simulations (streamlines of blood flow in left ventricle and aorta) (E). Credits: M. Fedele, I. Fumagalli.
Figure 4.
Image-based numerical simulation of patient-specific blood flow in the left ventricle and ascending aorta of a patient with SAM of the MV: pathologically strong aortic jet flow (left) and related vortical structures obtained by Q-criterion at systolic peak (right). SAM, systolic anterior motion; MV, mitral valve. Credits: I. Fumagalli.
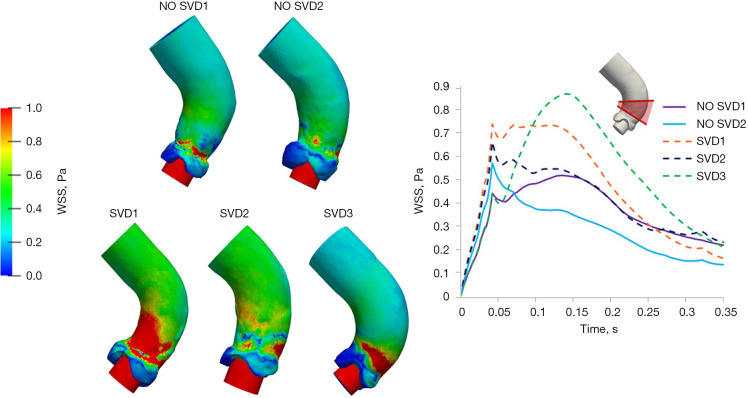
Another image-based computational model for hemodynamics was developed (93) for the investigation on transcatheter aortic valve implantation (TAVI) and the occurrence of structural valve degeneration (SVD) years after the intervention. Based only on pre-implantation CT acquisitions, we reconstructed the patient-specific geometries of the aorta for different patients (three that encountered SVD and two that did not), virtually implanted the prosthetic device, and simulated numerically the blood flow and its interaction with the prosthesis and the native valvular tissue, in a post-implantation scenario. This investigation unveiled preliminary correlations between the onset of SVD and the distribution of flow-induced wall shear stress (WSS) on the aortic wall (see Figure 5).
Figure 5.
WSS on the aortic wall of patients with TAVI (93): WSS distribution at systolic peak (left) and time evolution of average WSS in the orange area (right). High intensity and long persistence of WSS are predictive indicators of SVD. WSS, wall shear stress; TAVI, transcatheter aortic valve implantation; SVD, structural valve degeneration. Credits: R. Polidori, F. Renzi.
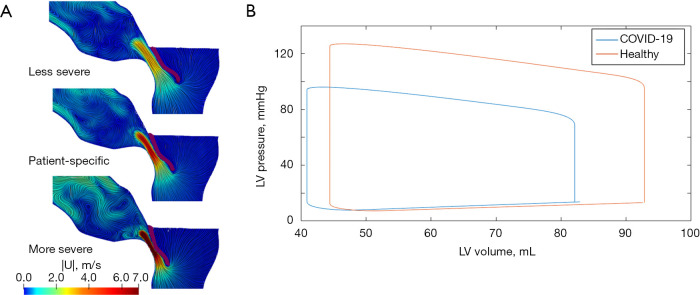
The effects of COVID-19 on the cardiovascular system of pediatric patients were investigated (94), based on a lumped-parameter model of the whole system developed (95). Patient-specific models of both asymptomatic and symptomatic children were obtained by calibration with measured clinical data. A correlation was found between myocardial compromise and the severity of the COVID-19 infection (see Figure 6), as observed also in clinical studies (96,97).
Figure 6.
Virtual scenario analyses: (A) 2D slices of the peak-systole blood velocity field in the left ventricle outflow tract of a patient with different levels of SAM (59); (B) pressure-volume loops of the LV of a healthy child and of a child with COVID-19 infection (94). SAM, systolic anterior motion; LV, left ventricle. Credits: L. Ruffino, A. Santoro, S. Sparvieri.
The computational models for the cardiovascular system developed in our group were described (98). Most of the simulations based on such models have been carried out in a high-performance computing environment, using the finite element software library lifex (https://lifex.gitlab.io/) (99-102). For the integration of clinical imaging data into the computational models, specific image- and surface-processing procedures have been devised and implemented based on VMTK (103,104), elastix (elastix.lumc.nl) (105), SimpleITK (simpleitk.org), MITK (www.mitk.org) (106,107).
The role of computational models in diagnostics and treatment planning
In our group, we developed a fully integrated multi-physics computational model of the heart function, encompassing the numerical modeling of several physiological processes, the development of computational tools for the analysis of clinical and imaging data, and the integration of such data in the model, for patient-specific analysis. The following discussion shows how the medical research and the clinical practice can benefit from computational modeling, exploiting its power at different levels: in the analysis of clinical data (see section “Analysis of patient data and clinical indicators”), in the quantitative assessment of clinical indicators and the uncovering of relations between quantities that are not directly measurable by diagnostic tools (see section “Investigation of physical processes underlying the heart function”), and in the prediction of long-term effects of treatments or development of pathologies (see section “Towards exploiting the predictive power of computational approaches”).
Analysis of patient data and clinical indicators
The assessment of the heart function in clinical practice entails the acquisition of diverse and possibly large datasets such as, e.g., diagnostic imaging data, time-dependent signals like ECG, pressure measurements, and the patient’s medical history. To assist the analysis and evaluation of a pathological condition, quantitative indicators and biomarkers are extracted from the patient’s data. These indicators, based on approved protocols and the physician’s experience, quantify the severity of a condition or the propensity to develop a certain pathology.
The main source of information about heart function is diagnostic imaging, acquired by CT, MRI or Doppler echocardiography. Indeed, several geometric measurements are used to assess the function of the heart—such as the stroke volume, the orifice area of valves, the diameters of the ventricles, or the thickness of the cardiac walls—and their deviation from physiological ranges is an important indicator of pathological states. Several reconstruction procedures have been developed to extract geometric and functional information from the data, either to create representative virtual models of the normal heart (108-110) or to develop a digital twin of a pathological heart in patient-specific conditions (45,83,84,111). In general, these procedures entail segmentation and registration algorithms, as shown in Figure 3. Segmentation refers to the reconstruction of surfaces—such as vessel or heart chamber walls (see Figure 3B)—from grey-scale images, and they rely on computational methods such as level-set methods based on partial differential equations combined with the marching-cubes algorithm (112). Registration, instead, aims to reconstruct the motion of such surfaces (see Figure 3C), by means of shape optimization and other optimization algorithms applied to images corresponding to different instants of the heartbeat (such as cine-MRI, multiple-time CT scans, or time-dependent echocardiography): see, e.g., (60,113).
More recently, machine-learning algorithms have also been employed for these reconstruction goals: the introduction of these algorithms aims at reducing the need for human intervention in the reconstruction procedure, by relying almost completely on data, and their reliability is based on the large number of data employed for their training (114,115).
In electrophysiology, in addition to anatomical data, electrical biomarkers guide the definition of ablation targets, which are those regions that are electrically isolated to avoid the development of new arrhythmic episodes. These indicators are calculated from electro-anatomical data, which consists of the set of intracardiac electrograms (EGMs) and the location of their measurement. These data are collected with mapping or diagnostic catheters (like, e.g., the coronary sinus catheter) equipped with multiple electrodes. Mapping systems process EGMs to reconstruct 3D maps depicting wavefront propagation in the cardiac chamber or areas of abnormal electrical activity (such as low voltage areas) (116).
Numerical methods improve the post-processing of electro-anatomical data by extracting even more representative indicators of arrhythmic propensity: slow conduction corridors or high rotational areas (pivot points). In the context of AF, these quantitative biomarkers, in addition to allowing a better stratification of patients explaining AF progression (86), are proven to affect the clinical outcome of an ablation procedure (117) (see Part I in section “Illustrative applications”). In the context of ventricular tachycardia, structural abnormalities can be distinguished from functional ones thanks to the quantitative comparison of indicators computed from electroanatomical maps in sinus rhythm and tachycardia (118). This highlights the importance of having computational tools that can combine information acquired using different modalities (e.g., imaging and catheter) or surrogate the lack of information with physics-based differential models.
Investigation of physical processes underlying the heart function
One of the main goals of medical research is to identify correlations between different physio-pathological processes and between different clinical indicators and measurable quantities, to explain the mechanisms of normal physiology, to investigate the causes and characteristics of pathologies, and to devise effective treatments. In this endeavor, important obstacles are represented by the uncertainty in clinical data, the difficulty of integrating information coming from different acquisition sources, and the intrinsic impossibility of analyzing different scenarios of pathology evolution or treatments.
Computational models can substantially address these issues through their encoded physics-based knowledge. Moreover, they can integrate subject-specific anatomical and functional data, as discussed in section “Analysis of patient data and clinical indicators”.
In this framework, computational investigation can be:
-
Complementary to diagnostics and clinical analysis, since:
It can quantify quantities of interest and biomarkers with a level of detail as high as needed;
It can fill up missing data in the measurements (e.g., the time evolution of quantities measured only in few time instants) or even give access to quantities that are not measurable in vivo;
Supplementary to clinical investigation, since it allows the analysis of different patient-specific scenarios associated with different stages of a pathology or with the application of different treatments.
These points will be discussed in the following, by referring to the clinical applications described in section “Illustrative applications”.
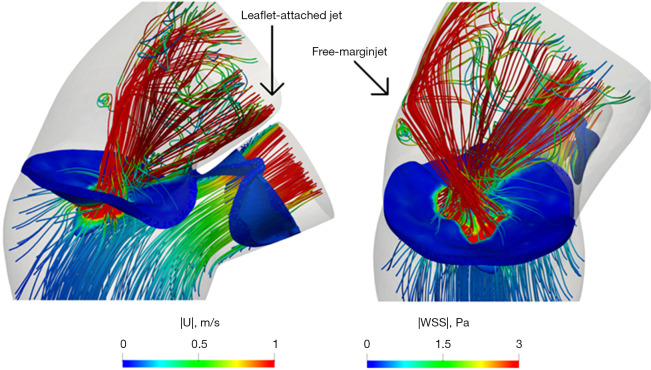
In terms of level of detail (point I-i), computational models can reach the scale of a single cell in representing contractile force generation in cardiac myocytes (80) or investigating slow conduction regions in the myocardium at the level of the fiber scale (19) or describing the generation of small-scale vortices and turbulence in the blood flow (45,48,119): examples of detailed vortical structures of flow jets in pathological conditions (HCM and mitral valve regurgitation), obtained by image-based computational fluid dynamics, are shown in Figures 4,7. Indeed, this kind of high-resolution information cannot be directly captured by standard in vivo measurements and clinical imaging. Moreover, multiscale models can describe how the abovementioned microscale effects affect the whole organ function, thus extending even further the relevance of the results.
Figure 7.
Systolic blood flow in a left heart with mitral valve regurgitation (113): instant of maximum regurgitant flow. Blood streamlines (colored by velocity magnitude) and WSS on the mitral valve leaflets due to the regurgitant jets. WSS, wall shear stress. Credits: L. Bennati.
In addition to enhancing the detail of measures of relevant clinical indicators, computational models can also provide data that are not directly measured by standard clinical measurements (point I-ii). Missing data can be of two types: they can be quantities that are in principle measurable but are not acquired to reduce the invasiveness of the diagnostic phase, or they can be quantities that are completely not measurable in vivo. An example of the first type is the acquisition of activation maps by catheterization of the epicardial veins or the interventricular septum: it was shown how the radiation exposure and the overall invasiveness of the procedure can be reduced by hinging upon an accurate numerical simulation of the electrical activity of the left ventricle (90) (cf. Part II in section “Illustrative applications”). The results of the computational model were validated against additional data in some subjects, such as the measured latest electrical activation segment (LEAS), as shown in Figure 2. In alternative, computational models combined with deep learning approaches can support the development of non-invasive reconstruction of the electrical activity in the ventricles (ECG imaging) (120).
In terms of hemodynamics, another example is represented by the lumped parameter model as the one proposed in some studies (34,38,121), which allowed to compute pressure-volume loops and the evolution of pressures and flows in the cardiovascular system with the need of only few non-invasive measurements of the systemic pressure and cardiac chamber volumes. A proper calibration of this model allowed to provide clinically relevant indications on the cardiopathies associated with COVID-19 infection in children (see Part V in section “Illustrative applications”).
Furthermore, the physical content of mathematical models can also give access to quantities that are not measurable in vivo. This is the case, for example, of the shear stress exerted by the blood flow on the ventricular (45) and aortic (93) wall or even on valve leaflets (113), as shown in Figure 7, the transmembrane electric potential in the atria (18) and ventricles (84,118), as shown in Figure 1, or the specific orientation of conduction fibers in atria (18,122). The relevance of quantifying these quantities lies in the established correlation they have with the heart function or the development of pathological conditions: e.g., fiber orientation strongly affects the overall electrical activity and contraction of the heart (123,124), and strongly oscillating values of the WSS are known to induce plaque formation in the vessels (125,126). Moreover, additional correlations can be found, that would not be directly detectable by classical clinical trials. This is the case, for example, of the correlation between TAVI structural degeneration and the flow-induced stress on the wall of the ascending aorta (cf. Part IV in section “Illustrative applications” and Figure 5), or the quantification of the intraventricular pressure gradient associated to hypertrophic obstructive cardiomyopathy (cf. Part III in section “Illustrative applications”).
A feature of computational models from which medical research and clinical practice can greatly benefit is the possibility to perform scenario analysis (point II). A common characteristic of all computational models is a separation between equations and parameters: the former describe physical processes, while the latter describe the specific settings in which such processes take place, in terms of geometry, boundary conditions, or other physical characteristics such as electrical conductivity or elastic modulus of the tissue. Acting on these parameters, one can compare different physio-pathological conditions of a single patient—such as the different severity levels of SAM analyzed in (60) (cf. Part III in section “Illustrative applications” and Figure 6A)—or else compare models representing different patients, as in the investigation (94) of COVID-19 effects on children’s cardiovascular system (cf. Part V in section “Illustrative applications” and Figure 6B) or electrical substrate characteristics (18). The strong relevance of scenario analysis lies in its non-invasiveness and relatively low cost, since it can provide new information with respect to diagnostic tests without the need for intervention or hospitalization.
All the abovementioned information that computational models provide can be used to investigate correlations between the patients anatomical and functional characteristics and the mechanisms underlying physiology and pathology.
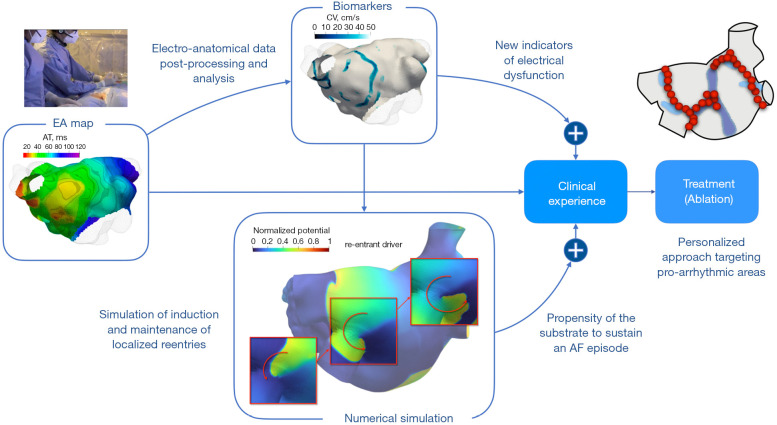
In cardiac electrophysiology, computational models allow us to associate the biomarkers extracted from electroanatomical maps to arrhythmic propensity: simulations have shown that slow-conducting areas provide anchor points for localized reentry, sustaining an arrhythmic episode (18). This link is crucial because, in addition to explaining a possible mechanism behind the higher duration and frequency of persistent fibrillation episodes, it confirms slow-conducting areas as suitable ablation targets (see Figure 8). Furthermore, in the absence of electrical data, computational models provide a surrogate that can be used to construct patient-specific ablation strategies starting from imaging data, as done in the OPTIMA (Optimal Target Identification via Modeling of Arrhythmogenesis) approach (127).
Figure 8.
Combination of quantitative post-processing of electro-anatomical maps with numerical simulations to analyze the arrhythmic propensity of a patient’s substrate and to design an optimal strategy for ablation. EA, electro-anatomical; AT, activation time; CV, conduction velocity; AF, atrial fibrillation. Credits: S. Pagani, A. Frontera.
This can then lead to the identification of predictive indicators for the onset or development of pathologies, as discussed in the next section.
Towards exploiting the predictive power of computational approaches
Hinging on the integration between patient-specific information and the fundamental physical laws governing the cardiovascular system, computational models can be used to model and predict virtual future scenarios. Indeed, based solely on the patient’s current situation, the development of a disease can be investigated for the next months or years, or else surgical treatments can be virtually applied and then compared at the pre-intervention stage.
An example of this is the investigation of TAVI degeneration described in Part IV in section “Illustrative applications”. We found preliminary predictive indicators for the onset of SVD on the basis of only pre-implantation CT scans. To make this possible, the reconstruction of patient-specific geometries was followed by the virtual implantation of the TAVI prosthesis, and a fluid-structure interaction simulation produced hemodynamics indicators in the resulting post-implantation settings. In the study, the intensity and persistence of WSS in the aorta were proved to be predictive for SVD by comparing their indication with the actual condition of the patients in follow-up exams (see Figure 5).
To further enhance the predictive power of computational models, the study of growth and remodeling of organs and living tissues, as well as of the development of pathological conditions such as plaques and aneurysms, is currently being brought forward (128-130). Adapted to reproduce specific pathological conditions, this kind of models will allow to shed more light on the development of cardiovascular diseases and to provide a more accurate environment for in-silico trials in the long term.
Conclusions
Computational cardiology combines the detailed description of physical processes provided by computational models with the patient-specific information retrievable by imaging acquisition and diagnostic data. Relying on representative applications investigated in our research group, we illustrated how computational models can positively impact diagnosis and treatment planning for several cardiovascular diseases, at different stages of clinical practice. Part of the results presented (see Part V in section “Illustrative applications” and the related discussion) regard the treatment of cardiovascular diseases in children, showing how the versatility of mathematical models allows for the translation of computational methods developed for adult patient care to the pediatric context.
In the investigative phase of diagnosis, reconstruction procedures based on segmentation and registration algorithms enable the extraction of anatomical and functional information from diagnostic images, possibly combining data acquired by different imaging techniques.
Then, such information can be enhanced in terms of physical information and space and time resolution, hinging upon a mathematical description of the physics comprised in the heart function and solving the resulting equations possibly at the level of the cell scale. In this regard, a single integrated computational model encompassing the different physical processes occurring in the heart and their coupling with the rest of the cardiovascular system is of the utmost importance, since it allows to represent and investigate the mutual effects that different components have on one another.
Moreover, exploiting the generality of this computational model, different scenarios can be generated in a completely non-invasive way, to investigate different severity levels of specific pathologies or to compare the effects of a disease on different subjects.
Finally, computational models can also predict the development of pathological conditions and the long-term effectiveness and adverse reactions of treatments: the very recent development of models for growth and remodeling showed promising results in this direction.
Overall, one of the main difficulties of using computational models in diagnosis and treatment design is related to certification. According to the current standards, validation of computational models usually requires extensive simulation campaigns and assessment on a great number of patient samples, that may require years. Moreover, there is no general definition of the requirements for a computational model or procedure to be certified, and each advancement needs an ad hoc evaluation. Nevertheless, the use of computational simulations has proved to be a powerful non-invasive tool for an effective investigation of specific pathologies and their treatments.
Supplementary
The article’s supplementary files as
Acknowledgments
We acknowledge all the clinical and academic partners that have contributed to the development of the projects that we review here. I.F., S.P., C.V., L.D., A.Q. are members of the INdAM (The National Institute for Advanced Mathematics) group-GNCS “Gruppo Nazionale per il Calcolo Scientifico” (National Group for Scientific Computing).
Funding: This work was supported in part by the funding that S.P., L.D., C.V., A.Q. received from the Italian Ministry of University and Research (MIUR) within the PRIN (research projects of relevant national interest 2017 “Modeling the heart across the scales: from cardiac cells to the whole organ” Grant Registration number 2017AXL54F). I. F., S. P., L. D., A. Q. acknowledge partial support by the project “Dipartimento di Eccellenza 2023-2027”, Dipartimento di Matematica, Politecnico di Milano. S.P. has been partially supported by the INdAM-GNCS Project 2023, CUP E53C22001930001, “Mathematical models and numerical methods for computational medicine in cardiovascular diseases”.
Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Footnotes
Provenance and Peer Review: This article was commissioned by the Guest Editor (Antonio F. Corno) for the series “The Impact of the Progresses of Knowledge and Technologies in Pediatrics” published in Translational Pediatrics. The article has undergone external peer review.
Reporting Checklist: The authors have completed the Narrative Review reporting checklist. Available at https://tp.amegroups.com/article/view/10.21037/tp-23-184/rc
Peer Review File: Available at https://tp.amegroups.com/article/view/10.21037/tp-23-184/prf
Conflicts of Interest: All authors have completed the ICMJE uniform disclosure form (available at https://tp.amegroups.com/article/view/10.21037/tp-23-184/coif). The series “The Impact of the Progresses of Knowledge and Technologies in Pediatrics” was commissioned by the editorial office without any funding or sponsorship. The authors have no other conflicts of interest to declare.
Reference
- 1.Cazeau S, Bordachar P, Jauvert G, et al. Echocardiographic modeling of cardiac dyssynchrony before and during multisite stimulation: a prospective study. Pacing Clin Electrophysiol 2003;26:137-43. 10.1046/j.1460-9592.2003.00003.x [DOI] [PubMed] [Google Scholar]
- 2.Karamitsos TD, Francis JM, Myerson S, et al. The role of cardiovascular magnetic resonance imaging in heart failure. J Am Coll Cardiol 2009;54:1407-24. 10.1016/j.jacc.2009.04.094 [DOI] [PubMed] [Google Scholar]
- 3.Litmanovich DE, Kirsch J. Computed Tomography of Cardiac Valves: Review. Radiol Clin North Am 2019;57:141-64. 10.1016/j.rcl.2018.08.011 [DOI] [PubMed] [Google Scholar]
- 4.Corrias G, Cocco D, Suri JS, et al. Heart applications of 4D flow. Cardiovasc Diagn Ther 2020;10:1140-9. 10.21037/cdt.2020.02.08 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Mangiafico V, Saberwal B, Lavalle C, et al. The role of CT in detecting AF substrate. Trends Cardiovasc Med 2021;31:457-66. 10.1016/j.tcm.2020.10.004 [DOI] [PubMed] [Google Scholar]
- 6.Quarteroni A, Dede’ L, Manzoni A, et al. Mathematical modelling of the human cardiovascular system: data, numerical approximation, clinical applications. Cambridge University Press 2019;33. [Google Scholar]
- 7.Morrison TM, Pathmanathan P, Adwan M, et al. Advancing Regulatory Science With Computational Modeling for Medical Devices at the FDA’s Office of Science and Engineering Laboratories. Front Med (Lausanne) 2018;5:241 . 10.3389/fmed.2018.00241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gray RA, Pathmanathan P. Patient-Specific Cardiovascular Computational Modeling: Diversity of Personalization and Challenges. J Cardiovasc Transl Res 2018;11:80-8. 10.1007/s12265-018-9792-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Martinolli M, Biasetti J, Zonca S, et al. Extended finite element method for fluid-structure interaction in wave membrane blood pump. Int J Numer Method Biomed Eng 2021;37:e3467 . 10.1002/cnm.3467 [DOI] [PubMed] [Google Scholar]
- 10.Tung L. A bi-domain model for describing ischemic myocardial dc potentials: PhD Dissertation. Massachusetts Institute of Technology 1978. [Google Scholar]
- 11.Romero D, Sebastian R, Bijnens BH, et al. Effects of the purkinje system and cardiac geometry on biventricular pacing: a model study. Ann Biomed Eng 2010;38:1388-98. 10.1007/s10439-010-9926-4 [DOI] [PubMed] [Google Scholar]
- 12.Trayanova NA. Whole-heart modeling: applications to cardiac electrophysiology and electromechanics. Circ Res 2011;108:113-28. 10.1161/CIRCRESAHA.110.223610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vergara C, Lange M, Palamara S, et al. A coupled 3D-1D numerical monodomain solver for cardiac electrical activation in the myocardium with detailed Purkinje network. Journal of Computational Physics 2016;308:218-38. [Google Scholar]
- 14.Prakosa A, Arevalo HJ, Deng D, et al. Personalized virtual-heart technology for guiding the ablation of infarct-related ventricular tachycardia. Nat Biomed Eng 2018;2:732-40. 10.1038/s41551-018-0282-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Niederer SA, Lumens J, Trayanova NA. Computational models in cardiology. Nat Rev Cardiol 2019;16:100-11. 10.1038/s41569-018-0104-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Del Corso G, Verzicco R, Viola F. A fast computational model for the electrophysiology of the whole human heart. Journal of computational physics 2022;457:111084. [Google Scholar]
- 17.Gillette K, Gsell MAF, Prassl AJ, et al. A Framework for the generation of digital twins of cardiac electrophysiology from clinical 12-leads ECGs. Med Image Anal 2021;71:102080 . 10.1016/j.media.2021.102080 [DOI] [PubMed] [Google Scholar]
- 18.Pagani S, Dede’ L, Frontera A, et al. A Computational Study of the Electrophysiological Substrate in Patients Suffering From Atrial Fibrillation. Front Physiol 2021;12:673612 . 10.3389/fphys.2021.673612 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Frontera A, Pagani S, Limite LR, et al. Slow Conduction Corridors and Pivot Sites Characterize the Electrical Remodeling in Atrial Fibrillation. JACC Clin Electrophysiol 2022;8:561-77. 10.1016/j.jacep.2022.01.019 [DOI] [PubMed] [Google Scholar]
- 20.Corrado C, Avezzù A, Lee AWC, et al. Using cardiac ionic cell models to interpret clinical data. WIREs Mech Dis 2021;13:e1508 . 10.1002/wsbm.1508 [DOI] [PubMed] [Google Scholar]
- 21.Courtemanche M, Ramirez RJ, Nattel S. Ionic mechanisms underlying human atrial action potential properties: insights from a mathematical model. Am J Physiol 1998;275:H301-21. 10.1152/ajpheart.1998.275.1.H301 [DOI] [PubMed] [Google Scholar]
- 22.ten Tusscher KH, Noble D, Noble PJ, et al. A model for human ventricular tissue. Am J Physiol Heart Circ Physiol 2004;286:H1573-89. 10.1152/ajpheart.00794.2003 [DOI] [PubMed] [Google Scholar]
- 23.Tomek J, Bueno-Orovio A, Passini E, et al. Development, calibration, and validation of a novel human ventricular myocyte model in health, disease, and drug block. Elife 2019;8:e48890 . 10.7554/eLife.48890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Baillargeon B, Rebelo N, Fox DD, et al. The Living Heart Project: A robust and integrative simulator for human heart function. Eur J Mech A Solids 2014;48:38-47. 10.1016/j.euromechsol.2014.04.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Fritz T, Wieners C, Seemann G, et al. Simulation of the contraction of the ventricles in a human heart model including atria and pericardium. Biomech Model Mechanobiol 2014;13:627-41. 10.1007/s10237-013-0523-y [DOI] [PubMed] [Google Scholar]
- 26.Genet M, Lee LC, Nguyen R, et al. Distribution of normal human left ventricular myofiber stress at end diastole and end systole: a target for in silico design of heart failure treatments. J Appl Physiol (1985) 2014;117:142-52. 10.1152/japplphysiol.00255.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Augustin CM, Neic A, Liebmann M, et al. Anatomically accurate high resolution modeling of human whole heart electromechanics: A strongly scalable algebraic multigrid solver method for nonlinear deformation. J Comput Phys 2016;305:622-46. 10.1016/j.jcp.2015.10.045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pfaller MR, Hörmann JM, Weigl M, et al. The importance of the pericardium for cardiac biomechanics: from physiology to computational modeling. Biomech Model Mechanobiol 2019;18:503-29. 10.1007/s10237-018-1098-4 [DOI] [PubMed] [Google Scholar]
- 29.Marx L, Gsell MAF, Rund A, et al. Personalization of electro-mechanical models of the pressure-overloaded left ventricle: fitting of Windkessel-type afterload models. Philos Trans A Math Phys Eng Sci 2020;378:20190342 . 10.1098/rsta.2019.0342 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gerach T, Schuler S, Fröhlich J, et al. Electro-mechanical whole-heart digital twins: a fully coupled multi-physics approach. MDPI Mathematics 2021;9:1247. [Google Scholar]
- 31.Salvador M, Fedele M, Africa PC, et al. Electromechanical modeling of human ventricles with ischemic cardiomyopathy: numerical simulations in sinus rhythm and under arrhythmia. Comput Biol Med 2021;136:104674 . 10.1016/j.compbiomed.2021.104674 [DOI] [PubMed] [Google Scholar]
- 32.Peirlinck M, Yao J, Sahli Costabal F, et al. How drugs modulate the performance of the human heart. Computational Mechanics 2022;69:1397-411. [Google Scholar]
- 33.Piersanti R, Regazzoni F, Salvador M, et al. 3D-0D closed-loop model for the simulation of cardiac biventricular electromechanics. Computer Methods in Applied Mechanics and Engineering 2022;391:114607. [Google Scholar]
- 34.Regazzoni F, Salvador M, Africa PC, et al. A cardiac electromechanical model coupled with a lumped-parameter model for closed-loop blood circulation. Journal of Computational Physics 2022;457:111083. [Google Scholar]
- 35.Chnafa C, Mendez S, Nicoud F. Image-based large-eddy simulation in a realistic left heart. Computers & Fluids 2014;94:173-87. [Google Scholar]
- 36.Mittal R, Seo JH, Vedula V, et al. Computational modeling of cardiac hemodynamics: current status and future outlook. Journal of Computational Physics 2016;305:1065-82. [Google Scholar]
- 37.Vedula V, Seo JH, Lardo AC, et al. Effect of trabeculae and papillary muscles on the hemodynamics of the left ventricle. Theoretical and Computational Fluid Dynamics 2016;30:3-21. [Google Scholar]
- 38.Hirschvogel M, Bassilious M, Jagschies L, et al. A monolithic 3D-0D coupled closed-loop model of the heart and the vascular system: Experiment-based parameter estimation for patient-specific cardiac mechanics. Int J Numer Method Biomed Eng 2017;33:e2842 . 10.1002/cnm.2842 [DOI] [PubMed] [Google Scholar]
- 39.Lassila T, Malossi C, Stevanella M, et al. Simulation of left ventricle fluid dynamics with mitral regurgitation from magnetic resonance images with fictitious elastic structure regularization. arXiv 2017;1707.03998.
- 40.Collia D, Zovatto L, Pedrizzetti G. Analysis of mitral valve regurgitation by computational fluid dynamics. APL Bioeng 2019;3:036105 . 10.1063/1.5097245 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Feng L, Gao H, Griffith B, et al. Analysis of a coupled fluid-structure interaction model of the left atrium and mitral valve. Int J Numer Method Biomed Eng 2019;35:e3254 . 10.1002/cnm.3254 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hirschhorn M, Tchantchaleishvili V, Stevens R, et al. Fluid-structure interaction modeling in cardiovascular medicine - A systematic review 2017-2019. Med Eng Phys 2020;78:1-13. 10.1016/j.medengphy.2020.01.008 [DOI] [PubMed] [Google Scholar]
- 43.Brenneisen J, Daub A, Gerach T, et al. Sequential Coupling Shows Minor Effects of Fluid Dynamics on Myocardial Deformation in a Realistic Whole-Heart Model. Front Cardiovasc Med 2021;8:768548 . 10.3389/fcvm.2021.768548 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Rigatelli G, Chiastra C, Pennati G, et al. Applications of computational fluid dynamics to congenital heart diseases: a practical review for cardiovascular professionals. Expert Rev Cardiovasc Ther 2021;19:907-16. 10.1080/14779072.2021.1999229 [DOI] [PubMed] [Google Scholar]
- 45.Fumagalli I, Vitullo P, Vergara C, et al. Image-Based Computational Hemodynamics Analysis of Systolic Obstruction in Hypertrophic Cardiomyopathy. Front Physiol 2021;12:787082 . 10.3389/fphys.2021.787082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Karabelas E, Longobardi S, Fuchsberger J, et al. Global Sensitivity Analysis of Four Chamber Heart Hemodynamics Using Surrogate Models. IEEE Trans Biomed Eng 2022;69:3216-23. 10.1109/TBME.2022.3163428 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kronborg J, Svelander F, Eriksson-Lidbrink S, et al. Computational Analysis of Flow Structures in Turbulent Ventricular Blood Flow Associated With Mitral Valve Intervention. Front Physiol 2022;13:806534 . 10.3389/fphys.2022.806534 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Zingaro A, Fumagalli I, Dede’ L, et al. A geometric multiscale model for the numerical simulation of blood flow in the human left heart. Discrete and Continuous Dynamical Systems-S 2022;15:2391-427. [Google Scholar]
- 49.Weinberg EJ, Mack PJ, Schoen FJ, et al. Hemodynamic environments from opposing sides of human aortic valve leaflets evoke distinct endothelial phenotypes in vitro. Cardiovasc Eng 2010;10:5-11. 10.1007/s10558-009-9089-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Votta E, Le TB, Stevanella M, et al. Toward patient-specific simulations of cardiac valves: state-of-the-art and future directions. J Biomech 2013;46:217-28. 10.1016/j.jbiomech.2012.10.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Halevi R, Hamdan A, Marom G, et al. Progressive aortic valve calcification: three-dimensional visualization and biomechanical analysis. J Biomech 2015;48:489-97. 10.1016/j.jbiomech.2014.12.004 [DOI] [PubMed] [Google Scholar]
- 52.Marom G. Numerical methods for fluid-structure interaction models of aortic valves. Archives of Computational Methods in Engineering 2015;22:595-620. [Google Scholar]
- 53.Fedele M, Faggiano E, Dedè L, et al. A patient-specific aortic valve model based on moving resistive immersed implicit surfaces. Biomech Model Mechanobiol 2017;16:1779-803. 10.1007/s10237-017-0919-1 [DOI] [PubMed] [Google Scholar]
- 54.Vergara C, Zonca S. Extended finite elements method for fluid-structure interaction with an immersed thick non-linear structure. In: Boffi D, Pavarino LF, Rozza G, Scacchi S, Vergara C. Mathematical and Numerical Modeling of the Cardiovascular System and Applications. Springer 2018;16. [Google Scholar]
- 55.Kaiser AD, McQueen DM, Peskin CS. Modeling the mitral valve. Int J Numer Method Biomed Eng 2019;35:e3240 . 10.1002/cnm.3240 [DOI] [PubMed] [Google Scholar]
- 56.Nestola MGC, Becsek B, Zolfaghari H, et al. An immersed boundary method for fluid-structure interaction based on variational transfer. Journal of Computational Physics 2019;398:108884. [Google Scholar]
- 57.Wu MCH, Muchowski HM, Johnson EL, et al. Immersogeometric fluid-structure interaction modeling and simulation of transcatheter aortic valve replacement. Comput Methods Appl Mech Eng 2019;357:112556 . 10.1016/j.cma.2019.07.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Sacks M, Drach A, Lee CH, et al. On the simulation of mitral valve function in health, disease, and treatment. J Biomech Eng 2019. [Epub ahead of print]. doi: . 10.1115/1.4043552 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Bosi GM, Capelli C, Cheang MH, et al. A validated computational framework to predict outcomes in TAVI. Sci Rep 2020;10:9906 . 10.1038/s41598-020-66899-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Fumagalli I, Fedele M, Vergara C, et al. An image-based computational hemodynamics study of the Systolic Anterior Motion of the mitral valve. Comput Biol Med 2020;123:103922 . 10.1016/j.compbiomed.2020.103922 [DOI] [PubMed] [Google Scholar]
- 61.This A, Morales HG, Bonnefous O, et al. A pipeline for image based intracardiac CFD modeling and application to the evaluation of the PISA method. Computer Methods in Applied Mechanics and Engineering 2020;358:112627. [Google Scholar]
- 62.Meschini V, Mittal R, Verzicco R. Systolic anterior motion in hypertrophic cardiomyopathy: a fluid-structure interaction computational model. Theoretical and Computational Fluid Dynamics 2021;35:381-96. [Google Scholar]
- 63.Hiromi Spühler J, Hoffman J. An interface-tracking unified continuum model for fluid-structure interaction with topology change and full-friction contact with application to aortic valves. International Journal for Numerical Methods in Engineering 2021;122:5258-78. [Google Scholar]
- 64.Vassilevski Y, Liogky A, Salamatova V. Application of hyperelastic nodal force method to evaluation of aortic valve cusps coaptation: Thin shell vs. membrane formulations. MDPI Mathematics 2021;9:1450. [Google Scholar]
- 65.Abbas SS, Nasif MS, Al-Waked R. State-of-the-art numerical fluid–structure interaction methods for aortic and mitral heart valves simulations: A review. Simulation 2022;98:3-34. [Google Scholar]
- 66.Terahara T, Kuraishi T, Takizawa K, et al. Computational flow analysis with boundary layer and contact representation: II. Heart valve flow with leaflet contact. Journal of Mechanics 2022;38:185-194. [Google Scholar]
- 67.Vankan WJ, Huyghe JM, Janssen JD, et al. Poroelasticity of saturated solids with an application to blood perfusion. International Journal of Engineering Science 1996;34:1019-31. [Google Scholar]
- 68.Chapelle D, Gerbeau JF, Sainte-Marie J, et al. A poroelastic model valid in large strains with applications to perfusion in cardiac modeling. Computational Mechanics 2010;46:91-101. [Google Scholar]
- 69.Cookson AN, Lee J, Michler C, et al. A novel porous mechanical framework for modelling the interaction between coronary perfusion and myocardial mechanics. J Biomech 2012;45:850-5. 10.1016/j.jbiomech.2011.11.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Papamanolis L, Kim HJ, Jaquet C, et al. Myocardial Perfusion Simulation for Coronary Artery Disease: A Coupled Patient-Specific Multiscale Model. Ann Biomed Eng 2021;49:1432-47. 10.1007/s10439-020-02681-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Di Gregorio S, Fedele M, Pontone G, et al. A computational model applied to myocardial perfusion in the human heart: from large coronaries to microvasculature. Journal of Computational Physics 2021;424:109836. [Google Scholar]
- 72.Di Gregorio S, Vergara C, Pelagi GM, et al. Prediction of myocardial blood flow under stress conditions by means of a computational model. Eur J Nucl Med Mol Imaging 2022;49:1894-905. 10.1007/s00259-021-05667-8 [DOI] [PubMed] [Google Scholar]
- 73.Barnafi Wittwer NA, Di Gregorio S, Dede’ L, et al. A multiscale poromechanics model integrating myocardial perfusion and the epicardial coronary vessels. SIAM Journal on Applied Mathematics 2022;82:1167-93. [Google Scholar]
- 74.Sugiura S, Okada JI, Washio T, et al. UT-Heart: A Finite Element Model Designed for the Multiscale and Multiphysics Integration of our Knowledge on the Human Heart. Methods Mol Biol 2022;2399:221-45. 10.1007/978-1-0716-1831-8_10 [DOI] [PubMed] [Google Scholar]
- 75.Kariya T, Washio T, Okada JI, et al. Personalized Perioperative Multi-scale, Multi-physics Heart Simulation of Double Outlet Right Ventricle. Ann Biomed Eng 2020;48:1740-50. 10.1007/s10439-020-02488-y [DOI] [PubMed] [Google Scholar]
- 76.Okada JI, Washio T, Sugiura S, et al. Clinical and pharmacological application of multiscale multiphysics heart simulator, UT-Heart. Korean J Physiol Pharmacol 2019;23:295-303. 10.4196/kjpp.2019.23.5.295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Santiago A, Aguado-Sierra J, Zavala-Aké M, et al. Fully coupled fluid-electro-mechanical model of the human heart for supercomputers. Int J Numer Method Biomed Eng 2018;34:e3140 . 10.1002/cnm.3140 [DOI] [PubMed] [Google Scholar]
- 78.Ahmad Bakir A, Al Abed A, Stevens MC, et al. A Multiphysics Biventricular Cardiac Model: Simulations With a Left-Ventricular Assist Device. Front Physiol 2018;9:1259 . 10.3389/fphys.2018.01259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Viola F, Spandan V, Meschini V, et al. FSEI-GPU: GPU accelerated simulations of the fluid-structure-electrophysiology interaction in the left heart. Computer Physics Communications 2022;273:108248. [Google Scholar]
- 80.Regazzoni F, Dedè L, Quarteroni A. Active force generation in cardiac muscle cells: mathematical modeling and numerical simulation. Vietnam Journal of Mathematics 2021;49:87-118. 10.1007/s10013-020-00433-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Bucelli M, Zingaro A, Africa PC, et al. A mathematical model that integrates cardiac electrophysiology, mechanics and fluid dynamics: application to the human left heart. International Journal for Numerical Methods in Biomedical Engineering 2022;39:e3678 . 10.1002/cnm.3678 [DOI] [PubMed] [Google Scholar]
- 82.Fedele M, Piersanti R, Regazzoni F, et al. A comprehensive and biophysically detailed computational model of the whole human heart electromechanics. Computer Methods in Applied Mechanics and Engineering 2023;410:115983. [Google Scholar]
- 83.Pagani S, Dede’ L, Manzoni A, et al. Data integration for the numerical simulation of cardiac electrophysiology. Pacing Clin Electrophysiol 2021;44:726-36. 10.1111/pace.14198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Salvador M, Regazzoni F, Pagani S, et al. The role of mechano-electric feedbacks and hemodynamic coupling in scar-related ventricular tachycardia. Comput Biol Med 2022;142:105203 . 10.1016/j.compbiomed.2021.105203 [DOI] [PubMed] [Google Scholar]
- 85.Frontera A, Limite LR, Pagani S, et al. Electrogram fractionation during sinus rhythm occurs in normal voltage atrial tissue in patients with atrial fibrillation. Pacing Clin Electrophysiol 2022;45:219-28. 10.1111/pace.14425 [DOI] [PubMed] [Google Scholar]
- 86.Frontera A, Limite LR, Pagani S, et al. Characterization of cardiac electrogram signals in atrial arrhythmias. Minerva Cardiol Angiol 2021;69:70-80. 10.23736/S2724-5683.20.05431-6 [DOI] [PubMed] [Google Scholar]
- 87.Zahid S, Cochet H, Boyle PM, et al. Patient-derived models link re-entrant driver localization in atrial fibrillation to fibrosis spatial pattern. Cardiovasc Res 2016;110:443-54. 10.1093/cvr/cvw073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Trayanova NA. Mathematical approaches to understanding and imaging atrial fibrillation: significance for mechanisms and management. Circ Res 2014;114:1516-31. 10.1161/CIRCRESAHA.114.302240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Stella S, Vergara C, Maines M, et al. Integration of activation maps of epicardial veins in computational cardiac electrophysiology. Comput Biol Med 2020;127:104047 . 10.1016/j.compbiomed.2020.104047 [DOI] [PubMed] [Google Scholar]
- 90.Vergara C, Stella S, Maines M, et al. Computational electrophysiology of the coronary sinus branches based on electro-anatomical mapping for the prediction of the latest activated region. Med Biol Eng Comput 2022;60:2307-19. 10.1007/s11517-022-02610-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Elliott PM, Anastasakis A, Borger MA, et al. 2014 ESC Guidelines on diagnosis and management of hypertrophic cardiomyopathy: the Task Force for the Diagnosis and Management of Hypertrophic Cardiomyopathy of the European Society of Cardiology (ESC). Eur Heart J 2014;35:2733-79. 10.1093/eurheartj/ehu284 [DOI] [PubMed] [Google Scholar]
- 92.Nicolò F, Lio A, Comisso M, et al. Surgical treatment of hypertrophic obstructive cardiomyopathy. In Cardiac Surgery Procedures: IntechOpen. 2019;107-119. [Google Scholar]
- 93.Fumagalli I, Polidori R, Renzi F, et al. Fluid-structure interaction analysis of transcatheter aortic valve implantation. Int J Numer Method Biomed Eng 2023;39:e3704 . 10.1002/cnm.3704 [DOI] [PubMed] [Google Scholar]
- 94.Ruffino L, Santoro A, Sparvieri S, et al. Computational analysis of cardiovascular effects of COVID-19 infection in children. Journal of Pediatric Advance Research 2023;2:1-10. [Google Scholar]
- 95.Dedè L, Regazzoni F, Vergara C, et al. Modeling the cardiac response to hemodynamic changes associated with COVID-19: a computational study. Math Biosci Eng 2021;18:3364-83. 10.3934/mbe.2021168 [DOI] [PubMed] [Google Scholar]
- 96.Tsankov BK, Allaire JM, Irvine MA, et al. Severe COVID-19 Infection and Pediatric Comorbidities: A Systematic Review and Meta-Analysis. Int J Infect Dis 2021;103:246-56. 10.1016/j.ijid.2020.11.163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Sharma C, Ganigara M, Galeotti C, et al. Multisystem inflammatory syndrome in children and Kawasaki disease: a critical comparison. Nat Rev Rheumatol 2021;17:731-48. 10.1038/s41584-021-00709-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Quarteroni A, Dede’ L, Regazzoni F, Vergara C. A mathematical model of the human heart suitable to address clinical problems. Japan Journal of Industrial and Applied Mathematics 2023;40:1547-67. [Google Scholar]
- 99.Africa PC. lifex: A flexible, high performance library for the numerical solution of complex finite element problems. SoftwareX 2022;20:101252. [Google Scholar]
- 100.Africa PC, Piersanti R, Fedele M, et al. lifex-fiber: an open tool based on lifex for myofibers generation in cardiac computational models. BMC Bioinformatics 2023;24:143 . 10.1186/s12859-023-05260-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Africa PC, Fumagalli I, Bucelli M, et al. lifex-cfd: an open-source computational fluid dynamics solver for cardiovascular applications. Computer Physics Communication 2024;296:109039. [Google Scholar]
- 102.Africa PC, Piersanti R, Regazzoni F, et al. lifex-ep: a robust and efficient software for cardiac electrophysiology simulations. BMC Bioinformatics 2023;24:389 . 10.1186/s12859-023-05513-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Public fork with additional features available online: https://github.com/marcofedele/vmtk, https://github.com/checkrenzi/vmtk/tree/merge-vmtk (last version).
- 104.Fedele M, Quarteroni A. Polygonal surface processing and mesh generation tools for the numerical simulation of the cardiac function. Int J Numer Method Biomed Eng 2021;37:e3435 . 10.1002/cnm.3435 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Klein S, Staring M, Murphy K, et al. Elastix: a toolbox for intensity based medical image registration. IEEE Transactions on Medical Imaging 2010;29:196-205. 10.1109/TMI.2009.2035616 [DOI] [PubMed] [Google Scholar]
- 106.Wolf I, Vetter M, Wegner I, et al. The medical imaging interaction toolkit. Med Image Anal 2005;9:594-604. 10.1016/j.media.2005.04.005 [DOI] [PubMed] [Google Scholar]
- 107.Nolden M, Zelzer S, Seitel A, et al. The Medical Imaging Interaction Toolkit: challenges and advances: 10 years of open-source development. Int J Comput Assist Radiol Surg 2013;8:607-20. 10.1007/s11548-013-0840-8 [DOI] [PubMed] [Google Scholar]
- 108.Strocchi M, Augustin CM, Gsell MAF, et al. A publicly available virtual cohort of four-chamber heart meshes for cardiac electro-mechanics simulations. PLoS One 2020;15:e0235145 . 10.1371/journal.pone.0235145 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Hoogendoorn C, Duchateau N, Sánchez-Quintana D, et al. A high-resolution atlas and statistical model of the human heart from multislice CT. IEEE Trans Med Imaging 2013;32:28-44. 10.1109/TMI.2012.2230015 [DOI] [PubMed] [Google Scholar]
- 110.Zygote Media Group, Inc. Zygote Solid 3D Heart Generation II Development Report. Technical report, 2014.
- 111.Baillargeon B, Costa I, Leach JR, et al. Human Cardiac Function Simulator for the Optimal Design of a Novel Annuloplasty Ring with a Sub-valvular Element for Correction of Ischemic Mitral Regurgitation. Cardiovasc Eng Technol 2015;6:105-16. 10.1007/s13239-015-0216-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Antiga L, Piccinelli M, Botti L, et al. An image-based modeling framework for patient-specific computational hemodynamics. Med Biol Eng Comput 2008;46:1097-112. 10.1007/s11517-008-0420-1 [DOI] [PubMed] [Google Scholar]
- 113.Bennati L, Vergara C, Giambruno V, et al. An Image-Based Computational Fluid Dynamics Study of Mitral Regurgitation in Presence of Prolapse. Cardiovasc Eng Technol 2023;14:457-75. 10.1007/s13239-023-00665-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Montalt-Tordera J, Muthurangu V, Hauptmann A, et al. Machine learning in Magnetic Resonance Imaging: Image reconstruction. Phys Med 2021;83:79-87. 10.1016/j.ejmp.2021.02.020 [DOI] [PubMed] [Google Scholar]
- 115.Quer G, Arnaout R, Henne M, et al. Machine Learning and the Future of Cardiovascular Care: JACC State-of-the-Art Review. J Am Coll Cardiol 2021;77:300-13. 10.1016/j.jacc.2020.11.030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Coveney S, Cantwell C, Roney C. Atrial conduction velocity mapping: clinical tools, algorithms and approaches for understanding the arrhythmogenic substrate. Med Biol Eng Comput 2022;60:2463-78. 10.1007/s11517-022-02621-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Kuo MJ, Ton AN, Lo LW, et al. Abnormal Conduction Zone Detected by Isochronal Late Activation Mapping Accurately Identifies the Potential Atrial Substrate and Predicts the Atrial Fibrillation Ablation Outcome After Pulmonary Vein Isolation. Circ Arrhythm Electrophysiol 2023;16:e011149 . 10.1161/CIRCEP.122.011149 [DOI] [PubMed] [Google Scholar]
- 118.Frontera A, Pagani S, Limite LR, et al. Outer loop and isthmus in ventricular tachycardia circuits: Characteristics and implications. Heart Rhythm 2020;17:1719-28. 10.1016/j.hrthm.2020.05.034 [DOI] [PubMed] [Google Scholar]
- 119.Zingaro A, Menghini F, Quarteroni A. Hemodynamics of the heart’s left atrium based on a Variational Multiscale-LES numerical method. European Journal of Mechanics-B/Fluids 2021;89:380-400. [Google Scholar]
- 120.Tenderini R, Pagani S, Quarteroni A, et al. PDE-aware deep learning for inverse problems in cardiac electrophysiology. SIAM Journal on Scientific Computing 2022;44:B605-B639. [Google Scholar]
- 121.Blanco PJ, Feijóo RA. A 3D-1D-0D computational model for the entire cardiovascular system. Mecánica Computacional 2010;29:5887-5911. [Google Scholar]
- 122.Fastl TE, Tobon-Gomez C, Crozier A, et al. Personalized computational modeling of left atrial geometry and transmural myofiber architecture. Med Image Anal 2018;47:180-90. 10.1016/j.media.2018.04.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Beyar R, Sideman S. A computer study of the left ventricular performance based on fiber structure, sarcomere dynamics, and transmural electrical propagation velocity. Circ Res 1984;55:358-75. 10.1161/01.res.55.3.358 [DOI] [PubMed] [Google Scholar]
- 124.Gil D, Aris R, Borras A, et al. Influence of fiber connectivity in simulations of cardiac biomechanics. Int J Comput Assist Radiol Surg 2019;14:63-72. 10.1007/s11548-018-1849-9 [DOI] [PubMed] [Google Scholar]
- 125.Ku DN, Giddens DP, Zarins CK, et al. Pulsatile flow and atherosclerosis in the human carotid bifurcation. Positive correlation between plaque location and low oscillating shear stress. Arteriosclerosis 1985;5:293-302. 10.1161/01.atv.5.3.293 [DOI] [PubMed] [Google Scholar]
- 126.Avgerinos NA, Neofytou P. Mathematical Modelling and Simulation of Atherosclerosis Formation and Progress: A Review. Ann Biomed Eng 2019;47:1764-85. 10.1007/s10439-019-02268-3 [DOI] [PubMed] [Google Scholar]
- 127.Boyle PM, Zghaib T, Zahid S, et al. Computationally guided personalized targeted ablation of persistent atrial fibrillation. Nat Biomed Eng 2019;3:870-9. 10.1038/s41551-019-0437-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Ramachandra AB, Humphrey JD, Marsden AL. Gradual loading ameliorates maladaptation in computational simulations of vein graft growth and remodelling. J R Soc Interface 2017;14:20160995 . 10.1098/rsif.2016.0995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Gebauer AM, Pfaller MR, Braeu FA, et al. A homogenized constrained mixture model of cardiac growth and remodeling: analyzing mechanobiological stability and reversal. Biomech Model Mechanobiol 2023;22:1983-2002. 10.1007/s10237-023-01747-w [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Pozzi S, Redaelli A, Vergara C, et al. Mathematical and numerical modeling of atherosclerotic plaque progression based on fluid-structure interaction. Journal of Mathematical Fluid Mechanics 2021;23:74. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The article’s supplementary files as