Confounder Adjustment Using the Disease Risk Score: A Proposal for Weighting Methods

Abstract

Propensity score analysis is a common approach to addressing confounding in nonrandomized studies. Its implementation, however, requires important assumptions (e.g., positivity). The disease risk score (DRS) is an alternative confounding score that can relax some of these assumptions. Like the propensity score, the DRS summarizes multiple confounders into a single score, on which conditioning by matching allows the estimation of causal effects. However, matching relies on arbitrary choices for pruning out data (e.g., matching ratio, algorithm, and caliper width) and may be computationally demanding. Alternatively, weighting methods, common in propensity score analysis, are easy to implement and may entail fewer choices, yet none have been developed for the DRS. Here we present 2 weighting approaches: One derives directly from inverse probability weighting; the other, named target distribution weighting, relates to importance sampling. We empirically show that inverse probability weighting and target distribution weighting display performance comparable to matching techniques in terms of bias but outperform them in terms of efficiency (mean squared error) and computational speed (up to >870 times faster in an illustrative study). We illustrate implementation of the methods in 2 case studies where we investigate placebo treatments for multiple sclerosis and administration of aspirin in stroke patients.

Abbreviations

ATE

average treatment effect in the entire population

ATT

average treatment effect in the treated population

DRS

disease risk score

EDSS

Expanded Disability Status Scale

IPW

inverse probability weighting

IST

International Stroke Trial

TDW

target distribution weighting

 

Nonrandomized studies are increasingly being used to study the effectiveness of therapeutic treatments. A key challenge in nonrandomized studies is the presence of confounding, which implies that treatments of interest are assigned according to variables that affect the outcome. If left unaddressed, confounding can lead to severely biased estimates of intervention effect.

To remove confounding, the propensity score plays a central role in nonrandomized, observational studies (1). Under a set of assumptions (i.e., no interference (or the “stable unit treatment value assumption”), consistency, the absence of unmeasured confounders, and positivity), conditioning on the propensity score—defined as the probability of receiving the treatment given the confounding variables—leads to comparability (or “exchangeability”) of the treatment groups by balancing the distribution of confounders, thus removing confounding and allowing estimation of causal treatment effects (1, 2). However, the use of the propensity score is challenged in some situations. For instance, violation of the positivity assumption can occur in finite samples due to chance, and in such cases, causal effects may be poorly identified (3). In such situations, it might be reasonable to opt for alternative methods.

The disease risk score (DRS), known as the prognostic analog of the propensity score, has garnered interest over the past few years. Initially developed for the case of binary exposures (4, 5), it has since been extended—for example, to multiple treatment exposure groups (6), survival analysis (7), or multiple outcomes (8). The DRS models the potential outcome that would be expected given the confounding variables, if individuals were to receive the control treatment. Hansen (5) shows that conditioning on the DRS allows a causal treatment effect estimation, under assumptions that are relatively similar to those needed for the propensity score: the stable unit treatment value assumption, consistency, the absence of unmeasured confounders, and a relaxed form of positivity—that is, a positive probability of treatment at all values of the DRS, instead of all values of the confounders. Therefore, the DRS offers an advantage when the overlapping values of confounders are limited between the treated and control individuals (i.e., near positivity violation). Wyss et al. (9) show that under different scenarios, the overlapping regions of the DRS are often larger than those of the propensity score. In practice, one can estimate the DRS using the same confounding variables as those used with the propensity score, and then perform matching (6, 9–13).

Matching can be computationally demanding—particularly in large data sets—and may involve some arbitrary choices (e.g., matching ratio, matching algorithm, sampling with replacement, use of a caliper, caliper width). In the case of the propensity score, weighting methods entail fewer choices and can be easily implemented (14–19). Yet, to our knowledge, no weighting methods have been described for the DRS. In this article, we propose 2 simple weighting methods for the DRS: One derives from inverse probability weighting (IPW); the other one, which we have named target distribution weighting (TDW), is a form of standardization that relates to importance sampling. Below, we elaborate on the theoretical framework behind the proposed methods, present a series of simulations, and illustrate the methods in 2 case studies investigating placebo treatments for multiple sclerosis and the administration of aspirin in stroke patients.

METHODS

Theoretical background

Let 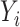denote the outcome, 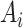the treatment status ( 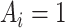denotes “treated”; 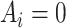denotes “control”) and 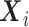the set of confounders. The effect caused by the treatment in individual 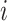, or simply the individual treatment effect, is defined as (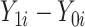). In this expression, 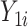and 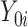are the potential (or “counterfactual”) outcomes that would be observed if 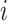were to receive the treatment and control exposures, respectively (20). Under consistency, that is, 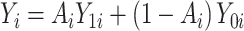, eithe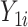r or 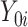is observed, since an individual cannot be simultaneously allocated to 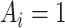and 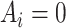. This fundamental problem implies that causal inference is generally impossible at the individual level (20).

When estimating treatment effects at a population level, a natural estimand is the average treatment effect in the entire population (ATE), defined as 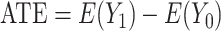. Yet, an estimand of particular interest is the average treatment effect in the treated population (ATT), for it informs on the effect of the treatment in the specific subpopulation for which it has been intended: 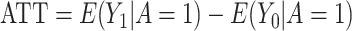. (In both equations (ATE and ATT), we have removed the index 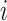due to averaging, and for the sake of notational simplicity, we omit this index in the remainder of the article.)

The DRS is defined as 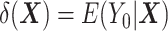, which—under the assumption of no unmeasured confounders, that is, 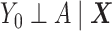—is equal to (5). The DRS can be estimated in several ways. One option is to fit a prognostic model in the control group; another option is to use a historical cohort including only control individuals. Compared with fitting a model to the same-sample control group, the use of a large historical cohort of control individuals may offer some advantages to reduce overfitting (5, 12) and limit bias amplification in cases where the assumption of no unmeasured confounders is not met (21). Hansen (5) shows that the DRS has a balancing property (called “prognostic balance”) that differs from that of the propensity score (“covariate balance”): While conditioning on the propensity score leads to balancing of the covariate distribution per se, conditioning on the DRS leads to balancing of the prognosis (i.e., the potential outcome that would be observed under control exposure, conditionally on the covariates). Thus, individuals sharing a same value for the DRS can be regarded as having the same risk (or prognosis) for the outcome, if they were to receive the control exposure. This assumes that, all over the range of the DRS, there exist control and exposed individuals who share similar values of the prognostic score rather than similar values of the covariates per se (i.e., the relaxed positivity assumption). Hansen shows that the use of the DRS is straightforward for the estimation of the ATT, as it requires no information on the existence of effect modifiers (5). This is because only the potential outcome under control exposure is modeled, thereby resulting in partial exchangeability, that is, 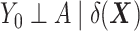, which is sufficient for the ATT. 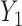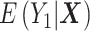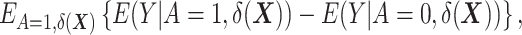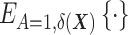(Estimating the ATE would also require exchangeability with respect to , and therefore either the use of a second DRS—that is, a prognostic score modeling —or the assumption that the two DRSs are parallel—that is, there are no effect modifiers (6).) Hansen shows that conditioning on the DRS suffices for the following unbiased estimator of the ATT: where denotes the expectation over the distribution of the DRSs within the treated group (5). This estimator can be regarded as the difference between 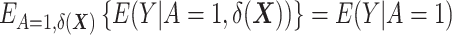, which is the outcome expectation in the treatment group, and 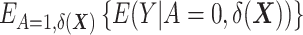, which is the outcome expectation in the control group conditional on having a distribution of 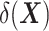similar to that in the treated arm. This conditioning can be performed, for instance, by matching (6, 9–13).

As alternatives to matching methods, we propose 2 weighting methods for estimating the ATT. One relates to importance sampling; the other is similar to IPW based on the propensity score (16, 18, 19).

First, to allow the DRS to be distributed as in the treated group, one can construct weights using the following function, for which we suggest the name TDW:

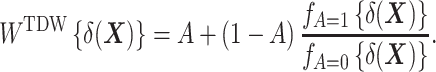Here, 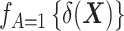denotes the probability density function of the DRS within the treated group, and 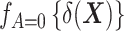denotes the probability density function of the DRS within the control group. To put it simply, the ratio 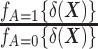standardizes the DRS distribution in the control group to that of the treated group (i.e., the “target distribution”), thereby allowing estimation of the ATT (see Web Appendix 1, available at https://doi.org/10.1093/aje/kwad196). These density functions can be estimated using a nonparametric kernel density estimator.

Second, in a manner akin to the construction of weights for IPW based on the propensity score (16, 18, 19), one can show that the following weighting function also allows unbiased estimation of the ATT (see Web Appendix 2):

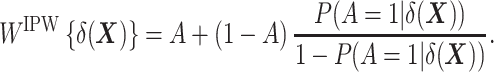Note that, as employed here for estimation of the ATT, this form of IPW is often referred to as “standardized mortality ratio weighting” in the epidemiologic literature (22). (We keep the term IPW throughout, which is used in the statistical literature to designate this class of estimators.) This method requires the estimation of 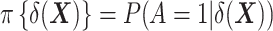, the “prognostic propensity score” or “focused propensity score” (23, 24), which is a propensity score including the DRS as the sole variable. Such a propensity score is not new; it has been previously proposed to balance the effect of variables that are strongly associated with the outcome (23, 24). In Web Appendix 3, we show how IPW actually relates to TDW.

Simulation study

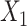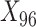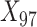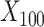We assessed the performance of the two proposed methods, TDW and IPW, in a simulation study. We adopted the design previously developed by Wyss et al. (9), who studied the performance of DRS matching methods in comparison with propensity score matching. We generated 100 confounders: to were drawn from a binomial distribution with a probability equal to 0.5, and to were drawn from a standard normal distribution (mean 0 and variance 1). Subsequently, we allocated the treatment exposure according to a Bernoulli distribution with a probability equal to 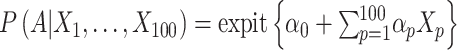, where 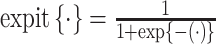. We generated the potential outcome that would be observed if all individuals were to receive the treatment, following a Bernoulli distribution with a probability equal to .

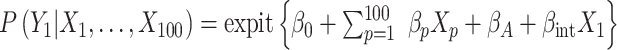Similarly, we generated the potential outcome that would be observed if all individuals were to receive control status, following a Bernoulli distribution with a probability .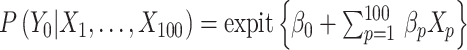

Finally, we generated the observed outcome using 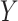in the consistency equation: 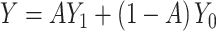. To allow the 100 confounders to have different magnitudes and directions, we drew their effect 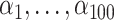on the treatment exposure and their effect 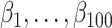on the outcome, following uniform distributions with bounds 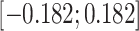(weak confounding scenarios), (moderate confounding scenarios), and 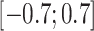(strong confounding scenarios). Finally, we set 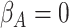(i.e., null treatment effect) and 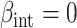in scenarios without effect modification and 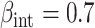in scenarios with effect modification. We set the sample size to 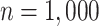and performed 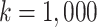iterations.

For each scenario and iteration, we used 5 estimators: 1) the naive estimator; 2) the nearest-neighbor matching estimator; 3) the optimal full matching estimator; 4) the IPW estimator; and 5) the TDW estimator. The naive estimator was simply the difference in average observed outcomes across the treated and control groups. All matching and weighting estimators were based on a DRS, which was estimated by fitting a logistic regression model to a simulated historical cohort including 10,000 control individuals (the generation of this cohort followed the same procedure as above, but without treatment exposure). Nearest-neighbor matching was performed without replacement using a 1:1 ratio and a caliper width of 0.025 standard deviation of the logit of the prognostic propensity score (9). Optimal full matching was performed without replacement and caliper. Contrary to nearest-neighbor matching, optimal full matching preserves the complete sample and allows many individuals to fall into the same “pair” (or subclass), such that the overall average distance between matches becomes optimal (25, 26). After matching, this approach assigns weights to the matched pairs (or subclasses) such that their distribution approximates that of the target population (e.g., the treated individuals). This rescaling is based on the probability (mass) function of the matched pairs. (See Nguyen and Debray (6) for application of optimal full matching on the DRS.) The IPW and TDW estimators were computed as the weighted difference in outcome across the treated and control arms after applying the aforementioned weighting functions. To estimate the density functions necessary for TDW, we used a Gaussian kernel estimator.

For each scenario, the true treatment effect was computed as 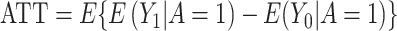over all 1,000 iterations. Based on this true treatment effect, we computed the bias and mean squared error (MSE) of each estimator over all 1,000 iterations: 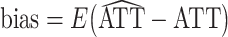and .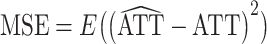

We present the R software code (R Foundation for Statistical Computing, Vienna, Austria) for the simulation study elsewhere (see Acknowledgments).

Illustrative case study 1

We applied the proposed estimators for DRS analysis using synthetic data from patients with relapsing-remitting multiple sclerosis. Our goal was to assess the effect of a treatment on the Expanded Disability Status Scale (EDSS) measured 36 weeks after baseline. The EDSS is a scale that quantifies disability in 0.5-unit increments, and scores range from 0 (no disability) to 10 (death due to multiple sclerosis). We combined the placebo arms from 4 clinical trials into 2 placebo treatment groups (27–30). We then generated synthetic data for new (artificial) patients by adopting multiple imputation by chained equations. To ensure that both placebo treatments had the same efficacy in the simulated data set, treatment allocation was not used to inform the generation of EDSS outcomes. This implies that the “true” mean difference in EDSS between the treatment groups was 0. Subsequently, to introduce baseline imbalance, we selectively removed simulated patients from the treatment groups. We labeled one group as “active” and the other as “control.” The resulting data set was then treated as a hypothetical observational nonrandomized study (see link in Acknowledgments), where the “true” treatment effect was expected to be 0.

We assessed the effect of the “active” treatment against the “control” treatment on the EDSS score after 36 weeks. To address confounding, we conducted a DRS analysis. First, a DRS was derived in the “control” group using linear regression. This model was then used to predict EDSS score at 36 weeks for all (treated and control) patients, using the baseline EDSS score and 20 additional baseline covariates. Subsequently, we estimated the effect of “active” treatment in the group of patients who received “active” treatment (i.e., ATT) using 4 DRS methods as in our simulation study: nearest-neighbor matching (1:1, no replacement, caliper width of 0.025 standard deviation of the logit of the prognostic propensity score), optimal full matching, IPW, and TDW. As a reference, we also fitted a (naive) linear regression model that only adjusted for received treatment to estimate EDSS score at 36 weeks.

Ninety-five percent confidence intervals around the ATT were obtained by bootstrapping (1,000 iterations), by taking the 2.5th and 97.5th percentiles of the bootstrap distribution. Each bootstrap loop included all analysis steps to take into account the total uncertainty.

Illustrative case study 2

We reanalyzed data from the International Stroke Trial (IST) (31). The IST was a large, multicenter, randomized, placebo-controlled trial including 19,435 stroke patients from 36 countries for which data are available in open access (32). The IST evaluated the effect of aspirin on a primary composite outcome of death or dependency (i.e., absence of autonomy) at 6 months (binary outcome) (31). While the investigators found a modest beneficial effect of aspirin versus placebo (−1.3% on an absolute risk difference scale: 62.2% of patients’ experiencing the outcome vs. 63.5%), patients included in the trial received the treatment at various initiation times (from 0 to 48 hours after the onset of symptoms) (31). Nowadays, it is recommended to initiate the administration of aspirin in stroke patients as soon as possible (33); nonetheless, it is unclear to what extent early administration of aspirin reduces the risk of the outcome. In this reanalysis, we assessed the effect of early aspirin administration (“treatment”; ≤8 hours after stroke symptoms) as compared with late aspirin administration (“control”; 9–48 hours after stroke symptoms). In this regard, we focused our reanalysis on the aspirin arm of the IST and analyzed it as an observational nonrandomized study, since aspirin might have been initiated at different time points due to confounding variables (e.g., age, sex, and stroke symptoms of patients).

To address confounding, we conducted a DRS analysis. First, a DRS was derived in the “control” group (i.e., patients who received aspirin after 8 hours), since no historical cohort of controls was available. We fitted a logistic regression model including the following variables: age, systolic blood pressure, sex, consciousness, previous computed tomography scan, visible infarct on computed tomography scan, stroke subtype, atrial fibrillation, aspirin intake within the previous 3 days, and 8 function deficit variables (face deficit, arm/hand deficit, leg/foot deficit, dysphasia, hemianopia, visuospatial disorder, brainstem/cerebellar signs, or other deficit). We used a restricted cubic spline with 3 knots to handle nonlinearity of continuous variables (age and systolic blood pressure). The fitted logistic model was used to return a predicted DRS in all patients. Then, we estimated the effect of early aspirin administration in the group of patients who received aspirin at an early time (i.e., ATT), using 4 DRS methods as in our simulation study and first illustrative case: nearest-neighbor matching (1:1, no replacement, caliper width of 0.025 standard deviation of the logit of the prognostic propensity score), optimal full matching, IPW, and TDW.

Ninety-five percent confidence intervals around the ATT estimate were obtained by bootstrapping (1,000 iterations), by taking the 2.5th and 97.5th percentiles of the bootstrap distribution. Each bootstrap loop included all analysis steps to take into account the total uncertainty. For the sake of simplicity and due to a low rate of missing data, we worked on complete cases (94.1%; 9,148 out of 9,720 patients who received aspirin).

RESULTS

Results of simulation study

Overall, the prevalence of the treatment exposure was equal to 32.1%; that of the outcome was equal to 52.5%. As shown in Figure 1, all 4 estimators based on the DRS consistently estimated the ATT. The nearest-neighbor matching and optimal matching methods led to a higher variability in the estimates, when compared with IPW and TDW (Figure 2). These two weighting methods performed best in terms of mean squared error (Table 1).

Figure 1.

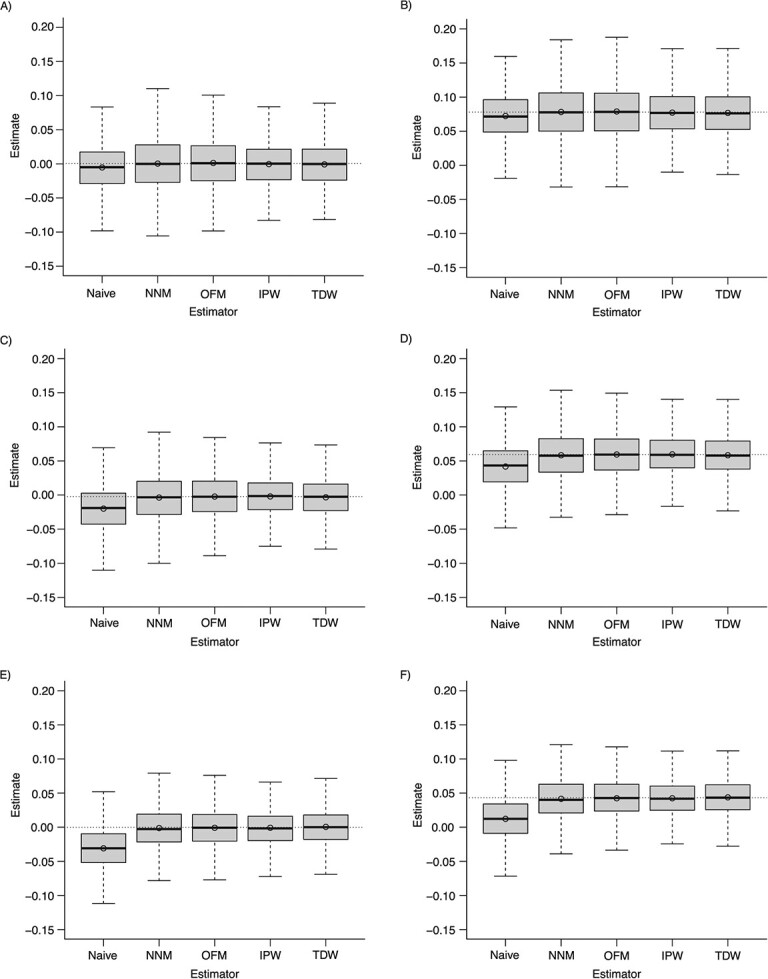
Estimates of the average treatment effect in the treated (ATT), according to different estimators based on the disease risk score across simulations. Scenarios: A) weak confounding and no effect modification; B) weak confounding and the presence of effect modification; C) moderate confounding and no effect modification; D) moderate confounding and the presence of effect modification; E) strong confounding and no effect modification; F) strong confounding and the presence of effect modification. NNM, nearest-neighbor matching; OFM, optimal full matching; IPW, inverse probability weighting; TDW, target distribution weighting. The top and bottom of the box represent the 75th and 25th percentiles; the horizontal line inside the box represents the median; and the whiskers extend to the most extreme data point, which is no more than 1.5 times the interquartile range from the box. The circle inside the box is the mean. The dotted line corresponds to the true ATT.

Figure 2.

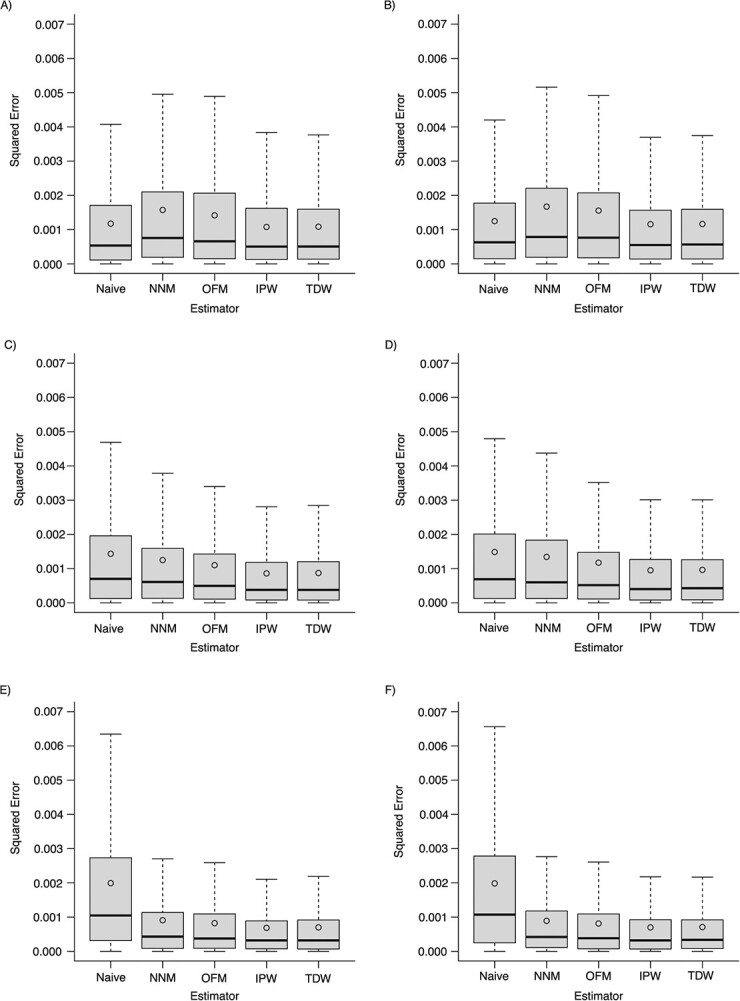
Squared error of estimates of the average treatment effect in the treated (ATT), according to different estimators based on the disease risk score across simulations. Scenarios: A) weak confounding and no effect modification; B) weak confounding and the presence of effect modification; C) moderate confounding and no effect modification; D) moderate confounding and the presence of effect modification; E) strong confounding and no effect modification; F) strong confounding and the presence of effect modification. NNM, nearest-neighbor matching; OFM, optimal full matching; IPW, inverse probability weighting; TDW, target distribution weighting. The top and bottom of the box represent the 75th and 25th percentiles; the horizontal line inside the box represents the median; and the whiskers extend to the most extreme data point, which is no more than 1.5 times the interquartile range from the box. The circle inside the box is the mean.

Table 1.

Performance of Different Estimators of the ATT Based on the Disease Risk Score, Derived Using Simulated Data (1,000 Replicated Samples)

Confounding Status	Effect Modification	Estimator	Bias (×100)	MSE (×100)
Weak	No	Naive	−0.5617	0.1176
Weak	No	NNM	0.0046	0.1575
Weak	No	OFM	0.1013	0.1419
Weak	No	IPW	−0.0659	0.1078
Weak	No	TDW	−0.1076	0.1086
Moderate	No	Naive	−1.7546	0.1435
Moderate	No	NNM	−0.1308	0.1251
Moderate	No	OFM	0.0130	0.1102
Moderate	No	IPW	0.0313	0.0862
Moderate	No	TDW	−0.0968	0.0873
Strong	No	Naive	−3.0799	0.1994
Strong	No	NNM	−0.1081	0.0910
Strong	No	OFM	−0.0664	0.0825
Strong	No	IPW	−0.0665	0.0688
Strong	No	TDW	0.0687	0.0702
Weak	Yes	Naive	−0.5617	0.1250
Weak	Yes	NNM	0.0301	0.1671
Weak	Yes	OFM	0.1013	0.1557
Weak	Yes	IPW	−0.0659	0.1159
Weak	Yes	TDW	−0.1076	0.1165
Moderate	Yes	Naive	−1.7546	0.1487
Moderate	Yes	NNM	−0.1001	0.1344
Moderate	Yes	OFM	0.0130	0.1175
Moderate	Yes	IPW	0.0313	0.0953
Moderate	Yes	TDW	−0.0968	0.0965
Strong	Yes	Naive	−3.0799	0.1986
Strong	Yes	NNM	−0.1496	0.0893
Strong	Yes	OFM	−0.0664	0.0815
Strong	Yes	IPW	−0.0665	0.0701
Strong	Yes	TDW	0.0687	0.0710

Abbreviations: ATT, average treatment effect in the treated population; IPW, inverse probability weighting; MSE, mean squared error; NNM, nearest-neighbor matching; OFM, optimal full matching; TDW, target distribution weighting.

On average, optimal full matching required the longest computation time (0.1828 seconds/analysis), followed by nearest-neighbor matching (0.0761 seconds/analysis). IPW and TDW ran much faster than matching methods (0.0055 seconds/analysis for IPW and 0.0049 seconds/analysis for TDW).

Supplementary simulations exploring different bandwidth choices for TDW are described in Web Appendix 4 (see results in Web Figures 1 and 2). We also performed an additional series of simulations to explore complex scenarios (Web Appendix 5), including positivity violation and model misspecification, and a comparison with propensity score weighting, direct substitution (i.e., G-computation), and a doubly robust estimator. These simulations followed the method of Kang and Schafer (34). Results are shown in Web Figures 3 and 4.

Results of illustrative case study 1

The nonrandomized study based on synthetic data contained 1,627 patients, with 500 receiving the “control” treatment. For most baseline covariates, the distribution substantially differed between the “control” and “active” groups (absolute standardized mean differences > 0.10), indicating potential confounding.

When estimating a naive treatment effect, without any adjustment for baseline covariates, we found in the “active” group an EDSS score at 36 weeks significantly lower than the one found in the “control” group (0.33 (standard error, 0.07) points lower). This effect was mainly caused by confounding due to baseline EDSS score, which was much lower in the “active” group (median, 2.0) than in the “control” group (median, 2.5). Although many other baseline covariates were imbalanced, their prognostic effect on EDSS score was much weaker.

When adjusting for differences in all of the observed baseline covariates using the DRS, we found that all estimates of the ATT were close to 0 (Table 2). In this illustrative study, this meant that those individuals who were included in the “active” group had, on average, no expected change in EDSS score compared with the hypothetical scenario where they were to receive the “control” placebo instead of the “active” exposure.

Table 2.

ATT Estimates of the Placebo Treatment Effect (Versus Other Placebo Treatment (i.e., Expected True Treatment Effect 0)) on EDSS Score at 36 Weeks in Patients With Relapsing-Remitting Multiple Sclerosis, on an Absolute Difference Scale, Derived Using Synthetic Data

Estimator	Estimation Time, seconds a	Point Estimate	95% CI a
Naive	2	−0.33	−0.57, −0.30
Nearest-neighbor matching	29	0.02	−0.12, 0.10
Optimal full matching	1,897	0.07	−0.11, 0.13
Inverse probability weighting	6	0.06	−0.08, 0.13
Target distribution weighting	4	0.04	−0.09, 0.10

Abbreviations: ATT, average treatment effect in the treated population; CI, confidence interval; EDSS, Expanded Disability Status Scale.

^a Results are based on 1,000 bootstrap samples (nonparametric 95% CI: 2.5th and 97.5th percentiles).

The matching approaches required the most computational time, especially when 95% confidence intervals were derived using bootstrapping (Table 2).

Results of illustrative case study 2

Among patients enrolled in the aspirin arm of the IST, fewer than one-quarter received the treatment within 8 hours following the onset of symptoms (23.6%; n = 2,161). In this group, 1,443 patients (66.8%) were recorded with death or dependency at 6 months versus 4,248 (60.8%) in the group of patients who received aspirin later (after 8 hours). After adjusting for confounding variables using the DRS, we found that early initiation of aspirin resulted in a moderate decrease in the outcome. This meant that patients who received aspirin within 8 hours after a stroke had, on average, an expected slight decrease in death/dependency at 6 months compared with the hypothetical scenario where they were to receive aspirin later (after 8 hours). Table 3 summarizes the effects of early aspirin administration obtained from the 4 DRS estimators.

Table 3.

ATT Estimates of the Effect of Early Aspirin Administration on Death or Dependency (i.e., Absence of Autonomy) at 6 Months in Ischemic Stroke Patients, on an Absolute Risk Difference Scale, Derived Using Data From the International Stroke Trial, 1991–1996

Estimator	Estimation Time, seconds a	Point Estimate	95% CI a
Naive	6	0.06	0.04, 0.08
Nearest-neighbor matching	582	−0.01	−0.04, 0.01
Optimal full matching	72,498	0.00	−0.03, 0.01
Inverse probability weighting	87	−0.01	−0.02, 0.01
Target distribution weighting	83	0.00	−0.02, 0.02

Abbreviations: ATT, average treatment effect in the treated population; CI, confidence interval.

^a Results are based on 1,000 bootstrap samples (nonparametric 95% CI: 2.5th and 97.5th percentiles).

Although comparable results were found across the 4 DRS estimators, the IPW and TDW estimators were much faster to compute than nearest-neighbor and optimal full matching. To complete the 1,000 bootstrap iterations, optimal full matching required 20 hours, nearest-neighbor matching 10 minutes, IPW 87 seconds, and TDW 83 seconds (i.e., TDW was more than 870 times faster than optimal full matching).

DISCUSSION

We propose 2 new weighting methods for estimating the ATT using the DRS in nonrandomized studies. Presently, the use of DRS analysis for confounder adjustment requires the implementation of matching methods, which can be inefficient and time-consuming. Results from our simulations demonstrate that the proposed weighting methods yield valid point estimates and outperform matching in terms of mean squared error and computation time. The results from the two illustrative case studies further support these findings.

Matching on the DRS allows researchers to estimate treatment effects in samples in which treated and control individuals are comparable in terms of potential outcomes. Matching methods are often used because they offer several practical advantages (e.g., nonparametric processing of data, approximation of experimental design, reduction of model-dependence (35)). However, implementing matching requires decisions on the matching technique (e.g., nearest-neighbor), sampling method (e.g., sampling with replacement), matching ratio, and caliper size. Many different combinations are possible, and it is not always clear how those different choices may affect the estimates and target estimands. Further, because the numbers of treated and control individuals usually differ in nonrandomized studies, techniques that are based on 1:1 matching necessarily prune out data. This is all the more problematic when a caliper is used to impose a maximal distance between matches, resulting in estimation of the treatment effect within an analytical subsample of the treated group (a subsample including only individuals for whom a match has been found) (36). (These analytical estimands are sometimes referred to as feasible sample ATTs.) Although optimal full matching has been proposed to preserve the complete sample (14, 25, 37, 38), its implementation requires substantial computation time, especially when bootstrapping is used to make inferences as shown in our illustrative case studies. This may particularly become problematic when using large data sets or when combined with methods such as multiple imputation of missing data.

We propose 2 simple weighting methods that may be regarded as alternatives or complements to matching. The first, which we called TDW, may be understood as the smoothed analog of full matching. Full matching involves a discretization of the DRS (i.e., creation of matched pairs or subclasses) before rescaling of the data according to the probability mass function of the discrete variable (i.e., the pair or subclass). In comparison, TDW preserves the continuous nature of the DRS and standardizes the entire distribution of the score to the one of the targeted population. For instance, the probability density function of the DRS can be approximated using a nonparametric kernel estimator. Note that the TDW function is not restricted to the DRS; it could also be applied to the propensity score or other variables. To our best knowledge, no such approach of kernel density weighting has been previously described.

In the econometrics literature, Heckman et al. (39–41) proposed kernel-based estimators in matching analysis, which weight untreated individuals proportionally to their distance from their paired treated individual according to a kernel smoothing bandwidth. In these studies, the kernel method was not used to ascribe weights based on counterfactual probability densities of the estimated propensity score. In 1996, DiNardo et al. (42) proposed a weighting method for estimating counterfactual densities, that is, probability densities that would be observed under their counterfactual. To this end, the authors presented a weighting function including the probability of being in the arm of interest, given a set of covariates (42). (DiNardo further described this method of “propensity score reweighting” for estimating the ATE in a later work (43); it is interesting to notice that this method corresponded, in fact, to IPW.)

A key parameter of TDW is the smoothing bandwidth of the kernel density estimator. Web Appendix 6 provides the R codes for computing TDW, including an argument for the bandwidth choice. The difficulty of selecting the optimal bandwidth for causal inference has been discussed in the econometrics literature by Imbens (44). This bandwidth defines the degree of contribution of neighbors around a particular value of the balancing score. The optimal choice of this value should be explored in further studies, in comparison with other methods of bandwidth selection, including more flexible adaptive or variable bandwidths. TDW should not be used in situations where the DRS is not continuous—for example, if it includes only a few confounders that are all categorical. In these unlikely situations, the direct use of full matching methods (e.g., exact matching) should be preferred. Further, because of relying on the nonparametric modeling of 2 density functions, TDW can be challenged in situations where nonparametric estimation is suboptimal. In general, nonparametric modeling can become sensitive in cases where outliers and misspecification are likely to be present—for instance, when the outcome to be modeled is not bounded or when underlying functional relationships are complex. In additional simulations based on the work of Kang and Schafer (34), we observed that such scenarios led TDW to perform worse than IPW (see Web Appendix 5). This is probably because the estimates of the two density functions required for TDW could be biased, which could in turn introduce bias in the density ratio used as weight. An alternative is to directly estimate the density ratio via a classifier; this relates in fact to our second proposed method, IPW (see Web Appendix 3 for theory).

The second weighting method we propose directly derives from the well-known IPW approach based on the propensity score. Applying IPW to the DRS requires the estimation of a prognostic propensity score—that is, a propensity score including the DRS as the sole variable (i.e., 1-to-1 mapping on the propensity score space). In our simulation study, we showed that both TDW and IPW were considerably faster to compute and more efficient than matching when estimating the ATT. Although this does not imply that weighting is superior to matching, we hope that our approach facilitates comparative effectiveness research in situations where matching is hardly feasible (e.g., a massive data set).

The additional series of simulations with scenarios of positivity violation and important misspecification led to complementary findings (see Web Appendix 5). First, under the positivity violation, DRS weighting was more efficient than propensity score weighting; this aligns with the theory that the use of the DRS relaxes the need for the positivity assumption. Second, under misspecification of the outcome model, balancing (via weighting) the DRS reduced bias in comparison with direct substitution with predicted outcome values (i.e., G-computation). This finding aligns with the missing-data literature, which recommends methods that rebalance the distribution of the imputed values by, for instance, borrowing an observed matched value (e.g., predictive mean matching), rather than directly imputing the predicted values returned by a parametric model (e.g., see Morris et al. (45)). In a way, DRS methods incorporate a nonparametric balancing step to mitigate bias due to misspecification of purely parametric methods. In this regard, the DRS methodology can be regarded as a semiparametric version of the use of the parametric G-formula. Third, under misspecification of both the outcome model and the propensity score model, the doubly robust estimator for the ATT proposed by Mercatanti and Li (46) was slightly less efficient than IPW based on the DRS. While the theory of Waernbaum (47) suggests that a misspecified DRS can still possibly remove confounding bias after matching, we emphasize that the generalizability of our finding is limited to our specific scenarios (see Maldonado and Greenland (48) for critical interpretation of simulation studies). It is important to underscore that further work is needed to assess how well our proposed methods generalize to settings not considered here.

Our study should be considered under the conditions of its limitations. Our weighting methods may depend on the different parameters of the density estimator (e.g., smoothing bandwidth, kernel, etc.) for TDW, and on the prognostic propensity score for IPW. We did not propose DRS weighting estimators for the ATE, since it would require weighting functions based on the joint probability distribution of the DRS and relevant effect modifiers. (See Hansen (5), who shows that conditioning jointly on the DRS and effect modifiers is necessary to estimate the ATE.) We did not compare our methods with propensity score methods. This comparison has been explored elsewhere (9, 11, 49, 50) and is outside the scope of our study. In this article, we aimed to extend the range of methods suitable for the DRS. We did not study the convergence rate of our estimators, nor did we provide estimators for their standard errors (which should include the uncertainty relating to all steps: from DRS estimation, prognostic propensity score estimation, or kernel density estimation to treatment effect estimation in the weighted sample). In our illustrative case studies, we show how these standard errors could be computed via bootstrapping. Our proposed methods were applied and evaluated only in the case of time-fixed settings. Yet, since the DRS is a semiparametric version of the parametric G-formula, extension to a longitudinal setting can be foreseen as long as the estimand is defined on 1 exposure group (e.g., ATT). Finally, further studies are needed to compare the performance of our proposed weighting methods with other alternatives to matching, such as fine stratification techniques (see Desai et al. (51)).

In conclusion, we propose DRS weighting methods for estimating causal effects in nonrandomized studies of treatments. These methods may be considered as alternatives or complementary approaches to DRS matching and propensity score methods. ATT estimates obtained by TDW and IPW are relatively close to those obtained by matching methods, and TDW and IPW are considerably faster than matching in terms of computational time. Future studies are needed to inform situations in which TDW and IPW methods may be challenged (e.g., multiple categorical confounders for TDW, extreme weights for IPW).