Perspective: Reference-potential Methods for the Study of Thermodynamic Properties in Chemical Processes: Theory, Applications, and Pitfalls

Abstract

In silico investigations of enzymatic reactions and chemical reactions in condensed phases often suffer from formidable computational costs due to a large number of degrees of freedom and enormous important volume in phase space. Usually, accuracy must be compromised to trade for efficiency by lowering the reliability of the Hamiltonians employed or reducing the sampling time. Reference-potential methods (RPM) offer an alternative approach to reaching high accuracy of simulation without much loss of efficiency. In this perspective, we summarize the idea of RPM and showcase some recent applications. Most importantly, the pitfalls of these methods are also discussed, and remedies to these pitfalls are presented.

Graphical Abstract

Computer simulation is widely used nowadays for the study of chemical process and enzymatic reactions. However, applications of computer simulation still inevitably face three fundamental challenges, as have been summarized in a recent review by Hansen and van Gunsteren, namely the insufficient/inefficient sampling of the phase space, limited accuracy of the Hamiltonian describing the interaction potential, and the statistical reliability of the methods for data post-processing.¹ Unfortunately, the first two difficulties require opposite solutions, thus posing a great dilemma. If one wants to reach a longer time scale (so interesting physical processes may take place), some further approximations to the Hamiltonian in use will be required. On the other hand, in order to achieve a higher accuracy, one needs to employ a higher-level Hamiltonian, which will further limit the simulation time scale. This dilemma becomes even irreconcilable when studying chemical reactions or enzymatic reactions, in which a hybrid quantum mechanical molecular mechanical (QM/MM) description (QM for atoms involved directly in bond forming/breaking and MM for solvent and enzyme atoms) is required. In order to fully converge the calculations of thermodynamic properties along a reaction, tens of ns of simulation time must be performed, while the time step for all-atom QM/MM molecular dynamics (MD) simulation is typically 0.5 or 1.0 fs. Each step of QM/MM MD propagation may take hundreds or thousands of seconds on a mainstream computer. Therefore, a single QM/MM MD simulation may take years or even tens of years of wall-clock time on a single computer. Although the simulation can be massively parallel on modern supercomputers, it is still too expensive for routine use. Therefore, it is essential to develop a more efficient methodology for sampling a large number of configurations. For the trajectory analysis, on the other hand, the calculations of statistical averages require independent and identically distributed (i.i.d.) samples. In order to avoid dependency among the sampled configurations, the sampling time interval should be no less than the correlation time of the physical properties in question. For simulations in condensed phase, the correlation time is on the order of ps. With a time step around 1 fs, only one configuration in every 1000 or more propagation steps can be used for further analysis, with the remaining 99.9% of the configurations discarded. Such a need to sample a large number of configurations of a condensed-phase system and then use only a small percentage of these configurations for subsequent analysis opens up the opportunity for more efficient sampling/analysis methodologies.

To this end, in the 1990s Gao and Warshel and his coworkers independently proposed the reference-potential method (RPM) for the calculations of hydration free energy and the free energy profiles for chemical reactions.^2-5 Basically, the RPM is an importance sampling method, which exploits the fact that the expectation

$$\mathrm{E}[f(\mathbf{X})]=\int f(x)p(x)\mathrm{d}x\approx \frac{1}{N}\sum _{n=1}^{N}f(x_n)$$

under the distribution function $p(x)$, which is unavailable or difficult to obtain, can be efficiently calculated via

$$\mathrm{E}[f(\mathbf{X})]=\int \frac{f(x)p(x)}{q(x)}q(x)\mathrm{d}x\approx \frac{1}{N}\sum _{n=1}^N\frac{f(x_n)p(x_n)}{q(x_n)}$$

with samples drawn from an easy-to-get distribution $q(x)$, if the surrogate distribution $q(x)$ is very close to the target distribution $p(x)$. In the RPM, an initial simulation is carried out utilizing some inexpensive (surrogate) potential energy functions, such as empirical valence bond (EVB)⁶ and AM1,⁷ which is expected to be close to the target potential-of-interest, usually the ab initio (ai) Hamiltonians. A perturbation rectification in the spirit of the second equation above is performed in a subsequent step to obtain the statistical properties at the level of the potential-of-interest. Inspired by these pioneering works, the RPM have emerged as powerful tools and have been applied in many studies, especially for the calculations of free energy landscapes. The pioneering work of Rod and Ryde in utilizing the RPM for the computation of free energy barriers in a methyl transfer reaction catalyzed by catechol O-methyltransferase is discussed. Their innovative approach of combining molecular mechanical calculations with density functional theory corrections has provided valuable insights into the underlying thermodynamics of this biologically important process.⁸ Beierlein et al. have made significant contributions to the field by applying the RPM to the calculation of free energy of protein-ligand binding,⁹ and two years later, Polyak et al. introduced a RPM called dual-Hamiltonian free energy perturbation (DH-FEP) for calculating free energy profiles of chemical reactions.¹⁰ König et al. have made notable progress by incorporating the Bennett acceptance ratio method into the RPM simulations, leading to the development of the non-Boltzmann Bennett acceptance ratio (NBB) method. This refined approach has demonstrated improved accuracy in free energy calculations, paving the way for more precise results in future studies. Dybeck et al. compared the performance of NBB and Multistate Bennett Acceptance Ratio (MBAR) in solvation free energy calculations and showed that the variances are marginally smaller for MBAR.¹¹ Jia et al. proved the superiority of the BAR+TP approach for RPM-based free energy calculations. Their comprehensive analysis has established the optimal path for accurate calculations.¹² Hudson et al. incorporated energy reweighting into the chain-of-replicas method and the non-equilibrium simulation method for the computations of free energy profiles.^13,14 Their pioneering work has opened up new avenues for the applications of RPM. Piccini and Parrinello combined the RPM with metadynamics for the first time to study the free energy profile of a S_N2 reaction.¹⁵ Giese and York integrated force matching into the molecular mechanics potential tuning process to enhance the similarity between MM and QM/MM potentials, resulting in a higher convergence rate of RPM.¹⁶ Rizzi et al. have advanced the field by integrating the RPM with machine learning, employing normalizing flow to assist in the correction from reference potential to target potential. Their innovative approach has the potential to revolutionize free energy calculations, offering a promising direction for future research in this area.¹⁷ Giese et al. have extended the idea of RPM by proposing the generalized weighted thermodynamic perturbation (gwTP) method.¹⁸ This novel approach, utilizing multiple reference potentials in umbrella sampling and piecing together free energy profile segments, can be used seamlessly with redundant neural network potentials from active learning and it has the potential to significantly advance the accuracy and efficiency of free energy calculations.^19,20

In this perspective, we will first briefly introduce the statistical basis of the RPM, and then showcase some applications of the RPM conducted in our own groups. Finally, we will discuss potential future directions in RPM-based free energy simulations.

Theory

Due to the large gap in spatial-temporal scales between experimental physical/chemical processes and all-atom simulations, enhanced sampling on multiple thermodynamic states is now routinely employed to accelerate the exploration in phase space. For the study of chemical reactions, the most widely used enhanced sampling method is the umbrella sampling (US) method, ²¹ in which a direct propagation from reactant to product is replaced by stratified windows aligned along a pre-assumed low-dimensional reaction pathway. For the simulation in each window, a (harmonic) restraining potential is applied to keep the system in the vicinity of a prescribed phase space and prevent it from falling back to the reactant or product states, which can be written as

$$U_k(\mathbf{r})=U_0(\mathbf{r})+{\Delta U}_k(\xi (\mathbf{r}))$$ (1)

for the kth thermodynamic state. $U_0$ and ${\Delta U}_k$ are the unbiased and the restraining potential energy functions, and $\xi$ is the collective variable (CV) describing the reaction process. In normal US calculations, $U_0$ is the Hamiltonian-of-interest. However, in the RPM, it is the reference Hamiltonian. In each sampling window, the degrees of freedom (DoF) orthogonal to $\xi$ need be adequately sampled before the convergence can be reached. However, hidden barriers may slow down the exploration of the orthogonal DoF, thus long-time simulations are sometimes desirable.

After running $K$ window simulations using a series of biased potential $U_k(\mathbf{r})$, each simulation contributes $N_k$ samples. All the samples are assembled together for the calculations of the expectation of any thermodynamics properties under the unbiased Hamiltonian $U_0$ via

$${\langle \widehat{O}\rangle }_0=\frac{\sum _{n=1}^N{\omega }_0({\mathbf{r}}_n)\widehat{O}({\mathbf{r}}_n)}{\sum _{n=1}^N{\omega }_0({\mathbf{r}}_n)},$$ (2)

where $N={\sum }_{k=1}^K{N}_k$ is the total number of samples, and ${\omega }_0({\mathbf{r}}_n)$ is the unnormalized weight of sample $n$ under the unbiased Hamiltonian $U_0$. Using the MBAR,²² the weight can be written as

$${\omega }_0(\mathbf{r})=\frac{e^{-\beta U_0(\mathbf{r})}}{\sum _{k=1}^K{N}_k{e}^{-\beta [U_k(\mathbf{r})-f_k]}},$$ (3)

where

$$f_k=-{\beta }^{-1}\text{ln}\sum _{n=1}^N\frac{e^{-\beta U_k({\mathbf{r}}_n)}}{\sum _{k^{\prime }=1}^K{N}_{k^{\prime }}{e}^{-\beta (U_{k^{\prime }}({\mathbf{r}}_n)-f_{k^{\prime }})}},\forall k=1,\dots ,K$$ (4)

is the estimated free energy of state $k$ and must be solved iteratively. The uncertainties can be estimated using the asymptotic covariance, bootstrapping or the block average.^22,23 With the estimated free energy of the unbiased state

$$f_0=-{\beta }^{-1}\text{ln}\sum _{n=1}^N\frac{e^{-\beta U_0({\mathbf{r}}_n)}}{\sum _{k=1}^K{N}_k{e}^{-\beta (U_k({\mathbf{r}}_n)-f_k)}},$$ (5)

the normalized weight under the unbiased Hamiltonian can be written as

$${\widehat{\omega }}_0(\mathbf{r})=\frac{e^{-\beta (U_0(\mathbf{r})-f_0)}}{\sum _{k=1}^K{N}_k{e}^{-\beta (U_k(\mathbf{r})-f_k)}}.$$ (6)

It can be seen from the formulation above that in US simulations we only carry out biased simulations, from which unbiased properties can be obtained. This is an extrapolation process in the Hamiltonian space, although this extrapolation is usually mild, and the calculated unbiased properties are reliable with small magnitude of uncertainties. Similarly, given sufficient samples, we can apply extrapolation to any other states, for instance to the target Hamiltonian in the RPM. The normalized weight under the target Hamiltonian $U_t$ is now written as

$$\begin{gathered} {\widehat{\omega }}_t(\mathbf{r})=\frac{e^{-\beta [U_t(\mathbf{r})-f_t]}}{\sum _{k=1}^K{N}_k{e}^{-\beta [U_k(\mathbf{r})-f_k]}} \\ =\frac{e^{-\beta \Delta U_t(\mathbf{r})}}{\sum _{k=1}^K{N}_k{e}^{-\beta [\Delta U_k(\xi (\mathbf{r}))-(f_k-f_t)]}}, \end{gathered}$$ (7)

with

$$e^{-\beta f_t}=\sum _{n=1}^N\frac{e^{-\beta [\Delta U_t({\mathbf{r}}_n)]}}{\sum _{k=1}^K{N}_k{e}^{-\beta [\Delta U_k(\xi ({\mathbf{r}}_n))-f_k]}}$$ (8)

being the normalization factor. The “agressiveness” of the extrapolation depends on the distribution width of the difference ${\Delta U}_t(\mathbf{r})$ between the target Hamiltonian $U_t$ and the reference Hamiltonian $U_0$. The second line of Eq. 7 indicates that it can be considered as a weighted free energy perturbation. Thermodynamic properties under the target Hamiltonian can thus be calculated via

$${\langle \widehat{O}\rangle }_t=\sum _{n=1}^N{\widehat{\omega }}_t({\mathbf{r}}_n)\widehat{O}({\mathbf{r}}_n).$$ (9)

The operator $\widehat{O}$ can, for instance, measure the bond length, the charge distribution, etc. When it is the indicator function

$$\delta ({\xi }_m-\xi ({\mathbf{r}}_n))=\{\begin{array}{cc}1,\hfill & \text{if}-\delta \xi ∕2<{\xi }_m-\xi ({\mathbf{r}}_n)\le \delta \xi ∕2\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}},$$ (10)

its ensemble average yields potential of mean force (PMF), up to an additive constant,

$$F_t({\xi }_m)=-{\beta }^{-1}\text{ln}\sum _{n=1}^N{\widehat{\omega }}_t({\mathbf{r}}_n)\delta ({\xi }_m-\xi ({\mathbf{r}}_n))$$ (11)

Applications

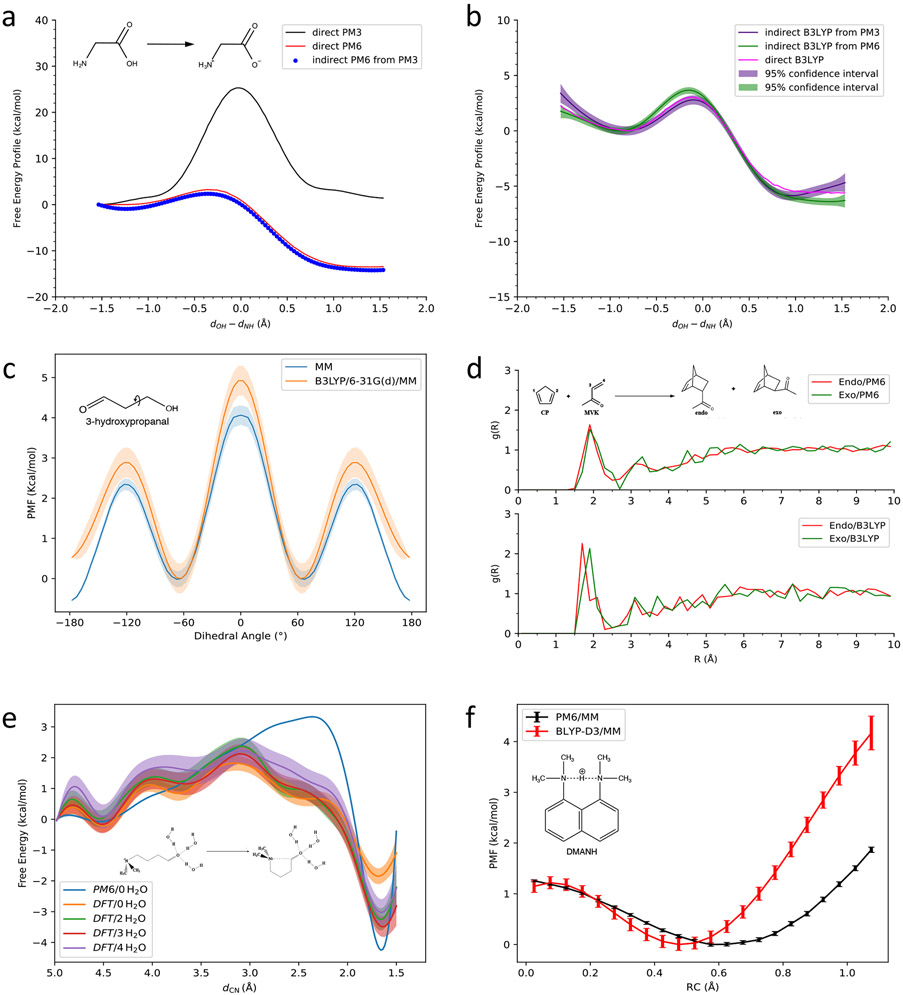
Proton transfer between titratable groups is ubiquitous in biomolecules. As a simplest model system, tautomerization reaction within a glycine molecule in aqueous solution was studied by us using the RPM.²⁴ The semiempirical methods PM3 and PM6 were chosen as the reference potential, and the target potential was the density functional theory with the B3LYP functional and 6-31G(d) basis set. The free energy profiles show significant Hamiltonian dependency. As shown in Fig. 1.a, under the PM3 level, the free energy profile is qualitatively wrong, where the reaction free energy is nearly zero. PM6 yields qualitatively correct free energy profile. However, it overestimates the reaction free energy as compared to the result under the DFT level of theory. As shown in Fig. 1.b, after the corrections from the PM3 and PM6 levels to the DFT level, the free energy profiles show much improved agreement with the direct DFT calculation, while the computational cost of this indirect approach is only 3.4% of the direct approach.

Figure 1:

Some applications of RPM. The PMF for proton transfer within glycine molecule in water solution (a) at semi-empirical levels, and (b) the ones at the DFT level after the correction using RPM. Reproduced from Ref. 24. Copyright [2018] American Chemical Society. (c) The PMF of the dihedral rotation in 3-hydroxypropanal at the MM level and the extrapolated B3LYP/6-31G(d)/MM level using RPM. (d) Solvent radial distribution near the oxygen atom in methyl vinyl ketone (MVK) averaged over the transition-state ensembles under PM6 Hamiltonian (top) and B3LYP Hamiltonian (bottom) for the endo pathway (red) and the exo pathway (green). Reproduced from Ref. 25. Copyright [2019] American Chemical Society. (e) Free energy profiles at the PM6 level without solvent molecules in the QM region and at the DFT/MM levels with different numbers of water molecules in the QM region. Reproduced from Ref. 26. Copyright [2021] American Chemical Society. (f) The PMF of the proton transfer in the protonated 1,8-bis(dimethylamino)naphthalene molecule under different levels of theory. Reproduced from Ref. 27. Copyright [2021] American Chemical Society.

With a continuous development of force fields, classical molecular modeling using force fields is becoming more and more accurate.^28-35 However, there is still room for further improvement. Currently, the quality of force fields is improved via either introducing more atomic types or the introduction of extra terms in the functional forms as in the polarizable force fields.^32,36,37 Both approaches require computation-intensive benchmarking. As an alternative solution, the RPM can be applied to improve the accuracy of classical force field based simulations. For 3-hydroxypropanal, for instance, the free energy profile for the dihedral rotation along the C─C bond (shown in Fig. 1.c) at the molecular mechanics (MM) level of theory was calculated via the MBAR analysis over the umbrella sampling trajectories, and it was extrapolated using RPM to the QM/MM level with the solute molecule in the QM region and the remaining atoms in the MM region. Figure 1.c shows the free energy profiles at the MM and B3LYP/6-31G(d)/MM levels, in which the shaded areas are the 95% confidence region. The profiles show different preference for the planar (dihedral angle ≈ 180°) and nonplanar (dihedral angle ≈ ±60°) structures at the MM and QM/MM levels of theory.

The microscopic explanation to the endo/exo stereoselectivity of the Diels–Alder (DA) reaction between cyclopentadiene and methyl vinyl ketone (MVK) in the aqueous solution has posed a challenge to the computational chemists.^38-43 Quantum mechanical calculations utilizing a continuum model for solvent often fail to accurately predict the reaction barrier. Therefore, sampling of the reaction at a high level of theory in explicit solvent model is needed. With the RPM, the US was performed at the PM6/MM level, and later an extrapolation to the B3LYP/MM level was carried out.²⁵ The statistical analysis at the B3LYP/MM level shows that the stereoselectivity mainly comes from the solvation effect. At their respective transition states, the first peak of the solvent distribution around the oxygen atom in MVK is slightly closer for the endo pathway than that for the exo pathway (shown in Fig. 1.d). Although one order of magnitude smaller than the experimental measurement, the predicted endo/exo ratio is qualitatively correct. A further improvement will require a more accurate QM/MM Hamiltonian as the target potential, longer simulations, and a more rational definition of the collective variable.

The accuracy of QM/MM calculations depends on not only the Hamiltonian of the QM region, but also the partitioning scheme of the QM and MM regions. With a small QM region, one achieves higher computational efficiency often at a sacrifice of the computational accuracy.^44-48 For most cases, the QM region is chosen with chemical intuition, and the convergence of the calculated properties with respect to the QM size is rarely checked in actual application projects due to the steep computational cost. Moreover, QM/MM calculations may face technical difficulties when the reactive region is varying over time. For instance, some solvent molecules may directly participate in the reaction beyond serving as a dielectric medium, and the exchange of water molecules between the reactive QM region and the surrounding MM region may occur on a time scale similar to the reaction time. In addition to the existing restrained QM/MM methods^49-51 and adaptive QM/MM methods,^52-59 RPM has been suggested as an alternative solution. The nucleophilic addition inside the 4-(dimethylamino)butanal molecule is a typical example. In this reaction, the solvent molecules stabilize the reaction product by accepting excess electrons from the aldehyde group. In the actual condensed phase system, the solvent molecules in different solvation layers surrounding the aldehyde group may exchange, resulting in a large scale of permutation. However, partitioning of the QM and MM regions with some solvent molecules included in the QM region breaks this symmetry, and once the exchange occurs, it may result in discontinuity in the QM region. Basically speaking, different QM/MM partition schemes correspond to different Hamiltonians. In order to avoid this technical difficulty, the lowest level of the partitioning scheme, where the QM region contains only the 4-(dimethylamino)butanal molecule, was utilized in our work as the reference potential, while the target potential encompasses several nearest solvent molecules in the QM region.²⁶ As shown in Fig. 1.e, by extrapolating from a semiempirical Hamiltonian to a DFT level of theory and from the minimal QM region to larger QM regions with different number of solvent molecules, the accuracy could be improved and the convergence with respect to the QM size can be examined with remarkably increased efficiency.

The RPM can be applied not only to the classical QM/MM trajectories but also to the path integral QM/MM molecular dynamics simulations for the studies of quantum delocalization of light particles such as protons. As a typical example, the protonated 1,8-bis(dimethylamino)naphthalene (DMANH) molecule has a short hydrogen donor-acceptor distance.⁶⁰ Therefore, the quantum tunneling effect for the proton transfer between the two nitrogen atoms can be nonnegligible. Using the RPM, the simulation time was extended by us to a scale of nanoseconds at the PM6/MM level with 16 beads for each QM atom, and then a PM6/MM to BLYP-D3/6-31G(d)/MM extrapolation was applied. Our results showed that the lowest-free energy structure at the PM6/MM level prefers a relatively more localized proton, while at the DFT level of theory a more diffused proton is preferred (See Fig. 1.f). A 545-fold reduction in the total CPU time was achieved while reaching the accuracy comparable to the DFT level of theory.²⁷

Remedies to Pitfalls

It can be seen from Eq. 7 that the RPM is fundamentally a free energy perturbation (FEP) method with energy difference appearing in the exponent in the numerator, only that each configuration has a unequal weight. Therefore, it naturally inherits the numerical difficulty of FEP, i.e. the width of the distribution of $U_t(\mathbf{r})-U_0(\mathbf{r})$ determines the convergence rate with respect to the sample size.^61-66 Any methods that can shrink the distribution width of $U_t(\mathbf{r})-U_0(\mathbf{r})$ can improve the convergence. Quantitative criteria to guide the convergence are long desired. So far, many criteria have been promoted, such as the variance of energy difference $\sigma$,^67,68 bias measure Π,^63,69 and overlap matrix.⁷⁰ To characterize the reliability of the TP calculation, the “reweighting entropy”⁷¹ is introduced, which is defined as

$${𝒮}_t({\xi }_m)=-\frac{\sum _{n=1}^N\delta ({\xi }_m-\xi ({\mathbf{r}}_n)){\widehat{\omega }}_t^m({\mathbf{r}}_n)\text{ln}{\widehat{\omega }}_t^m({\mathbf{r}}_n)}{\text{ln}\sum _{n=1}^N\delta ({\xi }_m-\xi ({\mathbf{r}}_n))},$$ (12)

for the samples collected in the mth bin around ${\xi }_m$, and

$${\widehat{\omega }}_t^m({\mathbf{r}}_n)=\frac{{\widehat{\omega }}_t({\mathbf{r}}_n)}{\sum _{n=1}^N\delta ({\xi }_m-\xi ({\mathbf{r}}_n)){\widehat{\omega }}_t({\mathbf{r}}_n)},$$ (13)

which are normalized in the mth bin. It measures the flatness of the distribution of weight ${\widehat{\omega }}_t({\mathbf{r}}_n)$. An even distribution of ${\widehat{\omega }}_t$ leads to ${𝒮}_t$ close to 1, while a sharply distributed ${\widehat{\omega }}_t$ (only a very small number of samples have a non-negligible weight) makes ${𝒮}_t$ close to 0.

Another metric is the smoothness of the density of states (DoS). Rewriting the definition of the potential of mean force under the target Hamiltonian as an integral in the space of $\Delta U(\mathbf{r})=U_t(\mathbf{r})-U_0(\mathbf{r})$

$$\begin{gathered} F_t({\xi }_m)=-{\beta }^{-1}\text{ln}\sum _{n=1}^N{\widehat{\omega }}_t({\mathbf{r}}_n)\delta ({\xi }_m-\xi ({\mathbf{r}}_n)) \\ =-{\beta }^{-1}\text{ln}{\int }_{-\infty }^{\infty }{\Omega (\Delta U)}_{{\xi }_m}\text{exp}(-\beta \Delta U)\mathrm{d}\Delta U+C, \end{gathered}$$ (14)

where

$${\Omega (\Delta U)}_{{\xi }_m}=\sum _{n=1}^N\frac{\delta (\Delta U-{\Delta U}_t({\mathbf{r}}_n))}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-{\beta \Delta U}_k(\xi ({\mathbf{r}}_n))]}\delta ({\xi }_m-\xi ({\mathbf{r}}_n))$$ (15)

is the DOS of $\Delta U$ in the mth bin around ${\xi }_m$,

$$\delta (\Delta U-{\Delta U}_t({\mathbf{r}}_n))=\{\begin{array}{cc}1,\hfill & \text{if}-\delta \Delta U∕2<\Delta U-{\Delta U}_t({\mathbf{r}}_n)\le \delta \Delta U∕2\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}\phantom{\}}$$ (16)

is again the indicator function, and C is an irrelevant constant.⁷² With a continuous energy function, the DOS should be continuous intrinsically. However, with finite samples, the estimated DOS can be noisy, especially in the rarely sampled region. This sampled noise in the low energy region may deteriorate the calculated ensemble averages. With a large number of samples, ${\Omega (\Delta U)}_{{\xi }_m}$ can be fitted to a Gaussian with the mean being

$${\overline{\Delta U}}_{{\xi }_m}=\frac{\sum _{n=1}^N\Delta U({\mathbf{r}}_n)\frac{\delta ({\xi }_m-\xi ({\mathbf{r}}_n))}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta {\Delta U}_k({\mathbf{r}}_n)]}}{\sum _{n=1}^N\frac{\delta ({\xi }_m-\xi ({\mathbf{r}}_n))}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta {\Delta U}_k({\mathbf{r}}_n)]}}$$ (17)

and the variance

$${\sigma }_{{\xi }_m}^2=\frac{\sum _{n=1}^N{\left(\Delta U({\mathbf{r}}_n)-{\overline{\Delta U}}_{{\xi }_m}\right)}^2\frac{\delta ({\xi }_m-\xi ({\mathbf{r}}_n))}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta {\Delta U}_k({\mathbf{r}}_n)]}}{\sum _{n=1}^N\frac{\delta ({\xi }_m-\xi ({\mathbf{r}}_n))}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta {\Delta U}_k({\mathbf{r}}_n)]}}.$$ (18)

With this Gaussian-shaped DoS, the probability of falling into the small energy bin with a width of $\delta \Delta U$ near $\Delta U$ is

$${\rho }_G\left(\left[\Delta U\pm \frac{1}{2}\delta \Delta U\right]\right)=\frac{1}{\sqrt{2\pi }{\sigma }_{{\xi }_m}}{\int }_{\Delta U-\frac{1}{2}\delta \Delta U}^{\Delta U+\frac{1}{2}\delta \Delta U}\text{exp}\left[-\frac{{\left(\Delta U-{\overline{\Delta U}}_{{\xi }_m}\right)}^2}{{2\sigma }_{{\xi }_m}^2}\right]\mathrm{d}\Delta U.$$ (19)

While, the sampled probability is

$${\rho }_S\left(\left[\Delta U\pm \frac{1}{2}\delta \Delta U\right]\right)=\frac{\sum _{n=1}^N\frac{\delta ({\xi }_m-\xi ({\mathbf{r}}_n))\delta (\Delta U-\Delta U({\mathbf{r}}_n))}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta {\Delta U}_k({\mathbf{r}}_n)]}}{\sum _{n=1}^N\frac{\delta ({\xi }_m-\xi ({\mathbf{r}}_n))}{\sum _{k=1}^K{N}_k\text{exp}[\beta f_k-\beta {\Delta U}_k({\mathbf{r}}_n)]}}.$$ (20)

By rescaling the sample weights via

$${\widehat{\omega }}_t^{\prime }({\mathbf{r}}_n)={\widehat{\omega }}_t({\mathbf{r}}_n)\cdot \frac{{\rho }_G\left(\left[\Delta U\pm \frac{1}{2}\delta \Delta U\right]\right)}{{\rho }_S\left(\left[\Delta U\pm \frac{1}{2}\delta \Delta U\right]\right)},$$ (21)

the potential of mean force becomes

$$F_t({\xi }_m)=-{\beta }^{-1}\text{ln}\sum _{n=1}^N{\widehat{\omega }}_t^{\prime }({\mathbf{r}}_n)\delta ({\xi }_m-\xi ({\mathbf{r}}_n)).$$ (22)

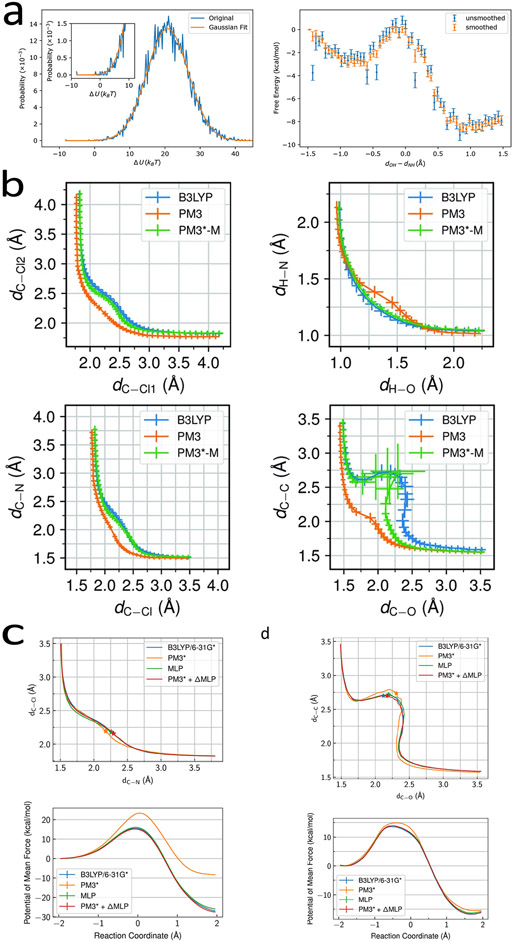
The results show that with this Gaussian smoothing over the DoS, the potential of mean force becomes much less noisy as shown in Fig. 2.a.

Figure 2:

a. Density-of-states in a certain CV bin and the free energy profiles for the glycine proton transfer. Reproduced from Ref. 72. Copyright [2020] American Chemical Society. b. Reaction pathways for the identity S_N2 reaction, Menshutkin reaction, glycine intramolecular proton transfer reaction in explicit TIP3P water molecule, and the chorismate to prephenate reaction in chorismate mutase. Reproduced from Ref. 73. Copyright [2019] the Royal Society of Chemistry. c. Sampled pathway and free energy profiles for the Menshutkin reaction and the chorismate mutase reaction. Reproduced from Ref. 74. Copyright [2021] American Chemical Society.

Most semiempirical QM/MM Hamiltonians show limited similarity to ab initio QM/MM Hamiltonians, therefore the important region in the phase space on a semiempirical QM/MM (free) energy surface does not necessarily cover the important region of ab initio QM/MM ones. It may lead to aggressive extrapolation if the RPM is employed, and a slow convergence may deteriorate the calculation results. Even when the free energy properties can be restored by the correction from the reference potential to the target potential, the recovery of the geometric properties, e.g. the reaction pathway in a two-dimensional or ever higher-dimensional space, can be much more difficult. By simply altering the importance of each sample, one does not gain access to the unsampled important configurations of the target Hamiltonian. In order to strength the similarity between the reference and the target Hamiltonians, calibration of semi-empirical Hamiltonians via force matching is one of the promising approaches. By constraining the parameters within ±5% of their original values, the parameters of the standard PM3 method were optimized using the force matching method against the B3LYP/6-31G(d) level of theory for a series of reactions in a recent work.⁷³ As shown in Fig. 2.b, the reparametrized PM3 method can produce a much improved reaction pathway projected in a 2D CV space for the chorismate mutase reaction. After a correction from this newly reparametrized PM3 Hamiltonian to the DFT Hamiltonian, the free energy profile was accurately reproduced. Although such a reparametrization of the semi-empirical Hamiltonian against high level QM methods for molecules of interest can improve the convergence rate of RPM, the magnitude of improvement is usually limited due to the relatively small number of parameters available for tuning. Artificial neural network (ANN) granted us a capability to further correct the semi-empirical Hamiltonians towards higher-level Hamiltonians. In a recent study, we trained a delta machine learning potential (ΔMLP) to reproduce the differences between the ai-QM/MM and semiempirical (se) QM/MM energies and forces. With this machine learning correction to the semi-empirical Hamiltonian, the ai-QM/MM energy and forces could be well reproduced with errors less than 1.0 kcal · mol⁻¹ and 1.0 kcal · mol⁻¹ · Å⁻¹, respectively, on average for representative configurations along the reaction pathway for Menshutkin and chorismate mutase reactions.⁷⁴ Thus, the free energy profiles and the reaction pathways show much improved agreement with the ground truth (at the DFT level of theory) as shown in Fig. 2.d. Such machine-learning assisted potential refinement can be greatly helpful for enhancing the applicability of RPM. It is important to note that the final results, such as the free energy barrier and reaction free energy, are highly dependent on the choice of target Hamiltonian, which we have intentionally set as density functional theory with a small basis set for the sake of convenience in presentation. However, a higher level of theory may be desirable for comparison with experimental measurements. For example, Brickel and Meuwly reported a barrier of 12.4 kcal/mol for the chorismate mutase reaction at the MP2/6-311++G(2d,2p) level of theory,⁷⁵ which closely agrees with our study’s result of 12.1 kcal/mol. In contrast, Turan et al. obtained a barrier of 18.0 kcal/mol for the Menshutkin reaction at the same MP2/6-311++G(2d,2p) level of theory,⁷⁶ which is 2.7 kcal/mol higher than our DFT level of theory result. The choice of a suitable target Hamiltonian or improving the density functional’s quality is beyond the scope of this perspective. Therefore, readers should exercise caution in selecting the target Hamiltonian, as the accuracy of the RPM method cannot exceed that of the chosen target Hamiltonian.

Parallel to the idea of improving the reference potential, the convergence of RPM can be facilitated by optimizing the mapping from the configurations from the reference potential sampling to those from the target potential utilizing elegant mathematical transformations, such as targeted free energy perturbation (TFEP)^77-79 and normalizing flow.¹⁷ The basic idea of TFEP is to find an optimal auxiliary state A′ (B′), which can be mapped from the sampled state A (B) via an invertible transformation $ℳ({ℳ}^{-1})$ and has more significant overlap with the target state B (A) than A (B) does. Therefore, the FEP from the auxiliary state to the target state converges faster than the original FEP from the sampled state to the target state.⁷⁷ However, for a complex system, the optimal $ℳ$ is difficult to find. Wirnsberger et al. proposed to use normalizing flow for the mapping and optimize the parameters⁷⁹ by minimizing the Kullback-Leibler (KL) divergence ($D_{KL}[P_{A^{\prime }}\mid \mid P_B]$ and/or $D_{KL}[P_{B^{\prime }}\mid \mid P_A]$). Rizzi exploited the fact that this idea can also be used for the calculation of free energy surfaces, and they applied this method to the analysis of the samples from umbrella sampling using

$$F_t({\xi }_m)=-{\beta }^{-1}\text{ln}\sum _{n=1}^N\frac{e^{-{\beta \Delta U}_t^{\prime }({\mathbf{r}}_n)}}{\sum _{k=1}^K{N}_k{e}^{-\beta [{\Delta U}_k(\xi ({\mathbf{r}}_n))-f_k]}}\delta ({\xi }_m-\xi ({\mathbf{r}}_n)),$$ (23)

where ${\Delta U}_t^{\prime }$ is the energy difference between the auxiliary state mapped from the target Hamiltonian and the reference Hamiltonian.¹⁷ Here, the equation has been reformulated instead of the weighted FEP form in their original paper. They showed that this configuration mapping using normalization flow can accelerate the convergence of RPM for an asymmetric S_N2 reaction.

Outlook

In this Perspective, we have reviewed the theory and applications of reference-potential methods, while also highlighting their limitations. Despite progress in improving the robustness of these methods, it is crucial for practitioners to be aware of potential sources of error and regularly assess convergence of results. Looking forward, we anticipate that further advancements in quantum chemistry and machine learning, such as the emergence of new semi-empirical quantum mechanical methods,^80,81 transfer learned and $\Delta$-machine learned potential energy functions,^82-84 and optimal transport theory⁸⁵ etc, will significantly improve the applicability of reference-potential methods in the near future. Moreover, we believe that these methods can help bridge the gap between computational studies and experimental investigations, and thereby strengthen the use of computational methods for understanding and interpreting experiments.

Biographies

Jia-Ning Wang is a Ph.D. student in Dr. Ye Mei’s group at East China Normal University. He received his B. S. degree from the National Base for Fundamental Sciences (Mathematics & Physics) at Inner Mongolia University, China, in 2013. His research interests lie in multiscale simulations and free energy methods

Yuanfei Xue is now pursuing her Ph.D. in Dr. Ye Mei’s group at East China Normal University. She obtained her master’s degree in chemistry from the University of Manchester, UK, in 2018. Her research interest spans from accelerated simulation methods to rational enzymatic evolution.

Dr. Pengfei Li holds a Bachelor of Science degree in Physics from Shandong Normal University, which he obtained in 2014. He completed his Ph.D. in Physics at East China Normal University in 2019, where his research focused on the development of multiscale free energy simulations for chemical reactions, solvation of small molecules, and protein-ligand binding free energy prediction. Following the completion of his Ph.D., Dr. Li joined Silicon Therapeutics LLC as a scientist, where he played a pivotal role in establishing a computational physics platform for in-silico design and optimization of small molecule drugs. He then moved on to TandemAI LLC in 2022 as a principal scientist, where he contributed to the development of computational platforms for predicting protein-ligand binding affinity. Currently, Dr. Li serves as a senior application scientist in the field of computational chemistry at Single Particle LLC, showcasing his expertise and contributions to the field.

Dr. Xiaoliang Pan received his Ph.D. in Physical Chemistry from Jilin University in 2012. He currently works as a postdoctoral researcher at the University of Oklahoma. Before that he also did research at the University of Arizona. His scientific interests are in simulating enzyme reactions and developing computational tools and algorithms to accelerate QM/MM free energy calculations. His most recent research includes combining physical-based models and machine learning techniques to model biomolecular systems.

Dr. Meiting Wang received her Ph.D. in computational biophysics from East China Normal University in 2019. She currently holds the position of postdoctoral fellow in the Department of Computational Chemistry at Lund University. Dr. Wang’s primary research interest centers around the development and application of free energy calculation methods, with a particular focus on accurately and efficiently predicting the binding free energy between proteins and small molecules using theoretical approaches. In addition, she is actively engaged in research related to computer-aided drug design, reflecting her diverse interests and expertise in the field of computational biophysics.

Dr. Yihan Shao obtained his Ph.D. in Physical Chemistry from the University of California at Berkeley in 2002. After a stint at the Q-Chem software company (as a staff, senior, and principal scientist), he joined the University of Oklahoma in 2016 as an Assistant Professor, and was promoted to Associate Professor in 2022. Lately, he got interested in exploring how chemical/photochemical/enzyme reactions and bioimaging probes work.

Dr. Yan Mo is an Associate Professor at East China Normal University. Her research mainly focuses on the theoretical and computational study of excitation energy transfer in light-harvesting systems, as well as the ultrafast dynamics of polymer and protein side chains at the air-water interface. Her expertise in these areas contributes to our understanding of complex molecular processes and their practical applications in renewable energy, materials science, and biophysics.

Dr. Ye Mei obtained his Ph.D. in Physical Chemistry from Nanjing University in 2007. He became an Associate Professor in the Department of Physics at East China Normal University in 2009 after completing his postdoctoral career at the Department of Physics of Nanjing University, and in 2012 he was promoted to Full Professor. His research mainly focuses on linear scale quantum mechanical methods for proteins and statistical methods for free energy calculations. He is also interested in rational enzymatic evolution and developing empirical interaction potentials for biomacromolecules, including force fields and machine learning potentials.